Abstract
Objective:
Continuous glucose monitoring (CGM) enables prediction of the future glucose concentration (GC) trajectory for making informed diabetes management decisions. The glucose concentration values are affected by various physiological and metabolic variations, such as physical activity (PA) and acute psychological stress (APS), in addition to meals and insulin. In this work, we extend our adaptive glucose modeling framework to incorporate the effects of PA and APS on the GC predictions.
Methods:
A wristband conducive of use by free-living ambulatory people is used. The measured physiological variables are analyzed to generate new quantifiable input features for PA and APS. Machine learning techniques estimate the type and intensity of the PA and APS when they occur individually and concurrently. Variables quantifying the characteristics of both PA and APS are integrated as exogenous inputs in an adaptive system identification technique for enhancing the accuracy of GC predictions. Data from clinical experiments illustrate the improvement in GC prediction accuracy.
Results:
The average mean absolute error (MAE) of one-hour-ahead GC predictions with testing data decreases from 35.1 to 31.9 mg/dL (p-value=0.01) with the inclusion of PA information, and it decreases from 16.9 to 14.2 mg/dL (p-value=0.006) with the inclusion of PA and APS information.
Conclusion:
The first-ever glucose prediction model is developed that incorporates measures of physical activity and acute psychological stress to improve GC prediction accuracy.
Significance:
Modeling the effects of physical activity and acute psychological stress on glucose concentration values will improve diabetes management and enable informed meal, activity and insulin dosing decisions.
Index Terms—: Glucose Concentration Prediction, Physical Activity, Acute Psychological Stress, Machine Learning, Diabetes
I. Introduction
FREQUENT measurement of glucose concentration (GC) is necessary to monitor and prevent diabetes-related complications [1–7]. Continuous glucose monitoring (CGM) provides information unattainable by intermittent self-monitoring of blood glucose, such as frequent (5-minute sampling time) GC information and its rate of change, proactive alerts and alarms for actual or impending glycemic excursions, and feedback for therapeutic decisions [5–14]. Accurate predictions of the future GC trajectory offer important information for making meal, activity and insulin dosing decisions [9–18]. Although accurate predictions of the future GC dynamics are important for effective diabetes management, maintaining a high level of GC prediction accuracy is challenging, particularly in free-living conditions, since future GC dynamics are affected by scheduled or spontaneous physiological and metabolic variations, caused by physical activity (PA) and acute psychological stress (APS), in addition to meals and insulin levels. Modeling the GC data enabled characterization of the effects of meals, insulin and exercise on future GC trajectory after these events have affected GCs and CGM readings [19–21]. Further improvement of GC control in people with Type 1 diabetes (T1D) necessitates the estimation of the characteristics of glycemic disturbances such as PA [22] and APS by using real-time data from convenient wearable devices, and the subsequent integration of the variables quantifying these disturbances in GC prediction models [13, 23, 24]. The models that use information about such disturbances have the advantage of estimating future GC variations before the effects of these disturbances start appearing in CGM values, consequently improving the accuracy of the predicted future GCs, and proactively suggesting insulin dose decisions that are cognizant of these PA [13, 25, 26] and APS events. Based on signals from a wristband device at high frequency, this paper reports the first results of incorporating the effects of PA and APS on GC predictions for people with T1D.
Recent publications have underlined the value of incorporating PA information in GC prediction models [27, 28], using signals that indicate the start of PA to adjust insulin infusions [29, 30] and employing variables computed based on armband signals in estimation of GC during exercise to modify control decisions on automated insulin delivery [13, 23, 26]. The use of readily measurable biosignals such as heart rate or accelerometer readings have been considered to indicate exercise [29, 30]. In our experience, additional biosignals and the variables derived from them enable more accurate GC predictions during PA [13, 23, 26]. The diversity in PA makes it difficult to predict glycemic excursions for different PA [31, 32]. The GC response to exercise is dependent on the type and intensity of the PA [31, 32]. While moderate-intensity PA can reduce GC due to increased glucose utilization, high-intensity PA can lead to elevated GC due to increased hepatic glucose production [31, 33]. The varied response to different types and intensities of spontaneous PA such as running to catch a bus or activities of daily living need to be characterized to improve GC regulation in diverse free-living conditions.
Little attention has been paid to incorporating APS to GC predictions [34] and using such information in insulin dosing decisions in T1D. Episodes of APS activate the hypothalamic-pituitary-adrenal axis and the sympathetic nervous system, resulting in the release of stress hormones, like adrenalin, noradrenalin, cortisol, glucagon and growth hormone, that affect glucose metabolism [35]. Various papers in psychology and neuroscience literature have reported APS detection in clinical environments by analyzing hormone samples or with sophisticated equipment for collecting physiological signals such as eye movement, skin conductivity, skin temperature, and heart rate variability [36–39]. Sensors for rapid and accurate measurement of these hormones in free living are not yet available. Hence, biosignals from wearable devices that can be used during daily free-living offer an attractive alternative for assessing the presence, type and intensity of APS.
The APS-induced transient increase in GC can be misconstrued as carbohydrate intake in automated insulin delivery systems, resulting in a bolus insulin infusion. However, the transitory increase in GC due to APS may be short-term, and a prompt recovery to the normal glucoregulatory state may leave excess insulin in the bloodstream, with a relatively longer duration of effect [40, 41]. This increases the risk of hypoglycemia as a result of an over-correction for the APS-induced increase in GC. The risk of incorrect insulin dosing must be overcome for automated insulin dosing algorithms to increase the time spent in the target euglycemic range, particularly in free-living scenarios where myriad disturbances can cause the dysregulation of GC [40, 41]. Further complicating the modeling of APS in GC prediction models is the lack of conveniently measurable biosignals that are indicative of the presence of APS. Hence, features based on physiological measurements such as heart rate and electrodermal activity need to be defined to detect, classify and quantify the level of various APS occurrences. The possibility of concurrent PA and APS provides additional challenges in detecting, discriminating and quantifying the PA and APS events. For example, the glycemic effects of PA during training and competition events are different, with the divergent responses caused by the presence of APS. Running to catch a bus, driving during rush hour, or receiving an alarm while performing house chores could also initiate concurrent PA and APS.
The exclusive reliance on CGM data is insufficient to resolve the multitude of disturbances affecting the GC and make appropriate corrective actions. Moreover, the use of only a limited set of biosignals may also confound the physiological effects of PA with the response to APS. Considering the use of this information in automated insulin delivery by an artificial pancreas generates additional constraints in the selection of physiological variables that can be used and wearable devices that can be worn continuously under daily free-living conditions. Various accurate sensor systems are appropriate in clinical environments, but a wristband is one of the few current choices for daily use. It overcomes the limitations of intrusive and invasive sampling techniques, which are not feasible for long-term use in diverse free-living conditions. Unfortunately, wristbands provide additional challenges such as high noise levels and artifacts in signals [24, 42].
Our previous work has used physiological measurements from a wristband to generate features and automatically detect the type and quantify the intensity of PA [24]. We also leveraged this information to discriminate different types of APS. Recently, we integrated these findings to enable the immediate evaluation of concurrent PA and APS, and to incorporate an estimate of the perceived APS level [34, 40].
Advances in classifying the type and estimating the intensity of PA and APS, and evaluating their concurrent presence, can enable personalized precision medicine by integrating the refined physiological assessments with GC information for more effective treatment of T1D. However, the mathematical relations between the physiological assessments and the glucose-insulin dynamics are complex and time-varying. Adaptive modeling can help identify the current relationships between the GC data and the quantifiable metrics of PA and APS [24, 34, 40].
Motivated by the above considerations, in this work we integrate adaptive GC prediction models with new features and metrics derived from biosignals to compute the effects of diverse PA and APS disturbances on GC predictions [24, 34, 40]. We conducted 34 experiments involving 12 people with T1D under various types of PA and APS inducements. The participants wore an Empatica E4 wristband that is convenient for use in free-living ambulatory conditions. The multiple physiological variables measured by Empatica E4 [43] capture the effects of PA and APS. A similar Empatica device, the Embrace2 is the only FDA-cleared wrist-worn wearable in epilepsy to predict seizures [44] and to evaluate stress and emotion. The biosignals from Empatica E4 include blood volume pulse, electrodermal activity, skin temperature and accelerometer. Blood volume pulse signals are used to estimate the heart rate values in the E4. We use these measurements to generate new quantifiable input features for PA and APS. Machine learning techniques are used with these variables and features to estimate the type and intensity of the PA and/or APS, and the possibly simultaneous presence of AP and APS [24, 34, 40]. The refined features and variables for PA and APS are integrated as exogenous inputs in an adaptive system identification technique to improve the accuracy of the predicted future GC trajectories. Data from the clinical experiments involving PA and APS are used to illustrate the improvement in GC prediction accuracy.
II. Preliminaries
A. Glucose Concentration Prediction Model
The GC modeling approach used in this work is the recursive version of the prediction-based subspace identification (rPBSID) algorithm [45, 46]. The approach identifies a state-space model in innovation form as
| (1) |
| (2) |
where , , and denote the state, output, input and innovation term variables, respectively, and A, B, C and D are system matrices with appropriate dimensions, and K is the Kalman filter gain.
In the modeling approach, we define stacked inputs and outputs as
where f and p are user-defined parameters for the future and past horizons, respectively. Similarly, we formulate the stacked vectors , , and , and the Hankel matrices U(f), U(p), E(f) and E(p).
By iterating the system equations, we can write the system using the Hankel matrices as
| (3) |
| (4) |
where
and Γ(f) is the extended observability matrix, H(f) and G(f) are two lower triangular Toeplitz matrices defined as
with and . Furthermore, the state evolution can also be expressed as
| (5) |
where . For a sufficiently large ‘p’, we can consider and
| (6) |
This leads to
| (7) |
The rPBSID approach works by estimating matrices H(f) and G(f) by using a vector autoregressive with exogenous (VARX) inputs model. The VARX model parameters are then used to construct estimates for the H(f) and G(f) matrices and subsequently obtain estimates for the system matrices [46–48].
III. Clinical Experiments
A. Data Collection
Clinical experiments involving 12 subjects with T1D (Table I) are conducted at the College of Nursing, University of Illinois at Chicago. The experiments were approved by the Institutional Review Board. Dexcom G5 CGM System [49] and E4 wristband are used in experiments. The E4 wristband has four sensors: electrodermal activity-sensor to measure the skin conductance (galvanic skin response), photoplethysmogram to measure the blood volume pulse, temperature sensor to measure skin temperature, and a three-axis accelerometer to measure movements [43]. The blood volume pulse data is used to derive heart rate and heart rate variability. The data collection activity in the experiments is divided into two subcategories: experiments for PA and APS (with APS inducement either alone or concurrent with PA). All experiments were open-loop, with subjects regulating their GC by manually adjusting their insulin infusions.
TABLE I.
Demographic Information of the Subjects with T1D (Male: M; Female: F; Standard Deviation: Stdev.)
| Weight (kg) | Height (cm) | Waist Size Size (cm) | Sex (F/M) | Age (yr) | Average Daily Basal Insulin (U/hr) | Duration of Diabetes (yr) | HbA1c (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| PA experiments (12 subjects) | Mean | 80.9 | 172.0 | 94.7 | 5/7 | 29.2 | 1.0 | 14.5 | 8.0 |
| Stdev. | 13.5 | 8.4 | 13.9 | - | 7.3 | 0.4 | 6.9 | 1.5 | |
| PA & APS experiments (8 subjects) | Mean | 83.8 | 170.1 | 98.8 | 4/4 | 32.1 | 1.14 | 13.5 | 8.21 |
| Stdev. | 14.0 | 8.4 | 15.0 | - | 6.5 | 0.3 | 8.1 | 1.5 |
1). Physical Activity Experiments (PA Exp.):
Twenty-four PA experiments involving 12 subjects with T1D are conducted (Table I). The duration of the experiments ranges between 6 to 9 hours. The experiments include at least one exercise session: treadmill run, stationary bicycle and resistance exercise. The exercise sessions are conducted more than one hour before or more than two hours after meal consumption. The GC measurements (CGM and self-monitoring of blood glucose during exercise), insulin administered, meal and snack information, PA information, and demographic information are recorded (Table I). The duration of treadmill and stationary bicycle exercises are fixed to 30 minutes. In addition to the structured exercise, subjects spent time sitting, reading books and watching videos. The experiments also involved activities of daily living through simulated household chores like doing laundry, cleaning or vacuuming. The treadmill exercise is conducted at various speeds in the range of 3.0 to 6.0 mph, which is calculated based on the 60 to 70% of maximum VO2 test, in addition to warm up and cool down periods (treadmill speeds below 1.7 mph). The stationary bicycle exercise is conducted with intensities in the range of 50 to 150 W. The intensity of treadmill and stationary bicycle exercises is determined for each individual subject according to the VO2 reserve method. After determining the maximum VO2 through the Bruce protocol treadmill test [50], the target intensities of the treadmill and stationary bicycle exercises are set between 60% to 70% of the maximum VO2. The resistance exercise sessions begin with a warm-up activity involving running on the treadmill at low speeds, followed by four sets of eight repetitions of dumbbell chest press, lateral pull down, seated row, dumbbell shoulder press, leg extension or leg curl. The subjects rest between sets for approximately one minute. The duration of the resistance exercise ranges between 30 to 120 minutes.
2). Acute Psychological Stress Experiments (APS Exp.):
Ten APS experiments with eight subjects with T1D (Table I) are conducted. There are several types of APS with varying impact on GC, ranging from the trauma of a traffic accident or news of job termination to taking exams, public speaking, and playing videogames. We focused on two types of APS: mental stress (MS) and emotional anxiety stress (EAS). CGM and self-monitoring of blood glucose data, insulin dosing, meal and snack information, and demographic information are recorded (Table I). The APS experiments are conducted at least two hours before or after any meals. Five different types of APS inducement are considered after consulting with psychologists and medical experts and conducting an exhaustive literature review for APS inducements techniques. MS inducement involves subjects solving mental arithmetic tests during a half-hour period, such as the multiplication or subtraction of numbers [51–53]. This is the only MS inducement used in our study, and the other four types are used for EAS inducement. Video games are one form of stress inducement method for EAS, with subjects playing video games for a half-hour period during the experiments [54, 55]. Trier social stress test is used for APS inducement, which involves public speaking and mental arithmetic lasting about 20 mins [56–58]. Stressor experiments induce APS and frustrate subjects by hindering or obstructing the completion of routine tasks by posing nuanced obstacles. The stressor experiments are conducted during sedentary state, daily activities or resistance exercise activities. Most APS inducements in this work, including video games, mental arithmetic and stressor, are conducted during structured exercise, such as playing computer games during treadmill exercise or mental arithmetic during stationary bicycle exercise, which augments the experiments with cases where the effects of PA and APS are confounded.
IV. Physical and Psychological Stress Assessment Algorithms
The PA experiments are used to classify the physical state (PS) and estimate the energy expenditure (EE), which are then incorporated into an adaptive GC prediction model (Fig. 1). The computations include the personalized plasma insulin concentration (PIC) estimation [59, 60] and meal effect estimation by using CGM and PIC values [19]. The APS experiments are used to derive an APS index and incorporate it in the GC prediction model (Fig. 1). The additional inputs for PA and APS are derived from the biosignals of E4 [43].
Fig. 1.
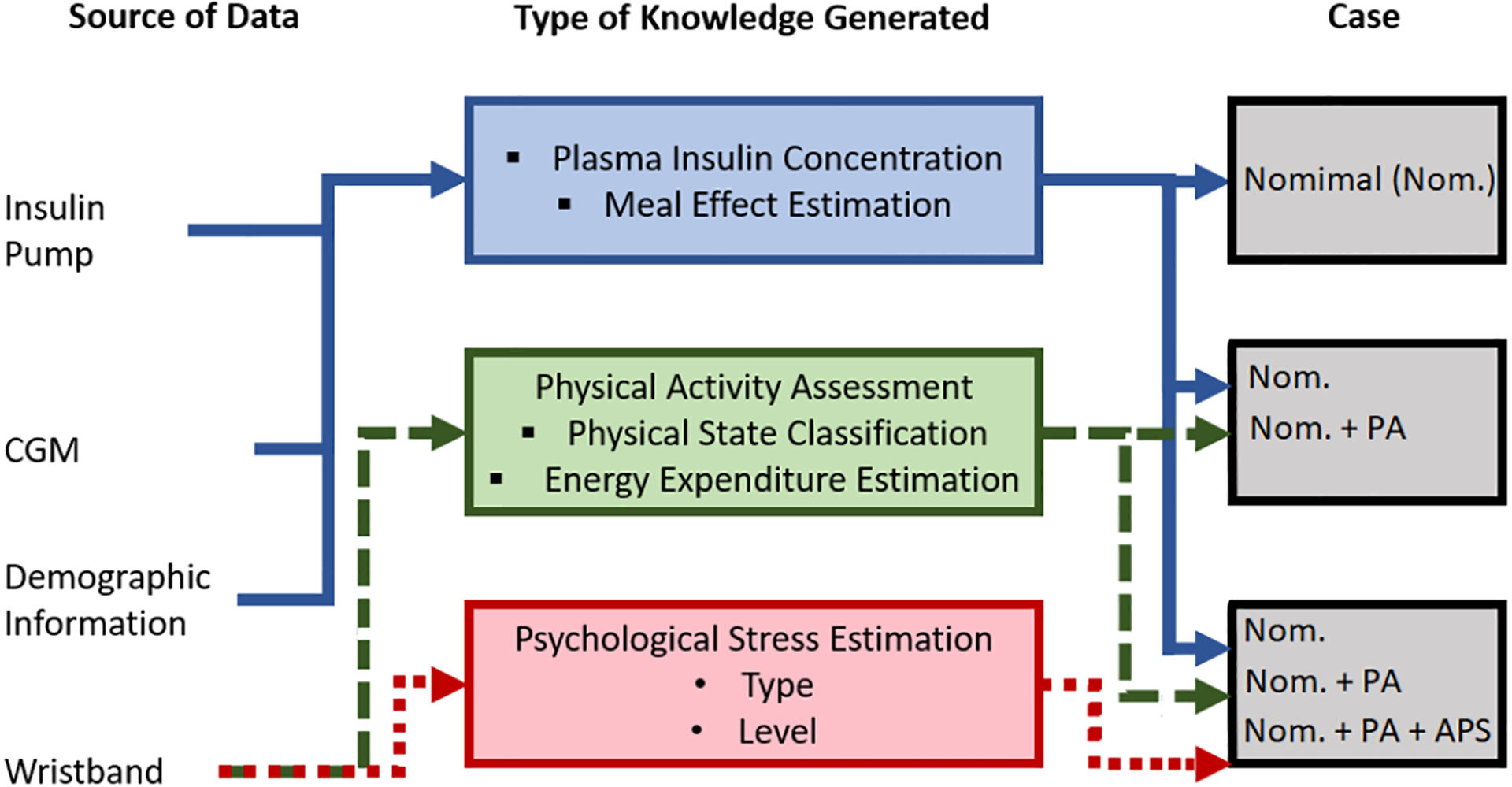
Incorporation of Psychological and Physiological State Estimates to GC Prediction Model
A. Physical Activity
The collected biosignals are preprocessed by using various filtering and artifact removal algorithms to improve the signal quality and remove artifacts and noise [24, 30]. The cleaned and preprocessed biosignals are used to generate feature variables that enhance the accuracy of the machine learning algorithms [24, 34, 40]. The feature variables are derived by using mathematical or statistical computations with the cleaned data. The feature variables are used with various supervised machine learning algorithms to classify the PS and estimate the EE. We consider k-nearest neighbors, linear discriminant analysis, decision trees, ensemble learning, support vector machines, Gaussian process regression, and deep neural networks with long short-term memory [24, 34, 40]. Since both PA and APS can be present, the use of heart rate or accelerometer alone may not provide accurate results. A computed variable such as EE and various feature variables are more effective in detecting, discriminating and characterising PA and APS. Equations that relate the measured variables to EE are developed using data collected simultaneously through the gold standard indirect calorimetry method with VO2 mask [61] and wristband data. The mean absolute error (MAE) values are calculated for the estimated EE compared to the indirect calorimeter measurements for the different machine learning algorithms for the testing dataset [24]. The deep neural networks with long short-term memory performed better than the other algorithms with an MAE of 0.25 MET [24]. PS classification accuracy is evaluated with different algorithms and deep neural networks with long short-term memory achieved a 94.8% with best testing classification accuracy [24].
The posterior probabilities (score values), denoted by P(sk,xk) for the PA class sk given the data xk, obtained by the PS classification algorithm are used to determine the additional input variable to the GC model. The posterior probabilities are not suitable for direct use as an input variable in the GC model because diverse PA affect glycemia to different degrees. Therefore, the posterior probabilities need to be integrated with a framework that recognizes the relative magnitude of glycemia effects for the various PA. A fuzzy logic algorithm comprised of fuzzification, rule-table design, and defuzzification stages is used to translate the posterior probabilities to the input variable [62]. The posterior probabilities are fuzzified using triangle fuzzy membership functions. The fuzzy membership functions are separated into five equal intervals to represent the different magnitudes of the glycemic effects for various PA, including very low [0, 0.2], low [0.2, 0.4], medium [0.4, 0.6], high [0.6, 0.8], and very high [0.8, 1] glycemic effects.
The rule-table is established through knowledge of the glycemic effects of the classified PA [25, 31–33] (Table II). The treadmill and stationary bicycle exercises are associated with the high output rule, as the moderate-intensity aerobic activity causes a decrease in GC. A high posterior probability of daily activities is associated with the medium output rule, which indicates a slight decrease in GC. High probabilities for resistance exercise and sedentary state are set to the low output rule, which indicate no significant changes in the GC. Therefore, the rules translate the highest posterior probability of the PS to the corresponding effect on GC, with the high effect rule associated with a rapid decrease in GC and a low effect rule associated with a small variation or steady GC value. The weighted average defuzzification method is used to determine the final fuzzy model output to the expected GC trajectory (Fig. 2) [62].
TABLE II.
Rule-Table for Fuzzy Logic Algorithm (Samples of Some Important Rules) (SS: Sedentary State, DA: Daily Activities, RE: Resistance Exercise, TR: Treadmill Exercise, BK: Stationary Bike)
| SS | DA | RE | TR | BK | Output Rule | Indication of the GC Effect |
|---|---|---|---|---|---|---|
| High | Low | Low | Low | Low | Low | Steady/Slight Variation |
| Low | Low | High | Low | Low | Low | Steady/Slight Decrease |
| Low | High | Low | Low | Low | Medium | Steady/Slight Variation |
| Low | Low | Low | High | Low | High | Sharp Decrease |
| Low | Low | Low | Low | High | High | Sharp Decrease |
Fig. 2.
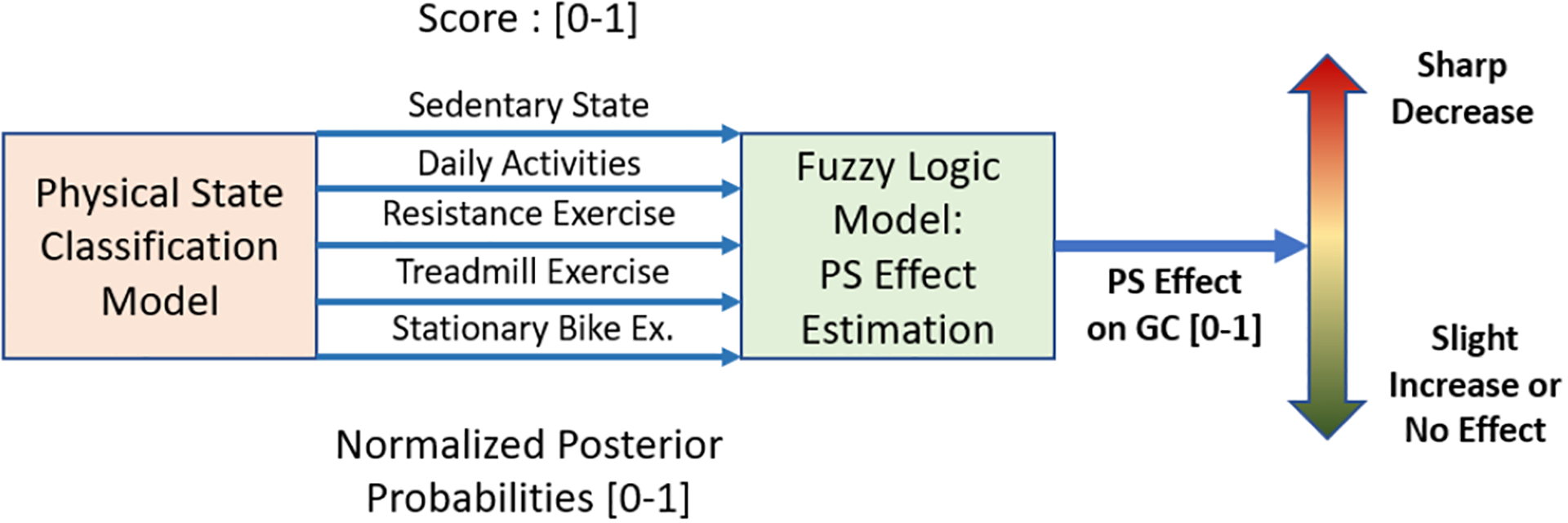
Physical State (PS) Effect Estimation
The fuzzy PS effect model enables the GC model to characterize the varying glycemic effects of the different PA. This is necessary since EE can be relatively high during both resistance exercise and aerobic PA, like treadmill and stationary bicycle, yet the glycemic effects are different. Relying solely on EE can result in less accurate predictions of GC. The fuzzy model converts the five PA class posterior probabilities by multiplying the probabilities by the associated rule system. The output of the fuzzy model is normalized and multiplied by the estimated EE, which is incorporated into the GC prediction model (Fig. 1). This enables the GC model to consider both the PS and the PA intensity in determining the glycemic effects of the PA.
The inputs to the GC prediction model are based on two groups of cases (Table III): (1) nominal model that considers only meal and insulin information (Nom.); and (2) meal, insulin and PA information, including EE and PS classification (Nom. + PA information) (Fig. 1). The insulin information incorporated as PIC estimates (Fig. 1) [60]. Demographic information is used to personalize the model (Fig. 1). A delay is incorporated in some of the GC model inputs to better represent the physiological time delay in the effect of PA on GC, with a delay of 25 mins (for 1-hour prediction) (five sampling times) (Table IV) considered for the EE and PS information. The output is the predicted GC value. Insulin and meal effect sensitivity and delay parameters computed in previous work [23, 60] are used (Table IV). PA sensitivity and delay parameters are determined by a genetic algorithm using a random set of selected experiments (training set). Optimized values are fixed and used for measuring the performance of the algorithms with the testing data set (Table IV).
TABLE III.
Data Collection and Separation
| Inducements ✔ - present, ✘ - absent | Information used in Addition to CGM and Insulin Pump | |||||
|---|---|---|---|---|---|---|
| Case | Meal | PA | APS | PS | EE | APS |
| PA Exp. with Nom. | ✔ | ✔ | ✘ | ✘ | ✘ | ✘ |
| PA Exp. with Nom. + PA | ✔ | ✔ | ✘ | ✔ | ✔ | ✘ |
| APS Exp. with Nom. | ✔ | ✔ | ✔ | ✘ | ✘ | ✘ |
| APS Exp. with Nom. + PA | ✔ | ✔ | ✔ | ✔ | ✔ | ✘ |
| APS Exp. Nom. + PA + APS | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
TABLE IV.
Optimized Parameter Values
| 1-hour GC Prediction | |||||||
|---|---|---|---|---|---|---|---|
| PA Exp.nd Case | Adaptation Period | Past Window (Sampling Time) | PIC and Meal Effect Sensitivity | PA Delay (Sampling Time) | PA Sensitivity | APS Delay (Sampling Time) | APS Sensitivity |
| Previous Research [23, 24, 59, 60] | 80 min | 3 | 0.2007 | — | — | — | — |
| PA Exp. Training (Nom.) | 80 min | 3 | 0.2007 | — | — | — | — |
| PA Exp. Training (Nom. + PA) | 80 min | 3 | 0.2007 | 5 | 0.1525 | — | — |
| APS Exp. Training (Nom.) | 80 min | 3 | 0.2007 | — | — | — | — |
| APS Exp. Training (Nom. + PA) | 80 min | 3 | 0.2007 | 5 | 0.1297 | — | — |
| APS Exp. Training (Nom. + PA + APS) | 80 min | 3 | 0.2007 | 5 | 0.1297 | 3 | 1.374 |
| 1.5-hour GC Prediction | |||||||
| Previous Research [23, 24, 59, 60] | 80 min | 3 | 0.2007 | — | — | — | — |
| PA Exp. Training (Nom.) | 80 min | 3 | 0.2007 | — | — | — | — |
| PA Exp. Training (Nom. + PA) | 80 min | 3 | 0.2007 | 2 | 0.1395 | — | — |
| APS Exp. Training (Nom.) | 80 min | 3 | 0.2007 | — | — | — | — |
| APS Exp. Training (Nom. + PA) | 80 min | 3 | 0.2007 | 2 | 0.1297 | — | — |
| APS Exp. Training (Nom. + PA + APS) | 80 min | 3 | 0.2007 | 5 | 0.1297 | 3 | 1.374 |
| 2-hour GC Prediction | |||||||
| Previous Research [23, 24, 59, 60] | 80 min | 3 | 0.2007 | — | — | — | — |
| PA Exp. Training (Nom.) | 80 min | 3 | 0.2007 | — | — | — | — |
| PA Exp. Training (Nom. + PA) | 80 min | 3 | 0.2007 | 5 | 0.1060 | — | — |
| APS Exp. Training (Nom.) | 80 min | 3 | 0.2007 | — | — | — | — |
| APS Exp. Training (Nom. + PA) | 80 min | 3 | 0.2007 | 1 | 0.999 | — | — |
| APS Exp. Training (Nom. + PA + APS) | 80 min | 3 | 0.2007 | 1 | 0.999 | 2 | 1.663 |
All parameters are fixed after optimization and used for the testing data sets for all cases
B. Acute Psychological Stress
The E4 [43] is used to detect, classify and quantify the level of APS experienced by a subject. We consider two types of APS, MS and EAS, for analyzing the effects of PA and APS, and we determine posterior probabilities for these two types of stress [34, 40]. We compute the score value for the type of APS (MS and EAS) during simultaneous PA (sedentary state, treadmill run exercise, and stationary bike exercise), which yields a total of six scenarios. The score value associated with likeliest PA type is used to find the accompanying MS and EAS score values, denoted P(mk ∣ x) as the probability of MS or EAS mk given the data x. Prior research [34, 40, 41, 63–65] indicates that EAS increases the GC, though intense MS can result in increased glucose consumption due to the mental burden of the tasks. To handle the differences in GC trajectories caused by the type of APS, we consider the difference in the score values between MS and EAS. The difference, dk = P(m1 ∣ x)−P(m2 ∣ x) is used as an additional input to the GC prediction model.
The incorporation of the APS in the GC prediction model is evaluated by using four cases (Table III): (1) nominal model without any APS or PA estimates as additional inputs (Nom.); (2) with PA estimates as additional inputs but without any APS estimates (Nom. + PA information); and (3) with PA and APS estimates as additional inputs (Nom. + PA + APS information) (Fig. 1). Retrospective data from the 10 open-loop experiments are used to assess the efficacy of the APS input to prediction accuracy of the GC model. The delay in the glycemic response to APS is optimized and found to be 3 sampling times, or 15 mins (Table IV), which pertains to the additional input indicating APS (dk). APS sensitivity and delay parameters are determined by a genetic algorithm using randomly selected training experiments. The PA delay and sensitivity parameters optimized for the Nom. + PA Info model are retained and used. Insulin and meal effect sensitivity and delay parameters are also kept the same (Table IV) [23, 24, 59, 60].
V. Results
In this section, we first report the efficacy of including the PA information in the GC prediction model. Then, we report the efficacy of including the APS information to the GC model by using the experiments that involve APS inducement with concurrent PA, which yields a GC prediction model with PS, EE, and APS estimates as additional inputs.
A. GC Predictions with Physical Activity Information
The PA clinical experiments are analyzed for three types of PA (sedentary state, treadmill run exercise, and stationary bike exercise) and the results are reported as the mean absolute error (MAE) for three different type of prediction horizons: 1-hour, 1.5-hour, and 2-hour prediction horizons (Table V). We compare the results of the nominal model, which predicts the future glucose with only glucose and insulin information, to the nominal model + PA information, which incorporates an additional input representing the type and intensity of the PA.
TABLE V.
Statistical Summary of MAE of GC Prediction Results with and without PA and APS information (mg/dL)
| PA Exp.: Training | PA Exp.: Testing | APS Exp.: Training | APS Exp.: Testing | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1-hour GC Prediction | ||||||||||
| Statistical Features | Nom. | Nom. + PA | Nom. | Nom. + PA | Nom. | Nom. + PA | Nm. + PA + APS | Nom. | Nom. + PA | Nm. + PA + APS |
| Min | Max | 7.6 | 41.4 | 4.4 | 28.5 | 18.6 | 69.1 | 12.3 | 55.0 | 20.7 | 107.2 | 15.8 | 96.9 | 17.4 | 99.4 | 8.3 | 29.1 | 7.8 | 24.4 | 7.5 | 24.0 |
| 1st | 3rd Quartile | 18.2 | 33.9 | 9.5 | 24.7 | 22.6 | 48.4 | 18.4 | 48.1 | 21.8 | 67.9 | 19.8 | 58.7 | 19.4 | 59.3 | 12.5 | 21.7 | 8.4 | 20.2 | 8.3 | 19.7 |
| Median | Total | 26.3 | 304 | 18.3 | 207 | 26.8 | 420 | 27.4 | 382 | 24.2 | 229 | 22.6 | 202 | 21.4 | 204 | 14.0 | 84 | 14.0 | 73 | 12.8 | 71 |
| Mean ± Stdev. | 25.3 ± 10.4 | 17.3 ± 8.1 | 35.1 ± 16.5 | 31.9 ± 15.5 | 45.8 ± 37.1 | 40.5 ± 33.5 | 40.8 ± 34.6 | 16.9 ± 7.8 | 14.7 ± 7.0 | 14.2 ± 6.9 |
| No. of Best | Worst Case | 1 | 11 | 11 | 1 | 2 | 10 | 10 | 2 | 1 | 4 | 1 | 1 | 3 | 0 | 0 | 5 | 0 | 0 | 5 | 0 |
| No. of Experiments | 12 | 12 | 5 | 5 | ||||||
| **Improvement | 28.5% | 10.3% | — | 11.9% | 11.9% | — | 12.4% | 15.7% | ||
| p-value | 0.001 (Wilcoxon Test) | 0.01 (Wilcoxon Test) | 0.09 (Friedman Test) | 0.006 (Friedman Test) | ||||||
| 1.5-hour GC Prediction | ||||||||||
| Min | Max | 6.2 | 50.7 | 5.6 | 52.3 | 21.3 | 89.1 | 18.6 | 85.2 | 21.9 | 169.4 | 15.8 | 155.0 | 14.5 | 151.9 | 11.5 | 38.7 | 11.1 | 31.5 | 10.7 | 33.8 |
| 1st | 3st Quartile | 23.0 | 47.1 | 16.6 | 33.9 | 34.1 | 68.9 | 28.4 | 70.9 | 24.1 | 93.6 | 21.7 | 87.1 | 21.1 | 86.2 | 13.5 | 34.7 | 16.1 | 30.5 | 13.2 | 31.4 |
| Median | Total | 35.1 | 403 | 21.5 | 299 | 47.5 | 621 | 47.3 | 593 | 32.7 | 317 | 30.0 | 289 | 29.0 | 283 | 28.0 | 125 | 19.4 | 110 | 30.1 | 119 |
| Mean ± Stdev. | 33.6 ± 15.2 | 24.9 ± 13.9 | 51.8 ± 23.5 | 49.5 ± 22.5 | 63.4 ± 62.0 | 57.8 ± 57.8 | 56.6 ± 56.6 | 25.1 ± 11.8 | 22.0 ± 8.6 | 23.8 ± 10.6 |
| No. of Best | Worst Case | 2 | 10 | 10 | 2 | 4 | 8 | 8 | 4 | 1 | 4 | 0 | 1 | 4 | 0 | 0 | 3 | 1 | 1 | 4 | 1 |
| No. of Experiments | 12 | 12 | 5 | 5 | ||||||
| **Improvement | 19.2% | 1.8% | — | 10.2% | 12.5% | — | 6.1% | 3.5% | ||
| p-value | 0.02 (Wilcoxon Test) | 0.4 (Wilcoxon Test) | 0.07 (Friedman Test) | 0.2 (Friedman Test) | ||||||
| 2-hour GC Prediction | ||||||||||
| Min | Max | 53.8 | 239.6 | 52.0 | 239.6 | 48.6 | 250.2 | 58.3 | 250.2 | 45.7 | 307.5 | 46.5 | 307.5 | 43.0 | 307.5 | 36.4 | 55.7 | 37.9 | 54.4 | 37.5 | 55.3 |
| 1st | 3st Quartile | 76.2 | 130.2 | 70.4 | 126.3 | 79.3 | 156.8 | 78.6 | 153.4 | 46.8 | 157.9 | 48.1 | 157.8 | 45.7 | 157.9 | 39.0 | 48.1 | 39.5 | 48.1 | 39.5 | 48.5 |
| Median | Total | 95.1 | 1336 | 85.6 | 1266 | 113.8 | 1502 | 104.6 | 1449 | 66.9 | 575 | 63.0 | 573 | 62.3 | 567 | 41.1 | 218 | 42.3 | 220 | 41.0 | 220 |
| Mean ± Stdev. | 111.4 ± 52.1 | 105.5 ± 54.8 | 125.2 ± 59.5 | 120.7 ± 61.0 | 115.1 ± 110. | 4 114.7 ± 110.5 | 113.5 ± 111.5 | 43.7 ± 7.4 | 44.1 ± 6.4 | 44.0 ± 7.0 |
| No. of Best | Worst Case | 2* | 8 | 8 | 2* | 3* | 7 | 7 | 3* | 1 | 2 | 1 | 2 | 3 | 1 | 3 | 1 | 1 | 2 | 1 | 2 |
| No. of Experiments | 12 | 12 | 5 | 5 | ||||||
| **Improvement | 8.3% | 3.4% | — | 0.2% | 2.7% | — | No Imp. | No Imp. | ||
| p-value | 0.01 (Wilcoxon Test) | 0.6 (Wilcoxon Test) | 0.7 (Friedman Test) | 0.5 (Friedman Test) | ||||||
| 4-hour GC Prediction | ||||||||||
| Min | Max | 104 | 230 | 104 | 230 | 106 | 168 | 106 | 168 | 91 | 170 | 91 | 169 | 91 | 169 | 117 | 181 | 118 | 181 | 125 | 179 |
| 1st | 3st Quartile | 126 | 201 | 126 | 201 | 113 | 131 | 113 | 131 | 114 | 154 | 113 | 153 | 113 | 153 | 132 | 168 | 132 | 168 | 136 | 167 |
| Median | Total | 149.8 | 1568 | 149.8 | 1568 | 124.0 | 1260 | 123.9 | 1259 | 137.8 | 537 | 137.7 | 535 | 137.1 | 535 | 151.3 | 601 | 151.2 | 602 | 151.2 | 607 |
| Mean ± Stdev. | 156 ± 43 | 156 ± 43 | 125 ± 17 | 125 ± 17 | 134 ± 32 | 133 ± 32 | 133 ± 32 | 150 ± 26 | 150 ± 26 | 151 ± 22 |
| No. of Best | Worst Case | 1**** | 1 | 1 | 1**** | 3* | 6 | 6 | 3* | 3 | 1 | 2 | 2 | 2 | 2 | 3 | 1 | 2 | 2 | 2 | 2 |
| No. of Experiments | 10 | 10 | 4 | 4 | ||||||
| **Improvement | No Imp. | 0.08% | — | 0.28% | 0.35% | — | No Imp. | No Imp. | ||
| p-value | 1 (Wilcoxon Test) | 0.57 (Wilcoxon Test) | 0.09 (Friedman Test) | 1 (Friedman Test) | ||||||
(PA Exp.: Experiments with Physical Activities) (APS Exp.: Experiments with Psychological Stress Inducement)
(2 cases have equal accuracy)
(Calculated based on average of MAPE (%))
(Improvements compared relative to Case 1))
(Statistical Significance Threshold: p < 0.05)
(8 cases have equal accuracy)
1). 1-Hour-Ahead GC Prediction:
The nominal model (without incorporating PA information) has the worst performance in 21 of the 24 experiments (12 training and 12 testing experiments), while the nominal model + PA information (with information of the type and intensity of PA incorporated in the GC predictions) has the best performance in 21 experiments (Table V). The average MAE of 12-step-ahead (one-hour-ahead) CGM prediction results for testing data improves from 35.1 mg/dL for the nominal model to 31.9 mg/dL for the nominal model + PA information. Across all the PA experiments (PA Exp.), incorporating PS and EE estimates (nominal model + PA information) improves the CGM prediction accuracy for training and testing by 28.5% and 10.3%, respectively. We evaluate the statistical significance of the results. Kurtosis and skewness analysis show that data are not normally distributed. The Wilcoxon test is used to compare the GC prediction results [66], and the improvement in prediction accuracy is found to be statistically significant for both training and testing data at the 95% confidence interval, with p-values of 0.001 and 0.01, respectively.
2). 1.5-Hours-Ahead GC Prediction:
The nominal model has the worst performance in 18 of the 24 experiments, while the nominal model + PA information has the best performance in 18 experiments (Table V). The average MAE of 16-steps-ahead CGM predictions for testing data (Te) improves from 51.8 mg/dL for the nominal model to 49.5 mg/dL for the nominal + PA model. Across all the PA experiments (PA Exp.), incorporating PS and EE estimates (nominal + PA information) improves the CGM prediction accuracy for training and testing by 19.2% and 1.8%, respectively. The improvement in the prediction accuracy is found to be statistically significant for the training data (p-value: 0.02), though the improvement using the testing data results is not statistically different (p-value: 0.4).
3). 2-Hours-Ahead GC Prediction:
The nominal model has the worst performance in 15 of the 24 experiments, while the nominal model + PA information has the best performance in 15 experiments (Table V). The average MAE of 24-steps-ahead CGM prediction results for testing data improves from 125.2 mg/dL for nominal model to 120.7 mg/dL for nominal + PA model. Across all the PA experiments (PA Exp.), incorporating PS and EE estimates improves the CGM prediction accuracy for training and testing by 8.3% and 3.4%, respectively. The improvement in the prediction accuracy is found to be statistically significant for the training (p-value: 0.01), though the improvement using the testing data set is not statistically different (p-value: 0.6).
4). 4-Hours-Ahead GC Prediction:
There is no improvement in the prediction accuracy for the nominal model + PA information relative to the nominal model possibly due to the use of the time-varying recursively identified model. The time-varying linear model updates the model parameters at each sampling time to increase the accuracy of short-term predictions for making insulin dosing decisions. Although a linear time-invariant model would have some improvement with the addition of PA information, it would not have good predictions without meal information being provided by users, while our proposed recursively identified models do not require any announcements from users for meals.
B. GC Predictions with Physical and Psychological Stress Information
The 10 clinical experiments with APS inducement are analyzed by considering three cases: the nominal model, the nominal model + PA information, and the nominal model + PA & APS information. The statistical details of the GC prediction results are presented as APS experiments in Table V.
1). 1-Hour GC Prediction:
The nominal model + PA & APS information case has better GC prediction accuracy compared to the nominal model, with 8 experiments showing an improvement in GC prediction accuracy out of the 10 experiments. The proposed method yields GC prediction accuracy (average MAE) with testing data of 14.2 mg/dL for the nominal model + PA & APS information, compared to 16.9 mg/dL for the nominal model, which is an improvement of 15.7% in prediction accuracy.
Since the CGM prediction results are not normally distributed based on skewness and kurtosis criteria, a we used Friedman’s statistical test for the comparison of three matched groups [66]. The case of the nominal model + PA & APS information results in a slight improvement in GC prediction accuracy relative to the nominal model + PA information. Both nominal model + PA information and nominal model + PA & APS information have a statistically significant improvement relative to the base nominal model (training data set) with a p-value of 0.006 (Table V). Training data set results are not statistically significant, with the p-value as 0.09, which is slightly greater than the significance threshold (0.05), although there is 11.9% improvement in the MAE.
2). 1.5-Hours-Ahead GC Prediction:
The nominal model + PA & APS information case has better GC prediction accuracy compared to the nominal model, with 8 experiments showing an improvement in GC prediction accuracy out of the 10 experiments. The proposed method yields GC prediction accuracy (average MAE) with testing data of 23.8 mg/dL for nominal model + PA & APS information, compared to 25.1 mg/dL for the nominal model, which is an improvement of 3.5% in prediction accuracy. Both testing and training data set results are not statistically significant, with the p-values as 0.07 and 0.2, which are slightly greater than the significance threshold (0.05), although there is 3.5% improvement in the MAE.
3). 2-Hour GC Prediction:
The nominal model + PA & APS information case has better GC prediction accuracy compared to the nominal model, with 8 experiments showing an improvement in GC prediction accuracy out of the 10 experiments. The proposed method yields GC prediction accuracy (average MAE) with testing data of 44.0 mg/dL for nominal model + PA & APS information, compared to 43.7 mg/dL for the nominal model, which equates to no improvement in prediction accuracy.
4). 4-Hours-Ahead GC Prediction:
The nominal model + PA & APS information case did not have better GC prediction accuracy compared to the nominal model for 4-hour-ahead GC predictions. This is again due possibly to the use of recursively identified models that prioritize accurate short-term predictions, the benefits of which overlap with the improvements due to the additional inputs at longer prediction horizons.
VI. Discussion
Incorporation of PA assessment information using PS and EE estimates for one-hour-ahead prediction horizon improves GC prediction accuracy for both the training and testing experiments during the periods of induced APS (APS Exp.), by 15.7% and 12.4%, respectively. These experiments also contain concurrent stress inducements. Incorporation of both PA and APS estimates yields a modest 3.3% improvement in GC prediction accuracy in comparison to the model incorporating only PA. The main reason for this marginal improvement, which reduces as the prediction horizon increases, is the low intensity of the APS inducements permitted by the IRB in clinical experiments. The resulting magnitude of the maximum change in GC is not very high and the duration of the change is short. Consequently, Their effects are not sustained in the glucose metabolism for 1.5 or 2 hours. Hence, the improvement in GC prediction is reduced as the prediction horizon is increased. Moreover, the subjects involved in APS inducement experiments are generally aware of the controlled laboratory conditions under which the experiments are conducted, and this may reduce the response of some subjects to the stress inducements. More significant APS such as getting hit by a car or participating in highly competitive races have more significant GC variations [33, 67], though the latter is also influenced by the high-intensity of the PA. A fellow researcher reported being hit by a car violating traffic rules, and the incident resulted in a large increase in GC. The GC was about 150 mg/dL before the accident, and the GC values increased to the 290–300 mg/dL range after the accident, even though there was no food consumption during this period. Olympic swimmer Gary Hall, Jr. has T1D and he reported that his blood glucose can spike from 100 mg/dL to 300 mg/dL in the 21 seconds of a 50 meter race [67].
The results illustrate that PA effect on GC is significant and relatively more influential than APS (for the APS inducements in our clinical experiments), and consideration of APS improves prediction accuracy. The experiments also show the more pronounced effects of PA are easier to capture in the GC prediction models relative to the effects of APS. The PA effects are typically more pronounced and longer in duration, as glucose is depleted and long-term effects of changes in insulin sensitivity result in prolonged decrease in CGM values. Under more stressful scenarios encountered in extremely traumatic or stressful situations, the glycemic effects of APS will be more significant and the model is anticipated to perform better.
The results of one experiment from APS Exp., testing data set is illustrated in Fig. 3. It allows the comparison of contributions of both PA and APS effects on GC prediction accuracy. The red (dashed line) curve (nominal model) has the poorest performance with MAE for predictions of 38.0 mg/dL, which could not track the blue curve (real CGM data, solid line) especially during APS inducement and PA. The purple curve (dotted line) has the best performance, taking into account both APS and PA information, which reduces the MAE to 12.9 mg/dL.
Fig. 3.
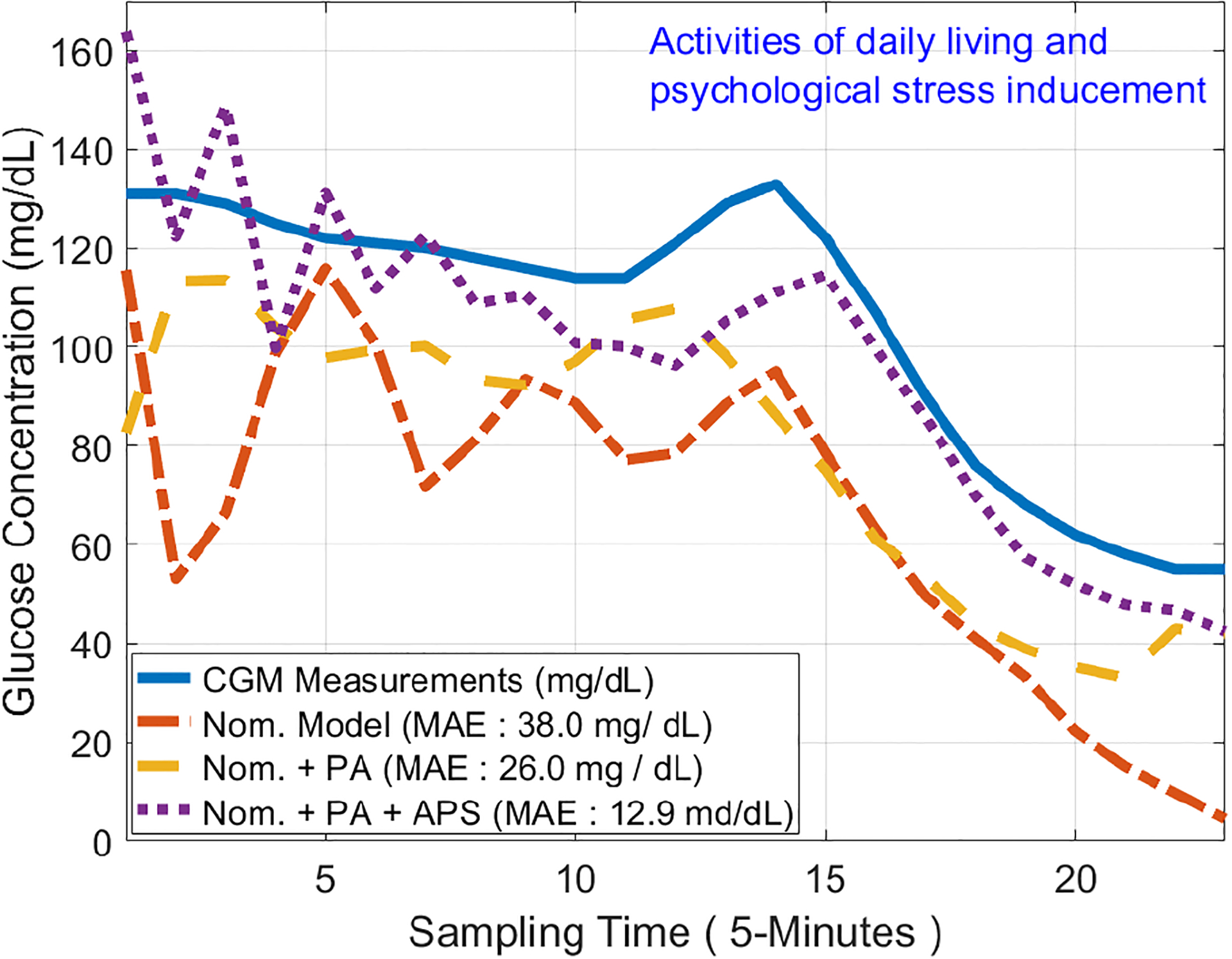
Illustration of GC Prediction Improvement by Using PA and APS Information (APS Exp.: Testing Data) (1-hour GC Prediction)
We leveraged the convenience and practicality of a wristband device that measures multiple physiological variables to detect and discriminate among the individual or simultaneous concurrent incidences of PA and APS [24, 25]. We chose a wristband because it is a device accepted by most people for use in free-living conditions and during diverse ambulatory activities. The additional information on the type and intensity of PA and APS is incorporated in GC prediction models to improve the prediction accuracy relative to conventional models that do not incorporate PA and APS information as additional inputs in making future GC predictions. The multiple physiological measurements are used to train machine learning models that generate informative signals on the type and intensity of PA and APS. Signal processing algorithms are used to remove the noise and motion artifacts from the measured physiological measurements before developing the models. The signal processing algorithms are also implemented on-line to process the measurements before using signals with the developed models to estimate the PA and APS information throughout daily life. We evaluated the effects of signal processing on improving the accuracy of the machine learning algorithms with testing data sets. The best accuracies with the raw signals are 98.6% and 96.2% for the classification of PS and APS, respectively. The classification accuracies improve to 99.3% and 98.3%, respectively, when the filtered signals are used.
Improving GC control in people with T1D is essential to realize numerous health benefits, yet achieving tight glycemic control is challenging because of the myriad disturbances affecting glycemia. Various disturbances like meals, PA, and APS need to be considered when making insulin dosing decisions. The performance of automated insulin delivery systems can be suboptimal if the various disturbances are not considered in estimating GC and computing the insulin doses. Advanced ML algorithms are needed to ensure that the disturbances are automatically evaluated and used for making insulin dosing decisions. To achieve a higher level of automation without requiring subjects to manually announce meal information, meal detection and carbohydrate estimation algorithms from CGM and insulin information is gaining popularity. However, insulin dose adjustments for structured exercise is often done manually, and spontaneous PA and effects of APS are usually not considered. The work reported in this paper provides a strong argument on the feasibility of using easy-to-measure biosignals to extract valuable and accurate information about the presence and characteristics of PA, APS and their concurrent occurrence, and using this information in improving the GC prediction accuracy.
Our work uses wristband biosignals to automatically detect and discriminate PA types, and evaluate the intensity of the PA, and predict the future glycemic effects of the PA [58–60]. APS is another glycemic disturbance that is not typically directly considered in automated insulin dosing decisions. We developed an approach to automatically assess the presence of APS, and the possible simultaneous concurrent PA, and subsequently incorporate the PA and APS information in making future GC predictions. The proposed algorithms will enable automated insulin dosing algorithms to explicitly consider psychological and physiological states in the insulin dose calculations without requiring users to manually provide information on the disturbances. The proposed algorithms will yield tighter glycemic control in people with T1D as they go about their diverse daily activities by simultaneously considering PA and APS in the future GC predictions. The proposed approach will also enable athletes with T1D participating in training or competitive events to better manage their glucose levels through simultaneously considering the effects of both PA and APS on the future GC values.
VII. Conclusions
The biosignals collected from a convenient-to-use wristband can generate new quantifiable input features for PA and APS. Machine learning algorithms can estimate the type and intensity of the PA, the presence and characteristics of APS, and the concurrent presence of PA and APS. The information determined for PA and APS can be integrated as exogenous inputs in an adaptive system identification technique to enhance GC estimation accuracy. Data from clinical experiments are used to demonstrate the improvement in GC prediction accuracy when explicitly considering PA and APS information in making GC predictions.
Acknowledgments
Financial support from the NIH under grants 1DP3DK101075 and 1DP3DK101077 and JDRF under grant 2-SRA-2017-506-M-B made possible through collaboration between the JDRF and The Leona M. and Harry B. Helmsley Charitable Trust is gratefully acknowledged.
Contributor Information
Mert Sevil, Department of Biomedical Engineering, Illinois Institute of Technology, Chicago, Illinois, 60616, USA.
Ali Cinar, Department of Biomedical Engineering, Illinois Institute of Technology, Chicago, Illinois, 60616, USA; Department of Chemical and Biological Engineering, Illinois Institute of Technology, Chicago, Illinois, 60616, USA.
References
- [1].Sparacino G, Zanderigo F, Corazza S et al. , “Glucose concentration can be predicted ahead in time from continuous glucose monitoring sensor time-series,” IEEE Transactions on Biomedical Engineering, vol. 54, no. 5, pp. 931–937, 2007. [DOI] [PubMed] [Google Scholar]
- [2].Kovatchev BP, Clarke WL, Breton M et al. , “Quantifying temporal glucose variability in diabetes via continuous glucose monitoring: mathematical methods and clinical application,” Diabetes Technology & Therapeutics, vol. 7, no. 6, pp. 849–862, 2005. [DOI] [PubMed] [Google Scholar]
- [3].Hovorka R, “Continuous glucose monitoring and closed-loop systems,” Diabetic Medicine, vol. 23, no. 1, pp. 1–12, 2006. [DOI] [PubMed] [Google Scholar]
- [4].Battelino T, Danne T, Bergenstal RM et al. , “Clinical targets for continuous glucose monitoring data interpretation: recommendations from the international consensus on time in range,” Diabetes Care, vol. 42, no. 8, pp. 1593–1603, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Dassau E, Cameron F, Lee H et al. , “Real-time hypoglycemia prediction suite using continuous glucose monitoring: a safety net for the artificial pancreas,” Diabetes Care, vol. 33, no. 6, pp. 1249–1254, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Turksoy K, Bayrak ES, Quinn L et al. , “Hypoglycemia early alarm systems based on multivariable models,” Industrial & Engineering Chemistry Research, vol. 52, no. 35, pp. 12 329–12 336, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Forlenza GP, Deshpande S, Ly TT et al. , “Application of zone model predictive control artificial pancreas during extended use of infusion set and sensor: a randomized crossover-controlled home-use trial,” Diabetes Care, vol. 40, no. 8, pp. 1096–1102, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Leal Y, Garcia-Gabin W, Bondia J et al. , “Real-time glucose estimation algorithm for continuous glucose monitoring using autoregressive models,” Journal of Diabetes Science and Technology, vol. 4, no. 2, pp. 391–403, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Taleb N, Emami A, Suppere C et al. , “Efficacy of single-hormone and dual-hormone artificial pancreas during continuous and interval exercise in adult patients with Type 1 diabetes: randomised controlled crossover trial,” Diabetologia, vol. 59, no. 12, pp. 2561–2571, 2016. [DOI] [PubMed] [Google Scholar]
- [10].Castle JR and Jacobs PG, “Nonadjunctive use of continuous glucose monitoring for diabetes treatment decisions,” Journal of Diabetes Science and Technology, vol. 10, no. 5, pp. 1169–1173, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Boiroux D, Hagdrup M, Mahmoudi Z et al. , “Model identification using continuous glucose monitoring data for Type 1 diabetes,” IFAC-PapersOnLine, vol. 49, no. 7, pp. 759–764, 2016. [Google Scholar]
- [12].Breton M, Farret A, Bruttomesso D et al. , “Fully integrated artificial pancreas in Type 1 diabetes: modular closed-loop glucose control maintains near normoglycemia,” Diabetes, vol. 61, no. 9, pp. 2230–2237, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Turksoy K, Quinn L, Littlejohn E et al. , “Multivariable adaptive identification and control for artificial pancreas systems,” IEEE Transactions on Biomedical Engineering, vol. 61, no. 3, pp. 883–891, 2013. [DOI] [PubMed] [Google Scholar]
- [14].Steil GM and Saad MF, “Automated insulin delivery for Type 1 diabetes,” Current Opinion in Endocrinology, Diabetes and Obesity, vol. 13, no. 2, pp. 205–211, 2006. [Google Scholar]
- [15].Hovorka R, Canonico V, Chassin LJ et al. , “Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes,” Physiological Measurement, vol. 25, no. 4, p. 905, 2004. [DOI] [PubMed] [Google Scholar]
- [16].Guerra S, Facchinetti A, Sparacino G et al. , “Enhancing the accuracy of subcutaneous glucose sensors: a real-time deconvolution-based approach,” IEEE Transactions on Biomedical Engineering, vol. 59, no. 6, pp. 1658–1669, 2012. [DOI] [PubMed] [Google Scholar]
- [17].Patek SD, Magni L, Dassau E et al. , “Modular closed-loop control of diabetes,” IEEE Transactions on Biomedical Engineering, vol. 59, no. 11, pp. 2986–2999, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Doyle FJ, Huyett LM, Lee JB et al. , “Closed-loop artificial pancreas systems: engineering the algorithms,” Diabetes care, vol. 37, no. 5, pp. 1191–1197, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Samadi S, Turksoy K, Hajizadeh I et al. , “Meal detection and carbohydrate estimation using continuous glucose sensor data,” IEEE Journal of Biomedical and Health Informatics, vol. 21, no. 3, pp. 619–627, 2017. [DOI] [PubMed] [Google Scholar]
- [20].Dassau E, Bequette BW, Buckingham BA et al. , “Detection of a meal using continuous glucose monitoring: implications for an artificial β-cell,” Diabetes Care, vol. 31, no. 2, pp. 295–300, 2008. [DOI] [PubMed] [Google Scholar]
- [21].Dalla Man C, Breton MD, and Cobelli C, “Physical activity into the meal Glucose-Insulin model of Type 1 diabetes: In silico studies,” pp. 56–67, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Riddell MC, Zaharieva DP, Yavelberg L et al. , “Exercise and the development of the artificial pancreas: One of the more difficult series of hurdles,” Journal of Diabetes Science and Technology, vol. 9, no. 6, pp. 1217–1226, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Hajizadeh I, Rashid M, Turksoy K et al. , “Incorporating unannounced meals and exercise in adaptive learning of personalized models for multivariable artificial pancreas systems,” Journal of Diabetes Science and Technology, vol. 12, no. 5, pp. 953–966, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Sevil M, Rashid M, Maloney Z et al. , “Determining physical activity characteristics from wristband data for use in automated insulin delivery systems,” IEEE Sensors Journal, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Turksoy K, Monforti C, Park M et al. , “Use of wearable sensors and biometric variables in an artificial pancreas system,” Sensors, vol. 17, no. 3, p. 532, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Turksoy K, Littlejohn E, and Cinar A, “Multimodule, multivariable artificial pancreas for patients with type 1 diabetes: regulating glucose concentration under challenging conditions,” IEEE Control Systems Magazine, vol. 38, no. 1, pp. 105–124, 2018. [Google Scholar]
- [27].Dadlani V, Levine JA, McCrady-Spitzer SK et al. , “Physical activity capture technology with potential for incorporation into closed-loop control for type 1 diabetes,” Journal of Diabetes Science and Technology, vol. 9, no. 6, pp. 1208–1216, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Kudva YC, Carter RE, Cobelli C et al. , “Closed-loop artificial pancreas systems: physiological input to enhance next-generation devices,” Diabetes Care, vol. 37, no. 5, pp. 1184–1190, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Breton MD, Brown SA, Karvetski CH et al. , “Adding heart rate signal to a control to range artificial pancreas system improves the protection against hypoglycemia during exercise in Type 1 diabetes,” Diabetes Technology & Therapeutics, vol. 16, no. 8, pp. 506–511, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Jacobs PG, Resalat N, El Youssef J et al. , “Incorporating an exercise detection, grading, and hormone dosing algorithm into the artificial pancreas using accelerometry and heart rate,” Journal of Diabetes Science and Technology, vol. 9, no. 6, pp. 1175–1184, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Turksoy K, Paulino TML, Zaharieva DP et al. , “Classification of physical activity: information to artificial pancreas control systems in real time,” Journal of Diabetes Science and Technology, vol. 9, no. 6, pp. 1200–1207, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Riddell MC, Gallen IW, Smart CE et al. , “Exercise management in Type 1 diabetes: a consensus statement,” The Lancet Diabetes & Endocrinology, vol. 5, no. 5, pp. 377–390, 2017. [DOI] [PubMed] [Google Scholar]
- [33].Riddell MC, Scott SN, Fournier PA et al. , “The competitive athlete with type 1 diabetes,” Diabetologia, vol. 63, no. 4, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Sevil M, Rashid M, Hajizadeh I et al. , “Assessing the effects of stress response on glucose variations,” in 2019 IEEE 16th International Conference on Wearable and Implantable Body Sensor Networks (BSN). IEEE, 2019, pp. 1–4. [Google Scholar]
- [35].Gaab J, Rohleder N, Nater UM et al. , “Psychological determinants of the cortisol stress response: the role of anticipatory cognitive appraisal,” Psychoneuroendocrinology, vol. 30, no. 6, pp. 599–610, 2005. [DOI] [PubMed] [Google Scholar]
- [36].Hosseini SA, Khalilzadeh MA, and Changiz S, “Emotional stress recognition system for affective computing based on bio-signals,” Journal of Biological Systems, vol. 18, no. spec01, pp. 101–114, 2010. [Google Scholar]
- [37].Giannakakis G, Grigoriadis D, Giannakaki K et al. , “Review on psychological stress detection using biosignals,” IEEE Transactions on Affective Computing, 2019. [Google Scholar]
- [38].Kurniawan H, Maslov AV, and Pechenizkiy M, “Stress detection from speech and galvanic skin response signals,” in Proceedings of the 26th IEEE International Symposium on Computer-Based Medical Systems. IEEE, 2013, pp. 209–214. [Google Scholar]
- [39].Haak M, Bos S, Panic S et al. , “Detecting stress using eye blinks and brain activity from eeg signals,” Proceeding of the 1st driver car interaction and interface (DCII 2008), pp. 35–60, 2009. [Google Scholar]
- [40].Sevil M, Hajizadeh I, Samadi S et al. , “Social and competition stress detection with wristband physiological signals,” in 2017 IEEE 14th International Conference on Wearable and Implantable Body Sensor Networks (BSN). IEEE, 2017, pp. 39–42. [Google Scholar]
- [41].Halford W, Cuddihy S, and Mortimer R, “Psychological stress and blood glucose regulation in type i diabetic patients.” Health Psychology, vol. 9, no. 5, p. 516, 1990. [DOI] [PubMed] [Google Scholar]
- [42].Askari MR, Rashid M, Sevil M et al. , “Artifact removal from data generated by nonlinear systems: Heart rate estimation from blood volume pulse signal,” Industrial & Engineering Chemistry Research, vol. 59, no. 6, pp. 2318–2327, 2020. [Google Scholar]
- [43].“Empatica E4,” https://www.empatica.com/research/e4/, Accessed: 2020-06-16.
- [44].“Empatica Embrace 2,” https://www.empatica.com/, Accessed: 2020-06-16.
- [45].Hajizadeh I, Rashid M, Turksoy K et al. , “Multivariable recursive subspace identification with application to artificial pancreas systems,” IFAC-PapersOnLine, vol. 50, no. 1, pp. 886–891, 2017. [Google Scholar]
- [46].Hajizadeh I, Rashid M, and Samadi S, “Adaptive personalized multivariable artificial pancreas using plasma insulin estimates,” Journal of Process Control, vol. 80, pp. 26–40, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wu P, Yang C, and Song Z, “Recursive subspace model identification based on vector autoregressive modelling,” IFAC Proceedings Volumes, vol. 41, no. 2, pp. 8872–8877, 2008. [Google Scholar]
- [48].Chiuso A, “The role of vector autoregressive modeling in predictor-based subspace identification,” Automatica, vol. 43, no. 6, pp. 1034–1048, 2007. [Google Scholar]
- [49].Food US and Administration Drug, “Approval order: Dexcom G5 mobile continuous glucose monitoring system,” PI20005. Silver Spring, MD: Department of Health and Human Services, 2016. [Google Scholar]
- [50].Will PM and Walter JD, “Exercise testing: improving performance with a ramped bruce protocol,” American Heart Journal, vol. 138, no. 6, pp. 1033–1037, 1999. [DOI] [PubMed] [Google Scholar]
- [51].Noto Y, Sato T, Kudo M et al. , “The relationship between salivary biomarkers and state-trait anxiety inventory score under mental arithmetic stress: a pilot study.” Anesthesia & Analgesia, vol. 101, no. 6, pp. 1873–1876, 2005. [DOI] [PubMed] [Google Scholar]
- [52].Goi N, Hirai Y, Harada H et al. , “Comparison of peroxidase response to mental arithmetic stress in saliva of smokers and non-smokers,” The Journal of Toxicological Sciences, vol. 32, no. 2, pp. 121–127, 2007. [DOI] [PubMed] [Google Scholar]
- [53].Specchia G, de Servi S, Falcone C et al. , “Mental arithmetic stress testing in patients with coronary artery disease,” American Heart Journal, vol. 108, no. 1, pp. 56–63, 1984. [DOI] [PubMed] [Google Scholar]
- [54].Karthikeyan P, Murugappan M, and Yaacob S, “A review on stress inducement stimuli for assessing human stress using physiological signals,” in 2011 IEEE 7th International Colloquium on Signal Processing and its Applications. IEEE, 2011, pp. 420–425. [Google Scholar]
- [55].Bosse T, Gerritsen C, de Man J et al. , “Inducing anxiety through video material,” in International Conference on Human-Computer Interaction. Springer, 2014, pp. 301–306. [Google Scholar]
- [56].Kudielka BM, Hellhammer DH, and Kirschbaum C, “Ten years of research with the Trier social stress test,” 2007.
- [57].Allen AP, Kennedy PJ, Cryan JF et al. , “Biological and psychological markers of stress in humans: focus on the Trier social stress test,” Neuroscience & Biobehavioral Reviews, vol. 38, pp. 94–124, 2014. [DOI] [PubMed] [Google Scholar]
- [58].Birkett MA, “The Trier social stress test protocol for inducing psychological stress,” JoVE (Journal of Visualized Experiments), no. 56, p. e3238, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Hajizadeh I, Rashid M, Turksoy K et al. , “Plasma insulin estimation in people with type 1 diabetes mellitus,” Industrial & Engineering Chemistry Research, vol. 56, no. 35, pp. 9846–9857, 2017. [Google Scholar]
- [60].Hajizadeh I, Rashid M, and Samadi, “Adaptive and personalized plasma insulin concentration estimation for artificial pancreas systems,” Journal of Diabetes Science and Technology, vol. 12, no. 3, pp. 639–649, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Perez-Suarez I, Martin-Rincon M, Gonzalez-Henriquez JJ et al. , “Accuracy and precision of the COSMED K5 portable analyser,” Frontiers in Physiology, vol. 9, p. 1764, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Yager RR and Zadeh LA, An introduction to Fuzzy-Logic applications in intelligent systems. Springer Science & Business Media, 2012, vol. 165. [Google Scholar]
- [63].Hinkle LE and Wolf S, “The effects of stressful life situations on the concentration of blood glucose in diabetic and nondiabetic humans,” Diabetes, vol. 1, no. 5, pp. 383–392, 1952. [DOI] [PubMed] [Google Scholar]
- [64].Gonder-Frederick LA, Carter WR, Cox DJ et al. , “Environmental stress and blood glucose change in insulin-dependent diabetes mellitus.” Health Psychology, vol. 9, no. 5, p. 503, 1990. [DOI] [PubMed] [Google Scholar]
- [65].Surwit RS, Schneider MS, and Feinglos MN, “Stress and diabetes mellitus,” Diabetes Care, vol. 15, no. 10, pp. 1413–1422, 1992. [DOI] [PubMed] [Google Scholar]
- [66].Zimmerman DW and Zumbo BD, “Relative power of the Wilcoxon test, the Friedman test, and repeated-measures ANOVA on ranks,” The Journal of Experimental Education, vol. 62, no. 1, pp. 75–86, 1993. [Google Scholar]
- [67].Colberg SR and Edelman SV, 50 Secrets of the longest living people with diabetes. Da Capo Lifelong Books, 2008. [Google Scholar]


