Role of efficient testing and contact tracing in mitigating the COVID-19 pandemic: a network modelling study

Abstract

Objectives

This study quantified how the efficiency of testing and contact tracing impacts the spread of COVID-19. The average time interval between infection and quarantine, whether asymptomatic cases are tested or not, and initial delays to beginning a testing and tracing programme were investigated.

Setting

We developed a novel individual-level network model, called CoTECT (Testing Efficiency and Contact Tracing model for COVID-19), using key parameters from recent studies to quantify the impacts of testing and tracing efficiency. The model distinguishes infection from confirmation by integrating a ‘T’ compartment, which represents infections confirmed by testing and quarantine. The compartments of presymptomatic (E), asymptomatic (I), symptomatic (Is), and death with (F) or without (f) test confirmation were also included in the model. Three scenarios were evaluated in a closed population of 3000 individuals to mimic community-level dynamics. Real-world data from four Nordic countries were also analysed.

Primary and secondary outcome measures

Simulation result: total/peak daily infections and confirmed cases, total deaths (confirmed/unconfirmed by testing), fatalities and the case fatality rate. Real-world analysis: confirmed cases and deaths per million people.

Results

(1) Shortening the duration between Is and T from 12 to 4 days reduces infections by 85.2% and deaths by 88.8%. (2) Testing and tracing regardless of symptoms reduce infections by 35.7% and deaths by 46.2% compared with testing only symptomatic cases. (3) Reducing the delay to implementing a testing and tracing programme from 50 to 10 days reduces infections by 35.2% and deaths by 44.6%. These results were robust to sensitivity analysis. An analysis of real-world data showed that tests per case early in the pandemic are critical for reducing confirmed cases and the fatality rate.

Conclusions

Reducing testing delays will help to contain outbreaks. These results provide policymakers with quantitative evidence of efficiency as a critical value in developing testing and contact tracing strategies.

Strengths and limitations of this study.

• This work provides efficiency as a new perspective when evaluating the impact of testing and tracing from three aspects: (1) the average time interval between infection and test confirmation/quarantine; (2) whether or not contacts of both symptomatic and asymptomatic infectors undergo testing and contact tracing; and (3) the delay to initiating testing and contact tracing after the first infection early in the outbreak.

• We quantified the effects of different kinds of testing and tracing efficiency using a self-designed model with a novel structure, and verified their important role in the control of the COVID-19 pandemic.

• This model is highly practicable, because the ideal average wait time between infection and quarantine can be simulated, and this value can be measured in practice for policymakers to assess whether their actions are efficient.

• A limitation of this work is that all simulations were conducted in a closed population that did not account for intercommunity social activity.

• Impacts of differences in population age ranges, medical resources and lockdown measures could be considered in this model in future work.

Introduction

COVID-19 has posed severe challenges to the physical and mental health of people worldwide since its outbreak in December 2019.1 New waves of cases in Asia, South America and the European Union continue to occur in the first quarter of 2021. It takes a long-time effort to achieve global herd immunity, especially when new strains predominate.2–4 In this condition, testing cases and tracing and quarantining their contacts are still key non-pharmaceutical interventions. SARS-CoV-2 is more contagious and has longer incubation time than SARS-CoV or Middle East respiratory syndrome coronavirus5 and can be transmitted during the incubation period.6–10 For example, approximately one-third of SARS-CoV-2 infectors in Spain were asymptomatic11 and contagious. Transmission via latent, presymptomatic and asymptomatic infected individuals may lead to more rapid spread. Due to the rapid spread of the epidemic and asymptomatic transmission, higher requirements are put forward for testing and tracing. Not only is a large number of tests necessary, but more importantly, efficiency of testing and tracing must be improved. Otherwise, it is difficult to avoid the epidemic rebound before herd immunity is achieved. Therefore, it is crucial to quantify the efficiency of the testing and contact tracing (ie, the timeliness of testing and tracing). This efficiency is related to three aspects: (1) the average time interval from infection to test confirmation and quarantine; (2) whether or not symptomatic, asymptomatic, and presymptomatic infectors are tested and traced; and (3) the delay to initiating testing and contact tracing after the first infection early in the outbreak.

The impact of testing and contact tracing (including quarantine) has been widely evaluated by various models. However, previous studies have focused on quantifying the volume of testing or the percentage of infections that should be traced, or they have highlighted a combination of other interventions.12–22 Few studies have quantified how the efficiency of testing and contact tracing limits disease spread. Lopes-Júnior et al23 published a protocol to evaluate the influence of testing capacity for symptomatic individuals on the control of COVID-19. We referred to this protocol and searched PubMed and Google Scholar in our literature review for studies evaluating the effect of testing and contact tracing through March 2021. We identified 14 modelling studies that were closely related to our work, but most of them did not investigate the effects of the time interval between infection and quarantine or delays to the implementation of testing and tracing procedures on epidemic control. Six of these 14 studies12 13 24–27 only determined the percentage of infections or contacts that needed to be tested and traced to stop the pandemic, but their models were not designed to quantify the effect of testing and tracing delays. For example, Ferretti et al27 concluded the contact tracing work could be overwhelming based on the transmission speed and active social interaction. Therefore, they compromised to strategies which covering only part of the contacts, and the assumptions were fit only for the exponential phase of the pandemic. Keeling et al25 found that 71% of contacts needed to be traced to reduce the basic reproductive number (R0) below 1 or to relax social distancing interventions, but these studies did not mention tracing efficiency (ie, the time interval needed for tracing). Other four articles12 13 24 26 also identified the proportion of contacts that should be traced. But because the number of infections is unknown in the real world, the usefulness for policymakers of these studies is limited. Five studies28–32 were simulations of specific environments (a university campus, care homes, and Dane County in the USA, and the USA); thus, the generalisability of their findings is limited. Three studies16 26 33 focused on policies of testing and tracing. For instance, McCombs and Kadelka33 compared different testing priority strategies (eg, people at high risk or low risk are tested first, people with recent/early symptoms are tested first) under the condition that the maximum test volume per day is fixed. Kucharski et al26 simulated the effect on transmission reduction of randomly mass testing 5% of the population each week and compared it with the effects of isolation and tracing, but the authors did not analyse different testing scenarios. Bilinski et al16 explored whether testing that includes all identified contacts or only those with symptoms alters the effective reproductive number. However, these models do not quantify the impacts of testing and tracing efficiency, which is a vital factor independent of the total amount of testing and tracing.

To quantify the impacts of testing and tracing efficiency on COVID-19 containment and supplement the deficiencies of existing research, we developed a novel individual-level network model, called CoTECT (Testing Efficiency and Contact Tracing model for COVID-19). Traditional population-level models cannot evaluate the time interval between infection and quarantine for each individual, and they do not define the interaction mode between individuals. Although some individual-level models have been developed, they are not directly suitable for modelling testing efficiency in COVID-19 transmission,34 because infectivity of SARS-CoV-2 during incubation period was not considered, and confirmed cases were not distinguished from infections. CoTECT distinguishes between confirmed and unconfirmed infections by integrating a T compartment, which refers to those who are confirmed to be infected by testing and then quarantined. The model also incorporates the following compartments: presymptomatic (E), asymptomatic (I), symptomatic (Is), and death with (F) or without (f) test confirmation. Regarding three aspects of efficiency, we simulated three scenarios using controlled variables with the aim of eliminating confounding factors, and investigated the average time interval between infection and quarantine, whether asymptomatic cases are tested, and initial delays to beginning a testing and tracing programme. Other key parameters used in our model were obtained from recent studies. Our model uses novel factors, strategies, and a unique model structure to evaluate how the efficiency of testing and contact tracing impacts the spread of COVID-19. An analysis of real-world data from four Nordic countries (with other similar confounders) revealed that delays in countermeasures adversely affect pandemic progression. Data from the second outbreak in Beijing were used to verify the importance of shortening the time interval between infection and quarantine. We provide a comprehensive and quantitative assessment of the critical factors related to testing and contact tracing that will help implement more effective measures to contain the pandemic.

Methods

CoTECT simulation model

CoTECT is a stochastic epidemiological network model that we developed specifically to evaluate how the efficiency of testing and contact tracing impacts the outcome of COVID-19 spread. The model was built with the R language and is based on EpiModel, a platform that can mathematically model infectious disease dynamics, allowing the user to construct a flexible network35 with the desired likelihood of connections conditional on specific network properties.36 37 The compartments and parameters were set in accordance with recent COVID-19 research. EpiModel supports stochastic network models developed with self-defined contact modes and interactions between different nodes (ie, different individuals). This differs from the typical differential equation (compartmental) mode, which assumes that human social activity is based on a large, homogeneous, well-mixed population. By contrast, every interaction is a stochastic process in CoTECT. The underlying network is an exponential family random graph model (ERGM),38 developed by Holland and Leinhardt.

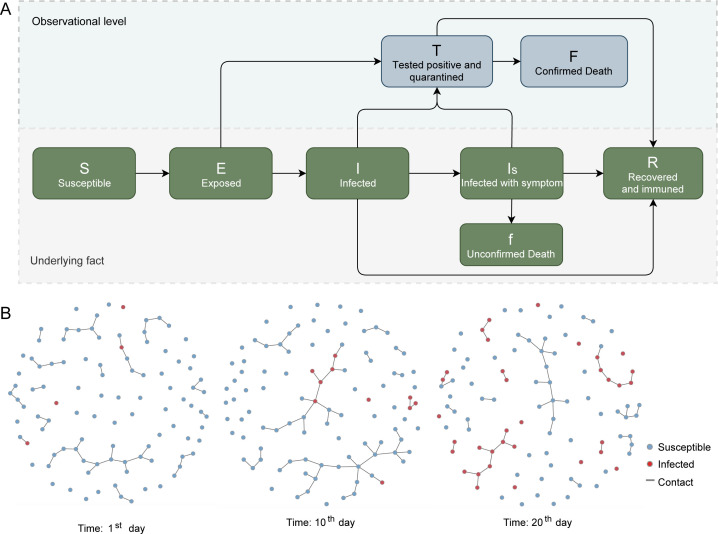
Building on the traditional Susceptible–Exposed–Infectious–Recovered structure, we designed the CoTECT model with eight compartments (figure 1):

Figure 1.

Introduction of the CoTECT model. (A) Structure of the network-based epidemiological model CoTECT. (B) Abbreviated version of the infection network progression. Snapshots shown are days 0, 10 and 20 after the first infected individual. Red and blue dots represent infected and susceptible individuals, respectively. Strings represent contact relationships. CoTECT, Testing Efficiency and Contact Tracing model for COVID-19.

1. Susceptible individuals (S).

2. Individuals exposed to the virus (E) (ie, cases in the incubation period). E cases are considered to be infectious based on the biological characteristics of SARS-CoV-2.

3. Infected individuals who do not have observable symptoms (I). Some I cases become symptomatic and transfer to the Is compartment.

4. Infected symptomatic cases (Is) are more likely to appear in the T compartment than I or E cases, as symptomatic cases are easier to detect.

5. Test-positive cases who are quarantined (T). We assumed all cases confirmed by testing are immediately quarantined.

6. Test-positive fatalities (F).

7. Fatalities without a positive test confirmation (f).

8. Recovered cases (R).

A schematic of the model is provided in figure 1. Arrows represent the transmission rate from one compartment to another, such as from Is to T, denoted as the IsT rate.

Infection occurs at the existing edge (real contact) between two nodes (people), with a given probability. In our model, the infection rate is determined by the SE rate and the times of contact between a susceptible person and an exposed person. SE rate related to the probability of a susceptible person become exposed (E) under the condition of existed connection with another infected nodes (E, I or Is). The exposed compartment represents the incubation period and contains individuals with a lower transmission ability than symptomatic, infected cases. This probability setting is based on the epidemiological characteristics of COVID-19. If the SE rate is p and the average time of contact is three, the infection probability between two connected nodes (people) is 1−(1−p).3 Meanwhile, the edge connecting two nodes is generated and dissolved by a stochastic process with particular conditions. The conditional probability of an edge forming and dissolving is based on a Bernoulli distribution of the module-specific parameter, and the resulting distribution is a binomial mixture.38 After infection, the status transmission rate (the combined IsT, IT and ET rate) is the reciprocal of the waiting interval. For example, an average 7-day waiting time from symptom onset to quarantine corresponds to a 1/7 transmission rate.

In addition to the infection process, the transmission rate from A to B implies a mean duration of remaining in the A status before changing to B status. For example, a 0.1 recovery rate (IR rate) indicates a 10-day recovery duration; thus, we defined the efficiency of testing and contact tracing as the time from E to T or from I to T, reflected as the ET rate and the IT rate, respectively. All transmissions of status of each node form a Bernoulli distribution over time. The value of R0 is determined based on the simulated result of changing the number of total infections (E+I+Is+T). To approach the SARS-CoV-2 R0 value reported by the WHO, we adjusted the network-related parameters in our baseline model, as shown in Figure 2A. Figure 1B displays the stochastic process of the edge generation and desolvation, representing the dynamic change of the social network. This dynamic change led to the abbreviated version of the contact network at various time steps.

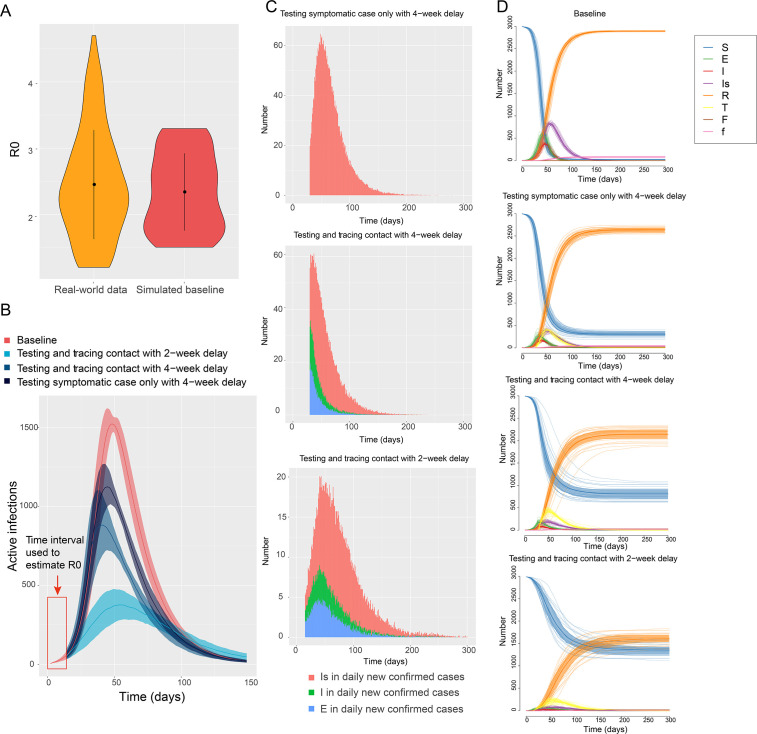
Figure 2.

Epidemic transmission for the baseline and intervention models. (A) Violin plots of R0 distributions for the real-world data and baseline model. (B) Infection curves for the baseline and different intervention models. (C) Daily new symptomatic, presymptomatic and asymptomatic cases confirmed by testing. (D) Compartment trends for the different models. E, exposed; F, confirmed death; f, unconfirmed death; I, infected; Is, infected with symptom; R, recovered and immune; R0, basic reproductive number; S, susceptible; T, tested positive and quarantined.

Parameter settings

The parameters used in the model were taken from published values from multiple sources,39–43 most of which were case-level statistics.8 44–46 The parameters are shown in online supplemental table 1 and include the incubation period,7 47 the average time from onset to a severe case,41 and the average recovery time45 for mild and severe cases. The sampled parameters were set at different grades within the scenarios, while fixed parameters remained constant across all experiments. A hypothetical population of 3000 people over 300 days was used. Our assumptions and network parameters are in line with ERGMs and are listed in online supplemental table 2. The R0 of the baseline model was 2.2 and was obtained by adjusting the edge density, maximum number of connections and probability of transmission between connected nodes (online supplemental table 2). Testing and tracing efficiency was defined as an individual’s average duration between exposure, infection, and symptom onset and test confirmation and quarantine. In CoTECT, the efficiency is translated as the transmission rate (the combined IsT, IT and ET rate is the reciprocal of the waiting interval). For example, an average 7-day waiting time from symptom onset to quarantine corresponds to a 1/7 transmission rate.

The efficiency parameters (IsT rate, IT rate and ET rate) were linked with all experiments setting according to table 1. The average time interval from E to I was 6 days; this was based on an average of 6.4 days7 10 40 43 from exposure to infection (ie, the incubation period). Therefore, the denominator of the IT rate is typically 6 days greater than that of the ET rate. The same logic applies to the IsT rate. Nevertheless, efficient contact tracing will boost both the IT and ET rates. CoTECT assumes that all COVID-19 tests have optimal sensitivity and specificity; therefore, false positives are described as small probability events.

Table 1.

Baseline and scenario 1, 2 and 3 model outcomes

	Delay (days) to targeted testing and contact tracing (T delay)	Average waiting interval (days) from Is to T (1/IsT rate)	Average waiting interval (days) from I to T (1/IT rate)	Total infections	Peak daily infections	Peak daily test confirmation	Total deaths	The proportion of unconfirmed deaths to total deaths
									Baseline	No testing	No IsT transformation	No IT transformation	2933.6	1553.2	0	78.1	100%
Scenario 1	0	4	Yes	344.3	48.7	38.1	5.6	36%
		6		1261.4	181.8	128.3	23	39%
		8		1789	328.5	208.9	37.3	49%
		10		2077.3	425	251.8	41.6	54%
		12		2330.8	581	318.3	50	56%
Scenario 2	0	7	No IT transformation	2510.9	800.4	315	57.2	67%
			13	1941.2	396.6	213	38.1	51%
			11	1614.6	285.5	168.9	30.8	45%
Scenario 3	10	7	Yes	1857.6	360.1	233.4	37.2	46%
	20			1922.6	456.2	294.4	37.8	49%
	30			2272.3	764.1	455.5	45.2	55%
	40			2649.8	1129.5	543	58.6	71%
	50			2866.7	1231.6	400.5	67.1	82%

I, infected; Is, infected with symptom; T, tested positive and quarantined.

Experiment setting

Efficient testing and contact tracing are crucial and include three aspects: (1) the average duration (in days) from exposure to self-quarantine for each individual during the pandemic; (2) whether or not symptomatic, asymptomatic, and presymptomatic infectors are tested and traced; and (3) the delay to initiating testing and contact tracing after the first infection early in the outbreak. To quantify the impacts of different kinds of efficiency of testing and tracing on transmission, CoTECT was used to simulate three different scenarios and one baseline scenario. The critical outcome indicators were cumulative infection (R+F+f), peak daily infections (E+I+Is), peak daily test-positive cases with quarantine (T), cumulative test-positive cases, total fatalities and case fatality rate (CFR).

The baseline scenario is the worst-case condition in which no testing or contact tracing is conducted. Thus, no quarantine measurements were carried out in this model. When the R0 is greater than 1, most of the population will eventually become infected. Using these assumptions, we also simulated different combinations of interventions as preliminary experiments to compare with the baseline scenario: (1) a 4-week delay in response (with no testing or contact tracing before the fourth week), and testing of symptomatic cases only; (2) a 4-week delay in response after which symptomatic, presymptomatic and asymptomatic cases are tested; and (3) a 2-week delay in response after which symptomatic, presymptomatic and asymptomatic cases are tested.

We designed the following three scenarios to investigate the importance of testing efficiency from three aspects. Only one condition was changed, with the other variables remaining consistent in each scenario. The average of 20 randomly repeated experiments were taken as the final result.

1. Scenario 1 evaluated the impact of overall testing and contact tracing efficiency by simulating five different levels of test efficiency, represented by five scales of daily transmission rate or average IsT rate. The intervals from symptom onset to positive test with quarantine were 4, 6, 8, 10 and 12 days. The corresponding IsT rates were 1/4, 1/6, 1/8, 1/10 and 1/12, thus reflecting different kinds of testing efficiency.

2. Scenario 2 evaluated the impact of tracing efficiency for presymptomatic and asymptomatic cases by simulating different IT and ET rates with a fixed IsT rate. Contact tracing for COVID-19 is critical due to the transmissibility of presymptomatic and asymptomatic infections. The IT and ET rates reflect contract tracing efficiency. In this scenario, the probability that latent and asymptomatic (or mild) cases would be tested and isolated (ET and IT rate) was adjusted by 0, 1/13 and 1/11. The fixed IsT rate was 1/7, which assumed 7 days waiting for an interval from onset to quarantine.

3. Scenario 3 evaluated the impact of delayed implementation of efficient testing and contact tracing. The response times are varied significantly worldwide. Many countries were not well prepared for the pandemic, and targeted testing and contact tracing measures were often not implemented until after many confirmed case fatalities. Therefore, we simulated different public health response delays in CoTECT. Five experiments were conducted with fixed IsT, IT and ET rates. The delay intervals between the first infection and implementation of targeted testing were set as 10, 20, 30, 40 and 50 days. The transmission rates from the E, I and Is compartments to T were set as 0 prior to the response.

Sensitivity analysis

We conducted the sensitivity analysis to elaborate how other factors (network parameters) would impact the transmission process. First, we evaluated transmission progression when no testing or contact tracing was in place for varying population sizes. For the three scenarios, the mean R0 was set as 2.2. The network density and contact duration between nodes were consistent across the main experiments.

Second, the sensitivity analysis also included tests of network-related parameters, which describe the disease transmission model’s underlying social activity patterns. In our study, the simulation model built on a graph model consisted of edges and nodes. The edge between two nodes reflects a relatively close contact that could result in disease transmission with a certain probability. In CoTECT, the edges can be interpreted, for example, as face-to-face conversations or sharing a car ride. Unlike the sensitivity analysis of the population size, which uses a constant infection ratio and transmission rate but applies different network sizes, the network-related parameter test demonstrates how these parameters impact disease transmission.

We tested each edge’s mean duration (contact), concurrent edges (how many simultaneous contacts happened per day) and the density of the entire network. The results are presented in the online supplemental figure 1 and online supplemental table 3. As previously mentioned, the final set of these parameters was tuned based on the R0 of the simulated baseline.

Patient and public involvement

No patients or other members of the public were involved in this study.

Results

We carried out preliminary experiments to show how the CoTECT model simulates transmission under different conditions of testing and contact tracing. We then demonstrated how disease transmission is impacted by (1) the efficiency of comprehensive testing and contact tracing, (2) the efficiency of contact tracing for presymptomatic and asymptomatic cases, and (3) delaying the implementation of efficient testing and contact tracing.

Preliminary results of CoTECT simulation

We first defined the baseline model as the worst-case scenario with no epidemiological interventions conducted in a closed population. The baseline R0 was 2.2, according to the average R0 estimated48 from 177 countries and territories49 (figure 2A), aligned with previously published studies.41 Then we compared the baseline model with different combinations of testing and contact tracing interventions to evaluate their respective impact on disease transmission. The infection curve is shown in figure 2B. We assumed each community responded a minimum of several weeks after the first infection. The dark blu

e line indicates the outcome for a delay of 4 weeks and testing only symptomatic cases. Total infections, peak daily infections, and total deaths were reduced by 13.2%, 43.7% and 27.3%, respectively, compared with baseline. The navy line shows the outcome of an open test policy (not only symptomatic cases) with a 4-week delay. Total infections, peak daily infections, and total deaths decreased by 23.4%, 43.1% and 41.3%, respectively, compared with baseline. The light blue line shows the outcome for a delay of 2 weeks after the first infection. Total infections, peak daily infections, and total deaths decreased by 44.1%, 75.8% and 61.0%, respectively, compared with baseline.

Daily new symptomatic, presymptomatic and asymptomatic cases confirmed by testing in three conditions are shown in figure 2C. Compared with condition 1 (only testing symptomatic cases with 4-week delay), condition 2 (testing and tracing presymptomatic and asymptomatic contacts with 4-week delay) could reduce 24.8% of total confirmed cases (from 125 to 94), and 26.5% of 94 confirmed cases were diagnosed before symptom onset (E+I). Condition 3 (tracing contacts and testing with a 2-week delay) could reduce 51.2% of total confirmed cases (from 125 to 61), 33.6% of 61 confirmed cases were diagnosed before symptom onset (E+I). Moreover, compared with condition 2, condition 3 also reduced daily peak confirmed Is, I, and E cases by 65.8% (from 38 to 13), 75.0% (from 16 to 4), and 75.0% (from 20 to 5), respectively. We further demonstrated trends of all compartments in baseline and different conditions (figure 2D). Compared with baseline, as infections decreased in three conditions, the S individuals (those who remain uninfected) of conditions 1, 2, 3 were 6.6, 11.6 and 20.7 times of S individuals of baseline model after 300 days of the epidemic, respectively. Meanwhile, 27.7%, 41.5% and 61.2% of deaths (confirmed and unconfirmed by testing) of the baseline model were saved in conditions 1, 2, 3, respectively. These results indicate that reduced time to action and better identification of presymptomatic and asymptomatic cases are critical factors in flattening the infection curve and decreasing the deaths.

Impacts of overall testing and contact tracing efficiency to all infectors

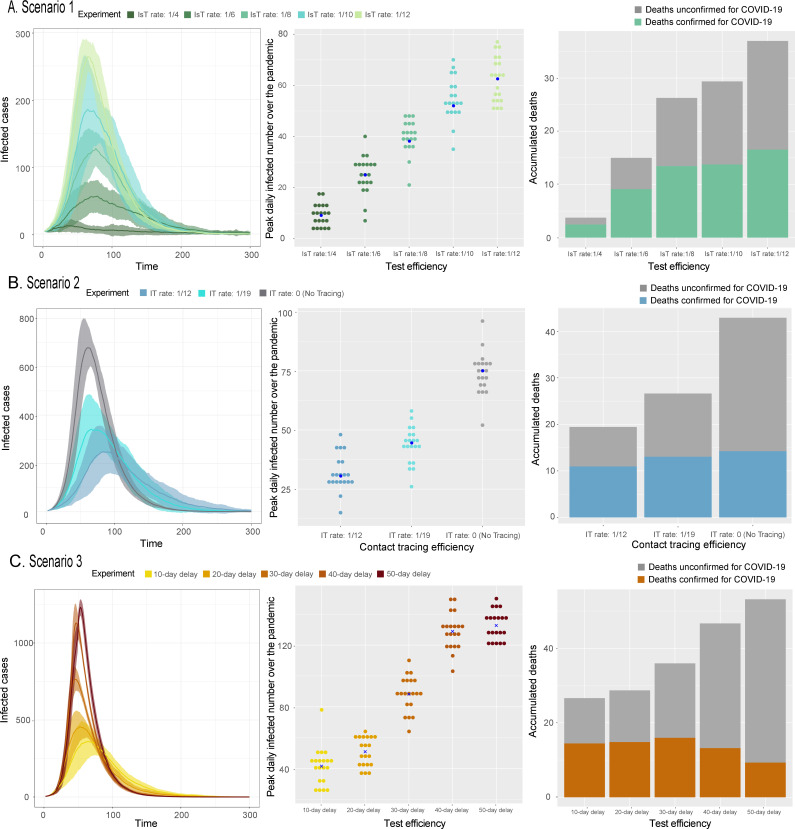
Scenario 1 simulated five different test efficiency levels represented by five different daily transmission rates from Is to T (IsT rate): 1/4, 1/6, 1/8, 1/10 and 1/12. The daily transmission rate from I to T (IT rate) and from E to T (ET rate) changed in accordance with the IsT rate. This scenario assumes that contact tracing efficiency changed with the IsT rate, and therefore latent, asymptomatic cases could also be tested. We found that longer public health response delays (ie, lower IsT rates) resulted in higher peak daily new transmitters, peak daily new diagnoses and overall cumulative infections. Besides, the number of diagnosed and undiagnosed fatalities and the proportion of undiagnosed fatalities increased as IsT rates declined, indicating that fewer tests and slower response times resulted in worse epidemic outcomes. We decreased the IsT delay from 12 to 4 days in 2-day intervals and found that, compared with baseline, total infections decreased by 20.5%, 29.2%, 39.0%, 57.0% and 88.3%, respectively, and total deaths decreased by 36.0%, 46.7%, 52.2%, 70.6% and 92.8%, respectively. Peak daily infections across the five experiments increased linearly as IsT rates decreased (table 1, figure 3A).

Figure 3.

Scenario 1, 2 and 3 outcomes. Total infections over time, peak daily infections for different public health response strategies (each dot represents a simulation) and accumulated deaths (both confirmed and unconfirmed cases) for (A) scenario 1, (B) scenario 2 and (C) scenario 3. I, infected; Is, infected with symptom; T, tested positive and quarantined.

Impacts of contact tracing efficiency for presymptomatic and asymptomatic cases

Scenario 2 quantified the importance of efficient contact tracing. Owing to asymptomatic transmissibility, contact tracing is critical for effective containment. The tracing efficiency is represented by either the IT or ET rate. Therefore, we designed simulations with a fixed IsT rate (1/7) and varied the IT (1/12, 1/19, 0) and ET rates (1/17, 1/24, 0). The results showed that larger ET and IT rates resulted in fewer overall infections, confirmed cases, and confirmed and unconfirmed fatalities. More efficient contact tracing (12-day delay from infected to testing for I cases) would prevent 36% of cumulative infections, 64% of peak daily infections, 46% of peak daily confirmed cases and 46% of total deaths compared with no contact tracing. Less efficient contact tracing (as a 19-day delay from infected to testing for I patients) prevented 23% of cumulative infections, 50% of peak daily infections, 32% of peak daily confirmed cases and 33% of total fatalities compared with no contact tracing. Thus, more efficient contact tracing resulted in fewer infections (table 1, figure 3B).

Impacts of delayed implementation of efficient testing and contact tracing

Scenario 3 evaluated the impact of delayed implementation of efficient testing and contact tracing. We found that cumulative infections and fatalities increased with increasing delay intervals. Compared with 50-day delay, delays of 10, 20, 30 and 40 days reduced total infections by 35.2%, 32.9%, 20.7% and 7.6%, respectively, and total deaths by 44.6%, 43.7%, 32.6% and 12.7%, respectively. The increase in peak daily transmitters as delay interval increased followed a sigmoid-shaped curve (table 1, figure 3C). Clearly, implementing a prompt testing response within 20 days of the first infection had much more impact than response 20 days later.

The critical impact of the prompt initiation of a testing programme is demonstrated in our simulation and is observed in real-world data. Measures of testing sufficiency are the number of tests conducted per confirmed case (TPC) and the number of tests per million people (TPM). Here, efficiency is measured as the average time interval between infection and a positive COVID-19 test. A sufficient testing capacity, estimated by TPC and TPM, is a prerequisite for efficient testing. Decreasing TPC trends indicate that disease transmission is outpacing testing and that efficiency is decreasing. The three indicators of epidemic control are CFR, confirmed cases per million people (CPM) and deaths per million people (DPM).

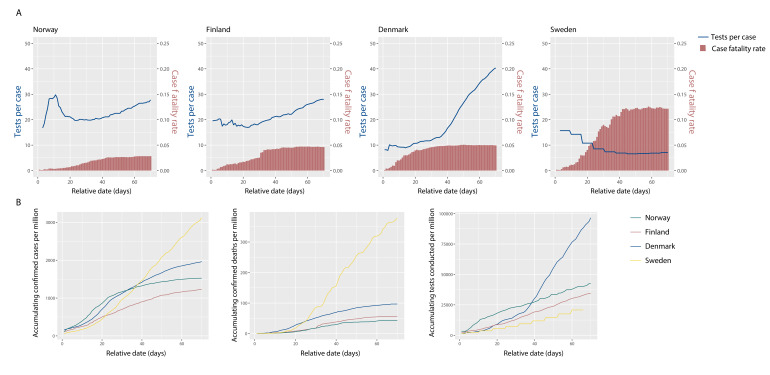
For comparison, we selected four Nordic countries that have similar medical resources, population age ranges, geography and climate (figure 4). Day 0 was defined as the day on which the daily DPM reached 0.1. Norway, Finland and Denmark experienced a similar lockdown duration in the first 70 days, and the TPC over the first 70 days increased in all countries. From day 0 to 14, TPC was highest in Norway, followed by Finland and Denmark. Between days 15 and 70, although the TPCs in Norway and Finland were similar, the CFR in Norway (2.8%) was lower than in Finland (4.6%). This implies that the early outbreak TPC values were a more significant factor than later TPC values in controlling the pandemic. Denmark had the lowest early outbreak TPC of these three countries. Even though its TPC later grew dramatically and far exceeded those of Norway and Finland, its CFR (4.9%) was higher than those of Norway and Finland. We also observed that the overall TPM in Denmark from day 0 to 70 was 2.7 times those of Norway and Finland. This implies that the early stage TPC may have a more significant influence on the overall CFR than the late-stage TPC, consistent with our hypothesis that early testing plays a critical role, without which testing efforts must be heavily increased as transmission rates worsen. In Sweden, the TPC gradually decreased. Sweden’s CFR (12%) was the highest of all four countries. This indicates that insufficient testing in the early stage might not be remedied by subsequently increasing the testing volume.

Figure 4.

Case fatality rate (CFR), confirmed cases per million people (CPM) and deaths per million people (DPM) trends in representative countries with different number of tests conducted per confirmed case (TPC) and tests per million people (TPM) levels. (A) Accumulating CFR by COVID-19 and the TPC for 4 countries, starting by the day since daily newdeaths due to COVID-19 reached 0.1 per million. (B) Accumulating CPM, DPM, and TPM of 4 countries.

Sensitivity analysis

To validate the rationality of our model’s network settings, we conducted sensitivity analyses using various population sizes and different settings of the parameters related to R0.

We first compared baseline models with population sizes of 1000, 2000, 3000, 4000 and 5000. The proportion of cumulative infections, peak daily infections and cumulative deaths were similar in all five models. However, there was considerably more variation between the 1000 and 2000 population models than between the models with population sizes of 3000 or more. These findings underpinned our rationale for using a representative population of 3000 (online supplemental figure 1, online supplemental table 3).

Second, a sensitivity analysis of R0-related parameters emphasised how the structure of a social network impacts disease transmission. In addition to the intrinsic properties of SARS-CoV-2, the value of R0 is determined by three parameters that we studied in the sensitivity analysis: the social network density, concurrent contacts (the number of people a person has contact with) and the average duration of contact between two people. The network density will directly impact the rate of disease spread (online supplemental figure 1, online supplemental table 3). An extremely low density is difficult to maintain in most areas. However, we can expect that a low density would occur in a town under lockdown for a short period of time. Decreasing the number of concurrent nodes with a fixed density will skew the infection number curve. This also affects the variance, because concurrent nodes become critical nodes that can spread the disease to many other nodes. The duration of an edge indicates the stability of the relationship between two nodes. The results revealed that increased stability would flatten the infection curve. It is clear that if we were to only contact the same group of people repeatedly, the possibility of infection would decrease. The value of R0 changed when the settings of these three parameters were altered. To improve the universality of our model, we selected suitable ranges for these parameters to achieve the average R0 reported in other studies (figure 2A). The R0 distribution in our baseline simulation corresponded to the average R0 estimated from 177 countries and territories.³⁸ The sensitivity analysis showed the validity of how we regulated parameters that are related to transmission dynamics. For all experiments, the mean R0 was set as 2.2. The network density, concurrent contacts and the relationship duration between nodes were consistent across all experiments.

Discussion

Principal findings

This work quantified how testing and contact tracing efficiency, investigated as the average duration between infection and quarantine and the delay in testing and tracing close contacts after the first identified infection, can influence COVID-19 transmission. Scenario 1 demonstrates that shortening the average time interval between symptom onset and quarantine from 12 days to 4 days results in an 85.2% reduction in infections and an 88.8% decrease in deaths. Scenario 2 indicates testing and tracing regardless of symptoms (a 7-day interval for Is to T, with the E/I to T intervals changing accordingly) reduce infections by 35.7% and deaths by 46.2% compared with testing symptomatic cases (Is) alone. Reducing the delay in implementing an efficient testing and tracing programme from 50 days to 10 days reduces infections and deaths by 35.2% and 44.6%, respectively. Scenario 3 implies that the delayed implementation of testing and contact tracing will lead to a massive demand in testing capacity, which is also supported by the analysis of data from the four Nordic countries. Thus, efficient testing and contact tracing can reduce disease transmission and the overall number of fatalities.

Strengths and weaknesses of the study

Strengths of this work include the following: (1) it provides a new perspective on evaluating the effect of testing and tracing in addition to the test volume at the individual level. This new perspective focuses on the efficiency of testing and tracing. Our work indicates that controlling the COVID-19 pandemic requires a rapid response to testing and tracing rather than solely relying on a massive testing capacity. (2) We quantified the effects of different kinds of testing and tracing efficiency using a self-developed model, called CoTECT, as well as real-world data to verify their important role in controlling the COVID-19 pandemic. The model quantified the additional percentage of infections and deaths that would occur when the implementation of these efficient measures is delayed. (3) This model is highly practicable. The ideal average wait time between infection and quarantine was simulated, and this time interval can be measured in practice for policymakers to determine whether their actions are efficient. Our main conclusions can be generalised to different circumstances, from megacities to small villages.

Weaknesses of this study include the following: (1) all simulations were conducted in a closed population; the model did not account for intercommunity social activity. (2) We assumed that nearly 100% of the tests were accurate because of false-positive tests result in an unnecessary self-quarantine. We also assumed that no infections would occur after self-quarantine.

Strengths and weaknesses in relation to other studies

While previous studies12 13 16 24–27 have typically emphasised the amount or percentage of infections or contacts that need to be tested and traced, our model simulates the ideal average wait time between infection and quarantine, which is a more practical criterion that is easily measured in real-world epidemiological investigations. In contrast, the percentage or number of infections that need to be tested and traced proposed by other modelling studies is less useful; this is because the true number of infections is difficult to estimate in the real world.

In addition, we did not limit our analysis to estimating a fixed, total amount of testing required because the capacity of testing changes over time. Instead, we focused on the duration between an exposure event and when an exposed person receives their test result (ie, the efficiency of testing and contact tracing). We found that more efficient testing can reduce the number of infections and deaths and decrease the fatality rate, and demand in testing capacity will increase as implementation of testing and contact tracing delayed. The testing and contact tracing capacity should be considered along with the demand for testing, which is related to the total number of infections.

In contrast to models that are suitable only for specific regions and conditions,28–32 our tool has potential to be used for various population sizes and is generalisable to different types of communities. The novelty of this method is reflected in the model’s structure and scenario design. Using the timeliness of individual testing, CoTECT can predict macro-perspective outcomes.

The weakness of our work in relation to other studies is that age ranges of the population, the medical resources and lockdown measures were not explicitly adjusted in this model (regarded as controlled variables). Impacts of these variables have been considered in other existed studies.15 18 27 33

Meaning of the study

Our results provide professionals and policymakers with quantitative evidence showing that efficiency is a critical value in the development of testing and contact tracing strategies. Our model is particularly useful for nations facing a potential second or third wave of COVID-19 or the spread of mutated virus strains or other emerging infectious diseases. We provide a novel tool, CoTECT, that policymakers can use to simulate the effects of delays to implementing testing and tracing systems, which could help them balance the costs against the risks. The model highlights that it is critical to consider the transmission rates from presymptomatic and asymptomatic cases, as well as the time delay between testing and quarantine.

The meaning of our conclusions drew from three scenarios: (1) according to scenario 1, an extra 4 days of waiting will lead to a considerable difference in total infections and deaths. At one point, the mean wait time between taking a COVID-19 test and receiving the result was 4.1 days in the USA, which is disadvantageous for controlling disease spread.50 So our study indicates the government and testers of some countries should improve the efficiency of testing. (2) An example of the value of efficient testing is the successful containment of the second COVID-19 outbreak in Beijing, China. Highly efficient testing (open to all regardless of symptoms) and contact tracing began immediately after the first case was identified51–54 and average time from onset to reporting of first 37 cases was 2.7 days (online supplemental tables 4 and 5). This is in marked contrast to the first outbreak in Wuhan when testing was less efficient and containment was slower, which verified our scenarios 1 and 2. (3) In scenario 3, we focused on the delay between the first infection and implementation of contact tracing and testing. In the real world, the longer the delay, the higher the initial positive rate would be (the lower TPC), which was analysed in Nordic countries. We recommend that the government should increase TPC as soon as possible in the early stage of a pandemic, which is critical in reducing the number of confirmed cases and the fatality rate.

Unanswered questions and future research

Some unanswered questions are the following: (1) How does intercommunity social activity affect our model?; (2) How do variables such as population age ranges, medical resources and lockdown measures lead to different results?; (3) Could the socioeconomic resources required for efficient testing be estimated? To solve these issues, we will introduce more variables and improve our model to study the impact of testing and contact tracing efficiency under different circumstances of constraints and countermeasures.

Data availability statement

Data are available in a public, open access repository. Data are available upon reasonable request. Data are available by emailing moehu@foxmail.com.

Ethics statements

Patient consent for publication

Not required.