2019 was a big year for metrology. The international system of units was revised on World Metrology Day, May 20th, that year [1]. What will 2020 bring? In this article we discuss five promising advances that we have on a watchlist for 2020. First, we describe the measurement of volume and gas pressure using electromagnetic waves. These measurements rely on the fixed value of the speed of light in vacuum c0. We then pivot to the Planck constant h. SI traceable measurements of mass and force can be obtained from h. Interesting developments are coming in mass metrology since the definition changed from the mass of the international prototype of the kilogram to the value of the Planck constant. Adding the elementary charge e to h gives access to resistance and impedance measurements via the quantum Hall effect. This has been a very interesting field for some time, since the discovery of graphene in 2004. The last section explains how the noise across a resistor can be used to measure thermodynamic temperature. As will be shown, the temperature can be linked to the quotient of the Boltzmann constant kB and the Planck constant.
While it is difficult to compete with the excitement in metrology of the last year, we are convinced that fun and exciting developments are in store for basic metrology in 2020.
Weighing a Gas with Microwave and Acoustic Resonances
Prior to the revision of the SI in May 2019, achieving better measurements of the Boltzmann constant kB using different methods was a priority. The method that achieved the lowest uncertainty relied on measuring acoustic and microwave resonances in a spherical cavity.
Today, the same equations that described those measurements can be rearranged to measure other quantities in novel ways. The example shown here is the development of a new apparatus which could eventually replace the present primary standard for gas flow [2] used by the National Institute for Standards and Technology (NIST). Flow measurements are economically important (the value of natural gas metered in US pipelines was about $90 billion in 2016 [3]). From the standpoint of metrology, the goal of the work described below is to reduce the number of steps in the present calibration chain by developing a gas-flow standard that operates at higher pressures and flow rates [3].
The main component of the prototype apparatus is referred to informally by the NIST researchers as the Big Blue Ball (BBB). Shown in Fig. 1, it has a nominal inner volume of 1.8 m3 (1800 liters) and can be pressurized to 7 MPa (70 atmospheres) for use as a flow standard. Three existing ports on the BBB were adapted to contain two microwave antennas, an acoustic speaker, and an acoustic microphone (one antenna and the speaker share the same port) [3].
Fig. 1.

The Big Blue Ball. It is made of carbon steel, has an inner volume of about 1800 liters, and weighs more than 1000 kg. (photo credit: NIST’s Fluid Metrology Group).
Volume Determined by Microwave Resonances
With a test gas—such as argon or nitrogen—filling the BBB, a simplified equation for a microwave resonance frequency fmicro is given by:
| (1) |
where a is the radius of the BBB inner volume, c0 is the speed of light in vacuum (which was defined exactly in 1983), ng is the refractive index of the gas filling the BBB, and ξmicro is an exactly calculable number related to the BBB’s geometry. The ratio in parentheses is the speed of microwaves in the gas. The volume needed is . Since the volume is a weak function of temperature T (due to thermal expansion) and internal pressure p, measurements of fmicro were made at a range of filling pressures from zero to 7 MPa and over a small range of temperatures (determined by thermistors placed on the outer surface of the BBB). The refractive index ng at the microwave frequencies used has been inferred from tabulated values of the dielectric constants of the test gas as a function of temperature and pressure. As a result, the inner volume of the BBB is known as a function of temperature and pressure to about two parts in 104, estimated at 95% confidence.
Mass of Fill Gas Determined by Acoustic Resonances
The speed of sound w in the gas is measured by acoustic resonances [3], [4]. To take the simplest case of the gas being in equilibrium at known pressure p and temperature T, the measured speed of sound is given by:
| (2) |
where facoust is the frequency of the measured acoustic resonance and ξacoust is an exactly known parameter (but different from ξmicro) [3]. Once w is known in m/s, the density ρ in kg/m3 for a particular gas as a function of p and w can be inferred from standard tables so that, finally, the mass of gas in the inner volume Macoust as determined from acoustic and microwave resonances is given by:
| (3) |
For the simplified equations it is assumed that the test gas within the BBB is at a uniform temperature, determined by thermistors placed on the outer wall. This is not usually the case. As Fig. 2 demonstrates, filling the sphere from 1 atmosphere to 70 atmospheres by passing the gas through a tube changes the temperature of the inflowing gas. The temperature distribution within the gas then stratifies due to convection, with temperature increasing from bottom to top. The approach to equilibrium is slow as inferred from the thermistors. However, inferring the temperature from the acoustic modes is much faster because of an inherent averaging effect [3], [4].
Fig. 2.
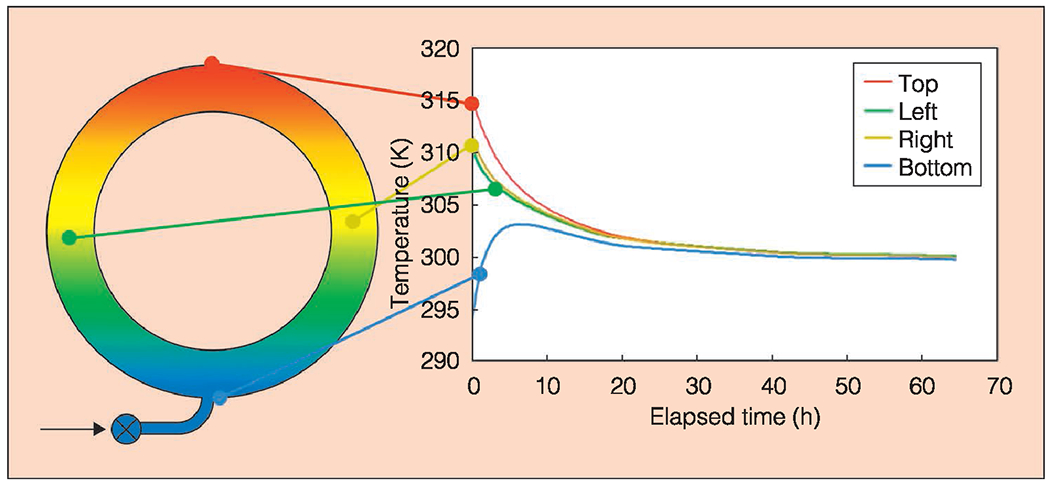
Temperature differences as a function of time as measured on the BBB after filling to 7 MPa. The temperatures are read from four thermistors placed as shown. Uniform temperature is reached after about 2 days (credit: NIST’s Fluid Metrology Group).
In [4], Pope et al. take the remaining step of calibrating secondary flow standards using this system, including determining the time derivative of Macoust, which is “dynamic” flow. Gas in the BBB is made to flow through the secondary standard under calibration. The authors also describe many cross checks with other techniques to support uncertainty claims. One of these tests is a calibration of secondary flow standards using the BBB as the primary standard, against results obtained using NIST’s current primary standard [2]. The authors show that dynamic flow can be conveniently monitored by measuring a particular acoustic resonance as a function of time. To do this, however, the resonance frequency must be acquired quickly; a novel positive-feedback circuit has been developed to speed up this measurement. Future steps are also presented in [4].
So, it seems possible to replace a classic flow system based on pVTt (pressure, volume, temperature, and time) with a system based on pVwt, where the temperature T of the gas is replaced by the speed of sound w measured within the gas using acoustic resonances, and the volume V is determined by microwaves resonances.
Using Light to Measure Pressure
The SI unit of pressure has the special name “pascal,” symbol Pa. In terms of the base units of the SI, Pa = kg m−1 s−2. The pascal can also be expressed as Pa = N/m2 = J /m3, where N is the symbol for the SI unit of force, the newton, and J is the symbol for the unit of energy, the joule.
Through four centuries, pressure has been measured with mercury manometers which, by the 21st century, have achieved a high degree of perfection [5]. Simply put, if one end of a U-tube that contains mercury is evacuated, the pressure p on the other end is proportional to the height difference Δh between the evacuated tube and the pressurized tube. To first order,
| (4) |
The density of mercury ρHg (about 13 600 kg/m3) must be accurately known as a function of temperature, and the local gravitational acceleration g (about 9.8 m/s2) must also be accurately known. The pressure p is then determined by a measurement of Δh. By dimensional analysis, it easy to see that when Δh is measured in meters, the unit on the right-hand side of (1) is kg m−1 s−2 —i.e., the pascal. The height difference Δh is about 760 mm at atmospheric pressure. The non-SI unit torr corresponds to 1 mm of mercury, but is now defined by the relation 1 Torr = 101 325/760 Pa. (In 1954, a standard atmosphere was defined to be 101 325 Pa.) The primary NIST manometer is 3 m tall and contains about 230 kg (500 pounds) of mercury. It takes about a minute for measurements to stabilize when the pressure is changed, and measurements are sensitive to vibration. The useful low-pressure limit is a few hundred pascals [6]. Mercury is a neurotoxin and so the goal is to replace this cumbersome apparatus by a new technology, described below. Until June 2019, NIST had two similar manometers but the second has been dismantled [7]. The first still serves as NIST’s primary realization of the pascal over a range of pressures of great interest.
New Ways to Realize the Pascal
Jousten et al. [8] have reviewed promising technologies for realizing the pascal over ranges from ultra-high vacuum (below 10−7 Pa) to pressures much higher than atmospheric. Here, we focus on replacing the mercury manometer by a technology that results in a compact package which is easy to replicate, and which uses the speed of light rather than the density of liquid mercury to determine pressure. A brief description is found in [9] and subsequent references.
Starting with the equation of state of an ideal gas:
| (5) |
where p is the pressure of the gas, V is its volume, T is its absolute temperature, N is the number of molecules in the volume, and kB is the Boltzmann constant. The value of kB has been defined to be exact since May 20, 2019. The unit of kBT is the joule. Dividing (5) by V yields:
| (6) |
The ratio N/V is the number gas molecules per unit volume. Since N is simply a number, the SI unit of the right-hand side of (6) is J/m3, which is identical to the pascal. The temperature T of the gas can be measured, but (6) does not yet reveal a way to measure p using light. The way forward is to see that N/V is proportional to n – 1, where n is the index of refraction of the gas [8]. A very rough approximation is:
| (7) |
where ϵ0 is the electric constant whose uncertainty is negligible, and α is the polarizability of the particular gas molecule. Equation (7) shows that the pressure of a gas is proportional to the difference of its index of refraction from 1, the index of refraction of vacuum. The full equation for real gases involves many additional terms (see e.g., [8], [9]).
At a known temperature T, the measurement of any particular pressure p requires a measurement of Δn = n – 1. This is analogous to the need to measure Δh in a mercury manometer, once ρHg, g, and T are known. For helium, the needed optical and other properties have been calculated more accurately than p can be measured using the full treatment of (7) [8]. A determination of (n – 1) in helium, either directly or indirectly [9], thus becomes a determination of pressure.
A prototype device to realize the pascal in this way, called the Fixed-Length Optical Cavity (FLOC), consists of two Fabry-Perot optical cavities of equal length, produced within a block of ultra-low expansion glass [8]. The cavity length is 15 cm. As shown in Fig. 3, the ends of both cavities are terminated by silicate-bonded, semi-reflective glass windows. In Fig. 3, the lower cavity can be evacuated, but the upper cavity has a slot that opens the cavity to the test gas. The FLOC is housed in a copper enclosure (Fig. 4) to help ensure uniform temperature.
Fig. 3.

The 15 cm long Fixed-Length Optical Cavity can be held in one hand (photo credit: NIST).
Fig. 4.

The Fixed-Length Optical Cavity is housed in a copper block, which helps to stabilize the temperature. In this photo, the upper plate of the block has been removed (photo credit: NIST).
Laser light in the evacuated cavity will be in resonance at some frequency, determined by the cavity’s length L. The speed of light is slower in the gas-filled cavity, whose length is also L. The resonance frequency is therefore different and n is determined from this difference [4]. A short video explains how the FLOC determines n [10].
Direct tests made several years ago with respect to NIST’s primary mercury standard demonstrated the superiority of the FLOC at the lower end of the mercury manometer’s range and had better precision throughout the entire range [10]. A recent feature in Nature Physics [11] gives an optimistic account of the program to replace the primary mercury manometer, although the conclusion of [9] is that much work still remains to be done to displace what the authors refer to as “the mechanical pascal,” by which they mean the pascal realized by force measurements.
Mass and Force Measurements Based on the Planck Constant
The Kibble balance, invented by the first contributor to the Basic Metrology column, Bryan Kibble [12], is an apparatus that can be used to realize the unit of mass from the Planck constant. Two building blocks are necessary to assemble a Kibble balance: a balance and quantum electrical standards. The balance itself is an electromechanical device that allows to counteract the weight of a mass standard with a force that is generated by a current carrying coil immersed in a magnetic field. The ingenious insight of Bryan Kibble was the fact that the conversion factor between the current in the coil and the resulting force is identical to the conversion factor between voltage and velocity, when the same system is used as a generator. In this mode, the (electrically) open coil is moved vertically through the magnetic field, while simultaneously measuring the coil’s velocity and the electro motive force that appears between the coil’s ends. By doing this with great care, the so-called geometric factor of the Kibble balance can be measured to with uncertainties that are smaller than a part in 108 (for the world’s best Kibble balances that is). And, by applying the geometric factor to the force mode, a device that converts current to a force with slightly larger uncertainties. In short, a known force can be generated relying upon measurements of voltage, current, and velocity.
To measure voltage and current, the quantum electrical standards are used. The quantum Hall effect provides a resistance standard that is an integer fraction of h/e2, about 25 812.807 kΩ. Here, h is the Planck constant, and e the elementary charge, two of the seven defining constants of the SI. Note: a Kibble balance does not need to be directly connected to a quantum Hall resistor; a standard resistor that has been calibrated against a quantum Hall resistor is all that is needed. By routing the coil current through this standard resistor, a voltage drop occurs. The resistive voltage drop, as well as the induced voltage in the velocity mode, can be precisely measured with the help of the Josephson effect [4]. This quantum mechanical phenomena that occurs at a tunnel barrier between two superconducting layers provides a voltage that is proportional to , where f is the frequency of a microwave current driven through the tunnel barrier. By combining two measurements of voltage with the quantum Hall resistor, the elementary charge drops out, but the Planck constant remains. Hence, force can be written as:
| (8) |
where β1is a known numerical factor that contains the number of Josephson junctions used, the integer in the quantum Hall effect and the ratio of h/e2 to the standard resistor used in the Kibble balance.
The Kibble balance is first and foremost a machine for a traceable force measurement; only by knowing the local gravitational acceleration g can it be used to realize mass, via the weight, mg. As an aside, the alternative method to realize the unit of mass at the kilogram level, the X-ray crystal density (XRCD) method does not require g. Here, the mass of a silicon crystal is given by a large known number multiplied by the electron mass which is precisely known, albeit with an insignificant uncertainty, from determinations of the Rydberg constant. In absence of a precise knowledge of g, the Kibble balance can be used to measure force and the XRCD method to measure mass. By combining both measurements, the local acceleration can be obtained. Of course, there are other ways to obtain g, for example by measuring the free fall acceleration of a mass in a vacuum chamber.
The Kibble balance and the XRCD method are usually seen as a replacement for the international prototype of the kilogram, the definition of the unit of mass from 1889 to 2019. As such, both methods would assign a number to a transfer standard, for example a national prototype, which would then be used to work-up and work-down to larger and smaller masses. It was always part of traditional mass metrology to produce multiples and submultiples of the kilogram. This task is achieved by substitution-weighing of combinations of masses that add up to the known standards together with comparisons of the individual masses within that combination. For example, a mass set comprised of a 500 g, two 200 g and two 100 g masses can be used to work-down from 1 kg to 100 g. A minimum of five substitution comparisons are required to solve a system of equations of the five unknown masses. In practice, more comparisons are performed, and the system of equations becomes overdetermined. It can be solved with a least-squares procedure which will result in the mass values and their uncertainties. The example above shows how the unit of mass is divided down by one order of magnitude. This division must occur for many orders of magnitudes. Some laboratories calibrate masses as small as 100 μg, a total of seven orders of magnitudes below 1 kg. Clearly, subdividing the unit of mass is an involved process that requires several weighings. Hence, it is an appealing option to build Kibble balances capable of measuring small mass directly via quantum electrical standards instead of subdividing a mass standard.
For smaller masses, smaller forces must be created with the coil and since the force is proportional to the current, smaller current is necessary. The last statement is true if the geometric factor remained the same. However, when designing a Kibble balance for smaller mass values, one could decide on a magnet system with a smaller geometric factor and, hence, maintain a large current. The problem with this approach is that the induced voltage in the generator mode will also go down and therefore be more difficult to measure. Increasing the velocity is often not a practical solution, either. Hence, it becomes clear that for smaller and smaller masses and forces, the Kibble balance may not be the ideal tool. An alternative solution is to use an electrostatic balance.
In an electrostatic force balance (EFB) [15], [16], the actuator is a capacitor with one fixed capacitor plate and a second moveable capacitor plate mounted to a balancing mechanism. The electrostatic energy of the capacitor is given by where C is the capacitance and V the potential difference between the capacitor plates. The force acting on each capacitance plate is given by
| (9) |
Like the measurement with the Kibble balance, the measurement with the EFB is performed in two modes. In the weighing mode, the force or weight that has to be measured is balanced against the electrostatic force. In this mode, the potential difference between the capacitor plates is measured against a voltage standard that is ultimately derived from a Josephson Voltage standard. In the second mode, the capacitance of the capacitor is obtained as a function of position C(z). From this measurement the capacitance gradient can be obtained. The capacitance is ultimately traceable to either the calculable capacitor or the ac quantum Hall effect. The capacitance per unit length of a calculable capacitor is given by
| (10) |
where the electric constant is given by
| (11) |
Here, e, h, and c 0 are defining constants in the SI and, hence, have no uncertainty. In contrast, the unitless fine structure constant, α has to be measured and, thus, carries a (negligible) uncertainty. The finite uncertainty in ϵ0 is collateral damage that was incurred with the introduction of the present SI last year. The other traceability chain starts with the ac quantum Hall effect, see below, where the capacitance is given by
| (12) |
Since the fine structure constant is a dimensionless number, no matter which of the two traceability chains are used the capacitance gradient is given by
| (13) |
where β2 is a known numerical factor. Combining this with the Josephson voltage measurements in the force mode,
| (14) |
yields a force given by
| (15) |
With
| (16) |
Again, the force is realized as the product of two frequencies and the Planck constant divided by the speed of light. Note, this assertion also holds for the Kibble balance, since the velocity of the coil can be seen as a tiny fraction of the speed of light.
While the final force equations are identical for the Kibble balance and the electrostatic balance, the differences occur in the steps needed to reach this result. The main advantage of the electrostatic balance over the Kibble balance is that calibration mode is carried out in a static fashion, whereas in the Kibble balance, the velocity mode is a dynamic measurement. For the Kibble balance, the induced voltage is measured simultaneously with the coil’s velocity while the coil is moving. This requires synchronization between the voltage measurement and the velocity measurement (usually an interferometer). For a highly precise measurement the synchronization is not trivial. In the electrostatic case, the movable capacitor plate needs to be servoed to different positions where the capacitance must be measured in order to obtain the capacitance gradient. Each of the measurements occurs statically, and no synchronization is required.
An advantage of the magnetic actuator in the Kibble balance is that it can be used to make forces in both directions. The force is proportional to the current and by reversing the direction of the current, the direction of the force can be reversed. This is not the case for the electrostatic capacitor, where the force is proportional to the square of the potential difference. Hence, if one capacitor plate is grounded, the force will be the same, whether there is a positive or negative voltage of the same magnitude applied to the other plate. The force is always in the direction that maximizes the capacitance. Lastly, the Kibble balance is ideally suited for larger forces (millinewton to newton), whereas the electrostatic balance is ideally suited for smaller forces (mirconewton and below). This can be easily seen, by the fact that geometric factor in the Kibble balance ranges from about 1 T m to 1000 T m, while is about 10−9 F/m. Hence, 1 mA in a coil of a Kibble balance produces a force between 1 mN and 1 N. A potential difference of 100 V in the electrostatic balance, however, only produces a force of 5 μN.
What are our expectations for 2020 regarding these technologies? Fig. 5 shows a comparison of different methods to measure mass. The data points represented by the red circles are taken from the entries that the NIST has at the calibration measurement capability database maintained at the International Bureau of Weights and Measures (BIPM). In blue and cyan are shown the uncertainties that were achieved with two Kibble balances named NIST-4 and KIBB-g1. The former is a Kibble balance that is optimized to measure 1 kg mass pieces and was formerly used to help established the now fixed value of the Planck constant. The latter is a table top Kibble balance that can be used to weigh 1 g masses. The intention for this balance is to bring Kibble balance technology to the factory floor. The uncertainties shown at the smaller mass range are obtained with the electrostatic force balance. These uncertainties are smaller than the uncertainties that are obtained with the traditional subdivision method.
Fig. 5.

Relative uncertainty of mass measurements from 50 μg to 5 kg. The red filled points are from the calibration measurement capability (CMC) of NIST. These points are obtained by a work-down and work-up down from the mass assigned to a prototype. NIST-4 and KIBB-g1 are two Kibble balances, the former working with 1 kg standards, the latter with 1 g standards. The green circles represent relative uncertainties that were obtained with the NIST electrostatic force balance (EFB).
The challenge for metrology in 2020 is twofold: First, to develop primary realization of the unit of mass in the range from 10 mg to 100 g. In this range, the subdivision of mass standards still outperforms the primary realization methods. Second, to achieve larger penetration of the existing technology. At NIST, efforts are under way to build a Kibble balance for 100 g masses with a stated relative uncertainty goal of a few parts in 108. Such a Kibble balance should be lower cost than a 1 kg balance and could be a good alternative for smaller national metrology institutes to realize the unit of mass. A larger penetration includes not only Kibble balances on the factory floor but also the application of these traceable measurement devices for other applications. One area that researchers at NIST are actively engaged in is measuring laser power with an electrostatic balance. There, the momentum transfer of light in reflection will cause a force on a mirrored surface that is measured with an electrostatic balance.
The Quantum Hall Effect for Resistance and Impedance Measurements
The quantum Hall effect was discovered by Klaus von Klitzing in 1980 [13]. Klitzing carried out measurements of electronic transport in silicon field effect transistors at low temperatures when he discovered the quantization of the Hall resistance, the quotient of transversal voltage to longitudinal current in the presence of a magnetic field. This resistance is quantized at a submultiple of the von-Klitzing constant which has a convenient exact value, which is approximately 25 813 Ω. The value is convenient in the sense that it is close to the geometric mean of 10 μΩ and 1 TΩ, a range that encompasses most electrical resistors used in technology. In the SI, the Planck constant and the elementary charge are both fixed, and hence, the von-Klitzing constant can be calculated to arbitrary precision.
For the quantum Hall effect to occur, three conditions must be met: the system must feature a two-dimensional electron gas; must be sufficiently cold; and must be immersed in a strong magnetic field that is perpendicular to the electron gas. While the discovery of the quantum Hall effect was made using silicon field-effect transistors, where a potential on the gate forced the electrons in a narrow 2d channel, most metrological applications used Gallium-Arsenide/Gallium-Aluminum-Arsenide heterostructures. Here, the electrical band structure is engineered such that the electrons are confined at a 10 nm thin interface layer between the two materials.
The research activity in the metrological application of the quantum Hall effect received a large impetus in 2004 with the discovery of graphene [17]. Graphene is a naturally 2D material and shows a much sparser set of submultiples of RK, which helps the quantized resistance to be maintained at higher temperatures. In recent years, the research in graphene devices for resistance realization has made significant strides. Initially, the devices were made from exfoliated graphene. This tedious process involved carefully isolating a single layer from natural crystals of graphite and allowed only for small devices capable of handling tiny currents. These days, epitaxial graphene layers grown on Silicon-Carbide substrates are widely used to fabricate devices.
The graphene-based quantum Hall devices operate at lower magnetic fields, higher currents, and larger temperatures than the GaAs devices. Hence, the graphene devices are more practical and less costly to operate than the early conventional devices. For example, a graphene device can operate at a temperature of 4 K, and a magnetic flux density of 5 T, while a conventional GaAs might require 1.2 K and 9 T. While the differences in the respective operating parameters are small, the technical benefits are enormous: the graphene device can be operated in a closed-cycle cryostat, and this overall decrease in complexity and cost enables primary laboratories to acquire and operate their own quantum Hall standard. In fact, at NIST, a table-top graphene quantum Hall device has been used as part of the calibration services in resistance metrology since 2017.
There are two exciting developments in this research field that we can look forward to in 2020: pn-junctions and topological insulators [18]. While the order of magnitude of RK/2 is practical, the numerical value 12.906 kΩ, is far away from the decadal sequence of standard resistors. An interesting solution to this problem is an array device that combines parallel and/or serial connection of quantum Hall devices. With gated graphene devices, researchers can control the density and even the polarity of charge carriers. For example, by applying an electric potential to gates electrically insulated from graphene, charge carrier density in the graphene can be adjusted (Fig. 6). With large enough electric potential difference on gates in different regions of the graphene, pn-junctions are created. Such junctions allow either multiples or fractions of RK. Hence, by changing the voltages on the various top gates the total resistance of the device can be programmed. Clearly, a programmable quantum Hall effect will have a huge benefit for the realization of the ohm.
Fig. 6.
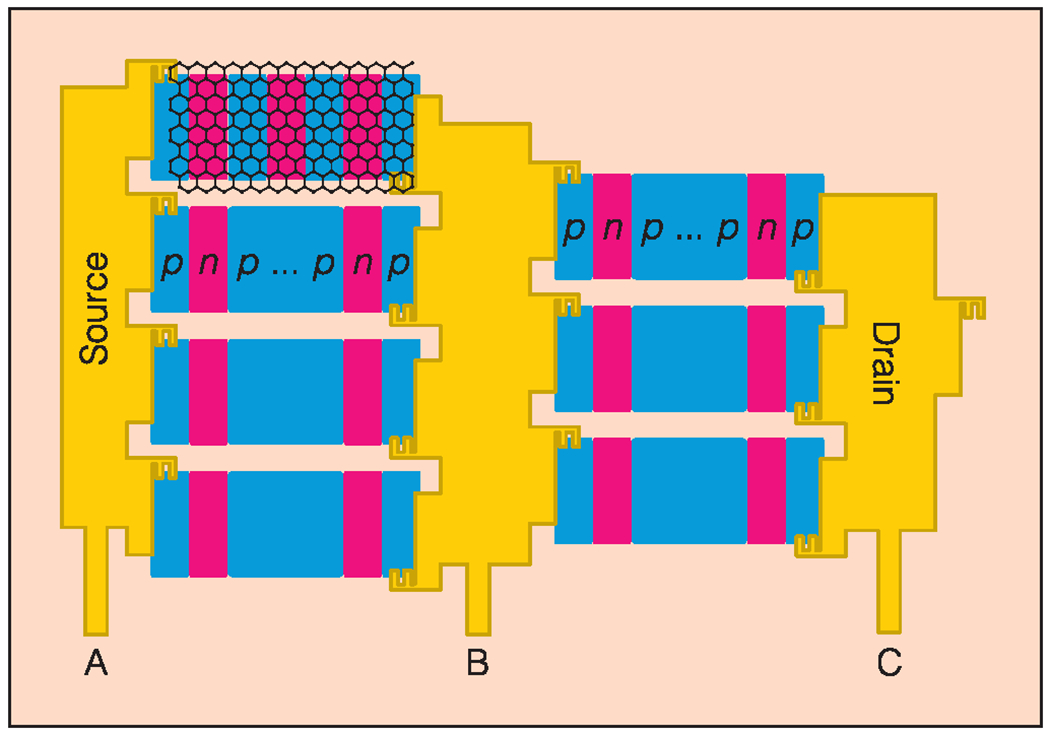
An example of a complex pn-junction graphene device the potential of the top gates can be changed to externally program various values of resistance (image courtesy of Albert Rigosi, NIST).
Broadly speaking, the quantum Hall effect falls in the category of topological quantum effects. In another class of materials, called topological insulators, electrical conduction occurs strictly along the surface and not in the bulk of the material. In the quantum Hall devices, the current travels along the edge of the device, in a so-called edge state, because the strong magnetic field restricts where current flow can occur. Interestingly, some new composite materials such as Cr-doped (Bi,Sb)2Te3 are topological insulators and can maintain similar edge effects without external magnetic fields. Several reports on observing the quantum Hall effect in such materials have been published in the literature. Currently, the required temperatures to achieve the quantum anomalous Hall effect in topological insulators are very low, tens of mK [9]. A focus of research is to find material systems that are topological insulators at higher temperature without an external magnetic field, which would substantially simplify the realization and dissemination chain of the unit of resistance.
So far, we discussed the application of the quantum Hall effect in direct current applications. What about applications in alternating current circuits? The dc unit of resistance can be transferred to ac by using calculable resistors [20]. These devices can be calibrated at dc values, and the calibration value can be extended to low frequencies because the frequency dependence of the resistor can be calculated from first principle. Once an ac value of a resistance is known, it can be transferred to capacitors and inductors using quadrature bridges. A second way to realize the farad is via the calculable capacitor, also known as the Thompson-Lampard capacitor [21]. In this capacitor the capacitance per unit length is given by
| (17) |
where ϵ0 is the electric constant. The Thompson-Lampard capacitor is an electro-mechanical device that is similarly complex as the Kibble balance. In theory, both the Kibble balance and the Thompson-Lampard capacitor seem simple, but most of the complexity of each experiment lies in managing the small imperfections that the real apparatus has in contrast to the idealized geometry on paper. Hence, using the quantum Hall resistance at ac as an impedance standard is an appealing idea.
The most significant difference between ac and dc metrology is the fact in ac currents can flow across insulating gaps via capacitive or inductive coupling. These couplings are especially troubling if the defining device is in cryostat which naturally requires long connections, prone to a lot of coupling, relative to the room-temperature measurement devices. In 2007, researchers at the Physikalisch-Technische Bundesanstalt (PTB), managed to solve these problems with a shielded GaAs device [12]. The quantum Hall effect is since a viable option to realize the farad. However, not many National Metrology Institutes (NMI) have been using the ac quantum Hall effect as the basis of their impedance measurements. The reason is that GaAs quantum Hall chips that are useable for ac are difficult to obtain. Graphene also, provides an optimal solution for ac measurements. Graphene chips are larger, thus having smaller edge-to-edge capacitance and they can be fabricated in house at several NMIs. As is the case for the dc quantum Hall measurement, the operating parameters are more forgiving. The devices can be operated at higher currents, higher temperature, and smaller magnetic field. In 2020, we hope to see some progress in the ac quantum Hall field. Hopefully more and more NMIs will embark on a journey to use the Quantum Hall device to realize impedance standards. Fig. 7 shows a possible geometry for an ac quantum Hall device made from epitaxial graphene.
Fig. 7.
An example of an ac quantum Hall device made from epitaxial graphene (image courtesy of Albert Rigosi, NIST).
Johnson Noise Thermometer (JNT)
Johnson Noise was first described in 1927 and largely explained in 1928 [16]. It concerns voltage fluctuations V that occur across a resistance R that is at a temperature T. In its simplest form, the mean square fluctuations within a frequency band Δf:
| (18) |
where kB is the Boltzmann constant, introduced above. Eq. (18) is known as the Nyquist equation, and gives the mean square voltage as a function of temperature, resistance, and bandwidth. We assume that R has no frequency dependence. The Nyquist equation then describes the power spectral density (PSD), of the voltage fluctuations across the resistor:
| (19) |
A resistor can therefore serve as a convenient source of PSD that is independent of frequency, i.e., “white noise.” Alternatively, if the PSD is known, the absolute temperature T can be determined. In this case, the device described by (19) becomes a JNT. There are unique advantages to measuring temperature this way. However, the great disadvantages of an absolute precision measurement are the need to measure SR against a known PSD, the elimination of extraneous noise sources—e.g., from amplifiers, and the need to integrate the signal over long times to reduce statistical uncertainty.
Nevertheless, the authors of [23] conclude that JNT “has appeal for metrological applications at temperatures ranging from below 1 mK up to 800 K. With the rapid advances in digital technologies, there are also expectations that noise thermometry will become a practical option for some industrial applications, perhaps reaching temperatures above 2000 K.” In [23], J. F. Qu et al. reviews the possibilities, giving ample references.
Redefining the kelvin
Because of the inherent difficulties in using a JNT, it was a remarkable achievement that such an experiment contributed to the redefinition of the kelvin. For this, it was necessary to measure the PSD of a resistance held at precisely 273.16 K, the triple point temperature of water (TTPW). To be competitive with other technologies being used to measure kB, the relative uncertainty needed to be about 3×10−6, corresponding to about 800 μK uncertainty at 273 K. What follows is a brief description of this remarkable measurement.
Resistor
The resistor is made from metal foils bonded to an alumina substrate [24], a design that minimizes the dependence of R on frequency. The nominal value is 100 Ω and is chosen to optimize the bandwidth over which SR is measured. The resistance value R is measured in terms of the quantum-Hall resistance where h is the Planck constant and e is the elementary charge. If we define the ratio X = R/RK, then (10) becomes:
| (20) |
PSD standard
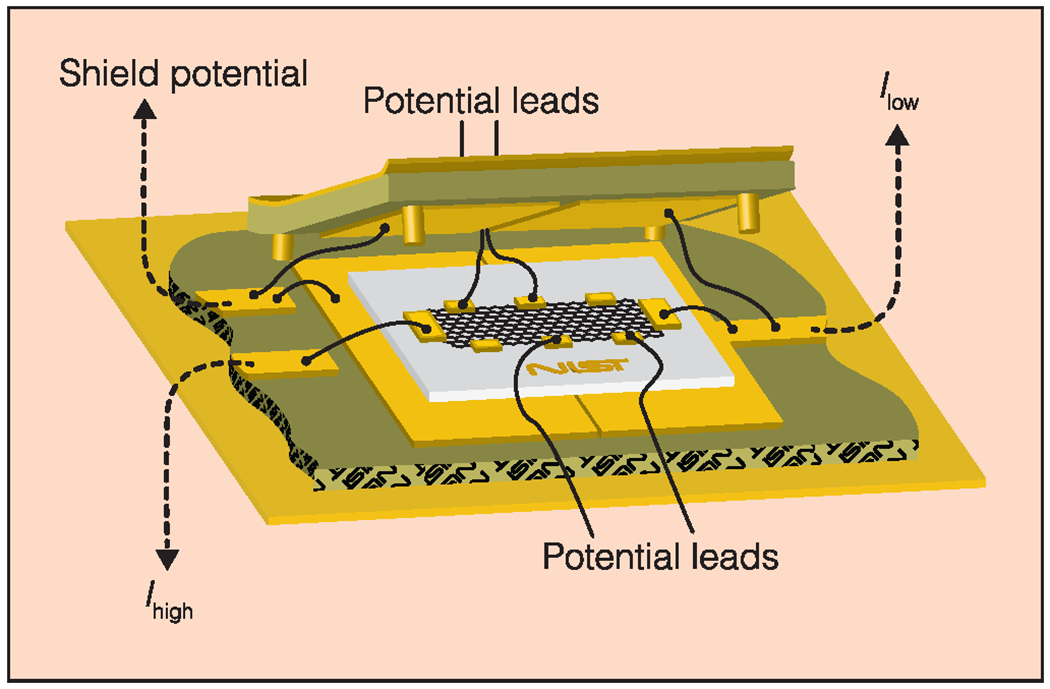
Perhaps the most important innovation for these JNT measurements was the synthesis of a quantum PSD standard, SQ, which depends on the Josephson effect [24]–[26]. Josephson “junctions” are maintained at 4 K. Fig. 8 shows a photograph of a chip with ten Josephson junctions. The technique results in a pseudo-random noise source with megahertz bandwidth from which the temperature of the Johnson noise can be determined. In [25], S. P. Benz et al. provide a good explanation of the pseudo-random noise generator and place it in the context of earlier work on a Josephson arbitrary-waveform synthesizer. The quantum noise source can be described by the following equation:
| (21) |
Fig. 8.

A Niobium based Johnson Noise Thermometry (JNT) chip. The chip generates a voltage with a power spectral density similar to a 100 Ω resistor at the temperature of the triple point of water. The US penny, which has a diameter of about 19 mm, is for scale (photo courtesy of Dan Schmidt, NIST).
where NJ is the number of Josephson junctions in the circuit, fs is a clock frequency, and a is a product of software parameters [25]. is the Josephson constant, whose unit is hertz per volt.
The electronics and software then provide the measurement ratio of the averaged PSDs:
| (22) |
showing how the measured PSD ratio and known T were used to measure kB/h with respect to TTPW before the revision of the SI on May 20, 2019. On that date, the constants kB and h were defined to have exact numerical values, and therefore (13) now shows how an arbitrary temperature T can be measured in terms those constants [26]. The ratio in square brackets is composed of dimensionless numbers. For those interested in the history of science, we note that both kB and h were invented by Max Planck to describe the black-body curve of electromagnetic radiation at a given T. We also point out that the measurement of kB/h reported in [24] was made using 1990 “conventional units” of voltage and resistance rather than their corresponding SI units. Since May 20, 2019, use of the conventional units has ended. However, it had been pointed out 20 years earlier that the measurement of kB/h using JNT could be made using conventional electrical units rather than SI units as defined prior to May 2019. This was essentially a measurement of kB because the relative uncertainty of h was already known to negligible uncertainty from other types of experiments.
Cross Correlation
Every available technique must be used to eliminate extraneous noise sources from the PDF signals. Cross correlation is used in JNT to minimize the effects of non-ideal low-noise preamplifiers. The signal to be measured is sent through two identical preamplifiers prior to further amplification and low-pass filtering. Each preamplifier adds a noise signal to the output, but the extraneous noise sources from the preamplifiers are uncorrelated. At a later stage, the common signal (the input signal to the preamplifiers) can be extracted by cross-correlation [24].
Integration Time
Finally, the uncertainty in the previous measurements of kB/h, or of present measurements of T using JNT, is limited by the integration time, which should be as long as possible to reduce statistical uncertainty [27]. Recent measurements of kB/h by JNT, as discussed in [28], had integration times of 33 days and 100 days. The uncertainty budgets of both these measurements are given in [29], where one can see that, despite several clever improvements to the apparatus, the improvement in the total uncertainty is due almost entirely to the integration time having been increased by a factor of 3, leading to a decrease in the variance of the statistical uncertainty by the same factor. Why go through all this trouble to decrease the relative uncertainty from 3.9×10−6 to 2.7×10−6 [28]? Because, before it would recommend redefinition of the kelvin, the Consultative Committee for Thermometry (CCT) set a goal of determining kB from at least two different types of experiments, with the relative uncertainty of at least one of these experiments being less than 3×10−6 [29]. As it turned out, the JNT value also agreed within uncertainties with the values determined by other technologies which met this goal [27].
Perspectives in JNT
An integration time of 100 days is a tribute to the stability of the equipment involved and the tenacity of the researchers, but this type of heroic effort is unlikely to be repeated, now that the kelvin has been redefined by fixing the numerical value of kB [28]. Nevertheless, JNT will be a hot topic in the future. Several interesting possibilities are discussed in [23]. JNT is a universal concept that applies in a broader temperature range than any other type of thermometer. The resistor used to sense the temperature can be calibrated in situ by a four-terminal measurement; removal of the resistor for recalibration is unnecessary. The sensing resistor can therefore be exposed to unusually harsh industrial environments. At cryogenic temperatures, superconducting quantum-interference devices (SQUIDs) can be used to amplify the signals.
The CCT has published on-line documents describing methods to realize the definition of the kelvin. These are updated periodically. The principal document [28] discusses JNT and cites an annexed document on low-temperature JNT and the challenges that must be met in the low-temperature regime [30].
Conclusion
With the revision in May 2019, the SI stepped into the 21st century. Mercury columns and the international prototype of the kilogram as symbols of 18th century metrology will soon be replaced by optical cavities and Kibble balances. The SI now is a good fit to quantum physics and is already inspiring new technologies that shorten calibration chains, make use of accurate theoretical calculations of useful gas properties, and a host of other possibilities. These possibilities may have been available before 2019, but they are facilitated and encouraged by the present SI.
We have chosen a diverse set of metrological research to illustrate these points: mass determinations, electrical measurements, flow metrology, pressure metrology, and thermometry. We could have mentioned many others. In addition, basic metrology is continuously evolving: Basic metrology in 2030 might include a redefinition of the second, based on the frequency of an optical clock.
Biographies
Richard Davis (richard.davis@ieee.org) joined the International Bureau of Weights and Measures (BIPM) in 1990 following eighteen years at NIST in Gaithersburg, Maryland. He began at NIST as a post-doctoral fellow in the electrical standards group. Later, he had technical responsibility for dissemination of the unit of mass from the United States’ national prototype of the kilogram. At the BIPM, he worked in the mass department until he retired in 2010 as department head. He continued as a consultant to the BIPM Director until June 2019. Richard is a Life Member of IEEE and a Fellow of the American Physical Society.
Stephan Schlamminger (stephan.schlamminger@nist.gov) is a Physicist at the National Institute of Standards and Technology in Gaithersburg, Maryland. He received a diploma in physics from the University of Regensburg, Germany and the Ph.D. degree in experimental physics from the University of Zurich, Switzerland. His research interests include precise measurements using mechanical and electrical apparatus.
Contributor Information
Richard Davis, International Bureau of Weights and Measures (BIPM) in 1990 following eighteen years at NIST in Gaithersburg, Maryland.
Stephan Schlamminger, Physicist at the National Institute of Standards and Technology in Gaithersburg, Maryland.
References
- [1].Davis R, “An introduction to the revised international system of units (SI),” IEEE Instrum. Meas. Mag, vol. 22, 2019. [Google Scholar]
- [2].SP 250-63 Gas Flow meter Calibrations with the 34 L and 677 L PVTt Standards, NIST. [Google Scholar]
- [3].Pope J, Gillis K, Moldover M, Mehl J, and Harman E, “Characterizing gas-collection volumes with acoustic and microwave resonances,” in Proc. 10th Int. Symp. Fluid Flow Measurements, Mar. 2018. [Google Scholar]
- [4].Pope J, Gillis K, Moldover M, Mehl J, and Harman E, “Progress towards a gas-flow standard using microwave and acoustic resonances,” Flow Meas. Instrum, vol. 69, 101592, Oct. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Tilford CR, “Three and a half centuries later–the modern art of liquid-column manometry,” Metrologia, vol. 30, pp. 545–552, 1994. [Google Scholar]
- [6].Egan P, Stone J, Ricker J, and Hendricks J, “Comparison measurements of low-pressure between a laser refractometer and ultrasonic manometer,” Rev. Sci. Instrum, vol. 87, 053113, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Lee JL, “No longer under pressure: NIST dismantles giant mercury manometer,” Jun. 2019. [Online]. Available: https://www.nist.gov/news-events/news/2019/06/no-longer-under-pressure-nist-dismantles-giant-mercury-manometer
- [8].Jousten K, Hendricks JH, Barker D, Douglas K et al. “Perspectives for a new realization of the pascal by optical methods,” Metrologia, vol. 54, no. 6, 2017. [Google Scholar]
- [9].Egan P, Stone J, Scherschligt J, and Harvey A, “Measured relationship between thermodynamic pressure and refractivity for six candidate gases in laser barometry,” J. Vacuum Science & Technol. A, vol. 37, 031603, 2019. [PMC free article] [PubMed] [Google Scholar]
- [10].Kelley S, Gauging pressure with light: a demonstration of the fixed length optical cavity (FLOC), video, Feb. 2019. [Online]. Available: https://www.nist.gov/video/gauging-pressure-light-demonstration-fixed-length-optical-cavity-floc.
- [11].Hendricks J, “Quantum for pressure,” Measure for Measure, Nature Physics, vol. 14, Jan. 2018. [Online]. Available: https://www.nature.com/articles/nphys4338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Kibble BP, “A measurement of the gyromagnetic ratio of the proton by the strong field method,” in Atomic Masses and Fundamental Constants, Sanders JH and Wapstra AH, Eds. New York, NY, USA: Plenum, 1976. [Google Scholar]
- [13].Klitzing K. v., Dorda G, and Pepper M, “New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance,” Phys. Rev. Lett, vol. 45, p. 494, 1980. [Google Scholar]
- [14].Josephson BJ, “Possible new effects in superconducting tunneling,” Phys. Lett, vol. 1, p. 251, 1962. [Google Scholar]
- [15].Shaw GA “Current state of the art in small mass and force metrology within the International System of Units,” Meas. Sci. Technol, vol. 29, 072001, 2018. [Google Scholar]
- [16].Shaw GA, Stirling J, Kramar J, Moses A et al. , “Milligram mass metrology using an electrostatic force balance,” Metrologia, vol. 53, no. 5, Sep. 2016. [Google Scholar]
- [17].Novoselov KS, Geim A, Morozov S, Jiang D et al. “Electric field effect in atomically thin carbon films,” Science, vol. 306, pp. 666–669, Oct. 2004. [DOI] [PubMed] [Google Scholar]
- [18].Rigosi AF and Elmquist RE “The quantum Hall effect in the era of the new SI,” Semicon. Sci. Technol vol. 34, no. 093004, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Fox EJ, Rosen I, Yang Y, Jones G et al. , “Part-per-million quantization and current-induced breakdown of the quantum anomalous Hall effect,” Phys. Rev., B, vol. 98, 075145, Aug. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Jeffrey A-M, Elmquist R, Lee L, Shields J, and Dziuba R et al. , “NIST comparison of quantized Hall resistance and the realization of the SI Ohm through the calculable capacitor,” IEEE Trans. Instrum, vol. 46, no. 2, pp. 262–268, Apr. 1997. [Google Scholar]
- [21].Thompson AM and Lampard DG, “A new theorem in electrostatics and its application to calculable standards of capacitance,” Nature, vol. 177, p. 888, 1956. [Google Scholar]
- [22].Schurr J, Ahlers F, Hein G, and Pierz K, “The ac quantum Hall effect as a primary standard of impedance,” Metrologia, vol. 44, no. 1, 2007. [Google Scholar]
- [23].Qu JF, Benz S, Rogalla H, Tew W et al. , “Johnson noise thermometry,” Meas. Sci. Technol, vol. 30, no. 11, Sep. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Qu J, Benz S, Pollarolo A, Rogalla H, et al. , Improved electronic measurement of the Boltzmann constant by Johnson noise thermometry, Metrologia, vol. 52, pp. S242–S256, Aug. 2015. [Google Scholar]
- [25].Benz SP, Martinis JM, Dresselhaus PD, and Nam SW, “An AC Josephson source for Johnson noise thermometry,” IEEE Trans. Instrum. Meas, vol. 52, pp. 545–549, Apr. 2003. [Google Scholar]
- [26].Moldover MR, Tew WL, and Yoon HW, “Advances in thermometry,” Nature Physics, vol. 12, pp. 7–11, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Mohr PJ, Newell D, Taylor B, and Tiesinga E, “Data and analysis for the CODATA 2017 special fundamental constants adjustment,” Metrologia, vol. 55, pp. 125–146, January. 2018. [Google Scholar]
- [28].Qu J, Benz S, Coakley K, Rogalla H et al. , “An improved electronic determination of the Boltzmann constant by Johnson noise thermometry,” Metrologia, vol. 54, no. 4, pp. 549–558, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].“Mise en pratique for the definition of the kelvin in the SI,” Consultative Committee for Thermometry, CIPM, SI Brochure, 9th ed., May 2019. [Online]. Available: https://www.bipm.org/utils/en/pdf/si-mep/SI-App2-kelvin.pdf. [Google Scholar]
- [30].Engert J and Kirste A, “MeP-K Low-temperature Johnson noise thermometry,” 2019, Open Access. [Online]. Available: https://www.bipm.org/utils/en/pdf/si-mep/MeP-K-2019-LT_Johnson_Noise_Thermometry.pdf. [Google Scholar]


