Machine Learning to Predict Transplant Outcomes: Helpful or Hype?

Abstract

An increasing number of studies claim machine learning (ML) predicts transplant outcomes more accurately. However, these claims were possibly confounded by other factors, namely supplying new variables to ML models. To better understand the prospects of ML in transplantation, we compared ML to conventional regression in a “common” analytic task: predicting kidney transplant outcomes using national registry data. We studied 133,431 adult deceased-donor kidney transplant recipients between 2005–2017. Transplant centers were randomly divided into 70% training set (190 centers/97787 recipients) and 30% validation set (82 centers/35644 recipients). Using the training set, we performed regression and ML procedures (gradient boosting [GB] and random forests [RF]) to predict delayed graft function, one-year acute rejection, death-censored graft failure, all-cause graft failure, and death. Their performances were compared on the validation set using C-statistics. In predicting rejection, regression (C=_0.6010.611_0.621) actually outperformed GB (C=_0.5810.591_0.601) and RF (C=_0.5690.579_0.589). For all other outcomes, the C-statistics were nearly identical across methods (delayed graft function, 0.717–0.723; death-censored graft failure, 0.637–0.642; all-cause graft failure, 0.633–0.635; and death, 0.705–0.708). Given its shortcomings in model interpretability and hypothesis testing, ML is advantageous only when it clearly outperforms conventional regression; in the case of transplant outcomes prediction, ML seems more hype than helpful.

INTRODUCTION

Machine learning (ML) algorithms have emerged as alternatives to conventional regression modeling, largely due to their ability to analyze non-tabular (e.g., image or natural language) and high-dimensional (typically >10,000 variables) data (Table 1) [1]. It seems natural that transplantation researchers are drawn to these methods, especially considering the frequent use of large registry data analyses in transplantation [2]. Indeed, this is a growing area of investigation [3–16], with several recent studies that reported superior predictive performance of ML in predicting delayed graft function, graft survival, and mortality after kidney or liver transplantation [3,4,6,16].

Table 1.

A brief comparison of regression and machine learning

	Regression	Machine learning
Mathematical assumptions	Several	Usually fewer
Analyzing high-dimensional data (e.g., >10,000 variables)	Possible, but labor intensive	Capable
Analyzing non-tabular data (e.g., images, clinical notes, etc)	Limited	Capable, but often requires extensive labor/resources
Model interpretability	Fully transparent and human-readable	Limited or absent
Ability to incorporate prior clinical/biological knowledge	Capable (e.g., assisted variable selection)	Limited or absent
Hypothesis testing	Built-in	Limited or absent

However, the reported improvements in predictive performance may not be fully attributable to ML, because those studies often supplied more clinical information to the ML models than to the conventional regression-based models. In other words, had the ML models been developed on the same set of variables as the regression-based models, we might have observed minimal or no gain in predictive performance. From a theoretical standpoint, the predictive performance of a regression model should at least match that of a ML algorithm under ideal conditions [17], and even violations of these conditions can mostly be addressed using statistical techniques. As such, a properly developed regression model is expected to perform similarly to ML.

Furthermore, a key limitation of most ML algorithms is that they deliver “black-box” predictions, whereas regression provides interpretable models, allows face validity checking, and enables biological hypothesis testing. These black-box predictions can sometimes be driven by senseless associations. For example, it was discovered that a ML algorithm, trained to determine malignancy from images of skin lesions, diagnosed lesions as malignant when a ruler was pictured near the lesion, because, in the training data, a ruler was drawn when the pathologist suspected a malignancy; identifying this harmful quirk was difficult because the ML was a black-box that did not show how it was evaluating the images [18,19]. Since ML is entirely data-driven and does not reveal its mechanism so that face validity can be checked, these approaches are not risk-free.

To better understand the possible role of ML in transplantation, we aimed to evaluate the performance of ML algorithms in a “common” study setup relevant to a wide gamut of transplantation research. Thus, we conducted a head-to-head comparison of ML algorithms versus regression in predicting various kidney transplant (KT) outcomes using the same populations and the same set of variables abstracted from the U.S. national registry data.

MATERIALS AND METHODS

Data source

This study used data from the Scientific Registry of Transplant Recipients (SRTR). The SRTR data system includes data on all donors, waitlisted candidates, and transplant recipients in the US, submitted by the members of the Organ Procurement and Transplantation Network (OPTN). The Health Resources and Services Administration (HRSA), US Department of Health and Human Services, provides oversight to the activities of the OPTN and SRTR contractors. A detailed description of the data has been provided elsewhere [2]. This study used de-identified registry data and was exempted by the Johns Hopkins Medicine Institutional Review Boards (NA_00042871).

Study population

Our study included 133,431 adult (18 or older) deceased-donor KT recipients at 272 KT centers from January 1, 2005 to December 31, 2017. The dataset was randomly divided at center-level into a 70% training set (190 centers; 97,787 recipients) and a 30% validation set (82 centers; 35,644 recipients).

Outcomes

We studied five outcomes: delayed graft function (DGF), one-year acute rejection (AR), death-censored graft failure (DCGF), death, and all-cause graft failure (ACGF). DGF was defined as the need for dialysis within the first week after transplant. AR included all acute rejection episodes reported up to one-year follow up. Since the exact dates of the episodes are not available on OPTN/SRTR data, AR were treated as a binary outcome, as opposed to a time-to-event outcome. DCGF was defined as the time from KT to graft failure (re-initiation of dialysis or re-KT), censoring for death. ACGF was defined as the time from KT to graft failure or death. Graft failure and death were collected by OPTN from multiple sources, including follow-up reports from transplant centers, Centers for Medicare & Medicaid Services ESRD Death Notification Form (CMS 2746), and the Social Security Death Master File. All recipients were censored at the end of study on December 31, 2017.

Model development

We developed prediction models on the 70% training set using generalized linear regression and two ML techniques: gradient boosting (GB) and random forests (RF).

For regression, we conducted logistic regressions on DGF and AR, and Cox regressions on DCGF, death, and ACGF. Missing values of the covariables were handled using multiple imputation with 10 iterations. To address any non-linear associations of continuous variables and clinical outcomes, we included linear spline terms into the models. Knots were determined based on previous literature and exploratory data analyses, which involved comparing the fit of univariable ACGF models using different sets of knots. The regression models were finalized using these knots (Supplementary Table 1).

GB was performed using the R package ‘XGBoost’ [20]. We used the logistic objective function for DGF and AR, and Cox proportional hazard objective function for DCGF, death, and ACGF. Missing values of the covariables were imputed during training in a way that is analogous to multiple imputation [20]. The tuning parameters were chosen via cross-validation on the 70% training dataset.

RF was performed using the R package ‘rfsrc’ [21]. We used the Gini splitting rule for DGF and AR, and the log-rank splitting rule for DCGF, death, and ACGF [21]. Similar to GB, missing values of the covariables were imputed during training. The tuning parameters were chosen via cross-validation on the 70% training dataset.

All prediction models included the same set of covariables, including donor variables (age, race, sex, ABO blood type, height, weight, stroke as the cause of donor death, terminal serum creatinine, cytomegalovirus (CMV), hepatitis C, diabetes, hypertension, donation after and cardiac death), recipient variables (age, sex, race, primary cause of end-stage renal disease, ABO blood type, primary insurer, body mass index (BMI), human immunodeficiency virus (HIV), CMV, hepatitis B, hepatitis C, Epstein-Barr virus, previous transplant, preemptive transplant, time on dialysis, panel reactive antibody (PRA), diabetes, hypertension, previous malignancy, symptomatic peripheral vascular disease, total serum albumin, and education level), and transplant variables (HLA-A/B/DR mismatches and cold ischemic time).

Evaluation of predictive performance: C-statistic

We used the 30% validation set to evaluate the predictive performance of the models. Our primary measure of predictive performance was the C-statistic. The C-statistic is a measure of discrimination, i.e., whether the model correctly assigns higher predicted risk to those who actually develop the outcome versus those who do not. Specifically, the C-statistic was derived using the area under the receiver operating characteristic curve (AUROC) for binary outcomes (DGF and AR), and Harrell’s concordance for time-to-event outcomes (DCGF, death, and ACGF) [22]. In addition, we conducted a sensitivity analysis in which the C-statistics for the time-to-event outcomes were estimated again using a novel method proposed by Uno and colleagues [23]. Unlike the conventional method, Uno’s C-statistic is independent from the censoring distribution of the study population.

We first estimated the C-statistic over the entire validation set, and then in 16 subgroups stratified by quartiles of Kidney Donor Profile Index (KDPI) and Estimated Post-Transplant Survival (EPTS) to identify whether the predictive performance of the models vary by donor and recipient risk level [24]. In 3965 (3.0%) recipients, KDPI and EPTS values could not be calculated due to missing values. These recipients were excluded from the stratified analysis.

Evaluation of predictive performance: Brier score

Our secondary measure of predictive performance was the Brier score [25]. The Brier score is a measure of calibration, i.e., how close the predicted risk is to the actual risk. A lower Brier score indicates a smaller difference between the predicted and actual risk, hence superior calibration. It is important to assess both discrimination and calibration as models with superior discrimination may have inferior calibration, with over- or under-predicted risk [26]. For time-to-event outcomes (DCGF, death, and ACGF), we used the integrated Brier score, an extension of the Brier score for time-to-event outcomes [27]. In addition, we created calibration plots to visualize the calibration of the prediction methods across the spectrum of predicted risk. We stratified the validation set into 20 equally distanced bins by the predicted risk of the outcome, and estimated the observed risk within each bin. The observed risk was defined as the incidence ratio for binary outcomes and as the cumulative incidence at 5 years post-KT for time-to-event outcomes.

Statistical analysis

All analyses were performed using R version 3.5.0. We used subscripts to indicate 95% confidence intervals as per the Louis and Zeger style [28].

RESULTS

Study population

Overall, the training set and the validation set showed similar characteristics. Median recipient age was 54 years in both sets. Median donor age was 41 years in the training set and 39 in the validation set. The training set included 39.7% female recipients, 32.6% African American recipients, 39.8% female donors, and 14.1% African American donors. The validation set included 39.7% female recipients, 34.7% African American recipients, 39.6% female donors, and 14.3% African American donors (Table 2).

Table 2.

Population characteristics

Clinical factor	Training set (n=97,787)	Validation set (n=35,644)
Recipient factors
Age (y), median (IQR)	54 (44, 63)	54 (43, 63)
Female	39.7%	39.7%
Race
White	42.5%	42.1%
African American	32.6%	34.7%
Hispanic/Latino	16.2%	15.0%
Other/multi-racial	8.6%	8.3%
Preemptive transplant	9.9%	10.7%
Time on dialysis (y), median (IQR)	3.5 (1.6, 5.7)	3.6 (1.6, 5.9)
Cause of ESRD
Glomerulonephritis	21.9%	22.3%
Diabetes	26.9%	27.6%
Hypertension	23.6%	24.3%
Others	27.7%	25.8%
Panel reactive antibody
0–9	54.1%	50.7%
10–79	23.3%	26.4%
80–100	16.8%	17.7%
Missing	5.7%	5.2%
BMI (kg/m2), median (IQR)	27.6 (24.1, 31.7)	27.8 (24.2, 31.8)
Previous Transplants	14.7%	14.6%
Cold ischemic time (hr), median (IQR)	17.0 (11.7, 23.0)	16.4 (11.0, 22.4)
Donor factors
Age (y), median (IQR)	41 (25, 52)	39 (25, 51)
Female	39.8%	39.6%
Race
White	69.0%	68.1%
African American	14.1%	14.3%
Hispanic/Latino	13.6%	14.2%
Other/multi-racial	3.3%	3.4%
Terminal serum creatinine (mg/dl), median (IQR)	0.9 (0.7, 1.3)	0.9 (0.7, 1.3)
Donation after cardiac death	16.4%	14.1%

IQR, interquartile range; ESRD, end-stage renal disease; and BMI, body mass index.

In the training set, 27.4% of the recipients developed DGF and 11.1% developed AR. The 5-year cumulative incidences were 13.8% for DCGF, 15.4% for death, and 24.5% for ACGF. The median follow up were 4.8 years for death and 4.2 years for DCGF and ACGF.

Predictive performance: C-statistic

In our comparison of predictive performance in the validation set, ML algorithms did not show superior discrimination over regression in any of the five outcomes we studied (Figure 1). Of note, regression actually showed higher C-statistic (C=_0.6010.611_0.621) than both ML algorithms, GB (C=_0.5810.591_0.601) and RF (C=_0.5690.579_0.589), in predicting one-year AR. For all other outcomes, the three methods showed nearly identical performance. For DGF, the C-statistics were _0.7140.721_0.727 for regression, _0.7170.723_0.729 for GB, and _0.7110.717_0.723 for RF. For DCGF, the C-statistics were _0.6290.637_0.646 for regression, _0.6330.642_0.650 for GB, and _0.6290.638_0.646 for RF. For death, the C-statistics were _0.7010.708_0.715 for regression, _0.6980.705_0.712 for GB, and _0.6980.705_0.713 for RF. For ACGF, the C-statistics were _0.6280.634_0.640 for regression, _0.6290.635_0.641 for GB, and _0.6270.633_0.639 for RF. Across the 16 subgroups of the 30% validation set stratified by the quartiles of KDPI and EPTS, regression, GB, and RF showed very similar predictive performance in all five outcomes (Supplementary Figure 1).

Figure 1. Predictive performance of regression (Reg), gradient boosting (GB), and random forests (RF) in predicting kidney transplant outcomes, as measured in the C-statistic.

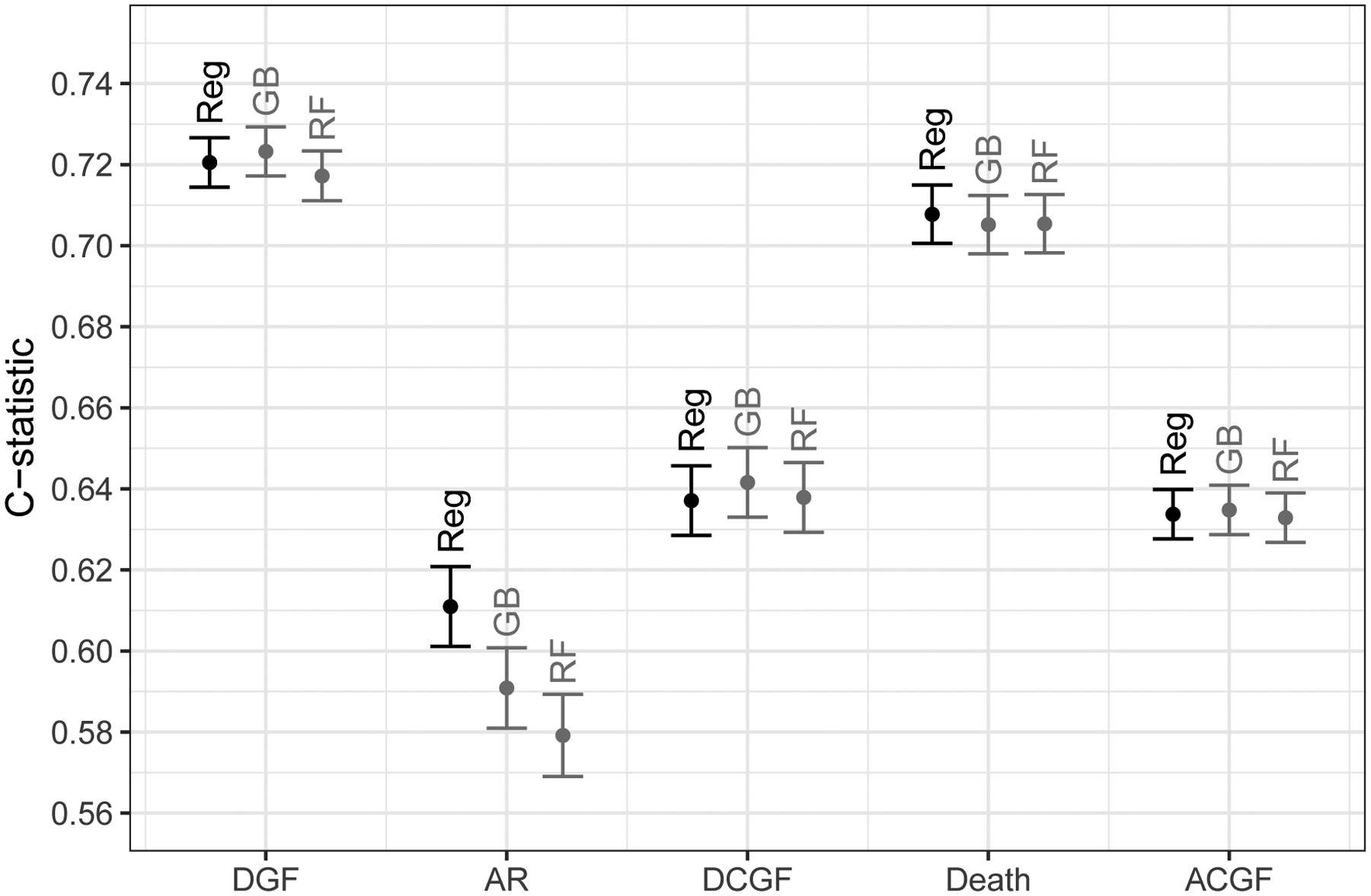
DGF, delayed graft function; AR, one-year acute rejection; DCGF, death-censored graft failure; and ACGF, all-cause graft failure. Regression represents logistic regressions for delayed graft function and acute rejection, and Cox regressions for death-censored graft failure, death, and all-cause graft failure. Y-axis indicates the area under the receiver operating characteristic curve (AUROC) for delayed graft function and acute rejection, and Harrell’s concordance statistic for death-censored graft failure, death, and all-cause graft failure.

We found similar trends in our sensitivity analysis where the C-statistics were estimated using Uno’s method for time-to-event outcomes. For DCGF, Uno’s C-statistics were 0.623 for regression, 0.624 for GB, and 0.611 for RF. For death, Uno’s C-statistics were 0.707 for regression, and 0.703 for both GB and RF. For ACGF, Uno’s C-statistics were 0.635 for both regression and GB, and 0.632 for RF.

Predictive performance: Brier score

All methods showed similar calibration in predicting binary outcomes (DGF and AR), whereas ML algorithms showed inferior calibration than regression in predicting time-to-event outcomes (DCGF, death, and ACGF). The Brier scores were very similar between the methods for DGF (regression, 0.161; GB, 0.160; and RF, 0.161) as well as for AR (regression, 0.089; GB, 0.090; and RF, 0.091). In contrast, regression showed lower Brier scores (i.e., smaller prediction errors) than ML algorithms for DCGF (regression, 0.179; GB, 0.187; RF, 0.185), death (regression, 0.183; GB, 0.206; and RF, 0.197), and ACGF (regression, 0.193; GB, 0.201; and RF, 0.208) (Table 3). In addition, our calibration plots suggested that all three prediction methods had comparable calibration across the spectrum of predicted risk (Figure 2).

Table 3.

Predictive performance of regression, gradient boosting, and random forests in predicting kidney transplant outcomes, as measured in the Brier score.

Outcome	Regression	Gradient boosting	Random forests
Delayed graft function	0.161	0.160	0.161
Acute rejection, one-year	0.089	0.090	0.091
Death-censored graft failure	0.179	0.187	0.185
Death	0.183	0.206	0.197
All-cause graft failure	0.193	0.201	0.208

Lower Brier score indicates superior calibration.

Figure 2.

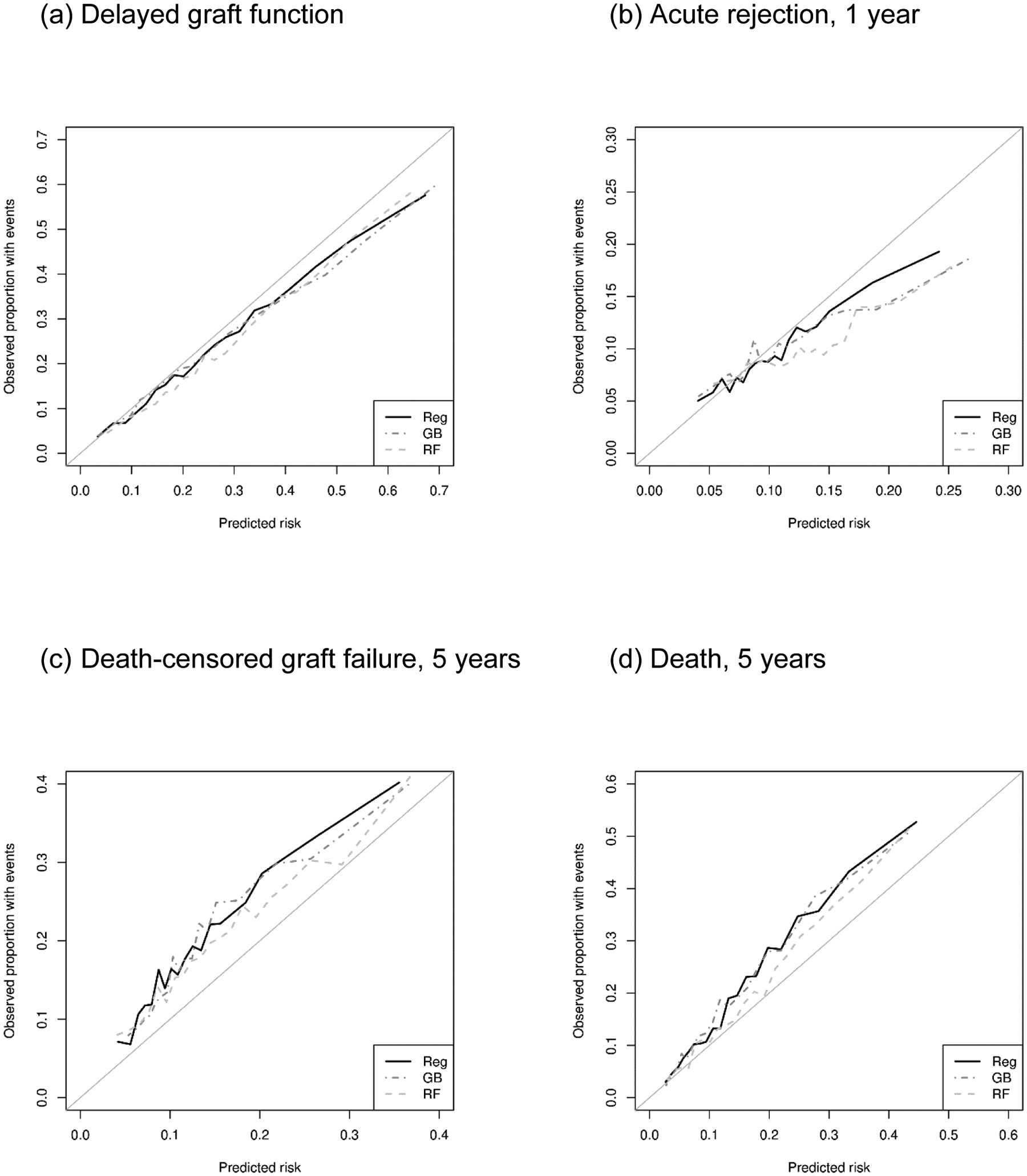
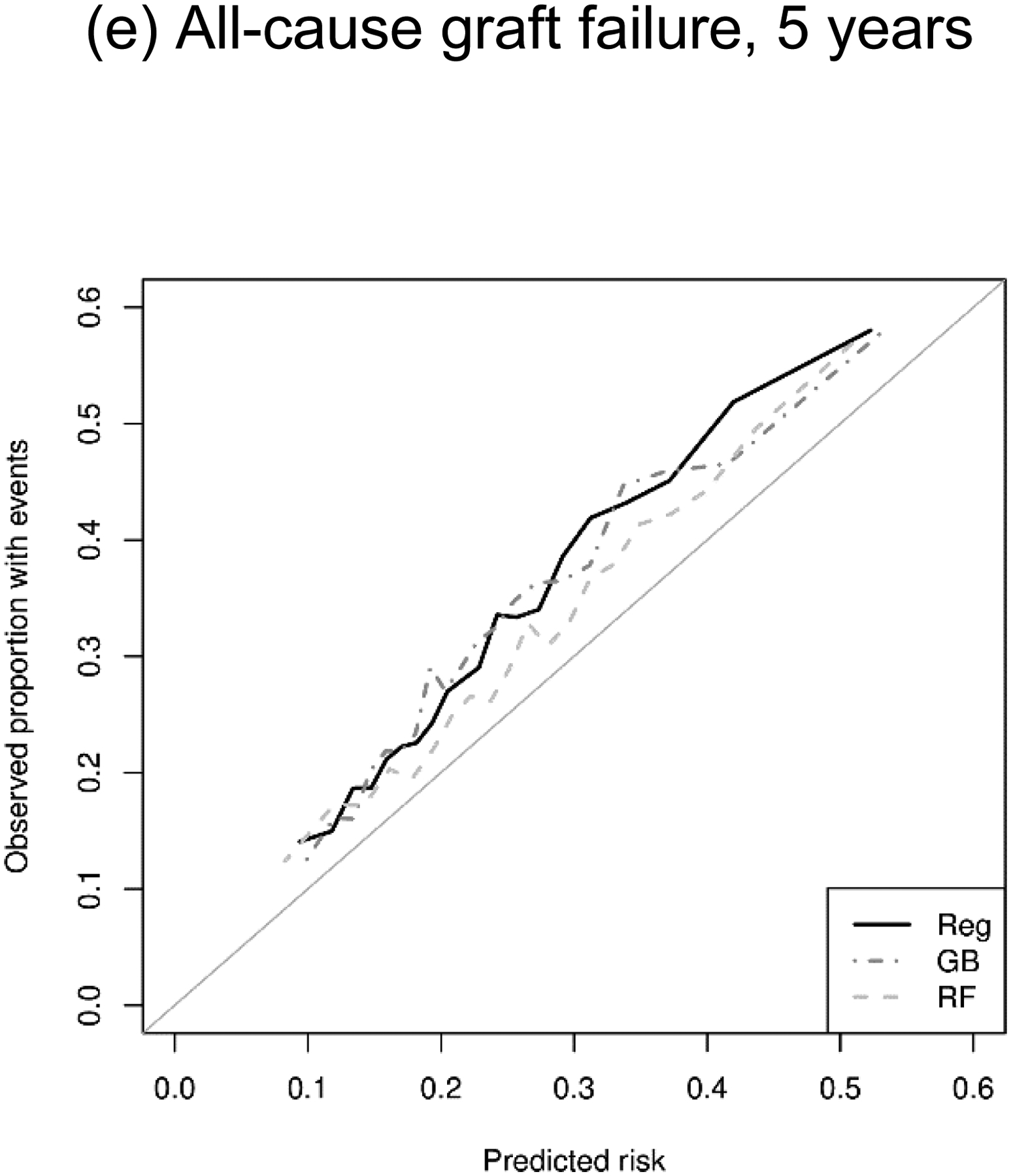
Calibration plot of regression (Reg), gradient boosting (GB), and random forests (RF) in predicting kidney transplant outcomes.

DISCUSSION

In this comparison of ML algorithms versus regression in predicting KT outcomes using large national registry data, ML did not outperform regression-based models. In terms of discrimination, we observed similar C-statistics across regression and ML algorithms in all transplant outcomes, with the exception of one-year AR where logistic regression actually showed a higher C-statistic than ML algorithms. Furthermore, in terms of calibration as measured in the Brier score, regression outperformed ML algorithms in predicting time-to-event outcomes (DCGF, death, and ACGF), whereas regression and ML algorithms showed similar performance in predicting binary outcomes (DGF and AR).

Predicting KT outcomes using the U.S. national registry data is perhaps one of the “generic” analytic tasks that pertain to a wide gamut of transplantation research, ranging from fine-tuning organ allocation policy [29,30] to informing clinical decision-making [14,31] to identifying independent effects by correctly adjusting for confounders [32,33]. The lack of ML’s advantage in this setting implies that, despite the recent successes, and recent claims of successes, surrounding ML in many areas of medicine, regression is a valuable, and sometimes a preferable, analytic method in transplantation research.

Our findings are consistent with a study in heart transplantation by Miller and colleagues [34] that found no meaningful difference in predicting 1-year survival between logistic regression and ML algorithms using the same set of variables, with C-statistics around 0.65 in most methods. We have extended this approach to kidney transplantation, to outcomes beyond 1 year, to Cox regression which is the typical method for evaluating survival, and to non-survival outcomes such as DGF and AR. Our findings are also consistent with studies [3–5,35] that reported only minor performance differences (e.g, C-statistic from 0.706 to 0.724); we extend these studies in the context of a true head-to-head comparison that shows no performance advantage of ML and, actually, some performance advantage of regression with some outcomes.

On the other hand, our findings are contrary to several recent studies that reported high predictive performance of ML algorithms. In some cases, the exact reason for the discrepancy is unclear due to the absence of a head-to-head, same-variable, same-population comparison against regression [7–10]. But more importantly, many of these studies purposefully explored ML as a tool to incorporate additional clinical information into prediction [6,13,16], rather than testing if ML outperforms regression on equal footing. For example, Lau and colleagues [16] reported that RF and neural network outperformed traditional models such as Donor Risk Index (DRI) in predicting graft survival after liver transplantation. However, the ML models included numerous key variables that are not included in DRI, such as recipient disease category, donor serum albumin level, and geographical location. Therefore, these studies have shown that ML methods identified potentially more influential clinical factors which led to better prediction. Purely in terms of predictive performance, these studies do not indicate that ML alone can achieve a new level of predictive performance that regression cannot reach, because an equally comprehensive regression-based model could have demonstrated similar performance. In that sense, our current study is a necessary follow-up to the previous ML prediction studies.

Although our findings do not support the application of ML on simple prediction of KT outcomes using routinely collected tabular data, there are research questions in organ transplantation that might be well suited for ML. Theoretically, ML methods are capable of handling interactions between predictors in a flexible manner [14,36], integrating non-tabular data such as clinical notes or graft biopsy images with tabular clinical data [13,37], and analyzing high-dimensional data such as genes or biomarkers [38]. Our study was not focused on evaluating these benefits, and our findings should not discourage future applications of ML on such research endeavors. However, in the context of straightforward outcome prediction, we emphasize that ML does not seem to provide a predictive advantage, yet suffers from a number of weaknesses that risk misleading modeling, limit our ability to assess face validity or test biological hypotheses, and diminish the interpretability of the models themselves.

Our study has several limitations. First, we cannot rule out the possibility that there exists a ML algorithm that outperforms the algorithms investigated in this study. However, considering that we observed nearly identical predictive performance from all three methods including regression, it is not unreasonable to assume that these performance measures are bound by the inherent variability of the data, not by the competency of the methods. Second, our findings are not generalizable to any analyses that include new types of data not present in the transplant national registry, especially non-tabular clinical information. As discussed above, ML might be actually advantageous in these cases. Lastly, there could be specific subgroups in which GB or RF outperforms regression models because of their ability to handle interactions without modeling assumptions. However, such effects were not observed in our analyses.

Our findings suggest that ML does not outperform conventional regression-based approaches in predicting various KT outcomes using routinely collected tabular data. Given that regression modeling presents an interpretable model and enables hypothesis testing, the advantage of using ML over regression in simple predictions of KT outcomes is questionable. The lack of ML’s advantage in our “generic”, controlled analytic setting implies that, in this case, ML is more hype than helpful.