Abstract
In this study, the motion and distribution of droplets containing coronaviruses emitted by coughing of an infected person in front of a classroom (e.g., a teacher) were investigated using CFD. A 3D turbulence model was used to simulate the airflow in the classroom, and a Lagrangian particle trajectory analysis method was used to track the droplets. The numerical model was validated and was used to study the effects of ventilation airflow speeds of 3, 5, and 7 m/s on the dispersion of droplets of different sizes. In particular, the effect of installing transparent barriers in front of the seats on reducing the average droplet concentration was examined. The results showed that using the seat partitions for individuals can prevent the infection to a certain extent. An increase in the ventilation air velocity increased the droplets’ velocities in the airflow direction, simultaneously reducing the trapping time of the droplets by solid barriers. As expected, in the absence of partitions, the closest seats to the infected person had the highest average droplet concentration (3.80 × 10−8 kg/m3 for the case of 3 m/s).
Keywords: COVID-19 particles, CFD simulation, Classroom, Seat partitions, Air change rate
Graphical Abstract
Nomenclature
- A
Surface area (m2)
- ACH
Air change per hour (h−1)
- CC
Cunningham coefficient
- Ci,s
Vapor concentration at the droplet surface (kgmol/m3)
- Ci,∞
Vapor concentration in the bulk gas (kgmol/m3), Nondimensional cough droplets' average concentration
- Cp
Specific heat capacity (J/kg K)
- d
Particle’s diameter (m)
- Di,m
Diffusion coefficient of vapor (m2/s)
- FD
Drag force
- g
Gravitational acceleration components (m/s2)
- h
Convective heat transfer coefficient (W/m2 K)
- hfg
Latent heat (J/kg)
- H
Height (m)
- k
Turbulent kinetic energy (J)
- K
Fluid thermal conductivity (W/m K)
- kC
Mass transfer coefficient (m/s)
- L
Length (m)
- Mw,i
Molecular weight of species i (kg/kg mol)
- m
Mass (kg), Mass flow rate of particles (kg/s)
- Ni
Molar flux of vapor (kg mol/m2-s)
- NTn
Total nondimensional numbers of droplets
- Nu
Nusselt number
- n
Number of particles
- P
Pressure (Pa)
- Pop
Operating pressure (Pa)
- R
Universal gas constant
- Re
Reynolds number
- S
Source term
- Sc
Schmidt number
- t
Time (s)
- T
Temperature (K)
- u, v, w
Velocity components (m/s)
- V
Velocity vector (m/s)
- W
Width (m)
- x, y, z
Cartesian direction
- X, Y
Non-dimensional Cartesian coordinates
Greek symbols
- α
Thermal diffusivity (m2/s)
- ɛ
Dissipation rate of the turbulent energy
- μ
Dynamic viscosity (m2/s)
- ρ
Density (kg/m3)
- τ
Total droplet removal time (s)
Subscripts
- d
Particle
- sat
Saturation
- T
Total
- x, y, z
Cartesian directions
1. Introduction
Governments worldwide are currently taking action to bring the students back to the schools after several months of COVID-19 pandemic closure, as they believe classrooms are an essential environment for the social, mental, and academic development of individuals. However, concerns still exist in ensuring safe and healthy classroom conditions due to many uncertainties on the COVID-19 infection pathways. Important questions that need to be addressed are how the ventilation systems affect the spread of the virus in the classroom. Also, how to minimize the chance for exposure. As the experimental study is challenging, computational fluid dynamics (CFD) provides a valuable tool to simulate the virus-laden droplets' distribution and spreading generated by the sneezing or coughing of an infected person in the classroom.
Over the past year, several studies have been reported on the flow-dynamic behavior of Covid-19. Bar-On et al. (2020) examined the biology and properties of the SARS-CoV-2 virus that causes Covid-19 infection and the characteristics of a human host. According to statistical results, transmission of COVID-19 in environment via aerosols, droplets, fomites, and feces affected on the people's health (Von Seidlein et al., 2020, Corburn et al., 2020, Mishra et al., 2020, Tellier et al., 2019, Mao et al., 2020). In addition, control of overcrowding can significantly reduce virus transmission. Asadi et al. (2020) studied the transmission of COVID-19 by direct or indirect contact, including airborne transmission during sneeze or cough or by physically touching infected surfaces. Diwan et al. (2020) examined the sneezing/coughing flows considering dry and wet conditions and included droplet evaporation using direct numerical simulations (DNS). They simulated the process of coughing as a turbulent jet/puff phenomenon. Kotb and Khalil (2020) used the ANSYS-Fluent code to simulate the transmission of Covid-19 by sneezing and coughing of an infected passenger moving inside the closed space of an aircraft cabin. Their results showed that sneezing droplets had more harmful effects than cough droplets, and both move long distances inside the cabin. Also, the faster a person moves, the more droplets are dispersed. Dispersion of Covid-19 infected droplets emitted by sneezing in a hospital room with three beds was investigated numerically by Wang et al. (2021). In their ANSYS-Fluent simulations, the particle trajectory and residence time were studied to estimate cross-infection probability.
Ventilation systems that are commonly used change the droplet concentration, temperature, and humidity of the indoor air environment. Evaluation of displacement and mixed ventilation systems and their effects on indoor air is of interest to human health and comfort (Van Hooff et al., 2011, Gilani et al., 2016). Many studies suggest that insufficient ventilation increases the risk of disease transmission in the indoor environment. Studies of indoor airflow regimes, room pressurization, and filtration for hospitals and chemical laboratories where infectious disease agents are handled were performed by Barbosa and Brum, 2018, Liu et al., 2017 to find low-risk conditions. Ren et al. (2021) studied numerical simulation of three typical ventilation strategies in a prefabricated Covid-19 inpatient ward in a hospital for a range of droplet diameters. They found that small particles move along with the main flow streams to long distances. Many of the droplets are removed by ventilation through the outlet(s). Large particles, however, cannot move with the flow streams, and most large particles deposit on solid surfaces by gravitational sedimentation in different regions of the ward for different ventilation strategies.
Due to the lack of experimental data on the fluid dynamics of COVID-19 infected droplets, reviewing the available simulations on spreading the droplet through sneezing/coughing are helpful for a better understanding of modeling the COVID-19 transmission. Laminar, transient, and turbulent indoor airflow significantly affect the dispersion and transport of suspended droplets (Liu et al., 2020, Liu et al., 2020, Liu and Chen, 2018). Furthermore, the indoor airflow becomes transient due to human behaviors involving walking, coughing, or sneezing. The analysis of the coughing airflow dynamics was performed experimentally by Gupta et al. (2009). They examined various cough velocities over time as a combination of gamma functions. They found that the direction of the cough and the area of mouth opening during coughing was not related to physiological parameters such as height, weight, and gender. The effects of human expiratory flows on respiratory infection in ventilated environments are investigated by Liu et al., 2020, Liu et al., 2020 to minimize the infection risk of breathing. Their results indicated the large droplets deposit within a short distance and are hardly affected by the thermal stratification; however, droplet infection to the susceptible people could happen at close contact with the infector. Yan et al. (2019) numerically studied the effect of the human thermal plume on the dispersion of evaporating droplets emitted by coughing over time. They used a three-dimensional Eulerian-Lagrangian model and investigated the effect of temperature and humidity on droplet evaporation. They found that the human thermal plume is significantly affected the droplet mass fraction and local air velocity distribution. They also reported that the droplets' size is reduced due to evaporation, which increases the chance that the droplets get inhaled in indoor spaces. Redrow et al. (2011) proposed a new model to simulate sputum droplets' evaporation and dispersion generated by human coughs or sneezes. They studied the effects of biological and chemical components of sputum on their evaporation rate, velocity, and temperature. Their results showed that droplet temperature decreases rapidly from the human body temperature to room temperature. In another numerical study, Li et al. (2018) used a multi-component Eulerian-Lagrangian approach to model the evaporation and dispersion of cough droplets in stagnant air. Their results showed that the vapor due to the supersaturated humid air escaping from the airways inhibits droplet evaporation. Zhang et al. (2017a) investigated the spreading and dispersion of cough droplets in a conference room using a Lagrangian model. The airflow was unsteady in their study, and gravity, drag force, and Brownian excitation of cough droplets were taken into account. They also examined the effect of air ventilation direction and the people's locations on the chance of exposure.
In an experimental study by Han et al. (2013), the size distribution of sneeze droplets expelled by twenty healthy individuals was recorded and fitted to a nonlinear distribution of droplets over time. Zhang and Chen (2007) compared the predictions of Eulerian and Lagrangian models of cough droplet concentration distribution in closed spaces. Their results showed that both models provide a reasonable prediction under steady conditions compared to measurements, but under unsteady conditions, the Lagrangian model performs better than the Eulerian model. The effect of a patient's movement on the distribution of cough droplets was studied using the Lagrangian trajectory analysis by Guan et al. (2014). They found that the patient's speed of movement affects the distribution of cough particles. Zhang et al. (2017b) numerically studied the distribution of cough droplets in a well-ventilated conference room using a Lagrangian particle trajectory analysis to assess the infection likelihood of people sitting around the conference table. Yang et al. (2020) investigated CFD simulation of droplet dispersion carrying viruses or bacteria in a bus. They showed droplet dispersion changes due to gravity, ventilation airflows, upward thermal body plume, and 85–100% of droplets deposit on surfaces.
The classroom as an environment for COVID-19 transmission among students has attracted the attention of researchers. Abuhegazy et al. (2020) investigated the transport of COVID-infected aerosols and their surface deposition in a classroom. Their numerical results presented the effects of particle size, aerosol source location, glass barriers, and windows. They found that most small particles exit through the air conditioning system, while large particles drop on the ground, desks, and other surfaces in the room by gravitational sedimentation. Comparisons of the airborne transmission by the method of Wells–Riley (Abuhegazy et al., 2020) and computational fluid dynamics (CFD) models (Wang et al., 2021) in a classroom with masked students for various ventilation conditions were reported by Foster and Kinzel (2021). They found that in the absence of forced ventilation, the two methods are in good agreement, but large differences are observed for forced ventilation. Curtius et al. (2021) tested four air purifiers equipped with HEPA filters in a classroom. Their measurements and calculation demonstrated that air purifiers potentially provide a well-suited measure to reduce the airborne transmission of COVID-19. Finally, the configuration of a closed space affects the distribution of COVID-19-infected droplets. Ugail et al. (2021, 2020) proposed a design optimization methodology that takes the dimensions and the other constraints and other requirements of a given physical space to provide optimal redesign solutions to minimize transmission. They used the social distancing criteria between people and the physical spaces such as doors, windows, walkways, and the variables related to the indoor airflow pattern to the optimization design of university buildings. Bañón and Bañón (2020) analyzed the seating distributing in various spaces for different uses and room sizes with equilateral triangle-based seat patterns. For COVID-19 condition, their study may help the schools, colleges, restaurants, libraries, and similar built environments where the seating capacity is crucial. With this approach, more seats are achieved in most situations, with mean increases of 13% and peaks from 25% to 50% in some specific circumstances.
The presented literature survey and the concerns and uncertainties surrounding the COVID-19 suggest that more research on coronavirus transmission in indoor spaces such as classrooms and developing strategies for reducing virus transmission are needed. The present study uses CFD to simulate the spreading of droplets containing the COVID-19 viruses expelled by coughing of an infective person standing in a partitioned and non-partitioned classroom. The turbulent airflow was simulated using the k-ɛ model. The governing equations for the flow and particles are solved using the ANSYS-Fluent software. The effects of the ventilation airflow speed, droplet diameters, and physical barrier on the virus distribution and concentration are also studied. The locations in the classroom that are safe are also identified.
2. Physical model
This work has investigated the transport and dispersion of droplets containing the COVD-19 viruses generated by coughing in a classroom with and without partitioning under summer weather conditions. The dimensions and the specifications of the classroom and the seats from the top view are presented in Fig. 1(a). The studied classroom floor is 6 m wide and 8 m long and is consistent with the 1.6 m2 per student requirement of Baker (2012). In addition, the classroom's height is 5 m, according to the design rules of educational buildings and classrooms. The student seating in the classrooms is with the appropriate distancing.
Fig. 1.
Classroom geometry and schematics. (a) Top view. (b) The 3D model without partition. (c) The 3D model with partition.
The 3D sketch of the simulated classroom with all considered details is presented in Fig. 1(b) and (c). Fig. 1(b) shows a typical classroom with no partitions, and Fig. 1(c) shows a classroom equipped with transparent partitions for every seat. In this study, we consider a COVID-19 infected person (with a height of 1.8 m and mouth area of 4 cm2) standing in front of the class suddenly coughs and expels the virus-infected droplets into the environment. The ventilation air is supplied from an intake on the wall behind the person and exits through the open door. Other dimensions are: windows are 2 × 2 m2, the board is 1 × 3 m2, the platform is 1.5 × 4.5 m2, seats are 0.6 × 0.6 m2, the table is 1 × 0.6 m2, the door is 1 × 2 /1 m2, and the supply air register (inlet) is 0.7 × 0.4 m2. The three-sided glass partitions for each seat that are modeled have a height of 2 m, and the wide of each side is 0.8 m (see Fig. 1(c)).
3. Mathematical model
In this study, numerical modeling of the flow dynamics of the transmission of the COVID_19 viruses was performed in two steps. First, a steady-state classroom's turbulent airflow condition was simulated used the RNG k-ɛ model. In the second step, various size water droplets presented in Table 1 (that could contain COVID-19 viruses) were expelled by coughing from the mouth of the infected person standing in front of the classroom and tracked using the Eulerian-Lagrangian method.
Table 1.
Injection conditions of droplets containing COVID-19 viruses.
| Diameter (μm) | Particles velocity (m/s) | Numbers of particles | Injection time (s) | Mass flow rate of particles (kg/s) |
|---|---|---|---|---|
| 0.150 | 10 | 1800 | 0.750 | 4.2413 × 10−15 |
| 1 | 10 | 1800 | 0.750 | 1.2566 × 10−12 |
| 10 | 10 | 1800 | 0.750 | 1.2566 × 10−09 |
| 50 | 10 | 1800 | 0.750 | 1.5706 × 10−07 |
| 100 | 10 | 1800 | 0.750 | 1.2566 × 10−06 |
| 150 | 10 | 1800 | 0.750 | 4.2413 × 10−06 |
3.1. Ventilation airflow modeling
The general equations of conservation of mass, momentum, and energy for the incompressible steady airflow are given as:
| (1) |
| (2) |
| (3) |
3.2. Turbulence modeling
The RNG k-ɛ turbulence model has been used extensively for simulating the airflow in indoor environments and was shown to be a suitable model (Tsan-Hsing et al., 1995). The corresponding transport equations for the turbulent kinetic energy k and dissipation rate ɛ are given as:
| (4) |
| (5) |
where Gk is the generation of turbulent kinetic energy due to the mean velocity gradients. Here, Sε and Sk are user-defined source terms, and Rε is the source term from renormalization. In (4), (5) αk and αε are effective inverse Prandtl numbers for the turbulent kinetic energy and its dissipation, and C1ɛ = 1.42 and C2ɛ = 1.68, are model constants.
3.3. Discrete phase modeling
For a dilute concentration of droplets in the present study, the airflow was first evaluated and then used for the particle trajectory analysis. The trajectories of virus-carrying droplets are evaluated using Newton’s second law in a Lagrangian framework (Wang et al., 2017, Verma et al., 2017, Dbouk and Drikakis, 2020, Li et al., 2020). The corresponding equation of motion is given as:
| (6) |
In Eq. (6), is Saffman lift force, and is the Brownian force (Li and Ahmadi, 1992), and FD is the coefficient of drag force given as:
| (7) |
| (8) |
Here CC is the Cunningham coefficient (Chen and Deng, 2017, Zhang et al., 2019).
Mass flow rate of particles is presented as:
| (9) |
where n and are the number and density of particles, respectively.
In this study, droplets of different sizes expelled from the mouth (with an area of 4 cm2) due to coughing are considered. A uniform distribution of droplet sizes from small (less than 10 µm), medium (10–100 µm) to large (more than 100 µm) are considered. Specifically, six droplet sizes within these ranges, as presented in Table 1, are used. These values were selected according to the recommendations of Kotb and Khalil (2020). The total number of droplets used was 10,800 (Redrow et al., 2011). The temperature of droplets is set to 37 °C. The velocity of particles at the mouth is 10 m/s, and their mass flow rates are calculated from Eq. (9). Particle injection conditions, including diameter, mass flow rate, velocity, injection time, and the number of droplets, are listed in Table 1. Effects of Brownian excitation (for droplets less than 1 µm) are also included in the simulation.
Assumptions used in this simulation are: (1) Temperature variations are negligible; (2) cough emits only particles/droplets; (3) droplet/particle sizes listed in Table 1 are those after evaporation of their water content, and there is no further evaporation (Shao et al., 2021; Narayanan and Yang, 2021; Nicas et al., 2005); (4) no-slip conditions between phases is assumed; (5) virus-infected droplets are treated as particles; (6) student bodies and their thermal plume (due heat generation) are neglected.
For the interactions between droplets and different surfaces, the trap condition is imposed on the solid walls, and the escape condition is used for the inlet and outlet. According to ASHRAE, the velocity of supply air is in the range of 500 ft/min (2.54 m/s) to 1500 ft/min (7.62 m/s). Three velocities in this range are used in the simulation, and the results are compared. The other boundary conditions used are velocity inlet and pressure outlet (temperature is an initial value for outlet) that are listed in Table 2. Furthermore, a 5% turbulence intensity at the inlet is considered.
Table 2.
Boundary conditions of airflow for cases 1, 2, and 3 in the absence and presence of partitions in the classroom.
| Case | T inlet (°C) | V inlet (m/s) | T outlet (°C) | P outlet (Pa) |
|---|---|---|---|---|
| 1 | 17 | 3 | 35 | 101,325 |
| 2 | 17 | 5 | 35 | 101,325 |
| 3 | 17 | 7 | 35 | 101,325 |
3.4. Numerical method
The governing equations were solved by the ANSYS-Fluent-19 code that uses the finite volume approach. The convergence criterion was also set to the value of 10−6 for the error between the two consecutive iterations for all variables.
3.5. Grid independence tests
For the grid independence study, the classroom without partitions shown in Fig. 1(b) and a supply air velocity of 3 m/s are investigated. An unstructured tetrahedral mesh was created using ANSYS-Fluent and is used in all simulations, as is shown in Fig. 2. Table 3 presents mesh size's effect on volume-average values of velocity, temperature, and pressure in the room. This table shows that the mean velocity, pressure, and temperature predicted using the 8 cm cell differ less than 1% from those of the 6 cm cells. Therefore, the mesh with dimensions of 8 cm was selected for subsequent simulations. Y+ less than 1 was considered for mesh generation, and the total number of grids was 1,550,000.
Fig. 2.
Classroom mesh of the computational model.
Table 3.
Grid independence study for Vin = 3 m/s in a classroom without partitions.
| Grid size (cm) | Number of grids | Volume average absolute pressure (Pa) | Volume average velocity (m/s) | Volume average temperature (K) |
|---|---|---|---|---|
| 14 | 250,530 | 101,325.20 | 0.26061 | 290.15013 |
| 12 | 574,653 | 101,325.23 | 0.28432 | 290.15009 |
| 10 | 915,266 | 101,325.24 | 0.29046 | 290.15008 |
| 8 | 1,540,323 | 101,325.26 | 0.30612 | 290.15007 |
| 6 | 3,762,091 | 101,325.27 | 0.30867 | 290.15007 |
3.6. Sensitivity to time steps
For the selected mesh with the 8 cm cells, the proper time step is selected by studying the injection of droplets (0.150, 1, 10, 50, 100, and 150 µm according to Table 1) in the classroom in the absence of partitions (Fig. 1(b)) with the supply air velocity of 3 m/s. In the present simulation, the droplet injection time is assumed to be 0.750 s (Redrow et al., 2011). A series of simulations are performed for time steps of 0.002 s, 0.001 s, 0.0005 s, and 0.00025 s, and the corresponding particle (0.150, 1, 10, 50, 100, and 150 µm according to Table 1) properties as a function of time are evaluated. The resulting volume-averaged concentration, velocity, and volume fraction at 0.5, 0.75, 1, and 2 s are reported, respectively, in Table 4, Table 5, Table 6. These tables show that as the time step becomes smaller, the differences in the model predictions reduce. Therefore, the time step of 0.0005 for which the model predictions are roughly the same as those for the shorter time step is selected for the subsequence simulations.
Table 4.
Time-step independence study of volume-average particle concentration in the classroom without partitions (Vin =3 m/s).
| Time step (s) | Volume-average concentration at 0.5 s | Volume-average concentration at 0.75 s | Volume-average concentration at 1 s | Volume-average concentration at 2 s |
|---|---|---|---|---|
| 0.002 | 1.224368 × 10−8 | 1.836470 × 10−8 | 1.835853 × 10−8 | 1.829874 × 10−8 |
| 0.001 | 1.224381 × 10−8 | 1.836484 × 10−8 | 1.835904 × 10−8 | 1.830452 × 10−8 |
| 0.0005 | 1.224385 × 10−8 | 1.836487 × 10−8 | 1.835911 × 10−8 | 1.830459 × 10−8 |
| 0.00025 | 1.224386 × 10−8 | 1.836488 × 10−8 | 1.835911 × 10−8 | 1.830460 × 10−8 |
Table 5.
Time-step independence study of volume-average particle velocity in the classroom without partitions
(Vin =3 m/s).
| Time step (s) | Volume-average velocity at 0.5 s | Volume-average velocity at 0.75 s | Volume-average velocity at 1 s | Volume-average velocity at 2 s |
|---|---|---|---|---|
| 0.002 | 8.152059 × 10−5 | 0.000110 | 0.000094 | 0.000462 |
| 0.001 | 8.559676 × 10−5 | 0.000119 | 0.000104 | 0.000476 |
| 0.0005 | 8.698910 × 10−5 | 0.000122 | 0.000107 | 0.000480 |
| 0.00025 | 8.635018 × 10−5 | 0.000125 | 0.000109 | 0.000481 |
Table 6.
Time-step independence study of volume-average particle volume fraction in the classroom without partitions (Vin =3 m/s).
| Time step (s) | Volume-average volume fraction at 0.5 s | Volume-average volume fraction at 0.75 s | Volume-average volume fraction at 1 s | Volume-average volume fraction at 2 s |
|---|---|---|---|---|
| 0.002 | 1.224347 × 10−11 | 1.836468 × 10−11 | 1.835854 × 10−11 | 1.829875 × 10−11 |
| 0.001 | 1.224378 × 10−11 | 1.836484 × 10−11 | 1.835904 × 10−11 | 1.830452 × 10−11 |
| 0.0005 | 1.224386 × 10−11 | 1.836490 × 10−11 | 1.835912 × 10−11 | 1.830455 × 10−11 |
| 0.00025 | 1.224388 × 10−11 | 1.836491 × 10−11 | 1.835916 × 10−11 | 1.830456 × 10−11 |
4. Results and discussion
4.1. Validation
The present numerical model for simulation of particle motion was validated by comparison with Li et al. (2018) for evaporation of a 10 µm droplet expelled by the coughing at a mass flow rate (5.24 × 10−11 kg/s) at the humidity of 0%. The evaporation model used is presented in Appendixes A and B. It is assumed that the droplets leave the mouth at a temperature of 37 °C, and the room temperature is 25 °C. Fig. 3 shows a good agreement between the present predictions and the results of Li et al. (2018). In addition, it is observed that the differences of the present work with the results of Li et al. (2018) are less than 1%.
Fig. 3.
Comparison of the result of the present study for evaporation of a 10 µm droplet with that of Li et al. (2018).
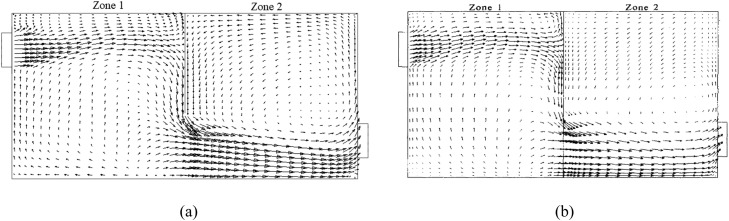
The second validation is presented for the airflow pattern in the three-dimensional two-zone room shown in Fig. 4 studied earlier by Lu et al. (1996). The room (L × H × W = 5 m × 2.4 m ×3 m) is separated using a partition in the middle with a small door opening on the centerline of the room. The door width and height are 0.7, 0.95 m, respectively. Also, the thickness of the partition is ignored compared with the size of the room. A supply and exhaust diffuser with the length, width, and height of, respectively, 1, 0.15, and 0.5 m are located on the front and the back walls, as shown in Fig. 4. The ventilation rate is ACH = 10.26 h−1. The airflow velocity vector patterns at the room mid-section (z = 1.5 m) are simulated, and the results are shown in Fig. 5(a). The earlier numerical study of Lu et al. (1996) is reproduced in Fig. 5(b) for comparison. It is seen that the present prediction of the velocity vector field is in good agreement with that of Lu et al. (1996).
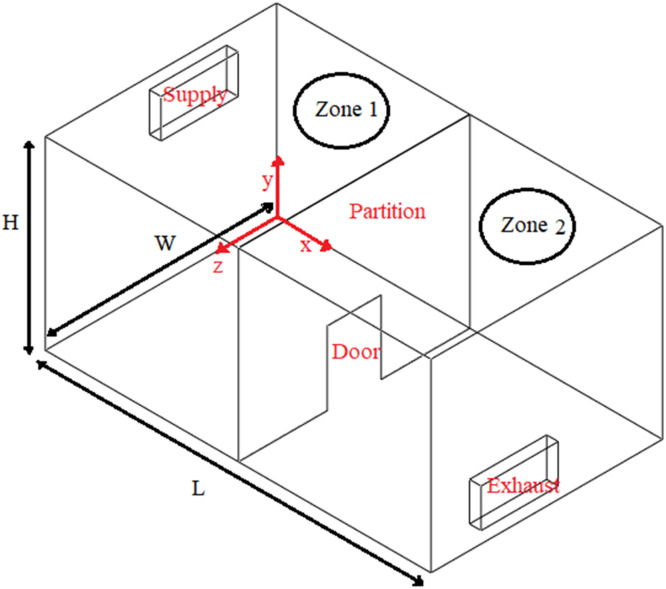
Fig. 4.
The Schematic of the three-dimensional two-zone room (Lu et al., 1996).
Fig. 5.
Comparison of airflow pattern in the centerline plane (width =1.5 m) (a) present work (b) Lu et al. (1996).
4.2. Particle distribution
In the present study, the steady airflow in the room is evaluated using the RNG k-ɛ model for cooler air entering from the inlet register and exiting the door. This is an example of a conventional classroom in Iran and other counties. Then the dispersion of cough droplets in the room is studied. Three different inlet air supply velocities were studied for both non-partitioned and partitioned seats in the classroom, as shown in Table 2.
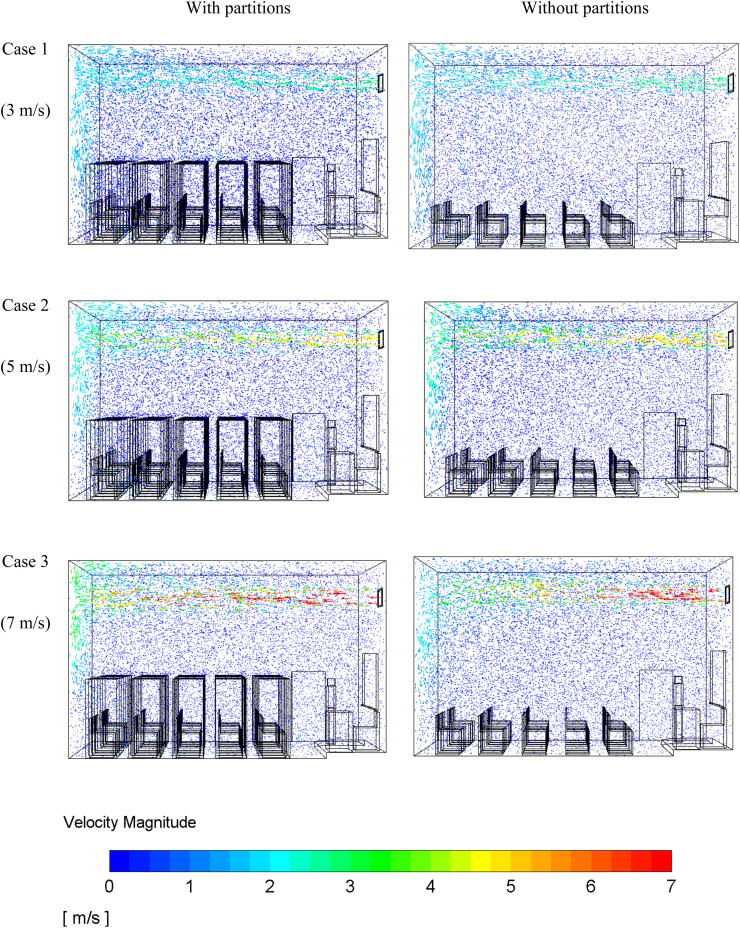
Fig. 6 illustrates the mean turbulent velocity vector field under steady flow conditions for different ventilation speeds. It is evident that the supply air forms a jet that extends across the room and creates a large circulating flow region. With the increase of the ventilation airspeed, the jet flow and the corresponding circulating flow become stronger. Fig. 7 presents velocity magnitude contours at the mid-plane of the inlet diffuser (y = 5 m see Fig. 2) in the classroom without and with partitions for different inlet airflow velocities. The inlet airflow jet is clearly seen in these figures. This figure also shows that the presence of the partitions reduces the spreading of the inlet airflow jet and causes it to penetrate deeper in the classroom.
Fig. 6.
Velocity vector fields in the rooms with and without partitions for different inlet airflow velocities. Case 1, 3 m/s. Case 2, 5 m/s. Case 3, 7 m/s.
Fig. 7.
Velocity magnitude contours at the mid-plane (y = 5 m see Fig. 2) of inlet in classroom with and without partitions for different inlet airflow velocities. Case 1, 3 m/s. Case 2, 5 m/s. Case 3, 7 m/s.
The behavior of particles of different sizes one second after coughing is illustrated in Fig. 8. Coughing generates a velocity of 10 m/s for a duration of 0.75 s. As expected, the larger and heavier droplets (100 µm and 150 µm) tend to drop faster due to the gravitational force. But, the smaller droplets (<1 µm) remain suspended for a longer duration and could infect the student in the classroom.
Fig. 8.
Particle distribution at one second after coughing for different diameters for ventilation velocity of 5 m/s (case 2).
The time variation of predicted distributions of cough droplets with different diameters (0.150, 1, 10, 50, 100, and 150 µm according to Table 1) emitted from the infected person’s mouth in the classroom is shown in Fig. 9 for the case without partitions. Similarly, Fig. 10 shows the particle distribution in the classroom with partitions. The particle distributions at different times for cases with various ventilation airflow velocity conditions in the classroom with and without partitions are shown in these figures. In these figures, the distributions of emitted particles at different times from 0.5 s to 100 s are shown. It is seen that the ventilation airflow significantly affects the dispersion and transport of the particle. Fig. 9 shows that for the ventilation airflow velocity of 3 m/s (Case 1), the particles seem to stay near the face up to about 1 s and then disperses more and spreads throughout the room at t = 100 s. The particles' dispersion rate increases as the ventilation speed increases to 5 m/s (Case 2) and 7 m/s (Case 3). For the latter case, the particles disperse in the entire room at about 10 s. The concentration then becomes gradually more dilute as air is leaving through the open door on the classroom side. For the ventilation speed of 7 m/s, the particle concentration in the classroom becomes dilute at t = 50 s. For the ventilation speed of 5 m/s, almost all particles leave the room at t = 100 s, while for the ventilation speed of 3 m/s, there is a roughly uniform concentration of particles in the classroom at t = 100. These results show that the higher air exchange rate speeds up virus-laden cough particles' dilution rate in the classroom.
Fig. 9.
Particles (0.150, 1, 10, 50, 100, and 150 µm according to Table 1) dispersion for different times for cases 1, 2 and 3 without partitions.
Fig. 10.
Particles (0.150, 1, 10, 50, 100, and 150 µm according to Table 1) dispersion for different times for cases 1, 2 and 3 with partitions condition.
Fig. 10 for the classrooms with partitions shows that the general trend of time variation of particle concentration is similar to Fig. 9. However, the students sitting on chairs in the partitions seem to be exposed to lower particle concentrations than the case in the absence of partitions. Comparing Fig. 9, Fig. 10, marked differences between classrooms with and without partitions are seen. For example, at 10 s, partitions significantly constrain the dispersion of the emitted particles compared to the classroom without partition for all ventilation flow rates. These trends are also seen for the ventilation speed of 3 m/s at t = 100 s and the ventilation speed of 7 m/s, respectively, at times of 10 s and 25 s after coughing.
The droplet concentration and the chance that students are infected for different cases are studied in this section. In this study, the student bodies' influence was not modeled, but the average droplet concentration at each seat in the classroom is evaluated. The total droplet removal time, τ, that when all emitted droplets (0.150, 1, 10, 50, 100, and 150 µm according to Table 1) are trapped on various surfaces or dropped on the ground and/or exited through the open door, for the cases with or without partitions are tabulated in Table 7. For all ventilation speeds, the values of τ for the classrooms with partitions are lower than the room without partitions due to an increase in the partition surface areas that increase particle trapping. Also, τ decreases with increasing the ventilation airflow velocity through the supply air.
Table 7.
Variations of τ for different ventilation cases for classrooms with and without partitions and different particle sizes (0.150, 1, 10, 50, 100, and 150 µm according to Table 1).
| τ (s) | ||
|---|---|---|
| With partitions | Without partitions | |
| Case 1 (3 m/s) | 361 | 411.5 |
| Case 2 (5 m/s) | 120.8 | 160 |
| Case 3 (7 m/s) | 61.5 | 77.5 |
The total nondimensional numbers of droplets, N Tn, that remain suspended in the classroom as a function of time for different ventilation speeds are shown in Fig. 11. For the low ventilation speed of 3 m/s, for the classroom with and without partitions, it takes longer to remove all droplets than case 3 with the ventilation speed of 7 m/s, which needs less time. This figure shows that for a given ventilation speed, for the classroom with partitions, τ is lower than that for the room without partitions.
Fig. 11.
Time variation of the total nondimensional numbers of droplets (NTn) in the classroom with and without partitions.
Fig. 12 shows the nondimensional cough droplets' average concentration in the classroom versus times for different ventilation speeds and different particle sizes (0.150, 1, 10, 50, 100, and 150 µm according to Table 1). It is seen that the mean concentration decreases with time for various ventilation speeds. Case 1, with the low ventilation speed of 3 m/s, takes a longer time than the other cases (ventilation speeds of 5 and 7 m/s) to reach a negligible particle concentration.
Fig. 12.
Time variation of the nondimensional cough droplets' average concentration) in the classrooms with and without partitions.
To find the high and low-average droplet concentration locations in the classroom after coughing of the infected person, the average droplet concentration for each seat at the height of 1 m (the height of a person sitting on a chair) as is shown in Fig. 1(b) and (c) using virtual planes at various times for different ventilation cases are shown in Figs. 13 and 14. As noted, before, the body of the students and the heat generated by them are not included in the present model, but the concentrations of droplets at different seats in the classroom are evaluated.
Fig. 13.
Average droplet concentration on the virtual plane (see Fig. 1(b) and (c)) for each seat (see Fig. 1(a)) at various times for the classroom without partitions.
For example, the average droplet concentration for seat 23 in the non-partitioned classroom for ventilation speed of 7 m/s (Case 3) at various times are given as:
At 0.5 s: 1 × 10−20-0 = 1 × 10−20 kg/m3 (negligible).
At 1 s: 2 × 10−20-1 × 10−20 = 1 × 10−20 kg/m3 (negligible).
At 5 s: 9.29 × 10−16-2 × 10−20 = 9.29 × 10−16 kg/m3.
At 10 s: 1.85 × 10−09-9.29 × 10−16 = 1.85 × 10−09 kg/m3.
At 30 s: 1.850625 × 10−09-1.85 × 10−09 = 6.26 × 10−13 kg/m3.
At 50 s: 1.8500000000001 × 10−09-1.85 × 10−09 = 1 × 10−20 kg/m3 (negligible).
At 100 s: 1.8500000000001 × 10−09-1.85 × 10−09 = 1 × 10−20 kg/m3 (negligible).
At 150 s: 1.8500000000001 × 10−09-1.85 × 10−09 = 1 × 10−20 kg/m3 (negligible).
The average droplet concentration of less than 10−20 kg/m3 is considered negligibly small and is neglected.
Figs. 13 and 14 show that, in general, the non-partitioned seats are at a higher average droplet concentration compared to the partitioned seats. Seat number 3 in the non-partitioned classroom has the highest average droplet concentration in all cases (with average droplet concentration of 3.61 × 10−10 kg/m3 at 50 s, 1.67 × 10−8 kg/m3 at 5 s, and 3.80 × 10−8 kg/m3 at 5 s, for the air supply cases of 1, 2, and 3, respectively). The location of high-average droplet concentration seat changes with supply air velocity for the partitioned seats. For the case of ventilation airflow velocity of 3 m/s, the high-average droplet concentration seat in terms of exposure is seat number 20 (with average droplet concentration of 6.29 × 10−12 kg/m3 at 150 s), while for the ventilation airflow velocity of 5 m/s and 7 m/s, it is seat number 2 (with average droplet concentration of 1.98 × 10−10 kg/m3 at 30 s and 2.48 × 10−9 kg/m3 at 30 s, respectively). Average droplet concentration on the virtual plane for the highest average droplet concentration seats of each case at various times are presented in Fig. 15.
Fig. 14.
Average droplet concentration on the virtual plane (see Fig. 1(b) and (c)) for each seat (see Fig. 1(a)) at various times for the classroom with partitions.
Fig. 15.
Average droplet concentration on the virtual plane (see Fig. 1(b) and (c)) for highest concentration seats (see Fig. 1(a)) at various times.
5. Conclusions
The flow dynamics and dispersions of droplets with different sizes expelled by coughing of a Covid-19 infected person standing in front of a classroom with seats with and without partitions were studied. The 3D simulations were carried out for different ventilation airflow velocities entering through the inlet register and exiting through the open classroom door. Based on the presented results, the following conclusions are drawn:
-
1.
At a given time after injection, the number of suspended droplets generally decreases as the ventilation velocity increases from 3 m/s to 5 m/s, and for the ventilation velocity of 5 m/s is higher than that for ventilation velocity of 7 m/s for both classrooms with and without partitions.
-
2.
The time duration to reach negligible droplet concentration, τ, is longer for the classroom without-partition than that with-partition.
-
3.
The value of τ decreases with increasing the ventilation speed.
-
4.
Average droplet concentration in the space decreases with time for all ventilation cases. Case 1, with the lowest ventilation airspeed of 3 m/s, shows the largest average droplet concentration compared to the other higher ventilation speeds.
-
5.
In general, seats in the classroom with partitions are exposed to a lower average droplet concentration than the room without partitions when the infected person coughs in front of the classroom.
-
6.
The highest average droplet concentration for the classroom without-partition occurs at Seat 3, at 50 s, 5 s, and 5 s after coughing, respectively, for ventilation air velocities of 3 m/s, 5 m/s, and 7 m/s. The corresponding peak average droplet concentrations at Seat 3 are, respectively, 3.61 × 10−10 kg/m3, 1.67 × 10−8 kg/m3, and 3.80 × 10−8 kg/m3 at the noted times.
-
7.
For the classroom with partitions at ventilation velocity of 3 m/s, Seat number 20 has the highest level of exposure with an average droplet concentration of 6.29 × 10−12 kg/m3 at 150 s after coughing. For the ventilation airflow velocities of 5 m/s and 7 m/s, Seat 2 experiences the highest exposure at 30 with the peak average droplet concentration of 1.98 × 10−10 kg/m3 and 2.48 × 10−9 kg/m3, respectively.
It should be emphasized that the findings of the present study were limited to the considered cases and the assumptions made. In particular, this study was concerned with the investigation of the dispersion and transport of cough droplets expelled by an infected person (teacher) standing in front of the classroom, and the exposure of students was assessed. The dispersion and transport of cough droplets emitted by infected students were not addressed in this study. In addition, the influence of the thermal plume generated by body heat is not included. Such studies are left for future work.
CRediT author contribution statement
Mahshid Mirzaie: Writing, Software, Simulation, Validation, Investigation. Esmail Lakzian: Methodology, Writing - review & editing, Supervision. Afrasyab Khan: Writing - review & editing, Supervision. Majid Ebrahimi Warkiani: Writing - review & editing, Supervision. Omid Mahian: Writing - review & editing, Supervision. Goodarz Ahmadi: Writing - review & editing, Supervision.
Declaration of Competing Interest
The authors do not have any potential conflict of interest to report.
Acknowledgments
Thanks are given to Dr. Ehsan Ebrahimnia-Bajestan (Postdoc fellow at the University of British Columbia) for mentioning the graduate student and comments on CFD simulations.
Editor: Dr. H. Zaher
Appendix A
Droplet evaporation model equations that were used in validation (part 5.3) are discussed in this appendix. The vaporization rate is governed by gradient diffusion. The flux of droplet vapor into the gas phase is related to the gradient of the vapor concentration between the droplet surface and the bulk gas. That is,
| (A-1) |
Here Ni is the molar flux of vapor, kc the mass transfer coefficient, Ci,s the vapor concentration at the droplet surface, and Ci, ∞ is the introduced vapor concentration in the bulk gas.
The concentration of vapor at the droplet surface and the bulk gas is evaluated as,
| (A-2) |
| (A-3) |
In the above equations, psat is the partial pressure of vapor at the interface and is equal to the saturation vapor pressure, Td is the particle droplet temperature, R is the universal gas constant, Xi is the local bulk mole fraction of species i, Pop is the operating pressure, and T∞ is the local bulk temperature in the gas.
The mass transfer coefficient is calculated from,
| (A-4) |
where is the Nusselt number, Di,m is the diffusion coefficient of vapor in bulk, Sc is the Schmidt number, and dd is the particle (droplet) diameter.
The mass of the evaporating droplet is reduced according to,
| (A-5) |
where Mw,i is the molecular weight of species i, md is the mass of the droplet, and Ad is the surface area of the droplet.
The droplet temperature is evaluated using the heat balance related to the sensible heat change in the droplet to the convective and latent heat transfer between the droplet and the continuous phase. That is,
| (A-6) |
here Cp is droplet heat capacity, h is the convective heat transfer coefficient, dmd/dt is the rate of evaporation, and hfg is the latent heat.
Appendix B
The material and characteristics of the COVID-19 virus are assumed to be the same as water. Due to the small size of viruses (150 nm), if we considered the evaporation of virus size droplets, all droplets would evaporate. Of course, viruses are made of protein and would not evaporate. In addition, while saliva droplets are mostly water, the droplet made of mucus contains a considerable amount of protein that would not evaporate. It is estimated that the radius of a mucus droplet would reduce to 44% of its original radius after complete evaporation of its water content.
In Fig. B1, water droplet distribution one second after coughing for different diameters for case 2 with evaporation in a low humidity room is compared with those without evaporation. As can be seen, the small size water droplets with diameters of 0.15, 1, 10, and 50 µm completely evaporate. Thus, in this study, the droplet evaporation phase is not included in the analysis, and the cough emitted particle sizes used in the simulations are those after the evaporation of their water content. Detailed studies of evaporating droplets with heterogeneous nuclei are planned for a future study. In such a study, water would evaporate, but the viruses and the nonvolatile compounds would remain as nuclei.
Fig. B1.
Comparison of droplet resident times in the absence of evaporation and with evaporation for case 2 (5 m/s).
References
- Abuhegazy M., Talaat K., Anderoglu O., Poroseva S.V. Numerical investigation of aerosol transport in a classroom with relevance to COVID-19. Phys. Fluids. 2020;32 doi: 10.1063/5.0029118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asadi S., Bouvier N., Wexler A.S., Ristenpart W.D. The coronavirus pandemic and aerosols: does COVID-19 transmit via expiratory particles. J. Aerosol Sci. Tech. 2020;54:635–638. doi: 10.1080/02786826.2020.1749229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker, L., 2012. A History of School Design and Its Indoor Environmental Standards, 1900 to Today. National Clearinghouse for Educational Facilities.
- Bañón L., Bañón C. Improving room carrying capacity within built environments in the context of COVID-19. Symmetry. 2020;12:1683. [Google Scholar]
- Barbosa B.P.P., Brum N.D.C.L. Validation and assessment of the CFD-0 module of CONTAM software for airborne contaminant transport simulation in laboratory and hospital applications. J. Build. Environ. 2018;142:139–152. [Google Scholar]
- Bar-On Y.M., Flamholz A., Phillips R., Milo R. SARS-CoV-2 (COVID-19) by the numbers. eLife. 2020;9 doi: 10.7554/eLife.57309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Deng Z. Hydrodynamics of a droplet passing through a microfluidic T-junction. J. Fluid Mech. 2017;819:401–434. [Google Scholar]
- Corburn J., Vlahov D., Mberu B., Riley L., Caiaffa W.T., Rashid S.F., Ko A., Patel S., Jukur S., Martínez-Herrera E., Jayasinghe S. Slum health: arresting COVID-19 and improving well-being in urban informal settlements. J. Urban Health. 2020;97:348–357. doi: 10.1007/s11524-020-00438-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtius J., Granzin M., Schrod J. Testing mobile air purifiers in a school classroom: reducing the airborne transmission risk for SARS-CoV-2. Aerosol Sci. Technol. 2021;25:586–599. [Google Scholar]
- Dbouk T., Drikakis D. On coughing and airborne droplet transmission to humans. Phys. Fluids. 2020;32 doi: 10.1063/5.0011960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diwan S.S., Ravichandran S., Govindarajan R., Narasimha R. Understanding transmission dynamics of COVID-19-type infections by direct numerical simulations of cough/sneeze flows. Trans. Indian Natl. Acad. Eng. 2020;5:255–261. doi: 10.1007/s41403-020-00106-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster A., Kinzel M. Estimating COVID-19 exposure in a classroom setting: a comparison between mathematical and numerical models. Phys. Fluids. 2021;33 doi: 10.1063/5.0040755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilani S., Montazeri H., Blocken B. CFD simulation of stratified indoor environment in displacement ventilation: validation and sensitivity analysis. J. Build. Environ. 2016;95:299–313. [Google Scholar]
- Guan Y., Ramesh A., Memarzadeh F. The effects of patient movement on particles dispersed by coughing in an indoor environment. Appl. Biosaf. 2014;19:172–183. [Google Scholar]
- Gupta J.K., Lin C.H., Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19:517–525. doi: 10.1111/j.1600-0668.2009.00619.x. [DOI] [PubMed] [Google Scholar]
- Han Z.Y., Weng W.G., Huang Q.Y. Characterizations of particle size distribution of the droplets exhaled by sneeze. J. R. Soc. Interface. 2013;10 doi: 10.1098/rsif.2013.0560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotb H., Khalil E.E. Sneeze and cough pathogens migration inside aircraft cabins. Energy. 2020;2:4. [Google Scholar]
- Li A., Ahmadi G. Dispersion and deposition of spherical particles from point sources in a turbulent channel flow. Aerosol Sci. Technol. 1992;16:209–226. [Google Scholar]
- Li X., Shang Y., Yan Y., Yang L., Tu J. Modelling of evaporation of cough droplets in inhomogeneous humidity fields using the multi-component Eulerian-Lagrangian approach. J. Build. Environ. 2018;128:68–76. doi: 10.1016/j.buildenv.2017.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y.Y., Wang J.X., Chen X. Can a toilet promote virus transmission? From a fluid dynamics perspective. Phys. Fluids. 2020;32 doi: 10.1063/5.0013318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F., Qian H., Luo Z., Wang S., Zheng X. A laboratory study of the expiratory airflow and particle dispersion in the stratified indoor environment. Build. Environ. 2020;180 doi: 10.1016/j.buildenv.2020.106988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W., Chen Q. Development of adaptive coarse grid generation methods for fast fluid dynamics in simulating indoor airflow. J. Build. Perform. Simul. 2018;11:470–484. [Google Scholar]
- Liu W., Liu D., Gao N. CFD study on gaseous pollutant transmission characteristics under different ventilation strategies in a typical chemical laboratory. J. Build. Environ. 2017;126:238–251. [Google Scholar]
- Liu W., van Hooff T., An Y., Hu S., Chen C. Modeling transient particle transport in transient indoor airflow by fast fluid dynamics with the Markov chain method. Build. Environ. 2020;186 doi: 10.1016/j.buildenv.2020.107323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu W., Howarth A.T., Adam N., Riffat S.B. Modelling and measurement of airflow and aerosol particle distribution in a ventilated two-zone chamber. Build. Environ. 1996;31:417–423. [Google Scholar]
- Mao N., An C.K., Guo L.Y., Wang M., Guo L., Guo S.R., Long E.S. Transmission risk of infectious droplets in physical spreading process at different times: a review. Build. Environ. 2020;185 doi: 10.1016/j.buildenv.2020.107307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra S.V., Haque S.M., Gayen A. COVID‐19 in India transmits from the urban to the rural. Int. J. Health Plan. 2020;35:1623–1625. doi: 10.1002/hpm.3047. [DOI] [PubMed] [Google Scholar]
- Narayanan S.R., Yang S. Airborne transmission of virus-laden aerosols inside a music classroom: effects of portable purifiers and aerosol injection rates. Phys. Fluids. 2021;33(3) doi: 10.1063/5.0042474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: emission of respirable pathogens. J. Occup. Environ. Hyg. 2005;2:143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redrow J., Mao S., Celik I., Posada J.A., Feng Z.G. Modeling the evaporation and dispersion of airborne sputum droplets expelled from a human cough. J. Build. Environ. 2011;46:2042–2051. [Google Scholar]
- Ren J., Wang Y., Liu Q., Liu Y. Numerical study of three ventilation strategies in a prefabricated COVID-19 inpatient ward. Build. Environ. 2021;188 doi: 10.1016/j.buildenv.2020.107467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao S., Zhou D., He R., Li J., Zou S., Mallery K., Kumar S., Yang S., Hong J. Risk assessment of airborne transmission of COVID-19 by asymptomatic individuals under different practical settings. J. Aerosol Sci. 2021;151 doi: 10.1016/j.jaerosci.2020.105661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tellier R., Li Y., Cowling B.J., Tang J.W. Reconocimiento de la transmisión de aerosoles de agentes infecciosos: un comentario. BMC Infect. 2019:19. [Google Scholar]
- Tsan-Hsing S., William W., Aamir S., Zhigang Y., Jiang Z. A new k-ε eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids. 1995;24:227–238. [Google Scholar]
- Ugail, H., Mehmood, I., Aggarwal, R., Iglesias, A., Suárez, P., Maqsood, M., Aadil, F., Campuzano, A., Tajouri, L., Gleghorn, S., Taif, K., 2020. On rearranging physical spaces for enhancing social distancing measures to combat the COVID-19 infection rates. In: Proceeding of the 2020 International Conference on Internet of Things and Intelligent Applications (ITIA), IEEE, pp. 1–5.
- Ugail H., Aggarwal R., Iglesias A., Howard N., Campuzano A., Suárez P., Maqsood M., Aadil F., Mehmood I., Gleghorn S., Taif K. Social distancing enhanced automated optimal design of physical spaces in the wake of the COVID-19 pandemic. Sustain. Cities Soc. 2021;68 doi: 10.1016/j.scs.2021.102791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hooff T., Blocken B., Aanen L., Bronsema B. A venturi-shaped roof for wind-induced natural ventilation of buildings: wind tunnel and CFD evaluation of different design configurations. J. Build. Environ. 2011;46(9):1797–1807. [Google Scholar]
- Verma T.N., Sahu A.K., Sinha S.L. Study of particle dispersion on one bed hospital using computational fluid dynamics. Mater. Today Proc. 2017;4:10074–10079. doi: 10.1016/j.matpr.2017.06.323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Seidlein L., Alabaster G., Deen J., Knudsen J. Crowding has consequences: prevention and management of COVID-19 in informal urban settlements. J. Build. Environ. 2020 doi: 10.1016/j.buildenv.2020.107472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Sun L., Zou M., Gao W., Liu C., Shang L., Gu Z., Zhao Y. Bioinspired shape-memory graphene film with tunable wettability. Sci. Adv. 2017;3 doi: 10.1126/sciadv.1700004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.X., Cao X., Chen Y.P. An air distribution optimization of hospital wards for minimizing cross-infection. J. Clean. Prod. 2021;279 doi: 10.1016/j.jclepro.2020.123431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan Y., Li X., Tu J. Thermal effect of human body on cough droplets evaporation and dispersion in an enclosed space. J. Build. Environ. 2019;148:96–106. doi: 10.1016/j.buildenv.2018.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X., Ou C., Yang H., Liu L., Song T., Kang M., Lin H., Hang J. Transmission of pathogen-laden expiratory droplets in a coach bus. J. Hazard. Mater. 2020;397 doi: 10.1016/j.jhazmat.2020.122609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C., Wu S., Yao F. Evaporation regimes in an enclosed narrow space. Int. J. Heat Mass Transf. 2019;138:1042–1053. [Google Scholar]
- Zhang Y., Feng G., Kang Z., Bi Y., Cai Y. Numerical simulation of coughed droplets in conference room. Procedia Eng. 2017;205:302–308. [Google Scholar]
- Zhang Y., Feng G., Kang Z., Bi Y., Cai Y. Numerical simulation of coughed droplets in conference room. Procedia Eng. 2017;205:302–308. [Google Scholar]
- Zhang Z., Chen Q. Comparison of the Eulerian and Lagrangian methods for predicting particle transport in enclosed spaces. Atmos. Environ. 2007;41:5236–5248. [Google Scholar]