A study of cation-dependent inverse hydrogen bonds and magnetic exchange-couplings in lanthanacarborane complexes

Summary

Ten lanthanacarborane complexes were synthesized to study the rare B−H^δ−∙∙∙Mⁿ⁺ inverse hydrogen bonds (IHBs). The average bonding energy of B−H^δ−∙∙∙Ln³⁺ is theoretically determined to be larger than 24 kJ/mol, which is comparable to moderately strong hydrogen bonds (21–56 kJ/mol). In addition to NMR and IR, magnetometer was used to study the exchange-coupling interaction via such B−H^δ−∙∙∙Ln³⁺ IHBs in detail, and the coupling constant is determined to be −2.0 cm⁻¹, which is strong enough to compare with single-atom bridged dysprosium(III) complexes. Two imidazolin-iminato incorporated complexes have shown energy barrier for magnetization reversal larger than 1000 K, and the exchange-biasing effects are evident. Moreover, the bonding strengths of B−H^δ−∙∙∙Mⁿ⁺ IHBs are cation-dependent. If M = Na, the B−H^δ−∙∙∙Na⁺ bonding energy is reduced to 14 kJ/mol, and the dimerization process is no longer reversible. The exchange-biasing effect is also disappeared. We believe such a finding extends our knowledge of IHBs.

Graphical abstract

Highlights

• •Cation-dependent inverse hydrogen bonds are found in lanthanacarborane complexes
• •The lanthanacarborane dimeric assembly via inverse hydrogen bonds is reversible
• •The average bonding energy of B−H^δ−∙∙∙Ln³⁺ is larger than 24 kJ/mol
• •Inverse hydrogen bonded dysprosiacarborane dimers are single-molecule magnets

Chemistry; Inorganic chemistry; Molecular inorganic chemistry; Magnetism.

Introduction

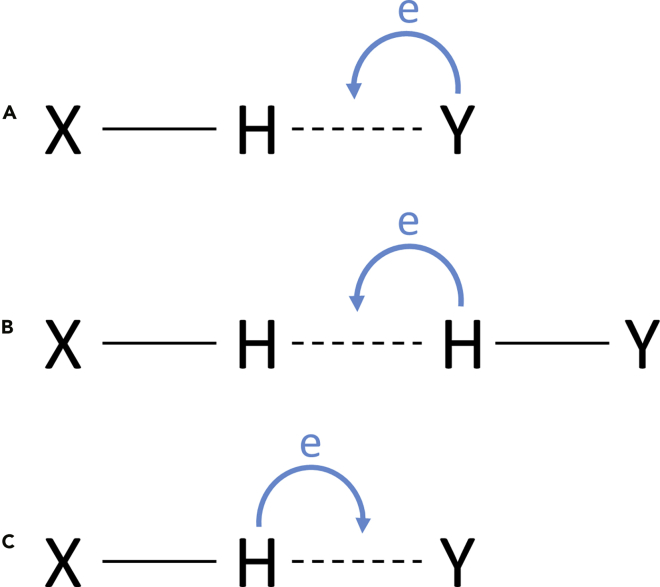
Hydrogen bond (HB) is a fundamental supramolecular interaction underpinning the complicated processes of self-assembly, molecular recognition, crystal engineering, material chemistry, catalytic cycle, and biological function (Steiner, 2002; Hannon, 2007; Braga, et al., 1999). Typical HB takes the form of X−H^δ+∙∙∙Y comprising a positively charged hydrogen atom between a pair of other electron donor-acceptor atoms (Scheme 1a). Interestingly, the bonding energy of HB varies widely, mostly depending on the electron affinity of two other atoms and the geometry among these three atoms (Rodham, et al., 1993). For instance, the bonding energy of weak C−H∙∙∙F HB is about 0.8 kJ mol⁻¹ (Howard, et al., 1996); for a typical water dimer, the bonding energy of O−H∙∙∙O HB is about 21 kJ mol⁻¹ (Gu, et al., 1999); while for linear bifluoride anion, the bonding energy of F−H∙∙∙F HB can go up to 161 kJ mol⁻¹ (Gronert, 1993). In some special cases, such as the dihydrogen bonds (Scheme 1b), the role of the H atom is divided — one H atom accepts the electrons from the other (Liu and Hoffmann, 1995).

Scheme 1.

Three kinds of hydrogen bonds

If the hydrogen atom acts as the electronic donor, such as the case shown in Scheme 1c, this type of X−H^δ−∙∙∙Y HB can be called as an inverse hydrogen bond (IHB) because the hydrogen atom is negatively charged and acts as an electron donor. IHB was initially proposed by Rozas et al., in 1997 when investigating the intermolecular interactions in metal hydrides due to the electronegativity of the hydrogen atom is much stronger than many metal atoms (Rozas, et al., 1997). Later, the IHBs were also found in nonmetal hydrides, such as SiH₄ and XeH₂ (Blanco et al., 2008; Yuan, et al., 2011). But as a whole, IHBs are still very scarce due to lower electron affinity of the hydrogen atom in most of the X-H bonds.

As boron atom is electron deficit, the electron tends to polarize to the hydrogen atom with a formal form of B^δ+−H^δ− (Pauling, 1960). This is widely observed in boron clusters (Núñez, et al., 2016) and carbon-boron clusters (carborane) (Hosmane, 2011; Zhao and Xie, 2016). Such boron-based clusters are found to be able to form B^δ+−H^δ−∙∙∙H^δ+−C^δ− dihydrogen bond (Cui et al., 2020; Xing et al., 2020) or B^δ+−H^δ−∙∙∙Mⁿ⁺ interactions (Hewes, et al., 1984; Baker, et al., 1978; Behnken, et al., 1985; Axtell, et al., 2016) when coordinating metal centers (Silva and Hardie, 2012). For M = lanthanide, several polymetallic lanthanacarborane systems bridged with B^δ+−H^δ−∙∙∙Ln³⁺ IHBs were reported previously, showing interesting and diversified structural motifs (Xie, et al., 1999; Cheung, et al., 2005; Wang, et al., 2003). However, the bonding energy was believed to be very weak due to the internal 4f orbitals of the lanthanide ions. Moreover, their physical properties are barely studied despite that dysprosiacarboranes are recently confirmed to be milestone entities for single-molecule magnets (SMMs) (Jin, et al., 2020), which may have potential applications in high-density information storage, spintronic devices, and quantum information processing, and so on (Gatteschi, et al., 2006; Mannini, et al., 2009; Leuenberger and Loss, 2001; Bogani and Wernsdorfer, 2008). In addition, the magnetic exchange coupling transferred by B^δ+−H^δ−∙∙∙Ln³⁺ IHBs is less studied although the magnetic properties affected by HBs have been discussed in some cases (Gupta et al., 2016a; 2016b; Norre, et al., 2020; Canaj, et al., 2018).

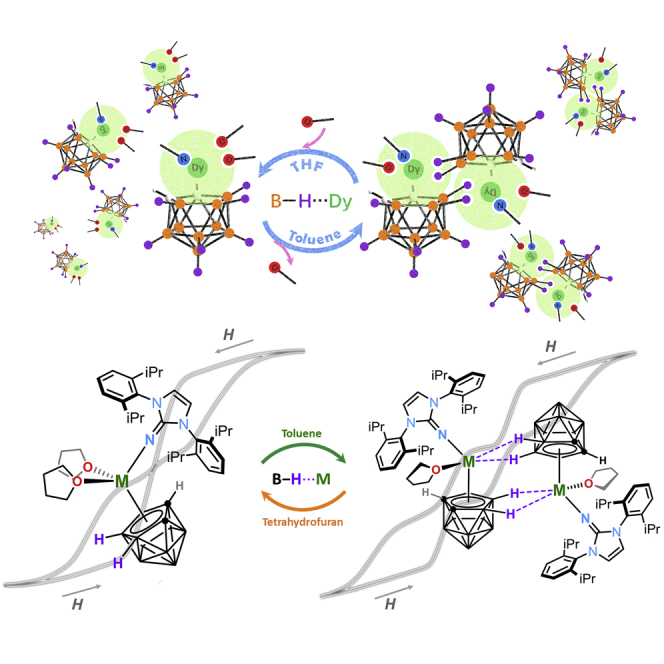
Herein, we utilize 1,3-bis(2,6-diisopropylphenyl)-imidazolin-2-iminato (Im^DippN⁻) and 2,6-bis(diphenylmethyl)-4-methylphenol (HOAr∗) to construct ten lanthanacarborane complexes. The Im^DippN⁻-based dimers namely [closo-nido-(η⁵-C₂B₉H₉) (μ-H₂)M(Im^DippN) (THF)]₂ (M = Dy, 2Dy; M = Y, 2Y) and [exo-nido-(μ-H₄-o-xylylene-C₂B₉H₉)Dy(Im^DippN) (THF)]₂ 4Dy are assembled from three respective monomeric precursors, [closo-nido-(η⁵-C₂B₉H₁₁)M(Im^DippN) (THF)₂], (M = Dy 1Dy; M = Y, 1Y), and [closo-nido-(η⁵-o-xylylene-C₂B₉H₉)Dy(Im^DippN) (THF)₂] 3Dy. We found the bonding energies of B−H^δ−∙∙∙Ln³⁺ IHBs in the dimeric complexes are larger than 24 kJ/mol, which are strong enough to construct the exchange biasing SMMs (Wernsdorfer, et al., 2002; Nava, et al., 2015; Nguyen, et al., 2016) with enhanced hysteresis loops and energy barriers (U_eff) for magnetization reversal.

More importantly, we found the bonding strength of B−H^δ−∙∙∙Mⁿ⁺ is cation-dependent. If the trivalent lanthanide is changed to the sodium(I) cation, the B−H^δ−∙∙∙Na⁺ interaction is much weakened (bonding energy of B−H^δ−∙∙∙Na⁺ is determined to be 15 kJ/mol). This is well demonstrated in two phenol-substituted dimeric derivatives [closo-nido-(OAr∗)M(THF) (η⁵-Et₂-C₂B₉H₆)Cl(μ-H)₃Na(THF)₂]₂ (M = Dy, 6Dy; M = Y, 6Y) which are respectively assembled from the monomers [exo-nido-(OAr∗)M(THF)₂(η³-Et₂-C₂B₉H₆)Cl][(μ-H)₃Na(THF)₃] (M = Dy, 5Dy; M = Y, 5Y). The reduced bonding strengths of these complexes are well reflected in their disappeared exchange-biasing effects (for details, see below).

Results and discussion

Synthesis

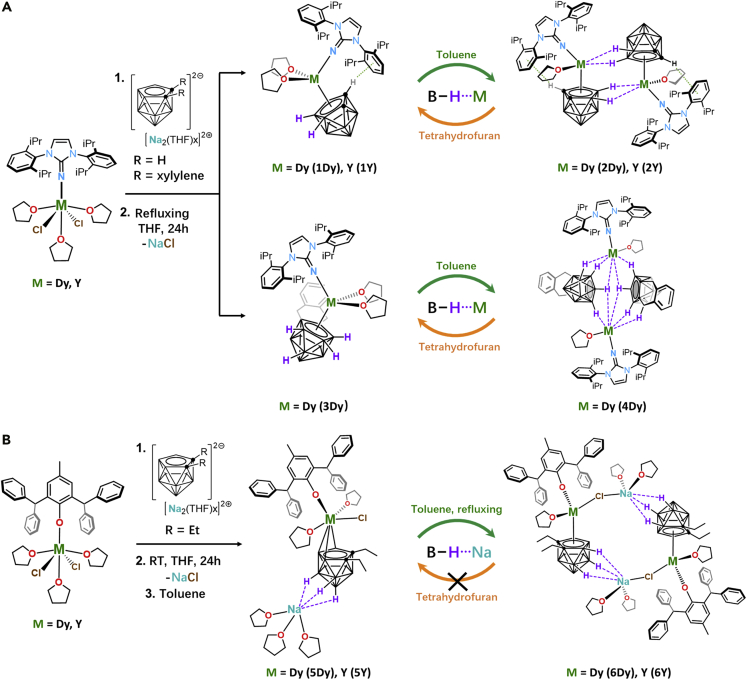
As shown in Figure 1A, the lanthanacarborane dimers (2Dy, 2Y, and 4Dy) are generated from the assembly of monomers of 1Dy, 1Y and 3Dy, respectively. The monomers 1Dy, 1Y, and 3Dy are generated from salt metathesis reaction between [(Im^DippN)MCl₂(THF)₃] (M = Dy, Y) and dicarbollide ligands nido-[C₂B₉H₁₁][Na]₂ and nido-[o-xylylene-C₂B₉H₉][Na]₂ ([{o-C₆H₄(CH₂)₂}C₂B₉H₉][Na]₂), respectively. Analogous to the synthesis of the above mentioned imidazolin-iminato incorporated lanthanacarboranes, the phenol derivative ligands OAr∗⁻ were introduced as well to have a better comparison with Im^DippN⁻. As showed in Figure 1B, bottom, a salt metathesis reaction between [Na₂][o-Et₂-C₂B₉H₉] and the dichlorides [(OAr∗)MCl₂(THF)₃] (M = Dy, Y) in THF solution produces 5Dy and its yttrium derivative 5Y. Moreover, complexes 5Dy and 5Y serve as intermediates further linking with each other to produce dinuclear structures 6Dy and 6Y. Supramolecular interaction between B−H^δ− and Ln³⁺ is verified via the reversible transformation processes of dimers (2Dy and 4Dy) and monomers (1Dy and 3Dy) under different solvent condition. However, monomers 5 cannot be reversibly isolated by simply treating dimers 6 with THF, which is different from the imidazolin-iminato incorporated complexes.

Figure 1.

The schematic diagram of the synthetic routes

(A) The synthetic routes to the imidazolin-iminato incorporated complexes 1Dy, 1Y, 2Dy, 2Y, 3Dy, and 4Dy and the reversible transformations between monomers (1Dy, 1Y and 3Dy) and dimers (2Dy, 2Y, and 4Dy).

(B) The synthetic routes to the phenol derivative incorporated complexes 5Dy, 5Y, 6Dy, and 6Y.

Structures

Single crystal X-ray diffraction measurement reveals the similar connectivity between the monomers and the dimers. Moreover, the yttrium(III) and dysprosium(III) complexes are isomorphous, so below we take the dysprosium(III) analog to discuss as a representative. Compounds 1Dy, 2Dy, and 3Dy crystallized in monoclinic space group P2₁/c, while 4Dy, 5Dy ,and 6Dy are in P-1.

For 1Dy, the pentagonal C₂B₃ bonding face of the dicarbollide ligand is η⁵-bound to the Dy(III) center and the Dy∙∙∙B/C distances to the η⁵-C₂B₃²⁻ face are ranging from 2.623(5) to 2.667(4) Å, while the Im^DippN⁻ ligand links to Dy(III) in an almost linear fashion (C‒N‒Dy angle of 176.05°) with a very short Dy‒N bond of 2.095(3) Å (Figure S1). In addition to the C₂B₉H₁₁²⁻and Im^DippN⁻ ligands, the coordination sphere of Dy(III) center is completed by two THFs to give a tetrahedral geometry with Dy‒O bond length at around 2.36 Å.

For 2Dy (Figure S3), the two asymmetric units connect to each other via four B−H^δ−∙∙∙Dy³⁺ IHBs with the distance of Dy³⁺∙∙∙Dy³⁺ of 4.081 Å. The angles of B−H∙∙∙Dy are ranging from 96.43° to 109.44°, and the H∙∙∙Dy distances are between 2.25 and 2.46 Å. In contrast to 1Dy, one THF molecule is eliminated. The Dy‒O distance remains unchanged, while the Dy‒N bond is a bit lengthened, to 2.107(3) Å. The bending angle of N−Dy−centroid (C₂B₃) is 117.27° and the Dy-centroid (C₂B₃) distance is 2.343 Å, similar to these of 1Dy.

The larger substituent group [o-xylylene-C₂B₉H₉]²⁻ results in the monomeric compound 3Dy (Figure S5), which has a wider bending angle N−Dy−centroid of 131.37° and a very short Dy‒N bond of 2.123(3) Å. The Dy∙∙∙B/C distances to the η⁵-C₂B₃²⁻ face have a wider range of 2.601(4) to 2.788(3) Å and a much shorted Dy∙∙∙ centroid (C₂B₃) distance of 2.275 Å.

However, due to the steric hindrance of [o-xylylene-C₂B₉H₉]²⁻ ligands the Dy³⁺ in 4Dy is no longer half sandwiched. Rather, it forms a pair of centrosymmetric exo-nido-dysprosiacarborane bridges (Figure S7). The Dy³⁺ ions are bridged by multiple B−H^δ−∙∙∙Dy³⁺ IHBs with Dy³⁺∙∙∙Dy³⁺ distance of 4.162 Å, among which the H1 atom is from the lower belt of the dicarbollide cage and other hydrogen atoms (H2, H3, and H4) are from the C₂B₃ pentagonal face. The distances of H−Dy range from 2.307 Å to 2.572 Å and the angles of B−H∙∙∙Dy range from 88.87° to 100.01°. Remarkably, the Dy−N bond length reduces to 2.066(2) Å, which is the shortest among these structures. This is probably due to the edge-coordinate mode of the dicarbollide ligand which less diverges the electrostatic attraction from the central cation.

For 5Dy (Figure S9), the Dy³⁺ ion has a slip distortion from the center of the C₂B₃ bonding face of the carboranyl ligand, which leads to much longer Dy–C(cage) and shorter Dy–B(cage) distances than that of 1Dy and 3Dy. The shortest Dy–C bond is 3.155(2) Å and Dy–B distances are ranging from 2.570(3) Å to 2.868(4) Å. The Dy(III) ion is bound to the (C₂H₅)₂C₂B₉H₉²⁻ ligand with η³ fashion. The Dy–O_(PhO) bond length is 2.112(2) Å, much shorter than the Dy–O_(THF) (2.432(3) Å and 2.455(2) Å). The solvated Na(I) ion is chelated by the carboranyl cages via triple B−H∙∙∙Na⁺ interactions and the H∙∙∙Na⁺ distances are between 2.601 and 2.724 Å, which are much longer than those of H∙∙∙M³⁺ in 1-4, indicative weaker IHBs.

For 6Dy (Figure S11), the Na(I) cation attaches to the chloride by electrostatic force with ionic bond length of 2.738(3) Å. The Na–Cl ionic bonds connect two adjacent units to produce a pair of centrosymmetric closo-nido-dysprosiacarborane bridges. Thus, the two Dy(III) centers in 6Dy are away from each other with Dy³⁺∙∙∙Dy³⁺ distance of 6.907 Å. Each Dy(III) ion in 6Dy has the similar coordination environment as those in 5Dy except for shorter H∙∙∙Na distances (2.356–2.659 Å). The Dy to the B/C of the η⁵-C₂B₃²⁻ face distances are ranging from 2.657(6) Å to 2.726(5) Å, and the Dy³⁺∙∙∙C₂B₃²⁻ face centroid distance is 2.268 Å. Other coordination sites were occupied by the oxygen atom of the [OAr∗]^– ligand and a Cl^– with Dy–O_(PhO) and Dy–Cl distances of 2.098(4) Å and 2.626(3) Å, respectively. Note that the Dy–O_(PhO) distance of 6Dy is shorter than that (2.112(2) Å) of 5Dy.

The crystal packing diagrams along a axis of 1Dy to 6Dy are shown in Figures S1–S12, respectively. The Dy(III) centers of different molecules are away from each other with the shortest intermolecular Dy³⁺∙∙∙Dy³⁺ distance 9.47 Å in 3Dy and the longest 12.48 Å in 6Dy.

NMR and IR spectra

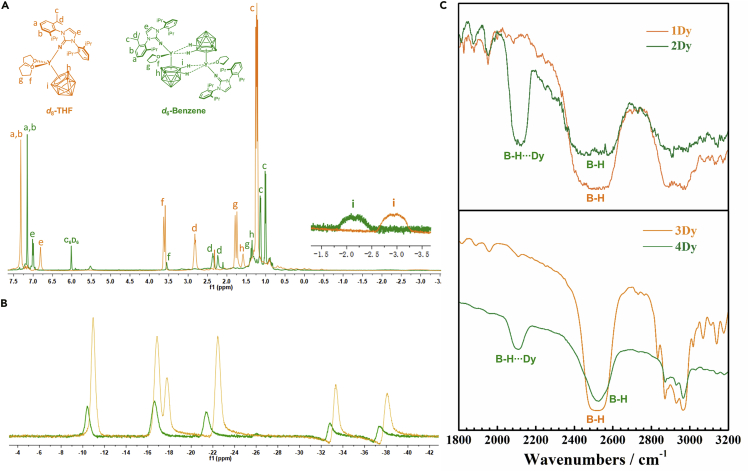
As the Y(III) is diamagnetic high-resolution ¹H NMR and ¹¹B NMR spectra can be obtained to study the strength of the B−H^δ−∙∙∙M³⁺ interaction (Figure 2A). These interactions can be well detected by the significant difference of the chemical shifts of 1Y in THF-d₈ and 2Y in Benzene-d₆. Besides, the signals of the alkyl hydrogen atoms of 2Y have the upfield shifts (a, b, c, d, f, g, h) while B-H broad signal (i) shifts downfield (from −2.6 ~ −3.5 ppm to −1.8 ~ −2.5 ppm) comparing with 1Y, which is attributed to the positive charge environment (Y³⁺) of B−H^δ−∙∙∙Y³⁺ linkages. In contrast, the transition from complexes 5Y to 6Y makes no difference to their chemical environment, giving very similar ¹H NMR spectrums and almost identical B-H signals in the range of −1.3 ~ −2.0 ppm (Figures S13 and S14). Moreover, for the dinuclear complex 2Y, the alkyl hydrogen atoms of two coordinated imidazolin-iminato ligands have non-equivalent chemical environment and are with slightly difference to give the separated C−H signals (e d and c). The smaller number of coordinated THF molecules in 2Y are also well detected with much weaker corresponding signals (f and g). The ¹¹B NMR shows the six resonances with 2:2:1:2:1:1 ratio from −10 to −40 ppm for 1Y and five resonances with 2:3:2:1:1 ratio for 2Y, whose signals shift downfield (Figure 2B). Most of peaks of monomer 1Y and dimer 2Y are asymmetrical except the two in −37.2 and −32.6 ppm of 2Y, giving the symmetric peaks which is mainly due to the existence of quadruple B−H^δ−∙∙∙Y³⁺ interactions in 2Y.

Figure 2.

The NMR and Infrared spectrums

(A and B) The ¹H NMR (A) and ¹¹B NMR (B) spectrum assignment for complexes 1Y (orange) and 2Y (olive-green). (Insert) Expanded view of the chemical shift from −3.5 to −1.5 ppm.

(C) Infrared spectrum of complexes 1Dy and 3Dy (orange) and 2Y and 4Dy (olive-green).

Solid-state infrared (IR) spectra of 1 to 6 exhibit broad resonance region at 2500 cm⁻¹, which is the characteristic peak of B−H stretches from carboranyl cages (Figures 2C and S17−S22). This is also a quick way to identify the existence of carboranyl ligands. Besides, an additional strong absorption is observed in ~2100 cm⁻¹ for 2Dy, 2Y, and 4Dy but not for 1Dy, 1Y, and 3Dy (Figures S17 and S18), which is suggestive of the existence of B−H^δ−∙∙∙M³⁺ stretching bands in 2Dy, 2Y, and 4Dy. Such M∙∙∙μ-H−B interactions have been noted previously (Chui, et al., 2000). In contrast, the IR spectra of complexes 5 and 6 give no extra B−H stretching peaks even at the presence of triple B−H^δ−∙∙∙Na⁺ interactions (Figures S19−S22), indicative of much weaker IHBs.

Computational studies

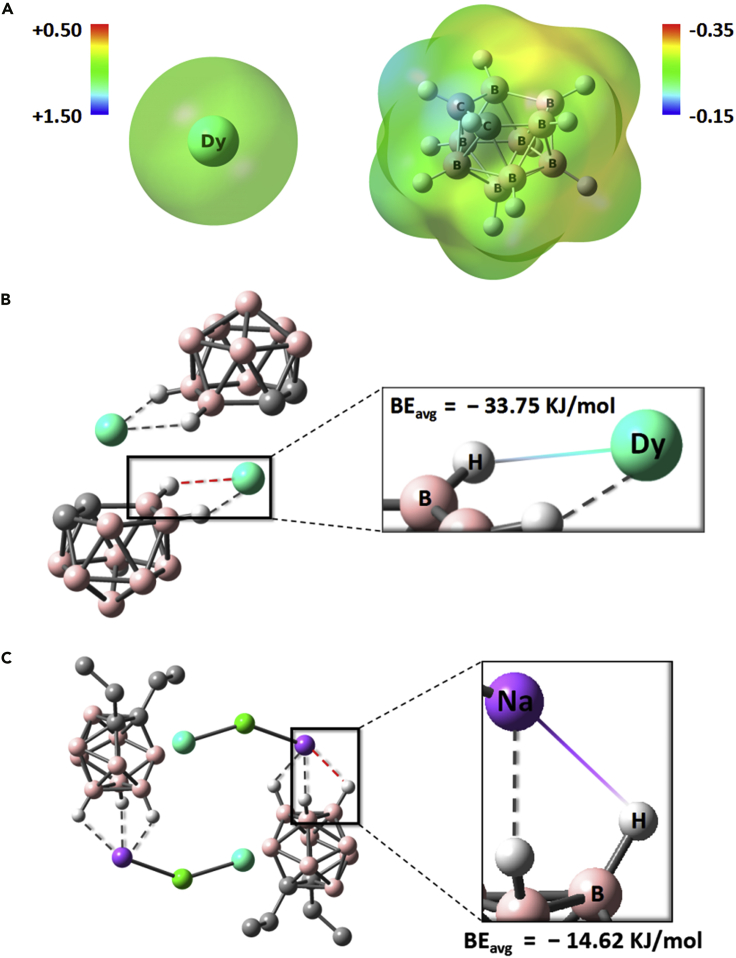
Density Function Theory (DFT) calculation was employed to acquire specific bonding energy for B−H^δ−∙∙∙Dy³⁺ and B−H^δ−∙∙∙Na⁺ IHBs using Gaussian 09. The B−H^δ− surface with negative electrostatic potential has strong interaction to Dy³⁺ (Figure 3A). The average bonding energy (BE_avg) is introduced by considering the complexes' centrosymmetry and similarity of Dy−H and Na−H distances. The calculation gives BE_{avg(B−H∙∙∙Dy)} = −33.75 kJ/mol for 2Dy, BE_{avg(B−H∙∙∙Dy)} = −24.99 KJ/mol for 4Dy, and BE_{avg(B−H∙∙∙Na)} = −14.62 KJ/mol for 6Dy (Figures 3B, 3C, and S77). The striking contrast of the binding energy between B−H^δ−∙∙∙Dy³⁺ and B−H^δ−∙∙∙Na⁺ is attributed to the cation dependent electrostatic interactions and exist one kind of relationship as BE_{avg(B−H∙∙∙Dy)} > BE_{avg(B−H∙∙∙Na)}. Nevertheless, these energy range is comparable to other hydrogen-bonded complexes which show B–H···π interactions with the binding energy ranging from −16.47 to −21.19 kJ/mol by using natural population analysis (Kolandaivel and Nirmala, 2004; Zhang, et al., 2016). Moreover, to confirm the strength relationship of B−H^δ−∙∙∙Dy³⁺ and B−H^δ−∙∙∙Na⁺, atoms in molecules (AIM) was adopted by using Multiwfn, which is a popular theory on electron density (ED) topological analysis (Bader, 1994; Lu and Chen, 2012a, 2012b). In this theory, the point of zero ED gradient in space is called critical point (CP), primarily consisting of four sorts: (3,-3), (3,-1), (3,+1), and (3,+3). Among them, the (3, −1) point, the second order saddle point of the ED function, is usually located between both adjacent atoms, called bond critical point (BCP) whose ED value can be employed to measure the strength of the same variety of interactions. Here for simplicity, these dimer molecules used in AIM analysis are the same as model dimer complexes in DFT calculations. All BCPs around B−H^δ−∙∙∙Mⁿ⁺ were found and their calculated total ED was listed in Table S40. Similarly, we introduced the average value of ED, named ρ_avg. It is evident that there is such a relationship: ρ_avg(2Dy) ≈ ρ_avg(4Dy) > ρ_avg(6Dy), which is consistent with the strength relation of calculated IHB binding energy, indicating the reliability of DFT calculations.

Figure 3.

Density Function Theory (DFT) calculation

(A) Electrostatic potentials of Dy(III) and nido-[C₂B₉H₁₁]^2- ((isovalue = 0.001)).

(B and C) Bonding energy between fragments for 2Dy (B) and 6Dy's (C) model complexes through DFT calculation. For clarity, certain hydrogen atoms in both complexes are omitted. (cyan for Dy, pink for B, gray for C, green for Cl, purple for Na and white for H).

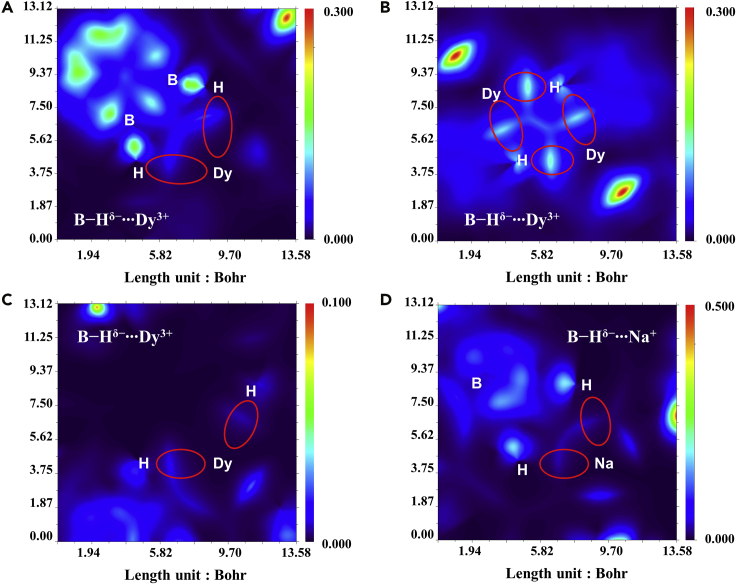
Intermolecular interaction region and its characteristics can be exhibited using Independent Gradient Model (IGM), which is a methodology based on ED (Lefebvre, et al., 2017). Generally, the gradients of ED between both atoms with interaction possess contrary signs. When the total gradient superposed in the region is zero, the position is exactly right BCP. Under normal circumstances, the total gradient at a certain point is regarded as the sum of the atomic gradients, denoted as $\left|\nabla \rho \right|$, while the IGM type density gradient ($\left|\nabla {\rho }^{\text{IGM}}\right|$) is defined as the sum of the absolute values of the individual atomic gradient. The so-called δg function is the difference between the above two quantities, as shown in Equation 1. The absolute value is introduced in calculation, thus the value of the function between both atoms, especially at BCP, is not relatively small, leading to the fact that the magnitude of δg is proportional to the strength of interactions and also outlines bonding regions between both atoms. To reveal distribution character of δg function, variable sections from their 3D isosurface representations based on this model have been plotted, showing existing B−H^δ−∙∙∙Dy³⁺ and B−H^δ−∙∙∙Na⁺ interactions in complexes 2Dy, 4Dy, and 6Dy using Multiwfn (Figure 4). For clarity, we adjusted the upper limits of δg function in these plots and the color from red to blue corresponds to the descending δg value. The part of each plot circled in red illustrates the existence of the B−H^δ−∙∙∙Mⁿ⁺. Compared with other regions, these interactions are evidently weaker than covalent bond.

$$\text{δ}g=\left|\nabla {\rho }^{\text{IGM}}\right|-\left|\nabla \rho \right|$$ (Equation 1)

Figure 4.

Cross section coloring maps

B−H^δ−∙∙∙Dy³⁺ and B−H^δ−∙∙∙Na⁺ interactions in 2Dy (A), 4Dy (B, C), and 6Dy (D) respectively.

Moreover, fingerprint plots and color-mapped isosurface graphs of Hirshfeld surface were produced by using Multiwfn and VMD (Figure S78) (Spackman and Jayatilakaa, 2009; Lu and Chen, 2012a; 2012b; Humphrey, et al., 1996). As we considered two Dy(III) (2Dy and 4Dy) and one Na(I) (6Dy) ion in the central area, the spikes at bottom of the finger plots mean existence of interactions between Dy(III) or Na(I) and other coordinated atoms in the peripheral areas. Meanwhile, the color from blue to red corresponds to ED varying from 0.0 to 0.015 a.u. in color-mapped isosurface graphs of Hirshfeld surface, indicating that red color area represents relatively large ED. All types of plots are in good agreement with X-ray diffraction analysis and DFT calculations, further proving that the interaction caused by boron-hydrogen bridging is crucial to the formation of binuclear compounds from mononuclear compounds in our system. At this point, we may conclude that there are two main advantages to form this kind of infrequent bonding interaction in our system: (1) the dual role of THF—reactant and solvent: abundant toluene goes against the coordination between THF and Dy(III); (2) more positive electrostatic potential of Dy(III) benefits the formation of B−H^δ−∙∙∙Dy³⁺ interaction.

Magnetic exchange-coupling interactions

For better understanding the exchange couplings transferred by B−H^δ−∙∙∙M³⁺ interactions between Ln³⁺ centers, we thoroughly investigate the magnetic properties of dysprosium(III)-based dinuclear complexes 2Dy, 4Dy, and 6Dy. Such couplings can be displayed in the field- and temperature-dependent magnetization (M) plots. The temperature-dependent molar magnetic susceptibilities (χ_m) under an applied field of 1000 Oe over the temperature range 2 K–300 K give the room temperature χ_mT products (in emu K mol⁻¹ and the same below) to be 27.48, 27.51, and 27.73 for 2Dy, 4Dy and 6Dy, respectively. These values are slightly below two free Dy(III) ions of 28.34 emu K mol⁻¹ calculated from S = 5/2, L = 5, and g = 4/3 (Figures S23−S27). For 2Dy and 4Dy, the χ_mT curves decrease slowly from 300 K to 30 K and rapidly afterward (Figures S24 and S26). In contrast, the decreasing trend in 6Dy is much slower largely due to the weaker interactions (Figure S27).

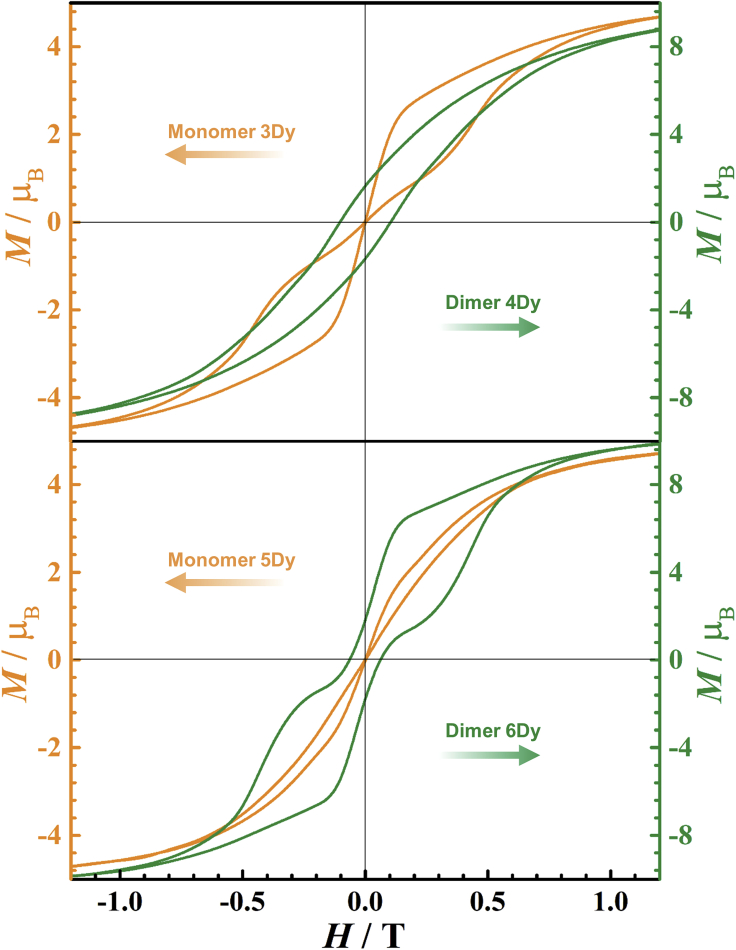
The effect of magnetic interaction is evident in the hysteresis loops (Figures 5 and S28−S33). For the monomers, namely complexes 1Dy, 3Dy and 5Dy, the hysteresis loops are waist-restricted with strong quantum tunneling of magnetization (QTM) effect at zero field. In contrast, the loops remain opened around zero field for dimers, namely complexes 2Dy, 4Dy, and 6Dy. Especially for 2Dy and 4Dy, in which the Dy(III) ions are bridged by B−H^δ−∙∙∙Dy³⁺ IHBs the coercive fields (H_c) are larger than 1000 Oe (Figure 5, top and S32, left); while for 6Dy, in which the Dy³⁺ ions are separated without B−H^δ−∙∙∙Dy³⁺ linkage gives much smaller H_c of 600 Oe (Figure S32, right). Interestingly, step-like hysteresis loop is clearly observed for 2Dy (Figure S28B). These steps are attributed to the level-crossing between the low-lying states of the dimer. If this complex is diluted with the yttrium(III) analog 2Y, the formed diluted sample 2Dy@2Y shows again waist-restricted shape (Figure S29, left), indicating the effect of intramolecular Dy³⁺∙∙∙Dy³⁺ interactions are absent.

Figure 5.

The magnetic hysteresis measurements

The comparison of magnetic hysteresis loops between polycrystalline samples 3Dy and 4Dy (top); 5Dy and 6Dy (bottom) at 2 K under an average sweep rate of 15 Oe s−1

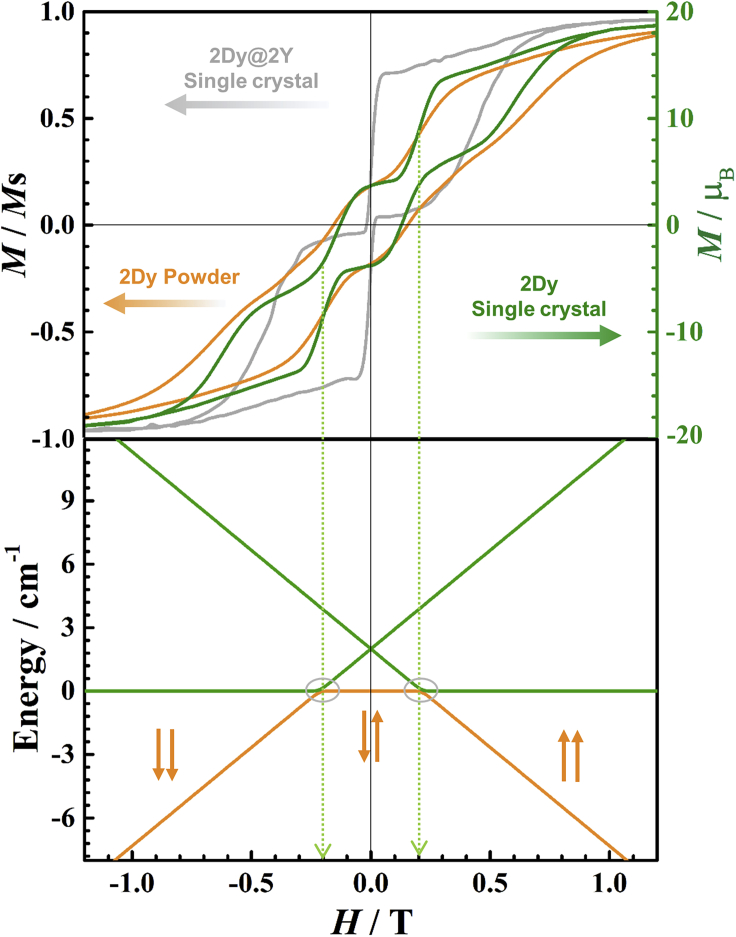
The QTM step-like hysteresis loop of 2Dy can also be well characterized with easy axis of single crystal sample (Figure 6, top, green), which is well explained with the Zeeman diagram of 2Dy (Figure 6, bottom). Upon decreasing the field, the saturated magnetic moment gradually flips from the |− −> configuration of the ferromagnetic state to the antiferromagnetic states (|+ −>, |− +>). When it comes to 0.2 T, about 40% moments undergo a transition due to the QTM process at the field of level crossing between the (|− −>) and the (|+ −>, |− +>) states. At field values away from the avoided level crossing, the dimer states are approximately frozen by the significant magnetic anisotropy barrier, demonstrated with plateaus in the hysteresis loop. The plateaus last until the next tunneling happens at −0.2 T from antiferromagnetic states (|+ −>, |− +>) to ferromagnetic state (|+ +>). The single crystal sample of 5% diluted 2Dy@2Y gives strong QTM at zero field, indicating the consequence of the absence of intra- and inter-molecular interactions (Figure 6, top, gray).

Figure 6.

The magnetic hysteresis measurements and Zeeman diagram

(Top) The magnetic hysteresis loop measurements (top) at 2.0 K for single crystal sample of 2Dy (green), 2Dy@2Y (gray) with sweep rate 7 Oe/s and powder sample of 2Dy (orange) with sweep rate 15 Oe/s.

(Bottom) the simulated Zeeman diagram for the single crystal sample of 2Dy.

To further understand the exchange biasing phenomenon in 2Dy, the intramolecular interaction between magnetic centers was studied through experimental data analysis and theoretical calculation. It has become a consensus that total interaction within both Dy(III) ion centers (J_total) primarily consist of magnetic exchange and dipole-dipole exchange whose coupling constants are expressed by J_exch and J_dip, respectively. Equation 2 is the Hamiltonian that expresses the relationship among the three coupling constants through J_total = J_exch + J_dip.

$$\hat{H}={\hat{H}}_{exch}+{\hat{H}}_{dip}=-J_{total}{\hat{\tilde{S}}}_{1z}{\hat{\tilde{S}}}_{2z}=-(J_{exch}{\hat{\tilde{S}}}_{1z}{\hat{\tilde{S}}}_{2z}+J_{dip}{\hat{\tilde{S}}}_{1z}{\hat{\tilde{S}}}_{2z})$$ (Equation 2)

$${\overline{J}}_{dip}=\frac{{{\mu }_B}^2}{{\left|r\right|}^3}\left[{\overline{g}}_1\cdot {\overline{g}}_2-3\left({\overline{g}}_1\cdot \stackrel{\rightharpoonup }{r}\right)\left(\stackrel{\rightharpoonup }{r}\cdot {\overline{g}}_2\right)\right]$$ (Equation 3)

Equation 3 is the expression for dipole-dipole interaction. By using the POLY_ANISO module, the magnetic data can be fitted (Figures S24, S26, and S27). Based on J_xx, J_yy, and J_zz, this module also outputs the Zeeman diagrams in three directions (Figure S76). As shown in Table 1, the magnitude of the J values is indicative of the strength of magnetic interactions and the sign of the J values represent ferro (+) and antiferro (−) magnetic interactions. The strength of total exchange coupling follows a trend of descending. With regard to J_exch, the values of 2Dy (−1.76 cm⁻¹) and 4Dy (−1.83 cm⁻¹) are approaching due to the similar distance between magnetic centers of 4.08 Å and 4.16 Å, respectively, hinting this part of magnetic exchange goes through resemble path, while longer distance of 6.91 Å for 6Dy creates less J_exch (−0.78 cm⁻¹). Under Ising approximation, g in Equation 2 can be replaced by g_z to calculated J_dip values. Despite approximate g_z values of their ground states, yet the angle between magnetic axis at both magnetic centers is different as well as the angle between magnetic axis and the connection of magnetic ions, leading to diverse dipole-dipole interactions with corresponding J_dip values 0.64 cm⁻¹, 1.14 cm⁻¹, and 0.37 cm⁻¹ of 2Dy, 4Dy, and 6Dy, respectively. 2Dy and 4Dy possess the same ligands, but the dipole-dipole interactions are distinctive, resulting from different closo- and exo-linkage coordination modes of C₂B₃ pentagonal facing to Dy(III). Consequently, the flexible coordination ways of carboranyl ligand can be realized by synthesis to control the magnetic exchange interaction via adjusting magnetic axis orientation. For 6Dy, because of the farthest distance between the magnetic centers, the J_dip is naturally the smallest. On the whole, the larger J_total values for 2Dy and 4Dy are presumably contributed from the B−H^δ−∙∙∙Dy³⁺ IHBs, which is much stronger than the B−H^δ−∙∙∙Na⁺ in 6Dy. Moreover, we analyzed dc magnetic data of single crystal sample of 2Dy and performed the fitting of magnetic interaction from z axis direction using PHI code. The coupling constant J_zz is coinciding with the sum of J_zz components of J matrix and the Zeeman diagram from POLY_ANISO (Figure 6, bottom), giving much reliable coupling constant of −2.01 cm⁻¹, which is comparable to the coupling values J = +4.4 cm⁻¹ and J = −4.6 cm⁻¹ transferred from single or double oxygen anion bridged Dy(III) dimers (Wang, et al., 2021; Xiong et al., 2017) and even larger than that of double chloride bridged Dy(III) dimers with J = −0.83 cm⁻¹ and J = −1.48 cm⁻¹, respectively (Han, et al., 2020; Han, et al., 2019).

Table 1.

Magnetic coupling constants (cm⁻¹) between two Dy(III) sites of 2Dy, 4Dy, and 6Dy

Complexes	Jexch	Jdip	Jtotal	Jzz
2Dy	−1.76(1)	0.64(2)	−1.12(2)	−2.01(2)
4Dy	−1.83(1)	1.14(1)	−0.69(2)	/
6Dy	−0.78(1)	0.37(2)	−0.41(2)	/

Dynamic magnetism

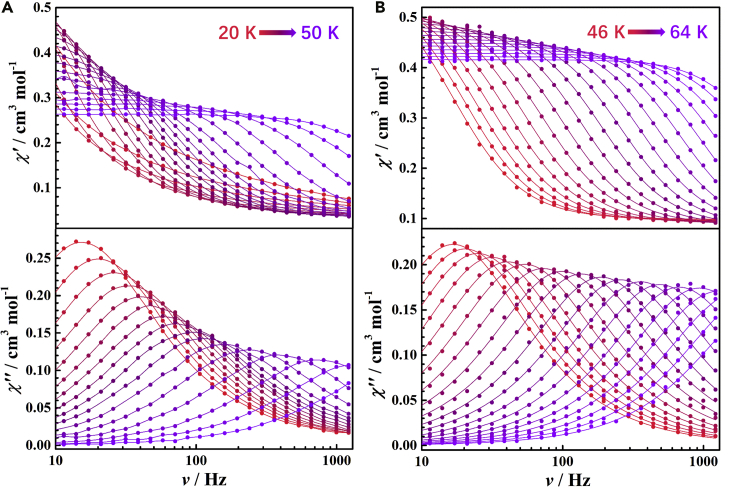
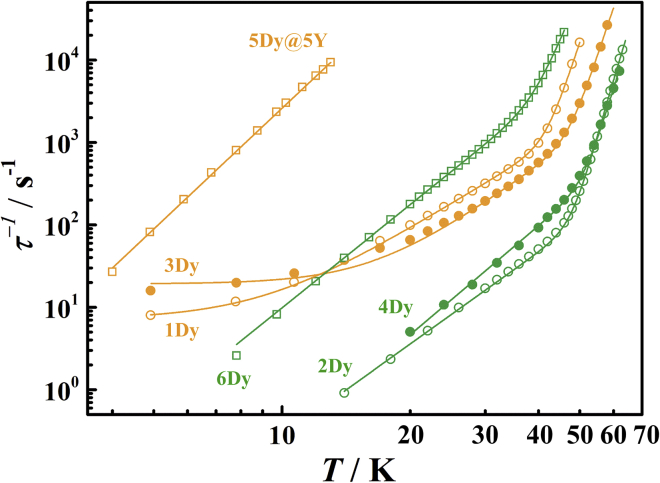
As these complexes demonstrate the SMM behavior, we analyze the dynamics of the magnetization using alternative current (ac) magnetic measurements (Figures 7 and S44–S65). The temperature- and frequency-dependent ac susceptibilities for 1Dy, 2Dy, 2Dy@2Y, 3Dy, 4Dy, 5Dy@5Y, 6Dy, and 6Dy@6Y are showed in Figures S44–S55, which can be fitted by CC-FIT program to obtain the log-log plots of ${\tau }^{-1}$ vs T (Figures 8, S64, and S65) (Chilton, 2014). All of the plots obey the Arrhenius law ${\tau }^{-1}={{\tau }_0}^{-1}{e}^{-U_{eff}/T}$ in the high temperature regime and are consistent with an Orbach relaxation mechanism over an effective energy barrier U_eff, except for 2Dy@2Y, which can be well fitted with ${\tau }^{-1}=C{T}^n$. The plots become power-law $C{T}^n$ temperature dependence along with the fall of temperature, which is the characteristic of a two-phonon Raman process. However, in contrast with 2Dy, 4Dy, and 6Dy, the magnetic relaxation process of 1Dy and 3Dy is accelerated below 10 K due to the zero-field QTM process. In this case, the relaxation times of dimers 2Dy, 4Dy, and 6Dy and monomers 1Dy and 3Dy could be well fitted by the Equation 3. The fitting gives parameters summarized in Table 2.

$${\tau }^{-1}={{\tau }_0}^{-1}{e}^{-U_{eff}/T}+C{T}^n+{{\tau }^{-1}}_{QTM}$$ (Equation 4)

Figure 7.

The AC magnetic susceptibility measurements

Frequency-dependence of the in-phase (χ′, top) and out-of-phase (χ", bottom) ac susceptibility signals for polycrystalline sample of 1Dy (A) and 2Dy (B) in zero DC field and an oscillating field of 3.5 Oe.

Figure 8.

Plot of natural log of the inverse relaxation time vs. temperature for 1Dy, 2Dy, 3Dy, 4Dy, 5Dy@5y, and 6Dy

The plots are from the ac susceptibility measurements. The lines are best fit with Equation 4.

Table 2.

The magnetic relaxation parameters of 1Dy, 2Dy, 2Dy@2Y, 3Dy, 4Dy, 5Dy@5Y, 6Dy, and 6Dy@6Y

Complexes	Ueff (K)	τ0 × 10−12 (s)	C (s−1 K−n)	n	τQTM (s)
1Dy	830(7)	4.2(2)	5.9(3)×10−3	3.2(1)	0.14(1)
2Dy	1089(6)	2.4(1)	5.5(2)×10−5	3.7(2)	/
2Dy@2Y	1089(6)	2.3(1)	1.3(2)×10−4	3.56(2)	/
3Dy	940(5)	3.9(1)	4.5(2)×10−4	3.78(1)	0.052(1)
4Dy	1106(5)	2.5(1)	9.0(1)×10−6	4.39(1)	/
5Dy@5Y	/	/	3.5(2)10−2	4.87(2)	/
6Dy	704(10)	12.8(2)	7.0(2)×10−4	4.16(2)	/
6Dy@6Y	704(10)	12.5(1)	2.0(1)×10−4	4.5(1)	/

From Table 2 we can see all the dimeric complexes (2Dy, 4Dy, and 6Dy) possess much higher energy barriers, U_eff = 1089(6) K for 2Dy, 1106(5) K for 4Dy, and 704(10) K for 6Dy, if compared to their corresponding monomers, U_eff = 830(7) K for 1Dy, 940(5) K for 3Dy and none for 5Dy@5Y (Table 2). It's worth noting that the U_eff values of 2Dy and 4Dy above 1000 K are very high for polynuclear SMMs (Wang, et al., 2021; Han, et al., 2020; Krylov, et al., 2017; Gould, et al., 2020; Meng, et al., 2020). The only higher value is reported in the compound Dy₂ScN@C₈₀-I_h with U_eff = 1735 ± 21 K (Krylov, et al., 2017). Moreover, the imidazolin-iminato incorporated dysprosium complexes 1Dy, 2Dy, 3Dy, and 4Dy exhibit larger U_eff than phenol derivative incorporated ones 5Dy and 6Dy do, which is attributed to the stronger electron donating ability of Im^DippN⁻ than that of OAr∗⁻ (Trambitas, et al., 2011; Liu, et al., 2019).

CASSCF-SO calculations were performed to gain insight into the electronic structure of Dy(III) ions and understand their magnetic properties. For 1Dy and 3Dy, as expected, pure |±15/2 > Kramers Doublets (KDs) have been stabilized by the crystal field in the two mononuclear complexes, reflecting a strong axial coordination to the central ion site. For 1Dy, the first and second excited KDs are fairly pure, 95.1% |±13/2> and 78.9% |±11/2 > respectively, but the proportion of |±9/2> in third excited KDs is only 43.5%, indicating that magnetic relaxation pathway passes between the second and third excited ones (778 K and 930 K), which is consistent with the experimental value. Naturally, those are the similar cases for 3Dy whose calculated barriers is 906 K–1026 K. Furthermore, 3Dy possesses higher barrier due to its purer KDs, demonstrating more fairly pure doublets benefit the increment of energy barrier in our system. For their dimer counterparts, their single ion fragments were considered to perform calculations at identical level, due to the fact that the energy barrier of binuclear compound primarily originates from single magnetic ion. These three fragments of centrosymmetric complexes 2Dy, 4Dy, and 6Dy possess much higher energy barriers owing to less equatorial coordinated THF solvent, which don't make evident QTM process emerging until higher KDs. In addition, the principal magnetic axis of the ground KD of 1Dy, 2Dy, 3Dy, 4Dy, 5Dy, and 6Dy are toward to N or O of Im^DippN⁻ and OAr∗⁻ instead of the C₂B₃ face centroid (Figures S66–S71), indicating the σ donor ligand has stronger influence on the magnetic anisotropy if compared to the π type dicarbollide ligand. Both results show their ground states agree with the Ising limit state (g_x = g_y = 0, g_z = 19.87 for 2Dy; g_x = g_y = 0, g_z = 19.83 for 4Dy); g_x = g_y = 0, g_z = 19.82 for 6Dy) (Tables S17, S19, and S21). Moreover, all the imidazolin-iminato incorporated dysprosiacarborane dimeric complexes show larger U_eff compared to pure dicarbollide-based dysprosium(III) SMMs.²⁶ Apart from magnetic coupling constants and Zeeman diagrams, the exchange energies and g_z values corresponding to the exchange doublets were also output by POLY_ANISO and listed in Tables S28–S30, where the exchange energies for 2Dy, 4Dy, and 6Dy are 1.676 cm⁻¹, 1.036 cm⁻¹, and 1.006 cm⁻¹, as well as g_z values of the first excited doublets 39.748, 39.757, and 39.650, respectively.

Conclusion

In conclusion, ten lanthanacarborane complexes were synthesized to study the unusual B−H^δ−∙∙∙Mⁿ⁺ IHBs, and found that the bonding strength is cation dependent and is determined to be 33.75 KJ/mol and 24.99 KJ/mol with the DFT calculations for 2Dy and 4Dy (M = Ln and n = 3), thereby can be used to switch on the exchange-biasing effect between the magnetic centers and resulting in a zero-field opened hysteresis loops up to 7.7 K and 5.9 K with large coercive fields of H_c = 1600 Oe and H_c = 1000 Oe at 2 K for 2Dy and 4Dy, respectively. In contrast, B−H^δ−∙∙∙Na⁺ interaction in 6Dy is much weaker (binding energy = 14.62 KJ/mol). Moreover, for 2Dy the step-like hysteresis loops of single crystal measurement along the easy-axis gives a coupling constant J_zz = −2.01(2) cm⁻¹, even larger than that of chloride bridged Dy(III) dimers. Intriguingly, the U_eff values of the imidazolin-iminato incorporated dysprosiacarborane complexes are much larger than those of the phenol analogs, suggesting stronger electron donating ability toward metal ions of the imidazolin-iminato ligand. Together, these results clearly demonstrate that the strength of B−H^δ−∙∙∙M³⁺ IHB is cation dependent and can be used to construct the exchange-biasing SMMs in a reversible way.

Limitations of the study

It should be noted that the step-like hysteresis loop of 2Dy is present only at relatively lower temperatures. In addition, the magnetic measurement for single crystal sample is only suitable for 2Dy, which can grow larger size crystals.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Crystal data for 1Dy	[CCDC]: [2047062]	Deposition Number: 2047062
Crystal data for 2Dy	[CCDC]: [2047063]	2047063
Crystal data for 2Y	[CCDC]: [2047064]	2047064
Crystal data for 3Dy	[CCDC]: [2047065]	2047065
Crystal data for 4Dy	[CCDC]: [2047066]	2047066
Crystal data for 5Dy	[CCDC]: [2058168]	2058168
Crystal data for 5Y	[CCDC]: [2058169]	2058169
Crystal data for 6Dy	[CCDC]: [2058167]	2058167
Crystal data for 6Y	[CCDC]: [2058170]	2058170
Software and algorithms
OPEN MOLCAS	Ignacio, et al., 2019	http://www.molcas.org/
Gaussian	Frisch, et al., 2009	http://gaussian.com/
Multiwfn	Lu and Chen (2012a), 2012b	http://sobereva.com/multiwfn/
VMD	Humphrey, et al., 1996	https://www.ks.uiuc.edu/Research/vmd/
COCO-FIT	Chilton (2014)	http://www.nfchilton.com/cc-fit.html.
PHI	Chilton, et al., 2013	http://www.nfchilton.com/phi.html

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Yan-Zhen Zheng (zheng.yanzhen@xjtu.edu.cn).

Materials availability

All materials generated in this study are available from the lead contact without restriction.

Data and code availability

Crystal data for (1Dy), (2Dy), (2Y), (3Dy), (4Dy), (5Dy), (5Y), (6Dy) and (6Y) are available from the Cambridge Crystallographic Data Centre under CCDC: 2047062, 2047063, 2047064, 2047065, 2047066, 2058168, 2058169, 2058167, 2058170. Computational output is available on request.

Method details

Synthesis

All experiments were performed under an atmosphere of dry argon with the rigid exclusion of air and moisture using standard Schlenk or in a glovebox. THF were dried and degassed by standard techniques. Anhydrous LnCl₃ (Ln = Dy) were prepared according to literature procedures (Reed, et al., 1939). [Me₃NH][C₂B₉H₉] (Xie, et al., 1997), [Me₃NH][o-C₆H₄(CH₂)₂-C₂B₉H₉] (Kwong, et al., 2004), Im^DippNH (Tamm, et al., 2007), (Im^DippNH represents 1,3-bis(2,6-diisopropylphenyl)imidazolin-2-imine), HOAr∗ (Liu, et al., 2019), (Ar∗ represents 2,6-bis(diphenylmethyl)-4-methylphenyl), [(Im^DippN)MCl₂(THF)₃] (M = Dy, Y) (Panda, et al., 2009) and [(OAr∗)MCl₂(THF)₃] (M = Dy, Y) (Liu, et al., 2019) were prepared according to the literature methods.

Synthesis of [(Im^DippN)DyCl₂(THF)₃]: A mixture of anhydrous DyCl₃ (810 mg, 3 mmol) and LiCH₂SiMe₃(5.4 mL, 3 mmol) (0.56M) was stirred with THF (30 mL) for 2 h. Then a solution of Im^DippNH (1212 mg, 3 mmol) in THF (10 mL) was added. The reaction mixture was allowed to stir for another 12 h. The solvent was evaporated, and the compound was repeatedly extracted with pentane (3x30 mL). The pentane was removed completely under vacuum to give pale yellow microcrystalline.

Synthesis of [(Im^DippN)YCl₂(THF)₃]: Following the procedure described for [(Im^DippN)DyCl₂(THF)₃]. The reaction of the solution of anhydrous YCl₃ (594 mg, 3 mmol), LiCH₂SiMe₃ (5.4 mL, 3 mmol) (0.56M) and Im^DippNH (1212 mg, 3 mmol) in THF(40 mL) gave [(Im^DippN)YCl₂(THF)₃] as white microcrystalline.

Synthesis of [(OAr∗)DyCl₂(THF)₃]:To a suspension of NaH (60 mg, 1.5 mmol, 60 w% dispersed in mineral oil) in 5 mL THF was added with 5 mL THF solution of HOAr∗ (441 mg, 1 mmol). The mixture was allowed to stirred for 2 hours at room temperature. The DyCl₃ (270 mg, 1.0 mmol) was added to suspension and stirred at room temperature overnight. The suspension was allowed to settle overnight. The white precipitate was filtered off and the solvent of the filtrate was removed completely under vacuum to produce [(OAr∗)DyCl₂(THF)₃] as pale yellow solid.

Synthesis of [(OAr∗)YCl₂(THF)₃]: Following the procedure described for [(OAr∗)DyCl₂(THF)₃]. The reaction of the solution of NaOAr∗ in THF with YCl₃ gave [(OAr∗)Cl₂(THF)₃] as white solid.

Synthesis of [(Im^DippN)Dy(C₂B₉H₁₁)(THF)₂] (1Dy): To a suspension of NaH (80 mg, 2 mmol, 60 w% dispersed in mineral oil) in 10 mL THF was added with 5 mL THF solution of [Me₃NH][C₂B₉H₁₁] (97 mg, 0.5 mmol). The mixture was allowed to refluxed overnight. The generated Me₃N was then removed to approximately half of the solvent under vacuum. The suspension was allowed to settle overnight. The resulting upper clear solution was regarded as [Na₂][C₂B₉H₁₁] and then was added dropwise through a cannula to a stirred suspension of [(Im^DippN)Dy(THF)₃Cl₂] (425 mg, 0.5mmol) in 20 mL THF. The reaction mixture was stirred at room temperature for 48 h and then allowed to settle. The white precipitate was filtered off and the solvent of the filtrate was removed completely under vacuum. The residue was dissolved in 5 mL THF, and X-Ray quality crystals of 1Dy were formed by diffusion with hexane after several days. Yield 175 mg, 41.6%. Elemental analysis found (calcd.)% for C₃₇H₆₃B₉DyN₃O₂: C 51.92 (52.75); N 4.85 (4.98); H 8.06 (7.48). IR spectra (cm⁻¹): 3601w, 3524w, 3469w, 3391w, 3334w, 3176w, 3136w, 3105w, 3078w, 2964m, 2890m, 2504s, 2082w, 2002w, 1953m, 1885w, 1824w, 1799w, 1648w, 1611w, 1559w, 1457m,1364w, 1260w, 1186m, 1044s, 967m, 887s, 810m, 770w, 671m.

Synthesis of [(Im^DippN)Y(C₂B₉H₁₁)(THF)₂] (1Y): According to the literature methods (Trambitas, et al., 2011), The reaction of the solution of [Na₂][C₂B₉H₁₁] (0.5 mmol) in THF with [(Im^DippN)YCl₂(THF)₃] (388 mg, 0.5 mmol) at room temperature gave 1Y as colorless crystals after several days. Yield 330 mg, 43.0%. ¹H NMR (THF-d₈, 400 MHz, 25°C): δ 7.32 (m, 6H, m-H, p-H), 6.81 (s, 2H, NCH), 3.60 (d, 8H, OCH₂-THF), 2.82 (m, 4H, CHMe₂), 1.76 (d, 8H, CH₂CH₂-THF), 1.58 (s, 2H, BCH), 1.39-1.13 (m, 24H, CHCH₃) ppm; the BH signals are very broad from -2.6 to -3.5 ppm. ¹¹B NMR (THF-d₈, 400 MHz, 25°C): δ -38.3 (1B), -33.5 (1B), -22.7 (2B), -17.9 (2B), -17.1 (1B), -11.2 (2B) ppm. Elemental analysis found (calcd.)% for C₃₇H₆₃B₉YN₃O₂: C 57.74 (57.23); N 5.46 (5.15); H 8.19 (8.44). IR spectra (cm⁻¹): 3600m, 3338m, 3176w, 3141w, 3101w, 2968s, 2924m, 2874m, 2508s, 1974w, 1895w, 1825w, 1652m, 1612s, 1464s, 1365m, 1296w, 1252w, 1202m, 1049s, 855m, 811m, 762m, 678m.

Synthesis of [(Im^DippN)(η⁵-C₂B₉H₁₁)Dy(μ-H₂-C₂B₉H₉)(THF)]₂ (2Dy): The complex 1Dy (420 mg, 0.5 mmol) was dissolved in toluene, filtrated and then was treated with hexane. The X-Ray quality crystals of 2Dy were formed after several days. Yield 244 mg, 63.4%. Elemental analysis found (calcd.)% for C₆₆H₁₁₀B₁₈Dy₂N₆O₂: C 50.95 (51.45); N 5.03 (5.46); H 6.88 (7.14). IR spectra (cm⁻¹): 3623m, 3466w, 3391w, 3330w, 3277w, 3173w, 3149w, 2988w, 2980w, 2503s, 2122s, 1953m, 1879m, 1814m, 1596w,1457w, 1361w, 1256w, 1213w, 1176w, 1112w, 1034m, 967m, 905m, 847m, 810m, 761m, 674w.

The alternative method for 1Dy: The complex 2Dy (154 mg, 0.1 mmol) was dissolved in THF and then was treated with hexane. The X-Ray quality crystals of 1Dy were formed after several days.

Synthesis of [(Im^DippN)(η⁵-C₂B₉H₁₁)Y(μ-H₂-C₂B₉H₉)(THF)]₂ (2Y): The complex 1Y (384mg, 0.5 mmol) was dissolved in toluene and then was treated with hexane. The X-Ray quality crystals of 2Y were formed after several days. Yield 227 mg, 65.3%. ¹H NMR (Benzene-d₆, 400 MHz, 25°C): δ 7.15 (m, 12H, m-H, p-H), 7.01, 7.69 (d, 4H, NCH), 3.55 (m, 8H, OCH₂-THF), 2.36, 2.23 (m, 8H, CHMe₂), 1.41 (m, 8H, CH₂CH₂-THF), 1.37, 1.35 (d, 4H, BCH), 1.13, 0.99 (d, 48H, CHCH₃) ppm; the BH signals are very broad from -1.8 to -2.5 ppm. ¹¹B NMR (Benzene-d₆, 400 MHz, 25°C): δ -37.2 (2B), -32.6 (2B), -21.1 (4B), -16.3 (6B), -10.2 (4B) ppm. Elemental analysis found (calcd.)% for 1391.99 C₆₆H₁₁₀B₁₈N₆O₂Y₂: C 56.13 (56.89); N 5.72 (6.03); H 8.23 (7.90). IR spectra (cm⁻¹): 3621s, 3463w, 3309w, 3131w, 3076w, 3027w, 2958s, 2928m, 2868m, 2508s, 2088m, 1953w, 1874w, 1805w, 1647m, 1593m ,1543m ,1464m, 1370m, 1212m, 1029m, 930w, 861m, 801m, 747m, 683m.

Synthesis of [(Im^DippN)Dy(η⁵-o-xylylene-C₂B₉H₉)(THF)₂] (3Dy): To a suspension of NaH (80 mg, 2 mmol, 60 w% dispersed in mineral oil) in 10 mL THF was added with 5 mL THF solution of [Me₃NH][o-C₆H₄(CH₂)₂-C₂B₉H₉] (148 mg, 0.5 mmol). The mixture was allowed to refluxed overnight. The generated Me₃N was then removed to approximately half of the solvent under vacuum. The suspension was allowed to settle overnight. The resulting upper clear solution was regarded as [Na₂][o-C₆H₄(CH₂)₂-C₂B₉H₉] and then was added dropwise through a cannula to a stirred suspension of [(Im^DippN)DyCl₂(THF)₃] (425 mg, 0.5 mmol) in 20 mL THF. The reaction mixture was stirred at room temperature for 48 h and then allowed to settle. The white precipitate was filtered off and the solvent of the filtrate was removed completely under vacuum. The residue was dissolved in 5 mL THF, and X-Ray quality crystals of 3Dy were formed by diffusion with hexane after several days. Yield 219 mg, 46.5%. Elemental analysis found (calcd.)% for C₄₅H₆₉B₉DyN₃O₂: C 56.88 (57.21); N 4.06 (4.45); H 7.68 (7.31). IR spectra (cm⁻¹): 3624m, 3464w, 3392w, 3327w, 3176w, 3137w, 3068w, 3023w, 2970m, 2931m, 2878m, 2832m, 2518s, 2105w, 1960w, 1887w, 1811w, 1651w, 1605m, 1468m, 1392w, 1367w, 1330w, 1258m, 1218m, 1108w, 1042s, 941m, 868w, 807m, 754m, 682m.

Synthesis of [(Im^DippN)(μ-H₄-o-xylylene-C₂B₉H₅)Dy(THF)]₂ (4Dy): The complex 3Dy (472mg, 0.5 mmol) was dissolved in toluene and then was treated with hexane. The X-Ray quality crystals of 4Dy were formed after several days. Yield 258 mg, 59.2%. Elemental analysis found (calcd.)% for C₈₂H₁₂₂B₁₈Dy₂N₆O₂: C 56.12 (56.44); N 4.56 (4.82); H 6.77 (7.00). IR spectra (cm⁻¹): 3609w, 3468w, 3327w, 3172w, 3141w, 2963w, 2928w, 2871w, 2522s, 2115s, 1945w, 1887w, 1811w, 1648m, 1605w, 1569w, 1532w, 1461m, 1363w,1330w, 1258w, 1212w, 1180w, 1042m, 937w, 858m, 807m, 750w, 698w.

The alternative method for 3Dy: The complex 4Dy (174 mg, 0.1 mmol) was dissolved in THF and then was treated with hexane. The X-Ray quality crystals of 3Dy were formed after several days.

Synthesis of [(OAr∗)Dy(THF)₂(η³-Et₂-C₂B₉H₉)Cl][(μ-H)₃Na(THF)₃] (5Dy): To a suspension of NaH (160 mg, 4 mmol, 60 w% dispersed in mineral oil) in 5 mL THF was added with 5 mL THF solution of [Me₃NH][o-Et₂-C₂B₉H₉] (250 mg, 1 mmol). The mixture was allowed to refluxed overnight. The generated Me₃N was then removed to approximately half of the solvent under vacuum. The suspension was allowed to settle overnight. The resulting upper clear solution was regarded as [Na₂][o-Et₂-C₂B₉H₉] and then was added dropwise through a cannula to a stirred suspension of [(OAr∗)DyCl₂(THF)₃] (890 mg, 1mmol) in 20 mL THF. The reaction mixture was stirred at room temperature for 24 h and then allowed to settle. The white precipitate was filtered off and the solvent of the filtrate was removed completely under vacuum. The residue was dissolved in 5 mL Toluene, and X-Ray quality crystals of 5Dy were formed by diffusion with hexane after several days. Yield 533 mg, 44.1%. IR spectra (cm⁻¹): 3086w, 3061w, 3022w, 2972m, 2927m, 2868m, 2520s, 1944w, 1891w, 1814w, 1602m, 1493s, 1448s, 1370s, 1319w, 1300s, 1216w, 1173w, 1139w, 1044s, 915m, 850s, 760m, 696s.

Synthesis of [(OAr∗)Y(THF)₂(η³-Et₂-C₂B₉H₉)Cl][(μ-H)₃Na(THF)₃] (5Y): Following the procedure described for 5Dy. The reaction of the solution of [Na₂][o-Et₂-C₂B₉H₉] (1 mmol) in THF with [(OAr∗)YCl₂(THF)₃] (818 mg, 1mmol) at room temperature gave 5Y as colorless crystals after several days. Yield 445 mg, 39.2%. ¹H NMR (Pyridine-d₅, 400 MHz, 25°C): δ 7.17-6.83 (m, 22H, Ar-H), 3.67-3.58 (m, 20H, THF), 2.85-2.76 (m, 2H, o-CH₂CH₃), 2.47-2.38 (m, 2H, o-CH₂CH₃), 2.20 (s, 2H, CH(Ph)₂), 1.97 (s, 3H, Me), 1.63-1.54 (m, 20H, THF), 1.34-1.30 (t, 3H, o-CH₂CH₃) 1.04-1.00 (t, 3H, o-CH₂CH₃) ppm; the BH signals are very broad from -1.3 to -2.0 ppm. ¹¹B NMR (Pyridine-d₅, 400 MHz, 25°C): δ -36.09 (1B), -34.81 (1B), -33.39 (1B), -18.03 (1B), -17.21 (1B), -13.66 (1B), -11.20 (1B), -9.77 (1B), -8.33 (1B) ppm. IR spectra (cm⁻¹): 3536s, 3086w, 3060w, 3028w, 2971m, 2926m, 2869m, 2514s, 1944w, 1885w, 1815w, 1758w, 1595m, 1493s, 1444s, 1373w, 1294m, 1184m, 1139w, 1030s, 908m, 862m, 748m, 696s.

Synthesis of [(OAr∗)Dy(THF)(η⁵-Et₂-C₂B₉H₆)Cl(μ-H)₃Na(THF)₂]₂ (6Dy): To a suspension of NaH (160 mg, 4 mmol, 60 w% dispersed in mineral oil) in 5 mL THF was added with 5 mL THF solution of [Me₃NH][o-Et₂-C₂B₉H₉] (250 mg, 1 mmol). The mixture was allowed to refluxed overnight. The generated Me₃N was then removed to approximately half of the solvent under vacuum. The suspension was allowed to settle overnight. The resulting upper clear solution was regarded as [Na₂][o-Et₂-C₂B₉H₉] and then was added dropwise through a cannula to a stirred suspension of [(OAr∗)DyCl₂(THF)₃] (890 mg, 1mmol) in 20 mL THF. The reaction mixture was refluxing for 48 h and then allowed to settle. The white precipitate was filtered off and the solvent of the filtrate was removed completely under vacuum. The residue was dissolved in 5 mL Toluene, and X-Ray quality crystals of 6Dy were formed by diffusion with hexane after several days. Yield 707 mg, 33.2%. IR spectra (cm⁻¹): 3523s, 3081w, 3060w, 3024w, 2965m, 2925m, 2870m, 2514s, 1944w, 1886w, 1802w, 1756w, 1602m, 1492s, 1444s, 1370m, 1300m, 1173m, 1076w, 1032s, 915w, 858m, 747m, 696s.

The alternative method for 6Dy: 5Dy (302 mg, 0.25mmol) was dissolved in 20mL THF. The mixture was refluxing for 24 h and then the solvent was removed completely under vacuum. The residue was dissolved in 5 mL Toluene, and X-Ray quality crystals of 6Dy were formed by diffusion with hexane after several days.

Synthesis of [(OAr∗)Y(THF)(η⁵-Et₂-C₂B₉H₆)Cl(μ-H)₃Na(THF)₂]₂ (6Y): Following the procedure described for 6Dy. The reaction of the solution of [Na₂][o-Et₂-C₂B₉H₉] (1 mmol) in THF with [(OAr∗)YCl₂(THF)₃] (818 mg, 1mmol) gave 6Y as colorless crystals after several days. Yield 591 mg, 29.8%. ¹H NMR (Pyridine-d₅, 400 MHz, 25°C): δ 7.71-6.83 (m, 44H, Ar-H), 3.64-3.61 (m, 24H, THF), 2.85-2.76 (m, 4H, o-CH₂CH₃), 2.47-2.38 (m, 4H, o-CH₂CH₃), 2.20 (s, 4H, CH(Ph)₂), 1.97 (s, 6H, Me), 1.62-1.55 (m, 24H, THF), 1.34-1.30 (t, 6H, o-CH₂CH₃) 1.04-1.00 (t, 6H, o-CH₂CH₃) ppm; the BH signals are very broad from -1.3 to -2.0 ppm. ¹¹B NMR (Pyridine-d₅, 400 MHz, 25°C): δ -36.15 (3B), -33.41 (3B), -18.02 (4B), -17.16 (2B), -11.27 (2B), -9.76 (4B) ppm. IR spectra (cm⁻¹): 3086w, 3060w, 3028w, 2977m, 2932m, 2874m, 2508s, 1944w, 1878w, 1803w, 1595m, 1492s, 1456s, 1371w, 1300s, 1216w, 1178w, 1139w, 1042s, 915m, 844s, 761s, 696s.

The alternative method for 6Y: 5Y (495 mg, 0.25mmol) was dissolved in 20mL THF. The mixture was refluxing for 24 h and then the solvent was removed completely under vacuum. The residue was dissolved in 5 mL Toluene, and X-Ray quality crystals of 6Y were formed by diffusion with hexane after several days.

Synthesis of 5% diluted sample 2Dy@2Y: Following the procedure described for 2Dy. The reaction of the solution of [Na₂][C₂B₉H₉] (1 mmol) in THF with [(Im^DippN)YCl₂(THF)₃] (737 mg, 0.95mmol) and [(Im^DippN)DyCl₂(THF)₃] (42.5 mg, 0.05mmol) at room temperature to give 1Dy@1Y, which was recrystallized in toluene to form 2Dy@2Y. The dilution ratio of dysprosium in 2Dy@2Y was determined by ICP-MS to be 7.7% ± 0.5%. 7.7%.

Synthesis of 5% diluted sample 5Dy@5Y: Following the procedure described for 5Dy. The reaction of the solution of [Na₂][o-Et₂-C₂B₉H₉] (1 mmol) in THF with [(OAr∗)YCl₂(THF)₃] (777 mg, 0.95mmol) and [(OAr∗)DyCl₂(THF)₃] (44.5 mg, 0.05mmol) at room temperature gave 5Dy@5Y as colorless crystals after several days. The dilution ratio of dysprosium in 5Dy@5Y was determined by ICP-MS to be 4.1% ± 0.5%.

Synthesis of 5% diluted sample 6Dy@6Y: Following the procedure described for 6Dy@6Y. The reaction of the solution of [Na₂][o-Et₂-C₂B₉H₉] (1 mmol) in THF with [(OAr∗)YCl₂(THF)₃] (777 mg, 0.95mmol) and [(OAr∗)DyCl₂(THF)₃] (44.5 mg, 0.05mmol) at 85 ºC gave 6Dy@6Y as colorless crystals after several days. The dilution ratio of dysprosium in 6Dy@6Y was determined by ICP-MS to be 10.6% ± 0.5%.

Characterization

NMR spectra were measured on a Bruker Avance-400 spectrometer and chemical shifts (δ) are reported in parts per million (ppm). ¹H NMR and ¹¹B NMR spectra were recorded at 400 MHz in NMR solvents and referenced internally to corresponding solvent resonance. Infrared spectra were collected on a Thermo Fisher Nicolet 6700 FT-IR spectrometer using ATR (Attenuated Total Reflectance) method. Absorption maxima (ν max) are reported in wavenumbers (cm^–1). Dilution ratios were determined with inductively coupled plasma mass spectrometry (ICP-MS; NexION350D).

X-Ray crystallography

All data were recorded on a Bruker SMART CCD diffractometer with MoKα radiation (λ = 0.71073 Å). The structures were solved by direct methods and refined on F² using Olex2 (Dolomanov, et al., 2009). CCDC 2047062 (1Dy), 2047063 (2Dy), 2047064 (2Y), 2047065 (3Dy), 2047066 (4Dy), 2058168 (5Dy), 2058169 (5Y), 2058167 (6Dy) and 2058170 (6Y) contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/conts/retrieving.html (or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB21EZ, UK; fax: (+44)1223-336-033; or deposit@ccdc.cam.ac.uk).

Magnetic measurements

Magnetic susceptibility measurements have been carried out with a Quantum Design MPMS-XL7 SQUID magnetometer upon cooling from 300 to 0.5 K in variable applied fields. Ac susceptibility measurements have been performed at frequencies of between 1 and 1218 Hz with an oscillating field of 3.5 Oe and with variable dc applied field. polycrystalline samples were embedded in eicosane to avoid any field induced crystal reorientation. A diamagnetic correction has been calculated from Pascal constants and embedding eicosane has been applied to the observed magnetic susceptibility. The magnetic hysteresis loops of 0.02 T/s and 0.05 T/s have been carried out with a Quantum Design MPMS-SQUID VSM-094 of Instrument Analysis Center of Xi'an Jiaotong University. The magnetic measurements for easy axis of single crystals were carried out with a sealed NMR tube in which the single crystal of 1.3-1.5 mg was immersed in crystal oil. The tube was then applied with 5 Tesla magnetic field for 10 min till the magnetic easy axis of single crystal along with the direction of magnetic field at 300 K. The 5 T magnetic field wasn’t removed until the temperature of sample space dropped to 150 K and settled for 30 min to freeze crystal oil in tube.

Ab initio calculation

We performed CASSCF-SO (completely active space self-consistent filed spin orbit) calculation though OPEN MOLCAS (Ignacio, et al., 2019) in order to gain insight into the electronic structure of Dy(III) ions and understand the observed exchange biasing effect. The geometry of these molecules was gained from X-ray crystal structure without optimization. The basic sets from MOLCAS ANO-RCC library (Roos, et al., 2004) were employed in whole calculation tasks: VTZP quality for paramagnetic ion, VDZP quality for all atoms at the first coordination sphere and VDZ quality for the rest atoms. The active space was composed of CAS (9,7),namely seven active f-orbitals and nine active f-electrons. The states of 21 sextets, 224 quartets and 490 doublets have been computed in the RASSCF module. The spin-orbit (SO) states were obtained in the RASSI module (Malmqvist, et al., 2002) by choosing 21 sextets, 128 quartets and 130 doublets, respectively. The magnetic properties for individual Dy(III) ions were obtained through SINGLE_ANISO module (Roos, et al., 2005) like g-tensors, crystal field parameters, transition magnetic moment matrix, magnetic susceptibility as well as magnetization plot. Here for calculating dimer complexes, one of two Dy(III) sites were replaced by diamagnetic ion Lu(III) treated as the same quality in basis set aspect. Considering saving the disk space and assuring calculation accuracy, we employed the Cholesky decomposition for two-election integrals in whole calculations. To further understand the interaction between two Dy(III) centers in two centrosymmetric complexes, magnetic exchange and dipole-dipole exchange were simulated though POLY_ANISO program based on the previous results of single-ion property. POLY_ANISO program has been performed to fit dinuclear even polynuclear complexes successfully and broadly (Chibotaru and Ungur, 2006; Katie, et al., 2017; Xiong et al., 2017; Zhang, et al., 2020; Kuduva, et al., 2018). Meanwhile, we also acquired the simulated magnetization and magnetic susceptibility plots and the total coupling parameter using PHI code in order to improve the credibility of the fitting process and found that both J values output from distinct codes are consistent (Chilton, et al., 2013). Considering the magnetic curves output by POLY_ANISO are scatter plots and to distinguish the simulated and experimental data better, we ultimately employed the continuous simulated curves generated by PHI code (Figures S23–S27).

DFT calculation

Population analysis calculations were performed using Gaussian 09D (Frisch, et al., 2009) to acquire electrostatic potentials (ESP) and specific interaction strength for B−H^δ−∙∙∙Dy³⁺ and B−H^δ−∙∙∙Na⁺. For interaction strength calculation, the geometry of these complexes was obtained from X-ray crystal structure without optimization. To avoid convergence problems, model complexes were considered extracted from centrosymmetric dimer complexes. We performed PBE density functional (Perdew, et al., 1997) with Grimme’s D3 dispersion correction (Grimme, 2004, 2006, 2011) in all calculation tasks. For Dysprosium, the CSDZ (Cundari Stevens double zeta) basis set and the corresponding pseudopotential (Cundari and Stevens, 1993; Yu, et al., 2020) was employed and the 6-311g+(d,p) basis set for other atoms like carbon, hydrogen, oxygen, nitrogen, boron sodium and chlorine. All converged wave functions are stable under the perturbations considered. The total bonding energy (BE_total) between fragments is defined as: BE_total = E_model – (E_frg1 + E_frg2), where E_model, E_frg1 and E_frg2 are the energy of model complex, fragment 1 and fragment 2, respectively. The first model complex has four B−H^δ−∙∙∙Dy³⁺ interactions, and the second model complex eight B−H^δ−∙∙∙Dy³⁺ interactions while 6Dy’s complex has six B−H^δ−∙∙∙Na⁺ interactions. Therefore, average bonding energy (BE_avg) is introduced considering complexes’ centrosymmetric and similarity of Dy-H and Na-H distance, namely BE_avg = BE_total / N (N= 4,8,6, respectively). It is noted that we initially employed geometry optimization towards nido-[C₂B₉H₁₁]^2- using the same method and basis sets before ESP calculation. All optimized structures were verified as stationary points on the potential energy surface through vibrational frequency calculations.

The related instructions and keywords we used in population analysis calculations are following: pbepbe/genecp em=gd3bj int=(ultrafine,acc2e=12) scf=qc stable=opt. The quadratically convergent SCF procedure was utilized to avoid convergence failures and the functions of the keyword “stable=opt” are to check the stability of wave function and to optimize it until stable if of instability.

Published: July 23, 2021