Reflection on modern methods: a common error in the segmented regression parameterization of interrupted time-series analyses

Abstract

Interrupted time-series (ITS) designs are a robust and increasingly popular non-randomized study design for strong causal inference in the evaluation of public health interventions. One of the most common techniques for model parameterization in the analysis of ITS designs is segmented regression, which uses a series of indicators and linear terms to represent the level and trend of the time-series before and after an intervention. In this article, we highlight an important error often presented in tutorials and published peer-reviewed papers using segmented regression parameterization for the analyses of ITS designs. We show that researchers cannot simply use the product between their calendar time variable and the indicator variable indicating pre- versus post-intervention time periods to represent the post-intervention linear segment. If researchers use this often-presented parameterization, they will get an erroneous result for the level change in their time-series. We show that researchers must take care to use the product between their intervention variable and the time elapsed since the start of the intervention, rather than the time since the beginning of their study. Thus, the second linear segment of the time-series indexing the post-intervention level and trend should be zero before intervention implementation and begin by counting from zero, rather than counting from the time elapsed since the beginning of the study. We hope that this article can clarify segmented regression parameterization for the analysis of ITS designs and help researchers avoid confusing and erroneous results in the level changes of their time-series.

Key Messages

• We highlight an important error in segmented regression parameterization for interrupted time-series (ITS) analyses often presented in turorials and peer-reviewed published papers.

• We show that researchers cannot simply use the often-presented product between their study time variable and their intervention dummy variable (for example, ${\mathit{\beta }}_3{\mathit{TX}}_{\mathit{t}}$) to represent the second linear segment in their analysis. T is the time elapsed since the start of the study, X_t is a dummy variable indicating the pre-intervention period (coded 0) or the post-intervention period (coded 1). Despite being commonly presented in the peer-reviewed literature, researchers using this parameterization will receive an erroneous and biased result for the main effect of the immediate level change of the time-series.

• To parameterize the second segment in a segmented regression analysis, researchers must centre their time variable in the interaction term of study time and their intervention dummy variable, subtracting out the study time (T_i) when the intervention starts (${\mathit{\beta }\mathbf{\text{'}}}_3{(\mathit{T}-{\mathit{T}}_{\mathit{i}})\mathit{X}}_{\mathit{t}}$), where X_t = 1 for T ≥T_i.

• In doing so, the first time point of the second linear segment should start indexing from zero instead of the time elapsed since the beginning of the study (as it does when a simple interaction term of ${\mathit{\beta }}_3{\mathit{TX}}_{\mathit{t}}$ is used).

Introduction

Interrupted time-series (ITS) designs are a robust and increasingly popular non-randomized study design for strong causal inference in the quantitative impact evaluation of public health interventions.^1,2 In an ITS design, an intervention (interruption) is introduced at a clear point in time, with repeated sequential measurements of the outcome of interest being recorded at equal intervals before and after the intervention. The impact of the intervention is estimated by comparing the trend and level of the outcome following the intervention with the ‘counterfactual’ scenario where the underlying pre-intervention level and trend continue unchanged as if the intervention had not occurred. Compared with before-and-after designs that measure exposure and outcome at only two time points (before and after the initiation of intervention), ITS designs have stronger internal validity by allowing for the statistical investigation of potential threats to validity, including the underlying secular trend, cyclical/seasonal patterns, short-term random fluctuations, regression to the mean and autocorrelation in the estimates of the effect of a given intervention.^3,4 Furthermore, the design allows for the analysis of the detailed functional form of intervention effect and takes advantage of repeated measurements of the same population, thus avoiding elements of selection bias due to group differences.¹

Segmented regression parameterization for the analysis of ITS designs and a common error

One of the most common techniques for model parameterization in the analysis of ITS designs is segmented regression, which uses a series of linear segments to represent the level and trend of the time-series before and after the intervention.^1,3 Bernal et al. (2017) have previously published a tutorial in the International Journal of Epidemiology highlighting a simple and commonly-used segmented regression model for ITS analyses which includes two linear segments with one trend pre-intervention and one trend post-intervention. This parameterization allows the evaluation of a main effect of the immediate level and slope changes in a time-series following an intervention (interruption) of interest³ (see Equation 1).

$$Y_t={\mathit{\beta }}_0\mathrm{ }+\mathrm{ }{\mathit{\beta }}_1\mathit{T}\mathrm{ }+{\mathit{\beta }}_2{\mathit{X}}_t\mathrm{ }+{\mathit{\beta }}_3{\mathit{TX}}_t\mathrm{ }$$ Equation 1

where Y_t is the outcome at time t, T is the time elapsed since the start of the study, X_t is a dummy variable indicating the pre-intervention period (coded 0) or the post-intervention period (coded 1). β₀ represents the baseline level of Y at T = 0, β₁ represents the underlying pre-intervention trend (the change in Y associated with a single-unit increase in time before the intervention), β₂ is purported to represent the immediate level (or intercept) change immediately following the intervention and β₃ is interpreted as the change in the slope of the trend following the intervention, compared with the pre-intervention trend.

This standard model (Equation 1) has been presented in numerous previous studies and tutorials on how to correctly conduct segmented regression analyses of ITS designs.^5–7 However, a different model has also been presented in both studies and tutorials,^8–11 and purported to represent the same main effect estimates (see Equation 2):

$$Y_t={\mathit{\beta }\mathrm{\text{'}}}_0\mathrm{ }+\mathrm{ }{\mathit{\beta }\mathrm{\text{'}}}_1\mathit{T}\mathrm{ }+{\mathit{\beta }\mathrm{\text{'}}}_2\mathrm{ }{\mathit{X}}_t\mathrm{ }+{\mathit{\beta }\mathrm{\text{'}}}_3\mathrm{ }{(\mathit{T}-{\mathit{T}}_{\mathit{i}})\mathrm{ }\mathit{X}}_t\mathrm{ }$$ Equation 2

where the interpretations of Y_t, T, X_t are the same as those in Equation 1, T_i represents the time point when the intervention starts (X_t = 1 for T ≥T_i) and the interpretations of β′_{0 ,} β′_1, β′₂ and β′₃ are the same as the purported interpretation of β_{0 ,} β_1, β₂ and β₃ in Equation 1, respectively. The singular difference between the two models is the parameterization of the second linear segment, corresponding to β′₃. In Equation 1, this second segment is parameterized by the product between the intervention dummy variable (X_t) and the time elapsed since the beginning of the study (T). In Equation 2, the second segment is parameterized by the product between the intervention (X_t) and the time elapsed since the beginning of the intervention (T-T_i).

The questions we ask now are the following: (i) are these models equivalent?; and ii) do they both yield the purported interpretation of interest for our cofficients? In order to answer this question, we generated a simple simulated dataset using hypothetical parameters in the R and Stata statistical programs (R version 3.5.3, Stata 15) and fit the two models to the data to compare the estimated coefficients with the parameters we initially used to simulate the data (see Supplementary File S1a, available as Supplementary data at IJE online, for R code and Supplementary File S1b, available as Supplementary data at IJE online, for Stata code). For the simulated data, the dependent variable is the weekly measurement of an outcome of interest from week 0 to 150; the outcome follows a linear trend with baseline level of 30 and a pre-intervention slope of 1/week. The intervention starts at T = 100 and is associated with an immediate level increase of 5 and an increase in the slope by 0.3/week. Normally-distributed noise was also added to the simulated dependent variable.

The results from the two models are presented in Table 1. The estimates of β_0, β_1, and β₃ from Equation 1 are very close to the simulated parameters (the truth), whereas the estimate of β₂ is different from the true immediate level change. All of the estimated coefficients, β′_0, β′_1, β₂ and β′₃, from Equation 2 are close to the simulated parameters and represent the baseline level, the pre-intervention slope, the immediate level change post-intervention and the post-intervention slope change, respectively.

Table 1.

Comparison of estimates from Equation 1 and Equation 2 to the ‘true’ parameters used in the data simulation

	Simulated parameters	Equation 1		Equation 2
		Point estimates	Standard error	Point estimates	Standard error
Baseline level	30.00	29.99 (β0)	0.06	29.99 (β′0)	0.06
Pre-intervention slope	1.00	1.00 (β1)	0.00	1.00 (β′1)	0.00
Purported level change	5.00	−25.20 (β2)	0.34	4.84 (β′2)	0.10
Slope change	0.30	0.30 (β3)	0.00	0.30 (β′3)	0.00

The intervention starts at Ti = 100; β₂ ≈ β'₂ − β₃*Ti; (−25.12 ≈ 4.84 − 0.3 × 100)

Based on our results in Table 1, it is clear that β₂ in Equation 1 does not represent the purported immediate level change associated with the intervention. In order to interpret β₂ and understand how it differs from β′₂ in Equation 2, we can rearrange Equation 1:

$$\begin{array}{cc}{Y}_t& ={\beta }_0+\end{array}{\beta }_{1}T+{\beta }_2{X}_t+{\beta }_{3}T{X}_t={\beta }_o+{\beta }_{1}T+{\beta }_2{X}_t+{\beta }_3[(T-T_i)+T_i]X_t={\beta }_o+{\beta }_{1}T+({\beta }_2+{\beta }_3{T}_i)X_t+{\beta }_3(T-T_i)X_t$$ Equation 1

$$Y_t={\mathit{\beta }\mathrm{\text{'}}}_0\mathrm{ }+\mathrm{ }{\mathit{\beta }\mathrm{\text{'}}}_1\mathit{T}\mathrm{ }+{\mathit{\beta }\mathrm{\text{'}}}_2\mathrm{ }{\mathit{X}}_t\mathrm{ }+{\mathit{\beta }\mathrm{\text{'}}}_3\mathrm{ }{(\mathit{T}-{\mathit{T}}_{\mathit{i}})\mathrm{ }\mathit{X}}_t\mathrm{ }$$ Equation 2

From Table 1 we notice that the estimated β_0, β_1, and β₃ from Equation 1 are equivalent to the estimated β′_0, β′_1, and β′₃ respectively from Equation 2. Moreover, the fitted values of the outcome from Equation 1 are exactly the same with those from Equation 2 (see Supplementary Dataset S1, available as Supplementary data at IJE online). Therefore, β₂ in the above transformation of Equation 1 should be equal to β′₂ - β₃T_i, indicating that the estimated immediate level change (if we incorrectly presume that it is represented by β₂) from Equation 1 is biased because of its negative association with the product of the slope change (β₃) and the time point when the intervention starts (T_i). Table 2 presents the deriviation and the relationships of the coefficients in Equation 1 and Equation 2, which further confirms that β₀ = β′₀; β₁ = β′₁; (β₂₊β₃T_i ) = β′₂; β₃ = β′₃, representing the baseline level, pre-intervention slope, level change and slope change for Equation 1 and Equation 2, respectively. For additional clarity, please see Table 3 for the differences in raw data structure for Equation 1 and Equation 2. Researchers should clearly note that in Table 3, both T (time elapsed since start of the study) and (T − T_i)X_t begin counting from zero and not one. To correctly estimate the main effect of the level change, (T − T_i)X_t must be zero at the first time point post intervention implementation (X_t=1). In addition, if researchers wish to interpret B₀ as the first time point in their time-series, T (time elapsed since the start of the study) must begin counting from zero.

Table 2.

Interpretation of the coefficients in Equation 1 and Equation 2 along with the relationships between the coefficeints of the two models

	Equation 1	Equation 2	Relationships
Baseline level: E(Yt|T = 0)	β0	β′0	β0 = β′0
Pre-intervention slope: E(Yt+1 − Yt | T ≤ Ti)	[β0 + β1(T+1)] − (β0 + β1T) = β1	[β′0 + β′1(T + 1)] − (β′0 + β′1T) = β′1	β1 = β′1
Post-intervention slope: E(Yt+1 − Yt | T>Ti)	[β0 +β1(T+1)+β2+β3(T + 1 − Ti)] − [β0 +β1T+β2+β3(T − Ti)] = β1+β3	[β′0 +β′1 (T + 1) + β′2 + β′3 (T + 1 − Ti)] − [β′0 +β′1 T + β′2 + β′3 (T − Ti)] = β′1+β′3	β3 = β′3
Slope change: E(Yt+1 − Yt | T>Ti) – E(Yt+1 − Yt | T≤Ti)	(β1+β3) − β1 = β3	(β′1+β′3) − β′1 = β′3
Immediate/level change: E(Yt |T = Ti & Xt = 1 ) − E(Yt | T=Ti & Xt = 0)	[β0 +β1T+(β2+β3Ti)]-[β0 +β1T] = β2+β3Ti	(β′0 + β′1T + β′2) − [β′0 + β′1T] = β′2	β2 + β3Ti = β′2

Where Y_t is the outcome at time t, T is the time elapsed since the start of the study, X_t is a dummy variable indicating the pre-intervention period (coded 0) or the post-intervention period (coded 1). T_i represents the time point when the intervention starts (X_t = 1 for T ≥ T_i). β₀ or β′₀ represents the baseline level of Y at T = 0, β₁ or β′₁ represents the underlying pre-intervention trend (the change in Y associated with a single-unit increase in time before the intervention), (β₂ + β₃T_i) or β′₂ both purport in the peer-reviewed literature to represent the immediate level (or intercept) change following the intervention, and β₃ or β′₃ is interpreted as the change in the slope of the trend following the intervention, compared with the pre-intervention trend

Table 3.

Example dataset structure for Equation 1 [erroneous results for β₂ (level change)] versus Equation 2 [correct results for β′₂ (level change)]

Equation 1 (erroneous)			Equation 2 (correct)
T	X t	TX t	T	X t	(T − Ti)Xt
0	0	0	0	0	0
1	0	0	1	0	0
2	0	0	2	0	0
…			…
99	0	0	99	0	0
100	1	100	100	1	0
101	1	101	101	1	1
102	1	102	102	1	2
…	1		…	1	…
150	1	150	150	1	50

Where T is the time elapsed since the start of the study, X_t is a dummy variable indicating the pre-intervention period (coded 0) or the post-intervention period (coded 1). T_i represents the time point when the intervention starts (X_t = 1 for T ≥ T_i). In this example, T_i = 100.

For illustration, Figure 1 visualizes the predicted trend based on the two models and the interpretation of the coefficients. As is seen in Figure 1, β₂ (shown as B-C) is the estimated level change from Equation 1, which is a an erroneous result and does not represent the immediate level change of interest. β′₂ (shown as B-A) is the estimated level change from Equation 2, and represents the immediate level change of interest in our analysis.

Figure 1.

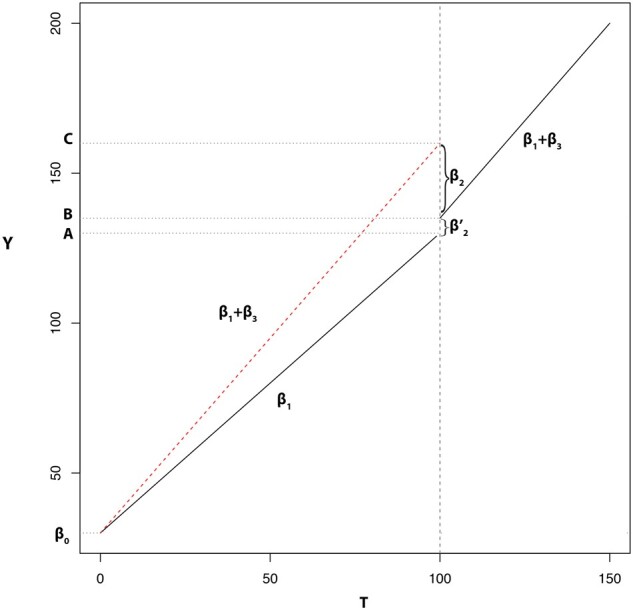
Interrupted time-series parameterized as a segmented regression model including a level and slope change. The solid lines represent the predicted trend based on the two models. β₂, demonstrated as (B-C), is the estimated level change from Equation 1, which is a an erroneous result and does not represent the immediate level change of interest. β’₂, demonstrated as (A-B), is the estimated level change from Equation 2, and is the correct result and represents the immediate level change of interest in our analysis

Conclusions

In this article we have highlighted an important error that is often presented in tutorials and published papers using segmented regression parameterization for the analyses of ITS designs. Specifically, Equation 1—which results in an erroneous result for the immediate level change of the time-series—is described as the correct method for parameterizing segmented regression analyses of interrupted time-series in a tutorial article recently published by Bernal et al. (2017) in the International Journal of Epidemology.

We have used a simulated case to show that care must be taken in parameterizing the second linear segment using segmented regression analyses for ITS designs. Researchers cannot use the often-presented parameterization of the simple product between study time and their intervention dummy variable (Equation 1). Using this model will lead to biased and erroneous findings for the main effect of the level change of their time-series. The correct parameterization is to use a second linear segment that is zero before intervention implementation, and then counts from zero (Equation 2) rather than the time elapsed since study start. This can be accomplished by centring the interaction term and subtracting the study time that intervention starts: ${\mathit{\beta }\mathrm{\text{'}}}_3{(\mathit{T}-{\mathit{T}}_{\mathit{i}})\mathrm{ }\mathit{X}}_t$. For clarity, researchers should take care to confirm that this second linear segment begins counting from zero and not one. That is, the second linear segment should be zero for the first time point after intervention initiation (X_t = 1). If the second segment starts counting from one instead of zero, the immediate level change may also be biased due to the inability to separate the effects of the level change and potential slope changes. Last, if researchers wish to be able to interpret B₀ as the first time point in their time-series they should confirm that their study time variable (T in our example) begins counting from zero and not one (see Table 3).

Supplementary Data

Supplementary data are available at IJE online.

Funding

B.H.W. was supported by grant number K01MH110599 from the US National Institute of Mental Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Conflict of interest: None declared.