A dynamical model for generating synthetic data to quantify active tactile sensing behavior in the rat

Significance

In recent years, increasing effort has been made to study sensorimotor integration within the context of the animal’s body and the environment. However, it is challenging to collect neurophysiological data under naturalistic conditions, and simulations have become an important part of neuroscience research. We developed a simulation framework, WHISKiT Physics, to model the dynamics of a complete sensorimotor system—the rodent vibrissal array—operating under ethologically relevant conditions. The tight link between sensing and motor control and the discrete somatotopy throughout the sensory pathway make the vibrissal array ideal to study sensorimotor circuits. WHISKiT Physics makes this widely used model system accessible to sensory research as well as to other disciplines including information theory, reinforcement learning, and artificial intelligence.

Abstract

As it becomes possible to simulate increasingly complex neural networks, it becomes correspondingly important to model the sensory information that animals actively acquire: the biomechanics of sensory acquisition directly determines the sensory input and therefore neural processing. Here, we exploit the tractable mechanics of the well-studied rodent vibrissal (“whisker”) system to present a model that can simulate the signals acquired by a full sensor array actively sampling the environment. Rodents actively “whisk” ∼60 vibrissae (whiskers) to obtain tactile information, and this system is therefore ideal to study closed-loop sensorimotor processing. The simulation framework presented here, WHISKiT Physics, incorporates realistic morphology of the rat whisker array to predict the time-varying mechanical signals generated at each whisker base during sensory acquisition. Single-whisker dynamics were optimized based on experimental data and then validated against free tip oscillations and dynamic responses to collisions. The model is then extrapolated to include all whiskers in the array, incorporating each whisker’s individual geometry. Simulation examples in laboratory and natural environments demonstrate that WHISKiT Physics can predict input signals during various behaviors, currently impossible in the biological animal. In one exemplary use of the model, the results suggest that active whisking increases in-plane whisker bending compared to passive stimulation and that principal component analysis can reveal the relative contributions of whisker identity and mechanics at each whisker base to the vibrissotactile response. These results highlight how interactions between array morphology and individual whisker geometry and dynamics shape the signals that the brain must process.

The nervous system of an animal species coevolves with its sensory and motor systems, which are in continuous interaction with the environment. Because these sensorimotor and environmental feedback loops are so tightly linked to neural function, there has been increasing effort to study neural processing within the context of the animal’s body and environment (e.g., in the fields of neuromechanics and embodied cognition). However, it is challenging to collect neurophysiological data under naturalistic conditions, and thus, simulations have become an increasingly important component of neuroscience. A wide variety of software platforms have been developed to enable simulations of neural populations and circuits (1–3), the biomechanics of motor systems (4), and the responses of sensory receptors (5–9). To date, however, no system has been able to fully account for the physical constraints imposed during active sensory acquisition behavior in a natural environment.

Here, we describe a simulation framework (WHISKiT Physics) that can model the dynamics of a complete sensory system—the rodent vibrissal array—operating under ethologically relevant conditions. The rat vibrissal array is one of the most widely used models in neuroscience to study active sensing and cortical processing. Although its biomechanics are relatively simple, the vibrissal array subserves a rich and complex repertoire of tactile sensing behavior. As nocturnal animals, rats are experts in using tactile cues from their whiskers to extract information from the environment, such as object distance (10, 11), orientation (12), shape (11, 13), and texture (14, 15). During tactile exploration, rats often use active, coordinated oscillatory movements of their whiskers (whisking) to sample the immediate space at frequencies between 5 to 25 Hz (16). These unique properties make this sensory system ideal to examine the dynamic relationship between motor control and sensory input during goal-directed and exploratory behavior.

A total of 30 whiskers are regularly arranged on each side of the rat’s face (mystacial pad) (11). Each whisker is embedded in a follicle where the mechanical signals generated at the whisker base are transduced by a variety of mechanoreceptors before they enter the sensory (trigeminal) pathway (17). Thanks to the clear whisker-based topographic maps reflected in central structures (18) and its parallels to human touch (dorsal column–medial lemniscal pathway), the entire pathway—from the primary sensory neurons, through brainstem and thalamus, up to primary somatosensory cortex—has been subject to extensive research. Nonetheless, to date, the field has lacked the ability to simulate such a system operating under naturalistic conditions (i.e., the full whisker array, active control of whiskers, etc.).

WHISKiT Physics incorporates a three-dimensional (3D) dynamical model of the rat vibrissal array to allow researchers to simulate the complete mechanosensory input during active whisking behavior. The model incorporates the typical shape and curvature of each individual whisker as well as the morphology of the rodent’s face and the arrangement of the whiskers on the mystacial pad. Each whisker can be actuated either according to typical equations of motion for whisking (19) or to directly match behavioral data. Because it permits direct control of whisker motion and simultaneous readout of mechanosensory feedback, WHISKiT Physics enables closed-loop simulations of the entire somatosensory modality in the rat, the first of its kind in any sensory modality. After validating models of individual whiskers in the array against several independent datasets, we use the full-array model to simulate vibrissotactile sensory input in four typical exploratory scenarios, both in the laboratory and in the natural environment, and discuss its use in future neural simulation systems. Each of the four scenarios generates unique patterns of data, illustrating that the model could be used to reveal the mechanisms that allow animals to extract relevant information about their environment. Although results are presented for the rat, they are easily extended to include the mouse.

Results

WHISKiT Physics is based on the Bullet Physics Library (20), an open-source physics engine with increasing contributions to game development, robotic simulation, and reinforcement learning (21). This engine provides our model with reasonable computational efficiency, the ability to model natural environments based on 3D polygon meshes, and visualization of the simulations.

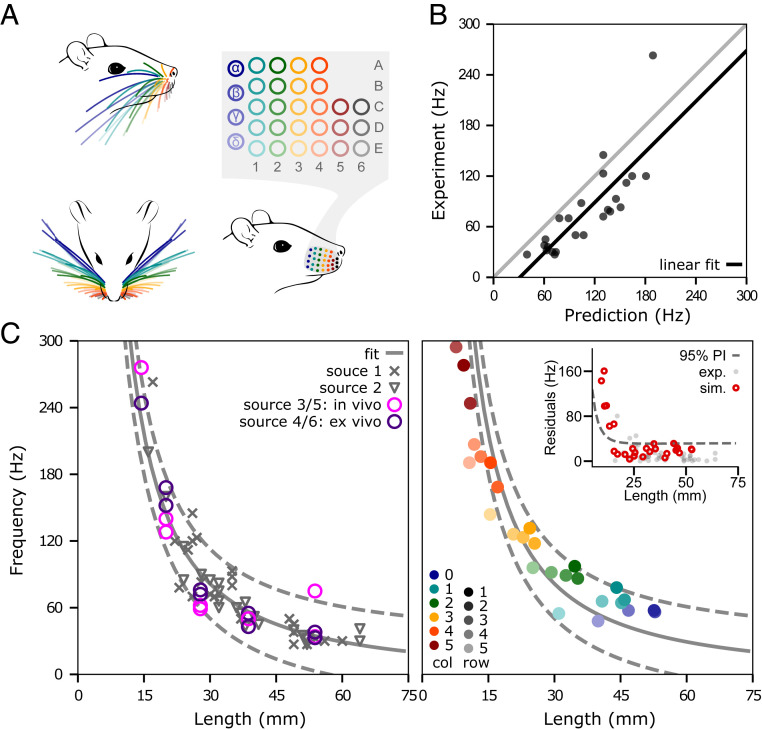
We aimed to model the complete rat vibrissal array, which typically consists of ∼60 whiskers, 30 on each side. The whiskers are organized in a grid-like manner on the mystacial pad, in five rows (A to E) and seven columns (1 to 6). Whiskers in the “zero” column are typically labeled with Greek letters (α, β, γ, δ) and the remaining columns are assigned their numerical values (1 to 6). The array organization for an average rat whisker array is schematized in Fig. 1A. The whisker geometry changes systematically with the whisker’s row and column identity and can be determined by using equations established in refs. 22 and 23. For example, the side and top views of the array in Fig. 1A, Left illustrate that the arc length of the whisker increases from rostral to caudal, while the curvature decreases. The radius slope of the whisker (i.e., its taper), which depends on its base and tip diameter as well as on its arc length, also decreases from rostral to caudal (22). The whisker’s taper is not illustrated but is included in the model.

Fig. 1.

The optimized model of the single whisker generalizes across the array. (A) The array of an average rat is organized in rows (A to E) and columns (1 to 6). The whiskers in column “0” are typically denoted by Greek letters (α, β, γ, δ). The side and top view of the array (Top, Left) show that the geometry of the whiskers changes considerably depending on the whisker’s row and column identity. (B) Predicted resonance frequencies from Hartmann et al. (24) (Dataset S1, source 1). Predictions were obtained from simulations that used the experimentally measured arc length and base/tip diameter. The gray line represents y = x. (C) The relationship between whisker length and resonance frequency obtained from experimental and simulated data. (Left): Experimentally measured resonance frequencies of the combined dataset from three laboratories including a total of 46 whiskers (Dataset S1). The gray solid line indicates the nonlinear fit $\left(\text{y}=8963{\hspace{0.17em}\mathrm{x}}^{\hspace{0.17em}\left(-1.4\right)}-3.8\right)$, while the dashed lines indicate the corresponding prediction intervals. (Right): Simulated resonance frequencies of average whiskers for all whiskers on the right side of the array (27 whiskers; left side is identical), color coded by whisker row and column identity. The solid and dashed gray lines are the identical nonlinear fit and prediction intervals shown in Left. (Inset) Residuals of experimental (gray) and simulated (red) resonance frequencies of the nonlinear fit. The dashed line indicates the prediction interval.

Resonant Frequencies with Optimized Material Parameters Generalize across Whisker Identities.

Before constructing the model of the full rat vibrissal array, we first developed a model of a single whisker (SI Appendix, Model of a single whisker and Fig. S1) and optimized its elastic and damping parameters based on experimental data (SI Appendix, Experiments for model optimization). The optimization yielded values of ${\theta }_E=5.0\hspace{0.17em}\mathrm{GPa}$ and ${\theta }_{\zeta }=0.33$ for elastic and damping parameters, respectively (SI Appendix, Optimization of single-whisker dynamics in two dimensions and Fig. S2). However, because the geometry of the whiskers varies so widely, it is not at all clear that these parameters will generalize over all whiskers and all geometries. We therefore quantified how well the model generalized over all whiskers in the array, without reoptimizing any parameters.

Using the optimized values for elasticity and damping, we quantified model performance against an experimental dataset that characterized the geometry and resonances of 24 whiskers from a single rat (see ref. 24 and Dataset S1, Source 1). The linear fit between predicted and measured resonant frequencies yields a slope of 1.0 and an intercept of −31 Hz (solid line; Fig. 1B). This fit closely matches that obtained from an analytical resonance model, which had a slope of 0.93 and an intercept of 6.4 Hz (24).

Model validation was then extended to incorporate additional experimental data for which only partial geometric and resonance information was available (Dataset S1). The study of Wolfe et al. extends the dataset by 22 whiskers (δ, D1, D2, D3, D4) from four different rats (25). Neimark et al. provides resonance frequencies of 10 whiskers of the C row (left and right) measured both in vivo and ex vivo (26). Because lengths for these whiskers were not published, we estimated them from the equations of Belli et al. (22). Resonance values for the entire dataset are plotted in Fig. 1 C, Left. Note that measurement condition (in vivo versus ex vivo) is associated with a large spread in the measurements; these differences provide an intuition for the error range associated with experimental data. Based on the inverse relationship between resonant frequency and whisker length, we fit a negative power function and obtained the model $\text{y}=8963{\hspace{0.17em}\mathrm{x}}^{\hspace{0.17em}\left(-1.4\right)}-3.8$ with a r² = 0.91 (solid line). The 95% prediction intervals are shown as dashed lines.

Based on this experimental fit, we validated the resonance response across all whiskers of the full array, using average geometry (arc length, base diameter, slope) for each whisker identity as predicted by the models published in Belli et al. (22). The whisker identities incorporated in the model are color coded in Fig. 1A. Fig. 1C, Right illustrates that the resonance frequencies of the averaged whiskers (colors consistent with Fig. 1A) are well within the prediction intervals obtained from the experimental data in Left (dashed lines). In addition, these resonance frequencies do not significantly differ from the resonance frequencies obtained from simulations using the actual geometry shown in Fig. 1B (two-sample t test: P = 0.93).

The residuals of the regression model in Fig. 1C reveal that only whiskers shorter than 15 mm (typically column 5 and higher) fall outside of the prediction intervals (Inset). This error is primarily attributable to the high stiffness and small size of these whiskers, which are challenging to simulate. However, note the large deviation in high-frequency measurements and sparsity of data points (Fig. 1C, Left), which also contribute to the mismatch between experimental data and simulation results. The whiskers in the most rostral column (column 6) are the smallest in the array and have extremely high resonance frequencies (>250 Hz) (24, 26), which lead to erroneous simulations. Therefore, this column was omitted from the model (Fig. 1A; gray column). These whiskers have the lowest probability of making contact with objects during exploratory behavior (27, 28), and thus, their removal is not a significant limitation on the model’s utility.

Dynamic Collision Behavior Matches Experimental Results for Straight and Curved Whiskers.

The results above validate model dynamics during motions of the whisker that do not involve contact. To test the model under conditions of contact and in collision scenarios, we compared it with an analytical model and with experimental data published previously (29). The analytical model of a straight whisker suggests that the mechanical response to a collision event scales with the collision’s velocity, while experimental data indicate that the associated deformation wave propagates approximately linearly from tip to base (29).

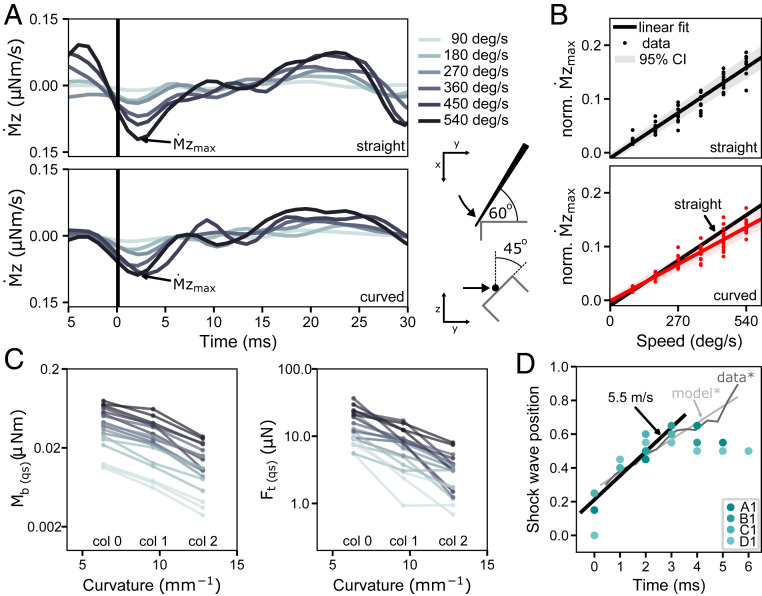
We selected 12 whiskers from four different rows (A, B, C, and D) from the model shown in Fig. 1 to test their collision response. To replicate the procedures used to test the analytical model of collision (29), we first simulated each whisker without curvature, as it was anchored at its base, and rotated it with constant velocity about the vertical axis through the base point until the 19th link (95% of whisker length from the base) collided with a rectangular edge. The collision angle between the whisker and the edge was set to 60° from the horizontal plane and 45° degrees from the vertical plane to generate mechanical responses in all three dimensions (Fig. 2A, Bottom Right). We simulated collisions at six different speeds.

Fig. 2.

Deformation waves resulting from collisions of straight and curved whiskers against a straight edge. (A) Mechanical response of a straight and curved whisker in response to a collision. The derivative of the moment at the base of the α-whisker is shown for six different whisker speeds (90, 180, 270, 360, 450, and 540 deg/s; color coded). Trials are aligned at the time of impact (black line). (Bottom, Right) Illustration of the top and side view of the corresponding experiment is given. (B) Relationship between normalized amplitude of the shock $\left({\dot{M}}_{z,max}\right)$ and whisker velocity for 12 straight and 12 curved whiskers (α, A1, A2, B1, β, B1, B2, γ, C1, C2, δ, D1, and D2). The linear fit is represented by a black solid line (95% CI shaded in gray). Note that the slope of the two regression lines is significantly different between straight and curved whiskers. (C) Bending moment $M_b$and transverse force F_t at time of the shock $\left({\dot{M}}_{z,max}\right)$ in respect to curvature of the whisker. Note that $F_t$ and $M_b$ are averaged values of the first 30 ms after collision, representing quasistatic (qs) measures. The slope of the linear regression curve is significant for $M_b$ (r² = 0.307, P < 0.001) as well as $F_t$ (r² = 0.467, P < 0.001). (D) Position of maximum deformation normalized to whisker length for whiskers A to D of the first column in the array. A linear fit to the first 4 ms is shown with a solid line and reveals a slope that is equivalent to 5.5 m/s. The light and dark gray lines illustrate the analytical (model*) and experimental (data*) results of Boubenec et al. (29), respectively.

We then repeated the simulation experiments for the same whiskers but with their intrinsic curvature as illustrated in Fig. 1A. One of the main advantages of the present numerical model is that the intrinsic curvature of the whisker can be included, which is expected to have a significant influence on the mechanical response at the base during collision (30).

Fig. 2A shows $\dot{M_z}$, the derivative of the moment at the base about the rotation axis for both a straight and curved α whisker, from 5 ms before to 30 ms after collision. In both cases, the first negative peak of $\dot{M_z}$ (shock, ${\dot{M}}_{z,max}$) occurs ∼3 ms after collision, and its magnitude clearly increases with velocity. These results are consistent with analytical solutions of a single straight whisker model (29). We then measured ${\dot{M}}_{z,max}$ for all trials and whiskers. For each whisker, ${\dot{M}}_{z,max}$ was normalized by its mean value across the six different speed trials. This normalization allowed us to compare trends across all 12 whiskers. Fig. 2B shows the normalized ${\dot{M}}_{z,max}$ value as a function of angular speed at the time of collision. ${\dot{M}}_{z,max}$ correlates with speed, achieving an adjusted r² of 0.92 for both straight and curved whiskers. However, the slopes of the regression lines are significantly different (P < 0.001).

The decrease in ${\dot{M}}_{z,max}$ for curved whiskers can be explained by the negative correlation between curvature and the transverse force $\left(F_t=\sqrt{F_y^2+F_z^2}\right)$ and between curvature and the bending moment $\left(M_b=\sqrt{M_y^2+M_z^2}\right)$ at the whisker base (Fig. 2C). This nearly linear inverse relationship between the quasistatic mechanical signals at the base and curvature matches predictions from a previous quasistatic numerical model (30).

Fig. 2D shows the position of the maximum deformation (deformation wave) relative to the normalized whisker length within the first 6 ms after collision for four whiskers (first four rows, first column). A linear regression was performed on the first four data points after collision. The slope is significant (r² = 0.90, P < 0.001) and corresponds to a deformation wave velocity of 5.5 m/s close to the analytical solution of 5.6 m/s and experimentally measured deformation wave velocity of 5.02 m/s (29). The analytical and experimental results from Boubenec et al. (29) are illustrated in light and dark gray, respectively. Boubenec et al. found the deformation wave propagation to be linear within the first 6 ms after collision. We attribute the nonlinearities in our model after 3 ms to the reduced spatial resolution of the whisker and increasing stiffness toward the whisker base. We found similar results for the Greek column, which yielded a deformation wave velocity of 4.3 m/s (r² = 0.97, P < 0.001).

Mechanical Signals across the Full Rat Vibrissal Array.

The organized morphology of the array plays an important role in shaping tactile input (31–33). WHISKiT Physics incorporates this morphology (23) to permit simulation of the complete mechanosensory input to the system. Moreover, as is the case for human touch, the rat vibrissal system is an active sensing system in which sensing typically occurs in conjunction with context-dependent finely controlled sensor movements. To incorporate this essential property in the model, each whisker is actuated at its base, allowing for rotation in three dimensions (pro/retraction, elevation, and roll). The protraction angle is controlled by the user, while elevation and roll follow the equations of motion for typical whisking behavior (see Simulation of Complete Vibrissotactile Input across the Array and Eqs. 4 and 5). These choices permit us to simulate passive stimulation (no protraction; Fig. 3A and B), stereotyped whisking behavior (equation-based protraction Fig. 3C and D), and data-based (e.g., tracking whisker motions from behavioral data) whisking. Examples for passive stimulation and equation-based whisking in the laboratory and natural environment are given below, and an example of simulating whisker motions from tracked behavioral data are available on GitHub (https://github.com/SeNSE-lab/whiskitphysics).

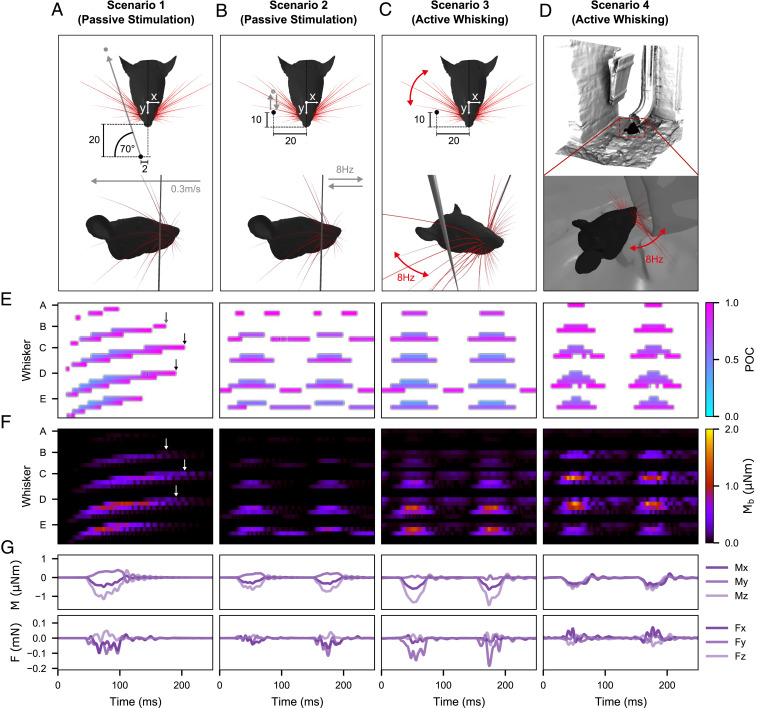
Fig. 3.

Mechanical response of the full rat whisker array for four scenarios. For simplicity, only results for the right side of the array are shown. Units are in millimeters if not indicated otherwise. (A) Visualization of the passive stimulation experiment simulating a vertical peg moving from rostral to caudal through the middle of the immobile right array. (B) Visualization of the passive stimulation experiment simulating a vertical peg moving back and forth in and out of the immobile right array at a pulse frequency of 8 Hz. (C) Visualization of active whisking against a fixed, vertical peg. The array performed a typical whisking motion as described in ref. 19 with a whisking frequency of 8 Hz. (D) Visualization of natural environment experiment. Whisking motions are the same as in C), but the array palpates the shape of a drainage pipe. (E) POCs for each whisker of the right array over time for each scenario. The POC is normalized to the length of the whisker and indicated by the color map. The whisker identities are grouped by row (dorsal to ventral) and sorted by column (caudal to rostral). Each letter on the y-axis indicates the first whisker of each group, the most caudal whisker of the corresponding row. (F) Magnitude of bending moment $\left(M_b\right)$ of each whisker indicated by color. The sorting of the whiskers is consistent with E. (G) Example of all six signal components at the base of the E2 whisker for each scenario. All panels share the same time scale (x-axis).

Fig. 3 compares the tactile signals of the rat vibrissal array for four scenarios. In Scenario 1 (Fig. 3A), a vertical peg is simulated to brush through the center of the immobile array. The peg moves at constant speed (0.3 m/s) from rostral to caudal. Scenario 2 (Fig. 3B) is similar to Scenario 1, but instead of a single sweep through the entire array, the peg oscillates back and forth between its start and end position (in the middle of the array) to repeatedly stimulate the array eight times per second (8 Hz). This scenario was carefully designed to replicate as closely as possible the stimulation distances, velocities, and frequencies associated with active whisking (Scenario 3). Scenario 3 (Fig. 3C) simulates active whisking against a fixed, vertical peg. Each whisker is driven at its base according to established kinematic equations for whisking motion (19). One cycle of protraction and retraction of the array lasts 125 ms, equivalent to a whisking frequency of 8 Hz. The peg is positioned laterally, 20 mm from the midline of the head with an offset of 10 mm from the nose tip. Finally, in Scenario 4 (Fig. 3D), the whiskers perform the identical whisking motion as in Scenario 3, but the array is positioned in front of the opening of a 3D scan of a drainpipe so that the rat is simulated to actively palpate a typical object found in its natural habitat. Movies S1–S4 show the simulations of Scenarios 1–4, respectively. Note that for simplicity, only the right side of the array is considered.

Fig. 3E shows the point of collision (POC) of each whisker in the array as a function of time for each of the four scenarios. The POC is normalized between 0 (whisker base) and 1 (whisker tip). For passive stimulation during a single sweep through the array (first panel), the spatial arrangement and geometry of the whiskers result in a systematic pattern of whisker activation. The moving peg first collides with the most rostral whiskers of the C, D, and E rows. The contact durations are short because the whiskers are small. As expected, contact durations increase as the peg collides with the more caudal and larger whiskers. Note that the slip-off of each whisker tip is clearly visible as reflected in high POC values at the very end of each whisker contact.

The systematic activation pattern is lost when a subset of whiskers is stimulated periodically as in the example of Scenario 2 (Fig. 3E, second panel). Since the peg moves only about halfway into the array, it does not collide with the more caudal (Greek and first column) whiskers. Very short (rostral) whiskers are also missed, which results in activated clusters consisting of the middle columns one to three. As deliberately designed in Scenario 2, these contact responses closely resemble those observed during the active whisking of Scenario 3 (Fig. 3E, third panel). However, the passive stimulation (Scenario 2) generates more slip-offs and therefore causes more contact patterns that are out of phase (B3, D4, E3) or doubled (A2), that is, the whiskers are hit by the peg during both rostral–caudal and caudal–rostral motion. A comparison of Scenario 2 and Scenarios 3 and 4 suggests that active whisking prevents more whiskers from slipping off the peg, likely because roll and elevation continuously change the orientation of the whiskers relative to the peg throughout the duration of the whisk.

Fig. 3F shows the magnitudes of the bending moment, $M_b$ $\left(=\sqrt{M_y^2+M_z^2}\right)$, at the base of each whisker during the first 250 ms of each behavioral condition. In Fig 3F, panel 1, oscillations in the bending moment near the end of several traces reflect the whiskers’ vibrations after they have slipped off the peg (black and white arrows). This effect is particularly visible for whiskers β, γ, and δ. Although less distinct, similar vibrations also cause $M_b$ to increase between whisks during both active whisking scenarios (Fig. 3F, panels 3 and 4). Also note that $M_b$ and POC tend to be inversely related, given that contact closer to the whisker base generally results in a greater mechanical response. Finally, because the head was stationary across all simulations, the more caudal whiskers tend to make contact closer to their bases (lower POC) and undergo larger deflections, leading to increased values of $M_b$ in this region of the array.

An example of the individual signal components at the base of a single whisker (in this case, E2) is shown in Fig. 3G. For this whisker, the mechanical signals during active whisking appear qualitatively similar between the peg and drainpipe conditions, with only a slight difference in amplitude. Similar results were found for the majority of the other individual whiskers in the array. However, these two conditions are clearly distinguishable at the level of the entire array (Fig. 3E).

Passive Stimulation and Active Whisking Result in Different Spatiotemporal Patterns of Mechanical Signals.

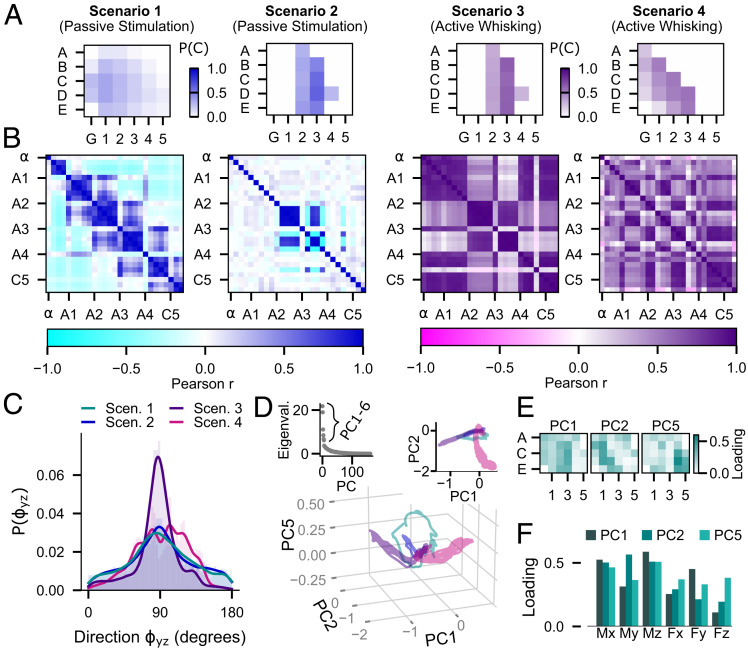
A quantitative analysis of the four scenarios in Fig. 3 clearly shows the differences between passive stimulation and active whisking. For example, the contact patterns in Fig. 3E can be used to compute the contact probability P(C) of each whisker within each trial (Fig. 4A), that is, the total time that each whisker is in contact with the object (peg or drainpipe) normalized to the trial duration. The mechanical signals, as shown for the bending moment $M_b$ in Fig. 3B, can then be used to quantify the relationships between whiskers by computing the Pearson correlation (Pearson r) of $M_b$ across whisker pairs (Fig. 4B).

Fig. 4.

Comparison of the mechanosensory signals acquired during the four example scenarios of Fig. 3. Different color schemes are used to illustrate results for the passive and active cases. (A) Contact probability P(C) for each whisker is computed as the duration that the whisker was in contact with the object normalized by the duration of the trial. (B) Correlation matrices (Pearson r) of the bending moment $\left(M_b\right)$ between whisker pairs across the array. The whiskers are arranged in groups of the same column and ordered by row number from dorsal to ventral. The labels indicate the first whisker of each group (most dorsal whisker in each column). (C) Histograms (probability distributions) of the direction of the bending moment ${\varphi }_{yz}$ in degrees. The distributions of ${\varphi }_{yz}$ during the two types of passive stimulation with a vertical peg are very similar (two-sample Kolmogorov–Smirnov test; P = 0.08). The distribution for active whisking against a vertical peg is peaked sharply at 90°, while the distribution for active whisking against a more naturalistic surface is broad and contains many peaks, reflecting the variety of contact angles. The distributions of ${\varphi }_{yz}$ for active whisking are significantly different from that observed during passive stimulation and from each other (two-sample Kolmogorov–Smirnov test; P < 0.001). (D) Projection of the 162-dimensional signal space (6 mechanical components × 27 whiskers) onto the principal components PC1, PC2, and PC5 for each of the scenarios. The color code is as in C. (Inset, Left) Eigenvalues of the PCs. (Inset, Right) Projection of the mechanosensory signals into the PC1 to PC2 plane. (E) Total loadings of each whisker for each of the PCs, obtained by summing over all six mechanical components. (F) Total loadings for each of the mechanical components for each of the PCs, obtained by summing over all whiskers.

As expected for the passive stimulation in Scenario 1, the caudal and longest whiskers in the Greek (G) and first column are more likely to be in contact, while rostral whiskers have a very low probability of contact (Fig. 4 A, panel 1). The corresponding correlation matrix in Fig. 4 B, panel 1 shows the strongest correlations between whiskers in the same column or in neighboring columns. Because the vertical peg moves from rostral to caudal, the whiskers within the given column are stimulated almost simultaneously, causing nearly synchronous oscillations after slip-off and therefore high Pearson r values. Depending on the location of slip-off, these correlations can also occur across neighboring columns (e.g., A1 is correlated with B2 and C2). However, the morphology of the array ensures that synchronized oscillations are unlikely beyond neighboring columns, leading to strong negative correlations with more distant whiskers (colored cyan in the correlation matrix). We suggest that these types of correlations during a single passive sweep could potentially be used by the animal to estimate the speed and direction of a moving object.

By design, the repeated peg stimulation of Scenario 2 generates contact probabilities P(C) that closely resemble those observed during active whisking against a peg (compare Fig. 4A, panels 2 and 3). However, correlations of the mechanical signals between whiskers are vastly different (Fig. 4B, panels 2 and 3). Most notably, active whisking increases the correlations for certain subsets of whiskers. For whisker columns 2 and 3, this increase is primarily caused by near-simultaneous activation of the whiskers when colliding with the peg. For columns G, 1, 4, and 5, the increased correlations are mainly due to inertial effects caused by the whisking motion. Similar effects appear in Scenario 4 (Fig. 4B, panel 4) but for different whisker groups. Notably, even though the whisking motion in Scenarios 3 and 4 only differ in amplitude (see Methods), the different shapes of the environment generate very different contact patterns over time and correlation matrices across whiskers (Fig. 4 A, panels 3 and 4 and B, panels 3 and 4). While whisking against the peg stimulates entire columns, whisking against the concave opening of the drainpipe activates the caudal–ventral half of the array.

Differences between active whisking and passive stimulation are not limited to signal magnitudes. As observed previously in the analysis of Fig. 3, the natural whisking motion includes the protraction-dependent elevation and roll of each whisker, which change the whisker’s orientation with respect to the environment during each whisk cycle. These orientation changes are clearly reflected in the direction of $M_b$ measured by ${\varphi }_{yz}=\left|{\tan }^{-1}\left(\frac{M_z}{M_y}\right)\right|$ in degrees; the four-quadrant inverse tangent was used such that ${\varphi }_{yz}\in \left[\mathrm{0,180}\right]$. The distributions of ${\varphi }_{yz}$ for each scenario are shown in Fig. 4C. Comparing Scenarios 2 and 3 (passive versus active) reveals that active whisking against the peg shifts ${\varphi }_{yz}$ toward 90°. An angle close to 90° indicates that the $M_y$ component is small and thus, $M_b$ points in the direction of $M_z$, which is defined as bending within the plane of the whisker’s curvature. These results suggest that active whisking against environmental features with substantial vertical components may help orient the whiskers so that they tend to bend in their plane of curvature, thereby generating a more uniform directional response at the base. However, objects that contain features with multiple orientations (e.g., the drainpipe) result in different distributions of ${\varphi }_{yz}$. Note that the distribution of ${\varphi }_{yz}$ for Scenario 4 has a unique multimodal shape that is significantly different from the other three scenarios (two-sample Kolmogorov–Smirnov test; P < 0.001).

Finally, we performed an analysis that allowed us to capture the mechanical response of the entire array simultaneously. Together, the six mechanical components and the 27 whiskers define a 162-dimensional space that can be reduced using principal component analysis (PCA). PCA was estimated by combining the data collected over time for each of the 162 variables in each scenario. Note that PCA does not consider the order in which the data were collected. The projection of the mechanosensory signals onto the first six principal components (PCs) suggests that PC1, PC2, and PC5 capture the differences between the four scenarios most clearly (SI Appendix, Fig. S4). In the corresponding PC space, the trajectories (i.e., the paths through the PC space according to the temporal evolution of the projected signals) corresponding to each of the four scenarios are clearly separated and occupy distinct regions of the space (Fig. 4D).

To understand the meaning of the trajectories in the PC space, it is useful to look at the loadings (i.e., squared coefficients) of each PC. Fig. 4E depicts the total loadings for each whisker (summed over all six mechanical components) for each of the three PCs. Each PC appears to represent a subset of whiskers. For example, PC1 (Fig. 4E, Left) receives the largest contribution from whiskers in column 2 and 3. These whiskers are highly active in Scenarios 2 and 3, thus explaining the corresponding large and overlapping excursions in the direction of PC1 (Fig. 4D, Right Inset). The loadings of the signal components indicate that $M_z$ is likely responsible for the larger extent in the negative PC1 direction of the trajectory in Scenario 3 compared to 2 (Fig. 4F). This PC analysis over all whiskers and all scenarios corroborates the result that active whisking tends to shift the direction of $M_b$ toward the direction of $M_z$ as shown in Fig. 4C.

In contrast, PC2 (Fig. 4E, Middle) is most strongly determined by the whiskers in a diagonal across the first three columns (β, B1, C1, D1, D2, E2). These whiskers are most strongly activated in Scenario 4, explaining the large excursion of the corresponding trajectory in the PC2 direction. The increase in variance of the signals in the PC2 direction in Scenario 4 compared to Scenario 1 is likely due to the signal components $M_x$, $M_y$, and $M_z$ (Fig. 4F). A difference in the magnitude of $M_y$ and $M_z$ manifests itself in a magnitude difference in $M_b$, visible in Fig. 3F, Left and Right.

Finally, for PC5 (Fig. 4E, Right), the loadings are largest for the rostral whiskers in column 4 and 5. In Scenario 2 and 3, these whiskers do not collide with the peg. However, the active whisking motion in Scenario 3 produces inertial signals at the base of these whiskers, which likely explains the offset in the PC5 direction that separates these two scenarios. Inertial effects are the strongest for the signal components $M_x$ and $M_z$, which are the main contributors to PC5 (Fig. 4F and SI Appendix, Fig. S5D). More details about the inertial signals during free-air whisking (no contact) are shown in SI Appendix, Fig. S5.

Discussion

We have developed a dynamic model of the whisker array of a “prototypical” rat, whose parameters and dynamics fall within the range of biological rats. This model is not intended to replicate the sensory input of a single individual rat at high precision. Instead, the model has been validated to generate reasonable approximations of real whisker dynamics, well within the naturally occurring variability within and across animals. Individual rats vary in size, age, sex, and strain, which ultimately manifest in different sizes, scales, shapes, material properties, and spatial arrangement of the vibrissae. Despite this variability, rat brains have found solutions that allow these animals to use their vibrissal systems to accomplish similar tasks in a similar manner. Understanding the underlying principles of the rat somatosensory pathway therefore cannot rely on modeling the sensors of an individual rat in detail (27).

The utility of the present model is that it begins to allow us to study the input to neural circuitry that has evolved with multiple sensors interacting with a 3D complex world. Behavioral studies have shown that natural rodent whisking behavior involves contact and collisions of many whiskers with the environment (33). Studies of the vibrissal-responsive primary somatosensory (“barrel”) cortex indicate that neural information is spatially integrated across multiple whiskers and that the statistics of the stimuli have a significant effect on the receptive fields due to adaptation mechanisms (28). These findings indicate that it is crucial to study neural activity in the vibrissal system in the context of natural behavior and the full whisker array. Although existing single-whisker models may be able to predict the dynamics of individual whiskers more accurately (29, 34, 35), the present work offers 3D simulations of the entire array in a wide range of simulated environments and experimental conditions.

Three technical caveats should be noted when using the present model. First, it cannot be used to simulate high-frequency vibrations because the spatial resolution of the whisker is limited to 20 data points (i.e., 20 links). Therefore, some dynamic behavior such as higher order resonance modes cannot be simulated. These modes are presumed to play a role in texture discrimination (25, 26, 36), which lies beyond the scope of the present model. Second, because each node is limited to two degrees of freedom, shear forces cannot be modeled. Beam theory indicates that shear forces are negligible in straight vibrating beams with aspect ratios greater than 100 (37). Whiskers have aspect ratios of 1,000 or greater, but it remains unclear how the taper and curvature of the whisker may affect the shear forces at the base and the extent to which these forces are transduced by the mechanoreceptors embedded in the follicle. These two technical limitations could be addressed in the WHISKiT simulator by adding more nodes and an extra degree of freedom to each node at the expense of increased computational load. Finally, the rostral-most macrovibrissae were not simulated. Previous work has indicated that these whiskers may be important when exploring object features that are small on the scale of the rat’s sensory volume (11) but that they are the whiskers least likely to make contact with a surface that is large on the scale of the rat’s vibrissal array. Therefore, when modeling how a rodent explores small objects, users of WHISKiT Physics should keep in mind that the simulated contact patterns will omit any potential contact with the most rostral whiskers.

In addition, all model validations are based on kinematic measurements (resonance and damping behavior, whisker shape, etc.) from experiments with real whiskers or on dynamics predicted from previously published models (which have also been validated against kinematic data) (29, 35). The reason is that it is not clear how one could ever obtain ground truth measurements of forces and moments in the real animal, as any sensor would interfere with the whisker’s dynamics. The relationship between kinematics and dynamics is primarily determined by material properties (density, Young’s modulus, damping) of the whisker and is therefore dependent on the model assumptions for these parameter values. Previous work has found that density as well as Young’s modulus vary between proximal and distal whisker regions (22, 38, 39). In WHISKiT Physics, parameters were chosen to be within the range of biological variation: density was approximated to increase linearly from base to tip, while Young’s modulus and damping properties were assumed to be homogeneous within and across whiskers.

Finally, experimental measurements of follicle compliance and translation on the mystacial pad are extremely limited at present (40). Our simulations showed that rigid boundary conditions in the single-whisker model are insufficient to match experimental data obtained when whiskers are deflected in situ, on the rat’s face (SI Appendix, Optimization of damping properties of the follicle and Fig. S3). Therefore, to model a compliant follicle, torsional springs were incorporated at the whisker base, and the spring constants were optimized to match the mechanics observed experimentally in the anesthetized animal (SI Appendix, Optimization of damping properties of the follicle and Fig. S3). However, the stiffness of the tissue surrounding the follicle in the awake animal likely depends on the degree of muscle contraction during each whisk cycle (41). These muscle contractions can also cause translational shifts of the entire mystacial pad in caudal–rostral as well as ventral–dorsal directions (40). WHISKiT Physics does not model these changes in follicle compliance and position during whisking but could potentially be extended to incorporate them if corresponding experimental data from the awake animal were available. Given that experimental data suggest that translational shifts of the mystacial pad are approximately uniform across whiskers and roughly maintain spatial relationships between whiskers (40), we expect that changes in follicle stiffness or position would affect deformation magnitude and resonance frequency relatively uniformly across the array. Thus, incorporating muscle contraction in the model is unlikely to change the results presented here.

The present work (Fig. 4) shows that WHISKiT Physics can be used to examine the spatiotemporal patterns of mechanical signals across the rat whisker array in ways that cannot currently be achieved in the real animal. For example, active whisking generates notably pulsatile patterns of contact associated with the whisking periodicity. We have previously proposed that these discrete patterns of contact suggest that rodents may employ a strategy of “windowed sampling” to extract an object’s spatial features (33, 35). More specifically, we have proposed that if the rat ensures that the whiskers remain in contact with an object for a sufficiently long duration (20 to 50 ms), the vibrations generated by collision with the object damp out (35). The animal could then spatially integrate quasistatic mechanical signals across whiskers to determine the object’s spatial features. Such a strategy closely resembles the periodic sampling strategy associated with sniffing behavior (42), an important means by which animals can identify elements and gradients within an olfactory plume.

Importantly, Fig. 4B demonstrates that even when a passive touch experiment is deliberately designed to match the periodic patterns of whisker–object contact observed in the awake animal, correlations between mechanical signals across whiskers are quite different. The results further suggest that active whisking helps to minimize slip-off and to ensure that the whisker deflects within its plane of curvature. Moreover, the PCs reveal how whisker identity and the mechanics at the base uniquely shape the signal trajectories, which is only possible with a model that captures the full input space of the sensor array.

We anticipate that WHISKiT Physics will soon allow us to examine how these patterns can be used to distinguish between stationary and moving objects, how the patterns would differ if the whisker array were altered, and the advantages of active compared to passive sensing. We also expect it to enable the field to leverage techniques such as information theory, virtual reality, and reinforcement and machine learning. These approaches will allow researchers to model both sensory information processing as well as control circuits, learning, and environmental interactions. For example, a similar but unvalidated model has already been used to make predictions about the processing architectures in the trigeminal pathway based on a goal-driven deep neural network approach (43). Finally, we expect that the simulation system can be used to bootstrap hardware implementation of artificial whisker systems, which could potentially accelerate and facilitate the design process of robots (44–49).

Methods

All experiments involving animals were approved in advance by the Animal Care and Use Committee of Northwestern University.

Extrapolation of Optimized Material Parameters across Whiskers with Varying Geometries.

After optimizing and validating dynamics for the single-whisker model (SI Appendix), we validated the resonance behavior of all whiskers across the array. To perform this validation, we searched the literature for studies that had published values of whisker resonance along with whisker length, base diameter, and tip diameter. We could find no study that had published all of these values for the same set of whiskers. However, Hartmann et al. (24) published resonance frequencies, arc length, and base diameter for 24 whiskers, and we were able to obtain tip diameter measurements for the same 24 whiskers from the original 2003 experiment (Dataset S1).

Based on these data, we simulated 24 straight whiskers with the measured arc lengths and base and tip diameters. The material parameters were set to the optimized values ${\theta }_E=5.0$ and ${\theta }_{\zeta }=0.33$. In simulation, the base of each whisker was rigidly clamped to a motor (defined as the origin) such that the whisker lay in the horizontal (x-y) plane and was aligned with the x-axis. The motor rotated the whisker about the vertical (z) axis. Each simulation lasted 1 s, sampled at 1 kHz. The angle from the original position $\nu \hspace{0.17em}\left(t\right)$ was changed according to a Gaussian-like function with ${\nu }_0=\frac{\pi }{3}$, $\mu =4\sigma$, and $\sigma =0.025$ to ensure smooth motor movement at the beginning of the actuation according to Eq. 1:

$$\nu \hspace{0.17em}\left(t\right)={\nu }_0{e}^{-\frac{1}{2}{\left(\frac{t-\mu }{\sigma }\right)}^2}\hspace{0.17em}.$$ [1]

The rotation of the motor was terminated abruptly after 0.128 s to induce vibrations of the whisker. The simulation was performed once for each whisker geometry.

The x, y, and z position of all 20 links was recorded at each time step, but only the y-component of the whisker tip (link 20) was used for further analysis. The data were cropped to contain only free whisker oscillations, whereas the fast Fourier transform (FFT) was performed to find the first resonant mode.

Extrapolation of Optimized Material Parameters to the Average Rat Vibrissal Array.

The arc length (S), base radius (r_base), and the radius slope of the whisker can be approximated as functions of whisker position (row, column) from which the tip radius can be calculated (22). The intrinsic curvature of the whisker is approximated by a quadratic function $y=A{x}^2$ in the x-y plane according to Belli et al. (23) in which $A$ represents the curvature coefficient. The value for $A$ can be calculated by using the relationship between the intrinsic curvature and arc length of the whisker. In our model, $N$ equidistant points along this quadratic curve represent the position of the nodes.

We tested whether the simulations using optimized parameters would generalize to explain the dynamics of all whiskers within the average whisker array as described by the equations found in Belli et al. (22). The simulations were identical to those described in Extrapolation of Optimized Material Parameters across Whiskers with Varying Geometries, but all 27 whiskers comprising the right side of the array (rows A to E, columns Greek to 5) were simulated.

The experimental data for comparison (resonance frequency and arc length) was compiled from Hartmann et al. (24), Wolfe et al. (25), and Neimark et al. (26) (Dataset S1).

Collision with a Straight Edge.

To validate simulation dynamics during collision, we compared results with a previously published analytical model (29) that simulated a straight whisker colliding with the edge of an object. For this purpose, each simulated whisker was rotated at its base at constant angular velocity about the vertical axis through the base point until the 19th link (95% of whisker length from the base) collided with a rectangular edge. The initial angular displacement from the edge was set to 5.6° $\left(\frac{\pi }{32}\hspace{0.17em}rad\right)$. When contact with the object was detected, the driving force at the base was set to zero, allowing natural deceleration of the whisker. The collision was set to be inelastic to avoid rebound.

The collision angle between whisker and edge was defined to be 60° in the horizontal and 45° in the vertical plane to generate mechanical responses in all three dimensions. We performed simulations with 12 whiskers from four different rows (α, A2, A2, B1, β, B1, B2, γ, C1, C2, δ, D1, and D2). In the first set of simulations, intrinsic curvature was omitted, that is, 12 straight whiskers replicated the experiment described in Boubenec et al. (29). In the second set of simulations, all whiskers were curved according to the model in Belli et al. (23). For each whisker, we simulated collisions for six velocities (90, 180, 270, 360, 450, and 540 deg/s) while recording all six components of the mechanical signals at the base $\left(F_x,F_y,F_z,M_x,M_y,M_z\right)$ as well as a binary “contact vector,” $C$, which indicated contact state (0 or 1) for each whisker link. The simulation output was sampled at 1 kHz, and simulations were terminated after 0.2 s.

For signal analysis, the mechanical components $F_x,\hspace{0.17em}{F}_y,F_z,\hspace{0.17em}{M}_x,M_y,\hspace{0.17em}\text{and}\hspace{0.17em}{M}_z$ were smoothed by convolving a 10th order Hanning window. The time of collision was obtained by finding the first nonzero value of $C$ of any whisker link.

To determine the magnitude of the shock immediately after the collision for each whisker, the derivative of the signal $M_z$ was rectified, and the maximum ${\dot{M}}_{z,max}$ at time $t_{max}$ within the first 10 ms after collision was found. The shock magnitude ${\dot{M}}_{z,max}$ was normalized for each whisker by dividing by the average across all six speeds. The bending moment and transverse force at time $t_{max}$ were computed using Eqs. 2 and 3:

$$M_b=\sqrt{M_y^2+M_z^2}$$ [2]

$$\text{and}$$

$$F_t=\sqrt{F_y^2+F_z^2}.$$ [3]

The propagation of the deformation wave from tip to base was determined for the two longest whiskers in each of the four rows (α, β, γ, δ, A1, B1, C1, and D1). Whiskers A2, B2, C2, and D2 were too small and stiff to exhibit a measurable deformation wave. To track the propagation of the deformation wave, the location of the maximum deflection point of each whisker relative to whisker length was measured in respect to position of first contact for five subsequent time samples.

Simulation of Complete Vibrissotactile Input across the Array.

The mechanical signals at the base of each whisker of the full rat whisker array were simulated for four scenarios: the motion of a vertical peg through the immobile array, 8 Hz oscillation of a peg within the immobile array, active whisking against a fixed, vertical peg, and active whisking against the 3D shape of a drainpipe, representing the natural environment. In all four scenarios, the whiskers were arranged according to the morphology of the rat whisker array described in Belli et al. (23). For visualization purposes, a scanned rat head was used to model the head to which the array is attached. In all simulations, collisions between the head and other objects were suppressed to increase the simulation speed.

Scenario 1 (passive stimulation).

The origin of the whisker array (base point average) was placed at the origin of the world frame and oriented such that the average row plane was approximately parallel to the horizontal plane. The whiskers remained at a resting position while a vertical peg moved with constant speed (0.3 m/s) from rostral to caudal through the middle of the array. The peg had a diameter of 1 mm and a length of 80 mm. An illustration of the simulation experiment is given in Fig. 3A and Movie S1.

Scenario 2 (passive stimulation).

Scenario 2 is the same as Scenario 1, but the peg was repeatedly moved back and forth between starting position and the middle of the array. The peg was moved with a velocity following a sinusoidal function with a maximum velocity of 0.3 m/s. An illustration of the simulation experiment is given in Fig. 3B and Movie S2.

Scenario 3 (active whisking against peg).

The origin of the whisker array (base point average) was placed at the origin of the world frame and oriented such that the average row plane was approximately parallel to the horizontal plane. Two vertical pegs were placed bilaterally with an offset of ±30 mm in the x-axis and −10 mm in the y-axis to cause collisions with the protracted whiskers. The position and orientation of the array and the pegs remains the same while the whiskers perform a typical whisking motion with a retraction angle of 15° and protraction angle of 30° as described below. An illustration of the simulation experiment is given in Fig. 3C and Movie S3.

Scenario 4 (active whisking in natural environment).

The position and orientation of the rat model was manually selected to ensure sufficient but not extreme contact between the surface of the 3D scan and the whisker array. The positions of the rat head and the 3D surface were held fixed while the whiskers performed a typical whisking motion. To model the natural environment of a rat, we collected 3D representations of a typical rat habitat (drainpipe) in the Evanston, IL area with a Kinect for Xbox V2 (Microsoft) and a Predator Helios 300 Laptop (Acer). The scans collected covered a volume of ∼2 m³. In Geomagic Design X (3D Systems, Inc.), the point cloud data were manually edited to remove holes and erroneous points before triangulation to generate a mesh with a maximum edge length of 3 mm. An illustration of the simulation experiment is given in Fig. 3D and Movie S4.

For both active whisking scenarios (Scenarios 3 and 4), the whiskers performed a sinusoidal whisking motion at a frequency of 8 Hz with a maximum protraction angle of 30 and 40°, respectively, and a maximum retraction angle of 15° from rest. Previous work (Knutsen, Biess, and Ahissar, 2008) found that natural whisking behavior involves elevation $\phi \left(t\right)$ and torsion $\zeta \left(t\right)$ of the whisker, both of which show a row-wise dependency on the angle of protraction $\theta \hspace{0.17em}\left(t\right)$. Based on these findings (19), we constructed equations of motion (Eqs. 4 and 5) for each row (A to E), which are used to drive angular rotation at the base point during active whisking:

$$\phi \left(t\right)=\theta \left(t\right)\mathrm{\Delta }{\phi }_j\hspace{0.17em}\mathrm{\Delta }{\phi }_j=\left\{0.398,\hspace{0.17em}0.591,\hspace{0.17em}0.578,\hspace{0.17em}0.393,\hspace{0.17em}0.217\right\},\hspace{0.17em}j=A,B,\hspace{0.17em}\dots E$$ [4]

$$\text{and}$$

$$\zeta \left(t\right)=\theta \left(t\right)\mathrm{\Delta }{\zeta }_j\hspace{0.17em}\mathrm{\Delta }{\zeta }_j=\left\{-0.9,-0.284,\hspace{0.17em}0.243,\hspace{0.17em}0.449,\hspace{0.17em}0.744\right\}\hspace{0.17em},\hspace{0.17em}j=A,B,\hspace{0.17em}\dots E.$$ [5]

Each simulation lasted 250 ms involving two whisk cycles and was sampled at 1 kHz. All six components of the mechanical signals at the base of each whisker $\left(F_x,F_y,F_z,M_x,M_y,M_z\right)$ and a binary vector $C$ indicating contact (1) or no contact (0) for each whisker link were recorded. For signal analysis, the mechanical components $F_x,F_y,F_z,M_x,M_y,\hspace{0.17em}\text{and}\hspace{0.17em}{M}_z$ were smoothed by convolving a 10th order Hanning window. The magnitude of the bending moment was computed according to equation Eq. 2.

POC was determined by the number of the links in contact relative to total number of links (base: $POC=0.0$, tip: $POC=1.0$).

Data Availability

All study data are included in the article and/or supporting information.