Significance
Wind comprised 6.1% of worldwide electricity generation in 2020. If this share is to substantially grow to decarbonize electricity systems, the size of future wind farms may extend far beyond that of current installations. The spatial scale of a wind farm affects both its mean generation per unit of land and the extension of wake shadowing on neighboring plants. As spatial scales increase, mean generation decreases and wake extension increases. Here, we characterize spatial constraints in the large-scale expansion of wind power plants to address the following: 1) How large a wind farm can be before its generation reaches energy replenishment limits, and 2) How far apart large wind farms must be spaced to avoid inter–wind-farm interference.
Keywords: wind energy, wind farm–atmosphere interaction, geophysical limits, spatial scales
Abstract
When wind turbines are arranged in clusters, their performance is mutually affected, and their energy generation is reduced relative to what it would be if they were widely separated. Land-area power densities of small wind farms can exceed 10 W/m2, and wakes are several rotor diameters in length. In contrast, large-scale wind farms have an upper-limit power density in the order of 1 W/m2 and wakes that can extend several tens of kilometers. Here, we address two important questions: 1) How large can a wind farm be before its generation reaches energy replenishment limits and 2) How far apart must large wind farms be spaced to avoid inter–wind-farm interference? We characterize controls on these spatial and temporal scales by running a set of idealized atmospheric simulations using the Weather and Research Forecasting model. Power generation and wind speed within and over the wind farm show that a timescale inversely proportional to the Coriolis parameter governs such transition, and the corresponding length scale is obtained by multiplying the timescale by the geostrophic wind speed. A geostrophic wind of 8 m/s and a Coriolis parameter of 1.05 × 10−4 rad/s (latitude of ∼46°) would give a transitional scale of about 30 km. Wind farms smaller than this result in greater power densities and shorter wakes. Larger wind farms result instead in power densities that asymptotically reach their minimum and wakes that reach their maximum extent.
In 2020, wind comprised a 6.1% share of electricity generated worldwide (1). This figure is expected to substantially grow as more renewable energy is used in the effort to limit carbon dioxide emissions and consequent global average temperature increases. Under some energy transition scenarios (2), wind energy provides more than one-third of global energy needs by 2050, indicating that the size of future wind farms may extend far beyond that of current installations.
When wind turbines are clustered in large groups, their performance is mutually affected, and the rate at which they extract energy from the atmosphere is reduced (3). To better characterize how wind farms function and interact with the atmosphere, researchers have focused on the wakes that the turbines generate (4) and the turbines’ power production (5), given in terms of power density per unit of land area for very large wind farms (6). Wakes are regions of reduced wind speed resulting from the turbine energy extraction. They are a function of wind speed and direction (7, 8), atmospheric turbulence intensity (9) and stratification (10), turbine operating conditions (11), and terrain topography (12). Because farm performance is directly affected by wakes and atmospheric transport mechanisms, power production or power density in wind farms exhibits the same qualitative dependence on the wind resource, turbulence, and stratification (5, 13–15).
Numerical- and observation-based studies have shown that there are substantial differences in wind farm performance and wake characteristics, depending on the horizontal size of the farm (16). For small wind farms, wind speed in wake regions recovers to undisturbed conditions within a distance of 10 to 15 times the rotor diameter (17), which corresponds to hundreds of meters, depending on the turbine dimensions. For large wind farms, wakes have been observed extending up to tens of kilometers downstream (18, 19), raising questions regarding the consequences that this could have on neighboring wind farms in terms of energy production and economic losses (20). As the number and density of turbines in a wind farm increase, so does their likelihood of being affected by an upstream turbine, diminishing energy generation. If wind farms are composed of a relatively small number of widely spaced turbines, the likelihood of a turbine being affected by an upstream one is low, and this likelihood can be further mitigated by optimal layout design (21, 22). For very large (mesoscale) wind farms, where all but the first row of turbines are mutually affected, a fully developed wind farm boundary layer is observed (6). At such scales, optimal siting of wind turbines is expected to have a more limited effect, with achievable gains in power generation of about 10%, depending on the layout (23). In fact, the power density reaches a limit that largely depends on the atmospheric pressure gradients and Coriolis forces, which ultimately control how much energy the turbines can extract from the atmosphere (24). While these limits are framed in terms of local pressure–gradient forces, these pressure–gradient forces are themselves a product of mesoscale processes that extend to global scale. These energy replenishment limits are reflected in the power density of wind farms at different scales: at small scales, it can exceed 10 W/m2, but it is in the order of 1 W/m2 at very large scales (25, 26).
These substantial differences among various wind farm sizes show the importance of understanding at which spatial scale a transition of wind farm performance and wake characteristics occurs. Because of the lack of field experiments aimed at answering this question, researchers have used numerical experiments to characterize this transition. Results from large-eddy simulations showed that the transition from submesocale to mesoscale—that is, the scale at which the wind farm boundary layer is fully developed—occurs well beyond 10 km in conventionally neutral boundary layers (27), and potentially at a few tens of kilometers (28, 29). Formulas based on scaling analyses considering canopy flows have also been provided to estimate the adjustment length (30). These analyses however did not consider the role of large-scale atmospheric physics such as the Coriolis force and atmospheric pressure gradients, which become important in large wind farms and for the characterization of the submesocale-to-mesoscale wind farm transition.
Here, we characterize spatial constraints in the large-scale expansion of wind power plants by identifying transitional scales in wind farm performance and wake characteristics. This will help determine how large a wind farm can be before its generation reaches lower mesoscale limits, and how far apart large wind farms must be spaced to avoid inter–wind-farm interference. In contrast to previous studies, we consider in our analysis the Coriolis and atmospheric pressure–gradient forces, which we show are important factors for a characterization of the transition. We run a set of idealized, atmospheric simulations with neutral atmospheric conditions using the Weather and Research Forecasting (WRF) model, in which the wind turbines are parametrized as momentum sinks. We give a physical explanation to the transitional scale, and we identify a timescale inversely proportional to the Coriolis parameter that defines at what length scale a wind farm can be said to have reached mesoscale characteristics (fully developed wind farm boundary layer). We also show the implications that this scale has on the power density and wakes when we consider different wind farm sizes. Ultimately, the goal of this study is to provide both mechanistic understanding and a quantitative rule of thumb, indicating when the primary factor reducing wind power generation would be shadowing by wakes from individual turbines, or the formation of the wake behind the wind farm as a whole.
Timescales in the Ekman Boundary Layer
To study and characterize the timescales in a wind farm, we consider an idealized case of planetary boundary layer flowing over a wind farm, as depicted in Fig. 1. The wind farm has flat regions both upstream and downstream. The balance of a constant pressure–gradient and Coriolis forces drives a geostrophic flow over the flat regions and the wind farm. An Ekman turbulent boundary layer develops close to the ground, resulting from the interaction of the pressure–gradient, Coriolis, and turbulent friction forces (31). We assume that the Ekman layer is fully developed and in equilibrium in the flat region upstream of the wind farm. The wind farm can be considered as a sudden change in surface roughness, and once the air flows over it, the Ekman layer responds and adjusts to a new equilibrium, up to a fully developed state if the wind farm is long enough. Another sudden change in surface roughness is present at the end of the wind farm, where the Ekman layer has to readjust to the downwind flat region.
Fig. 1.
The dynamic response of an Ekman boundary layer flowing over and off a mesoscale wind farm is characterized by the turbulent () and Coriolis () timescales. A geostrophic wind () is driven over the flat regions and the wind farm by the balance of a constant pressure–gradient () and Coriolis () forces. An Ekman turbulent boundary layer develops close to the ground, resulting from the interaction of the pressure–gradient (), Coriolis (), and turbulent friction () forces.
If we assume that such a system is in steady-state conditions, the adjustment that the flow undergoes can be characterized with length scales. These length scales are derived by considering how far an air parcel travels at the given wind speed and for a certain time. This time is a characteristic property of the system and, as such, defined as a fundamental timescale of its dynamic response. To understand the characteristic timescales of an Ekman layer, we first recall its governing equations. The momentum equations of the geostrophic flow above the Ekman layer are the following (31):
| [1] |
| [2] |
where the geostrophic wind is given by the following:
The momentum equations for the steady-state Ekman layer over varying surface roughness are the following (31):
| [3] |
| [4] |
The three terms on the right-hand side are the forces at play (pressure–gradient, Coriolis, and turbulent friction) that control the evolution of the Ekman turbulent boundary layer.
Various experimental and numerical studies have looked at the dynamic response of an Ekman boundary layer, particularly when subject to a varying pressure–gradient forcing or to a change in surface roughness. Lewis and Belcher (32) showed with mathematical and numerical models the different response times of the forces at play in transient ocean Ekman currents (with governing equations similar to atmospheric boundary layers). They highlighted that, given a wind forcing, the earliest response is driven by diffusive momentum transfer, followed by the Coriolis acceleration, and lastly by inertial oscillations that slowly decay. Momen and Bou-Zeid (33, 34) studied by means of large-eddy simulations the unsteady Ekman layer under sinusoidal pressure forcing, and identified two characteristic timescales, an inertial and a turbulent timescale. They also demonstrated that, under certain regimes, the unsteady Ekman layer behaves as a dynamic second-order system (i.e., a mass-spring-damper system), in which the mass corresponds to the flow inertia, the spring to the conservative Coriolis force, and the damper to the frictional dissipation. Taylor (35), Jensen (36), and Wright et al. (37) studied with numerical models the Ekman layer over a change in surface roughness with a constant pressure forcing. The response to this change in roughness showed an asymptotic adjustment of the Ekman layer to the new equilibrium, without the inertial oscillations typical of an underdamped second-order system. Overall, these studies suggest that three different timescales may define the response of an Ekman layer flowing over and off a wind farm: the turbulent timescale (34),
| [5] |
where is the height of the Ekman layer and the surface friction velocity; the Coriolis timescale (32),
| [6] |
and the inertial timescale (34),
| [7] |
which controls inertial oscillations.
With regard to the turbulent timescale, the height of the Ekman layer, , has been shown to be directly proportional to the surface friction velocity and inversely to the Coriolis parameter (38), with a proportionality coefficient, , in the range from 0.12 to 0.4 (36, 39, 40). This variability is usually attributed to a dependence on stability conditions (41), and more advanced analyses show how to properly account for it through empirical formulas (42). The height of the Ekman layer can be written as the following:
| [8] |
which allows a rewrite of the turbulent timescale as the following:
| [9] |
All three of these timescales are, therefore, inversely related to the Coriolis parameter.
We hypothesize that these timescales govern the transition from submesoscale to mesoscale wind farms and, therefore, that this transition occurs on a timescale that is inversely related to the Coriolis parameter. However, the constant coefficients in Eqs. 6, 7, and 9 vary by more than an order of magnitude. Because the Coriolis parameter increases with latitude, this implies that higher-latitude wind farms would undergo the submesoscale-to-mesoscale transition at a larger size than would a lower-latitude wind farm. Furthermore, this would suggest that, with other things equal, wind farm wakes at higher latitudes would be replenished with momentum and kinetic energy more rapidly than they would at lower latitudes.
For this system, the geostrophic winds above the boundary layer provide a characteristic velocity. Thus, a characteristic horizontal length scale can be defined for each of these three timescales, in which this length scale is the geostrophic velocity times the characteristic timescale. This yields a turbulent length scale,
| [10] |
a Coriolis length scale,
| [11] |
and an inertial length scale,
| [12] |
The surface roughness length, of either the actual terrain or the wind farm, does not appear in the present analysis. It is possible to argue that that parameter could be important for the response behavior of an Ekman layer. Because the geometry, operating conditions, and arrangement of the wind turbines concur in determining a wind farm equivalent surface roughness, the conclusions of the present study might not be general if the importance of the surface roughness length were indeed substantial. In The Response of an Ekman Boundary Layer Flowing over a Very Large Wind Farm, we will see that different operating conditions of a wind farm do not modify the response behavior of the Ekman layer, while in Power Density and Wakes as a Function of Wind Farm Size, we will see that different turbines arrangements in a wind farm result in limited differences in terms of both power densities and wake extension. In SI Appendix, Supplementary Note 2, we provide an estimation of the surface roughness lengths in our simulations, and we show that despite their values changing by orders of magnitude, the response of the Ekman layer is substantially unchanged. Lastly, in SI Appendix, Supplementary Note 3, we provide a nondimensional analysis of the governing equations, showing that the surface roughness length has indeed a minor role in the evolution of an Ekman layer after a change in surface roughness. Research on surface roughness in nonrotating flows also supports that, as long as the vertical length is greater than a few (actual) roughness heights, and the roughness is appreciably smaller than the boundary layer height, the specific details of the roughness become less important (43). We speculate that this minor effect is embedded in the empirical coefficient of Eq. 8, which is then reflected in the turbulent length scale of Eq. 10. A proper determination of this coefficient and its dependence on the surface roughness length (among other factors) is, however, beyond the scope of the present study. Rather, we are instead interested in providing a first-order characterization of the time and length scales in wind farms.
The Response of an Ekman Boundary Layer Flowing over a Very Large Wind Farm
To test our hypothesis, we run a set of idealized, numerical atmospheric simulations with the WRF simulation tool (44, 45), version 4.2.1, in which the wind turbines are parametrized as sinks of momentum and sources of turbulence kinetic energy (46–48). Idealized, numerical simulations are widely used to study the fundamental mechanisms that govern large wind farms (6, 8, 14, 23, 27–29, 49, 50). They allow, in fact, to isolate and study only some specific mechanisms and disentangle them from other concurring phenomena. In the present simulations, we consider a limited-sized doubly periodic domain with horizontal dimensions of 1,000 × 50 km2 and a height of 10 km, where a geostrophic flow runs along the longest dimension. In this domain, a wind farm extends for 500 km along the stream-wise direction, covering the 50-km cross-wise dimension. The wind farm is composed of Vestas V164-9.0MW wind turbines on a uniform arrangement with 1-km spacings in the stream- and cross-wise directions. This idealized scenario, equivalent in substance to the representation of Fig. 1, results in two regions with different surface roughness, one given by the actual ground and one (equivalent) given by the wind farm, and a sufficient length for the flow to fully adjust after the two sudden changes in roughness. The set of simulations that we perform with this scenario uses a combination of three geostrophic wind speeds (8, 12, and 16 m/s) and two Coriolis parameters (0.55 × 10−4 and 1.05 × 10−4 rad/s; latitudes of ∼22° and ∼46°, respectively), resulting in six cases. These settings in the boundary conditions implicitly assume a driving constant pressure–gradient field for each of the considered combinations, as given by Eqs. 1 and 2. Furthermore, for each combination of geostrophic wind and Coriolis parameter, we perform additional simulations that consider a 50 × 50 km2 domain either without turbines or with turbines covering the entire ground. Given the periodic boundary conditions and uniform surface conditions, these simulations are used to calculate the fully developed flow conditions that would be reached if enough distance is present after a sudden change in surface roughness. Note that in all the simulations, we assume neutral atmospheric conditions (i.e., no thermal convection or stratification) and dry air.
In Fig. 2, we plot the two-dimensional flow field obtained by each combination of geostrophic wind and Coriolis parameter. More specifically, we plot the contours of absolute value of wind speed normalized by the geostrophic value, and we indicate with dotted lines the region where the wind farm is present, with vertical solid lines the location at which the wind farm begins and ends, and with vertical dash-dotted and dashed lines the distance that an air parcel travels over the turbulent and Coriolis timescales, respectively, from either the beginning or end of the wind farm. The darker blue above, within and downstream the wind farm, indicates a wind speed reduction generated by the drag of the wind turbines on the airflow. We can see that the adjustment of the airflow once it travels over or off the wind farm tends to occur in shorter distances for weaker geostrophic winds and larger Coriolis parameter, suggesting that both these parameters play an important role in the flow transition. These qualitative visualizations of our results, however, do not fully show the effect of the different timescales discussed earlier.
Fig. 2.
Contours of the absolute value of wind speed normalized by the geostrophic value, showing the slowing of winds as they pass over the mesoscale wind farm (Left to Right). Each panel is for a combination of the geostrophic combination of geostrophic wind (8, 12, and 16 m/s) and Coriolis parameter (0.55 × 10−4 and 1.05 × 10−4 rad/s; ∼22 and ∼46° latitude). and are the turbulent and Coriolis length scales, respectively. is plotter for a value of . Dotted lines indicate the region where the wind farm is present, vertical solid lines the location at which the wind farm begins and ends, and vertical dash-dotted and dashed lines the distance that an air parcel travels over the turbulent and Coriolis timescales, respectively, from either the beginning or end of the wind farm. The adjustment of the airflow once it travels over or off the wind farm occurs in shorter distances for weaker geostrophic winds and larger Coriolis parameter.
We further analyze the results of the six cases considered by looking at the wind speed and direction at different altitudes over the length of the domain. In Fig. 3, we plot these quantities at the turbine hub height and two other altitudes above the wind farm for each combination of geostrophic wind and Coriolis parameter. In the same figures, we also indicate with horizontal dashed and dash-dotted lines the value that the wind speed or direction would be without turbines or with an infinite wind farm, respectively. A more quantitative analysis is presented in Fig. 4 A–D, in which we plot the percentage difference between the wind speed at the turbulent () or Coriolis () stream-wise distances over the wind farm or in the wake region and its respective fully developed wind speed. In Fig. 4 E–H, we plot the same quantitative difference for the wind direction. is evaluated for a value of , which is a reasonable approximation for neutral, atmospheric boundary layers (39).
Fig. 3.
Changes in the absolute value of wind speed normalized by the geostrophic value (Left axis) and wind direction (Right axis) at three different altitudes, as winds flow over the mesoscale wind farm (Left to Right). Each panel is for a combination of geostrophic wind (8, 12, and 16 m/s) and Coriolis parameter (0.55 × 10−4 and 1.05 × 10−4 rad/s; ∼22 and ∼46° latitude). Vertical solid lines indicate the location at which the wind farm begins and ends, and vertical dash-dotted and dashed lines indicate the distance that an air parcel travels over the turbulent and Coriolis timescales, respectively, from either the beginning or end of the wind farm. is plotter for a value of . Horizontal dash-dotted and dashed lines indicate the wind speed or direction values for the fully developed case with or without turbines, respectively.
Fig. 4.
Difference between the wind speed (A–D) or direction (E–H) and its respective fully developed value. For the four panels on the left (A, B, E, and F), the fully developed conditions are the ones obtained with an infinite wind farm, whereas for the four panels on the right (C, D, G, and H), the fully developed conditions are the ones obtained without turbines. The locations considered are the beginning and the end of the wind farm (blue shades for wind speed and gray shades for wind direction) and a distance equal to the turbulent () or Coriolis () length scale after the beginning and the end of the wind farm (pink shades for wind speed and red shades for wind direction). is calculated for a value of . Bands correspond to ± 1 SD with respect to the average difference calculated, when considering all the cases with different geostrophic winds and Coriolis parameters.
By looking at the plots of wind speed in Fig. 3, it is possible to see that most of the flow adjustment after sudden changes in surface roughness occurs within a length given by the turbulent length scale, , and the flow becomes almost completely adjusted after a length given by the Coriolis length scale, . From Fig. 4, the percentage difference between the wind speed and its respective fully developed conditions drops from about 50 to 60% at the beginning of the wind farm to about 0 to 6% and 0 to 5% after distances equal to and , respectively, when considering the region over the wind farm. When we consider the wake region, the percentage difference drops from about 35 to 40% at the end of the wind farm to about 0 to 7% and 0 to 5% after distances equal to and , respectively. The turbulent timescale identifies the turnover time of the largest eddies over the boundary layer height and therefore gives a measure of the diffusion rate of any change in boundary conditions, such as a change in surface roughness. The wind speed at the highest plotted altitude takes, in fact, a slightly longer horizontal distance to respond to the change in roughness because the change in turbulence propagates upward from the ground. In contrast, the Coriolis force acts more slowly on the flow field, and once an air parcel has traveled for a timescale equal to the Coriolis timescale after a change in surface roughness, the wind speed becomes nearly constant.
For lower geostrophic wind speeds and higher Coriolis parameters, the velocity field shows some of the characteristics of a second-order system, as discussed in Timescales in the Ekman Boundary Layer. Simulated wind speeds show some very minor oscillations (for example, for a geostrophic wind of 8 m/s) in response to the sudden change in surface roughness. These oscillations are expected to have a frequency inversely proportional to the inertial timescale, . However, the full oscillations are not seen in our results because these are quickly damped by turbulent dissipation, and because the current wind farm length, 500 km, does not allow them to be fully captured (for example, the shorter inertial timescale given by the case with geostrophic wind of 8 m/s and Coriolis parameter of 1.05 × 10−4 rad/s would give a length of roughly 450 km).
The response of wind direction to a change in surface roughness is also influenced by wind speed and Coriolis parameter (Fig. 3). Even though the wind direction response to a change in surface roughness is consistent with the wind speed response (i.e., more rapid adjustment with weaker geostrophic winds or larger Coriolis parameters), the response of wind direction to changes in surface roughness is generally slower than the response of wind speed. In Fig. 4, the difference between the wind direction and its respective fully developed value drops from about 7 to 13° at the beginning of the wind farm to about 0 to 6° and 0 to 3° after distances equal to and , respectively, when considering the region over the wind farm. When we consider the wake region, the difference drops from about 7 to 13° at the end of the wind farm to about 1 to 7° and 0 to 3° after distances equal to and , respectively.
Furthermore, the wind direction response to changes in surface roughness is more commonly associated with oscillations. This behavior was also noticed by Taylor (35) and suggests that because only the Coriolis force causes the flow to deflect, the response of the wind direction to a sudden change in surface roughness is characterized primarily by the Coriolis timescale. Also, the adjustment of the wind direction appears to be uniform across the height of the boundary layer rather than propagating from the bottom, as was the case for the wind speed adjustment driven initially by turbulent diffusion. Additionally, our results show that inertial oscillations, with wind direction variation generally within a ± 5° of the mean, affect much more the wind direction than the wind speed. This can be explained by considering that turbulent dissipation acts on the kinetic energy of the flow, which is proportional to the wind speed squared, and does not directly affect wind direction. A change in wind direction requires an application of a force with a component normal to the direction of flow, such as is provided by Coriolis forces. Because these oscillations have a length scale that is in many cases longer than the wind farm size as discussed previously, the wind direction in our simulations never reaches a fully developed state.
Lastly, we show in Fig. 5 the thrust and power generated by each row of turbines and for each of the cases considered. In the same figure, we also plot their values (with horizontal dash-dotted lines) for the fully developed case of an infinite wind farm. The behavior of the thrust and power generation closely mimics the behavior of wind speed: The first rows of turbines operate at the maximum performance for the given wind speed, whereas, within a length proportional to the turbulent timescale, the thrust and power undergo most of their reduction, after which their value is already very close to the fully developed case. Our results show that full adjustment is reached after a length proportional to the Coriolis timescale.
Fig. 5.
Thrust (Left axis) and power generation (Right axis) of the wind turbines. Each panel is for a combination of geostrophic wind (8, 12, and 16 m/s) and Coriolis parameter (0.55 × 10−4 and 1.05 × 10−4 rad/s; ∼22 and ∼46° latitude). Vertical solid lines indicate the location at which the wind farm begins and ends, and vertical dash-dotted and dashed lines indicate the distance that an air parcel travels over the turbulent and Coriolis timescales, respectively, from the beginning. is plotter for a value of . Horizontal dash-dotted lines indicate the thrust and power values for the fully developed case with turbines.
Overall, the results of our idealized simulations provide substantial confirmation of the hypothesis that the turbulent and Coriolis timescales govern the transition from submesoscale to mesoscale wind farms and, therefore, that this transition occurs on a timescale that is inversely related to the Coriolis parameter. By considering simple scenarios with a widely used three-dimensional (3D) numerical model, we showed that the adjustment of a planetary boundary layer flowing over or off a wind farm occurs for the most part within a length that is directly proportional to the geostrophic wind and turbulent timescales. An almost full adjustment occurs after the Coriolis force has had time to deflect the flow toward the fully developed conditions, which occurs within a Coriolis timescale. Minor inertial oscillations are sometimes seen in the wind speed evolution, but these are quickly damped by the turbulent dissipation. More evident inertial oscillations are seen for the wind direction, in which the turbulent dissipation has a smaller impact, and decay much more slowly. In SI Appendix, Supplementary Note 5, we provide a preliminary analysis of the effect of stratification on the spatial scales that we identified in our analysis. The results suggest that a stratified atmosphere results in a shorter turbulent length scale and a more rapid wind speed adjustment, while the wind direction response remains characterized by the Coriolis length scale.
Power Density and Wakes as a Function of Wind Farm Size
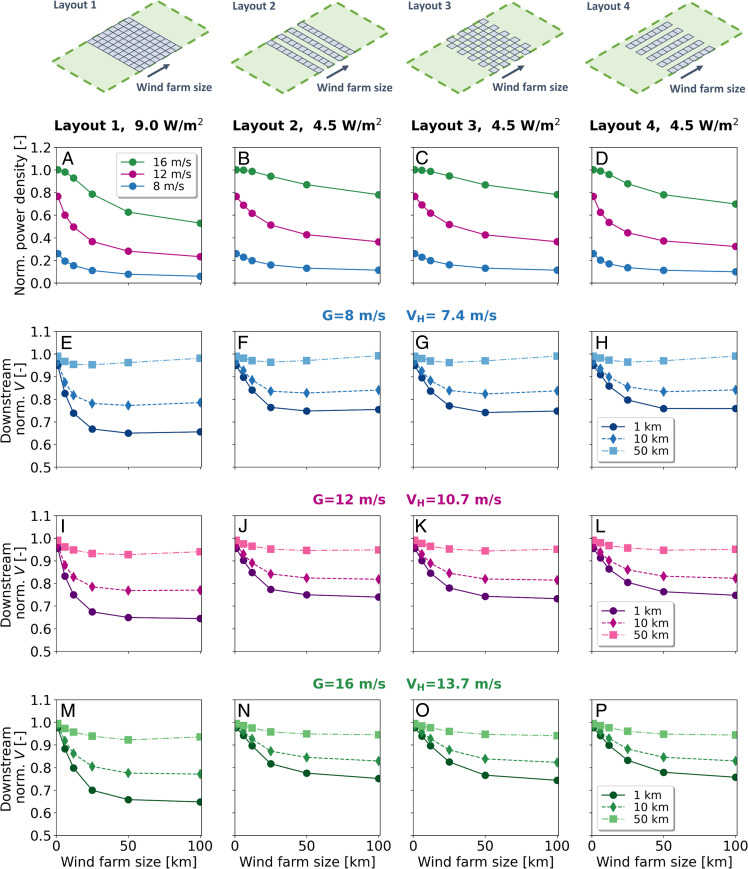
To understand the implications that the timescales previously studied would have for a more realistic scenario, we consider wind farms with a varying number of wind turbines, different layouts, and installed power densities, as illustrated at the top of Fig. 6. The wind farms use the same Vestas V164-9.0MW wind turbines of the previous simulations, arranged on a uniform grid with 1-km spacings. Each simulated wind farm has a different size that defines the number of rows perpendicular to the geostrophic flow direction (we identify the columns as parallel to the geostrophic flow direction). In these cases, the wind farm size ranges from a single row of turbines to multiple rows extending 100 km, reflecting more realistic installations, as opposed to the 500 km length of the previous cases. In layout 1, all the rows and columns are occupied by one turbine; in layout 2, the rows are occupied alternately; in layout 3, both rows and columns are occupied alternately; and in layout 4, the columns are occupied alternately. The resulting installed capacity density is 9 W/m2 for layout 1 and 4.5 W/m2 for layouts 2, 3, and 4. The installed capacity indicates the maximum instantaneous power production possible from a wind turbine or farm with ideal winds. The simulations of these cases are performed with settings similar to the previous ones: the domain is doubly periodic with dimensions of 500 × 50 km2, and a geostrophic flow runs along the longest dimension. These simulations use a combination of three geostrophic wind speeds (8, 12, and 16 m/s) and one Coriolis parameter (1.05 × 10−4 rad/s).
Fig. 6.
Normalized average power density (A–D) and normalized wind speed in the wind farm wakes (E–P) as a function of wind farm size, turbine layout, and geostrophic wind speed. The normalized average power density is calculated as the total power produced by the farm divided by its total area and normalized by the installed capacity density. The installed capacity density is 9 W/m2 in layout 1 and 4.5 W/m2 in layouts 2, 3, and 4. The wind speed is shown at three distances downstream of each simulated wind farm (1, 10, and 50 km), and it is normalized by its undisturbed value at the hub height (). Above the panels, we show the layouts considered in the simulations. The wind farm size defines the number of rows perpendicular to the geostrophic flow direction (we identify the columns as parallel to the geostrophic flow direction).
In Fig. 6 A–D, we plot the normalized, average power density resulting from the cases simulated. It is calculated as the total power produced by the farm divided by its total area and normalized by the installed power density. The power density is influenced by both the wind farm size and installed power density. The mean power density of small wind farms can reach values that are much greater than those found for large wind farms. The first rows in these farms, in fact, experience undisturbed wind conditions and can be operated at the maximum performance for the given wind speed, whereas turbines operating in the wake of others see a reduction in power generation. For wind farms with very few wind turbines, the concept of power density is less relevant because the wind turbines can be placed much closer to each other without affecting one another (even closer than what has been simulated in this study), and land availability is usually not an issue. Small wind farms can in fact have power densities that are an order of magnitude higher (51). As the wind farm size increases, the power density decreases and reaches a limit that is governed by how much of the energy supplied by the pressure gradient is transported to the turbines (24).
When the turbine density is lower, such as in layouts 2 and 3, the decrease in power density is less sensitive to the wind farm size because the wind turbines are less affected by upstream ones, and the wind speed that they face has more likely recovered to almost undisturbed conditions. The lower sensitivity to the wind farm size is also true for layout 4, in which the turbines are arranged in columns aligned to the geostrophic flow and almost aligned to the local wind direction. Here, the wind speed has less distance to recover before reaching a downstream turbine, but the wider intercolumn spacing allows for a larger sidewise entrainment that promotes a faster wind speed recovery and higher power generation (52). If we decreased even more the installed capacity density, we would reach a condition for which the spacing would be enough for the wind speed to fully recover before reaching a downstream turbine. In this case, there would not be any decrease in the generated power density as the wind farm size increases.
The results of layouts 2, 3, and 4 also show that for large enough wind farms the power density is not affected by the turbines arrangement as much as the turbine density or geostrophic wind (driven by a combination of pressure gradient and Coriolis force). If we consider a 100-km-long wind farm with layout 1 and a geostrophic wind of 12 m/s as a reference case, layouts 2, 3, and 4 provide increases of 56.4, 56.6, and 38.6% in normalized power density with respect to the reference case. Layouts 2 and 3 provide an increase of about 12.8% with respect to layout 4. This result is consistent with a previous study (23) about aligned and staggered layouts in very large wind farms using large-eddy simulations. The authors show that staggered layouts provide a power output that is about 10% higher than aligned layouts. While confirming that for large enough wind farms the turbines arrangement becomes less important (49), the results also suggest that the power extraction becomes limited by atmospheric pressure gradients and Coriolis forces (24). In such conditions, the turbine density (turbines per unit area) becomes a dominant parameter, which is also consistent with the theoretical analysis of large wind farm aerodynamics performed by Nishino and Dunstan (53). This is unlikely to be true for a wind farm with few turbines, where optimal layouts have been shown to substantially increase the wind farm power output (21, 22, 54).
The results in terms of power density as a function of the wind farm size confirm that there is a transitional scale that separates the behavior of submesoscale and mesoscale wind farms. If we consider the turbulent timescale, over which most of the flow adjustment occurs, and we multiply it by the three geostrophic wind speeds, we obtain transitional scales equal to about 30, 45, and 61 km, respectively, which are reflected in the power density, especially for the layout 1. Similar transitional length scales were observed by Wu and Porté-Agel (28), such that for a geostrophic wind of 10 m/s and a Coriolis parameter of 1.195 × 10−4 rad/s, they inferred from large-eddy simulations an adjustment distance of 24 km in conventionally-neutral atmospheric boundary layers. Our analysis with the same geostrophic wind and Coriolis parameter predicts a transitional scale of about 33 km in neutral, atmospheric boundary layers (see SI Appendix, Supplementary Note 5 for the effects of stratification on the Ekman boundary layer adjustment). However, as we showed in our analysis, this length scale is not universal but depends on the geostrophic wind and Coriolis parameter.
In Fig. 6, we also plot the wind speed downstream of the last row of each wind farm simulated to analyze the wake characteristics. The wind speed is normalized by its undisturbed value at the hub height () and is plotted at three distances downstream of the wind farm (1, 10, and 50 km). We can see that, for small wind farms, the wind speed reduction is small and recovers quickly to its undisturbed value. As the wind farm size increases, the wind speed reduction is more significant, and wakes can extend up to 50 km and potentially more. This is consistent with the observation of wakes in large wind farm, where wakes extended up to tens of kilometers downstream (18, 19). Note that beyond a certain wind farm size (larger for larger geostrophic winds), wake extensions remain substantially unchanged regardless of wind farm size. The wind speed downstream of the farm is also dependent on the installed power density, with greater wind speed reductions for denser wind farms. This behavior is consistent with the results of power density and indicates that denser wind farms are able to extract more kinetic energy from the boundary layer, which is then reflected in the deeper kinetic energy deficit of wakes. For a geostrophic wind of 8 m/s and when considering large enough wind farms, the normalized wind speed at hub height shows an increasing trend after 50-km downstream of the farm, as illustrated in Fig. 6 E–H. This behavior was observed also in the results of the previous section. In fact, for low geostrophic wind speeds and high-Coriolis parameters, the velocity field presents some of the characteristics of a second-order system, and the wind speeds show some minor oscillations at the inertial frequency. In contrast, if a wind farm is small, the boundary layer does not have enough distance to adjust to the wind farm and, consequently, does not undergo a subsequent adjustment after the wind farm.
Conclusions
By combining atmospheric and wind energy sciences, we have characterized transitional scales in wind farm performance and wake characteristics. These transitional scales are useful to understand constraints in the large-scale expansion of wind power plants relevant to energy system planners and policy makers. Such scales define the transition between when a wind turbine is primarily affected by individual upstream turbines, and when it is primarily affected by the upstream farm in aggregate. We have hypothesized that timescales related to the forces at play could give a physical explanation to and characterize such a transition. We have performed a set of idealized, atmospheric simulations of a very large wind farm with neutral atmospheric conditions using the WRF model, and we looked at the response behavior of the Ekman turbulent boundary layer to a sudden change in surface roughness given by the presence of the wind farm. We verified that, within a turbulent timescale, most of the flow adjusts to the new surface roughness, whereas the flow becomes almost completely adjusted after a length given by the Coriolis timescale. We have also shown that, consistent with field observations, wind farms smaller than a length scale given by the geostrophic wind and the turbulent timescale result in higher power densities and shorter wakes. Increasingly larger wind farms result instead in power densities that asymptotically reach their minimum and wakes that reach their maximum extent.
Our simulations used an idealized scenario; assumed neutral atmospheric conditions and dry air; and did not consider other phenomena such as evaporation, precipitation, stratification, or inversion layers, which all have an effect on the flow characteristics (9, 14, 50, 55). However, our results, obtained with a widely used 3D numerical model, confirm the theoretical foundation of our analysis and provide a first-order characterization of the transitional scales in wind farm performance and wake characteristics. While our idealized analysis might not be readily applicable to onshore wind energy development (on complex terrains, for example), it could instead be suited for offshore applications, in which more homogeneous conditions, both geometric and atmospheric, are present. Winds are generally higher and more persistent over oceans, changes in surface roughness are minimal, and large dimensions are more easily achievable. In future wind energy expansion, offshore installations will likely have a dominant role. For example, Europe envisions between 230 and 450 GW of offshore wind by 2050, up from the 25 GW installed at the end of 2020 (210 GW is Europe's total installed wind capacity at the end of 2020) (56). In the United States, offshore wind installed capacity is expected to grow to about 160 GW by 2050 (2). It is estimated that the US offshore wind resources can potentially produce 7,000 TWh/y, while the total national electricity generation is about 4,000 TWh/y at the end of 2020 (57). Asia is expected to dominate global offshore wind power installations with a total capacity exceeding 600 GW by 2050 (2).
Our findings, in contrast to previous studies, show that there is a transitional length scale that depends on the state of the Ekman turbulent boundary layer and, more specifically, on the wind speed and response time of the forces at play. We have shown that the timescales that characterize the flow adjustment (mostly, turbulent and Coriolis timescale) are independent of the Ekman boundary layer and are, to a first approximation, a function of the Coriolis parameter only, which in turn depends on latitude. The geostrophic wind, on the other hand, is driven by a pressure gradient and is variable in space and time. This indicates that the actual length scale that an Ekman layer requires to adjust to a new surface condition (the presence of the wind farm) is not universal but depends on the local wind resource.
The characterization of dimensional scales for wind farms is of crucial importance for the planning of the next-generation wind farms. Our analysis provides a better understanding and a physical explanation of the scalability of wind farms, and defines the dimensions under which a wind farm can be considered submesoscale, or above which it can be considered mesoscale. Whereas for submesoscale wind farms the turbines are less likely to be affected by an upstream one and power densities can be greater, for very large wind farms all turbines are mutually affected and a fully developed wind farm boundary layer develops, resulting in lower power density. With these understanding, wind farm designers could predict how a prospective wind farm would operate, and whether an optimal layout design would more effectively mitigate any energy losses generated by wakes. At the submesoscale level, current methodologies that neglect the effect of Coriolis and focus on wake interaction minimization will remain the preferred choice. At the mesoscale level, choosing the combination of installed power density and wind farm size will likely become a matter of optimization to find the best economically viable solution. Also, designers could explore the possibility of designing multiple small wind farms as opposed to a larger one in the effort to maximize the energy generation over a given area and with a given number of turbines. While there exists an upper bound on the replenishment of momentum and kinetic energy within the boundary layer for mesoscale wind farms, this bound does not identify what fraction of momentum and energy will ultimately reach the wind turbine blades. Optimal turbine layout and operation will still need to be considered by wind farm developers even for very large wind farms. Despite energy replenishment limits, the turbine layout of fully developed wind farms can increase power density by about 10%. As wind energy development grows and suitable locations for potential wind farms becomes more populated, the length of wind farm wakes could be better predicted to understand their potential impact on neighboring wind farms in terms of energy production and economic losses.
Methods
The idealized simulations are conducted with the WRF simulation tool (44, 45), version 4.2.1. The WRF model has been extensively used to simulate wind farms, their interaction with the atmospheric boundary layer, and their potential impacts on the environment (20, 55, 58–61). The model has been validated and refined over the years by comparing it against field observations (62–66) and higher-fidelity models, such as large-eddy simulations (67, 68). We use the native parametrization for the wind turbines, which represents them as sinks of momentum (the turbine drag proportional to the thrust coefficient data) and sources of turbulence kinetic energy (the fraction of kinetic energy not transferred into electricity) (46–48). We use the default value for the correction factor (= 0.25) to the turbulent kinetic energy produced by the turbines (68).
We perform atmospheric simulations on three domains. The first is used to study the response of an Ekman boundary layer flowing over a very large wind farm and has a horizontal size of 1,000 × 50 km2 with a uniform grid resolution of 1 km. The second is used to calculate the fully developed flow conditions without turbines or with turbines covering the entire ground and has a horizontal size of 50 × 50 km2 with a uniform grid resolution of 1 km. The third is used to analyze power density and wakes as a function of wind farm size and has a horizontal size of 500 × 50 km2 with a uniform grid resolution of 1 km. The vertical dimension is always 10 km with a variable, stretching resolution, finer at the bottom (23 levels in the first 1 km) and coarser at the top (37 levels in the remaining 9 km). Such domains to evaluate spatial scales of large wind farms (10 to 100 km) can be effectively handled by WRF, whereas these requirements are currently incompatible with higher-fidelity models, such as large-eddy simulations, in which space and time discretizations are at least an order of magnitude higher (6, 50).
Here, we consider wind farms with a set of Vestas V164-9.0MW, one of the largest wind turbines currently available with a hub height of 130 m. The performance curves (nominal power and thrust coefficient) for each of these turbines are reported in SI Appendix, Fig. S1.
For each domain, we consider different wind farm sizes. With the first domain, we consider a wind farm that extends for 500 km along the stream-wise direction, covering the 50-km cross-wise dimension, in a uniform arrangement with 1-km spacings in the stream- and cross-wise directions. The wind farm is placed in the middle of the domain, i.e., there are 250 km both upstream and downstream the wind farm (we could have chosen other arrangements without affecting the results because the domain is doubly periodic). With the second domain, we consider a wind farm that covers the entire ground in a uniform arrangement with 1-km spacings in the stream- and cross-wise directions. With the third domain, we consider wind farm sizes ranging from a single row of turbines to multiple rows extending 100 km. The wind farms all start at 50 km from the beginning of the domain (we could have chosen other arrangements without affecting the results because the domain is doubly periodic). For the third domain, we consider also different wind farm layouts (Fig. 6): In layout 1, all the rows and columns are occupied by one turbine; in layout 2, the rows are occupied alternately; in layout 3, both rows and columns are occupied alternately; and in layout 4, the columns are occupied alternately.
We parametrize the wind farms on the eight layers intersecting the rotor area in a doubly periodic domain. On this domain, we specify a set of vertically, uniform, and geostrophic wind values (8, 12, and 16 m/s) and Coriolis parameters (0.55 × 10−4 and 1.05 × 10−4 rad/s). These settings in the boundary conditions implicitly assume a driving constant pressure–gradient field for each of the considered combinations (see Eqs. 1 and 2). The bottom boundary is defined as a sea surface with a roughness length of 10−4 m. We use a dry atmosphere with no surface heat, radiation, or moisture fluxes. The planetary boundary layer physics is parameterized using the Mellor–Yamada–Nakanishi–Niino Level-2.5 model (69, 70). Each simulation is run with a time step of 10 s for a total of 10 d of simulation time in order to reach stationary conditions. Resulting variables are then averaged horizontally over the last 12 h. The power produced by each turbine is calculated with the power curve provided by the manufacturer (SI Appendix, Fig. S1) according to the wind speed at the turbine-containing levels where the turbine is located.
Supplementary Material
Acknowledgments
This work was supported by a gift from Gates Ventures, LLC to the Carnegie Institution for Science.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2103875118/-/DCSupplemental.
Data Availability
Code, input data, and instructions required to reproduce the work reported in the manuscript are available in the GitHub repository at https://github.com/eantonini/Spatial_scales_of_wind_farms. All other study data are included in the article and/or SI Appendix.
References
- 1.Our World in Data , Wind power generation, 2020. Our World in Data (2021). https://ourworldindata.org/grapher/wind-generation. Accessed 1 March 2021.
- 2.International Renewable Energy Agency (IRENA) , Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects (IRENA Publications, 2019). [Google Scholar]
- 3.Porté-Agel F., Bastankhah M., Shamsoddin S., Wind-turbine and wind-farm flows: A review. Boundary Layer Meteorol. 174, 1–59 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barthelmie R. J., et al., Modelling and measuring flow and wind turbine wakes in large wind farms offshore. Wind Energy 12, 431–444 (2009). [Google Scholar]
- 5.Barthelmie R. J., et al., Quantifying the impact of wind turbine wakes on power output at offshore wind farms. J. Atmos. Ocean. Technol. 27, 1302–1317 (2010). [Google Scholar]
- 6.Calaf M., Meneveau C., Meyers J., Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22, 015110 (2010). [Google Scholar]
- 7.Barthelmie R. J., Jensen L. E., Evaluation of wind farm efficiency and wind turbine wakes at the Nysted offshore wind farm. Wind Energy 13, 573–586 (2010). [Google Scholar]
- 8.Porté-Agel F., Wu Y.-T., Chen C.-H., A numerical study of the effects of wind direction on turbine wakes and power losses in a large wind farm. Energies 6, 5297–5313 (2013). [Google Scholar]
- 9.Hansen K. S., Barthelmie R. J., Jensen L. E., Sommer A., The impact of turbulence intensity and atmospheric stability on power deficits due to wind turbine wakes at Horns Rev wind farm. Wind Energy 15, 183–196 (2012). [Google Scholar]
- 10.Han X., Liu D., Xu C., Shen W. Z., Atmospheric stability and topography effects on wind turbine performance and wake properties in complex terrain. Renew. Energy 126, 640–651 (2018). [Google Scholar]
- 11.Zhan L., Letizia S., Valerio Iungo G., LiDAR measurements for an onshore wind farm: Wake variability for different incoming wind speeds and atmospheric stability regimes. Wind Energy 23, 501–527 (2020). [Google Scholar]
- 12.Makridis A., Chick J., Validation of a CFD model of wind turbine wakes with terrain effects. J. Wind Eng. Ind. Aerodyn. 123, 12–29 (2013). [Google Scholar]
- 13.Volker P. J. H., Hahmann A. N., Badger J., Jørgensen H. E., Prospects for generating electricity by large onshore and offshore wind farms. Environ. Res. Lett. 12, 034022 (2017). [Google Scholar]
- 14.Abkar M., Porté-Agel F., Influence of atmospheric stability on wind-turbine wakes: A large-eddy simulation study. Phys. Fluids 27, 035104 (2015). [Google Scholar]
- 15.Antonini E. G. A., Romero D. A., Amon C. H., Improving CFD wind farm simulations incorporating wind direction uncertainty. Renew. Energy 133, 1011–1023 (2019). [Google Scholar]
- 16.Veers P., et al., Grand challenges in the science of wind energy. Science 366, eaau2027 (2019). [DOI] [PubMed] [Google Scholar]
- 17.Vermeer L. J., Sørensen J. N., Crespo A., Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 39, 467–510 (2003). [Google Scholar]
- 18.Platis A., et al., First in situ evidence of wakes in the far field behind offshore wind farms. Sci. Rep. 8, 2163 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schneemann J., Rott A., Dörenkämper M., Steinfeld G., Kühn M., Cluster wakes impact on a far-distant offshore wind farm’s power. Wind Energy Sci. 5, 29–49 (2020). [Google Scholar]
- 20.Lundquist J. K., DuVivier K. K., Kaffine D., Tomaszewski J. M., Costs and consequences of wind turbine wake effects arising from uncoordinated wind energy development. Nat. Energy 4, 26–34 (2019). [Google Scholar]
- 21.Antonini E. G. A., Romero D. A., Amon C. H., Continuous adjoint formulation for wind farm layout optimization: A 2D implementation. Appl. Energy 228, 2333–2345 (2018). [Google Scholar]
- 22.Antonini E. G. A., Romero D. A., Amon C. H., Optimal design of wind farms in complex terrains using computational fluid dynamics and adjoint methods. Appl. Energy 261, 114426 (2020). [Google Scholar]
- 23.Abkar M., Porté-Agel F., The effect of free-atmosphere stratification on boundary-layer flow and power output from very large wind farms. Energies 6, 2338–2361 (2013). [Google Scholar]
- 24.Antonini E. G. A., Caldeira K., Atmospheric pressure gradients and Coriolis forces provide geophysical limits to power density of large wind farms. Appl. Energy 281, 116048 (2021). [Google Scholar]
- 25.Enevoldsen P., Jacobson M. Z., Data investigation of installed and output power densities of onshore and offshore wind turbines worldwide. Energy Sustain. Dev. 60, 40–51 (2021). [Google Scholar]
- 26.Miller L. M., Keith D. W., Observation-based solar and wind power capacity factors and power densities. Environ. Res. Lett. 13, 104008 (2018). [Google Scholar]
- 27.Allaerts D., Meyers J., Boundary-layer development and gravity waves in conventionally neutral wind farms. J. Fluid Mech. 814, 95–130 (2017). [Google Scholar]
- 28.Wu K. L., Porté-Agel F., Flow adjustment inside and around large finite-size wind farms. Energies 10, 2164 (2017). [Google Scholar]
- 29.Sharma V., Cortina G., Margairaz F., Parlange M. B., Calaf M., Evolution of flow characteristics through finite-sized wind farms and influence of turbine arrangement. Renew. Energy 115, 1196–1208 (2018). [Google Scholar]
- 30.Markfort C. D., Zhang W., Porté-Agel F., Turbulent flow and scalar transport through and over aligned and staggered wind farms. J. Turbul. 13, 1–36 (2012). [Google Scholar]
- 31.Jacobson M. Z., Fundamentals of Atmospheric Modeling (Cambridge University Press, 2005). [Google Scholar]
- 32.Lewis D. M., Belcher S. E., Time-dependent, coupled, Ekman boundary layer solutions incorporating Stokes drift. Dyn. Atmos. Oceans 37, 313–351 (2004). [Google Scholar]
- 33.Momen M., Bou-Zeid E., Large-eddy simulations and damped-oscillator models of the unsteady Ekman boundary layer. J. Atmos. Sci. 73, 25–41 (2016). [Google Scholar]
- 34.Momen M., Bou-Zeid E., Mean and turbulence dynamics in unsteady Ekman boundary layers. J. Fluid Mech. 816, 209–242 (2017). [Google Scholar]
- 35.Taylor P. A., The planetary boundary layer above a change in surface roughness. J. Atmos. Sci. 26, 432–440 (1969). [Google Scholar]
- 36.Jensen N. O., Change of surface roughness and the planetary boundary layer. Q. J. R. Meteorol. Soc. 104, 351–356 (1978). [Google Scholar]
- 37.Wright S. D., The adaptation of the atmospheric boundary layer to a change in surface roughness. Boundary Layer Meteorol. 89, 175–195 (1998). [Google Scholar]
- 38.Monin A. S., The atmospheric boundary layer. Annu. Rev. Fluid Mech. 2, 225–250 (1970). [Google Scholar]
- 39.Panofsky H. A., Dutton J. A., Atmospheric Turbulence: Models and Methods for Engineering Applications (John Wiley & Sons, 1984). [Google Scholar]
- 40.Peña A., Gryning S.-E., Hasager C. B., Measurements and modelling of the wind speed profile in the marine atmospheric boundary layer. Boundary Layer Meteorol. 129, 479–495 (2008). [Google Scholar]
- 41.Koracin D., Berkowicz R., Nocturnal boundary-layer height: Observations by acoustic sounders and predictions in terms of surface-layer parameters. Boundary Layer Meteorol. 43, 65–83 (1988). [Google Scholar]
- 42.Zilitinkevich S. S., Esau I. N., The effect of baroclinicity on the equilibrium depth of neutral and stable planetary boundary layers. Q. J. R. Meteorol. Soc. 129, 3339–3356 (2003). [Google Scholar]
- 43.Jiménez J., Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196 (2004). [Google Scholar]
- 44.Powers J. G., et al., The weather research and forecasting model: Overview, system efforts, and future directions. Bull. Am. Meteorol. Soc. 98, 1717–1737 (2017). [Google Scholar]
- 45.W. R. F. , Version, 4.2.1. https://github.com/wrf-model/WRF/releases/tag/v4.2.1. Accessed 1 September 2020.
- 46.Fitch A. C., et al., Local and mesoscale impacts of wind farms as parameterized in a mesoscale NWP model. Mon. Weather Rev. 140, 3017–3038 (2012). [Google Scholar]
- 47.Fitch A. C., Notes on using the mesoscale wind farm parameterization of Fitch et al. (2012) in WRF. Wind Energy 19, 1757–1758 (2016). [Google Scholar]
- 48.Lee J. C. Y., Lundquist J. K., Evaluation of the wind farm parameterization in the Weather Research and Forecasting model (version 3.8.1) with meteorological and turbine power data. Geosci. Model Dev. 10, 4229–4244 (2017). [Google Scholar]
- 49.Stevens R. J. A. M., Gayme D. F., Meneveau C., Effects of turbine spacing on the power output of extended wind-farms. Wind Energy 19, 359–370 (2016). [Google Scholar]
- 50.Allaerts D., Meyers J., Large eddy simulation of a large wind-turbine array in a conventionally neutral atmospheric boundary layer. Phys. Fluids 27, 065108 (2015). [Google Scholar]
- 51.Dabiri J. O., Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 3, 043104 (2011). [Google Scholar]
- 52.Andersen S. J., Sørensen J. N., Mikkelsen R. F., Turbulence and entrainment length scales in large wind farms. Philos. Trans. A Math. Phys. Eng. Sci. 375, 20160107 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Nishino T., Dunstan T. D., Two-scale momentum theory for time-dependent modelling of large wind farms. J. Fluid Mech. 894, A2 (2020). [Google Scholar]
- 54.Dhoot A., Antonini E. G. A., Romero D. A., Amon C. H., Optimizing wind farms layouts for maximum energy production using probabilistic inference: Benchmarking reveals superior computational efficiency and scalability. Energy 223, 120035 (2021). [Google Scholar]
- 55.Rajewski D. A., et al., Crop wind energy experiment (CWEX): Observations of surface-layer, boundary layer, and mesoscale interactions with a wind farm. Bull. Am. Meteorol. Soc. 94, 655–672 (2013). [Google Scholar]
- 56.European Commission . A Clean Planet for all. A European strategic long-term vision for a prosperous, modern, competitive and climate neutral economy. https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52018DC0773. Accessed 1 June 2020.
- 57.Musial W., Heimiller D., Beiter P., Scott G., Craxl C., “2016 offshore wind energy resource assessment for the United States” (Tech. Rep. NREL/TP-5000-66599, National Renewable Energy Laboratory, Golden, CO, 2016).
- 58.Miller L. M., et al., Two methods for estimating limits to large-scale wind power generation. Proc. Natl. Acad. Sci. U.S.A. 112, 11169–11174 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Fitch A. C., Lundquist J. K., Olson J. B., Mesoscale influences of wind farms throughout a diurnal cycle. Mon. Weather Rev. 141, 2173–2198 (2013). [Google Scholar]
- 60.Vautard R., et al., Regional climate model simulations indicate limited climatic impacts by operational and planned European wind farms. Nat. Commun. 5, 3196 (2014). [DOI] [PubMed] [Google Scholar]
- 61.Jiménez P. A., Navarro J., Palomares A. M., Dudhia J., Mesoscale modeling of offshore wind turbine wakes at the wind farm resolving scale: A composite‐based analysis with the Weather Research and Forecasting model over Horns Rev. Wind Energy 18, 559–566 (2015). [Google Scholar]
- 62.Jiménez P. A., et al., Surface wind regionalization over complex terrain: Evaluation and analysis of a high-resolution WRF simulation. J. Appl. Meteorol. Climatol. 49, 268–287 (2010). [Google Scholar]
- 63.Jiménez P. A., Dudhia J., Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 51, 300–316 (2012). [Google Scholar]
- 64.Siedersleben S. K., et al., Turbulent kinetic energy over large offshore wind farms observed and simulated by the mesoscale model WRF (3.8.1). Geosci. Model Dev.. 13, 249–268 (2020). [Google Scholar]
- 65.Tomaszewski J. M., Lundquist J. K., Simulated wind farm wake sensitivity to configuration choices in the Weather Research and Forecasting model version 3.8.1. Geosci. Model Dev. 13, 2645–2662 (2020). [Google Scholar]
- 66.Tomaszewski J. M., Lundquist J. K., Observations and simulations of a wind farm modifying a thunderstorm outflow boundary. Wind Energy Sci. 6, 1–13 (2021). [Google Scholar]
- 67.Shin H. H., Dudhia J., Evaluation of PBL parameterizations in WRF at subkilometer grid spacings: Turbulence statistics in the dry convective boundary layer. Mon. Weather Rev. 144, 1161–1177 (2016). [Google Scholar]
- 68.Archer C. L., Wu S., Ma Y., Jiménez P. A., Two corrections for turbulent kinetic energy generated by wind farms in the WRF model. Mon. Weather Rev. 148, 4823–4835 (2020). [Google Scholar]
- 69.Nakanishi M., Niino H., An improved Mellor-Yamada level-3 model with condensation physics: Its design and verification. Boundary Layer Meteorol. 112, 1–31 (2004). [Google Scholar]
- 70.Nakanishi M., Niino H., Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteorol. Soc. Jpn. 87, 895–912 (2009). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code, input data, and instructions required to reproduce the work reported in the manuscript are available in the GitHub repository at https://github.com/eantonini/Spatial_scales_of_wind_farms. All other study data are included in the article and/or SI Appendix.