Abstract
Iontophoresis employs low-intensity electrical voltage and continuous constant current to direct a charged drug into a tissue. Iontophoretic drug delivery has recently been used as a novel method for cancer treatment in vivo. There is an urgent need to precisely model the low-intensity electric fields in cell culture systems to optimize iontophoretic drug delivery to tumors. Here, we present an iontophoresis-on-chip (IOC) platform to precisely quantify carboplatin drug delivery and its corresponding anti-cancer efficacy under various voltages and currents. In this study, we use an in vitro heparin-based hydrogel microfluidic device to model the movement of a charged drug across an extracellular matrix (ECM) and in MDA-MB-231 triple-negative breast cancer (TNBC) cells. Transport of the drug through the hydrogel was modeled based on diffusion and electrophoresis of charged drug molecules in the direction of an oppositely charged electrode. The drug concentration in the tumor extracellular matrix was computed using finite element modeling of transient drug transport in the heparin-based hydrogel. The model predictions were then validated using the IOC platform by comparing the predicted concentration of a fluorescent cationic dye (Alexa fluor 594®) to the actual concentration in the microfluidic device. Alexa fluor 594® was used because it has a molecular weight close to paclitaxel, the gold standard drug for treating TNBC, and carboplatin. Our results demonstrated that a 50 mV DC electric field and a 3 mA electrical current significantly increased drug delivery and tumor cell death by 48.12%±14.33 and 39.13%±12.86, respectively (n=3, p-value<0.05). The IOC platform and mathematical drug delivery model of iontophoresis are promising tools for precise delivery of chemotherapeutic drugs into solid tumors. Further improvements to the IOC platform can be made by adding a layer of epidermal cells to model the skin.
1. INTRODUCTION
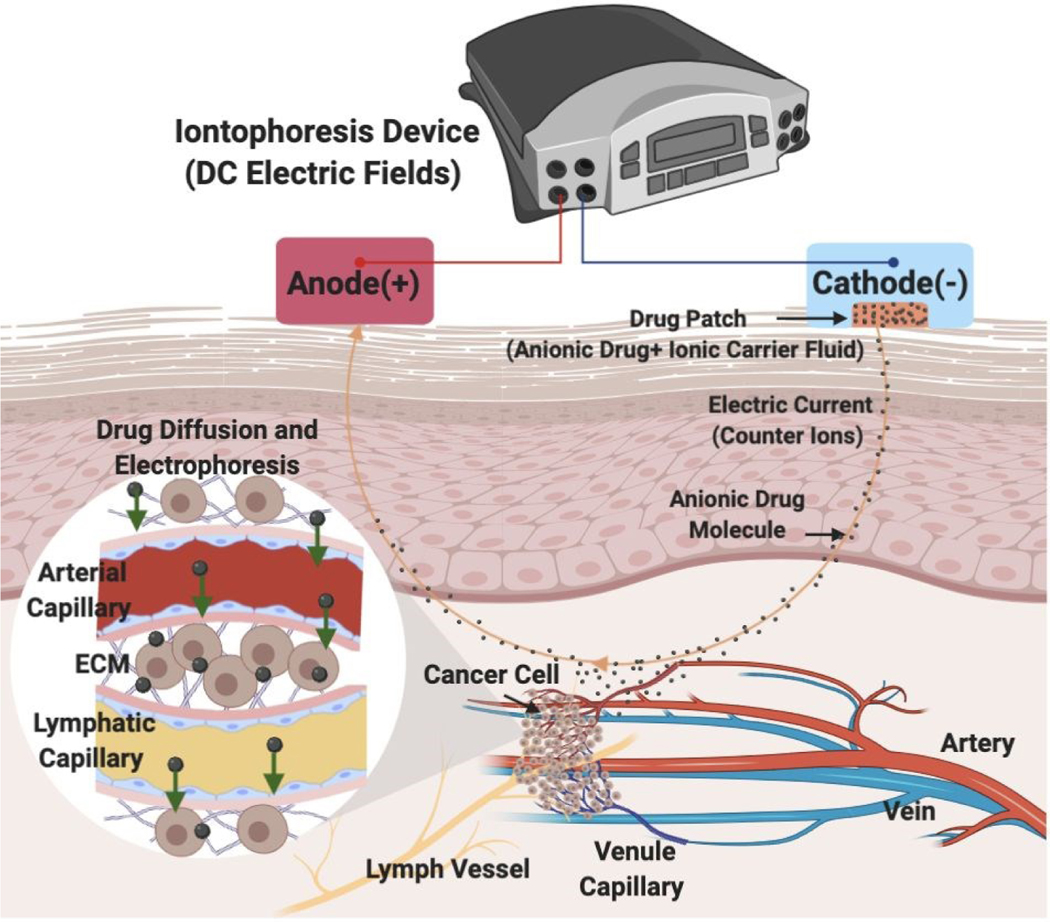
Intravenous chemotherapy is the traditional method for administering cytotoxic agents to cancer patients. Unfortunately, the full potential of anti-cancer drugs is limited because of systemic toxicity and poor tumor perfusion. In an attempt to improve the efficacy of anti-cancer drugs while mitigating their side effects, many groups have reported on the clinical use of electric fields to improve drug delivery. Most studies focus on the electropermeabilization of cells via high-intensity electric fields [1–7]. More recently, however, the use of iontophoresis via low intensity electric fields [8] was reported in animal models [9–13] and in humans [14–17]. Iontophoresis enhances drug delivery by electrophoresis, the movement of charged drug molecules in the tumor’s extracellular matrix surrounding tumor capillaries. During cancer treatment, iontophoretic devices with external power and drug flow controls are implanted proximal to the tumor or onto the skin of the patient [17–19]. However, iontophoretic delivery of chemotherapeutic drugs into the tumor microenvironment is still not well-defined [20, 21]. After passing the epidermis, iontophoresis enhances drug delivery via three mechanisms in the tumor vasculature (Fig. 1): 1) The electric field and current drives ions through the endothelial membrane of the blood vessels; 2) The ion-electric field interaction provides electrophoretic movement of ions, which increases ion delivery out of the blood vessel; and 3) Electroosmotic flow produces bulk motion of the solvent itself, which carries ions or neutral species within the solvent ‘stream’ [19, 22]. To date, most in vitro [21, 23–26] and in vivo [27, 28] studies focused on overcoming human epidermal membrane (HEM) drug resistance by using iontophoresis with a short delivery duration of the electric field. There is a need, however, to precisely control and predict the rate, direction, and distance of drug delivery in the tumor extracellular matrix (ECM) when using iontophoresis techniques. After passing through the HEM, iontophoretic drug delivery is still blocked by the ECM. Physiological and biological barriers within the ECM not only decrease the efficacy of chemical compounds, but also delay the compounds from reaching tumor cells in concentrations sufficient enough to exert a therapeutic effect [14, 17]. Barriers to iontophoretic drug delivery created by the ECM is a critical issue that must be addressed. Using a diffusion-based model, our groups has previously [29] described that a 70% porosity, heparin-based hydrogel was a biomimetic scaffolding for modeling the chemoresistance of MDA-MB-231 triple-negative breast cancer (TNBC) ECM [29]. Therefore, we chose to use a heparin-based hydrogel with 70% porosity to represent the ECM of an in vivo tumor [30, 31].
Figure 1. Iontophoretic transdermal drug delivery into the tumor vasculature in vivo.
The schematic shows the in vivo transport of an anionic drug from the artery to the tumor where it eventually drains into the lymph vessel. Iontophoretic transdermal drug delivery includes insertion of the cathode along with the drug patch on the skin from where the anionic drug molecules move to the tumor facilitated by the transport of the counter ions (from carrier solvent) to the anode.
Previous microfluidic in vitro studies have been conducted to mimic the three-dimensional microenvironments of tumors using on-chip technologies including the tumor vasculature network, which promotes drug resistance in the tumor microenvironment. Recent studies have utilized microfluidic platforms to obtain further insights into the mechanisms of electric field stimulation on cancer cells in 3D as well as the specific parameter values that affect tumor growth but do not harm surrounding, non-cancerous cells present in the tissue [32]. The microfluidic approach facilitates numerous advantages including: (1) the precise control of the biomaterials’ physical and chemical properties to resemble the physiological ECM; (2) Nanoliter volumes reduce reagent usage and facilitates reproducibility [33]; and (3) Controlling the physics of drug transport phenomena in the presence of an applied electric field aids in the design and testing of new therapeutic approaches [34–36].
In silico simulations are well-suited for testing combinations of multiple physical laws (e.g., diffusion and electrophoresis) and are used for estimating drug concentration profiles in the tumor [37–39]. However, the fundamental mathematical model that incorporates the physics of electrophoresis transport is not well-defined. Based on the work of Pascal et al. [40], it was demonstrated in their electrokinetics drug delivery model [41] that the application of an electric field enhances drug delivery at both micro- and macro-scales. However, a validated electrokinetics model [42] that can be used for the prediction of the tumor response to chemotherapy in the presence of an applied low-intensity DC electric field has not been reported.
To address these issues, we developed both iontophoresis-on-chip (IOC) platform and mathematical model of iontophoretic drug delivery. Our iontophoresis-on-chip (IOC) platform allows for three unique applications: (1) Acupuncture electrodes facilitate electrode insertion into the microfluidics and precise control over the location and direction of the applied electric field. (2) Incorporation of heparin-based hydrogels into fluidic channels to mimic and precisely control the physiology of the tumor ECM [43–51].; (3) The open microfluidic platform facilitates exchange of the cell medium so as to maintain a constant pH and expose cancer cells to a drug of interest up to 48 h after 3D cell culture. Our mathematical model enabled us to predict optimal parameters (electric field intensity, direction), which were then validated in vitro. Our iontophoresis-on-chip (IOC) platform is the first microfluidic system in the literature to offer the opportunity to investigate the effects of electrophoretic carboplatin delivery into TNBC cells (MDA-MB-231) that are encapsulated in a heparin-based hydrogel.
2. MATERIALS AND METHODS
2.1. Design and fabrication of the microfluidic iontophoresis platform
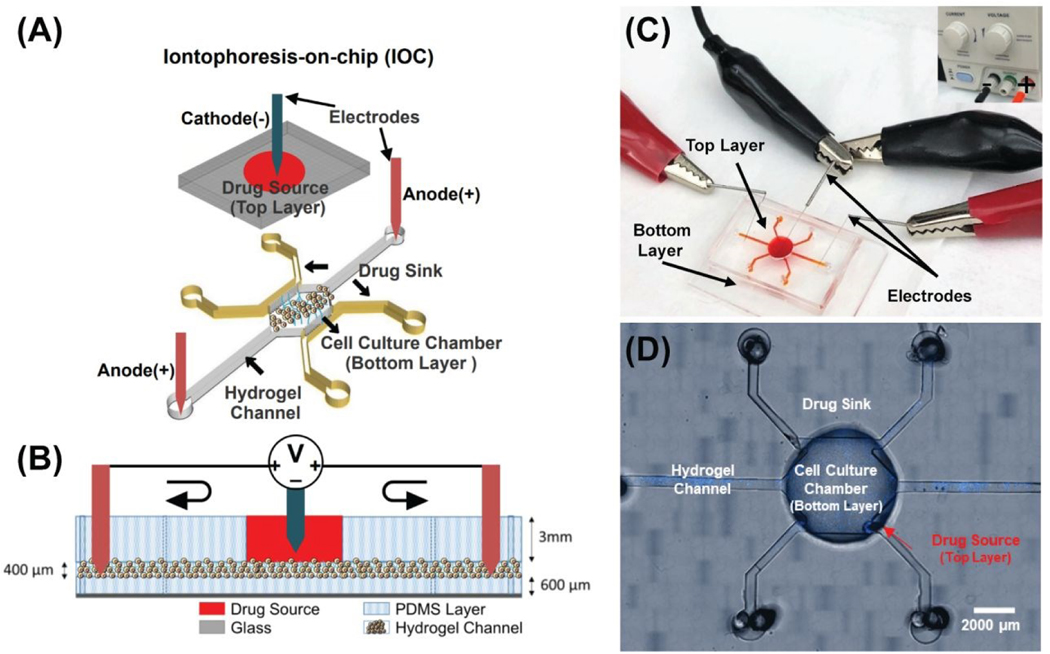
The iontophoresis-on-chip (IOC) platform was designed to mimic tumor vasculature by providing a top layer of arterial capillaries and two side channels of lymph capillaries in the bottom layer (Fig. 2A). The heparin-based hydrogel and cell culture medium (DMEM/F-12+10% FBS) is found between the top and the bottom layers and plays the role of a salt bridge. Sterile stainless-steel acupuncture needles with a diameter of 0.12 mm (Kingli, China) were used as electrodes to construct the DC electric field circuit (Fig. 2B&C). The negative electrode was placed in the top layer and the positive electrodes were placed in the inlet and outlet of the bottom layer’s hydrogel channel (Fig. 2A&B). The master mold was patterned using two layers of photoresist: (i) The first layer (i.e., the top layer) consists of a central well (1.5 mm wide and 3 mm thick) and has the role of supplying media to cells that are encapsulated in hydrogel in the bottom layer; (ii) The second layer (i.e., the bottom layer) consists of a cell culture chamber that has the dimensions of 3X3 mm2, two sink channels with the dimensions of 0.5X3 mm2, 15 ports with the dimensions of 0.15X0.15 mm2 between the cell culture chamber and each sink channel, and two side hydrogel channels with the dimensions of 0.5X5 mm2 (Fig. 2A). The thickness of the bottom layer was optimized to 400 μm using the SU8–2100 photoresist and was fabricated according to the manufacturer’s (MicroChem Corp.) instructions. Microfluidic devices were produced by replica molding using Polydimethylsiloxane, (PDMS, Sylgard 184; Ellsworth Adhesives, Wilmington, MA, USA) on the master wafer, and fabricated using standard microfabrication techniques [52]. We aligned and bonded the two PDMS layers of the microfluidic platform using a Nikon SMZ-1 stereo microscope and a Nordson MARCH (AP-300) oxygen plasma bonder, respectively. After bonding the two layers, the inlets and outlets were punched using a 0.75 mm biopsy puncher (Fig. 2D). Finally, a 6‐well glass‐bottom plate (MatTek, Ashland, MA, USA) was plasma-treated along with the PDMS IOC devices and the devices were bonded to the plate using a hot plate (85°C for 10 min).
Figure 2. Iontophoresis-on-chip (IOC) for quantifying iontophoretic delivery of chemotherapeutic drugs in vitro.
(A) Microfluidic experiment setup, three-dimensional top view of microfluidic device, negative electrode inserted in drug source well and positive electrodes added to the bottom tumor region layer. (B) Side view of the open microfluidic device and the electric field circuit. (C) Image of experimental setup and application of a DC electric field for drug delivery from the top layer into the tumor region in the bottom layer. (D) Microfluidic device designed to measure iontophoresis drug delivery. Bottom layer includes: 1) Drug sink. 2) Cell culture chamber for MDA-MB-231 cells (blue, Hoechst stain). 3) Electrophoresis channels for the delivery of drugs from the cell culture chamber to the side channels through electrophoresis and diffusion. Top layer is the drug source.
2.2. Hydrogel preparation and dose response curve
The HyStem-HP Hydrogel Kit w/ PEGSSDA (ESI BIO GS315P) was used to prepare the heparin hydrogel. The kit is composed of lyophilized solids of Heprasil® (thiol-modified sodium hyaluronate with thiol-modified heparin), Gelin-S® (thiol-modified gelatin), and PEGSSDA™ (disulfide containing polyethylene glycol di-acrylate), as well as degassed deionized water (DG Water). Gels were prepared as per manufacturer’s directions. Cell seeding density and drug concentration optimization experiments were done in 384 well-plates with a 0.06 cm2 growth area, which is approximately the growth area of the fabricated microfluidic device (0.09 cm2). The drug was applied after 48 h of incubation. Cells were stained using a live and dead cell fluorescent assay (Abcam, Cambridge, MA) after 72 h of incubation. Dose-response curves of paclitaxel (Sigma-Aldrich, St. Louis, MO) and carboplatin (Sigma-Aldrich, St. Louis, MO) were obtained in single cells using a 10K cell density in 30 μL of heparin-hydrogel. The paclitaxel dose response curve showed that 11 nM was the 90% effective dose (EC90) and the carboplatin dose response curve showed that 12 nM of carboplatin killed the maximum fraction of cells (85%) (Fig. S1A). Because of these dose response curves, we chose to use 2 nM of the drugs to use doses less than the EC90 for both paclitaxel and carboplatin in the microfluidic in vitro environment. We tested the effect of electric field on the delivery of paclitaxel and carboplatin separately to examine this effect on both charged (carboplatin) and neutral (paclitaxel) drug delivery.
2.3. Cell culture and iontophoresis-on-chip (IOC) assay
The human TNBC cells used in this study were from an invasive ductal carcinoma cell line (MDA-MB-231, American Type Cell Culture HTB-26). Gibco™ Dulbecco’s Modified Eagle’s Medium F-12 (DMEM/F-12), containing high levels of glucose and GlutaMAX™ supplemented with 10% (v/v) fetal bovine serum (FBS, ATCC, Manassas, VA) and 1% (v/v) penicillin-streptomycin (100 units/mL penicillin and 0.1 mg/mL streptomycin), was used as a complete culture medium for the TNBC cells. The encapsulated breast cancer cells were studied using heparin hydrogel in complete media (DMEM + 10% FBS+1% P/S). The cells were suspended in the Heprasil and Gelin-S mixture before adding the PEGSSDA crosslinker at a density of 10K single cells in 30 μL of hydrogel. 2 nM concentrations of paclitaxel and carboplatin were used because they kill approximately 71% of cells without an applied electric field (Fig. S1A). We used cells on top of the gel, and encapsulated cells inside the gel for 3D cell culture in the microfluidic device. The encapsulated cells in the hydrogel were introduced into the device through manual injection using a syringe and tubing until a uniform distribution of cells was attained in the cell culture chamber. In our study, we set the flow rate to zero (eliminating electroosmotic flow) and focused on electrophoresis transport only. To model the iontophoresis, we needed to define: 1) ECM porosity; 2) drug concentration; 3) cell density; and 4) drug charge. We set the drug concentration to be less than the effective dose of 90% (ED90), which we measured in both standard well plates and in the microfluidic device (Fig. S1). Application of an external electric voltage resulted in faster delivery of anionic drugs compared to cationic drugs [35]. We compared an anionic drug [53, 54], carboplatin, to the gold standard non-ionized drug, paclitaxel. We also studied TNBC cells cultured in heparin-based hydrogel as a tumor ECM biomaterial [29, 55]. In our device, we validated the application of a 50 mV electric field to an ECM of 70% porosity to increase drug delivery to a tumor’s single cells. We also varied the drug type (charge). In this study, we controlled low-intensity DC electric fields for electrophoretic drug delivery in the tumor’s single cells. We quantified the effect of a 50 mV DC electric field and a 3 mA electric current on the percent of dead cells both mathematically and experimentally using a mass transfer model and a microfluidic platform, respectively. Our IOC mimics the tumor extracellular matrix through the use of MDA-MB-231 single cells in a heparin-based hydrogel, the lymph capillary (drug sink), and the blood capillary (drug source). We initially used a physics based mathematical model [41] for sensitivity analysis and parameter optimization to reduce the number of in vitro experiments. To experimentally prove the chosen electric field intensity of 50 mV derived from the sensitivity analysis, we showed the effect of electrophoresis transport on increasing ionic macromolecule delivery in heparin-based hydrogel.
The experiment was conducted for a total of 72 h where the cells were initially seeded and allowed to grow for 48 h and then treated with 2 nM of the drug and 50 mV of electric field for 5 h. The electric field was discharged after 5 h, however, the cells were left in the drug solution for an additional 19 h. Finally, the cells were stained with live and dead cell fluorescent assay medium (Abcam, Cambridge, MA) after 72 h (Fig. S3).
2.2. Electrokinetics and mass transfer model
To reduce the number of in vitro experiments, we employed a physics-based model to predict the minimum electric field intensity needed to affect the maximum fraction of cells killed by simulating the effect of iontophoresis on carboplatin delivery. The model was then validated with a biomimetic three-dimensional microfluidic experiment by comparing the measured and predicted percentage of dead cells. See the supplementary materials for a more detailed description of the coupled electrokinetics and mass transfer model.
2.3. Drug delivery model optimization and sensitivity analysis
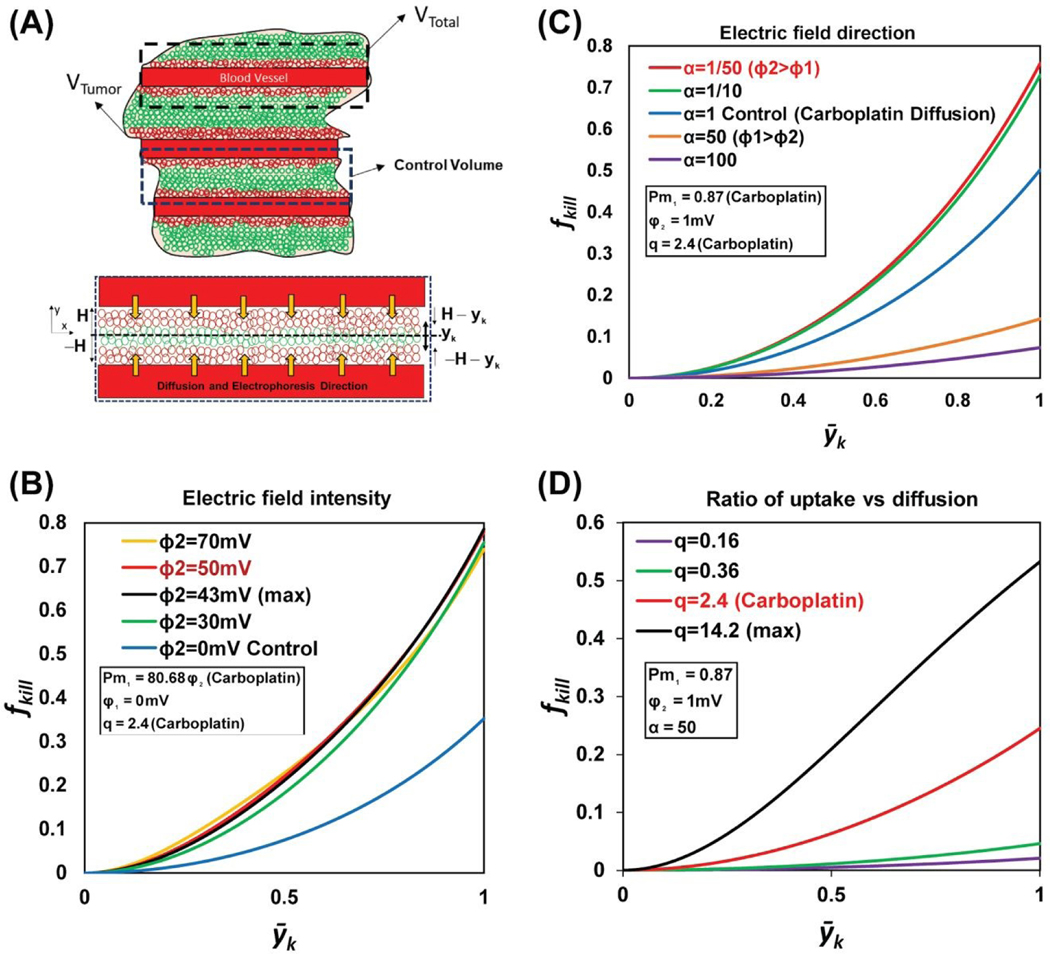
Sensitivity analysis was used to eliminate a trial and error approach for determining the electric field intensity when conducting the IOC experiments. Sensitivity analysis of the electric field potential, between 0 and 70 mV, at the blood vessel wall showed 43.01 mV as the optimum electric field intensity to obtain a 79% cell death rate (Fig. 3B).
Figure 3. Mathematical model sensitivity analysis of the fraction of tumor cells killed model.
(A) The schematic illustrates the volume of the analytical domain under study (VTotal), which is the sum of the volume of a single blood vessel and the surrounding tumor mass (VTumor). VTumor includes both the live and dead tumor cells, represented by the green and red circles, respectively. Vcontrol depicts the volume between two consecutive blood vessels and is used as the control volume for the mathematical model, with idealized system boundaries (𝐻, ― 𝐻, ― 𝑦𝑘, ― 𝐻 ― 𝑦𝑘). (B) The graph shows the variation in the fraction of tumor cells killed (fkill) over a dimensionless kill distance yk, for different values of Pm1 and electric field intensities. The sensitivity analysis predicted 43 mV as the optimal electrical voltage required to maximize the fraction of tumor cells killed (0.79). (C) The graph shows the variation in the fraction of tumor cells killed (fkill) over a dimensionless kill distance, yk, for different values of 𝛼 (which is the ratio of electric potential in the drug source (𝜑1) to the electric potential in the tumor (𝜑2)). When 𝜑2 is 50 times more than 𝜑1, the diffusion and electrophoretic movement of the charged drug molecules are in the same direction, and the fraction of tumor cells killed is at its maximum (0.75). (D) The graph shows the variation in the fraction of tumor cells killed (fkill) over a dimensionless kill distance, yk, for different values of q (the ratio of the drug uptake rate to the drug diffusion). For carboplatin q=2.4, where the fraction of cells killed is 0.25.
Three non-dimensional numbers and the electric potential in the tumor region were optimized using GRG (Generalized Reduced Gradient) nonlinear solver [56]. The optimal value of 𝜑2 (electric field intensity), 43.01 mV, was instrumental in eliminating multiple microfluidic in vitro experiments for electric field intensity optimization. Table S1 and Table S2 show the dependent and independent variables, their sensitivity ranges, and optimum value to obtain the maximum fraction of cells killed.
2.4. Transport of macromolecules into heparin-based hydrogel
The first experimental setup was used to determine the ionized fluorescent dye concentration with and without applying a 50 mV of DC electric field. Sensitivity analysis and model optimization show that the electric potential of 43.01 mV resulted in the maximum fraction of tumor cells killed. Due to the restriction in the precision of our DC power supply (DC power supply must be >10 mV), we had to choose between 40 mV and 50 mV. We loaded a heparin-based hydrogel in the bottom layer, closed the outlets to eliminate gravitational flow, placed the device under a Nikon TiE time lapse microscope, and allowed the hydrogel to solidify (10–15 min). 30 μL of dye was added to the top layer and live imaging was started simultaneously. Live images were taken every 1 minute for 5 h in two 1 mm2 x-y planes in the central chamber and the hydrogel channel over a 1.2 mm distance. The fluorescence intensity was measured over 10 different depths (40 μm) within the hydrogel (400 μm). The average intensity was determined over the 1 mm2 x-y plane. The final average intensity is the average of x-y plane intensities at 10 different hydrogel depths. The calibration curve was used (Fig. S2) to convert average dye intensity to dye concentration. We used Alexa fluor 594® fluorescent dye with a molecular weight of 819.85 g/mol, which is similar to paclitaxel’s molecular weight (853.91 g/mol) and close to carboplatin molecular weight (371.25 g/mol). The experimental result of Alexa fluor 594® concentration versus time validated the finite element model of dye concentration (diffusion and electrophoresis delivery with 50 mV electric potential gradient) in the porous hydrogel region.
2.5. Confocal microscopy and image processing
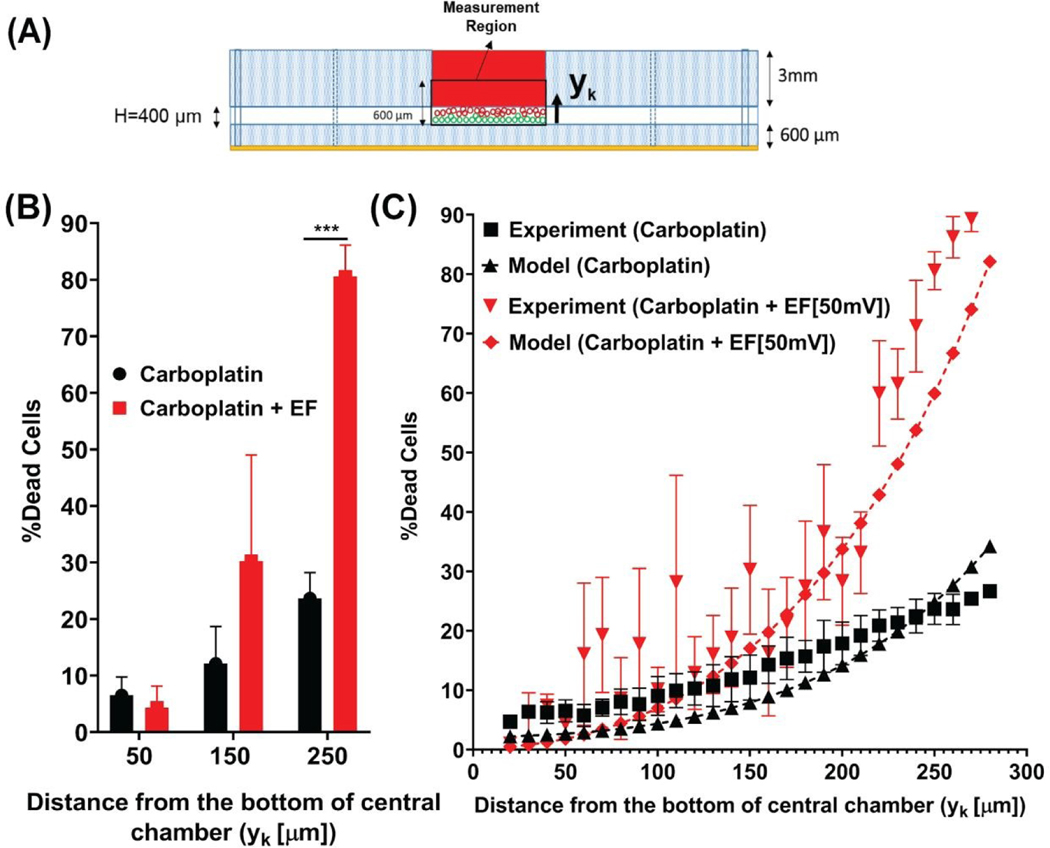
Confocal microscopy was used to measure the fraction of cells killed with and without applying a 50 mV DC electric field. A confocal microscope (ZEISS LSM 880 with Airyscan) fitted with a ZEISS Axiocam 503 mono camera and a computerized stage was used to take fluorescent images. The microscope was controlled using ZEN software (Carl Zeiss Microscopy GmbH, Germany). Images were processed using ImageJ (NIH, Bethesda, MD). To calculate the fraction of cells killed (or the percentage of dead cells), the fluorescent light intensities from Tetramethyl Rhodamine Iso-Thiocyanate (TRITC, red: dead cells) were divided by the total fluorescent light intensities from TRITC (red: dead cells) and Fluorescein isothiocyanate (FITC, green: live cells) in each 10 μm plane along the hydrogel’s z-axis. Results from the confocal images were used for validation of the fraction of cells killed model [41] (Fig. 6C).
Figure 6. Percent dead tumor cells model validation shows that low-intensity electric field promotes iontophoretic delivery of carboplatin into breast cancer cells.
(A) Representative of the experimental measurement region in the cell culture chamber of the device, for calculating the percent dead tumor cells when treated with 2 nM of carboplatin with and without 50 mV of electric field. (B) Graph shows increase in percent dead tumor cells that are seeded at 50 μm,150 μm, and 250 μm distance from the bottom of the cell culture chamber and treated with 2 nM of carboplatin with and without 50 mV of electric field; the difference in the percent dead cells when treated with 2 nM of carboplatin with electric field is significantly higher at 250 μm (closest to drug source) compared to other distances. (C) Percent dead tumor cells model validation with the in vitro experiment shows an accurate correlation between model and experiment (Table S3).
2.5. Microfluidics in vitro experiment statistical analysis
Statistical analyses were performed using Prism version 8.1.2 (332) software (GraphPad Software, La Jolla, CA) with a confidence level of α = 0.05. Two-way analysis of variance (ANOVA) was used to test for differences in the number of dead cells after electrophoresis treatment (n = 3) in our microfluidic device (n = 3). When results of ANOVA were significant, Tukey post hoc comparisons were used to examine differences among treatment groups. Data are presented as the arithmetic mean ± SD.
3. RESULTS AND DISCUSSION
The combined mathematical and experimental approach in our study included four steps. First, we used a physics-based mathematical model [41], sensitivity analysis, and parameter optimization to eliminate trial and error in conducting in vitro experiments to determine the optimal electric voltage. Second, we showed the effect of electrophoresis transport on cationic macromolecule concentration (Alexa fluor 594®) in the porous region (heparin-based hydrogel) using a transient electrokinetics drug release computational model, which was validated by a microfluidic in vitro experiment. Third, the IOC device was used to study carboplatin and paclitaxel delivery to TNBC cells in an in vitro experiment using 50 mV of electric field (EF) and 3 mA of electric current. Fourth, the in vitro experimental results were used to validate the fraction of cells killed in the mathematical model.
3.1. Drug delivery mathematical model optimization and sensitivity analysis
The physics-based model development is shown in the supplemental documents. In the final fraction of tumor killed function, equation 24, three non-dimensional numbers relate to the physics of uptake, diffusion, and electrophoresis drug transport and needed to be analyzed. 𝑃𝑚1 is the ratio between the electric potential and diffusivity, is the ratio 𝑞 between the uptake rate of the carboplatin and diffusivity, and α is the ratio of electric potential in the drug source to the electric potential in the tumor. Three non-dimensional numbers and the electric potential in the tumor region were optimized using GRG (Generalized Reduced Gradient) nonlinear solver [56].
The first non-dimensional number, , is the ratio between the electric potential and the diffusion coefficient. We consider the problem of maximizing the fraction of cells killed subject to varying non-dimensional numbers. The 𝑃𝑚1 number is the function of the electric potential in the tumor region. Except for 𝜑2, other terms in 𝑃𝑚1 are constant properties of carboplatin. We only look at the carboplatin property because it is a charged drug candidate for studying the effect of electric field on its delivery. At a large 𝑃𝑚1 (3.47), the electric potential 𝜑2 has the highest value (43.01 mV); therefore, the fraction of cells killed is maximized (0.79) (Fig. 3B). Our results show the positive effect that electric potential has on the fraction of cells killed and that it can overcome carboplatin’s low diffusion coefficient. As 𝑃𝑚1decreases, the fraction of cells killed also decreases due to a decrease in 𝜑2. When 𝑃𝑚1 is zero, the result indicates the fraction of cells killed (0.37) without applying an electric field.
The direction of electrophoresis can be opposite the direction of drug diffusion. The second non-dimensional number is 𝛼, which is the ratio of electric potential in the drug source to the electric potential in the tumor. The fraction of cells killed decreases when 𝛼 is close to 1, i.e., when there is no electric potential gradient. Therefore, when 𝛼 = 1 (𝜑1 = 𝜑2) the fraction of cells killed is minimized (0.44) (Fig. 3C). As 𝛼 increases (𝜑1 > 𝜑2), the electrical potential gradient is in the opposite direction of the concentration gradient, so the fraction of cells killed decreases. Note that 𝛼 = 1/50 means 𝜑2 is 50 times more than 𝜑1, at which point the fraction of cells killed is maximized (0.79).
The non-dimensional number is analyzed to examine the fraction of cells killed based on drug uptake rate and diffusion. 𝑞 is the ratio of the drug uptake rate to drug diffusion. Since 𝑞 is always positive, the model always increases (monotonic) with different values of positive 𝑞. At small 𝑞 values (0.16), carboplatin diffusion dominates over the uptake rate. High carboplatin diffusion can occur due to a decrease in the tumor drug uptake rate. Therefore, the number of cells killed at high carboplatin uptake (𝑞 = 14.2) leads to a maximized fraction of cells killed (0.55) and a decrease in tumor drug resistance (Fig. 3D). When 𝑞 is 2.4 for carboplatin, the uptake rate of carboplatin is smaller than its diffusion where the fraction of tumor cells killed is 0.25. The fraction of cells killed reaches an asymptote by increasing the value of 𝑞, which depends on the properties of the drug. Therefore, applying an electric field to enhance chemotherapy delivery of carboplatin is essential to kill the maximum fraction of cells (0.79). The graph shows that the primary sources of uncertainty in percent dead cells are the drug uptake rate and diffusivity, and this type of sensitivity analysis allows drug designers to assess the effects of the physical properties of the drugs in the interest of building robust drug delivery models. Our model investigated diffusion and electrophoresis drug transport into single cells. Increasing the electric field intensity increases the fraction of cells killed; however, the new physics of transport, such as joule heating and electroosmotic flow, should be added to the model for a more accurate prediction.
3.2. Delivery of cationic fluorescent dye into the hydrogel using a low intensity electric field
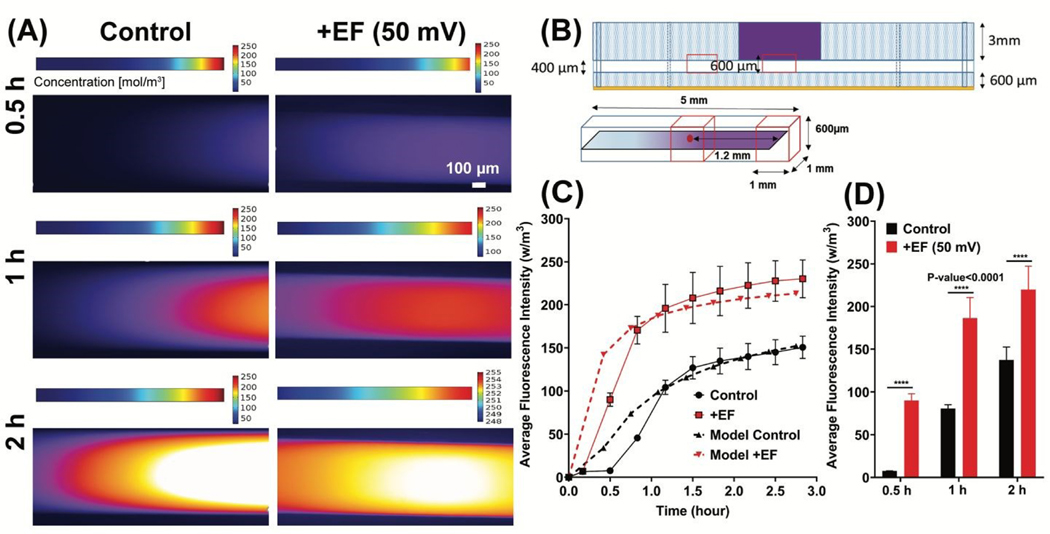
Sensitivity analysis and electric potential gradient optimization showed that an electric potential of 43.01 mV resulted in the maximum fraction of tumor cells being killed (0.7–0.8 or 70%−80%). Based on mathematical model sensitivity analysis, we used a 50 mV electric field intensity for drug delivery experiments on single cells. Because of the restriction in the precision of our DC power supply (DC power supply must be >10 mV), we had to choose 50 mV instead of 43.01 mV. To test our hypothesis using a 50 mV electric field in transient condition, finite element modeling of macromolecule transport in hydrogel was computed. The model was validated with an electrophoresis microfluidic experiment using the IOC device by comparing the measured and predicted normalized fluorescence intensity of the dye. Alexa fluor 594® cationic dye diffusion and electrophoretic delivery were investigated in a 3 h experiment and a transient continuum mass transfer model. The regions in the cell culture chamber and hydrogel channel of the device for the measurement of dye transient concentration (Top: experimental regions, Bottom: computational domain) are shown in Fig. 4B. The in-silico simulation and in vitro experiment showed an increase (48.12%, n=46, p-value<0.0001) in the average fluorescence intensity of the dye by applying 50 mV electric potential gradient in the hydrogel microchannel (Fig. 4A, C&D). The finite element model of the concentration profile in the microchannel was validated with an in vitro experiment of Alexa fluor 594® cationic dye diffusion and electrophoretic delivery (Fig. 4C).
Figure 4. Low-intensity electric fields increase cationic macromolecule transport into the hydrogel.
(A) Snapshots comparing the transient concentration of the Alexa fluor 594® dye in the hydrogel channel at 0.5 h, 1 h, and 2 h time points under the following conditions: Left: Diffusion only (Top: finite element model result, Bottom: experimental result); Right: Diffusion and electrophoresis at 50 mV electric fields (Top: finite element model result, Bottom: experimental result). (B) Representation of the regions in the cell culture chamber and the hydrogel channel of the device, for the measurement of dye transient concentration (Top: experimental regions, Bottom: computational domain). (C) The graph shows the validation of finite element model results for the dye transient concentration obtained experimentally by measuring average fluorescence intensity in the hydrogel channel under the following conditions: (i) Control (diffusion only), (ii) Diffusion and electrophoresis at 50mV electric fields. (D) Summary of the average fluorescence intensity of Alexa fluor 594® dye at 0.5 h, 1 h, and 2 h time points under the same conditions as C. Graph show an increase (48.12%, n=46, p-value<0.0001) in the average fluorescence intensity of the dye by applying 50 mV of electric potential gradient in the hydrogel microchannel after 2 h.
3.3. A low-intensity electric field increases carboplatin delivery in breast cancer single cells
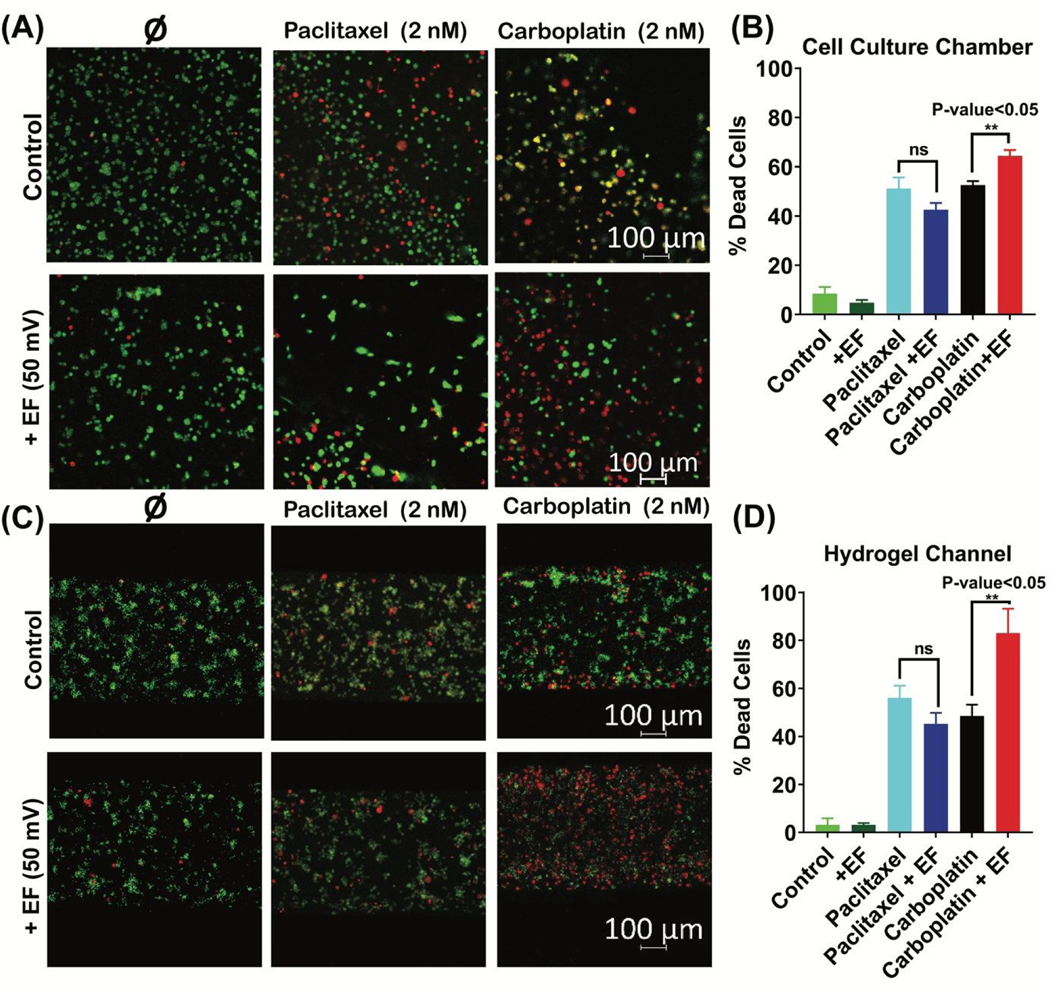
Based on model sensitivity analysis (section 3.2), we specified the low-intensity electric field to be 50 mV. Drug concentration optimization (Fig. S1A) showed that 2 nM of paclitaxel and carboplatin have around a 59% and 71% tumor cell death rate, respectively. Therefore, we specified operating at 2 nM drug concentrations, which is less than the EC90 (effective concentration for 90% of the cells being dead). A significant difference was observed in the percent of dead cells by applying a 50 mV electric field and 3 mA electric current for 3 h (Fig. 5A&C). The percent of dead cells increased by 22% (n=3, p-value<0.05) in the cell culture chamber (Fig. 5B) and 39% (n=3, p-value<0.05) in the hydrogel channel (Fig. 5D).
Figure 5. Low-intensity electric fields increase the delivery of carboplatin to single tumor cells.
Confocal microscope images showing the live-dead cell staining of single tumor cells when exposed to the following treatments: cell culture medium, DMEM/F-12 (no drug); 2 nM of paclitaxel (non-ionized drug); and 2 nM of carboplatin (anionic drug), with and without 50 mV of electric field in the device’s (A) cell culture chamber and (C) hydrogel channel. Graph shows the percent dead tumor cells when exposed to the following treatments: (i) control (cell culture medium, DMEM/F-12 (no drug, no electric field), (ii) cell culture medium, DMEM/F-12 (no drug, with 50 mV of electric field),(iii) 2 nM of paclitaxel (non-ionized drug, no electric field), (iv) 2 nM of paclitaxel(non-ionized drug, with 50 mV of electric field), (v) 2 nM of carboplatin(anionic drug, no electric field), and (vi) 2 nM of carboplatin(anionic drug, with 50 mV of electric field), in the device’s (B) cell culture chamber and (D) hydrogel channel, respectively. Tumor cells that are treated with 2 nM of carboplatin in the presence of 50 mV electric field showed the least viability of all the treatments, with dead cell percent about 64% (n=3, p<0.05) in cell culture chamber and 83% (n=3, p<0.05) in hydrogel channel.
3.4. Fraction of cells killed model validation with in vitro experiment
The “fraction of cells killed” model was developed to facilitate the prediction of the iontophoresis outcome. The in vitro results of percent dead cells versus hydrogel depth were used for model validation (Fig. 6A). A summary of results of the percent of dead cells at different distances from the bottom of the chamber shows an increase in percent dead cells when delivering carboplatin using electrophoresis (Fig. 6B). The validated fraction of cells killed model shows an increase in the percent of dead cells when applying a 50 mV electric field and 3 mA electric current for 3 h experimentally and mathematically (Fig. 6C).
Our results demonstrate that 50 mV of DC electric field and 3 mA of electric current increases drug delivery by 48.12% and increases cell death by 39.13%. Our obtained experimental results validated our recent drug transport model [41].
The correlation between the fraction of cells killed model and the in vitro experiment was measured using two different methods (Table 3S) [57] : 1. RNMSE (Root normalized mean square error) and 2. FB (Fraction of bias). The correlation between cationic dye concentration in hydrogel experimental and theoretical values was calculated using the same methodologies. We found that the FB (fractional bias) value was equal to 0.02, where a positive FB indicated that the model is under prediction, and an RNMSE (root normalized mean square error) [54] equal to 0.3 indicated low scattering from the mean. Overall, the statistical analysis indicated a strong correlation between the model and the microfluidic experiment.
4. CONCLUSION
This paper demonstrates, for the first time, an iontophoresis-on-chip platform that mimics the outcome of iontophoretic drug delivery for the treatment of breast cancer. The mathematical model for the carboplatin concentration profile between two blood vessels in a confined tumor volume was able to accurately predict our in vitro microfluidic results. In this study, we varied the drug type (charge) and cell density as the two main parameters for the on-chip experiments. As expected, iontophoresis was only effective in increasing the charged drug (carboplatin) delivery to the individual tumor cells. Our device could potentially be used for high-throughput screening of charged drug candidates for iontophoretic treatment for breast cancer. Our modeling and experimental results show that an applied electric field intensity of 50–70 mV of DC electric fields and 3 mA of electric current led to the maximum percentage of dead cells (70%−90%). This low intensity electric field has been reported to have minimal side effects on healthy tissues and is significantly lower than that following electroporation. The on-chip platform allows us to precisely control the physics of transport phenomena by adjusting the device geometries, boundary conditions, and initial values of drug dose and electric field intensity to match the mathematical model. The predictive models that we developed in this manuscript define the influence of DC electrical fields and electric current on iontophoretic drug delivery to tumors and may possibly assist physicians in designing an effective treatment regimen for breast cancer patients [58]. (B) We proved the synergy between our mathematical models and our in vitro experiments, which led to a reduction in the number of electric field intensity trials using the mathematical model sensitivity analysis. We then proved the accuracy of the chosen electric field intensity values from the sensitivity analysis by macromolecule electrophoretic delivery into the heparin-based hydrogel microfluidics experiment. The results of the macromolecule electrophoresis delivery into the porous hydrogel was used to validate a transient electrokinetics mass transfer model.
In the future, our device also has the capability to vary flow, ECM porosity, electric field intensity, tumor size, and tumor type. This model is the first step towards generating a predictive model for in vivo applications. Further improvements to the model for transdermal iontophoretic drug delivery can be made and validated by adding additional components in the microfluidic device, mimicking the human epidermis. Currently, iontophoresis is only used for transdermal drug delivery to accessible tumors. In the future, endoscopic surgeries may enable the implantation of 3D printed hydrogels and electrodes [59–62] for electrically-controlled drug delivery into inaccessible solid breast tumors.
Supplementary Material
7. ACKNOWLEDGEMENTS
The authors would like to thank Dr. Jiangtao Cheng for kindly providing us with the electrical instruments required for the experimental work. We also acknowledge support from Fralin Life Sciences Institute of Virginia Tech for facilitating confocal imaging and the Micro & NanoFabrication Laboratory at Virginia Tech’s Bradley Department of Electrical and Computer Engineering for master mold fabrication. We would also like to thank Dr. Janet Webster for critically reading and editing the manuscript.
6. FUNDING
Research materials and equipment for this study were funded by CNJ startup funds from the Department of Biological Sciences at Virginia Tech and The National Institute of General Medical Sciences of the National Institutes of Health under award number R35GM133610. MM was supported by the VT-Initiative for Maximizing Student Development (IMSD) (NIGMS 2R25GM072767-05A1) and the Department of Mechanical Engineering at Virginia Tech.
Footnotes
8. CONFLICTS OF INTEREST
There are no conflicts to declare.
Publisher's Disclaimer: Accepted Manuscripts are published online shortly after acceptance, before technical editing, formatting and proof reading. Using this free, service, authors can make their results available to the community, in, citable form, before we publish the edited article. We will replace this, Accepted Manuscript with the edited and formatted Advance Article as, soon as it is available.
12. REFERENCE
- 1.Neumann E, et al. , Gene transfer into mouse lyoma cells by electroporation in high electric fields. The EMBO journal, 1982. 1(7): p. 841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.OKINO M and MOHRI H, Effects of a high-voltage electrical impulse and an anticancer drug on in vivo growing tumors. Japanese Journal of Cancer Research GANN, 1987. 78(12): p. 1319–1321. [PubMed] [Google Scholar]
- 3.Orlowski S, et al. , Transient electropermeabilization of cells in culture: increase of the cytotoxicity of anticancer drugs. Biochemical pharmacology, 1988. 37(24): p. 4727–4733. [DOI] [PubMed] [Google Scholar]
- 4.Sersa G, et al. , Electrochemotherapy in treatment of tumours. European Journal of Surgical Oncology (EJSO), 2008. 34(2): p. 232–240. [DOI] [PubMed] [Google Scholar]
- 5.Wichtowski M, et al. , Electrochemotherapy in Breast Cancer - Discussion of the Method and Literature Review. Breast Care, 2017. 12(6): p. 409–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bourke MG, et al. , Effective treatment of intractable cutaneous metastases of breast cancer with electrochemotherapy: Ten-year audit of single centre experience. Breast cancer research and treatment, 2017. 161(2): p. 289–297. [DOI] [PubMed] [Google Scholar]
- 7.Wichtowski M, et al. , Electrochemotherapy in the Treatment of Breast Cancer Metastasis to the Skin and Subcutaneous Tissue - Multicenter Experience. Oncology Research and Treatment, 2019. 42(1–2): p. 47–51. [DOI] [PubMed] [Google Scholar]
- 8.Banga AK, Bose S, and Ghosh TK, Iontophoresis and electroporation: comparisons and contrasts. International journal of pharmaceutics, 1999. 179(1): p. 1–19. [DOI] [PubMed] [Google Scholar]
- 9.Banerjee A, et al. , Intestinal iontophoresis from mucoadhesive patches: a strategy for oral delivery. Journal of Controlled Release, 2019. 297: p. 71–78. [DOI] [PubMed] [Google Scholar]
- 10.Dalmolin LF and Lopez RFV, Nanoemulsion as a Platform for Iontophoretic Delivery of Lipophilic Drugs in Skin Tumors. Pharmaceutics, 2018. 10(4): p. 214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liang H, et al. , Effects of methycobal iontophoresis combined with balance acupuncture on peripheral facial paralysis. Zhongguo zhen jiu= Chinese acupuncture & moxibustion, 2018. 38(9): p. 955–960. [DOI] [PubMed] [Google Scholar]
- 12.Pikal MJ, The role of electroosmotic flow in transdermal iontophoresis. Advanced Drug Delivery Reviews, 2001. 46(1): p. 281–305. [DOI] [PubMed] [Google Scholar]
- 13.Patel SR, et al. , In vitro and in vivo evaluation of the transdermal iontophoretic delivery of sumatriptan succinate. European journal of pharmaceutics and biopharmaceutics, 2007. 66(2): p. 296–301. [DOI] [PubMed] [Google Scholar]
- 14.Byrne JD, Yeh JJ, and DeSimone JM, Use of iontophoresis for the treatment of cancer. Journal of Controlled Release, 2018. 284: p. 144–151. [DOI] [PubMed] [Google Scholar]
- 15.Sloan JB and Soltani K, Iontophoresis in dermatology: a review. Journal of the American Academy of Dermatology, 1986. 15(4): p. 671–684. [DOI] [PubMed] [Google Scholar]
- 16.Byrne JD, et al. , Impact of formulation on the iontophoretic delivery of the FOLFIRINOX regimen for the treatment of pancreatic cancer. Cancer Chemotherapy and Pharmacology, 2018. 81(6): p. 991–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Byrne JD, et al. , Local iontophoretic administration of cytotoxic therapies to solid tumors. Science Translational Medicine, 2015. 7(273): p. 273ra14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wolinsky JB, Colson YL, and Grinstaff MW, Local drug delivery strategies for cancer treatment: Gels, nanoparticles, polymeric films, rods, and wafers. Journal of Controlled Release, 2012. 159(1): p. 14–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Karpiński T, Selected Medicines Used in Iontophoresis. Pharmaceutics, 2018. 10(4): p. 204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Eljarrat-Binstock E and Domb AJ, Iontophoresis: A non-invasive ocular drug delivery. Journal of Controlled Release, 2006. 110(3): p. 479–489. [DOI] [PubMed] [Google Scholar]
- 21.Eljarrat-Binstock E, et al. , In Vitro and In Vivo Evaluation of Carboplatin Delivery to the Eye Using Hydrogel-Iontophoresis. Current Eye Research, 2008. 33(3): p. 269–275. [DOI] [PubMed] [Google Scholar]
- 22.Kirby BJ, Micro-and nanoscale fluid mechanics: transport in microfluidic devices. 2010: Cambridge university press. [Google Scholar]
- 23.Li SK, et al. , In vitro and in vivo comparisons of constant resistance AC iontophoresis and DC iontophoresis. Journal of controlled release, 2003. 91(3): p. 327–343. [DOI] [PubMed] [Google Scholar]
- 24.Sylvestre J-P, Guy RH, and Delgado-Charro MB, In Vitro Optimization of Dexamethasone Phosphate Delivery by Iontophoresis. Physical Therapy, 2008. 88(10): p. 1177–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eljarrat-Binstock E, et al. , Charged nanoparticles delivery to the eye using hydrogel iontophoresis. Journal of Controlled Release, 2008. 126(2): p. 156–161. [DOI] [PubMed] [Google Scholar]
- 26.Eljarrat-Binstock E, et al. , Methylprednisolone delivery to the back of the eye using hydrogel iontophoresis. Journal of Ocular Pharmacology and Therapeutics, 2008. 24(3): p. 344–350. [DOI] [PubMed] [Google Scholar]
- 27.Jia H-Z and Peng X-J, Efficacy of iontophoresis-assisted epithelium-on corneal cross-linking for keratoconus. International journal of ophthalmology, 2018. 11(4): p. 687–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jung JH, et al. , Ocular drug delivery targeted by iontophoresis in the suprachoroidal space using a microneedle. Journal of Controlled Release, 2018. 277: p. 14–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Menon N, et al. , Heparin-based hydrogel scaffolding alters the transcriptomic profile and increases the chemoresistance of MDA-MB-231 triple-negative breast cancer cells. Biomaterials Science, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Karuppuswamy P, et al. , Functionalized hybrid nanofibers to mimic native ECM for tissue engineering applications. Applied surface science, 2014. 322: p. 162–168. [Google Scholar]
- 31.Loh QL and Choong C, Three-dimensional scaffolds for tissue engineering applications: role of porosity and pore size. Tissue Engineering Part B: Reviews, 2013. 19(6): p. 485–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pavesi A, et al. , Engineering a 3D microfluidic culture platform for tumor-treating field application. Sci Rep, 2016. 6: p. 26584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lee IC, Cancer-on-a-chip for Drug Screening. Curr Pharm Des, 2018. 24(45): p. 5407–5418. [DOI] [PubMed] [Google Scholar]
- 34.Murdan S, Electro-responsive drug delivery from hydrogels. Journal of Controlled Release, 2003. 92(1): p. 1–17. [DOI] [PubMed] [Google Scholar]
- 35.Curcio M, et al. , On demand delivery of ionic drugs from electro-responsive CNT hybrid films. RSC Advances, 2015. 5(56): p. 44902–44911. [Google Scholar]
- 36.Rahman SM, et al. , Evaluation of intercellular communication between breast cancer cells and adipose-derived stem cells via passive diffusion in a two-layer microfluidic device. Lab on a Chip, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Aroesty J, et al. , Tumor growth and chemotherapy: Mathematical methods, computer simulations, and experimental foundations. Mathematical Biosciences, 1973. 17(3–4): p. 243–300. [Google Scholar]
- 38.Siepmann J and Siepmann F, Modeling of diffusion controlled drug delivery. Journal of Controlled Release, 2012. 161(2): p. 351–362. [DOI] [PubMed] [Google Scholar]
- 39.Mircioiu C, et al. , Mathematical Modeling of Release Kinetics from Supramolecular Drug Delivery Systems. Pharmaceutics, 2019. 11(3): p. 140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pascal J, et al. , Mechanistic patient-specific predictive correlation of tumor drug response with microenvironment and perfusion measurements. Proceedings of the National Academy of Sciences, 2013. 110(35): p. 14266–14271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Moarefian M and Pascal JA, Fundamental mathematical model shows that applied electrical field enhances chemotherapy delivery to tumors. Mathematical biosciences, 2016. 272: p. 1–5. [DOI] [PubMed] [Google Scholar]
- 42.Sung JH, Kam C, and Shuler ML, A microfluidic device for a pharmacokinetic–pharmacodynamic (PK–PD) model on a chip. Lab on a Chip, 2010. 10(4): p. 446–455. [DOI] [PubMed] [Google Scholar]
- 43.McGuire MF, et al. , Formalizing an Integrative, Multidisciplinary Cancer Therapy Discovery Workflow. Cancer Research, 2013. 73(20): p. 6111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Enderling H and Rejniak K, Simulating Cancer: Computational Models in Oncology. Frontiers in Oncology, 2013. 3(233). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Choe SC, et al. , Model for in vivo progression of tumors based on co-evolving cell population and vasculature. Scientific Reports, 2011. 1: p. 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Frieboes HB, et al. , Physical Oncology: A Bench-to-Bedside Quantitative and Predictive Approach. Cancer Research, 2011. 71(2): p. 298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu C, et al. , Use of mathematical models to understand anticancer drug delivery and its effect on solid tumors. Pharmacogenomics, 2011. 12(9): p. 1337–1348. [DOI] [PubMed] [Google Scholar]
- 48.Michor F, et al. , What does physics have to do with cancer? Nature Reviews Cancer, 2011. 11: p. 657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Byrne HM, Dissecting cancer through mathematics: from the cell to the animal model. Nature Reviews Cancer, 2010. 10: p. 221. [DOI] [PubMed] [Google Scholar]
- 50.Swierniak A, Kimmel M, and Smieja J, Mathematical modeling as a tool for planning anticancer therapy. European Journal of Pharmacology, 2009. 625(1): p. 108–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dogra P, et al. , Mathematical modeling in cancer nanomedicine: a review. Biomedical Microdevices, 2019. 21(2): p. 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Brittain S, et al. , Soft lithography and microfabrication. Physics World, 1998. 11(5): p. 31. [Google Scholar]
- 53.Di Pasqua AJ, et al. , Activation of Carboplatin by Carbonate. Chemical Research in Toxicology, 2006. 19(1): p. 139–149. [DOI] [PubMed] [Google Scholar]
- 54.Ciancetta A, et al. , Activation of carboplatin by carbonate: A theoretical investigation. Vol. 41. 2012. 12960–9. [DOI] [PubMed] [Google Scholar]
- 55.Kim M, et al. , Heparin-based hydrogel as a matrix for encapsulation and cultivation of primary hepatocytes. Biomaterials, 2010. 31(13): p. 3596–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lasdon LS, Fox RL, and Ratner MW, Nonlinear optimization using the generalized reduced gradient method. Revue française d’automatique, informatique, recherche opérationnelle. Recherche opérationnelle, 1974. 8(V3): p. 73–103. [Google Scholar]
- 57.Soni M, et al. , A performance evaluation of WRF model using different physical parameterization scheme during winter season over a semi-arid region, India. International Journal of Earth and Atmospheric Science, 2014. 1(3): p. 104–114. [Google Scholar]
- 58.Calvert A, et al. , Carboplatin dosage: prospective evaluation of a simple formula based on renal function. Journal of Clinical Oncology, 1989. 7(11): p. 1748–1756. [DOI] [PubMed] [Google Scholar]
- 59.Simeunovic A and Hoelzle DJ. Coupled Dynamics of Material Delivery and Robotic Manipulator Axes in Endoscopic Additive Manufacturing. in 2019 American Control Conference (ACC). 2019. [Google Scholar]
- 60.Adib AA and Hoelzle D. Hybrid System Model of Microextrusion-Based Direct-Write Additive Manufacturing. in 2019 American Control Conference (ACC). 2019. [Google Scholar]
- 61.Bloomquist CJ, et al. , Controlling release from 3D printed medical devices using CLIP and drug-loaded liquid resins. Journal of Controlled Release, 2018. 278: p. 9–23. [DOI] [PubMed] [Google Scholar]
- 62.Oh HJ, et al. , 3D Printed Absorber for Capturing Chemotherapy Drugs before They Spread through the Body. ACS Central Science, 2019. 5(3): p. 419–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bird RB, Stewart WE, and Lightfoot EN, Transport phenomena. 2007: John Wiley & Sons. [Google Scholar]
- 64.Probstein RF, Physicochemical hydrodynamics: an introduction. 2005: John Wiley & Sons. [Google Scholar]
- 65.Geankoplis CJ, Transport processes and separation process principles:(includes unit operations). 2003: Prentice Hall Professional Technical Reference. [Google Scholar]
- 66.Johansson L, Elvingson C, and Loefroth JE, Diffusion and interaction in gels and solutions. 3. Theoretical results on the obstruction effect. Macromolecules, 1991. 24(22): p. 6024–6029. [Google Scholar]
- 67.Boyce WE, DiPrima RC, and Meade DB, Elementary Differential Equations and Boundary Value Problems, Loose-Leaf Print Companion. 2017: John Wiley & Sons. [Google Scholar]
- 68.Pampel A, Michel D, and Reszka R, Pulsed field gradient MAS-NMR studies of the mobility of carboplatin in cubic liquid-crystalline phases. Chemical Physics Letters, 2002. 357(1): p. 131–136. [Google Scholar]
- 69.Gust R and Schnurr B, Investigations on the stability of carboplatin infusion solutions. Monatshefte für Chemie/Chemical Monthly, 1999. 130(5): p. 637–644. [Google Scholar]
- 70.Binks SP and Dobrota M, Kinetics and mechanism of uptake of platinum-based pharmaceuticals by the rat small intestine. Biochemical Pharmacology, 1990. 40(6): p. 1329–1336. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.