Abstract
We consider models for the importation of a new variant COVID-19 strain in a location already seeing propagation of a resident variant. By distinguishing contaminations generated by imported cases from those originating in the community, we are able to evaluate the contribution of importations to the dynamics of the disease in a community. We find that after an initial seeding, the role of importations becomes marginal compared to that of community-based propagation. We also evaluate the role of two travel control measures, quarantine and travel interruptions. We conclude that quarantine is an efficacious way of lowering importation rates, while travel interruptions have the potential to delay the consequences of importations but need to be applied within a very tight time window following the initial emergence of the variant.
Keywords: COVID-19, Variants, Importation risk
1. Introduction
SARS-CoV-2 is an RNA virus and as a consequence is prone to mutations. However, mutations in coronaviruses occur not as fast as for viruses such as HIV or Influenza because of copy editing (Otto et al., 2021). During most of its early spread in 2020, few mutations were observed that became established. Then, in December 2020, the United Kingdom announced that its intensive sequencing efforts had led to the discovery of a variant, B.1.1.7, which seemed to be both in the process of establishing itself there and to be more transmissible than the “historic” variant. Since then, this variant has become the dominant source of infection in the UK and, at the time of writing, in several European countries and elsewhere. Other variants have also been detected. See a review in (Otto et al., 2021).
In reaction, many countries took measures to limit the entry of passengers hailing from countries where the novel variants were prevalent. Quarantine measures were also either implemented de novo or continued. See an extensive review of the types of measures used in (Burns et al., 2021).
The pattern has repeated itself since with, using the US CDC classification (Centers for Disease Co, 2019), various variants of interest (VOI), of concern (VOC) or of high consequence (VOHC) such as B.1.1.7, B.1.351, P.1 or B.1.617 and can be described as follows. Following the identification of a novel variant in some jurisdiction, local public health authorities communicate this information to their international counterparts and to the media. An amplification phase in the media and social media follows that results almost invariably, in other jurisdictions, to calls for stringent measures to be imposed, from quarantine all the way to the closing of borders. Whether or not countries followed through on these calls has varied greatly and has resulted from arbitration between arguments in favour of and arguments against such measures.
There are factual and scientific arguments in favour of strict travel control, besides the implicit need for politicians to heed the call of social and established media. From the perspective of international law, the World Health Organisation provides, through the International Health Regulations (IHR), a practical framework to deal with Public Health Emergencies of International Concern (PHEIC) such as COVID-19. The IHR provide guidelines for the inter-state dissemination of information about PHEIC, but also delineate the actions that states can take to safeguard the health security of their populations. In the context of international mobility, they set for instance the rights and responsibilities of states vis-à-vis international non-citizen travellers arriving on their soil in terms of testing, quarantine or treatment. At the start of the first wave, stringent border control measures allowed to identify cases. For instance, among the first cases detected in Hong Kong, numbers #1 and #7 were imported cases detected at the border (Kwok et al., 2020). Some modelling work also argues in favour of travel bans; see, e.g., (Costantino et al., 2020; Russell et al., 2021).
However, there are also arguments against strict travel control. Firstly, in the context of international law, the pendant for individuals to the IHR is framed by the mobility articles (Articles 13–15) in the Universal Declaration of Human Rights (UDHR) and its derived international and national treaties of application (e.g., the Canadian Charter of Rights and Freedoms). There have been discussions, in particular, about the necessity of allowing states to temporarily go counter to Article 13 (“Everyone has the right to leave any country, including his own, and to return to his country”) or its equivalent in national laws (Baum & Hai, 2020; Magendzo & Osler, 2020; Saliba & do Valle, 2020). At this point, law courts have mostly sided with governments. However, a recent ruling in France shows that as the crisis continues, courts will likely start to rule in favour of Article 13. On January 30, 2021, the French Government decreed that French citizens living outside the European Union could return to France only if they had an “imperious motive”. Some French expatriates took this to the Council of State, which struck down the decree because it was in violation of Article 13 of the UDHR (d’État, 2021). Secondly, as the fight against COVID-19 continues, governments that were, at the beginning of the crisis, able to take stringent measures aimed only at curtailing the spread of COVID-19, now have to take into account many different aspects, including in particular some related to maintaining economic activity. In the modern global economy, interconnections are crucial and even with the tightest of border controls, there are still many aspects of economic activity that require transborder movement of goods and, as a consequence, of those in charge of assuring this movement. Downturns in economic activity have a demonstrable and quantifiable effect on the health of populations; see, e.g., (Chang et al., 2013; Hone et al., 2019; Maruthappu et al., 2016).
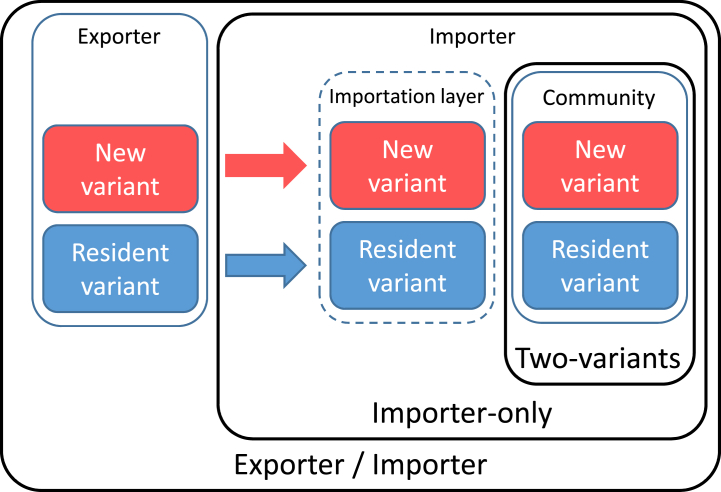
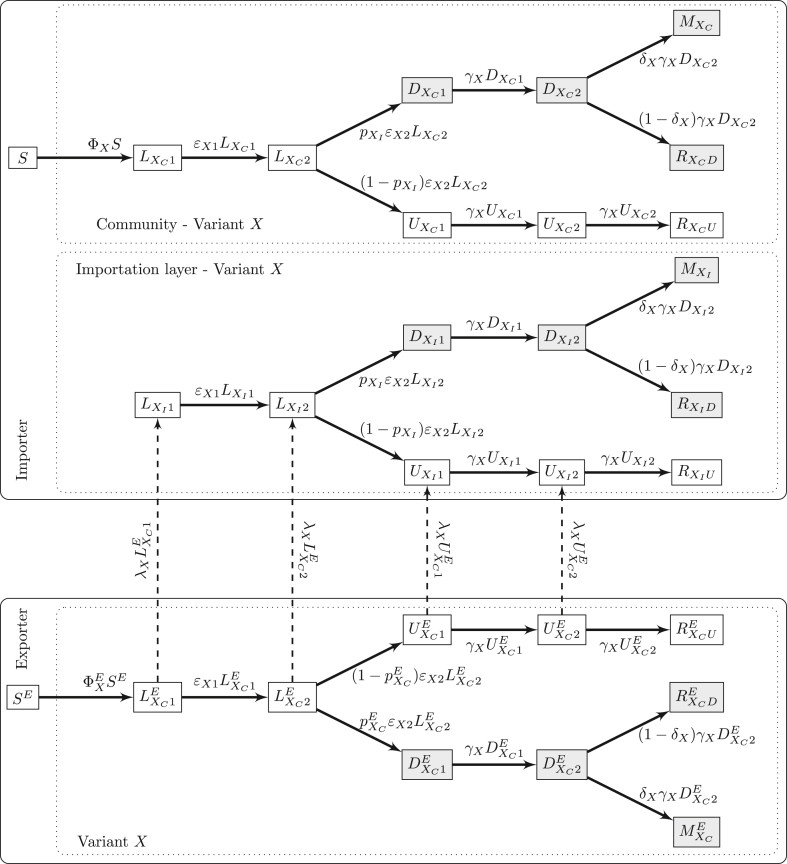
Thus, when taking their decisions, governments have to weigh the direct human costs of the ongoing crisis versus the societal and indirect human costs of the measures taken to curtail it. As such, understanding the role of importations and the effect of border control measures is critical. To contribute to a better understanding of these issues, we extend a model for the importation of SARS-CoV-2 to locations seeing little or no local transmission (Arino et al., 2020), to consider the risk of importing a variant to a population in which a resident virus is already circulating. This is done through three different models of increasing complexity that are schematised in Fig. 1.The first model describes the spread of two variants in an isolated population. The second model adds an importation layer to the first model, allowing to tackle the specific roles of imported and community generated cases in local spread. The last model introduces a metapopulation-type structure to study the relationship between an exporting and an importing jurisdiction. Each model is an extension of the one before and we present and study them in succession.
Fig. 1.
The three models under consideration: Two-variants, Importer-only and Exporter/Importer.
In this preliminary background work, we present the three models and some early mathematical and numerical investigations of their properties. Real-life work considering specific scenarios will be considered in further work. As was done in (Arino et al., 2020), while the models are formulated using ordinary differential equations (ODE), their continuous time Markov chain (CTMC) equivalents are used in practice. The advantage of using ODE is that some quantities are easy to derive in this context, such as the effective reproduction number . By simulating the models as CTMC, on the other hand, we are able to track individuals as well as events and to incorporate stochasticity in trajectories.
2. The model for two variants
2.1. Case detection-based modelling
All three models in the paper are based on the compartmental model in (Arino et al., 2020), with notation adapted to better reflect the nature of the compartments. Deviating from a classic SLIAR model (Arino et al., 2006), we replace the compartments for symptomatic and asymptomatic infections, I and A respectively, by compartments for detected and undetected cases, denoted D and U respectively. This better reflects the reality of COVID-19: detected individuals are those with a positive test for the disease, whether or not they show symptoms, while undetected individuals are those who finish their infection having never been tested or having been wrongly declared negative by a test. The parameter p used to represent the proportion of detected cases (see Section 2.2) is thus a theoretical parameter representing testing effort given perfect knowledge of the burden of the epidemic. To precisely estimate p, one would indeed need, after the epidemic is over, to compare the total detected and total burdens of the epidemic, i.e., perform a posteriori testing of the entire population, including all deaths having occurred during the epidemic. While a precise estimation of p is thus nigh impossible, this parameter does provide a way to rank testing effort between different locations or groups.
Progression through undetected compartments ultimately ends in removal, which happens because of recovery or death, i.e., using a Kermack-McKendrick type interpretation of removal. For detected compartments, in order to potentially reconcile model outputs with data, removal is explicitly split between recovery and death; the latter is denoted M (for mort in French). As in (Arino et al., 2020), compartments L, U and D are split into sub-compartments, with two used here for simplicity, in order have Erlang-distributed times of sojourn in these types of states; see details in (Arino & Portet, 2020). We call unobserved compartments and denote the latent and undetected compartments, i.e., those where individuals bear the disease but have not yet been detected or are not detected altogether.
2.2. Two-variants model formulation
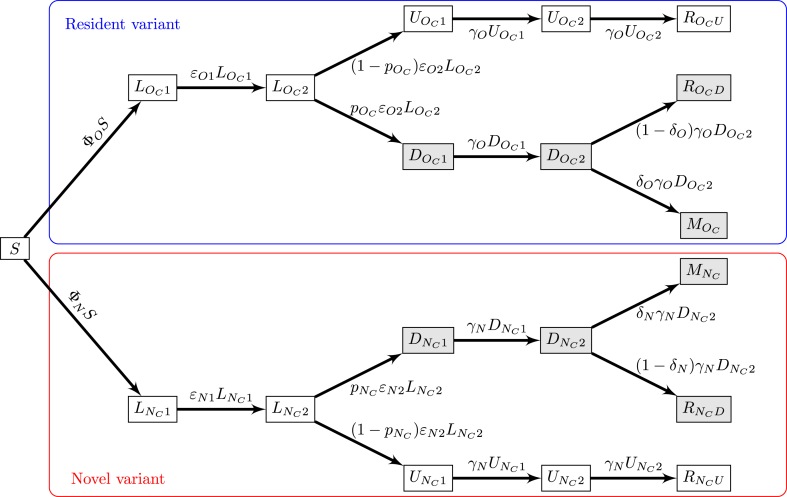
The model for two variants in an isolated location is a straightforward extension of the compartmental model in (Arino et al., 2020), with notation modified as explained in Section 2.1. To describe the spread of two variants, the structure in the model of (Arino et al., 2020) is doubled, with one branch containing the original or resident variant, denoted with the index O, and another containing the novel or new variant, denoted with the index N. The model structure is shown in Fig. 2. To keep notation consistent throughout the paper, we write these indices OC and NC, where C indicates infections acquired from individuals in the community.
Fig. 2.
Flow diagram of the two-variants model. Shaded compartments include detected (observable or observed) cases; blue and red boxes show resident and novel variants, respectively. ΦO and ΦN are the forces of infection for the original (resident) and the novel variants, respectively, and take the form for X ∈{O, N}; see (A.2) in Appendix A.
The model is formulated using ordinary differential equations, which are shown in Appendix A, while simulations of the model are performed as continuous-time Markov chains. It is assumed that the period of time under consideration is sufficiently small that demographic effects do not play a role. As a consequence, the only demographic parameter used is the total population P in the location. Epidemiological parameters of the model are summarised in Table 1 and are allowed to vary between the original and the novel variant, to reflect that characteristics of the novel variant may differ substantially from those of the resident variant. The durations of stages were chosen to reflect the general timeline of SARS-CoV-2 infections in individuals, in particular with respect to generation intervals, i.e., the time between the infection of a primary case and one of its secondary cases. The mean of the generation interval is given by (Svensson, 2007)
In terms of model parameters and given the exponential and Erlang distributions used, it thus equals, for variant X ∈{O, N},
so, with the values in Table 1, the mean generation interval is 5.875 days, commensurate with estimates in the literature (Alene et al., 2021; Hussein et al., 2021; Prete et al., 2020; Zaki & Mohamed, 2021). Note that most studies on disease characteristics date back to the first wave and it is not impossible that some of these characteristics have evolved since or that they would be different for some of the variants.
Table 1.
Parameters for variant X ∈{O, N}. Typically, and .
| Parameter | Meaning | Value or range |
|---|---|---|
| Reproduction number | [0.5, 3.0] | |
| βX | Disease transmission parameter | Computed |
| ηX | Modulation of transmissibility for latent individuals | [0, 1] |
| ξX | Modulation of transmissibility for detected individuals | [0, 1] |
| 1/ϵX1 | Average duration of the noninfectious incubation period | 3 days |
| 1/ϵX2 | Average duration of the infectious incubation period | 1 days |
| 2/γX | Average duration of the infectious period | 3 days |
| δX | Case fatality ratio | 0.53% (Salje et al., 2020) |
| Efficacy of detection in community cases | [0, 1] |
For variant X ∈{O, N}, parameters are as follows. The rates of moving through latency (assumed to completely match incubation) are ϵX1 and ϵX2, respectively, for the non-infectious and infectious latent periods, giving an average duration of the latent period of 1/ϵX1 + 1/ϵX2. Because of the Erlang distribution resulting from using two compartments for the infectious period with same rates of outflow, 2/γX is the average duration of the infectious period. Testing intensity is described by the parameter , while the case fatality ratio is δX ∈ [0, 1]. Recall that we distinguish between recovery and death only for detected individuals; for undetected individuals, both processes are aggregated within “removal” and as a consequence, δX only acts on detected individuals. Finally, βX is the disease transmission parameter. In terms of units, and δX are proportions, ϵX and γX are per capita, while βX is per capita per contact.
2.3. Mathematical properties of the two-variants model
We first consider properties of the ODE model, since some of these properties carry through to the CTMC model. First, there are two types of reproduction numbers; see Appendix A.2 and Appendix A.4 for details of their computation. The variant-specific reproduction number is given, for variant X ∈{O, N}, by
| (1) |
where ηX and ξX are the modulation (typically attenuation) factors for transmission by incubating and detected cases and S(0) is the susceptible population at the initial time, computed by subtracting the total non-susceptible population from the total population P. There is also a “system-wide” reproduction number,
| (2) |
When considering a single variant in isolation, it is possible to derive a final size relation, i.e., to obtain the overall attack rate of the variant should the other variant not be present; see Appendix A.3.
2.4. Setting up simulations of the two-variants model
The free parameters ξX, ηX, ϵX1, ϵX2, , γX and are estimated from the literature or by calibrating model responses to data. Our aim in this work is not to be extremely precise with regards to parameter values but rather to use values compatible with the general characteristics of COVID-19. The disease transmission parameter βX for variant X ∈{O, N} is obtained from the reproduction number for this variant by solving (1) for βX as a function of , finding the transmission coefficient for variant X as
| (3) |
For simplicity, in this introductory work, we take the values of the rate of progression through the incubation and infectious periods and the disease induced death rate to be constants and vary only the reproduction number (and through it βX) and the efficacy of detection .
We use the R package GillespieSSA2 to perform numerical simulations of the CTMC. The package allows to track individual firings of the CTMC, i.e., the reactions that activate to change the state of the system. We utilise this feature and, in the remainder of the text, denote Y → Z the event in the CTMC that results in the switch of an individual from state Y to state Z. If transitions are “obvious”, some information is omitted; for instance, the transition is written , since it is evident from model structure that transition from latent to detected occurs between the second latent compartment and the first detected compartment (Fig. 2). We denote #(⋅) the number of events of a certain type per unit time; e.g., is the number per unit time of cases bearing the resident variant detected in the community. When considering different types of events, we use the logical or notation ∨; e.g.,
| (4) |
is the fraction of newly detected cases that are bearing the novel variant. Finally, new infections are denoted in a manner making explicit what type of individuals are involved. For instance, denotes new infections in the community by detected individuals bearing the resident variant, while are infections by unobserved (latent or undetected) individuals.
To ensure that simulations run in a way where the start of importations of the new variant has a direct effect on the system, we first run the system without the new variant over a burn-in period of three weeks. The initial condition for the original variant used for the system with the new variant is the state of the system after this initial burn-in period. The original variant is assumed to propagate with , while the reproduction number for the novel variant used is unless otherwise indicated.
In the figures throughout the remainder of the text, when a range is shown, it is the range containing x% of simulation results at each time point (typically 90% or 95%), between the (100 − x)/2-percentile and 100 − (100 − x)/2-percentile of values for that time point. Because each realisation of the CTMC has a different sequence of jump times, envelopes as well as mean and percentiles are obtained by interpolating each solution on a fine time grid.
2.5. Numerical investigation of the two-variant model
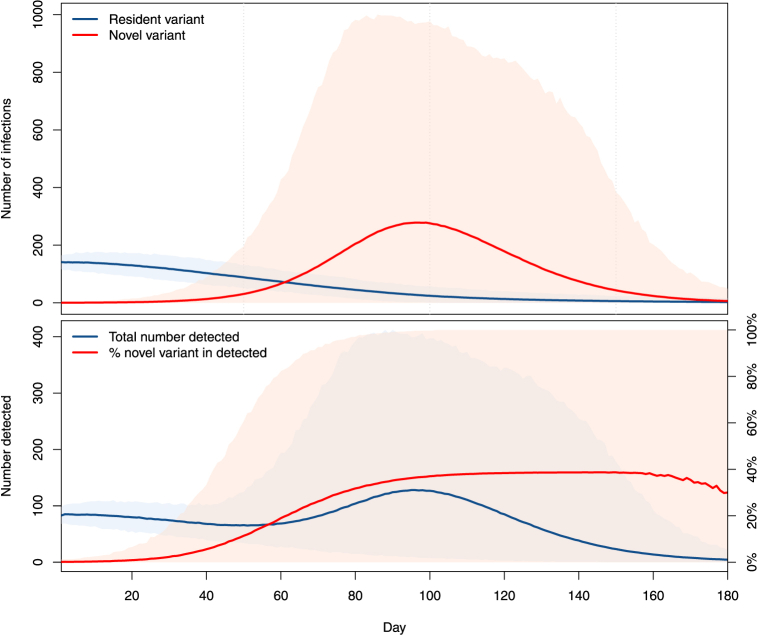
Fig. 3 shows the 95% range and the mean of 1000 simulations where P = 100, 000, , , ξO = 0.15, ξN = 0.3 and there is initially a single individual in the compartment. The top panel shows the numbers of infections that are with the resident variant (blue) and the novel variant (red). The slow decrease of the average number of new infections with the resident variant is due to the fact that S(t) decreases with time. This implies that the effective reproduction number for resident variant O, obtained at time t by replacing S(0) with S(t) in (1), decreases. As initially, this means for all t > 0.
Fig. 3.
Top: number of infections with the resident (blue) and novel (red) variants in an isolated location, when one case of the novel variant is introduced at time t = 0. Bottom: total number of new cases detected (blue, scale on left axis) and percentage of these cases that are with the novel variant (red, scale on right axis). Ranges are 95% of the solutions, lines represent the mean of all solutions.
The bottom panel in Fig. 3 shows the corresponding total number of detected cases, i.e., the denominator in (4), and the percentage of novel variants in these detected cases given by (4), when the percentages of resident and novel variants detected are, respectively, 60% and 40%. By the design of the model, the time to detection is underestimated, i.e., we find detection times earlier on average than they should be. Indeed, recall that a case is detected, for variant X ∈{O, N}, when a transition LX → DX occurs, whereas in “real life”, this transition can happen at any point during the transition through compartments downstream from latent compartments in the flow diagram of Fig. 2. Thus, detection timing results presented in this work are best-case scenarios where detection occurs at the end of the incubation period.
The initial number of individuals infected with the new variant greatly influences the latter's capacity to become established in the population. We illustrate this in Fig. 4, which shows the dependence of the percentage of simulations seeing an extinction of the novel variant in the six months time window considered on the number of individuals initially infected with that variant. Parameters are as used in Fig. 3. For consistency of results, we assume that at time t = 0, all individuals infected with the novel variant are in compartment . Also shown on this figure is the probability of a minor epidemic given by Whittle's formula (Whittle, 1955), where I0 is the number of individuals initially infected with the disease. Whittle establishes that when , there can only be minor or major epidemics, where minor epidemics correspond to those where we observe significantly fewer cases and disease extinction generally occurs more quickly than in the case of a major epidemic (Becker, 1976; Tritch & Allen, 2018). In the present case, since , the complement to the probability of a minor epidemic is the probability of a major epidemic (Milliken, 2017; Tritch & Allen, 2018; Whittle, 1955), corresponding here to the case where the novel variant does not become extinct. In (Arino et al., 2020), the latter probability was used to characterise critical successful importations.
Fig. 4.
Percentage of 1000 simulations seeing extinction of the novel variant within a six months period as a function of the initial number of individuals in , with all other compartments for the novel variant starting empty. Also shown is the theoretical value of the probability of a minor epidemic obtained by using Whittle's formula (Whittle, 1955), which here roughly approximates the probability of novel variant extinction; see text for details.
3. The importer-only model
To study the role of importations and the effect of control measures implemented to limit them, we now add compartments that contain all individuals bearing the disease and arriving in the location of interest from outside the location of interest. We focus here on the dynamics of importation within the location of interest and thus call this the importer-only model.
3.1. Formulation of the importer-only model
We consider a model with the same structure as in Section 2 but subjected to introductions, which we call importations here. We adopt the same language as in (Arino et al., 2020): importations are all events when someone infected with the disease in another location arrives in the location of interest; successful importations are those importations that result in the transmission of the disease to at least one individual in the location of interest, i.e., success is from the perspective of the pathogen.
We assume that importations can only be of individuals incubating with the disease (L compartments) or with an undetected active infection (U compartments); individuals with detected active infections are not able or allowed to travel.
In order to distinguish between infections happening because of contacts with imported and community cases, we introduce an importation layer. Individuals in the importation layer and in the community are distinguished using indices I and C, respectively. Thus, for variant X ∈{O, N}, cases are distinguished by the indices XI and XC, depending on whether infection was acquired by contact with someone infected in another location or in the community. Each disease state is therefore indexed by of one of four types: resident variant acquired in the community OC, imported resident variant OI, novel variant acquired in the community NC and imported novel variant NI.
By model construction, new infections in the importation layer can only originate from an importation, i.e., there is no within-group transmission of the pathogen there. These importations occur at Poisson distributed times with rate constant λX for variant X ∈{O, N} and enter compartments , , and with probabilities , , and , respectively, where . Individuals in the importation layer make contacts with individuals in the community freely.
We assume that detection efficacy can differ between imported and community cases for a given variant. Indeed, individuals entering a jurisdiction are often subject to different detection protocols than individuals already in the jurisdiction. For instance, Canada and the United Kingdom have been using “day 0” testing, where an individual needs, additionally to a negative PCR test less than 72 h before undertaking travel, to submit to a PCR test upon entry into the jurisdiction.
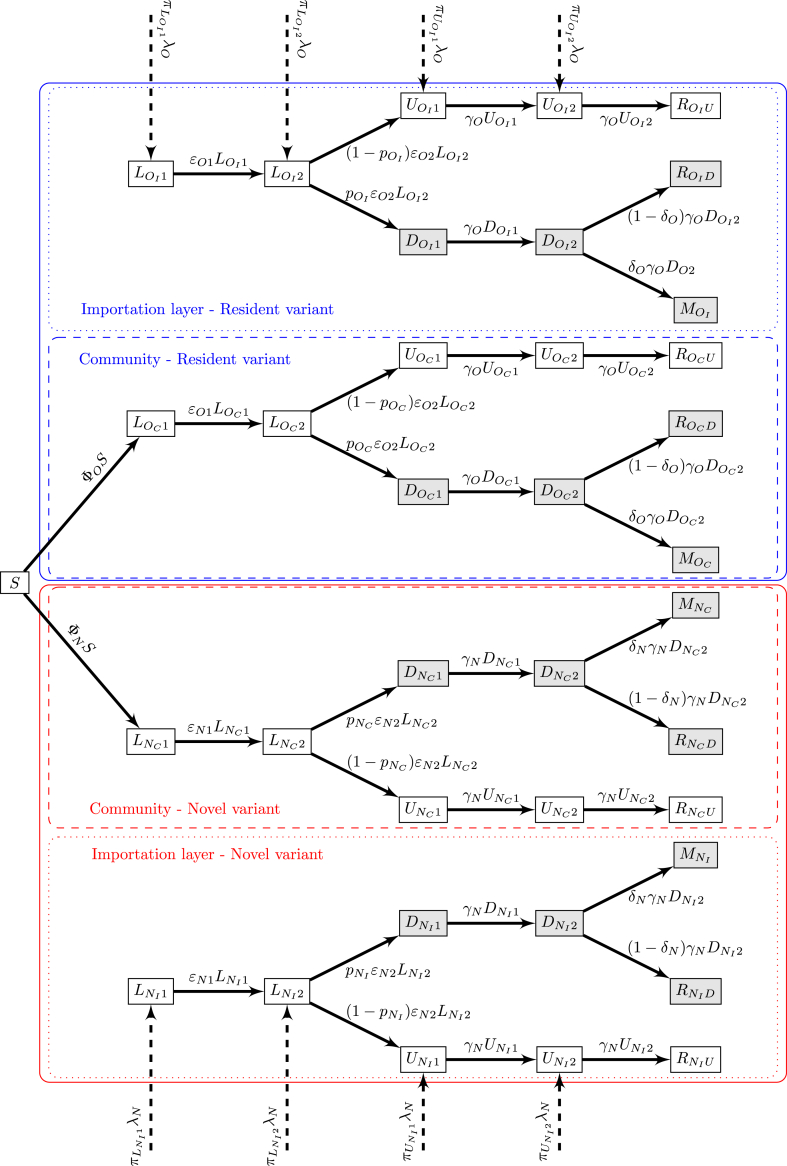
As is the two-variants model in Section 2, we assume that the total population in the location of interest is P. The model structure is shown in Fig. 5.
Fig. 5.
Flow diagram of the importer-only model. Shaded compartments are detected; blue and red boxes show resident and novel variants, respectively. For variant X ∈{O, N}, ΦX is the force of infection (B.2) in Appendix B.
3.2. Properties of the importer-only model
Because importations always enter and remain in the importation layer, P is constant for the community but the total population in the location of interest is increasing.
The importer-only model does not admit a disease-free equilibrium, because of the inflow of individuals into infected compartments. As a consequence, it is not possible to compute a reproduction number for the entire system. See, e.g. (Almarashi & McCluskey, 2019), for a discussion of this issue and some leads into addressing it. It is still possible to use, and we do, formula (1) for the reproduction number for a single variant without importation, but this reproduction number must be understood to apply in this specific situation.
3.3. No travel control
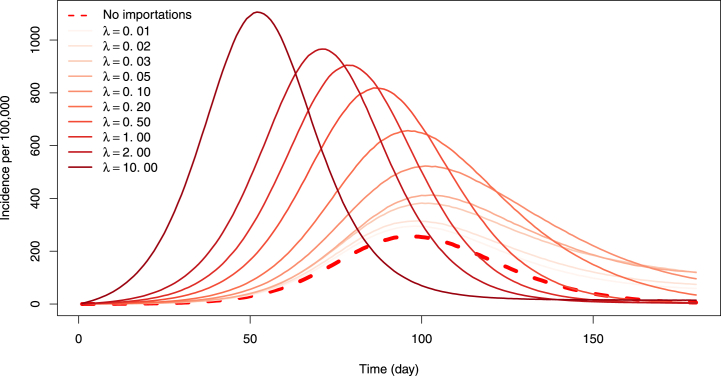
Let us start with the case with no travel control, to understand the baseline response of the model. To visualise the role of importations, we compare solutions of the model without importations of Section 2 with solutions of the importer-only model, for increasing values of the rate of importation λX. In Fig. 6, we focus on incidence of the novel variant, when .As expected, importations speed up spread: the base case without importations (dashed line) sees the slowest rate of increase of the incidence of the novel variant, while increasing importation rates result in increasingly fast epidemics. Simulations shown are run with an importer population of 100,000 and at high importation rates, we observe that the epidemic peak is reached much earlier than for lower or zero importation rates.To investigate the likelihood of detection of new variants, let us consider the pendant of the lower panel in Fig. 3, i.e., the evolution of the fraction of detection of the novel variant among all detections,
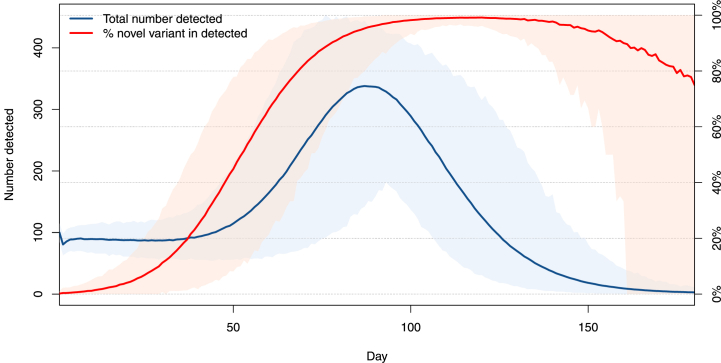
The evolution of this quantity is shown in Fig. 7, when the percentages of resident and novel variants detected are, respectively, 60% and 40%. For the parameters used, we observe that the introduction of the novel variant does not have an immediate effect on the total number of detected cases (blue curve). On the other hand, detection of the novel variant occurs more rapidly here than it does in the isolated case with no importation of the lower panel of Fig. 3. This phenomenon was observed in many locations when more transmissible variants started propagating there and highlights the importance of frequent and extensive sequencing. Indeed, if testing only establishes presence or absence of the infection without distinguishing between variants, then it takes a substantial amount of time before the presence of the novel variant is detected through an increase of the overall number of cases detected.
Fig. 6.
Incidence of the novel variant in the two-variants model without importation (dashed line) and in the importer-only model with increasing importation rates λ≔λO = λN. Here, .
Fig. 7.
Mean total number of new cases detected (blue, scale on left axis) and mean percentage of new variants detected within these (red, scale on right axis). Here, λO = λN = 1/2.
3.4. Effect of quarantine
To consider the effect of quarantine, we use the method developed in (Arino et al., 2020) and detailed in Appendix B.2. Note that we assume that all incoming individuals follow the quarantine for its entire duration. In “real life”, there have been exemptions allowing some to not quarantine, and some individuals having to quarantine have either failed to do so or have terminated the process early.
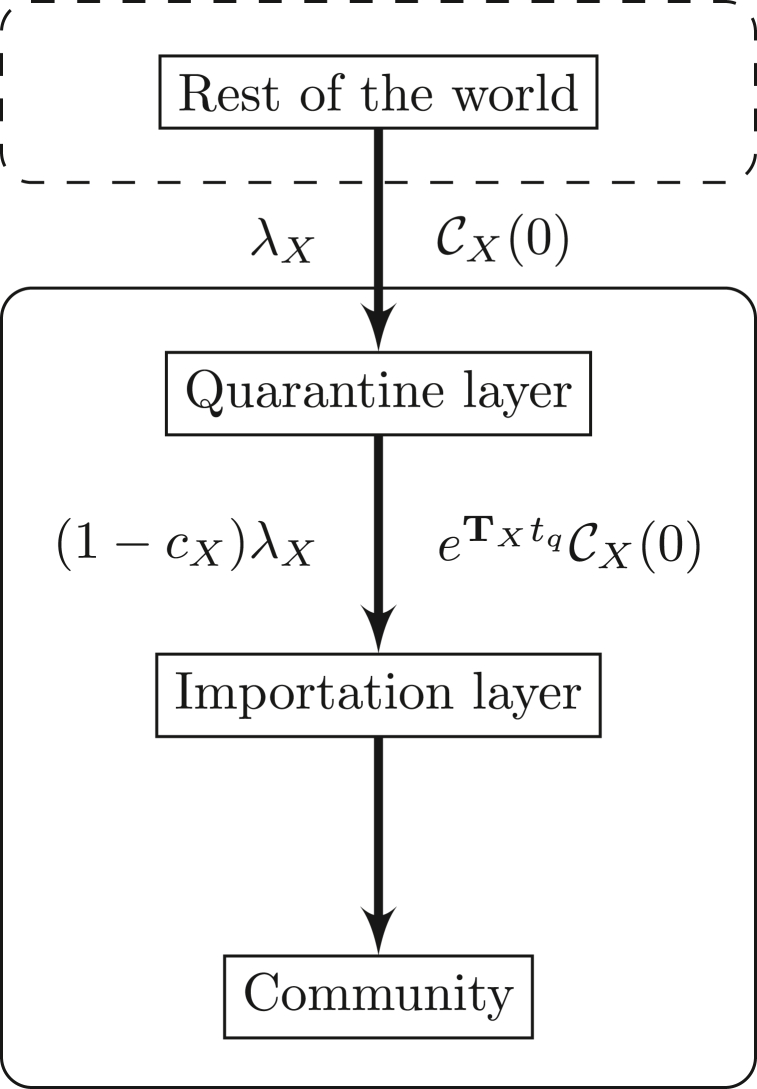
We proceed in several steps illustrated in Fig. 8. We assume that what is happening in the rest of the world translates, for variant X ∈{O, N}, into an importation rate λX with distribution of states , where .
Fig. 8.
Setup of the quarantine simulations.
Here, for simplicity, we assume that not-yet-detected or undetected cases are equally likely, i.e., . From this and model parameters, we deduce both the quarantine efficacy cX and the distribution of probability of being in the different compartments given by (B.4). This is the output of the quarantine layer and is fed into the importation layer. Using the indicator vector u defined in Appendix B.2, inputs to , , and in the importation layer occur at rate given by the nonzero entries in , where are the probabilities of transition between states for individuals over tq units of time and tq is the quarantine duration.
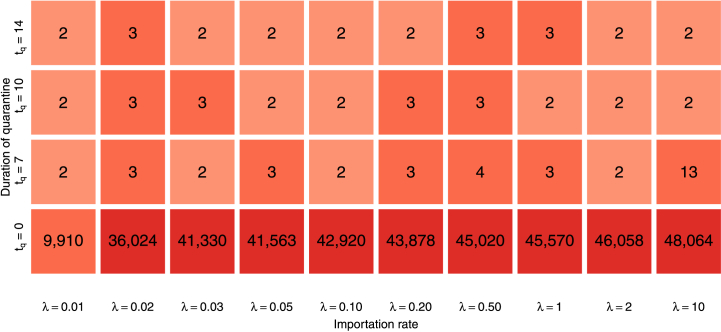
In Fig. 6, we observe that importations can be disastrous in terms of overall disease burden, so it is natural to try to limit them. In order to evaluate the capacity of quarantine in this context, we compare the outcome of simulations without quarantine as in Fig. 6 and with three durations of quarantine that have been used by different countries, tq = 7, 10 and 14 days. One thousand simulations are run for each combination of importation rate and quarantine duration. For each simulation, we compute the numeric final size of the novel variant by counting how many infections with the novel variant take place over the period of interest of six months. Fig. 9 then shows the median value of the final sizes and indicates that quarantine has a very distinguishable effect. Indeed, with the model parameters used, a quarantine with tq = 7 is 98.4% efficacious (see Appendix B.2), implying a multiplication of the mean time between importations by about 60 or, equivalently, an importation rate λ ≃ 0.008 instead of λX = 1/2.
Fig. 9.
Median over 1000 simulations of the final size of the novel variant over the period of interest of six months, as a function of the importation rate λ≔λO = λN and the duration tq of quarantine (in days). The bottom row corresponds to final sizes of the solutions shown in Fig. 6.
3.5. Effect of complete border closures
To evaluate the role of complete interruption of travel, we proceed to the following experiment. We choose a day td for the start of travel control. On the interval [0, td], we run the system as in Section 3.3. Then, starting on day td, full travel interruption is implemented by setting λO = λN = 0.
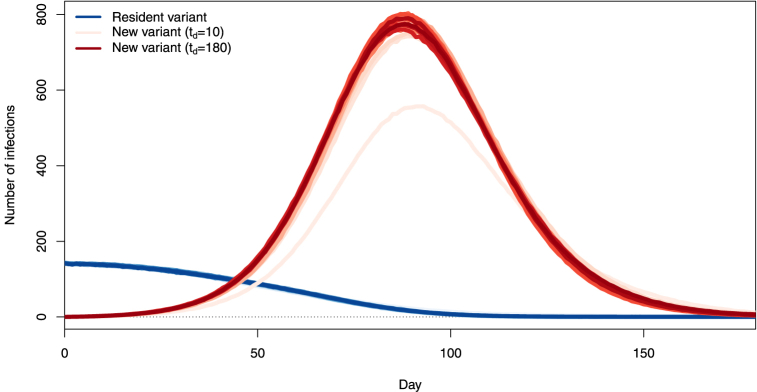
Fig. 10 shows the mean trajectories of 1000 simulations, i.e., the mean numbers of transmission events, in the same setting as Fig. 7 and with a moderate importation rate λO = λN = 1/2 prior to border closures, for values of td = 10, 20, …, 180. (The case td = 180 means there is never an interruption of travel.)
Fig. 10.
Number of transmission events involving the original (blue) and novel (red) variants, with a complete interruption of importations occurring at td = 10, 20, …, 180 days. Scales (most not shown) range from lightest when td = 10 days to darkest when td = 180 days. Each curve is the mean of 1000 simulations.
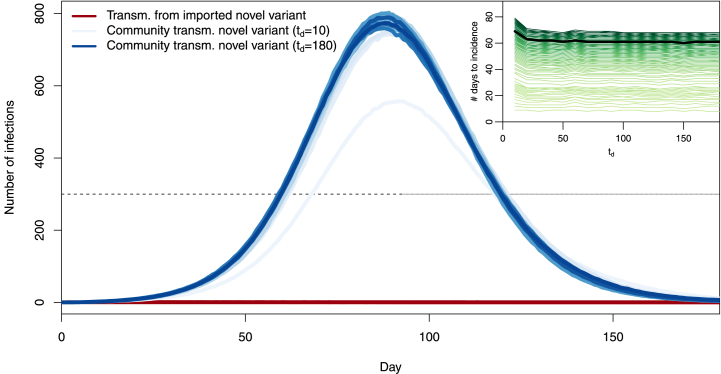
We see that the trajectory most advantageous in terms of control of the variant is that corresponding to td = 10 days, with other trajectories being roughly similar to one another. Interruption of importations does not affect the already spreading resident variant. Thus, it appears that unless they are implemented very soon after the novel variant starts being imported, travel restrictions play very little role. To understand why this is, consider the main panel in Fig. 11.There, we observe that community transmission quickly becomes the main source of transmission of the new variant, while transmission from imported cases to the community remains very low. Thus, very little seeding by imported variant cases is required to start a local outbreak. Early efforts (td = 10) substantially delay passage times through set incidence values. The likely reason for this is that for such values of td, we fail to import a case. Indeed, from the model, the probability of no successful variant introduction is approximately over the period [0, T]. This value becomes less than 5% when . The mean time to introduction of the first novel variant is 1/λ and mean time to the first successful introduction is . Longer times to travel shutdown, starting with td = 20 days, change very little to the outcome.
Fig. 11.
Number of transmission events involving importation cases bearing the new variant (, red) and transmission of the new variant within the community (, blue), when a complete interruption of importations occurs at td = 10, 20, …, 180 days. Scales (most not shown) range from lightest when td = 10 days to darkest when td = 180 days. Each curve is the mean of 1000 simulations. Inset: mean first passage time (MFPT) to a prescribed incidence value as a function of the number td of days from the start of importations to complete travel interruption. Lightest coloured curve: MFPT to an incidence of 1; darkest colour: MFPT to an incidence of 555; green curves correspond to MFPT to 1,2, …,15,20, …,555. Highlighted in black: incidence of 300 (main figure) and corresponding MFPT (inset).
To confirm this, consider the inset in Fig. 11, which shows the d’État which each of the blue curves in the main panel in the figure passes through a given incidence value, i.e, the mean first passage time (MFPT) through that value. Curves are ordered and coloured from the MFPT for an incidence of 1 at the bottom in light green to the MFPT for an incidence of 555 at the top in dark green, which is the maximum incidence at 94 days along the blue curve for td = 10. The example of the MFPT through an incidence of 300 is shown, with the black curve in the inset corresponding to the points of intersection of the different blue curves with the dashed black line at an incidence of 300.
One way to read the MFPT curves is as follows. Set a target maximum daily incidence, say 300 as highlighted in Fig. 11, and pick the MFPT curve corresponding to this value (the black one, in the case of an incidence of 300). The right endpoint of that curve corresponds to the situation where no action is ever taken, i.e., td = 180. Following the curve left, we observe that there is initially virtually no change, meaning that reacting with this delay achieves almost no benefit in timing. Then, as td reaches td = 10, there is a marked change in curve slope, meaning that time was “bought”. Observe that, as the threshold is decreased, so is the value of td for which meaningful time delays are achieved, to the point that for the lowest thresholds, only td = 10 achieves more than a two day increase in MFPT.
It is possible for the novel variant to become extinct during the period of interest, since there are no new importations after td. Indeed, the blue curves in Fig. 11 show the mean of 1000 realisations of the stochastic process. It is likely that individual realisations have the prevalence of the novel variant become zero after td, corresponding to a successful use of border closures, since there can be no further introductions of the novel variant after td. Let us focus on the pre-peak period: indeed, extinctions are very likely in the latter phase of the 6 months period under consideration; however they occur not because of control measures but because the epidemic has run its course. The average time of the peaks in Fig. 11 is 89.3 days and prior to that date, extinctions occur in 23.5%, 4.5% and 1% of (1000 each) simulations for td equal to 10, 20 and 30 days, respectively, and never for td ≥ 40. This further confirms that the (time) window of opportunity during which complete border closures can be expected to contribute substantially to the curtailing of the disease is quite narrow.
This is all the more relevant when one considers the process for declaring an emergent novel variant a VOI or VOC, as it is indeed unreasonable to think that a remote public health authority would act to block travel from a country before a variant is declared a VOI/VOC by local authorities there. There is no consensus on the definition of VOI or VOC; the following is the one proposed by WHO in February 2021; see also the already cited US CDC definition (Centers for Disease Co, 2019). A SARS-CoV-2 isolate is a variant of interest (VOI) if it is phenotypically changed compared to a reference isolate or has a genome with mutations that lead to amino acid changes associated with established or suspected phenotypic implications AND has been identified to cause community transmission/multiple COVID-19 cases/clusters, or has been detected in multiple countries; OR is otherwise assessed to be a VOI by WHO in consultation with the WHO SARS-CoV-2 Virus Evolution Working Group. In view of this definition, the time it takes before a variant is declared of interest will vary based on local authorities as well as the efficiency of local surveillance. This suggests that there is a lower bound for td that may well be greater than or equal to the threshold of 30–40 days after which the novel variant is shown to almost always establish.
3.6. Comparing the effect of quarantine and border closures
To compare the effect of quarantine and complete travel interruptions, we consider the final size of infections with the novel variant using both modalities of importation control. The result is shown in Fig. 12. Parameters used are as in Sections 3.4, 3.5 and we consider the moderate value of λO = λN = 1/2, i.e., one importation event on average every two days.
Fig. 12.
Final sizes of infections with the novel variant over a six months period, in the base case (importation without control, left “middle” row), with quarantine (right lower row) and with complete travel interruptions (upper row). The number indicated below the type of control is the final size.
To understand why a total travel interruption, even one starting ten days after the beginning of novel variant spread, is far less effective than a 7 days quarantine, recall that the numbers presented are medians over 1000 simulations. We saw in Section 3.5 that with complete travel interruptions after 10 days, a little over 20% of simulations saw complete extinction of the novel variant prior to the mean time of incidence peaks. However, other than these favourable simulations, other simulations with td = 10 had on average 5 or 6 introductions before complete shutdown of importations. On the other hand, as remarked in Section 3.4, with the model parameters used, a quarantine with tq = 7 is 98.4% efficacious and results in a considerable decrease of the rate of importation. So, while in 20% of the cases, total travel interruptions offer a more desirable outcome, the rest of the time they do not, which is reflected in the figure.
4. The exporter-importer model
In our considerations in Section 3, importation rates λO and λN are held constant throughout simulations. In Section 3.4, they are modulated by quarantine, while in Section 3.5 they are set to zero after td days to mimic border closures. However, they do not depend on the evolution of the epidemic situation in locations from which imported cases originate.
As a consequence, when considering the number of infections involving imported infectious individuals versus those in the community, we find that the number of new infections generated by imported cases is essentially a function of the importation rates λO and λN and remains roughly constant through time.
To better understand the role of detection in relation to border closures, we therefore extend the model to take into account the epidemic situation in the location where imported cases originate from.
4.1. Formulation of the exporter-importer model
We extend our study to the mechanism generating the importations received by the model in Section 3. For this, we derive a metapopulation-type model (Arino, 2017) with only two spatial locations: an exporter, where amplification of the novel variant is taking place, and an importer, which uses the model formulated in Section 3.
We use the superscript E to indicate state variables and parameters in the exporting jurisdiction. In the exporter, we use a replica of the model in Fig. 2 for propagation of two variants within a community in Section 2. We suppose that individuals in compartments , , and , X ∈{O, N}, in the exporter travel to the importer at the per capita mobility rates λX. As previously, we assume detected individuals do not move between locations. Most parameters are assumed to take the same values as in the importer, except for the contact parameter β and the proportion of detection p. The total population of the exporter is PE initially, while the total population of the community in the importer is fixed and equals P. See Fig. 13, which details the model structure for one of the variants X ∈{O, N}. Model equations for the ODE exporter-importer model are given in Appendix C.1.
Fig. 13.
Export-import model for one variant X ∈{O, N}. Recall that S and SE are also connected to the other variant Y ∈{O, N} ≠ X.
4.2. Properties of the exporter-importer model
Taken together with individuals in the importation layer of the importer, the total number PE of individuals in the exporter is constant, although the population in each patch varies. (Note that this includes death.) The total population in the community in the importer is also constant.
One major difference between the import-only and export-import models is that because importations are not considered in the exporter, the export-import model behaves like a regular metapopulation model and has, in particular, a disease-free equilibrium. This implies that it is possible to compute a basic reproduction number for each variant and for the whole system.
However, one can also consider the exporter in isolation from the importer, since the latter plays no role in the dynamics of the former. This is useful to set the reproduction number in the exporter patch. The computation in Appendix A.2 is virtually unchanged in this case, with the only difference being that matrix VX takes the form
This changes the expression for as follows; for variant X ∈{O, N} in the exporter patch,
In simulations, the value of is set by solving this formula for a given , giving a complicated expression that is not shown here.
4.3. Sample behaviour of the exporter-importer system
The set up of numerical investigations of the exporter-importer system is similar to earlier models. To compute the movement rate λ from exporter to importer, we proceed as in (Arino & Portet, 2015): we consider the evolution of the number PE of individuals in the exporter due to movement of passengers from the exporter to the importer. Over a very short time period, we can assume that there are no other significant sources of change to PE, so that . Solving this simple linear ODE for one day and equating PE(0) − PE(1) = ΔE, where ΔE is the number of passengers travelling from the exporter to the importer in one day, we find λ = − ln(1 −ΔE/PE).
Note one fundamental difference between the importation rates used in the second model (Section 3) and those used here. In the second model, the effect of importation rates is additive, in the sense that because of competing risks, the importer population is subject to importations at the combined rate λO + λN.Here, on the other hand, the rate λ derived above applies per capita to the entire population PE in the exporter patch. Therefore, in the present model, λO and λN are modulations of this rate. If they are taken equal to λ (which is what is typically done), travel takes place at the same rate for all individuals regardless of their epidemic status. Values of λO and λN smaller than the general λ may be used for instance to indicate that negative PCR tests are required for travel.
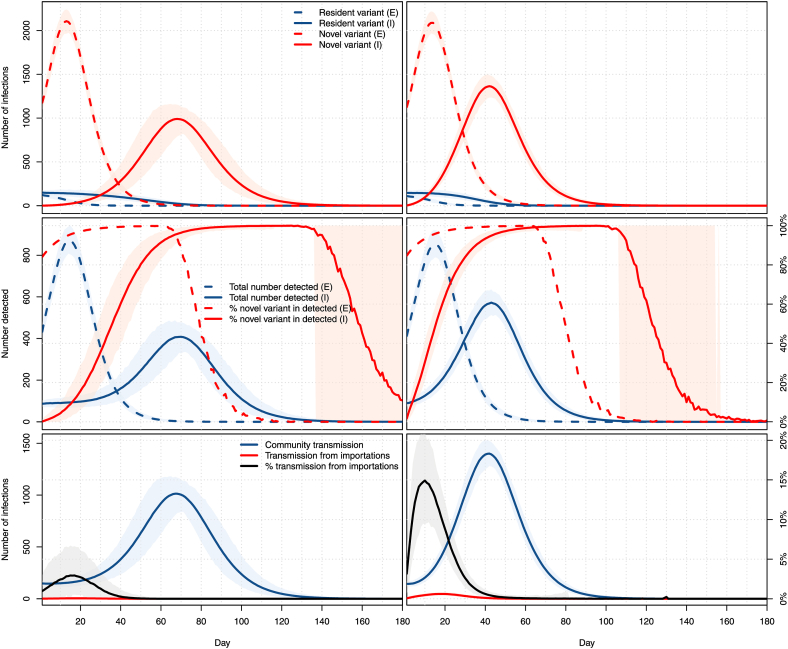
In Fig. 14, we show results when the two locations have the same population of 1 million people and for per capita movement rates from the exporter to the importer corresponding to 500 and 5000 passengers per day. A 21-days burn-in period is used prior to the dates shown, in which it is assumed that the resident variant is propagating in both the exporter and the importer with , while the novel variant is propagating only in the exporter with , starting the burn-in period there with a prevalence equal to that of the resident variant. To illustrate the effect of the duration of stages on the duration of the epidemic, we use here longer stages, with a latent period of 5 days and an infectious period of 10 days, on average.
Fig. 14.
Top: number of infections with the resident (blue) and novel (red) variants in the exporter (dashed) and importer (plain). Middle: total number of detected cases (blue) and percentage of these detected cases that are with the novel variant (red) in the exporter (dashed) and importer (plain). Bottom: Number of infections in the importer patch resulting from contacts with individuals infected in the community (blue) or in the exporter patch (red). Both locations have a population of 100,000. Left column: travel of a maximum of 50 passengers per day; right column: travel of a maximum of 500 passengers per day. All panels: means of 1000 simulations and ranges of 95% of these simulations.
The inflow numbers used represent 0.05% of the population per day for the low inflow case and 0.5% of the population per day for the high inflow case. To get a sense of the validity of such numbers, let us compare this with international entries into Canada, for which data is available (Statistics Canada. Table, 2531). In 2019, there were a total number of 96,810,028 people-entries into Canada, i.e., roughly 0.7% of its population per day. From April 2020 to February 2021 inclusive (the latest data available at the time of writing), the number of international people-entries dropped to 10,105,865, roughly 0.08% of the population per day. Thus the situation shown in Fig. 14 is roughly consistent with unabated (right column) and abated (left column) movement rates.
The first row in Fig. 14 shows the dynamics of infection of the two variants in the two locations. At low per capita importation rates, the peak of infections, due entirely to the novel variant, is delayed by 55 days in the importer. This delay falls to 28 days for regular per capita importation rates.
This delay is also observed when considering detections, which are shown in the second row of Fig. 14. Note one interesting difference in these compared to Fig. 7: even in the case of low importation rates, the percentage of detections of the new variant rises more quickly than it did there. In practice, though, the build-up of transmissions of the novel variant is more progressive. Indeed, recall that in Fig. 14, we have assumed that the variant was completely absent from the importer while it was already spreading at high levels in the exporter, to the point that it already accounts for over 80% of the detected cases in the exporter at time t = 0.
Consequently, the influence of imported cases on the dynamics is also more important, as can be seen from the third row in Fig. 14. In the case of pandemic-era mobility rates, the mean percentage of transmissions in the importer resulting from contacts with someone infected in the exporter (i.e., an individual in the importation layer of the importer) reaches a peak mean of about 2.9% at 17 days. When mobility is similar to what it was in the pre-pandemic era, this peak reaches 14.9% sooner, after 10 days. Note that as mobility rates increase, the relative locations of the peak mean incidence in the exporter (top row in the figure) and the peak mean percentage of transmissions from importations change. For low mobility, the peak in the exporter precedes its direct effect in the importer, while the situation is reversed for higher mobility rates.
5. Discussion
We present three increasingly complex models for the importation and spread of two variants of COVID-19, which we specialise to the context of spread of a novel variant in a population already experiencing spread of another variant. These models are, at present, not tailored explicitly to data, but in view of existing data on the spread of variants, we are satisfied they do a reasonable job already without fitting and will later seek to use them in real life situations. Note, however, that this will require high quality data on the spread of variants, in particular in terms of times of initial importation in the different jurisdictions.
The first model (Section 2 and Appendix A) is used mainly to evaluate the baseline responses of the paradigm used in the three models to describe the spread of two variants in a population. From this simplest model, we draw two main conclusions, illustrated respectively by Fig. 3, Fig. 4. The first is that it takes quite a while before a novel variant is becomes established to the point that it is detected frequently compared to the resident variant. Since actual identification of the novel variant involves further tests (sequencing, etc.), this means that it is likely that a novel variant is well established before it is effectively detected. Fig. 4 points to one of the issues arising in travel control measures: the likelihood that a novel variant successfully establishes itself in a population is highly dependent on the size of the initial number of individuals bearing this variant introduced in the population. While we do not consider the problem of importation size in our investigation of later models, this is indicative of the importance of ensuring that travel is safe. Indeed, consider the case where a location would receive a single transport conveyance before it completely shut down travel. In the conditions of Fig. 4, if this conveyance contained a single infected individual, then the probability of a successful importation would be about 1/3. On the other hand, if, while aboard the conveyance, transmission took place and the location received 4 infected individuals, then the importation would be successful in over 80% of the cases.
The second model (Section 3 and Appendix B) focuses on the role of importations. Fig. 6 shows the potential strong effect of importations. Other aspects we consider with the second model are the role of quarantine and of complete travel interruptions. Quarantine is found to be a very efficacious way to limit the effects of variant importation; see Fig. 9. This is due to the fact that we use reasonably high detection rates and quarantine lengths longer than the mean generation interval. We have not considered here shorter quarantines, with for instance tq = 3 days as has been considered in some countries. These, being shorter than the mean generation interval, would require higher testing levels in order to achieve the same efficacy (the efficacy of a three-day quarantine, with the parameters used here, drops to 85% from the 98% of a seven-day quarantine). Total interruption of travel, on the other hand, is found to be effective only when it is used in the very early stages of propagation of the variant, i.e, within at most 10 days of the start of potential importations; see Fig. 10, Fig. 11. Thus, the window of opportunity during which a complete interruption of travel would allow a jurisdiction to successfully forbid entry of a more transmissible variant is very narrow. As initial detection of a novel variant may take several weeks or even months in countries carrying out little sequencing of test results, while exportation may start very soon after emergence, it follows that in most cases, total travel interruption is not an efficacious method to fight variant introductions. Further to this, one should bear in mind that there is a high degree of network plasticity, for instance in the air transportation network: cutting an edge typically leads to a reconfiguration of itineraries between points rather than to a substantial attrition of volumes. Altogether, quarantine, a mitigation measure that controls inflow “passively” and can be left in place for extended time periods, outperforms travel bans while also being less stigmatising.
On the positive side, though, travel interruptions are often implemented in locations that are already enforcing quarantine and as such, are subject to lowered rates of importation. We have not investigated the compounding of both measures, but expect that this would indeed lower even further the risk of importation of a novel variant.
To better understand the dynamics of importations, we consider a third model (Section 4 and Appendix C), written as a simple metapopulation with an exporter and an importer patch connected by movement that is frequency-dependent rather than fixed as in the previous model. A limited preliminary numerical investigation of this complex model shows some interesting characteristics, summarised in Fig. 14. The first, seen on both the top and middle row in that figure, is the (entirely expected) existence of a lag between activity in the exporter patch and its “translation” into the importer patch. This lag is (still not unexpectedly) a decreasing function of movement rates. The curve of the percentage of infections resulting from importations in the lower row of Fig. 14 is less obvious to interpret. For mobility rates of the order experienced these days (left column), it remains relatively low, representing no more than one infection out of 20 in the left column. Also, it culminates at the same time as infection peaks in the exporter patch. For higher movement rates consistent with pre-pandemic travel (right column), importations at times contribute to about 15% of infections, this time with a marked advance on the peak of infection in the exporter patch.
The number of parameters is lower than the apparent complexity of the models implies, but these remain nonetheless systems whose behaviours warrant more investigation than what was performed here. In future work, we will seek to use this framework in conjunction with the vast amount of data (of varying quality) available regarding the spread of COVID-19. In particular, rather than taking travel restrictions decisions based on timing, it would be of interest to let them depend on the state of the system, for instance that of the exporter in the exporter-importer model. We expect that success in this setting would depend to a large extent on the detectability of both types of variants, which we have not explored here.
To conclude, during crises of all types, governments the world over have often resorted to a repli sur soi: the peril comes from the rest of the world, not from what is done to address the crisis of the day within one's borders. As noted by (Chetail, 2020), “a powerful expression of state's sovereignty, immigration control provides a typical avenue for governments to reassure their citizens and bolster a national sense of belonging, while providing an ideal scapegoat for their own failure or negligence.” As a consequence, when faced with public health emergencies, travel and border control measures like those discussed here but also of other types (e.g., screening) have been used time and time again. In terms of disease importations, it is indeed true that danger originally does come from the rest of the world. However, as can be seen here, a given jurisdiction's status can very quickly change from being free of infection with a variant to experiencing local transmissions in a context where importations represent but a fraction of the origin of transmission chains.
Acknowledgements
JA and SP are supported in part by NSERC Discovery Grants and through the Emerging Infectious Disease Modelling consortium. JA is supported in part by CIHR through the Fields Institute Mathematical Modelling of COVID-19 Task Force and acknowledges past support both financial and logistical from the Public Health Agency of Canada. PYB acknowledges support form ISCD (Institut des Sciences du Calcul et de la Donnée) and the EU grant MOOD (H2020-874850).
Handling Editor: Dr. J Wu
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Appendix A. The base ODE model for two variants
Appendix A.1 Model equations
The ODE model takes the following form. First, the equation for the evolution of S is given by
| (A.1a) |
Then, for variant X ∈{O, N},
| (A.1b) |
| (A.1c) |
| (A.1d) |
| (A.1e) |
| (A.1f) |
| (A.1g) |
| (A.1h) |
| (A.1i) |
| (A.1j) |
with force of infection
| (A.2) |
where ηX and ξX are the attenuation factors for transmission by incubating and detected cases. Note that the coupling between the resident and new variants dynamics only occurs in the equation for S, depicting an implicit competition between the two variants through their infectiousness. This ODE model, as well as the ones following, is considered with nonnegative initial conditions such that at least one of the infected state variables is positive in order to avoid trivial solutions.
Appendix A.2 Reproduction number for a single variant
We use the method of (Arino et al., 2007). Let us consider variant X ∈{O, N} in isolation, i.e., in the absence of the other variant. First, we identify the infected variables as
and consider them in that order. Then, using the notation in (Arino et al., 2007), D = 1 since with m = 1. The matrix ΠX is a vector, ΠX = (1,0,0,0,0,0)T, since all new infections move to the compartment. The row vector bX describes relative horizontal transmissions and takes the form bX = (0, ηX, ξX, ξX, 1, 1). The function denoted β(x, y, z) in (Arino et al., 2007) is the constant βX here. Finally, the matrix VX describing transitions between and out of infected states for variant X takes the form
| (A.3) |
and therefore has inverse
| (A.4) |
From (Arino et al., 2007), the basic reproduction number for variant X ∈{O, N} is
where S(0) is the susceptible population at the initial time. Thus, the basic reproduction number for variant X ∈{O, N} in the absence of another variant takes the form given by (1).
Appendix A.3 Final size for the single variant model
With the notation and considerations in Appendix A.2, we can also use (Arino et al., 2007) to derive a final size relation for the single variant cases, finding a result similar to that found in (Arino & Portet, 2020).
Appendix A.4 Reproduction number for the two-variant model
The method in (Arino et al., 2007) cannot be applied to the two variant case because the multigroup nature of the problem leads to a vector incidence function rather than a scalar one. As a consequence, in order to compute the reproduction number for the two-variant system, we use the method of (van den Driessche & Watmough, 2002), which is easily applied from the considerations in Appendix A.2. With infected variables listed and notation as in Appendix A.2, the matrix F used in (van den Driessche & Watmough, 2002) takes the form
where, for X ∈{O, N}, FX has first row given by βXbXS(0) and all other rows zero. For X ∈{O, N}, VX takes the same form as VX in Appendix A.2. It follows that
Note that this is as far as the application of (van den Driessche & Watmough, 2002) can proceed; in particular, it is not possible to apply their Theorem 2 to this epidemic (as compared to endemic) situation. Indeed, there is no situation in the present model where the DFE is unstable; also, the DFE is always locally stable but never locally asymptotically stable.
Intuitively, the issue of final sizes is harder in this setting, as the following thought experiment confirms. Suppose that the two variants each have a value of such that the final size for that variant in isolation is larger than S(0)/2. Clearly, the final size for the entire system is not larger than S(0), so final sizes are not additive. However, they cannot operate as the max either, as does, since one can expect to see more cases than the maximum implied by either of the final sizes. Refer to, e.g. (Andreasen, 2011; Lunelli & Pugliese, 2018; Magal et al., 2018), for more considerations and some results concerning final sizes in multi-group models.
Appendix B. The ODE importer-only model
Appendix B.1 Model equations
The ODE model takes the form
| (B.1a) |
and, for variant X ∈{O, N}, assuming no importation of detected cases, dynamics in the importation layer are governed by
| (B.1b) |
| (B.1c) |
| (B.1d) |
| (B.1e) |
| (B.1f) |
| (B.1g) |
| (B.1h) |
| (B.1i) |
| (B.1j) |
while dynamics in the community are governed by
| (B.1k) |
| (B.1l) |
| (B.1m) |
| (B.1n) |
| (B.1o) |
| (B.1p) |
| (B.1q) |
| (B.1r) |
| (B.1s) |
The force of infection takes the form
| (B.2) |
where, for X ∈{O, N} and Z ∈{I, C},
Because of the term λX in equations (B.1b), (B.1c), (B.1f) and (B.1g), there is no disease-free equilibrium in the importation layer and as a consequence, it is impossible to compute a reproduction number there, nor for the whole importer-only system.
A reproduction number can however be computed in the community in the absence of connection with the importation layer, giving the same expression as in Appendix A.2. We also use this reproduction number to approximate the value of βX in the importation layer in the absence of importation. Indeed, as disease propagation parameters are the same, for variant X ∈{O, N}, in the importation layer and in the community and that contacts from individuals in the importation layer are with susceptible individuals in the community, the S(0) used in the computation of in Appendix A.2 is that of the community. This is the reason why, in (B.2), we use the same βX for both the importation layer and the community.
Appendix B.2 Quarantine efficacy
To compute quarantine efficacy, we proceed as in (Arino et al., 2020). Suppose an individual arrives in the importation layer while in one of the unobserved infected states for variant X ∈{O, N},
| (B.3) |
The individual remains in quarantine for tq time units, during which time they have no contact with anyone else (βX = 0) and progress through disease stages following the model in the importation layer. If, at the end of the quarantine period, when they start making contacts in the community, they are still in a compartment in , then quarantine has failed since they can still infect individuals in the community. Quarantine efficacy is thus the complement of the probability that an imported case in is still, after spending tq time units in quarantine, in one of the states in .
Consider the matrix of transition rates between stages of infection, where the last three columns of all zeros are omitted:
| −ϵX1 | 0 | 0 | 0 | 0 | 0 | |
| ϵX1 | −ϵX2 | 0 | 0 | 0 | 0 | |
| 0 | − γX | 0 | 0 | 0 | ||
| 0 | 0 | γX | − γX | 0 | 0 | |
| 0 | 0 | 0 | − γX | 0 | ||
| 0 | 0 | 0 | 0 | γX | − γX | |
| 0 | 0 | 0 | (1 − δX)γX | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | γX | |
| 0 | 0 | 0 | δXγX | 0 | 0 |
Let TX = [tij] be the matrix whose entries are given in this table (including the three columns of zeros not shown), with tij the rate at which individuals in compartment j transition to compartment i. Denote the distribution of probabilities of belonging to compartment i = 1, …, n at time t, with and compartments indexed as in the columns of TX. Then satisfies the differential equation
whose solutions are, using the matrix exponential ,
Specifically, entries of are the probabilities an individual is in the corresponding row-stage at time t conditional on having started in the corresponding column-stage at time 0.
If infected individuals with states distributed according to are placed in quarantine for tq time units starting at time t = 0, then the states at time tq have distribution
| (B.4) |
Further, the probability that individuals are in one of the compartments in at time t ≥ 0 is given by
where u = (1, 1, 0, 0, 1, 1, 0, 0, 0) is the characteristic vector for undetected infections.
If, after tq days, the individual is still in an unobservable state , then quarantine has failed. Otherwise, quarantine is a success. (Recall that, in the model, D and M individuals have been detected by authorities, explaining why , and individuals are considered a success of quarantine.) We therefore define the efficacy cX of quarantine for variant X ∈{O, N} as the probability
| (B.5) |
that the imported case is either in an observable state (, , or ) or in the unobserved but recovered state . Remark that cX depends on model parameters through TX but also on the distribution . Typically, it is assumed that , i.e., importation of all four unobservable states is equally likely.
Finally, one easily verifies (see (Arino et al., 2020) for details) that the quarantine-regulated importation rate is expressed as
| (B.6) |
Appendix C. The ODE exporter-importer model
Appendix C.1 Model equations
In the exporter, the ODE model takes the following form. First, the dynamics of SE follows
| (C.1a) |
Then, for variant X ∈{O, N} and assuming no exportation of detected cases, the dynamics are governed by
| (C.1b) |
| (C.1c) |
| (C.1d) |
| (C.1e) |
| (C.1f) |
| (C.1g) |
| (C.1h) |
| (C.1i) |
where the force of infection takes the form
| (C.2) |
In the importer,
| (C.3a) |
and, for variant X ∈{O, N} and assuming no importation of detected cases, dynamics in the importation layer are governed by
| (C.3b) |
| (C.3c) |
| (C.3d) |
| (C.3e) |
| (C.3f) |
| (C.3g) |
| (C.3h) |
| (C.3i) |
| (C.3j) |
while dynamics in the community are governed by
| (C.3k) |
| (C.3l) |
| (C.3m) |
| (C.3n) |
| (C.3o) |
| (C.3p) |
| (C.3q) |
| (C.3r) |
| (C.3s) |
with force of infection
| (C.4) |
where, for X ∈{O, N} and Z ∈{I, C},
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Alene M., Yismaw L., Assemie M.A., Ketema D.B., Gietaneh W., Birhan T.Y. Serial interval and incubation period of COVID-19: A systematic review and meta-analysis. BMC Infectious Diseases. 2021;21(1):1–9. doi: 10.1186/s12879-021-05950-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almarashi R.M., McCluskey C.C. The effect of immigration of infectives on disease-free equilibria. Journal of Mathematical Biology. 2019;79(3):1015–1028. doi: 10.1007/s00285-019-01387-8. [DOI] [PubMed] [Google Scholar]
- Andreasen V. The final size of an epidemic and its relation to the basic reproduction number. Bulletin of Mathematical Biology. 2011;73(10):2305–2321. doi: 10.1007/s11538-010-9623-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arino J. Spatio-temporal spread of infectious pathogens of humans. Infectious Disease Modelling. May 2017;2(2):218–228. doi: 10.1016/j.idm.2017.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arino J., Bajeux N., Portet S., Watmough J. Quarantine and the risk of COVID-19 importation. Epidemiology and Infection. 2020;148:e298. doi: 10.1017/S0950268820002988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arino J., Brauer F., van den Driessche P., Watmough J., Wu J. Simple models for containment of a pandemic. Journal of The Royal Society Interface. June 2006;3(8):453–457. doi: 10.1098/rsif.2006.0112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arino J., Brauer F., van den Driessche P., Watmough J., Wu J. A final size relation for epidemic models. Mathematical Biosciences and Engineering. 2007;4(2):159–175. doi: 10.3934/mbe.2007.4.159. [DOI] [PubMed] [Google Scholar]
- Arino J., Portet S. Epidemiological implications of mobility between a large urban centre and smaller satellite cities. Journal of Mathematical Biology. 2015;71(5):1243–1265. doi: 10.1007/s00285-014-0854-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arino J., Portet S. A simple model for COVID-19. Infectious Disease Modelling. 2020;5:309–315. doi: 10.1016/j.idm.2020.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum T., Hai N.T.T. International Journal of Contemporary Hospitality Management; 2020. Hospitality, tourism, human rights and the impact of COVID-19. [Google Scholar]
- Becker N. Estimation for an epidemic model. Biometrics. 1976;32(4):769–777. [PubMed] [Google Scholar]
- Burns J., Movsisyan A., Stratil J.M., Biallas R.L., Coenen M., Emmert-Fees K.M., Geffert K., Hoffmann S., Horstick O., Laxy M., Klinger C., Kratzer S., Litwin T., Norris S., Pfadenhauer L.M., Philipsborn P.von, Sell K., Stadelmaier J., Verboom B.…Rehfuess E. International travel-related control measures to contain the COVID-19 pandemic: A rapid review. Cochrane Database of Systematic Reviews. 2021;3 doi: 10.1002/14651858.CD013717.pub2. CD013717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang S.-S., Stuckler D., Yip P., Gunnell D. Impact of 2008 global economic crisis on suicide: Time trend study in 54 countries. BMJ. 2013;347 doi: 10.1136/bmj.f5239. f5239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chetail V. Crisis without borders: What does international law say about border closure in the context of Covid-19? Frontiers in Political Science. 2020;2(12) [Google Scholar]
- C. d’État. Décisions 449743-449830. https://www.conseil-etat.fr/Media/actualites/documents/2021/03-mars/449743-449830.pdf. Accessed: 2021-04-27.
- Costantino V., Heslop D.J., Raina MacIntyre C. The effectiveness of full and partial travel bans against COVID-19 spread in Australia for travellers from China during and after the epidemic peak in China. Journal of Travel Medicine. 2020;27(5) doi: 10.1093/jtm/taaa081. taaa081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hone T., Mirelman A.J., Rasella D., Paes-Sousa R., Barreto M.L., Rocha R., Millett C. Effect of economic recession and impact of health and social protection expenditures on adult mortality: A longitudinal analysis of 5565 Brazilian municipalities. The Lancet Global Health. 2019;7:e1575–e1583. doi: 10.1016/S2214-109X(19)30409-7. [DOI] [PubMed] [Google Scholar]
- Hussein M., Toraih E., Elshazli R., Fawzy M., Houghton A., Tatum D., Killackey M., Kandil E., Duchesne J. Meta-analysis on serial intervals and reproductive rates for SARS-CoV-2. Annals of Surgery. 2021;273(3):416–423. doi: 10.1097/SLA.0000000000004400. [DOI] [PubMed] [Google Scholar]
- Kwok K.O., Wong V.W.Y., Wei W.I., Wong S.Y.S., Tang J.W.-T. Epidemiological characteristics of the first 53 laboratory-confirmed cases of COVID-19 epidemic in Hong Kong. Euro Surveillance. April 2020;25 doi: 10.2807/1560-7917.ES.2020.25.16.2000155. 13 February 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunelli A., Pugliese A. Final attack ratio in SIR epidemic models for multigroup populations. Ricerche di Matematica. 2018;67(1):49–68. [Google Scholar]
- Magal P., Seydi O., Webb G. Final size of a multi-group SIR epidemic model: Irreducible and non-irreducible modes of transmission. Mathematical Biosciences. 2018;301:59–67. doi: 10.1016/j.mbs.2018.03.020. [DOI] [PubMed] [Google Scholar]
- Magendzo A., Osler A. The covid-19 pandemic: A challenge and an opportunity for human rights educators. Human Rights Education Review. 2020;3(2):68–82. [Google Scholar]
- Maruthappu M., Watkins J., Noor A.M., Williams C., Ali R., Sullivan R., Zeltner T., Atun R. Economic downturns, universal health coverage, and cancer mortality in high-income and middle-income countries, 1990-2010: A longitudinal analysis. The Lancet. 2016;388:684–695. doi: 10.1016/S0140-6736(16)00577-8. [DOI] [PubMed] [Google Scholar]
- Milliken E. The probability of extinction of infectious salmon anemia virus in one and two patches. Bulletin of Mathematical Biology. 2017;79(12):2887–2904. doi: 10.1007/s11538-017-0355-5. [DOI] [PubMed] [Google Scholar]
- Otto S.P., Day T., Arino J., Colijn C., Dushoff J., Li M., Ogden N.H. The origins and potential future of SARS-CoV-2 variants of concern in the evolving COVID-19 pandemic. Current Biology. 2021 doi: 10.1016/j.cub.2021.06.049. (To appear) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prete C.A., Jr., Buss L., Dighe A., Porto V.B., Candido D.da S., Ghilardi F., Pybus O.G., de Oliveira W.K., Croda J.H.R., Sabino E.C., Faria N.R., Donnelly C.A., Nascimento V.H. Serial interval distribution of SARS-CoV-2 infection in Brazil. Journal of Travel Medicine. 2020;28(2) doi: 10.1093/jtm/taaa115. 7. taaa115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell T.W., Wu J.T., Clifford S., Edmunds W.J., Adam J.K., Jit M. Effect of internationally imported cases on internal spread of COVID-19: A mathematical modelling study. The Lancet Public Health. 2021;6(1) doi: 10.1016/S2468-2667(20)30263-2. e12–e20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saliba A.T., do Valle F.M.V. Stranded at the border: An analysis of the legality of international travel restrictions adopted by states in the COVID-19 pandemic in light of the right to return to one's country. Wis. Int’l LJ. 2020;38(39) [Google Scholar]
- Salje H., Tran Kiem C., Lefrancq N., Courtejoie N., Bosetti P., Paireau J., Andronico A., Hozé N., Richet J., Dubost C.-L. Estimating the burden of SARS-CoV-2 in France. Science. 2020;369(6500):208–211. doi: 10.1126/science.abc3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Statistics Canada. Table 24-10-0041-01 International travellers entering or returning to Canada, by type of transport. 10.25318/2410004101-eng. Accessed: 2021-04-30. [DOI]
- Svensson Å. A note on generation times in epidemic models. Mathematical Biosciences. 2007;208(1):300–311. doi: 10.1016/j.mbs.2006.10.010. [DOI] [PubMed] [Google Scholar]
- Tritch W., Allen L.J.S. Duration of a minor epidemic. Infectious Disease Modelling. 2018;3:60–73. doi: 10.1016/j.idm.2018.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- US Centers for Disease Control and Prevention SARS-CoV-2 variant classifications and definitions. https://www.cdc.gov/coronavirus/2019-ncov/cases-updates/variant-surveillance/variant-info.html Accessed: 2021-05-10.
- van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- Whittle P. The outcome of a stochastic epidemic – a note on Bailey's paper. Biometrika. 1955;42(1–2):116–122. 6. [Google Scholar]
- Zaki N., Mohamed E.A. The estimations of the COVID-19 incubation period: A scoping reviews of the literature. Journal of Infection and Public Health. 2021;14(5):638–646. doi: 10.1016/j.jiph.2021.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]