Abstract
Because of the rapid spread and wide range of the clinical manifestations of the coronavirus disease 2019 (COVID-19), fast and accurate estimation of the disease progression and mortality is vital for the management of the patients. Currently available image-based prognostic predictors for patients with COVID-19 are largely limited to semi-automated schemes with manually designed features and supervised learning, and the survival analysis is largely limited to logistic regression. We developed a weakly unsupervised conditional generative adversarial network, called pix2surv, which can be trained to estimate the time-to-event information for survival analysis directly from the chest computed tomography (CT) images of a patient. We show that the performance of pix2surv based on CT images significantly outperforms those of existing laboratory tests and image-based visual and quantitative predictors in estimating the disease progression and mortality of COVID-19 patients. Thus, pix2surv is a promising approach for performing image-based prognostic predictions.
Keywords: Unsupervised deep learning, Survival analysis, COVID-19, Computed tomography
Graphical abstract
1. Introduction
The rapid global spread of the coronavirus disease 2019 (COVID-19) has placed major pressures on healthcare services worldwide. During the year of 2020, over 70 million COVID-19 infections and over 1.6 million deaths due to COVID-19 were reported worldwide (WHO, 2020). Because of the wide range of the clinical manifestations of COVID-19, fast and accurate estimation of the disease progression and mortality is vital for the management of patients with COVID-19.
Chest computed tomography (CT) is the most sensitive chest imaging method for COVID-19 (Harmon et al., 2020; Mei et al., 2020). Recently, several computer-assisted image-based predictors have been reported for prognostic prediction of COVID-19 patients based on chest CT images. The basic idea of these predictors has been to extract various features from CT images, and to subject these features to a classifier (logistic regression) or a survival prediction model. Most studies have used a small number of well-understood manually defined size, shape, or texture features that are extracted from regions of interest, such as those of segmented ground-class opacities, semi-consolidation, and consolidation (Colombi et al., 2020; Huang et al., 2020; Lanza et al., 2020; Liu et al., 2020; Matos et al., 2020; Wang et al., 2020; Yu et al., 2020; Zhang et al., 2020). Other studies performed a radiomic analysis by extraction of a large number of radiomic features from a segmented complete lung region, followed by feature selection to determine a manageable set of key features (Homayounieh et al., 2020; Wu et al., 2020). After the calculation of the prognostic features, the prognostic prediction has usually been performed by use of logistic regression, which limits the analysis to a binary prediction of the disease severity or survival at a specific time point (Colombi et al., 2020; Homayounieh et al., 2020; Lanza et al., 2020; M. D. Li et al., 2020; Li et al., 2020; Matos et al., 2020; Xiao et al., 2020). Instead of logistic regression, some methods performed a traditional survival analysis by subjecting the features to a Cox regression analysis for the calculation of the time-to-event information which is needed to perform a complete survival analysis for clinical tasks (Francone et al., 2020; Wu et al., 2020; Zhang et al., 2020).
These previous studies had several limitations. Semi-automated quantification of CT images requires manual guidance and suffers from inter- and intra-observer variability. Extraction of features from segmented regions of interest is vulnerable to segmentation errors, it can exclude important information from non-segmented lung regions, and manually or mathematically defined features may not be ideal for the construction of optimal prognostic predictors. Furthermore, few studies have made use of traditional survival analysis, which enables the calculation of the survival probability at any time point for performing important clinical tasks, such as the calculation of survival curves. Finally, the role of deep learning in these methods has been limited to a segmentation of CT images, and such deep learning models were trained with a supervised learning approach that requires the availability of an annotated training dataset. Therefore, there is an unmet need for an objective survival analysis system that would automatically extract, select, and combine image-based features for the calculation of complete time-to-event information for optimally predicting the prognosis of patients with COVID-19, without the laborious and expensive annotation effort that is required by supervised learning schemes.
Recently, an adversarial time-to-event model based on a conditional generative adversarial network (GAN) has been shown to be able to generate predictions for the survival analysis of epidemiologic data at a higher accuracy than those of traditional survival methods (Chapfuwa et al., 2018). The model focused on the estimation of time-to-event distribution rather than event ordering, and it also accounted for missing values, high-dimensional data, and censored events. Such an approach has the advantage that the distribution of the survival time can be estimated directly from the input predictor. However, to the best of our knowledge, no conditional GAN-based methods have been proposed for estimating the survival time directly from images.
In this study, we developed a weakly unsupervised conditional GAN, called pix2surv, which enables the estimation of the distribution of the survival time directly from the chest CT images of patients. The model avoids the technical limitations of the previous image-based COVID-19 predictors discussed above, because the use of a fully automated conditional GAN makes it possible to train a complete image-based end-to-end survival analysis model for producing the time-to-event distribution directly from input chest CT images without an explicit segmentation or feature extraction efforts. Also, because of the use of weakly unsupervised learning, the annotation effort is reduced to the pairing of input training CT images with the corresponding observed survival time of the patient.
We show that the prognostic performance of pix2surv based on CT images compares favorably with those of existing laboratory test results computed by the traditional Cox proportional hazard model (Cox, 1972) and those of image-based visual and quantitative predictors in estimating the disease progression and mortality of patients with COVID-19. We also show that the time-to-event information calculated by pix2surv based on CT images enables stratification of the patients into low- and high-risk groups with a wider separation than do those of the other predictors. Thus, pix2surv is a promising approach for performing image-based prognostic prediction for the management of patients.
2. Background
The intent of a time-to-event model is to perform a statistical characterization of the future behavior of a subject in terms of a risk score or time-to-event distribution. A time-to-event dataset can be formulated as , where are the predictors, is a time-to-event of interest, is a binary censoring indicator, and N is the size of the dataset. A value of indicates that the event is observed, whereas a value of indicates censoring at .
Let T denote a continuous random variable (or survival time) with a cumulative distribution function F(t). The survivor function of T is defined as the fraction of the population that survives longer than some time t, as (Kleinbaum and Klein, 2012)
| (1) |
where h(It) is a hazard function that describes the rate of the occurrence of an event over time. Given a set of predictors, x, the relationship between the corresponding conditional hazard and conditional survival functions can be expressed as
| (2) |
where is the conditional survival density function. Time-to-event models typically characterize the relationship between the predictors x and a time-to-event t by estimation of the conditional hazard function of Eq. (2) by use of the relationships of
| (3) |
and
| (4) |
where is the cumulative conditional hazard function.
Cox proportional hazard model (Cox, 1972) is a popular time-to-event model, which is based on the assumption that the effect of the predictors is a fixed, time-independent, multiplicative factor on the value of the hazard function (or hazard rate). The estimation depends on event ordering rather than on the time-to-event itself, which is undesirable in applications where the prediction is of the highest importance. The accelerated failure time (AFT) model (Wei, 1992) is another time-to-event model, which is based on the assumption that the effect of the predictors either accelerates or delays the event progression relative to a parametric baseline time-to-event distribution. The parametric time-to-event distribution is represented by use of a limited parametric form, such as exponential distribution, which is often violated in practice due to the inability of the model to capture unobserved variation.
A deep adversarial time-to-event (DATE) model is yet another type of time-to-event model, which makes use of a conditional GAN to estimate the time-to-event distribution, , where t is a non-censored time-to-event from the time at which the predictors x were observed (Chapfuwa et al., 2021, 2018). This makes it possible to implicitly specify the time-to-event distribution via sampling, rather than by learning the parameters of a pre-specified distribution. Also, the use of a GAN penalizes unrealistic samples, which is a known issue in likelihood-based models (Karras et al., 2018). For censored events, the likelihood of should be high, whereas for non-censored events, the pairs should be consistent with the data generated by , where is the (empirical) marginal distribution for the predictors from which we can sample but whose explicit form is unknown.
The generator function of the conditional GAN of the DATE model can be modeled as
| (5) |
where is a simple distribution such as uniform distribution, and denotes the parameters of the generator. The generator defines an implicit non-parametric approximation of the non-censored samples of . Ideally, the pairs generated by Eq. (5) should be indistinguishable from the observed data .
Given a discriminator function with a parameter set , the cost function of the conditional GAN for non-censored data can be expressed as
| (6) |
where is the empirical joint distribution for the non-censored subset . The expectation terms are estimated through the samples and only.
To leverage the censored subset for updating the parameters of the generator, a second cost function is introduced as
| (7) |
where the role of is to incur no loss from as long as the sampled time is larger than the censoring point.
For cases where the proportion of the observed events is low, the cost functions of Eqs. (6) and (7) do not account for mismatches between the time-to-events and the ground truth, t. To penalize for not being close to the event time t for non-censored events, a third cost function, or distortion loss, is introduced as
| (8) |
where
The conditional GAN of the DATE model is trained by optimizing the combination of the cost functions of Eqs. (6)–(8), , by maximizing it with respect to and . It has been demonstrated that the use of the DATE model yields a significant performance gain in the survival analysis of epidemiologic data over those of traditional methods (Chapfuwa et al., 2018), such as the Cox-Efron (Efron, 1974), the random survival forest (Ishwaran et al., 2008), or a deep regularized AFT model (Chapfuwa et al., 2018).
In Section 3, we describe how we generalized the concepts of the DATE model to convolutional neural networks for performing prognostic prediction for COVID-19 based on the CT images of patients in this study.
3. Methods and materials
3.1. pix2surv
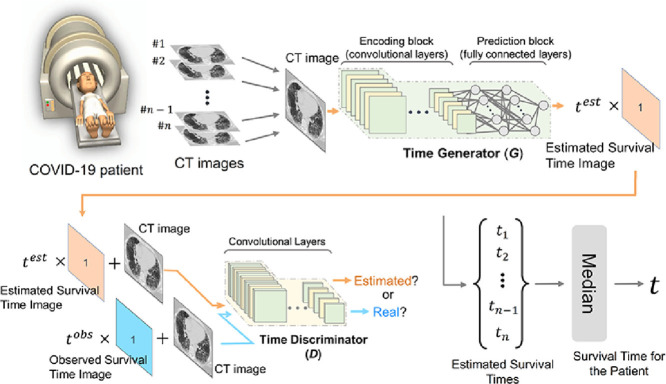
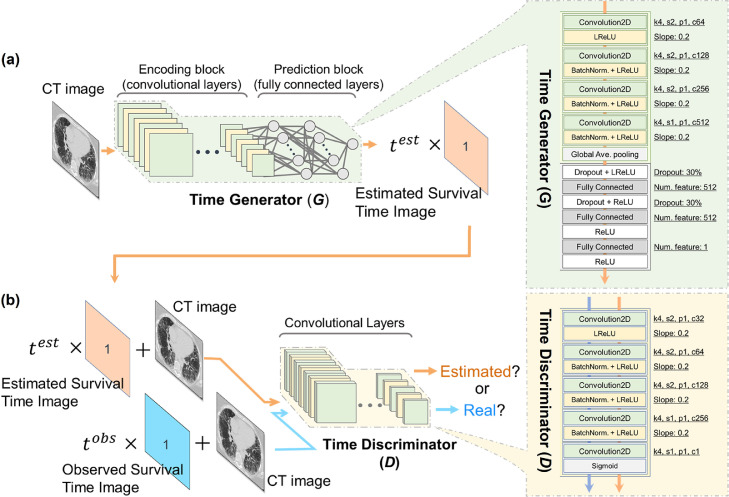
Fig. 1 shows a schematic structure of the pix2surv survival prediction model for CT images. The training of the model involves the optimization of a time generator (Fig. 1a) and a time discriminator (Fig. 1b). The time generator, G = Gθ, is used to convert an image into an estimated survival time by converting the feature maps of a fully convolutional encoder network into a scalar time value by use of a fully connected network. The details of the implementation of G are discussed in Section 3.3. During training, the estimated survival time, , is converted into an estimated survival time image (orange rectangle in Fig. 1a), which contains as a scalar value at each pixel and is provided as input to the time discriminator.
Fig. 1.
Schematic structure of pix2surv. (a) An overview of the time generator, including the construction of the estimated survival time image during training. (b) An overview of the time discriminator. The architectural details of the time generator and the discriminator networks are shown on the right margin.
The time discriminator, D = Dϕ, is trained to differentiate “real pairs” of an input image and the corresponding observed (true) survival time image (blue rectangle in Fig. 1b), which is based on the observed true survival time, , from “estimated pairs” of an input image and a corresponding estimated survival time image (orange rectangle in Fig. 1b) generated by G. The implementation details of D are described in Section 3.3.
The training of pix2surv involves the optimization of G and D based on the images of a training dataset. The cost function is a modified min-max objective function
| (9) |
which contains three distinct loss functions adapted from Eqs. (6)–(8). The first of these loss functions,
| (10) |
is the standard loss function of a conditional GAN (Isola et al., 2017; Mirza and Osindero, 2014), where denotes the empirical joint distribution of an input image x and a survival time image t, pz(z) denotes a Gaussian distribution, and z is a latent variable. The loss function of Eq. (10) encourages D to identify incorrect survival times (or survival time images) generated by G, whereas G is encouraged to generate survival times that have a low probability of being incorrect, according to D. The two other loss functions of Eq. (9),
| (11) |
and
| (12) |
further constrain G to generate survival times that are similar to the observed true survival times of censored and non-censored patient images, respectively. The trade-off between and relative to is controlled by the parameters and of Eq. (9).
3.2. Prognostic prediction for patients based on their CT images
In this study, the image-based prediction by pix2surv for estimating the survival time of a patient was performed based on an analysis of the 2D CT image slices of the patient. For this purpose, the pix2surv was first trained by use of the individual 2D CT images of patients, where the CT images were paired with the observed survival time of the corresponding patient.
After the training, the survival time of a patient was estimated by subjecting the CT images of a patient to the time generator (see Section 3.1), which yielded an estimated survival time for each CT image. The survival time of the patient was then calculated as the median of the estimated survival times of the CT images of the patient. We used the median value because, in our experiments, this yielded more accurate predictions than the use of other first-order statistics for estimating the image-based survival time.
3.3. Implementation of pix2surv
To reduce the computation time of the training step, we subsampled the input CT images from their original 512×512-pixel matrix size to a 256×256-pixel matrix size. Also, we constrained the number of CT images per patient to a maximum of 100, by a random selection of the CT images whenever the CT acquisition series of a patient contained more than 100 CT image slices. These two steps reduced the training time by 80% with essentially no change in the performance of the prognostic prediction (see Appendix A for an ablation study). Thus, these two steps substantially improved the throughput without compromising the prognostic performance.
The architectural details of G (the time generator) which we used in our experiments are shown on the right margin of Fig. 1a. There were four convolution layers and three fully connected layers. The architectural details of D (the time discriminator) are shown on the right margin of Fig. 1b. We implemented D as a patch-based fully convolutional neural network (PatchGAN), similar to that of the pix2pix GAN model (Isola et al., 2017; Li & Wand, 2016). There were five convolution layers. The PatchGAN is designed to penalize unrealistic structures at the scale of small image patches by averaging the outputs of the network convolutions across the input image into an aggregate output likelihood that is used to determine if the input image is considered as real or synthetic.
We implemented the pix2surv model by use of PyTorch 1.5 Paszke et al., 2019). The calculations were performed by use of Linux graphics processing unit (GPU) servers equipped with 48GB RTX 8000 GPUs (NVIDIA Corporation, Santa Clara, CA) and 10-core 3.7 GHz Core i9-10900X CPUs (Intel Corporation, Santa Clara, CA). No data augmentation was performed. The values of the free parameters of pix2surv were determined during training by use of grid search, where the time generator and time discriminator of pix2surv were trained by use of the Adam optimizer with and . The dropout ratio was set to 0.3, batch size was 64, the learning rate was 2.0×10-4, and the trade-off parameters of Eq. (9) of the censored and non-censored loss functions of Eqs. (11) and ((12) with respect to the standard loss of Eq. (10) were set to and .
3.4. Materials
This study was approved by our institutional review board (IRB). All procedures involving human participants were performed in accordance with the ethical standards of the IRB and with the 1964 Declaration of Helsinki and its later amendments. The informed consent of the patients was waived for this study.
We established a retrospective multi-center database of COVID-19 cases with the associated CT image acquisitions, where the cases were collected between March 1 and June 28, 2020, from the medical records of the Massachusetts General Hospital and the Brigham and Women's Hospital through the Research Patient Data Registry and the COVID-19 Data Mart at the Mass General Brigham (Boston, MA), and they were followed up until July 28, 2020. The medical records were reviewed by an expert pulmonologist to include patients who (1) were at least 18 years old, (2) had been diagnosed as COVID-19 positive based on a positive result for severe acute respiratory syndrome coronavirus 2 (SARS-COV-2) by reverse transcriptase-polymerase chain reaction (RT-PCR) with samples obtained from the nasopharynx, oropharynx, or lower respiratory tract, and (3) had a high-resolution chest CT examination available. The resulting cohort consisted of 302 patients. After excluding the patients whose CT examinations had been performed for diseases other than COVID-19, we established a database of 214 COVID-19 patients for this study. All these patients were included in the study regardless of the diagnostic quality of their CT images.
Table 1 summarizes the demographics, clinical characteristics, and CT acquisition parameters of the two types of patient cohorts used in this study. All 214 patients were considered for mortality analysis, whereas only 141 patients were considered for progression analysis because patients who had their CT examination after the intensive care unit (ICU) admission were excluded from the progression analysis.
Table 1.
The demographics, clinical characteristics, and CT parameters of the progression and mortality analysis patient cohorts. IQR = interquartile range.
| Progression cohort | Mortality cohort | |
|---|---|---|
| Available # of patients | 141 | 214 |
| Gender, # females : # males | 64 : 77 | 86 : 128 |
| Age (years), median [IQR Q1, Q3] | 69 [59, 80] | 67 [58, 78] |
| Survival time (days), median [IQR Q1, Q3] | 8 [2, 24] | 17 [8, 40] |
| # of events | 51 | 46 |
| CT image size, width x height | 512 x 512 | 512 x 512 |
| # of CT images, median [IQR Q1, Q3] | 385 [326, 463] | 374 [325, 436] |
| Slice thickness (mm) | 0.625 – 3.0 | 0.625 – 3.0 |
| Pitch | 0.3 – 3.0 | 0.3 – 3.0 |
| Tube voltage (kVp) | 80 - 140 | 80 - 140 |
The chest CT images of the patients were acquired by use of a single-phase low-dose acquisition with a multi-channel CT scanner (Canon/Toshiba Aquilion ONE, GE Discovery CT750 HD and Revolution CT/Frontier, Siemens SOMATOM Definition AS/AS+/Edge/Flash, SOMATOM Force, Biograph 64, and Sensation 64) that used auto tube-current modulation and the parameter settings shown in Table 1. The CT images were reconstructed by use of a neutral or medium sharp reconstruction kernel.
The 214 patients generated a total of 84,971 CT images for the study. As a pre-processing step, the intensity values of the CT images were clipped to a Hounsfield unit (HU) range of -1024 to 1024 HU and mapped linearly to the range of -1 to +1.
Because not all of the values of some of the reference predictors were available for all the patients, we evaluated the comparative performance of the predictors both in terms of the maximum number of patients that were available individually for each predictor, as well as in terms of specific subcohorts of patients, called “common cases”, where the values of all the reference predictors were available for all patients of the subcohort. In progression analysis, there were 105 such common cases, whereas, in mortality analysis, there were 171 common cases.
3.5. Reference predictors
We compared the prognostic performance of pix2surv with those of reference predictors that had been reported in the peer-reviewed literature for COVID-19 by the time our experiments were carried out. These reference predictors included (1) a combination of the laboratory tests of lactic dehydrogenase, lymphocyte, and high-sensitivity C-reactive protein (abbreviated as Lab) (Ji et al., 2020; Yan et al., 2020), (2) visual assessment of the CT images in terms of a total severity score (TSS) (K. Li et al., 2020; Lyu et al., 2020), (3) visual assessment of the CT images for the total severity score for crazy paving and consolidation (CPC) (Lyu et al., 2020), and (4) semi-automated assessment of the CT images in terms of the percentage of well-aerated lung parenchyma (%S-WAL) (Colombi et al., 2020).
The results of the laboratory tests (Lab) were collected from the patient records. The TSS (value range: 0-20) was estimated by an internist with over 20-year experience (C.W.) based on the descriptions of previously published studies (Bernheim et al., 2020; Lyu et al., 2020), as a sum of the visually assessed degree of acute lung involvement at each of the five lung lobes on the chest CT images. The CPC was assessed as the sum extent of crazy paving and consolidation in terms of the TSS criteria, where the sum involvement of the five lung lobes was taken as the total lung score (value range: 0-20) (Lyu et al., 2020). The %S-WAL was calculated by use of previously published image processing software (Kawata et al., 2005), based on the descriptions of a previously published study (Colombi et al., 2020), as the relative volume of the well-aerated 3D lung region determined by the density interval of -950 HU and -700 HU with respect to the volumetric size of the complete segmented 3D lung region on the chest CT images.
The predictions by Lab were calculated by use of the elastic-net Cox proportional hazard model (Simon et al., 2011). To calculate the time-to-event distributions provided by the image-based reference predictors, each predictor was subjected to the conditional GAN of the pix2surv model of Section 3.1 except that, for each predictor, there was only one input image per patient, where the input image was constructed by storing the feature value of the predictor in the channel dimension for each pixel. The other computations were performed as described in Section 3.1. Previously, we have demonstrated that, when the time-to-event distribution of a single-valued predictor is estimated by use of pix2surv as described above, the resulting prognostic performance is similar or even higher than if the predictor had been subjected to a traditional Cox proportional hazards model ()(Uemura et al., 2020). This observation is consistent with the previously reported result that the predictions generated by the DATE model (see Section 2), the inspiration behind our pix2surv model, are more accurate than those generated by traditional survival models (Chapfuwa et al., 2018).
3.6. Evaluation methods
3.6.1. Training and validation with bootstrapping
To obtain an unbiased estimate and 95% confidence intervals of how well our model would generalize to external validation patients, we performed the evaluations by use of the bootstrap-based procedure recommended by the Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD) consensus guideline (Moons et al., 2015). The bootstrapping evaluations were performed with 100 bootstrap replicates on the pix2surv model as well as on the reference predictors described in Section 3.5. The associated statistical analyses were performed by use of R 4.0.2 (R Core Team, 2020).
The bootstrap evaluations were performed by use of per-patient bootstrapping, i.e., when a patient was assigned to a training or test set in the bootstrap procedure, all the CT images of the patient were assigned to that set. See Appendix B for details about the implementation of the per-patient bootstrap procedure. It took approximately 276 hours (11.5 days) to perform 100 bootstrap replicates for 214 patients on a single GPU by the use of the architecture and parameter settings of pix2surv described in Section 3.3.
3.6.2. Prediction performance
We measured the performance of the prognostic prediction in terms of survival time. For the analysis of COVID-19 progression, the survival time was defined as the number of days from the baseline CT image acquisition to that of either ICU admission or death (for uncensored patients), or to the most recent follow-up date (for censored patients). For the analysis of COVID-19 mortality, the survival time was defined as the number of days from the baseline CT image acquisition to the death of the patient (for uncensored patients), or to the most recent follow-up date (for censored patients).
We used the concordance index (C-index) (Harrell et al., 1996) as the primary metric of the performance of the prognostic prediction. The C-index is technically similar to the area under the receiver operating characteristic (ROC) curve (AUC) that is used for evaluating classification performance for binary outcomes, except that the C-index estimates the concordance between predicted and observed outcomes in the presence of censoring. The C-index is focused on the estimation of usable pairs, in which one patient is known to have an outcome before the other patient, who may have an outcome later or who may be censored. The C-index has a value range of 0%–100%, where 50% indicates random prediction and 100% indicates perfect prediction.
As a secondary metric of the prognostic performance, we calculated the relative absolute error (RAE) of the predictions with respect to the range of the events. The RAE is defined as , where and are the estimated and observed survival time for patient i, respectively. For censored events, the relative error for patient i is defined as .
It should be noted that we did not include the Lab reference predictor in the RAE or survival time estimation results of Section 4. As noted in Section 2, the estimate of the Cox proportional hazard model that was used for calculating the prediction of Lab (Section 3.5) is based on event ordering rather than on time. Thus, it does not provide the time-to-event distribution necessary for the calculation of the RAE or the distribution of the survival time.
We also quantified the uncertainty in the predictions of the progression and mortality across the predictors by use of the coefficient of variation as a metric (Chapfuwa et al., 2021, 2020). The details and results of this analysis are provided in Appendix C.
3.6.3. Risk stratification
We evaluated the performance of the pix2surv model in risk stratification by use of the Kaplan-Meier estimator (Kaplan and Meier, 1958). The Kaplan-Meier estimator is a non-parametric statistic for estimating a survival probability function of a population as a function of time from time-to-event data. A plot of the Kaplan-Meier estimator, called a Kaplan-Meier survival curve, results in a series of declining horizontal steps which, with a large enough sample size, approaches the true survival function for that population.
For each patient in a cohort, the predicted survival time from pix2surv was calculated by use of the per-patient bootstrapping (Section 3.6.1). Then, the median of the predicted survival times of all the patients in the cohort was used as a cut point (Harrell et al., 1996) for stratifying the patients into low- and high-risk groups, i.e., the patients whose predicted survival times were shorter than the cut-point time value were categorized into the high-risk group, whereas those whose predicted survival times were longer than the cut-point value were categorized into the low-risk group. For each group, the Kaplan-Meier survival curve was generated by use of the Kaplan-Meier estimator, and the difference between the survival curves of the two risk groups was evaluated by use of the log-rank test (Mantel, 1966), which is a non-parametric test for testing the null hypothesis that there is no difference between populations regarding the probability of an event at any time point. The log-rank test is based on the same assumptions as those of the Kaplan-Meier survival curves (Harrington, 2005; Harrington and Fleming, 1982).
3.6.4. Equivalence of estimated versus observed survival curves
We evaluated the equivalence of the estimated Kaplan-Meier survival curve with that of the patient cohort by use of a non-parametric equivalence test (Möllenhoff and Tresch, 2020), where the equivalence margin was set to 0.15. The null hypothesis on the difference of the two survival curves over the entire period, , was tested at a significance level of 0.05. If the null hypothesis was not rejected, the survival curves were considered equivalent.
4. Results
4.1. Prognostic prediction performance
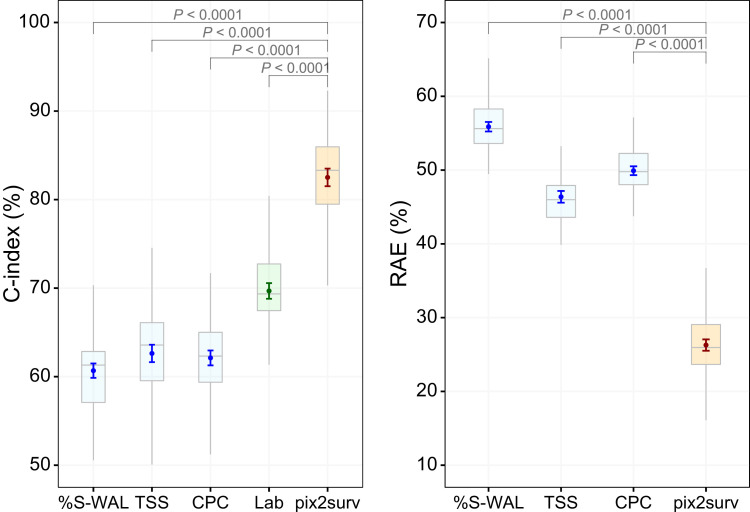
Fig. 2 shows the comparative performance of the pix2surv and the reference predictors in the prediction of COVID-19 progression, as measured by the C-index and RAE with the 100 bootstrap replicates. This progression analysis of common cases (see Section 3.4) included 105 patients, of whom 38 either had been admitted to the ICU (n = 26) or who had expired (n = 12). For the C-index, the prediction performance of pix2surv (82.5% with a 95% confidence interval of [81.5%, 83.5%]) was significantly higher than those of %S-WAL (60.7% [59.9%, 61.5%]), TSS (62.6% [61.7%, 63.6%]), CPC (62.1% [61.3%, 63.0%]), and Lab (69.8% [69.5%, 70.1%]) (P < 0.0001). For the RAE, the prediction error of pix2surv (26.3% [25.5%, 27.0%]) was significantly lower than those of %S-WAL (55.9% [55.2%, 56.5%]), TSS (46.4% [45.6%, 47.2%]), and CPC (49.9% [49.3%, 50.5%]) (P < 0.0001).
Fig. 2.
Comparative performances of the pix2surv and the reference predictors in the prediction of the progression of COVID-19 measured by (left) C-index and (right) RAE. The boxplot shows the bootstrap results, and the confidence bars inside the boxplots show the 95% confidence intervals of the prediction performance.
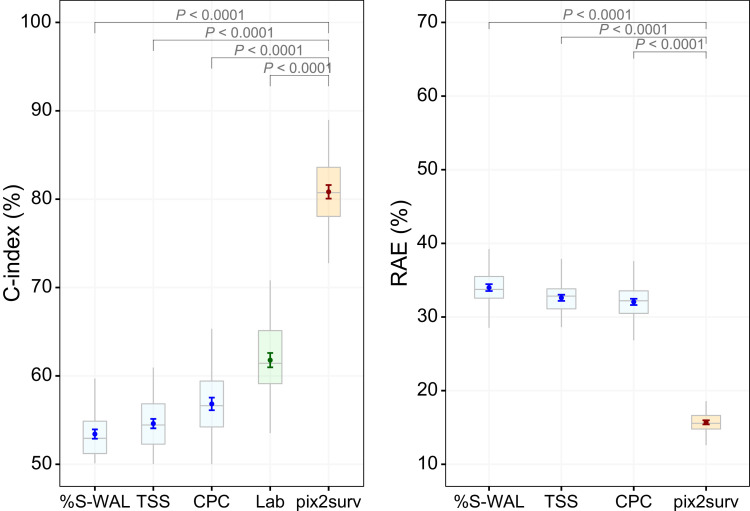
Fig. 3 shows the comparative performance of the pix2surv and the reference predictors in the prediction of mortality, as measured by the C-index and RAE with 100 bootstrap replicates. This mortality analysis of common cases (see Section 3.4) included 171 patients, of whom 40 had expired. For the C-index, the prediction performance of pix2surv (80.8% [80.1%, 81.6%]) was significantly higher than those of %S-WAL (53.4% [52.9%, 53.9%]), TSS (54.6% [54.1%, 55.1%]), CPC (56.8% [56.1%, 57.5%]), and Lab (62.5% [62.3%, 62.8%]) (P < 0.0001). For the RAE, the prediction error of pix2surv (15.7% [15.4%, 16.0%]) was significantly lower than those of %S-WAL (34.0% [33.5%, 34.5%]), TSS (32.6% [32.2%, 33.0%]), and CPC (32.1% [31.6%, 32.5%]) (P < 0.0001).
Fig. 3.
Comparative performances of the pix2surv and the reference predictors in the prediction of the mortality from COVID-19 measured by (left) C-index and (right) RAE. The boxplot shows the bootstrap results, and the confidence bars inside the boxplots show the 95% confidence intervals of the prediction performance.
Table 2 shows the comparative performance of pix2surv and the reference predictors in the prediction of the COVID-19 progression (left) and mortality (right) for the subcohorts of patients, in which the maximum numbers of patients that were available individually for each predictor, as indicated in the second and fifth columns for the progression and mortality, respectively, were used to calculate the result for the predictor. For pix2surv, the C-index values for both progression and mortality were increased by 2.7% from those shown in Fig. 2 and Fig. 3. The RAE values of pix2surv for progression and mortality were decreased by 3.1% and 0.5%, respectively. Similar to the trend shown in Figs. 2 and 3, pix2surv statistically significantly (P < 0.0001) outperformed the other predictors.
Table 2.
Comparative performance of pix2surv and the reference predictors in the prediction of the COVID-19 progression (left) and mortality (right) for the subcohorts of patients, where, for each predictor, all available patients (as shown in the second and fifth columns) were used.
The above results indicate that pix2surv outperforms the reference predictors by a large margin in prognostic prediction. The results of the quantification of the associated uncertainties that are provided in Appendix C also show that pix2surv is at least as precise in prognostic prediction as the reference predictors.
4.2. Risk stratification performance
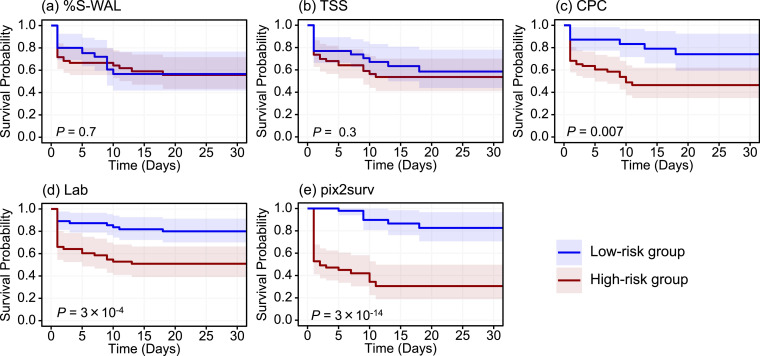
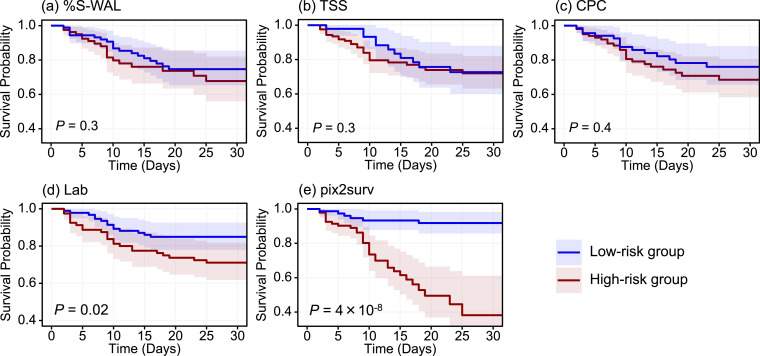
Figs. 4 and 5 show the Kaplan-Meier survival curves, stratified into low- and high-risk groups, of the common cases of COVID-19 patients included in Figs. 2 and 3, respectively. In both progression and mortality analysis, both visual assessment and the P-values of the log-rank test indicated that the separation between the two curves was largest with pix2surv, indicating that pix2surv was the most effective predictor in the stratification of the progression and mortality risk of COVID-19 patients.
Fig. 4.
The Kaplan-Meier survival curves, stratified into low- and high-risk patient groups, of the common cases in the progression analysis cohort included in Fig. 2. The estimated survival curves for the low-risk group (n = 52) and high-risk group (n = 53) are shown in blue and red, respectively, with shaded areas representing the 95% confidence intervals. The P values were obtained by application of the log-rank test to the two survival curves. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 5.
The Kaplan-Meier survival curves, stratified into low- and high-risk patient groups, of the common cases in the mortality analysis cohort included in Fig. 3. The estimated survival curves for the low-risk group (n = 85) and high-risk group (n = 86) are shown in blue and red, respectively, with shaded areas representing the 95% confidence intervals. The P values were obtained by application of the log-rank test to the two survival curves. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4.3. Equivalence of survival curves
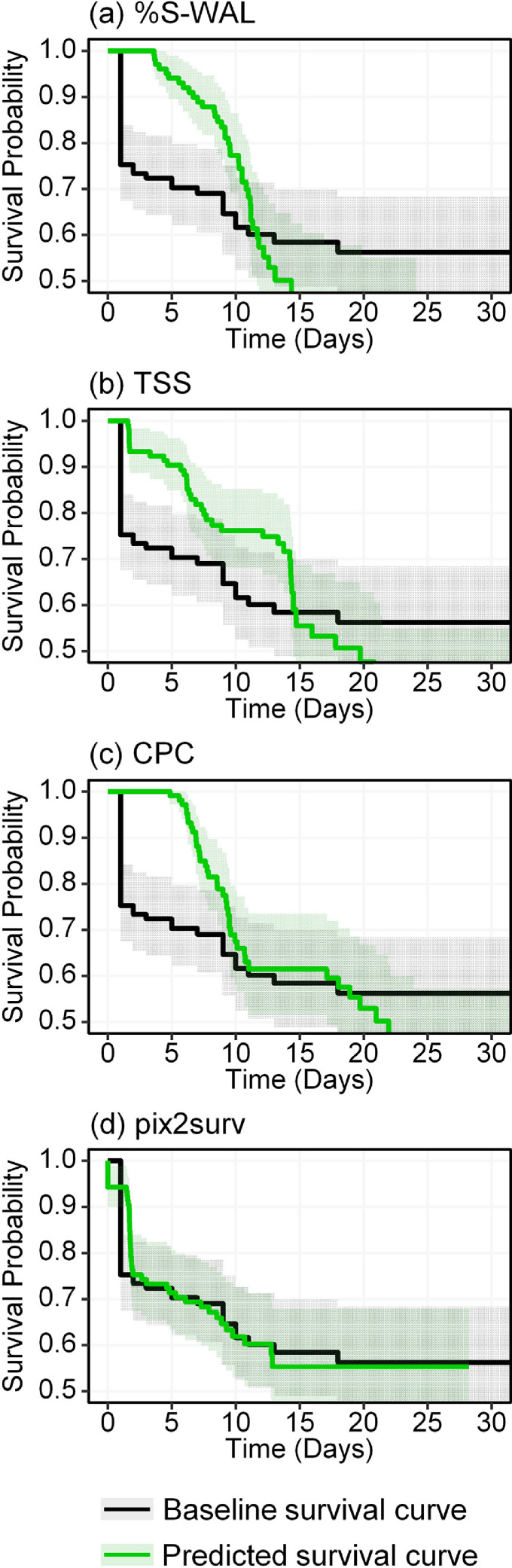
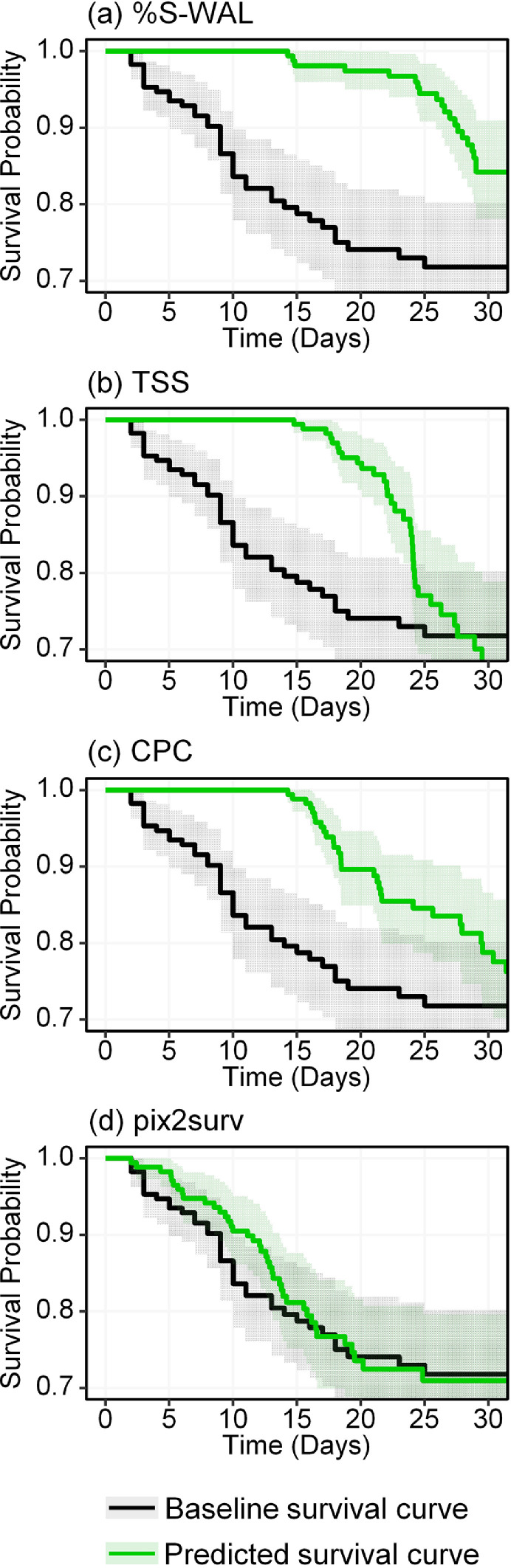
Figs. 6 and 7 show the Kaplan-Meier survival curves estimated by pix2surv and the three image-based reference predictors for the progression and mortality of the common cases of COVID-19 patients included in Figs. 2 and 3, respectively, in comparison with the actual (baseline) survival curves of these patient cohorts. The non-parametric equivalence test described in Section 3.6.4 showed that, in both progression and mortality predictions, the survival curves estimated by use of pix2surv were identified as equivalent to the actual survival curves over the period of 0 to 30 days, whereas those estimated by the reference predictors were not. Also, visual assessment indicates that pix2surv approximates the actual survival time better than do the reference predictors.
Fig. 6.
Kaplan-Meier survival curves for the progression of COVID-19 in the patient cohort of common cases, as estimated by the four image-based predictors used in this study (green curves), in comparison with the actual survival curve of the patients (black). The shaded areas represent the 95% confidence intervals. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 7.
Kaplan-Meier survival curves for mortality in the patient cohort of common cases, as estimated by the four image-based predictors used in this study (green curves), in comparison with the actual survival curve of the patients (black). The shaded areas represent the 95% confidence intervals. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4.4. Survival time estimation
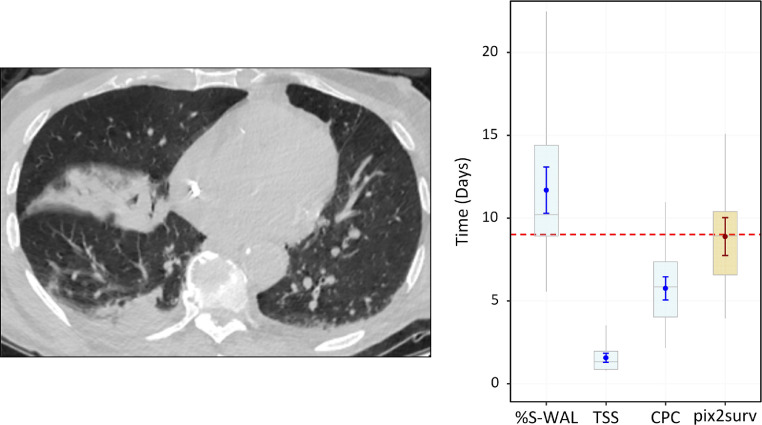
Figs. 8–10 show examples of the prediction of survival time for individual COVID-19 patients by use of pix2surv and the three image-based reference predictors. Fig. 8 shows a 71-year-old male who was admitted to the ICU nine days after the chest CT examination. The feature values of the %S-WAL, TSS, and CPC predictors for this patient were 81%, 8, and 6, respectively. The estimated survival times (the small circle inside the box plots) and their confidence intervals (bars) that were estimated by %S-WAL, TSS, CPC, and pix2surv were 11.7 [95% CI: 10.3, 13.0], 1.6 [1.3, 1.8], 5.8 [5.1, 6.4], and 8.9 [7.8, 10.0] days, respectively.
Fig. 8.
An example of the predicted progression-free survival time of a 71-year-old male who was admitted to the ICU nine days (indicated by the horizontal red dotted line on the plot on the right) after the chest CT examination. The image on the left shows a representative example of the CT images. The plot on the right shows the predicted survival times (circles) by pix2surv and the image-based reference predictors, with 95% confidence interval bars superimposed on the boxplots that represent the bootstrap results. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
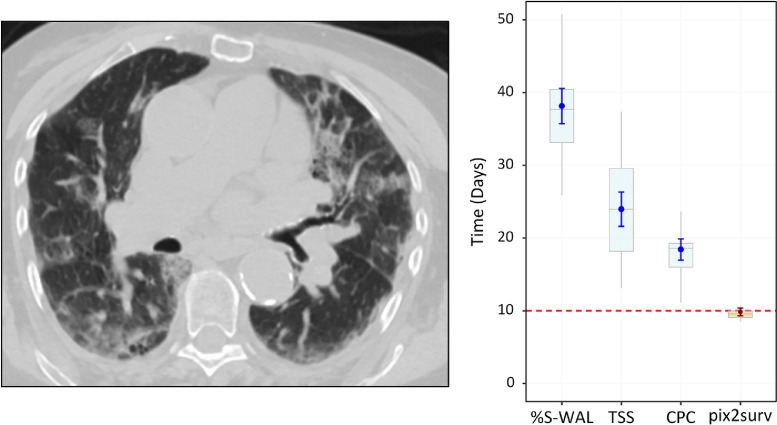
Fig. 10.
An example of the predicted overall survival time (mortality) of a 47-year old male who expired 2 days (red dotted line on the plot on the right) after a chest CT examination. The image on the left shows a representative example of the CT images. The plot on the right shows the predicted survival times (circles) by pix2surv and the image-based reference predictors, with 95% confidence interval bars superimposed on the boxplots that represent the bootstrap results. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
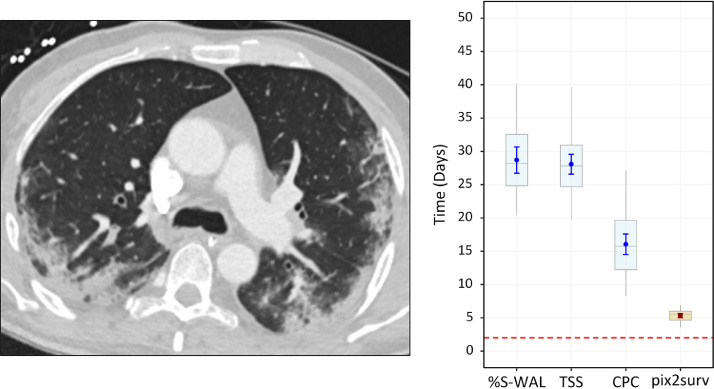
Fig. 9 shows a 67-year old male who expired 10 days after the chest CT examination. The %S-WAL, TSS, and CPC values for this patient were 67%, 12, and 7, respectively. The survival times estimated by %S-WAL, TSS, CPC, and pix2surv were 38.1 [95% CI: 35.8, 40.5], 24.0 [21.7, 26.2], 18.4 [17.0, 19.8], and 9.8 [9.3, 10.3] days, respectively.
Fig. 9.
An example of the predicted overall survival time (mortality) of a 67-year old male who expired 10 days (red dotted line on the plot on the right) after the chest CT examination. The image on the left shows a representative example of the CT images. The plot on the right shows the predicted survival times (circles) by pix2surv and the image-based reference predictors, with 95% confidence interval bars superimposed on the boxplots that represent the bootstrap results. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 10 shows a 47-year old male who expired two days after the chest CT examination. The %S-WAL, TSS, and CPC values for this patient were 75%, 8, and 6, respectively. The survival times estimated by %S-WAL, TSS, CPC, and pix2surv were 28.7 [95% CI: 26.8, 30.6], 28.1 [26.6, 29.5], 16.0 [14.5, 17.5], and 5.3 [5.0, 5.6] days, respectively.
For the cases in Figs. 8 and 9, the two-one-sided t-test (TOST) (Schuirmann, 1987) with an equivalence margin of 15% and confidence interval of 95% showed that the survival times predicted by pix2surv were equivalent to the observed survival time (P < 0.0001), whereas those of the reference predictors were not, indicating the potential usefulness of the pix2surv model for the prediction of survival times of COVID-19 patients. For the case shown in Fig. 10, all the predictors yielded a longer survival time than what was observed, possibly because the involvement of the consolidation is limited to the posterior and peripheral lung on the CT images. However, pix2surv still approximated the observed survival time more accurately than did the reference predictors.
5. Discussion
Fast and accurate clinical assessment of the disease progression and mortality is vital for the management of COVID-19 patients. Although several computer-assisted image-based predictors have been proposed for prognostic prediction of COVID-19 patients based on chest CT, those previous predictors were limited to semi-automated schemes with manually designed features and supervised learning, and the survival analysis was largely limited to logistic regression. To the best of our knowledge, the weakly unsupervised conditional GAN model (pix2surv) that we developed in this study is the first prognostic deep-learning model that can be trained to estimate the distribution of the survival time of a patient directly from the CT images of the patient without image segmentation. The use of deep learning as an integral part of pix2surv makes it possible to train a complete image-based end-to-end survival analysis model for estimating the time-to-event distribution directly from input images without explicit segmentation or feature extraction. Also, our weakly unsupervised approach eliminates the time, costs, and uncertainties plagued by manual image annotation efforts that are still required by traditional supervised learning approaches and that can slow down the development of solutions for addressing new diseases such as COVID-19 (Greenspan et al., 2020).
We demonstrated that the prognostic performance of pix2surv based on chest CT images for estimating the disease progression and mortality of patients with COVID-19 is significantly better than those based on established laboratory tests or existing image-based visual and quantitative predictors. The time-to-event information calculated by pix2surv for chest CT images also enabled stratification of COVID-19 patients into low- and high-risk groups by a wider margin than those calculated by the reference predictors.
The nominal performance of pix2surv could be improved in a number of ways. One approach would be to use data augmentation for enhancing the training dataset (Shorten and Khoshgoftaar, 2019). Another approach could be to expand our COVID-19 dataset by use of public imaging repositories that are currently being constructed. However, it is not clear if such repositories will include chest CT examinations and the kinds of specific clinical information that were available to our study.
For this study, we implemented the pix2surv as a 2D deep learning model, where the prediction is based on an analysis of a stack of 2D CT image slices of a patient, rather than on a volumetric analysis of the chest CT volume. At present, effective use of 3D deep learning is constrained by the limitations of the currently available datasets and GPUs, which introduce several obstacles (Singh et al., 2020). First, the use of 3D volume as a basic unit would reduce the amount of training data over using 2D images. Because of the 2D implementation, we were able to perform the training and evaluations by the use of up to 84,971 CT images, whereas with a 3D implementation we could have used only up to 214 CT image volumes, thus introducing a convergence problem in the training phase. Second, in clinical practice, chest CT studies are still being acquired at an anisotropic image resolution, which makes their volumetric analysis less meaningful than an independent analysis of the image slices. Third, because of the memory limitations of the currently available GPUs, it is not straightforward or sometimes not even possible to fit an isotropic high-resolution chest CT volume and a 3D deep learning model into a single GPU, at least not without compromising performance. However, in the future, we anticipate that the use of a 3D pix2surv model with a large enough training dataset of isotropic chest CT volumes could be used to yield an even higher performance than that reported in this study.
It should be noted that most of the COVID-19 data of this study were collected during the first six months of the pandemic outbreak, at a time when relatively little was known about COVID-19. Since then, rapid developments in COVID-19 treatments and vaccinations have substantially improved the patients’ survival, and survival models that have been trained only on previously collected COVID-19 data may have limited relevance in today's context. Thus, topics such as generalization of previously developed prediction models to more recently collected COVID-19 data, including issues such as “Long COVID” (Sudre et al., 2021), provide ideas for future studies.
The reference COVID-19 predictors of this study were limited to those that had been published in peer-reviewed literature at the time our experiments were carried out. The purpose of this study was to develop and to demonstrate the feasibility of a weakly unsupervised pix2surv model for performing prognostic prediction for COVID-19 based on chest CT images, rather than to perform an exhaustive evaluation with any potentially available predictors. This is a topic to be explored in a future study.
The main limitations of this study include that this was a retrospective study based on early COVID-19 data, and that the evaluation was limited to an internal validation with bootstrapping. The proposed method only considers image-based information, and therefore, integration of non-imaging clinical data to the model could improve the accuracy of the predictions. Potential future topics include the application of the pix2surv model to more recently collected COVID-19 data and to other diseases that are manifested in medical images, as well as an external validation with prospective cases.
6. Conclusions
We developed a weakly unsupervised conditional GAN, called pix2surv, that can be used to calculate time-to-event information automatically from images for performing prognostic prediction. We showed that the prognostic performance of pix2surv based on chest CT images compares favorably with those of currently available laboratory tests and existing image-based visual and quantitative predictors in the estimation of the disease progression and mortality of COVID-19 patients. We also showed that the time-to-event information calculated by pix2surv based on chest CT images enables stratification of the patients into low- and high-risk groups by a wider margin than those of the other predictors. Thus, pix2surv is a promising approach for performing image-based prognostic prediction for the management of patients.
CRediT authorship contribution statement
Tomoki Uemura and Janne J. Näppi contributed to methodology, software development, experiment, formal analyses, and writing the manuscript. Chinatsu Watari contributed to clinical data collection and formal analyses. Toru Hironaka contributed to data collection and software developments. Tohru Kamiya provided technical consultation. Hiroyuki Yoshida conceptualized and supervised the study, developed methodology, carried out formal analyses, and reviewed and edited the manuscript.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. During the conduct of this study, Janne J. Näppi received NIH grants R21EB024025 and R21EB22747, as well as Massachusetts General Hospital (MGH) Executive Committee on Research (ECOR) Interim Support Funding, as the PI of the grants; Hiroyuki Yoshida received NIH grants R01EB023942 and R01CA212382 as the PI of the grants; Tomoki Uemura was partly supported by the NIH grant R01EB023942; and Toru Hironaka was partly supported by the NIH grants R21EB024025, R21EB22747, R01CA212382, and R01EB023942.
Acknowledgments
The authors are thankful for the support from the Department of Radiology, especially Dr. Gordon Harris, at the Massachusetts General Hospital, as well as the Research Patient Data Repository and the COVID-19 Data Mart at the Mass General Brigham.
Appendix A. Ablation study
Table A.1 provides an ablation study regarding the prediction performance of the pix2surv model when it was trained using the method of Section 3.3 (“256×256×100”), i.e., by subsampling of the original input CT images to a 256×256-pixel matrix size and by constraining the number of CT images per patient to a maximum of 100, in comparison to using all the available CT images of patients (“256×256xAll”) or using the original 512×512-pixel matrix size of the CT images (“512×512×100”). The results of Table A.1 indicate that the method of Section 3.3 for reducing training time yields a reasonable approximation of the prediction performance.
Table A.1.
Prediction performance of the pix2surv model when trained with the method of Section 3.3 (“256×256×100”) in comparison to using all the CT images (“256×256xAll”) or using the original matrix size of CT images (“512×512×100”).
| Progression |
Mortality |
|||
|---|---|---|---|---|
| Width x Hight x Depth | C-index % [95% CI] | RAE % [95% CI] | C-index % [95% CI] | RAE % [95% CI] |
| 256 x 256 x 100 | 85.2 [84.6, 85.9] | 23.2 [22.6, 23.7] | 83.5 [82.8, 84.2] | 15.2 [14.9, 15.5] |
| 256 x 256 x All | 84.1 [83.4, 84.8] | 18.6 [17.9, 19.4] | 82.8 [82.0, 83.7] | 12.8 [12.3, 13.3] |
| 512 x 512 x 100 | 81.2 [80.1, 82.2] | 32.8 [31.9, 33.6] | 82.3 [81.4, 83.2] | 16.7 [16.0, 17.4] |
Appendix B. Per-patient bootstrap procedure
Let N be the number of patients included in a patient cohort (i.e., progression or mortality analysis cohort in Table 1), and let denote the CT images of patient . Let be the set of all CT images for the cohort of the N patients. Let denote the value of a C-statistic (e.g., C-index or RAE) that is obtained when pix2surv is trained on the training set and tested on the test set . Here, the training and test of pix2surv are performed as described in Sections 3.1 and 3.2. The per-patient bootstrap evaluation of pix2surv for obtaining a bias-corrected estimate of the C-statistic value is performed as follows (Efron and Tibshirani, 1993; Sahiner et al., 2008):
-
(1)
First, we initialize pix2surv with random weights, and then calculate a resubstitution estimate of the C-statistic value, , by training pix2surv on the cohort of patients and by testing it on the same cohort of patients .
-
(2)
Next, we generate B bootstrap replicates (also called bootstrap samples), , where each replicate is obtained by randomly drawing N patients, with replacement, from . It can be shown that, for a large N, each of these bootstrap replicates contains, on average, of all the patients (Efron and Tibshirani, 1997).
-
(3)
We then train pix2surv on each bootstrap replicate , and test it on and to obtain the following bias of the resubstitution estimate: . Here, the first term of can be regarded as the resubstituting C-statistic value in a so-called “bootstrap world” (Boos, 2003), whereas the second term of can be regarded as the test C-statistic value in the bootstrap world.
-
(4)
The average of over the B bootstrap replicates provides an estimated bias of the resubstitution estimate. Thus, the bias-corrected bootstrap estimate of the C-statistic is obtained by .
Appendix C. Quantification of uncertainty
Predictions made by artificial intelligence suffer from various uncertainties, such as those related to the input data or the correctness of the underlying prediction model (Ghoshal et al., 2020). One of the metrics to measure such uncertainties is the coefficient of variation (CoV), which characterizes the dispersion of predictions around the mean in a distribution. In practice, it is desirable for a time-to-event prediction model to generate concentrated predictions. Thus, a low value of CoV indicates that a prediction is more precise than those obtained with a large value of CoV.
Table C.1 shows the CoV of pix2surv and those of the reference predictors in the prediction of the COVID-19 progression (left) and mortality (right). It should be noted that predictions based on the Cox model (Lab) have been excluded from this analysis, because the Cox model estimates a risk score and thus predictions based on the Cox model cannot be evaluated on CoV.
Table C.1.
Quantification of the uncertainty of predictions in terms of coefficient of variation (CoV).
References
- Bernheim A., Mei X., Huang M., Yang Y., Fayad Z.A., Zhang N., Diao K., Lin B., Zhu X., Li K., Li S., Shan H., Jacobi A., Chung M. Chest CT findings in coronavirus disease-19 (COVID-19): relationship to duration of infection. Radiology. 2020;295(3) doi: 10.1148/radiol.2020200463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boos D.D. Introduction to the bootstrap world. Statis. Sci. 2003;18(2):168–174. [Google Scholar]
- Chapfuwa P., Li C., Mehta N., Carin L., Henao R. ACM CHIL 2020 - Proceedings of the 2020 ACM Conference on Health, Inference, and Learning. 2020. Survival cluster analysis; pp. 60–68. [DOI] [Google Scholar]
- Chapfuwa P., Tao C., Li C., Khan I., Chandross K.J., Pencina M.J., Carin L., Henao R. Calibration and uncertainty in neural time-to-event modeling. IEEE Trans. Neural Networks Learn. Syst. 2021 doi: 10.1109/tnnls.2020.3029631. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapfuwa P., Tao C., Li C., Page C., Goldstein B., Carin L., Henao R. Proceedings of the 35th International Conference on Machine Learning. 2018. Adversarial time-to-event modeling; pp. 734–743. [PMC free article] [PubMed] [Google Scholar]
- Colombi D., Bodini F.C., Petrini M., Maffi G., Morelli N., Milanese G., Silva M., Sverzellati N., Michieletti E. Well-aerated lung on admitting chest CT to predict adverse outcome in COVID-19 pneumonia. Radiology. 2020;296(2):E86–E96. doi: 10.1148/radiol.2020201433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D.R. Regression models and life-tables. J. Roy. Statist. Soc. Ser. A. 1972;34(2):187–220. [Google Scholar]
- Efron B, Tibshirani R.J. Monographs on Statistics and Applied Probability (Vol. 57) Chapman & Hall; 1993. An introduction to the bootstrap. [Google Scholar]
- Efron B. The efficiency of Cox’s likelihood function for censored data. J. Am. Statist. Assoc. 1974;72(359):557–565. [Google Scholar]
- Efron Bradley, Tibshirani R. Improvements on cross-validation: The .632+ bootstrap method. J. Am. Statist. Assoc. 1997;92(438):548–560. doi: 10.1080/01621459.1997.10474007. [DOI] [Google Scholar]
- Francone M., Iafrate F., Masci G.M., Coco S., Cilia F., Manganaro L., Panebianco V., Andreoli C., Colaiacomo M.C., Zingaropoli M.A., Ciardi M.R., Mastroianni C.M., Pugliese F., Alessandri F., Turriziani O., Ricci P., Catalano C. Chest CT score in COVID-19 patients: correlation with disease severity and short-term prognosis. Eur. Radiol. 2020;30(12):6808–6817. doi: 10.1007/s00330-020-07033-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghoshal B., Tucker A., Sanghera B., Lup Wong W. Estimating uncertainty in deep learning for reporting confidence to clinicians in medical image segmentation and diseases detection. Comput. Intell. 2020 doi: 10.1111/coin.12411. September, 1–34. [DOI] [Google Scholar]
- Greenspan H., San José Estépar R.J., Niessen W., Siegel E., Nielsen M. Position paper on COVID-19 imaging and AI: from the clinical needs and technological challenges to initial AI solutions at the lab and national level towards a new era for AI in healthcare. Med. Image Anal. 2020;66 doi: 10.1016/j.media.2020.101800. April. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harmon S.A., Sanford T.H., Xu S., Turkbey E.B., Roth H., Xu Z., Yang D., Myronenko A., Anderson V., Amalou A., Blain M., Kassin M., Long D., Varble N., Walker S.M., Bagci U., Ierardi A.M., Stellato E., Plensich G.G., Franceschelli G., Girlando C., Irmici G., Labella D., Hammoud D., Malayeri A., Jones E., Summers R.M., Choyke P.L., Xu D., Flores M., Tamura K., Obinata H., Mori H., Patella F., Cariati M., Carrafiello G., An P., Wood B.J., Turkbey B. Artificial intelligence for the detection of COVID-19 pneumonia on chest CT using multinational datasets. Nat. Commun. 2020;11(1):4080. doi: 10.1038/s41467-020-17971-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrell F.E., Lee K.L., Mark D.B. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat. Med. 1996;15(4):361–387. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. http://www.doi.wiley.com/10.1002/%28SICI%291097-0258%2819960229%2915%3A4%3C361%3A%3AAID-SIM168%3E3.0.CO%3B2-4 [DOI] [PubMed] [Google Scholar]
- Harrington D. Encyclopedia of Biostatistics. Wiley Interscience; 2005. Linear rank tests in survival analysis. https://doi.org/doi: [DOI] [Google Scholar]
- Harrington D., Fleming T. A class of rank test procedures for censored survival data. Biometrika. 1982;69(3):553–566. [Google Scholar]
- Homayounieh F., Ebrahimian S., Babaei R., Mobin H.K., Zhang E., Bizzo B.C., Mohseni I., Digumarthy S.R., Kalra K.M. CT radiomics, radiologists and clinical information in predicting outcome of patients with COVID-19 pneumonia. Radiol. Cardiothorac. Imaging. 2020;2(4) doi: 10.1148/ryct.2020200322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L., Han R., Ai T., Yu P., Kang H., Tao Q., Xia L. Serial quantitative chest CT assessment of COVID-19: deep-learning approach. Radiol. Cardiothorac. Imaging. 2020;2(2) doi: 10.1148/ryct.2020200075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishwaran H., Kogalur U.B., Blackstone E.H., Lauer M.S. Random survival forests. Ann. App. Statist. 2008;2:841–860. [Google Scholar]
- Isola P., Zhu J.-Y., Zhou T., Efros A.A. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017. Image-to-image translation with conditional adversarial networks; pp. 1125–1134.http://arxiv.org/abs/1611.07004 [Google Scholar]
- Ji D., Zhang D., Xu J., Chen Z., Yang T., Zhao P., Chen G., Cheng G., Wang Y., Bi J., Tan L., Lau G., Qin E. Prediction for progression risk in patients with COVID-19 pneumonia: the CALL score. Clin. Infect. Dis. 2020;71(6):1393–1399. doi: 10.1093/cid/ciaa414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan E.L., Meier P. Nonparametric estimation from incomplete observations. J. Am. Statist. Assoc. 1958;53(282):457–481. [Google Scholar]
- Karras T., Aila T., Laine S., Lehtinen J. 6th International Conference on Learning Representations (ICLR) 2018. Progressive growing of GANs for improved quality, stability, and variation. [Google Scholar]
- Kawata Y., Kubo H., Niki N., Ohmatsu H., Moriyama N. A study of three-dimensional curvatures and curvatures of four-dimensional hypersurface for analyzing pulmonary nodules on high-resolution CT images. Syst. Comput. Japan. 2005;36(10):16–29. doi: 10.1002/scj.20178. [DOI] [Google Scholar]
- Kleinbaum D.G., Klein M. Springer; 2012. Survival Analysis: a Self-Learning Text (Third) [Google Scholar]
- Lanza E., Muglia R., Bolengo I., Santonocito O.G., Lisi C., Angelotti G., Morandini P., Savevski V., Politi L.S., Balzarini L. Quantitative chest CT analysis in COVID-19 to predict the need for oxygenation support and intubation. Eur. Radiol. 2020;30(12):6770–6778. doi: 10.1007/s00330-020-07013-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C., Wand M. Europan Conference on Computer Vision (ECCV) 2016. Precomputed real-time texture synthesis with markovian generative adversarial networks; pp. 702–716. [DOI] [Google Scholar]
- Li K., Fang Y., Li W., Pan C., Qin P., Zhong Y., Liu X., Huang M., Liao Y., Li S. CT image visual quantitative evaluation and clinical classification of coronavirus disease (COVID-19) Eur. Radiol. 2020;30(8):4407–4416. doi: 10.1007/s00330-020-06817-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, M. D., Arun, N. T., Gidwani, M., Chang, K., Deng, F., Little, B. P., Mendoza, D. P., Lang, M., Lee, S. I., O'Shea, A., Parakh, A., Singh, P., & Kalpathy-Cramer, J. (2020). Automated assessment of COVID-19 pulmonary disease severity on chest radiographs using convolutional Siamese neural networks. In medRxiv. https://doi.org/10.1101/2020.05.20.20108159 [DOI] [PMC free article] [PubMed]
- Liu F., Zhang Q., Huang C., Shi C., Wang L., Shi N., Fang C., Shan F., Mei X., Shi J., Song F., Yang Z., Ding Z., Su X., Lu H., Zhu T., Zhang Z., Shi L., Shi Y. CT quantification of pneumonia lesions in early days predicts progression to severe illness in a cohort of COVID-19 patients. Theranostics. 2020;10(12):5613–5622. doi: 10.7150/thno.45985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu P., Liu X., Zhang R., Shi L., Gao J. The performance of chest CT in evaluating the clinical severity of COVID-19 pneumonia: identifying critical cases based on CT characteristics. Invest. Radiol. 2020;55(7):412–421. doi: 10.1097/RLI.0000000000000689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantel N. Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemother. Rep. 1966;50(3):163–170. [PubMed] [Google Scholar]
- Matos J., Paparo F., Mussetto I., Bacigalupo L., Veneziano A., Perugin Bernardi S., Biscaldi E., Melani E., Antonucci G., Cremonesi P., Lattuada M., Pilotto A., Pontali E., Rollandi G.A. Evaluation of novel coronavirus disease (COVID-19) using quantitative lung CT and clinical data: prediction of short-term outcome. Eur. Radiol. Exp. 2020;4(1):39. doi: 10.1186/s41747-020-00167-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mei X., Lee H.-C., Diao K.-Y., Huang M., Lin B., Liu C., Xie Z., Ma Y., Robson P.M., Chung M., Bernheim A., Mani V., Calcagno C., Li K., Li S., Shan H., Lv J., Zhao T., Xia J., Long Q., Steinberger S., Jacobi A., Deyer T., Luksza M., Liu F., Little B.P., Fayad Z.A., Yang Y. Artificial intelligence-enabled rapid diagnosis of patients with COVID-19. Nat. Med. 2020;26(8):1224–1228. doi: 10.1038/s41591-020-0931-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirza, M., & Osindero, S. (2014). Conditional generative adversarial nets. https://doi.org/1411.1784
- Möllenhoff, K., & Tresch, A. (2020). Survival analysis under non-proportional hazards: investigating non-inferiority or equivalence in time-to-event data. http://arxiv.org/abs/2009.06699 [DOI] [PMC free article] [PubMed]
- Moons K.G.M., Altman D.G., Reitsma J.B., Ioannidis J.P.A., Macaskill P., Steyerberg E.W., Vickers A.J., Ransohoff D.F., Collins G.S. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): explanation and elaboration. Ann. Intern. Med. 2015;162(1):W1–W73. doi: 10.7326/M14-0698. [DOI] [PubMed] [Google Scholar]
- Paszke A., Gross S., Massa F., Lerer A., Bradbury J., Chanan G., Killeen T., Lin Z., Gimelshein N., Antiga L., Desmaison A., Köpf A., Yang E., DeVito Z., Raison M., Tejani A., Chilamkurthy S., Steiner B., Fang L., …, Chintala S. 33rd Conference on Neural Information Processing Systems (NeurIPS 2019) 2019. PyTorch: an imperative style, high-performance deep learning library.http://arxiv.org/abs/1912.01703 [Google Scholar]
- R Core Team . R Foundation for Statistical Computing; Vienna: 2020. R: A Language and Environment for Statistical Computing.http://www.r-project.org/ [Google Scholar]
- Sahiner B., Chan H.-P., Hadjiiski L. Classifier performance prediction for computer-aided diagnosis using a limited dataset. Med. Phys. 2008;35(4):1559–1570. doi: 10.1118/1.2868757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuirmann D.J. A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability. J. Pharmacokinet. Biopharm. 1987;15(6):657–680. doi: 10.1007/BF01068419. [DOI] [PubMed] [Google Scholar]
- Shorten C., Khoshgoftaar T.M. A survey on image data augmentation for deep learning. J. Big Data. 2019;6(60) doi: 10.1186/s40537-019-0197-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon N., Friedman J., Hastie T., Tibshirani R. Regularization paths for Cox’s proportional hazards model via coordinate descent. J. Stat. Softw. 2011;39(5):1–13. doi: 10.18637/jss.v039.i05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh, S. P., Wang, L., Gupta, S., Goli, H., Padmanabhan, P., & Gulyás, B. (2020). 3D deep learning on medical images: a review. Sensors (Switzerland), 20(18), 1–24. https://doi.org/10.3390/s20185097 [DOI] [PMC free article] [PubMed]
- Sudre C.H., Murray B., Varsavsky T., Graham M.S., Penfold R.S., Bowyer R.C., Pujol J.C., Klaser K., Antonelli M., Canas L.S., Molteni E., Modat M., Cardoso M.J., May M.J., Ganesh A., Davies S., Nguyen R., L. H., Drew D.A., Astley C.M., Joshi A.D., Merino J., Tsereteli N., Fall T., Gomez M.F., Duncan E.L., Menni C., Williams F.M.K., Franks P.W., Chan A.T., Wolf J., Ourselin S., Spector T., Steves C.J., C. J. Attributes and predictors of long COVID. Nat. Med. 2021 doi: 10.1038/s41591-021-01292-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uemura T., Watari C., Näppi J.J., Hironaka T., Kim H., Yoshida H. GAN-based survival prediction model from CT images of patients with idiopathic pulmonary fibrosis. Proc SPIE Medical Imaging. 2020;11318:11318F. doi: 10.1117/12.2551369. [DOI] [Google Scholar]
- Wang Y., Chen Y., Wei Y., Li M., Zhang Y., Zhang N., Zhao S., Zeng H., Deng W., Huang Z., Ye Z., Wan S., Song B. Quantitative analysis of chest CT imaging findings with the risk of ARDS in COVID-19 patients: a preliminary study. Ann. Transl. Med. 2020;8(9) doi: 10.21037/atm-20-3554. 594–594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei L.J. The accelerated failure time model: a useful alternative to the Cox regression model in survival analysis. Stat. Med. 1992;11(14–15):1871–1879. doi: 10.1002/sim.4780111409. [DOI] [PubMed] [Google Scholar]
- WHO. (2020). COVID-19 Weekly Epidemiological Update(Issue December). https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/
- Wu Q., Wang S., Li L., Wu Q., Qian W., Hu Y., Li L., Zhou X., Ma H., Li H., Wang M., Qiu X., Zha Y., Tian J. Radiomics analysis of computed tomography helps predict poor prognostic outcome in COVID-19. Theranostics. 2020;10(16):7231–7244. doi: 10.7150/thno.46428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao L., Li P., Sun F., Zhang Y., Xu C., Zhu H., Cai F.-Q., He Y.-L., Zhang W.-F., Ma S.-C., Hu C., Gong M., Liu L., Shi W., Zhu H. Development and validation of a deep learning-based model using computed tomography imaging for predicting disease severity of coronavirus disease 2019. Front. Bioeng. Biotechnol. 2020;8:898. doi: 10.3389/fbioe.2020.00898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan L., Zhang H.-T., Goncalves J., Xiao Y., Wang M., Guo Y., Sun C., Tang X., Jing L., Zhang M., Huang X., Xiao Y., Cao H., Chen Y., Ren T., Wang F., Xiao Y., Huang S., Tan X., Huang N., Jiao B., Cheng C., Zhang Y., Luo A., Mombaerts L., Jin J., Cao Z., Li S., Xu H., Yuan Y. An interpretable mortality prediction model for COVID-19 patients. Nat. Mach. Intell. 2020;2(5):283–288. doi: 10.1038/s42256-020-0180-7. [DOI] [Google Scholar]
- Yu Q., Wang Y., Huang S., Liu S., Zhou Z., Zhang S., Zhao Z., Yu Y., Yang Y., Ju S. Multicenter cohort study demonstrates more consolidation in upper lungs on initial CT increases the risk of adverse clinical outcome in COVID-19 patients. Theranostics. 2020;10(12):5641–5648. doi: 10.7150/thno.46465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K., Liu X., Shen J., Li Z., Sang Y., Wu X., Zha Y., Liang W., Wang C., Wang K., Ye L., Gao M., Zhou Z., Li L., Wang J., Yang Z., Cai H., Xu J., Yang L., Cai W., Xu W., Wu S., Zhang W., Jiang S., Zheng L., Zhang X., Wang L., Lu L., Li J., Yin H., Wang W., Li O., Zhang C., Liang L., Wu T., Deng R., Wei K., Zhou Y., Chen T., Lau J.Y-N., Fok M., He J., Lin T., Li W., Wang G. Clinically applicable AI system for accurate diagnosis, quantitative measurements, and prognosis of COVID-19 pneumonia using computed tomography. Cell. 2020;181(June):1423–1433. doi: 10.1016/j.cell.2020.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]