Invisible Hands and Fine Calipers: A Call to Use Formal Theory as a Toolkit for Theory Construction

Abstract

In recent years, a growing chorus of researchers have argued that psychological theory is in a state of crisis: theories are rarely developed in a way that indicates an accumulation of knowledge. Paul Meehl raised this very concern more than 40 years ago. Yet, in the ensuing decades, little has improved. We aim to chart a better path forward for psychological theory by revisiting Meehl’s criticisms, his proposed solution, and the reasons his solution failed to meaningfully change the status of psychological theory. We argue that Meehl identified serious shortcomings in our evaluation of psychological theories and that his proposed solution would substantially strengthen theory testing. However, we also argue that Meehl failed to provide researchers with the tools necessary to construct the kinds of rigorous theories his approach required. To advance psychological theory, we must equip researchers with tools that allow them to better generate, evaluate, and develop their theories. We argue that formal theories provide this much needed set of tools, equipping researchers with tools for thinking, evaluating a theory’s capacity to explain, strengthening measurement, informing theory development, and moving toward the collaborative construction of psychological theories.

“The power of the physicist does not come from exact assessment of probabilities that a difference exists […]. The physicist’s scientific power comes from two other sources, namely, the immense deductive fertility of the formalism and the accuracy of the measuring instruments. The scientific trick lies in conjoining rich mathematics and experimental precision, a sort of ‘invisible hand wielding fine calipers’.”

—Meehl, 1978, p. 825

1. Introduction

In a trenchant critique published more than 40 years ago, Paul Meehl argued that theories in the domains of clinical, counseling, social, and personality psychology rarely develop. Instead, they tend to fade away, uncorroborated and unrefuted (Meehl, 1978). This critical appraisal of “soft psychology” reached a wide audience. It has been cited more than 2,000 times and subsequent articles expanding on these ideas have been cited hundreds more (e.g. Meehl, 1990a, 1990b). Yet, decades later, the status of theory in these domains has not appreciably improved and a growing number of researchers have argued that psychological theory is in a deep-seated state of crisis (Oberauer & Lewandowsky, 2019; Muthukrishna & Henrich, 2019; Smaldino, 2019).

In this article, we aim to chart a path forward for psychological theory by looking back to Meehl’s criticisms, the solutions he proposed, and the reasons why those solutions failed to produce meaningful change in the status of psychological theories. We will argue that Meehl identified fundamental flaws in the ways we test psychological theories, especially in our use of null hypothesis significance testing. We will further argue that his proposed solution would substantially strengthen theory testing. However, we will also argue that Meehl failed to provide researchers with the tools necessary to construct the kinds of rigorous theories his approach required and, thus, failed to provide a viable alternative to null hypothesis significance testing. We will then propose that formal theories provide this much needed set of tools for theory construction, including tools for thinking, evaluating explanation, enhancing measurement, informing theory development, and promoting the collaborative construction of psychological theories.

2. Sir Ronald, Sir Karl, and Professor Meehl

Meehl believed that the problems facing psychological theory were rooted in the field’s reliance on Sir Ronald Fisher’s null hypothesis significance tests as a tool for theory development. Meehl’s core concern was that a null hypothesis significance test provides very little information about a theory. Because any given psychological variable tends to be at least weakly correlated with any other (for a critical review of this idea, see Orben & Lakens, 2019), it can reasonably be assumed that, with a sufficient sample size, most null hypotheses will be rejected. Consequently, rejecting a null hypothesis does little to corroborate a theory. Worsening matters, failing to reject the null hypothesis is similarly uninformative. Because theories are necessarily tested alongside a host of auxiliary hypotheses (e.g., assumptions about one’s sample, measures, tasks, etc.), failing to reject the null hypothesis at best demonstrates that the combination of the theory and these auxiliary hypotheses are false, not that the theory itself is false. Null hypothesis testing thus neither strongly corroborates nor clearly refutes psychological theories and, consequently, does little to help us move them forward.

In the years following Meehl’s criticisms, others extended his critiques. Prominent researchers echoed his concerns about null hypothesis significance testing (Cohen, 1994), labeling these tests a “disaster,” an “intellectually trivial and scientifically sterile” pursuit, and “the most boneheadedly misguided procedure ever institutionalized in the rote training of science students” (Rodgers, 2010, p.3, Hunter, 1997, p.3, Rozeboom, 1997, p.335). Others argued that we frequently mistake statistical hypotheses, data fitting, and other aspects of psychological research for substantive theories (Borsboom, 2013; Gigerenzer, 1998). As a result, we often proceed with our research unaware whether a substantive theory is present or absent. We have developed a kind of “theoretical amensia,” forgetting what a good theory is and what it is good for (Borsboom, 2013; Gigerenzer, 2010).

Meehl proposed that, to address the problems facing psychological theory, we must abandon null hypothesis testing in favor of Sir Karl Popper’s risky tests: testing predictions that would be highly improbable were it not for the theory. In Meehl’s framework, this improbability was primarily achieved by making very specific predictions, ideally to the point of specifying a numerical point prediction (e.g. a correlation of 0.55). Because such a prediction would be unlikely in the absence of the theory, the test puts the theory at “grave risk of refutation” and any theory that survives such risk is strongly corroborated (Meehl, 1978, p. 821). In subsequent work, Meehl revised and elaborated on these ideas, but he never deviated from his emphasis on testing as the primary vehicle for developing psychological theory (Meehl, 1990a).

So why, more than four decades after Meehl raised the alarm, does psychological theory remain in a state of crisis? We believe that there is a fundamental and relatively straightforward reason: Meehl failed to provide, and “soft psychology” continues to lack, a concrete and well-established set of tools for theory construction. Mesmerized by Sir Karl, Meehl focused almost exclusively on testing as the vehicle for advancing scientific knowledge. Although his proposed solution would strengthen theory testing, he had little to say about how to generate the kinds of highly specific theories needed to carry out the risky tests for which he advocated. Further, he provided minimal guidance for how to continue to develop an initial theory after it has failed a risky test. Meehl, of course, is not alone in this regard. The broader hypothetico-deductive framework that dominates psychological research is almost exclusively focused on theory testing as a vehicle for advancing psychological theories (Rozeboom, 1961, 1990; Haig, 2014) and there is minimal emphasis on theory construction in the education of most psychologists (Borsboom, van der Maas, Dalege, Kievit, & Haig, 2020). Lacking concrete and accessible alternatives, researchers continue to rely on null hypothesis significance tests as the primary means of developing theories. Consequently, little has improved in the status of psychological theory since Meehl’s critique.

In response to concerns about the state of theory development in psychology, some have proposed more comprehensive approaches to theory construction that place greater emphasis on the initial generation and subsequent development of psychological theories (e.g., Haig, 2005; Borsboom et al., 2020; Haslbeck, Ryan, Robinaugh, Waldorp, & Borsboom, 2019). These approaches provide valuable frameworks, delineating a sequence of steps or stages to be followed when aiming to construct a strong theory. However, we believe that for these frameworks to be successful, two needs must be addressed. First, we must correct our theoretical amnesia and establish what we are aiming for in our theory construction efforts. Second, we must provide theorists with a set of tools that allow them to better generate, evaluate, and develop theories within these recently proposed frameworks for theory construction. In the remainder of this paper, we address these needs.

3. The Nature and Value of Formal Theories

3.1. Theories, Target Systems, and Phenomena

Scientific theories have two characteristic functions: they explain and they represent. Theories explain phenomena: the robust, generalizable features of the world that we as scientists seek to understand (Bogen & Woodward, 1988; Haig, 2014), such as the Flynn Effect (Trahan, Stuebing, Fletcher, & Hiscock, 2014), the matching phenomenon (Feingold, 1988), or the simple observation that some individuals experience recurrent panic attacks (Kessler et al., 2006). Much of psychological science is focused on establishing these phenomena, and much of the recent efforts to improve psychological science have focused on bolstering our ability to confidently conclude that genuine phenomena have been observed (Munafò et al., 2017; Shrout & Rodgers, 2018). These efforts are critically important to the progress of theory in psychology, as carefully established phenomena are a prerequisite for the development of theories to explain them.

Theories aim to explain phenomena by representing the components of the real world that give rise to the phenomena of interest. We will refer to these components of the real world and the relationships among them as the target system (cf. Elliott-Graves, 2014). We will refer to the components of the theory and the relationships among those components as the theory’s structure. Among philosophers of science, there has been a growing consensus that representation is crucial to the practice of science (Bailer-Jones, 2009; Suárez, 2010). Theories can be understood as models that represent the target system (Suárez & Pero, 2019). As representations of the target system, theories allow us to engage in surrogative reasoning (Swoyer, 1991), using the theory to make predictions about the target system. Just as we can learn to navigate the streets of Paris by consulting a map that represents the city, we can learn about, predict, and even control what will happen in the real world by reasoning from our theory. Theories thus equip us to achieve our most fundamental aims in psychological science: the explanation, prediction, and control of psychological phenomena. To achieve these aims, we must develop theories that are sufficiently good representations of the target system that they allow for surrogative reasoning.

3.2. The “Immense Deductive Fertility” of Formal Theories

The ability to engage in surrogative reasoning hinges on our ability to deduce from a theory how the target system will behave (e.g., how the components of the target system will evolve over time). Unfortunately, for most theories in “soft psychology,” it is difficult to make precise predictions about the target system’s behavior. The reason for this shortcoming is that most psychological theories are verbal theories: they express the structure of the theory in words and, thus, are limited by the imprecision of natural language (Smaldino, 2017). In contrast, formal theories express the structure of the theory in a more precise language, such as the language of mathematics (i.e., a “mathematical model”), formal logic, or a computational programming language (i.e., a “computational model”). By doing so, formal theories allow researchers to precisely deduce the behavior implied by the theory.

3.2.1. Example 1: A Theory of Panic Attacks

Consider the “vicious cycle” theory of panic attacks. Panic attacks are a robust phenomenon characterized by sudden and spontaneous surges of arousal and perceived threat that often seem to arise “out of the blue” (American Psychiatric Association, 2013). In a highly influential verbal theory, Clark posited that if some initial arousal-related bodily sensations (e.g., increased heart rate) are perceived as threatening (e.g., indicating a heart attack), that perceived threat will elicit more arousal which, in turn, will exacerbate the sense of perceived threat; a “vicious cycle” that culminates in a panic attack (Clark, 1986). This verbal theory uses words to express the theory’s structure: positing two core components (arousal and perceived threat) with positive (amplifying) effects on one another. It asserts that the target system represented by this theory can give rise to spontaneous surges of arousal and perceived threat, thereby offering an explanation of panic attacks.

We can create a formal “vicious cycle” theory by expressing this same structure using the language of mathematics. For example, we could use a difference equation to define how the state of arousal (A) evolves over time as a function of itself and perceived threat (T): A_τ+1 = A_τ + α(νT_τ – A_τ), where α constrains the rate at which arousal can change and ν specifies the strength of a linear effect of perceived threat on arousal. Difference and differential equations are often used to model target systems in this way because they allow us to determine how the theory components will evolve over time (in discrete and continuous time, respectively). For this model, if the product of ν and T is greater than the current level of A, A will increase at the next time step; if it is less than the current level of A, A will decrease at the next time step. If we define a similar equation specifying how perceived threat evolves as a function of arousal, these coupled difference equations provide us with a formal theory of the target system (see Appendix A for further details). We can then use this formal theory to deduce what we will refer to as the target system’s theory-implied behavior: the theory’s prediction about how the components of the target system will evolve together over time.

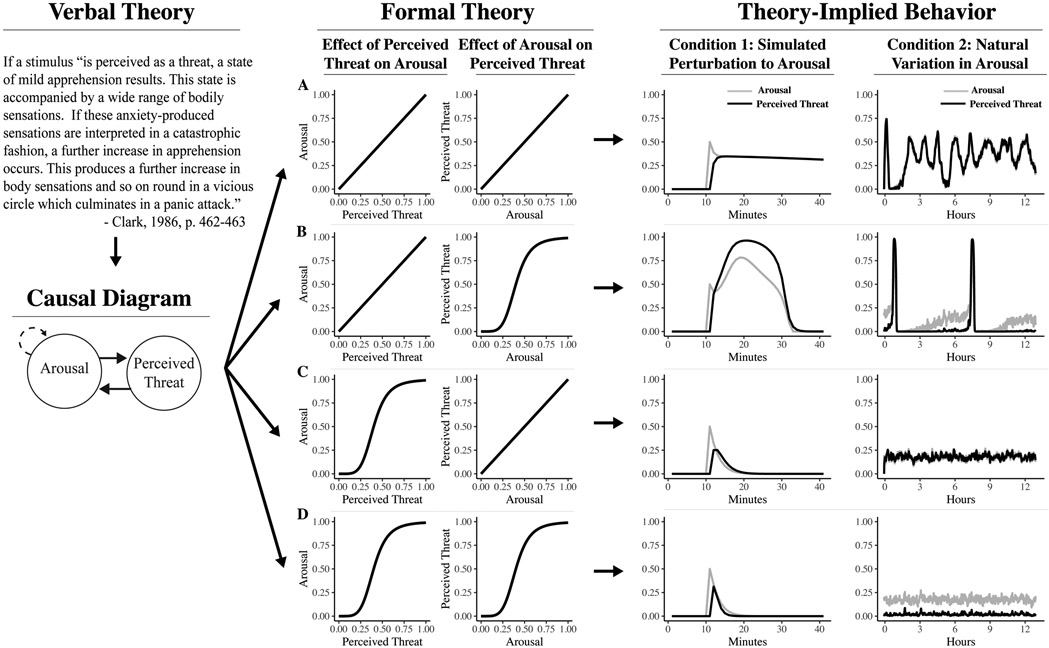
In Figure 1 we present four possible formalizations of the verbal theory of panic attacks.¹ In each, we define the two key effects in the system as being either linear or sigmoidal (note that these are only two of many possible forms this relationship could take). Alongside these effects, we also incorporated a regulating effect of homeostatic feedback on arousal that returns arousal to its baseline in the event that arousal becomes substantially elevated. The effect of homeostatic feedback was the same across each of the four implementations of the verbal “vicious cycle” theory. We specified each of these effects as difference equations and implemented those equations as computational models using the programming language R (R Core Team, 2019), thereby providing us with four distinct formal theories (see Appendix A). Using these formal theories, we are now able to precisely deduce the theory-implied behavior of the target system. That is, we are able to determine precisely how arousal and perceived threat will behave over time within an individual according to each formal theory.

Figure 1:

The verbal theory of panic attacks expresses the theory’s structure in words, positing a positive feedback loop between arousal and perceived threat. This structure can be expressed as a causal diagram, where solid arrows represent amplifying effects and dashed arrows represent dampening effects. The dampening self-loop on arousal represents the effect of homeostatic feedback on elevated arousal (see Appendix A). Due to its imprecision, the verbal theory can be interpreted in many ways. We present four possible formalizations (A-D), defining the effects of arousal on perceived threat and the effect of perceived threat on arousal as being either linear or sigmoidal. We then simulated how an individual’s target system would evolve over time according to each formalization of this theory. We did so in two conditions. In Condition 1, we perturbed the system by inducing a specified level of arousal (0.50) at time point 10 and evaluating how the system responds. In Condition 2, we did not perturb the system, but rather incorporated stochastic variation in arousal to represent natural fluctuations in arousal from internal or external stimuli.

As seen in Figure 1, despite being an implementation of the same verbal theory, each of the four formal theories predicts different system behavior (for a similar illustration of this point from cognitive psychology, see Lewandowsky & Farrell, 2010, p.39-56). For example, consider the formal theory depicted in Panel A. In Condition 1, we induced a specified level of arousal (0.50 at minute 10), with no direct manipulation of perceived threat. The system responded to this perturbation with a sustained moderate level of both arousal and perceived threat for the duration of the simulation. In Condition 2, we induced stochastic variation around a low mean level of arousal, representing natural fluctuations in arousal experienced throughout the day. The system responds to this stochastic variation with persistent and fairly severe oscillations in both arousal and perceived threat. The formal theory depicted in Panel B predicts qualitatively distinct behavior. In response to perturbation (Condition 1), the system quickly enters a state of runaway positive feedback, leading to a surge of both arousal and perceived threat that subsequently subsides. In Condition 2, arousal fluctuates around a relatively low mean and perceived threat remains largely absent for much of the simulation, interrupted by two sudden surges of arousal and perceived threat. Accordingly, despite being a faithful implementation of the same verbal theory, these two formal theories predict qualitatively distinct target system behavior, and only one (Panel B) predicts behavior resembling that of a panic attack. It is thus impossible to deduce precisely what the verbal theory predicts, because what it predicts depends upon information not specified in the verbal theory.

Notably, even if the verbal theory was expressed with greater precision, it would still be limited because it does not provide a means of deduction. For example, we can specify in words that there is a perfect linear effect of arousal on perceived threat and of perceived threat on arousal, thereby approaching the specificity of the formal theory depicted in Panel A. However, to deduce the behavior implied by this verbal theory, we are limited to performing some unspecified mental derivation or simulation. Typically, the accuracy of such mental simulations are unknown. However, in this case, we can compare the theory-implied behavior derived from our mental simulations with the theory-implied behavior derived from our computational model simulations (see Figure 1 Panel A). We encourage the reader to give it a try. In our opinion, it is prohibitively difficult to mentally simulate something resembling the actual theory-implied behavior, even in this very simple system. In a more complex system, mentally simulating the theory-implied behavior would be all but impossible.

3.2.2. Example 2: A Theory of The Matching Phenomenon

Difference equation models are not the only modeling approach that provides a means of deducing what a theory predicts. Another popular class of models are agent-based models (e.g., Wilensky & Rand, 2015), which we will illustrate with a theory from a another domain of “soft psychology.”

Researchers have consistently observed that romantic partners tend to resemble one another on a range of traits, including physical attractiveness, mental abilities, and personality (Buss & Barnes, 1986; Feingold, 1988). Some theorists have posited that this “matching phenomenon” arises because we strategically seek out mates who match our own level of attractiveness (e.g., a mate who is comparably intelligent or physically attractive; Berscheid, Dion, Walster, & Walster, 1971). We will refer to this as the Maximize Similarity Theory. An alternative theory posits that the matching phenomenon arises, not from deliberate attempts to find a mate with comparable attractiveness, but as a consequence of everyone seeking to partner with the mate to whom they are most attracted (Kalick & Hamilton, 1986; Burley, 1983). We will refer to this as the Maximize Attraction Theory.

In a recently developed computational model, Conroy-Beam and colleagues incorporated the Maximize Attraction Theory (Conroy-Beam et al., 2019) as part of a broader theory of mating behavior. Like the “vicious cycle” theory of panic attacks, their theory has a structure that we can express in words. The theory components are the male and female members of a population, each having a set of traits (representing things like intelligence, physical appearance, etc.) and a set of preferences (i.e., traits they find desirable in a potential mate). The relationships among these components are the rules guiding their interaction with one another, which occur in three stages. In the attraction stage, individuals determine how attracted they are to members of the opposite sex based on their preferences across a range of traits. In the selection stage, each individual is paired with the available partner to whom they are most attracted (i.e., following the Maximize Attraction Theory). Finally, in the reproduction stage, these romantic partners produce offspring that inherit their parent’s traits and preferences. Reproductive success is determined by the degree to which the parents possess certain traits, thereby creating a selection pressure in favor of those traits. Following reproduction, this three stage process repeats in the new generation. It is this target system, the theory posits, that gives rise to the matching phenomenon.

Conroy-Beam and colleagues went beyond this verbal description and expressed the structure of their theory in the programming language R as an agent-based model, a common way of formalizing theories of social processes. In this type of model, individuals are represented as agents who interact with one another according to a set of rules specified in the model. Here, the rules specify how agents become attracted to one another, select romantic partnerships, and reproduce.² Like the difference equation models in the example of panic attacks, agent-based models require these relationships to be precisely specified. For example, the Maximize Attraction Theory posits that the matching phenomenon arises from individuals seeking the available partner to whom they are most attracted. Although a seemingly straightforward assertion, it is unclear from this statement precisely how the level of attraction to another individual is determined. How does one go about integrating information across a range of traits in order to inform which partner to select? Is it based on the number of traits that fall within an acceptable range (i.e., a so-called aspiration mechanism) or the difference between preferences and traits in multi-variate space (i.e., a euclidean distance mechanism)? This level of detail is easy to overlook when generating a verbal theory, but is unavoidable when formalizing the theory.

Conroy-Beam et al. (2019) thoroughly investigated how trait information is integrated by formalizing several possible integration mechanisms in distinct agent-based models. In Appendix B, we use two of these models to deduce precisely what the Maximize Attraction Theory predicts when adopting these distinct mechanisms. Just as we saw with the theory of panic attacks (see Figure 1), details left unspecified when expressing the theory in words prove critical to determining what the theory predicts: the matching phenomenon follows when adopting one integration mechanism (i.e., the euclidean distance mechanism), but not another (i.e., the aspiration mechanism; cf. Conroy-Beam et al. (2019)). It is only because the agent-based model allows us to precisely deduce the implications of adopting these distinct mechanisms that the importance of this information to the Maximize Attraction Theory becomes clear.

3.2.3. “Invisible Hand” Formal Theories

As seen in both the difference equation model of panic attacks and the agent-based model of the matching phenomenon, formal theories provide a means of precisely deducing theory-implied behavior. Meehl referred to this as the “immense deductive fertility” of formal theories and he was clear in his belief that theories should ideally be formalized (Meehl, 1978, p. 825). And for good reason: formal theories are all but required for the precise numerical point predictions he viewed as central to the progress of science. Yet, Meehl’s interest in formal theory seemed to run deeper than theory testing alone. Meehl referred to formal theories as “invisible hand theories,” a locution borrowed from Robert Nozick’s “invisible hand explanations” (Nozick, 1974). Invisible hand explanations show how a phenomenon emerges from the interactions among a set of components, as if guided by an invisible hand. Nozick argued that such “fundamental explanations” deepen our understanding of a phenomenon and Meehl spoke admiringly of their ability to produce behavior that would be difficult to anticipate were it not for the careful specification of how the components interact. Verbal theories are limited in their ability to reveal emergent phenomena and, thus, are limited in their ability to provide “fundamental explanations.” Although somewhat oblique, we believe Meehl’s use of this phrase is important because it suggests that Meehl recognized what we regard as a formal theory’s chief virtue: the support it provides for a theory’s ability to explain phenomena (a point to which we will return in the next section).

Like Meehl, we believe formal theories are a key pillar of good science. The deductive fertility of formal theories substantially strengthens our ability to engage in surrogative reasoning and, in doing so, strengthens our ability to make use of a theory. Formal theories support clear and demonstrable explanations, supply precise predictions about the behavior expected from the theory, and provide more precise information about how to control the psychological phenomenon of interest. Yet, while commonly used in some areas of psychology (e.g., mathematical psychology, cognitive psychology, and computational psychiatry), formal theories are much less common in “soft psychology.” If we take the explanation, prediction, and control of psychological phenomena as our joint aims in these domains of psychology, then we must address this relative absence and support the construction of formal theories.

4. Formal Theory as a Set of Tools for Theory Construction

If constructing well-developed formal theories were as simple as setting our sights on them, there would be no theory crisis to address. We suspect that, to the extent most psychologists have thought about formal theories, they regard them as a long-term aspiration; one that is unattainable in the current state of our field. Meehl’s own beliefs were in this vein. He concluded his otherwise lively polemic on a decidedly pessimistic note, questioning whether the formal theories he called for were even possible in “soft psychology.” (Meehl, 1978)

We are more optimistic. We believe the very ideas advocated by Meehl point toward a promising path forward: one that leverages the precision and deductive fertility of formal theories not for theory testing, but for theory construction. In the remainder of this paper, we will argue that the surest path to a good formal theory is a bad formal theory (cf. Smaldino, 2017; Wimsatt, 1987), identifying five ways in which formal theories support theory construction.

4.1. A Tool for Thinking

Formal theories require an intimidating level of specificity. In the early stages of theory generation, psychologists may be reluctant to posit relationships with a level of precision that goes beyond what is known from empirical research. However, avoiding inaccuracies by remaining imprecise is detrimental to progress. Theories that are imprecise give an illusion of understanding and agreement by masking assumptions, omissions, contradictions, and other theory shortcomings (Smaldino, 2016). Formalizing a theory uncovers these shortcomings and, in doing so, clarifies how the theory can be improved. Further, formalizing theory instills a “scientific habit of mind,” forcing the theorist to think critically and carefully about all aspects of the theory and committing them to uncovering what remains unknown (Epstein, 2008; Muthukrishna & Henrich, 2019). Formalization thus acts both as a thinking tool and as a guide for future empirical research.

For example, we recently endeavored to formalize the “vicious cycle” theory of panic attacks (cf. Figure 1); an effort which revealed that there is little empirical guidance for specifying the precise form of these effects, emphasizing the need for further descriptive research on the relationship between arousal and perceived threat (Robinaugh et al., 2019). In the absence of clear empirical guidance, we were required to think carefully about the form of these relationships. For example, we posited that individuals are able to experience low level fluctuations in arousal without elicitation of perceived threat, and we embodied this theoretical position by specifying a sigmoidal rather than linear effect of arousal on perceived threat (cf. Figure 1, Panel B). Formalizing each causal effect posited by the theory in this way required us to think deeply about the nature of each of these relationships and shone a light on the considerable amount of information about this target system that remains unknown (for further detail, see Robinaugh et al., 2019).

The value of formal theory as a thinking tool can similarly be seen in the agent-based model presented in the previous section (Conroy-Beam et al., 2019). Even in our cursory overview of this work, one is immediately struck by the rigorous thought that must be invested to specify each aspect of this model. By forcing theorists to think carefully and critically about each aspect of their theory, formalization can uncover questions previously unrecognized (e.g., how do we integrate information across traits when determining the attractiveness of a potential mate?). Further, by making each aspect of the theory explicit, formalization can reveal areas where theorists hold differing views, even when working from seemingly straightforward and well understood verbal theories. In doing so, formalization provides opportunity for constructive disagreement among theorists on issues that may have been masked when working from verbal theories alone (for an example of such a disagreement from the matching phenomenon literature, see Kalick & Hamilton, 1986, 1988; Aron, 1988). The act of formalizing the theory thus provides a vehicle for rigorous theory generation and sets the stage for subsequent theory development.

4.2. A Tool for Evaluating Explanation

Formalization is not an end unto itself. It is the beginning of an ongoing process of theory evaluation and development. We believe the primary way a theory should be evaluated is by its ability to explain phenomena (cf. Borsboom et al., 2020; van Rooij & Baggio, 2020). Typically, a verbal theory’s ability to explain a phenomenon is simply asserted. This is problematic because to demonstrate that the theory explains the phenomenon, we must first show that the phenomenon does indeed follow as a matter of course from the theory. In other words, explanation presumes accurate deduction (Hempel & Oppenheim, 1948). The deductive infertility of verbal theories thus substantially constrains their ability to provide clear explanations.

Consider again the the “vicious cycle” theory of panic attacks. Of the four possible formalizations of the verbal theory presented in Figure 1, only one shows panic attacks following from the theory. It is thus unclear whether the verbal theory explains panic attacks because the answer to that question depends on how one interprets and implements the verbal theory. In contrast, formal theories allow us to precisely deduce what the theory predicts, thereby strengthening our ability to evaluate what the theory can and cannot explain. For example, the formal theory presented in Panel A of Figure 1 is a plausible interpretation of the verbal “vicious cycle” theory. Yet it fails to produce the characteristic surge of arousal and perceived threat from low-level variations in arousal. From this failure, we learn that the formal theory does not explain panic attacks. Where the verbal theory is imprecise and inconclusive, the formal theory is precise and wrong. Here again, we would argue that it is better to be precise and wrong than to be imprecise. Theories that are wrong move us forward, clarifying the direction we should (and should not) go in further developing the theory. When we arrive at a formal theory that does produce the phenomenon of interest (e.g., Figure 1, Panel B), our confidence in that explanation is increased because the theory showed us, rather than merely told us, that it can account for that phenomenon. Formal theories thus provide a tool for evaluating what is perhaps the most important function of a theory: its ability to explain phenomena. Given this strength, we believe that theorists should operate under a simple guiding principle: “don’t trust an explanation that you can’t simulate” (Westermann, 2020).

In the early stages of theory construction, we suspect that theorists will be best served by focusing on one or a narrow set of robust and likely qualitative phenomena to explain, such as the matching phenomenon (Borsboom et al., 2020; Haslbeck et al., 2019). However, it is critical that theory evaluation does not end there. Researchers should continue to evaluate the theory, investigating its explanatory breadth (i.e., the number of phenomena for which the theory can account) and explanatory precision (i.e., the specificity with which the theory can explain the phenomena of interest). This expansion in scope and precision is needed to guard against the possibility that the initial explanatory successes achieved by a formal theory are the result of “overfitting” the theory to a specific phenomenon. As the breadth and precision of explanation increases, the more confident we can be that the theory’s explanatory successes are attributable to its adequacy as a representation of the target system.

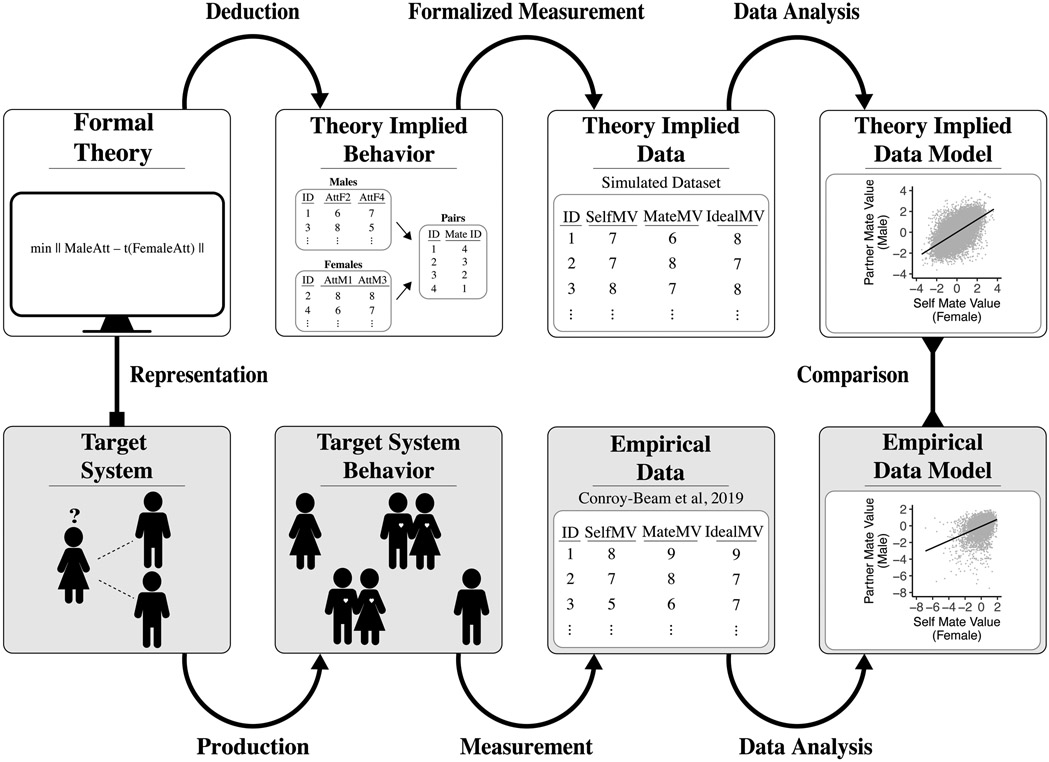
Evaluating a theory’s explanatory breadth can simply entail examining its ability to account for additional qualitative phenomena expected to arise from the target system beyond those the theorist initially set out to explain. However, to evaluate a theory’s explanatory precision requires that we move beyond visual inspection of qualitative theory-implied behavior (e.g., as depicted in Figure 1) and focus instead on a comparison between empirical data models and theory-implied data models. Empirical data models are any representation of data collected from the real world, such as a mean, correlation coefficient, latent factor structure, or any other summary of the data. Empirical data models are used in the appraisal of theories because data themselves are idiosyncratic, error prone, and subject to many causal influences beyond those that are of core interest (Bogen & Woodward, 1988). Theory-implied data models are these same representations of data (e.g., mean, correlation, and many other commonly performed statistical analyses) but using data that are deduced by the combination of our theory and our auxiliary hypotheses (for an extended discussion, see Haslbeck et al., 2019).

To illustrate this process, consider again the example of the matching phenomenon. The model of mating behavior developed by Conroy-Beam and colleagues adopted the Maximize Attraction Theory: agents seek the available partner to whom they are most attracted (Conroy-Beam et al., 2019). To create a formal Maximize Similarity Theory, we adapted this model so that agents instead seek the partner who is most similarly attracted to the agent as the agent is to them. All other aspects of the original model were retained. To evaluate this formal Maximize Similarity Theory, we used the model to simulate the theory-implied target system behavior (see Figure 2). We then used a set of formalized assumptions regarding measurement to produce theory-implied data and examined the correlation between an agent’s mate value (i.e., how attractive the agent is to member’s of the opposite sex in general) and the mate value of their partner, the same statistical analysis that Conroy-Beam et al. (2019) performed on their empirical data when examining the matching phenomenon. As seen in Figure 2, the Maximize Similarity Theory produces a strong positive association between an agent’s mate value and the mate value of their partner, thus demonstrating that it can indeed account for the matching phenomenon. However, there is some cause for concern. In empirical data collected by Conroy-Beam et al. from 45 different countries, the mean correlation between an agent’s mate value and their partner’s mate value across samples was r = 0.38 (cf. Feingold, 1988). In contrast, the mean correlation across the simulations performed with the formal theory was notably higher (r = 0.64). Thus, while the theory can explain the matching phenomenon, it does not provide an especially precise account of the phenomenon.

Figure 2:

Formal theories can be used to precisely deduce the data models we should expect from our theory. First, the deductive fertility of formal theory is leveraged to deduce the theory-implied target system behavior (e.g., how attraction and mate selection choices play out across generations). Second, using a formalized set of assumptions about how the components of that system are measured, we can produce theory-implied data (e.g., calculating an overall "mate value" for each agent on the basis of their traits and the preferences of potential partners). Finally, we can analyze the data to produce a theory-implied data model using the same statistical analyses used in our empirical data. Here, we examined the correlation between an agent’s mate value (calculated as the euclidean distance from the agent’s traits to the average preferences of members of the opposite sex) and that of their selected partner, with correlations examined within a series of individual samples (each of 45 countries in which data was collected for the empirical data and each of 225 simulation iterations for the formal theory). By comparing the theory-implied data model with a data model derived from empirical data, we can gain insight into the adequacy of the theory as an explanation of a given phenomena and as a representation of the target system. Just as importantly, we can use any discrepancies between these data models to improve the theory, inferring the best explanation for the observed discrepancy and, thereby, identifying potential avenues for further theory development. Here, the theory-implied data model produced by the formal Maximize Similarity Theory demonstrates that the theory can account for the matching phenomenon: agents with higher mate value tended to partner with other high mate value agents.

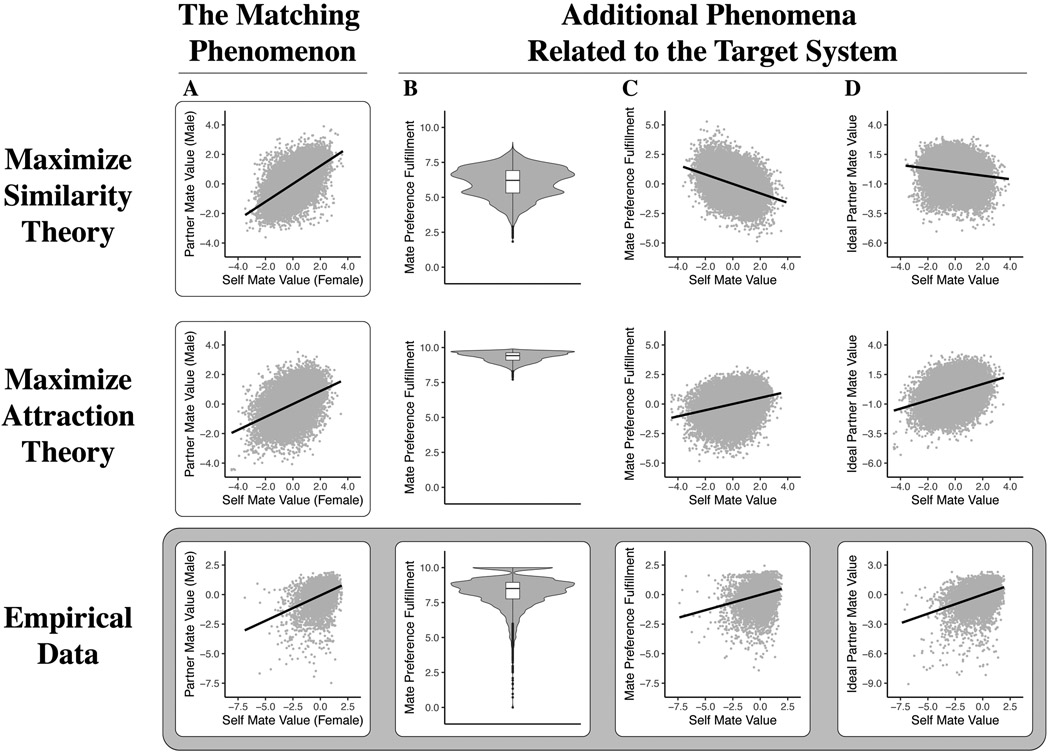
We next examined whether the Maximize Similarity Theory can explain additional phenomena related to mate selection. In their empirical data, Conroy-Beam et al. (2019) found that (a) individuals generally fulfill their mate preferences, (b) fulfillment is highest among those with high mate value, and (c) those with higher mate value tend to set their sights on higher mate value partners (i.e., they report that their ideal partner has higher mate value than do lower mate-value individuals). As seen in Figure 3, the Maximize Similarity Theory fails to account for each of these additional phenomena, thus exhibiting limited explanatory breadth.

Figure 3:

A comparison between data models based on empirical data and the data models implied by two theories of mate selection: the Maximize Similarity Theory and Maximize Attraction Theory (for further information about these empirical data, see Conroy-Beam et al. (2019)). We compared theory-implied and empirical data models relating to four phenomena: (A) the association between an individual’s mate value and that of their partner (i.e., the matching phenomenon), (B) the distribution of mate preference fulfillment, where preference fulfillment is scaled from 0 (no fulfillment) to 10 (complete fulfillment), (C) the association between an individual’s (or agent’s) mate value and their mate preference fulfillment, and (D) the association between an individual’s mate value and their ideal partner value. For all associations, the data were standardized within samples (i.e., individual countries in the empirical data; distinct iterations of the model simulations in the formal theories). The Maximize Similarity Theory accounts for the matching phenomenon (A), but fails to produce each of the other phenomena observed in the empirical data (B-D). In contrast, the Maximize Attraction theory accounts well for each of the phenomena, though it does appear to overestimate the level of mate preference fulfillment we should expect to see in the empirical data.

The Maximize Attraction Theory embedded in the original model by Conroy-Beam et al. (2019) fares much better (see Figure 3). As expected, the theory produces a positive association between an agent’s mate value and their partner’s mate value, thereby demonstrating that the theory can explain the matching phenomenon (cf. Conroy-Beam et al., 2019; Kalick & Hamilton, 1986, 1988). In contrast to the Maximize Similarity Theory, the Maximize Attraction Theory suggests a moderate association between these variables (mean correlation of r = 0.46) accounting reasonably well for the strength of this phenomenon. Furthermore, the Maximize Attraction Theory is able to provide an account for each of the additional phenomena we examined (see Figure 3; cf. Conroy-Beam et al., 2019, Figures 1 & 2). The Maximize Attraction theory thus exhibits both greater explanatory precision and greater explanatory breadth, giving us more confidence that its explanatory successes are due to its adequacy as a representation of the target system. These relative merits of the Maximize Attraction Theory would have been missed had we focused our evaluation only on the matching phenomenon, especially if had we limited our evaluation to a null hypothesis significance test. To better evaluate our theories, we must rigorously assess their explanatory breadth and precision, efforts that all but require formal theories.

4.3. A Tool for Measurement

A close examination of the simulation results presented in the previous subsection reveal that the explanatory shortcomings of the Maximize Similarity Theory arise, at least in part, because of how this formalized mate selection strategy interacts with auxiliary hypotheses embedded in the model regarding reproduction. Because agents do not necessarily choose the most attractive mate available to them, mate preferences in future generations do not converge on the traits optimal for reproduction and, thus, there is little relationship between an agent’s mate value and their ideal partner’s mate value. As Meehl would have noted (Meehl, 1978, 1990a), the discrepancy between our theory-implied data models and our empirical data models does not necessarily mean that our theory of mate selection has failed, only that the conjunction of the theory and our auxiliary hypotheses has failed. The fault may not lie in the formal theory, but in the auxiliary hypotheses. Formalization does not eliminate this fundamental difficulty in drawing inferences from explanatory failures (nor failed hypothesis tests). However, formal theories do confer advantages in addressing this difficulty. By forcing us to explicate both the theory and our auxiliary hypotheses, formalization allows us to interrogate both and consider both as potential explanations for the inability to produce a phenomenon of interest. If we deem the auxiliary hypotheses implausible, we can revise them and investigate them. If we deem the auxiliary hypotheses well-supported, we may conclude that the theory is indeed the most likely explanation for our observed explanatory shortcomings. It is thus critical that we not only formalize and critically examine our theory, but also our auxiliary hypotheses.

Among these formalized auxiliary hypotheses, we believe formalized measurement warrants particular attention. In recent years, measurement in psychology has been critically appraised, leading some to call for more precise and transparent measurement practices (Flake & Fried, 2019; Fried & Flake, 2018). Formalizing measurement addresses these needs. Formalization not only requires that we specify precisely and transparently what variables are being assessed, but also our assumptions about how those variables relate to components of the real world. In other words, researchers must specify the measurement function that links the component of the target system to the measured variable in the data (for an extended discussion, see Kellen, Davis-Stober, Dunn, & Kalish, 2020).

Consider again the example of panic attacks presented in Figure 1. To determine what we should expect to see in an empirical study of perceived threat and physiological arousal, we must specify our assumptions about how people reflect on their thoughts and emotions when responding to our assessments (cf. van der Maas, Molenaar, Maris, Kievit, & Borsboom, 2011). Do they report the average level of perceived threat over the specified time period? A weighted average that favors the moments immediately prior to the assessment? Or, as some research suggests, will their responses reflect the most intense perceived threat they experienced over the time window (Schuler et al., 2019)? Similar questions arise in our examination of mate selection strategies. In our adapted computational model, we assumed that individuals can and do accurately self-report their traits. There is good reason to question this auxiliary hypothesis (Kenealy, Gleeson, Frude, & Shaw, 1991). To better derive theory-implied data would require us to consider the function that relates objective trait values with self-report trait values. The measurement assumptions we make will affect the data models we expect from our theories and any misspecification of measurement functions has the potential to both give rise to and mask differences between theory-implied and empirical data models. For example, it is well-known that in 2 × 2 factorial designs, not all interaction effects are robust against monotonic transformations (Loftus, 1978; Wagenmakers, Krypotos, Criss, & Iverson, 2012). This means that an interaction effect may be observed when adopting one measurement function, but not when adopting a monotonic transformation of that function. Our expectations regarding measurement will, thus, determine what we are able to learn from empirical data, not only in the approach proposed here, but in any effort to use empirical data to evaluate predictions made by a theory.

It is thus critical to make our assumptions about measurement transparent. Just as formalizing a theory reveals hidden assumptions and unknowns in the theory, we suspect that formalizing measurement will similarly reveal many hidden measurement assumptions and raise important questions about precisely what our data have captured. Formalizing measurement will thus strengthen what Meehl identified as the second pillar of good science: the “fine calipers” of precise experiments and accurate measuring instruments. Indeed, we believe that the comparison of theory-implied and empirical data models laid out in Figure 2 achieves what Meehl saw as the key to good science: joining together rich formal theories with precise measurement.

4.4. A Tool for Informing Theory Development

The process of comparing theory-implied and empirical data models closely resembles what Meehl referred to as a consistency test: a comparison between a theory-derived parameter value and the actual value of that parameter derived from empirical data (Meehl, 1978). However, there is a critical distinction between Meehl’s approach and the approach we wish to advocate here. Rather than using this consistency test with an eye toward refutation or corroboration of the theory, we propose that the consistency test be used as a tool for theory development, informing how the theory can be revised and refined (Haslbeck et al., 2019). That is, we propose that if a discrepancy between the theory-implied and empirical data models is observed, researchers should not necessarily abandon the theory, but rather should consider the best explanation for the discrepancy and use this information to consider revisions to the theory that would bring it more in line with robust findings from empirical research.

For example, the Maximize Attraction Theory accounted reasonably well for a range of phenomena related to mating behavior (see Figure 3), but there were limits to the theory’s explanatory success. The model overestimated the extent to which mates achieve their partner preference. In the empirical data, even high mate value individuals have limits in their ability to realize their ideal mate preferences, whereas in the theory-implied data model, high mate-value individuals achieve near complete fulfillment (see Figure 3). These limits suggest areas in which the theory or its auxiliary hypotheses could be further developed. One plausible explanation for the discrepancy is that the ability to fulfill one’s preferences may be constrained by the structure of one’s social network. In the theory we evaluated here, we assumed a fully connected network. That is, each agent had the potential to partner with every agent of the opposite sex. In computational models adopting more realistic assumptions about the structure of one’s social network, the strength of the matching phenomenon becomes attenuated as that network becomes more sparse, a decline driven by high mate value agents who are unable to partner with other high value agents due to the constraints on their social network (Jia, Spivey, Szymanski, & Korniss, 2015). Accordingly, incorporating more realistic assumptions about social network structure may allow the theory examined here to more precisely explain the empirically observed rates of preference fulfilment.

We suspect that nearly all theories will benefit from an extended period of revisions and refinements such as this before being subjected to the kinds of “risky tests” advocated by Meehl. Accordingly, we regard the ability to inform theory development to be among the most valuable tools in the formal theory toolkit. It is important to note, however, that there are unique challenges and unanswered questions about precisely how best to use data models to inform formal theories in this way. For example, it remains unclear how best to balance parsimony and explanatory breadth when revising a theory. For an extended discussion of how data models can best inform theory development, see Haslbeck et al., 2019. Here, one point is of particular importance. Theorists must be careful to ensure that the data models they are using to inform theory development are robust. Just as the hardest findings to explain are those that are not true (Lykken, 1991), the most misguided revisions to a theory will be those made to accommodate a data model that cannot be reproduced or replicated. The need for robust empirical findings to inform theory generation and development underscores that our call to strengthen theory construction is not in lieu of or at odds with calls to strengthen the empirical rigor of psychological science (e.g., Munafò et al., 2017; Shrout & Rodgers, 2018); rather, it complements these efforts by calling for similar rigor in the construction of psychological theories.

4.5. A Tool for Collaboration and Integration

Finally, formal theories provide a tool for open and collaborative theory construction. The social psychologist Walter Mischel once quipped that theories are like toothbrushes, “no self-respecting person wants to use anyone else’s” (Mischel, 2008). We suspect this siloed development of theories ‘owned’ by a specific theorist arises at least in part because verbal theories do not lend themselves to collaborative development. To know what a theory asserts, it is often necessary to consult with the theorist who, as noted, may themselves be uncertain about the specifics of their verbal theory. This slows development, failing to marshal the efforts of a wide range of theorists and limiting the domains of expertise brought to bear in developing a theory. This is especially problematic in psychology where most phenomena straddle biological, psychological, and social realms. Further, it leads to a fractured theoretical landscape in which the theories within one domain play a limited role in the theories within another. Formal theories remedy these limitations by making the theory explicit, transparent, and expressed in languages used across domains of science. Formal theories are available to any theorist to advance, revise, or refute as they see fit and can be collaboratively developed by researchers across domains of expertise. Indeed, our ability to access, adapt, and evaluate the computational model of mating behavior developed by Conroy-Beam and colleagues is a clear illustration of the way in which formal theories support open and collaborative theory development. Furthermore, because formal theories are specified in a common language, they can be more readily integrated with other formal theories and commonalities across theories may be more readily identified. Formal theories thus have the potential to support the integration of theories across domains and the development of theories that cut across multiple target systems (Muthukrishna & Henrich, 2019). In other words, formal theories set the stage for precisely the type of cumulative and integrative growth that Meehl wanted to see in psychology.

5. Conclusion

The advancement of scientific knowledge depends on the development of scientific theories. This notion is implicit in Meehl’s classic critique and perhaps in the minds of many psychologists, but it warrants making explicit because it clarifies the target of our scientific endeavors. As psychologists, we should be striving for well-developed theories that are sufficiently good representations of a target system that they support the explanation, prediction, and control of psychological phenomena. In this article, we have argued that formalizing theories early in the process of theory construction will help move us toward this aim (cf. Guest & Martin, 2020). We illustrated the advantages of formal theory using a simple difference equation model from the clinical psychology literature and a more well-developed agent-based model from the social psychology literature. Together, we believe these examples illustrate how formal theories equip us with a set of tools for theory construction that can be applied across domains of “soft psychology.”

Importantly, our argument is not that extant verbal theories should be discarded. The theory crisis in psychology is not due to an absence of good ideas about how the brain, mind, and human behavior work. To the contrary, there are numerous rich and insightful verbal theories in the psychology literature. The value of formal theories is that they equip us with tools to better develop, evaluate, and integrate these verbal theories. For example, we regard the verbal “vicious cycle” theory of panic attacks used throughout this paper to be among the best theories clinical psychology has to offer. Yet this theory has seen little development in the past three decades, despite thousands of published articles on panic disorder during that time (Asmundson & Asmundson, 2018). Formalizing the theory provides an avenue for advancing it and, by doing so, strengthening our ability to explain, predict, and treat panic disorder. In the coming years, we expect that most efforts to develop formal theories in “soft psychology” will be similarly rooted in existing verbal theories, taking them as a starting point for continued theory construction. Further, we suspect that any newly generated formal theory will begin with a rich verbal theory from researchers with substantive expertise in the target system and phenomena of interest. Theorizing is, thus, not limited to those with mathematical or computational modeling expertise. Nonetheless, we believe that psychology as a whole will benefit from bringing more mathematical and computational modeling expertise into its ranks (Borsboom et al., 2020) and that individual theorists will benefit from utilizing the tools provided by formal theory, either through collaboration or by developing their own expertise in formal theory construction.

It is also important to note that formal theory provides a toolkit, not a panacea. Like any set of tools, formal theories can be misused. We see two dangers of particular note. First, theory can be used as a tool of intimidation: a shield used to make the theory less accessible and, thus, less susceptible to criticism and revision. This danger is heightened in areas of psychology where readers may lack the training to readily interpret the equations or algorithms with which the structure of the theory is expressed. To avoid this danger, researchers should strive not only to be transparent, but also clear and thorough in annotating, explaining, and providing the rationale for each aspect of the formal theory. Doing so will strengthen each of the advantages of formal theory described here and assist in bringing formalization into regular practice within “soft psychology.”

Second, formal theory can be used as a tool for wishful thinking, giving the theorist an inflated sense of their theory’s strengths and thereby leading to over-interpretation of model parameters and complacency in theory evaluation (Brown, Sokal, & Friedman, 2013). This danger may arise, especially, following the initial stage of generating a formal theory, when a particular model with a particular set of parameters has demonstrated an ability to explain a phenomenon of interest. The remedy to this danger is straightforward: the initial act of formalization must be treated not as a culminating act, but rather as the beginning of a process of ongoing theory development (for frameworks detailing this process, see Haslbeck et al., 2019; Guest & Martin, 2020). This process requires rigor in all aspects of psychological research; not only in the generation of formal theories, but also in the collection and analysis of data for the purposes of informing and evaluating those theories. It will be especially important to use robust empirical findings to investigate the theory’s explanatory breadth, as these efforts increase our confidence that the theory’s explanatory successes are not a result of mathematical fishing but rather are the result of having constructed a theory that is an adequate representation of the target system that gives rise to the phenomena of interest.

Although the approach we have advocated for here is not without its dangers, there is reason to be optimistic about its potential. Formal theories have been fruitfully used in other domains of psychology, including in mathematical psychology (Estes, 1975), cognitive psychology (Ritter, Tehranchi, & Oury, 2019), and computational psychiatry (Friston, Redish, & Gordon, 2017; Huys, Maia, & Frank, 2016). This work provides clear examples to follow, colleagues with whom to collaborate, and guides for developing mathematical and computational models (e.g., Jaccard & Jacoby, 2019; Smaldino, 2020; Farrell & Lewandowsky, 2018; van Rooij & Blokpoel, 2020). In addition, although it represents a small portion of the work in “soft psychology,” there have been valuable efforts to incorporate formal theory in clinical psychology (e.g., Fradkin, Adams, Parr, Roiser, & Huppert, 2020; Schiepek, Aas, & Viol, 2016), personality psychology (e.g., Pickering, 2008), and social psychology (e.g., Smith & Conrey, 2007; Read & Monroe, 2019; Conroy-Beam et al., 2019; Denrell & Le Mens, 2007). By building upon this work, we believe that the “invisible hand” formal theories championed by Meehl will be considerably more achievable than he believed them to be and we are optimistic that embracing formal theory as a tool for theory construction will allow us to make genuine progress in our ability to explain, predict, and control psychological phenomena.

Appendix

A. Four “Vicious Cycle” Theories of Panic Attacks

In Figure 1, we generated four formal theories implementing a verbal “vicious cycle” theory of panic attacks. We did so by posing two questions: what is the precise effect of perceived threat (T) on arousal (A)? and what is the precise effect of arousal on perceived threat? We limited ourselves ourselves to considering only linear or sigmoidal relationships for each. Note that even with this constraint, there is no limit to the number of possible implementations through the selection of different parameter values defining these equations. For the purposes of this illustration, we chose a single set of parameter values for the linear effect of arousal on perceived threat, the sigmoidal effect of arousal on perceived threat, the linear effect of perceived threat on arousal, and the sigmoidal effect of perceived threat on arousal. The four formal theories here represent the four possible combinations of these effects. Notably, one parameter value (i.e., the parameter value defining the half saturation point in the sigmoidal effect of arousal on perceived threat) was selected because we knew it to be associated with vulnerability to panic attacks from our prior development of a vicious cycle theory of panic attacks (Robinaugh et al., 2019).

In addition to this positive feedback loop between the two core theory components, we incorporated a third component: homeostatic feedback (H). We then specified a negative feedback loop between arousal and this homeostatic feedback component. Importantly, the effects of homeostatic feedback on arousal remained consistent across each of the four formal theories and, thus, is not a source of any differences between these implementations of the verbal theory. It is incorporated only to account for the processes that bring physiological arousal back to homeostasis following substantial increases to arousal.

The difference equations and parameter values used for each formal theory are as follows:

I. Formal Theory A (Linear - Linear)

$$\begin{gathered} A_{\tau +1}=A_{\tau }+.5(T_{\tau }-A_{\tau })-10H_{\tau } \\ {T}_{\tau +1}=T_{\tau }+1(A_{\tau }-T_{\tau }) \\ {H}_{\tau +1}=H_{\tau }+.01(\frac{A_{\tau }^8}{A_{\tau }^8+{.75}^8}-H_{\tau }) \end{gathered}$$

II. Formal Theory B (Linear - Sigmoidal)

$$\begin{gathered} A_{\tau +1}=A_{\tau }+.5(T_{\tau }-A_{\tau })-10H_{\tau } \\ {T}_{\tau +1}=T_{\tau }+1(\frac{A_{\tau }^5}{A_{\tau }^5+{.4}^5}-T_{\tau }) \\ {H}_{\tau +1}=H_{\tau }+.01(\frac{A_{\tau }^8}{A_{\tau }^8+{.75}^8}-H_{\tau }) \end{gathered}$$

III. Formal Theory C (Sigmoidal - Linear)

$$\begin{gathered} A_{\tau +1}=A_{\tau }+.5(\frac{T_{\tau }^5}{T_{\tau }^5+{.5}^5}-A_{\tau })-10H_{\tau } \\ {T}_{\tau +1}=T_{\tau }+1(A_{\tau }-T_{\tau }) \\ {H}_{\tau +1}=H_{\tau }+.01(\frac{A_{\tau }^8}{A_{\tau }^8+{.75}^8}-H_{\tau }) \end{gathered}$$

IV. Formal Theory D (Sigmoidal - Sigmoidal)

$$\begin{gathered} A_{\tau +1}=A_{\tau }+.5(\frac{T_{\tau }^5}{T_{\tau }^5+{.5}^5}-A_{\tau })-10H_{\tau } \\ {T}_{\tau +1}=T_{\tau }+1(\frac{A_{\tau }^5}{A_{\tau }^5+{.4}^5}-T_{\tau }) \\ {H}_{\tau +1}=H_{\tau }+.01(\frac{A_{\tau }^8}{A_{\tau }^8+{.75}^8}-H_{\tau }) \end{gathered}$$

To derive the target system behavior implied by these formal theories, we implemented them as a set of difference equations in R (R Core Team, 2019). We conducted two sets of simulations. In Condition 1, we induced a specified level of arousal (A=.5), at time step 10, in order to evaluate how each system would respond to a perturbation. In Condition 2, we added a red noise function (van Nes & Scheffer, 2004) to the equation defining arousal in order to incorporate variation around a low mean level of arousal. This condition was intended to capture how the system would respond to natural variation in arousal arising from either internal or external stimuli. The results of these simulations are presented in Figure 1 of the main text. The R code for all models and simulations can be found at: https://osf.io/gcqnf/. For readers interested in learning more about a formal theory of the vicious cycle theory of panic attacks or the behavior of the system under different parameter settings, see Robinaugh et al. (2019).

B. The Deductive Fertility of Formal Theories: The Example of the Matching Phenomenon

In this Appendix, we illustrate the value of what Paul Meehl referred to as the “immense deductive fertility” of formal theories using an agent-based model of mating behaviour developed by Conroy-Beam and colleagues (Conroy-Beam et al., 2019). The model created by Conroy-Beam and colleagues is an agent-based model in which a population of male and female agents interact with each other in three stages: an attraction stage in which each agent determines how attracted they are to all other agents of the opposite sex; a selection stage in which each agent is paired with a partner; and a reproduction stage in which partners produce offspring that inherit the traits and preferences of their parents.

In the selection stage of this model, the researchers adopted what we will call the Maximize Attraction Theory. The Maximize Attraction Theory aims to explain the robust observation that individuals tend to resemble their partners across a range of desirable traits (e.g., physical attractiveness), a phenomenon known as the matching phenomenon. The Maximize Attraction Theory posits that this phenomenon arises when each individual member of a population seeks out the partner to whom they are most attracted. Accordingly, in the agent-based model, agents are paired with the available partner to whom they are most attracted, based on a range of desirable traits. The verbal Maximize Attraction Theory does not specify how an individual goes about integrating information across traits to inform which partner to select. However, to formalize the theory, an integration mechanism must be specified. Conroy-Beam et al. (2019) investigated which mechanism is most appropriate by formalizing and evaluating several possible mechanisms by which this integration may occur.

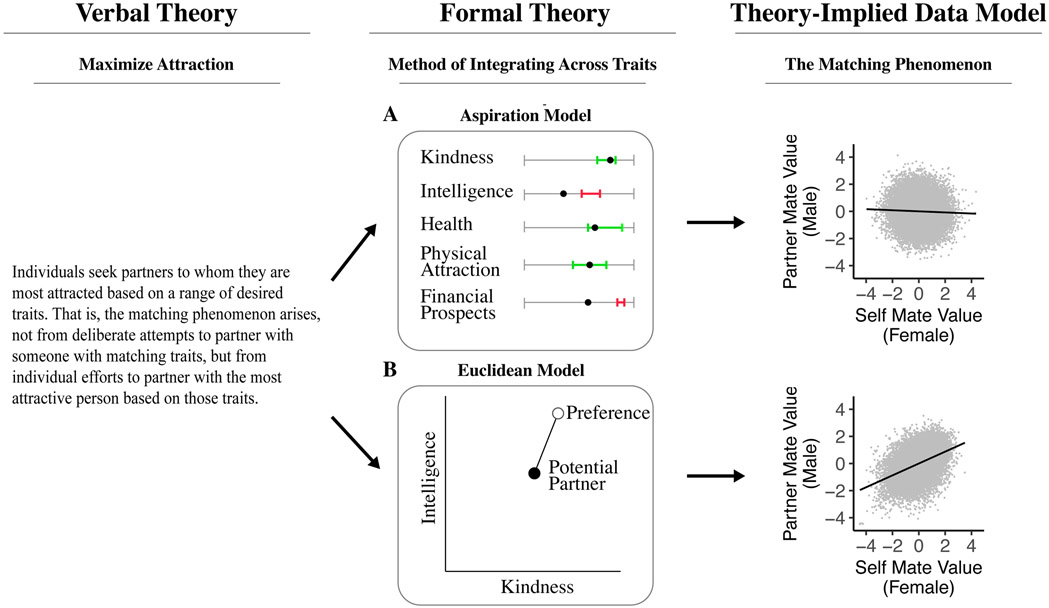
In Figure 4, we conduct a set of analyses similar to those conducted by Conroy-Beam et al. (2019), comparing two formalized integration mechanisms.³ The first is based on the number of traits in a potential partner that fall within an acceptable range (i.e., an aspiration mechanism). The second is based on the difference between preferences and traits in multi-variate space (i.e., a euclidean distance mechanism), with smaller distance indicating greater attraction. Though both of these formalized integration mechanisms are consistent with the verbal Maximize Attraction Theory, they make very distinct predictions and only one (the euclidean distance mechanism) produces the matching phenomenon (i.e., a positive association between an individual’s mate value and their partner’s mate value). Accordingly, it is impossible to say precisely what the verbal Maximize Attraction Theory theory predicts, because what it predicts depends upon aspects of the theory that we have left unspecified in our verbal description (cf. Figure 1). In contrast, with the formal theory we are able to deduce precisely what the theory predicts, a capacity that undergirds the formal theory’s ability to better support theory evaluation and development.

Figure 4:

Due to its imprecision, the verbal Maximize Attraction theory can be interpreted in multiple ways. For example, it is unclear from the verbal theory precisely how we integrate information across traits to determine who is the most appropriate partner. To illustrate the impact of failing to make these aspects of the theory explicit, we reproduced findings from two computational models developed and evaluated by Conroy-Beam et al. (2019). In the first (Panel A), a so-called “aspiration” model, individuals have an ideal range for each of a set of traits and the more traits that fall within the ideal range, the higher the agent’s attraction to the potential mate. In the second (Panel B), attraction is determined by the Euclidian distance between an agent’s preferences and the potential partner’s traits in the multi-variate space defined by all traits of interest. As seen in the final column, these models make very different predictions. When adopting the aspiration mechanism, there is no association between an agent’s mate value (defined as the euclidean distance from the agent’s traits to the average preferences of potential partners) and the mate value of their partner. In contrast, when adopting the euclidean distance mechanism, a strong positive association (i.e., the matching phenomenon) is observed.