A new method for quantification and 3D visualization of brain tumor adhesion using slip interface imaging in patients with meningiomas

Abstract

Objectives

To develop an objective quantitative method to characterize and visualize meningioma-brain adhesion using MR elastography (MRE)-based slip interface imaging (SII).

Methods

This retrospective study included 47 meningiomas (training dataset: n = 35; testing dataset: n = 12) with MRE/SII examinations. Normalized octahedral shear strain (NOSS) values were calculated from the acquired MRE displacement data. The change in NOSS at the tumor boundary (ΔNOSS_bdy) was computed, from which a 3D ΔNOSS_bdy map of the tumor surface was created and the probability distribution of ΔNOSS_bdy over the entire tumor surface was calculated. Statistical features were calculated from the probability histogram. After eliminating highly correlated features, the capability of the remaining feature for tumor adhesion classification was assessed using a one-way ANOVA and ROC analysis.

Results

The magnitude and location of the tumor adhesion can be visualized by the reconstructed 3D ΔNOSS_bdy surface map. The entropy of the ΔNOSS_bdy histogram was significantly different between adherent tumors and partially/completely non-adherent tumors in both the training (AUC: 0.971) and testing datasets (AUC: 0.900). Based on the cutoff values obtained from the training set, the ΔNOSS_bdy entropy in the testing dataset yielded an accuracy of 0.83 for distinguishing adherent versus partially/non-adherent tumors, and 0.67 for distinguishing non-adherent versus completely/partially adherent tumors.

Conclusions

SII-derived ΔNOSS_bdy values are useful for quantification and classification of meningioma-brain adhesion. The reconstructed 3D ΔNOSS_bdy surface map presents the state and location of tumor adhesion in a “clinician-friendly” manner, and can identify meningiomas with a high risk of adhesion to adjacent brain parenchyma.

Introduction

Meningiomas are commonly treated by resective surgery and complete resection is the preferred treatment. In addition to the surgeon’s experience and ability, the success of tumor resection commonly depends on tumor characteristics such as tumor size, consistency, and adherence to the adjacent brain parenchyma or other critical structures. The adhesion of meningiomas to adjacent normal yet critical tissue has long been recognized to impact the rate of surgical complications and to influence surgical aggressiveness [1-3]. Adhesion can lead to longer operative times, increase the risk of stroke, or result in permanent neurologic deficits, especially when the meningioma location involves eloquent areas of the cortex or cranial nerves [4]. Therefore, preoperative imaging aimed at identifying tumor adhesion could allow better risk assessment, alter the surgical approach, or even change treatment to a non-invasive technique such as radiotherapy/radiosurgery.

Since magnetic resonance imaging (MRI) is widely used in the surgical planning and evaluation of meningiomas, many MRI features have been proposed to predict the adherence of a tumor to the brain surface, such as the peritumoral cerebrospinal fluid (CSF) cleft [5, 6], peritumoral edema [7, 8], tumor rim pattern [9], and tumor vascularity [7, 8]. However, these static methods do not directly measure tumor mobility relative to adjacent brain parenchyma (adhesion), but rather measure the indirect consequences of tumor adhesion. A strategy to overcome this limitation lies in the ability to noninvasively assess the motion of the brain tumor relative to the brain parenchyma. A new imaging technique, named slip interface imaging (SII), has been recently developed to determine tumor-brain adhesion by directly assessing the relative motion between the tumor and the adjacent brain parenchyma with the introduction of gentle external dynamic vibration [10, 11]. Another MRI-based technique that subtracts T2-weighted images in systolic and diastolic phases of the cardiac cycle has also been developed to evaluate meningioma-brain adhesion by visualizing the CSF pulsation at the brain/tumor interface [12]. However, the cardiac cycle-dependent motion amplitude of MRI detectable CSF flow varies in different intracranial locations and is minimal toward the vertex. SII, in contrast, uses extrinsically applied mechanical vibrations at a much higher frequency and its measurement approach is more sensitive to micron-range shear motion throughout the brain.

SII is based on the principles of brain MR elastography (MRE), which is performed by gently vibrating the head with a mechanical driver and simultaneously imaging the brain tissue displacements using a phase-contrast type MRI sequence [13]. Previous SII work has defined the presence of a slip interface when a large shear strain (i.e., normalized octahedral shear strain, NOSS) is detected as two adjacent surfaces move relative to each other [11]. A hyper-intense NOSS tumor interface is the characteristic of a slip boundary, where a tumor is not adherent to the adjacent brain parenchyma. Conversely, a high NOSS is not seen along the tumor interface when the tumor is tightly bonded to the adjacent tissue. Although SII characterization of tumor adhesion has been shown to agree well with intraoperative assessments, the evaluation method is subjective and relies on the visual perception of the NOSS signal at the tumor-brain interface compared to the adjacent parenchyma [11]. Therefore, objective quantitative characterization of brain tumor adhesion is needed, as it will contribute to the establishment of a standard method for grading tumor adherence and improve patient management. Moreover, the SII results are displayed in 2D images, which require interpolation to translate into a 3D representation. A 3D direct visualization of tumor adhesion would further assist precise adhesion localization for surgical planning.

Toward these goals, we have developed a new methodology based on SII in which the change of NOSS across the tumor boundary was used to create a quantitatively objective measurement to discriminate between adhesion groups. A 3D tumor surface map was also generated to represent the location and magnitude of tumor adhesion. The aim of this study was to evaluate the effectiveness of this newly developed quantitative method for analyzing and visualizing the SII data of tumor adherence.

Materials and methods

Patients

The research was approved by our Institutional Review Board, and all patients provided written informed consent. Between October 2013 and October 2019, patients that met all the following criteria were identified: (a) patients had brain MRE; (b) tumors were histopathologically confirmed as meningiomas; (c) surgical resection was performed within 7 days after the MRE examination. Exclusion criteria were as follows: (a) recurrent tumors; (b) intraosseous tumors; (c) tumors with no surgical information about their adhesion to surrounding structures; (d) small tumors with maximum tumor diameter <2.5 cm; and (e) unsuccessful MRE acquisitions. The following information was collected for all patients: sex and age at surgery, tumor size in maximum dimension, tumor location (convexity, falx/parasagittal, and skull base tumors), and tumor WHO grade [14].

Surgical grading of meningioma–brain adhesion

Surgical findings of tumor adhesion to the adjacent brain tissue were evaluated by one neurosurgeon (J.J.V.G., with 15 years of experience) blinded to SII results as described in prior work [11]. The degree of tumor adhesion was grouped into complete adhesion, partial adhesion, and no adhesion. The definitions were as follows: (1) complete adhesion—separating the tumor from the adjacent brain was difficult and dissection had to be performed in a subpial fashion in more than 2/3 of the total tumor-cortex interface. (2) No adhesion—a clear surgical plane was found in more than 2/3 of the surface between the tumor capsule and brain surface. (3) Partial adhesion—a clear surgical plane was partially lost where the pial membrane was adherent to the tumor in more than 1/3 and less than 2/3 of the interface.

SII acquisition

SII is based on MRE acquisitions using a single-shot, flow-compensated, spin-echo (SE), echo-planner-imaging (EPI) MRE pulse sequence performed on 3-T MRI scanners [11]. Fourteen meningioma patients were scanned using the GE whole-body 3-T HDxt system (GE Healthcare); 16 patients were scanned using the GE Discovery whole-body 3-T MR750 system (GE Healthcare); and 16 patients were scanned on a recently developed high-performance compact 3-T scanner [15, 16]. All scans were acquired with standard 8-channel receive-only head coils. Briefly, low-amplitude mechanical vibrations at 60 Hz were introduced into the brain with a soft, pillow-like passive driver placed underneath the subject’s head (Fig. 1(a)). The three-dimensional brain motion was encoded into the phase of the MR signal with the following imaging parameters: repetition time (TR) / echo time (TE) = 3600/64.3 ms for the HDxt scanner; TR/TE = 4000/57.3 ms for the MR750 scanner; TR/TE = 4000/58.7 ms for the compact 3 T scanner; field of view (FOV) = 24 cm; 80 × 80 image acquisition matrix reconstructed to 128 × 128; 48 continuous axial slices with a slice thickness of 3 mm; 2xASSET acceleration; 8 phase offsets sampled over one period of the 60 Hz motion; 6 MRE motion encoding directions with ±x, ±y, ±z.

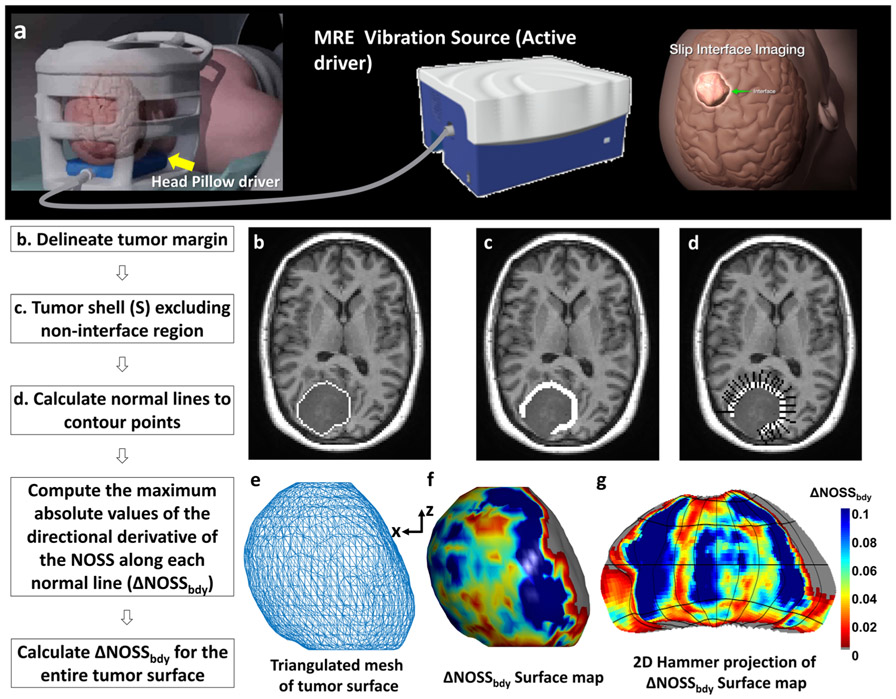
Fig. 1.

(a) Brain MR elastography (MRE) setup. (b–g) The diagram of the ΔNOSS_bdy calculation. (b) An example slice of T1W image with a manually delineated tumor margin. (c) The tumor shell after dilation, erosion, and exclusion of non-interface regions. (d) Black lines orthogonal to the tumor surface placed at contour points. For illustration purposes, only half of the orthogonal lines are shown. (e) The surface mesh is generated by MATLAB from the tumor volume and smoothed by a box filter with the kernel size of 3 × 3 × 3. (f) The 3D surface map with ΔNOSS_bdy values projected onto the 3D surface. The gray color indicates a non-interface region that was not included in the calculation. (g) A 2D Hammer projection of the ΔNOSS_bdy surface map unfolded along the z-direction to facilitate the 3D data visualization

Anatomical image acquisition

A 3-dimensional T1-weighted (T1W) image was also collected. On the HDxt scanner, the T1W image was acquired with an inversion recovery-prepared spoiled gradient echo (IR-SPGR) pulse sequence with the following parameters: sagittal orientation; superior-inferior frequency-encoding direction; TR/TE = 7.0/2.8 ms; 11° flip angle; inversion time = 400 ms; FOV = 27 cm; 256 × 256 acquisition matrix; 1.75× array spatial sensitivity encoding technique acceleration; and 196 slice locations with 1.2-mm spacing. On the MR750 scanner and the compact 3-T scanner, the T1W image was acquired with a magnetization-prepared rapid gradient echo (MP-RAGE) pulse sequence with the following parameters: sagittal orientation; superior-inferior frequency encoding direction; TR/TE = 7.4/3.0 ms; 8° flip angle; inversion time = 900 ms; FOV = 26 cm; 256 × 256 acquisition matrix; and 166 slice locations with 1.2-mm spacing.

Brain and tumor segmentation

All tumors were manually segmented by manually delineating the tumor boundaries on each slice by an experienced radiologist (X.L., with 20 years of experience) who was blinded to the clinical information of the patients using an in-house developed Matlab-based program. The boundaries were agreed upon by one other investigator (Z.Y., an MRI scientist with 10 years of experience in MRE) at the time of segmentation. Brain masks were computed by segmentation of the T1W images to produce probabilistic maps of gray matter, white matter, and CSF using SPM5 [17]. A brain mask was defined by voxels in which the gray matter content plus the white matter content was greater than the CSF content. The T1W image, brain mask, and tumor mask were then registered and resliced to the MRE space. Trilinear interpolation was used for resampling the T1W image and the brain and tumor masks were resampled with nearest-neighbor interpolation.

Quantitative SII analysis and 3D visualization

For each patient, the NOSS map was calculated from the unwrapped phase image as described in prior work [11]. The phase data was unwrapped with an iterative 3D graph cuts-based unwrapping algorithm [18, 19]. The OSS was calculated for each phase offset [20] and a final OSS map was calculated as the mean of the eight sets of OSS data. The NOSS map was generated by normalizing OSS to the combined amplitude (square root of the sum of squares) of the first harmonic of the complex x/y/z-axis shear waves.

The change in NOSS at the tumor boundary (ΔNOSS_bdy) was calculated from the tumor periphery as illustrated in Fig. 1. First, with morphological operations (erosion and dilation) in 3D, a 3-pixel wide tumor shell was created, consisting of the one-pixel layer just outside the tumor mask and the two outermost pixel layers inside the tumor mask. A brain shell was also created, consisting of the outermost three pixel layers inside the brain mask. Because the focus is on the interface between the tumor and brain surface, the non-brain interface regions were excluded from the tumor shell by excluding the intersection of the tumor shell and the brain shell.

The following processing was performed in 2D using an in-house developed Matlab-based program. For each slice containing the tumor, lines orthogonal to the tumor surface were created at each contour point (only half of these normal lines are shown in Fig. 1d for illustration purposes). The absolute values of the directional derivative of the NOSS values along these lines were calculated for the three points in the tumor shell, using finite differences. The ΔNOSS_bdy value at each contour point was taken to be the largest of these three values, to allow for possible errors in segmentation. The ΔNOSS_bdy values were calculated for the entire tumor surface, allowing for the creation of a 3D ΔNOSS_bdy map of the tumor surface (Fig. 1f). The 3D surface map can also be visualized using a Hammer projection in which spatial ratios are maintained (Fig. 1g) [21]. A non-adherent region with a visible NOSS contour is expected to have a large ΔNOSS_bdy value as it represents the NOSS variation of voxels across the tumor boundary.

Statistical analysis

Statistical analyses were performed using JMP software (v. 14.1.0, SAS Institute). Continuous variables were expressed as mean ± one standard deviation (SD); categorical variables were reported as counts or percentages. All tests were 2 sided andp <0.05 was considered statistically significant. To build and validate the predictive model using ΔNOSS_bdy, the enrolled patients were split semi-randomly (complete:partial:no adhesion ratio retained) into two subsets (3:1 ratio): 35 for training and 12 for testing. The one-way ANOVA test (for continuous variables) and chi-square test (for categorical variables) were used to assess differences in demographic and clinical data within and between the training and testing sets.

To compare ΔNOSS_bdy values among three adhesion groups, the probability distribution of ΔNOSS_bdy over the entire tumor surface was constructed by quantizing the ΔNOSS_bdy values into 40 bins spanning the range from 0 to 0.4. We chose 5 commonly used statistics features to describe the ΔNOSS_bdy distribution at the tumor boundary: mean, standard deviation, skewness, kurtosis, and entropy. To test for significant group-wise differences while controlling for nuisance variables, a linear model was then fit to each ΔNOSS_bdy feature with predictors including age, sex, scanner system, and group. The ΔNOSS_bdy features were then corrected for age, sex, and scanner system.

In the training cohort, to eliminate the redundant features, we removed highly correlated features by calculating the absolute correlation coefficient (ACC) between the features with Spearman’s rank correlation. If two variables had a strong correlation (ACC > 0.7), we calculated the mean absolute correlation of each variable and kept only the variable with the smallest mean absolute correlation, removing the variable with the larger absolute correlation. The discrimination ability of the remaining age-/sex-/scanner-corrected features (mean and entropy) to classify tumor adhesion was investigated by using a one-way ANOVA with post hoc Steel-Dwass multiple comparisons. For comparison, the mean and entropy of absolute NOSS values calculated from the tumor margin (also corrected for age, sex, and scanner system) were also analyzed (see Appendix-E1). To further evaluate the classification ability of the ΔNOSS_bdy feature, the receiver operating characteristics (ROC) curves were derived in both the training and testing cohorts. The optimal cutoff value of the ΔNOSS_bdy feature determined by the ROC curve in the training cohort was applied to the testing set to derive the accuracy. Area under the curve (AUC) and diagnostic accuracy to distinguish the degree of adhesion was derived in both the training dataset and testing dataset.

Results

Demographic and clinical characteristics of patients

Between October 2013 and October 2019, a total of 60 patients with a meningioma were diagnosed via histopathology. Among these patients, 14 patients were excluded because of recurrent tumors (n = 2), intraosseous tumors (n = 4), tumors with no surgical information about their adhesion to surrounding structures (n = 3), small tumors with maximum tumor diameter < 2.5 cm (n = 3), and unsuccessful MRE acquisition owing to large patient motion (n = 1) and mechanical failure (n = 1). A total of 47 meningiomas in 46 patients (one patient had two meningiomas) were included in the study (Fig. 2).

Fig. 2.

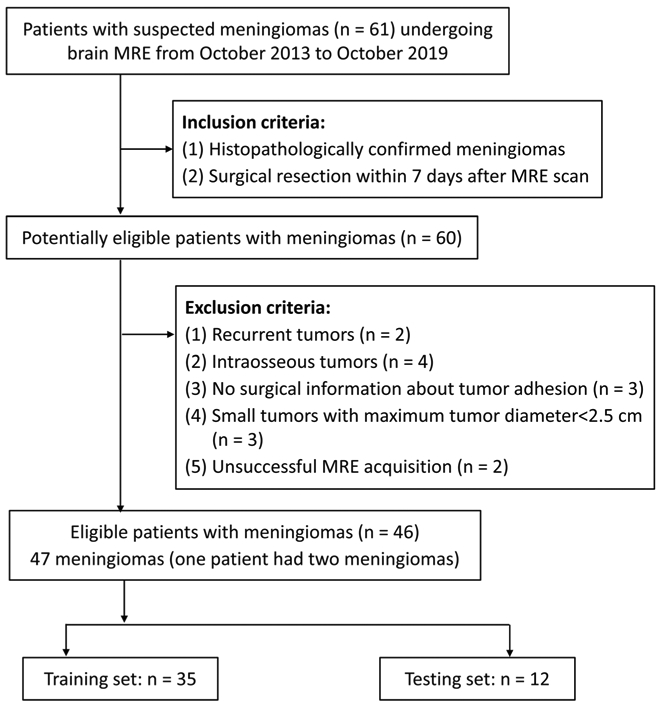
Flowchart of patient selection

The patients’ demographic and clinical data in the training and testing cohorts are presented in Table 1. The mean age of patients was 59.76 (age range of 38–80 years), 35 of which (74%) were female. It was determined at surgery that the interface between the tumor capsule and the adjacent brain parenchyma in the 47 cases showed complete adhesion in 8 (17%), partial adhesion in 16 (34%), and no adhesion in 23 (49%). No significant differences were found between the training and testing datasets for all demographic and clinical characteristics. Age, sex, tumor size, and tumor location did not correlate with meningioma adhesiveness in both training and testing datasets. The correlation between the WHO grade and adhesion groups was significant in the training dataset (p = 0.01). All WHO grade II tumors in the training set (n = 6) were found to be adherent to the brain parenchyma in more than 1/3 of the tumor interface, suggesting that WHO grade II meningiomas are more likely to be adherent tumors. However, by dividing into histological subtypes, no significant difference was observed between tumor histological subtype and adhesion (p >0.1).

Table 1.

Demographic data and clinical characteristics according to surgical adhesion groups and training/testing groups

	Full data set	Trainiang (n = 35)					Testing (n = 12)					Between- group p value
		Total	Complete adhesion (n = 6)	Partial adhesion (n = 12)	No adhesion (n = 17)	Within- group p value	Total	Complete adhesion (n = 2)	Partial adhesion (n = 4)	No adhesion (n = 6)	Within- group p value
Age Mean (SD)	59.76 (9.78)	60.71 (10.05)	65 (8.56)	61.75 (9.17)	58.47 (11.01)	0.37	56.5 (12.3-3)	50.0 (5.66)	59.5 (16.74)	56.67 (11.6-4)	0.71	0.24
Sex (female)	35 (74%)	26 (74%)	4 (67%)	9 (75%)	13 (76%)	0.88	9 (75%)	1 (50%)	3 (75%)	5 (83%)	0.73	1.0
Tumor size (cm) Mean (SD)	4.44 (1.36)	4.38 (1.39)	4.25 (0.76)	4.88 (1.89)	4.08 (1.09)	0.31	4.63 (1.31)	4.5 (0.71)	3.93 (0.53)	5.15 (1.67)	0.38	0.58
Site (Falx and parasagittal/convexity/skull base*)	9/3/35	7/2/26	1/0/5	3/1/8	3/1/13	0.95	2/1/9	0/0/2	1/0/3	1/1/4	1.0	1.0
WHO grade (I/II)	38/9	29/6	4/2	8/4	17/0	0.01	9/3	1/1	3/1	5/1	0.73	0.67
Histological subtype (meningothelial/fibrous/transitional/psammomatous/-aytipical)	25/3/8/2/9	19/1/7/2/6	3/1/0/0/2	5/0/2/1/4	11/1/4/1/0	0.23	6/2/1/0/3	1/0/0/0/1	1/1/1/0/1	4/1/0/0/1	0.91	0.40

^*Skull base location was defined as cavernous sinus, cerebellopontine angle, clinoid, clivus, foramen magnum, jugular foramen, middle fossa, olfactory groove, petroclival, petrous, planum sphenoidale, posterior fossa, and sphenoid wing

Note: Numbers in bold are significant at p < 0.05

ΔNOSS_bdy features

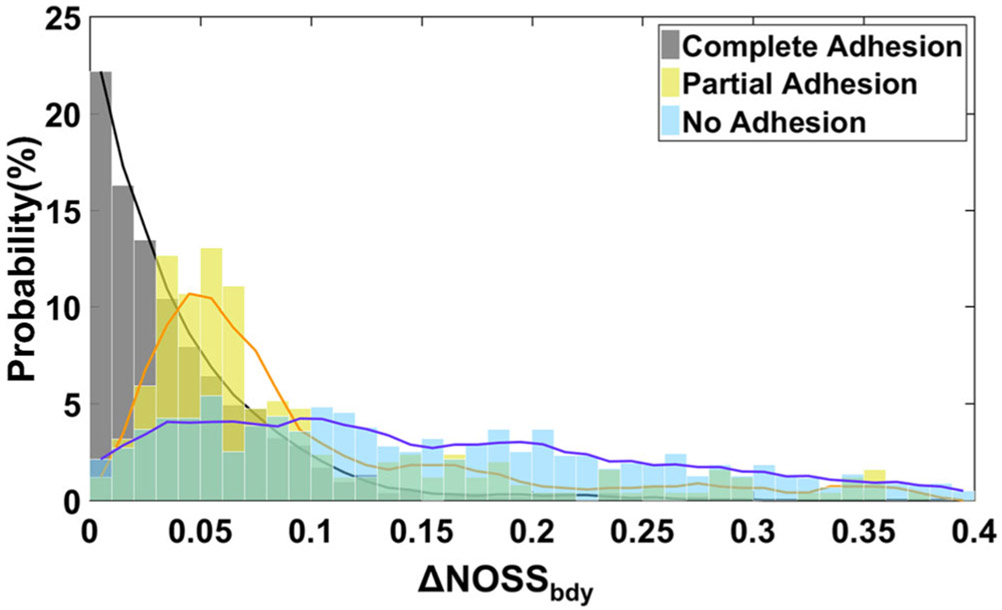
Figure 3 shows representative probability histograms of ΔNOSS_bdy values from one completely adherent, one partially adherent, and one non-adherent meningioma. Note that the distributions change with the degree of adhesion; the histograms broaden and shift toward the right from complete adhesion to no adhesion, implying both an increase in ΔNOSS_bdy and its variation in the tumor periphery with decreasing adhesion. Among the five histogram parameters (mean, standard deviation, skewness, kurtosis, and entropy) after correction for age, sex, and scanner system, ACC tests were performed on each pair of parameters to remove highly correlated features in the training group. After this analysis, 2 histogram parameters remained (mean and entropy). Spearman’s correlation coefficients are summarized in Table 2.

Fig. 3.

The probability histograms of ΔNOSS_bdy values generated from the tumor shells for representative complete, partial, and non-adherent tumors. The histogram fitting curve of the adherent tumor is high and sharp, while the histogram fitting curve of the non-adherent tumor is wide and flat

Table 2.

Spearman’s correlation coefficients in absolute correlation coefficient test for ΔNOSS_bdy features after age, sex, and scanner system correction in the training cohort

	Mean	Standard deviation	Skewness	Kurtosis	Entropy
Mean	1	0.40	0.23	0.26	−0.17
Standard deviation	–	1	0.90	0.85	−0.95
Skewness	–	–	1	0.98	−0.84
Kurtosis	–	–	–	1	−0.76
Entropy	–	–	–	–	1

Relationships between ΔNOSS_bdy features and tumor surgical grading

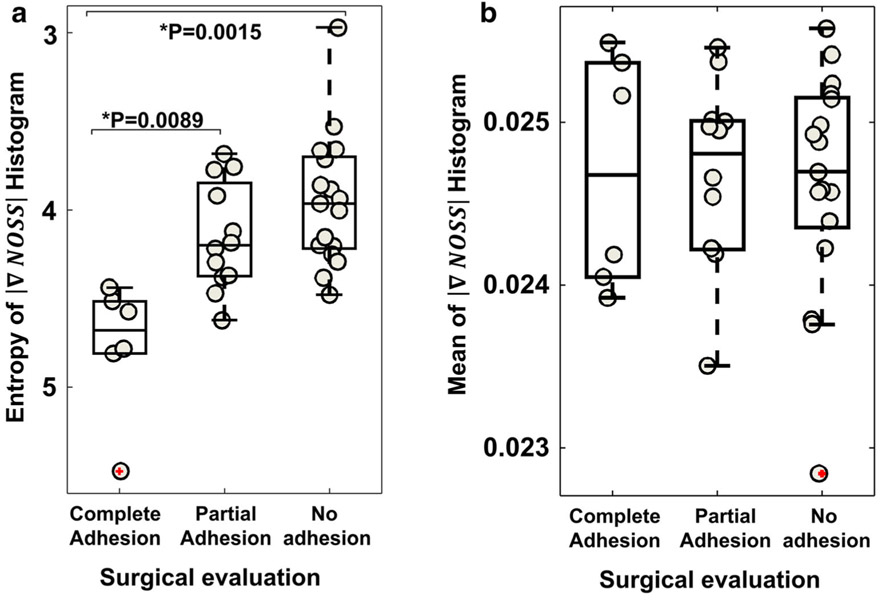
The entropy of the probability histogram of ΔNOSS_bdy (Fig. 4) proved to be significant for distinguishing completely adherent meningiomas from partially (p = 0.0089) and non-adherent meningiomas (p = 0.0015) in the training dataset. No significant difference was found between the partially and non-adherent tumors. The mean of the probability histogram did not show significant inter-group differences.

Fig. 4.

Group comparison of (a) entropy and (b) mean of the probability histogram of ΔNOSS_bdy values among completely, partially, and non-adherent meningiomas in the training cohort. *p was tested with one-way ANOVA with post hoc Steel-Dwass multiple comparisons

Predictive Performance of ΔNOSS_bdy Features

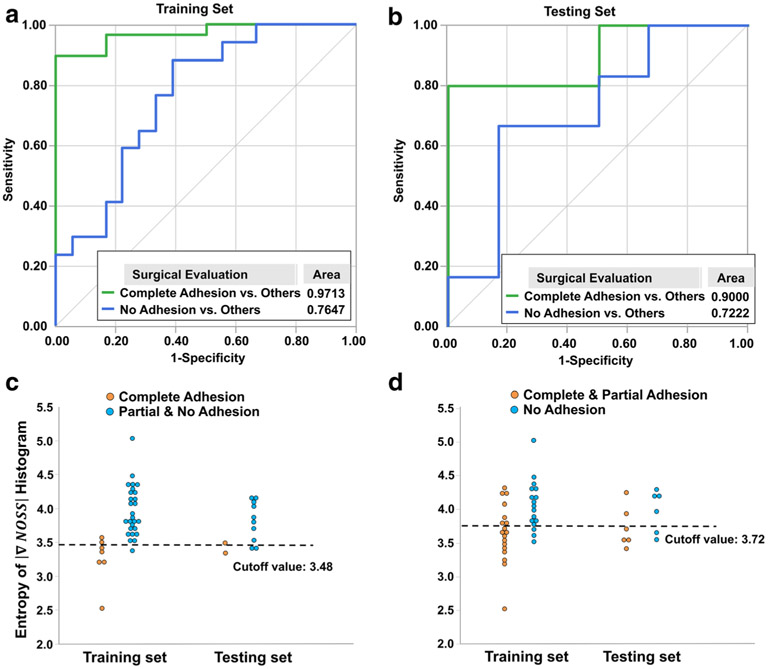
Figure 5 a and b show the ROC analyses of tumor adhesion prediction using the entropy of the probability histogram of ΔNOSS_bdy in both training and testing cohorts. The entropy has excellent predictive performance with an AUC of 0.971 (95% CI: 0.924–1.108) in the training set and an AUC of 0.900 (95% CI: 0.815–0.985) in the testing set for distinguishing complete adhesion versus partial/no adhesion. The AUC was 0.765 (95% CI: 0.645–0.885) and 0.722 (95% CI: 0.595–0.849) for distinguishing no adhesion versus partial/complete adhesion in the training and testing sets, respectively. Based on the cutoff value obtained from the training set (3.48 for distinguishing complete versus partial/no adhesion), the entropy of ΔNOSS_bdy yielded an accuracy of 0.91 in the training set and 0.83 in the testing set. The cutoff (3.72) for distinguishing no versus complete/partial adhesion yielded an accuracy of 0.71 and 0.67 for the training and testing sets, respectively. The ΔNOSS_bdy entropy for each patient in the training and testing cohorts sorted by the classification of tumor adhesion is depicted in Fig. 5 c and d.

Fig. 5.

Receiver operating characteristic (ROC) curves for the entropy of the probability histogram of the ΔNOSS_bdy values in the (a) training and (b) testing cohorts. (c, d) The ΔNOSS_bdy entropy for each patient sorted by the classification of tumor adhesion in the training and testing cohorts. (c) Complete adhesion versus partial/no adhesion. (d) No adhesion versus partial/complete adhesion. The dotted lines represent the best cutoff values for distinguishing tumor adhesion

Illustrative cases

Examples from the SII evaluations are presented in Fig. 6 that include 3D surface maps and the corresponding 2D Hammer projections of ΔNOSS_bdy from patients with completely, partially, and non-adherent meningiomas. A small ΔNOSS_bdy indicates less NOSS change at the tumor periphery, therefore a more adhesive tumor. Compared to the 2D slice, the 3D display of ΔNOSS_bdy on the tumor surface enables better visualization of the magnitude and location of the tumor adhesion.

Fig. 6.

Illustrative cases. (a) A 46-year-old female. The surgeons described the brain-tumor interface as extremely poor, and there was sub-pial invasion all around this tumor. Although the NOSS map shows a faint line of slightly increased NOSS value at the tumor periphery (arrow), both the 3D surface map of the ΔNOSS_bdy and the 2D Hammer map indicate that the majority of the tumor surface was adhesive. (b) A 52-year-old female. It was noted at the surgery that this tumor had no adhesion on the medial side adjacent to the falx, but was adherent to the lateral side of the brain, which correlates well with the ΔNOSS_bdy surface map. The NOSS map shows a faint hyper-intensity NOSS contour. (c) A 51-year-old female. This was a non-adherent tumor. Both the NOSS map and 3D surface map of the ΔNOSS_bdy agreed well with the surgical evaluation. Rotating 3D animation of the tumor surface maps are shown in the electronic supplementary material

Discussion

In this study, we have developed a new methodology based on SII to quantify and visualize tumor adhesion. NOSS data were utilized to build a quantitative metric (i.e., ΔNOSS_bdy) from the periphery pixels at the tumor margin. A color-encoded ΔNOSS_bdy surface map of the tumor can be generated to enable the 3D visualization of the tumor adhesion. A ΔNOSS_bdy-based statistical feature (i.e., entropy) was constructed and was found to successfully distinguish completely adherent tumors, which require tedious dissection away from surrounding tissues, from non-adherent tumors.

Meningiomas arise from arachnoidal cap cells and most are well isolated from the brain surface. However, some meningiomas (such as type II atypical) may behave invasively, leading to adherence with adjacent brain parenchyma. We found that the WHO grading is significantly correlated with the surgical adhesion grading in the training dataset, but not in the testing set. When dividing into different subtypes, no significant differences were found. We believe this may be due to the small sample size, and uneven distribution of adhesions groups and pathological subtype groups.

Evaluation of tumor-brain adhesion with SII is based on the dynamic relationship between the tumor and adjacent brain parenchyma motion while undergoing vibration introduced from an external source. In previous studies, a qualitative assessment of the presence of a hyper-intense NOSS contour was performed based on the relative contrast within the image [11]. This can be performed directly from the scanner as the first evaluation of tumor adhesion by neuroradiologists. However, because of its qualitative nature, NOSS has limited use when it comes to quantification. We have demonstrated that the absolute values of NOSS did not show a significant difference between the three adhesion groups (Figure A in Appendix). Although NOSS has been normalized to eliminate wave amplitude variations at the interface within each patient, its value may still vary between subjects due to differences in the head-driver mechanical coupling. Therefore, it is important to develop another metric that could provide predictive value in the quantification of tumor adhesion in addition to the visual inspection. As a result, ΔNOSS_bdy was developed to reduce the within-subject variation by calculating the maximum change of NOSS across the tumor surface. ΔNOSS_bdy values thus quantify the slip-induced change of shear strain and its distribution reflects different adhesion patterns at the tumor periphery.

We have found that a histogram feature, the entropy of ΔNOSS_bdy over the entire tumor surface, is an important index to quantify the tumor adhesion. In previous work with a visual inspection, NOSS correlated well with the etermination of partial and no adhesion [11]. In our study, the ability of ΔNOSS_bdy entropy in distinguishing between partial and no adhesion is limited. This may be partially due to the different sample sizes, and partially due to the qualitative nature of our reference standard and visual inspection, where the current overall results of the tumor adhesion are determined by the surgeon’s impression, so the evaluations were generally descriptive. Moreover, brain tumor resection is performed piece-by-piece in a small operation field, making it difficult at times to accurately quantify the percentage of tumor adhesion. It is also interesting to find that there is no difference in the histogram means between adhesion groups. This may be due to the heterogeneity of the adhesion across the tumor surface within each group.

The grade of adhesion can be heterogeneous across the tumor surface. With a 2D representation, the neurosurgeon and neuroradiologist routinely rely on the 2D images to create a 3D mental image of the lesion and its surrounding structures. However, 2D images cannot accurately convey the complexities of human anatomy and hence interpretation of complex anatomy in 2D images requires training and experience. Non-experienced individuals may have difficulty integrating the 3D anatomy or adjusting to the variabilities in 3D space. The 3D surface map of ΔNOSS_bdy and its Hammer projection demonstrated both the anatomical and adhesive relationship between the tumor and the surrounding brain tissue. This approach could facilitate preoperative adhesion localization as well as patient-specific planning, and together with navigation, potentially provide the surgeon with interactively displayed 3D visual information about the tumor adhesion during surgery.

Our study has some limitations. First, the ΔNOSS_bdy calculation is highly dependent on accurate tumor segmentation. In this study, the tumors were segmented manually, which is tedious and time-consuming. Utilizing an automated or semi-automated tumor segmentation tool may increase the precision of tumor boundary demarcation. As state-of-the-art computerized segmentation is introduced into clinical practice, SII could be integrated into daily clinical practice for presurgical 3D planning and intraoperative navigation during routine neurosurgical procedures. Second, the current EPI-based MRE pulse sequence is relatively low-resolution and prone to image distortion caused by local susceptibility-induced B0 in homogeneities, which may distort the displacement field near the tumor boundary. This hinders the ability to detect tumor adhesion with other critical structures (such as cranial nerves or vessels) especially near a bone interface such as the skull base. This could be addressed in future studies by acquiring high-resolution distortion-free MRE images with multiband DIADEM-MRE [22]. In addition, the current processing only calculates ΔNOSS_bdy values in-plane. This may lead to loss of spatial complexity in the slice direction. This could be addressed in future work by defining the center of the mass for the tumor and then calculating the 3D normal lines to the tumor surface. Finally, this study was retrospective and included only a relatively small number of meningiomas as brain MRE is not widely available in clinical practice due to the required specialized hardware.

Despite these limitations, ΔNOSS_bdy has demonstrated potential usefulness in providing surgeons with the degree of tumor-brain adhesion preoperatively. This technique has the potential to be widely applicable to target the adhesive relationships between all tumors and their surrounding structures. With the increasing evidence and technical development, ΔNOSS_bdy could contribute to the establishment of a standard method for grading tumor adherence and facilitate the clinical evaluation of tumor adhesion preoperatively.

Conclusion

In conclusion, this study demonstrated that SII-derived ΔNOSS_bdy values are useful for quantification and classification of meningioma-brain adhesion. The reconstructed 3D ΔNOSS_bdy surface map presents the state and location of tumor adhesion in a comprehensible, “clinician-friendly” manner. This technology can be used to identify meningiomas that have a high risk of adhesion with the adjacent brain parenchyma.

Key points.

• MR elastography (MRE)–based slip interface imaging shows promise as an objective tool to preoperatively discriminate meningiomas with a high risk of intraoperative adhesion.

• Measurement of the change of shear strain at meningioma boundaries can provide quantitative metrics depicting the state of adhesion at the tumor-brain interface.

• The surface map of tumor adhesion shows promise in assisting precise adhesion localization, using a comprehensible, “clinician-friendly” 3D visualization.

Methodology.

• retrospective

• observational

• performed at one institution

Abbreviations

ACC

Absolute correlation coefficient

EPI

Echo planner imaging

FOV

Field of view

IR-SPGR

Inversion recovery-prepared spoiled gradient echo

MP-RAGE

Magnetization-prepared rapid gradient echo

MRE

Magnetic resonance elastography

NOSS

Normalized octahedral shear strain

OSS

Octahedral shear strain

SE

Spin echo

SII

Slip interface imaging

TE

Echo time

TR

Repetition time