Building predictive signaling models by perturbing yeast cells with time-varying stimulations resulting in distinct signaling responses

Summary

This protocol provides a step-by-step approach to perturb single cells with time-varying stimulation profiles, collect distinct signaling responses, and use these to infer a system of ordinary differential equations to capture and predict dynamics of protein-protein regulation in signal transduction pathways. The models are validated by predicting the signaling activation upon new cell stimulation conditions. In comparison to using standard step-like stimulations, application of diverse time-varying cell stimulations results in better inference of model parameters and substantially improves model predictions.

For complete details on the use and results of this protocol, please refer to Jashnsaz et al. (2020).

Graphical abstract

Highlights

• •Diverse time-varying cell stimulations result in distinct signaling activation dynamics
• •Signaling models fit step stimuli responses well but result in poor predictions
• •Distinct responses upon diverse time-varying stimulations improve model predictions
• •Temporal stimulation of pathways result in novel signaling dynamics and mechanisms

This protocol provides a step-by-step approach to perturb single cells with time-varying stimulation profiles, collect distinct signaling responses, and use these to infer a system of ordinary differential equations to capture and predict dynamics of protein-protein regulation in signal transduction pathways. The models are validated by predicting the signaling activation upon new cell stimulation conditions. In comparison to using standard step-like stimulations, application of diverse time-varying cell stimulations results in better inference of model parameters and substantially improves model predictions.

Before you begin

Timing: 1 day

Cells in their natural environment experience stimuli that change gradually over time. We have demonstrated that the rates by which these changes occur are critical for cellular responses and fate decisions (Johnson et al., 2021; Thiemicke et al., 2019; Thiemicke and Neuert, 2021). By implementing an integrated experimental and computational modeling framework, we have found that diverse time-varying cell stimulations result in distinct signaling response dynamics, which better constrain signaling model parameters, and improve predictions of WT and mutant pathway responses as compared to models identified using standard step-like stimulation responses (Jashnsaz et al., 2020). We have demonstrated the applicability of our time-varying cell stimulations approach to discriminate competing signaling models and signaling mechanisms (Jashnsaz et al., 2020). This protocol describes the steps for measuring and modeling signaling pathways using signaling activation measurements under time-varying stress gradients. The framework is generalizable to build signaling models using measured signaling data from the literature for other pathways, and under other stimuli. The utility of this framework is demonstrated on osmotic stress signaling data measured in the High Osmolarity Glycerol (HOG) pathway in the model system S. cerevisiae yeast. The experimental section in this protocol outlines the steps to measure the HOG signaling activation dynamics upon time-varying osmotic stress conditions in yeast. We have also used this protocol to quantify signaling dynamics in human cells (Jurkat and THP1) (Thiemicke et al., 2019; Thiemicke and Neuert, 2021).

Preparation to measure and quantify signaling activation in experiment

• 1.Media. [Timing: 4 h]. Prepare buffers and solutions that are needed for cell growth (e.g., CSM) and cell stimulations (e.g., osmotic stress stimuli) in advance. Prepare 5 M sodium chloride (NaCl) concentrated stock in growth media (CSM 1×). Prepare 1 mL stocks of 0.1 mg/mL Concanavalin A (ConA) by diluting 1 mg/mL ConA into sterile H20 and store them in −20°C. See materials and equipment table.

Note: It is recommended to prepare all solutions and especially the 5M NaCl large enough (750ml) for all the experiments at once for reproducibility.

• 2.Colonies. [5 min]. At least 3 days before the start of the experiment, streak the strains of interest on appropriate selection plates and incubate for 2–3 days at 30°C. Keep plates on the bench at around 25^oC after visible single colonies are formed.
• 3.Cell stimulation profile. [1 h]. Set up the cell stimulation profiles and load them to syringe pumps to be used to perturb cells according to the desired time-varying cell stimulation profile. See Ref. (Thiemicke et al., 2019) for algorithm and key resources table to download the codes and instructions.
• 4.Cell culture. [1 h]. The day before the start of the experiment, in the morning, pick single colonies for each strain/condition from a fresh plate and inoculate each colony in 5 mL medium (pre-cultures) in round bottom tubes. Grow the pre-cultures for 3–6 h in the shaking incubator (200 rpm, 30°C). At the end of the day, measure OD of the pre-cultures at 600 nm. Dilute each pre-culture into 30–50 mL fresh growth media in a 125 mL flask and grow them in the shaking incubator (200 rpm, 30°C), to reach a target OD600 of 0.5 the next day at the time of the experiment.

Note: It is ideal to start cell cultures from pre-cultures with OD600 of 0.2 to 0.6.

Note: The exponential growth curve could be used to estimate the amount of pre-culture cells needed to be added to the fresh media given the initial and the target OD600, the volume of the media, and the duration between the dilution and the experiment (use OD600_calculation.m in Jashnsaz_et_al_dir07_CellGrowth, see key resources table).

Note: Multiple dilution of cells at multiple flasks could be prepared to have cells with OD600 = 0.5 at multiple timepoints at the day of the experiment.

Note: For multiple biological replica experiments, inoculate multiple cell cultures each from an independent single colony.

• 5.Acryl slide. [20 min]. Prepare acryl slide with tubing (see key resources table). Cut 5 cm (2in) long tubing pieces, stick them into the holes in the slide and seal them with epoxy glue using a 20–200ul pipette tip. Let the glue dry at 37°C for a minimum of 1 h. Prepare many of them for a set of experiments on the next day.
• 6.Microscope cover glass. [20 min]. In the morning at least 1 h before the experiment, rinse 22×50 mm glass coverslips with 100% ethanol and dry with Kimwipe. Flash centrifuge the 0.1 mg/mL ConA (allow to sit at 25°C for 5 min after removing from −20°C) at max speed to remove undissolved ConA protein. Take 100ul of the 0.1 mg/mL ConA, coat coverslips with a stripe, and incubate at 37°C for at least 1 h before the experiment. The yeast cells stick to ConA in an unspecific manner. Prepare many of these slides for a set of experiments for the day, but old coverslips lose their ability to keep the yeast cells attached (use coated coverslips up to 24 h).
• 7.Software. [10 min]. Download the image processing codes that are used for cell segmentation and quantification of time-lapse images. See key resources table.

Note: To assay the nuclear enrichment of Hog1 in single cells using time-lapse fluorescent microscopy, a strain with a yellow-fluorescent protein (YFP) tagged to the C-terminus of endogenous Hog1 in Saccharomyces cerevisiae BY4741 yeast cells through homologous DNA recombination was used.

Download the modeling codes

• 8.Download the codes available at https://github.com/neuertlab/Jashnsaz_STARProtocols_2021.
• 9.Install MATLAB on the local or cluster computers. The codes are generated in MATLAB R2019a. Refer to README.txt in the main directory as well as the README.txt in each sub directories for instructions.

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Critical commercial assays
New Era Syringe Pumps	https://www.syringepump.com/index.php	New Era, NE-1200
Tubing	Scientific Commodities	Catalog#: BB31695-PE/4
Dispensing needles	https://www.cmlsupply.com/dispensing-needle-20ga-1-0-tip-yellow/	CML Supply 20ga × 1.0" Yellow Blunt Tip Dispensing Fill Needles (SKU:901-20-100, MPN:901-20-100)
Acrylic Side	Grace Bio-Labs	Custom 0.125 Clear Acrylic Side w/3-Ports (product code: RD440562)
T-shape Adhesive Spacer	Grace Bio-Labs	SecureSeal Adhesive Spacer, "T", 1L Adhesive, 44040 (product code: 440556)
Deposited data
Signaling model and data	Jashnsaz et al, 2020	MATLAB codes and data
Experimental models: organisms/strains
Saccharomyces cerevisiae (BY4741)	Thiemicke et al, 2019	MATahis3Δ1 leu2Δ0 met15Δ0 ura3Δ0
Saccharomyces cerevisiae (Hog1-YFP)	Johnson et al, 2021	MATahis3Δ1 leu2Δ0 met15Δ0 ura3Δ0 HOG1- YFP::HIS3
Software and algorithms
Algorithms to set the pump profiles	Thiemicke et al, 2019	Algorithms to generate time-varying cell stimulation profiles
Codes to generate the pump profiles	This study	Jashnsaz_et_al_dir06_GeneratePumpProfiles
Codes to calculate the inoculation volumes for cell cultures	This study	Jashnsaz_et_al_dir07_CellGrowth
Image processing codes	Neuert et al, 2013; Kesler et al, 2019	https://osf.io/kwbe6/
Signaling modeling codes	Jashnsaz et al, 2020	https://github.com/neuertlab/Jashnsaz_STARProtocols_2021
Other
Microscope	Nikon	Nikon Eclipse Ti
Perfect Focus System (PFS)	Nikon	TI-PFS-CON 596216
X-cite fluorescent light source	Excelitas	Series 120 Q
Fluorescent filter for YFP	Semrock	YFP-2427B-NTE
100× VC DIC lens	Nikon	MRD01901
Orca Flash 4v2 CMOS camera	Hamamatsu	C11440-22CU
Automated XYZ high-resolution stage	ASI	ME-2000
Microscope cover glass	Fisherbrand	12-545-E 22x50-1

Materials and equipment

CSM 1× growth liquid media 750mL

Reagent	Final concentration	Amount
CSM 10×	5.925 g CSM (Formedium DCS0019) in 750 mL ddH2O	75mL
YNB 10×	51.75 g Yeast Nitrogen Base w/o Amino Acids (YNB) (Formedium, CYN0410) in 750 mL ddH2O	75mL
Glucose 20%	150 g Glucose (Fisher, Dextrose Anhydrous 147, M-15722) in 750 mL ddH2O	75 mL
ddH2O	n/a	525mL

CSM 1× could be stored at 25°C, and be used up to 6 months.

NaCl 5M 750 mL

Reagent	Final concentration	Amount
CSM 1×	n/a	750mL (final volume)
NaCl	Sodium chloride (Sigma-Aldrich, S7653-1KG, Formula weight, 58.44 g/mol)	219.15g

NaCl 5 M solution could be stored at 25°C, and be used up to 6 months.

Concanavalin A (0.1 mg/mL)

Reagent	Final concentration	Amount
Concanavalin A	1 mg/mL (in ddH2O)	100ul
ddH2O	n/a	900ul

Con A solutions (both 1 mg/mL and 0.1 mg/mL) are stored at −20°C up to 36 months.

Software and algorithms

Software	Use
MATLAB	programming and computing platform to analyze data, develop algorithms, and build models

Step-by-step method details

Measure signaling activation dynamics upon time-varying cell stimulation conditions

Timing: 1–4 days

Timing: 3 h for step 1

Timing: 2 h per time-lapse for step 3

To mimic physiological conditions, we have reported general experimental methodologies to precisely control the temporal changes of extracellular stimuli for different cell types (Thiemicke et al., 2019). Here, we outline the steps to perturb yeast single cells with osmo-stress concentrations that change over time and to measure and quantify the HOG signaling pathway activation dynamics upon different osmostress gradients (Figure 1). We used a strain with a yellow-fluorescent protein (YFP) tagged to the C-terminus of endogenous Hog1 in Saccharomyces cerevisiae BY4741 yeast (through homologous DNA recombination) and quantified the nuclear enrichment of Hog1 terminal kinase in single cells as a readout for the pathway activation using time-lapse fluorescent microscopy.

Note: Yeast cells are grown (200 rpm, 30°C) prior to the experiment to reach the target OD600 of 0.50 at the start of the experiment (see section before you begin).

• 1.
  Generate the pump profile.

  • a.
    Download the codes to generate the pump profiles and see Ref. (Thiemicke et al., 2019) for the algorithm used to set up the pump profiles (codes: Jashnsaz_STARProtocols_2021/Jashnsaz_et_al_dir06_GeneratePumpProfiles).
  • b.
    In the above directory, follow steps 1 to 5 in README.txt, to use the MATLAB codes and excel files to set up and generate the desired pump profiles and load them to the syringe pump to be used to perturb cells according to time-varying profiles (Figure 1A) during the time-lapse experiments.
• 2.
  Prepare the flow setup.

  • a.
    Prepare the experimental setup of the microfluidic flow chamber on a microscope according to Figure 2C in Ref. (Thiemicke et al., 2019). A programmed pump (see step 1) adds a concentrated stimulus gradually to a mixing beaker at constant magnet stirring. A second pump of a constant low rate delivers the time-varying stimulus generated in the mixing beaker to the cells loaded into a flow chamber (see step 3) through tubing. A 3-way valve determines if the cells are exposed to normal media (0 M) or to a temporal gradient generated in the mixing beaker.

Note: Loading cells into flow chamber according to the following protocol provides an optimal cell density under the microscope for cells of OD600 between 0.40 and 0.55.

Note: For reproducibility, we recommend using at least three biological replicates for each cell stimulation profile condition. The ideal biological replicates are independently grown cell cultures initiated from independent pre-cultures each inoculated from different single colonies.

• 3.
  Assemble the flow chambers.

  • a.
    Use a razor blade to cut off all the access glue and tubing on the bottom of the acryl slide.
  • b.
    Glue one side of the double sticky T-shaped spacer on the Pyrex slide with the tubing. Make sure all the tubing inlets are accessible. Use a plastic pen and move it over the T-shaped spacer to remove all the air bubbles. This helps to reduce air leaking into the flow chamber later in the experiment.
  • c.
    Remove second sticky tape cover and place the ConA coated coverslip onto the fluidic channel so that the ConA stripe matches with the T-shaped space. Use again a plastic pen to remove the bubbles. The fluid cell is now ready to use. Prepare many of them for a set of experiments.
• 4.
  Load cells to the flow chambers.

  • a.
    Measure the OD of the cells in the morning before the experiment to be OD = 0.5 at 600 nm.
  • b.
    Transfer 1.5 mL of cells (OD600–0.5) into each of three 1.5 mL centrifugation tubes at 500G (rcf) for 5 min to concentrate the cells. Remove access liquid until ∼100ul are left in each tube. Centrifuge the tubes on the bench-top centrifuge for 10 s, remove supernatant (∼60ul), then re-suspend and combine the remaining 40ul pellets from all three tubes to one.
  • c.
    Load the cells to the flow chamber using a pipette and 100ul tips. After loading the cells into the flow chamber, hookup the chamber onto the microscope, and wait 5 min to allow the cells to stick to the ConA coverslip.
• 5.
  Image acquisition with time-lapse microscopy.

  • a.
    Image acquisition setup. An inverted microscope (Nikon Eclipse Ti) which is equipped with perfect focus (Nikon), a 100× VC DIC lens (Nikon), a fluorescent filter for YFP (Semrock), an X-cite fluorescent light source (Excelitas) and an Orca Flash 4v2 CMOS camera (Hamamatsu) was controlled with a Micro-Manager program (Figure 1C).
  • b.
    By moving in xy-plane, select a field of view with optimal density of the cells in a single z-plane. Adjust the z-focus to see the boundary of the majority of the cells as a white ring.
  • c.
    Record time-lapse images with both bright field (e.g., every 10 s) and fluorescent (e.g., every minute) channels (Figure 1D, Methods video S1).

Figure 1.

Experimental procedure to perturb cells with stimulant concentrations that change over time and to measure and quantify signaling activation response dynamics upon different cell stimulation profiles

(A) To mimic physiologically relevant cell environments, time-varying cell culture environments are implemented. Experimental setup to generate and perturb cells with stimulant concentrations that change over time in the laboratory is reported in Ref (Thiemicke et al., 2019).

(B and C) (B) Cell cultures treated with time-varying stimulations (C) are followed over time in a microfluidic flow chamber on a fluorescent microscope.

(D) Measured bright field and fluorescent images of yeast cells (gray) are collected overtime showing nuclear localization of the yellow fluorescent protein (YFP) tagged Hog1 mitogen-activated protein kinase (MAPK, red). Scalebar is 2 μm. (see Methods video S1 for the time-lapse microscopy images of multiple cells).

(E) Image processing codes for cell segmentation and quantification of single cell data are reported in Refs (Johnson et al., 2021; Kesler et al., 2019). Signaling activation time-traces measured and quantified using immunoblotting such as in Ref (English et al., 2015) or using fluorescent flow cytometry as in Ref (Thiemicke and Neuert, 2021) could also be used to parametrize the underlaying signaling models following this protocol.

(F) MAPK Hog1 nuclear localization dynamics upon step increases in NaCl to different final concentrations.

(G) Hog1 dynamics upon step, linear or quadratic increases from 0 M to 0.4 M NaCl in 10 min then switch back to growth media of 0 M. Lines are means and shaded areas are the standard deviations of the means from six (control condition) or three (remaining conditions) biological replicates measured and quantified following (A) to (E). Data presented in (F and G) are from Ref (Jashnsaz et al., 2020) with permission.

(H) A schematic (cartoon) representative summary of experimental results showing how different extracellular time-varying stimulations (left) activate a signaling pathway (middle) and result in distinct dynamics of kinase signaling and nuclear localization (right). See also Methods video S1.

Figure 2.

Model signal transduction networks as dynamic ODE system with parameters inferred from experimental signaling data

(A) The signaling pathway is represented as a network diagram with nodes representing proteins and lines representing regulation activities. Arrow-headed lines represent positive regulations; dash-headed lines represent negative regulations; dashed lines represent basal regulations on each node; top nodes represent sensors stimulated by the input; and the final node represents the terminal kinase.

(B) Regulation graphs are represented as square matrices with the number of rows equal to the number of network nodes, where a +1 (or -1) in the (i,j) entry denotes a positive (or negative) influence of j^th input, basal regulator or enzyme on the regulation of the i^th node.

(C) The MATLAB code implementation of the matrix arrangement of the network.

(D) Each regulation is modeled as a Michaelis-Menten (MM) reaction. A representative positive regulation, where the active form of node x₃ converts node x₄ from its inactive to its active form (orange box in B) through a Michaelis-Menten function consisting of two parameters, the catalytic rate constant ($k_{cat}$) and the Michaelis-Menten constant ($K_{MM}$).

(E) The pathway is compiled as a dynamic ordinary differential equation (ODE) system by calling the appropriate MM function (positive, negative, none) using the arranged matrices form in (B and C), with the vector of parameters $\mathbf{\Lambda }=\left({\lambda }_1,{\lambda }_2,\dots \right)$ arranged such that odd entries correspond to catalytic rate constants and even entries correspond to the MM constants.

(F) Optimization algorithm to parametrize the model using signaling data. The algorithm consists of a customized Genetic Algorithm (GA) and the MATLAB built-in fminsearch function. The algorithm takes a model and a set of training data and returns a set of best parameters (Λ∗) that maximizes the likelihood of observing the training data. This task is done by minimizing the objective function (blue boxes) defined as the sum of squared residuals between the model and data over the time-traces of all the training datasets. Refer to section Optimization algorithm in step 2 for details.

(G) The HOG pathway is modeled as a 4-node network of SLN1 and SHO1 branches each stimulated by the input, both regulating Pbs2, that in turn regulates Hog1 terminal kinase (see step 2 for details).

(H) Ten independent fits (red) of model in (G) simultaneously to measured Hog1 nuclear localization data (black) upon steps of 0.2 M and 0.4 M NaCl (Figure 1F). Out of multiple independent training, the parameter set resulting in best predictions for signaling activation upon new experimental conditions (Figure 1G) are given in Table S1 (${\mathbf{\Lambda }}^0$) in Ref (Jashnsaz et al., 2020). This set (referred to as the “true parameter set”) is used to simulate synthetic data upon wider time-varying stimulation inputs (Figure 3). Figures 2A, 2B, 2D, 2E, and 2H are reprinted with permission from Ref (Jashnsaz et al., 2020).

• 6.
  Perturb cells with time-varying stimuli.

  • a.
    Connect the flow chamber inlet with the 3-way valve (to media and mixing beaker) and its outlet to the pump2 in the flow setup according to the step 2 (a) above.
  • b.
    Switch the inlet valve to the media (0 M). On the outlet syringe pump, set the flow rate to 9 mL/min, turn on the pump and wash off any unbound cells with osmolyte free media. Stop pump after all the unbound cells are gone (∼ 1 min). This ensures the air bubble is pumped out of the tubing and the fluid chamber.
  • c.
    Reduce the outlet pump flow rate to 0.1 mL/min (see the rate for pump2 in profile setup codes in step 1).
  • d.
    After the flow is stabilized, turn off the pump, close the valve to the media w/o osmolyte and switch the inlet tubing to the mixing beaker (osmolyte containing media). Start the data acquisition (see step 5) and turn on the pumps simultaneously. Make sure there are at least 3 YFP images taken before the cells experience osmotic stimuli.
• 7.
  Quantify single cell signaling activation.

  • a.
    Image processing codes for cell segmentation and quantification (Kesler et al., 2019) are available in the public OSF repository: https://osf.io/kwbe6/. All codes used for image processing and analysis in this study to quantify signaling activation dynamics (Figures 1E–1H) (Johnson et al., 2021; Munsky et al., 2018; Neuert et al., 2013; Thiemicke et al., 2019) are available at https://osf.io/kwbe6/ for download and use.

Methods video S1. Time-lapse microscopy images of yeast cells, related to step 1

Time-lapse microscopy images of yeast cells (gray) showing nuclear localization of the yellow fluorescent protein (YFP) tagged Hog1 mitogen-activated protein kinase (MAPK, red) following a 0.2 M NaCl step stimulation at t=0 min (the 1^st frame). Movie frames are shown at every minute. The Hog1 nuclear localization peaks at 4–5 min and perfectly adapts to pre-stimulus level at +12 min (see Figure 1F for quantification).

Model signal transduction network as dynamic ODE system and infer parameters using signaling activation measurements

Timing: 1–4 days

• 8.
  Model signal transduction networks as a dynamic ODE system. The signal transduction network is modeled as a dynamic ordinary differential equations (ODEs) system where proteins regulate each other through biochemical reactions (Figure 2).

  • a.
    Download the MATLAB codes at Jashnsaz_STARProtocols_2021/Jashnsaz_et_al_dir01_Models to generate the models. Figures 2A–2E outlines the implementation of the model3 in this code; the network topology diagram (Figure 2A), the regulation matrices (Figure 2B), the MATLAB implementation code (Figure 2C), and the compiled dynamic ordinary differential equations (ODEs) system (Figure 2E). Figures 2A–2E provide the necessary details to use the codes to convert a specific network topology (Figure 2A) to its corresponding ODE model (Figure 2E).
  • b.
    Use the MATLAB code visualize_models.m to import the models (Models.mat that is generated by running get_models.m) and using the customized network_plot.m function to visualize the network diagrams for all the models (similar to Figure 2A).

    Note: This framework is general to map arbitrary regulatory networks to their corresponding ODE models and it is implemented in MATLAB 2019a. The framework takes arbitrary number of regulatory nodes based on the proteins involved in the pathway (Figure 2A). The framework allows the user to model network topologies with user-specified connections (by manually entering the elements of the regulation matrices) or to model all the possible regulation networks (by generating all the possible permutations of the elements of the regulation matrices) (Figures 2B and 2C).

  • c.
    Specify protein states and the type of regulation functions. The formulation of the rate equations of the model is adopted from Ref. (Ma et al., 2009). In our model, each node representing a protein (or a group of proteins) is modeled as two-state (active and inactive) species, and it has a fixed total concentration that is interconverted between active and inactive states via regulations from the stimuli inputs, fixed basal regulators, or other nodes of the network (Figure 2B). The total rate is the sum of all such regulations that a node receives (Figure 2E). We implement each regulation (link) as Michaelis-Menten kinetics (Figure 2D), however, the framework is easily generalizable to other types of regulations such as mass action, Hill functions, and any other type of function.

    Note: The total regulation that a node receives could also be combined through a multiplicative AND-gate function where two or more proteins cooperatively regulate another protein (Mangan and Alon, 2003).

    Note: In the model, sensors receive extracellular stimulation, they relay the signal to a downstream node, which in turn regulate the final node as the pathway readout (e.g., the terminal kinase phosphorylation and/or nuclear transport). Each node receives a constant basal regulation to take into account the role of constitutively active phosphatases and autoregulation. Feedforward and feedback loop (FFL/FBL) regulations are also considered that enable dynamic behaviors like adaptation (Figure 2A).

  • d.
    Reduce model complexity by grouping proteins together as nodes. Although this framework allows the user to model a network of regulations at different complexity levels, here we considered a 4-node network topology (Figure 2A) with the proceeding argument. The signal transduction networks, despite their topological complexity, broadly could be simplified into a general 4-node topology:

    • i.
      First, the recurrent core network topologies (“circuit motifs”) that are capable of robustly executing biological functions are well supported (Milo et al., 2002; Shen-Orr et al., 2002; Wagner, 2005).
    • ii.
      Second, multiple of the proteins involved in signaling networks can be grouped together and considered a virtual node in a reduced ODE model to describe pathway activation dynamics and cellular responses with sufficient accuracy (Huang et al., 2010; Jeong et al., 2018).
    • iii.
      Third, many signaling pathways are branched; two or more upstream multi-component branches (e.g., consisting of the sensors, phosphorelays, and kinases) are stimulated by extracellular changes, that converge at a common downstream component, which in turn regulates a terminal signaling protein to trigger a cellular response.
    • iv.
      In this protocol, as a proof of principle, we will model the well-characterized stress sensing Hog1 MAPK signaling pathway in S. cerevisiae as a reduced 4-node topology.

• 9.
  Infer model parameters using signaling data (optimization algorithm). The optimization algorithm is provided in Figure 2F. We ran this algorithm over 21 iterations for the training conditions provided throughout the manuscript that resulted in fits converging within the standard deviation of the data. Each iteration consists of two Genetic Algorithm (GA, a MATLAB built-in function) calls each followed by the MATLAB fminsearch function (light blue boxes, Figure 2F) through the following steps:

  • a.
    Divide the timepoints of data. The first GA and its following fminsearch uses only a portion of the timepoints of each training dataset (25% selected randomly). This reduces getting stuck in local minima of the parameters space. Then the second GA and its consequent fminsearch use all timepoints of the training data.
  • b.
    Define the objective function. The objective function is defined as one half of the sum of squared residuals of the model fit to the data given in Equation 1.

    $$OBJ=\sum _{n=1}^d\sum _{k=1}^N\frac{{\left(x_n\left(t_k\right)-O_n\left(t_k\right)\right)}^2}{2{\sigma }_n{\left(t_k\right)}^2},$$ (Equation 1)
    N is the number of timepoints (25% selected randomly for the 1^st GA, 100% for the 2^nd GA) in each dataset, d is the total number of datasets in the training data, X_n(t) is the model, O_n(t) is the data mean, and $\sigma$_n(t) is the standard error of the mean (experimental data) or additive noise (simulated data) for the pathway activation dynamics of dataset n.
  • c.
    Sample parameter space. At the first 4 iterations ($i\le 4$) as well as at every 4^th iteration of the algorithm, the 1^st GA takes 200 parameter sets sampled uniformly in [−3,+3] in the logarithmic scale base 10, and returns a parameter set, that feeds into its following fminsearch. Sampling 200 parameter sets uniformly between −3 and +3 results in an average spacing of 0.03 for each parameter. This uniform sampling of parameter space multiple times in the beginning and through each optimization process helps to sample larger parameter space and reduces getting stuck in local minima. The iteration interval (i) can be adjusted if needed. Each fminsearch takes the parameter sets that GA outputs and minimizes the objective function given in Equation 1. During each iteration, the best parameter sets after the 2^nd fminsearch are collected. These parameter sets are used to resample 200 new parameter sets for the 1^nd and 2^nd GA (Figure 2F, purple boxes). These parameter sets are sampled within the range [−0.5,+0.5] so that parameter space could be searched with finer spacing (0.005).
  • d.
    Customize the GA parameters. Each GA runs for 20 generations, passes on one parameter set that has the minimum objective value among the 200 sets at each generation. The GA implements a mutation function that uses the best parameter sets from the previous generation (parents) to guess the new parameter sets.

    Note: Objective values are updated during the 2^nd fminsearch if their value is improved. In total, 168,042 (= 2$\times$21$\times$20$\times$200 + 2$\times$21) number of parameter sets are evaluated for each model fit through this optimization process.

• 10.
  Model stress sensing HOG pathway as a 4-node branched network topology. As a proof of principle of our approach, in this protocol, we model the well-characterized stress sensing Hog1 MAPK signaling pathway in S. cerevisiae as a reduced 4-node topology (Figure 2G). The HOG pathway serves as a blueprint to study eukaryotic signaling pathways (Hohmann et al., 2007). In the context of the HOG pathway (Figure 1G), each SLN1 or SHO1 branch is grouped into a node given their fast (millisecond) activation dynamics before they activate Pbs2 in comparison to the longer activation dynamics of the Hog1 terminal kinase (that is in the order of 5 min) (Saito and Posas, 2012; Tatebayashi et al., 2015) as following.

  • a.
    The node x₁ (Figure 2A) represents the SLN1 branch (Figure 2G) (including the proteins Sln1, Ypd1, Ssk1, Ssk2/ Ssk22) that utilizes a two-component phosphorelay mechanism to transmit its signal, with b₁ representing the constant deactivation of the SLN1 branch (Hohmann et al., 2007; Maeda et al., 1994).
  • b.
    The node x₂ describes the SHO1 branch of the HOG pathway that utilizes protein kinases to relay its information. The SHO1 branch consists of the proteins Sho1, Msb2, Hkr1, Opy2, Cdc42, Ste20/Cla4, Ste11 and Ste50, with b₂ modeling the basal deactivation of the SHO1 branch (Tatebayashi et al., 2015). The SHO1 branch is also regulated by the Hog1 kinase through a feedback loop (Hao et al., 2007; O’Rourke and Herskowitz, 1998; Westfall and Thorner, 2006).
  • c.
    The node x₃ represents a MAPKK such as Pbs2 that integrates information flow from two branches and has basal regulation (b₃) through phosphatases such as Ptc1/2/3.
  • d.
    Lastly, x₄ represents a terminal kinase such as Hog1 that is activated by Pbs2. Hog1 is deactivated through phosphatases Ptc1/2/3 and Ptp2/3 (Mattison and Ota, 2000; Warmka et al., 2001; Young et al., 2002). Deactivation of Hog1 via constitutively active phosphatases is modeled as the act of basal deactivator b₄ on x₄.

Note: The details on how a 4-node model among a class of expandable network topologies that is considered in this protocol is discussed in Ref. (Jashnsaz et al., 2020) in the context of other HOG models from the literature (English et al., 2015; Granados et al., 2017; Hersen et al., 2008; Klipp et al., 2005; Muzzey et al., 2009; Schaber et al., 2012; Zi et al., 2010).

• 11.
  Parametrize the HOG model with experimentally measured Hog1 nuclear localization data.

  • a.
    We parametrized the biologically-inspired HOG 4-node model (Figure 2G) by fitting the model to a set of experimental Hog1 nuclear localization data (Figure 2H) over multiple independent training processes.
  • b.
    Using the parameter sets inferred from each of the multiple independent training processes, we predicted the Hog1 signaling dynamics upon new cell stimulation inputs (Figure 1G) that were held out during model training.
  • c.
    For each condition, we evaluated the model’s ability to predict the held out experimental Hog1 dynamics.
  • d.
    We defined the parameter set (Table S1 in Ref. (Jashnsaz et al., 2020)) resulting in the smallest prediction errors (i.e., the difference between the model and the data) as the “true parameter set”.
  • e.
    Using the combination of the “true parameter set” and the 4-node model (hereafter, the “true model”), we simulate synthetic signaling data upon multiple cell stimulation conditions (see next section, step 12).

Simulate signaling data using the parametrized model upon diverse time-varying cell stimulation conditions to validate the model inference approach

Timing: 1 day

Diverse cell stimulation inputs that change according to a step, linear, or quadratic function over time resulted in distinct pathway activation dynamics (Figure 1G). To establish whether and how model prediction depends on the type of the cell stimulation inputs and the resulting pathway activation dynamics, synthetic signaling data were simulated from the “true model” under different time-varying stimulation inputs (Figure 3A).

CRITICAL: Using the combination of a biologically inspired model (the “true model” as a simplified HOG pathway model) and biologically representative simulated signaling data (that recapitulate experimental observations of the HOG pathway activations) provide a ground truth to quantitatively benchmark whether different time-varying cell stimulations impact model predictability without the challenges of modeling experimental data. Simulation also allows generating signaling data over a wide range of cell stimulation conditions (Figure 3B).

• 12.
  Simulate signaling data. Upon numerous cell stimulation input conditions of different temporal profiles in the form of polynomial functions each to multiple different final concentrations (Figure 3B), we simulated signaling data for the pathway activation dynamics (Figures 3C–3H).

  • a.
    Upon each cell stimulation input condition, the “true model” is solved for the activation of the terminal kinase protein (final node) for the “true parameter set” under each corresponding stimulus input s(t) profile (Figure 3A).
  • b.
    To capture cell-to-cell variability and measurement noise, single-cell trajectories are generated by adding experimentally realistic Gaussian white noise to the model ODE solutions, and the mean and standard deviation from single-cell trajectories over time are calculated as signaling activation data for each condition.

    Note: Here, the implementation of Gaussian white noise is based on the experimental observation that the distribution of single-cell Hog1 signaling variations at the same time and same conditions is well captured by a Gaussian distribution.

  • c.
    We simulated 30 independent synthetic data sets for each condition under independent single-cell noise. We refer to these as 30 “synthetic replicates” of the same data that will be used to initiate 30 independent fits for each training condition (see next section, step 15).

    Note: The implemented cell stimulation profiles are feasible in a lab setting and are mutually independent such that each of the profiles stimulates the pathway to express a unique temporal activation dynamic.

    CRITICAL: The “true parameter set” that is used for this task is determined based on the quality of generated simulated data among many parameters sets from multiple independent training processes (see step 11). This ensures that the resulting simulated signaling data (Figure 3) qualitatively and quantitatively recapitulate the experimental Hog1 pathway activation dynamics (Figures 1F and 1G), such as activation levels, measurement noise, onset of activation, maximum activation time and perfect adaptation time. Importantly, from step stimulation inputs to the highest polynomial inputs the peak response shifts to the right as a result of a delay in the rate and concentration of higher order polynomial stimulation inputs. The resulting simulated data allowed us to investigate which set among these signaling data is best suited to train the model such that the remaining conditions could be predicted.

Figure 3.

Generate simulated signaling data over a wide range of cell stimulation types and intensities

Temporal stimulations of signaling pathways result in distinct dynamic pathway activation responses

(A) Diverse time-varying perturbations corresponding to step ($t^0$), root ($\sqrt{t}$), linear ($t^1$), quadratic ($t^2$), quints ($t^5$), and heptic ($t^7$) changes over time (left) are applied to the true model (middle) resulting in synthetic signaling activation dynamics (right). In synthetic signaling data, gray lines are the ODE model solutions for $x_4\left(t\right)$ and blue lines represent 10 single cells by adding Gaussian white noise to the solution for each condition (Jashnsaz et al., 2020).

(B–H) (B) A table of diverse kinetic inputs reaching different final concentrations result in 54 distinct simulated signaling datasets. (I) Red, blue, yellow, and green colors indicate each dataset belonging to traindata, testdata1, testdata2, and testdata3, respectively, to be used to train the model and to test model predictions (Figures 4 and 5). Synthetic pathway activation data simulated from the true model upon diverse kinetic stimulations (inserts) as step ($t^0$, C), root ($\sqrt{t}$, D), linear ($t^1$, E), quadratic ($t^2$, F), quints ($t^5$, G), and heptic ($t^7$, H) functions over time each to final concentrations of 0.050, 0.10, 0.20, 0.30, 0.50, 0.70 M. All kinetic stimulations start at 0 min, all except steps reach their final concentrations at 25 min and then keep constant from 25 min to 50 min (insets). Lines are means and shaded areas are the standard deviations of the means from five simulated biological replicates each containing 10 single cell trajectories (similar to A). 30 “synthetic replicates” of each data is simulated under independent Gaussian single-cell noise. See step 3 for details, and Ref (Jashnsaz et al., 2020).

Infer signaling model parameters by training the model with simulated data

Timing: 3 days

As a common practice of systems biology, the dynamics of biological processes (i.e., signaling pathways) are often modeled as ODEs and the unknown dynamics and parameters (i.e., experimentally unobserved species and the unknown parameters such as reaction rates) are inferred from the measurements of the dynamics for a few species of the system. In this section, we explored what effects different cell stimulation inputs have on signaling model parameter inference.

• 13.We trained the true model with independent sets of simulated data that are generated using the true model with experimentally realistic noise that is Gaussian distributed (step 12). For each condition, we quantified the fit errors, best parameter sets, and the uncertainty in the model parameters.

Note: The extensive analysis under different training datasets conditions is performed in Ref. (Jashnsaz et al., 2020).

• 14.Here, we used two conditions that include the same amount of training data that are generated upon step cell stimulations (Figures 4A–4C) in comparison to diverse time-varying cell stimulation inputs (Figures 4D–4F).
• 15.This task was repeated upon multiple independent training processes each using independent noise in simulated data and randomized optimization initialization. Beside reproducibility, this ensures that the final results are independent of the noise in the data and initial parameter guesses.
• 16.Under each training condition, each model’s fit convergence is confirmed to maximize the likelihood of observing the training data and the fit errors are evaluated. Under both conditions (Figures 4A and 4D), the model fits the simulated data equally well (Figures 4B and 4E). The fit errors, defined as the mean absolute difference of the fit and their corresponding synthetic data over time, is within one standard deviation of the experimental noise considered for the data (Figures 4C and 4F).

CRITICAL: The question is whether different training conditions that result in models with indistinguishable fit errors lead to different predictions. To answer this question, next we evaluated the model predictions from each training condition (see next section, steps 17–18).

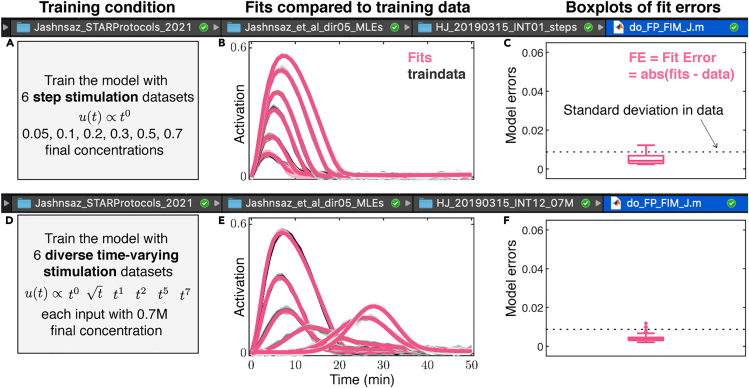
Figure 4.

Model fits equally well to simulated signaling data upon six step stimulation inputs and six diverse time-varying stimulation inputs

(A and B) (A) Upon training to six simulated step input responses at different concentrations, (B) model fits (red) of signaling activation dynamics are compared to their corresponding training data (gray). Thick lines and shaded areas in red show median and interquartile range out of 10 independent model fits, and in gray they show means and standard deviations of the synthetic data.

(C) A box plot of model fit errors, defined as the mean absolute difference of the model fit and their corresponding simulated training data over time, is shown compared to the standard deviation of the simulated data (dashed line). Box plot is quantified out of 60 fit error values (6 training data, 10 independent fits).

(D and E) (D) Upon training to six simulated diverse time-varying input responses of ($t^0\text{to}{t}^7$), (E) model fits (red) of signaling activation dynamics are compared to their corresponding training data (gray).

(F) A box plot of model fit errors is shown compared to the standard deviation of the simulated data (dashed line). Box plot is quantified out of 60 fit error values (6 training data, 10 independent fits). Figures 4B and 4E are reprinted with permission from Ref (Jashnsaz et al., 2020).

Validate model by predicting signaling responses for the new conditions

Timing: 1 day

Being able to predict the system’s behavior upon new conditions provides a testable way to validate or invalidate whether the observations that were used to train the model have sufficiently constrained the model structure and parameters. Using simulated data allowed us to generate numerous signaling data sets (step 12), of which we use a portion to train the model (steps 13–16) and use the remaining data for testing the model predictions (next, steps 17 and 18).

• 17.
  Using the best parameter set resulting from the model fit to six step ($t^0)$training datasets (Figures 4A–4C), we predicted the signaling dynamics upon new cell stimulation conditions (Figures 5A–5C).

  • a.
    We compared model predictions of signaling dynamics upon different concentrations of linear cell stimulations in the form of $u\left(t\right)\propto t^1$ and upon nonlinear cell stimulations of $u\left(t\right)\propto t^9$to their corresponding synthetic data (Figure 5B, blue and green compared to gray).

    Note: An input of $u\left(t\right)\propto t^9$ is comparable to a shifted step function and describes an upper limit on the polynomial functions used.

  • b.
    We calculated the model prediction errors upon different sets of test data that exclude the training step data. These resulted in uncertain parameters that gave inaccurate predictions for testing data that are collected when using a different type of cell stimulation input (Figure 5C).

• 18.
  Using the best parameters set resulting from the model fit to signaling dynamics under diverse time-varying cell stimulation profile types ($t^0-t^7$) simultaneously (Figures 4D–4F), we predicted the signaling dynamics upon new cell stimulation conditions (Figures 5D–5F).

  • a.
    We compared model predictions of signaling dynamics upon different concentrations of linear cell stimulations in the form of $u\left(t\right)\propto t^1$ and upon nonlinear cell stimulations of $u\left(t\right)\propto t^9$to their corresponding synthetic data (Figure 5E, blue and green compared to gray). These results indicate that the predictions are substantially improved when the model is trained with data under diverse inputs.
  • b.
    We calculated the model errors upon test datasets and the quantification indicate that model predictions for all new testing conditions are as good as the model fits (Figure 5F).

CRITICAL: For all the conditions, we evaluate the model predictions using sets of test data upon cell stimulation conditions that are different than those of the training datasets (either in the type of input or its final concentration).

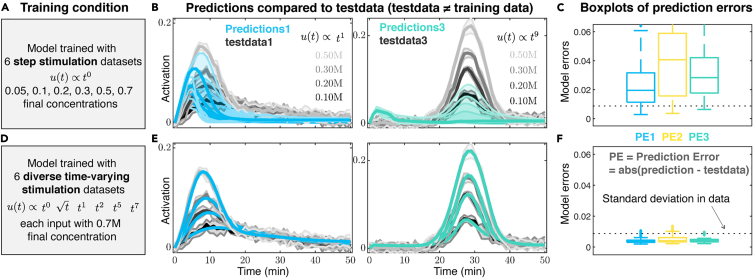
Figure 5.

Diverse time-varying cell stimulations improve model predictions

(A and B) (A) Upon training to six simulated step input responses at different concentrations (Figure 4A–4C), (B) model predictions of signaling activation dynamics upon different concentrations of linear input stimulations (predictions1 in blue) or different concentrations of nonlinear inputs of the shape t⁹ (predictions3 in green) are compared to their corresponding simulated test data (gray). Thick lines and shaded areas in blue and green show median and interquartile range of predictions corresponding to the 10 independent fits from Figure 4, and in gray they show means and standard deviations of the synthetic data.

(C) A box plot of prediction errors, defined as the mean absolute difference of the model prediction and their corresponding simulated test data over time, is shown compared to the standard deviation of the simulated data (dashed line). Box plots of PE1, PE2, and PE3 are quantified from prediction errors of testdata1 (30 data sets over 10 independent fits), testdata2 (12 data sets over 10 independent fits), and testdata3 (6 data sets over 10 independent fits), respectively, that each excludes the training data.

(D and E) (D) Upon training to six simulated diverse time-varying input responses to $t^0\text{to}{t}^7$ (Figure 4D–4F), (E) model predictions of signaling activation dynamics upon linear (blue) and nonlinear (green) input stimulations are compared to their corresponding test data (gray).

(F) Box plots of predictions errors are quantified similar to (C) where test data excludes the training data. Figures 5B and 5E are reprinted with permission from Ref (Jashnsaz et al., 2020).

Expected outcomes

Our results indicate that under step-like cell stimulation conditions, despite excellent model fits of the signaling dynamics data (Figure 4C), the lack of cell stimulation diversity limits model prediction power (Figure 5C). We found that diversified cell stimulations of different time-varying profile inputs overcome this problem and substantially improve model predictions (Figure 5F).

Quantification and statistical analysis

Multiple training processes. Each training condition was performed over 30 independent training processes each using an independent normal noise in the simulated data and a randomized optimization initialization. For each condition, the analysis result was presented for the 10 best converged fits out of the 30 (the 10 optimizations with lowest final objective function values). The analysis of all the 30 independent trainings did not change the overall results. Implementing multiple training processes ensured reproducibility and that the results are independent of the noise in the data and the initial guesses for parameters before optimization.

Multiple test datasets. For each training condition, different sets of test datasets were simulated to ensure unbiased testing conditions. Simulating data under numerous stimuli conditions of diverse temporal profile types and different final concentrations (Figure 3B) allowed us to quantify how predictions depend on the choice of the test data in comparison to each training dataset. Our detailed analysis (Figure S4A–S4I in Ref. (Jashnsaz et al., 2020)) indicated that test data that is temporally similar to the training data are usually predictable, while prediction errors increase for test data in conditions that are substantially different than those of the training data. Therefore, it is important to test the model predictions under new conditions that are different than the training data; not only in terms of their final concentrations, but also in terms of how the two (test versus training) stimulation profiles change over time.

Model errors quantifications. The model error was defined as the mean absolute difference of the model fit and their corresponding simulated training data over time. The box plots for the model fit errors (FE) and each of the prediction errors (PE1, PE2, PE3) is quantified out of their corresponding training or test data each over the 10 independent trainings. For the shaded plots of the model fits (red) and predictions (blue or green) for the pathway activations (Figures 4B, 4E, 5B, and 5E), the 1st, 2nd and 3rd quartiles are used such that the thick line, upper and lower shaded areas represent Q2, (Q3-Q2), and (Q2-Q1), respectively.

Limitations

The basic requirement for applying this protocol fully to other signal transduction pathways is that (1) different time-varying environmental gradients can be generated with timescales that are appropriate to the networks under consideration, (2) that the pathway response changes over time in response to time-varying cell stimulation conditions, (3) that the pathway response time is homogenous from cell-to-cell and (4) that the central limit theorem (CLT) is fulfilled in single cells (Gaussian noise). The requirements 3 and 4 ensure that the ODE models capture the dynamics of single cells within experimental errors. For the condition where signaling response is heterogeneous from cell-to-cell or over time, stochastic models are needed to be implemented and the model parameters need to be inferred using single-cell distributions data – rather than ODE models parametrized with population mean data as we implemented in this study.

Troubleshooting

Problem 1

Yeast cells vacuole formation upon cold shock (steps 3–6).

The yeast cells upon cold shock form vacuole that happens even at temperatures as low as 25°C.

Potential solution

It is important to keep the cells at 30°C over the course of the experiment duration (loading the cells to tubes, centrifugation time, loading to flow chamber, and during the time-lapse experiment). To reduce this effect, it is recommended to keep the tubes, mixing flasks, flow chambers, and buffers at the 30°C incubator before the experiment for temperature control.

Problem 2

Image segmentation (steps 6 and 7).

The image segmentation codes identify the boundary of the single cells based on the white rings around the cells in bright field images and this requires sharp cell boundaries.

Potential solution

It is important to adjust the z-focus to have the boundary of the majority of the cells as a clear white ring.

Problem 3

Differential signaling activation (steps 1, 2, 6, 7, and 12).

A requirement for our approach in this protocol is that distinct signaling data can be generated from the pathway under diverse cell stimulation profiles.

Potential solution

When designing time-varying cell stimulation profiles it is important that the profiles are distinct from each other over time, they are physiologically feasible in a lab setting, and that they result in distinct signaling activation dynamics of the pathway under study.

Problem 4

Generalization of the approach (steps 5 and 7).

Generalization of the protocol to measure and model other pathways activation using other reporters.

Potential solution

Although we have used an endogenous YFP tag on Hog1 as a reporter to quantify its nuclear localization as pathway activation readout, signaling data using other reporters such as in immunoblotting in Ref (English et al., 2015) or using fluorescent flow cytometry as in Ref (Thiemicke and Neuert, 2021) could also be used to parametrize the signaling models using this protocol. A list of pathways in different cell types with potential for time-varying cell stimulation with different stimuli types is provided in the discussion section of the Ref. (Jashnsaz et al., 2020).

Problem 5

CLT requirement and noise in data (steps 7–12).

It is important to quantify the distributions of single-cell activation dynamics from the experimental measurements. The type of single cell activation distribution is important in determining the best modeling approach.

Potential solution

Homogeneous single cell activation where the noise is Gaussian among single cells ensures that the ODE models capture the dynamics of single cells within experimental noise. For heterogeneous conditions, stochastic modeling approaches should be considered to infer model parameters using single-cell distributions data rather than the population means.

Problem 6

The fitting issues for different models (step 9).

The optimization algorithm was validated using the “true model” (Figure 2A) that has 20 unknown parameters and for the range of the training data up to 306 timepoints (6 datasets each with 51 timepoints). Under these conditions, we considered different values for the following parameters and the ranges in the Genetic Algorithm (Figure 2F) and they did not have significant impact on the results: the GA Initial Population size (50 to 500 with increments of 50), the GA number of generations (5 to 95 with increments 5), number of time-points to drop for the 1^st GA call (0%–95% with increments of 5%), the absolute value of the models parameters range in the logarithmic base 10 space (1 to 6 with increments of 1). One of the above parameters was sampled in the specified range each time by setting the remaining parameters to values similar in the Figure 2F.

Potential solution

If the signaling model complexity increases, or the amount or the type of the signaling data changes, optimization parameters may be required to be adjusted to ensure the convergence of the fits.

Problem 7

Model complexity range (step 8).

To determine whether the complexity of the proposed signaling models are sufficient.

Potential solution

Our modeling approach in this protocol allows to simplify complex signaling networks to a class of expandable network topologies of increasing complexities by grouping proteins into nodes (Figure 2), and models are trained with signaling data under diverse stimuli inputs (Figure 4). Then models are tested in their ability to make biologically relevant predictions (Figure 5). If the simplified (e.g., 4-node) model doesn’t fit the diverse signaling data quantified in experiment, model complexity could be increased by adding additional regulations and nodes. Predictions of new conditions should be used to eliminate the over-fitting of complex models. We have validated this approach in Ref. (Jashnsaz et al., 2020).

Problem 8

Parameters bounds (steps 9 and 13–16).

The range of model parameters are another important factor to consider when fitting complex signaling models to signaling data in particular to experimental data. Too narrow parameter ranges do not provide enough flexibility in the model to fit the data, while too wide of parameter ranges result in numerical issues when solving the ODEs.

Potential solution

Specific attention should be given to the relation of the specific parameters range and their biological relevance. Fitting could be started with parameter range within a narrow range, and the range for the parameters that always end up at an extreme value could be expanded.

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, [Gregor Neuert] (gregor.neuert@vanderbilt.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

This study includes multiple datasets and codes as following:

The published articles (Johnson et al., 2021; Kesler et al., 2019; Munsky et al., 2018; Neuert et al., 2013; Thiemicke et al., 2019) include the image processing codes for cell segmentation and quantification that are used to analyze the Hog1 experimental data during this study. The codes are available at https://osf.io/kwbe6/.

The datasets and code generated during this study are available at https://github.com/neuertlab/Jashnsaz_STARProtocols_2021. The previously published article (Jashnsaz et al., 2020) and this article include all datasets generated and analyzed during this study.