Novel approach to solve singularly perturbed boundary value problems with negative shift parameter

Abstract

Singularly perturbed boundary value problems with negative shift parameter are special types of differential difference equations whose solution exhibits boundary layer behaviour. A simple but novel numerical method is developed to approximate the numerical solution of the problems of these types. The method gives accurate solutions for $h\ge \epsilon$ in the inner region of the boundary layer where other classical numerical methods fail to give smooth solution. The present method is proved to be point-wise uniformly convergent with second order rate of convergence.

Finite difference method; Delay differential equations; Singular perturbation problem

1. Introduction

Singularly perturbed differential-difference equations arise frequently in the mathematical modelling of real-life phenomena in science and engineering. Scientifically, any differential equation in which the highest order derivative is multiplied by a small positive parameter and containing at least one negative/positive shift parameter is known as a singularly perturbed differential-difference equation. Such types of problem have a variety of applications in the mathematical modelling of various physical and biological phenomena. For example, population ecology, control theory, viscous elasticity, and materials with thermal memory, hybrid optical system, in models for physiological processes, red blood cell system, predator-prey models, and so on as the detailed descriptions given in ([1], [2], [3], [4], [5]). A series of papers developed ([6], [7], [8], [9], [10], [11], [12], [13], [14], [15]), and many more to obtain an approximate solution for different classes of singularly perturbed differential-difference equations. A variety of different numerical approaches have been suggested in an attempt to obtain accurate and reliable schemes for the treatment of boundary value problems of singularly perturbed differential-difference equations with a small negative shift in the convection term [9, 12]. They also tried to discuss the effect of small shifts on the solution of the problem.

However, the main concern with such problems is the swift growth or deterioration of their solutions in one or more narrow boundary layer region(s). In most cases, not only determining analytical solutions to such problems is difficult, but also the convergence analysis due to the presence of boundary layers and multi-scale characters in their solution. In fact, the classical finite difference methods are not reliable to preserve the stability property unless they applied with very fine meshes inside the boundary layers, which requires more computational cost. Even in contrary to the usual expectation, the maximum point-wise error does not decrease as the mesh is refined. As a result, these methods could not capture the solutions in the layer region of the domain as the solution profile depends on the perturbation parameter and their convergence is also highly dependent on the value of the perturbation parameter that also affect their accuracy. To avoid such shortcomings, it is imperative to develop simple and more accurate computational methods for solving the problem under consideration.

In this paper, simple but novel numerical method that gives accurate solutions is formulated for reasonable mesh size compared to the value of perturbation parameter in the inner region of the boundary layer where other classical numerical methods fail to give smooth solution. The scheme is developed by introducing of a fitting parameter in a new finite difference scheme that derived by the application of the finite difference approximation approaches and the theory of singular perturbations.

2. Problem formulation

Consider the following singularly perturbed delay convection-diffusion boundary value problems:

$$\epsilon y^{″}(x)+a(x)y^{\prime }(x-\delta )+b(x)y(x)=f(x),x\in (0,1)$$ (1)

subject to the interval-boundary conditions

$$y(x)=\varphi (x),-\delta \le x\le 0,y(1)=\gamma$$ (2)

with small perturbation parameter, $0<\epsilon \ll 1$ and δ is a small delay parameter to be order of $o(\epsilon )$. The functions $a(x),b(x)$, and $f(x)$ are assumed to be sufficiently smooth with $a(x)\ge a^{⁎}>0$ and $b(x)\le -\beta <0$ for $x\in [0,1]$. When the shift parameter δ is smaller than ε the use of Taylor's series expansion for the term containing shift argument is valid [16]. In this work, the case when $\delta <\epsilon$ is considered. Thus, to approximate the term with delay parameter, Taylor's series expansion is applied as follows:

$$y^{\prime }(x-\delta )=y^{\prime }(x)-\delta y^{″}(x)+O({\delta }^3)$$ (3)

Now, substituting Eq. (3) into Eq. (1), we obtain an asymptotically equivalent singularly perturbed two point boundary value problem of the form:

$$c_{\epsilon }{y}^{″}(x)+a(x)y^{\prime }(x)+b(x)y(x)=f(x)$$ (4)

subject to the boundary conditions

$$y(0)=\varphi (0),y(1)=\gamma$$ (5)

where $c_{\epsilon }=\epsilon -a(x)\delta$ and assumed to be positive throughout the interval $[0,1]$. Since δ is smaller than ε, the effect of the value of the truncated term with $O({\delta }^3)$ is negligible. Hence, the solution of the asymptotically equivalent problem is equivalent to that of the original problem. Further, its error bound is also equivalent to that of the original problem.

The differential operator $Ly(x)=c_{\epsilon }{y}^{″}(x)+a(x)y^{\prime }(x)+b(x)y(x)$ defined on Eq. (4) satisfies the continuous minimum principle given below.

Lemma 2.1

(Continuous minimum principle) Suppose that $\psi (x)$ be the solution function of Eqs. (4)–(5) satisfying $\psi (0)\ge 0,\psi (1)\ge 0$ and $L\psi (x)\le 0,\forall x\in (0,1)$. Then $\psi (x)\ge 0,\forall x\in [0,1]$.

Proof

(See [10], [15]). □

Theorem 2.2

(Stability estimate). The solution $y(x)$ of problem (4)–(5) satisfies

$$|y(x)|\le \frac{\Vert f\Vert }{\beta }+\max \{|\varphi (0)|,\left|\gamma \right|\}$$

where, $\Vert .\Vert$ is the maximum norm defined as $\Vert f\Vert ={\max }_{[0,1]}|f(x)|$.

Proof

(See [10], [15]). □

3. The numerical scheme

In this section, we use finite difference method for the numerical solution of (4)–(5) with a uniform step size. Let we divide the interval $[0,1]$ into N equal parts with constant mesh length h. Then, we have $x_i=ih,i=0.1,2,\cdots ,N,h=1/N$. For convenience, denote $y(x_i)$ by $y_i$ at the nodal point $x_i$. Then, applying Taylor series expansion on $y(x_{i\pm 1})$ upto the term with order 9 and adding the two, we obtain:

$$y_{i-1}-2y_i+y_{i+1}=\frac{2h^2}{2!}{y}_i^{″}+\frac{2h^4}{4!}{y}_i^{(4)}+\frac{2h^6}{6!}{y}_i^{(6)}+\frac{2h^8}{8!}{y}_i^{(8)}+O(h^{10})$$ (6)

and

$$y_{i-1}^{″}-2y_i^{″}+y_{i+1}^{″}=\frac{2h^2}{2!}{y}_i^{(4)}+\frac{2h^4}{4!}{y}_i^{(6)}+\frac{2h^6}{6!}{y}_i^{(8)}+\frac{2h^8}{8!}{y}_i^{(10)}+O(h^{12})$$ (7)

Further, from Eq. (6) and Eq. (7), we obtain the relation:

$$y_{i-1}-2y_i+y_{i+1}=\frac{h^2}{30}(y_{i-1}^{″}+28y_i^{″}+y_{i+1}^{″})+R$$ (8)

where, $R=\frac{h^4}{20}{y}_i^{(4)}-\frac{13h^6}{302400}{y}_i^{(8)}+O(h^{(10)})$.

Writing Eq. (4), in its discrete form:

$$\epsilon y_{i+1}^{″}=-a_{i+1}{y}_{i+1}^{\prime }-b_{i+1}{y}_{i+1}+f_{i+1}$$ (9)

$$\epsilon y_i^{″}=-a_i{y}_i^{\prime }-b_i{y}_i+f_i$$ (10)

and

$$\epsilon y_{i-1}^{″}=-a_{i-1}{y}_{i-1}^{\prime }-b_{i-1}{y}_{i-1}+f_{i-1}$$ (11)

Now, approximating $y_{i+1}^{\prime },y_i^{\prime }$ and $y_{i-1}^{\prime }$ by non symmetric finite differences, we have:

$$y_i^{\prime }\approx \frac{y_{i+1}-y_{i-1}}{2h}+O\left(h^2\right)$$ (12)

$$y_{i+1}^{\prime }\approx \frac{3y_{i+1}-4y_i+y_{i-1}}{2h}-h{y}_i^{\prime }+O\left(h^2\right)$$ (13)

$$y_{i-1}^{\prime }\approx \frac{-y_{i+1}+4y_i-3y_{i-1}}{2h}+h{y}_i^{\prime }+O\left(h^2\right)$$ (14)

Substituting Eqs. (12), (13) and (14) into Eqs. (10), (9) and (11) respectively, utilizing the results into Eq. (8) and simplifying, we obtain:

$$\begin{gathered} (c_{\epsilon }+\frac{a_{i-1}h}{30}-\frac{a_{i+1}h}{30})\left(\frac{y_{i-1}-2y_i+y_{i+1}}{h^2}\right)=(\frac{3a_{i-1}}{60h}-\frac{b_{i-1}}{30}+\frac{28a_i}{60h}-\frac{a_{i+1}}{60h})y_{i-1} \\ +(\frac{-4a_{i-1}}{60h}-\frac{28b_i}{30}+\frac{4a_{i+1}}{60h})y_i+(\frac{a_{i-1}}{60h}-\frac{28a_i}{60h}-\frac{3a_{i+1}}{60h}-\frac{b_{i+1}}{30})y_{i+1} \\ +\frac{1}{30}(f_{i-1}+28f_i+f_{i+1}) \end{gathered}$$ (15)

Now, by introducing a fitting parameter $\sigma (\rho )$ in Eq. (15) above, we obtain:

$$\begin{gathered} (\sigma (\rho )c_{\epsilon }+\frac{a_{i-1}h}{30}-\frac{a_{i+1}h}{30})\left(\frac{y_{i-1}-2y_i+y_{i+1}}{h^2}\right)=(\frac{3a_{i-1}}{60h}-\frac{b_{i-1}}{30}+\frac{28a_i}{60h}-\frac{a_{i+1}}{60h})y_{i-1} \\ +(\frac{-4a_{i-1}}{60h}-\frac{28b_i}{30}+\frac{4a_{i+1}}{60h})y_i+(\frac{a_{i-1}}{60h}-\frac{28a_i}{60h}-\frac{3a_{i+1}}{60h}-\frac{b_{i+1}}{30})y_{i+1} \\ +\frac{1}{30}(f_{i-1}+28f_i+f_{i+1}) \end{gathered}$$ (16)

Multiplying Eq. (16) by h and taking the limit as $h\to 0$, provides:

$$\underset{h\to 0}{\lim }\sigma (\rho )c_{\epsilon }\left(\frac{y_{i-1}-2y_i+y_{i+1}}{h}\right)=\frac{a(0)}{2}(y_{i+1}-y_{i-1})$$ (17)

For problems with layer at the left end of the interval, from the theory of singular perturbations it is known that the solution of Eqs. (4)–(5) is of the form [17] (page 22-26):

$$y(x)\approx y_0(x)+\frac{a(0)}{a(x)}({\varphi }_0-y_0(x))\exp (-a(x)\frac{x}{c_{\epsilon }})+O(\epsilon )$$ (18)

where $y_0(x)$ is the solution of reduced problem

$$a(x)y_0^{\prime }(x)+b(x)y_0(x)=f(x),with,y_0(0)={\varphi }_0$$

By taking the Taylor's series expansion for $a(x)$ about the point $\prime 0^{\prime }$ and restricting to its first terms, Eq. (18) becomes

$$y(x)\approx y_0(x)+({\varphi }_0-y_0(0))\exp (-a(0)\left(\frac{x}{c_{\epsilon }}\right))+O(c_{\epsilon })$$ (19)

By considering Eq. (19) at $x_i=ih$ as $h\to 0$, we obtain

$$\underset{h\to 0}{\lim }y(ih)\approx y_0(0)+({\varphi }_0-y_0(0))\exp (-a(0)\left(i\rho \right))+O(c_{\epsilon })$$ (20)

where $\rho =\frac{h}{c_{\epsilon }}$.

Now, using Eq. (20) into Eq. (17), we get:

$$\frac{\sigma (\rho )}{\rho }(e^{a(0)\rho }-2+e^{-a(0)\rho })=\frac{a(0)}{2}(e^{a(0)\rho }-e^{-a(0)\rho })$$

On simplifying, we get

$$\sigma \left(\rho \right)=\frac{a(0)\rho }{2}\coth \left(\frac{a(0)\rho }{2}\right)$$ (21)

which is a required fitting parameter.

Finally, using Eq. (16) and the value of $\sigma \left(\rho \right)$ given by Eq. (21), we obtain the three term recurrence relation:

$$E_i{y}_{i-1}+F_i{y}_i+G_i{y}_{i+1}=H_i,i=1,2,\cdots ,N-1$$ (22)

where,

$$\begin{gathered} E_i=\frac{\sigma ({\rho }_i)c_{\epsilon }}{h^2}-\frac{a_{i-1}}{60h}-\frac{28a_i}{60h}-\frac{a_{i+1}}{60h}+\frac{b_{i-1}}{30} \\ {F}_i=-\frac{2\sigma ({\rho }_i)c_{\epsilon }}{h^2}+\frac{28b_i}{30} \\ {G}_i=\frac{\sigma ({\rho }_i)c_{\epsilon }}{h^2}+\frac{a_{i-1}}{60h}+\frac{a_{i+1}}{60h}+\frac{28a_i}{60h}+\frac{b_{i+1}}{30} \\ {H}_i=\frac{1}{30}(f_{i-1}+28f_i+f_{i+1}) \end{gathered}$$

The recurrence relation Eq. (22) represents a system of $(N-1)$ equations with $(N+1)$ unknowns. These $(N-1)$ equations together with the boundary conditions $y(0)$ and $y(1)$ given by Eq. (5) are sufficient to solve for the unknowns $y(x_1)$ to $y(x_{N-1})$.

4. Convergence analysis

In this section, we proved the boundness of truncation error and the convergence of the method.

Lemma 4.1

If $y\in C^3(0,1)$, then

$$\left|{\tau }_i\right|\le \underset{x_{i-1}\le x\le x_{i+1}}{\max }\left\{\frac{28a{h}^2}{180}|y^{(3)}(x)|\right\}+O\left(h^3\right),i=1,2,\cdots ,N-1$$ (23)

Proof

By definition of local error estimates, we have

$${\tau }_i=-\sigma c_{\epsilon }\{\frac{y_{i-1}-2y_i+y_{i+1}}{h^2}-y_i^{″}\}+\frac{a_{i-1}}{30}\{(\frac{-3y_{i-1}+4y_i-y_{i-1}}{2h}+h{y}_i^{″})-y_{i-1}^{\prime }\}+\frac{28a_i}{30}\{\frac{y_{i+1}-y_{i-1}}{2h}-y_i^{\prime }\}+\frac{a_{i+1}}{30}\{(\frac{y_{i+1}-4y_i+3y_{i+1}}{2h}-h{y}_i^{″})-y_{i+1}^{\prime }\},i=1(1)N-1\Rightarrow {\tau }_i=-\sigma c_{\epsilon }\{\frac{h^2}{12}{y}_i^{(4)}+\frac{h^4}{360}{y}_i^{(6)}+\cdots \}+\frac{a_{i-1}}{30}\{h{y}_i^{″}-\frac{2h^2}{3}{y}_i^{(3)}+\cdots \}+\frac{28a_i}{30}\{\frac{h^2}{6}{y}_i^{(3)}+\frac{h^4}{120}{y}_i^{(5)}+\cdots \}+\frac{a_{i+1}}{30}\{-h{y}_i^{″}-\frac{2h^2}{3}{y}_i^{(3)}+\cdots \}\Rightarrow \left|{\tau }_i\right|\le \underset{x_{i-1}\le x\le x_{i+1}}{\max }\left\{\frac{\sigma h^2{c}_{\epsilon }}{12}|y^{(4)}(x)|\right\}+\underset{x_{i-1}\le x\le x_{i+1}}{\max }\left\{\frac{28}{180}a{h}^2|y^{(3)}(x)|\right\}$$

Using the relation (22) with $M=\frac{a(0)}{2}\coth \left(\frac{a(0)\rho }{2}\right)$ we get,

$$\Rightarrow \left|e_i\right|\le \underset{x_{i-1}\le x\le x_{i+1}}{\max }\left\{\frac{M{h}^3}{12}|y^{(4)}(x)|\right\}+\underset{x_{i-1}\le x\le x_{i+1}}{\max }\left\{\frac{28}{180}a{h}^2|y^{(3)}(x)|\right\}$$

$$\Rightarrow \left|{\tau }_i\right|\le \underset{x_{i-1}\le x\le x_{i+1}}{\max }\left\{\frac{28}{180}a{h}^2|y^{(3)}(x)|\right\}+O\left(h^3\right)$$

$$\Rightarrow \left|{\tau }_i\right|\le O\left(h^2\right),i=1,2,\cdots ,N-1$$

Thus, the desired result is obtained. This result guarantee the boundness of the truncation error and in turn it implies the stability estimate of the scheme. □

Theorem 4.2

Let $y(x_i)$ be the solution of problem (4) and $y_i$ be the solution of the discrete problem (22). Then, we have the following estimate:

$$|y(x_i)-y_i|\le C{h}^2$$ (24)

Proof

Rewriting Eq. (22) in matrix vector form as:

$$Zy=D$$ (25)

where $Z=\left(m_{i,j}\right),1\le i,j\le N-1$ is a tri-diagonal matrix of order $N-1$ with

$$\begin{gathered} m_{i,i-1}=\frac{\sigma ({\rho }_i)c_{\epsilon }}{h^2}-\frac{a_{i-1}}{60h}-\frac{28a_i}{60h}-\frac{a_{i+1}}{60h}+\frac{b_{i-1}}{30} \\ {m}_{i,i}=-\frac{2\sigma ({\rho }_i)c_{\epsilon }}{h^2}+\frac{28b_i}{30} \\ {m}_{i,i+1}=\frac{\sigma ({\rho }_i)c_{\epsilon }}{h^2}+\frac{a_{i-1}}{60h}-\frac{a_{i+1}}{60h}+\frac{28a_i}{60h}+\frac{b_{i+1}}{30} \end{gathered}$$

and $D=(H_i)$ is a column vector with $H_i=\frac{1}{30}(f_{i-1}+28f_i+f_{i+1})$ for $i=1,2,\cdots ,N-1$, with local truncation error ${\tau }_i$:

$$\left|{\tau }_i\right|\le O\left(h^2\right)$$ (26)

we also have

$$Z\bar{y}-\tau (h)=D$$ (27)

where, $\bar{y}={({\bar{y}}_0,{\bar{y}}_1,\cdots ,{\bar{y}}_N)}^T$ and $e(h)={({\tau }_1(h),{\tau }_2(h),{\tau }_2(h),\cdots ,{\tau }_N(h))}^T$ denote the actual solution and the local truncation error respectively.

From Eqs. (25) and (27), we get

$$Z(\bar{y}-y)=\tau (h)$$ (28)

Thus, the error equation is

$$ZE=\tau (h)$$ (29)

where, $E=\bar{y}-y={(e_0,e_1,e_2,\cdots ,e_N)}^t$. Let S be the sum of elements of the $i^{th}$ row of Z, then we have

$$S_1=\sum _{j=1}^{N-1}{m}_{1,j}=-\frac{\sigma ({\rho }_i)c_{\epsilon }}{h^2}+\frac{a_{i+1}}{60h}+\frac{a_{i-1}}{60h}+\frac{28b_i}{30}+\frac{b_{i+1}}{30}+\frac{28a_i}{60h}$$

$$S_{N-1}=\sum _{j=1}^{N-1}{m}_{N-1,j}=-\frac{\sigma ({\rho }_i)c_{\epsilon }}{h^2}-\frac{a_{i+1}}{60h}-\frac{a_{i-1}}{60h}+\frac{28b_i}{30}+\frac{b_{i-1}}{30}-\frac{28a_i}{60h}$$

$$S_i=\sum _{j=1}^{N-1}{m}_{i,j}=s_i+O\left(h^2\right)=B_{i0};i=2\left(1\right)N-2$$

where, $B_{i0}=s_i=\frac{1}{30}(f_{i-1}+28f_i+f_{i+1})$

For sufficiently small h the matrix Z is irreducible and monotone. Then, it follows that $Z^{-1}$ exists and its elements are non-negative. Hence, from Eq. (29), we obtain

$$E=Z^{-1}\tau (h)$$ (30)

and

$$\Vert E\Vert \le \Vert Z^{-1}\Vert \Vert \tau (h)\Vert$$ (31)

Let ${\bar{m}}_{ki}$ be the ${\left(ki\right)}^{th}$ elements of $Z^{-1}$. Since ${\bar{m}}_{ki}\ge 0$ by the definition of multiplication of matrices with its inverses, we have:

$$\sum _{i=1}^{N-1}{\bar{m}}_{ki}{S}_i=1,k=1,2,\cdots ,N-1$$ (32)

Therefore, it follows that

$$\sum _{i=1}^{N-1}{\bar{m}}_{ki}\le \frac{1}{{\min }_{0\le i\le N-1}{S}_i}=\frac{1}{B_{i,0}}\le \frac{1}{\left|B_{i0}\right|}$$ (33)

for some i0 between 1 and $N-1$, and $B_{i0}=s_i$.

From equations (25), (31) and (33), we obtain

$$e_i=\sum _{i=1}^{N-1}{\bar{m}}_{ki}\tau (h),i=1\left(1\right)N-1$$

which implies

$$e_i\le \frac{O\left(h^2\right)}{\left|s_i\right|}i=1\left(1\right)N-1$$ (34)

Therefore,

$$\Vert E\Vert \le O\left(h^2\right)$$ (35)

This implies that the proposed method is convergent of second order. □

5. Numerical results and discussion

To check the validity of the theoretical results obtained by the proposed method, we considered some model examples of singularly perturbed delay convection-diffusion equations. As the exact solutions of these examples are not known, the maximum absolute error for the given examples are computed by using the double mesh principle [18] defined by:

$$E_{\epsilon ,\delta }^N=\underset{1\le i\le N-1}{\max }|y_i^N-y_{2i}^{2N}|$$

where $y_i^N$ and $y_{2i}^{2N}$ are the $i^{th}$ components of the computed numerical solutions on meshes N and 2N respectively. For any value of N, the ε-uniform errors are calculated using

$$E^N=\underset{\epsilon ,\delta }{\max }{E}_{\epsilon ,\delta }^N$$

The computational rate of convergence of the proposed scheme is calculated by the formula

$$r^N={\log }_2\left(\frac{E^N}{E^{2N}}\right).$$

Example 5.1

$\epsilon y^{″}(x)-e^x{y}^{\prime }(x-\delta )-xy(x)=0$, subject to the interval and boundary conditions, $y(x)=1,-\delta \le x\le 0,y(1)=1$.

Example 5.2

$\epsilon y^{″}(x)-(1+x)y^{\prime }(x-\delta )-e^{-x}y(x)=1$, subject to the interval and boundary conditions, $y(x)=1,-\delta \le x\le 0,y(1)=-1$.

Example 5.3

$\epsilon y^{″}(x)+y^{\prime }(x-\delta )+y(x)=0$, subject to the interval and boundary conditions, $y(x)=1,-\delta \le x\le 0,y(1)=1$.

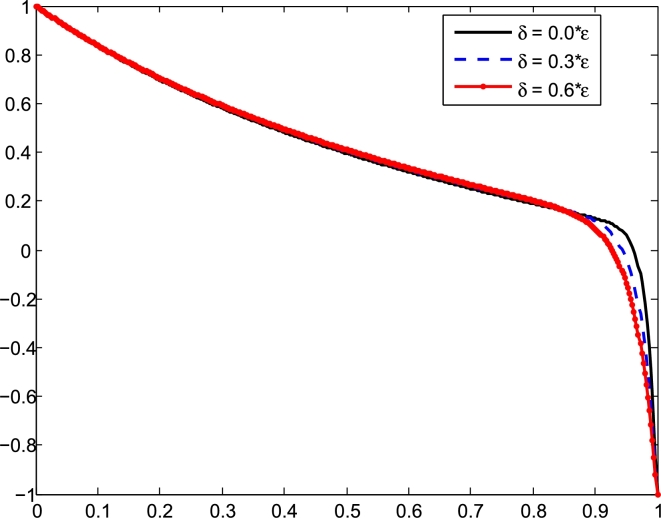
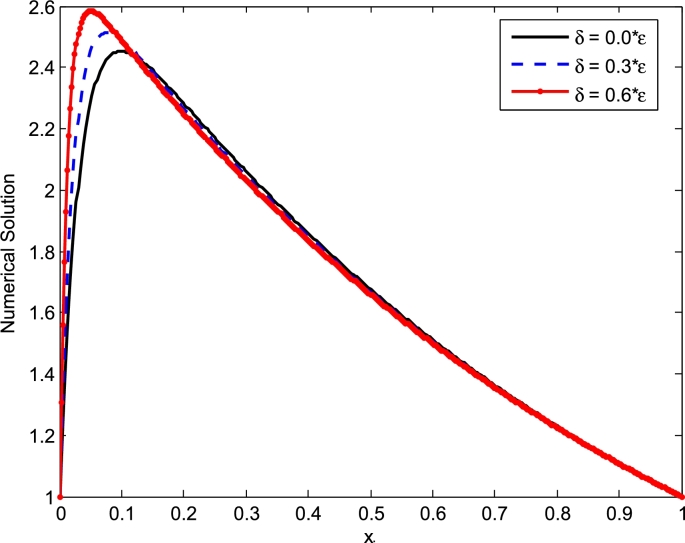
The maximum absolute errors ($E_{\epsilon ,\delta }^N$) of Example 5.1, Example 5.3 are presented in Tables 1 and 2 for different values of δ, N and ε. The uniform error estimate, $E^N$ and rate of convergence, $r^N$ for Example 5.1, Example 5.3 are presented in Table 3. As can be seen from the tabular results presented in Table 2, the maximum absolute error decreases rapidly as the mesh size decreases. The solution behaviour of the problem in the layer regions is depicted in Fig. 1 and revealed that as the value of the delay parameter increases the thickness of the right boundary layer also increases. The effect of small shifts on the boundary layer behaviour of the solutions are also shown in Figs. 2 and 3 for varying values of δ with fixed $\epsilon =2^{-5}$ and $N=400$ for the test Example 5.2, Example 5.3 respectively. These figures clearly show that as the value of the delay parameter increases, the thickness of the layer increases for the case when the solution of the problem manifests layer behaviour at the right end of the solution domain and vice versa for the left end boundary layer.

Table 1.

Maximum absolute errors obtained by the proposed method for different values of δ, N and ε = 0.1.

δ↓ N→	23	25	27	29	211
Example 1
0.03	1.8773e-03	1.2473e-04	7.8243e-06	4.8914e-07	3.0571e-08
0.05	1.5524e-03	1.0187e-04	6.3843e-06	3.9908e-07	2.4941e-08
0.07	1.3187e-03	8.5539e-05	5.3586e-06	3.3496e-07	2.0935e-08
0.09	1.1409e-03	7.3473e-05	4.5998e-06	2.8752e-07	1.7971e-08
Example 2
0.03	7.8120e-03	5.1772e-04	3.2466e-05	2.0295e-06	1.2685e-07
0.05	6.4652e-03	4.2158e-04	2.6415e-05	1.6513e-06	1.0321e-07
0.07	5.4621e-03	3.5313e-04	2.2121e-05	1.3828e-06	8.6424e-08
0.09	4.6929e-03	3.0211e-04	1.8924e-05	1.1830e-06	7.3936e-08
Example 3
0.03	2.4155e-02	1.6227e-03	1.0172e-04	6.3592e-06	3.9745e-07
0.05	3.4122e-02	2.4758e-03	1.5568e-04	9.7362e-06	6.0853e-07
0.07	5.3192e-02	4.4352e-03	2.8433e-04	1.7796e-05	1.1124e-06
0.09	7.0034e-02	1.2727e-02	9.4159e-04	5.9527e-05	3.7231e-06

Table 2.

Maximum absolute errors obtained by the proposed method for different values of ε, N and δ = 0.5 × ε.

ε↓N→	28	210	212	214	216
Example 1
2−8	4.5193e-05	2.8548e-06	1.7854e-07	1.2027e-08	7.4998e-10
2−10	1.5714e-04	1.1355e-05	7.1698e-07	4.8313e-08	3.0214e-09
2−12	2.5560e-04	3.9395e-05	2.8424e-06	1.9331e-07	1.2092e-08
2−14	2.5754e-04	6.4111e-05	9.8555e-06	7.6445e-07	4.8341e-08
2−16	2.5754e-04	6.4600e-05	1.6041e-05	2.5966e-06	1.9113e-07
2−18	2.5754e-04	6.4600e-05	1.6163e-05	4.0212e-06	6.4919e-07
2−20	2.5754e-04	6.4600e-05	1.6163e-05	4.0417e-06	1.0054e-06
Example 2
2−8	2.0046e-04	1.4336e-04	7.9239e-07	5.3521e-08	3.3349e-09
2−10	6.9471e-04	1.4336e-04	3.1949e-06	2.1583e-07	1.3494e-08
2−12	1.1352e-03	1.7425e-04	1.2673e-05	8.6459e-07	5.4081e-08
2−14	1.1428e-03	2.8467e-04	4.3601e-05	3.4173e-06	2.1628e-07
2−16	1.1428e-03	2.8657e-04	7.1221e-05	1.1494e-05	8.5447e-07
2−18	1.1428e-03	2.8657e-04	7.1697e-05	1.7849e-05	2.8736e-06
2−20	1.1428e-03	2.8657e-04	7.1697e-05	1.7928e-05	4.4624e-06
Example 3
2−8	1.4446e-03	1.0091e-04	6.3550e-06	3.1651e-07	4.9760e-08
2−10	2.5932e-03	3.6576e-04	2.5562e-05	1.2873e-06	8.5270e-08
2−12	2.6284e-03	6.5314e-04	9.1851e-05	5.1467e-06	3.2573e-07
2−14	2.6284e-03	6.6201e-04	1.6359e-04	1.9155e-05	1.2890e-06
2−16	2.6284e-03	6.6201e-04	1.6581e-04	3.9977e-05	4.7910e-06
2−18	2.6284e-03	6.6201e-04	1.6581e-04	4.1471e-05	9.9958e-06
2−20	2.6284e-03	6.6201e-04	1.6581e-04	4.1471e-05	1.0369e-05

Table 3.

Uniform errors Estimate (E^N) and rate of convergence (r^N) obtained by the proposed scheme when ε = 0.1 and δ = 0.03.

ε↓ N→	26	27	28	29	210
Example 1
EN	3.1276e-05	7.8243e-06	1.9565e-06	4.8914e-07	1.2229e-07
rN	1.9990	1.9997	2.0000	1.9999
Example 2
EN	1.2976e-04	3.2466e-05	8.1177e-06	2.0295e-06	5.0738e-07
rN	1.9988	1.9998	1.9999	2.0000
Example 3
EN	4.0663e-04	1.0172e-04	2.5436e-05	6.3592e-06	1.5898e-06
rN	1.9991	1.9997	2.0000	2.0000

Figure 1.

The numerical solution of Example 5.1 when ε = 0.1, N = 64 and for different values of δ.

Figure 2.

The numerical solution of Example 5.2 for different values of δ, ε = 2⁻⁵ and N = 400.

Figure 3.

The numerical solution of Example 5.3 for different values of δ, ε = 2⁻⁵ and N = 400.

Moreover, Table 2, shows that the presented method gives accurate solution for both cases of the values of perturbation parameter; that is when it is much much less and greater than mesh sizes. Some methods in the literature such as methods in [10], [12], [13], and [19] lacks the quality that the present method have. Further, the thickness of layer behaviour in Fig. 1 is exactly same as the property that the result in [19] depicted. Hence, the proposed method is more advantageous than some existing methods in the literature.

6. Conclusions

A simple and accurate numerical scheme is proposed for solving singularly perturbed convection-diffusion equation with a small negative shift. The scheme is developed based on the Taylor's series expansion for the approximation of term with negative shift parameter and the finite difference method is applied to approximate the resulting singularly perturbed differential equation. The Efficiency of the scheme is shown by taking some model examples. The scheme is shown to be pointwise uniformly convergent of second-order.

Declarations

Author contribution statement

G.F. Duressa: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

No data was used for the research described in the article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.