Hybrid hyperalignment: A single high-dimensional model of shared information embedded in cortical patterns of response and functional connectivity

Abstract

Shared information content is represented across brains in idiosyncratic functional topographies. Hyperalignment addresses these idiosyncrasies by using neural responses to project individuals’ brain data into a common model space while maintaining the geometric relationships between distinct patterns of activity or connectivity. The dimensions of this common model capture functional profiles that are shared across individuals such as cortical response profiles collected during a common time-locked stimulus presentation (e.g. movie viewing) or functional connectivity profiles. Hyperalignment can use either response-based or connectivity-based input data to derive transformations that project individuals’ neural data from anatomical space into the common model space. Previously, only response or connectivity profiles were used in the derivation of these transformations. In this study, we developed a new hyperalignment algorithm, hybrid hyperalignment, that derives transformations based on both response-based and connectivity-based information. We used three different movie-viewing fMRI datasets to test the performance of our new algorithm. Hybrid hyperalignment derives a single common model space that aligns response-based information as well as or better than response hyperalignment while simultaneously aligning connectivity-based information better than connectivity hyperalignment. These results suggest that a single common information space can encode both shared cortical response and functional connectivity profiles across individuals.

1. Introduction

Hyperalignment models shared information that is embedded in idiosyncratic cortical patterns across brains. Modeling shared information makes it possible to compare functional anatomy across brains at a fine spatial scale. Hyperalignment projects cortical pattern vectors into a common, high-dimensional information space (Haxby et al., 2020). Derivation of this common space can be based on either neural response profiles (e.g. data collected during tasks, such as movie viewing (Haxby et al., 2011)) or functional connectivity profiles (Guntupalli et al., 2018). Common spaces based on each of these data types differentially improve between-subject alignment. Response-based common spaces better align held-out response data, whereas connectivity-based common spaces better align held-out connectivity data. However, it has remained unclear whether optimizations of both response hyperalignment and connectivity hyperalignment would converge on the same common information space.

While both response- and connectivity-based hyperalignment significantly improve intersubject correlations (ISCs) of response profiles relative to anatomical alignment, response-based hyperalignment (RHA) results in slightly higher ISCs for response profiles than does connectivity-based hyperalignment (CHA) (Guntupalli et al., 2018). Similarly, RHA yields better alignment of cortical response patterns for two additional tests of between-subject alignment: between-subject multivariate pattern classification (bsMVPC) and ISC of representational geometry (Guntupalli et al., 2016, 2018). At the same time, CHA yields higher ISCs of dense connectivity profiles than RHA (Guntupalli et al., 2018). In other words, RHA outperforms CHA on response-based metrics of alignment, whereas CHA outperforms RHA on connectivity-based metrics. The common information spaces derived from RHA and CHA are correlated yet different, which suggests that the information contained in population response patterns versus functional connectomes may be fundamentally distinct. Alternatively, RHA and CHA may both be imperfect estimates of a single common information space that can accommodate both shared response information and shared connectivity information.

If the first hypothesis holds and the common spaces derived by RHA and CHA each capitalize on distinct aspects of the same data, then two separate optimal common spaces exist. In this case, adding response information to connectivity-based hyperalignment would move the CHA common space toward the RHA optimum and away from the optimal CHA space, degrading ISC of connectivity profiles. Likewise, moving closer to the shared CHA space by adding connectivity information to response-based hyperalignment should degrade response-based benchmarks of between-subject alignment: ISC of response profiles and bsMVPC of response patterns. If the second hypothesis holds, both RHA and CHA are imperfect estimates of a single optimal shared-information space. In this case, deriving a common space based on combined response and connectivity data should maintain or improve ISCs of response and connectivity profiles as well as bsMVPC of response patterns.

To test these two possibilities, we developed a new algorithm, hybrid hyperalignment, that derives a common space based on both response and connectivity data from the same task fMRI dataset. We measured the performance of hybrid hyperalignment using fMRI data collected while participants watched one of three movies: The Grand Budapest Hotel (Visconti di Oleggio Castello et al., 2020A), Raiders of the Lost Ark (Nastase, 2018), or Whiplash. We found that a single common model computed using both response and functional connectivity information aligned neural response and connectivity patterns across participants as well as or better than RHA or CHA alone, supporting the second hypothesis of a single, optimal shared-information space.

2. Materials and methods

2.1. Participants

We used three separate data sets for our analyses. All participants gave written, informed consent, and all studies were approved by the Institutional Review Board of Dartmouth College. In data set one (Budapest), we scanned 21 participants (11 female, 27.29 years ± 2.35 SD) as they watched the second half of the film The Grand Budapest Hotel ((Visconti di Oleggio Castello et al., 2020A). This dataset had 25 total participants. We used a subset of 21 participants with customized headcases for this analysis. In data set two (Raiders), we scanned 23 participants (12 female, 27.26 years ± 2.40 SD) as they watched the second half of the film Raiders of the Lost Ark (Nastase, 2018). In the third study (Whiplash), 29 participants (15 female, 18.30 years ± 0.79 SD) watched part of the film Whiplash. In the Whiplash data set, we chose 29 participants with the least head motion (measured as average framewise displacement) from a set of 62 participants who viewed this video as part of another study.

2.2. Stimuli and design

In each of these studies, participants viewed part of an audio-visual film in the MRI scanner. In the Budapest data set, participants watched the audio-visual film The Grand Budapest Hotel. They viewed the first portion of the movie outside of the scanner and the second portion (final 50.9 min) in the scanner during fMRI data collection. This second portion of the film was broken into 5 separate runs, each approximately 10 min long, with a short break between each run (Visconti di Oleggio Castello et al., 2020A). In the Raiders data set, fMRI responses were measured while participants watched the second half of the film Raiders of the Lost Ark (approximately 57 min) over 4 runs, each roughly 15 min. Again, participants viewed the first half of the movie outside of the scanner just prior to the scanning session. In the Whiplash data set, participants watched a 29.5 min edit of the film Whiplash. FMRI data were collected in a single run, and we divided the data into 4 pseudoruns of approximately 8 min to approximately match the length of the runs in the two other data sets.

For each data set, the videos were projected using an LCD projector, which the participant could view on a mirror mounted on the head coil in the scanner. Audio was played using MRI-compatible in-ear headphones. Participants were simply instructed to pay attention and enjoy the movie.

2.3. MRI data acquisition and preprocessing

All fMRI data were collected in the Dartmouth Brain Imaging Center with a 3T Siemens Magnetom Prisma MRI scanner (Siemens, Erlangen, Germany) with a 32-channel phased-array head coil with TR/TE = 1000/33 ms, flip angle = 59°, resolution = 2.5 × 2.5 × 2.5 mm isotropic voxels, matrix size = 96 × 96, FoV = 240 × 240 mm, with anterior-posterior phase encoding. For Budapest and Whiplash 52 axial slices were obtained. For Raiders 48 axial slices were obtained. Both volumes provided roughly full brain coverage with no gap between slices.

Anatomical data were acquired using a high-resolution 3-D magnetization-prepared rapid gradient echo sequence (MP-RAGE; 160 sagittal slices; TR/TE, 9.9/4.6 ms; flip angle, 8°; voxel size, 1 × 1 × 1 mm). Data acquisition and conversion to BIDS was performed using the ReproIn specification and tools (Visconti di Oleggio Castello et al., 2020B) and organized into BIDS format with DataLad (Gorgolewski et al., 2016; Halchenko et al., 2017). Data was preprocessed using fMRIprep 20.0.3 (Esteban et al., 2018). The Budapest, Raiders, and Whiplash data sets had 3052, 2570, and 1770 total TRs, respectively. Confound regression was used to mitigate the effects of head motion, physiological fluctuations (e.g. aCompCor), and slow trends. Detailed information on anatomical and functional preprocessing can be found in previous publications for the Budapest (Visconti di Oleggio Castello et al., 2020A) and Raiders (Nastase, 2018) data sets or under Supplemental Methods for the Whiplash data set.

2.4. Intersubject alignment

Our analysis consisted of four types of intersubject alignment beginning with traditional anatomical alignment described in the previous section (and displayed in Fig. 1A). Anatomical alignment (AA) non-linearly registered each participant’s individual BOLD response data to FreeSurfer’s high-resolution fsaverage cortical template based on sulcal curvature (Fischl, 2012). For computational efficiency, and to more closely match the native resolution of the functional data, we then decimated this surface grid to fsaverage5 by selecting the first 10,242 vertices per hemisphere. This lower-resolution fsaverage5 mesh is equivalent to downsampling a participant’s volume data to a 5-order icosahedron tessellation ( “icoorder5”). The AA data were then used to perform hyperalignment with three different algorithms. Response-based hyperalignment (RHA) mapped data from the anatomical space to a common information space based on time-point response patterns across cortical vertices. Connectivity-based hyperalignment (CHA) mapped data from the anatomical space to a separate common information space based on functional connectivity patterns derived from the movie response data. Finally, the novel hybrid hyperalignment (H2A) algorithm began with RHA followed by hyperalignment that used both response and connectivity patterns as input to calculate a single common information space (Fig. 1). All hyperalignment was performed with python code utilizing the PyMVPA toolbox version 2.6.5 (Hanke et al., 2009).

Fig. 1.

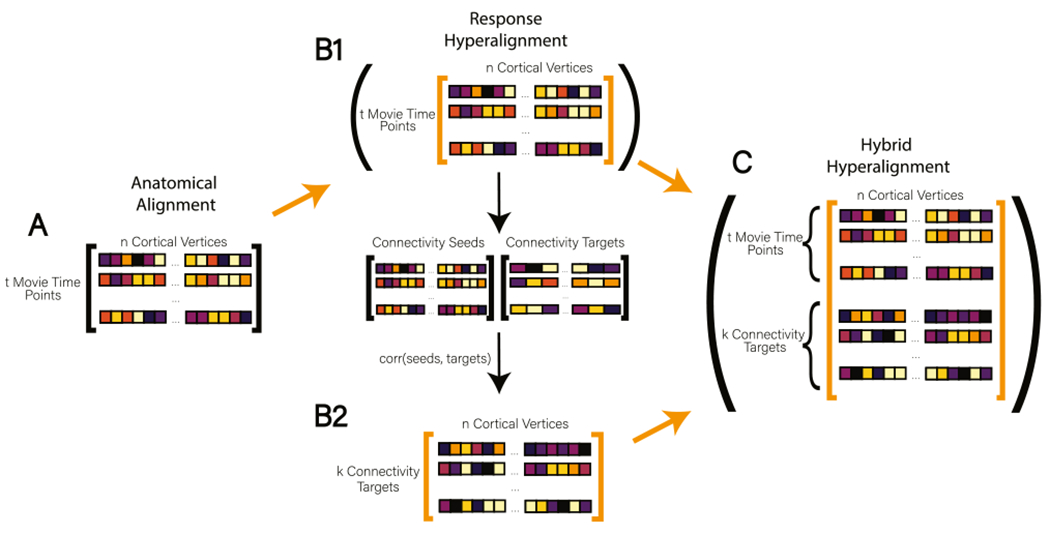
The Hybrid Hyperalignment Algorithm. Orange arrows indicate a data matrix being passed to searchlight hyperalignment. (A) In Anatomical Alignment (AA) response profiles are aligned to a common anatomical template with t movie time points as rows and n cortical vertices as columns. (B1) To perform Response Hyperalignment (RHA), AA data are passed directly to the searchlight hyperalignment algorithm to derive transformation matrices based on local response patterns. Dimensions in the RHA common space are associated with the cortical vertices in a reference brain (Guntupalli et al. 2016). (B2) After mapping AA data into the newly derived RHA common space, the time series of each cortical vertex is correlated with the average time series of vertices aggregated into coarse connectivity targets across the brain (here, 1076 searchlights). The resulting connectome has k connectivity targets as rows and n cortical vertices as columns. (C) In our new method, Hybrid Hyperalignment, the response-hyperaligned time series from B1 and the corresponding functional connectome from B2 are combined, resulting in (t movie time points + k connectivity targets) rows and n cortical vertices as columns. This combined data matrix is then passed to the searchlight hyperalignment algorithm to derive transformations based on both local response and brain-wide connectivity profiles (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

2.4.1. Response-based hyperalignment

To perform response-based hyperalignment we began with the AA data consisting of responses across cortical vertices (over time) in the downsampled fsaverage5 surface (“icoorder5”, 3 mm resolution). We removed vertices within the medial wall for this analysis, which resulted in 9372 and 9370 vertices remaining in the left and right hemispheres respectively. The resulting data matrix for each participant consisted of a row for each TR (response patterns) and a column for each cortical surface vertex (18,742 total combined across left and right hemispheres; Fig. 1B). Each column of the matrix (time series) was z-scored to have zero mean and unit variance. These data served as input to the searchlight response hyperalignment algorithm, which utilizes Procrustes transformations to calculate a transformation matrix for each participant that maps their AA data into a shared high-dimensional information space shared across participants (Guntupalli et al., 2016).

The searchlight hyperalignment algorithm centers a searchlight on each cortical surface vertex and computes a common information space across participants for each searchlight. Because searchlights are highly overlapping, each cortical-vertex-to-model space-dimension pair will be assigned transformation weights from multiple searchlight transformation matrices (Haxby et al., 2020). These transformation weights are summed and z-scored for each vertex-to-dimension pair to produce a single, whole-brain transformation matrix for each participant, which maps data into a single common space for the whole cortex. The use of searchlights serves to constrain the Procrustes transformations of response profiles to a neuroanatomically meaningful radius. In other words, functional data from a vertex in the occipital lobe cannot be aligned to a vertex in the prefrontal cortex. Our analyses used a 20 mm searchlight radius (Guntupalli et al., 2016; Nastase, 2018; Feilong et al., 2018).

2.4.2. Connectivity-based hyperalignment

The implementation of connectivity-based hyperalignment is identical to that of RHA, except that CHA takes a connectivity data matrix as input, rather than a response data matrix. In a functional connectivity matrix, each row is a pattern of connectivity strengths across vertices (columns) for a “connectivity target” elsewhere in the brain. In this way, CHA distinguishes itself from RHA by functionally aligning brain data based on the co-activation of cortical vertices with the rest of the brain in contrast to using purely local response profiles.

To compute each participant’s connectome, we began with the same data matrix as used as input to the RHA algorithm described above (fsaverage5 or “icoorder5” surface, 3 mm resolution) and then defined our connectivity seeds and targets. In this analysis, our connectivity seeds were of the same resolution (3 mm) as our data: each seed was an icoorder5 surface vertex. Our connectivity targets were defined on a sparser surface for two main reasons. By downsampling to a lower resolution, we reduced the number of data points and increased computational efficiency. More notably, defining dense connectivity targets (for example, vertex-to-vertex) on anatomically-aligned data yields poor functional correspondence across participants (as shown in the results presented for anatomical alignment in Fig. 4). By aggregating these targets into searchlights instead of individual vertices, we ensure more reliable seed-target correspondence, which the hyperalignment algorithm assumes. We define the vertices at the center of each connectivity target as each vertex on a lower resolution surface mesh (icoorder3, yielding 588 and 587 vertices in the left and right hemispheres, respectively after masking the medial wall). We then centered a 13 mm searchlight on each of these vertices and computed an average time series for each searchlight, which served as a connectivity target. We calculated the participant’s connectome as the correlation between the average time series of 1175 connectivity target searchlights and the time series of 18472 connectivity seeds (icoorder5 vertices). Each column of a subject’s connectome was then z-scored to have zero-mean and unit variance, and the connectomes were passed to the searchlight hyperalignment algorithm in exactly the same process described above for response patterns in RHA. We used 13 mm searchlights with local averaging to define connectivity targets to reduce the similarity of connectivity patterns for neighboring targets. However, the searchlight hyperalignment step of CHA was performed with 20 mm searchlights in order to match those used in RHA and H2A. This produced a transformation matrix for each participant, which, like RHA, mapped each brain’s cortical vertices into common information space dimensions, but these were based on alignment of each participant’s connectome (derived in AA space) into a connectivity-based common information space.

Fig. 4.

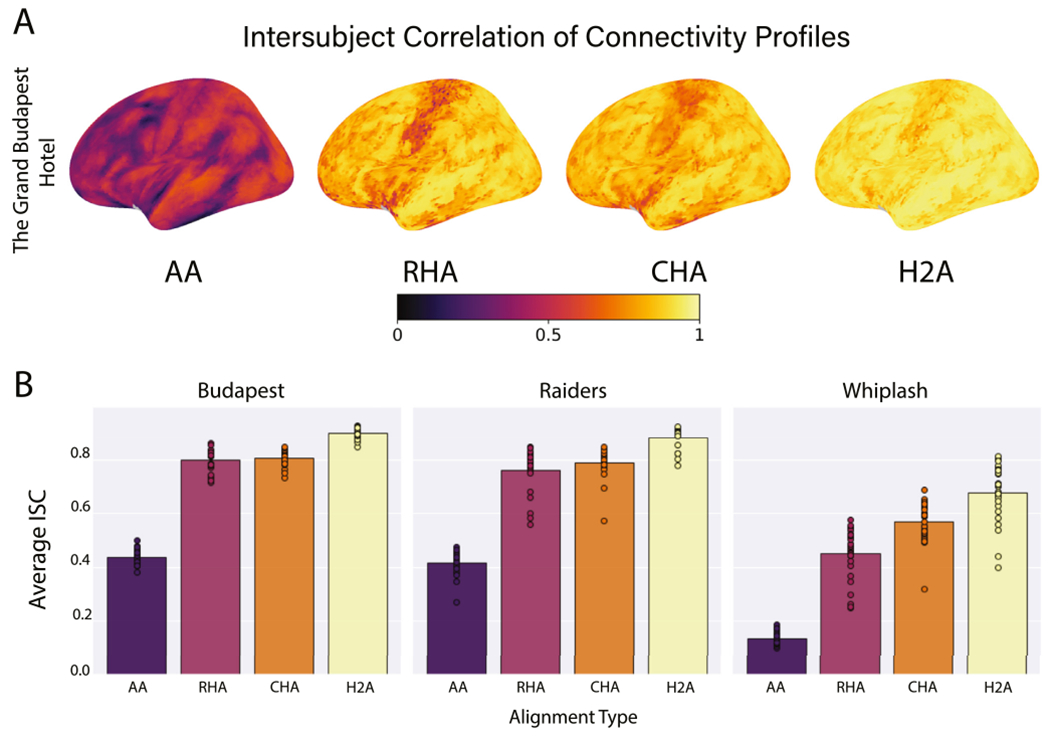
The average intersubject correlation of connectivity profiles. (A) Correlations are presented for each vertex on the left lateral cortical surface averaged over data folds and participants. Brain image figures of results with lateral, medial, and ventral views of both hemispheres are shown in Supplemental Figs. S4–S6. (B) Correlations are shown for each alignment algorithm for each data set. Bars represent the average intersubject correlation over all vertices, data folds, and participants. Circles represent the average intersubject correlation for an individual participant over all vertices and data folds.

2.4.3. Hybrid hyperalignment

The hybrid hyperalignment method starts with response hyperalignment (Fig. 1B1). The response-hyperaligned time series data is then used to compute a functional connectome (Fig. 1B2) using the same procedure as preparing anatomical data for CHA (Section 2.4.2). The time series data and the RHA connectome are then combined and used as input for searchlight hyperalignment to define a common model space based on both patterns of response and patterns of connectivity (Fig. 1C). These two data matrices do not necessarily have the same number of samples, as the samples of the response data represent the number of TRs collected and the samples of the connectome represent the number of connectivity targets we defined. Though each column in both of these matrices already had zero mean and unit variance, we wanted to ensure that the overall magnitudes of the variance of both response and connectivity input data were the same, such that both information types would be equally weighted by the Procrustes transformation. We therefore applied a multiplier to every element of whichever input matrix contained fewer rows. To determine the multiplier, we calculated the Frobenius norm of both the response profile matrix and the connectome matrix for each participant. A ratio of the two Frobenius norms was then computed: the numerator of the ratio was the Frobenius norm of whichever input matrix contained more samples, and the denominator of the ratio was the Frobenius norm of whichever input matrix contained fewer samples.

Once this multiplier was applied, we vertically concatenated the connectome to the response data matrices (Fig. 1C). The resulting matrix was of dimensions t time points plus 1176 connectivity targets (rows/samples) by 18,742 vertices (columns/features). This matrix was then passed to the searchlight hyperalignment algorithm as described above with a 20 mm searchlight radius. Again, searchlight hyperalignment produced a transformation matrix for each participant that maps their AA cortical data into a common information space based on both response and connectivity information.

It is important to note that all three hyperalignment methods made use of the same original neural data but used different sets of patterns derived from those data to compute individual transformation matrices and a common model space.

2.5. Alignment benchmarking

2.5.1. Intersubject correlation of response and connectivity profiles

To investigate the relative efficacy of the hyperalignment procedures in aligning shared information processing across brains, we computed the vertex-by-vertex intersubject correlation (Nastase et al., 2019) of both movie-viewing response profiles (time series responses) (Figs. 2 and 3) and functional connectivity profiles (dense functional connectomes; Guntupalli et al., 2018; Fig. 4). First, the transformation matrices for each participant were calculated by RHA, CHA, and H2A separately using a leave-one-run-out data folding scheme described below. Next, participants’ held-out movie-viewing response profiles (test data) were mapped from anatomical space (fsaverage5) into each common space (derived from training data). Within anatomical space and each common space a dense, vertex-by-vertex functional connectome was computed by correlating each cortical vertex’s response time series with all 18,741 other vertices’ time series for every participant. The Pearson correlation was then calculated across participants for every vertex on both (1) the held-out response profile data and (2) the held-out dense functional connectomes in each of the 3 common information spaces. Differences in the distributions of ISCs across alignment algorithms were tested using a one-sided permutation test for each hyperalignment method vs. AA, or a two-sided permutation test for comparing hyperalignment methods to each other (null distributions were created by shuffling alignment method labels 10,000 times in all tests). Mean ISCs across vertices, participants, and data folds were projected onto the fsaverage template with nearest neighbor interpolation for visualization.

Fig. 2.

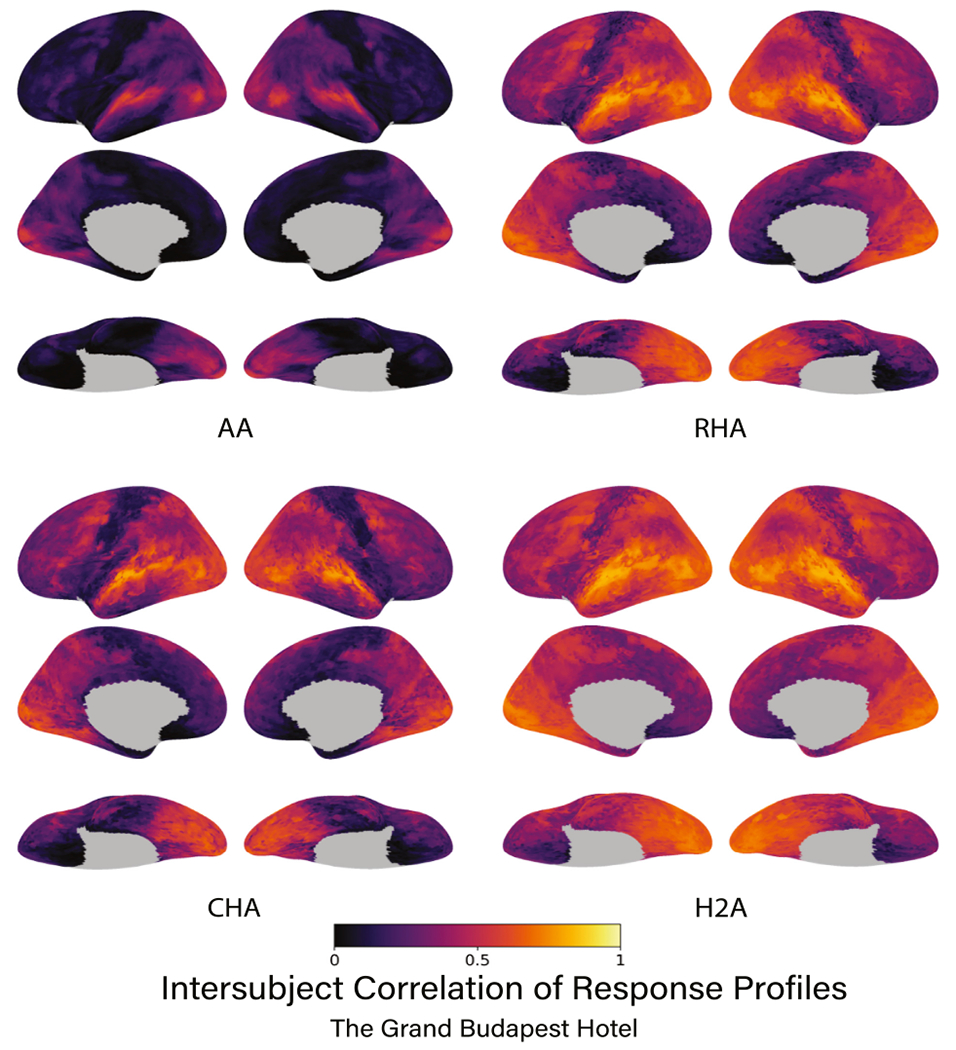
The intersubject correlation of response profiles using the Budapest data for each type of alignment algorithm. Correlations are presented for each vertex on the cortical surface averaged over data folds and participants. Subsequent figures show only left lateral hemisphere views of results. Brain image figures of results for all three datasets with lateral, medial, and ventral views are shown in Supplemental Figs. S1,S2.

Fig. 3.

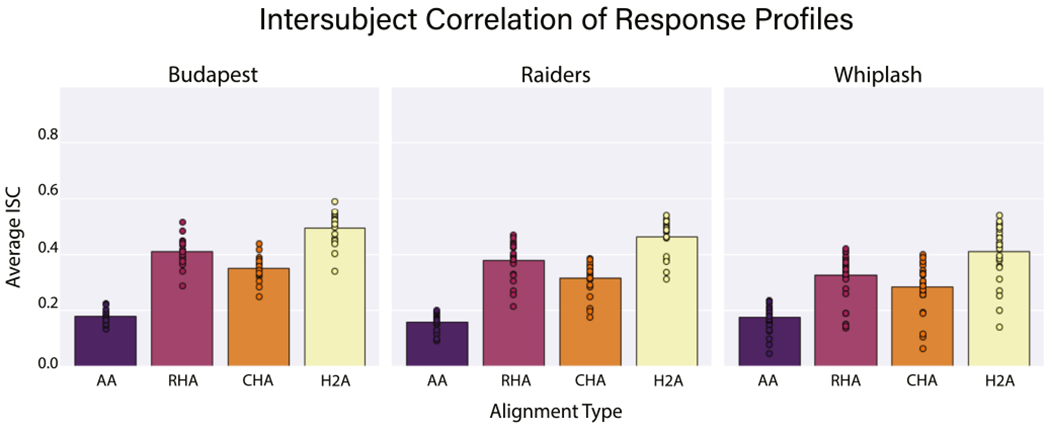
The average intersubject correlation of response profiles is shown for each alignment algorithm for each data set. Bars represent the average intersubject correlation over all vertices, data folds, and participants. Circles represent the average intersubject correlation for an individual participant over all vertices and data folds.

2.5.2. Movie segment classification

We computed the classification accuracies, searchlight-by-searchlight, of 5 s movie segments from a held-out run of movie data. To do this, we compared each searchlight’s activity pattern (averaged across all vertices within a searchlight) in one participant with the average activity pattern over all other participants in the same searchlight for every 5 s movie segment (5 TRs) using a sliding window. Ten-second buffer periods were added to both ends of every target segment such that no target segment was compared to a time segment within 10 s of itself. Thus, each analysis was a 1/3023, 1/2541, or 1/1741 classification for the Budapest, Raiders, or Whiplash datasets, respectively.

The searchlights used for movie segment classification were centered on each cortical vertex and included all other vertices within a 13 mm radius of the center vertex. If a participant’s searchlight pattern of activation for a given segment was most similar to the group average response for the corresponding segment (relative to average group patterns for all other movie segments) it was considered correctly classified. We quantified “most similar” as the segment with the highest Pearson’s correlation coefficient. Differences in the distributions of accuracies for each subject across alignment algorithms were tested using a one-tailed permutation test for AA vs. each hyperalignment method or a two-tailed permutation test for comparing hyperalignment methods to each other. Null distributions were simulated by shuffling alignment method labels 10,000 times in all tests. Mean classification accuracies across searchlights, participants, and data folds were projected onto the fsaverage template with nearest neighbor interpolation for visualization.

We consider movie segment classification to be a strong test of the quality of alignment of shared information across participants. Movies combine complex visual and auditory information with higher-order information about social interactions and narrative arc. Each person encodes this information in idiosyncratic cortical topographies. If hyperalignment successfully aligns these idiosyncratic representations in a common information space, the response pattern at each time point in model space dimensions will be more similar across brains, leading to higher time segment classification accuracies. Previous hyperalignment studies have used 15 s segments (Haxby et al. 2011; Guntupalli et al. 2016, 2018), which contain more neural information and are therefore more easily classified. We opted here for a more exacting classification task with 5 s segments.

2.5.3. Data folding

We used a leave-one-run-out data folding scheme to validate hyperalignment training on an unseen portion of data. For each movie, hyperalignment parameters for each subject were trained on all but one run, and the held-out run was mapped into the trained space using the derived transformation matrix. Once this unseen data was mapped into the common model, alignment performance was benchmarked using our three chosen tests of intersubject alignment: response profile ISC, dense connectome ISC, and movie segment classification. ISC and classification analyses were therefore iteratively performed on every run of every movie after deriving a common space from all other runs from the same movie. Correlations and classification accuracies are reported as the average of these measures across data folds for each movie.

3. Results

3.1. Intersubject correlation

3.1.1. Response profiles

All three hyperalignment algorithms in all three data sets yielded significant improvements in intersubject correlation of vertex time series response profiles across participants relative to AA alone (p < 0.001 for all). Further, H2A aligned response profiles significantly better than RHA in all three data sets. In the Budapest data set, AA produced an average ISC of 0.179, while RHA, CHA, and H2A produced ISCs of 0.411, 0.349, and 0.495, respectively (Figs. 2, 3). RHA and H2A aligned response profiles significantly better than CHA (p < 0.001 for both), and H2A aligned response profiles significantly better than RHA (p < 0.001). In the Raiders data set, AA produced an average ISC of 0.160, while RHA, CHA, and H2A yielded ISCs of 0.378, 0.314, and 0.462, respectively (Fig. 3). Again, RHA and H2A significantly outperformed CHA (p < 0.001 for both), and H2A significantly outperformed RHA (p < 0.001). Finally, in the Whiplash data set, AA produced an average ISC of 0.175, while RHA, CHA, and H2A produced ISCs of 0.324, 0.282, and 0.408, respectively (Fig. 3). In this dataset RHA and H2A performed significantly better than CHA (p < 0.001 for both), and H2A performed significantly better than RHA (p < 0.001). Of note, the Whiplash data set was only about half the duration of the other two data sets, which may partially account for why the ISCs across alignment methodologies are lower for these participants.

3.1.2. Dense connectivity profiles

All three hyperalignment procedures significantly improved the intersubject alignment of dense connectivity profiles relative to AA alone across data sets (p < 0.001 for all), with H2A consistently producing the highest ISCs of any method. In the Budapest data set, AA produced an average ISC of 0.437, while RHA, CHA, and H2A produced ISCs of 0.800, 0.807, and 0.902, respectively (Fig. 4A, B). The ISCs of CHA and RHA were not significantly different (p = 0.848), but the ISC of H2A was significantly higher than both CHA and RHA (p < 0.001 for both). In the Raiders data, AA produced an average ISC of 0.417, and RHA, CHA, and H2A yielded ISCs of 0.762, 0.790, and 0.884, respectively (Fig. 4B). Again, the ISCs of CHA and RHA were not significantly different (p = 0.985), but the ISC of H2A was significantly higher than both CHA and RHA (p < 0.001 for both). Finally, in the shorter Whiplash data set, AA had an average ISC of 0.135, and RHA, CHA, and H2A resulted in ISCs of 0.450, 0.568, and 0.679, respectively (Fig. 4B). In this data set, the ISCs of both CHA and H2A were significantly greater than RHA (p < 0.001 for both). Further, the ISCs of H2A were significantly greater than those of CHA (p < 0.001). The shorter duration of the Whiplash movie-viewing session may partially account for the lower ISCs across alignment algorithms.

3.2. Movie segment classification

Hyperalignment, regardless of the specific algorithm, showed significant improvements relative to AA in classifying 5 s movie segments (p < 0.001 for all). In nearly every common space across data sets, the individual with the lowest hyperaligned classification accuracy had better accuracy than the individual with the highest AA accuracy (Fig. 5B). We present results here as the average classification accuracy across searchlights, participants, and data folds. In the Budapest data set, AA produced an average accuracy of 0.023, while RHA, CHA, and H2A had accuracies of 0.166, 0.115, and 0.162, respectively (Fig. 5A, B). In this data set, RHA and H2A both classified time segments better than CHA (p < 0.001 for both), and RHA significantly outperformed H2A (p = 0.049). In the Raiders data set, AA produced an average classification accuracy of 0.015, and RHA, CHA, and H2A yielded accuracies of 0.117, 0.076, and 0.108, respectively (Fig. 5B). Again, RHA and H2A were both significantly better than CHA at classifying time segments (p< 0.001 for both), but RHA and H2A were not significantly different from each other in accuracy (p = 0.083). Finally, in the Whiplash data set, AA had an average accuracy of 0.022, while RHA, CHA, and H2A produced accuracies of 0.129, 0.086, and 0.137 (Fig. 5B). In this data set RHA and H2A significantly outperformed CHA (p < 0.001 for both), and again, RHA and H2A were not significantly different from each other in accuracy (p = 0.808).

Fig. 5.

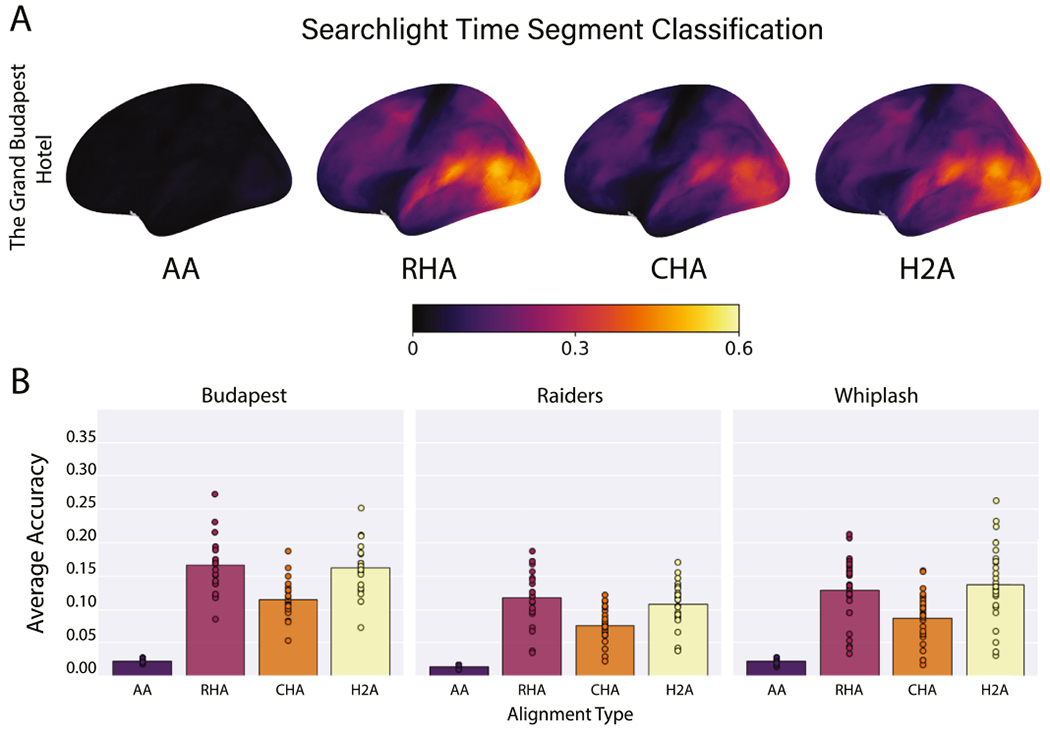
Average time segment classification accuracies. (A) Accuracies are presented for all searchlights on the left lateral cortical surface averaged over data folds and participants. Brain image figures of results with lateral, medial, and ventral views of both hemispheres are shown in Supplemental Figs. S8–S10. (B) Correlations are shown for each alignment algorithm for each data set. Bars represent the average classification accuracies over all searchlights, data folds, and participants. Circles represent the average classification accuracy for an individual participant over all vertices and data folds.

4. Discussion

A major objective of the hyperalignment algorithm is to map the shared information originally found in idiosyncratic cortical topographies into a common space in which this information is better aligned across participants. Previously, RHA was shown to align response-based data better than CHA, whereas CHA was shown to better align connectivity-based data than RHA. In this study we used three separate data sets to show that a hybrid hyperalignment algorithm, H2A, which uses both response and connectivity information from the same dataset, is capable of aligning both types of data in a single common information space. Adding response information in the derivation of the common information space clearly improves the alignment of connectivity information. Adding connectivity information clearly improved alignment of response information on one measure - ISC of response profiles - and maintained performance on another - bsMVPC of movie time segments.

H2A showed significantly greater ISCs of response profiles than both RHA and CHA across all 3 data sets. H2A also showed significantly larger ISCs of dense connectivity profiles than both RHA and CHA across all 3 data sets. Finally, in the most stringent test of the alignment of cortex-wide response patterns, we classified 5 s movie time segments by comparing each individual’s response pattern to the average group response pattern (See Movie Segment Classification above). In the Budapest data, RHA outperformed H2A in classification accuracy by a difference of 0.004 (p = 0.049). In both the Raiders and Whiplash data sets, RHA and H2A classification accuracies were not significantly different. Together, these results show that H2A produces a single common information space that aligns both response and connectivity information as well as or better than RHA or CHA can alone.

Our findings indicate that functional alignment based upon either response or functional connectivity information alone provides an imperfect estimate of an optimal common space that would maximize the shared information we can account for between brains. By combining both types of information, H2A provides a significantly better estimate of this single optimal common space. However, the sequential nature of the H2A method is crucial in aligning both types of information. Anatomical alignment provides poor correspondence of connectivity information (Fig. 4, AA bars; S3, S7, S11). Thus, using anatomically defined data to compute the functional connectome for H2A provides a more noisy estimate of the common space. To address this, we first hyperaligned participants’ response information and then computed the functional connectome within the RHA common space. Because this information passed to H2A is better aligned across participants, the connectivity targets are better aligned for calculating the connectivity patterns that serve as input for H2A (Figs. S3, S7, S11).

We applied a multiplier to the H2A input data such that the Frobenius norms of both the response and connectivity data matrices were equal. One consideration for future exploration is whether equal Frobenius norms for both information types are optimal. It is possible that unequal weighting of the two types of data may in fact be optimal for deriving H2A transformation matrices. For example, it may be preferable to weight RHA more heavily in visual areas and CHA more heavily in prefrontal areas. We plan to investigate this idea further in future studies.

Despite H2A’s evident improvement in aligning functional connectomes compared with CHA, there are some intrinsic limitations that apply to H2A but not CHA. H2A and RHA both require that participants share the same time-locked stimulus with the same number of time points, so they cannot be applied to resting-state data or data sets that implement different stimuli. Because CHA aligns functional connectivity profiles rather than time series data, it alone can be used with datasets that don’t have time-locked stimuli (Guntupalli et al. 2018; Nastase et al., 2020). Although we derive the RHA and CHA estimates from the same movie stimulus in the current application of H2A, the CHA component of the algorithm could also be applied to subjects with both movie and resting-state scans.

In comparison to other methods of functional alignment, our novel H2A method aligns both response and connectivity information using a single algorithm. Many researchers are interested in discerning both specific vertex-wise patterns of activation and patterns of functional network connectivity that correspond to different cognitive states. Previously, fully leveraging hyperalignment to conduct both of these types of analyses would require implementing RHA to derive a response-based common information space and implementing CHA separately to derive a connectivity-based common information space. With H2A researchers can investigate both types of neural information with an estimate of the single optimal information space.

5. Conclusions

Our results show that a single common information space can model both response and connectivity information that is shared across brains. If optimization of shared response and connectivity information resulted in two separate common spaces, the derivation of a single common space using both types of information should vitiate its alignment capabilities. Instead, we found that a hybrid common space aligns response data better than RHA and connectivity data better than CHA. This suggests that the two methods individually produce imperfect estimates of a single optimal information space. The H2A algorithm capitalizes on the strengths of different types of information to provide a more robust estimate of this optimal information space. This makes the H2A algorithm a preferable method for aligning stimulus response data when one wants to evaluate both connectivity and response data. However, H2A does require data collected while participants are shown a time-locked stimulus such as a movie. In cases where this type of data is unavailable, CHA can still be used to align shared information. Our new algorithm is a powerful tool for elucidating the underlying space that encodes various forms of information represented in the brain.

Data/code availability

The Grand Budapest Hotel data are publicly available on Scientific Data (Visconti di Oleggio Castello et al., 2020A). The Raiders of the Lost Ark and Whiplash data will be made available upon request.

Response and connectivity based hyperalignment implementations are available publicly as part of the PyMVPA software package (Hanke et al., 2009). The hybrid hyperalignment implementation and all analysis scripts are available at github.com/ericabusch/hybrid_hyperalignment_neuroimage. The hybrid hyperalignment implementation will be made available via PyMVPA as well.