The impact of social distancing, contact tracing, and case isolation interventions to suppress the COVID-19 epidemic: A modeling study

Abstract

Introduction

Most countries are dependent on nonpharmaceutical public health interventions such as social distancing, contact tracing, and case isolation to mitigate COVID-19 spread until medicines or vaccines widely available. Minimal research has been performed on the independent and combined impact of each of these interventions based on empirical case data.

Methods

We obtained data from all confirmed COVID-19 cases from January 7th to February 22nd 2020 in Zhejiang Province, China, to fit an age-stratified compartmental model using human contact information before and during the outbreak. The effectiveness of social distancing, contact tracing, and case isolation was studied and compared in simulation. We also simulated a two-phase reopening scenario to assess whether various strategies combining nonpharmaceutical interventions are likely to achieve population-level control of a second-wave epidemic.

Results

Our study sample included 1,218 symptomatic cases with COVID-19, of which 664 had no inter-province travel history. Results suggest that 36.5 % (95 % CI, 12.8–57.1) of contacts were quarantined, and approximately five days (95 % CI, 2.2–11.0) were needed to detect and isolate a case. As contact networks would increase after societal and economic reopening, avoiding a second wave without strengthening nonpharmaceutical interventions compared to the first wave it would be exceedingly difficult.

Conclusions

Continuous attention and further improvement of nonpharmaceutical interventions are needed in second-wave prevention. Specifically, contact tracing merits further attention.

1. Introduction

The Coronavirus disease 2019 (COVID-19) caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has had a substantial global impact on almost all countries (WHO Coronavirus Disease (COVID-19), 2021). Despite this, there is a large variability in the public health response and impact among countries. Countries such as South Korea and Canada have been able to reduce the impact of the pandemic after initial large outbreaks (WHO Coronavirus Disease (COVID-19), 2021), while the United States, India, Brazil, and many others are continuing to experience a sustained caseload and high mortality (WHO Coronavirus Disease (COVID-19), 2021).

Due to the lack of effective treatment and limited supplements of vaccines, most countries are dependent on non-pharmaceutical public health interventions to suppress the epidemic curve. Although interventions such as social distancing, contact tracing, and case isolation were widely implemented across countries (Panovska-Griffiths et al., 2020; Aleta et al., 2020), between-country implementation has differed with some countries employing all interventions together while others are more selective. Given the expectation that COVID-19 will continue to circulate and be a public health threat for months to come (Berwick, 2020), strategies that could suppress the epidemic with minimal impact on normal life are needed (Choi et al., 2020; Sebhatu et al., 2020). Although studies have attempted to model the impact of various strategies (Panovska-Griffiths et al., 2020; Aleta et al., 2020; Koh et al., 2020; Kucharski et al., 2020; Quilty et al., 2020), many are theoretical explorations. A few have combined models and data (Flaxman et al., 2020; Davies et al., 2020a; Cowling et al., 2020) to evaluate the effectiveness of combined strategies of multiple interventions but did not distinguish the contribution of each intervention. In resource-limited settings, understanding the impact of distinct strategies utilized so far, and how this might impact future control efforts would be critically important for policymaking.

To address these knowledge gaps, we used a comprehensive COVID-19 patient database in Zhejiang Province, China prior to February 23rd in 2020 with social contact data and timing of community-level interventions. Detailed COVID-19 patient’ data and records of NPI policy enable us to calibrate models for parameter estimations. Often impacts of specific NPIs are estimated by aggregated data or extracted from multiple secondary studies both cannot well control heterogeneity and will cause bias. We explored the impact of single and/or multiple nonpharmaceutical interventions to stymie the COVID-19 pandemic and the possibility of a second wave in the province using a mathematical model.

2. Materials and methods

2.1. Data sources

Zhejiang province, geographically adjacent to Shanghai city, is an eastern coastal province encompassing a population of over 54 million individuals (Bureau of Statistics, 2014). The 1st case in Zhejiang had disease onset on January 7th 2020, followed by a major outbreak until February 22nd, 2020. After this date, only sporadic single-case events were observed, most of which were imported from other provinces. We obtained all confirmed cases at and prior to February 22nd, 2020.

Zhejiang implemented social distancing, contact tracing, and case isolation at the beginning of the epidemic. On January 23rd, the provincial government changed its infectious disease alert category to the highest level. Subsequently, they implemented a comprehensive set of restrictions (Backer et al., 2020) on February 1st. The core interventions (Chong et al., 2020) may be summarized as: 1) using mass symptom-based screening to find cases; 2) isolating all detected cases; 3) quarantining persons exposed to another individual with diagnosed Covid-19 for at least 14 days; 4) ordering mass masking and social distancing to all residents. Trained health professionals investigated each confirmed case with a predefined questionnaire by which basic health and demographic information were collected.

2.2. Model structure

To explore the potential effect of social distancing, contact tracing and case isolation, we built an age-stratified ordinary differential equation (ODE) model to fit the observed data of Zhejiang, China.

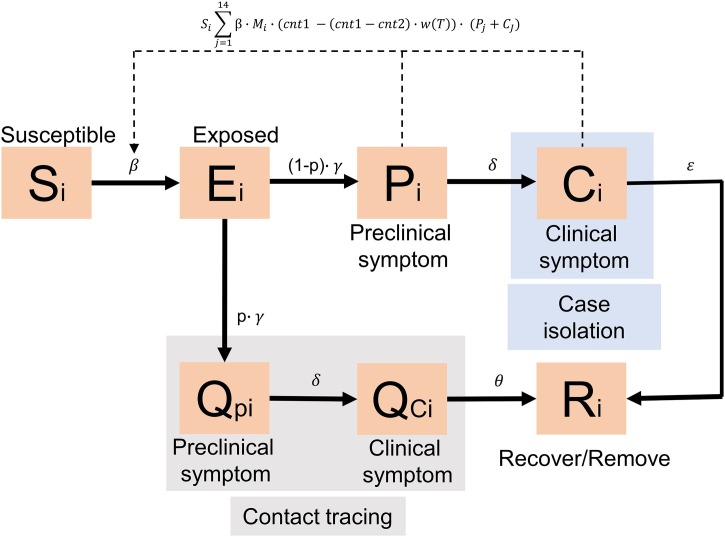
Our model contained 14 age groups and seven compartments per age group. The seven compartments included: 1) susceptible individuals (S); 2) exposed individuals (E); 3) preclinical symptomatic cases (P, infectious but not symptomatic); 4) clinical symptomatic cases (C, infectious and symptomatic); 5) removed/recovery individuals (R); 6) preclinical symptomatic cases in quarantine (Qp); and 7) clinical symptomatic cases in quarantine (Qc). Cases in compartments of individuals under quarantine (i.e., Qp and Qc) were considered in closed-off management making the assumption that they do not contribute to transmission.

To better represent interventions in Zhejiang, we assumed individuals exposed to persons with COVID-19 were partially (with a proportion of p) put into quarantine by contact tracing. Those exposed but lost in contact tracing (1-p), depending on local testing capacity, would be isolated later (with the speed of $\epsilon$) due to mass screening and testing. For each age group, the model is given in Fig. 1 .

Fig. 1.

Model compartments diagram.

2.3. Social contacts

We used contact matrices between age groups with surveys conducted in Shanghai (Zhang et al., 2020; Zhang et al., 2019) along with sensitivity analyses to check possible deviations from different geographic areas. The surveys provided two different strengths of contact (before and during the epidemic). Contact strengths were estimated by age-specific contact rates (number of contacts per person per day).

The first survey conducted in 2017–2018 in Shanghai was considered as a baseline of the strength of contact (Zhang et al., 2019). The second survey with the same design was conducted during the epidemic (from February 1st, 2020, to February 10th, 2020). We modeled the process of contact strength changes between two cross-sectional surveys by a sigmoid function of time (days). The baseline social contact strength was assumed to start declining around January 23rd when the highest level of infectious disease alert category was announced, and smoothly transitioning into the strength of the outbreak period around February 1st, when a comprehensive set of restrictions were implemented. As a result, the decreasing of contact frequency among age groups between two periods (before and during the epidemic) can be modeled as $w\left(t\right)=\frac{1}{1+{{\displaystyle e}}^{-a\left(t-b\right)}},$ where t is the time of day, a and b are two parameters controlling the declining speed of contact strength, and the starting point of the decline, respectively.

2.4. Model parameters

We obtained the total population and age distribution of Zhejiang from China's sixth census (Bureau of Statistics, 2014). We assumed the average time from exposure to preclinical symptomatic status (γ) to be 2 days (Lauer et al., 2020; Backer et al., 2020), the average time from preclinical symptomatic (pre-symptomatic) to symptomatic (δ) to be 4 days (Kong et al., 2020; Wei et al., 2020), and the average time from symptom onset to recover close to 20 days (Deng et al., 2020). Our social contact data were extracted from studies conducted in Shanghai which is a metropolitan city adjacent to Zhejiang Province. Although the two regions share similar social, cultural and economic characteristics, discrepancies in the social contact activities are expected. Therefore, we let the social contact strength of Zhejiang could be variated around the observed value and fitted it by model. To account the potential COVID-19 susceptibility (M) difference between age group, we used estimations from a previous study (Davies et al., 2020b). Details of the mathematical formulas and parameters are listed below and in Table 1 :

$$\begin{array}{l}\lambda =\sum _{j=1}^{14}\beta \cdot {{\displaystyle M}}_{ji}\cdot \left({{\displaystyle cnt1}}_{ji}-\left({{\displaystyle cnt1}}_{ji}-{{\displaystyle cnt2}}_{ji}\right)\cdot w\left(t\right)\right)\cdot \left({{\displaystyle P}}_j+{{\displaystyle C}}_j\right)\\ {{\displaystyle \dot{S}}}_i=-{{\displaystyle S}}_i\lambda \\ {{\displaystyle \dot{E}}}_i={{\displaystyle S}}_i\lambda -E/\gamma \\ {{\displaystyle \dot{P}}}_i=\left(1-p\right)E/\gamma -{{\displaystyle P}}_i/\delta \\ {{\displaystyle \dot{C}}}_i={{\displaystyle P}}_i/\delta -{{\displaystyle C}}_i/\in \\ {{\displaystyle \dot{Q}}}_{pi}=pE/\gamma -{{\displaystyle Q}}_{pi}/\delta \\ {{\displaystyle \dot{Q}}}_{ci}={{\displaystyle Q}}_{pi}/\delta -{{\displaystyle Q}}_{ci}/\theta \\ {{\displaystyle \dot{R}}}_i={{\displaystyle C}}_i/\in +{{\displaystyle Q}}_{ci}/\theta \end{array}$$

Table 1.

Parameters list for model fitting.

Parameter	Meaning	Setting	Notes
Si	Population size in the i-th age group	45 million (Bureau of Statistics, 2014)	Fixed
R0	Basic reproduction number	Uniform (3, 4) (Anderson et al., 2020; Sanche et al., 2020; Viceconte and Petrosillo, 2020; Mizumoto et al., 2020)	R0 = 3.5 was used in the heatmap.
$1/\gamma$	Average time from exposure to preclinical symptomatic (pre-symptomatic)	Gamma (θ = 0.1, k = 20) days (Lauer et al., 2020; Backer et al., 2020)	$1/\gamma$ = 2 days was used in the heatmap
$1/\delta$	Average time from preclinical symptomatic to clinical symptomatic	Gamma (θ = 0.2, k = 20) days (Kong et al., 2020; Wei et al., 2020)	$1/\delta$ = 4 days was used in the heatmap
$\theta$	Average time from clinical symptomatic to recover for those quarantined	20 days (Deng et al., 2020)	Fixed (No influence on model fitting)
$cnt{1}_{ij}$	Social contact from j-th to i-th age groups before the outbreak		From surveys (Zhang et al., 2020; Zhang et al., 2019)
$cnt{2}_{ij}$	Social contact from j-th to i-th age groups during the outbreak		From surveys (Zhang et al., 2020; Zhang et al., 2019)
p	The proportion of exposure get quarantined (contact tracing)	Range: (0, 0.8)	Fitted by the data
$\epsilon$	Case isolation speed (days), from clinical symptomatic to remove for those not in quarantined	Range: (1, 15) days	Fitted by the data
a	Parameter of the sigmoid function	Uniform (0.5, 1.5)	a = 1 was used in the heatmap
b	Parameter of the sigmoid function	Uniform (17, 20)	b = 19 was used in the heatmap
scnt1	Scale parameter of social contact before the outbreak	Range: (0.9, 1.3)	Fitted by the data; final social contact = $\text{s}\text{c}\text{n}\text{t}1\text{*}cnt{1}_{ij}$
scnt2	Scale parameter of social contact during the outbreak	Range: (0.9, 1.3)	Fitted by the data; final social contact = $\text{s}\text{c}\text{n}\text{t}2\text{*}cnt{2}_{ij}$

2.5. Model fitting

We modeled the transmission of COVID-19 in Zhejiang province with cases who had no recent travel histories between provinces. Therefore, only cases without inter-province travel histories were used in the modeling, and we assumed that they were infected by community transmission. Their onset dates were extracted to fit our model. The model with parameters minimizing the sum of the squared differences between the observed and the fitted daily new cases was identified as the best-fit model. The Subplex (Box, 1965) and Nelder-Mead (Nelder and Mead, 1965) simplex algorithms were used in fitting.

2.6. Model simulation

Subsequently, we used parameters estimated from the best-fit model to explore the influence of varied combinations of social distancing, contact tracing proportion, and case isolation speed on outbreak size. We further explored a two-phase reopening scenario to explore what proportion of contact tracing and speed of case isolation are needed to avoid a significant second wave. We assumed that social contact activities in each age group would gradually return to pre-outbreak levels after reopening. However, recommendations of social distancing would not completely end before the elimination of sporadic single-case events. Therefore, we explored potential consequences as the social distancing effect gradually fades off conditioning on different intervention strategies. We proposed a hypothetical two-phase reopening simulation to study these nonpharmaceutical interventions. The first phase of the reopening was assumed to start from the 90th day after the date of the first confirmed cases until the 180th day when the strength of the contact matrix recovered to 50 % of the baseline level (cnt1). Subsequently, the second phase of the reopening was assumed to start after the 180th day and cause the strength of the contact matrix to recover to the level of 80 % of the baseline (cnt1). The entire simulated timeframe was truncated at 12 months, and the predicted counts of cases were used to compare strategies.

2.7. Uncertainty assessment

We repeatedly sampled parameters defined in Table 1 and then re-fit models 1,000 times. In these 1,000 models, we assessed uncertainty of target parameter estimations (isolation speed and quarantine proportion) by mean and credible interval. The uncertainty of epidemic curves of multiple scenarios, and reopening predictions were assessed by the predicted means and 95 % prediction intervals.

All analyses were conducted in R version 4.0.2 (R Core Team, 2020). The deSolve (Soetaert et al., 2010) and nloptr (Ypma et al., 2014) packages were used. The R scripts to reproduce all results are provided as part of the Supplementary Appendix.

3. Results

3.1. Data description

As of February 22nd, 2020 there were 1,218 symptomatic cases in Zhejiang of which 664 cases (54.5 %) reported no inter province travel history. The symptom onset dates of the first and last case were January 7th and February 22nd, 2020, respectively. The peak was observed between January 25th and 31st, 2020.

3.2. Model fitting results

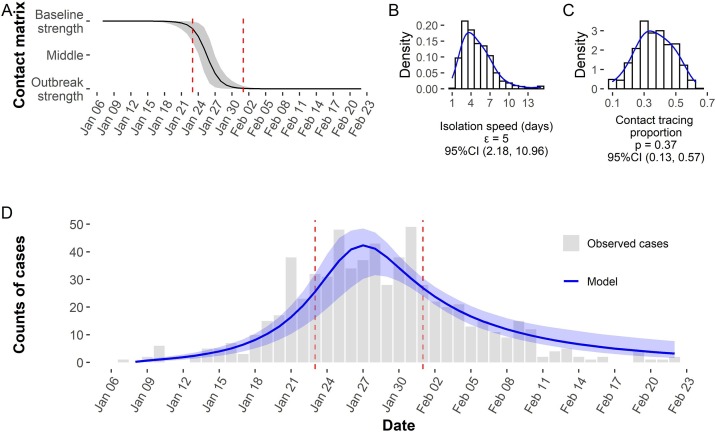
The best-fit model suggested that around 36.5 % (95 % CI, 12.8–57.1 %) of infected contacts were expected to be quarantined and the average case isolation speed ($\epsilon$) was 5 (95 % CI, 2.2–11.0) days. The contact matrix scale parameter scnt1 and scnt2 were 1.3 (95 % CI, 0.9–1.3) and 1.0 (95 % CI, 0.9–1.3). The strength of social contact between age groups began to decrease around January 21st, then reached the level of strict social distancing around February 1st, 2020 (Fig. 2 ).

Fig. 2.

Epidemic curve of the COVID-19 outbreak in Zhejiang and model fitting results. (A) Fitted sigmoid function of social contact change. Zhejiang changed its infectious disease alert category to the highest level on January 23rd, 2020 (left red vertical line) and started a comprehensive set of restrictions on February 1st, 2020 (right red vertical line). (B) The distribution of isolation speed (days). (C) The distribution of contact tracing proportion. (D) Model fitting curve and observed counts of confirmed symptomatic cases by their symptom onset date.

3.3. Scenario analysis

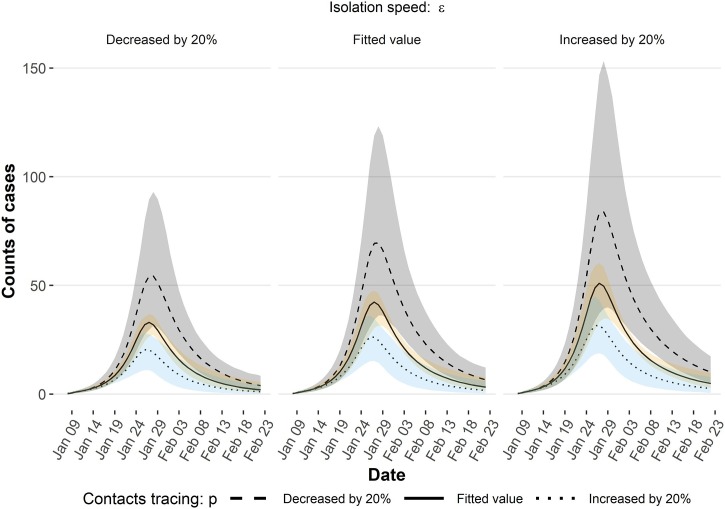
As shown in Fig. 3 , combinations of case isolation speed ($\epsilon$) and contact tracing proportion (p) were associated with different patterns of curves. We simulated scenarios with different $\epsilon$ and p values by increasing or decreasing 20 % of the fitted value. When the contact tracing proportion varied by decreasing 20 %, the peak was significantly elevated. In comparison, a 20 % improvement of isolation days may not compensate for the impact from a 20 % reduction of contact tracing proportion.

Fig. 3.

Scenarios of the epidemic curve with varied case isolation speed ($\epsilon$) and contact tracing proportion (p) by increasing or decreasing 20 %. For example, contact tracing proportion decreased by 20 % means the proportion changed from p to 0.8*p; isolation speed decreased by 20 % means days need for a case’s isolation changed from ε to 0.8*ε days. Line: mean value, color band: 95 % prediction interval.

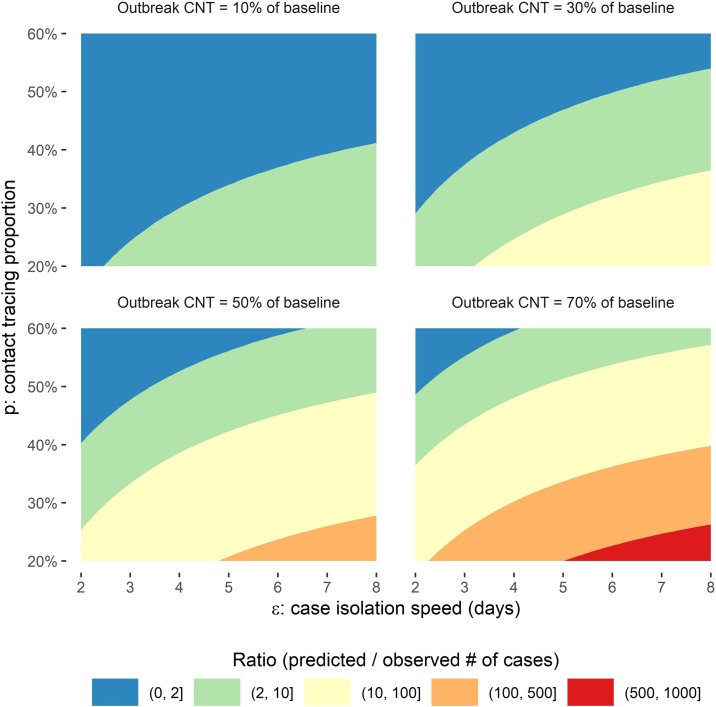
Based on estimated parameters, the ratio of the largest eigenvalue of the social contact strength during and before outbreak was 9 % (95 %CI, 7 %–15 %) in Zhejiang. Therefore, we presented a heatmap with varied social contact strength during the outbreak (10–70 % of the strength prior to the outbreak) to study the relationship between case isolation speed, contact tracing proportion and social contacts (Fig. 4 ). Each of these interventions were able to determine the final case counts. When the observed strength of the contact matrix during the outbreak period hold, the final case counts increased with either decreasing tracing proportion or delay of isolation. As social contact strength during the outbreak increases from 10 % to 70 %, strategies reflected by possible combinations of contact tracing proportion and case isolation speed become less likely to suppress the epidemic to the observed incidence level that ratio of predicted/observed total case number increased fast. In the bottom two panels of Fig. 4, limited strategies space was left for controlling the outbreak closed to the observed level.

Fig. 4.

Heatmap of the ratio of the predicted total number of cases over observed values with different contact tracing proportion, case isolation speed and social contact strength during the outbreak. When the strength of the contact matrix (the CNT level during the outbreak) increased, potential alternative strategies related to case tracing and isolation speed which could suppress the epidemic curve closed to the observed level (ratio close to 1, the blue area) drop quickly.

3.4. The two-phase reopening

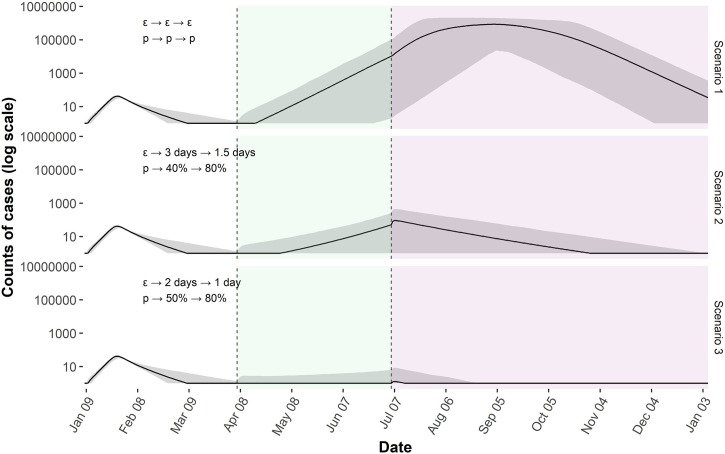
As the decision of society reopening is inevitable, we explored scenarios in which the strength of social contact recovers in two stages. We assumed that the strength of social contact would gradually recover to the level of baseline (before the outbreak). Specifically, the two-phase reopening includes a 1st phase starting at the 90th day after the reporting of the first cases, which will observe the strength of social contact recovered to 50 % of the baseline level by the 180th day, and a 2nd phase (from 180th to 365th day) during which the strength of social contact will reach 80 % of the baseline level at the end of 12 months (Fig. 5 ).

Fig. 5.

The two-phases reopening with varied case isolation speed and contact quarantine proportion. Green area was the 1st phase, purple area was the 2nd phase. Case isolation speed and contact quarantine proportion were hold at the fitted value of the outbreak period through reopening phases in the scenario 1 but varied in scenario 2 and 3. There was an apparent second wave in the first scenario, but much smaller in the second one and almost avoid in the last scenario. In these theoretical simulations, the second wave heavily depended on case isolation speed and contact quarantine proportion.

Based on fitted values of parameters, we simulated the epidemic curves of the two-phase reopening for qualitative comparison. The first scenario assumed the nonpharmaceutical interventions hold at the same level of the outbreak period through the 1st and 2nd phases of reopening. The second scenario assumed the case isolation speed to be 3 and 1.5 days, and the corresponding quarantine proportion at 40 % and 80 % in the 1st and 2nd phases, respectively. In the last scenarios, the case isolation speed was set as 2 and 1 days, with the quarantine proportion of 50 % and 80 % in the 1st and 2nd phases, respectively. A late second wave was observed in the first scenario. The simulated second wave combined with the first outbreak infected around 90 % of the entire population. When isolation speed or quarantine proportion were continuously improved, the overall trajectory would be highly dependent on the combinations of the two. In the scenario 2, the second wave produced additional 3847 cases with an “M” shape, while scenario 3 avoided a second outbreak.

4. Conclusions

We fit an age-stratified, compartmental model based on detailed contact information pre- and post-epidemic in Zhejiang Province, China. The impact of three nonpharmaceutical interventions, including social distancing, case isolation, and contact tracing on transmission control, and safety reopening were subsequently studied using simulation models with parameters estimated from the best-fit model. This study estimated the impact of certain combinations of NPIs in the control of COVID-19 transmission based on local data. This evidence may assist policy makers when deciding on specific interventions to implement.

Social distancing can effectively reduce potential contacts between infectious and susceptible individuals, but it cannot eliminate all contacts (Lau et al., 2020; Seale et al., 2020). Early on in the epidemic, China implemented massive lockdowns and electronic surveillance (Zhang et al., 2020). Zhejiang province declared the highest provincial level public health emergency on January 23rd, 2020, started to suspend all inter-province land and water passenger transportation on January 27th, and restricted city-level gatherings and travels on February 1st, 2020 (Chong et al., 2020). Lockdowns may severely interrupt social activities and/or are less enforceable in many other regions (Kupferschmidt and Cohen, 2020). Our results suggest that a combined effort of better contact tracing and quicker case isolation may compensate for less stringent social distancing implementations.

Our estimation of the case isolation speed at 5 (95 %CI, 2.18–10.96) days was close to the finding from a previous study, in which the average speed of case isolation was reported as 4.6 days (Bi et al., 2020). Case isolation requires quick and reliable identification of the infected person (Raffle et al., 2020). Massive screening and testing were commonly implemented across countries. Even though hospitals and laboratories could reduce the amount of time between testing and isolation, timely testing and isolation remain challenging (GOS, 2021; BBC News, 2021). The virus shedding typically drops in the first few days (Zou et al., 2020), sharply decreasing the sensitivities of testing (Zhao et al., 2020) and suppressing the time window left for accurate case identification. Delayed testing deployment complicates the control efforts further (Pulia et al., 2020). Based on our simulation, if the time period from symptom onset to final isolation cannot be controlled to a maximum of 5 days, which is arguably the case in most places especially the developing countries at this stage, intensive contact tracing will be needed to mitigate the speed of the disease spread.

In Fig. 3, Fig. 4, simulations showed that proportional changes in contact tracing impact the shapes of the epidemic curve more significantly than the changes in case isolation speed. Contact tracing heavily depend on the public health system (Iacobucci, 2020) and is a pre-requisite of rapid case isolation. With a professional investigation of every confirmed case, a large proportion of contacts were traced and put into quarantine. As a result, the scale of secondary cases was chopped heavily. Studies have suggested that reaching 80 % of the contacts of all people tested positive is needed for controls to be effective (Iacobucci, 2020). We found that with stringent social distancing and quick case isolation, Zhejiang province suppressed the curve with a contact tracing effort covering 36.5 % (95 %CI, 12.8%–57.1%) of all exposed individuals, while in the reopening scenarios, higher contact tracing percentages close to 80 % may be necessary.

We found a successful reopening not only depends on the maintenance of previous interventions but also requires continuous improvement, otherwise a second wave would be hard to avoid. Our simulation showed that the isolation speed and quarantine proportion which were able to control the first wave are not sufficient to prevent the second wave. The process of reopening may cause the strength of social contact to arise compared to the observed strength during the outbreak period.

We acknowledge that multiple nonpharmacist interventions mandated in Zhejiang province during the outbreak, such as mass masking, mandatory case isolation and quarantine require significant resources that may be difficult to implement in resource limited locations. Studies assessing cost-effectiveness are needed to understand efficiency and feasibility further. Furthermore, Covid-19 vaccinations are becoming widely available in several countries however are largely unused in the majority of the world. Although our model did not take vaccination into consideration, our study will be instructive to countries with a lack of vaccine supply, where new variants emerge, and also useful for future outbreaks of novel pathogens.

There are some limitations to this analysis. Our model focused on measuring the community transmission of COVID-19. However, the source of imported cases may introduce some biases in the parameter estimations even though we excluded cases with confirmed travel history. We did not adjust for the transmission role of asymptomatic cases, which is still in the debate in the existing literature and hard to be quantified. The SEIR model is sensitive to assumptions of latent and infectious periods when NPIs effectiveness are aimed to be estimated (Wearing et al., 2005). The distribution of infectious and latent periods can impact the model calibration as the trajectory matching was closely related to the key statistics of the curve’s growth and peak (Lloyd, 2001a; Lloyd, 2001b). We used gamma distributions similar as previously published studies on modeling COVID-19 transmission (Lauer et al., 2020; Backer et al., 2020; Kong et al., 2020; Wei et al., 2020). However, such assumptions are with limitations as previously suggested (Wearing et al., 2005; Lloyd, 2001a; Lloyd, 2001b). Nevertheless, the constant recovery/progression model can indeed be a good approximation provided the average duration of the infectious/latent periods is short. Our model needs to be interpreted with caution, as it was built upon assumptions which may not hold in locations where COVID-19 had actively spread longer. Our second wave simulations were based on hypothetical strategies reflected by case isolation speed and contact quarantine proportion, which cannot be easily connected with real-world policies. Potential social distancing dynamic fluctuations after reopening were not further studied. In addition, our approach did not count for virus mutation due to limited data. We expected a more transmissible variant might cause more cases than our estimation. Therefore, our estimations may be conservative. Although these limitations are unlikely to reverse the effect direction of interventions, they would impact the uncertainty assessment of the estimated effectiveness of the interventions.

Social distancing, case isolation, and contact tracing are all necessary to suppress the epidemic curve and to ensure a safe reopening (Flaxman et al., 2020). Based on the differential impact of various intervention strategies identified in our study, contact tracing should be prioritized in strategy generation.

Author statement

Yang Ge: Conceptualization, Methodology, Software, Writing- Original draft preparation, Formal analysis

Zhiping Chen: Conceptualization, Methodology, Investigation, Data Curation, Resources

Andreas Handel: Conceptualization, Methodology

Leonardo Martinez: Conceptualization, Methodology

Qian Xiao: Writing, Reviewing and Editing, Conceptualization

Changwei Li: Writing, Reviewing and Editing, Conceptualization

Enfu Chen: Conceptualization, Investigation, Resources

Jinren Pan: Conceptualization, Investigation, Resources

Yang Li: Conceptualization, Methodology, Writing, Reviewing and Editing, Project administration, Data Curation

Feng Ling: Conceptualization, Writing, Reviewing and Editing, Project administration, Data Curation

Ye Shen: Conceptualization, Methodology, Validation, Supervision, Writing, Reviewing and Editing, Project administration, Resources

Funding sources

This study is funded by Zhejiang Basic Public Welfare Research Project grant LGF21H260003. Li’s work is supported by Platform of Public Health & Disease Control and Prevention, Major Innovation & Planning Interdisciplinary Platform for the “Double-First Class” Initiative, Renmin University of China.

Declaration of Competing Interest

None.

Appendix A. Supplementary data

The following are Supplementary data to this article: