Revisiting the Neural Architecture of Adolescent Decision-Making: Univariate and Multivariate Evidence for System-Based Models

Abstract

Understanding adolescent decision-making is significant for informing basic models of neurodevelopment as well as for the domains of public health and criminal justice. System-based theories posit that adolescent decision-making is guided by activity related to reward and control processes. While successful at explaining behavior, system-based theories have received inconsistent support at the neural level, perhaps because of methodological limitations. Here, we used two complementary approaches to overcome said limitations and rigorously evaluate system-based models. Using decision-level modeling of fMRI data from a risk-taking task in a sample of 2000+ decisions across 51 human adolescents (25 females, mean age = 15.00 years), we find support for system-based theories of decision-making. Neural activity in lateral PFC and a multivariate pattern of cognitive control both predicted a reduced likelihood of risk-taking, whereas increased activity in the NAcc predicted a greater likelihood of risk-taking. Interactions between decision-level brain activity and age were not observed. These results garner support for system-based accounts of adolescent decision-making behavior.

SIGNIFICANCE STATEMENT Adolescent decision-making behavior is of great import for basic science, and carries equally consequential implications for public health and criminal justice. While dominant psychological theories seeking to explain adolescent decision-making have found empirical support, their neuroscientific implementations have received inconsistent support. This may be partly because of statistical approaches used by prior neuroimaging studies of system-based theories. We used brain modeling, an approach that predicts behavior from brain activity, of univariate and multivariate neural activity metrics to better understand how neural components of psychological systems guide decision behavior in adolescents. We found broad support for system-based theories such that neural systems involved in cognitive control predicted a reduced likelihood to make risky decisions, whereas value-based systems predicted greater risk-taking propensity.

Introduction

Adolescent decision-making has important implications for basic science (Blakemore and Mills, 2014; Larsen and Luna, 2018; Sharp and Wall, 2018; Yeager et al., 2018) as well as public health, civic matters, and criminal justice policy (Cohen and Casey, 2014; Cohen et al., 2015; Oosterhoff and Wray-Lake, 2021). Influential theories posit that adolescent decision-making is governed by psychological “systems” that compete (or in some cases, complement) to guide behavior (Casey, 2015; Shulman et al., 2016). While system-based theories have enjoyed broad success at describing the psychological underpinnings of adolescent decision behavior, they have yielded mixed findings when used to describe the neurobiology underlying said behavior (e.g., Pfeifer and Allen, 2012). This discrepancy between psychological and neural data may be due in part to prior neuroimaging work using brain mapping (predicting brain from behavior) instead of brain modeling (predicting behavior from brain) approaches, testing theory between- instead of within-subjects, and not considering multivariate neural patterns. The current neuroimaging study sought to overcome these methodological limitations, and to more rigorously test the validity of system-based models for predicting adolescent risky decision-making.

A number of system-based theories have been used to explain risky decision-making and related motivated behaviors in adolescence (Ernst et al., 2006; Strang et al., 2013; Casey, 2015). Most of these theories contain two key elements. First, they posit the existence of two (though some posit three) adversarial systems: a value-based system oriented toward immediate incentives, increasing the propensity for risk-taking; and a cognitive control system that restrains the former system to avoid risks. Second, these prominent theories argue the value-based system is primed to “overpower” the cognitive-control system in adolescence (i.e., they interact with age), ostensibly leading adolescents to take more risks than children and adults, particularly in socioemotional contexts (Shulman et al., 2016; Steinberg et al., 2018). System-based models tend to perform well at explaining adolescent behavior in observational and experimental studies (Botdorf et al., 2017; Steinberg et al., 2018; Ellingson et al., 2019). However, neuroscientific evidence for these theories is far less consistent (van Duijvenvoorde et al., 2016a, 2016b; Flannery et al., 2017; Lee et al., 2018), prompting calls to update system-based theories (Pfeifer and Allen, 2012, 2016; Casey, 2015), or revise them so drastically as to be categorically different from existing versions (Harden et al., 2017; Romer et al., 2017). Without outright rejecting these possibilities, we propose an alternative interpretation for why system-based theories receive inconsistent neuroscientific support.

Most prior neuroscientific investigations of adolescent decision-making have relied on univariate brain mapping methods to compare individuals who differ in terms of age or risk-taking behavior. Brain mapping refers to statistically predicting brain activity from stimulus or task characteristics, or task behavior (Kragel et al., 2018). An alternative to brain mapping is brain modeling (Kragel et al., 2018), which uses neuroscientific data to predict cognitions and behavior (i.e., any kind of neural metric predicting behavior). Having recently grown in popularity, brain modeling approaches have seen broad applications, some of which involve within-person modeling, including prediction of food craving (Cosme et al., 2019; Cosme and Lopez, 2020), emotion regulation tendencies (Doré et al., 2017), negative affect (Chang et al., 2015), chronic pain (Wager et al., 2013), and vision (Liu et al., 2018; Gardner and Liu, 2019). While brain mapping has generated key discoveries in neuroscience (e.g., Kanwisher, 2017), it can be problematic for evaluating system-based theories. Statistically, brain modeling may be preferable to brain mapping because individual units of analysis (e.g., voxels or neurons) are more predictive when used in concert (e.g., as in a multivariate signature) to predict task behavior, as opposed to the opposite (e.g., behavioral responses predicting brain activity) (Zhao et al., 2021). That is, treating individual voxels as the outcome of an analysis is less informative than examining how multiple voxels collectively predict a phenomenon of interest. Unfortunately, prior brain-mapping studies testing system-based theories of decision-making have largely overlooked the cumulative information that comes from many voxels. Another advantage of brain modeling is that it is better suited for trial-level, within-subject modeling, which tends to be better powered than classic between-subject analyses. Philosophically, system-based theories make predictions about how underlying neural processes drive behavior; for example, “when value-based brain activity is high, individuals will be more likely to take a risk,” which almost by definition aligns with brain modeling. Relatedly, system-based theories of decision-making are implicitly geared toward explaining within-subject behavior (Strang et al., 2013), yet most prior studies of adolescent risky decision-making have focused on between-subject differences (van Duijvenvoorde et al., 2016a; Flannery et al., 2017; Rudolph et al., 2017). Understanding within-adolescent fluctuations in decision-making carries critical translational implications for understanding why the same individual may be law-abiding most of the time but occasionally engage in destructive or maladaptive behavior. The aforementioned limitations of prior work motivated the present study to use novel methodology to test the validity of system-based accounts for predicting adolescent decision-making.

Materials and Methods

Overview

The current study is, to the best of our knowledge, the first within-subject, brain modeling investigation of system-based theories of adolescent decision-making. Using fMRI, we predicted trial-by-trial risky decision-making in healthy adolescents as a function of brain activity from value-based and cognitive control systems, the first premise posited by system-based models. We then tested to see if the two systems interacted with age, testing the second premise posted by system-based models. Critically, we examined two versions of value-based and cognitive control systems: a “classic” univariate version and a newly posited “switchboard” multivariate version. The classic variant of the theory assumes that the value-based system that prioritizes immediate rewards is primarily housed in the NAcc, whereas the cognitive control system is located in lateral PFC (lPFC) (Shulman et al., 2016). This variant is clearly modular, in that it posits that psychological functions are represented in isolated brain regions, or modules, that independently and locally perform their respective function. While evidence exists to suggest that some degree of modularity may be present in the brain (Kanwisher, 2017), this assumption is inconsistent with much other work in cognitive neuroscience that shows psychological processes are encoded in distributed, multivariate signatures (e.g., Chang et al., 2015; Huth et al., 2016; Parkinson et al., 2017). To that end, we additionally tested a “switchboard” version of the model wherein we predict risky behavior as a function of multivariate neural signatures of value and cognitive control (via the use of multivoxel pattern analysis). The advantage of this approach is that it does not hypothesize the localization of mental function to any given ROI but instead assumes that mental functions are encoded in distributed patterns. Another way to summarize the two variants of the model is that the functional units of the classic model lie in particular ROIs, whereas the functional units of the switchboard model are comprised by patterns of activity that cut across brain regions. We used multilevel logistic regression to examine how linear combinations of these brain metrics predicted within-person risky behavior. Last, for thoroughness, we also implemented a between-subjects version of the brain model (predicting risky behavior as a function of brain metrics using only between-subjects information) while considering between-subject variables, including age and sex as predictors, in addition to a traditional univariate analysis.

Procedures and measures

Participants

The N = 51 participants (mean age = 15.00 years, SD = 3.66, range = 9.11-22.60, 25 females) in the current study were part of a broader longitudinal study investigating the impact of early life experiences on the neural bases of socioemotional development. This age range is consistent with recent scientific advances that suggest adolescence in human development may last nearly 15 years (Kinghorn et al., 2018). Participants in the current set of analyses were those who provided usable data from an fMRI scanning session and did not have a history of early social deprivation. Ethnically, 8 participants identified as Hispanic/Latinx (15.7%). Racially, 26 participants identified as white (51%), 6 participants (11.8%) identified as Asian/Asian American, no participants identified as Black (0%), 1 participant (2%) identified as Native Hawaiian/Other Pacific Islander, 7 participants (13.7%) identified as African American, no participants (0%) identified as Native American/Alaskan Native, 4 participants (7.8%) identified as being mixed race, 4 participants identified as belonging to an unlisted race (7.8%), and 3 participants (5.9%) declined to report their race. Sample size was dictated by the number of participants willing to participate in this wave of data collection. Participants were compensated $50 for participating in fMRI scanning. The research was completed at the University of California, Los Angeles. All participants under 18 years provided informed assent, and their parents provided informed consent; all participants 18+ years provided informed consent. All research practices were approved by the Institutional Review Board at the University of California, Los Angeles. Data and analysis code are publicly available on the Open Science Framework (www.osfi.io/fphn4).

Experimental design

Risky decision-making paradigm

Participants completed the Yellow Light Game (YLG) while undergoing fMRI scanning (Fig. 1A) (Op de Macks et al., 2018). An adaptation of a widely used adolescent risk-taking task (the stoplight game) (Gardner and Steinberg, 2005; Chein et al., 2011; Peake et al., 2013), the YLG is a computerized driving simulation in which participants drive along a straight road and encounter a series of intersections. Consistent with prior studies, participants in our study were told the objective of the game was to drive through the set of intersections as quickly as possible. The traffic light at each intersection turned yellow for 1000 ms before crossing each intersection, and participants were faced with a choice to brake (“stop”) or drive through the intersection (“go”). A choice to brake at the intersection resulted in a delay of 2500 ms. A choice to accelerate through the intersection resulted in one of two outcomes: (1) participants would drive straight through the intersection with no delay, or (2) a car from the cross-street would crash into them resulting in a 5000 ms delay. A 10,000 ms delay was imposed if participants failed to respond on a trial. Participants made their choices by pressing one of two buttons on a button box using their index and middle fingers.

Figure 1.

Schematic of data collection, processing, and analysis. For visualization of head motion metrics for fMRI data, see Extended Data Figure 1-1. A, Data acquisition of the YLG while participants were undergoing fMRI scanning. B, LSS modeling implemented as a preprocessing step. C, Schematic of extracting the set of univariate and multivariate metrics from resulting β-series in B.

Figure 1-1

Most extreme frame displacements. Values are randomly jittered along the x axis. Frame displacement values are in millimeter units. The dotted line corresponds to our frame displacement cutoff of 0.9. Revisiting the Neural Architecture of Adolescent Decision Making: Univariate and Multivariate Evidence for System-Based Models Download Figure 1-1, TIF file ^{(769.8KB, tif)} .

Participants completed three runs of the task, consisting of 15 trials each (n = 45 total trials). Unbeknownst to participants, five intersections per run were set to result in a crash if participants chose to accelerate through them, meaning that the probability of crashing was equal to one-third. Participants were not made aware of this probability. Each run had specific intersections that were rigged to crash, and the order in which runs were administered was counterbalanced across participants. Buttons indicating “go” and “stop” were also counterbalanced between subjects among the index and middle fingers. The task was self-paced but typically took participants ∼2.5 min to complete each run. Participants completed two, 10-trial practice runs before scanning to eliminate any potential confounds associated with learning. The YLG was programmed in Java and ran off Apache Tomcat, a program that creates an http web-server environment.

fMRI data acquisition

Imaging data were acquired on a 3T Siemens Prisma scanner using a 32-channel head coil and a parallel image acquisition system (GRAPPA). A high-resolution T1-weighted, MPRAGE image was acquired for registration to functional runs (TR = 2400 ms, TE = 2.22 ms, flip angle = 8°, FOV = 256 mm², 0.8 mm³ isotropic voxels, 208 slices). Functional images were acquired using a T2* EPI BOLD sequence. Thirty-three axial slices were collected with a TR of 2000 ms and a 3 × 3 × 4 mm³ voxel resolution (TE = 30 ms, flip angle = 75°, FOV = 192 mm²). Participants completed the YLG by using a head-mounted mirror on the coil to view an LCD back projector screen.

fMRI analysis

The following sections describe our approach to analyzing the fMRI data using both univariate activity estimates of the NAcc and lPFC and multivariate pattern expression (PE) values for reward and cognitive control signatures (signature definitions described below). We first describe our preprocessing steps and then outline the single-trial analysis procedure used to produce both univariate activity estimates and multivariate metrics for each trial during the task. Because we were interested in within-subject variability in decision-making, we estimated univariate and multivariate values for each trial across all subjects. Single-trial metrics were used for both the within-person (in disaggregate form) and between-person (in aggregate form) analyses, for consistency. We also detail how we conducted the traditional univariate analysis of the YLG.

Preprocessing

Before preprocessing, functional images were visually inspected for artifacts and biological abnormalities. No images contained obvious artifacts or biological abnormalities that warranted exclusion from further analysis. fMRI data were preprocessed and analyzed using the fMRI Expert Analysis Tool (version 6.00) of the FMRIB Software Library package (FSL, version 5.0.9; www.fsl.fmrib.ox.ac.uk). Preprocessing consisted of the following steps: We used the brain extraction tool to remove nonbrain tissue from functional and structural runs, spatially realigned functional volumes to the middle image to correct for head motion using MCFLIRT, and high-pass filtered the data with a 100 s cutoff. We used fsl_motion_outliers to identify volumes that exceeded a 0.9 mm frame displacement threshold for head motion (Siegel et al., 2014), although most participants failed to record any volumes exceeding this threshold (Extended Data Table 1-1; Extended Data Fig. 1-1). No participant had >10% of their volumes in a given run exceed the aforementioned framewise displacement threshold; thus, no participants were excluded on the basis of head motion in our sample. Spatial smoothing was not conducted during preprocessing and was instead applied later when extracting data from single-trial activity estimates because the extent of smoothing depended on the type of information that was being extracted from the single trial (average ROI activation warrants greater smoothing than PE analysis). We prewhitened the data to correct for autocorrelated residuals across time. Functional data were registered to each subject's high-resolution MPRAGE scan with FSL's boundary-based registration (Greve and Fischl, 2009) while maintaining the 3 × 3 × 4 mm voxel size. To preserve the fine-grained spatial resolution of the data, we did not register the functional runs to standard MNI space at this stage but did so for the traditional group analyses (see Table 7). As detailed below, masks and neural signatures were defined in standard space and then transformed to subject space.

Table 7.

Brain regions that showed significant activation Go > Stop and Stop > Go

Region		x	y	z	Z	k
Go > Stop
Occipital pole	L	−18	−90	0	7.51	13,177b
Striatum	R	10	6	8	4.22	b
pSTS	L	−52	−36	28	5.18	491
ACC	R	12	10	42	5.15	406
Amygdala	L	−30	−10	−14	5.60	372
Amygdala	R	30	−12	−12	5.86	229
Insular cortex	L	−56	4	12	4.49	216
SPL	R	24	−52	56	5.34	146
Stop > Go
TPJ	R	50	−56	42	4.97	566
TPJ	L	−46	−60	46	4.52	204

R, Right; L, left; x, y, and z, MNI coordinates; Z, z statistic at those coordinates (local maxima); pSTS, posterior superior temporal sulcus; SPL, superior parietal lobule; TPJ, temporoparietal junction. Regions that share the same superscript (^b) are part of the same cluster.

Within-subject analyses

Single-trial activity estimation

We used a least squares analytic framework to obtain trial-level estimates of the BOLD signal (i.e., a β-series) (Rissman et al., 2004). Here we opted to use the least squares single (LSS) (Fig. 1B) method because of its advantageous statistical properties over the least squares all estimator, especially considering the fast timing of the YLG (Mumford et al., 2012, 2014). Accordingly, a fixed-effects GLM was created for the decision period on each trial of the YLG game within each participant. A decision period was defined as the time between the onset of the yellow light (i.e., when the light at the traffic intersection switched from green to yellow as the car approached the intersection) and when participants pressed a button to signify their decision. A GLM was modeled for the i-th decision period (target decision) such that the target decision received its own regressor, all other decision periods were modeled in a single, separate nuisance regressor, and outcomes of all decisions (delays because of the braking, successful passes after running the light, or crashes) were modeled in another regressor.

Head motion was statistically controlled for across all GLMs by adding FSL's extended motion parameters (6 regressors for x, y, z, pitch, roll, yaw directions, their squares, and the derivatives of both, comprising 24 regressors) in addition to regressors for single volumes that exceeded a frame displacement threshold of 0.9 mm (i.e., censoring). The first temporal derivative of all task and motion regressors were also entered into the model to account for slice timing and motion effects, respectively. Parameter estimates from each trial-specific GLM were used to create a linear contrast image comparing the target decision period to the implicit baseline (unmodeled events). We then used the unthresholded z statistics of this contrast to extract univariate and multivariate estimates of the BOLD signal in ROIs.

Extracting univariate ROI activity from single-trial estimates (classic model)

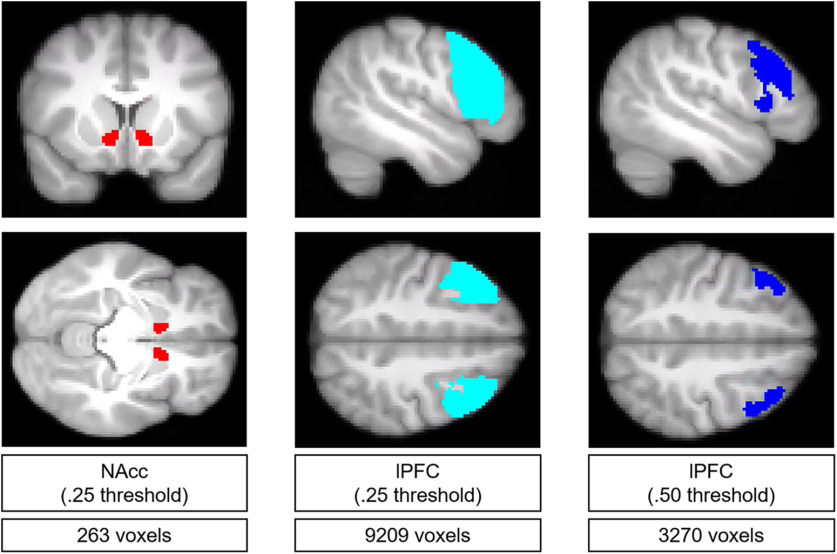
Masks were defined to extract univariate activity from the NAcc and lPFC. Both masks were defined using the Harvard-Oxford probabilistic atlas as rendered in FSL's viewer (fslview) on the MNI152 NLIN sixth-generation T1 template image at 2 mm³ voxel resolution (avg152T1_brain.nii.gz) (Brett et al., 2002). This atlas contains probabilistic masks to various bilateral structures that articulate the probability that a given voxel within the mask falls in the specified brain region. We created a bilateral NAcc mask by merging the atlas' left and right NAcc probabilistic images into a nifti volume and thresholding the image at p = 0.25. We selected the NAcc because of prior empirical and theoretical accounts of this region's importance in adolescent risk-taking (Galvan et al., 2006; Steinberg, 2010). The 0.25 threshold was selected with the goal of creating a mask that was relatively inclusive but did not also possess clear outlying voxels (i.e., voxels with a very low probability of landing in the accumbens). A similar procedure was used to create a bivariate lPFC mask by selecting and merging left and right interior frontal gyrus masks (both the pars opercularis and pars triangularis) and thresholding the image at p = 0.50. We chose a 0.50 threshold for this mask because lPFC activation reported in prior adolescent neuroimaging studies tends to be spatially broad. However, we also created another version of this mask by thresholding at p = 0.25 to be consistent with the NAcc mask and found consistent results (masks shown in Fig. 2).

Figure 2.

NAcc and lPFC masks used to extract univariate activation estimates. NAcc refers to ventral striatum. Thresholds were applied to probabilities values from the Harvard-Oxford cortical and subcortical atlases. Masks are depicted in MNI standard space and projected onto an average of all subjects' high-resolution anatomic images.

Once our masks were defined, we transformed the masks into the native space for each single-trial activity map using FLIRT (i.e., whole brain zstat) and then extracted activity estimates using the nilearn software package (Abraham et al., 2014). We used the package's NiftiMasker() function to mask each single-trial activity estimate with the aforementioned NAcc mask and then again with the aforementioned lPFC mask and extract the mean of all voxels within each respective mask (Fig. 1C). It was at this step that we applied smoothing to the extracted data (6 mm, FWHM), as the NiftiMasker() function allows one to smooth a masked image when extracting data. This step produced a set of NAcc and lPFC activation estimates for each trial on the task across all subjects (i.e., each subject had as many NAcc and lPFC activation estimates as they did decisions in the YLG).

Computing PE from single-trial estimates (switchboard)

We used PE analyses to quantify the extent to which whole-brain patterns of brain activity corresponded to neural signatures of cognitive control and value-based computations (Fig. 1C). Such an analysis allows one to determine how strongly a given pattern of brain activity is expressed as a function of a neural signature of interest (Wager et al., 2013; Chang et al., 2015; Kragel et al., 2018). Neural signatures are thought to be the fingerprints of brain activity that encode a particular psychological process or state of interest. In practice, they are frequently defined as maps of the brain containing weights that quantify the strength and direction of association between each voxel and the psychological process of interest.

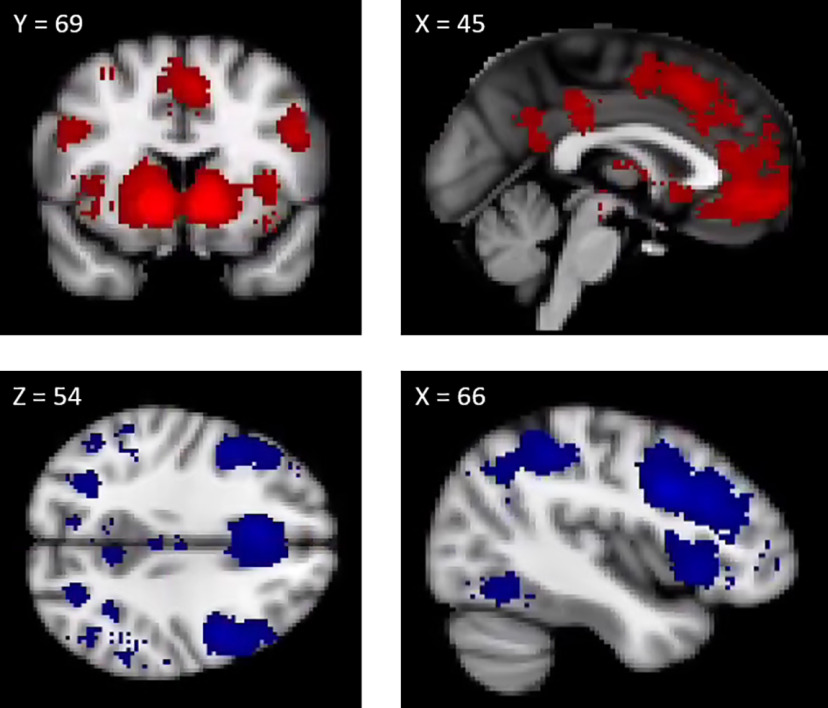
The first step in this analysis involved defining neural signatures of cognitive control and value-based computation. To this end, we used Neurosynth, a web-based platform that automates meta-analysis over a large set of published fMRI studies (Yarkoni et al., 2011), to retrieve meta-analytic maps for the terms “value” (470 studies) and “cognitive control” (598 studies). We chose these terms based on system-based theories such that “value” references one system which drives adolescents to make risky decisions in service of acquiring immediate hedonic rewards, whereas “cognitive control” references a second system which modulates the drive toward immediate rewards (Steinberg, 2013; Shulman et al., 2016). A benefit of using meta-analytic maps as neural signatures is that they “allow the data to speak for themselves” by allowing us to select voxel weights that are most strongly associated to our psychological processes of interest (in contrast to approaches that posit singular ROIs that might exclude meaningful voxels). To our knowledge, the majority of data used to calculate these analytic maps come from traditional univariate studies, although we note that the high volume of studies should theoretically allow for identification of the most sensitive voxels. To ensure the robustness of results, we used both the uniformity and association maps (reported in Table 3). While a review of the differences between these two types of images is beyond the scope of this paper (see Neurosynth.org/faq), we briefly note here that association maps provide greater selectivity about the relationship between a voxel and a given term by incorporating information about base rates. To be comprehensive, we reran all analyses with the Neurosynth term “reward” and observed nearly identical results. Maps of the two signatures (uniformity) are depicted in Figure 3.

Table 3.

Log-odds of risky choice from within-subjects analysis of switchboard system-based models

Term	A: Estimate	B: Estimate	C: Estimate
Intercept	0.581 (0.123)***	0.510 (0.122)***	0.619 (0.122)***
Value PE	0.051 (0.048)	0.008 (0.054)	−0.004 (0.052)
Cognitive control PE	−0.123 (0.047)**	−0.119 (0.060)*	−0.154 (0.055)**
Age	0.113 (0.087)	0.134 (0.079)†	0.122 (0.087)
Gender	−0.104 (0.181)	0.054 (0.181)	−0.176 (0.174)
Variance component	A: Estimate	B: Estimate	C: Estimate
Var(π0ij)	0.259	0.253	0.284
Var(π1ij)	0.000	0.006	0.010
Var(π2ij)	0.003	0.039	0.022
Fit statistic	A: Statistic	B: Statistic	C: Statistic
AIC	2894.3	2892.6	2888.1
BIC	2957.1	2955.4	2950.9

Value PE refers to value-based PE; Cognitive control PE refers to cognitive control PE. Var() refers to a variance component of a given random effect from the model. Results come from a multilevel logistic regression model, with log-odds of a risky choice as the dependent variable. Column A, Results using Neurosynth association maps for PE analysis; Column B, Results using Neurosynth uniformity maps; Column C, Results from a PE analysis using only unique voxels among the value and cognitive control Neurosynth uniformity maps (i.e., common voxels between the two masks were removed).

*p < 0.05.

**p < 0.01.

***p < 0.001.

†p < 0.10.

Figure 3.

Multivariate signatures of value (top row) and cognitive control (bottom row). Both signatures obtained from Neurosynth. Uniformity signatures are depicted. Voxels weights differed between each mask (i.e., a hypothetical voxel could be included in both signatures, but its weight likely varied between signatures). This is important to note because these maps were used as multivariate signatures, which ultimately meant that the same brain regions included in both masks possessed a different multivariate signature.

Once the neural signatures were defined, we transformed each signature into the native space of each single-trial activity map (i.e., whole-brain zstat), and extracted multivariate patterns from both the transformed neural signatures and activity estimates using NiftiMasker(). Multivariate patterns were minimally smoothed (1 mm FWHM) (Weaverdyck et al., 2020), and then the dot product between voxels in the two patterns (activity estimate, neural signatures) was taken (we reran all analyses with a greater smoothing kernel, 4 mm FWHM, and obtained highly similar results). This resulted in two PE estimates per trial: one quantifying the expression of value patterns in brain activity during a given decision and another quantifying the expression of cognitive control patterns in brain activity during the same decision. Barring missing decision data (Fig. 4), each subject had 90 PE estimates: 45 for value and 45 for cognitive control, each corresponding to a decision during the YLG.

Figure 4.

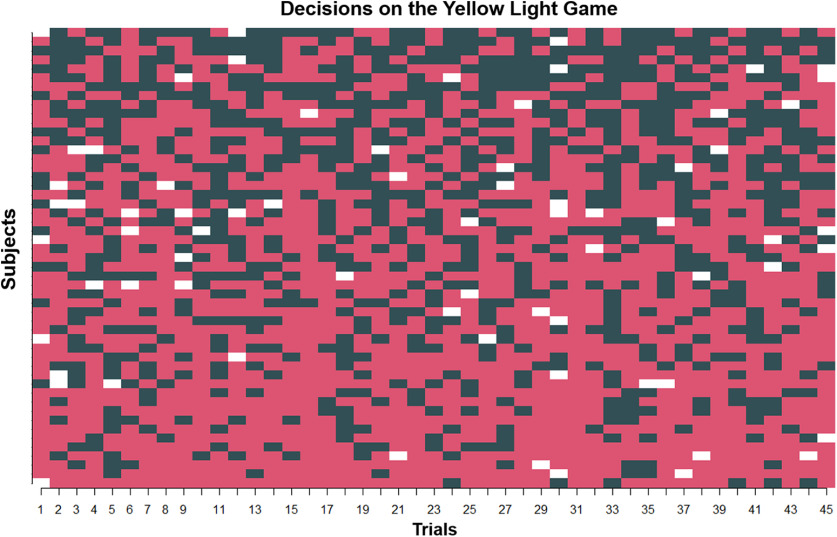
Visualizing risky and safe decisions on the YLG for all participants. Red squares represent risky decisions. Black squares represent safe decisions. White squares represent no decision (i.e., failure to respond). Columns represent decision (trial) number, arranged chronologically. Rows represent subjects (arranged in order of descending rate of risky decisions). Entries into the matrix represent whether a given subject made a risky or safe decision on a given trial.

Notably, we were aware of previous work using PE analyses with a preprocessing stream that involved normalizing images to standard space (Wager et al., 2013; Chang et al., 2015). We note that our decision to keep images in subject space for PE calculation is not necessarily at odds or incompatible with these prior studies, best practices for PE analyses, or even the broader multivoxel pattern analysis literature. Unlike these prior studies, our goal was not to create a biomarker or construct a neural signature that can be applied across an entire population (Weaverdyck et al., 2020). Because our focus was on intra-individual fluctuations in activity and links to decision-making behavior, it was appropriate to refrain from normalizing to preserve fine-grain spatial information.

Between-subject analyses

Aggregation of trial-level data for between-subjects analysis

In order to conduct between-subject analyses, we aggregated the trial-level univariate and PE data. We did this by taking the average of the aforementioned brain activity metrics for each subject.

Group-level brain mapping analysis

We conducted traditional, group-level brain mapping (mass univariate) analyses to serve as a comparison point and complement our between-subject analyses (Chein et al., 2011; Telzer et al., 2015; Op de Macks et al., 2018). To this end, we first submitted each participant's run-level data to a fixed GLM analysis in FSL. For this purpose, the YLG was modeled consistent with other prior univariate studies by including a regressor for Go decisions, a regressor for Stop decisions, and a regressor for outcomes (regardless of type, e.g., successful pass, crash). This differed from the LSS analysis in that all events from each condition of interest (Go decisions, Stop decisions, outcomes) are put into a single regressor for that condition, whereas the LSS analysis assigns a target decision trial (regardless of type) its own regressor, and all other decisions and outcomes are modeled as two separate nuisance regressors. The same preprocessing decisions steps were taken as in all other analyses (e.g., slice timing correction via adding temporal derivatives, adding extended motion parameters, censored volumes, etc.). The only exception was that we smoothed our data for this model (6 mm, FWHM), and nonlinearly registered high-resolution anatomic images to the MNI152 template image (10 mm warp resolution), and used the subsequent transformation matrix to register the functional images to standard space.

Parameter estimates from this GLM were used to create linear contrast images comparing the Go and Stop conditions (Go-Stop, Stop-Go). Random effects, group-level analyses were performed on this contrast using FSL's FLAME1 module. A cluster defining threshold of Z = 3.1 was used in conjunction with a familywise error rate of p < 0.05 and Random Field Theory cluster correction to address the problem of multiple comparisons. An additional whole-brain analysis regressed age (mean centered) on these contrasts but found no age effects.

Statistical analysis

Overview

Our analytic approach consisted of two parts. The first set of analyses examined neural systems underlying within-subject variability in decision-making, using both classic and switchboard models. The second set of analyses examined between-subject variability in decision-making. Here, we again compared classic and switchboard dual-systems models. A detailed description of both approaches follows below. For thoroughness, we also report a traditional between-subjects univariate analysis of the YLG in Table 7.

Within-subjects: modeling trial-level influences of brain on behavior

We executed our within-subjects test of the classic and switchboard models with a series of multilevel logistic regression models. For each theory (classic, switchboard), we conducted a multilevel logistic regression model, including trial-level estimates of brain activity and subject-level controls (age, gender). The form and specification of the statistical models for both variants follow:

Trial-level, Classic:

$$\mathrm{Logit}\left({\mathrm{Decision}}_{ij}\right)={\pi }_{0j}+{\pi }_{1j}\left({\mathrm{NAcc}}_{ij}\right)+{\pi }_{2j}\left({\mathrm{lPFC}}_{ij}\right)$$

Trial-level, Switchboard:

$$\mathrm{Logit}\left({\mathrm{Decision}}_{ij}\right)={\pi }_{0j}+{\pi }_{1j}\left(\mathrm{Value}{\mathrm{PE}}_{ij}\right)+{\pi }_{2j}\left(\mathrm{Cognitive}\mathrm{Control}{\mathrm{PE}}_{ij}\right)$$

Decisions (1 = risky [Go], 0 = safe [Stop]) at the i-th trial for the j-th individual were modeled as a function of a subject-specific intercept (π_0j), and brain activity metrics. The brain activity metrics in the classic model were average activations in the ventral striatum (NAcc_ij) and lPFC (lPFC_ij) at the i-th trial for the j-th individual. Said activity metrics in the switchboard model were PE estimates for value (Value PE_ij) and cognitive control (Cognitive Control PE_ij) for the i-th trial for the j-th individual. Subject-specific parameters for all within-person predictors (π_1j and π_2j) correspond to the subject-specific expected change in the log-odds of making a risky decision given a 1 unit increase in the predictor (e.g., average univariate brain activity, PE score) holding the other predictors constant. All trial-level predictors were standardized using the grand mean. Rerunning main analyses while standardizing trial-level predictors within-person produced statistically significant results with comparable parameter estimates (magnitude and sign).

As noted above, we controlled for the following between-subject variables: gender (dummy coded, 0 = male, 1 = female) and age. The form of the between-subjects component of the model for both classic and switchboard follows (i.e., this component of the model was the same for both classic and switchboard models):

$${\pi }_{0j}={\gamma }_{00}+{\gamma }_{01}\left({\mathrm{Gender}}_j\right)+{\gamma }_{02}\left({\mathrm{Age}}_j\right)+{\text{u}}_{0j}$$

$${\pi }_{1j}={\gamma }_{10}+u_{1j}$$

$${\pi }_{2j}={\gamma }_{20}+u_{2j}$$

This component of the model reflects how all trial-level parameters are allowed to vary randomly between subjects (indicated by the u_j's, random effects) while showing the main effect of between-subject predictors (γ₀₁ and γ₀₂). The other gammas in the model (γ₁₀ and γ₂₀) represent the fixed effect of the trial-level predictors (i.e., the portion of trial-level effects that are common to all participants). Random coefficient regression models were implemented with the lme4 package in R (Bates et al., 2014), and significant tests were obtained using the lmerTest package (Kuznetsova et al., 2017). Here we note that this analytic framework affords us greater statistical power than we would focusing on a model exclusively testing between-subjects differences because we have many decisions nested within individuals. Because our predictors of interest occurred at the level of the decision, we were able to reach ∼80% statistical power to detect a meaningful trial-level effect (Schoeneberger, 2016; Astivia et al., 2019). We also tested permutations of these models that allowed age to interact with the trial-level brain activity metrics, effectively testing the possibility that the strength of the two neural systems changes with age.

Modeling between-subject brain-behavior associations

Using the aggregated univariate activity (i.e., the average of each subjects' trial-level brain activity metrics) and aggregated PE estimates (obtained via averaging over estimates within each subject), we sought to examine between-subject brain-behavior associations. To do so, we conducted two multiple regression analyses. The first analysis examined the contribution of univariate NAcc and lPFC activity on the percentage of risky decisions during the task while controlling for age and gender. The second analysis swapped out the univariate predictors for the multivariate PE metrics.

Results

Baseline models and descriptive data visualizations

Individual decisions across all subjects are plotted in Figure 4. This figure highlights the variability in risky behavior both within and between subjects. Additionally, we ran two “baseline” multilevel logistic regression models on the trial-level risky decision-making data from the YLG. The first model was an empty model, modeling trial-level decisions only as a function of an intercept, effectively estimating the unconditional likelihood of making a risky decision on the task (Table 1). The second model included gender and age as predictors (“covariate-only model”) so as to examine the effects of these variables unconditioned on the brain activity data (Table 1); neither was related to risky decision likelihoods.

Log-odds of risky choice from empty and covariate-only models

	Empty	Covariate-only
Term	Estimate
Intercept	0.527 (0.087)***	0.599 (0.119)***
Trial number	—	−0.009 (0.047)
Age	—	0.104 (0.085)
Gender	—	−0.144 (0.169)
Variance component	Estimate
Var(intercept)	0.282	0.268
Var(trial number)	—	0.006
Fit statistic	Statistic
AIC	2887.1	2892.8
BIC	2898.5	2932.8

Sex was dummy coded (0 = male; 1 = female). SEs of parameter estimates are given in parentheses. Var() refers to a variance component of a given random effect from the model.

***p < 0.001.

Table 1-1

Head motion statistics. Download Table 1-1, DOCX file ^{(24.2KB, docx)} .

Within-subjects results

Results from our within-subject models are summarized in Tables 2–4 and Figure 5. All are described in greater detail below.

Table 2.

Log-odds of risky choice from within-subjects analysis of classic system-based models

Term	A: Estimate	B: Estimate
Intercept	0.580 (0.121)***	0.575 (0.121)***
NAcc	0.140 (0.063)*	0.135 (0.064)*
lPFC	−0.147 (0.057)*	−0.123 (0.058)*
Age	0.105 (0.086)	0.104 (0.086)
Gender	−0.084 (0.172)	−0.077 (0.172)
Variance component	A: Estimate	B: Estimate
Var(π0ij)	0.267	0.267
Var(π1ij)	0.041	0.043
Var(π2ij)	0.024	0.024
Fit statistic	A: Statistic	B: Statistic
AIC	2888.7	2888.7
BIC	2951.5	2951.5

Gender was dummy coded (0 = male; 1 = female). NAcc refers to univariate ventral striatum activity; lPFC refers to univariate lPFC activity. Var() refers to a variance component of a given random effect from the model. Results come from a multilevel logistic regression model, with log-odds of a risky choice as the dependent variable. Column A, Results using an lPFC mask thresholded at 0.25; Column B, Results using an alternate, more conservative mask (thresholded at 0.50) that covered less cortical area.

*p < 0.05.

***p < 0.001.

Table 4.

Models testing interactions with age

Term	A: Estimate	B: Estimate
Intercept	0.583 (0.121)***	0.508 (0.122)***
NAcc (A) | Value PE (B)	0.120 (0.063)†	0.007 (0.054)
lPFC (A) | Cognitive control PE (B)	−0.139 (0.057)*	−0.117 (0.061)†
Age	0.107 (0.087)	0.120 (0.086)
Gender	−0.088 (0.171)	−0.056 (0.182)
NAcc (A) | Value PE (B) × Age	−0.090 (0.063)	0.004 (0.056)
lPFC (A) | Cognitive control PE (B) × Age	0.045 (0.057)	0.019 (0.062)
Variance component	A: Estimate	B: Estimate
Var(π0ij)	0.266	0.252
Var(π1ij)	0.033	0.006
Var(π2ij)	0.022	0.036
Fit statistic	A: Statistic	B: Statistic
AIC	2890.8	2896.5
BIC	2965.0	2970.7

Gender was dummy coded (0 = male; 1 = female). NAcc refers to univariate ventral striatum activity; lPFC refers to univariate lPFC activity. Var() refers to a variance component of a given random effect from the model. Results come from a multilevel logistic regression model, with log-odds of a risky choice as the dependent variable. Column A, Results from the classic model (lPFC threshold = 0.25); Column B, Results from the switchboard model (association maps). In order to be concise, differing terms for each model (any term involving a metric of brain activity) are included in the same line of the first column, separated by “|.”

*p < 0.05.

***p < 0.001.

†p < 0.10.

Figure 5.

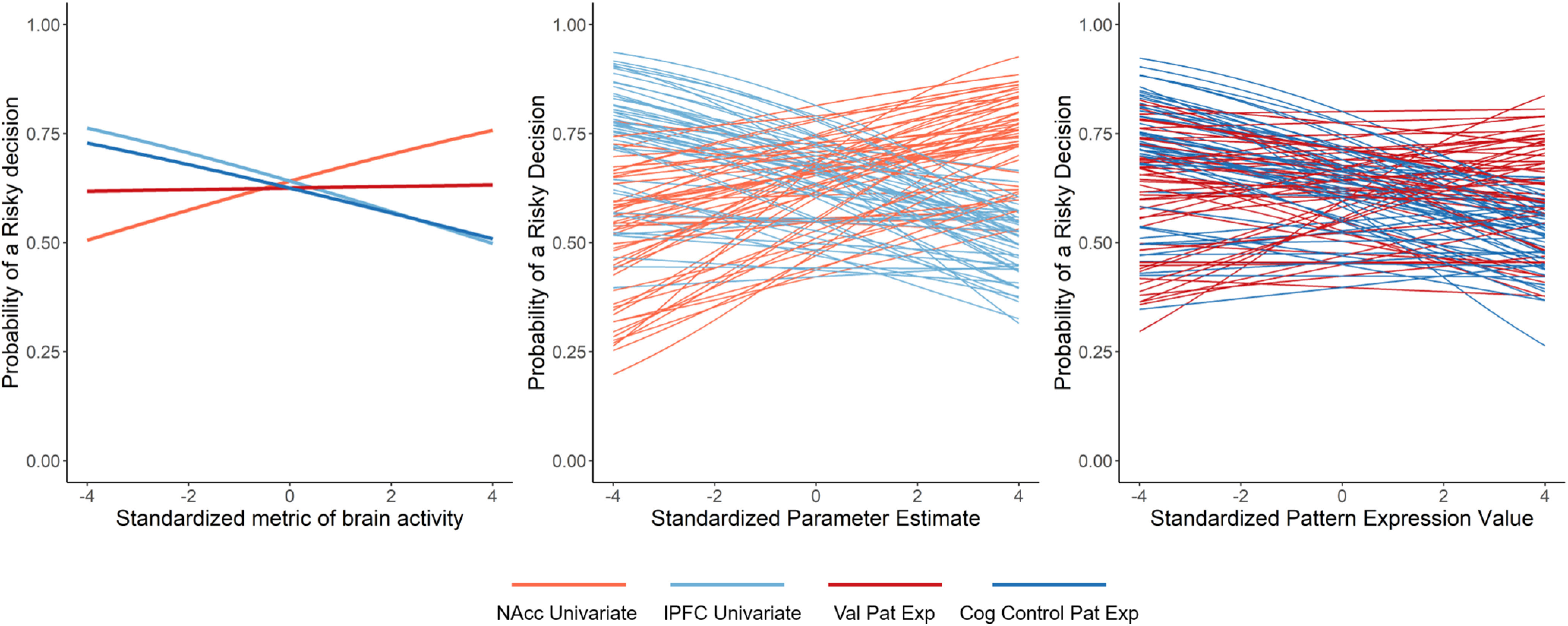
Associations between univariate and multivariate brain activity and probability of making a risky decision. NAcc Univariate, trial-level univariate NAcc activity estimates; lPFC Univariate, trial-level univariate lPFC activity estimates; Cog Control Pat Exp, trial-level cognitive control PE estimates; Value Pat Exp, trial-level value-based PE estimates. Left, Fixed effects of brain activity metrics from both models. Middle, Subject-specific random effects of associations between risky decision-making probability and univariate NAcc and univariate lPFC activity. Right, Subject-specific random effects of associations between risky decision-making probability and, value-based PE, and cognitive control PE values.

Classic

Using the classic system-based model, we found that trial-level univariate NAcc and lPFC activity was independently associated with decision tendencies in the YLG in a manner consistent with theory. Within-person increases in NAcc activity were associated with an increased likelihood of making a risky decision, whereas within-person increases in lPFC activity were associated with a decreased likelihood of making a risky decision. The magnitudes of the effects were comparable: a 1 unit increase in NAcc activity was associated with a 15.03% increase in the expected odds of making a risky decision, whereas a 1 unit increase in lPFC activity corresponded with a 13.67% decrease in the expected odds of making a risky decision (calculated using coefficients reported in Table 2, Column A). Notably, these results remained highly similar when using an alternate, more conservative lPFC mask (results still significant, same direction, comparable effect sizes; Table 2, Column B). Age did not interact with either NAcc or lPFC activity (Table 4, Column A).

Switchboard

Results from the switchboard system-based model are summarized in Table 3. These results are partially consistent with system-based theories, in that cognitive control PE estimates were significantly associated with risky decision-making on the YLG. A 1 unit increase in cognitive control PE corresponded with an 11.57% decrease in the expected odds of making a risky decision (obtained from Table 3, Column A). Sensitivity analyses indicated that this effect was robust to variations in neural signatures (e.g., when using uniformity and association maps, unique voxels in uniformity maps; see Table 3, Columns B, C) and these effects were not present when using theoretically orthogonal neural signatures (“vision” and “auditory,” see Table 5). Collectively, these results indicate that multivariate pattern-based activity related to cognitive control encodes meaningful information about risk-taking tendencies. Simultaneously, and inconsistent with system-based theories, value-based PE estimates were not significantly associated with risky decision propensities (coefficient: 0.051, SE 0.048, not significant; Table 3). To ensure our value-based results were not driven via the selection of an erroneous pattern, we reran analyses using Neurosynth's “reward” term and obtained near-identical results (reward coefficient: 0.043, SE = 0.048, not significant). Importantly, multivariate patterns and univariate activity metrics were modestly correlated (correlations ranged between ∼0.09 and 0.4), and overlap between the lPFC and cognitive control multivariate signature, the only system that was significant in both model variants, was minimal (only 7.9% of the voxels in the cognitive control signature were also present in the lPFC mask). We reiterate here that univariate activity metrics and multivariate PE scores represent different aspects of brain activity, and these descriptive statistics emphasize this point. As with the classic model, age did not interact with either value or cognitive control patterns.

Table 5.

Log-odds of risky choice from models with additional Neurosynth patterns to gauge uniqueness of cognitive control PE findings

Term	Estimate
Intercept	0.569 (0.120)***
Vision PE	0.096 (0.054)†
Auditory PE	0.075 (0.050)
Age	0.072 (0.083)
Gender	−0.072 (0.168)
Variance component	Estimate
Var(π0ij)	0.292
Var(π1ij)	0.027
Var(π2ij)	0.011
Fit statistic	Statistic
AIC	2888.4
BIC	2951.2

Gender was dummy coded (0 = male; 1 = female). The alternate maps correspond to the terms listed in the table (Vision, Auditory). Association maps for each term were used. Var() refers to a variance component of a given random effect from the model. Results come from a multilevel logistic regression model, with log-odds of a risky choice as the dependent variable.

***p < 0.001.

†p < 0.10.

We conducted post hoc analyses to interrogate the lack of a relationship between value-based PE estimates and risky behavior. We first examined whether multivariate signatures within the NAcc were associated with behavior given that univariate signals within this region were, operating under the logic that value-based patterns may be more localized to a given region than cognitive control. We reran the PE analyses with the value-based neural signature, but this time only included voxels in the NAcc in our mask. Again, this analysis showed a nonassociation between value-based PE scores in the NAcc and risky decision-making (coefficient = 0.000, not significant). Given this result and the nature of PE analysis, it was puzzling why univariate activity in the NAcc tracked with behavior (especially when considering a bulk of the pattern was comprised of NAcc voxels; Fig. 3), but value-based signatures, even if localized to the NAcc, did not. This led us to believe that perhaps it was the homogeneity of multivariate activity in NAcc that related to risky decision tendencies. Multivariate patterns necessarily encode spatial variability, but it could be that homogeneity or uniformity of activity is more strongly predictive of behavior, suggesting that PE estimates that inherently capture this variability may be poor predictors of behavior. To test this, we re-extracted multivariate patterns from the NAcc and lPFC and computed Gini coefficients for each region for each trial. Traditionally used in macroeconomics but recently applied in neuroscience (Guest and Love, 2017; Guassi Moreira et al., 2019), Gini coefficients in this context can describe the extent to which brain activity in a given region is homogeneous (uniform) or heterogeneous. Indeed, as shown in Table 6, a lower Gini coefficient in the NAcc (i.e., more uniform activation) was associated with an increased propensity to take risks on the YLG, suggesting a strong, one-dimensional encoding of value signatures during decision-making.

Table 6.

Models with predicting decision activity from trial-level Gini coefficients

Term	Estimate
Intercept	0.629 (0.121)***
NAcc Gini	−0.115 (0.048)*
lPFC Gini	0.057 (0.047)
Age	0.080 (0.088)
Gender	−0.198 (0.172)
Variance component	Estimate
Var(π0ij)	0.270
Var(π1ij)	0.009
Var(π2ij)	0.004
Fit statistic	Statistic
AIC	2894.1
BIC	2956.9

Gender was dummy coded (0 = male; 1 = female). Var() refers to a variance component of a given random effect from the model. Results come from a multilevel logistic regression model, with log-odds of a risky choice as the dependent variable.

*p < 0.05.

***p < 0.001.

Between-subject results

Results from between-subject analyses indicate that none of the between-subject brain activity metrics (univariate or pattern based) was related to proportion of risky decisions (univariate NAcc: b = 0.223, SE = 0.316, p > 0.250; univariate lPFC: b = −0.209, SE = 0.270, p > 0.250; value PE: 8.725e-5, SE = 1.823e-4, p > 0.250; cognitive control PE: −1.435e-4, SE = 1.219e-4, p = 0.245). A traditional brain mapping (mass univariate) analysis of the YLG showed significant ACC activity for the Go > Stop contrast in addition to significant amygdala and dorsal striatal activity (Fig. 6; Table 7).

Figure 6.

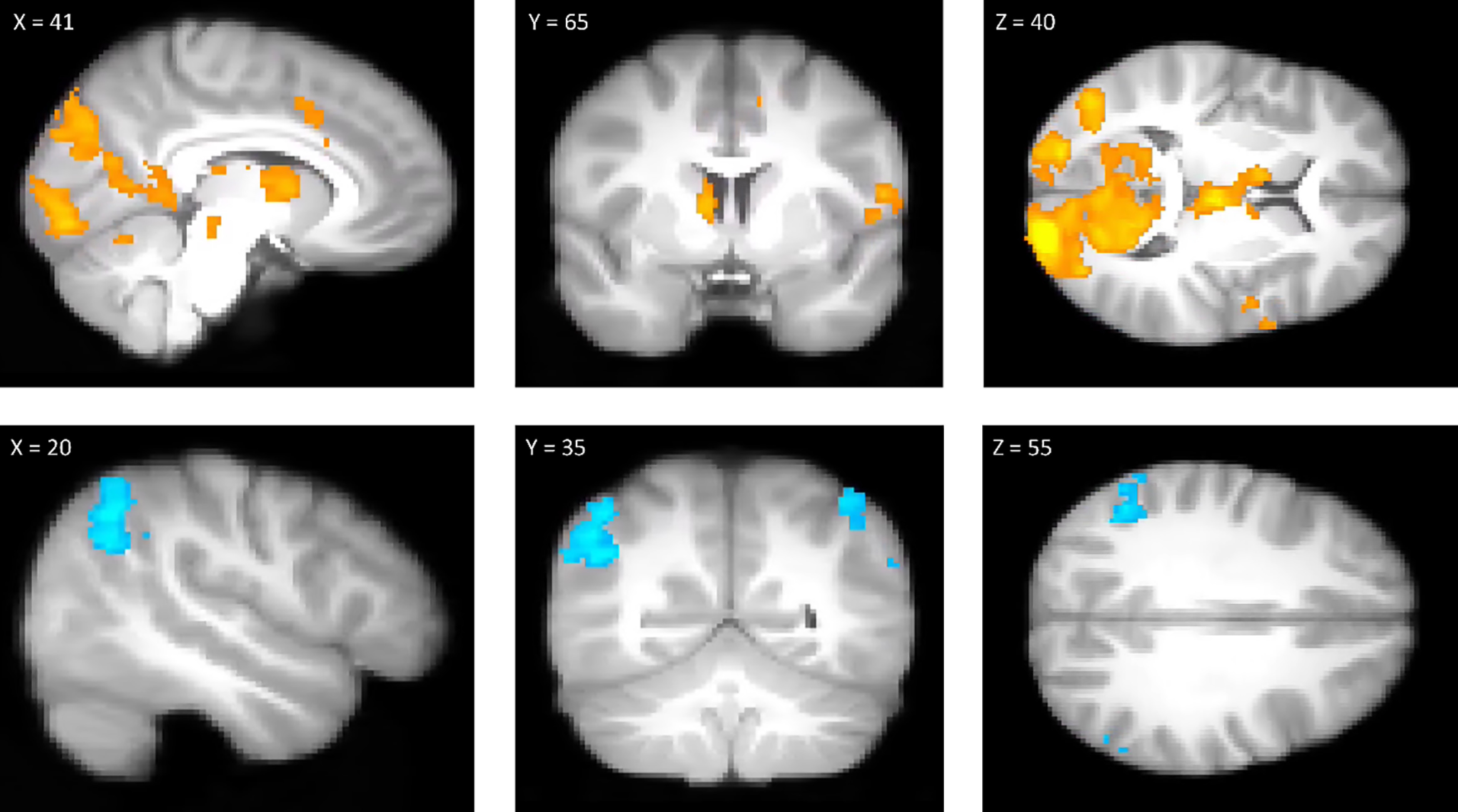
Results from the Go > Stop (top row) and Stop > Go (bottom row) contrasts. x, y, z indicate voxel coordinates in MNI standard space. Clusters rendered here were obtained using a cluster-defining threshold of Z = 3.1, correct for multiple comparisons at p < 0.05 using Random Field Theory. Clusters are rendered on bg_image, FSL's average of all subjects' high-resolution anatomic images.

Discussion

The current study used a brain modeling philosophy (Kragel et al., 2018) in conjunction with within-subject multilevel logistic regression to test system-based theories of adolescent decision-making. In doing so, we also expanded on traditional neuroscientific implementations of system-based theories by examining the role of multivariate neural signals. We found that features of brain activity predicted behavior in a manner consistent with system-based theories. We observed this in two variants of the model: a classic implementation assuming modularity among ROIs and a novel variant that included information for multivariate signatures. These findings have a number of ramifications for neuroscientific models of adolescent decision-making.

Implications for system-based theories of adolescent decision-making

We observed that value-based and cognitive control systems generally predicted behavior in a manner consistent with system-based theories: univariate estimates of NAcc and lPFC activity were directly and inversely, respectively, associated with the probability of making risky decision, while cognitive control PE was predictive of a reduced likelihood to make a risky decision. Our between-subject analyses, along with traditional mass univariate brain mapping analyses, failed to show any such trends. Two broad conclusions follow from these results. First, these findings support the utility of brain modeling techniques for testing system-based theories of decision-making in developmental neuroscience and beyond, reinforcing that brain modeling and brain mapping philosophies are not simply inverse functions of the other that yield equivalent results (Kragel et al., 2018). Second, and perhaps more importantly, these results suggest features of system-based theories of decision-making carry evidentiary value, despite compelling arguments to the contrary (Pfeifer and Allen, 2012). The present findings suggest that system-based theories may offer interim frameworks for relatively young fields, such as cognitive neuroscience, as they continue to incrementally extend theory on the basis of novel evidence (Baddeley, 2012; Pfeifer and Allen, 2016). Even as these theories are eventually replaced by stronger accounts that consider more nuanced relationships between cognitive control and value systems as well as other biological influences (Harden et al., 2017; Davidow et al., 2018), their use as “baseline” models may facilitate novel theoretical insights so long as they are not subscribed to too rigidly. Furthermore, that features of system-based models have evidentiary value is not tantamount to saying they are optimal (indeed, a comparison of model fit statistics between system-based models and empty or covariate-only models in the present study suggests otherwise), but rather points to the need to develop and test more nuanced quantitative models of the neurodevelopment of decision-making behavior. Relatedly, we failed to observe interactions between brain activity metrics and age, a major tenet of developmental system-based models. This null finding underscores our call for greater nuance in quantitative models of decision-making neurodevelopment: clear age-related behavioral differences in risk-taking behavior (Duell et al., 2018; Defoe et al., 2019) are necessarily encoded in brain activity, yet current modeling approaches have been unable to consistently link age differences in the association between neurobiology and behavior.

Modularity and population coding in system-based theories of decision-making

On a more granular level, our results speak to two long-discussed concepts in neuroscience: modularity and population coding (Erickson, 2001). These two concepts are reflected by univariate and multivariate analyses, respectively, in neuroimaging data. Most system-based theories of adolescent decision-making originate from disciplines within psychological science that espoused modularity at the psychological level (Steinberg et al., 2008). Although it is not a given that psychological modularity necessitates neural modularity, this assumption has been preserved in many neuroscientific implementations of system-based theories (Strang et al., 2013; Shulman et al., 2016), despite evidence in adults that multivariate patterns reflect meaningful information about decision-making (Hampton and O'Doherty, 2007). Our univariate and multivariate results, somewhat surprisingly, provide support for both modularity and population coding, respectively (Cosme and Lopez, 2020); specifically, results revealed that univariate NAcc and lPFC activity was associated with decision behavior, and also that PE of a multivariate cognitive control (but not value) signature predicted decisions. The former (evidence of modularity) is surprising, given the limited support for neural modularity that prior studies have found (Erickson, 2001), whereas the latter (population coding) is notable because no prior studies, to our knowledge, have found evidence of such in the context of brain modeling decision behavior (i.e., using multivariate metrics to model behavior/cognition).

These findings carry notable implications. Although our results suggest that modularity may be a feature of adolescent decision behavior, we cannot conclude with certainty what activation in those modules (i.e., NAcc and lPFC) reflects. While such activation could index computations related to value and cognitive control, respectively, it is more difficult to infer psychological processes from ROI-based activity than from multivariate signatures, which tend to be more specific in what they reflect (Poldrack, 2006; Wager et al., 2013). Our data are roughly consistent with an amplifier model, which would allow for reconciliation of our classic and switchboard results. In such a model, multivariate patterns may code for the psychological process of interest and the modules observed here act as “volume” knobs that amplify their magnitude. In other words, the multivariate patterns code for a given psychological process, whereas the univariate activity of the modules controls the intensity of the process. Indeed, such multidimensional coding schemes appear to support decision behaviors in monkeys (Zhang et al., 2019), and similar findings from human samples in other domains (eating behavior) further hint at the neural plausibility of a modular-population hybrid scheme (Cosme and Lopez, 2020). Further work could also examine whether there is a qualitative shift between coding schemes across development (Gee et al., 2013). Although we found no such evidence in our own data, future work could broaden age ranges to include young children and adults to determine the extent to which system-based models explain decision-making at different developmental stages. Overall, it is clear that additional work is needed to characterize the relative contributions of neural modules and population codes in system-based theories of decision-making, involving the use of different behavioral tasks, different multivariate signatures, and evaluation of decision behaviors in different contexts.

Building on system-based theories of adolescent decision-making

Our findings suggest system-based models provide at least some explanatory utility, but it is critical that future work improves on existing models in several key ways. One future step will be to determine the algebraic form of influential system-based theories. Existing neuroscientific system-based theories of human decision-making are virtually exclusively expressed in linguistic terms without specifying a computational model (i.e., they are explained qualitatively, instead of with an algebraic equation). This means one could posit a number of algebraic forms that satisfy qualitative requirements of system-based theories that each carry very different implications. We assumed a linear relationship between the log-odds of a risky choice and metrics of brain activity, but an alternate statistical model may be more appropriate. Future studies could test a set of candidate algebraic formulations of system-based decision-making theories (e.g., estimating latent value and linking to decision likelihoods, etc.). This could facilitate cross-study and cross-discipline comparison by setting an objective framework that supports falsifiability. Future work must also directly address our null findings involving value-based PE values. While we tested “reward” and “value” patterns and obtained null results with both, it is possible an alternative untested pattern computed in a different manner (i.e., not relying on meta-analytic maps) would yield positive results. To rigorously test this possibility, we recommend future studies systematically create and test patterns that vary iteratively on psychological processes relevant for system-based theories (Wager et al., 2013; Chang et al., 2015). This process should also involve understanding how such maps change with development, as it may be unrealistic to assume a reward signature derived in one age group is readily applicable to all ages. Taking such an approach would also have the benefit of providing insights into what specific psychological features these patterns encompass, for example, by examining subcomponents of cognitive control (e.g., working memory). Finally, it is worth noting that interactions between each system and age were null, defying a core feature of system-based theories, suggesting that more bottom-up exploratory work is needed to better understand how the dynamic potency of each system changes with age. Ideally, such work would involve repeated sampling at both the decision- and subject-level (i.e., longitudinal assessments).

Limitations and future directions

The current study has several limitations that point directly to future directions in this line of research. The first is that the effect sizes found from key results are somewhat modest. Though not a traditional “limitation” per se, this points to the possibility that other untested computational signals in the brain may also contribute to decision behavior. Another limitation is that the present results were obtained in a single, moderately sized sample and ought to be replicated (Helmer et al., 2020; Marek et al., 2020). That said, our concerns about sample size are partially assuaged by the fact that we leveraged multilevel models to maximize statistical power when examining brain-behavior associations (Schoeneberger, 2016). Three additional limitations also exist regarding generalizability. First, in terms of adolescent decision-making, prior work shows adolescent decision behaviors are prone to tremendous diversity across the world and even within individuals (Steinberg et al., 2018), forcing us to consider that these results, even ignoring other limitations, may not reflect a “common ground truth” among all humans or even within a single human (to the extent such a “ground truth” actually exists). Second, it is possible that a different pattern of results would emerge for decision behaviors in other contexts (e.g., moral, financial decisions). Third, it is unclear whether these findings are specific to adolescence or generalize to general decision-making processes across the lifespan. A final limitation is that we did not compare our implementation of system-based theories to alternative theories. While this is mainly because system-based theories have dominated the field and alternative approaches have been relatively atheoretical (Pfeifer and Allen, 2012, 2016), we look forward to future work aimed at rigorously comparing alternate explanations.

In conclusion, system-based theories of adolescent decision-making have drawn tremendous scholarly interest, yet the veracity of their neuroscientific implementation has been the subject of much debate. This investigation was the first, to our knowledge, to test system-based theories of adolescent decision-making using a methodological approach that is more consistent with the core tenets of such theories (i.e., brain modeling). We found evidence that system-based theories are indeed predictive of adolescent risk-taking behaviors, showing that univariate and multivariate brain activity metrics of cognitive control and value-based processes predict trial-by-trial risky decision tendencies. We did not, however, observe evidence that these neural systems interacted with age, at odds with a key element of system-based theories. Overall, this work contributes knowledge about the neural bases of adolescent decision behavior.