Does the 2,6-didehydropyridinium cation exist?

Abstract

Reactive intermediates are key species involved in many chemical and biochemical processes. For example, carbon-centered aromatic σ,σ-biradicals formed in biological systems from naturally occurring enediyne antitumor antibiotics are responsible for the irreversible cleavage of double-stranded DNA caused by these prodrugs. However, because of their high reactivity, it is very difficult or impossible to isolate and investigate these biradicals. The aromatic σ,σ-biradical, 2,6-didehydropyridine, has been speculated for many years to be formed in certain organic reactions; however, no definitive proof of its generation has been obtained. We report here the successful generation of protonated 2,6-didehydropyridine and the examination of its chemical properties in the gas phase by using a Fourier transform ion cyclotron resonance mass spectrometer. The results suggest that a mixture of singlet (ground) state and triplet (excited) state 2,6-didehydropyridinium cations was generated. The two different states show qualitatively different reactivity, with the triplet state showing greater Brønsted acidity than that of the singlet state. The triplet state also shows much greater radical reactivity than that of the singlet state, as expected because of the coupling of the nonbonding electrons in the singlet state.

INTRODUCTION

The discovery that the DNA-cleaving ability of the enediyne family of naturally occurring compounds is associated with in situ formation of aromatic biradicals (often para-benzyne derivatives) has led to the publication of a large number of theoretical and experimental studies on organic biradicals since the 1990s.^[1–18] Some of the studies, aimed at facilitating the design of novel DNA-cleaving anticancer drugs based on formation of biradicals, were devoted to better understanding of the factors controlling the reactivity of aromatic biradicals.^[3–5] For example, several experimental and theoretical studies have focused on meta-benzynes and the possibility of tuning their properties for specific applications.^[5–18]

The first experimental observation of a meta-benzyne (and related meta-arynes) was achieved relatively recently.^[19] However, it is still unclear whether meta-benzynes were actually generated in some of these early experiments.^[20–23] 2,6-Didehydropyridine is an example of such a meta-aryne. This molecule was claimed to be an intermediate in the Chichibabin reaction of 3-substituted pyridines almost 40 years ago.^[24] It was also claimed to be responsible for the resin formation observed when 2-halopyridines were treated with lithium piperidide.^[24–29] However, reinvestigations of both reactions resulted in the conclusion that 2,6-didehydropyridine was not formed as an intermediate.^[28,29] These findings were supported by theoretical investigations, which showed that 2,6-didehydropyridine is the least stable of all possible didehydropyridine isomers because of a destabilizing 3-center and 4-electron interaction between the bonding combination of the two nonbonding σ-orbitals and the nitrogen lone pair.^[17,30] Protonation of 2,6-didehydropyridine, leading to 2,6-didehydropyridinium cation, 1, is calculated to significantly increase its stability compared with other isomeric didehydropyridinium cations.^[10] However, the partial positive charge on the central NH moiety is believed to contribute to some destabilization of this cation relative to meta-benzyne, on the basis of calculations of biradical stabilization energies.^[10]

Here, evidence is provided in support of the existence of 2, 6-didehydropyridinium cation (1) in the gas phase on the basis of experimental and computational studies on this biradical and several isomeric didehydropyridinium cations, the 2,4-didehydropyridinium, 3,5-didehydropyridinium, 2,5-didehydropyridinium, and 1,2-didehydropyridinium cations (2, 3, 4, and 5, respectively; Chart 1).

Chart 1.

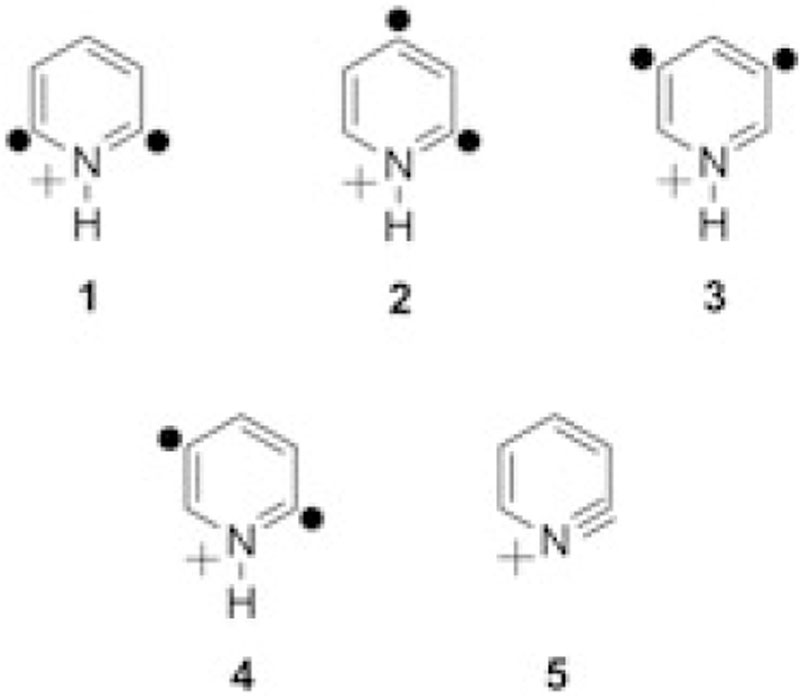
Chemical structures of 2,6-didehydropyridinium cation (1) and isomeric 2,4-didehydropyridinium (2), 3,5-didehydropyridinium (3), 2,5-didehydropyridinium (4), and 1,2-didehydropyridinium (5) cations

EXPERIMENTAL SECTION

Radical precursors and neutral reagents

The precursors for biradicals 4 and 5, 2,5-diiodopyridine and 2-iodopyridine, respectively, were purchased from Sigma–Aldrich (St. Louis, MO, USA) and used as received. Biradicals 1, 2, and 3 were generated from 2,6-diiodopyridine, 2,4-diiodopyridine, and 3,5-diiodopyridine, respectively, synthesized using literature methods.^[31–33] The neutral reagents studied, tetrahydrofuran, cyclohexane, allyl iodide, dimethyl disulfide, and tert-butyl isocyanide, as well as those used to bracket proton affinities, were purchased from Sigma–Aldrich and used as received.

Gas-phase experiments

All experiments were carried out on a Finnigan Model 2001 Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometer equipped with a Sun Sparc 20 data station running Odyssey version 4.0 software and a stored-waveform inverse Fourier transform^[34,35] (SWIFT) cell controller. This instrument consists of a differentially pumped reaction chamber that contains two identical cubic 2-inch cells and is aligned collinearly with the magnetic field produced by a 3.0-T superconducting magnet. The two cells are separated by a common wall (the conductance limit plate) that contains a 2 mm hole in the center. The nominal base pressure in the cells was less than 10⁻⁹ torr, as maintained by two Edwards (Sanborn, NY, USA) diffusion pumps 160P/700 (800 L s⁻¹), each backed with an Alcatel mechanical pump. The pressure was measured with two Bayard–Alpert ionization gauges: one located on each side of the dual cell. The pressure readings were corrected for the sensitivity of the ion gauges toward each neutral reagent^[36] and for the pressure differential between the cell and the ion gauge, as reported previously.^[37] The latter correction factor was obtained by measuring the rate of an exothermic electron transfer from the neutral reagents of interest to carbon disulfide radical cation and comparing this with a theoretically derived collision rate.^[38]

The radical precursors were introduced at a nominal pressure of (1.0–1.5) × 10⁻⁸ torr into one side of the dual cell by using a heated solids’ probe or a variable leak valve. The precursors were subjected to electron ionization (typically 30 eV electron energy, 7µA emission current, and 50–300ms ionization time), and the resulting radical cations and their fragment ions were allowed to ionize the neutral precursors by proton transfer (self-chemical ionization; reaction times ranged from 1–10 s). Alternatively, protonated methanol or acetone was generated via self-chemical ionization to transfer a proton to the radical precursors. The precursor ions formed in these experiments were transferred into the second cell by grounding the conductance limit plate for 100–160 µs. Unless otherwise stated, this plate and the other two trapping plates were maintained at +2 V. Quadrupolar axialization was used in some cases to enhance ion transfer.^[39–44] All the ions in the other side of the dual cell were removed prior to ion transfer by changing the remote trapping plate voltage from +2.0 V to −3.5 V for 15 ms. The transferred ions were cooled for 1 to 5 s by collisions with the neutral molecules present in this cell (the reagent to be used in the final stage of the experiment) and via infrared emission. To generate radical sites, the precursor ions were subjected to to sustained off-resonance irradiation collision-activated dissociation (SORI-CAD).^[45] SORI-CAD experiments utilized off-resonance excitation of the isolated ion at a frequency ±1000 Hz of the cyclotron frequency of the ion. This experiment was carried out for about 0.3 s in the presence of an inert gas (about 10⁻⁵ torr of Ar). The number of SORI-CAD events was dependent on the specific radical precursor used, being either one or two. The product ions were cooled for 1 s through collisions with the neutral molecules present in the cell and via infrared emission. The SWIFT^[34,35] excitation pulse to the excitation plates of the cell (Finnigan SWIFT module) was used to isolate desired ions by ejecting all unwanted ions from the cell. The isolated ions were allowed to react with a neutral reagent for a variable period of time (typically 0.005–40 s). Nominal base pressures of the neutral reagent used varied from 1.2 × 10⁻⁸ to 1.4 × 10⁻⁸ torr, as measured by ion gauges. After reaction, all ions were excited for detection by using “chirp” excitation at a bandwidth of 2.7 MHz and a sweep rate of 3 200 Hz µs⁻¹. The spectra are an average of at least five transients and were recorded as 64 or 128k data points with an acquisition rate of 8000 kHz and subjected to one zero fill prior to Fourier transformation.

Reactions studied under the conditions described follow pseudo-first-order kinetics. The second-order rate constants (k_exp) were obtained from a semi-logarithmic plot of the relative abundance of the reactant ion as a function of time. The collision rate constants (k_coll) were calculated by using a parameterized trajectory theory.^[38] The reaction efficiencies are given by k_exp/k_coll. The accuracy of the rate constant measurements is estimated to be ±50%, whereas the precision is usually better than ±10%. Primary products were distinguished from secondary products on the basis of their constant relative abundances at short reaction times and, in some cases, isolation of a product ion and examination of its reactivity.

The proton affinity of 2,6-didehydropyridine was measured by bracketing experiments employing a series of reference bases with known proton affinities. The protonated biradical was generated in a dual-cell FT-ICR mass spectrometer as described. After isolation, 2,6-didehydropyridinium cation was allowed to interact with reference bases. The 2,6-didehydropyridinium cation was found not to transfer a proton to 2-butanol (PA = 194.8 kcal mol^−1[46]), but it transferred a proton to ethylene glycol (PA = 195.0 kcal mol^−1[46]) and dimethyl carbonate (PA = 198.4 kcal mol^−1[46]). Therefore, the proton affinity of 2,6-didehydropyridine (or gas-phase acidity of 2,6-didehydropyridinium cation) must be very close to 195 kcal mol⁻¹, and it is assigned to be 195.0 ± 2.6 kcal mol⁻¹.

COMPUTATIONAL METHODS

Geometries for all species were computed by using density functional theory (DFT) with either the correlation-consistent polarized valence-double-ζ (cc-pVDZ^[47]) basis set or the correlation-consistent polarized valence-triple-ζ (cc-pVTZ^[47]) basis set. These DFT calculations use the gradient-corrected exchange functional of Becke,^[48] which is combined with either the gradient-corrected correlation functional of Lee, Yang, and Parr^[49] (BLYP) or that of Perdew et al.^[50] (BPW91). All DFT geometries were verified to be local minima by computation of analytic vibrational frequencies, and these (unscaled) frequencies were used to compute zero-point vibrational energies and 298K thermal contributions (H₂₉₈ – E₀) for all species. DFT calculations for triplet states of biradicals employed an unrestricted formalism – total spin expectation values for Slater determinants formed from the optimized Kohn–Sham orbitals did not exceed 2.02. For singlet biradicals, the DFT “wave function” was allowed to break spin symmetry by using an unrestricted formalism.^[51–55] Total spin expectation values for Slater determinants formed from the optimized Kohn–Sham orbitals in these cases ranged widely between 0.0 and 1.0. Geometry optimization using the unrestricted formalism has been shown to give more accurate geometries for a number of relevant aromatic biradicals.^[9,16,51,56]

Coupled cluster calculations for single-configuration reference wave functions were carried out for all species except one (discussed later in text) by using the cc-pVTZ basis set and including all single and double excitations and a perturbative estimate for triple excitations (RHF-(U) CCSD(T)/cc-pVTZ). For these calculations, the T1 diagnostic did not exceed 0.030 (with the exception of the 2,3-[H] shift transition state for 1, 0.049). For biradical 4, coupled-cluster calculations expanded in Brueckner^[65] orbitals were carried out. Brueckner orbitals eliminate contributions from single excitations in the coupled-cluster ansatz, and this alleviates instabilities^[66] associated with very large singles amplitudes in the more common CCSD(T) method that have previously been observed for aromatic biradicals having low degrees of symmetry.^[53]

Proton affinities (PAs) for the aromatic biradicals were calculated at the RHF-(U)CCSD(T)/cc-pVTZ//(U)BPW91/cc-pVDZ level of theory by using an isodesmic reaction involving proton transfer from the charged aromatic biradical to pyridine to produce pyridinium cation and the neutral biradical. The calculated enthalpy change for this isodesmic reaction was then combined with the experimentally determined PA for pyridine^[46] to derive PAs for the biradicals.

Molecular orbital calculations were carried out with the Gaussian 03^[67] and Molpro^[68] electronic structure program suites.

RESULTS AND DISCUSSION

The examination of the reactivity of the 2,6-didehydropyridinium, 2,4-didehydropyridinium, and 3,5-didehydropyridinium cations, 1, 2, and 3, respectively, yielded unexpected results (Table 1). These meta-didehydropyridinium cations react with cyclohexane and tetrahydrofuran by abstraction of two hydrogen atoms, with allyl iodide by two consecutive iodine atom abstractions and with dimethyl disulfide by two consecutive thiomethyl group abstractions (Table 1). However, while these reactions in most cases are the fastest or among the fastest reactions for 2 and 3, the major reaction observed for 1 with tetrahydrofuran, allyl iodide, dimethyl disulfide and tert-butyl isocyanide is proton transfer, a non-radical reaction (Table 1). This finding was surprising because, on the basis of earlier studies,^[18] meta-benzynes with smaller singlet–triplet (S–T) splittings are expected to react faster (via radical mechanisms) than meta-benzynes with larger S–T splittings, and 1 has the smallest S–T splitting among these three biradicals.

Table 1.

Reaction efficiencies and branching ratios for primary products

	1		2		3		4/14		5
S–T splittinga (kcal mol−1)	−11.1		−24.3		−21.6		−4.9b		−58.0
Relative energiesa (kcal mol−1)	0		−15.7		−11.6		4.7/−22.8		−35.8
	H+ trns (2°) add	78%	Hydride abs	36%	2 × H abs	72%	H+ trns	100%	H2O abs	48%
	H2O abs	10%	CH2O abs	26%	C2H4 abs	20%			CH2O abs	27%
	Hydride abs	5%	C2H4O abs	20%	C3H3 abs	8%			Hydride abs	22%
	CH2O abs	4%	H2O abs	14%					2 × H abs	2%
	2 × H abs	3%	2 × H abs	4%					C2H4O abs	1%
	Efficiency = 85%		Efficiency = 28%		Efficiency = 1%		Efficiency = 99%		Efficiency = 84%
	2 × H abs	64%	2 × H abs	100%	2 × H abs	100%	No Reaction		Hydride abs	52%
	Hydride abs	22%							2 × H abs	48%
	C2H4 abs	9%
	C3H6 abs	5%
	Efficiency = 39%		Efficiency = 0.03%		Efficiency = 0.1%				Efficiency = 70%
	Less reactive isomer: 62%								Less reactive isomer: 23%
	Efficiency too low to be measured accurately								Efficiency = 8%
	H+ trns	54%	Allyl abs	49%	I abs	69%	H+ trns	100%	Iodide abs	54%
	I abs		(2°) I abs		(2°) I abs
	(2°) I abs		(2°) Allyl abs		(2°) Allyl abs
	(2°) Allyl abs	36%	I abs	42%	Allyl abs (2°) I abs	29%			Allyl-H abs	27%
			(2°) I abs		(2°) Allyl abs
			(2°) Allyl abs
	Allyl abs (2°) I abs	6%	Allyl-H abs	9%	Allyl-H abs	2%			HI abs	19%
	Allyl-H abs	4%
	Efficiency = 34%		Efficiency = 15%		Efficiency = 15%		Efficiency = 31%		Efficiency = 65%
	H+ trns	65%	SCH3 abs	73%	SCH3 abs	82%	H+ trns	100%	HSCH3 abs	83%
			(2°) SCH3 abs		(2°) SCH3 abs
	SCH3 abs	17%	SSCH3 abs	23%	SSCH3 abs	12%			SCH2 abs	14%
	(2°) SCH3 abs		(2°) SCH3 abs		(2°) SCH3 abs
	e− trns	8%	HSCH3 abs	4%	HSCH3 abs	3%			SCH3 abs	3%
	(2°) SCH3 abss
	HSCH3 abs	8%			SCH2 abs + CH3 abs	3%
	SSCH3 abs	2%
	Efficiency = 93%		Efficiency = 47%		Efficiency = 58%				Efficiency = 100%
	H+ trns	48%	HCN abs	53%	HCN abs	79%	H+ trns and diss	76%	Cyanide abs	58%
			(2°) C4H8 abs		(2°) C4H8 abs
	Cyanide abs	28%	Cyanide abs	47%	Cyanide absc	21%	C4H8 abs	24%	HCN abs	42%
									(2°) C4H8 abs
	C4H8 abs	15%
	HCN abs	9%
	(2°) C4H8 abs
	Efficiency = 98%		Efficiency = 82%		Efficiency = 68%		Efficiency = 99%		Efficiency = 98%

Reaction efficiencies are reported as k_reaction/k_collision ×100.

abs, abstraction; trns, transfer; diss, dissociation; add, addition; LI, less reactive isomer; secondary products are noted as (2°) and are listed under the primary products that produce them.

^aCalculated at the RHF-UCCSD(T)/cc-pVTZ//UBPW91/cc-pVDZ level of theory and corrected for zero-point vibrational energy differences at 298 K by using the (unscaled) UBPW91/cc-pVDZ frequencies.

^bCalculated at the BD(T)/cc-pVTZ//UBPW91/cc-pVDZ level of theory; corrected for zero-point vibrational energy differences at 298 K by using the (unscaled) UBPW91/cc-pVDZ frequencies.

^cNote that proton transfer was erroneously reported^[83] earlier.

BD(T), Brueckner; RHF, restricted Hartree–Fock; CCSD(T), coupled cluster with singles, doubles, and perturbative triples; cc-pVTZ, correlation-consistent polarized valence-triple-ζ; BPW91, gradient-corrected exchange functional of Becke combined with the gradient-corrected correlation functional of Perdew et al.; cc-pVDZ, correlation-consistent polarized valence-double-ζ.

To explain the aforementioned findings, the PAs of the conjugate bases of 1, 2, and 3 and the relevant neutral reagents were compared. At the RHF-UCCSD(T)/cc-pVTZ//UBPW91/cc-pVDZ level of theory, the calculated PAs for 1, 2, and 3 are 213.5, 207.7, and 215.6 kcal mol⁻¹, respectively. The experimentally determined PAs of tetrahydrofuran, cyclohexane, dimethyl disulfide, and tert-butyl isocyanide are 196.5, 164.2, 194.9, and 208.1 kcal mol⁻¹, respectively.^[46] The PA of allyl iodide has not been experimentally measured; however, on the basis of calculations at the RHF-RCCSD (T)/6–311G(d,p)//B3LYP/6–311G(d,p) level of theory, the value is estimated to be 193.4 kcal mol⁻¹.^[69] Therefore, it was surprising that despite the high PA of 1, it efficiently transfers a proton to all neutral reagents studied, with the exception of cyclohexane. Investigation of the reactivity of 1 toward cyclohexane revealed that only part of the ion population thought to be 1 was reactive toward cyclohexane (Table 1). A possible explanation for the mentioned observations is that the reactant ion population contains 1 and also one or more isomeric species that are unreactive toward cyclohexane and much more acidic than 1.

Previous computational studies on meta-benzyne 6 and its derivatives provided insights into the possible identity of the unknown isomer of 1.^{[19,31,70–76]} If given enough energy, meta-benzyne 6 may undergo ring opening followed by a [1,2]-hydrogen shift to yield enediyne 8, which also is produced via ring opening of para-benzyne 7 (Scheme 1).^{[19,70,73–75]} The activation enthalpy for the transformation of 6 to a carbene intermediate was estimated to be 48.5 kcal mol⁻¹ at the B3LYP/6–31G(d,p) level of theory. The subsequent [1,2]-H shift was predicted to occur with a very low (about 0.1 kcal mol⁻¹) energy barrier.^[70] In comparison, the calculated activation enthalpy for ring opening of para-benzyne 7 to form 8 is only 20.2 kcal mol⁻¹.^[70] Hence, ring opening of meta-benzyne is not particularly favorable kinetically. However, experimental studies by Sander et al. have shown that ring opening followed by a 1,2-hydride shift does occur for 2,6-didehydropyridine (10) during its generation by flash vacuum pyrolysis of 2,6-diiodopyridine (9) (Scheme 2).^[31]

Scheme 1.

Ring opening of meta- and para-benzyne with activation enthalpies (ΔH^ǂ) and reaction enthalpies (ΔH) of each transformation calculated at the B3LYP/6–31G(d,p) level of theory.^[70] All enthalpies are given relative to the enthalpy of 6

Scheme 2.

Rearrangement of 2,6-didehydropyridine after generation by flash vacuum pyrolysis (FVP)^[31]

In light of these observations, ring-opening and a 1,2-hydride shift to form the aza-enediyne 14 (Scheme 3) may occur for 1 in the gas-phase experiments discussed here. The PA of the conjugate base of the aza-enediyne 14 has been computed at the RHF-UCCSD(T)/cc-pVTZ//UBPW91/cc-pVDZ level of theory to be 190.7 kcal mol⁻¹.^[69] This PA is consistent with the proton transfer reactions observed for the unknown ion population thought to be 1. The same aza-enediyne 14 is likely to be formed upon the spontaneous ring opening (calculated barrier 10.1–33.4 kcal mol⁻¹, depending on the level of theory^{[7,53,57–64,77]}) of gaseous 2,5-didehydropyridinium cation 4 (Scheme 3),^{[69,74,77,78]} an analog of para-benzyne 7, and thus, data^[69] for 4 (14) are included in Table 1. The ion population generated from 4, thought to correspond to 14, does indeed transfer protons to all reagents except cyclohexane. Additional support for the formation of 14 from 1 was provided by studying 15 (Chart 2), which has a structure similar to that of 14. This cation was found to transfer a proton to all examined reagents with the exception of cyclohexane. In addition, C₄H₈ group abstraction was observed for reaction of 15 with tert-butyl isocyanide. This particular reaction also occurs for 1 and 4 with this neutral reagent (Table 1).

Scheme 3.

Possible isomerization reactions of 2,6-didehydropyridinium cation 1 and 2,5-didehydropyridinium cation 4 when generated by sustained off-resonance irradiated collision-activated dissociation (SORI-CAD)

Chart 2.

Chemical structures of 14 and 15

However, the overall reactivity observed for ions thought to be 1 is not entirely consistent with a mixture of isomers 1 and 14. For example, proton transfer from 4/14 to tert-butyl isocyanide is so exothermic that spontaneous fragmentation occurs, which was not observed for 1 (Table 1). Further, the reactivity of 1 toward cyclohexane is three orders of magnitude greater than that for the isomeric 2 and 3 and hence highly unusual for a singlet meta-benzyne derivative. The aza-enediyne 14 is entirely unreactive toward this reagent. For these reasons, other possible rearrangement pathways of 1 were examined computationally.

The computational results suggest that the two most likely rearrangements of 1 generate cations 14 and 5 that are energetically greatly favored over biradical 1 (Fig. 1). Formation of both 14 and 5 is preceded by an initial C–N bond cleavage (ΔH^ǂ 31.5 kcal mol⁻¹) to generate a carbene (downhill by about 4 kcal mol⁻¹; Fig. 1). The formation of the protonated aza-enediyne 14 from the carbene is barrierless (−0.4 kcal mol⁻¹). Hence, if ring opening can occur, formation of 14 is feasible. However, formation of 5 after ring opening requires an additional 11.3 kcal mol⁻¹ (Fig. 1).

Figure 1.

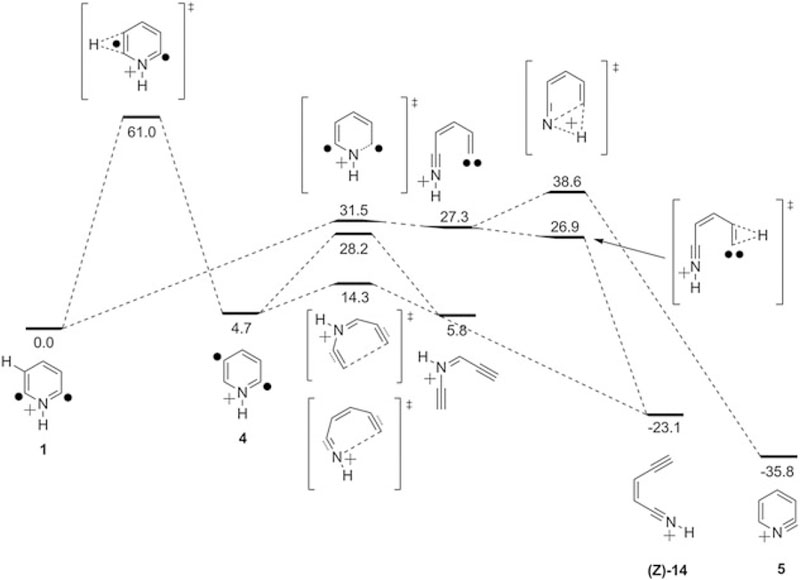
Energy diagram for rearrangements of 1 as calculated at the RHF-UCCSD(T)/cc-pVTZ//(U)BLYP/cc-pVTZ level of theory (all enthalpies in kcal/mol)

The formation of 5 can be ruled out on the basis of a comparison of the reactivities of the ion population initially thought to be 1 and 1,2-didehydropyridinium cation 5. Although similarities in the product distributions with tetrahydrofuran, cyclohexane, dimethyl disulfide, and tert-butyl isocyanide were observed, the branching ratios of the products (ignoring proton transfer observed for 1) are different. The reactivity toward allyl iodide is especially noteworthy. It was reported previously that two consecutive iodine atom abstractions from allyl iodide molecules indicate the presence of two radical sites in meta-didehydropyridinium cations.^[79] This reaction has been observed for all such biradicals studied thus far, including the 2,6-isomer 1 (Table 1). On the other hand, ortho-didehydropyridinium cations have been shown to abstract HI instead of two iodine atoms, which was also observed for 5 (Table 1).^[80,81] Moreover, allyl-H group abstraction is only a minor reaction for the ion population thought to be 1, whereas it is the main reaction for 5. For dimethyl disulfide, while two thiomethyl group abstractions were observed for the ion population thought to be 1, as well as for other meta-benzyne analogs (Table 1),^[80,81] only one thiomethyl group abstraction was observed for 5. Hence, rearrangement of 1 to 5 can be ruled out.

Rearrangement of 1 to 14 is energetically unfeasible. The calculated barrier for ring opening (ΔH^ǂ = 31.5 kcal mol⁻¹) is too high to be overcome by the solvation energy (typically 5–20 kcal mol⁻¹) of a gas-phase collision complex of 1 with the neutral reagents studied. If an isomerization takes place, it more likely occurs during the generation of the biradical upon SORI-CAD (Scheme 3) used to cleave two iodine atoms from the kinetically excited 2,6-diiodopyridinium cation precursor via energetic collisions with Ar. Indeed, our previous studies^[69] have demonstrated that some excess energy can be deposited to a biradical generated upon SORI-CAD, although the upper limit for this excess energy was determined to be 14 kcal mol⁻¹ for biradicals with two heavy atoms between the radical sites.^[69] Hence, ring opening of 1 does not appear possible upon SORI-CAD. However, it might be possible to access the triplet state of 1 that lies only about 11 kcal mol⁻¹ above the singlet state (calculated S–T splitting −11.1 kcal mol⁻¹; Table 1). The proton affinity of the conjugate base of the triplet state of 1 was calculated to be only 196.9 kcal mol⁻¹, which is 16.6 kcal mol⁻¹ lower than the PA of the singlet state. The high PA of the neutral singlet state is caused by repulsive interactions between the two radical sites and the nitrogen lone pair. This destabilizing interaction disappears upon protonation of the nitrogen atom. The neutral triplet state does not suffer from such an interaction and hence has a lower PA.

The low PA calculated for the conjugate base of the triplet state of 1 suggests that the triplet state may be responsible for the unexpected proton transfer reactions observed for 1. Under the high vacuum conditions used here, the triplet state is not rapidly converted to the singlet state via molecular collisions.

To further explore this possibility, the PA of the conjugate base of the ion population thought to be 1 was determined to be 195.0 ± 2.6 kcal mol⁻¹ by using bracketing experiments. This value is in excellent agreement with the PA calculated for the triplet state of 1. Hence, the proton transfer reactions observed for 1 are likely explained by the formation of its triplet state either upon SORI-CAD or within the collision complex with the neutral reagents used.

Cyclohexane is the only reagent studied with no dipole moment, and hence, it is the reagent that provides the smallest amount of solvation energy (expected to be much less than 11 kcal mol⁻¹) when forming a collision complex with 1. For this reagent, promotion of the singlet state of 1 to the triplet state via solvation energy is not possible. However, fast-reacting (likely the triplet state) and slow-reacting (likely the singlet state) components were observed (for possible mechanisms, see Schemes 4 and 5). This finding suggests that a mixture of the singlet and triplet states of 1 is generated upon SORI-CAD before the formation of a gas-phase collision complex with a neutral reagent. The presence of the strong magnetic field (as in FT-ICR) may facilitate the conversion of the singlet state to the higher-energy triplet state,^[82] because in a mass spectrometer with no magnetic field (a linear quadrupole ion trap), only a trace amount of the more reactive form was observed. Furthermore, when argon was replaced with a heavy atom, xenon (expected to facilitate triplet-to-singlet intersystem crossing), in the experiments to generate the biradical in the FT-ICR, the percentage of the more reactive (triplet) form decreased from 38% to 24%.

Scheme 4.

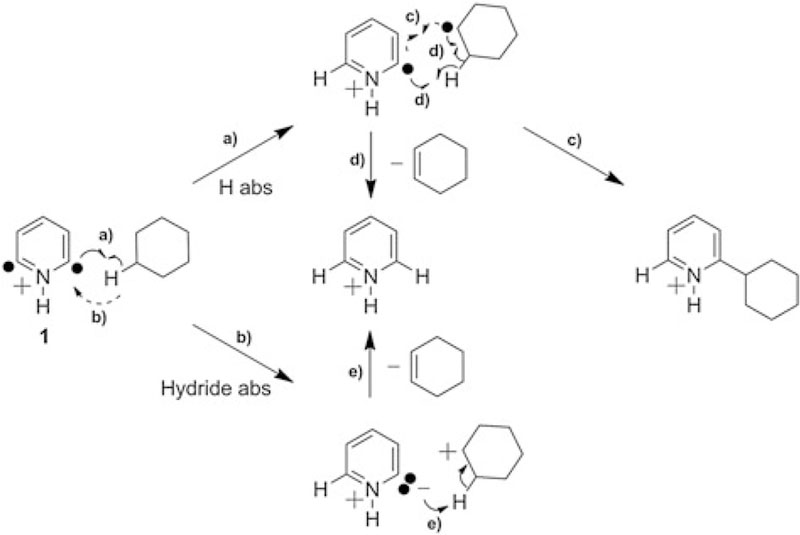
Possible mechanisms for the reactions of 2,6-didehydropyridinium cation (1) with cyclohexane to form the hydride abstraction product (bottom), the product formally formed upon abstraction of two hydrogen atoms (center) and the adduct (right) that is not stable but fragments further, possibly, as shown in Scheme 5

Scheme 5.

Possible mechanisms for further fragmentation of the adduct of 1 and cyclohexane to yield the C₂H₄ (top) and C₃H₆ (bottom) abstraction products. The observation^[83] that phenylcyclohexane radical cation fragments via similar pathways indicates that the nitrogen atom does not play an important role in these reactions

One final issue needs to be addressed. This is the observation of only one reactive species upon reactions of 1 with allyl iodide, dimethyl disulfide, tetrahydrofuran, and tert-butyl isocyanide as opposed to cyclohexane (Table 1). As stated, cyclohexane provides the smallest amount of solvation energy to the reactant collision complex. It also does not contain heavier atoms than those of carbon. Hence, within a collision complex with this reagent, the mixture of singlet and triplet states of 1 created upon SORI-CAD will react with no intersystem crossing. Indeed, fast-reacting and slow-reacting ions were observed. The use of Xe as the collision gas instead of Ar, however, resulted in less of the triplet state, likely because a heavy atom such as this facilitates intersystem crossing. For the other reagents, the solvation energy may be large enough to allow conversion of the singlet state to the more reactive triplet state prior to reactions. All these reagents also contain atoms heavier than carbon, which may facilitate intersystem crossing. This may explain why only one reactive species, with a specific bimolecular rate constant, was observed. This species is likely to be triplet 1 because it is expected^[5] to undergo much more facile radical reactions than the singlet, and it is also much more acidic than the singlet state.

CONCLUSIONS

Based on a detailed analysis of the available experimental and computational data, 2,6-didehydropyridinium cation 1 is generated from 2,6-diiodopyridinium cation 12 upon collision-induced consecutive cleavage of the two carbon–iodine bonds in a strong magnetic field. Because of a relatively small S–T splitting (about 11 kcal mol⁻¹), a mixture of singlet and triplet states is likely generated. Upon interaction with cyclohexane, the triplet state reacts rapidly by abstraction of two hydrogen atoms, whereas the singlet state reacts slowly by abstraction of a hydride followed by a proton transfer. The use of Xe instead of Ar as the collision gas to generate the radical sites resulted in a reduced amount of the triplet state. For all other reagents, only one highly reactive species, likely to be the triplet state, was observed. The triplet reacts much faster via radical reactions than the isomeric singlet biradicals 2 and 3 (with large S–T splittings), as expected. Furthermore, triplet 1 is much more acidic than singlet 1 and transfers a proton to all reagents except cyclohexane.