A New Framework for CNN-Based Speech Enhancement in the Time Domain

Abstract

This paper proposes a new learning mechanism for a fully convolutional neural network (CNN) to address speech enhancement in the time domain. The CNN takes as input the time frames of noisy utterance and outputs the time frames of the enhanced utterance. At the training time, we add an extra operation that converts the time domain to the frequency domain. This conversion corresponds to simple matrix multiplication, and is hence differentiable implying that a frequency domain loss can be used for training in the time domain. We use mean absolute error loss between the enhanced short-time Fourier transform (STFT) magnitude and the clean STFT magnitude to train the CNN. This way, the model can exploit the domain knowledge of converting a signal to the frequency domain for analysis. Moreover, this approach avoids the well-known invalid STFT problem since the proposed CNN operates in the time domain. Experimental results demonstrate that the proposed method substantially outperforms the other methods of speech enhancement. The proposed method is easy to implement and applicable to related speech processing tasks that require time-frequency masking or spectral mapping.

I. Introduction

SPEECH enhancement is the task of removing or attenuating additive noise from a speech signal, and it is generally concerned with improving the intelligibility and quality of degraded speech. Speech enhancement is employed as a preprocessor in many applications such as robust automatic speech recognition, teleconferencing and hearing aids design. The purpose of monaural (single-channel) speech enhancement is to provide a versatile and cost-efficient approach to the problem that utilizes recordings from only a single microphone. Single-channel speech enhancement is considered a very challenging problem especially at low signal-to-noise ratios (SNRs). This study focuses on single-channel speech enhancement in the time domain.

Traditional monaural speech enhancement approaches include statistical enhancement methods [1] and computational auditory scene analysis [2]. In the last few years, supervised methods for speech enhancement using deep neural networks (DNNs) have become the mainstream [3]. Among the most popular deep learning methods are denoising autoencoders [4], feedforward neural networks [5], [6], and CNNs [7]–[9].

Most frequently employed methods for supervised speech enhancement use T-F masking or spectral mapping [3]. Both of these approaches reconstruct the speech signal in the time domain from the frequency domain using the phase of the noisy signal. It means that the learning machine learns a mapping in the frequency domain but the task of going from the frequency domain to the time domain is not subject to the learning process. Integrating the domain knowledge of going from the frequency domain to the time domain, or the other way around, could be helpful for the core task of speech enhancement. A similar approach of incorporating such domain knowledge inside the network is found to be useful in [10], which employs a time-domain loss for T-F masking. Recently in [11], the authors integrate a fixed number of steps of the iterative Multiple Input Spectrogram Inversion (MISI) algorithm [12] inside DNN, which is found to be helpful for the speaker separation task.

We design a fully convolutional neural network that takes as input the noisy speech signal in the time domain and outputs the enhanced speech signal in the time domain. One way to train this network is to minimize the mean squared error (MSE) or the MAE loss between the clean speech signal and the enhanced speech signal [8], [9]. However, our experiments show that, using a time domain loss, some of the phonetic information in the estimated speech is distorted probably because the underlying phones are difficult to distinguish from the background noise. Also, using a loss function in the time domain does not produce a good speech quality. So, we believe that it is important to use a frequency domain loss, which can discriminate speech sounds from nonspeech noises and produce speech with high quality.

Motivated by the above considerations, we propose to add an extra operation in the model at the training time that converts the estimated speech signal in the time domain to the frequency domain. The conversion from the time domain to the frequency domain is differentiable, so a loss in the frequency domain can be used to train a network in the time domain. We propose to use the MAE loss between the clean STFT magnitude and the estimated STFT magnitude.

The two approaches proposed in [10], [11] employ a DNN in the frequency domain and use a loss function in the time domain to train the DNN. However, these methods use the noisy phase to reconstruct a time domain signal, and may suffer from the well-known invalid STFT problem [13]. In our approach, a model is employed in the time domain and trained using a loss function in the frequency domain, so the generated signal is always a valid signal and we do not need to use the phase of the noisy signal. The neural network learns a phase structure itself in the process of optimizing the proposed loss. We show in Section VI that the learned phase is better than the noisy phase.

Other researchers have explored speech enhancement in the time domain using deep learning. In [9], authors explore CNNs for speech enhancement and claim that fully connected layers inside a DNN are not suitable for the time domain enhancement and instead propose to use a fully-convolutional neural network. Similar to our work, a time domain network has been proposed using a loss based on a short-term objective intelligibility metric [14]. In [8], authors propose a generative adversarial network [15] for speech enhancement in which the generator is an autoencoder based fully-convolutional network that is trained with the help of a discriminator. Recently, the Bayesian wavenet [16] has been explored for speech enhancement followed by [17], which makes the wavenet [18] faster and uses a discriminative approach rather than a generative approach. Very recently, a fully convolutional network is proposed for speaker separation in the time domain [19] and it is trained using a loss based on scale-invariant signal-to-noise ratio (SI-SNR).

The work presented in this paper is an extension of our preliminary work in [20]. Here, we present more extensive experiments, provide a justification for the observed behavior, and evaluate the proposed model in a speaker- and noise-independent way. The rest of the paper is organized as follows. In the next Section, we describe the method to compute a frequency domain loss for a CNN in the time domain. Section III explains the details about the model architecture. In Section IV, we briefly describe the invalid STFT problem. Experiments and comparisons are described in Sections V and VI. Section VII concludes the paper.

II. Frequency Domain Loss Function

Given a real-valued vector x_t of size N in the time domain, we can convert it to the frequency domain by multiplying it with a complex-valued discrete Fourier transform (DFT) matrix D using the following equation

$${\mathit{x}}_f={\mathit{Dx}}_t$$ (1)

where x_f is the DFT of x_t and D is of size N × N. Since x_t is real-valued, the relation in (1) can be rewritten as

$${\mathit{x}}_f=({\mathit{D}}_r+i{\mathit{D}}_i){\mathit{x}}_t={\mathit{D}}_r{\mathit{x}}_t+i{\mathit{D}}_i{\mathit{x}}_t$$ (2)

where D_r and D_i are real-valued matrices formed by taking the element-wise real and imaginary part of D and i denotes the imaginary unit. This relation can be separated into two Equations involving only real-valued vectors as given in the following Equation.

$$\begin{gathered} {\mathit{x}}_{f_r}={\mathit{D}}_r{\mathit{x}}_t \\ {\mathit{x}}_{f_i}={\mathit{D}}_i{\mathit{x}}_t \end{gathered}$$ (3)

Here, x_fr and x_fi are real-valued vectors formed by taking element-wise real and imaginary part of x_f. A frequency domain loss can thus be defined using x_fr and x_fi. One such loss defined as the average of the MSE losses on the real and imaginary part of x_f is:

$$\begin{gathered} L({\widehat{\mathit{x}}}_f,{\mathit{x}}_f)=\frac{1}{N}\sum _{n=1}^N(({\widehat{x}}_{f_r}(n)-x_{f_r}(n){)}^2 \\ +({\widehat{x}}_{f_i}(n)-x_{f_i}(n){)}^2) \end{gathered}$$ (4)

where ${\widehat{\mathit{x}}}_f$ is an estimate of x_f. x(n) denotes the n^th component of x. It should be noted that this loss function has both magnitude and phase because it uses the real as well as the imaginary part. However, we find that using both the magnitude and the phase does not give as good performance as using only the magnitude. So, we use the following loss function defined using only the magnitudes.

$$\begin{gathered} L({\widehat{\mathit{x}}}_f,{\mathit{x}}_f)=\frac{1}{N}\sum _{n=1}^N\mid (\mid {\widehat{x}}_{f_r}(n)\mid +\mid {\widehat{x}}_{f_i}(n)\mid ) \\ -(\mid x_{f_r}(n)\mid +\mid x_{f_i}(n)\mid )\mid \end{gathered}$$ (5)

This loss can also be described as the MAE loss between the estimated STFT magnitude and the clean STFT magnitude when the magnitude of a complex number is defined using the L₁ norm. We also compare the proposed loss function with an L₂ loss defined as:

$$\begin{gathered} L({\widehat{\mathit{x}}}_f,{\mathit{x}}_f)=\frac{1}{N}\sum _{n=1}^N\mid \sqrt{{\widehat{x}}_{f_r}(n{)}^2+{\widehat{x}}_{f_i}(n{)}^2+\alpha } \\ -\sqrt{x_{f_r}(n{)}^2+x_{f_i}(n{)}^2+\alpha }\mid \end{gathered}$$ (6)

Here, α is a small positive constant added to stabilize the training. Our use of the MAE loss is partly motivated by a recent observation that the MAE loss works better in terms of objective quality scores when a spectral mapping based DNN is trained [21]. In the present study we have confirmed that the MAE loss performs better than the MSE loss for objective intelligibility and quality.

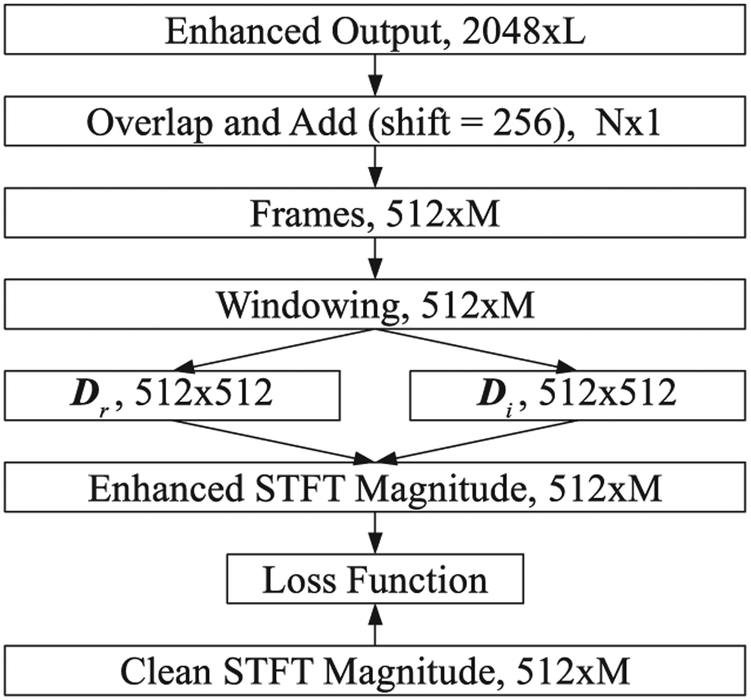
Fig. 1 shows a schematic diagram for computing a frequency domain loss from enhanced time domain frames. The proposed model operates on the frame size of 2048 samples, meaning that it takes as input a frame of duration 128 ms with the sampling frequency of 16 kHz, and outputs a frame of the same length. All the enhanced frames of an utterance at the network output are combined using the overlap-and-add (OLA) method to obtain the enhanced utterance. A frame shift of 256 samples is used for OLA. The enhanced utterance is then divided into frames of size 512. The obtained frames are multiplied by the Hamming window and then separately with two matrices D_r and D_i, each of size 512 × 512 as defined in Equation (2). The matrix multiplication gives the real and imaginary part of the STFT. Next, the real and imaginary part of the STFT are combined to get the STFT magnitude. The computed STFT magnitude is compared with the clean STFT magnitude to obtain a frequency domain loss.

Fig. 1.

Block diagram showing the steps involved in computing a frequency domain loss from the time domain frames at the output of network. L denotes the number of frames of size 2048, and N the length of the enhanced utterance obtained after overlap-and-add. M is the number of frames of size 512. D_r and D_i represent the real and the imaginary part of the DFT matrix, respectively.

III. Model Architecture

We use a fully convolutional neural network that is comprised of a series of convolutional and deconvolutional layers. We first describe the convolution and deconvolution operation and then the proposed model.

A. Convolution

Formally, a 1-D discrete convolution operator *, which convolves signal f with kernel k of size 2m + 1 and with stride r, is defined as

$$(\mathit{f}\ast \mathit{k})(p)=\sum _{s+t=(r\times p)}f(s)k(t)$$ (7)

where p, $s\in \mathbb{Z}$ and $t\in [-m,m]\cap \mathbb{Z}$. Here, $\mathbb{Z}$ denotes the set of integers. A strided convolution used in this work is a convolution meant to reduce the size at the output by sliding the kernel over the input signal with a step greater than one. For example, given an input of length 2N, a kernel of size 2m + 1 and zero padding of size m on both sides of the input, a convolution with stride 2 will produce an output of size N. Hence the input of size 2N is effectively downsampled to an output of size N.

B. Deconvolution

A deconvolution layer [22], also known as transposed convolution, is a convolution meant to increase the size at the output. For a deconvolution with stride length r, r − 1 zeroes are first inserted between the consecutive samples of the input signal. Then it is zero padded on both sides with an appropriate amount so that the convolution with a kernel of size k and stride 1 produces the output of desired size. For example, given an input of length N, kernel of size (2m + 1), and stride of 2, first, one zero will be inserted between the consecutive samples of the input, giving a signal of length 2N − 1. Then the signal will be zero-padded on left and right by m and m + 1 respectively to get the signal of length 2N + 2m. After this, a convolution with a filter of size 2m + 1 will produce an output of size 2N. Hence the input of size N is effectively upsampled to an output of size 2N.

C. Proposed Model

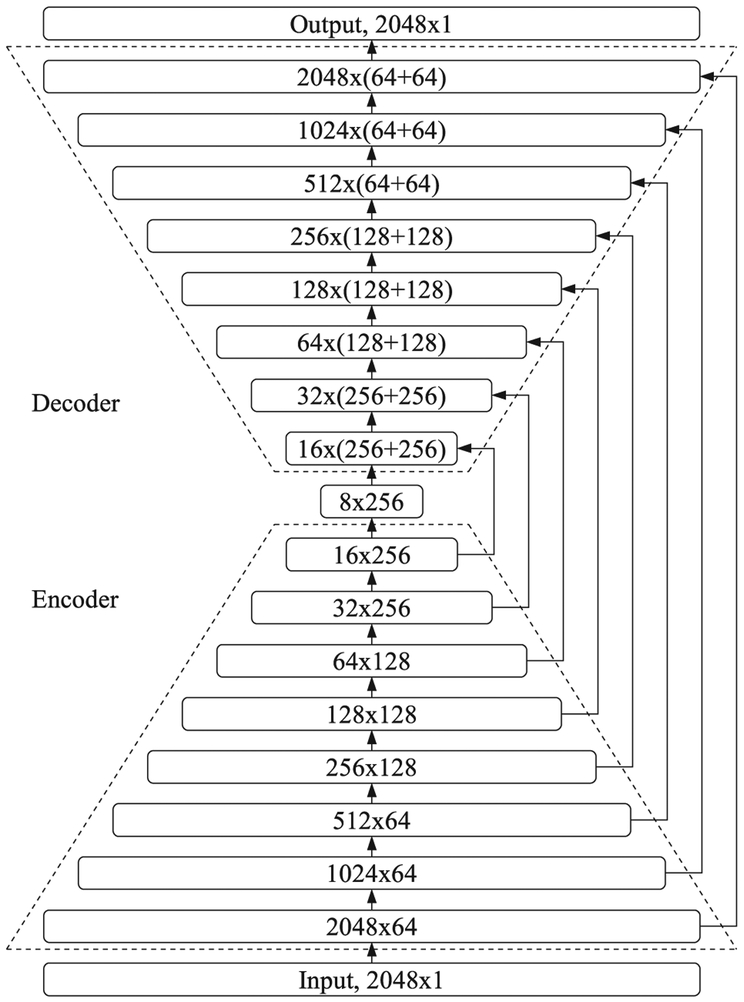
We use an autoencoder based fully convolutional neural network with skip connections first proposed for time domain speech enhancement in [8], which was adopted from U-Net [23]. The schematic diagram of the proposed model is shown in Fig. 2, which illustrates the processing of one frame. The first layer of the encoder is a convolutional layer that increases the number of channels from 1 to 64. Each of the next eight layers successively reduces the dimension of the input signal to half using convolutions with a stride of 2, while either doubling or maintaining the number of channels. The final output of the encoder is of size 8 with 256 channels. The decoder mirrors the encoder, consisting of a series of eight deconvolutional layers [22] with a stride of 2 that double the dimension of its input making the number of channels the same as in the corresponding symmetric layer of the encoder. The output of each layer in the decoder is concatenated with the output from the corresponding symmetric layer of the encoder along the channel axis.

Fig. 2.

A schematic diagram illustrating the architecture of the proposed model. The numbers represent the output dimension after each layer where M × N denotes a signal with dimension M and number of channels equal to N. Note that the number of channels in the decoder is double of that in the encoder because of the concatenation of the incoming connection from the symmetric layer of the encoder. Arrows denote skip connections.

The skip connections are included because a signal can not be well reconstructed from the final output of the encoder as it has a much reduced dimension compared to the input and is a bottleneck. Furthermore, the skip connections help to provide gradients to the layers close to the input layer and avoid the vanishing gradient problem [24]. The final output layer is a simple convolutional layer which reduces the number of channels from 64 to 1. Each layer in the network uses the activation of parametric ReLU non-linearity [25] except for the output layer which uses the Tanh. A dropout [26] rate of 0.2 is applied at every 3 layers. To summarize, the dimensionality of the outputs from the successive layers in the proposed network is 2048 × 1 (input), 2048 × 64, 1024 × 64, 512 × 64, 256 × 128, 128 × 128, 64 × 128, 32 × 256, 16 × 256, 8 × 256, 16 × 512, 32 × 512, 64 × 256, 128 × 256, 256 × 256, 512 × 128, 1024 × 128, 2048 × 128, 2048 × 1 (output).

For the speaker- and noise-independent model trained on the WSJ0 SI-84 dataset [27] (see Section V-A), we use a deeper network that takes as input a frame of size 16384 samples. The model mentioned above gives good performance for this task but is not able to improve the state-of-the-art performance. For the enhancement task on this dataset, the importance of future and past context was first established in [28]. We also observe a considerable performance improvement when the context is increased by increasing the frame size. The dimensionality of the successive layers in the network used for this task is 16384 × 1 (input), 16384 × 32, 8192 × 32, 4096 × 32, 2048 × 64, 1024 × 64, 512 × 64, 256 × 128, 128 × 128, 64 × 128, 32 × 256, 16 × 256, 8 × 256, 16 × 512, 32 × 512, 64 × 256, 128 × 256, 256 × 256, 512 × 128, 1024 × 128, 2048 × 128, 4096 × 64, 8192 × 64, 16384 × 64 (output).

IV. Invalid Short-Time Fourier Transform

The STFT of a signal is obtained by taking the DFT of overlapped frames of a signal. The overlap between consecutive frames causes the adjacent frames to have common samples at the boundary of frames. This correlation between adjacent frames appears in the frequency domain as well and results in a certain relationship between the STFT magnitude and the STFT phase. This relationship needs to be maintained to reconstruct the original signal in the time domain. In [13], the authors show that not all 2-dimensional complex-valued signals correspond to a valid STFT. A 2-dimensional complex-valued signal, X (m, k) is a valid STFT if and only if the following holds.

$$\text{STFT(ISTFT}(X(m,k)))=X(m,k)$$ (8)

Here, ISTFT denotes inverse STFT, m frame number, and k is frequency index. An STFT obtained by taking the STFT of a real signal in the time domain is always a valid STFT. It means that given a real signal x(t) in the time domain, the following relations will always hold.

$$\begin{gathered} \text{ISTFT(STFT}(x(t)))=x(t) \\ \text{STFT(ISTFT(STFT}(x(t))))=\text{STFT}(x(t)) \end{gathered}$$ (9)

The problem arises when the STFT magnitude of a given real or the STFT phase of the signal are altered separately. In such a case, the required relationship between the STFT magnitude and STFT phase is not guaranteed, and Equation (6) may not hold. In the frequency domain speech enhancement, popular approaches are T-F masking and spectral mapping. Both of these methods require using the STFT phase of the noisy speech with enhanced STFT magnitude to reconstruct a time domain signal. The combination of the noisy phase with the enhanced magnitude of STFT is unlikely a valid STFT, as recently demonstrated in [29]. Invalid STFT causes unpleasant signal distortions. To deal with this problem, an iterative method has been proposed to get a signal in the time domain which produces the STFT magnitude close to the enhanced STFT magnitude while maintaining the valid STFT [13].

The proposed framework can be thought of as a supervised way of resolving the invalid STFT problem by a CNN, which produces a speech signal in the time domain but is trained with a loss function which minimizes the distance measured in terms of the STFT magnitudes.

The proposed model generates consecutive frames one by one and combines them using the OLA method as we find that OLA is better than a simple concatenation. Even though we use a loss function based on the magnitude of a valid STFT at the training time, this does not guarantee that generated consecutive frames will have matching samples at the boundary. But we use a frame size of 128 ms so that, even though the analysis window size is 32 ms, the validity of signal is guaranteed over the duration of 128 ms. The proposed model does not guarantee the whole utterance to be a valid signal. The simple concatenation of consecutive frames would give a valid signal, but it exhibits boundary discontinuity, giving worse objective scores than OLA. A different approach to generate a valid signal at the utterance level is to design a model that produces one sample at a time. But, such models based on deep learning are very slow and have not been established for speech enhancement. One such example is wavenet [18], which has been explored for denoising in [16] and [17]. The proposed model in [16] is very slow, and in [17], it operates at the frame level for efficiency and hence suffers from the same problem.

V. Experimental Settings

A. Datasets

In our first set of experiments, we evaluate and analyze the proposed framework on the TIMIT dataset [30] which consists of utterances from many male and female speakers. We use 2000 randomly chosen utterances from the TIMIT training set as the training utterances. The TIMIT core test set consisting of 192 utterances is used as the test set. We evaluate models for the noise-dependent and noise-independent case. Five noise-dependent models are trained on the following five noises: babble, factory1, oproom, engine, and speech-shaped noise (SSN). A single noise-independent model is trained using the five noises mentioned above and evaluated on two untrained noises: factory2 and tank. All the noises except SSN are from the NOISEX [31] dataset. All noises are around 4 minutes long. The training set is created by mixing random cuts from the first half of noises at the SNRs of −5 dB and 0 dB. The test set is created by adding random cuts from the second half of the noises at the SNRs of −5 dB, 0 dB, and 5 dB. Here, 5 dB is an untrained SNR condition that is used to asses SNR generalization of the trained models. The datasets are similar to the ones used in [21], [32].

Further, we evaluate the proposed framework in a speaker-dependent way on the IEEE database[33]. This experiment is performed to evaluate if the proposed framework scales well for untrained noises after training using a large number of noises. The IEEE database consists of 720 utterances of a single male speaker. We create a large training set by mixing randomly selected 560 IEEE sentences with 10000 non-speech sounds from a sound-effect library (available at www.sound-ideas.com). The remaining 160 utterances are used as test utterances. The training set consists of 640000 noisy utterances. To create a training utterance an IEEE sentence is first randomly selected from the 560 training utterances. The selected utterance is then mixed at a fixed SNR of −2 dB with a random segment of a randomly selected noise. The total duration of the training noises is around 125 hours, and that of the training mixtures is around 380 hours. The test set is created by mixing the selected 160 test sentences with babble and cafeteria noise from the Auditec CD (available at http://www.auditec.com) at the SNRs of −5 dB, −2 dB, 0 dB and 5 dB. Here, −5 dB, 0 dB and 5 dB are untrained SNRs. The training and test set used in this experiment are similar to the ones used in [34], hence facilitating a direct comparison.

We also evaluate the proposed framework on the WSJ0 SI-84 dataset [27] that consists of 7138 utterances from 83 speakers. A speaker- and noise-independent model is trained using a large training set. Seventy-seven speakers are selected to produce training utterances. The test set is created from the utterances of 6 speakers that are not included in the training set. The training and test mixtures are generated in the same manner as described in the previous paragraph. The only difference is that, in this experiment, 320000 utterances are generated at five SNRs of −5 dB, −4 dB, −3 dB, −2 dB, −1 dB. An utterance, a noise, and an SNR value are randomly selected first. Then the selected utterance is mixed with a random cut from the selected noise at the selected SNR. The SNRs used for evaluation are −5 dB, 0 dB and 5 dB. The training and the test set for this experiment are the same as in [35], again facilitating quantitative comparisons.

B. System Setup

As described in the last subsection, we perform training on three datasets: TIMIT, IEEE, and WSJ0 SI-84. All the utterances are resampled to 16 kHz. The noisy and the clean utterances are normalized to the value range [−1, 1], and frames are extracted from the normalized utterances. A frame size of 2048 samples (128 ms) is used for the experiments on the TMIT and IEEE databases. A frame size of 16384 samples is used, as mentioned in Section III, for the experiments on WSJ0 SI-84. The frame shift to generate training frames is half of the frame size for IEEE and WSJ0 and 256 samples for the experiments on TIMIT.

A filter size of 11 is used. All the weights in CNNs are initialized using the Xavier initializer with normally distributed random initialization [36]. The Adam optimizer [37] is used for SGD (stochastic gradient descent) based optimization with a batch size of 4 utterances. The shorter utterances in a batch are zero padded to match the size of the longest utterance. The loss value computed over the zero padded region is ignored for gradient computation. The learning rate is set to 0.0002.

The major difference between the architecture of the generator in SEGAN [8] and the architecture of our model is that the input frame size to SEGAN is equal to 16384 samples whereas our input frame size is 2048 samples. The filter size in SEGAN is 31 as compared to 11 in our model. The total number of parameters in the SEGAN model is around 58 million whereas our model has around 6.4 million parameters.

C. Baseline Models

To compare the noise-dependent and noise-independent models trained on the TIMIT dataset, we use three baseline models. First, we train a DNN model using the MAE loss to estimate the ideal ratio mask (IRM) [32]. This model is a 3-layered fully connected DNN that takes as input the noisy STFT magnitudes of five consecutive frames (centered at the current frame) concatenated together and outputs the IRM of the corresponding five frames together. Multiple predictions of the IRM are averaged. The second baseline is the SEGAN model [8]. In the method in [8], the generator of the generative adversarial network (GAN) [15] is trained using two loss functions; adversarial loss and MAE loss in the time domain. We train two versions of this model. The first is trained using both the loss functions, adversarial loss and the MAE loss as in the original paper. We call this model SEGAN. The second is trained using only the loss on time domain samples. We call this model SEGAN-T in our experiments.

The model trained on the IEEE dataset is compared with a five-layered DNN model proposed in [34] which uses the same dataset as in our work, and generates the training and test mixtures in the same manner. The input to their DNN is the concatenation of the power ($\frac{1}{15}$) compressed cochleagram of 23 consecutive frames (centered at the current frame) of noisy speech. The output of the DNN is the IRM of 5 consecutive frames. Multiple predictions of the IRM are also averaged. Each hidden layer has 2048 units.

Our speaker- and noise-independent model trained on WSJ0 SI-84 dataset is compared with a recently proposed model [35]. This gated residual network (GRN) model is a 62-layer deep fully convolutional network with residual connections. It takes as input the spectrogram of the whole utterance at once and outputs the phase-sensitive mask (PSM) [38] of the whole utterance. The layers in this model are comprised of dilated convolutional layers having gated linear units with an exponentially increasing rate of dilation. This model has the state-of-the-art performance for this speaker- and noise-independent enhancement task.

D. Evaluation Metrics and Comparisons

In our experiments, models are compared using short-term objective intelligibility (STOI) [39], perceptual evaluation of speech quality (PESQ) [40], and scale-invariant signal-to-distortion ratio (SI-SDR) [41] scores, all of which represent the standard metrics for speech enhancement. STOI has a typical value range from 0 to 1, which can be roughly interpreted as percent correct. PESQ values range from −0.5 to 4.5.

All the time domain models are compared for both the MAE loss and the MSE loss training. For the experiments on the TIMIT dataset, the first comparison is done between the baseline models and the proposed model trained using different loss functions. The proposed model can be trained using a loss in the time domain or different types of loss in the frequency domain. For a frequency domain loss, two possible loss functions are a loss on both the real and the imaginary part of STFT and a loss on the STFT magnitude. We call our model autoencoder convolutional neural network (AECNN). The corresponding abbreviated names for our models trained using different loss functions are AECNN-T for using a loss on time domain samples, AECNN-RI for using a loss on both the real and the imaginary part of the STFT, and AECNN-SM for using a loss on STFT magnitudes. AECNN-SM1 denotes the loss defined on L₁ norm and AECNN-SM2 denotes the loss defined on L₂ norm of STFT coefficients.

Note that a model trained using a loss in the time domain or a loss on both the real and the imaginary part of the STFT utilizes phase information during training and hence training is supposed to learn both the magnitude and the phase. The model proposed in [42] also uses a loss on the real and imaginary part of the STFT but it operates in the frequency domain and thus is fundamentally different from our approach.

AECNN-SM trains a given model using a loss on STFT magnitudes, with no phase used at the training time. With the proposed time-domain enhancement, however, AECNN learns a phase structure itself. It is interesting to explore whether the learned phase is better than the mixture phase. We compare the learned phase with the mixture phase and the clean phase. First, we combine the STFT magnitude of the noisy utterance with two different kinds of phase: the learned phase and the clean phase. These are named MIX-SM and MIX-CLN respectively. Second, we combine the STFT magnitude predicted by the baseline IRM estimator with three kinds of phase: the noisy phase, the learned phase, and the clean phase. They are named IRM-MIX, IRM-SM, and IRM-CLN respectively. The STOI, PESQ and SI-SDR scores are compared at the SNRs of −5, 0, and 5 dB.

VI. Results and Discussions

First, we present the results of noise-dependent models trained on the TIMIT dataset. Table I lists the average results over all the five noises at −5 dB, 0 dB, and 5 dB SNR. We divide our loss functions into two categories, those with phase, i.e., AECNN-T, SEGAN-T or AECNN-RI, and those without phase, i.e., AECNN-SM1 and AECNN-SM2. We observe that the models trained with a loss with phase perform better using MSE whereas the models trained with a loss without phase perform better using MAE. The SEGAN-T, AECNN-T, and AECNN-RI, have better STOI and SI-SDR scores with MAE but significantly worse PESQ. AECNN-SM1 and AECNN-SM2 produce better scores with the MAE loss. AECNN-SM1 and AECNN-SM2 have similar STOI and PESQ scores but AECNN-SM1 is consistently better in terms of SI-SDR.

TABLE I.

Performance Comparison Between Various Loss Functions and Network Models for Noise-Dependent Models Trained on the TIMIT Dataset

SNR		−5 dB			0 dB			5 dB
Metric		STOI (%)	PESQ	SI-SDR	STOI (%)	PESQ	SI-SDR	STOI (%)	PESQ	SI-SDR
Mixture		56.5	1.41	−4.8	68.2	1.72	0.1	78.9	2.05	5.1
DNN		69.7	1.88	2.8	80.4	2.34	7.5	87.7	2.74	11.9
SEGAN		76.8	1.77	7.1	86.0	2.28	10.3	90.2	2.60	12.5
SEGAN-T	MAE	77.7	1.73	7.6	87.2	2.22	11.2	91.3	2.57	13.5
	MSE	77.9	2.01	7.7	87.3	2.46	11.2	91.5	2.78	13.6
AECNN-T	MAE	78.9	1.88	8.2	88.2	2.41	11.7	92.3	2.80	14.3
	MSE	78.6	2.00	8.0	88.0	2.60	11.5	92.2	2.90	13.9
AECNN-RI	MAE	80.0	1.92	8.6	89.0	2.48	12.0	92.8	2.86	14.3
	MSE	78.6	2.00	8.1	88.1	2.56	11.6	92.2	2.90	14.1
AECNN-SM1	MAE	80.3	2.20	8.0	89.0	2.68	11.4	92.8	3.01	13.7
	MSE	78.9	2.20	7.5	88.0	2.60	11.1	92.2	2.90	13.6
AECNN-SM2	MAE	80.2	2.20	7.8	89.0	2.70	10.8	92.7	3.02	12.7
	MSE	78.9	2.20	7.3	88.1	2.60	10.7	92.1	2.9	12.9

Next, we observe that AECNN-T is significantly better than SEGAN-T and SEGAN, suggesting that the AECNN architecture is better than SEGAN for speech enhancement in the time domain. Additionally, the time domain models are much better than the baseline IRM based DNN model. The proposed AECNN-SM1 is significantly better in terms of STOI and PESQ compared to the AECNN-RI with MSE. AECNN-RI is marginally better in terms of SI-SDR. Note that the SI-SDR of AECNN-RI with MAE is better than AECNN-SM1, but its PESQ score is very low, implying that the AECNN-SM1 is better as it substantially improves PESQ while maintaining SI-SDR. In summary, the proposed AECNN-SM1 is the best in terms of STOI and PESQ, whereas AECNN-RI is the best for SI-SDR.

A similar performance profile is observed for the noise-independent models at the three SNRs as given in Table II. AECNN-SM1 and AECNN-SM2 are the best in terms of STOI and PESQ. AECNN-RI is the best for SI-SDR at 5 dB but AECNN-SM1 is better at 0 dB and −5 dB. Note that we compare AECNN-SM1-MAE with AECNN-RI-MSE. AECNN-SM1 and AECNN-SM2 have similar STOI and PESQ scores but AECNN-SM1 is consitently better in terms of SI-SDR, making it the better enhancement approach.

TABLE II.

Performance Comparison Between Various Loss Functions and Network Models Noise-Independent Models Trained on the TIMIT Dataset

SNR		−5 dB			0 dB			5 dB
Metric		STOI (%)	PESQ	SI-SDR	STOI (%)	PESQ	SI-SDR	STOI (%)	PESQ	SI-SDR
Mixture		66.8	1.63	−4.8	76.3	2.00	0.1	84.4	2.35	5.1
DNN		76.3	2.21	6.5	84.8	2.64	10.7	90.0	2.99	14.6
SEGAN		83.3	2.15	9.1	89.1	2.56	11.5	91.3	2.77	12.8
SEGAN-T	MAE	83.9	2.01	10.3	90.4	2.47	13.2	93.0	2.75	15.0
	MSE	84.0	2.33	10.1	90.1	2.70	13.0	92.7	2.94	14.9
AECNN-T	MAE	84.7	2.14	10.7	91.1	2.64	13.8	93.6	2.93	15.7
	MSE	84.5	2.35	10.1	90.8	2.79	13.1	93.3	3.05	14.8
AECNN-RI	MAE	84.8	2.12	11.0	91.3	2.66	13.9	93.8	2.96	15.7
	MSE	84.5	2.36	10.1	90.7	2.79	13.3	93.2	3.05	15.2
AECNN-SM1	MAE	85.7	2.50	10.6	91.7	2.93	13.4	93.9	3.15	14.9
	MSE	85.1	2.50	10.2	91.0	2.85	13.2	93.4	3.08	15.1
AECNN-SM2	MAE	85.9	2.51	10.0	91.9	2.94	12.6	94.2	3.19	14.0
	MSE	85.1	2.51	9.7	91.3	2.87	12.7	93.7	3.10	14.4

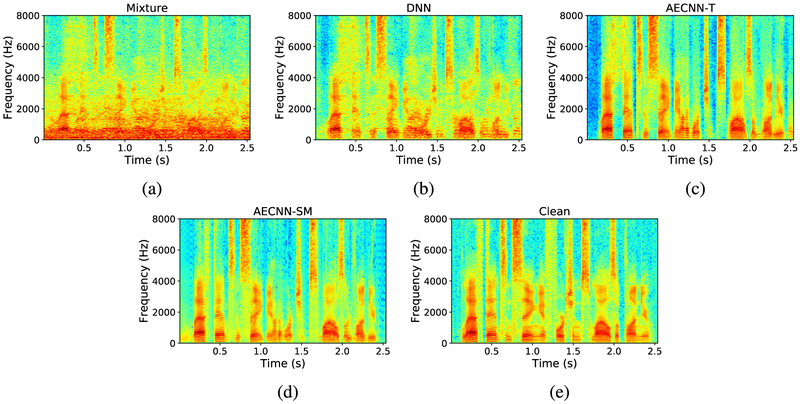
For illustration, we plot spectrograms of a sample utterance in Fig. 3. We can observe that the DNN based IRM estimator does not appear to distort the speech signal by much but is not able to remove some of the noise as can be seen for low-frequency regions around 1.25s. AECNN-T reduces the noise more but still retains some noise as can be observed in the low-frequency region around 2.5s. The enhanced spectrogram using the STFT magnitude loss looks closest to the clean spectrogram, and is better not only for noise reduction but also seems to introduce relatively negligible distortions compared to the clean spectrogram.

Fig. 3.

Spectrogram of a sample utterance mixed with babble noise at −5 dB SNR, and its enhanced spectrograms using different models. (a) Noisy spectrogram. (b) Spectrogram enhanced using a DNN based IRM estimator. (c) Spectrogram enhanced using AECNN trained with a time domain loss. (d) Spectrogram enhanced using AECNN trained with an STFT magnitude loss. (e) Clean spectrogram.

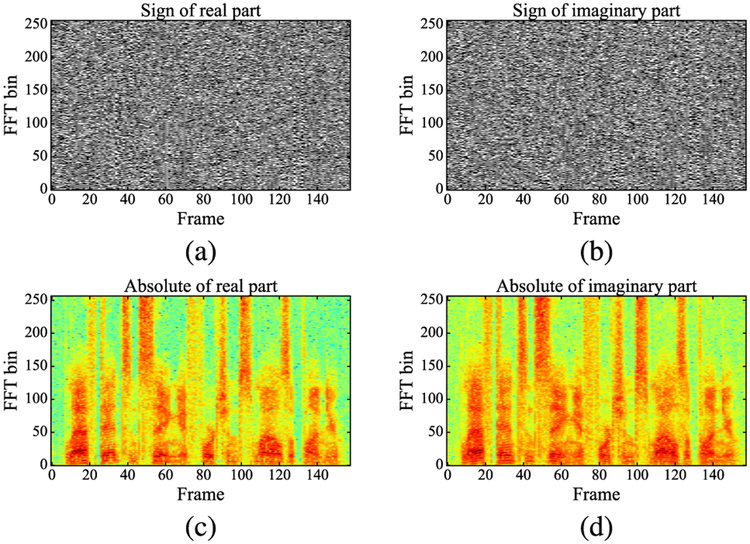
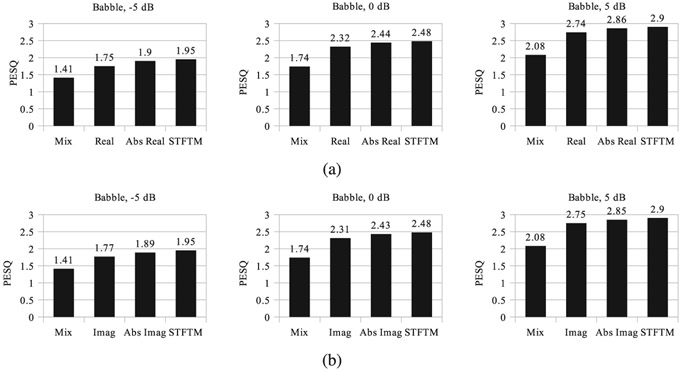
The frequency domain loss functions using the real and imaginary part of the STFT do not perform as well as a loss based on the STFT magnitude. One explanation for this observation is that the STFT magnitude exhibits clearer temporal structure than the real part or imaginary part. Also, it is non-negative, and likely easier to learn. As analyzed in [43], structure exists in the absolute of the real and the imaginary part of the STFT of a speech signal. Fig. 4 shows the signs and the absolute values of the real and imaginary parts of STFT for a sample utterance. To plot the absolute values, we first normalize the relevant data to the value range [10⁻⁸, 1] and then take their logarithm. We observe that the signs of real and imaginary parts are very noisy whereas there is a clear structure in their absolute values. This suggests that the real and the imaginary parts that are obtained by multiplying the signs and the absolute values would be unstructured. It further suggests that a model trained using a loss on the absolute values of the real or the imaginary part of STFT should perform better than a loss defined directly on the real and imaginary parts. To verify, we have trained models using a loss on the absolute value of the real and the imaginary part of the STFT. The PESQ scores for noise-dependent models trained on babble noise are plotted in Fig. 5. We can see that using the absolute values improves the PESQ score and makes the performance comparable to the AECNN-SM1 model. We obtain similar results for the other four noises and noise-independent models.

Fig. 4.

STFT structure. Plots of the sign of real and imaginary part of STFT of a sample utterance are shown in (a) and (b). In these plots, black and white dots denote −1 and 1 respectively. The signs of the real and imaginary parts of STFT are very noisy. Plots (c) and (d) show the structure of the absolute of the real and imaginary part of STFT of the same utterance.

Fig. 5.

PESQ comparisons of real-valued and absolute-valued loss functions. (a) PESQ scores of the models trained on the real part and the absolute of the real part of STFT. (b) PESQ scores of the models trained on the imaginary part and the absolute of the imaginary part of STFT.

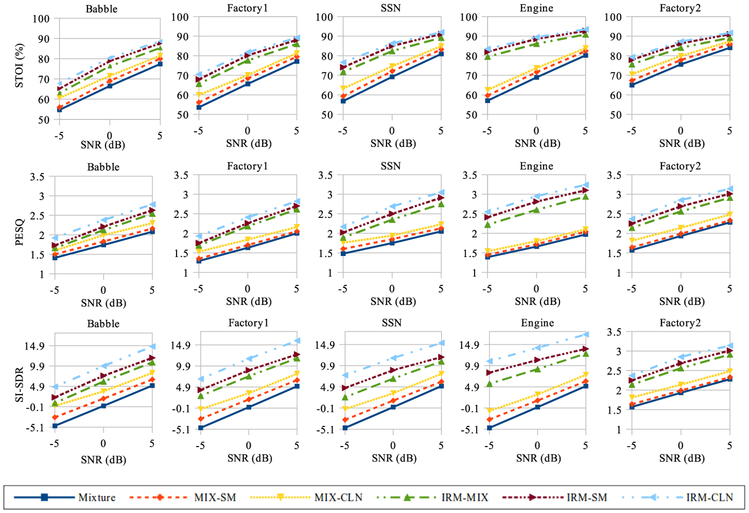
Next, we compare learned phase with noisy phase and clean phase. The noisy test utterances constructed from the TIMIT corpus are used to obtain two STFT magnitudes: noisy STFT magnitude and STFT magnitude enhanced by the baseline DNN estimator. The two magnitudes are combined with three kinds of phase: noisy phase, learned phase and clean phase, to reconstruct a signal in the time domain. STOI, PESQ and SI-SDR values are compared with their corresponding mixture values. These scores at 3 SNR conditions are plotted in Fig. 6. Note that the last column is for the factory2 noise which is enhanced using the noise-independent model. In all the plots, the three lower lines are for the speech reconstructed from the noisy STFT magnitudes and upper three lines are for the speech reconstructed using the enhanced STFT magnitude. We observe that the results with the learned phase are consistently better than those with the mixture phase. This suggests that the learned phase is better than the noisy phase for both the noise-dependent and noise-independent models. Using the clean phase all the scores are significantly better over the noisy phase. This performance gap is partly filled by using the learned phase. On the other hand, there is room for improvement if a neural network can learn to estimate a phase closer to the clean phase.

Fig. 6.

STOI, PESQ, and SI-SDR comparisons between learned phase, noisy phase, and clean phase.

The proposed method is further evaluated on the IEEE dataset for speaker-dependent but noise-independent training on a large number of noises. The performance and comparison with the DNN baseline in STOI are given in Table III. The DNN model improves the STOI score by 16.6% at the −5 dB SNR, which is a difficult and untrained SNR condition. In this cndition the proposed framework improves the STOI score by 23.3%, which represents a substantial improvement. The STOI improvement over the baseline is 5.5% at −2 dB, 4% at 0 dB and 1.6% at 5 dB.

TABLE III.

Performance Comparison Between the Baseline DNN and the Proposed Framework for Noise-Independent Models Trained on the IEEE Dataset. The Scores Denote the Percent Improvement in STOI Over Mixture

	Babble		Cafeteria
	DNN	AECNN-SM1	DNN	AECNN-SM1
5 dB	12	13.6	13.3	14.4
0 dB	17.1	21.1	18.1	21.1
−2 dB	18	23.5	18.7	22.5
5 dB	16.6	23.3	17.5	21.5

The baseline DNN used here has 20.5 million parameters whereas our model has only 6.4 million parameters. The DNN takes the acoustic features of 23 consecutive frames and outputs the IRM of 5 consecutive frames. It means that it uses information from 240 ms of speech and outputs 60 ms of speech. Our model operates on a speech of duration 128 ms and outputs a speech of duration 128 ms.

Finally, we evaluate the proposed method for noise- and speaker-independent speech enhancement trained on a large training set created from the WSJ0 SI-84 dataset. The evaluation results for untrained speakers on untrained babble and cafeteria are given in Table IV. Again, the proposed framework produces substantially better STOI and PESQ scores than the baseline GRN which is 62-layer deep and operates on a whole utterance. It means that the past and future context are maximal for the baseline model. Our model operates on a frame of duration 1024 ms. For this difficult task, the past and future contexts are very important, as analyzed in [34]. We can increase the context in our model by increasing the size of the input frame, but we find that the performance does not improve further by increasing the frame size. One explanation for our better performance is that the GRN model uses the mixture phase whereas our model learns the phase itself, which we have shown is better than the mixture phase.

TABLE IV.

Comparison Between the Baseline GRN and the Proposed Method for Speaker- and Noise-Independent Model Trained on the WSJ0 S1-84 Dataset and Tested on Untrained Speakers. The Scores Denote the Improvement Over Mixture

		STOI		PESQ
		GRN	AECNN-SM1	GRN	AECNN-SM1
Babble	−5 dB	17.3	22.6	0.43	0.61
	−2 dB	17	21.9	0.59	0.84
Cafeteria	−5 dB	17.8	22.5	0.67	0.77
	−2 dB	17.7	21.9	0.77	0.93

VII. Concluding Remarks

In this paper, we have proposed a novel approach to train a fully convolutional neural network for speech enhancement in the time domain. The key idea is to use a frequency domain loss to train the CNN. We have investigated different types of loss function in the frequency domain. Our main observation is that frequency domain loss is better than a time domain loss. Using a frequency domain loss helps to improve objective quality and intelligibility. The highest improvement is obtained using an MAE loss computed on STFT magnitudes defined using L₁ norm. The best SI-SDR score is achieved using a loss on the real and imaginary part of STFT. We have evaluated our method for speech enhancement in speaker-dependent but noise-independent, and speaker- and noise-independent scenarios. In all the cases, the proposed method substantially outperforms the current state-of-the-art methods.

Other frequency domain losses do not perform as well as an STFT magnitude loss. This might be due to better structure in the STFT magnitude. We also observe that there is clear structure in the absolute of the real and imaginary part of the STFT. Training a model with a loss on the absolute value of the real and imaginary part of the STFT gives comparable performance to the STFT magnitude based loss.

We have also tried to make the real and imaginary part of STFT bounded or squashed with a Tanh or sigmoidal function, but not much improvement is obtained. Also, one might think that the logarithm of STFT magnitude should perform better, but that is not what we observe, probably because of a log operation involved in the training process. We also find that the performance of the proposed framework drops significantly when input and output lengths are reduced to one frame from four frames. Future research needs to develop methods for real-time implementation with comparable performance.

Although trained with a loss on only the STFT magnitudes, the proposed framework learns a phase structure itself as it generates a signal in the time domain. We find that learned phase is better than mixture phase but not as good as clean phase. A future research direction is to explore ways to train a deep model to improve phase estimation.

Biography

Ashuosh Pandey received the B.Tech. degree in electronics and communication engineering from Indian Institute of Technology Guwahati, Guwahati, India, in 2011. He is currently working toward the Ph.D. degree at The Ohio State University, Columbus, OH, USA. His research interests include speech separation and deep learning.

DeLiang Wang’s photograph and biography not available at the time of publication.