Feature Selection Algorithms Enhance the Accuracy of Frailty Indexes as Measures of Biological Age

Abstract

Biological age captures some of the variance in life expectancy for which chronological age is not accountable, and it quantifies the heterogeneity in the presentation of the aging phenotype in various individuals. Among the many quantitative measures of biological age, the mathematically uncomplicated frailty/deficit index is simply the proportion of the total health deficits in various health items surveyed in different individuals. We used 3 different statistical methods that are popular in machine learning to select 17–28 health items that together are highly predictive of survival/mortality, from independent study cohorts. From the selected sets, we calculated frailty indexes and Klemera–Doubal’s biological age estimates, and then compared their mortality prediction performance using Cox proportional hazards regression models. Our results indicate that the frailty index outperforms age and Klemera–Doubal’s biological age estimates, especially among the oldest old who are most prone to biological aging-caused mortality. We also showed that a DNA methylation index, which was generated by applying the frailty/deficit index calculation method to 38 CpG sites that were selected using the same machine learning algorithms, can predict mortality even better than the best performing frailty index constructed from health, function, and blood chemistry.

Aging occurs with the passage of time. Calendar age is associated with adverse changes, including chronic diseases and mortality for which it is a risk factor. However, studies of model organisms indicate that the passage of time is not the direct cause of aging: life spans can be altered by genetic, nutritional, or pharmaceutical interventions (1,2). If chronological age was the direct and main cause of aging, delay or reversal of aging that has been observed using model organisms would be impossible. Moreover, chronological age alone cannot account for the wide variation in age-related phenotypes among age peers or in birth cohorts (3–5).

Biological aging is characterized by a gradual decline in health and body functioning over time, with increasing risks of disability, disease, and mortality. Biological age gauges progression of functional aging that occurs independently of chronological age (6,7). Functional decline can be associated with quantitative measures of various biomolecules and health-related items that change with calendar age. Chronological age is a confounder that underlies all aspects of biological aging. It can be likened to the time period taken for chemical reactions to occur, but it is the reactants and products that characterize chemical reactions, not the time.

For estimation of biological age from biomarkers, researchers usually rely on calendar age (8). For example, the approach based on multiple linear regression uses calendar age to derive coefficients for individual biomarkers. In the approach based on principal component analysis, without calendar age, no dominant principal components can be found that can account for the bulk of the data variation, and biological age measures derived from one or more principal components are outperformed by those derived from multiple linear regressions (8–10). The Klemera–Doubal (KD) method has been popular because KD’s biological age estimates outperform age in mortality prediction (11). The KD method proposes 2 main equations for biological age estimation: Eq. (25) termed BE and Eq. (34) termed BEC. However, the BE estimate requires 2 age-derived parameters and BEC requires age as another biomarker in addition to the 2 age-derived parameters used for BE. Thus, the outperformance of BE and BEC over age in mortality prediction makes sense in that the KD measures incorporate both age and health data. This is especially true for BEC, which explicitly uses age as an additional biomarker.

The frailty index (FI, also called deficit index) is simply the proportion of health deficits in various health items surveyed for any individual at any given time (12,13). The health items usually include blood test results, survey data on physical activities, and cognitive and physical functional abilities. The frailty index is fully quantitative and has been extensively studied and well characterized as a measure of biological age (14–16). In this study of 3 independent population samples, we selected 17–28 health items that were predictors of all-cause mortality, using statistical algorithms that are popular in machine learning for predictive modeling. From the selected sets, we calculated frailty indexes, BE, and BEC, and compared their mortality prediction performance using Cox proportional hazards regression models. Our results indicate that the frailty index outperforms age, BE, and BEC, especially in nonagenarians. We also found that a DNA methylation index, called DmI, calculated using only 38 DNA methylation measurements selected with the same statistical algorithms can predict mortality better than the best performing frailty index.

Method

Louisiana Healthy Aging Study

Louisiana Healthy Aging Study (LHAS) data were from 592 Caucasian subjects aged from 21 to 103 (17). Previously, FI34 had been constructed from 34 randomly selected health items, as described (18). In this study, we constructed FI28 from 28 items selected for their ability to predict mortality. The data set contained 188 health variables with <10% missing data points and intervariable correlation coefficient <0.6. The missing data points were imputed using the preProcess function (method = “bagImpute”) in the R caret package. In selecting the 28 items, we used the random forest regression for survival (an ensemble learning method based on decision trees; the R ranger package, num.trees = 500, num.random.splits = 1, alpha = 0.5, importance = permutation), elastic net cox regression (a regularized regression method that combines lasso and ridge methods; the R glmnet package, family = cox, alpha = 0.5), and CoxBoost (Cox regression modeling based on likelihood-based boosting; the R coxBoost package, maxstepno = 500, K = 10, penalty = 1000, type = verweij). The 28 items, present in common in all 3 outputs, are from surveys of physical activities, medical histories, physical examinations, cognitive functioning, and blood test results (Supplementary Table 1).

National Health and Nutrition Examination Survey

Various health items can be grouped into 4 categories: physical activities, physical function abilities, cognitive functioning, and blood counts and chemistry data. In preparing data sets from public databases, we wanted to have public data sets in which health items are from all these 4 categories. Another critical factor that affected our data selection is the availability of sufficient mortality data for survival/mortality analysis. Earlier data sets contain more mortality data but fewer or no health items for one or more of the 4 categories. For example, we chose the 1999–2000 cycle data for National Health and Nutrition Examination Survey (NHANES) because unlike the previous (older) data sets, this cycle data set has cognitive functioning variables. The same principle applied to selection of the Health and Retirement Study (HRS) data set (below). Unlike older data sets, the 2006 data have “sensitive biomarker” data (6 blood test results) and sufficient mortality data. So, selection of a data set from each public database is a balance between mortality data and availability of diverse data categories.

NHANES data sets consist of demographics, dietary, laboratory, and examination data from interviews and Mobile-Exam Center examinations (19). From NHANES 1999–2000, we initially gathered 2568 variables, comprising demographics, laboratory, and examination data, for 4972 subjects whose mortality status was known. However, this data set lacked health items about cognitive and physical functioning. To include more body systems, we added variables in cognitive functioning (CFQ, 7 variables in 1834 subjects) and muscle strength (MSX, 16 variables in 2156 subjects). After removing variables unrelated to health, variables with missingness > 10%, and a variable from each intercorrelated variable pair (r > .6), we obtained a data set consisting of 811 subjects with 70 variables. These NHANES subjects, consisting of 24% Mexican American, 62% Caucasian, and 14% African American, were 60–85 years old (in NHANES 1999–2000, age ≥ 85 is coded 85). The 3 statistical algorithms were applied, and 17 health items were selected and coded to calculate FI17 (Supplementary Table 2). The majority of the 17 items were from blood tests. Cox proportional hazards regression models using NHANES data were adjusted for races, sample weights, strata, and clusters, using the R survey package.

Health and Retirement Study

The HRS is sponsored by the National Institute on Aging (grant number NIA U01AG009740) and is conducted by the University of Michigan (20). We used the 2006 wave in the RAND HRS Longitudinal File. To have many diverse health items, we combined 635 public variables for 42 053 subjects with 343 sensitive biomarker variables for 6735 subjects, resulting in 978 variables for 6735 subjects. Selection of variables with complete data points and non-Hispanic Caucasians further reduced the data to 71 variables for 3894 subjects. The 3 statistical algorithms were applied to this data set and 18 health items were selected (Supplementary Table 3). The subjects were 30–96 years old, and the final set includes items of blood tests, cognitive and physical abilities, and several diseases, among others. Cox proportional hazards regression models using HRS data were adjusted for sample weights, strata, and clusters, using the R survey package.

Klemera–Doubal’s Measures of Biological Age

The data set of coded variables in each population sample that was used to calculate the corresponding frailty index was used to calculate KD’s BE and BEC estimates of biological age using the R WGCNA package with the default setting (21).

Calculation of DmI From 38 DNA Methylation Measurements

We used DNA methylation data obtained using the Infinium HumanMethylation450 BeadChip assay from 211 LHAS DNA samples aged 60–103, as described previously (22). DNA methylation measurements (β values) that failed quality control measures and those highly correlated (one from each intercorrelated pair, r > .6) were removed. From the resulting 56 949 DNA methylation level measurements, 2842 CpG sites whose variable importance scores were within the top 10% were collected using the random forest survival regression, 38 CpG sites with nonzero coefficients using the elastic net Cox regression, and 19 CpG sites with nonzero coefficients using the boosted Cox regression as described above. These 3 sets of selected CpG sites partially overlapped with each other, indicating the presence of many CpG sites with DNA methylation levels predictive of mortality and a wide variation in selection of such CpG sites depending on the feature selection method used (and parameters set). Hannum et al. (23) built a predictive model of aging using 71 DNA methylation sites using the elastic net regression. DNA methylation levels at these sites were highly correlated with chronological age. Using the same method, Horvath (24) proposed DNA methylation age measures based on 353 CpG sites. Thus, the elastic net method appeared prolific with DNA methylation data. Furthermore, 18 of the 19 CpG sites selected by the boosted were also found in the 38 CpG sites selected by the elastic net. As stated in “Discussion” section, Weidner et al. (25) showed that only 3 age-related CpG sites were sufficient for a predictive model in blood. Thus, although the 18 or 19 CpG sites should work as well, to increase the applicability of the DmI to other tissues, we decided to use the 38 CpG sites selected by the elastic net method (Supplementary Table 4).

Beta values of these sites are associated with mortality either positively or negatively (inversely). Positively correlated DNA methylation sites predict higher risk of death for subjects with higher beta values of the sites. Thus, for each of the 9 positively correlated CpG sites, the following coding using quartile (Q) values was applied: if β < Q₁, 0; if Q₁ ≤ β < Q₃, 0.5; if β > Q₃, 1. On the other hand, negatively correlated DNA methylation sites predict lower risk of death for subjects with higher beta values of the sites. For this type of CpG site, the following coding was applied: if β < Q₁, 1; if Q₁ ≤ β < Q₃, 0.5; if β > Q₃, 0. DmI is the average of these coded values. A separate DmI calculated from raw beta values from positively correlated CpG sites and (1 − β) values from the negatively correlated CpG sites gave very similar results.

Estimation of Mortality Prediction Effect Size

The end point of biological aging is death, so the accuracy of biological age estimates is best evaluated by their effect sizes in mortality prediction. The Cox proportional hazards regression analysis is a popular method for survival/mortality analysis of censored data. To show the age adjustment effect in Cox regression analysis, we compared z scores (coefficients divided by standard errors). In comparing effect sizes of predictors, we used the standardized Cox regression coefficient, which estimates the effect of 1 SD change in a continuous predictor variable on the hazard of death. We also used likelihood ratio test and concordance statistics, the latter of which is the same as the area under the curve (AUC) in the receiver operating characteristic (ROC) analysis. The difference in goodness-of-fit of 2 nested models can be ascribed to the added predictor variable in the extended model, and the statistical significance of the difference (Δlog-likelihood) can be assessed using the likelihood ratio χ ² test, which was provided by the R anova function. For analysis of complex survey data, we used the design-adjusted Rao–Scott likelihood ratio test, provided by the regTermTest function in the R survey package. The null hypothesis of this test is that the regression coefficient of the term being tested is zero. Concordance (C-index) is another model fit measure, and the performance of 2 predictors can be compared by noting the change in concordance as each of the predictors is added to a common model. Concordance scores were provided by the coxph function of the R survival package or by the svycoxph function of the R survey package. All analyses were adjusted for sex and race (in the NHANES data).

Results

FI28 in LHAS

We used 3 different statistical algorithms to select 28 health items in LHAS that are highly predictive of survival/mortality, according to Cox proportional hazards regressions analysis. Comparison of z scores of raw coefficients for the 28 items before and after age adjustment indicated that age adjustments substantially reduced z scores of the health variables in all regressions (Supplementary Figure 1). One possible explanation for this reduction is that being age-related changes, these health items are correlated with age. FI28 and KD’s BE (BE28) and BEC (BEC28) were calculated using these 28 health items. FI34 had been previously constructed using randomly selected 34 health items, and BE34 and BEC34 were calculated using the same set. Although this study was cross-sectional, we can infer longitudinal properties of these biological age measures. All these measures of biological age increased exponentially with age, which coincides with the exponential increase in mortality with age (Supplementary Figure 2). We can conveniently infer how closely these biological age measures are related to age by assuming linear relationships. All were significantly correlated with age (p < .001; Kendall’s τ = .54 for FI34, .65 for BE34, and .81 for BEC34, .63 for FI28, .66 for BE28, .82 for BEC28).

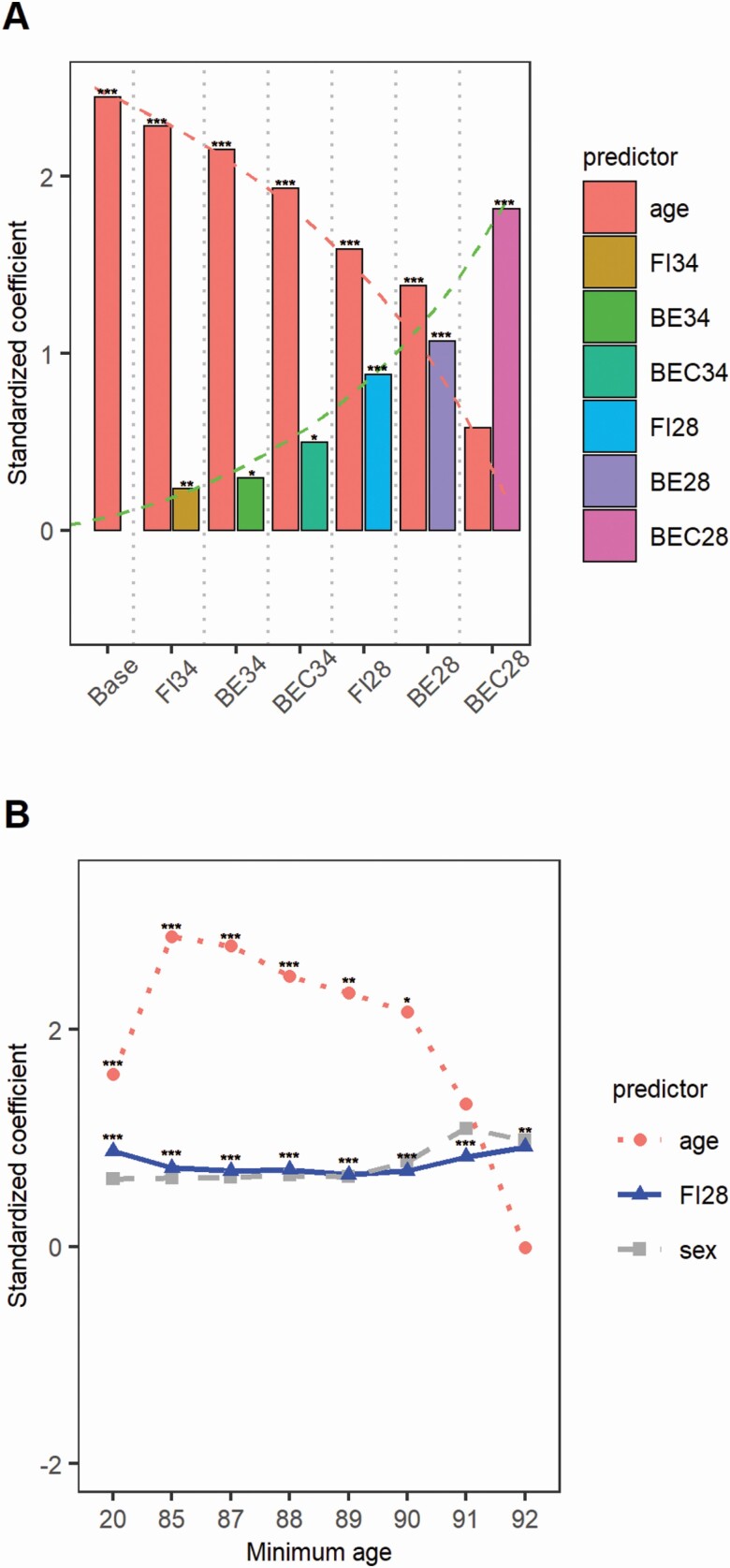
The prediction effect size of each biological age measure was estimated using sex-adjusted Cox regression models for the whole LHAS cohort analyzed (Figure 1A). Age in the base model showed the largest standardized coefficient, confirming that age is the best predictor of mortality in the general population. When biological age measures derived from 34 health items were individually added to the base model, the effect size of age was reduced, with the amount of the reduction proportional to the degree of correlation of the biological measure with age: The reduction was smallest with FI34 but largest with BEC34. Further reduction of the effect size of age was observed when biological age measures derived from the 28-item set were added, and again the reduction was proportional to the correlation of the biological measure with age. These results indicate that KD measures, especially BEC28, are largely redundant with age. The same results were obtained from analysis of sex-separated data (Supplementary Figure 3).

Figure 1.

Effect size (standardized coefficient on y-axis) of mortality predictors (x-axis) in Cox regression models in Louisiana Healthy Aging Study (LHAS) (A) and changes in effect size of FI28 in nested age groups of the LHAS data (B). The base model contains age and sex, and other models additionally contain individual biological age measures. The numbers on x-axis in (B) indicate individuals whose ages are greater than the numbers (eg, the age group “20” means subjects older than age 20, and “85” older than age 85, etc.). Note that the x-axis scale is not proportional. The numbers of deceased/total were 205/592 for age > 20, 151/172 for age > 80, 101/106 for age > 90, 69/72 for age > 91, 45/47 for age > 92, and 26/27 for age > 93. * .01 < p ≤ .05. ** .001 < p ≤ .01. ***p ≤ .001.

Although all biological age measures were significant predictors of mortality after adjustment for age, BEC28 seemed to have the largest effect size (Figure 1A). However, comparisons of concordance and Δlog-likelihood values indicate that the best model was that containing FI28 (Table 1). Furthermore, addition of BE28 or BEC28 to models containing age and FI28 did not improve the model fit, indicating that these measures are essentially redundant with both age and FI28.

Table 1.

Model Comparison Using the Concordance and Likelihood Ratio Test Statistics in Cox Regression Analysis of LHAS

Model 1	Model 2	Concordance (SE)	ΔLog-Likelihood	Significance
Sex	Model 1 + age	.883 (.01)	232.601	***
Sex + age	Model 1 + FI34	.887 (.01)	3.63	**
Sex + age	Model 1 + BE34	.886 (.01)	3.10	*
Sex + age	Model 1 + BEC34	.886 (.01)	3.10	*
Sex + age	Model 1 + FI28	.896 (.009)	24.05	***
Sex + age	Model 1 + BE28	.893 (.009)	18.26	***
Sex + age	Model 1 + BEC28	.893 (.009)	18.26	***
Sex + age + FI28	Model 1 + BE28	.896 (.009)	0.22	n.s.
Sex + age + FI28	Model 1 + BEC28	.896 (.009)	0.22	n.s.
Sex + age + BE28	Model 1 + FI28	.896 (.009)	6.00	***
Sex + age + BEC28	Model 1 + FI28	.896 (.009)	6.00	***

Notes: LHAS = Louisiana Healthy Aging Study. The concordance estimates the accuracy of Model 2. The Δlog-likelihood and significance are to assess the significance of the added predictor (Model 1 + an added predictor = Model 2) in each pair of nested models. N = 592, age range = 21–103, 205/592 deceased.

* .01 < p ≤ .05. ** .001 < p ≤ .01. ***p ≤ .001; n.s. = p > .05.

Mortality from biological aging is more relevant to the elderly than the young; therefore, the Cox regression modeling involving sex, age, and a biological age measure was applied to nested age groups in which the lower age limit increased toward the upper age limit (103). The effect size of age was larger than that of FI28 until the lower age cutoff reached 90 (Figure 1B). After that, however, the effect size of age decreased and became no longer significant. In contrast, the effect size of FI28 remained relatively stable, maintaining its significance in all age groups. The same nested age group analysis was applied to sex-separated data and similar results were obtained (Supplementary Figure 4). The dominance of the frailty index over age was also observed with FI34 (Supplementary Figure 5A). Thus, among subjects aged greater than 91 (69 deceased out of 71), both FI34 and FI28 remained significant, whereas age was no longer significant in predicting mortality.

The Cox regression analysis of nested age groups was also repeated using age, BEC28, and FI28 in the same models (Supplementary Figure 5B). Unlike age and FI28, BEC28 was not a significant predictor of mortality in all age groups. At age older than 91 years, only FI28 was a significant predictor. Similar observations were made using BE28 + FI28, BE34 + FI34, or BEC34 + FI34 (data not shown).

Frailty Indexes Using NHANES and HRS Data

The comparisons of biological age measures in LHAS indicate that the frailty index calculated using selected health items can outperform BE and BEC as a biological age measure. Using independent public data sets, we tested the generalizability of the finding. The same feature selection methods were applied to the processed 1999–2000 NHANES data set, and 17 health items were selected (Supplementary Table 2). As in LHAS, the age adjustment substantially reduced z scores of most of the variables, indicating that these health items constitute age-related changes (Supplementary Figure 6). The coded data were used to calculate biological age measures. The prediction effect size of these biological age measures was estimated using survey-weighted Cox regression modeling. The design-adjusted likelihood ratio test value of FI17 was higher than that of BE17 or BEC17 (Table 2). Furthermore, in the presence of age and FI17, BE17 or BEC17 was not significant at all, confirming the redundancy of the KD measures with age and the frailty index. In the NHANES data, accurate estimation and comparison of effect sizes was not possible because the age of 85 years and older was combined as age 85.

Table 2.

Model Concordance and Likelihood Ratio (Rao–Scott) Test Statistics of Biological Age Measures in Survey-Weighted Cox Regression Analysis of NHANES Data

Survey-Weighted Cox Model	Concordance (SE)	Term Tested	2Log LR	Significance
Base (sex + race + age)	.686 (.021)	Age	128.83	***
Base + BE17	.744 (.019)	Age	6.89	**
		BE17	38.87	***
Base + BEC17	.744 (.019)	Age	1.59	n.s.
		BEC17	38.87	***
Base + FI17	.760 (.018)	Age	19.29	***
		FI17	135.70	***
Base + FI17 + BE17	.762 (.018)	Age	8.07	**
		FI17	55.34	***
		BE17	2.79	n.s.
Base + FI17 + BEC17	.762 (.018)	Age	0.44	n.s.
		FI17	55.34	***
		BEC17	2.79	n.s.

Notes: LR = likelihood ratio; NHANES = National Health and Nutrition Examination Survey. The concordance estimates the accuracy of each model. The 2logLR and significance are to assess the significance of the indicated term.

** .001 < p ≤ .01. ***p ≤ .001; n.s. = p > .05.

We applied the same selection methods to the 2006 wave of HRS data and selected 18 health items (Supplementary Table 3). As in LHAS and NHANES, age adjustment substantially reduced z scores of most of the variables in mortality prediction (Supplementary Figure 7). The adjusted likelihood ratio test value of FI18 was higher than that of BE18 or BEC18, and the model containing FI18 showed the highest concordance (Table 3). Also, at age older than 83 years (173 deceased of 223 total), age became not significant while FI18 remained significant (Supplementary Figure 8).

Table 3.

Model Concordance and Likelihood Ratio (Rao–Scott) Test Statistics of Biological Age Measures in Survey-Weighted Cox Regression Analysis of HRS Data

Survey-Weighted Cox Model	Concordance (SE)	Term Tested	2logLR	Significance
Base (sex + age)	.759 (.012)	Age	678.23	***
Base + BE18	.812 (.01)	Age	327.22	***
		BE18	423.07	***
Base + BEC18	.812 (.01)	Age	177.94	***
		BEC18	423.07	***
Base + FI18	.816 (.009)	Age	409.37	***
		FI18	489.39	***

Notes: HRS = Health and Retirement Study; LR = likelihood ratio. The concordance estimates the accuracy of each model. The 2logLR and significance are to assess the significance of the indicated term.

***p ≤ .001.

DmI Calculated From DNA Methylation Measurements in LHAS

We applied the feature selection methods to genomic DNA methylation measurements and selected 38 CpG sites whose DNA methylation levels were highly predictive of mortality. Cox regressions of the 38 DNA measurements with and without age adjustment showed that z scores of many DNA methylation measurements were noticeably inflated after age adjustment (Supplementary Figure 9). This is contrary to the reduction observed with general health items. DmI was calculated by averaging coded beta values over the 38 selected CpG sites. Like many of the individual CpG sites, DmI and age strengthened the prediction effect of each other when present together in a model (Supplementary Figure 10). DmI was significantly correlated with FI28 (p < .001) and FI34 (p < .001) but not with age (p >> .1). Despite the lack of significant correlation with age, DmI was the most significant predictor of mortality, surpassing the frailty indexes and KD’s measures (Table 4).

Table 4.

Model Comparison Using Concordance and Likelihood Ratio Test Statistics in Cox Regression Analysis of LHAS

Model 1	Model 2	Concordance (SE)	ΔLog-Likelihood	Significance
Sex	Model 1 + age	.756 (.022)	53.26	***
Sex	Model 1 + DmI	.709 (.023)	25.40	***
Sex + age	Model 1 + DmI	.860 (.015)	69.19	***
Sex + age	Model 1 + FI34	.783 (.021)	5.68	***
Sex + age	Model 1 + BEC34	.775 (.021)	3.29	*
Sex + age	Model 1 + FI28	.796 (.021)	15.96	***
Sex + age	Model 1 + BEC28	.782 (.022)	11.40	***

Notes: LHAS = Louisiana Healthy Aging Study. The concordance estimates the accuracy of Model 2. The Δlog-likelihood and significance are to assess the significance of the added predictor (Model 1 + an added predictor = Model 2) in each pair of nested models.

* .01 < p ≤ .05. ***p ≤ .001.

Discussion

The Frailty/Deficit Index

Chronological age has been the major tool in describing or predicting many time-dependent phenomena, including aging and aging-related diseases. This is mainly because chronological age is intuitive and readily available. Consciously or unconsciously, however, people recognize differences in aging, independent of chronological age. This recognition comes from the heterogeneity and plasticity of biological aging. The heterogeneity of aging is easy to appreciate; for example, “One man may be 60 years old, another man may be 60 years young,” as Benjamin Harris (7) states in his paper published in the second issue of the original Journal of Gerontology. Chronological age cannot account for all the heterogeneity. The plasticity of aging is revealed by the observations from model organisms that aging can be delayed or even reversed. Invariant, chronological age cannot accommodate the plasticity of aging at all. Thus, the heterogeneity and plasticity fits well into the idea of healthy aging, in contrast to the traditional idea of longevity. In daily life, we use chronological age as a quick and convenient way of measuring progression of aging and aging-associated diseases. In science, however, we endeavor to attain the highest accuracy in describing or predicting scientific phenomena. In pursuing the biology of aging, we must use an accurate measure of biological age that can account for not only the heterogeneity and plasticity but also other aging-related biological events.

To estimate the variable pace of biological or functional aging that occurs independently of the invariant pace of chronological aging, researchers began to develop various biological age measures. Rockwood et al. (14) and Fried et al. (26) quantitated the concept of frailty by counting small numbers of functional losses or deficits without including chronological age itself. It is Mitnitski et al. (12) who developed a fully quantitative frailty index as a biological age metric by averaging proportions of defective health items among 92 health variables. The health items are usually from diverse body domains, and the resulting composite index is considered to reflect functional changes occurring at various biological levels. Based on this principle, without employing any selection strategies, we collected 34 health items from LHAS data and calculated FI34, which has been instrumental as a biological age measure in studying various aspects of healthy aging (3,27).

A significant predictor of mortality, FI34 is associated with changes in various physiological processes, such as resting metabolic rate, body composition, tissue damage, and gut dysbiosis (28,29). FI34 is heritable and associated with mitochondrial uncoupling protein genes UCP2 and UCP3, programmed cell death genes LASS1 and XRCC6, and a noncoding regulatory region at 12q13-14 (18,30–32).

To see whether we can enhance the performance of the frailty index in mortality prediction, we used feature selection algorithms for survival/mortality analysis to gather 28 health items from the LHAS data for construction of FI28. Thus, FI28 is different from FI34 in that FI28 is from a set of health items that were selected for their ability to predict mortality, whereas FI34 is derived from health items chosen without such a selection strategy. Only 3 items are common in both FI34 and FI28 (cataracts, heart attack, and Mini-Mental State Examination). However, FI34 and FI28 are directly comparable because the health items were from the same study and frailty indexes calculated from statistically valid numbers of health items (≥ ~20) are known to yield comparable results (33). Therefore, differences in these 2 frailty indexes can be attributed largely to the selection of desired health items in FI28. We also calculated KD’s BE and BEC estimates of biological aging using the same sets of health items. By comparing Cox regression models containing the biological age measures and calendar age, we found (i) FI28 performed better than FI34 as a mortality predictor, (ii) FI28 was the best predictor, outperforming chronological age, BE, and BEC, especially among the oldest subjects who are highly prone to risks of biological aging, and (iii) BE and BEC outperformed chronological age.

Our results with FI34 agree with the previous results obtained by Mitnitski et al (4) using FI-CSHA, which, like FI34, is a standard frailty index calculated using 38 health variables from the Canadian Study of Health and Aging. In their study, BEC was the best predictor of mortality, followed by chronological age, BE, and FI-CSHA. Levine (9) also observed the outperformance of BEC over BE or other linear regression or principle component-derived biological age measures using NHANES III data. Thus, in our study, the observation that FI28 surpassed BEC in mortality prediction clearly demonstrates that the performance of the frailty index can be dramatically improved by selecting constituent health variables.

It should be noted that no health items are commonly present in all 3 selected sets that were used to calculated FI28, FI18, and FI17. Fried et al. (26) regarded frailty as a clinical syndrome and categorized subjects into 3 levels (normal, prefrail, and frail) based on 5 fixed descriptive items, which could be useful in clinical settings. On the other hand, the frailty index by Mitnitski et al. (12) is the proportion of deficits present in aging individuals. The number of health items used to calculate the frailty index typically varies from ~20 to ~100. Thus, unlike the Fried et al.’s (26) frailty or any similar qualitative or semi-quantitative index, the frailty/deficit index is based on the probability concept and it has been shown that different frailty indexes calculated from different sets of health items show similar properties if health items are diverse. Besides the theoretical reason, there is a practical reason why fixing a set of specific health items for the frailty index calculation is not recommended: It is difficult to find the same health items among different studies and data sets. Even if there had been many health items commonly present in all 3 data sets, the likelihood that the same health items would be selected and included in the final sets would be low partly because of the population and ethnicity-specific effect of a health variable and partly because of its varying interactions with other health variables present in statistical modeling. Detection of underlying common physiological processes may require systematic in-depth analyses of large-scale, longitudinal data sets (34,35).

Other types of biological age metrics have been proposed, but most of them rely on chronological age as a surrogate biological age measure, and thus these types of biological age measures are highly correlated with chronological age (8). Indeed, “a perfect correlation between a biomarker and chronological age yields the biomarker as perfectly useless as an alternative to chronological age as a predictor of anything” (36). Likewise, any biological age metrics that are made to perfectly correlate with chronological age or made to predict chronological age with high accuracy will be useless.

Recently, several aging metrics have been reported that are less dependent on chronological age. For example, Levine et al. (37) selected 9 biomarkers by applying a penalized Cox regression method to NHANES III data. By incorporating the 9 biomarkers and chronological age into a parametric model based on the cumulative distribution function of the Gompertz model, they estimated 10-year mortality risks of individuals. At the final step, the mortality scores were converted to “PhenotypicAge” using another cumulative distribution function based on a univariate Gompertz regression model involving only age. Thus, calculation of the phenotypic age involves several assumptions and parametric models. It should be noted that the phenotypic age is highly correlated with chronological age (r = .94 using NHANES IV). On the other hand, calculation of the frailty index is straightforward, without using any assumptions or models or derivation of parameters using chronological age.

DNA Methylation Index

We selected 38 CpG sites that were commonly present among the top performing CpG sites identified by the statistical algorithms. Interestingly, neither the 38 DNA methylation levels nor the DmI calculated from them was correlated with age (p >> .1). However, DmI was significantly correlated with FI28 and with FI34. Surprisingly, the effect size of DmI in mortality prediction was greater than that of FI28 (Table 4), suggesting that accurate biological age metrics do not have to be highly correlated with chronological age.

Aging genomes tend to lose DNA methylation, with the exception of some regions where CpG sites gain DNA methylation (38–40). For example, CpG islands gain DNA methylation in many tissues, including blood (41). Thus, DNA methylation levels at many genomic CpG sites correlate with chronological age either negatively or positively (42,43). A cross-sectional compilation found up to 56 579 CpG sites significantly associated with age, and about 30% of them significantly change longitudinally (44).

Theoretically, a single CpG site whose DNA methylation level perfectly correlates with chronological age could be used as an accurate age predictor. However, DNA methylation is tissue, environment, and population specific; therefore, prediction models usually employ multiple CpG sites to increase model predictability in multiple tissues and cohorts. Thus, subsets of age-related CpG sites, up to several hundred in number, have been used as epigenetic predictors of chronological age or in epigenetic models of aging (23,24). Using multivariate linear regression modeling, Weidner et al. (25) found that only 3 age-related CpG sites were sufficient to predict chronological age reasonably well in blood samples.

Efforts have been made to find CpG sites that are associated with functional phenotypes of biological aging, independently of chronological age. These phenotypes include blood pressure, lung function, hand grip strength, blood metabolic markers, cognitive functioning, and mortality (23,44–47). Svane et al. (47) identified 2806 CpG sites associated with all-cause mortality after adjustment for age and other relevant covariates. Thus, although an order of magnitude smaller in number compared with the age-associated CpG sites, there are CpG sites whose DNA methylation levels are associated with functional declines. Furthermore, certain CpG sites are associated with cognitive functioning and survival but not with age, indicating that age-related changes alone may not be sufficient to explain the biology of aging (48). Recently Levine et al. (37) came up with DNAm PhenoAge, which is based on 513 CpG sites associated with the Gompertz model-based phenotypic age described above. In contrast, our DmI is based on only 38 CpG sites, without employing any complicated models.

There are several considerations related to DmI that need to be addressed. First, its performance relative to other DNA methylation age metrics, such as DNAm PhenoAge, is unknown. Second, it is yet to be determined what underlies the increase in effect size of DmI in the presence of calendar age, which is applicable to any of the DNA methylation-based measures. This could be a type of statistical enhancement in which a variable increases the relationship of another variable with the dependent variable when both independent variables are present together in a regression model. We suspect complex statistical interactions of the variables involving one or more hidden variables. Third, we are uncertain about the replicability of the properties of DmI calculated from the 38 CpG sites. Svane et al. (47) built a good mortality prediction model using 14 CpG sites but it did not perform well in independent samples. Therefore, it is not surprising that none of our 38 CpG sites overlap with the 14 CpG sites or any of the top 24 CpG sites that were most significantly associated with mortality among the CpG sites compiled by Svane et al. (47). All these results highlight the varying nature of epigenetic measurements across different human populations. Fourth, it is unclear what biological properties, if any, the 38 CpG sites bear. Gene ontology analysis of genes linked to the 38 CpG sites found none significant (the number is too small for gene enrichment analysis). It is possible that these CpG sites constitute the mortality nodes in the network model of the frailty index (49). In contrast to the frailty nodes in this model, we suggest that mortality nodes may have a probability of damage that may increase with chronological age. Such a scenario would explain the enhancement of the effect size of Dml with calendar age.

In sum, using 3 independent population data sets, we showed that the frailty/deficit index constructed from selected health items performs best, especially among the oldest old groups where mortality caused by biological aging is most prevalent. We also showed that a frailty index based on DNA methylation, which was generated by applying the frailty index calculation method, can predict mortality even better than the best performing frailty index.

Funding

This work was supported by grants from the National Institutes of Health (AG022064, AG027905, and GM103629), the Louisiana Board of Regents through the Millennium Trust Health Excellence Fund (HEF[2001–2006]-02), and the Louisiana Board of Regents RC/EEP Fund through the Tulane–LSU CTRC at LSU Interim University Hospital.

Conflict of Interest

None declared.