Abstract

This article reports the syntheses, characterization, structural description, together with magnetic and spectroscopic properties of two isostructural molecular magnets based on the chiral ligand N,N′-bis((1,2-diphenyl-(pyridine-2-yl)methylene)-(R,R/S,S)-ethane-1,2-diamine), L1, of general formula [Ln2(RR-L1)2(Cl6)]·MeOH·1.5H2O, (Ln = Ce (1) or Nd (2)). Multifrequency electron paramagnetic resonance (EPR), cantilever torque magnetometry (CTM) measurements, and ab initio calculations allowed us to determine single-ion magnetic anisotropy and intramolecular magnetic interactions in both compounds, evidencing a more important role of the anisotropic exchange for the NdIII derivative. The comparison of experimental and theoretical data indicates that, in the case of largely rhombic lanthanide ions, ab initio calculations can fail in determining the orientation of the weakest components, while being reliable in determining their principal values. However, they remain of paramount importance to set the analysis of EPR and CTM on sound basis, thus obtaining a very precise picture of the magnetic interactions in these systems. Finally, the electronic structure of the two complexes, as obtained by this approach, is consistent with the absence of zero-field slow relaxation observed in ac susceptibility.
Short abstract
Multifrequency electron paramagnetic resonance (EPR), cantilever torque magnetometry (CTM) measurements, and ab initio calculations lead to determination of both the single-ion magnetic anisotropy and the intramolecular magnetic interactions in two new chloro-bridged NdIII and CeIII dimers. The combination of these techniques appears to be fundamental for determining the weak intramolecular exchange interactions characterizing lanthanide-based polynuclear complexes, which play a subtle but relevant role in determining the magnetic properties of these systems.
Introduction
The discovery by Ishikawa and co-workers1 of slow magnetic relaxation in terbium-phthalocyaninate provoked a growing interest in the use of lanthanide complexes as single molecule magnets (SMMs)2−6 and, more recently, for quantum information processing (QIP).7−10 The interesting magnetic behavior of these complexes benefits from their large unquenched orbital angular moments, resulting from strong spin–orbit coupling and weak ligand fields, which impart strong magnetic anisotropy.
Looking forward to these ambitious applications, it is important to understand all the possible variables that can play a relevant role in determining the dynamic magnetic properties of these molecular systems. In this framework, the intramolecular exchange interaction between lanthanide (Ln) ions is a still scarcely investigated parameter,11−16 because of the complexity of its determination.17 The exchange interaction strongly influences the magnetization relaxation pathways of SMMs, e.g., by reducing the effect of quantum tunneling of magnetization (QTM) at zero-field. This effect is analogous to exchange bias in permanent magnets, thus allowing zero-field magnetic remanence.18 On the other hand, the observed relaxation under an applied field is often faster in weakly exchange-coupled systems than in mononuclear ones, as a consequence of state mixing induced by the interaction.19 The use of this exchange-bias approach to reduce the effectiveness of tunneling is applicable for weak 4f–4f interactions. In contrast, stronger interactions yield a coupled system behaving as a single giant spin.20,21 This requires the presence of additional 2p or 3d paramagnetic centers,22,23 resulting in a slowdown of the relaxation. Indeed, a multistep Orbach process is favored, while competitive processes such as Raman and direct ones become less efficient.20,24 An intramolecular exchange interaction between two Ln ions can also be a way to achieve entanglement between two spins, which is required for the realization of two-quantum-bit gates.25,26 This approach presents the advantage of being spatially precise as the distance between the two spins is imposed by the molecular structure. However, this interaction must be finely tuned, with respect to the anisotropic features of the constitutive ions, and this, in turn, requires a deep understanding of the factors affecting it. Obviously, the surroundings of the qubits must also be chosen with care, since the presence of any other spin provides a pathway that accelerates the relaxation, limiting their usefulness.
All aforementioned applications require a quantitative interpretation of the magnetic data, in terms of exchange interaction for LnIII-based complexes. However, this is not straightforward, since ligand field strength is usually one order of magnitude larger than exchange coupling, and a large deviation from Curie-type behavior is observed, even in the absence of exchange interactions. Furthermore, the isotropic exchange Hamiltonian, which provides a simple conceptual framework to analyze the data in case of orbitally nondegenerate systems, cannot be applied to these systems. Indeed, the orbital degeneracy requires the effective exchange Hamiltonian to be expressed in terms of both spin and orbital operators.27,28 Finally, one must consider that magnetic dipolar interactions are of comparable magnitude to superexchange ones, because of the large magnetic moment of LnIII ions. Thus, the exchange interaction in polynuclear LnIII systems cannot be obtained by simple powder magnetic measurements but requires a multitechnique approach that involves magnetic and spectroscopic measurements backed up by ab initio calculations, and possibly the use of single-crystal measurements.12,13,15
In this work, we investigate and compare the magnetic properties of two isostructural chiral bimetallic molecular magnets with general formula [Ln2(RR-L1)2(Cl6)]·MeOH·1.5H2O, where the [LnIII2] core is based on Ln = Ce (1) or Nd (2), and L1 = N,N′-bis((1,2-diphenyl-(pyridine-2-yl)methylene)-(R,R/S,S)-ethane-1,2-diamine).
The choice of bis-bidentate Schiff bases ligands originates from the ease of the synthetic procedure, which occurs by condensation of a diamine with two aldehydes or ketones, and from their high versatility. The use of substituted diamines with chiral centers as the starting reagent is a simple and elegant synthetic route for obtaining chiral ligands that can be useful for enantioselective catalysis29,30 or for introducing chiroptical or magnetochiral properties in new complexes.31−35 On the other hand, the focus on complexes of two early Ln ions stems from the importance of characterizing the exchange interaction for these more-abundant and less-expensive rare-earth ions. Indeed, exchange and anisotropy effects in these elements are at the heart of the remarkable magnetic features of classical hard magnets,36 and they offer a great case study for our aim.
To provide a clear picture of the magnetic anisotropy of these systems and to quantify the magnetic exchange interactions, we use a multitechnique investigation including dc magnetometry, continuous wave electron paramagnetic resonance (cw-EPR), and cantilever torque magnetometry (CTM) experiments, flanked by complete active space self consistent field (CASSCF) calculations. This study allows us to discuss, in depth, a methodology to determine the intramolecular interaction and anisotropy with precision. Our results provide a good understanding of complexes of interacting early Ln ions, which is a step forward for improved control and design of such systems.
Results
Synthesis
Complexes 1 and 2 were synthesized by direct reaction of the Schiff base with the corresponding lanthanide trichloride in methanolic solution, according to Scheme 1.
Scheme 1.
The size of the cation determines that dimeric complexes with double chloro bridge and octacoordinated LnN4Cl4 environment can be obtained for the larger lanthanides (from CeIII to SmIII), whereas monomeric complexes with formula [Ln(L1)Cl3] and LnN4Cl3 heptacoordination were previously reported for the smaller ones (from EuIII to YbIII).37 We also tried to obtain the isostructural diamagnetic LaIII derivative, following the same procedure but all our attempts were unsuccessful. Electronic circular dichroism spectra of the representative pair of dimeric complexes 2RR, and 2SS show absorptions with positive Cotton effect at λmax = 270 and 221 nm and negative Cotton effect at 300 and 210 nm for 2RR and a mirror image for 2SS, confirming its enantiomeric identity (see Figure S1 in the Supporting Information).
Structural Description
Monocrystal X-ray diffraction (XRD) experiments were performed for complexes 1RR, 2RR, and 2SS. These complexes are isostructural (see Table S1 in the Supporting Information), and a common description is provided in order to avoid repetitions.
[Ln2(L1)2(Cl6)] (Ln = Ce, (RR-L1), 1RR·1.5H2O; Ln = Nd, (RR-L1), 2RR·0.5MeOH·0.75H2O; Ln = Nd, SS–(L1), 2SS·2.5H2O)
A view of the molecular structure is shown in Figure 1 (top), while the main structural parameters are summarized in Table S2 in the Supporting Information.
Figure 1.

Top: Molecular structure of complexes 1 (Ln = Ce) and 2 (Ln = Nd), with the principal atoms labeled. Small gray balls represent C atoms; H atoms have been omitted for the sake of clarity. Bottom: intermolecular hydrogen bonds that determine the arrangement of the dimers and a view of the layers of solvent and dimers in the network.
The structure consists of a neutral LnIII complex in which the two cations are linked by two μ-Cl bridges. Each cation is octacoordinated by the four N atoms of one L1 ligand, two terminal chloro ligands, and the two bridging chloro donors. The pyridyl groups of L1 ligand are slightly bent, with respect to the main plane, with the cations placed ∼0.63 Å out of the plane determined by the four N-donors and toward the other cation. The neighbor N-donors of L1, linked by one ethylene spacer, determine a narrow bite with N–Ln–N bond angles close to 63°, allowing one of the chloro ligands to be placed in the same plane of the coordination polyhedron. The two μ-Cl bridges and the other terminal chloro ligands are placed in the axial positions above and below the NdN4Cl plane. The shorter bond distances correspond to the Nd–N bonds, average ∼2.6 Å, whereas the longer ones are those related to the Ln–(μ)–Cl bonds: these average to 2.85 Å but for each metal center there is clearly a long (2.90 Å) and a short (2.80 Å) Ln–Cl bond. The Ln1–Cl–Ln2 bond angles take a value at ∼109.7°, thus yielding a Ln1–Ln2 intramolecular distance of 4.65 Å. SHAPE38 analysis provides evidence that the coordination polyhedra around the two lanthanoid ions are largely distorted, with only a slight preference for bicapped trigonal prisms (BTPR-8, Ln1) and triangular dodecahedra (TDD-8, Ln2), respectively (see Table S3 in the Supporting Information).
According to a survey in the CSD, the LnN4Cl4 (Ln = CeIII, NdIII) coordination environment has been previously reported only for a couple of nonpolymeric structures:39,40 interestingly, both are dimeric, double chloro-bridged structures. For the noncentrosymmetric structures reported in ref (39) the coordination polyhedra are distorted with slight preference for BTPR-8 and TDD-8, while a square antiprism is clearly favored for the centrosymmetric Nd dimer reported in ref (40). In both cases, bond lengths and angles are consistent with those reported in this study.
A complex set of intramolecular and intermolecular weak CH···Cl and CH···OH interactions relating the dimers and the solvent molecules is observed. Among them, the intramolecular CH···Cl interactions involving H atoms from the pyridinic groups and the bridging chlorides and in-plane terminal chloro ligands are of particular relevance. Indeed, they determine the parallel arrangement of dimers in the network, with layers of dimers separated by layers of crystallization solvents (see bottom of Figure 1).
The powder diffraction spectra of 1 and 2 were performed to check their purity and phase consistence prior to magnetic characterization. The spectra corroborated the isostructurality of the complexes but were surprisingly different from the spectrum expected by the single-crystal data (see Figure S2). To verify if such a difference could be attributed to a loss of solvent, the crystals of the analogous SmIII (3) complex, obtained following the same procedure, were maintained at open air for 24 h and single-crystal data were collected after this time.
After 24 h of open-air exposure, the crystals do not visually evidence apparent changes; however, the quality of their diffraction pattern is reduced, thus lowering the quality of the solved molecular structure. Nonetheless, we report it here since it is necessary to interpret the powder diffraction pattern (vide infra) and its main features (unit cell parameters, connectivity, major packing features) can be safely determined. The arrangement of the dimers in 2D planes and bond parameters of the first coordination sphere of the lanthanides are identical in the general trends to the above-described structure for 1 and 2 (Tables S1 and S2). However, the layers of methanol and water molecules of crystallization in the ab plane of the nonaged crystals are completely lost (Figure S3 in the Supporting Information): we thus label this complex as 3b. While its a- and b-cell parameters are practically identical (9.707(1) and 11.853(1) Å) to those of 1 and 2, the c-parameter of the cell becomes 12.593(1) Å (that is ∼2.6 Å shorter than in the structures containing the layer of solvents). The powder X-ray spectrum (PXRD) simulated from the monocrystal structure of the desolvated form matches perfectly with those obtained from the powdered samples of 1 and 2, indicating that those are desolvated species (see Figure S2).
DC Magnetic Characterization
A preliminary investigation of the magnetic properties of 1 and 2 was performed on microcrystalline powder samples. The temperature dependence of the magnetic susceptibility in the 2–300 K range for the two complexes is shown in Figure S4 in the Supporting Information, as χMT vs T plots. For both molecules, χMT at room temperature is close to the free ion value for two corresponding magnetically independent lanthanide cations (2F5/2 for CeIII and 4I9/2 for NdIII). When the temperature is lowered, the χMT product reduces for both compounds, reaching a final value of 0.55 cm3 mol–1 K for 1 and 1.52 cm3 mol–1 K for 2. This decrease can be attributed to the thermal depopulation of the energy levels of the ground multiplet split by Crystal Field effects. At the lowest temperature, intramolecular interactions, which are expected to be rather weak in these systems, might also contribute.
The magnetic-field-dependent magnetization was measured in the range of 0–5 T and at three different temperatures (see Figure S5 in the Supporting Information). Magnetization does not saturate, and the reduced magnetization shows quasi-superimposable plots: this indicates an almost-complete population of the ground doublet.
Electron Paramagnetic Resonance
EPR is a useful tool for investigating the magnetic anisotropy and exchange interactions of lanthanides with an odd number of unpaired electrons, such as CeIII and NdIII.13,41,42 For this reason, powder samples of complexes 1 and 2 were investigated at helium temperature, using cw-EPR at two frequencies (∼9 GHz for the X-band and ∼94 GHz for the W-band).
Figure 2 shows the experimental powder EPR spectra of complex 1 at 5 K in the X-band. The spectrum presents a first absorption band at ∼200 mT and a second broader one at ∼950 mT. The shape of the spectrum is as expected for a single, well-isolated anisotropic doublet, where the second line is the component of a rhombic doublet rather than the perpendicular one in an axial system. On the other hand, there are no evidence of intramolecular exchange or dipolar interactions, nor any indication about difference in magnetic behavior between the two structurally inequivalent lanthanide centers.
Figure 2.

Experimental (red) and simulated (black) X-band EPR spectrum of a polycrystalline powder sample of compound 1 measured at 5 K. Dashed line represents the simulated spectrum by assuming noncollinear single-ion anisotropy and calculated dipolar interactions.
A simulation of the EPR spectrum of 1 could then be obtained by assuming an effective Spin Hamiltonian,
| 1 |
where μB is
the Bohr magneton, 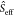 the effective spin angular
moment,
the effective spin angular
moment, 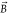 the dc magnetic field,
and geff the effective Landé g tensor
of the ground doublet. A good agreement with the experimental data
is found assuming as principal values of geff, gx < 0.5, gy = 0.72, and gz= 2.98. Note that gx is not observed as it occurs
at magnetic fields outside our accessible field range.
the dc magnetic field,
and geff the effective Landé g tensor
of the ground doublet. A good agreement with the experimental data
is found assuming as principal values of geff, gx < 0.5, gy = 0.72, and gz= 2.98. Note that gx is not observed as it occurs
at magnetic fields outside our accessible field range.
For the NdIII derivative, complex 2, the powder X-band EPR spectrum at 5 K is depicted in the top portion of Figure 3. The observed number of spectral lines is clearly not compatible with a single effective ground doublet with geff anisotropy. The extra bands in the spectrum can be, in principle, due to the presence of low-lying excited states (which can allow intradoublet transitions), to intramolecular magnetic interactions (either dipolar or exchange in nature), or to appreciable differences in the magnetic features of the two magnetic centers. The three hypotheses can be verified by measuring the spectrum at a different frequency, since each of them would result in a completely different pattern. Indeed, if the splitting between lines is due to intramolecular interactions, it should be frequency-independent. On the other hand, if the separation is due to intermultiplet transitions within each center or to different magnetic anisotropy of the two structurally inequivalent lanthanides, it should vary on varying frequency.
Figure 3.

Experimental (red lines) and simulated (black lines) powder EPR spectra of 2, measured at the X-band and 5 K (top) and at the W-band and 14 K (bottom). Simulations are performed using the Hamiltonian of eq 2 and assuming a collinear single-ion anisotropy. The asterisk marks an unavoidable cavity impurity in the W-band spectrometer.
W-band EPR spectrum (ν ∼ 94 GHz) on a powder sample was then performed at 14 K (Figure 3, bottom). The splitting of the two lowest field lines is the same observed at low frequency. This suggests a non-negligible intramolecular interaction between the anisotropic doublets. Following this interpretation, we simulated the spectra at the two frequencies, on the basis of the following spin Hamiltonian:
| 2 |
where we assumed the two NdIII centers as equivalent, with an effective spin S = 1/2, and D is a traceless interaction tensor collinear to geff. In this approach, each pair of lines is centered at gi (i = x, y, z) with a separation of Dii/giμB. The best simulation was obtained with principal geff values of gz = 4.16 gy = 1.52 gx = 1.08 and a traceless anisotropic interaction between NdIII ions with principal values D = [0.08 0.08 −0.16] cm–1. It is worth stressing that, due to the assumption of collinearity between the two centers, the inclusion of an isotropic exchange coupling in eq 2 does not change the spectral appearance, but only the intensity of the simulated spectrum, as a function of temperature. Because of the low magnitude of the isotropic coupling, these effects are however not large enough to allow its determination.
The traceless nature of the D tensor would suggest a dipolar nature of the interaction in 2. However, its principal values are ca. 50% larger than those calculated on the basis of point dipole approximation and structural parameters, even in the assumption of the maximum geff component being oriented along the Nd1–Nd2 direction, which is not demonstrated at this stage. This suggests that further contributions, mainly due to anisotropic exchange, are not negligible. To clarify this point it is necessary to know the orientation of the geff tensor with respect to the molecular frame, which is a problem that we tackled using CTM and ab initio calculations.
Cantilever Torque Magnetometry
CTM allows one to determine the magnetic anisotropy of coordination compounds and its correlation with the molecular structure. It is especially useful when applied to low-symmetry lanthanide complexes, because of the not-easily predictable nature and orientation of their magnetic anisotropy.43−45
With this aim, single crystals of the two compounds were indexed by XRD and placed on the cantilever. To reconstruct the principal magnetic tensors, rotations around two orthogonal axes were performed under a static magnetic field with a fixed orientation (Rot1 and Rot2; see Figure 4) perpendicular to the rotation axis. The initial position of the crystal, with respect to the laboratory frame in each of the two rotations, is described in Figure S6 in the Supporting Information. During the experiment, the crystal is rotated and each time the magnetic field is parallel to the projection of one principal magnetic axis on the scanned plane, then the measured torque component is null: τY = MzBx – MxBz = 0. For the first rotation, Rot1, this occurs at θ = 27° and 117° for compound 1 and for compound 2 at θ = 60° and 150°; in both cases, the expected 90° periodicity is fulfilled (see Figure 4). The complete set of experimental data and the corresponding fits are reported in Figures S7 and S8 in the Supporting Information.
Figure 4.

Experimental and best fit CTM data for 1 (upper) and 2 (lower) at 2 K and 1 T using the principal geff values from EPR and leaving the orientation of the anisotropy axis free to refine. The best-fit orientations are shown in Figure 5.
For the second rotation measurement set, Rot2, the crystals were first manually rotated by 90° on the sample holder with respect to Rot1 configuration and the experiment was repeated: for 1, the zeros of the torque occur at θ = 54° and 144°, and they are at θ = 10° and 100° for 2 (Figure 4). For both complexes, low-temperature CTM data could be reproduced by using eq 1. This implies the assumption that the ground anisotropic effective doublet is selectively populated, and the two structurally distinct paramagnetic centers have the same geff tensor, as for EPR interpretation. Furthermore, we did not include the intramolecular interaction term determined by EPR for 2, since its magnitude is too weak to be effective in determining CTM results.
In the fitting procedure, the effective g values were kept fixed to those determined by EPR (with the exception of gz for 1, for which an upper bound of 0.5 was set), while the Euler angles (zyz convention) describing the orientation of geff, with respect to the crystal frame, were left free to refine and provided best-fit results (α, β, γ) = (94.0°, 39.2°, 7.4°) and (α, β, γ) = (202.6°, 84.5°, 208.9°) for 1 and 2, respectively. An overall scale factor was refined to account for the incertitude on the masses of the two crystals, which were too small to be determined accurately. The resulting director cosines of the easy axis, with respect to the ab′c* orthogonalized coordinate crystal system, are reported in Table S4 in the Supporting Information, while the orientation of the geff tensors of the ground doublets, with respect to the complexes, are graphically sketched in Figure 5.
Figure 5.

Orientation of effective principal directions of geff tensors of the ground doublet, with respect to the molecular frame, as determined by fit of CTM data assuming collinear centers and principal g-values as determined by EPR for 1 (upper) and 2 (lower). Green, orange, and red rods refer to the principal components of geff in decreasing order of magnitude; green balls represent Cl atoms, and cyan balls represent N atoms.
In both cases, no clear correlation between the principal directions of geff and the structural features of the complexes emerges from the analysis of the experimental data. For 1, the only appreciable feature is the orthogonality of the intermediate component to one Ce–Cl direction, while the major component is only very approximately oriented along the bisector of Cl–Ce–Cl. For 2, the only evident structural correlation is the major component of the ground doublet lying in the Nd2Cl2 plane, almost orthogonal to the two long Nd–Cl bonds in this plane (95° angle).
It is interesting to note that, for 1, the fit is of very good quality up to high temperature (see Figure S7 in the Supporting Information), thus suggesting that the ground doublet is well-isolated from the excited ones. However, since the use of the only ground state to reproduce CTM data might be an oversimplification, we turned to ab initio calculations to obtain a complete picture of the anisotropic features of these systems.
Ab Initio Results
Multiconfigurational CASSCF calculations are the most accurate ab initio methods to rationalize the magnetic properties of lanthanide complexes.46,47 The widespread use of this type of calculations in this field is due to their ability to provide information that is otherwise inaccessible by most spectroscopic techniques, such as excited states’ energies and magnetic anisotropy tensors. However, they are far from being perfect and use of the results obtained by this method requires a preliminary benchmarking against a set of accurately determined properties.17 This approach is gaining increasing momentum in the literature: the calculated properties include low-temperature luminescence,48,49 EPR spectroscopy,13,50,51 single-crystal magnetometry,15,52−54 inelastic neutron scattering,55,56 and advanced spectroscopic techniques.57−59 With this aim, ab initio calculations were performed on 1 and 2, and the results are compared with EPR and CTM data. This provides a sound basis for the following discussion on the magnetic properties of these systems.
For both complexes, CASSCF calculations predict similar but distinguishable properties for the two structurally distinct LnIII centers. The energy difference between the ground and first excited doublet is above 300 cm–1 for both CeIII centers in 1, while for 2, it lies at ∼40 cm–1 and all the 4I9/2 excited doublets are within 300 cm–1. In agreement with the interpretation of EPR data and with the highly distorted coordination symmetry, the calculated compositions of the ground doublets for all the paramagnetic centers are highly mixed. Indeed, all |mJ⟩ components contribute by more than 5% (see Tables S5–S12 in the Supporting Information). With this electronic structure, the field-dependent magnetization curves at low temperature are correctly reproduced (see Figure S5 in the Supporting Information). As for the temperature dependence of the susceptibility, the agreement with the experimental curve is less satisfactory, suggesting some discrepancies between calculated and real energy and composition of the excited states (see Figure S4 in the Supporting Information).
For complex 1, the computed geff values of the ground doublet are, on average, in very good agreement with those obtained by simulating EPR spectrum; in particular, the highest geff value, arbitrarily chosen as gz, is perfectly reproduced. The agreement with the spectral features of 2 is somehow less satisfactory, with an overestimation of the rhombicity of the ground doublet compared to the experimental EPR results, while the easy axis anisotropy is slightly underestimated. This is at variance with the overestimation of axiality commonly reported for ab initio calculations.50 An important point evidenced by ab initio results is the different orientation of the magnetic anisotropy axes calculated for the two centers. This offset is just 10° for 2, but it reaches values up to 34° for the lowest geff components of 1 (see Table 1). Furthermore, the average orientations of the principal directions of the two centers are also quite different from the one obtained by assuming the two centers to be collinear (see Table S4 in the Supporting Information for director cosines). We checked the accuracy of the theoretical results by comparing the angular, magnetic field, and temperature dependencies of the torque calculated using ab initio results with the experimental ones. As reported in Figure S9 in the Supporting Information, the calculated CTM data for 1 are clearly offset, with respect to the experimental ones. On the other hand, for 2, while the agreement between theoretical and experimental data is quite good for Rot2, the two are almost in phase opposition for Rot1 (see Figure S10 in the Supporting Information).
Table 1. Experimental EPR and Ab Initio Calculated geff Principal Values for the Ground Doublets of the Two LnIII Centers in Cerium and Neodymium Complexes, and Angles between the Calculated Principal Orientations on the Two Sites.
| EPR | Ln1 | Ln2 | angle Ln1–Ln2 | ||
|---|---|---|---|---|---|
| Ce | gx | <0.5 | 0.527 | 0.272 | 34.0400 |
| gy | 0.71 | 0.894 | 0.623 | 32.2988 | |
| gz | 3.0 | 3.065 | 3.066 | 17.9347 | |
| Nd | gx | 1.08 | 0.586 | 0.743 | 10.3943 |
| gy | 1.52 | 1.857 | 2.028 | 10.8398 | |
| gz | 4.16 | 3.970 | 3.925 | 9.8956 |
To obtain a good reproduction of the CTM data, the orientations of the anisotropy axes were then left free to be refined with respect to those calculated ab initio, while keeping the crystal field parameters (or the geff values of the ground doublet) fixed to the calculated values (see Figure 4, as well as Figures S6 and S7 in the Supporting Information). The best fit orientation of the geff tensors, with respect to the ab′c* molecular frames obtained by following this procedure is reported graphically in Figure S11 in the Supporting Information and in tabular form in Table S4 in the Supporting Information.
For both derivatives, the calculated direction of the easy axis is close to that obtained by the best fit of the experimental CTM curve (angles between experimentally determined and theoretical directions ranging between 5° and 15°; see Table S13 and Figure S11 in the Supporting Information), whereas much difference is observed in the hard plane. The overestimation of rhombicity results in the intermediate and hard axes being almost swapped between calculated and experimentally derived values for Nd1 in 2 and differing by ∼50° for Nd2. Furthermore, the best fit parameters of the CTM curves are consistent with the noncollinearity of the geff tensors of the two centers (see Table S4 and Figure S11).
To check whether this discrepancy is due to the neglecting of dynamical correlation effects on the CASSCF wave function we performed N-electron valence state perturbation theory (NEVPT2) calculations60 with ORCA 4.2 software61 (see Tables S14–S21 in the Supporting Information). However, the electronic structure description of the ground Kramers’ doublets in both compounds is not substantially modified. We can conclude that the CASSCF level of theory appears adequate and reliable for the reproduction of ground-state properties and low-temperature magnetic measurements. The discrepancies among experiment and theory should be attributed to other factors, principally the correct reproduction of the Madelung potential inside the crystal cell62 or the refinement of the structure by geometry optimizations.
AC Susceptibility
Of the many lanthanide complexes presenting slow relaxation of the magnetization,63−65 the vast majority contains ions of the second half of the series. DyIII is, by far, the most diffuse, because of its large magnetic moment and its Kramers’ nature. CeIII and NdIII cations can also present slow relaxation of the magnetization in zero field with a proper design of the crystal field, but only a few of them have been reported.66−69 For the sake of complete characterization, we measured the ac susceptibility of both 1 and 2, to observe how the electronic structure determined above is reflected on their dynamic magnetic properties. As expected on the basis of the large transversal components of the ground doublets of these systems, the two derivatives do not show slow relaxation in zero field, because of extremely efficient QTM. However, a frequency- and temperature-dependent out-of-phase susceptibility appears on application of a dc field, more easily measurable for 2 (see Figures S12 and S13 in the Supporting Information). The temperature dependence of the relaxation times (Figure S14 in the Supporting Information) extracted by using a generalized Debye approach70,71 clearly points to a mix of direct and Raman contributions rather than to an Orbach process for both derivatives.72 This is again consistent with the largely rhombic nature of these systems indicated by EPR and CTM experiments and with the absence of a reliable anisotropy barrier evidenced by ab initio calculations. In this respect, despite 1 and 2 being part of the scarce number of CeIII and NdIII complexes reported until now that present slow relaxation of the magnetization under certain conditions,42,50,66−69,73−75 we cannot consider them as SMM. Indeed, neither a value for an effective anisotropy barrier Ueff nor a blocking temperature can be defined for these complexes.3 It is also interesting to note that for 2, two relaxation processes are active. While this might be, in principle, attributed to the two different single-ion properties, their largely different values rather suggest that the slowest of the two is to be attributed to a collective process. However, given the small number of points and the impossibility of obtaining an isostructural diamagnetic analogue, we refrain here from drawing any further conclusions from these data.
Discussion
The above-reported results point to the absence of evident correlation between the coordination sphere of the lanthanides in the two complexes and the orientation of the magnetic anisotropy axes at low temperature. This is to be attributed to the absence of a pronounced axial charge distribution of the ligand environment around the lanthanide center, which would favor pure easy axis anisotropy for both CeIII and NdIII, oblate ions,76 in agreement with the largely distorted coordination polyhedra.
The comparison of the experimental and theoretical results further indicates that, while ab initio calculations work remarkably well in determining the orientation of the easy magnetization directions of the lanthanide centers, it does not provide results that are as reliable as those for the orientation of the hard directions. The same is true for the accuracy of the reproduction of the principal values, which is highest for the largest geff values but decreases for the hardest directions. However, the most relevant result obtained by ab initio methods is for sure the indication that the geff tensors of the two centers are far from being collinear. In this respect, our previous analysis of the EPR spectrum, based on collinearity assumption, is somehow oversimplified. A refinement of the model would then require performing simulations on the basis of the following Spin Hamiltonian:77
| 3 |
Here, geff,i are the g-tensors expressed in the molecular reference frame, which were fixed at the principal geff values obtained by preliminary EPR interpretation and principal directions obtained by the CTM fits based on ab initio results; Ddip is the dipolar interaction tensor, which can be calculated using a point dipole approximation; J represents the exchange interaction tensor, which, in principle, has no symmetry and can be decomposed into antisymmetric, anisotropic, and isotropic components.78 For 1, the simple inclusion of the noncollinearity of geff tensors on the two sites and of the calculated dipolar tensor, with J constrained to be isotropic with an absolute value smaller than 0.02 cm–1 provides a clear improvement with respect to the original simulation (Figure 2). This set of parameters is indeed able to partially reproduce the series of weak signals which might otherwise have been misassigned as a nonstatistical distribution of the microcrystals.
The situation is more complex for 2, given the large noncollinearity of the two tensors indicated by ab initio calculations and CTM, and the large discrepancy between the two sets of calculated and experimental results (see Figure S10 in the Supporting Information). At any rate, by considering a noncollinearity of the single ion geff, inclusion of the calculated dipolar interaction and of an isotropic exchange coupling is not enough to provide a reasonable simulation of the multifrequency EPR spectra, thus confirming the relevance of the anisotropic component of the interaction. As a whole, this analysis confirms that the intramolecular anisotropic exchange coupling interactions are larger in 2 than in 1, being however small, in terms of absolute values.
To the best of our knowledge, these are the first (di)chloro-bridged CeIII and NdIII dimers structurally characterized for which an in-depth analysis of the magnetic properties has been performed. Previous reports were indeed only of qualitative nature and did not provide any hint as to the intramolecular magnetic interactions in these systems.79,80 More-detailed studies have been reported for dichloro-bridged heavy lanthanide complexes (Dy- and Er-based), given their interest as SMM81−86 and, more recently, for other halogen-bridged complexes.87,88 In those systems, the large easy-axis anisotropy of the single-ion, which is a prerequisite for observing SMM behavior, provides a much stronger dipolar interaction (more than one order of magnitude) than in the present case. At the same time, the exchange contribution, either ferromagnetic or antiferromagnetic, turned out to be weak but crucial in determining specific features of the magnetization dynamics. The situation is evidently much different for 1 and 2. Here, the single-ion rhombic anisotropy hampers SMM behavior and the dipolar interaction is weak and oriented along a direction which requires single-crystal experimental study to be determined.
Conclusions
Here, we have reported an in-depth study of the single-ion anisotropy and intramolecular magnetic interactions for two chloro-bridged dinuclear lanthanide complexes. EPR, CTM, and ab initio calculations, for both systems, point to a clearly rhombic magnetic anisotropy, the orientation of which has no direct relation to structural features. EPR spectroscopy clearly indicates that intramolecular interactions for the cerium dimer, 1, are weak and essentially of a dipolar nature, whereas for the neodymium dimer, 2, anisotropic exchange provides a major contribution. From a methodological point of view, this study demonstrates that, in the case of largely rhombic systems, ab initio calculations are still reliable in determining the principal values of the anisotropy tensors but can fail in determining the orientation of their weakest component. In turn, however, the result obtained by ab initio methods may help to fix some of the unknowns in the analysis of EPR and CTM results. The combination of all these techniques appears of fundamental importance to unravel the determination of the weak intramolecular exchange interactions characterizing lanthanide-based polynuclear complexes, which play a subtle but relevant role in determining the magnetic properties of these systems.
Experimental Section
Synthesis
All the starting materials were purchased from TCI and were used without further purification.
The L1 ligand resulted from the condensation of 2-pyridinecarboxaldehyde (0.053 g, 0.5 mmol) and 1R,2R-1,2-diphenylethylendiamine (0.053 g, 0.25 mmol) in 20 mL of methanol stirred at room temperature for 1 h.
Ligand was used in situ for the preparation of the complexes.
All the complexes were prepared following the same procedure. The previously prepared ligand solution was added to an equimolar quantity of the corresponding lanthanide chloride, LnCl3·xH2O (0.25 mmol, x = 7, 0.093 g for Ce, x = 6, 0.098 g for Nd, x = 6, 0.91 g for Sm), dissolved in 10 mL of methanol. The resulting solution was stirred at room temperature for 1 h. Orange (1) and white (2 and 3) crystals suitable for XRD were obtained from slow diffusion of the solution in diethyl ether, with a yield of ∼30% for all the complexes. These were used for the instrumental measurements. Calculated/found elemental analysis (dried samples) were as follows: for 1: C, 49.03/49.2; N, 8.80/8.8; H, 3.48/3.3%; for 2: C, 48.71/48.6; N, 8.74/8.7; H, 3.46/3.7%; and for 3: C, 48.25/48.4; N, 8.66/8.9; H, 3.43/3.6%.
X-ray Crystallography
Prismatic crystals of 1 and 2 were used for single-crystal X-ray crystallographic analysis. Measurements were performed after exposing 3 for 24 h to ambient conditions, resulting in 3b. The X-ray intensity data were collected on a D8 Venture system equipped with a multilayer monochromator and a Mo microfocus (λ = 0.71073 Å). The frames were integrated with the Bruker SAINT software package, using a narrow-frame algorithm. Data were corrected for absorption effects using the multiscan method (SADABS). The structures were solved and refined using the Bruker SHELXTL software package. Further crystallographic details can be found in the corresponding CIF files provided in the Supporting Information.
Indexation for monocrystal studies was performed in a SCD Oxford Xcalibur3 X-ray diffractometer.
Powder XRD spectra were acquired with a PANalytical X’Pert PRO MPD θ/θ powder diffractometer of 240 mm of radius in a configuration of convergent beam with a focalizing mirror and transmission geometry with flat samples sandwiched between low absorbing films and Cu Κα radiation (λ = 1.5418 Å). Comparison between the calculated spectrum from the single-crystal structures of 3b is an accurate match with the experimental powder diffraction of 1, 2, and 3.
Physical Characterization
All the physical measurements on single crystals were performed on fresh samples corresponding to the solvated structures. Measurements on powders should be considered as being performed on desolvated structure (see the section on Structural description).
EPR Spectroscopy
X-band (∼9 GHz) and W-band (∼94 GHz) EPR spectra were recorded using commercial Bruker E500 and E600 spectrometers. The samples were microcrystalline ground powders, undiluted. For W-band spectra, sample was embedded in wax to avoid torquing effects. Cryogenic temperatures were obtained by using a CF935 continuous flow cryostat for W-band spectrometer and a ESR900 for X-band spectrometer, both from Oxford Instruments. Simulation of the spectra was performed using the Matlab toolbox Easyspin.89
Cantilever torque magnetometry
CTM measurements were performed by using a homemade two-legged CuBe cantilever separated by 0.1 mm from a gold plate. The cantilever was inserted into an Oxford Instruments MAGLAB2000 platform with automated rotation of the cantilever chip in a vertical magnet. The capacitance of the cantilever was detected with an Andeen-Hegerling 2500A Ultra Precision Capacitance Bridge. The faces of the measured crystal were indexed by using XRD in the above-described setup. This procedure resulted in an estimated uncertainty of the actual orientation of the crystal of ∼5°.90 The fit of the data was performed using home-developed codes based either on FORTRAN44 or on MATLAB exploiting EasySpin toolbox.91
Magnetic Measurements
Magnetic measurements were performed using a Quantum Design MPMS SQUID magnetometer and the dynamic measurements were performed in a Quantum Design PPMS in the ac mode on powders pressed in a pellet to avoid field-induced orientations. Diamagnetic corrections were calculated using Pascal’s constants.92
Electronic Circular Dichroism
Electronic circular dichroism spectra were recorded in methanolic solutions on a JASCO Model 815 spectropolarimeter.
Computational Details
All calculations have been performed with the MOLCAS 8.0 quantum chemistry package.93 The geometries resolved by XRD were employed without further geometry optimizations. The calculations for each ion in each dimer were performed by substituting the second lanthanide ion in the molecule with its diamagnetic equivalent, lanthanum. The energy ladder of the electronic states for every lanthanide ion has been computed within the Complete Active Space Self Consistent Field approach, followed by Spin Orbit State Interaction calculation (the CASSCF/CASSI-SO method).94 The employed ANO-RCC basis sets95,96 and contractions are reported in Table S22 in the Supporting Information. The chosen active space for the lanthanides consists of the unpaired electrons in the seven 4f -orbitals of the lanthanide ion in the oxidation state +3: CAS (1,7) for Ce and CAS (3,7) for Nd, respectively. Because of hardware limitations, only the states with the highest spin multiplicity for each lanthanide were included in the following CASSI-SO calculation: 7 doublets for Ce, 35 quadruplets for Nd. The geff for each Kramers’ doublet were computed with the SINGLE_ANISO module.62 The magnetic anisotropy was investigated within the pseudospin framework and their anisotropy axes were calculated with a pseudospin S = 1/2.
Acknowledgments
Dr. M. Perfetti is acknowledged for fruitful discussion about CTM and corresponding data fitting procedure.
Glossary
ABBREVIATIONS
- CTM
cantilever torque magnetimetry
- cw-EPR
continuous wave electron paramagnetic resonance
- CASSCF
complete active space self consistent field
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.1c00647.
ECD spectrum, PXRD spectra, further crystallographic figures and crystallographic tabular materials, dc and ac magnetic characterization curves, full CTM measurements, ab initio calculated Stevens’ parameters for the four paramagnetic centers, orientations of the anisotropy axis for different models, in both tabular and graphic mode (PDF)
Accession Codes
CCDC 2057194–2057197 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.
Author Present Address
∇ Instituto de Ciencia Molecular (ICMol), University of Valencia, Catedrático José Beltran 2, 46980 Paterna (Valencia), Spain.
Author Present Address
⊥ Institute of Physical Chemistry, University of Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany.
Author Present Address
# Department of Chemistry, Federal University of Parana, Centro Politecnico, Jardim das Americas, 81530-900 Curitiba-PR, Brazil.
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
This work was supported by the Italian MIUR through “Progetto Dipartimenti di Eccellenza 2018–2022 allocated to the Department of Chemistry “Ugo Schiff” (ref B96C1700020008) and PRIN project QCNaMoS (2015-HYFSRT).
The authors declare no competing financial interest.
Supplementary Material
References
- Ishikawa N.; Sugita M.; Ishikawa T.; Koshihara S.-Y.; Kaizu Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125 (29), 8694–8695. 10.1021/ja029629n. [DOI] [PubMed] [Google Scholar]
- Sessoli R.; Powell A. K. Strategies towards Single Molecule Magnets Based on Lanthanide Ions. Coord. Chem. Rev. 2009, 253 (19–20), 2328–2341. 10.1016/j.ccr.2008.12.014. [DOI] [Google Scholar]
- Woodruff D. N.; Winpenny R. E. P.; Layfield R. A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113 (7), 5110–5148. 10.1021/cr400018q. [DOI] [PubMed] [Google Scholar]
- Zhang P.; Zhang L.; Tang J. Lanthanide Single Molecule Magnets: Progress and Perspective. Dalt. Trans. 2015, 44 (9), 3923–3929. 10.1039/C4DT03329A. [DOI] [PubMed] [Google Scholar]
- Goodwin C. A. P.; Ortu F.; Reta D.; Chilton N. F.; Mills D. P. Molecular Magnetic Hysteresis at 60 K in Dysprosocenium. Nature 2017, 548, 439–442. 10.1038/nature23447. [DOI] [PubMed] [Google Scholar]
- Guo F. S.; Day B. M.; Chen Y. C.; Tong M. L.; Mansikkamäki A.; Layfield R. A. Magnetic Hysteresis up to 80 K in a Dysprosium Metallocene Single-Molecule Magnet. Science (Washington, DC, U. S.) 2018, 362, 1400–1403. 10.1126/science.aav0652. [DOI] [PubMed] [Google Scholar]
- Pedersen K. S.; Ariciu A.-M.; McAdams S.; Weihe H.; Bendix J.; Tuna F.; Piligkos S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138 (18), 5801–5804. 10.1021/jacs.6b02702. [DOI] [PubMed] [Google Scholar]
- Luis F.; Repollés A.; Martínez-Pérez M. J.; Aguilà D.; Roubeau O.; Zueco D.; Alonso P. J.; Evangelisti M.; Camón A.; Sesé J.; Barrios L. A.; Aromí G. Molecular Prototypes for Spin-Based CNOT and SWAP Quantum Gates. Phys. Rev. Lett. 2011, 107 (11), 117203. 10.1103/PhysRevLett.107.117203. [DOI] [PubMed] [Google Scholar]
- Shiddiq M.; Komijani D.; Duan Y.; Gaita-Ariño A.; Coronado E.; Hill S. Enhancing Coherence in Molecular Spin Qubits via Atomic Clock Transitions. Nature 2016, 531 (7594), 348–351. 10.1038/nature16984. [DOI] [PubMed] [Google Scholar]
- Bertaina S.; Gambarelli S.; Tkachuk A.; Kurkin I. N.; Malkin B.; Stepanov A.; Barbara B. Rare-Earth Solid-State Qubits. Nat. Nanotechnol. 2007, 2 (1), 39–42. 10.1038/nnano.2006.174. [DOI] [PubMed] [Google Scholar]
- Habib F.; Murugesu M. Lessons Learned from Dinuclear Lanthanide Nano-Magnets. Chem. Soc. Rev. 2013, 42 (8), 3278–3288. 10.1039/c2cs35361j. [DOI] [PubMed] [Google Scholar]
- Moreno Pineda E.; Chilton N. F.; Marx R.; Dörfel M.; Sells D. O.; Neugebauer P.; Jiang S.-D.; Collison D.; van Slageren J.; McInnes E. J. L.; Winpenny R. E. P. Direct Measurement of Dysprosium(III)···dysprosium(III) Interactions in a Single-Molecule Magnet. Nat. Commun. 2014, 5, 5243. 10.1038/ncomms6243. [DOI] [PubMed] [Google Scholar]
- Giansiracusa M. J.; Moreno-Pineda E.; Hussain R.; Marx R.; Martínez Prada M.; Neugebauer P.; Al-Badran S.; Collison D.; Tuna F.; van Slageren J.; Carretta S.; Guidi T.; McInnes E. J. L.; Winpenny R. E. P.; Chilton N. F. Measurement of Magnetic Exchange in Asymmetric Lanthanide Dimetallics: Toward a Transferable Theoretical Framework. J. Am. Chem. Soc. 2018, 140 (7), 2504–2513. 10.1021/jacs.7b10714. [DOI] [PubMed] [Google Scholar]
- Katoh K.; Asano R.; Miura A.; Horii Y.; Morita T.; Breedlove B. K.; Yamashita M. Effect of F-f Interactions on Quantum Tunnelling of the Magnetization: Mono- and Dinuclear Dy(III) Phthalocyaninato Triple-Decker Single-Molecule Magnets with the Same Octacoordination Environment. Dalt. Trans. 2014, 43 (21), 7716–7725. 10.1039/c4dt00042k. [DOI] [PubMed] [Google Scholar]
- Gysler M.; El Hallak F.; Ungur L.; Marx R.; Hakl M.; Neugebauer P.; Rechkemmer Y.; Lan Y.; Sheikin I.; Orlita M.; Anson C. E.; Powell A. K.; Sessoli R.; Chibotaru L. F.; van Slageren J. Multitechnique Investigation of Dy3-Implications for Coupled Lanthanide Clusters. Chem. Sci. 2016, 7 (7), 4347–4354. 10.1039/C6SC00318D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giansiracusa M. J.; Al-Badran S.; Kostopoulos A. K.; Whitehead G. F. S.; McInnes E. J. L.; Collison D.; Winpenny R. E. P.; Chilton N. F. Magnetic Exchange Interactions in Symmetric Lanthanide Dimetallics. Inorg. Chem. Front. 2020, 7 (20), 3909–3918. 10.1039/D0QI00854K. [DOI] [Google Scholar]
- Liddle S. T.; van Slageren J. Improving f-Element Single Molecule Magnets. Chem. Soc. Rev. 2015, 44 (19), 6655–6669. 10.1039/C5CS00222B. [DOI] [PubMed] [Google Scholar]
- Gatteschi D.; Sessoli R.; Sorace L.. Magnetic Bistability in Lanthanide-Based Molecular Systems: The Role of Anisotropy and Exchange Interactions. In Handbook on the Physics and Chemistry of Rare Earths, Vol. 50; 2016, pp 91–139 10.1016/bs.hpcre.2016.09.003. [DOI] [Google Scholar]
- Long J.; Habib F.; Lin P.-H.; Korobkov I.; Enright G.; Ungur L.; Wernsdorfer W.; Chibotaru L. F.; Murugesu M. Single-Molecule Magnet Behavior for an Antiferromagnetically Superexchange-Coupled Dinuclear Dysprosium(III) Complex. J. Am. Chem. Soc. 2011, 133 (14), 5319–5328. 10.1021/ja109706y. [DOI] [PubMed] [Google Scholar]
- Liu F.; Krylov D. S.; Spree L.; Avdoshenko S. M.; Samoylova N. A.; Rosenkranz M.; Kostanyan A.; Greber T.; Wolter A. U. B.; Büchner B.; Popov A. A. Single Molecule Magnet with an Unpaired Electron Trapped between Two Lanthanide Ions inside a Fullerene. Nat. Commun. 2017, 8 (1), 16098. 10.1038/ncomms16098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rinehart J. D.; Fang M.; Evans W. J.; Long J. R. Strong Exchange and Magnetic Blocking in N23–-Radical-Bridged Lanthanide Complexes. Nat. Chem. 2011, 3 (7), 538–542. 10.1038/nchem.1063. [DOI] [PubMed] [Google Scholar]
- Demir S.; Jeon I.-R.; Long J. R.; Harris T. D. Radical Ligand-Containing Single-Molecule Magnets. Coord. Chem. Rev. 2015, 289–290 (1), 149–176. 10.1016/j.ccr.2014.10.012. [DOI] [Google Scholar]
- Patrascu A. A.; Briganti M.; Soriano S.; Calancea S.; Allão Cassaro R. A.; Totti F.; Vaz M. G. F.; Andruh M. SMM Behavior Tuned by an Exchange Coupling LEGO Approach for Chimeric Compounds: First 2p-3d-4f Heterotrispin Complexes with Different Metal Ions Bridged by One Aminoxyl Group. Inorg. Chem. 2019, 58 (19), 13090–13101. 10.1021/acs.inorgchem.9b01998. [DOI] [PubMed] [Google Scholar]
- Demir S.; Nippe M.; Gonzalez M. I.; Long J. R. Exchange Coupling and Magnetic Blocking in Dilanthanide Complexes Bridged by the Multi-Electron Redox-Active Ligand 2,3,5,6-Tetra(2-Pyridyl)Pyrazine. Chem. Sci. 2014, 5 (12), 4701–4711. 10.1039/C4SC02154A. [DOI] [Google Scholar]
- Aromí G.; Aguilà D.; Gamez P.; Luis F.; Roubeau O. Design of Magnetic Coordination Complexes for Quantum Computing. Chem. Soc. Rev. 2012, 41 (2), 537–546. 10.1039/C1CS15115K. [DOI] [PubMed] [Google Scholar]
- Macaluso E.; Rubín M.; Aguilà D.; Chiesa A.; Barrios L. A.; Martínez J. I.; Alonso P. J.; Roubeau O.; Luis F.; Aromí G.; Carretta S. A Heterometallic [LnLn′Ln] Lanthanide Complex as a Qubit with Embedded Quantum Error Correction. Chem. Sci. 2020, 11 (38), 10337–10343. 10.1039/D0SC03107K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy P. M. Rare-Earth-Iron Exchange Interaction in the Garnets. I. Hamiltonian for Anisotropic Exchange Interaction. Phys. Rev. 1964, 135 (1A), A155–A165. 10.1103/PhysRev.135.A155. [DOI] [Google Scholar]
- Borrás-Almenar J. J.; Clemente-Juan J. M.; Coronado E.; Palii A. V.; Tsukerblat B. S. Magnetic Exchange between Orbitally Degenerate Ions: A New Development for the Effective Hamiltonian. J. Phys. Chem. A 1998, 102 (1), 200–213. 10.1021/jp971701u. [DOI] [Google Scholar]
- Pellissier H. Recent Developments in Enantioselective Lanthanide-Catalyzed Transformations. Coord. Chem. Rev. 2017, 336, 96–151. 10.1016/j.ccr.2017.01.013. [DOI] [Google Scholar]
- Mikami K.; Terada M.; Matsuzawa H. “Asymmetric” Catalysis by Lanthanide Complexes. Angew. Chem., Int. Ed. 2002, 41 (19), 3554–3572. . [DOI] [PubMed] [Google Scholar]
- Crassous J. Chiral Transfer in Coordination Complexes: Towards Molecular Materials. Chem. Soc. Rev. 2009, 38 (3), 830–845. 10.1039/b806203j. [DOI] [PubMed] [Google Scholar]
- Zinna F.; Di Bari L. Lanthanide Circularly Polarized Luminescence: Bases and Applications. Chirality 2015, 27 (1), 1–13. 10.1002/chir.22382. [DOI] [PubMed] [Google Scholar]
- Taniguchi K.; Nishio M.; Kishiue S.; Huang P. J.; Kimura S.; Miyasaka H. Strong Magnetochiral Dichroism for Visible Light Emission in a Rationally Designed Paramagnetic Enantiopure Molecule. Phys. Rev. Mater. 2019, 3 (4), 045202 10.1103/PhysRevMaterials.3.045202. [DOI] [Google Scholar]
- Gendron F.; Di Pietro S.; Abad Galán L.; Riobé F.; Placide V.; Guy L.; Zinna F.; Di Bari L.; Bensalah-Ledoux A.; Guyot Y.; Pilet G.; Pointillart F.; Baguenard B.; Guy S.; Cador O.; Maury O.; Le Guennic B. Luminescence, Chiroptical, Magnetic and: Ab Initio Crystal-Field Characterizations of an Enantiopure Helicoidal Yb(III) Complex. Inorg. Chem. Front. 2021, 8 (4), 914–926. 10.1039/D0QI01194K. [DOI] [Google Scholar]
- Atzori M.; Dhbaibi K.; Douib H.; Grasser M.; Dorcet V.; Breslavetz I.; Paillot K.; Cador O.; Rikken G. L. J. A.; Le Guennic B.; Crassous J.; Pointillart F.; Train C. Helicene-Based Ligands Enable Strong Magneto-Chiral Dichroism in a Chiral Ytterbium Complex. J. Am. Chem. Soc. 2021, 143 (7), 2671–2675. 10.1021/jacs.0c13180. [DOI] [PubMed] [Google Scholar]
- Pathak A. K.; Khan M.; Gschneidner K. A.; McCallum R. W.; Zhou L.; Sun K.; Dennis K. W.; Zhou C.; Pinkerton F. E.; Kramer M. J.; Pecharsky V. K. Cerium: An Unlikely Replacement of Dysprosium in High Performance Nd-Fe-B Permanent Magnets. Adv. Mater. 2015, 27 (16), 2663–2667. 10.1002/adma.201404892. [DOI] [PubMed] [Google Scholar]
- Mayans J.; Sorace L.; Font-Bardia M.; Escuer A. Chiral Mononuclear Lanthanide Complexes Derived from Chiral Schiff Bases: Structural and Magnetic Studies. Polyhedron 2019, 170, 264–270. 10.1016/j.poly.2019.05.051. [DOI] [PubMed] [Google Scholar]
- Ruiz E.; Alemany P.; Alvarez S.; Cano J. Toward the Prediction of Magnetic Coupling in Molecular Systems: Hydroxo- and Alkoxo-Bridged Cu(II) Binuclear Complexes. J. Am. Chem. Soc. 1997, 119 (6), 1297–1303. 10.1021/ja961199b. [DOI] [Google Scholar]
- Kano S.; Nakano H.; Kojima M.; Baba N.; Nakajima K. An Effect of the Ionic Radii of Lanthanide(III) Ions on the Structure and Catalytic Properties of Chiral Schiff Base-Lanthanide(III) Complexes. Inorg. Chim. Acta 2003, 349, 6–16. 10.1016/S0020-1693(03)00052-5. [DOI] [Google Scholar]
- Lhoste J.; Henry N.; Loiseau T.; Abraham F. Molecular Assemblies of Trichloride Neodymium and Europium Complexes Chelated by 1,10-Phenanthroline. Polyhedron 2011, 30 (7), 1289–1294. 10.1016/j.poly.2011.02.020. [DOI] [Google Scholar]
- Amjad A.; Madalan A. M.; Andruh M.; Caneschi A.; Sorace L. Slow Relaxation of Magnetization in an Isostructural Series of Zinc-Lanthanide Complexes: An Integrated EPR and AC Susceptibility Study. Chem. - Eur. J. 2016, 22 (36), 12849–12858. 10.1002/chem.201601996. [DOI] [PubMed] [Google Scholar]
- Lucaccini E.; Baldovi J. J.; Chelazzi L.; Barra A.-L.; Grepioni F.; Costes J.-P.; Sorace L. Electronic Structure and Magnetic Anisotropy in Lanthanoid Single-Ion Magnets with C3 Symmetry: The Ln(Trenovan) Series. Inorg. Chem. 2017, 56 (8), 4728–4738. 10.1021/acs.inorgchem.7b00413. [DOI] [PubMed] [Google Scholar]
- Lucaccini E.; Briganti M.; Perfetti M.; Vendier L.; Costes J.-P.; Totti F.; Sessoli R.; Sorace L. Relaxation Dynamics and Magnetic Anisotropy in a Low-Symmetry Dy-III Complex. Chem. - Eur. J. 2016, 22 (16), 5552–5562. 10.1002/chem.201505211. [DOI] [PubMed] [Google Scholar]
- Perfetti M. Cantilever Torque Magnetometry on Coordination Compounds: From Theory to Experiments. Coord. Chem. Rev. 2017, 348, 171–186. 10.1016/j.ccr.2017.08.013. [DOI] [Google Scholar]
- Mihalcea I.; Perfetti M.; Pineider F.; Tesi L.; Mereacre V.; Wilhelm F.; Rogalev A.; Anson C. E.; Powell A. K.; Sessoli R. Spin Helicity in Chiral Lanthanide Chains. Inorg. Chem. 2016, 55 (20), 10068–10074. 10.1021/acs.inorgchem.6b01010. [DOI] [PubMed] [Google Scholar]
- Ungur L.; Chibotaru L. F. Ab Initio Crystal Field for Lanthanides. Chem. - Eur. J. 2017, 23 (15), 3708–3718. 10.1002/chem.201605102. [DOI] [PubMed] [Google Scholar]
- Ungur L.Introduction to the Electronic Structure, Luminescence, and Magnetism of Lanthanides. In Lanthanide-Based Multifunctional Materials: From OLEDs to SIMs; Elsevier, 2018; pp 1–58, 10.1016/B978-0-12-813840-3.00001-6. [DOI] [Google Scholar]
- Guégan F.; Jung J.; Le Guennic B.; Riobé F.; Maury O.; Gillon B.; Jacquot J. F.; Guyot Y.; Morell C.; Luneau D. Evidencing Under-Barrier Phenomena in a Yb(III) SMM: A Joint Luminescence/Neutron Diffraction/SQUID Study. Inorg. Chem. Front. 2019, 6 (11), 3152–3157. 10.1039/C9QI00726A. [DOI] [Google Scholar]
- Brunet G.; Marin R.; Monk M. J.; Resch-Genger U.; Gálico D. A.; Sigoli F. A.; Suturina E. A.; Hemmer E.; Murugesu M. Exploring the Dual Functionality of an Ytterbium Complex for Luminescence Thermometry and Slow Magnetic Relaxation. Chem. Sci. 2019, 10 (28), 6799–6808. 10.1039/C9SC00343F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset E.; Piccardo M.; Boulon M.-E.; Gable R. W.; Soncini A.; Sorace L.; Boskovic C. Slow Magnetic Relaxation in Lanthanoid Crown Ether Complexes: Interplay of Raman and Anomalous Phonon Bottleneck Processes. Chem. - Eur. J. 2018, 24 (55), 14768–14785. 10.1002/chem.201802779. [DOI] [PubMed] [Google Scholar]
- Vieru V.; Ungur L.; Cemortan V.; Sukhanov A.; Baniodeh A.; Anson C. E.; Powell A. K.; Voronkova V.; Chibotaru L. F. Magnetization Blocking in Fe 2III Dy 2III Molecular Magnets: Ab Initio Calculations and EPR Spectroscopy. Chem. - Eur. J. 2018, 24 (62), 16652–16661. 10.1002/chem.201803821. [DOI] [PubMed] [Google Scholar]
- Boulon M.-E.; Cucinotta G.; Liu S.-S.; Jiang S.-D.; Ungur L.; Chibotaru L. F.; Gao S.; Sessoli R. Angular-Resolved Magnetometry beyond Triclinic Crystals: Out-of-Equilibrium Studies of Cp*ErCOT Single-Molecule Magnet. Chem. - Eur. J. 2013, 19 (41), 13726–13731. 10.1002/chem.201302600. [DOI] [PubMed] [Google Scholar]
- a Jung J.; Le Natur F.; Cador O.; Pointillart F.; Calvez G.; Daiguebonne C.; Guillou O.; Guizouarn T.; Le Guennic B.; Bernot K. Experimental and Theoretical Evidence That Electrostatics Governs Easy-Axis Orientation in DyIII-Based Molecular Chains. Chem. Commun. 2014, 50 (87), 13346–13348. 10.1039/C4CC05062B. [DOI] [PubMed] [Google Scholar]; b Pointillart F.; Flores Gonzalez J.; Montigaud V.; Tesi L.; Cherkasov V.; Le Guennic B.; Cador O.; Ouahab L.; Sessoli R.; Kuropatov V. Redox- And Solvato-Magnetic Switching in a Tetrathiafulvalene-Based Triad Single-Molecule Magnet. Inorg. Chem. Front. 2020, 7 (12), 2322–2334. 10.1039/D0QI00319K. [DOI] [Google Scholar]
- Briganti M.; Lucaccini E.; Chelazzi L.; Ciattini S.; Sorace L.; Sessoli R.; Totti F.; Perfetti M. Magnetic Anisotropy Trends along a Full 4f-Series: The fN+7 Effect. J. Am. Chem. Soc. 2021, 143, 8108. 10.1021/jacs.1c02502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen K. S.; Ungur L.; Sigrist M.; Sundt A.; Schau-Magnussen M.; Vieru V.; Mutka H.; Rols S.; Weihe H.; Waldmann O.; Chibotaru L. F.; Bendix J.; Dreiser J. Modifying the Properties of 4f Single-Ion Magnets by Peripheral Ligand Functionalisation. Chem. Sci. 2014, 5 (4), 1650. 10.1039/C3SC53044B. [DOI] [Google Scholar]
- Giansiracusa M. J.; Vonci M.; Van Den Heuvel W.; Gable R. W.; Moubaraki B.; Murray K. S.; Yu D.; Mole R. A.; Soncini A.; Boskovic C. Carbonate-Bridged Lanthanoid Triangles: Single-Molecule Magnet Behavior, Inelastic Neutron Scattering, and Ab Initio Studies. Inorg. Chem. 2016, 55 (11), 5201–5214. 10.1021/acs.inorgchem.6b00108. [DOI] [PubMed] [Google Scholar]
- Marx R.; Moro F.; Dörfel M.; Ungur L.; Waters M.; Jiang S. D.; Orlita M.; Taylor J.; Frey W.; Chibotaru L. F.; van Slageren J. Spectroscopic Determination of Crystal Field Splittings in Lanthanide Double Deckers. Chem. Sci. 2014, 5 (8), 3287–3293. 10.1039/c4sc00751d. [DOI] [Google Scholar]
- Rechkemmer Y.; Fischer J. E.; Marx R.; Dörfel M.; Neugebauer P.; Horvath S.; Gysler M.; Brock-Nannestad T.; Frey W.; Reid M. F.; van Slageren J. Comprehensive Spectroscopic Determination of the Crystal Field Splitting in an Erbium Single-Ion Magnet. J. Am. Chem. Soc. 2015, 137 (40), 13114–13120. 10.1021/jacs.5b08344. [DOI] [PubMed] [Google Scholar]
- Hallmen P. P.; Rauhut G.; Stoll H.; Mitrushchenkov A. O.; van Slageren J. Crystal Field Splittings in Lanthanide Complexes: Inclusion of Correlation Effects beyond Second Order Perturbation Theory. J. Chem. Theory Comput. 2018, 14 (8), 3998–4009. 10.1021/acs.jctc.8b00184. [DOI] [PubMed] [Google Scholar]
- Schapiro I.; Sivalingam K.; Neese F. Assessment of N-Electron Valence State Perturbation Theory for Vertical Excitation Energies. J. Chem. Theory Comput. 2013, 9 (8), 3567–3580. 10.1021/ct400136y. [DOI] [PubMed] [Google Scholar]
- Neese F. Software Update: The ORCA Program System, Version 4.0. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8 (1), 1327. 10.1002/wcms.1327. [DOI] [Google Scholar]
- Briganti M.; Garcia G. F.; Jung J.; Sessoli R.; Le Guennic B.; Totti F. Covalency and Magnetic Anisotropy in Lanthanide Single Molecule Magnets: The DyDOTA Archetype. Chem. Sci. 2019, 10 (30), 7233–7245. 10.1039/C9SC01743G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Z.; Guo M.; Li X. L.; Tang J. Molecular Magnetism of Lanthanide: Advances and Perspectives. Coord. Chem. Rev. 2019, 378, 350–364. 10.1016/j.ccr.2017.10.030. [DOI] [Google Scholar]
- Day B. M.; Guo F. S.; Layfield R. A. Cyclopentadienyl Ligands in Lanthanide Single-Molecule Magnets: One Ring to Rule Them All?. Acc. Chem. Res. 2018, 51 (8), 1880–1889. 10.1021/acs.accounts.8b00270. [DOI] [PubMed] [Google Scholar]
- Liu J. L.; Chen Y. C.; Tong M. L. Symmetry Strategies for High Performance Lanthanide-Based Single-Molecule Magnets. Chem. Soc. Rev. 2018, 47 (7), 2431–2453. 10.1039/C7CS00266A. [DOI] [PubMed] [Google Scholar]
- Gupta S. K.; Shanmugan S.; Rajeshkumar T.; Borah A.; Damjanović M.; Schulze M.; Wernsdorfer W.; Rajaraman G.; Murugavel R. A Single-Ion Single-Electron Cerrous Magnet. Dalt. Trans. 2019, 48 (42), 15928–15935. 10.1039/C9DT03052B. [DOI] [PubMed] [Google Scholar]
- Gupta S. K.; Rajeshkumar T.; Rajaraman G.; Murugavel R. An Unprecedented Zero Field Neodymium(III) Single-Ion Magnet Based on a Phosphonic Diamide. Chem. Commun. 2016, 52 (44), 7168–7171. 10.1039/C6CC03066A. [DOI] [PubMed] [Google Scholar]
- Chen Y. C.; Huang X. S.; Liu J. L.; Tong M. L. Magnetic Dynamics of a Neodymium(III) Single-Ion Magnet. Inorg. Chem. 2018, 57 (18), 11782–11787. 10.1021/acs.inorgchem.8b01957. [DOI] [PubMed] [Google Scholar]
- Hino S.; Maeda M.; Yamashita K.; Kataoka Y.; Nakano M.; Yamamura T.; Nojiri H.; Kofu M.; Yamamuro O.; Kajiwara T. Linear Trinuclear Zn(II)-Ce(III)-Zn(II) Complex Which Behaves as a Single-Molecule Magnet. Dalt. Trans. 2013, 42 (8), 2683–2686. 10.1039/c2dt32812g. [DOI] [PubMed] [Google Scholar]
- Gatteschi D.; Sessoli R.; Villain J.. Molecular Nanomagnets; Oxford University Press: Oxford, U.K., 2007, 10.1093/acprof:oso/9780198567530.001.0001. [DOI] [Google Scholar]
- Reta D.; Chilton N. F. Uncertainty Estimates for Magnetic Relaxation Times and Magnetic Relaxation Parameters. Phys. Chem. Chem. Phys. 2019, 21 (42), 23567–23575. 10.1039/C9CP04301B. [DOI] [PubMed] [Google Scholar]
- Orbach R. Spin-Lattice Relaxation in Rare-Earth Salts: Field Dependence of the Two-Phonon Process Spin-Lattice Relaxation in Rare-Earth Salts: Field Dependence of the Two-Phonon Process. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1961, 264 (1319), 485–495. [Google Scholar]
- Le Roy J. J.; Korobkov I.; Kim J. E.; Schelter E. J.; Murugesu M. Structural and Magnetic Conformation of a Cerocene [Ce(COT″) 2]- Exhibiting a Uniconfigurational F1 Ground State and Slow-Magnetic Relaxation. Dalt. Trans. 2014, 43 (7), 2737–2740. 10.1039/C3DT53280A. [DOI] [PubMed] [Google Scholar]
- Le Roy J. J.; Gorelsky S. I.; Korobkov I.; Murugesu M. Slow Magnetic Relaxation in Uranium(III) and Neodymium(III) Cyclooctatetraenyl Complexes. Organometallics 2015, 34 (8), 1415–1418. 10.1021/om501214c. [DOI] [Google Scholar]
- Khélifa A. B.; Belkhiria M. S.; Huang G.; Freslon S.; Guillou O.; Bernot K. Single-Molecule Magnet Behaviour in Polynuclear Assembly of Trivalent Cerium Ions with Polyoxomolybdates. Dalt. Trans. 2015, 44 (37), 16458–16464. 10.1039/C5DT02377G. [DOI] [PubMed] [Google Scholar]
- Rinehart J. D.; Long J. R. Exploiting Single-Ion Anisotropy in the Design of f-Element Single-Molecule Magnets. Chem. Sci. 2011, 2 (11), 2078. 10.1039/c1sc00513h. [DOI] [Google Scholar]
- Bencini A.; Gatteschi D.. EPR of Exchange-Coupled Systems; Springer–Verlag; Berlin, 1990. [Google Scholar]
- Sorace L.; Sangregorio C.; Figuerola A.; Benelli C.; Gatteschi D. Magnetic Interactions and Magnetic Anisotropy in Exchange Coupled 4f-3d Systems: A Case Study of a Heterodinuclear Ce3+-Fe3+ Cyanide-Bridged Complex. Chem. - Eur. J. 2009, 15 (6), 1377–1388. 10.1002/chem.200801638. [DOI] [PubMed] [Google Scholar]
- Lhoste J.; Pérez-Campos A.; Henry N.; Loiseau T.; Rabu P.; Abraham F. Chain-like and Dinuclear Coordination Polymers in Lanthanide (Nd, Eu) Oxochloride Complexes with 2,2′:6′,2″-Terpyridine: Synthesis, XRD Structure and Magnetic Properties. Dalt. Trans. 2011, 40 (36), 9136–9144. 10.1039/c1dt10485c. [DOI] [PubMed] [Google Scholar]
- Chakoumakos B. C.; Custelcean R.; Ramey J. O.; Kolopus J. A.; Jin R.; Neal J. S.; Wisniewski D. J.; Boatner L. A. Cerium Chloride-Methanol Adduct Crystals, CeCl3(CH 3OH)4: Preparation, Crystallography, and Scintillation Properties. Cryst. Growth Des. 2008, 8 (7), 2070–2072. 10.1021/cg800136p. [DOI] [Google Scholar]
- Han T.; Ding Y. S.; Li Z. H.; Yu K. X.; Zhai Y. Q.; Chilton N. F.; Zheng Y. Z. A Dichlorido-Bridged Dinuclear Dy(Iii) Single-Molecule Magnet with an Effective Energy Barrier Larger than 600 K. Chem. Commun. 2019, 55 (55), 7930–7933. 10.1039/C9CC02436K. [DOI] [PubMed] [Google Scholar]
- Sulway S. A.; Layfield R. A.; Tuna F.; Wernsdorfer W.; Winpenny R. E. P. Single-Molecule Magnetism in Cyclopentadienyl-Dysprosium Chlorides. Chem. Commun. 2012, 48 (10), 1508–1510. 10.1039/C1CC14643B. [DOI] [PubMed] [Google Scholar]
- Burns C. P.; Wilkins B. O.; Dickie C. M.; Latendresse T. P.; Vernier L.; Vignesh K. R.; Bhuvanesh N. S.; Nippe M. A Comparative Study of Magnetization Dynamics in Dinuclear Dysprosium Complexes Featuring Bridging Chloride or Trifluoromethanesulfonate Ligands. Chem. Commun. 2017, 53 (60), 8419–8422. 10.1039/C7CC02457F. [DOI] [PubMed] [Google Scholar]
- Hilgar J. D.; Flores B. S.; Rinehart J. D. Ferromagnetic Coupling in a Chloride-Bridged Erbium Single-Molecule Magnet. Chem. Commun. 2017, 53 (53), 7322–7324. 10.1039/C7CC02356A. [DOI] [PubMed] [Google Scholar]
- Pajerowski D. M.; Li Q.; Hyun J.; Dennis C. L.; Phelan D.; Yan P.; Chen P.; Li G. Chloride-Bridged, Defect-Dicubane {Ln4} Core Clusters: Syntheses, Crystal Structures and Magnetic Properties. Dalt. Trans. 2014, 43 (31), 11973–11980. 10.1039/C4DT01329H. [DOI] [PubMed] [Google Scholar]
- Han T.; Giansiracusa M. J.; Li Z. H.; Ding Y. S.; Chilton N. F.; Winpenny R. E. P.; Zheng Y. Z. Exchange-Biasing in a Dinuclear Dysprosium(III) Single-Molecule Magnet with a Large Energy Barrier for Magnetisation Reversal. Chem. - Eur. J. 2020, 26 (30), 6773–6777. 10.1002/chem.202000719. [DOI] [PubMed] [Google Scholar]
- Wu H.; Li M.; Xia Z.; Montigaud V.; Cador O.; Le Guennic B.; Ke H.; Wang W.; Xie G.; Chen S.; Gao S. High Temperature Quantum Tunnelling of Magnetization and Thousand Kelvin Anisotropy Barrier in a Dy2 single-Molecule Magnet. Chem. Commun. 2021, 57 (3), 371–374. 10.1039/D0CC06993K. [DOI] [PubMed] [Google Scholar]
- Hilgar J. D.; Bernbeck M. G.; Rinehart J. D. Million-Fold Relaxation Time Enhancement across a Series of Phosphino-Supported Erbium Single-Molecule Magnets. J. Am. Chem. Soc. 2019, 141 (5), 1913–1917. 10.1021/jacs.8b13514. [DOI] [PubMed] [Google Scholar]
- Stoll S.; Schweiger A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006, 178 (1), 42–55. 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- Perfetti M.; Lucaccini E.; Sorace L.; Costes J.-P.; Sessoli R. Determination of Magnetic Anisotropy in the LnTRENSAL Complexes (Ln = Tb, Dy, Er) by Torque Magnetometry. Inorg. Chem. 2015, 54 (7), 3090–3092. 10.1021/acs.inorgchem.5b00288. [DOI] [PubMed] [Google Scholar]
- Rigamonti L.; Bridonneau N.; Poneti G.; Tesi L.; Sorace L.; Pinkowicz D.; Jover J.; Ruiz E.; Sessoli R.; Cornia A. A Pseudo-Octahedral Cobalt(II) Complex with Bispyrazolylpyridine Ligands Acting as a Zero-Field Single-Molecule Magnet with Easy Axis Anisotropy. Chem. - Eur. J. 2018, 24 (35), 8857–8868. 10.1002/chem.201801026. [DOI] [PubMed] [Google Scholar]
- Bain G. A.; Berry J. F. Diamagnetic Corrections and Pascal’s Constants. J. Chem. Educ. 2008, 85 (4), 532. 10.1021/ed085p532. [DOI] [Google Scholar]
- Aquilante F.; Autschbach J.; Carlson R. K.; Chibotaru L. F.; Delcey M. G.; De Vico L.; Fdez. Galván I.; Ferré N.; Frutos L. M.; Gagliardi L.; Garavelli M.; Giussani A.; Hoyer C. E.; Li Manni G.; Lischka H.; Ma D.; Malmqvist P. Å.; Müller T.; Nenov A.; Olivucci M.; Pedersen T. B.; Peng D.; Plasser F.; Pritchard B.; Reiher M.; Rivalta I.; Schapiro I.; Segarra-Martí J.; Stenrup M.; Truhlar D. G.; Ungur L.; Valentini A.; Vancoillie S.; Veryazov V.; Vysotskiy V. P.; Weingart O.; Zapata F.; Lindh R. Molcas8: New Capabilities for Multiconfigurational Quantum Chemical Calculations across the Periodic Table. J. Comput. Chem. 2016, 37 (5), 506–541. 10.1002/jcc.24221. [DOI] [PubMed] [Google Scholar]
- Chibotaru L. F.; Ungur L. Ab Initio Calculation of Anisotropic Magnetic Properties of Complexes. I. Unique Definition of Pseudospin Hamiltonians and Their Derivation. J. Chem. Phys. 2012, 137 (6), 064112. 10.1063/1.4739763. [DOI] [PubMed] [Google Scholar]
- Roos B. O.; Lindh R.; Malmqvist P. Å.; Veryazov V.; Widmark P.-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108 (15), 2851. 10.1021/jp031064+. [DOI] [Google Scholar]
- Roos B. O.; Lindh R.; Malmqvist P. Å.; Veryazov V.; Widmark P. O.; Borin A. C. New Relativistic Atomic Natural Orbital Basis Sets for Lanthanide Atoms with Applications to the Ce Diatom and LuF3. J. Phys. Chem. A 2008, 112 (45), 11431–11435. 10.1021/jp803213j. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



