Coordination of movement via complementary interactions of leaders and followers in termite mating pairs

Abstract

In collective animal motion, coordination is often achieved by feedback between leaders and followers. For stable coordination, a leader's signals and a follower's responses are hypothesized to be attuned to each other. However, their roles are difficult to disentangle in species with highly coordinated movements, hiding potential diversity of behavioural mechanisms for collective behaviour. Here, we show that two Coptotermes termite species achieve a similar level of coordination via distinct sets of complementary leader–follower interactions. Even though C. gestroi females produce less pheromone than C. formosanus, tandem runs of both species were stable. Heterospecific pairs with C. gestroi males were also stable, but not those with C. formosanus males. We attributed this to the males' adaptation to the conspecific females; C. gestroi males have a unique capacity to follow females with small amounts of pheromone, while C. formosanus males reject C. gestroi females as unsuitable but are competitive over females with large amounts of pheromone. An information-theoretic analysis supported this conclusion by detecting information flow from female to male only in stable tandems. Our study highlights cryptic interspecific variation in movement coordination, a source of novelty for the evolution of social interactions.

1. Introduction

Animals often move as a group while searching for a safe place or feeding site. Coordinated group movements are achieved by rules for interactions among group members, with individuals often playing different roles [1,2]. One or a few individuals initiate movement, and other members follow the leader [3,4]. Such leadership strongly affects the collective outcome of group movements [5]. When a pair of individuals explore the environment together, a leader–follower relationship is almost inevitable; the first to move is the leader, and the other has no option but to follow [6]. Thus, many studies on pairs have focused on how partners respond to each other to control movement speed and turning angle [7–11]. As successful coordination results from social feedback, innate behavioural differences between partners can promote or hinder coordination [12]. Especially, if the pair shares a common goal, leader phenotypes should complement follower phenotypes to maintain stable coordination, resulting in a species-specific manner of social interaction.

Tandem running in termites is among the simplest leader–follower relationships. Unlike ants, where tandem runs recruit colony members to specific resource locations [13,14], termite mating pairs perform tandems after dispersal, while seeking sites for colony foundation [15]. The female leads the tandem and releases a short-range sex pheromone to guide the male [16,17], and the male touches the female's abdomen with its antennae and mouthparts, indicating its continued presence [15,18]. As the sex pheromone varies among species [16], female behaviour can also vary in order to transmit species-specific signals efficiently [19]. We predict that males coevolved species-specific following capacity to form stable tandems with conspecific females.

To disentangle the contributions of leaders and followers to behavioural coordination, we made heterospecific pairings between related species, Coptotermes gestroi (Wasmann) and C. formosanus (Shiraki). These two termites evolved in allopatry in the course of 18 million years of evolution [20], but both are now invasive and found in sympatry in some coastal regions, including Taiwan, Hainan and southeast Florida [21–23]. In south Florida, USA, heterospecific mating events have been observed, resulting in hybrid colonies [24]. Heterospecific pairing can occur because the species share the same pairing (sex) pheromone, (3Z,6Z,8E)-dodeca-3,6,8-trien-1-ol, emitted from tergal glands at the tip of the abdomen of females [25] (figure 1a). The main difference is the quantity of pheromone, and thus the strength of the transmitted signal; C. formosanus females produce approximately 10× more pheromone than C. gestroi females [25]. Based on this difference, we hypothesized that males of these species evolved different tandem following capacities matched to their conspecific female's signal strength.

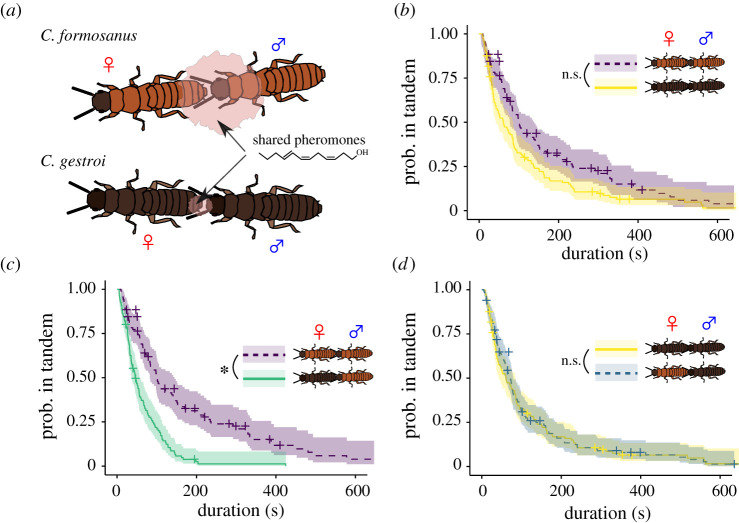
Figure 1.

Interspecific variation of tandem running in Coptotermes termites. (a) During tandem runs, the female leader releases a short-range pheromone that attracts the male follower. The chemical is shared between C. formosanus and C. gestroi, but the quantity is much larger in C. formosanus. (b–d) Comparison of the duration of tandem running until separation across different combinations. Kaplan–Meier survival curves were generated for each pairing combination. Asterisk (*) indicates significant difference (mixed effect Cox model, p < 0.05). + indicates censored data due to the end of observations. Shaded regions show 95% confidence intervals. (Online version in colour.)

Here, we study the heterospecific tandem runs of C. formosanus and C. gestroi. We show that C. formosanus males do not maintain heterospecific tandem runs because they only follow females that release large amounts of sex pheromone, while C. gestroi males are accustomed to small quantities and are not challenged in following the larger amount released by C. formosanus females. During this process, males of C. formosanus may have difficulty detecting small amounts of pheromone, or they may instead lack the motivation to follow weak pheromone signals. Thus, we next investigate their motivation by observing males' responses when they become separated from their leader. After separation, the female pauses while the male engages in active local search, and this dimorphism enhances re-encounter rates [19]. By moving slowly just after separation, males increase their re-encounter rate with the same partner. By instead moving quickly, they can more efficiently search for a new partner [26]. The former tactic is often used in lower-density conditions, while the latter is used in higher-density conditions where the availability of alternative mates reduces the relative value of a separated partner [26]. Thus, the male's movement speed right after separation can reflect a male's evaluation of the female; slow movement indicates a relatively positive evaluation of the separated female and preference to reunite; fast movement means a lower rating and a preference for finding a new partner. Finally, we explore the outcome of competition between C. formosanus male and C. gestroi male over C. formosanus female, as C. formosanus females are attractive to males of both species. Combined, we show that partner selection has shaped the species-specific association of termite mating pairs.

2. Material and methods

(a) . Termites and experimental arena

We collected alates of C. formosanus and C. gestroi using a light-trapping system at dusk between 18 and 20 April 2020 in Broward County (Florida, USA) during synchronized dispersal flights. All alates were collected at a single site. We brought the alates to the laboratory and maintained them on wet cardboard at 28°C. We used individuals who shed their wings by themselves and observed their behaviour within 12 h after the flight. Each individual was used only once.

We performed all observations in an experimental arena made by filling a Petri dish (ø = 140 mm) with moistened plaster. The Petri dish had a clear lid during observations. A video camera above the arena was adjusted so that the arena filled the camera frame. We extracted the coordinates of termite movements from all obtained video, using the video-tracking system UMATracker [27]. All data analyses were performed using R v. 4.0.1 [28].

(b) . Comparing tandem run stability across different pair combinations

To explore interspecies differences in tandem running behaviour, we introduced one female and one male to the experimental arena and recorded their behaviour for 30 min. We tested four different species combinations: conspecific pairs of C. formosanus (Cf-Cf), conspecific pairs of C. gestroi (Cg-Cg), heterospecific pairs of female C. gestroi and male C. formosanus (Cg-Cf), and heterospecific pairs of female C. formosanus and male C. gestroi (Cf-Cg). We prepared 10 replicates for each combination.

During observations, termite pairs were in one of three states: (i) tandem running, (ii) interacting but not tandem running and (iii) searching (two are at a distance). Following a previous study [26], we classified the pairing states based on the coordination of a female and a male. We defined them as interacting (or tandem running) when the distance between their centroids was less than 1.3×mean body length. This value was 11.57 mm for C. formosanus, 9.75 mm for C. gestroi and 10.65 mm for heterospecific pairs, respectively. We selected this distance to slightly exceed the average body length because termites in a tandem run are nearly in physical contact [19]. An interacting pair was considered to be performing a tandem run only if they met the following criteria [26]. First, the interaction needed to last for more than 5 s; a very short separation (less than 2 s) was not regarded as a separation event unless the distance between individuals was greater than 20 mm. Second, both termites needed to move more than 30 mm while interacting. After separation, we considered that individuals engage in separation search until they interact with an individual again for more than 1 s. We down-sampled all videos to a rate of five frames per second (FPS) (= every 0.2002 s) for this analysis.

We obtained 103, 110, 120 and 132 tandem run events for Cf-Cf, Cg-Cg, Cg-Cf and Cf-Cg, respectively. We compared tandem duration between the two conspecific pairs and between heterospecific and conspecific pairs for each male species. We used the mixed-effects Cox model (coxme() function in the coxme package in R [29]), with female species as a fixed effect and video id as a random effect. The random effect accounted for the inclusion of multiple tandem events for each pair of termites. The likelihood ratio test was used to determine the statistical significance of each explanatory variable (type II test). Observations interrupted by the end of the video were treated as censored data. We also fitted a variety of distributions to the tandem survival curves, including exponential, Weibull, gamma and power-law distribution. After calculating the maximum log-likelihood for each model, we determined the best fitting model using Akaike's information criterion (AIC). For model fitting, we removed censored data.

(c) . Moving speed during tandem runs

We compared moving speed during tandem runs across different pair combinations to further explore the role of females and males for heterospecific behavioural coordination. We first calculated the moving step length between two successive frames at 5FPS. The step length distribution was bimodal, with two peaks around 0 and 3 mm (electronic supplementary material, figure S2). The two peaks can be regarded as representing pauses and moves, respectively. Based on the histogram of each pairing combination using 0.1 mm bins, we obtained the value representing the second peak of moving speed (electronic supplementary material, figure S2). Then, we defined thresholds to distinguish movements from pauses by multiplying the value of the 2nd peak by a factor of 0.2 (Cf-Cf, 3.4 mm; Cg-Cg, 2.9 mm; Cf-Cg, 3.5 mm; Cg-Cf, 2.9 mm) [19]. A pause was defined as a step length shorter than or equal to the threshold. By removing data for pause durations, we obtained a dataset only including moving speed. Finally, we used a linear mixed model to analyse moving speed, where the species of female and male were included as fixed effects and video id as a random effect. The likelihood ratio test was used to determine the statistical significance of each explanatory variable (type II test). Note that, although we present results applying species-specific thresholds, we reached the same conclusions when we used one identical threshold (=2.9 mm, obtained from the histogram of a pooled dataset).

(d) . Information transfer between females and males

We used transfer entropy to quantify the degree to which the female leader's motion predicts that of the male follower, a measure of coupling strength within the pair. Transfer entropy quantifies how well knowledge of present behaviour of the sender reduces uncertainty about the future of behaviour of the receiver, after taking account of the receiver's history [30,31]. This value can be determined for both directions, with the difference giving a measure of the net direction and amount of information flow. We calculated transfer entropy by coarse-graining their movement trajectories into a sequence of discrete behaviours. During tandem runs, the female explores the environment to look for a potential nest site with the following male [15]. In a random search, both move/pause patterns and turning patterns link to search efficiency [32]. We discretized trajectories of each runner to obtain time-series describing the pausing and rotation pattern [9]. The behaviour of each runner was classified into three states: pause (P), motion with clockwise rotation (M-CW) and motion with counterclockwise rotation (M-CCW). The pause state was distinguished from others using the threshold obtained in the moving speed analysis. As this threshold was computed on the basis of data sampled at 5 FPS (sampling period = 0.2002s), we simply rescaled this threshold by the ratio of sampling periods to obtain that for other sampling periods. If the step length between successive frames was shorter than the threshold, the state of the frame was recorded as a pause P. Otherwise, the state was either M-CW or M-CCW depending on the direction of motion computed as the cross product of movement vectors between successive time steps. If no rotation was detected (i.e. cross-product equal to 0), the rotation direction was copied from the previous time step.

We employed transfer entropy to investigate the coupling between female leaders and male followers during tandem runs (refer to [9] for a detailed description of this methodology). Transfer entropy is an information-theoretic measure that quantifies the predictive power given by knowledge of the present state of an individual about the future state of a different individual. In other words, it measures causal interactions between a sender and a receiver in terms of Granger causality [33]. If L and F are behavioural sequences representing the leading female and the following male, then transfer entropy from L to F is defined as

$$T_{L\to F}=\sum _{\hspace{0.17em}{f}_{i+1},f_i^{(k)},l_i}p(\hspace{0.17em}{f}_{i+1},f_i^{(k)}{l}_i){\log }_2\frac{\hspace{0.17em}p(f_{i+1}|f_i^{(k)}{l}_i)}{\hspace{0.17em}p(\hspace{0.17em}{f}_{i+1}|f_i^{(k)})},$$

where l_i is the value of sequence L at time i, f_i+1 is the value of sequence F at time i + 1 and $f_i^{(k)}$ is the k-history of F at time i (i.e. the last k states in the sequence). As range of values of transfer entropy is determined by the encoding of states in the sequences, we can normalize its value to obtain a coupling measure in the range of [0;1] by dividing it for its maximum [9,34]. Normalized transfer entropy indicates the proportion of the follower's future behaviour that is predicted by the leader's present behaviour: it is 1 when the follower behaviour is entirely determined by the behaviour of the leader, and 0 when the two are independent from each other. Furthermore, transfer entropy can be computed in both directions, from leader to follower and from follower to leader. By comparing these values, T_L→F and T_F→L, we can obtain the predominant direction of information flow. The difference in transfer entropy between the two directions, T_L→F − T_F→L, is called net transfer entropy [9,34]. The value is positive when information flow from leader to follower is predominant (T_L→F > T_F→L) and negative when flow from follower to leader (T_L→F < T_F→L) predominates.

To test that our results were significant, and not an artefact of finite sample size, we artificially created surrogate datasets by pairing time series obtained from leaders and followers, not tandem running together; then, we computed transfer entropy for these datasets and compared it with the experimental results [9,34]. To produce a surrogate dataset, we paired randomly selected leaders and followers belonging to different tandem runs. Although females and males from different tandems are still influenced by the same environmental cues of the experimental arena, this randomization process ensures that there are no causal interactions within the surrogate pair. For each pairing combination and parameter configuration, we repeated the randomization process and obtained 100 surrogate datasets. We used these to estimate the mean and standard error of transfer entropy for surrogate datasets with the same size of the experimental ones. Finally, measurements of transfer entropy for the experimental data were discounted by a correction factor given by the mean values estimated from surrogate datasets to account for their finite sample sizes.

Our information-theoretic analysis depended on setting the values of two parameters: the sampling period of continuous spatial trajectories and the history length of transfer entropy, k. The optimal choice of these parameters varies for different pairing combinations and focal behavioural patterns due to behavioural, morphological, and cognitive differences manifesting at different time scales [9]. To find good parameterizations, we computed net transfer entropy for 900 different parameter configurations for each species (history length k ∈ {1, … , 20} and sampling period {0.0334s, … , 1.5015s}). The resulting landscapes of net transfer entropy show robustness to different parameter values over most of the tested range (electronic supplementary material, figure S3). We selected the parameter configurations that maximize the net transfer of information (electronic supplementary material, table S1).

For the chosen parameter configurations, we performed two statistical tests. First, we tested if the experimental data showed significantly greater values of transfer entropy with respect to the surrogate data. We used one-sided two-sample Wilcoxon rank-sum tests with continuity correction. Second, we tested differences in the flows of information between the two possible directions (from leaders to followers and from followers to leaders) to determine which among the leader and the follower was the predominant source of information. We used one-sided paired Wilcoxon signed-rank tests with continuity correction. All information-theoretic measures were computed using the rinform-1.0.1 package in R [35].

(e) . Moving speed after separation

When termites in a pair are accidentally separated, females pause while males move to enhance the chances to reunite [19]. As moving speed is related to reunion efficiency [26], we measured the change in movement speed, focusing on a time window around separation events. We compared movement speed between the last 2 s before separation and the first 2 s after separation. For each separation event, we measured the mean movement speed for both time windows. Then, we used linear mixed models (LMM), with the time window treated as a fixed effect and video ID included as a random effect. The model was fit for each combination of pairs. The likelihood ratio test was used to determine the statistical significance of each explanatory variable (type II test). Finally, we examined if re-encounter after separation resulted in a tandem run or not.

(f) . Interspecific competition over a female

Because males of both species show stable tandem runs with C. formosanus females, we introduced one female C. formosanus, one male C. formosanus, and one male C. gestroi to the experimental arena to study interspecific competitions. We prepared 13 replicates and recorded their behaviour for 30 min. Tandem runs were identified using the method described in §2b. By doing so, we obtained the time series of states observed among three individuals. There were four different states: (i) no tandem run is observed; (ii) tandem run between female C. formosanus and male C. formosanus; (iii) tandem run between female C. formosanus and male C. gestroi; and (iv) tandem run involving three individuals. We counted tandem runs of three individuals when both males were concurrently interacting with the female. When three individuals were in a straight line, we regarded it as a tandem run of heading female and the male just after her. Then, we counted the number of transitions from one state to another. Usually, state (i) can transit to (ii) or (iii), state (ii) or (iii) to (i) or (iv), and state (iv) to (ii) or (iii) (figure 4a). Then we compared the tendency of state transition using binomial tests. We also checked if there is a different state transition trend from (ii) or (iii), using Fisher's exact test.

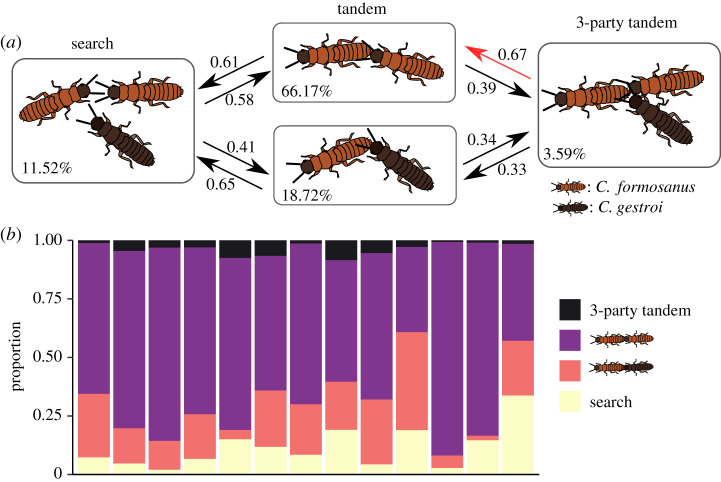
Figure 4.

Competition between C. formosanus and C. gestroi males to follow one C. formosanus female. (a) State transition diagram for a 3-party tandem run with a C. formosanus female, a C. formosanus male and a C. gestroi male. The transition from search to 3-party tandem is not shown (approx. 0.01). The percentage in each box indicates overall time in that state. (b) Proportion of time in each state during observation. Each bar indicates replicate. Overall, the conspecific tandem of C. formosanus was the most frequent state. (Online version in colour.)

3. Results

(a) . Comparison of movement coordination across pairs

Despite the relatively small quantity of sex pheromone involved, C. gestroi conspecific tandem runs lasted as long as those of C. formosanus (mixed-effects Cox model, χ²₁ = 0.942, p = 0.332; figure 1b). As for heterospecific tandem runs, their durations were asymmetric. When the male was C. gestroi, heterospecific tandems lasted as long as conspecific ones (mixed-effects Cox model, χ²₁ = 0.01, p = 0.91; figure 1d). When the male was C. formosanus, heterospecific tandems ended sooner than conspecific ones (mixed-effects Cox model, χ²₁ = 19.52, p < 0.001; figure 1c). Thus, tandem runs were unstable only for the combination of a C. gestroi female and a C. formosanus male, as predicted in [24,25]. For the stable combinations, tandem breakups appeared to happen accidentally, as their durations were best fitted by exponential distributions (i.e. a smaller AIC comparing to gamma, Weibull and power-law distributions). On the other hand, tandem durations of the unstable combination of a C. gestroi female and a C. formosanus male followed a gamma distribution.

Moving speeds of females and males were highly correlated across all pairing combinations (electronic supplementary material, figure S1). However, modal moving speed was higher for conspecific C. formosanus pairs (17.0 mm sec⁻¹) than for conspecific C. gestroi pairs (14.5 mm s⁻¹; electronic supplementary material, figure S2). Thus, for heterospecific pairs to synchronize their movement, one or both partners need to adjust their speed. We found evidence that males make this speed adjustment; the modal speed of heterospecific pairs was similar to that of the female's conspecific tandem runs (C. formosanus female–C. gestroi male: 17.5 mm s⁻¹, C. gestroi female–C. formosanus male: 14.5 mm s⁻¹; electronic supplementary material, figure S2). Also, across all tandem runs, speed depended on the female species (LMM; female moving speed, female species: ${\chi }_1^2=14.888$, p < 0.001, male species: χ²₁ = 2.0802, p = 0.1492; male moving speed, female species: χ²₁ = 12.2442, p < 0.001, male species: χ²₁ = 1.5145, p = 0.21845).

The asymmetry between heterospecific pairings was further supported by an information-theoretic analysis. The future behaviour of males was significantly predicted by the present behaviour of females in all stable combinations—that is, conspecific pairs or heterospecific pairs of C. formosanus females and C. gestroi males (Wilcoxon rank-sum test, p < 0.001; figure 2; electronic supplementary material, table S2). In these pairs, information flow from females to males was significantly stronger than in the opposite direction (Wilcoxon signed-rank test, p < 0.05; electronic supplementary material, table S2). However, in the unstable heterospecific pairs of C. gestroi females and C. formosanus males, neither female nor male behaviour was significantly predicted by their partner's behaviour (Wilcoxon rank-sum test, p > 0.05); thus, there was no predominant direction of information flow (Wilcoxon signed-rank test, p > 0.05; figure 2; electronic supplementary material, table S2). The lack of predictive power by female behaviour of male behaviour indicates deficient following by males in this combination.

Figure 2.

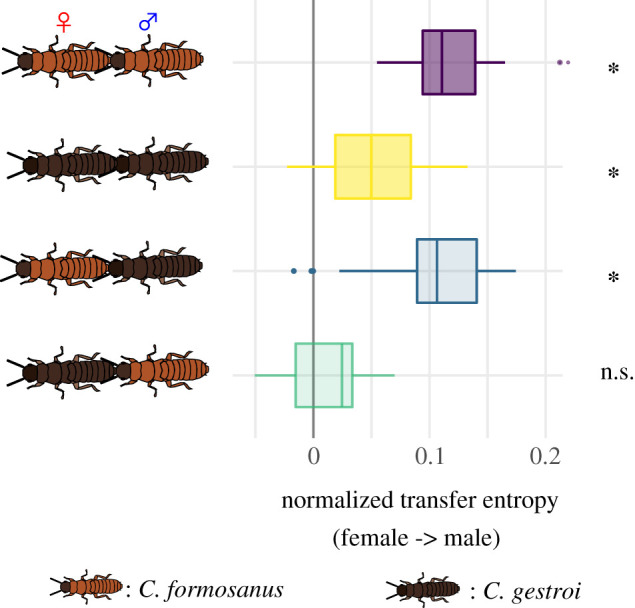
Comparison of the strength of information flow during tandem runs. The predominant direction of predictive information is given by the proportion of uncertainty reduction explained by the interaction between leading females and following males. * indicates the combination with significant information flow from female to male. (Online version in colour.)

(b) . Evaluation of leader females by follower males

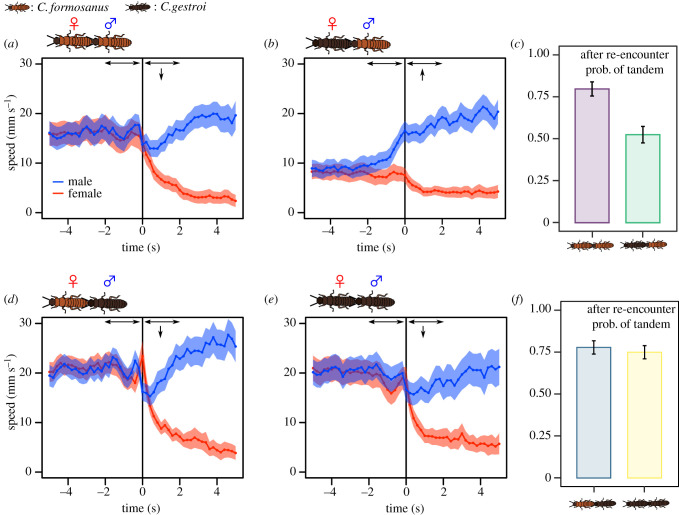
After separation, females of both species slowed down significantly irrespective of partner species (comparison of mean speed two seconds before and two seconds after separation, LMM, p < 0.01; figure 3a,b,d,e). Males of C. gestroi evaluated both conspecific and C. formosanus females as good leaders because they slowed down just after the separation to enhance re-encounter rates (LMM, p < 0.05; figure 3d,e). On the other hand, C. formosanus males slowed down upon separation from conspecific females (LMM, estimate ± s.e. = −0.4409 ± 0.2217, ${\chi }_1^2=3.9546$, p = 0.04674; figure 3a), whereas they increased their speed after separating from C. gestroi females (LMM, estimate ± s.e. = 1.1553 ± 0.1981, χ²₁ = 34.003, p < 0.0001; figure 3b). Moreover, when the original partners did re-encounter each other, their probability of resuming a tandem run was lower for pairings of a C. formosanus male and a C. gestroi female than for other pairing combinations (GLMM, Tukey's test, p < 0.01; figure 3c,f). These results suggest that a C. formosanus male evaluates a C. gestroi female as a poor leader and begins to search for another partner upon separation. Thus, male preference plays an important role in the success of heterospecific tandem runs.

Figure 3.

Behavioural change of tandem runners before and after separation events. (a,b,d,e) The time development of speed across different combinations of mating pairs. Pair separation occurs at 0 s. Shaded regions indicate mean speed ± 2 s.e. Arrows indicate significant increase (upwards) or decrease (downwards) of male speed compared with before separation. (c,f) The probability of resumption of a tandem run upon re-encounter following a separation event. We obtained this probability by observing if a separated female and a male started a tandem run (=1) or not (=0) when they first came close enough for interaction after the separation event. Bars indicate the mean ± s.e. (Online version in colour.)

(c) . Interspecific competition over females

When one C. formosanus male and one C. gestroi male competed over one C. formosanus female, the termites could be in one of four different states (figure 4a): search (no tandem run), conspecific tandem run of C. formosanus, heterospecific tandem run of C. formosanus female and C. gestroi male, and three-partner tandem run with the two competing males side by side behind the female. When two individuals were in tandem, there was no interspecific difference in the probability to return to the search state (Fisher's exact test, p = 0.5174). However, when three individuals were in tandem, the probability of state transition was asymmetrical; competitions were twice as likely to end with victory by the C. formosanus male than by the C. gestroi male (binomial test, p < 0.001). As a result, the most frequently observed state was conspecific tandem running by C. formosanus (figure 4b). These results demonstrate that C. formosanus males are superior to C. gestroi when competing over a female, possibly because of their better-matched moving speed and body size.

4. Discussion

Our study has demonstrated that tandem coordination depends on a close association between the behaviour of male followers and the signal strength of female leaders. Males of C. gestroi, whose females produce only a tenth of the amount of sex pheromone as C. formosanus [25], are adapted to follow a weak signal and so can maintain stable tandem runs with C. formosanus females. On the other hand, C. formosanus males are adapted to follow females with stronger signals and display a poor ability to maintain tandem runs with C. gestroi females. When they become separated from a female with a weak signal, C. formosanus males search for an alternative leader. This result demonstrates active behavioural mate choice in termites, hypothesized in previous studies but not shown empirically [36,37]. Note that females behaved the same regardless of male species, implying that they maintain the tandem passively through pheromone production, rather than actively choosing their potential mate. In summary, our results suggest that behavioural coordination in termite tandem runs is a product of coevolution between females and males. The species-specific association of leader and follower phenotypes may explain previous observations on the collective behaviour of mixed-species groups; some function as well as conspecific groups, while others show a loss of coordination [38–40].

Leadership may be more likely in some individuals, due to traits like body size or personality (reviewed in e.g. [6,41,42]). In such a group, coordination may be difficult when there is a conflict of interest among members (e.g. about where to go). However, this is not the case in termite tandem runs. There is no conflict over leadership because roles are usually fixed by sex, with females leading and males following, although this is flexible in occasional same-sex pairs [43]. Additionally, it is reasonable to assume that the pair share the same goal of successful colony foundation. Predation risk is high during tandem [44], so pairs must establish a nest as soon as possible regardless of combinations [45]. Their highest priority is not who they found a colony with but simply to found as soon as possible [46]. Indeed, C. formosanus males were willing to approach C. gestroi females and formed tandem pairs with them, although they evaluated conspecific females more highly upon separation events (figure 3). Thus, we conclude that unstable tandem runs result not from conflicts of interest but from a communication mismatch between C. gestroi females and C. formosanus males, where female signalling is not sufficient for the males to follow.

Laboratory experiments have shown that individual behaviour underlying group coordination can evolve in just a few generations [47,48]; however, such changes have yet to be documented in the field. Species invasions provide opportunities to observe evolutionary changes in behaviour [49,50]. In our study of an invasive population, we found less stable tandem runs than those previously observed in a native population of C. formosanus in Japan [19] (electronic supplementary material, figure S4). This suggests modification of tandem coordination following invasion, although such differences may have already existed between the source population and other native ranges [51]. Further investigation is needed to determine what is the cause of evolutionary change in behaviour of C. formosanus from Florida, as invasive populations often have different populational structures from native populations (e.g. high density or relatively low genetic diversity [51]). Moreover, colony foundation experiments have confirmed that hybrid colonies can last greater than 2 years [52]. Research on female pheromone production and male following ability of hybrid adults will tell us the inheritance mechanism of movement coordination in termites.

Evolutionary theory predicts that the development of conserved morphological structures can involve significant modifications in their regulatory mechanisms [53,54]. We argue that this is possible even in behavioural systems. For example, similar group-level patterns can emerge from different individual-level behavioural rules regulating social interactions [55,56]. In this study, we show that a similar level of behavioural coordination can be achieved from different leader/follower combinations. In C. formosanus, the leader produces an abundant signal tracked by a competitive follower; in C. gestroi, the leader produces a weaker signal, but the follower has enhanced tracking ability. Tandem runs are seen across most termite taxonomic groups [16]. However, our results imply that their underlying mechanisms for coordination can vary, because the adaptiveness of a tandem run is not determined by how they coordinate but by how well they maintain contact during nest site search in a vulnerable period. By emphasizing that there are multiple solutions for the same coordination problem, our study has implications beyond pair coordination and gives insight into the convergent evolution of collective behaviour across different taxa.

Data accessibility

All data are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.9w0vt4bf9 [57].

Authors' contributions

N.M.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, validation, visualization, writing—original draft; S.-B.L.: investigation, methodology, writing—review and editing; G.V.: formal analysis, methodology, validation, visualization, writing—review and editing; T.C.: conceptualization, funding acquisition, methodology, writing—review and editing; S.C.P.: conceptualization, supervision, writing—review and editing. All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

N.M. is supported by a JSPS Overseas Research Fellowship, a JSPS Research Fellowships for Young Scientists CPD (20J00660), and a Grant-in-Aid for Early-Career Scientists (21K15168). G.V. is supported by research funds from Arizona State University to Prof. Bert Hölldobler. T.C. is supported by a grant from USDA National Institute of Food and Agriculture Hatch projects number FLA-FLT 005660, and by an NSF-DEB grant, under agreement no. 1754083.