Abstract
Coronavirus disease 2019 (COVID-19) is a contagious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). It may cause severe ailments in infected individuals. The more severe cases may lead to death. Automated methods which can detect COVID-19 in radiological images can help in the screening of patients. In this work, a two-stage pipeline composed of feature extraction followed by feature selection (FS) for the detection of COVID-19 from CT scan images is proposed. For feature extraction, a state-of-the-art Convolutional Neural Network (CNN) model based on the DenseNet architecture is utilised. To eliminate the non-informative and redundant features, the meta-heuristic called Harris Hawks optimisation (HHO) algorithm combined with Simulated Annealing (SA) and Chaotic initialisation is employed. The proposed approach is evaluated on the SARS-COV-2 CT-Scan dataset which consists of 2482 CT-scans. Without the Chaotic initialisation and the SA, the method gives an accuracy of around 98.42% which further increases to 98.85% on the inclusion of the two and thus delivers better performance than many state-of-the-art methods and various meta-heuristic based FS algorithms. Also, comparison has been drawn with many hybrid variants of meta-heuristic algorithms. Although HHO falls behind a few of the hybrid variants, when Chaotic initialisation and SA are incorporated into it, the proposed algorithm performs better than any other algorithm with which comparison has been drawn. The proposed algorithm decreases the number of features selected by around 75% , which is better than most of the other algorithms.
Keywords: COVID-19 detection, Convolutional Neural Network, Harris Hawks optimisation, Simulated Annealing, Chaotic initialisation, CT scan image
1. Introduction
COVID-19 is a contagious respiratory disease caused by SARS-CoV-2. It first emerged in Wuhan, China in December 2019 and has resulted in an ongoing global pandemic. The usual symptoms include fever, dry cough, fatigue, breathlessness, and, loss of smell and taste. Serious complications may lead to death. The standard method for detection is by real-time reverse transcription polymerase chain reaction (rRT-PCR). However, the method also has a high sensitivity value and can take a few hours to produce the results. Therefore, conventional radiological imaging modalities (X-rays, CT-scans, etc.) have also been widely used as a quick screening measure.
In the past years, Deep Learning (DL) has been successfully applied in several cross-domain tasks to achieve state-of-the-art results. This can be explained by the increase in the available computing power as well as an increase in the availability of large datasets. DL has also been widely adopted for the purpose of automatic feature extraction from data as opposed to manual feature engineering. In particular, Convolutional Neural Networks (CNNs) have been successfully utilised for the classification of many complex datasets in the domain of image processing and computer vision among others.
FS is the method of selecting a subset of features or attributes that contribute most to the variable we are keen on predicting. FS aims to get rid of redundant attributes while predicting using a learning model so that it takes lesser time to train the model and delivers good performance. If there are dimensions in the feature vector, then a total of combinations are possible. Therefore, FS is a NP-hard problem, and solutions to such problems can only be found in exponential time. Evaluation of FS algorithms is also not practically feasible due to high cost of computation. Several methods have been proposed to deal with the FS problem. These approaches can be broadly classified in to the following three categories:
-
1.
Filter methods: Here, some statistical process is conducted to identify the correlation between the features and the output variable and metrics. Based on this, the suitable features are then selected. A few examples of such methods include Fisher score [1], Mutual Information [2] and Relief [3].
-
2.
Wrapper methods: Here a model is trained using some learning algorithm. Some examples include binary particle swarm optimisation [4] and ant colony optimisation [5].
-
3.
Embedded methods: This is a combination of the above two methods. Notable examples would be LASSO [6] and RIDGE [7].
In general, filter methods are much faster than wrapper methods. This is because wrapper methods use some supervised learning procedure which is a time-consuming step. On the other hand, wrapper methods generally achieve higher classification performance than filter methods.
Meta-heuristic algorithms are computational paradigms applied to find solutions to optimisation or FS problems. Heuristic algorithms carry out a guided search over the entire search space to discover a reasonably good feature vector which may not be the best possible solution but is admissible within computational limitations. Meta-heuristics find their applications in a wide range of fields [8] for solving FS problems such as handwriting recognition, medical diagnosis, gene selection, benchmark problems and so on. Meta-heuristic algorithms are generally preferred due to their flexibility, non-derivative nature, ability to avoid local optima and ease of implementation.
Meta-heuristic algorithms generally consist of two broad phases of exploration and exploitation. An efficient algorithm must achieve a good trade-off between the two phases to produce competent results. This requires a good deal of tuning of the underlying parameters in order to obtain the final results. In addition, the above two phases must also be efficient so as to be able to obtain the solution in an acceptable amount of time. It is also noted that these algorithms do not guarantee the best solution since the entire search space is not explored. There may be a few reasons for this: the search space where the optimum solution lies is not explored, the area of the search space with the optimum solution is found but the algorithm does not converge properly, or both of the above may occur. Furthermore, the existence of the No Free Lunch (NFL) theorem [9] states that no single algorithm exists which is able to guarantee good performance on all the datasets. The above facts encourage further research into the creation of new or hybrid meta-heuristic algorithms. Keeping the above facts in mind, in this paper, we have proposed a hybrid meta-heuristic FS algorithm for the classification of COVID-19 using CT-Scans images.
Myriad meta-heuristic algorithms have been proposed for the purpose of FS. Each algorithm has its own advantages and drawbacks. The performance is also reliant on the inherent traits of the dataset on which our model is trained. Often, the dataset is trained with hybridised algorithms so that the shortcomings of one algorithm is overcome by the other algorithm(s) [10]. Suppose if an algorithm with good exploration properties is coupled with an algorithm that exhibits good exploitation, it will enhance the performance of the entire system as a whole and establish a trade-off between the two properties in the system. Here, the local optima problem that HHO suffers from is overcome by integrating the SA algorithm and the population diversity of the search space is augmented by applying Chaotic initialisation.
Hybridisation of meta-heuristics is a known approach for FS. An early work in [11] proposed the hybridisation of GA with local search. In [12], Memetic algorithm and late hill climbing are hybridised for FS to aid in facial emotion recognition. A similar work [13] on hybridisation also obtained good results on UCI datasets. A very recent work in [14] hybridised Harmony Search with Artificial Electric Field Algorithm for the purpose of FS. The work by [15] is another recent work in hybridisation where FS has been performed for Indic script classification. Here, the Binary Particle Swarm Optimisation and the Binary Gravitational Search Algorithm have been combined.
Most of the hybridisation approaches mentioned above also suffer from the problem of parameter tuning. In addition, the time required to obtain a solution is also more due to the combination of two algorithms. Some works have also noted that parallelised algorithms can be explored in future research which can mitigate the time consumption issue. Furthermore, the NFL theorem is also applicable in this case as well. No single hybridised approach can guarantee performance, and several works in the same direction continue to be proposed.
In this work, a two-stage pipeline for the detection of COVID-19 in CT-scan images is proposed. The first stage is feature extraction, which is followed by the second stage of FS and classification. We use a state-of-the-art CNN model, DenseNet [16], for the purpose of extracting discriminative features from the input CT-scans. The models are first pre-trained on the ImageNet dataset and then evaluated on SARS-COV-2 CT-Scan dataset. This increases the performance and robustness of the model, despite the small amount of training data available for the problem under consideration.
In the second stage, FS is performed on the features extracted in the previous stage. In general, the features that are extracted by the CNNs may contain some redundant and highly correlated features. If such features are removed, then the classification performance of models using the optimal subset of features is expected to improve. At the same time, a reduction in the total number of features helps to reduce the computational time taken by various classification algorithms using these features.
In this study, Harris Hawks optimisation (HHO) [17] with Simulated Annealing (SA) [18] and Chaotic initialisation or in short Chaotic Harris Hawks optimisation Algorithm (CHHO) [19] has been utilised for the purpose of FS. This leads to a better performance in terms of accuracy as compared to the CNN model used for classification. It is also noted that this stage also reduces the number of features to a large extent, thereby reducing training time and memory requirement by the model.
Simulated Annealing (SA) is applied here to improve the exploitation capability of HHO while dealing with the high dimensional feature vector. Previously, SA has been successfully incorporated into algorithms to enhance the local search property of such algorithms. For example, it was used to evaluate the performance of FS [20], to improve the best solution after each iteration [21], to enhance the exploitation search capability [22], and to evaluate PSO performance as a wrapper-based method [23]. The enhanced performance that was obtained by employing the SA in these previous studies inspired us to include the SA into HHO algorithm to enhance the local search during FS.
For the purpose of training and testing of the present approach, the SARS-COV-2 CT-Scan dataset [24] is used. It consists of 2482 CT-scan images in total: 1252 are from COVID-19 positive patients and 1230 are from COVID-19 negative patients. The presented method obtains an accuracy of 98.85%.
To sum it up, the highlighting points of this work are as follows:
-
1.
A two-stage pipeline for the detection of COVID-19 in CT-scan images is proposed.
-
2.
The first stage is the feature extraction from the CT-scans using a DenseNet based CNN model.
-
3.
The second stage is the selection of relevant features using the HHO algorithm combined with SA and Chaotic initialisation.
-
4.
Experimental results indicate that the present approach obtains better results than when only using the DenseNet model, and also when compared to some state-of-the-art methods applied on the same dataset considered here.
-
5.
The method is also evaluated on some real-world engineering problems, and the results are comparable with current state-of-the-art approaches.
The remaining part of this work is as follows: Section 2 provides an overview of previous works on the topic. Section 3 discusses the present method. Section 4 contains the experimental results and we end with the concluding remarks in Section 5.
2. Related work
Over the last decade, DL techniques have been widely used in various domains, including medical image processing. This is mainly due to the increase in computing power as well as due to the availability of large datasets. Many works have been proposed in domains such as image classification, image segmentation, computer aided diagnosis, etc. which utilise these DL based methods to achieve state-of-the-art results. Recently, several DL based works have also been proposed to aid in detecting COVID-19 in medical images.
DL based models generally require a large amount of data for generalisability. However, it is often difficult to get a large quantity of data, especially in new domains. Waheed et al. [25], in their work, have proposed an Auxiliary Classifier Generative Adversarial Network (ACGAN) based model termed as CovidGAN. The authors have used the CovidGAN model to generate synthetic chest X-ray images corresponding to COVID-19 positive and COVID-19 negative classes. They have prepared a dataset by combining three publicly available datasets: IEEE Covid Chest X-ray dataset, COVID-19 Radiography Database and COVID-19 Chest X-ray Dataset Initiative. The final dataset contains 1124 chest X-rays of which are 403 are COVID-19 positive and 721 are normal. They demonstrate that the inclusion of the synthetic images in a VGG16 classifier improves the accuracy and F1 score values to 95% and 0.95 respectively from 85% and 0.85 respectively.
Jaiswal et al. [26] in their work have employed transfer learning to improve the performance of their DL models. The authors have first trained the models on the ImageNet dataset. Thereafter, the pre-trained models are again trained on the SARS-CoV-2 CT-scan dataset to classify the input images into two classes of COVID-19 infected and COVID-19 negative. The authors have observed that the DenseNet architecture provides the better result as compared to other architectures such as VGG, ResNet and InceptionResNet. An accuracy score of 96.25% is reported on the test set.
Pruning and ensembling are common approaches for improving the performance of DL models. The authors in [27] have utilised such techniques to detect pneumonia and COVID-19 related artefacts in chest X-rays. They have proposed an end-to-end pipeline for the same task. The authors have also used modality specific training where the models are trained on a pneumonia-related dataset before being trained on the COVID-19 data. The reported accuracy and AUC values are 99.01% and 0.9972 respectively.
In [24], the authors have put forward a COVID-19 related dataset named as the SARS-CoV-2 CT-scan dataset for the benefit of the research community. In addition to this, they have provided a baseline model for the purpose of comparison. An explainable deep neural network (xDNN) has been employed for the purpose of detecting COVID-19 in the CT scan images. The method has obtained accuracy and AUC values of 97.38% and 97.36% respectively.
FS is a process in which a subset of features is chosen from a given feature vector. The idea is to select the relevant features from the original features. This generally removes redundancy in the features and provides several benefits such as reduced training times, better performance, etc. Meta-heuristic algorithms have been widely used in the literature for the purpose of FS.
Elaziz et al. [28] have proposed a framework to detect COVID-19 in chest X-rays in which they have used Fractional Multichannel Exponent Moments (FrMEMs) for the purpose of feature extraction. Following the feature extraction stage, FS was performed using the Manta Ray Foraging optimisation (MRFO) algorithm based on Differential Evolution (DE). For testing their approach, the authors have utilised two datasets. The first is a combination of the Cohen dataset and a pneumonia dataset from Kaggle. It consists of 216 COVID-19 positive X-rays and 1675 COVID-19 negative X-rays. The second dataset consists of 219 COVID-19 positive images and 1341 COVID-19 negative images. It was collected by a team of researchers and doctors. The reported accuracies are 96.09% and 98.09% respectively on the first and second datasets respectively.
In a similar work, Sahlol et al. [29] have used a CNN as the feature extractor and a combination of fractional-order calculus with the Marine Predators Algorithm (FO-MPA) for the purpose of FS. They have used the same two datasets as the work by Elaziz et al. and reported the accuracies as 98.7% and 99.6% respectively.
In [30], the authors have used a 2D curvelet transform for the purpose of getting features from an input grayscale X-ray. Thereafter, the coefficients of the obtained feature matrix have been optimised using the Chaotic Salp Swarm Algorithm (CSSA). Ultimate, a DL model, EfficientNet-B0, has been used for classification. They have used a dataset consisting of 2905 X-rays of which 219 are from COVID-19 patients, 1341 are normal, and 1345 are from viral pneumonia patients. They have further generated synthetic data so as to produce 7980 images in total equally split into the three classes. The authors have reported the accuracy and F-measure values as 99.69% and 99.53% respectively.
Whereas the above works utilised meta-heuristic algorithms for the purpose of FS, the work by Goel et al. [31] utilised the same for a different purpose. The authors have proposed an optimised CNN (OptCoNet) for the purpose of detecting COVID-19 in chest X-rays. The CNN models is a conventional one with the usual layers such as convolution, pooling, dense, fully-connected, etc. However, the authors have used the Grey Wolf optimisation (GWO) algorithm for tuning the hyperparameters of the CNN. The authors have compared the approach with other state-of-the-art CNNs and have found that it performs better. A combination of six publicly available datasets has been used by the authors. The datasets contain chest X-rays corresponding to normal, pneumonia and COVID-19 categories. There were 2700 X-rays in total, and 900 of these were from COVID-19 affected patients. The authors reported the accuracy, sensitivity, specificity, precision, and F1 score values as 97.78%, 97.75%, 96.25%, 92.88% and 95.25% respectively.
A similar work by Ezzat et al. [32] used the Gravitational Search Algorithm (GSA) to optimise the hyperparameters of a DenseNet121 model. The authors have prepared a dataset which has been named as the Binary COVID-19 dataset. It is a combination of the Cohen dataset and the Kaggle chest X-ray dataset. There are 99 images from COVID-19 positive patients and 207 from COVID-19 negative patients. Among the 207, 104 are from healthy patients, whereas the remaining are from patients suffering from diseases such as pneumonia, SARS, etc. The authors reported the accuracy and F1 score of their method as 98.38% and 98% respectively.
3. Proposed work
3.1. Feature extraction
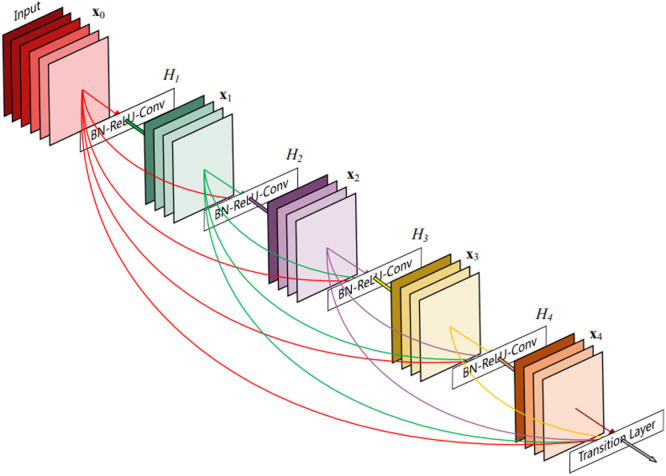
In this work, for the purpose of feature extraction, a CNN based model is used. In particular, the DenseNet201 model architecture, proposed in the work by Huang et al. [16], is used. The DenseNet architecture is similar to conventional CNNs in many respects. However, the main difference is that the output of a particular layer is connected to all the subsequent layers. This is highlighted in Fig. 1. These direct or dense connections provide an increased parameter efficiency. This is because redundant features are not learned by the later layers as the earlier layers already contain the same information. The inclusion of the dense connections also leads to an improved flow of gradients through the network which helps in the training stage.
Fig. 1.
A pictorial representation of the dense connections in the DenseNet architecture [16].
In the training stage, transfer learning is employed where the model is first trained on the ImageNet dataset before training on the CT-scan dataset. After training on ImageNet, the last dense layer is replaced with a custom dense layer of dimension 2 with softmax activation representing the two output classes of COVID-19 positive and COVID-19 negative. It is noted that the layer before the custom dense layer is a global pooling layer which produces a 1D vector of dimension 1920. This vector represents the extracted features which are used in the next stage of FS. The model is trained for 40 epochs at a learning rate of 0.001 using the Adam [33] optimisation algorithm. The training-testing ratio is 85%–15% with an additional 20% of the training data being used for validation.
3.2. CHHO algorithm
HHO algorithm [17] is a meta-heuristic population-based optimisation algorithm developed by Heidari and Mirjalili et al. in 2019. It is influenced by the manner in which Harris Hawks’ track a prey in nature. The Harris Hawks’ exhibit a special kind of technique to hunt the prey named surprise pounce. HHO algorithm conveys various exploration and exploitation approaches, that are affected by the exploring of the target, surprise pounce, and then attacking the prey in a distinctive style. A mathematical prototype is put forward to replicate the way in which Harris Hawks’ hunt in nature. Now, the various steps that HHO algorithm comprise to emulate the attacking style of nature’s Harris Hawks’ are described.
3.2.1. Initialisation
Chaotic initialisation is done when assigning values to the vectors initially. The feature vectors are initialised using the Sine Chaotic map. The first feature vector is initialised randomly and the other feature vectors are derived from the first one by using the Sine Chaotic map. Additionally, all the other parameters are set to some starting values. Using Chaotic maps [34] [35] to look for global optimum solutions aids in enhancing the diversity of the solutions. Let denotes the th feature vector. Then the formula for obtaining the , the feature vector, given the values of the th feature vector can be obtained by any of the following Chaotic maps.
-
1.Sine Chaotic Map:
(1) -
2.Singer Chaotic Map:
(2) -
3.Sinusoidal Chaotic Map:
(3) -
4.Chebyshev Chaotic Map:
(4) -
5.Tent Chaotic Map:
(5) -
6.Logistic Chaotic Map:
(6) -
7.Iterative Chaotic Map:
(7)
3.2.2. Exploration
In this phase, all the Harris Hawks are considered as possible solutions to the FS problem. The Harris Hawks are one of the most intelligent birds and they can effortlessly trace a prey with their keen eyes but at times, the prey cannot be seen. In HHO, each Harris Hawk is considered a possible solution and the prey is taken to be the Harris Hawk which yields the minimum value when passed to the objective function (the best possible solution amongst the current set of Harris Hawks, one which yields maximum classification accuracy selecting the minimum number of features possible). There are two possible ways to imitate the exploration strategy of Harris Hawks as stated in Eq. (8).
| (8) |
Here, denotes the position of a Harris Hawk in the th iteration. is the new position of the Harris Hawk at the end of the th iteration. is the location of the prey. signifies an arbitrary solution chosen from the current population of the Harris Hawks. Here, , are numbers that are randomly chosen from the range (0, 1). denotes the lower limit or bound and stands for the upper limit or bound. stands for average position of the current generation of hawks. And the formula for is given by Eq. (9).
| (9) |
where, the size of the current population is M and the position of every hawk in the th iteration is given by .
This first perspective gives rise to solutions based on the position of a randomly chosen hawk and the locations of other hawks. The second perspective initiates solutions based on the position of the prey, mean position of the hawks at the beginning of the current iteration, and other arbitrary scaled factors. Here, is a scaling factor and as the value of tends towards 1, it aids in enhancing the randomness of this method. To the Lower Limit (), a random length is added. It ensures that more domains of the feature space are discovered.
3.2.3. Changeover between exploration and exploitation
The HHO algorithm can exhibit a changeover between the exploration and exploitation aspects. It can also show alteration between various exploitative actions based on the escaping energy of the rabbit and the probability of the rabbit escaping. As the prey attempts to escape, its escaping energy diminishes. If the initial energy of the prey is depicted by , the current iteration is denoted by m and the total iterations are denoted by , then the escaping energy of prey in the th iteration (say, X) can be depicted by Eq. (10).
| (10) |
The value of varies in the range [−1, 1] randomly. When the value of decreases from 0 to −1, it signifies that the prey gets tired and when it increases from 0 to 1, it means that the prey gets revitalised. Normally, decreases as the iterations progress. Exploration is favoured when and exploitation is done when .
3.2.4. Exploitation
In this stage of the HHO, neighbourhood of the feature vectors are exploited. The Harris Hawks execute the surprise pounce (seven kills strategy [36]) by charging on the target spotted in the exploration phase. It utilises four separate approaches based on the location of the chase that was determined in the previous stage. The four approaches comprise soft besiege, hard besiege, soft besiege with progressive rapid dives and hard besiege with progressive rapid dives. When , then it is opted for soft besiege else hard besiege, where stands for the current energy of the prey. There is also another parameter , which designates the probability of the prey escaping and it is taken randomly in the interval (0, 1). Lower value of means that the prey has higher chances of fleeing. The four methods are discussed below.
Soft besiege is opted for when and . The prey or the rabbit has ample energy but the hawks surround the rabbit when it tries to deceive the Harris Hawks and get away. Finally, the hawks carry out the surprise dive on the prey. This can be drafted mathematically as given in Eq. (11) to Eq. (13).
| (11) |
| (12) |
| (13) |
Here, is a random number between 0 and 1, and depicts the random Jump Strength of the prey while it is striving to get away. stands for the difference between the location of the prey and the position of the current Harris Hawk in the th iteration.
Hard besiege is selected when and . The rabbit is worn out and the amount of energy it has to escape is low. The Harris Hawks barely need to perform the surprise dive.
| (14) |
Soft besiege with continuous or progressive rapid dives is the next technique. When the prey has and , it has more energy to get away, and also good chances of escaping. Here the Harris Hawks carry out the surprise dive in two moves.
In the first move, the Hawks surround the prey and move to a location after assessing the next move of the prey.
| (15) |
In the next move, the Harris Hawks choose whether to perform the jump after contrasting with the result of the preceding dive and its corresponding result, and if it is seen that such a dive is not reasonable, then based on the Levy Flight idea, uneven irregular dives are performed. The Levy Flight (LF) idea is used to imitate the misleading manner in which preys behave while trying to escape the swift, non-uniform descents of Hawks around the prey while it strives to get away. It is backed by observations in real life in the way in which various animals such as monkeys and sharks chase preys [37], [38] .
| (16) |
denotes the dimension of the solution. is a random vector of the dimensions . Here, is the Levy Flight function [39], calculated using the equation written below.
| (17) |
where the value of is set to 1.5 and the other two parameters, are generated randomly in the range 0 to 1 (both inclusive). In the method of soft besiege with progressive rapid dives, the position of the Harris Hawk at the end of the iteration is updated according to the formula stated in Eq. (18).
| (18) |
where denotes the value obtained when x is passed as parameter to the fitness or the objective function.
The last technique is Hard besiege with continuous or progressive rapid dives, when . There is not much energy left in the prey to escape and the hawks implement rapid jumps before exhibiting the surprise dive on the prey. The motion of the Hawks can be mathematically shown as in Eq. (18).
The values of and are obtained from the Eqs. (19) and (20).
| (19) |
| (20) |
where is obtained as described in Eq. (3).
3.3. Simulated annealing
SA [40] is a local search algorithm which is incorporated into the HHO to enhance the exploitation properties of the latter, so that it looks for global optimum and does not get stuck in any local optima. It is a probabilistic technique. At each iteration inside the SA, the neighbour of the current solution is assigned to the feature vector if a lower cost than the original feature vector is obtained using the objective function. A neighbour yielding a higher cost in the objective function can also be assigned to the feature vector with a pre-specified probability, to search for the global optimum and avoid local optimum. Hence, the algorithm is hill-climbing, barring the fact that instead of the best move from a point, it chooses a random one. Probability of accepting an uphill move is equal to , where . Hence, is equal to the difference in the value of fitness function() obtained by passing the current state() and the randomly chosen neighbour() of the current state and it is analogous to the difference in the energy levels of the two states in the annealing method. The variable is comparable to Temperature in the actual process of Annealing. It is decreased gradually by a constant until it reaches some value.
3.4. Fitness function
This part is for assessing the quality of a feature vector. Since the FS algorithm used here is a wrapper-based method, a learning algorithm is required. The K-Nearest Neighbours (KNN) classifier [41] is employed for calculating the accuracy of the proposed method. In the method of FS, the main objectives are to increase the accuracy and also decrease the number of features selected. The classification error needs to be minimised for this purpose. Hence it is required to minimise the number of traits selected as well as the error in classifying. The fitness function or the objective function computes the fitness as written in Eq. (21).
| (21) |
where denotes the number of features selected by the current feature vector, denotes the total number of features present in the dataset, stands for the error in classification of the current feature vector and stands for the error in classification when all the features are used. Here, is a parameter in the range 0 to 1(both inclusive) that gives us the relative weightage of the classification error and the number of features selected. After training over the training dataset, it is observed that optimal performance is obtained when the value of is set at 0.2
3.5. Proposed algorithm for feature selection
In the process of FS, our main aims are to minimise the number of attributes chosen and to maximise the accuracy of the model. It was observed in earlier studies, HHO outperformed many other optimisation algorithms. However, the HHO algorithm has two major drawbacks. Firstly, the solutions are not very diverse and secondly, the solutions may get stuck in local optima. To overcome the first drawback, the initialisation is done using the Sine Chaotic map, which ensures solution diversity. Whereas SA algorithm is integrated into the algorithm to augment the exploitation property of the HHO and ensure that the HHO looks for global optima. The SA algorithm boosts the local searchability of the HHO algorithm. When the SA algorithm is invoked from the HHO algorithm, the solution returned is accepted only if the fitness of that solution is not worse than the original solution by some particular value (the tuning settings are recorded in Table 4).
3.5.1. Computational complexity
The FS algorithm that is implemented is the HHO along with SA and Chaotic initialisation. If there are S features vectors initially, the time and space complexity for the initialisation are . If there are M iterations and is the dimension of the search space of the algorithm, then the complexity for updating the location of the feature vectors by the HHO method is O(SM) O(SM ). For SA, the computational complexity is (M ), where denotes the number of iterations inside the SA method and denotes the number of neighbours of the current feature vector generated for choosing a random neighbour, inside the SA method. Hence, the computational complexity of the entire method for FS is: O(S(1MM ) S ). Fig. 2 displays the flowchart for the entire process.
Fig. 2.

Flowchart of the proposed work for the detection of COVID-19 from CT-scans.
4. Results and discussion
4.1. Dataset used
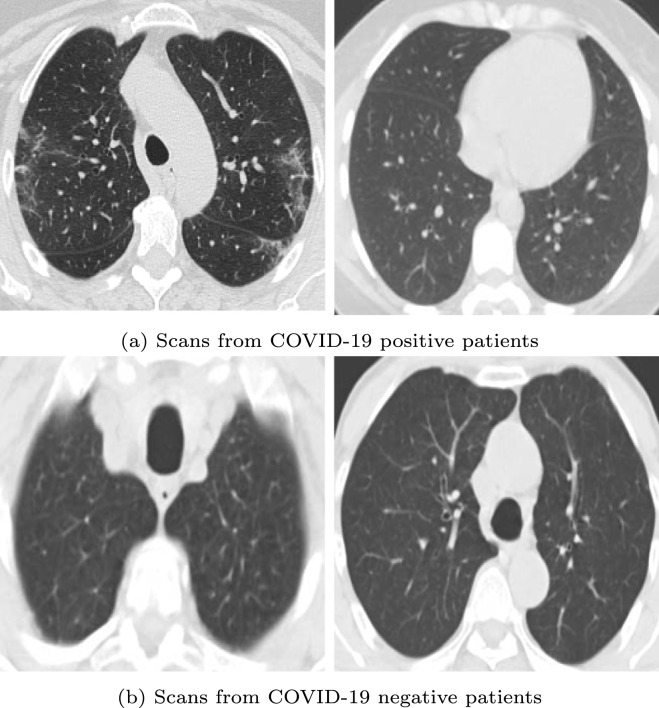
The SARS-COV-2 CT-Scan Dataset1 [24], available on Kaggle, is used in this work for the purpose of training and testing. It contains 2482 CT scan images in total. Among them, 1252 scans are from COVID-19 positive patients whereas the remaining 1230 scans are from COVID-19 negative patients. Fig. 3 shows some representative images from the dataset.
Fig. 3.
Some sample CT scan images from the SARS-COV-2 CT-Scan dataset.
The images are resized to a fixed dimension of 224 × 224 before being passed to the DenseNet model. Online data augmentation is employed to increase the variation in the training data. The augmentation methods include the following: random rotation up to 45 degrees, random zoom up to a factor of 0.2, and random horizontal flip. Thereafter, all the images are normalised into the range of before being passed to the DenseNet model.
4.2. Choice of chaotic map
Table 1 contains the results of the experiments performed with different Chaotic maps to judge the performance of each one. It is noted that a lot of the maps achieve similar accuracies. Finally, we select the Sine Chaotic map which achieves the best accuracy score in the present case.
Table 1.
The experimental results that are obtained with various types of Chaotic maps.
| Chaotic map | Final fitness | Accuracy (%) | No. of features | Time (mm:ss) |
|---|---|---|---|---|
| No map | 0.763453 | 98.48 | 498 | 51:03 |
| Sine | 0.573282 | 98.85 | 469 | 48:12 |
| Singer | 0.596292 | 98.59 | 399 | 51:43 |
| Sinusoidal | 0.581294 | 98.68 | 342 | 49:04 |
| Chebyshev | 0.824525 | 98.03 | 902 | 47:13 |
| Tent | 0.792435 | 98.11 | 758 | 48:59 |
| Logistic | 0.601328 | 98.65 | 528 | 52:02 |
| Iterative | 0.593123 | 98.57 | 405 | 53:43 |
4.3. Tuning of parameters in FS
In this step, a set of parameters are assigned values for the FS algorithm to yield the best performance. The values that the parameters in FS are allocated influence the overall performance of the optimisation algorithm. For each parameter, we run the algorithm over a set of possible values that the parameter can be allotted and then we choose the particular value for which the algorithm gives the best fitness value. In this case, it is aimed to reduce the error rate in the process of classification as well as the number of features selected for FS.
4.3.1. Parameter tuning in SA algorithm
Here we discuss the results of tuning the various parameters in SA. Table 2 highlights the experimental results of tuning the initial and final temperatures. Table 3 highlights the experimental results of tuning the alpha value. Based on the results, the initial and final temperatures are chosen as 20 and 16 respectively. Also, the cooldown factor in SA has been chosen to be 0.2 based on the results.
Table 2.
Parameter tuning for the temperatures in Simulated Annealing.
| Initial temp | Final temp | Initial fitness | Final fitness |
|---|---|---|---|
| 5 | 1 | 0.715347 | 0.715763 |
| 10 | 6 | 0.715347 | 0.715868 |
| 15 | 11 | 0.715347 | 0.759687 |
| 20 | 16 | 0.715347 | 0.714409 |
| 25 | 21 | 0.715347 | 0.716493 |
Table 3.
Parameter tuning for cooldown factor (alpha) in SA.
| Alpha | Initial fitness | Final fitness |
|---|---|---|
| 0.5 | 0.715347 | 0.714930 |
| 0.4 | 0.715347 | 0.715659 |
| 0.3 | 0.715347 | 0.804340 |
| 0.2 | 0.715347 | 0.714409 |
| 0.1 | 0.715347 | 0.715034 |
4.3.2. Parameter tuning for the acceptance threshold
This parameter decides how worse a solution should be accepted from the SA algorithm when it is invoked from the overall HHO algorithm. The exact statement is in line 27 of Algorithm 1 mentioned above.
The values of the constraint are tabulated in Table 4 and as evident from the table, discarding the solutions that are worse than 0.00010 with respect to the original solution leads to the best performance. The solution from the local search (SA) is accepted based on this parameter. If the improvement that it provides is worse than this constraint value (0.00010 as obtained from the table) then the solution is rejected else we take up the value in the future iterations.
Table 4.
Value of constraint parameter such that the feature vectors with fitness worse than the original feature vector should be discarded if they exceed this margin.
| Value of the parameter | Initial fitness | Final fitness |
|---|---|---|
| 0.00005 | 0.725451 | 0.725320 |
| 0.00010 | 0.725451 | 0.724218 |
| 0.00020 | 0.725451 | 0.724888 |
| 0.00030 | 0.725451 | 0.725159 |
| 0.00040 | 0.725451 | 0.725334 |
| 0.00050 | 0.725451 | 0.725343 |
| No constraint | 0.725451 | 0.725409 |
4.3.3. Parameter tuning in HHO algorithm
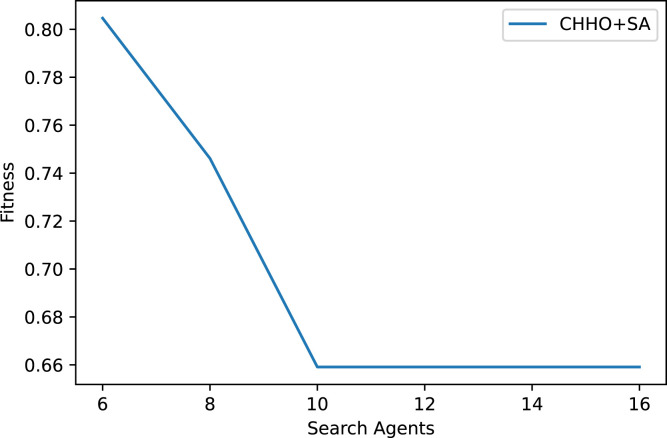
In the HHO algorithm, the first parameter that is encountered for tuning is the number of search agents. From Fig. 4, it can be seen that if the number of search agents is set beyond 10, the outcomes are not affected significantly. Hence, there are 10 search agents initially. If the number of search agents are taken to be more than 10, the least fitness amongst the Harris Hawks is not affected. Hence, it can be inferred that 10 search agents suffice for this case.
Fig. 4.
Graph demonstrating that increasing the number of search agents beyond a particular limit does not yield any major change in the fitness value of the best search agent.
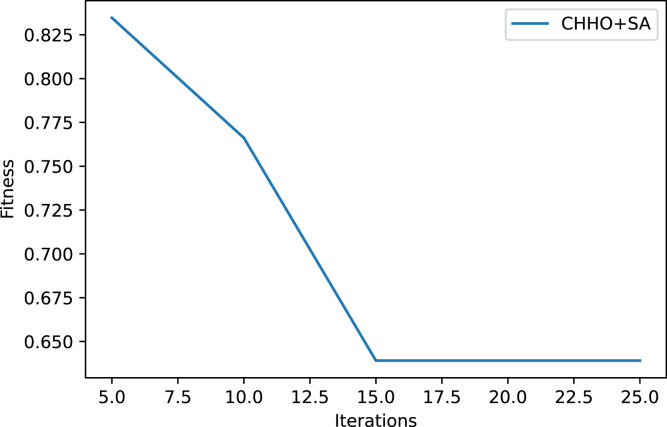
The other parameter that is tuned here is the maximum number of iterations in each run of the FS algorithm. As evident from Fig. 5, the maximum number of iterations is set at 15. Increasing the value of this parameter only increases the time required for the algorithm to execute without any change in the fitness value of the best search agent.
Fig. 5.
Graph illustrating that increasing the maximum number of iterations beyond a particular value does not cause any notable change in the fitness value of the best search agent.
4.4. Parameter settings of the other FS algorithms
The parameters that are used for the other FS algorithms considered in the paper for comparison are mentioned in Table 5. The parameter names stated in the table are taken directly from their respective papers or are commonly used as such. Also, a parameter lying in the range [a, b] signifies that the parameter varies from a to b over the iterations.
Table 5.
The parameter settings for some of the other FS algorithms that are used for comparison.
| Algorithm | Parameters |
|---|---|
| GA | rate_of_crossover 0.4 |
| rate_of_mutation 0.3 | |
| GSA | |
| GWO | lies in [2 0] |
| PSO | Weight lies in [1 0] |
| HS | 0.9 |
| MA | rate_of_mutation 0.2 |
| pos_attraction_constan | |
| pos_attraction_constan 1.5 | |
| init_nuptial_dance_coeff 0.1 | |
| init_random_walk_coeff 0.1 | |
| gravitational_coeff 0.8 | |
| visibility_coeff 2 | |
| BBA | |
| rate_of_pulse_emission 0.15 | |
| loudness_val 1 | |
| WOA | lies in [2 0] |
| SCA | |
| lies in [1 0] | |
| RDA | |
| Upper_Bound 5 | |
| Lower_Bound −5 | |
| EO | |
| size_of_pool 4 | |
| 0.5 | |
4.5. Results
Other than the FS algorithm selected in this paper, many meta-heuristic algorithms such as Genetic Algorithm (GA) [42], Whale optimisation Algorithm (WOA) [43], Grey Wolf optimisation (GWO) [44], Particle Swarm optimisation (PSO) [45], Harmony Search (HS) [46], Binary Bat Algorithm (BBA) [47], Gravitational Search Algorithm (GSA) [48] can also be chosen as FS algorithms. Comparative results have shown that he selected method delivers better performance than the other meta-heuristic FS algorithms and some state-of-the art methods as listed in Table 7.
Table 6 illustrates that the performance of the basic DL model can be boosted by carrying out FS after feature extraction. The other FS algorithms are run till the value of fitness obtained for the leading feature vector is the same for five consecutive iterations or for fifteen iterations (as the number of iterations for the CHHO has been found out to be fifteen by tuning the hyperparameter), whichever is more. The percentage increase column in Table 6 is with respect to the classification accuracy obtained from the DenseNet201 model without using any FS algorithm, which is 93.52%. There is a significant enhancement in the accuracy of the overall model after the process of FS. The HHO algorithm gets stuck in local optima, and hence another meta-heuristic algorithm called SA is used to ameliorate the exploitation property of the HHO algorithm. Also, another demerit of the HHO is the limited population diversity. Hence, the first feature vector is initialised randomly and the rest of the population is initialised using the Sine Chaotic map. The augmented population diversity while initialising , by using the Sine Chaotic map speeds up the convergence rate of the algorithm.
Table 6.
Comparison of the present method with other optimisation based FS methods.
| Algorithm | Pop size | Max_itn | % Acc | % inc(acc) | Features | % decrease | Fit Evn | hh:mm:ss |
|---|---|---|---|---|---|---|---|---|
| DenseNet | N/A | N/A | 93.52 | 0.00 | 1920 | 0 | N/A | N/A |
| GA [42] | 15 | 15 | 97.70 | 4.18 | 642 | 66.56 | 730 | 00:05:19 |
| GSA [48] | 15 | 15 | 98.28 | 4.76 | 1346 | 29.89 | 256 | 00:03:26 |
| GWO [44] | 15 | 15 | 97.63 | 4.11 | 704 | 63.33 | 650 | 00:03:46 |
| PSO [45] | 15 | 15 | 97.63 | 4.11 | 918 | 52.19 | 256 | 00:03:15 |
| HS [46] | 10 | 15 | 98.34 | 4.82 | 642 | 66.56 | 271 | 00:03:09 |
| MA [49] | 15 | 15 | 98.34 | 4.82 | 1346 | 29.89 | 2521 | 00:37:29 |
| BBA [47] | 15 | 15 | 98.34 | 4.82 | 607 | 68.38 | 490 | 00:04:38 |
| WOA [43] | 15 | 15 | 98.34 | 4.82 | 812 | 57.71 | 720 | 00:04:12 |
| SCA [50] | 15 | 15 | 98.12 | 4.60 | 619 | 67.76 | 432 | 00:03:57 |
| RDA [51] | 15 | 15 | 98.03 | 4.51 | 402 | 79.06 | 1230 | 00:12:48 |
| EO [52] | 15 | 15 | 98.12 | 4.60 | 662 | 65.52 | 398 | 00:03:21 |
| HS-MA [53] | 20 | 20 | 98.34 | 4.82 | 912 | 52.50 | 12342 | 02:30:47 |
| SSD-LAHC [54] | 30 | 25 | 98.52 | 5.00 | 902 | 53.02 | 9234 | 02:19:53 |
| HAGWO [55] | 15 | 15 | 98.36 | 4.84 | 1236 | 35.62 | 2000 | 01:28:36 |
| RTHS [56] | 15 | 20 | 98.24 | 4.72 | 179 | 90.68 | 2925 | 00:10:32 |
| HHO | 10 | 15 | 98.42 | 4.90 | 476 | 75.21 | 776 | 00:02:30 |
| 10 | 15 | 98.85 | 5.33 | 469 | 75.57 | 3861 | 00:48:12 | |
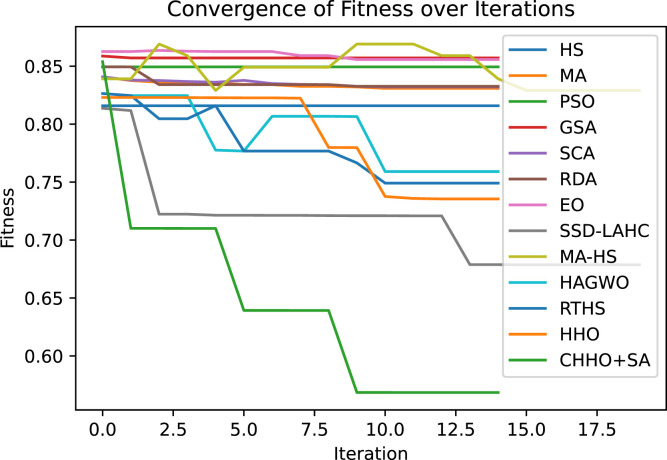
The proposed FS algorithm thus performs better than many other meta-heuristic algorithms. The convergence curves for the algorithms considered for comparison are shown in Fig. 6
Fig. 6.
The convergence curves for a few of the algorithms considered here for comparison of the proposed method.
Table 6 also underlines the number of features selected and the reduction in the number of features selected after running the optimisation algorithms at the end of the proposed method. As evident, the FS process chooses only those features that help in the procedure of classification. The number of features selected by the optimisation algorithm presented in this paper is less than most of the other optimisation algorithms considered here for comparison. The method that we have proposed for FS reduces the number of features selected by more than 75 percent of the original features and around one-fourth of the initial total number of features present are selected for classification. Also, the performance of the system is augmented and error in classification decreases by a significant margin.
Table 7 compares the performance of the presented approach and other state-of-the-art methods. In terms of accuracy, the present method can be compared to the other state-of-the-art methods and delivers performance on a par with the other methods.
From the observed results, it can be inferred that performing FS after the feature extraction process ameliorates the performance of the system. Not only is the number of selected features drastically reduced, but also the accuracy of classification increases by a good margin, by discarding the redundant and insignificant features. It enhances the performance of the system, apart from conserving space and time. It can also be noted that adding the SA and Sine Chaotic maps boosts the accuracy of the HHO each time.
HHO has already been shown to deliver results that are comparable (if not better) to the existing meta-heuristic algorithms [17]. Also, SA has been used previously with the meta-heuristic algorithms to enhance their performance [21], [22], [23]. The enhanced local search property of SA has inspired us to incorporate the SA into the HHO algorithm. The Chaotic maps [34], [35] have been observed to enhance the diversity of the solutions, and hence it has also been integrated into the algorithm.
4.6. Real-world optimisation problems
In this section, we also evaluate the performance of the present approach on some real-world constrained optimisation problems. In the subsections below, we present a brief outline of the problem statements, and also present the results in corresponding tables. In the tables, denotes the value of the function to be minimised, and is a penalisation factor based on the inequality and equality constraints which should be 0 in the ideal case. We have also included the results of some recent algorithms (COLSHADE, sCMAgES, SASS) in addition to the popular and standard algorithms (like GA, GSA, GWO, etc.) for the purpose of comparison. The problems are taken from [57] and the exact definitions of the problems are provided below. To deal with the constraints, a simple boundary penalty based approach is used.
Table 7.
Comparison with state-of-the-art approaches.
4.6.1. RC08: Process synthesis problem
The results obtained by the various algorithms are highlighted in Table 8 and the problem details are defined below.
Table 8.
Results of the various algorithms on the RC08 problem.
| Algorithm | ||
|---|---|---|
| GA | 0.000000000 | 0.416666667 |
| WOA | 2.000000000 | 0.000000000 |
| GWO | 2.000000635 | 0.000000000 |
| PSO | 2.000000000 | 0.000000000 |
| HS | 2.000742969 | 0.000000000 |
| BBA | 2.014718336 | 0.000000000 |
| GSA | 2.000044044 | 0.000000000 |
| COLSHADE | 2.000000000 | 0.000000000 |
| sCMAgES | 2.000000000 | 0.000000000 |
| SASS | 2.000000000 | 0.000000000 |
| SA | 2.826997797 | 0.000000000 |
| HHO | 2.000000000 | 0.000000000 |
| CHHOSA | 2.000000000 | 0.000000000 |
Minimise
subject to the constraints
-
1.
-
2.
with bounds
-
1.
-
2.
4.6.2. RC13: Process design problem
The results obtained by the various algorithms are highlighted in Table 9 and the problem details are defined below.
Table 9.
Results of the various algorithms on the RC13 problem.
| Algorithm | ||
|---|---|---|
| GA | 24 614.05506 | 3.616334258 |
| WOA | 26 888.88250 | 0.000000000 |
| GWO | 26 887.44540 | 0.000000000 |
| PSO | 26 887.42221 | 0.000000000 |
| HS | 26 890.44140 | 0.000000000 |
| BBA | 27 863.88673 | 0.000000000 |
| GSA | 27 536.85742 | 0.000000000 |
| COLSHADE | 26 887.42200 | 0.000000000 |
| sCMAgES | 26 887.42221 | 0.000000000 |
| SASS | 26 887.42200 | 0.000000000 |
| SA | 25 467.04135 | 0.000000000 |
| HHO | 26 887.42339 | 0.000000000 |
| CHHOSA | 26 887.42221 | 0.000000000 |
Minimise
subject to the constraints
-
1.
-
2.
-
3.
with bounds
-
1.
-
2.
-
3.
4.6.3. RC21: Multiple disc clutch brake design problem
The results obtained by the various algorithms are highlighted in Table 10 and the problem details are defined below.
Table 10.
Results of the various algorithms on the RC21 problem.
| Algorithm | ||
|---|---|---|
| GA | 0.5505580258 | 59.324530710 |
| WOA | 0.2352424579 | 0.000000000 |
| GWO | 0.2352430476 | 0.000000000 |
| PSO | 0.2352424579 | 0.000000000 |
| HS | 0.2488310738 | 0.000000000 |
| BBA | 0.2693890470 | 0.000000000 |
| GSA | 0.2412716274 | 0.000000000 |
| COLSHADE | 0.2352424600 | 0.000000000 |
| sCMAgES | 0.2352424679 | 0.000000000 |
| SASS | 0.2352424600 | 0.000000000 |
| SA | −0.8015697572 | 0.000000000 |
| HHO | 0.2352424579 | 0.000000000 |
| CHHOSA | 0.2352424679 | 0.000000000 |
Minimise
subject to the constraints
-
1.
-
2.
-
3.
-
4.
-
5.
-
6.
-
7.
-
8.
where
-
1.
N.mm
-
2.
rad/s
-
3.
mm2
-
4.
N/mm2
-
5.
mm/s
-
6.
mm
-
7.
-
8.
mm
-
9.
mm
-
10.
-
11.
m/s
-
12.
mm
-
13.
-
14.
s
-
15.
rpm
-
16.
Kg m2
-
17.
Nm
-
18.
Nm
-
19.
with bounds
-
1.
-
2.
-
3.
-
4.
-
5.
4.6.4. RC31: Gear train design problem
The results obtained by the various algorithms are highlighted in Table 11 and the problem details are defined below.
Table 11.
Results of the various algorithms on the RC31 problem.
| Algorithm | ||
|---|---|---|
| GA | 252.1980357000 | 0.000000000 |
| WOA | 0.0000000000 | 0.000000000 |
| GWO | 0.0000000000 | 0.000000000 |
| PSO | 0.0000000000 | 0.000000000 |
| HS | 0.0000000039 | 0.000000000 |
| BBA | 0.0000204294 | 0.000000000 |
| GSA | 0.0000000000 | 0.000000000 |
| COLSHADE | 0.0000000000 | 0.000000000 |
| sCMAgES | 0.0000000000 | 0.000000000 |
| SASS | 0.0000000000 | 0.000000000 |
| SA | 0.4060476713 | 0.000000000 |
| HHO | 0.0000000000 | 0.000000000 |
| CHHOSA | 0.0000000000 | 0.000000000 |
Minimise
subject to the constraints
-
1.
-
2.
4.6.5. RC02: Heat exchanger network design (Case 2)
The results obtained by the various algorithms are highlighted in Table 12 and the problem details are defined below.
Table 12.
Results of the various algorithms on the RC02 problem.
| Algorithm | ||
|---|---|---|
| GA | 1982341.232347 | 1 052 226.253000 |
| WOA | 7627.294131 | 4134.68254 |
| GWO | 14079.909500 | 41.47897 |
| PSO | 7043.365909 | 5000.49975 |
| HS | 7149.418361 | 8332.36337 |
| BBA | 6808.191262 | 338 700.38450 |
| GSA | 6565.456142 | 6565.45614 |
| COLSHADE | 7049.037000 | 0.00000 |
| sCMAgES | 7049.036954 | 0.00000 |
| SASS | 7049.037000 | 0.00000 |
| SA | 581.480853 | 876 462.75750 |
| HHO | 6989.986571 | 6001.39413 |
| CHHOSA | 7047.767548 | 245.29036 |
Minimise
subject to the constraints
-
1.
-
2.
-
3.
-
4.
-
5.
-
6.
-
7.
-
8.
-
9.
with bounds
-
1.
-
2.
-
3.
-
4.
-
5.
-
6.
-
7.
5. Conclusion
In this work, a two-stage pipeline composed of feature extraction followed by FS is proposed for the detection of COVID-19 from CT-scan images. For feature extraction, a state-of-the-art CNN architecture, DenseNet, is used. For the purpose of FS from the extracted features, a hybrid meta-heuristic optimisation algorithm combining HHO with SA is used. The naive HHO’s drawbacks are overcome by incorporating SA and Chaotic initialisation. The results indicate that the inclusion of the feature extraction stage provides better performance as compared to the vanilla CNN. It is also observed that the proposed method achieves better accuracy than some state-of-the-art methods. Additionally, the present method also provides a significant reduction in the number of relevant features as compared to some well-known optimisation algorithms.
It is seen that on increasing the population size beyond a certain point, there is no increase in the classification accuracy, the best fitness among the Harris Hawks does not increase beyond a particular margin however much the population size or the number of iterations is increased. It performs best when the population size is set at 10, and the maximum number of iterations is set at 15, as discussed in Section 4. The primary limitation of this algorithm is that it consumes too much time, mainly due to the time complexity of SA. The SA algorithm after being added to the HHO increases the time consumed by the optimisation algorithm by a good margin. Besides, the attention mechanism in the CNN model can be explored to improve the feature extractor and ameliorate the performance. The optimisation algorithm used here can solve complex optimisation problems as well as high-dimensional FS problems.
CRediT authorship contribution statement
Rajarshi Bandyopadhyay: Conceptualisation, Methodology, Software, Validation, Investigation, Writing – original draft. Arpan Basu: Methodology, Software, Validation, Investigation, Writing – original draft. Erik Cuevas: Writing – review & editing, Supervision. Ram Sarkar: Conceptualisation, Writing – review & editing, Supervision.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
References
- 1.Gu Quanquan, Li Zhenhui, Han Jiawei. 2012. Generalized fisher score for feature selection. arXiv preprint arXiv:1202.3725. [Google Scholar]
- 2.Huang Jinjie, Cai Yunze, Xu Xiaoming. A hybrid genetic algorithm for feature selection wrapper based on mutual information. Pattern Recognit. Lett. 2007;28(13):1825–1844. [Google Scholar]
- 3.Kira Kenji, Rendell Larry A. Machine Learning Proceedings 1992. Elsevier; 1992. A practical approach to feature selection; pp. 249–256. [Google Scholar]
- 4.Wei Jiaxuan, Zhang Ruisheng, Yu Zhixuan, Hu Rongjing, Tang Jianxin, Gui Chun, Yuan Yongna. A BPSO-SVM algorithm based on memory renewal and enhanced mutation mechanisms for feature selection. Appl. Soft Comput. 2017;58:176–192. [Google Scholar]
- 5.Kashef Shima, Nezamabadi-pour Hossein. An advanced ACO algorithm for feature subset selection. Neurocomputing. 2015;147:271–279. [Google Scholar]
- 6.Tibshirani Robert. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996;58(1):267–288. [Google Scholar]
- 7.Zhang Han, Zhang Rui, Nie Feiping, Li Xuelong. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) IEEE; 2018. A generalized uncorrelated ridge regression with nonnegative labels for unsupervised feature selection; pp. 2781–2785. [Google Scholar]
- 8.Al-Tashi Qasem, Abdulkadir Said Jadid, Rais Helmi Md, Mirjalili Seyedali, Alhussian Hitham. Approaches to multi-objective feature selection: A systematic literature review. IEEE Access. 2020;8:125076–125096. [Google Scholar]
- 9.Wolpert David H., Macready William G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1(1):67–82. [Google Scholar]
- 10.Talbi E.-G. A taxonomy of hybrid metaheuristics. J. Heuristics. 2002;8(5):541–564. [Google Scholar]
- 11.Oh Il-Seok, Lee Jin-Seon, Moon Byung-Ro. Hybrid genetic algorithms for feature selection. IEEE Trans. Pattern Anal. Mach. Intell. 2004;26(11):1424–1437. doi: 10.1109/TPAMI.2004.105. [DOI] [PubMed] [Google Scholar]
- 12.Ghosh Manosij, Kundu Tuhin, Ghosh Dipayan, Sarkar Ram. Feature selection for facial emotion recognition using late hill-climbing based memetic algorithm. Multimedia Tools Appl. 2019;78(18):25753–25779. [Google Scholar]
- 13.Mafarja Majdi, Abdullah Salwani. Investigating memetic algorithm in solving rough set attribute reduction. Int. J. Comput. Appl. Technol. 2013;48(3):195–202. [Google Scholar]
- 14.Sheikh Khalid Hassan, Ahmed Shameem, Mukhopadhyay Krishnendu, Singh Pawan Kumar, Yoon Jin Hee, Geem Zong Woo, Sarkar Ram. EHHM: Electrical harmony based hybrid meta-heuristic for feature selection. IEEE Access. 2020;8:158125–158141. [Google Scholar]
- 15.Guha Ritam, Ghosh Manosij, Singh Pawan Kumar, Sarkar Ram, Nasipuri Mita. A Hybrid Swarm and Gravitation-based feature selection algorithm for handwritten Indic script classification problem. Complex Intell. Syst. 2021;7(2):823–839. [Google Scholar]
- 16.Huang G., Liu Z., Van Der Maaten L., Weinberger K.Q. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017. Densely connected convolutional networks; pp. 2261–2269. [Google Scholar]
- 17.Heidari Ali Asghar, Mirjalili Seyedali, Faris Hossam, Aljarah Ibrahim, Mafarja Majdi, Chen Huiling. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019;97:849–872. [Google Scholar]
- 18.van Laarhoven Peter J.M., Aarts Emile H.L. Simulated Annealing: Theory and Applications. Springer Netherlands; 1987. Simulated annealing; pp. 7–15. [Google Scholar]
- 19.Elgamal Zenab Mohamed, Yasin Norizan Binti Mohd, Tubishat Mohammad, Alswaitti Mohammed, Mirjalili Seyedali. An improved harris hawks optimization algorithm with simulated annealing for feature selection in the medical field. IEEE Access. 2020;8:186638–186652. [Google Scholar]
- 20.Al-Tashi Qasem, Kadir Said Jadid Abdul, Rais Helmi Md, Mirjalili Seyedali, Alhussian Hitham. Binary optimization using hybrid grey wolf optimization for feature selection. IEEE Access. 2019;7:39496–39508. [Google Scholar]
- 21.Mafarja Majdi M., Mirjalili Seyedali. Hybrid whale optimization algorithm with simulated annealing for feature selection. Neurocomputing. 2017;260:302–312. [Google Scholar]
- 22.Wang Jun, Zhou Bihua, Zhou Shudao. An improved cuckoo search optimization algorithm for the problem of chaotic systems parameter estimation. Comput. Intell. Neurosci. 2016;2016:1–8. doi: 10.1155/2016/2959370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Moradi Parham, Gholampour Mozhgan. A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy. Appl. Soft Comput. 2016;43:117–130. [Google Scholar]
- 24.Soares Eduardo, Angelov Plamen, Biaso Sarah, Froes Michele Higa, Abe Daniel Kanda. SARS-CoV-2 CT-scan dataset: A large dataset of real patients CT scans for SARS-CoV-2 identification. MedRxiv. 2020 [Google Scholar]
- 25.Waheed A., Goyal M., Gupta D., Khanna A., Al-Turjman F., Pinheiro P.R. CovidGAN: Data augmentation using auxiliary classifier GAN for improved Covid-19 detection. IEEE Access. 2020;8:91916–91923. doi: 10.1109/ACCESS.2020.2994762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jaiswal Aayush, Gianchandani Neha, Singh Dilbag, Kumar Vijay, Kaur Manjit. Classification of the COVID-19 infected patients using DenseNet201 based deep transfer learning. J. Biomol. Struct. Dyn. 2020:1–8. doi: 10.1080/07391102.2020.1788642. PMID: 32619398. [DOI] [PubMed] [Google Scholar]
- 27.Rajaraman S., Siegelman J., Alderson P.O., Folio L.S., Folio L.R., Antani S.K. Iteratively pruned deep learning ensembles for COVID-19 detection in chest X-Rays. IEEE Access. 2020;8:115041–115050. doi: 10.1109/ACCESS.2020.3003810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Elaziz Mohamed Abd, Hosny Khalid M., Salah Ahmad, Darwish Mohamed M., Lu Songfeng, Sahlol Ahmed T. New machine learning method for image-based diagnosis of COVID-19. PLOS ONE. 2020;15(6):1–18. doi: 10.1371/journal.pone.0235187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sahlol Ahmed T., Yousri Dalia, Ewees Ahmed A., Al-Qaness Mohammed A.A., Damasevicius Robertas, Abd Elaziz Mohamed. COVID-19 image classification using deep features and fractional-order marine predators algorithm. Sci. Rep. 2020;10(1):1–15. doi: 10.1038/s41598-020-71294-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Altan Aytaç, Karasu Seçkin. Recognition of COVID-19 disease from X-ray images by hybrid model consisting of 2D curvelet transform, chaotic salp swarm algorithm and deep learning technique. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Goel Tripti, Murugan R., Mirjalili Seyedali, Chakrabartty Deba Kumar. OptCoNet: an optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl. Intell. 2020:1–16. doi: 10.1007/s10489-020-01904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ezzat Dalia, Hassanien Aboul Ella, Ella Hassan Aboul. An optimized deep learning architecture for the diagnosis of COVID-19 disease based on gravitational search optimization. Appl. Soft Comput. 2021;98 doi: 10.1016/j.asoc.2020.106742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kingma Diederik P., Ba Jimmy. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. [Google Scholar]
- 34.Ewees Ahmed A., Elaziz Mohamed Abd. Performance analysis of Chaotic Multi-Verse Harris Hawks Optimization: A case study on solving engineering problems. Eng. Appl. Artif. Intell. 2020;88 [Google Scholar]
- 35.Menesy Ahmed S., Sultan Hamdy M., Selim Ali, Ashmawy Mohamed G., Kamel Salah. Developing and applying chaotic harris hawks optimization technique for extracting parameters of several proton exchange membrane fuel cell stacks. IEEE Access. 2020;8:1146–1159. [Google Scholar]
- 36.Bednarz James C. Cooperative hunting Harris’ hawks (Parabuteo unicinctus) Science. 1988;239(4847):1525–1527. doi: 10.1126/science.239.4847.1525. [DOI] [PubMed] [Google Scholar]
- 37.Sims David W., Southall Emily J., Humphries Nicolas E., Hays Graeme C., Bradshaw Corey J.A., Pitchford Jonathan W., James Alex, Ahmed Mohammed Z., Brierley Andrew S., Hindell Mark A., Morritt David, Musyl Michael K., Righton David, Shepard Emily L.C., Wearmouth Victoria J., Wilson Rory P., Witt Matthew J., Metcalfe Julian D. Scaling laws of marine predator search behaviour. Nature. 2008;451(7182):1098–1102. doi: 10.1038/nature06518. [DOI] [PubMed] [Google Scholar]
- 38.Viswanathan G.M., Afanasyev V., Buldyrev Sergey V., Havlin Shlomo, da Luz M.G.E., Raposo E.P., Stanley H. Eugene. Lévy flights in random searches. Physica A. 2000;282(1–2):1–12. [Google Scholar]
- 39.Yang Xin-She. Luniver press; 2010. Nature-Inspired Metaheuristic Algorithms. [Google Scholar]
- 40.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 41.Altman N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Amer. Statist. 1992;46(3):175–185. [Google Scholar]
- 42.Whitley Darrell. A genetic algorithm tutorial. Stat. Comput. 1994;4(2):65–85. [Google Scholar]
- 43.Mirjalili Seyedali, Lewis Andrew. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. [Google Scholar]
- 44.Mirjalili Seyedali, Mirjalili Seyed Mohammad, Lewis Andrew. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. [Google Scholar]
- 45.Kennedy J., Eberhart R. Proceedings of ICNN’95-International Conference on Neural Networks, Vol. 4. IEEE; 1995. Particle swarm optimization; pp. 1942–1948. View Article. [Google Scholar]
- 46.Geem Zong Woo, Kim Joong Hoon, Loganathan Gobichettipalayam Vasudevan. A new heuristic optimization algorithm: harmony search. Simulation. 2001;76(2):60–68. [Google Scholar]
- 47.Mirjalili Seyedali, Mirjalili Seyed Mohammad, Yang Xin-She. Binary bat algorithm. Neural Comput. Appl. 2014;25(3–4):663–681. [Google Scholar]
- 48.Rashedi Esmat, Nezamabadi-pour Hossein, Saryazdi Saeid. GSA: A gravitational search algorithm. Inform. Sci. 2009;179(13):2232–2248. [Google Scholar]
- 49.Zervoudakis Konstantinos, Tsafarakis Stelios. A mayfly optimization algorithm. Comput. Ind. Eng. 2020;145 [Google Scholar]
- 50.Mirjalili Seyedali. SCA: a sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016;96:120–133. [Google Scholar]
- 51.Fathollahi-Fard Amir Mohammad, Hajiaghaei-Keshteli Mostafa, Tavakkoli-Moghaddam Reza. Red deer algorithm (RDA): a new nature-inspired meta-heuristic. Soft Comput. 2020:1–29. [Google Scholar]
- 52.Boettcher Stefan, Percus Allon G. 1999. Extremal optimization: Methods derived from co-evolution. arXiv preprint math/9904056. [Google Scholar]
- 53.Bhattacharyya Trinav, Chatterjee Bitanu, Singh Pawan Kumar, Yoon Jin Hee, Geem Zong Woo, Sarkar Ram. Mayfly in harmony: A new hybrid meta-heuristic feature selection algorithm. IEEE Access. 2020;8:195929–195945. [Google Scholar]
- 54.Chatterjee Bitanu, Bhattacharyya Trinav, Ghosh Kushal Kanti, Singh Pawan Kumar, Geem Zong Woo, Sarkar Ram. Late acceptance hill climbing based social ski driver algorithm for feature selection. IEEE Access. 2020;8:75393–75408. [Google Scholar]
- 55.Singh Narinder, Hachimi Hanaa. A new hybrid whale optimizer algorithm with mean strategy of grey wolf optimizer for global optimization. Math. Comput. Appl. 2018;23(1):14. [Google Scholar]
- 56.Ahmed Shameem, Ghosh Kushal Kanti, Singh Pawan Kumar, Geem Zong Woo, Sarkar Ram. Hybrid of harmony search algorithm and ring theory-based evolutionary algorithm for feature selection. IEEE Access. 2020;8:102629–102645. [Google Scholar]
- 57.Kumar Abhishek, Wu Guohua, Ali Mostafa Z., Mallipeddi Rammohan, Suganthan Ponnuthurai Nagaratnam, Das Swagatam. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput. 2020;56 [Google Scholar]
- 58.Jaiswal Aayush, Gianchandani Neha, Singh Dilbag, Kumar Vijay, Kaur Manjit. Classification of the COVID-19 infected patients using DenseNet201 based deep transfer learning. J. Biomol. Struct. Dyn. 2020:1–8. doi: 10.1080/07391102.2020.1788642. [DOI] [PubMed] [Google Scholar]
- 59.Wang Zhao, Liu Quande, Dou Qi. Contrastive cross-site learning with redesigned net for COVID-19 CT classification. IEEE J. Biomed. Health Inf. 2020;24(10):2806–2813. doi: 10.1109/JBHI.2020.3023246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Silva Pedro, Luz Eduardo, Silva Guilherme, Moreira Gladston, Silva Rodrigo, Lucio Diego, Menotti David. COVID-19 detection in CT images with deep learning: A voting-based scheme and cross-datasets analysis. Inf. Med. Unlocked. 2020;20 doi: 10.1016/j.imu.2020.100427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Goel Chirag, Kumar Abhimanyu, Dubey Satish Kumar, Srivastava Vishal. Cold Spring Harbor Laboratory; 2020. Efficient Deep Network Architecture for COVID-19 Detection Using Computed Tomography Images. [Google Scholar]