How Specific Are Learning Disabilities?

Abstract

Despite historical emphasis on “specific” learning disabilities (SLDs), academic skills are strongly correlated across the curriculum. Thus, one can ask how specific SLD truly are. To answer this question, we used bifactor models to identify variance shared across academic domains (academic g), as well as variance unique to reading, mathematics, and writing. Participants included 686 children aged 8 to 16. Although the sample was overselected for learning disabilities, we intentionally included children across the full range of individual differences in this study in response to growing recognition that a dimensional, quantitative view of SLD is more accurate than a categorical view. Confirmatory factor analysis identified five academic domains (basic reading, reading comprehension, basic math, math problem solving, and written expression); spelling clustered with basic reading and not writing. In the bifactor model, all measures loaded significantly on academic g. Basic reading and mathematics maintained variance distinct from academic g, consistent with the notion of SLDs in these domains. Writing did not maintain specific variance apart from academic g, and evidence for reading comprehension-specific variance was mixed. Academic g was strongly correlated with cognitive g (r=.72) but not identical to it. Implications for SLD diagnosis are discussed.

The diagnostic classification system for specific learning disorders (SLD) changed in substantive ways from Diagnostic and Statistical Manual of Mental Disorders (DSM)—IV (American Psychiatric Association, 1994) to DSM-5 (American Psychiatric Association, 2013), including both “lumping” (grouping all learning disorders together under a single umbrella) and “splitting” (better distinguishing basic from complex academic skills for reading, writing, and math). Although some research supported these decisions, as discussed further below, important questions remain unresolved. In particular, the degree to which reading and writing are separable remains a subject of debate (Berninger & Abbott, 2010; Kaufman, Reynolds, Liu, Kaufman, & McGrew, 2012). Further, some of the possible types of SLD identified by DSM-V are not yet well validated (Pennington, McGrath, and Peterson, 2019), and limited research has examined whether each academic domain delineated by DSM-5 has specific variance that can be reliably distinguished from variance shared across academic measures. To address these unanswered questions, the current study had two interrelated aims: 1) explore the structure of academic skills including variance shared across domains as well as variance unique to reading, writing, or math; and 2) test the validity of the structure of SLDs proposed by the DSM-5. We utilized bifactor models which simultaneously model variance shared across academic skills and variance specific to an academic domain. The specific domains we modeled in this study were basic reading (word reading accuracy and fluency), complex reading (comprehension), basic math (calculation/fluency), complex math (problem solving), basic writing (spelling/handwriting), and complex writing (sentence- and paragraph-level composition).

DSM-5 Structure of SLDs

A notable change in the diagnostic structure of SLDs between DSM-IV and DSM-5 is the collapsing of four different diagnoses (Reading Disorder, Mathematics Disorder, Disorder of Written Expression, and Learning Disorder—Not Otherwise Specified) into a single overarching category (Specific Learning Disorder) with specifiers to identify the academic skill(s) impacted. This decision reflects the high correlations among academic skills (Deary, Strong, Smith, & Fernandes, 2007; Kaufman et al., 2012) and corresponding high comorbidity among SLDs. For example, SLDs in reading and math are estimated to co-occur at least 25-30% of the time (Landerl & Moll, 2010), and the overlap between reading and writing disabilities is even higher. An epidemiologic study of specific writing disorder (Katusic, Colligan, Weaver, & Barbaresi, 2009) documented that 75% of children meeting criteria for SLD writing also had SLD reading.

Like DSM-IV, DSM-5 recognizes three primary academic domains (reading, writing, and math). Unlike DSM-IV, for each domain, DSM-5 distinguishes basic academic skills from complex or higher-level skills. In the case of reading, basic skills include word recognition, decoding, and fluency, all of which are emphasized in the first few years of elementary school as children learn to read. Once reasonable mastery of these basic skills is attained, the primary focus of reading instruction shifts to reading comprehension (or reading to learn). Gough and Tunmer argued more than three decades ago with “the simple view of reading” (1986) that reading comprehension is determined by both basic reading and listening comprehension. Substantial research evidence has since accrued supporting the simple view (e.g., García & Cain, 2014), and parallel simple models of writing and math have been proposed (Berninger, Vaughan, Abbott, Begay, Coleman, Curtin, et al., 2002; Pennington & Peterson, 2015). In each case, the higher-level academic skill (written expression or math problem solving) depends on both basic skills (e.g., handwriting/spelling or number sense/calculation) as well as complex cognitive non-academic skills (narration or complex problem solving). At early stages of basic skill acquisition (or in individuals who have basic skill weaknesses due to a learning disability), these skills demand significant cognitive resources, thus limiting resources available for higher-level comprehension or problem solving (Perfetti, 1998). As automaticity in basic skills develop, cognitive resources are freed up to devote to reading comprehension, written expression, or math problem solving. Nonetheless, proficiency in a complex academic skill will still be limited by proficiency in the corresponding basic academic skill, providing another reason (in addition to academic g) for why SLDs cannot be fully specific. Thus, there is both theoretical and empirical support for the updated DSM-5 definition of SLD, including the grouping of all SLD diagnoses together under a single umbrella category as well distinguishing basic from complex skills for reading, writing, and math; questions remain about how specific each of these six SLDs are.

Validity of DSM-5 SLD Symptom Clusters

The DSM-5 definition of SLD recognizes six symptom clusters, at least one of which must be present for diagnosis (Criterion A). These clusters include basic reading (word reading accuracy and fluency), complex reading (comprehension), basic writing (spelling), complex writing (sentence- and paragraph-level composition), basic math (number sense, math facts, and calculation), and complex math (mathematical reasoning). These symptom clusters map onto three main academic domain specifiers (reading, mathematics, and written expression), and clinicians are instructed to identify all impacted subskills, which encompass the basic and complex skills identified in Criterion A. However, not all SLD subtypes based on the six symptom clusters have been well validated by previous research, as discussed next.

Basic Reading

SLD in basic reading (also known as dyslexia) is the best validated of the six possible DSM-5 SLD subtypes, with decades of research documenting that this is a genetically- and environmentally-influenced, brain-based disorder that is manifest across cultures, languages, and developmental stages (Peterson & Pennington, 2012). Like all behaviorally defined disorders, SLD in basic reading represents the low tail on a continuum rather than a discrete category, so any particular cut-off is inevitably somewhat arbitrary. However, membership in the low tail of basic reading ability is associated with functional impairment, including reduced educational and occupational opportunities (McLaughlin, Spiers, & Shenassa, 2014).

Complex Reading

Consistent with the simple model of reading, difficulties with word recognition can cause downstream difficulties with reading comprehension, but there are also people with intact basic reading skills who struggle to understand what is read because of other cognitive weaknesses (Swanson & Alexander, 1997). Such individuals who have relatively specific difficulty in reading comprehension have been called “poor comprehenders” in the research literature. In this manuscript, we prefer terms such as “reading comprehension difficulties” especially in light of the dimensional nature of this skill. Not surprisingly, individuals with reading comprehension difficulties have associated weaknesses in oral language skills including vocabulary knowledge and listening comprehension (Catts, Adoph, & Weismer, 2006; Nation, Cocksey, Taylor, & Bishop, 2010). This profile has sometimes been conceptualized as a type of language disorder (Nation, Clarke, Marshall, & Durand, 2004; Spencer, Quinn, & Wagner, 2014). While it is clear that word decoding and comprehension are partly distinguishable academic skills, even showing independent genetic influences (Keenan et al, 2006), what is less clear is whether reading comprehension difficulties in the absence of word decoding problems can be fully accounted for by oral language comprehension weaknesses (Christopher, et al., 2016; Spencer & Wagner, 2018). A related practical problem in assessing the validity of an SLD in reading comprehension is that measures vary considerably in the skills they assess, with some emphasizing decoding and others emphasizing language comprehension (Cutting & Scarborough, 2006; Keenan, Betjemann, & Olson, 2008). These measures have been shown to identify different individuals as having an SLD in reading comprehension (Keenan & Meenan, 2014). As a result, the current study takes a latent modeling approach to emphasize the shared variance of reading comprehension measures.

Basic and Complex Mathematics

Substantial evidence supports the validity of an SLD in math across levels of analysis. Problems with math achievement are known to have both genetic and environmental influences (Haworth, Kovas, and Harlaar, 2009), to be related to aberrant activation of widely distributed, bilateral brain networks (Kauffmann et al., 2011) and to be associated with long-term functional impairment (Geary, 2011). However, some questions remain. First, the distinction between SLD in basic versus complex math is not well validated, and the field has yet to converge on operational definitions of math disability subtypes or dimensions (Szucs & Goswami, 2013). Second, etiologic and cognitive influences on math appear largely shared with those on intelligence and other academic skills (Harlaar, Kovas, Dale, Petrill, and Plomin, 2012; Peng Peng et al., 2019; Peterson et al., 2017), raising questions about how “specific” math learning problems are.

Basic Writing

The simple view of writing (Berninger, 2002) holds that basic writing encompasses tasks required for transcription, or the process of converting oral language to written form. These include spelling and handwriting (or keyboarding). The DSM-5 includes problems in spelling accuracy as a symptom that should trigger diagnosis of SLD with impairment in written expression. The primary problem with this approach is spelling and word reading development are well known to be intricately connected (e.g., Ehri, 1997) and extensive evidence links spelling problems to dyslexia (Vellutino, Fletcher, Snowling, & Scanlon, 2004), so it is not clear that a separate diagnosis for SLD in spelling is warranted, at least for English-speaking children. Isolated or “specific” spelling difficulties may be more likely in highly regular orthographies, although even in these cases, spelling problems may reflect the same underlying neurobiological liability that leads to basic reading problems in more complex orthographies (Paulesu et al., 2001; Wimmer & Mayringer, 2002)

DSM-5 includes spelling as the sole manifestation of an SLD in basic writing and does not identify handwriting problems as a manifestation of SLD. Existing evidence does not clearly support the notion of SLD impacting handwriting. Few standardized measures of handwriting are available, and only limited research has explored contributors to poor handwriting at the etiologic, brain, or neuropsychological levels. Of course, it remains possible that future research could help validate handwriting problems as part of an SLD in basic writing. To provide a more comprehensive test of whether problems in basic writing should be distinguished as a type of SLD, we included a measure of handwriting in the current study.

Complex Writing

The final type of SLD recognized by DSM-5 is in complex written expression, which is also not currently well validated. We identified only two epidemiologic studies of writing disabilities, both of which used the same sample and did not clearly distinguish basic from complex writing (Katusic, Colligan, Weaver, & Barbaresi 2009; Yoshimasu, Barbaresi, Colligan, Killian, Voigt, Weaver, & Katusic, 2011). This research showed a very high overlap between reading and writing problems. Among those with writing difficulties who did not meet criteria for a reading disability, nearly 30% met criteria for ADHD, and language disorder was not accounted for. This work suggests that there may be relatively few children with writing problems whose difficulties are not accounted for by another better validated diagnosis.

Summary

Of the six SLD symptom clusters identified in DSM-5, SLD with impairment in basic reading (or dyslexia) is best validated. SLD in math has been fairly well validated; distinguishing learning difficulties in basic versus complex math is theoretically defensible but further empirical work on this question is still needed. Many people have reading comprehension problems that cannot be explained by dyslexia alone, and they likely have some of the same underlying etiologic, brain-based, and neuropsychological risk factors that characterize oral language disorders (Pennington et al., 2019). Although there are certainly individuals who have weaknesses in basic and/or complex writing, these problems may overlap too heavily with other, better validated disorders (primarily dyslexia) to warrant distinct behavioral diagnoses.

Common and Unique Variance in Academic Skills

Academic skills are normally distributed (e.g., Shaywitz, Escobar, Shaywitz, Fletcher, & Makuch, 1992) due to their multifactorial etiology (e.g., Snowling, Gallagher, & Frith, 2003). Research at the etiologic, brain, and cognitive levels of analysis has consistently demonstrated that the same risk factors which operate in the low tail of the distribution of academic skills also influence individual differences across the full range (Haworth et al., 2009; Kaufmann et al., 2011; Szucs, 2016). These findings have led to calls for researchers to move away from a categorical approach to the study of learning disorders and instead to adopt dimensional, quantitative methods (Casey, Oliveri, & Insel, 2014; Kovas & Plomin, 2006; Peters & Ansari, 2019). Thus, factor analyses of the most widely used individually administered measures of academic achievement, such as the Wechsler Individual Achievement Test (WIAT; e.g., WIAT-III; Breaux, 2009), Woodcock-Johnson Tests of Achievement (WJ; e.g., WJ-IV; Shrank, McGrew, & Mather, 2014), and Kaufman Test of Educational Achievement (KTEA; e.g., KTEA-III; Kaufman & Kaufman, 2014), are relevant to understanding relations among learning disorders. This work has consistently supported the distinctness of math from literacy skills. Findings regarding reading and writing have been mixed; tests tapping these domains have sometimes been reported to load on a single factor and at other times to load on two different factors (Kaufman et al, 2012; Shrank et al., 2014; Woodcock, McGrew, & Mather, 2001).

All academic skills are correlated (Shrank et al., 2014). Although examples of extreme discrepancies within an individual can be found and have historically been the subject of great scientific and clinical attention (Morgan, 1896), it turns out that such individuals are the exception rather than the rule. A student with difficulties in one area of the curriculum is more likely to have difficulties in other areas. This finding has led to the proposal that there is an academic “g” which underlies variance shared across academic skills (akin to Spearman’s or cognitive g which explains variance common to various intellectual skills; Spearman, 1904). Multiple research groups have reported evidence for academic g by applying second order factor or bifactor models to a battery of academic tests (Deary et al., 2007; Kaufman et al., 2012; Shuldt & Sparfeldt, 2016). These findings are consistent with the high rates of comorbidity among learning disabilities and with the umbrella SLD diagnosis in DSM-5.

Relationship Between Cognitive and Academic g

What is academic g? It overlaps substantially with cognitive g, but the two appear not to be identical. Studies that have directly tested the association between academic and cognitive g have reported associations between .5 and .9 (Deary, 2007, Rindermann & Neubauer, 2004; Shuldt & Sparfeldt, 2016), with the most comprehensive study on this question reporting an overall mean correlation of .83 as well as some evidence for an increasing relationship with age (Kaufman et all, 2012). More research is needed to understand the variance in academic g unaccounted for by cognitive g, but it seems likely to relate to a variety of individual, familial, educational, and institutional risk and resilience factors. Many of these same risk and resilience factors influence cognitive g as well, so it will be important to distinguish shared and distinctive environmental influences. It may also be that academic skills emphasize some underlying cognitive processes that are partly distinct from those tapped by traditional IQ measures.

The Current Investigation

We sought to better characterize the structure of academic skills and by extension, to test the validity of the DSM-5 structure of SLD in children overselected for learning disabilities who had completed a large battery of tests assessing reading, writing, math, and IQ. Given our questions of interest and mounting calls for researchers to embrace dimensional rather than categorical approaches to the study of SLDs, we included children with skills spanning the full range of individual differences. In order to explicitly model academic g, we used a bifactor approach. Bifactor models are conceptually similar to, yet mathematically distinct from, second order factor analyses (Chen, West, & Sousa, 2006). The bifactor model has advantages for this study by allowing investigation of whether specific academic domains continue to cluster together while accounting for variance shared across academic skills.

We addressed three main questions, which are listed below along with our hypotheses.

Question 1) How many factors describe our academic battery?

Hypothesis 1) We expected to find at least four factors: basic reading (accuracy and fluency), complex reading, complex writing, and mathematics. We were agnostic as to whether tasks emphasizing basic versus complex mathematics would load on a single factor or two factors. Based on extensive evidence that spelling is linked to SLD in basic reading, we expected spelling to load at least as strongly on basic reading as on writing but were also open to the possibility that spelling could be part of a distinctive basic writing cluster. Thus, we planned to test two competing models: one in which spelling loaded with handwriting and a second in which spelling loaded with basic reading.

Question 2) Can reliable variance in basic and complex reading, math, and writing be identified that is distinct from academic g?

Hypothesis 2) Based on the established validity of SLDs in basic reading and math, we predicted that variance distinct from academic g would be identified in at least these two domains.

Question 3) What is the relationship between academic and cognitive g?

Hypothesis 3) We expected to replicate previous findings that academic g is strongly but not perfectly correlated with cognitive g.

Method

Participants

Participants included 686 children and adolescents (367 [53.5%] were identified as male by parent report and 319 were identified as female by parent report [46.5%]). Mean age was 11.25 years (SD=2.17; range = 8-16), mean maternal years of education was 15.98 (SD = 2.43), and mean Wechsler Full Scale IQ (FSIQ) was 107.23 (SD = 12.17). The racial identification of the sample was 87% White, 10% multiracial, 1% Black, 1% Native American/American Indian/Alaska Native/Indigenous, and 1% preferring to self-describe their race¹. The ethnic identification of the sample was 3% Hispanic or Latino, 10% multiethnic, and 87% Not Hispanic or Latino.

The participants were recruited as part of the Colorado Learning Disabilities Research Center (CLDRC) twin study, which is an ongoing study of learning disorders. In brief, twins living within 150 miles of metropolitan Denver were identified through 22 local school districts or through the state’s twin registry. For both recruitment sources (schools or twin registry), all twins were invited to participate with subsequent screening for eligibility conducted after families indicated interest in the study. Parents who provided informed consent completed a phone questionnaire to screen for history of reading or attention problems. Questions related to history of reading problems included whether the child had had difficulty learning to read, had current reading difficulties, or had been diagnosed with a learning disability in reading. Parents were also asked to provide scores on state-based standardized tests, when available, and performance below the proficient range on literacy tests was considered indicative of reading problems. Questions related to history of attention problems included whether the child had difficulties paying attention, had a history of hyperactivity, had ever been diagnosed with ADHD/ADD, or had been prescribed stimulant medication. Parents also completed a rating scale measure of DSM-IV symptoms of ADHD, and permission was requested to send a parallel questionnaire to each twin’s primary classroom teacher. If either member of a twin pair had a history of reading or attention difficulties, the pair was invited to participate in the study. A comparison group of twins in which neither twin met the screening criteria for learning problems matched on age, zygosity, and parent-identified sex was also recruited.

Inclusion criteria were: (1) primarily English-speaking home, (2) no evidence of neurological problems or history of brain injury, (3) no uncorrected visual impairment, (4) not Deaf or hard-of-hearing, and (5) no known genetic disorders or syndromes. Additional criteria specific to this study were (1) FSIQ ≥ 70 and Verbal IQ > 85 or Nonverbal IQ > 85 (2) testing completed in 2006 or later, since assessment of a more limited number of academic domains had been completed in earlier years. To preserve the statistical assumption of independence, one twin was randomly chosen from each family, regardless of diagnostic status, to be included in the analyses for this study. In the final sample, 28.4% of participants had a school history of reading difficulties and 24.3% had a history of attention problems.

Procedure

The study protocol was approved by the Institutional Review Boards at the University of Colorado, Boulder and the University of Denver. After obtaining informed consent at both institutions, two testing sessions were completed at the University of Colorado, and two additional testing sessions were scheduled approximately one month later at the University of Denver. Participants taking psychostimulant medication were asked to withhold medication for 24 hours prior to each testing session.

Measures

Basic reading (accuracy and fluency) was assessed with Peabody Individual Achievement Test (PIAT) Reading Recognition (Dunn & Markwardt, 1970), Time-Limited Word Recognition Test (TLWRT; Olson, Wise, Connors, Rack, & Fulker, 1989), Test of Word Reading Efficiency (TOWRE) Word Reading Efficiency (Torgesen, Wagner, & Rashotte, 1999), and Gray Oral Reading Tests-Third Edition (GORT-3) Fluency (Wiederholdt & Bryant, 1992). PIAT Spelling (Dunn & Markwardt, 1970) was included in this construct because it is essentially a single word reading task involving spelling recognition, not production.

Complex reading was assessed with PIAT Reading Comprehension (Dunn & Markwardt, 1970), the Qualitative Reading Inventory (QRI) Reading Questions (Leslie & Caldwell, 2001), Woodcock-Johnson-III (WJ-III) Passage Comprehension (Woodcock, McGrew, & Mather, 2001), and GORT-3 Comprehension (Wiederholdt & Bryant, 1992).

Basic mathematics was assessed with Wide Range Achievement Test-Revised (WRAT-R) Arithmetic (Jastak & Wilkinson, 1984), which heavily emphasizes knowledge of calculation procedures and, WJ-III Math Fluency (Woodcock et al., 2001) which requires completion of simple arithmetic problems under time pressure.

Complex mathematics was assessed with the Arithmetic subtest from the Wechsler Intelligence Scale for Children (WISC-R or WISC-III) (Wechsler, 1974, 1991) and WJ-III Applied Problems (Woodcock et al., 2001), both of which emphasize math reasoning by requiring participants to solve orally presented word problems.

Basic writing was assessed with WRAT-R Spelling (Jastak & Wilkinson, 1984) and Handwriting Copy (Graham, Berninger, Weintraub, & Schafer, 1998).

Complex writing was assessed with two sentence-level writing measures (WJ-III Writing Fluency and Writing Samples (Woodcock et al., 2001)) as well as two measures of essay-length written composition (Wechsler Individual Achievement Test-III (WIAT-III) Essay Composition (Breaux, 2009) and Test of Written Language-4^th Edition (TOWL-4) Story Composition (Hammill, 2009)).

Cognitive g was estimated from the FSIQ estimate from a Wechsler instrument (WISC-R: 2% of the sample; WISC-III: 57% of the sample; WISC-III short-form [Information, Coding, Arithmetic, Block Design, Vocabulary, Object Assembly, and Digit Span subtests]: 41% of the sample).

Data Cleaning

We used standard scores whenever possible and raw scores if the test was not standardized (i.e., TLWRT, QRI, Handwriting Copy). Even though standard scores should already be corrected for age, we regressed both standard scores and raw scores on age and age squared, to control for any residual linear and nonlinear age effects to ensure that any evidence for academic g was not due to maturational factors. We also regressed all scores on sex. Residuals were saved for further analyses. Outliers were winsorized to 4 SD. Distributional characteristics were found to be satisfactory.

Missing Data

Because some measures were introduced to the battery later than others, there were patterns of missingness that were unrelated to participant characteristics other than year of recruitment. Specifically, the following measures were included from 2012 on: WJ-III Math Fluency and Applied Problems, WRAT-R Arithmetic, TOWL-4 Story Composition, and WIAT-III Essay Composition. WRAT-R Arithmetic had also been included in an earlier phase of the project but was not administered between 2007 and 2011. The remaining 12 measures were included in all phases of the project from which the current study drew participants. Average level of missingness for the academic variables was 19% (range 0-64%; Table 1). To ensure that missing data patterns were not unduly influencing the results, we conducted follow-up analyses including only the 12 academic measures with low missingness (< 20%). No participants were missing Full Scale IQ.

Table 1.

Sample Sizes, Means, SDs, and Reliability Estimates for Academic Measures and Full Scale IQ

Construct/Measure	N	Mean	SD	Reliability (N pairs)
Basic Reading
PIAT Reading Recognition SS	679	105.25	11.59	.83 (883)
PIAT Spelling SS	679	103.06	12.70	.73 (885)
Time Limited Oral Reading rs	686	120.96	41.83	.87 (879)
TOWRE Word Reading SS	682	102.23	12.34	.70 (195)
GORT-3 Fluency ss	570	11.28	4.39	.86 (269)
Complex Reading
PIAT Reading Comprehension SS	678	106.86	12.19	.70 (883)
QRI rs	574	4.62	1.04	.48 (268)
WJ-III Passage Comprehension SS	573	102.14	10.41	.69 (273)
GORT-3 Comprehension ss	568	11.61	3.36	.46 (266)
Basic Mathematics
WRAT-R Arithmetic SS	293	105.31	17.48	.79 (544)
WJ-III Math Fluency	283	96.49	13.56	.72 (72)
Complex Mathematics
Wechsler Arithmetic ss	686	11.26	3.42	.61 (886)
WJ-III Applied Problems SS	283	108.36	11.09	.73 (72)
Basic Writing
WRAT-R Spelling SS	681	101.96	16.20	.87 (665)
Handwriting Copy rs	656	102.50	37.80	.73 (192)
Complex Writing
WJ-III Writing Fluency SS	671	104.53	14.54	.55 (193)
WJ-III Writing Samples SS	671	110.98	13.42	.65 (194)
WIAT Essay Composition	342	110.52	13.21	.41 (94)
TOWL-4 Story Composition	249	12.24	2.84	.52 (71)
Cognitive g
Full Scale IQ SS	686	107.23	12.17	.83 (879)

Note. Reliability was estimated based on MZ twin intraclass correlation. SS = Standard score with mean = 100 and SD = 15, ss = scaled score with mean = 10 and SD = 3, rs = raw score.

Analyses

Raw correlations were computed in IBM SPSS Statistics 25.0. Confirmatory factor analyses were run with Mplus 8.2 using maximum likelihood estimation, and missing data were handled with full information maximum likelihood estimation. Because χ² tests are sensitive to sample size, we relied on the following fit indices and guidelines to assess model fit: Comparative Fit Index (CFI) > 0.90, Root Mean Square Error of Approximation (RMSEA) < 0.08, Standardized Root Mean Square Residual (SRMR) <.08. For comparing non-nested models, the Bayesian Information Criterion (BIC) and Akaike Information Criterion (AIC) were used as indices of absolute fit. The BIC was prioritized in evaluating models because it has a larger penalty for model complexity, but AIC is provided for reference. Because of the large number of path loadings included in these complex models, we set our alpha value at p<.001 for statistical significance.

Results

Descriptives for all of the academic and cognitive measures are provided in Table 1. We also included a lower-bound approximation of test-retest reliability of each measure in our sample using intraclass correlations of monozygotic (MZ) twin scores. The correlations between MZ twins can be considered an estimate of test-retest reliability because MZ twins share both their genes and family environment. They are a conservative estimate because even though MZ twins share genes and family environment, nonshared environmental influences may reduce the correlation (Plomin, DeFries, McClearn, & McGuffin, 2001). But nonshared environmental influences on academic skills tend to be small (e.g., Keenan, et al., 2006), so the MZ correlations can be considered estimates of test-retest reliability. Subsequent analyses only included one twin from each family to preserve the assumption of statistical independence.

Structure of Academic Skills

Correlations

Table 2 shows the zero-order correlations (Pearson’s r) among individual academic measures, grouped according to hypothesized construct. Each measure’s correlation with FSIQ is also provided. All measures were significantly and positively correlated, with effect sizes falling mainly in the medium to large range (r = .3-.5), consistent with the notion of academic g. The median correlation value for the full table (excluding FSIQ) was 0.45. All measures were also positively and significantly correlated with FSIQ.

Table 2.

Correlations (Pearson’s r) Among Measures of Reading, Mathematics, Writing, and Cognitive G

	Reading									Mathematics				Writing
	Basic					Complex				Basic		Complex		Basic		Complex
	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.	16.	17.	18.	19.
Reading
Basic
1.PIAT Reading
2.PIAT Spelling	.71
3.TLWRT	.87	.74
4.TOWRE	.66	.56	.82
5.GORT-3 Fluency	.79	.70	.82	.70
Complex
6.PIAT Comprehension	.69	.57	.67	.52	.61
7. WJ-III Passage Comp	.66	.54	.64	.49	.62	.65
8.QRI Questions	.36	.24	.36	.26	.37	.38	.45
9.GORT-3 Comprehension	.44	.34	.41	.28	.41	.46	.49	.39
Mathematics
Basic
10. WRAT-R Arithmetic	.53	.46	.55	.42	.54	.49	.50	.26	.28
11. WJ-III Math Fluency	.43	.35	.45	.48	.56	.34	.36	.19	.22	.64
Complex
12.Wechsler Arithmetic	.52	.45	.53	.43	.55	.48	.52	.32	.35	.70	.52
13.WJ-III Applied Problems	.48	.41	.52	.32	.49	.47	.51	.34	.39	.64	.46	.68
Writing
Basic
14.WRAT-R Spelling	.82	.76	.85	.63	.79	.61	.59	.25	.33	.55	.48	.53	.46
15.Handwriting Copy	.36	.33	.39	.45	.46	.30	.27	.10	.16	.35	.45	.30	.23	.40
Complex
16.WJ-III Writing Fluency	.54	.46	.59	.56	.60	.46	.50	.27	.32	.54	.47	.47	.46	.56	.57
17.WJ-III Writing Samples	.47	.42	.48	.30	.51	.46	.45	.29	.40	.48	.33	.43	.46	.51	.33	.44
18.TOWL-4 Story	.38	.29	.39	.36	.38	.30	.42	.18	.23	.36	.39	.33	.38	.37	.42	.46	.40
19.WIAT-III Essay	.45	.33	.47	.36	.44	.32	.41	.32	.27	.37	.28	.35	.38	.41	.24	.41	.34	.33
Cognitive g
20. FSIQ	.54	.47	.56	.42	.57	.59	.62	.47	.50	.51	.26	.64	.34	.48	.31	.50	.46	.27	.32

Note. All correlations were significant at the p<.001 level.

White boxes represent intra-construct correlations at either the basic or complex level. Light gray boxes represent intra-construct correlations across basic and complex measures. Darker gray boxes represent cross-construct correlations.

PIAT: Peabody Individual Achievement Test; TLWRT: Time Limited Word Recognition Test; TOWRE: Test of Word Reading Efficiency; GORT-3: Gray Oral Reading Tests—Third Edition; QRI: Qualitative Reading Inventory; WIAT-III: Wechsler Individual Achievement Test—Third Edition; WJ-III: Woodcock Johnson Tests of Achievement—Third Edition; WRAT-R: Wide Range Achievement Test—Revised; FSIQ: Full Scale IQ

In most cases, intra-domain correlations were larger than inter-domain correlations. As predicted, single word spelling was an exception to this pattern; it consistently correlated more strongly with basic reading measures (r values range from .63 to .85) than with other basic (.40) or complex writing measures (r values range from .37 to .56).

Table 3 summarizes the intra- and interdomain correlations among the academic measures. The left-most column shows the median estimated test-retest reliability (based on monozygotic twin correlations) among all the measures in each academic domain, which sets an approximate upper bound for the values in the other columns of the table. Notably, across all three primary academic domains, median reliability was higher for basic than complex skills. The pattern of lower estimated reliability for more complex tasks extended to variation within complex reading and complex writing measures included in the current study. For complex reading, previous research (Keenan et al., 2008) has demonstrated that two of the measures we included (WJ-III Passage Comprehension and PIAT Reading Comprehension) emphasize decoding skills relatively more than comprehension, while the other two measures (QRI Reading Questions and GORT-3 Fluency) emphasize comprehension relatively more than decoding. Median estimated reliability for the more decoding-heavy complex reading tasks was .70, compared to just .47 for the other two tasks. Similarly, for complex writing, estimated reliability for the two measures of sentence-level written composition was .60, compared to .47 for the two measures of essay-level written composition.

Table 3.

Median Correlation Values for Academic Measures by Academic Domain

		Relations among academic measures in Table 2
	MZ Intraclass Correlation	Within domain and complexity	Within domain, across complexity	Across domain
Basic Reading	.83	.73	.47	.46
Complex Reading	.59	.46	.47	.34
Basic Math	.76	.64	.58	.44
Complex Math	.67	.68	.58	.46
Basic Writing	.80	.40	.41	.45
Complex Writing	.54	.41	.41	.40

The next column shows the median intradomain correlation (i.e., among basic reading measures, among complex reading measures, etc.), and the next shows the median correlation among measures in the same primary academic domain but across levels of complexity (i.e., median correlations of basic reading measures with complex reading measures, basic math measures with complex math measures, and basic writing measures with complex writing measures). The right-most column shows median interdomain correlations (e.g.., basic reading measures with all math and writing measures; basic math with all reading and writing measures, etc.). The structure of SLD proposed in the DSM-5 predicts that the values should be highest on the left side of the table and decline in each subsequent column. This predicted pattern emerged most clearly for math. For reading, the pattern varied for basic versus complex skills. Basic reading was more related to itself than to other constructs, but similarly related to complex reading as to the other academic domains. On the other hand, complex reading was as related to basic reading as it was to itself. Writing did not follow the predicted pattern; both basic and complex writing were as related to other domains as they were to themselves.

In summary, the zero-order correlations among academic measures: 1) provide evidence for academic g; 2) suggest that the basic reading and basic math measures have adequate reliability and discriminant validity to support individual diagnosis of SLD in those domains, while results were more mixed for complex reading and complex math; and 3) cast doubt on whether writing measures capture writing-specific variance that is distinct from the other academic domains. These results were next explored further with confirmatory factor and bifactor analyses.

Factor Analyses

Correlated Factors Model.

We conducted confirmatory factor analyses to examine the structure of academic skills and test the validity of the DSM-5 framework of SLDs. A priori, we planned to undertake several steps to select the best correlated factors model. These steps started with a six-factor model corresponding to the DSM-5 symptom clusters (basic/complex reading, basic/complex math, basic/complex writing) with sequential steps to test whether: 1) spelling was better conceptualized as part of a basic writing or basic reading factor; 2) the correlation between basic and complex factors within academic domain could be set to unity; and 3) whether correlations across academic domains could be set to unity. After selecting a correlated factors model, the final step was to test a bifactor model that allowed us to jointly represent both the relationships among all the measures (i.e., academic g) as well as the evidence for domain specificity. We planned to compare the final correlated factors model to the bifactor solution. Fit statistics are summarized in Table 4.

Table 4.

Comparison of Confirmatory Factor Analysis Models

Model	X2(df), p-value	CFI	RMSEA (90% CI)	SRMR	BIC	AIC
1.Six factors (Table 1)	Not positive definite: correlation between basic reading and basic writing >1.
2. Five factors (move WRAT-R Spelling to Basic Reading, drop Handwriting Copy) (Figure 1)	X2(125) = 401.08, p<.001	.96	.057 (.051-.063)	.039	64800.52	64510.54
3. Four factors (Basic Reading, Complex Reading, Math, Complex Writing) (Supplementary Figure 1)	X2(129) = 423.82, p<.001	.96	.058 (.052-.064)	.042	64797.14	64525.28
4. Bifactor with four domain-specific factors (based on Model 3) (Figure 2)	X2(117) = 382.22, p<.001	.96	.057 (.051-.064)	.040	64833.90	64507.68
5. Bifactor with writing-specific factor removed (Supplementary Figure 2)	X2(121) = 407.05, p<.001	.96	.059 (.052-.065)	.041	64832.61	64524.51
6. Second-order with four first-order factors (based on Model 3) (Supplementary Figure 4	X2(131) = 436.31, p<.001	.96	.058 (.052-.064)	.044	64796.56	64533.77

The initial six-factor model (Model 1 in Table 4) was mis-specified (not positive definite) because the correlation between basic reading and basic writing exceeded 1. A Wald test indicated that the correlation between basic reading and basic writing was not distinguishable from 1 (p = .09). Based on previous research, our a priori hypothesis was that spelling would cluster strongly with decoding measures, which was confirmed by the high correlation between the basic reading and basic writing factors. As such, we modified the model to a five-factor model with WRAT-R Spelling loading on the basic reading factor. We dropped handwriting from the five-factor model (since none of the theoretical frameworks we were considering identify handwriting as a basic reading skill and there were no longer multiple measures of basic writing). The five-factor model with WRAT Spelling loading on basic reading (Model 2 in Table 4 and Figure 1) resulted in an admissible solution with adequate fit. We selected Model 2 over Model 1 and next tested whether the relationship between basic and complex skills could be set to 1 for math and reading. The correlation for basic reading and complex reading was .84 and the correlation for basic and complex math was .90. In both cases, the correlations were significantly less than 1 (p<.001) according to a Wald test. As such, we did not continue with additional steps to test whether factors across academic domains could be collapsed because our first series of tests indicated this approach would result in reduced model fit. We thus selected Model 2 as the final correlated factors model (Figure 1). This model had five factors: basic reading (including spelling production), complex reading, basic math, complex math, and complex writing. Correlations among the latent factors were high, ranging from .66-.90.

Figure 1. Correlated Factors Model – 5 Factors (Model 2 in Table 4).

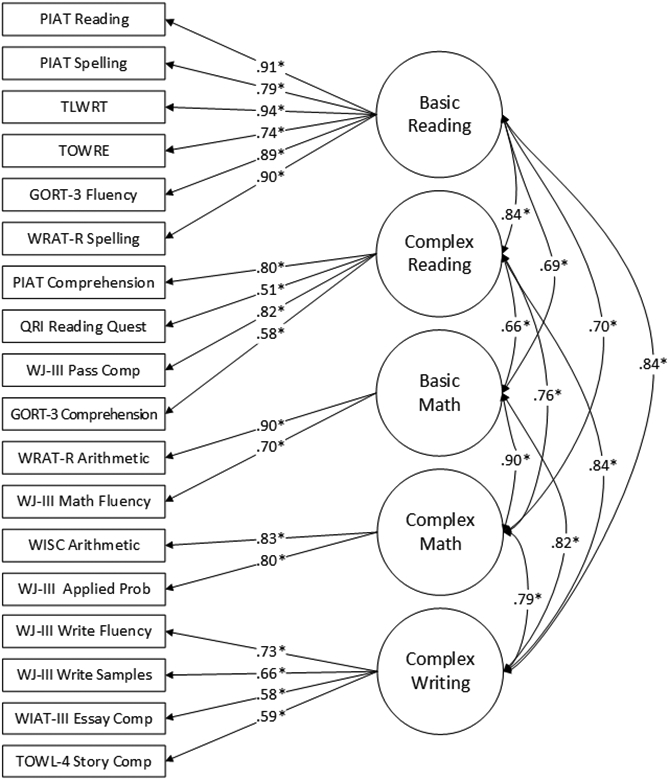
Note. Model fit: X²(125)=401.08, p<.001, CFI = .96, RMSEA=.057 (90% CI=.051-.063), SRMR=.039, BIC=64800.52, AIC=64510.54, *p < .001

Abbreviations

PIAT: Peabody Individual Achievement Test Reading

TLWRT: Time Limited Word Recognition Test

TOWRE: Test of Word Reading Efficiency

GORT-3: Gray Oral Read ing Test—Third Edition

WRAT-R: Wide Range Achievement Test—Revised

ORI Reading Quest: Qualitative Reading Inventory – Reading Questions

WJ-III: Woodcock-Johnson Tests of Achievement—Third Edition

WIAT-III: Wechsler Individual Achievement Test – Third Edition

TOWL-4: Test of Written Language – Fourth Edition

Pass Comp: Passage Comprehension

Applied Prob: Applied Problems

Comp: Composition

Bifactor Model.

We next tested a bifactor model in which each measure had loadings on both the academic g latent factor and its domain-specific latent factor from the correlated factors model. However, bifactor models require at least three indicators for model identification and both basic and complex math had only two indicators each. Based on limited previous theoretical and empirical work clearly delineating these two constructs as well as the high correlation between latent basic and complex math in the current study (.90), we tested a correlated factors model in which all four math measures loaded on a single factor. While we know from the Wald test mentioned above that this .90 correlation was significantly less than 1, a four-factor model with basic reading, complex reading, math, and complex writing (Model 3 in Table 4; Supplementary Figure 1) still produced a solution with adequate fit. The four-factor (Model 3) and five-factor (Model 2) were comparable based on ΔBIC = 3.38 with a slight preference for the simpler four-factor model. The AIC favored the five-factor model (ΔAIC = 14.74), likely because it has less of a penalty for model complexity.

We selected the four-factor solution with basic reading, complex reading, math, and complex writing (Model 3 in Table 4; Supplementary Figure 1) to adapt for a bifactor model. Consistent with canonical bifactor models, the domain-general and domain-specific latent factors were modeled to be uncorrelated. This bifactor model (Model 4 in Table 4; Figure 2) fit the data adequately and was statistically preferred to the correlated-factors model based on the chi-square difference test (Model 4 versus Model 3: Δχ²(12) = 41.60, p<.001). The chi-square difference test is appropriate because the correlated factors and bifactor models are nested (Reise, 2012). The correlated factors model can be derived from the bifactor model by setting the general factor paths to 0 and freeing the orthogonality constraints on the group factors (Reise, 2012). We prioritized the results of the chi-square difference test, but we note that the BIC (ΔBIC = 36.76) favored the correlated-factors model and the AIC (ΔAIC = 17.60) favored the bifactor model.

Figure 2. Bifactar Madel (Madel 4 in Table 4).

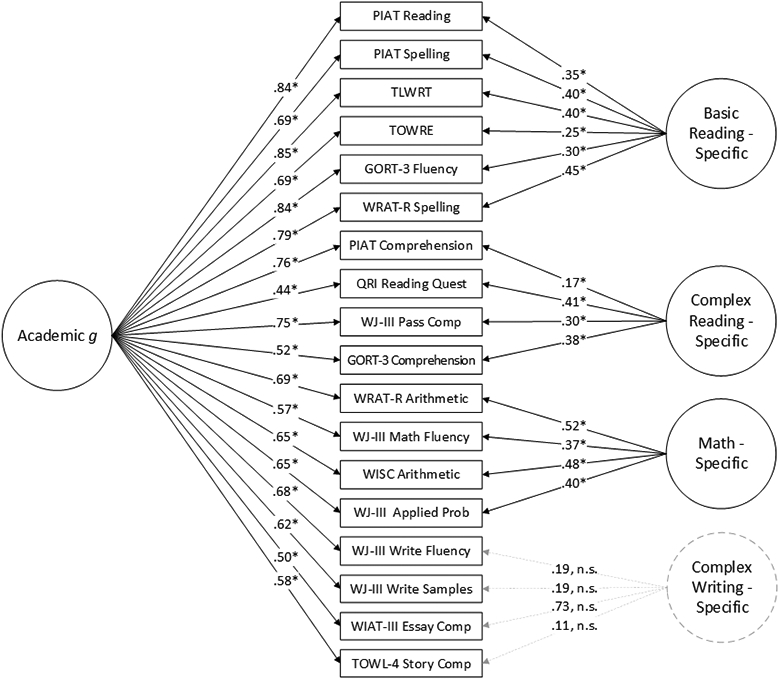
Note. Model fit: X²(117)=382.22, p<.001, CFI=.96, RMSEA=.057 (90% CI=.051-.064), SRMR = .040, BIC=64833.90, AIC=64507.68, *p < .001

Abbreviations

PIAT: Peabody Individual Achievement Test Reading

TLWRT: Time Limited Word Recognition Test

TOWRE: Test of Word Reading Efficiency

GORT-3: Gray Oral Reading Test—Third Edition

WRAT-R: Wide Range Achievement Test—Revised

QRI Reading Quest: Qualitative Reading Inventory – Reading Questions

WJ-III: Woodcock-Johnson Tests of Achievement—Third Edition

WIAT-III: Wechsler Individual Achievement Test – Third Edition

TOWL-4: Test of Written Language – Fourth Edition

Pass Comp: Passage Comprehension

Applied Prob: Applied Problems

Comp: Composition

All measures loaded significantly on the academic g factor (p<.001), with values ranging from .44 to .85. After accounting for this shared variance, loadings on academic constructs decreased as expected, but remained statistically significant for basic reading, complex reading, and mathematics. Variances of the basic reading-specific and mathematics-specific latent factors were statistically greater than 0, while the variance of complex reading-specific latent factor was not (p = .099). In contrast, all individual loadings on the complex writing-specific factor were nonsignificant and the variance of the writing-specific factor was not significantly different from 0, suggesting that the writing-specific factor could not be statistically distinguished from academic g. The final bifactor model with the complex writing-specific factor dropped (Model 5 in Table 4; Supplementary Figure 2) showed a satisfactory fit to the data and was selected as the final bifactor model.

We examined the extent to which missing data might be impacting this model by running the bifactor model with only academic tests with <20% missingness (Supplementary Figure 3) (X²(55) = 257.61, p<.001, CFI=.97, RMSEA=.073 (90% CI .064-.082), SRMR = .029 BIC = 54683.22, AIC = 54461.20). This model retained basic and complex reading-specific factors, but we were unable to test for a math-specific or writing-specific factor because only one measure met missingness criteria for math and only two measures met missingness criteria for writing. Most importantly, the academic g factor was robust to changes in the indicators with loadings remaining quite stable; none of the standardized path loadings changed more than .02 units (Supplementary Figure 2 vs. Supplementary Figure 3).

The bifactor model has come under criticism recently for problems with over-fitting and statistical anomalies that generalize across datasets (Bonifay, Lane, & Reise, 2017; Reise, Kim, Mansolf, & Widaman, 2016; Eid et al., 2017). Because of these limitations, we also ran a second-order confirmatory factor analysis model with the same four first-order factors (basic reading, complex reading, math, and writing) that were used in the initial bifactor model. The second-order model also fit the data well (Model 6 in Table 4 and Supplementary Figure 4). As with the bifactor model, there was evidence of an over-arching academic g factor with strong loadings from all four domains (writing =.94, complex reading = .92, basic reading =.90, and math =.83). The fact that writing had the highest loading factor is consistent with the result that writing was also the most difficult to distinguish from academic g in the bifactor model. The second-order factor model is nested within the bifactor model (Mansolf & Reise, 2017), which allowed us to directly compare the models with the chi-square difference test. Results favored the bifactor model (Model 6 versus Model 4 in Table 4: Δχ²(14) = 54.09, p<.001). In terms of the absolute fit indices, the BIC favored the second-order model (ΔBIC = 37.34), while the AIC favored the bifactor model (ΔAIC= 26.09). It is not too surprising that the chi-square difference test and some of the fit indices would favor the bifactor model because they are known to be biased in favor of the bifactor. In fact, current work casts doubt on the validity of fit indices and the chi-square difference test to distinguish between the second-order and bifactor models (Mansolf & Reise, 2017). We chose the bifactor model a priori because it is best suited theoretically to answer our primary research question about shared variance among individual tests from different academic domains. We provide these results from the second-order model for comparison purposes.

Relationship between Cognitive and Academic g

To test the association between academic and cognitive g, we modeled cognitive g as a latent factor with a single indicator (FSIQ from the WISC) (Supplementary Figure 5). The error variance in FSIQ is established through test-retest reliability in the norming sample (r=.94 for WISC-III; Wechsler, 1991). We also estimated error variance in our sample through the MZ twin correlation which provides a lower bound for test-retest reliability; as can be seen in Table 2, for FSIQ, the MZ twin correlation was .83. From these data points, we estimated reliability to be .90 and set the error variance of FSIQ to (1-reliability)*sample variance (Muthen & Muthen, 2009). The model fit was adequate, X²(135) = 461.44, p<.001, CFI=.96, RMSEA=.059 (90% CI .053-.065), SRMR = .043, BIC=69642.53, AIC= 69307.24. The correlation between cognitive and academic g was high (r = .72, p<.001), indicating that approximately half of the variance in academic g overlaps with cognitive g. We conducted a sensitivity analysis using the lower-bound (.83) and upper-bound (.94) reliability estimates. The correlation between academic and cognitive g ranged from .71 to .75, using the upper-bound and lower-bound estimates, respectively. Cognitive g was significantly correlated with variance in complex reading that was distinct from academic g (r=.39, p<.001, sensitivity range r=.38-.40) as well as the variance in math distinct from academic g (r=.36, p<.001, sensitivity range r=.35-.37). Cognitive g showed no relationship with the variance in word reading/fluency distinct from academic g (r=−.05, p=.24, sensitivity range =−.05 - −.06).

One issue with the analyses above is that the Wechsler Full Scale IQ includes Arithmetic and we modeled the Arithmetic subtest as a math measure loading on academic g. In a follow-up analysis, we dropped the Arithmetic measure from the math-specific factor (X²(119) = 441.38, p<.001, CFI=.95, RMSEA=.063 (90% CI .057-.069), SRMR = .043, BIC= 66539.81, AIC= 66222.65). All of the relationships were stable from the previous analyses (cognitive g with academic g, r=.71, p<.001, cognitive g with the complex reading specific factor, r=.40, p<.001, cognitive g with the math specific factor, r=.38, p<.001, and no relationship between cognitive g and the word reading specific factor, r=−.04, p=.41).

Developmental Differences

While the current study was primarily concerned with individual differences, we conducted an initial set of analyses to examine potential developmental differences in the bifactor academic g model (Supplementary Figure 6). We used a median split on age to obtain approximately equal samples in each age group: ages 8-10.99 years (N=348), ages 11-16 (N=338). We conducted a multi-group CFA of the final academic g bifactor model with group-specific factors for basic reading, complex reading and math (Supplementary Figure 2). There was evidence of configural invariance with the academic g model fitting adequately in both the younger and older age group with the same factor structure (younger: X²(121) = 228.90, p<.001, CFI=.97, RMSEA=.051 (90% CI .040-.061), SRMR = .047, BIC= 32900.44, AIC= 32638.49; older: X²(121) = 316.48, p<.001, CFI=.94, RMSEA=.069 (90% CI .060-.078), SRMR = .054, BIC= 32126.96, AIC= 31866.99). There was evidence for partial measurement invariance across the older and younger age groups. All the intercepts could be equated across groups without a significant decrease in model fit (ΔX2 = 5.26, df=18, p=.998), but there was not metric invariance across all factor loadings (ΔX2 = 91.43, df=32, p<.001). Twenty-five of the thirty-two factor loadings could be equated across groups without a significant decrease in model fit from the unconstrained model. Supplementary Figure 6 illustrates the seven factor loadings that were freed across groups. Interestingly, five of the seven factor loadings that were freed were for timed academic tasks. For these five measures, the pattern was such that speeded academic measures loaded more strongly on academic-specific factors and less strongly on academic g as children got older.

Discussion

Despite historical emphasis on the “specific” nature of learning disabilities, considerable evidence demonstrates that individual differences in academic skills across the curriculum are correlated. We sought to better understand shared and unique variance across academic domains using a bifactor modeling approach, with a focus on the implications for SLD diagnosis. We replicated previous findings that a reliable academic g factor captures variance shared across basic and complex reading, writing, and math measures. Also similar to previous investigators, we found that academic g overlaps substantially with but is not identical to cognitive g. The most important novel contribution of the current study was that after accounting for academic g, reliable variance in basic literacy (word reading, fluency, and spelling) and math was identified, but this was not the case for writing. Evidence for reliable complex reading -specific variance was mixed.

Different theoretical frameworks disagree about the degree to which reading and writing are separable constructs. Cattell-Horn-Carroll (CHC) theory, the dominant theory on the structure of human intelligence (Schneider & McGrew, 2018), specifies a single factor (“Grw”) for basic reading and writing skills. Consistently, in recent factor analyses of academic test batteries based on CHC theory (e.g., WJ-IV, KTEA-III), reading and writing subtests load on a single factor (e.g., Kaufman et al., 2012; Shrank et al., 2014). On the other hand, both the cognitive neuropsychology and SLD literatures have often emphasized that reading and writing tap partly distinct neurocognitive systems (e.g., Berninger & Abbott, 2010; Tainturier & Rapp, 2001). More consistent with the latter approach, the DSM has historically provided separate diagnoses for reading and writing problems. In DSM-5, the provision of distinct specifiers for different aspects of reading and writing continues to imply that partly separable learning processes underlie these skills. However, if the CHC approach is a more accurate depiction of the structure of academic skills, perhaps a single specifier for SLD in literacy would be more appropriate.

In the final correlated-traits models, the current academic battery was best described by five distinct but strongly related constructs: basic literacy (including reading accuracy, reading fluency, and spelling), complex reading, basic math, complex math, and complex writing. Results therefore are more consistent with the current DSM framework separating reading and writing than with a single SLD in literacy. However, in contrast to the DSM structure, we found no evidence to support an SLD impacting spelling in isolation. Instead, our results were consistent with spelling problems being part of the dyslexia profile, and with recent evidence showing that the latent-trait correlation between word-reading and spelling accuracy is .96 (Olson, Hulslander, & Treiman, 2018).

We tested the distinction between basic and complex skills for reading, writing, and math. For all three domains, estimated test-retest reliabilities (based on MZ twin intraclass correlations) were higher for basic than complex skills. These results call into question whether existing measures can assess complex academic skills with sufficient reliability to be practical for individual diagnosis. At the group level, our results further validated the distinction between basic and complex reading. There was some evidence for the validity of the distinction between basic and complex math in the raw correlations and in confirmatory factor analyses. However, the correlation between latent basic math and complex math factors was very high (.9), and a four-factor solution in which all math tasks loaded on a single factor fit the data comparably to the five-factor solution. We did not identify a basic writing factor that could be distinguished from basic reading but did identify a complex writing factor in the correlated traits model that was distinct from reading skills.

We found strong evidence for academic g, consistent with our prediction. Also consistent with our hypothesis, even while accounting for this shared variance, distinct variance in basic reading and math was identified. These results support a degree of specificity in these areas. In other words, the bifactor results supported the “specific” nature of variance in SLDs for basic literacy and math, but not writing. This conclusion is consistent with considerable prior work validating these diagnoses and suggest that there are children who show strengths and weaknesses in these two academic domains (basic literacy and math) that are not fully accounted for by academic g. Results for complex reading were mixed; although individual measures continued to load significantly on a complex reading -specific factor in the bifactor model, its variance was not statistically greater than 0.

The mixed evidence for SLD in complex reading (comprehension) is not necessarily surprising. The current study raised questions about this diagnosis based on both the relatively low reliability of reading comprehension measures (particularly those that emphasized more complex skills) and the final bifactor model in which the reading comprehension-specific factor had negligible variance. While we did hypothesize that reading comprehension would be distinguishable from the other academic skills in this battery, it remains an open question whether SLD reading comprehension is distinct from oral language comprehension difficulties (Nation et al., 2004; Spencer et al., 2014) which could also be described diagnostically as a language disorder. Our group has shown a very high correlation between latent reading comprehension and listening comprehension (Christopher et al., 2016), and it would be important to see if the same pattern holds when academic g is explicitly modeled.

We found no evidence for a specific writing construct that could be reliably distinguished while accounting for general academic abilities. This pattern of one residual factor showing negligible variance and/or negligible loadings is not uncommon in bifactor models (Eid, Geiser, Koch, & Heene., 2017) so we considered whether this finding could be an artefact of our modeling approach. We were reassured by the fact that inspection of the raw correlations among measures supports the same basic conclusion, which is that the writing measures show weak discriminant validity and do not clearly assess a distinctive writing construct. Together with the questions about the reliability of the measurement of complex writing noted earlier, this casts doubt on the practical value of these measures for individual diagnosis. More generally, along with previous research (Katusic et al., 2009) suggesting that most children meeting criteria for SLD with impairment in writing also have dyslexia, these findings question the validity of an SLD in written expression. While our findings cast doubt on the notion of specific writing problems, they do not question the fact that some children experience writing difficulties that warrant intervention. One implication is that children with isolated writing difficulties should be rare. The more common profile should be that children with writing difficulties experience broad challenges across academic domains.

We replicated previous findings of a strong correlation between academic and cognitive g. Interestingly, cognitive g was moderately correlated with the complex reading-specific variance; a similar result was found for math but not for basic literacy. Although basic literacy and FSIQ are known to be correlated (e.g., Vellutino, 2001) this relationship appears to be fully accounted for by skills that are shared across a wide range of academic and cognitive tasks. On the other hand, the complex reading and math tests share some variance with FSIQ that is different from the variance shared by all academic measures in the battery. We hypothesize that in both cases, this relationship reflects higher-level thinking and reasoning abilities that support complex skills such as problem solving and inferencing.

Limitations & Future Directions

Future studies should address the limitations of the current work, including more comprehensive measurement of basic and complex mathematics so that the distinctions between skills could be tested with latent factors in the context of a bifactor model. It is possible that with more reliable measures of complex reading and writing, stronger evidence for specific factors in these domains would emerge. Since the current battery included a range of widely used measures chosen for the best available reliability and validity, this likely reflects a more general challenge in the field. Extension to children from a broader range of racial, ethnic, and socioeconomic backgrounds will be important, including consideration of bilingual learners and languages other than English. We opted for a bifactor modeling approach a priori on the grounds that it allowed the most direct test of whether specific academic domains continue to cluster together while accounting for variance shared across academic skills. However, some scholars have recently described theoretical and practical concerns with the bifactor model, including that it may overfit data (Bonifay, Lane, & Reise, 2017; Reise, Kim, Mansolf, & Widaman, 2016) and that there can be “vanishing” factors (Eid et al., 2017). Our study found writing to behave like one of the “vanishing” factors that have been problematic in other datasets. Therefore, it is important to interpret our difficulty in specifying the writing factor with appropriate caution. However, writing also had the highest loading factor in the second-order model (.94). Furthermore, a careful examination of the raw correlations among academic measures revealed concerns about the reliability and discriminant validity of writing measures, raising questions about whether they could adequately support SLD diagnosis. Nonetheless, it will be important to know whether future studies utilizing other modeling strategies (e.g., Eid, et al., 2017) reach similar conclusions.

Consistent with the growing recognition of the value of a dimensional approach to the study of SLDs (Peters & Ansari, 2019), we included children with academic skills across the full range of individual differences. Although we believe this approach was most appropriate given our questions about shared and specific variance, this study did not directly address categorical diagnosis of SLDs. The current study included a broad age range of children from 8-16 years and further work should delve more deeply into potential developmental changes over time in a longitudinal sample. Preliminary cross-sectional analyses of younger and older age groups in this study showed that the bifactor academic g model fit reasonably well in both age groups, with some minor variations particularly in timed tasks. The pattern was such that some timed tasks became stronger indices of academic-specific factors than academic g over time. Further developmental work is needed to more fully understand this pattern. Finally, much prior research has examined which cognitive factors predict various academic outcomes, but these studies have generally not carefully accounted for general versus specific academic skills, so applying the current approach to longitudinal studies with fine-grained cognitive, language, and academic measures will also be important.

Summary and Conclusions

In summary, our results support aspects of the structure of academic skills endorsed by the DSM-5, but also highlight some problems with that model. First, the DSM-5 structure implies a hierarchical structure to academic skills by having a single umbrella SLD category with various specifiers. Overall, this structure appears reasonable. However, our findings help confirm that a specific learning disability in spelling alone does not appear to be a meaningful diagnosis, since spelling problems are highly interconnected with word reading problems and thus best conceptualized as part of SLD in basic reading or dyslexia. Further, based on the lack of evidence for specificity in individual differences in writing skills other than spelling (at least with available measures), it is not clear that identifying a “specific” learning disability in writing is meaningful. Although there are students who struggle with writing and need support in this area, our results suggest that many of these same students would benefit from support for other academic skills as well.

An important question for our current diagnostic system concerns how to classify children who struggle across academic domains. Clearly, because of the large amount of common variance underlying different academic skills, many children with difficulties in one domain should also be expected to have difficulties in other academic domains (i.e., due to underlying weaknesses in academic g). Current and previous results suggest that these more pervasive difficulties would likely be evident on a standard intelligence test to some extent as well, since the correlation between cognitive and academic g is high (r=.72 in this study, reflecting approximately 50% overlapping variance). Although some children have learning difficulties severe enough to qualify for the more generalized diagnosis of intellectual disability, many others have milder learning difficulties resulting in relatively low yet fairly even performance across numerous cognitive and academic measures. Based on our experience, clinicians and educators are sometimes reluctant to identify such children as having SLD, since there is so little specificity to their profile. However, it seems illogical to deny these children supports for learning difficulties because they have more widespread difficulties than children who do qualify for services. In other words, academic g accounts for a prominent amount of variance in diverse academic skills, and yet our current DSM-5 diagnostic system does not have an adequate specifier to describe children who have widespread academic difficulties and subsequent need for educational services.