Abstract
Background
Already at hospital admission, clinicians require simple tools to identify hospitalized COVID-19 patients at high risk of mortality. Such tools can significantly improve resource allocation and patient management within hospitals. From the statistical point of view, extended time-to-event models are required to account for competing risks (discharge from hospital) and censoring so that active cases can also contribute to the analysis.
Methods
We used the hospital-based open Khorshid COVID Cohort (KCC) study with 630 COVID-19 patients from Isfahan, Iran. Competing risk methods are used to develop a death risk chart based on the following variables, which can simply be measured at hospital admission: sex, age, hypertension, oxygen saturation, and Charlson Comorbidity Index. The area under the receiver operator curve was used to assess accuracy concerning discrimination between patients discharged alive and dead.
Results
Cause-specific hazard regression models show that these baseline variables are associated with both death, and discharge hazards. The risk chart reflects the combined results of the two cause-specific hazard regression models. The proposed risk assessment method had a very good accuracy (AUC = 0.872 [CI 95%: 0.835–0.910]).
Conclusions
This study aims to improve and validate a personalized mortality risk calculator based on hospitalized COVID-19 patients. The risk assessment of patient mortality provides physicians with additional guidance for making tough decisions.
Keywords: Cause-specific hazard regression, COVID-19, Mortality, Prognosis, Risk assessment, Risk chart
Background
The ongoing coronavirus disease 2019 (COVID-2019) pandemic changed priorities all over the world. More than 119 million confirmed infections and over 2.6 million deaths worldwide have been reported [1, 2]. Approximately 20% of such confirmed cases were severe, among which most were admitted in the intensive care unit (ICU) and required early intubation and mechanical ventilation. The health systems thus face financial and facility challenges in light of managing this condition. As the pandemic continuous, hospitals seek effective methods for managing such severe patients. Present guidelines on COVID-19 treatment identify ICU admission, ventilation, and mortality risk as typical outcomes in high-risk patients and consider these patients as potential candidates for medical treatment [3, 4]. Many studies reported the clinical characteristics and outcomes of COVID-19 patients, but few research studies focused on the risk assessment of outcomes [5, 6]. Personal risk profiles can help physicians make the correct decision for optimal patient treatment and hospital capacity management.
The risk assessment procedure and the resulting risk charts have been well documented in community-based cardiovascular Cohorts [7–11]. In such studies, the risk of having an event by the end of the cohort follow-up is estimated using the time-to-event analysis based on Cox proportional hazard regression [12]. By contrast, the analysis of in-hospital data requires special attention. Standard Cox regression models lead to inaccurate results when competing events exist [13]. For example, discharge alive is a competing event when hospital death is the event of interest. Such information should not be ignored since it results in an incomplete reflection of treatment effects [14] and creates competing risk bias. Moreover, standard logistic regression could not be used when some active cases are still hospitalized at the last follow-up date [13, 15]. In fact, excluding such patients creates selection bias.
Recently, machine learning methods were used for survival analysis. Methods, such as Random Survival Forests (RSF), were compared with standard Cox regression models [16]. Although RSF could select significant nonlinear interactions to improve the discrimination ability, they do not provide direct clinical interpretation information and should be further studied before the clinical application [17, 18]. Also, time-to-event data analysis could not be performed appropriately using classification systems, in which the event-of-interest is only used, and time-to-event data is discarded with the same reason mentioned above for the standard logistic regression.
This paper introduces an absolute cause-specific risk regression approach to perform risk assessment [19–21] for patients hospitalized with COVID-19. The event-of-interest is death in the hospital, and discharge alive is considered as the competing event. To demonstrate the methodology, the Khorshid COVID-19 Cohort (KCC) dataset [22] with 630 patients is used. To the best of our knowledge, this is the first study in which absolute risk assessment is performed on in-hospital COVID-19 patients considering the competing events. We also provide a death risk chart as a simple tool for clinical applications.
Methods
Absolute risk estimation for hospital mortality
First, we introduce the absolute risk estimation approach, which is used for the risk assessment.
We denote D the event outcome, where D = 1 if the event of interest (e.g., hospital death) occurred, and D = 2 if the competing event (e.g., discharge alive) happened. Then, the probability (i.e., absolute risk) that an event of type 1 (i.e., D = 1) occurred by time t is given by the Eq. (1) [20, 21]:
| 1 |
where denotes the right-sided limit, is the conditional event-free survival function, is the hazard of the event of interest dependent on the baseline covariate vector x, and z is a set of strata variables. The event-free survival function,, is the probability to be still hospitalized at time s and thus depends on the patients’ length of hospital stay which is directly linked to both the death hazard, and the discharge hazard, This is in contrast to the classical time-to event settings with only one event of interest (here: death) and without competing events (here: discharge). Thus, the absolute risk of hospital mortality is preliminary determined by the death hazard but also by the discharge hazard. As many clinical factors and biomarkers are associated with the discharge hazard, it is therefore necessary to use competing risk methodology to identify potential predictors for hospital mortality.
To estimate , we first need to estimate the event-free survival function. It is done by estimating both cause-specific hazards and then using the product integral estimator [21]. The stratified Cox regression model for cause j, j = 1 or 2 [21, 23], is given by the Eq. (2):
| 2 |
where βj is the vector of log-hazard ratios of the covariate vector x and λ0j,z(t) is the baseline hazard function.
Thus, the absolute risk estimation includes estimating the cause-specific hazards for both event types and then calculating the integral Eq. (1).
Obtaining the risk chart
We use the absolute risk estimation procedure to obtain a detailed risk chart for patients hospitalized for COVID-19 (see Fig. 1). First, two cause-specific Cox proportional hazards models for the outcome events death in the hospital and discharged alive are fitted. It is done by using the “csc” function of the “riskRegression” package in R [21, 24]. The cause-specific hazard ratios show how the risk factors affect each hazard rate. Both cause-specific hazard ratios have to be considered to conclude the effects of the risk factors on the absolute risk. Thus, even if a variable does not affect the death hazard, it may indirectly affect hospital mortality by in- or decreasing the discharge hazard. By contrast, the subdistribution hazard ratio combines the direct and the indirect effects in a single coefficient. To show how variables may indirectly influence hospital mortality, we additionally estimate the subdistribution hazard for the outcome of death. It is done using the “crr” function of the “cmprsk” package in R [25–27].
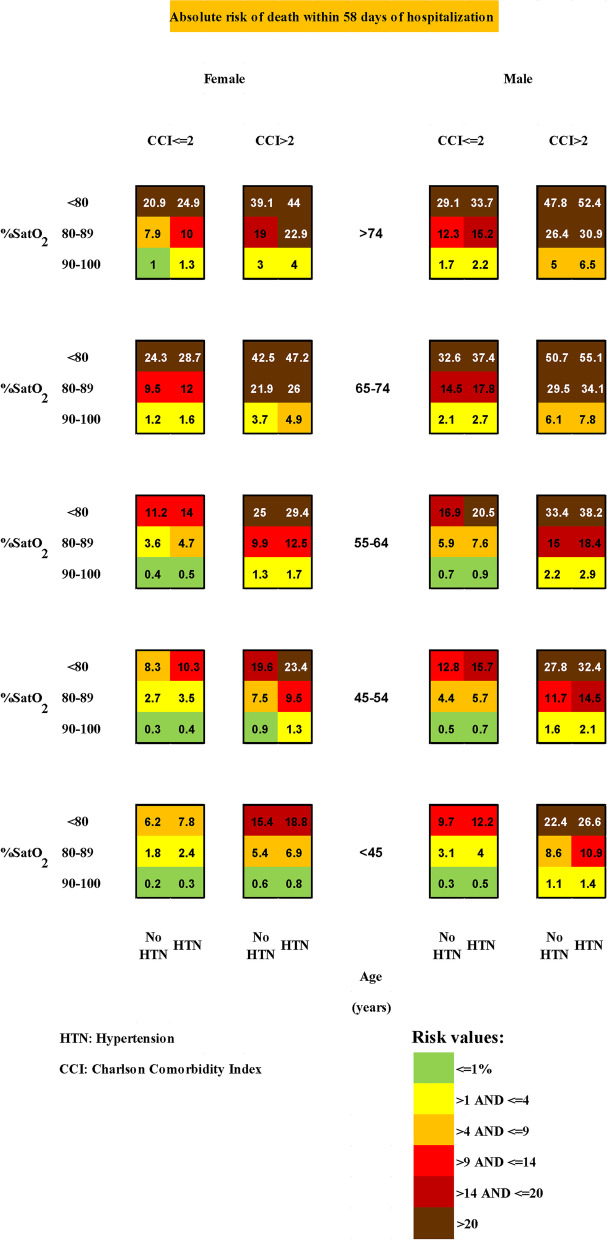
Fig. 1.
The absolute mortality risk chart for COVID-19 hospitalized patients based on sex, age, oxygen saturation, hypertension, and Charlson Comorbidity Index
Nonetheless, the absolute risk approach is based on the two cause-specific hazards, as was explained above. Thus, we apply the “predict” function on the csc-object to obtain the estimates of for all patient groups. For each patient, we obtain an individual risk based on the baseline covariates of the patients. Finally, the risk chart as shown in Fig. 1 can be constructed. By color-coding, high-risk and low-risk patients are directly identifiable from the chart.
The area under the curve (AUC) of the receiver operator curve (ROC), defined in Eq. (3) [28–30], could be used to assess accuracy for discrimination between patients discharged alive and dead:
| 3 |
where m is the number of patients who died, n is the number of patients discharged alive, Pi and Pj are the estimated mortality risks of the data points i and j. The kernel is defined in Eq. (4).
| 4 |
It is done using the “colAUC” function of the “caTools” package in R [31, 32].
Results were reported as mean ± standard deviation (for interval variables) and frequencies (for categorical variables). All data processing was performed using R version 4.0.3 [33].
Dataset and variable selection
In our study, the Khorshid COVID-19 Cohort (KCC) dataset [22, 34] was used. It is a hospital-based open cohort from Isfahan, which was a hot outbreak zone in central Iran. COVID-19 patients were admitted to the Khorshid referral hospital in Isfahan from February 2020 until September 2020. The patient recruitment phase finished at the end of August 2020, and the follow-up continues until the end of August 2021. The patients are followed up for the first, fourth, 12th weeks, and the first year after discharge. In total, 630 COVID-19 patients were enrolled in our study.
Among the recorded data for each COVID-19 patient, the baseline parameters sex, age, hypertension, oxygen saturation (SaO2) at hospital admission, and Charlson Comorbidity Index (CCI) [35, 36] were used as the non-lab input measurements to the model. Such parameters were selected based on clinical knowledge and previous papers published in the literature on the COVID-19 clinical outcome prediction [37, 38]. Age was categorized as less than 45 (years) (B0), 45–54 (B1), 55–64 (B2), 65–74 (B3), and more than 75 (B4) as in Petrilli et al. [39]. Oxygen saturation was categorized as more than or equal to 90% (A0), 80–89 (A1), and less than 80 (A2) by merging some SaO2 sub-categories as mentioned by Mejía et al. [38]. CCI was dichotomized as low (CCI < 3) or high (CCI ≥ 3). Such an optimal cut-off was estimated to minimize the (Error-Rate) ER-criteria of the Receiver operating characteristic curve (ROC) [40] for optimal mortality discrimination (AUC = 0.767 [CI 95%: 0.697–0.837]). Such a threshold previously was used in the literature for risk stratifications of hospitalized COVID-19 patients [41]. A reference group is considered with the following categories: sex (Female), age (B0), oxygen saturation (A0), and low CCI. Time-to-event was considered until hospital discharge, and the status at discharge (dead or alive) is taken into account. The risk assessment procedure was performed for the time from admission until 58 days of hospitalization.
Results
Among 630 patients, 38.7% were female. The average age of the admitted patients was 57.1 ± 15.4 years. The average of the CCI was 2.3 ± 2.1. 34.9% of the participants had hypertension. Forty-five patients died in the hospital. The descriptive statistics of the admitted patients categorized by the vital state at discharge are listed in Table 1. The cause-specific hazard ratios and their 95%-CIs are shown in Table 2. The subdistribution hazard ratios and their CI 95% for mortality based on the Fine and Gray model [26], with the competing event of discharge alive, are listed in Table 3. For example, we find that low oxygen saturation significantly increases the death hazard rate and decreases the discharge hazard. If it drops below 80%, the death hazard is more than five times higher than for patients in the reference group. At the same time, the discharge hazard is 40% lower. The subdistribution hazard ratio quantifies the combined effect: patients with 80% oxygen saturation or less have a more than ten times higher risk of death in the hospital. This effect is not only explained by the increased death hazard but also by the decreased discharge hazard. Due to the decreased discharge hazards, the patients stay longer in the hospital and therefore longer at risk and thus also at higher risk of dying in the hospital within 58 days.
Table 1.
The baseline characteristics of 630 patients, discharged alive or dead
| Parameter | Discharged alive n = 585 |
Dead n = 45 |
|---|---|---|
| Sex (male) | 359 (61.4) | 27 (60.0) |
| Age | 56.1 ± 15.1 | 70.0 ± 13.4 |
| Oxygen saturation | 90.0 ± 6.1 | 80.1 ± 12.6 |
| CCI | 2.1 ± 2.0 | 4.2 ± 2.2 |
| Hypertension | 193 (33.0) | 27 (60.0) |
CCI Charlson Comorbidity Index. Data are Mean ± SD or numbers (%)
Table 2.
The multivariable Cox proportional hazard regression model for mortality and hospital discharge
| Parameter | Category | Death Hazard Ratio | Discharge Hazard Ratio |
|---|---|---|---|
| Sex | |||
| Female, ref | - | - | |
| Male |
1.52 [0.77–2.99] |
0.93 [0.78–1.11] |
|
| Age (years) | |||
| < 45, ref | - | - | |
| 45–54 |
1.02 [0.14–7.33] |
0.82 [0.64–1.05] |
|
| 55–64 |
1.81 [0.36–9.07] |
0.93 [0.73–1.19] |
|
| 65–74 |
3.84 [0.78–18.87] |
0.77 [0.57–1.04] |
|
| > 74 |
2.74 [0.51–14.80] |
0.73 [0.50–1.05] |
|
| Oxygen Saturation (%) | |||
| 90–100, ref | - | - | |
| 80–89 |
3.19 [1.33–7.65] |
0.57 [0.47–0.69] |
|
| < 80 |
5.48 [2.18–13.78] |
0.38 [0.27–0.53] |
|
| CCI | |||
| 0–2, ref | - | - | |
| ≥ 3 |
2.10 [0.90–4.86] |
0.80 [0.61–1.05] |
|
| Hypertension |
1.14 [0.55–2.37] |
0.92 [0.75–1.12] |
|
CCI Charlson Comorbidity Index
Table 3.
The multivariable subdistribution hazards model for hospital mortality
| Parameter | Category | Subdistribution Hazard Ratio | CI 95% | p-value |
|---|---|---|---|---|
| Sex | ||||
| Female, ref | - | - | - | |
| Male | 1.41 | 0.72–2.78 | 0.320 | |
| Age (years) | ||||
| < 45, ref | - | - | - | |
| 45–54 | 0.91 | 0.14–6.10 | 0.920 | |
| 55–64 | 1.53 | 0.32–7.39 | 0.600 | |
| 65–74 | 3.49 | 0.70–17.56 | 0.130 | |
| > 74 | 2.40 | 0.42–13.72 | 0.330 | |
| Oxygen Saturation (%) | ||||
| 90–100, ref | - | - | - | |
| 80–89 | 5.37 | 2.27–12.74 | < 0.001 | |
| < 80 | 10.94 | 3.90–30.66 | < 0.001 | |
| CCI | ||||
| 0–2, ref | - | - | - | |
| ≥ 3 | 2.18 | 0.94–5.05 | 0.068 | |
| Hypertension | 1.41 | 0.72–2.76 | 0.320 | |
CCI Charlson Comorbidity Index
The absolute mortality risk was then calculated within 58 days of hospitalization of COVID-19 patients. Its color-coded risk chart is provided in Fig. 1. The proposed risk assessment method had an excellent accuracy (AUC = 0.872 [CI 95%: 0.835–0.910]). The ROC of the proposed system is shown in Fig. 2.
Fig. 2.
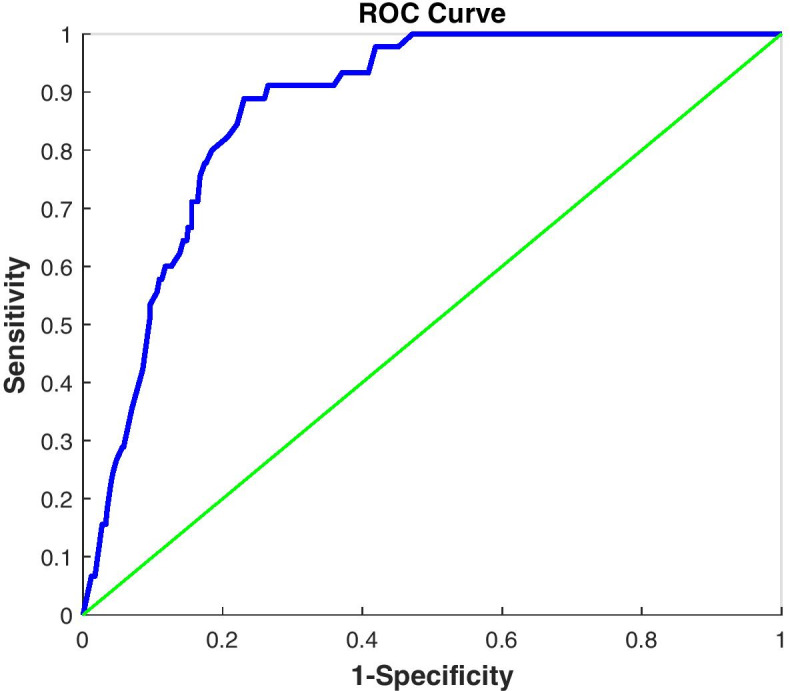
The Receiver operating characteristic (ROC) curve of the proposed risk assessment method for discrimination between the dead and discharged alive patients. The parameters Sensitivity (Specificity) are the proportion of patients who died (discharged alive) that were correctly identified by the model
The risk chart reflects the combined results of the two cause-specific hazard ratios. We find that the risk of hospital death within each group is about ten times higher for patients with an oxygen saturation lower of 80%.
Discussion
Suitable identification of hospitalized COVID-19 patients at high risk of mortality can significantly improve resource allocation and patient management within hospitals. This study aims to improve and validate a personalized mortality risk calculator based on hospitalized COVID-19 patients. The risk assessment of patient mortality provides physicians with additional guidance for making tough decisions. The presented tool showed a very good accuracy. In this model, baseline clinical parameters collected at hospital admission were used. It requires commonly available demographic and comorbidity data. Also, the oxygen saturation level could be measured using a traditional pulse oximeter. Thus, it does not require advanced blood testing and could be considered as a non-laboratory-based risk chart. The proposed risk assessment procedure is not limited to the input factors used in this paper. In fact, it could be applied to any input variables such as repeated COVID-19 infection, vaccination category, and body mass index.
Predicted mortality increased for patients with low oxygen saturation, corroborating findings that link hypoxemia to mortality [42], as well as the observed prevalence of shortness of breath in severe patients [43]. This measurement additionally serves as a signal of respiratory distress, and respiratory failure has been found clinically as one of the significant causes of COVID-19 mortality [44]. It can also appear in silent hypoxia cases where shortness of breath is not observed [45]. Age was another critical determinant of mortality in the model: older patients have higher mortality risk, as observed in the retrospective patient analysis [46] and subsequently reflected in public health guidance [47]. Similar to our study, it was shown in the literature that a higher CCI score is significantly associated with mortality and disease severity in COVID-19 patients [41, 48].
Moreover, the increase in mortality risk for patients with elevated blood pressure levels is consistent with the reports in other studies [49, 50]. Such findings could have been expected a priori as logical, but the proposed assessment permits quantifying them as a function of time after patient admission. In our analysis, a dichotomized version of CCI was used (CCI < 3 vs. CCI ≥ 3). However, more categories of CCI were used in the literature, such as: CCI = 0, CCI score of 1–2, and CCI score of ≥ 3 [41]. Due to the collinearity between age and CCI, our model consisted of a dichotomized version of CCI.
In our dataset, no active patients were in the hospital, and follow-up was complete for hospital mortality. Thus, in principle, the logistic regressions could be alternatively used instead of the absolute risk regression model in our data situation. However, it does not account for time-to-event and censoring. It could only display effects on a cumulative incidence function on a plateau [15]. Moreover, since we aim to use the proposed risk assessment procedure in dynamic situations and integrate it into the hospital information system (HIS), only predictions based on cause-specific regression could be used as there are always active cases in the hospital proceeding time frames.
The example of oxygen saturation categories demonstrated the possible incomplete picture of risk assessment if the competing risk of discharge alive is ignored. In the Cox regression, where discharge alive is not considered (cause-specific hazard ratio of death Tables 2 and 3), the effect of oxygen saturation would have been estimated to be 5.48. However, considering the competing risk, discharge alive showed an indirect effect on hospital mortality via an increased length of stay. Thus, in contrast to a classical survival situation without competing risks, the cause-specific hazard ratio has no one-to-one relationship with the absolute risk. Estimating the subdistribution hazard ratio combined direct and indirect effects and showed that the mortality risk is increased tenfold rather than only fivefold. Such differences affect the estimated mortality risks.
The available data limit our prediction model. Considering more comprehensive variables such as IL-6 levels, D-Dimer, and radiographic diagnosis, may yield more accurate results in the laboratory-based risk charts. While the proposed model focused on the COVID-19 dataset at the national level, some studies considered multi-center region-specific data to measure how major risk factors identify the mortality rate [51]. Furthermore, the variability in treatment protocols across countries and individual organizations might lead to different results [22, 52]. External validation of the proposed risk assessment method is the focus of our future work.
Conclusions
In conclusion, we provided a personalized mortality risk chart based on hospitalized COVID-19 patients to provide physicians with additional guidance for making tough decisions.
Acknowledgements
We would like to acknowledge the Khorshid hospital nurses and interns for this study, who recruited patients and collected follow-up data. Most importantly, we would like to acknowledge all the patients who consented to participate in this study.
Abbreviations
- AUC
Area under the curve
- CCI
Charlson Comorbidity Index
- CI
Confidence Interval
- COVID-2019
Coronavirus disease 2019
- HR
Hazard Ratio
- HIS
Hospital information system
- ICU
Intensive care unit
- KCC
Khorshid COVID Cohort
- SaO2
Oxygen saturation
- RSF
Random Survival Forests
- ROC
Receiver operator curve
Authors' contributions
HRM, MVC, MM, RH, HB, and MW participated in the Conceptualization, Investigation, and Methodology. HRM, MM, MVC, and MW participated in the Visualization, Software, and Validation. RS, SHJ, MM, PA, and MW participated in the Project administration. HRM, MVC, SHJ, MM, BA, FS, MoM, PA, MAM, HB, and MW participated in the formal analysis. RS, SHJ, MM, BA, FS, MoM, PA, NK, NSH, and AT participated in the data acquisition. HRM, RS, MM, NK, NSH, and AT participated in the data curation. RS, SHJ, MM, MAM, and MW participated in funding acquisition. MVC, MAM, and MW participated in supervision. MVC, RS, RH, MAM, and MW participated in the interpretation of the results. HRM, MVC, MM, and MW participated in Writing – original draft, while RS, SHJ, BA, FS, MoM, PA, NK, NSH, AT, RH, MAM, and HB participated in Writing – review & editing. All authors read and approved the final manuscript and agreed to be accountable for all aspects of the work.
Funding
The research leading to these results has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 712949 (TECNIOspring PLUS), and from the Agency for Business Competitiveness of the Government of Catalonia (TECSPR18-1–0017). The TECSPR18-1–0017 project provided the APC. These funders had no role in study design, data collection, analysis, decision to publish, or manuscript preparation.
Availability of data and materials
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Declarations
Ethics approval and consent to participate
The experimental protocol was approved by the ethics committee of the Isfahan University of Medical Sciences (IUMS) and the other national authorities (Longitudinal epidemiologic investigation of patients' characteristics with coronavirus infection referring to Isfahan Khorshid Hospital: IR.MUI.MED.REC.1399.029, Modeling of incidence and outcomes of COVID-19: IR.MUI.RESEARCH.REC.1399.479), conforming to the Declaration of Helsinki. The ethics committee of the IUMS granted permission to use the raw data of the KCC study. Also, the entire subjects gave written informed consent to the experimental procedure. It was given by the first relative family of patients with severe conditions. No minors participated in our study.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Hamid Reza Marateb, Email: h.marateb@eng.ui.ac.ir, Email: hamid.reza.marateb@upc.edu.
Maja von Cube, Email: cube@imbi.uni-freiburg.de.
Ramin Sami, Email: r.sami@med.mui.ac.ir.
Shaghayegh Haghjooy Javanmard, Email: sh_haghjoo@med.mui.ac.ir.
Marjan Mansourian, Email: marjan.mansourian@upc.edu, Email: j_mansourian@hlth.mui.ac.ir.
Babak Amra, Email: amra@med.mui.ac.ir.
Forogh Soltaninejad, Email: f.soltaninejad@med.mui.ac.ir.
Mojgan Mortazavi, Email: m_mortazavi@med.mui.ac.ir.
Peyman Adibi, Email: adibi@med.mui.ac.ir.
Nilufar Khademi, Email: nilufarkhademi@yahoo.com.
Nastaran Sadat Hosseini, Email: nastaran.h97@gmail.com.
Arash Toghyani, Email: arasht_75@yahoo.com.
Razieh Hassannejad, Email: rhassannejad@hlth.mui.ac.ir.
Miquel Angel Mañanas, Email: miguel.angel.mananas@upc.edu.
Harald Binder, Email: binderh@imbi.uni-freiburg.de.
Martin Wolkewitz, Email: wolke@imbi.uni-freiburg.de.
References
- 1.COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE), JHC [https://www.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6]. Accessed 1 June 2021.
- 2.Dong E, Du H, Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis. 2020;20(5):533–534. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shang Y, Pan C, Yang X, Zhong M, Shang X, Wu Z, Yu Z, Zhang W, Zhong Q, Zheng X, et al. Management of critically ill patients with COVID-19 in ICU: statement from front-line intensive care experts in Wuhan, China. Ann Intensive Care. 2020;10(1):73. doi: 10.1186/s13613-020-00689-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.COVID-19 Treatment Guidelines Panel. Coronavirus Disease 2019 (COVID-19) Treatment Guidelines. National Institutes of Health, [https://www.covid19treatmentguidelines.nih.gov/]. Accessed 1 June 2021. [PubMed]
- 5.Barda N, Riesel D, Akriv A, Levy J, Finkel U, Yona G, Greenfeld D, Sheiba S, Somer J, Bachmat E, et al. Developing a COVID-19 mortality risk prediction model when individual-level data are not available. Nat Commun. 2020;11(1):4439. doi: 10.1038/s41467-020-18297-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Das AK, Mishra S, Saraswathy Gopalan S. Predicting CoVID-19 community mortality risk using machine learning and development of an online prognostic tool. PeerJ. 2020;8:e10083–e10083. doi: 10.7717/peerj.10083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.D’Agostino RB, Lee M-L, Belanger AJ, Cupples LA, Anderson K, Kannel WB. Relation of pooled logistic regression to time dependent cox regression analysis: The framingham heart study. Stat Med. 1990;9(12):1501–15. [DOI] [PubMed]
- 8.Schnabel RB, Sullivan LM, Levy D, Pencina MJ, Massaro JM, D’Agostino RB Sr, Newton-Cheh C, Yamamoto JF, Magnani JW, Tadros TM, et al. Development of a risk score for atrial fibrillation (Framingham Heart Study): a community-based cohort study. The Lancet. 2009;373(9665):739–45. [DOI] [PMC free article] [PubMed]
- 9.Conroy RM, Pyörälä K, Fitzgerald AP, Sans S, Menotti A, De Backer G, De Bacquer D, Ducimetière P, Jousilahti P, Keil U, et al. Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J. 2003;24(11):987–1003. doi: 10.1016/S0195-668X(03)00114-3. [DOI] [PubMed] [Google Scholar]
- 10.Sarrafzadegan N, Hassannejad R, Marateb HR, Talaei M, Sadeghi M, Roohafza HR, Masoudkabir F, OveisGharan S, Mansourian M, Mohebian MR et al: PARS risk charts: A 10-year study of risk assessment for cardiovascular diseases in Eastern Mediterranean Region. PLOS ONE 2017, 12(12):e0189389. [DOI] [PMC free article] [PubMed]
- 11.Kaptoge S, Pennells L, De Bacquer D, Cooney MT, Kavousi M, Stevens G, Riley LM, Savin S, Khan T, Altay S, et al. World Health Organization cardiovascular disease risk charts: revised models to estimate risk in 21 global regions. Lancet Glob Health. 2019;7(10):e1332–e1345. doi: 10.1016/S2214-109X(19)30318-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.D’Agostino RB, Pencina MJ, Massaro JM, Coady S. Cardiovascular Disease Risk Assessment: Insights from Framingham. Glob Heart. 2013;8(1):11–23. [DOI] [PMC free article] [PubMed]
- 13.Wolkewitz M, Lambert J, von Cube M, Bugiera L, Grodd M, Hazard D, White N, Barnett A, Kaier K. Statistical Analysis of Clinical COVID-19 Data: A Concise Overview of Lessons Learned, Common Errors and How to Avoid Them. Clin Epidemiol. 2020;12:925–928. doi: 10.2147/CLEP.S256735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Latouche A, Allignol A, Beyersmann J, Labopin M, Fine JP. A competing risks analysis should report results on all cause-specific hazards and cumulative incidence functions. J Clin Epidemiol. 2013;66(6):648–653. doi: 10.1016/j.jclinepi.2012.09.017. [DOI] [PubMed] [Google Scholar]
- 15.Poguntke I, Schumacher M, Beyersmann J, Wolkewitz M. Simulation shows undesirable results for competing risks analysis with time-dependent covariates for clinical outcomes. BMC Med Res Methodol. 2018;18(1):79. doi: 10.1186/s12874-018-0535-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang H, Li G. A Selective Review on Random Survival Forests for High Dimensional Data. Quantitative bio-science. 2017;36(2):85–96. doi: 10.22283/qbs.2017.36.2.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kurt Omurlu I, Ture M, Tokatli F. The comparisons of random survival forests and Cox regression analysis with simulation and an application related to breast cancer. Expert Syst Appl. 2009;36(4):8582–8588. doi: 10.1016/j.eswa.2008.10.023. [DOI] [Google Scholar]
- 18.Miao F, Cai Y-P, Zhang Y-T, Li C-Y: Is Random Survival Forest an Alternative to Cox Proportional Model on Predicting Cardiovascular Disease? In: 6th European Conference of the International Federation for Medical and Biological Engineering: 2015// 2015; Cham: Springer International Publishing; 2015: 740–743.
- 19.Gerds TA, Scheike TH, Andersen PK. Absolute risk regression for competing risks: interpretation, link functions, and prediction. Stat Med. 2012;31(29):3921–3930. doi: 10.1002/sim.5459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Benichou J, Gail MH. Estimates of absolute cause-specific risk in cohort studies. Biometrics. 1990;46(3):813–826. doi: 10.2307/2532098. [DOI] [PubMed] [Google Scholar]
- 21.Ozenne B, Sørensen AL, Scheike T, Torp-Pedersen C, Gerds TA. riskRegression: Predicting the Risk of an Event using Cox Regression Models. R J. 2017;9(2):440. doi: 10.32614/RJ-2017-062. [DOI] [Google Scholar]
- 22.Sami R, Soltaninejad F, Amra B, Naderi Z, Haghjooy Javanmard S, Iraj B, Haji Ahmadi S, Shayganfar A, Dehghan M, Khademi N et al: A one-year hospital-based prospective COVID-19 open-cohort in the Eastern Mediterranean region: The Khorshid COVID Cohort (KCC) study. PLoS One 2020, 15(11):e0241537. [DOI] [PMC free article] [PubMed]
- 23.Cox DR: Regression Models and Life-Tables. In: Breakthroughs in Statistics: Methodology and Distribution. edn. Edited by Kotz S, Johnson NL. New York, NY: Springer New York; 1992: 527–541.
- 24.Gerds TA, Ozenne B: riskRegression: Risk Regression Models and Prediction Scores for Survival Analysis with Competing Risks. R package version 2020.02.05. 2020.https://CRAN.R-project.org/package=riskRegression.
- 25.Gray B: cmprsk: Subdistribution Analysis of Competing Risks. R package version 2.2–10. 2020.https://CRAN.R-project.org/package=cmprsk.
- 26.Fine JP, Gray RJ. A Proportional Hazards Model for the Subdistribution of a Competing Risk. J Am Stat Assoc. 1999;94(446):496–509. doi: 10.1080/01621459.1999.10474144. [DOI] [Google Scholar]
- 27.Gray RJ. A Class of K-Sample Tests for Comparing the Cumulative Incidence of a Competing Risk. Ann Stat. 1988;16(3):1141–1154. doi: 10.1214/aos/1176350951. [DOI] [Google Scholar]
- 28.Fawcett T. ROC graphs: Notes and practical considerations for researchers. Mach Learn. 2004;31(1):1–38. [Google Scholar]
- 29.Mason SJ, Graham NE. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q J R Meteorol Soc. 2002;128(584):2145–2166. doi: 10.1256/003590002320603584. [DOI] [Google Scholar]
- 30.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics. 1988;44(3):837–845. doi: 10.2307/2531595. [DOI] [PubMed] [Google Scholar]
- 31.Muschelli J. ROC and AUC with a Binary Predictor: a Potentially Misleading Metric. J Classif. 2020;37(3):696–708. doi: 10.1007/s00357-019-09345-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tuszynski J: caTools: moving window statistics, GIF, Base64, ROC, AUC, etc. R package version 1.18. 1. In.; 2021. https://CRAN.R-project.org/package=caTools.
- 33.R_Core_Team: R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2013.http://www.R-project.org/.
- 34.Vedaei SS, Fotovvat A, Mohebbian MR, Rahman GME, Wahid KA, Babyn P, Marateb HR, Mansourian M, Sami R. COVID-SAFE: An IoT-Based System for Automated Health Monitoring and Surveillance in Post-Pandemic Life. IEEE Access. 2020;8:188538–188551. doi: 10.1109/ACCESS.2020.3030194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Charlson ME, Pompei P, Ales KL, MacKenzie CR. A new method of classifying prognostic comorbidity in longitudinal studies: development and validation. J Chronic Dis. 1987;40(5):373–383. doi: 10.1016/0021-9681(87)90171-8. [DOI] [PubMed] [Google Scholar]
- 36.Radovanovic D, Seifert B, Urban P, Eberli FR, Rickli H, Bertel O, Puhan MA, Erne P: Validity of Charlson Comorbidity Index in patients hospitalised with acute coronary syndrome. Insights from the nationwide AMIS Plus registry 2002–2012. Heart (British Cardiac Society) 2014, 100(4):288–294. [DOI] [PubMed]
- 37.Cho KH, Kim SW, Park JW, Do JY, Kang SH: Effect of Sex on Clinical Outcomes in Patients with Coronavirus Disease: A Population-Based Study. Journal of clinical medicine 2020, 10(1). [DOI] [PMC free article] [PubMed]
- 38.Mejía F, Medina C, Cornejo E, Morello E, Vásquez S, Alave J, Schwalb A, Málaga G: Oxygen saturation as a predictor of mortality in hospitalized adult patients with COVID-19 in a public hospital in Lima, Peru. PLOS ONE 2021, 15(12):e0244171. [DOI] [PMC free article] [PubMed]
- 39.Petrilli CM, Jones SA, Yang J, Rajagopalan H, O’Donnell L, Chernyak Y, Tobin KA, Cerfolio RJ, Francois F, Horwitz LI: Factors associated with hospital admission and critical illness among 5279 people with coronavirus disease 2019 in New York City: prospective cohort study. BMJ 2020, 369:m1966. [DOI] [PMC free article] [PubMed]
- 40.Unal I. Defining an Optimal Cut-Point Value in ROC Analysis: An Alternative Approach. Comput Math Methods Med. 2017;2017:3762651. doi: 10.1155/2017/3762651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tuty Kuswardhani RA, Henrina J, Pranata R, Anthonius Lim M, Lawrensia S, Suastika K. Charlson comorbidity index and a composite of poor outcomes in COVID-19 patients: A systematic review and meta-analysis. Diabetes Metab Syndr. 2020;14(6):2103–2109. doi: 10.1016/j.dsx.2020.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bertsimas D, Lukin G, Mingardi L, Nohadani O, Orfanoudaki A, Stellato B, Wiberg H, Gonzalez-Garcia S, Parra-Calderón CL, Robinson K, et al. COVID-19 mortality risk assessment: An international multi-center study. PLoS ONE. 2020;15(12):e0243262–e0243262. doi: 10.1371/journal.pone.0243262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ora J, Liguori C, Puxeddu E, Coppola A, Matino M, Pierantozzi M, Mercuri NB, Rogliani P. Dyspnea perception and neurological symptoms in non-severe COVID-19 patients. Neurol Sci. 2020;41(10):2671–2674. doi: 10.1007/s10072-020-04632-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hasan SS, Capstick T, Ahmed R, Kow CS, Mazhar F, Merchant HA, Zaidi STR. Mortality in COVID-19 patients with acute respiratory distress syndrome and corticosteroids use: a systematic review and meta-analysis. Expert Rev Respir Med. 2020;14(11):1149–1163. doi: 10.1080/17476348.2020.1804365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chandra A, Chakraborty U, Pal J, Karmakar P: Silent hypoxia: a frequently overlooked clinical entity in patients with COVID-19. BMJ Case Reports 2020, 13(9):e237207. [DOI] [PMC free article] [PubMed]
- 46.Heras E, Garibaldi P, Boix M, Valero O, Castillo J, Curbelo Y, Gonzalez E, Mendoza O, Anglada M, Miralles JC et al: COVID-19 mortality risk factors in older people in a long-term care center. European Geriatric Medicine 2020. [DOI] [PMC free article] [PubMed]
- 47.WHO: Guidance on COVID-19 for the care of older people and people living in long-term care facilities, other non-acute care facilities and home care. 2020.
- 48.Varol Y, Hakoglu B, Kadri Cirak A, Polat G, Komurcuoglu B, Akkol B, Atasoy C, Bayramic E, Balci G, Ataman S et al: The impact of charlson comorbidity index on mortality from SARS-CoV-2 virus infection and A novel COVID-19 mortality index: CoLACD. International journal of clinical practice 2020:e13858. [DOI] [PMC free article] [PubMed]
- 49.Du Y, Zhou N, Zha W, Lv Y: Hypertension is a clinically important risk factor for critical illness and mortality in COVID-19: A meta-analysis. Nutrition, Metabolism and Cardiovascular Diseases 2020. [DOI] [PMC free article] [PubMed]
- 50.Liang X, Shi L, Wang Y, Xiao W, Duan G, Yang H, Wang Y. The association of hypertension with the severity and mortality of COVID-19 patients: Evidence based on adjusted effect estimates. J Infect. 2020;81(3):e44–e47. doi: 10.1016/j.jinf.2020.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Garg P, Joshi D: A region-specific clustering approach to investigate risk-factors in mortality rate during COVID-19: comprehensive statistical analysis from 208 countries. Journal of medical engineering & technology 2021:1–6. [DOI] [PubMed]
- 52.Rieg S, von Cube M, Kalbhenn J, Utzolino S, Pernice K, Bechet L, Baur J, Lang CN, Wagner D, Wolkewitz M et al: COVID-19 in-hospital mortality and mode of death in a dynamic and non-restricted tertiary care model in Germany. PLoS One 2020, 15(11):e0242127. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.