Effectiveness of non-pharmaceutical interventions against local transmission of COVID-19: An individual-based modelling study

Abstract

The outbreak of the novel coronavirus disease 2019 (COVID-19), caused by the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), has caused global transmission, and been spread all over the world. For those regions that are currently free of infected cases, it is an urgent issue to prevent and control the local outbreak of COVID-19 when there are sporadic cases. To evaluate the effects of non-pharmaceutical interventions against local transmission of COVID-19, and to forecast the epidemic dynamics after local outbreak of diseases under different control measures, we developed an individual-based model (IBM) to simulate the transmission dynamics of COVID-19 from a microscopic perspective of individual-to-individual contacts to heterogenous among individuals. Based on the model, we simulated the effects of different levels of non-pharmaceutical interventions in controlling disease transmission after the appearance of sporadic cases. Simulations shown that isolation of infected cases and quarantine of close contacts alone would not eliminate the local transmission of COVID-19, and there is a risk of a second wave epidemics. Quarantine the second-layer close contacts can obviously reduce the size of outbreak. Moreover, to effectively eliminate the daily new infections in a short time, it is necessary to reduce the individual-to-individual contacts. IBM provides a numerical representation for the local transmission of infectious diseases, and extends the compartmental models to include individual heterogeneity and the close contacts network. Our study suggests that combinations of self-isolation, quarantine of close contacts, and social distancing would be necessary to block the local transmission of COVID-19.

1. Introduction

The pandemic of novel coronavirus disease 2019 (COVID-19), caused by the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), is spreading globally over the world. As of 11 January 2021, more than 89 million confirmed cases and 1930 thousand death have been reported worldwide (World Health Organization, 2020c). COVID-19 have a basic reproduction number larger than 1 (about 2.0 ~ 3.0), and a death rate of 0.3% ~ 0.6% (Gudbjartsson et al., 2020; Flaxman et al., 2020). The rapid spreading of COVID-19 has become a major issue of global public health and economic development. Non-pharmaceutical interventions (NPIs) are certainly needed in order to control the COVID-19 outbreak (Ferguson et al., 2020; Flaxman et al., 2020; Lai et al., 2020). Especially, in regions that are currently free of infected cases, such as many area away from big cities, and most regions in mainland China, it is a challenging issue to prevent the spreading of COVID-19 while minimizing the economic and social costs.

The novel coronavirus was first reported in Wuhan, China, in December 2019, and spread rapidly within the city and across the country (Li et al., 2020b). Starting from 20 January 2020, a series of NPIs were implemented to contain the virus spreading and to reduce the epidemic size across China, including the intercity travel restrictions, early identification, isolation of infected patients and close contacts management, and measures of contact restrictions and social distancing (Chen et al., 2020). These NPIs effectively slowdown the spreading process and result in a rapid decline in daily infected cases, however at high economic and social costs (World Health Organization, 2020a,b). Similar control measures were also applied in many other counties and regions, and effectively slow down the spreading of diseases. SRAS-CoV-2 was completely contained in China, and the indigenous transmission was mostly stopped 4 months after the early outbreak (Li et al., 2020c). However, there are still high risks of the re-occurrence of community transmission from import-related cases. Local outbreak of COVID-19 re-emergence in multiple places, including Harbin in Heilongjiang Province (April 2020), Shulan in Jilin Province (May 2020), Beijing (June), and Xinjiang (August 2020) (Fig. 1). These local outbreaks are quickly contained thanks to the strong suppression efforts of containment measures.

Fig. 1.

Daily indigenous new cases in mainland China from 2020/01/01 to 2020/09/30. Inset shows sporadic outbreaks.

The experience in China suggests that NPIs are effective public health responses to control the local outbreaks of COVID-19. However, it remains debates on the trade-off between epidemic control and social costs. A comprehensive and quantitative studies of the effectiveness of different NPIs are lacked when we try to come out with a precise prevention and control strategy, including the timing at which they should be implemented, and the forecasting of epidemic dynamics upon different measures.

In this study, to evaluate the effectiveness of NPIs, we constructed an individual-based model (IBM) based on heterogenous responses and close contacts tracing to simulate the transmission dynamics of COVID-19 in a local region. The model is consists of a network of individuals that are connected through a relation of close contacts. Each individual follows a stochastic state transition of susceptible-exposed-infectious-hospitalized-quarantine-removed (SEIHQR), and the susceptible individual can be infected while contacting with infectious. The confirmed cases are isolated through hospitalized. We studied the effects of different level control measures, and predicts how these measures play roles in the reduction of outbreak size and to stop local transmission. We concluded that combination of second layer close contacts quarantine and contacts restriction can effectively reduce the size of COVID-19 outbreak, and it may usually take one month to contain the virus spreading.

2. Methods

2.1. Individual-based model

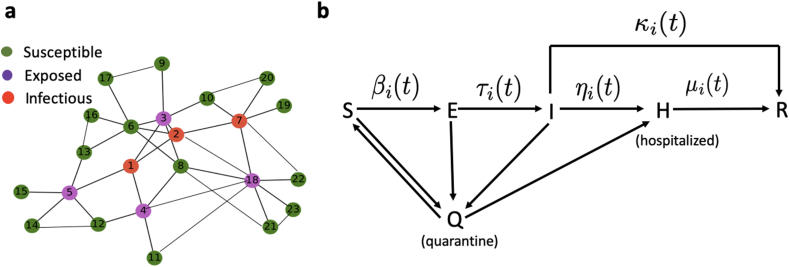
To simulate the transmission of COVID-19, we established an individual-based model. In the model, population of individuals are represented by nodes in a close contact network, in which each node transits among different states, and the close contact relationships are represented by edges between nodes (Fig. 2a).

Fig. 2.

Sketch of the individual-based model of COVID-19 transmission. a Illustration of a close contact network of individuals. Each node represents a person, with different colors for its state, and the edges represent the relationship of close contact between individuals. b The SEIHQR model of each individual, each person can transit among the states of susceptible (S), exposed (E), infectious (I), hospitalized (H), quarantined (Q), or recovered (R), following the direction of arrows. The transition rates can vary with time, and individual dependent.

Each individual may at different states, including susceptible (S), exposed (E), infectious (I), hospitalized (H), quarantined (Q), or removed (R), in accordance with the basic assumptions of the SEIHQR compartmental model (Fig. 2B). In the model, heterogeneity and dynamic changes of the individuals were highlighted. Here, by exposed we mean a person who has exposed to and infected with SARS-CoV-2, however not yet show symptoms, and may has the risk to infect other susceptible persons (Gao et al., 2020; Xia et al., 2020).

The state of each individual is represented by a multi-components tensor as

$$S_i(t)=\{C_i^1(t),C_i^2(t),C_i^3(t),\dots ,C_i^5(t)\},(i=1,2,\dots ,N).$$ (1)

Here, N represents the total number of individuals in the population, and S_i represents the states/properties of the i'th individual. The meanings of each component $C_i^m(t)$ are listed below,

• 1.$C_i^1(t)\in {\mathbb{R}}_{+}$ represents the age.
• 2.$C_i^2(t)\in \{0,1,2,3,4,5\}$ stands for the epidemiological status, the numbers 0, 1, 2, 3, 4, 5 represent respectively susceptible (S), exposed (E), infected (I), hospitalized (H), quarantined (Q), removed (R). Here, the recovered individuals are assumed to be resistance to SARS-CoV-2 and would not be infected again.
• 3.$C_i^3(t)\in \{0,1\}$ represents the quarantined status (0 for not quarantined, 1 for quarantined).
• 4.$C_i^4(t)\in (0,14]$ represents the number of days an individual is quarantined (maximum 14 days).
• 5.$C_i^5(t)$ is a vector to store the indexes of close contacts in the last 14 days.

2.2. Contact network

The real contact network can be highly dynamics and difficult to trace. Here, we would not consider the real contact network, instead, we considered a virtual network that share similar statistical properties as the real network. The statistical properties of social networks have been extensively studied, evidences shown that both social networks and simulated contact networks display the features of small-world networks (Hartvigsen et al., 2007; Masuda et al., 2004). Here, we applied the Watts-Strogatz small-world network to represent the contact relationship among individuals (Watts & Strogatz, 1998).

There are three parameters in a small-world network according to the Watts-Strogatz construction algorithm (Watts & Strogatz, 1998), the population size N, the degree of contacts number K, and the probability P of random reconnections. The parameters K and N determine the distribution of contact numbers of the individuals in a network. Given a close contact network, let ${\{{\phi }_{i,j}\}}_{1\le i,j\le N}$ to represent the contact relationship between individuals, with φ_i,j = 1 when individuals i and j are contacted, and other wise φ_i,j = 0. The contact number of individual i is given by $n_i={\sum }_{j=1}^N{\phi }_{i,j}$. Fig. 3a shows the distribution of contact numbers ${\{n_i\}}_{i=1}^N$ with varying values of K and P.

Fig. 3.

Illustration of model parameters. a. Distributions of close contact numbers defined by small-world networks with different values of K and P. Here, N = 2000 in all cases. b. Density of incubation periods defined by Gamma distribution Γ(τ; a, b) with a = 3.07 and b = 2.35.

2.3. State transition

To model the dynamics of individual state transition, we need to formulate the transition rate between different states.

2.3.1. Infection

In the model, we assumed that a susceptible individual can be infected with SARS-CoV-2 when he/she contacts with an exposed or infectious person. Let β (day⁻¹) the infection rate when a susceptible persons contacts with an infectious, and there is factor θ to the infection rate when a susceptible person contacts with an exposed person. Thus, the effective infectious rate of an individual i at the susceptible state is

$${\beta }_i(t)=\beta \left(\theta \sum _{1\le j\le N,C_j^2(t)=1}{\phi }_{i,j}+\sum _{1\le j\le N,C_j^2(t)=2}{\phi }_{i,j}\right).$$ (2)

Accordingly, the probability that a susceptible individual i is infected within a time interval of [t, t + Δt] is given by (Keeling et al., 2008):

$$P_1(t)=1-e^{-{\beta }_i(t)\mathrm{\Delta }t}.$$ (3)

2.3.2. Incubation period

After a susceptible individual is infected, he/she becomes exposed, and becomes infectious after a period of incubation τ_i. The incubation period is heterogenous for different patients. Here, we adopt a gamma distribution Γ(τ; a, b) of incubation periods, with the shape parameter a = 3.07 and the scale parameter b = 2.35 in accordance with the epidemic dynamics of COVID-19 in China (Li et al., 2020a) (Fig. 3b).

2.3.3. Infectious patient confirmation

Each infectious patient is confirmed with a rate η(t), the probability that an infectious individual is confirmed in a time interval [t, t + Δt] is

$$P_2(t)=1-e^{-\eta (t)\mathrm{\Delta }t}.$$ (4)

The confirmation rate may vary with the epidemic evolution, especially during the early stages of the outbreak of a novel epidemic disease (He et al., 2020; Tang et al., 2020). After a patient is confirmed, he/she is hospitalized and lose the contact with other individuals.

2.3.4. Recovery or death

The confirmed (hospitalized) patients are removed (recovery or death) with a rate μ, so that the probability of being removed in Δt is given by

$$P_3(t)=1-e^{-\mu (t)\mathrm{\Delta }t}.$$ (5)

Moreover, infectious patients (slight symptom patients) are removed (recovery or death) by themselves with a rate κ, and hence the probability

$$P_4(t)=1-e^{-\kappa (t)\mathrm{\Delta }t}.$$ (6)

2.4. Non-pharmaceutical interventions

To model the effectiveness of non-pharmaceutical interventions (NPIs), we considered two control measures: quarantine of close contacts and restriction of social contacts.

In our model, the contact relations were traced along the transmission process. Once an infected person was confirmed, the close contacts are identified and quarantined. Moreover, we may also consider the second layer contacts tracing if necessary. Moreover, to quantify various execution potential of local governments, we assumed different tracing rates, which is defined as the probability of successful quarantine of a close contact person. For peoples in the quarantined state, the infected individuals (either exposed or infected state) can be diagnosed effectively and become hospitalized. The un-infected individuals are moved back to the susceptible state after 14 days quarantine.

To model the control measure of social contract restriction, we varied the small-world network parameter K to mimic the situation of reducing the average contact number.

In summary, three level responses were considered:

Level III: Close contact tracing and quarantine.

Level II: Level III response and social contact restriction so that the average contact number reduce to half of the normal level.

Level I: Level III response and strict restriction of social contacts so that the average contact number is limited to a minimum level.

Specifically, control measures considered in this study are listed in Table 1.

Table 1.

NPI control measures considered in this study. Measures M-1 to M-9 are listed, including level III response with layer 1 (III-L1) or layer 2 (III-L2) close contact quarantine (with quarantine rates 0.5, 07, 0.9 and 0.3, 0.5, 0.7, respectively), level II response with K = 10 (II–K10) (starts when there are 10 or 5 daily confirmed cases, respectively), and level I response with K = 4 (I–K4) (starts when there are 5 daily confirmed cases).

Measure	III-L1			III-L2			II-K10		I–K4
	0.5	0.7	0.9	0.3	0.5	0.7	10	5	5
M-1	+	−	−	−	−	−	−	−	−
M-2	−	+	−	−	−	−	−	−	−
M-3	−	−	+	−	−	−	−	−	−
M-4	−	+	−	+	−	−	−	−	−
M-5	−	+	−	−	+	−	−	−	−
M-6	−	+	−	−	−	+	−	−	−
M-7	−	+	−	−	+	−	+	−	−
M-8	−	+	−	−	+	−	−	+	−
M-9	−	+	−	−	+	−	−	−	+

2.5. Parameter estimation

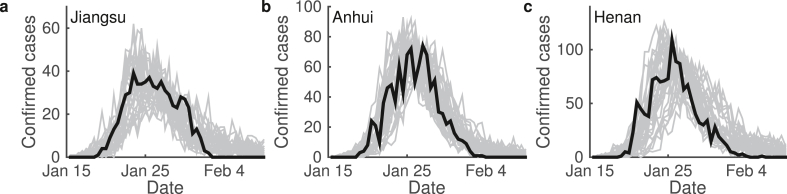
To verify the proposed model and estimate the parameters, we applied the approximate Bayesian computation (ABC) algorithm to estimated model parameters and fitted model simulation with epidemic data (Toni et al., 2009). This study was intended to consider the control measures in China, and hence referred the situation of early COVID-19 spreading in China. We compared model simulation with the data of daily confirmed cases in Jiangsu, Anhui, and Henan provinces from January to March 2020. Fitting results are shown in Fig. 4, and the estimated parameters in the studies below are given in Table 2. In simulations below, we referred the parameters values obtained from Jiangsu Province.

• ^(a) Here, K = 14 corresponds to the situation with control measures. In simulations, we set K = 20 for the normal situation without control measures.

• ^(b) In the current situation, all infections were diagnosed and hospitalized, and hence the self-recovery rate κ = 0.

• ^(c) In the case of early 2020, the diagnose rate varied with time from early slow confirmation to latter fast confirmation, so that the confirmation rate η = (η₁ − η₂)e^−rt + η₂. In our simulation, to consider the situation with stable confirmation rate, we take η = η₂.

• ^(d) In model simulations, we varied the quarantine rate according to Table 1.

Fig. 4.

Model simulation and epidemic data. Figures show the daily increased confirmed cases in provinces (a) Jiangsu, (b) Anhui, and (c) Henan in China. Both epidemic data (black) and model simulations (gray) are shown. For each province, model simulations were performed 50 independent runs.

Table 2.

Parameter values obtained by fitting model simulation with epidemic data of Jiangsu province. In all cases, we set the duration of quarantine as 14 days.

Parameter	Definitions	Range	Value
N	The number of contact network nodes	[2000, 5000]	3566
	(the number of individuals)
K	The number of regular network neighbors	[10, 30]	14(a)
	(the average number of close contacts)
P	The probability of the random reconnection	(0, 1)	0.1854
β	The probability of successful infection	(0, 0.5)	0.0879
θ	The moderator for the probability of	(0, 0.5)	0.1703
	transmission from exposed individuals
κ	The self-recovery rate (day−1)	(0, 0.1)	0(b)
η1	the initial diagnose rate (day−1)	(0, 0.3)	0.2314(c)
η2	The fastest diagnose rate (day−1)	(0.3, 0.6)	0.4756(c)
r	The exponential decreasing rate (day−1)	(0, 1)	0.4351(c)
μ	The remove rate (day−1)	(0, 0.2)	0.1029
q	Quarantine ratio	(0.2, 0.9)	0.5114(d)

3. Results

3.1. Epidemic dynamic without control measures

First, we considered the situation with initially one infection and no control measures. Consequently, the disease may spread to cover most individuals in the contact network (Fig. 5a). Since there is a time lag between infection and diagnosis, disease outbreak may occur before the first diagnosis of infected cases. Model simulations shown that the number of infected cases may range from a few to more than 50 cases at the time of the first diagnosis, and an average of 9 ~ 10. Moreover, most infected cases belong to layer 1–3 contacts of the diagnosed patient (Fig. 5b). At the time when 5 cases are diagnosed, there are on average up to about 50 infected person, and many of them (27%) belong to close contacts of layer 4 or further (Fig. 5b). These results indicate the fact of fast transmission of COVID-19 in the case without control measures, and hence quick response upon the diagnosis is required in order to control the epidemic outbreak.

Fig. 5.

Epidemic dynamics without control measures. (a). Cumulative infected cases without control measures. Black shows 50 random simulations based on the IBM model, red line shows the result from deterministic the SEIR model. (b). Statistics of infection numbers upon the confirmation of 1 or 5 cases after disease outbreak. Pie graphs show the percentages of infections in layer 1 (L1), layer 2 (L2), layer 3 (L3), or other layer close contacts of the confirmed cases. In each situation, data were obtained from 500 independent runs.

3.2. Effects of non-pharmaceutical interventions

Now, we considered the effects of NPIs. Nine measures listed in Table 1 were evaluated, the results are summarized in Fig. 6. When level III response with only layer-1 contact isolation (M-1, M-2, M-3), both daily new infections and total infected cases obviously decrease with the isolation rate (Fig. 6a–b & g-h), hence increasing the isolation rate can effective reduce the epidemic size. Nevertheless, the peak time of daily new infection do not change with the isolation rate, which are on average at 30 days after the occurring of the first infection (Fig. 6d and e).

Fig. 6.

Effectiveness of different control measures. (a) Peak value of daily new cases under different control measures. For each measure, results from 30 independent runs are shown. (b) Error bar plot of peak values for different measures. (c) Epidemics of daily new cases under control measure 5 (M-5), 8 (M-8) and 9 (M-9) in Table 1. Here, shadows show the range of 30 runs, and solid lines show the average numbers. (d) Peak time of daily new cases under different control measures. (e) Error bar plot of peak times for different measures. (f) Boxplots of total cases for three control measures. (g) Total cases under different control measures. (h) Error bar plot of total cases for different measures. (i) Day of eliminating the disease under different control measures. Here, control measures M-1 to M-9 are listed in Table 1.

When the level III response with second layer contacts isolation was implemented (M-4, M-5, M-6), both peak value of daily new cases and the total infected numbers obviously decease in comparing with layer-1 contact isolation alone (Fig. 6a–b & g-h). Furthermore, implementation of layer-2 isolation can shorten the peak time of daily new infections (Fig. 6d and e), and hence shift the turning point to earlier date. We note that layer-2 isolation obviously improve the effects of layer-1 isolation alone, and variances in the rate of layer-2 isolation do not result in significant differences in the epidemic dynamics. Hence, layer-2 isolation is necessary to effectively control the spreading of disease, even the isolation rate can be low.

Nevertheless, we note that layer-2 contact isolation alone may not effective eliminate the disease, and second wave outbreak or prolong epidemic dynamics may occur (Fig. 7a). Hence, we need to carry out further restrictions on social distancing.

Fig. 7.

Second wave outbreak and disease elimination. (a) Epidemic dynamics of daily infected cases under level III response (M-5). Magenta and black lines show two sample dynamics with second wave outbreak and prolong transmission, respectively. (b) Epidemic dynamics of daily infected cases under level II response (M-8). Magenta and black lines show two sample dynamics. (c) Distribution of the days of disease elimination under measure M-5 and M-8. Red ‘∗’ shows the maximum simulation date, some samples do not lead to disease elimination.

Level II response with the contact parameter K reduced to half of the normal level (K = 10, M-7 and M-8) can effectively reduce both the daily new infections and the total infected population size (Fig. 6a–b & g-h), and show much lower daily cases in the later stage (Fig. 6c). Moreover, implementation of level II response can effectively eliminate the daily new infections (Fig. 7b). Statistical analysis of the time of disease elimination shown that level II response can significantly reduce the time of disease spreading (Fig. 7b).

We further reduced the average number of close contacts according to level I response (K = 4, M-9). Level I response further improve the effect of level II response (Fig. 6c), obviously reduced the infected population to a very low level, and shorten the day of disease elimination from average 48.3 days with level II response to 33.3 days under level I response (Fig. 6i). From Fig. 6f and i, level II and I responses can obviously reduce the total epidemic size and shorten the epidemic duration.

3.3. Epidemic dynamics after suspension of control measures

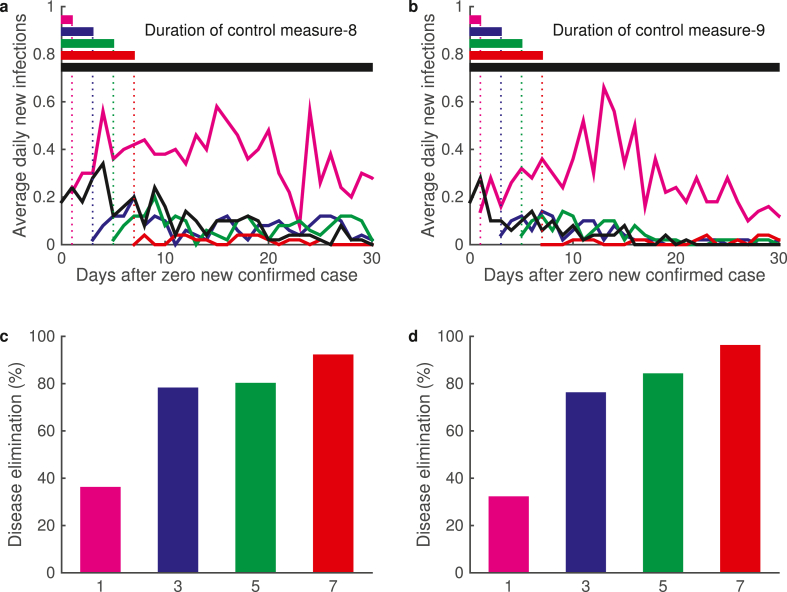
Now, we examined the effects of control measures suspension under various conditions, including zero new confirmed cases for continuous 1, 3, 5, or 7 days (Fig. 8). Simulations shown that if the control measures (level II or level I responses) were suspended when there is zero confirmed cases for only 1 day, the disease would mostly recur, and the probability of disease elimination is only as low as 40%. Nevertheless, the probability of disease elimination increase to 80% if the control measures are suspended after continuously 3–5 days zero new confirmed cases, and to 90% when continuously 7 days zero new confirmed cases. These results suggest the control measure should be terminated at least 7 continuous days of zero new confirmed cases in order to reach 90% probability of elimination.

Fig. 8.

Epidemic dynamics after the suspension of control measures. (a)–(b) Daily new infections after control measures were suspended under different conditions. Results for control measures (a) M-8 and (b) M-9 are shown. The suspension conditions include continuous 1 (magenta), 3 (blue), 5 (green), and 7 (red) days with zero new confirmed cases. The default situation with continuous measure is also shown. Here, day 0 corresponds to the first day of zero new confirmed case after disease outbreak. (c)–(d) Percentages of disease elimination after the suspension of control measures. Results for control measures (c) M-8 and (d) M-9 are shown. Different color bars correspond to the situations in (a)–(b).

In summary, the above simulations show that second-layer contacts isolation is required to prevent the spreading of disease, and social restriction is necessary in order to effectively eliminate the disease. Strict restriction in social contact can shift the date of disease elimination to earlier, however with higher social cost. Hence, the trade-off between epidemic dynamics control and the social cost should be highlighted while applying the measure of social contacts restriction.

3.4. Effects of control measures with continuous import cases

Now, based on the discussion previously, we simulated the effect of different control measures under the situation of continuous import cases. We assumed a circumstance that new cases occurred randomly for continuously 5 days, the number of daily new cases follow a poisson distribution with the parameter λ = 3. Four control measures in Table 3 were compared through model simulations (Fig. 9). The simulation results show that the second layer contacts isolation (measure B) obviously reduce the peak value of daily new cases and the total epidemic size (Fig. 9). Further restrictions in the social contacts (measures C and D) can significantly reduce the final size of cumulative infected cases (Fig. 9d).

Table 3.

Control measure with continuous import cases for continuously 5 days.

Measure	Description
A	Level III response with layer-1 contact isolation with the
	isolation rate 0.7.
B	Measure A control from the beginning, and layer-2 contact
	isolation when daily new confirmed cases exceeded 3 per day.
C	Measure B control, and start level II response when the daily
	new confirmed cases exceeds 5 per day.
D	Measure C control, and start level I response when the daily
	new confirmed cases exceeds 8 per day.

Fig. 9.

Effects of NPI control measures with continuous import cases. (a) Daily new cases under control measures A, B, C, and D in Table 3. (b)–(d) Boxplot of (b) peak values, (c) peak time, and (d) total case for different measures.

4. Discussion

This study introduces an individual-based model of epidemic dynamics to evaluate the effectiveness of NPIs against local transmission of COVID-19. Our study was intended to provide suggestions on the control measures in a local area when there are occasional occurrence of new cases of confirmed COVID-19 patients. COVID-19 has a basic reproduction number R₀ larger than 1, and COVID-19 patients can potentially infect other peoples before showing typical symptoms. Hence, by the time when the first patients was diagnosed, the disease may have already locally spread. The proposed individual-based model is capable of simulating the process of individual-to-individual transmission under different circumstance, and hence provide precise informations for the control measures.

We considered different level control measures, including the close contact isolation and social contact restriction. Model simulations shown that close contact isolation upon the diagnosed of the first patient is certainly required in order to control the disease spreading. Moreover, second-layer contact isolation can significantly reduce the final infected population size and the peak of daily new cases, and hence is strongly suggested in applying the control measures. The measure of close contact isolation can constrain the disease spreading for a while, it may not finally eliminate disease transmission. Our study suggested that further implementation of social contact restriction is required to achieve the goal of eliminating the infected cases.

In summary, our studies suggest the following strategies as normal measures to prevent the local outbreak of COVID-19:

• 1.Second-layer contact isolation should be put into effect once a COVID-19 patient was diagnosed.
• 2.Social distancing is important to prevent the disease spreading, and restriction of social contact should be considered in order to eliminate the disease.
• 3.Strict restriction of social contact can shift the date of disease elimination earlier, and effectively decrease of total number of cases.

Moreover, we also verified the simulations with various size, the results are independent to the population size (data not shown). The simulation results in our study is insensitive with the changes in the individual number N, which suggest the existence of an upper bound of populations may be affected, and hence localized control measure is enough to prevent further disease transmission.

The proposed individual-based model provides a framework to simulate the process of local transmission of epidemic diseases. The proposed model framework is flexible to model different circumstances through the modification of contact networks and the personalized individual state transition rates, which is important to model the early epidemic stages from sporadic cases to clusters of community spread. Individual-based models highlight the heterogeneity in personal features and the contact networks, and can give details of the transmission trajectory, which are important for making the precise control strategies.

Declaration of competing interest

The authors declare that they do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Handling editor: Dr. J Wu