Forecasting fully vaccinated people against COVID-19 and examining future vaccination rate for herd immunity in the US, Asia, Europe, Africa, South America, and the World

Abstract

Coronavirus disease 2019 (COVID-2019) has spread rapidly all over the world and it is known that the most effective way to eliminate the disease is vaccination. Although the traditional vaccine development process is quite long, more than ten COVID-19 vaccines have been approved for use in about a year. The COVID-19 vaccines that have been administered are highly effective enough, but achieving herd immunity is required to end the pandemic. The motivation of this study is to contribute to review the countries’ vaccine policies and adjusting the manufacturing plans of the vaccine companies. In this study, the total number of people fully vaccinated against COVID-19 was forecasted in the US, Asia, Europe, Africa, South America, and the World with the Autoregressive Integrated Moving Average (ARIMA) model, which is a new approach in vaccination studies. Additionally, for herd immunity, the percentage of fully vaccinated people in these regions at the beginning of 2021 summer was determined. ARIMA results show that in the US, Asia, Europe, Africa, South America, and the World will reach 139 million, 109 million, 127 million, 8 million, 38 million, and 441 million people will be fully vaccinated on 1 June 2021, respectively. According to these results, 41.8% of the US, 2.3% of Asia, 17% of Europe, 0.6% of Africa, 8.8% of South America, and 5.6% of the World population will be fully vaccinated people against the COVID-19. Results show that countries are far from the herd immunity threshold level desired to reach for safely slow or stop the COVID-19 epidemic.

1. Introduction

The coronavirus was reported as pneumonia of unknown etiology in Wuhan, China in December 2019. In January 2020, it was determined that the disease agent was a new coronavirus (2019-nCoV) that was not previously detected in humans. Because of its high similarity to SARS coronavirus (SARS-CoV), it was named SARS-CoV-2, and the disease that occurred was later named coronavirus disease 19 (COVID-19) [1].

The virus spread rapidly around the world, as there is no treatment and vaccine for COVID-19 disease. In the first three months, 114 countries were affected by the virus, and 4291 deaths occurred. As a result of the rapid spread of the disease, it was declared as a global pandemic by the World Health Organization (WHO) on March 11, 2020 [2].

SARS-CoV-2 can be transmitted from an infected person without symptoms and can lead to a pandemic disease within a week. This situation shows how important and mandatory vaccination is in controlling SARS-CoV-2 [3]. Therefore, a lot of effort has been made recently to develop vaccines against human coronavirus infections such as MERS and SARS. However, the fact that antiviral agents or vaccines have not been developed against MERS and SARS viruses until today has made COVID-19 a global threat [4], [5], [6].

Developed SARS-CoV-2 vaccines are based on mRNA, viral vector, inactive and protein. mRNA type vaccines provide the genetic code (DNA or RNA) for our cells to produce viral proteins. Once the proteins (non-disease causing) are produced, the body develops immunity against the virüs [7]. The first COVID-19 vaccine is Pfizer–BioNTech and is of the mRNA type. In viral vector-based vaccines, the genetic material of the virus is inserted into other viruses that do not cause genetic disease and applied to humans. Inactivated or weakened virus vaccine technique is the classical method. Here, the weakened or dead virus is used. In protein-based vaccine, virus proteins are used either directly isolated from the virus or artificially produced. Developed SARS-CoV-2 vaccines and properties of these vaccines are given in Table 1.

Table 1.

SARS-CoV-2 vaccines and properties of vaccines.

Vaccine	Efficacy	Type	Storage	Doses
Pfizer–BioNTech [8]	95%	mRNA	−70 °C	2
Moderna [9]	94%	mRNA	−20 °C	2
SputnikV [10]	91%	Viral vector	<=−18 °C	2
AstraZeneca [9]	70%	Viral vector	2–8 °C	2
Convidecia [11]	66%	Viral vector	2–8 °C	1
Janssen [12]	76.7–85.4%	Viral vector	2–8 °C	1
CoviVac [12]	–	Inactivate	2–8 °C	2
Sinopharm [13]	79%	Inactivate	2–8 °C	2
CoronaVac/Sinovac [12]	50%–91%	Inactivate	2–8 °C	2
Covaxin [12]	81%	Inactivate	2–8 °C	2
EpiVacCorona [12]	100%	Protein	2–8 °C	2
ZF2001/RBD-Dimer [14]	70%–95%	Protein	2–8 °C	3
Novavax [15]	89%	Protein	2–8 °C	2

Vaccines have proven to be the most effective and economical way to prevent and control infectious diseases [32]. Although COVID-19 vaccines are highly efficacy enough, herd immunity is required to end the pandemic. Herd immunity can be achieved by vaccination or natural immunization. The fastest way to achieve herd immunity is vaccination. Herd immunity for the COVID-19 disease may vary from country to country because not every individual in the community can be vaccinated (for example, babies, pregnant women, those with medical problems, or those who do not want to be vaccinated). For this reason, reaching the minimum vaccination rate determined in order to achieve herd immunity is important in terms of eliminating the COVID-19 pandemic. The percentage of people who need to be immune to ensure herd immunity varies with each disease. Because this may vary depending on the vaccine, the population, the populations prioritized for vaccination, and other factors [33]. By forecasting the total number of fully vaccinated people by country, it can be observed that approximately how much of the population will be vaccinated and how close the threshold level for herd immunity has been reached.

Estimating the future values of an observed time series plays an important role in many sciences and engineering fields. The main idea of the ARIMA model is to identify mathematical and statistical theory and then used it to forecast time-series data. Integrated Moving Average (ARIMA) model is frequently used to predict future values due to its simple structure, flexibility, fast applicability and captures many different patterns [18]. In the past epidemics and health studies, the ARIMA time series model was successfully used [34], [35], [36], [37], [38]. ARIMA models are also widely and successfully used for current COVID-19 epidemic research. Some studies using the ARIMA model for the COVID-19 epidemic are given in Table 2.

Table 2.

Various studies on COVID-19 epidemic using ARIMA.

Authos(s)	Forecasting	Study area
Alzahrani et al. [16]	Case	Sudi Arabistan
Dehesh et al. [17]	Case	China, Italy, South Korea, Iran, Thailand
Ceylan [18]	Case	Italy, Spain, France
Anne [19]	Case	India
Kumar et al. [20]	Case and death	Fifteen countries
Tandon et al. [21]	Case	Eight countries and Asia regions
Ilie et al. [22]	Case	Nine countries
Kufel [23]	Case	Selected European
Sharma [24]	Case	India
Chaurasia [25]	Death	World
Argawu [26]	Case	Ten countries
Lukman et al. [27]	Case	SA, Nigeria, Ghana, Egypt
Perone [28]	Case	Italy, Russia, USA
Maheshwari et al. [29]	Case and death	India
Katoch et al. [30]	Case	India
Kırbaş et al. [31]	Case	Eight countries

In the literature, there are many studies on estimating the number of COVID-19 cases and/or deaths using the ARIMA models. Nevertheless, there is a gap in the literature in estimating the prevalence trend of the COVID-19 vaccinations by using the ARIMA time series model.

The main purpose of this study is to forecast the number of people fully vaccinated against COVID-19 in the US, Asia, Europe, Africa, South America, and the World and to analyze whether it has reached a sufficient rate for herd immunity. ARIMA model was used to forecast the future number of fully vaccinated people for selected regions. Thus, the number of vaccinations and vaccine supply plans needed in these regions in the future for herd immunization can be helped. The contributions of this paper are as follows;

• •Forecasting the number of people fully vaccinated against COVID-19 in the near future with ARIMA, which is the new approach in the COVID-19 vaccination studies,
• •To identify the most successful ARIMA models in estimating the number of fully vaccinated people against COVID-19 in the US, Asia, Europe, Africa, South America, and the World,
• •To forecast the total number of fully vaccinated people in the US, Asia, Europe, Africa, South America, and the World in the near future,
• •To determine the people fully vaccinated against COVID-19 rate of the population at the begging of the summer in the US, Asia, Europe, Africa, South America, and the World to achieve herd immunity.

2. Material and method

2.1. Data collection

In this study, the number of people fully vaccinated against COVID-19 in the US, Asia, Europe, Africa, South America and the World were used to model and validate the ARIMA. The dataset were obtained from the Our World in Data [39]. The datasets used in the study start from the first date of fully vaccinated people against COVID-19 and ends on May 22, 2021. So the number of data varies for each region. The date of the first fully vaccinated people of the investigated regions and data size are given in Table 3.

Table 3.

Date of first fully vaccinated people of the regions and the size of the dataset.

Region	Date	Data size
US	January 14, 2021	129
Asia	January 04, 2021	139
Europe	December 27, 2020	147
Africa	February 03, 2021	109
South America	January 13, 2021	130
World	December 27, 2020	147

2.2. ARIMA model

ARIMA, also known as the Box-Jenkins model, is shown as ARIMA (p, d, q). Parameter p in the model is the order of autoregression, parameter d is the degree of difference, and parameter q is the order of the moving average. The ARIMA model consists of Autoregressive (AR), Moving Average (MA) and “I” stands for integration sections. Three basic ARIMA models for a stationary time series are mathematically representing as follows [40];

Autoregressive model of order p or AR(p) model:

$$y_t={\varphi }_1{y}_{t-1}+{\varphi }_2{y}_{t-2}+\cdots +{\varphi }_p{y}_{t-p}+{\varepsilon }_t$$ (1)

Moving-average model of order q or MA(q):

$$y_t={\theta }_1{\varepsilon }_{t-1}+{\theta }_2{\varepsilon }_{t-2}+\cdots +{\theta }_q{\varepsilon }_{t-q}+{\varepsilon }_t$$ (2)

Autoregressive moving average model of order p and q or ARMA(p,q):

$$y_t=\delta +{\varphi }_1{y}_{t-1}+\cdots +{\varphi }_p{y}_{t-p}+{\varepsilon }_t+{\theta }_1{\varepsilon }_{t-1}+\cdots +{\theta }_q{\varepsilon }_{t-q}$$ (3)

Where, $\varphi$ is the autoregression and $\theta$ is the moving average parameters. $y_t$ is the actual value at a time t. $\delta$ is the constant. The random disturbance term ${\varepsilon }_t$ is assumed to be white noise which means it is independently identically distributed with mean 0 and a common variance for all terms.

2.3. Model selection criteria

Akaike Information Criterion (AIC), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE) criteria were used to select the most successful ARIMA models for the dataset. The AIC shows how well the model fits the observed series. The most suitable model for the dataset is that have smallest AIC, RMSE and MAPE value [41]. These performance criteria can be calculated by using Eqs. (4), (5), (6), respectively.

$$\mathrm{AIC}\left(\mathrm{m}\right)=-2\text{logL}+2m$$ (4)

Where, L is the likelihood function, m is the total number of parameters in the model.

$$\text{RMSE}=\sqrt{\frac{{\left({\mathrm{a}}_1-{\mathrm{p}}_1\right)}^2+{\left({\mathrm{a}}_2-{\mathrm{p}}_2\right)}^2+\cdots +{\left({\mathrm{a}}_{\mathrm{n}}-{\mathrm{p}}_{\mathrm{n}}\right)}^2}{\mathrm{n}}}$$ (5)

$$\mathrm{MA}\mathrm{P}\mathrm{E}=100\text{\%}\times \frac{|{\mathrm{a}}_1-{\mathrm{p}}_1|+|{\mathrm{a}}_1-{\mathrm{p}}_1|+\cdots +|{\mathrm{a}}_{\mathrm{n}}-{\mathrm{p}}_{\mathrm{n}}|}{\mathrm{n}}$$ (6)

Where, p is the predicted value, a is the actual value. It is desirable for the above three error measurement criteria to be lower. Error is zero indicates that it is a statistically perfect model.

3. Results

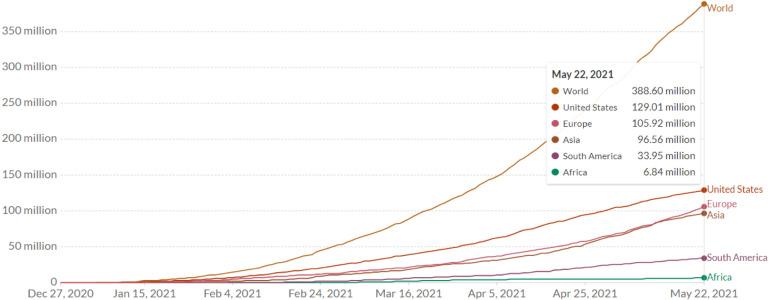
Vaccination has started to be administered in countries on different dates. Until May 22, 2021, 129.01 million in the US, 96.56 million in Asia, 105.92 million in Europe, 33.95 million in South America, 6.84 million in Africa, and 388.60 million people fully vaccinated against COVID-19 in the World (Fig. 1).

Fig. 1.

Number of people fully vaccinated against COVID-19 in the examined regions [39].

The process of ARIMA modeling consists of four consecutive steps: identification of model, parameters estimation, diagnostic checking, and forecasting. In the first step, it is identified whether the time series variable is stationary and non-stationary. If the series is non-stationary, it is converted to stationary.

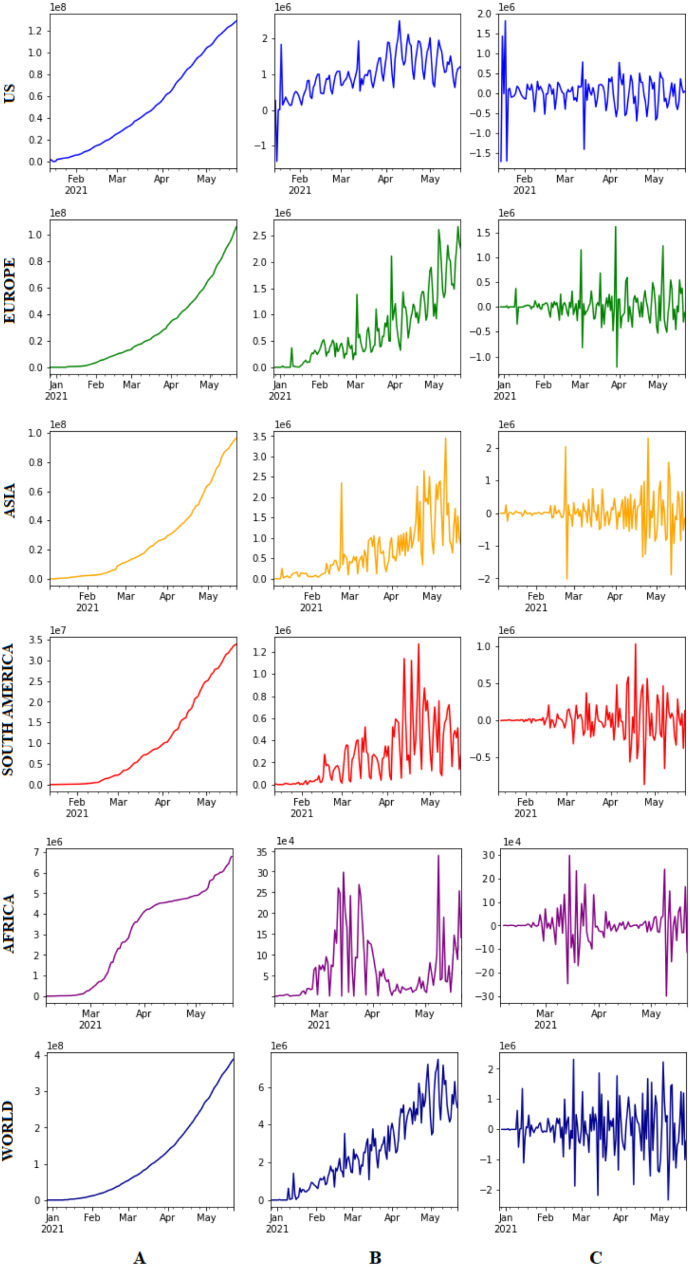
Time-series graphs are given in Fig. 2 to observe the stationarity of the dataset. Original time-series graphs are shown in Fig. 2 A. It is seen that there is an upward trend in all regions examined, that is, the original series is non-stationary. Therefore, the first-order difference was applied to the original data to stabilize the mean of the people fully vaccinated against COVID-19. The first-order difference of the series is shown in Fig. 3B. When the first-difference series are examined, trends of all series still observed, so the second-order difference was applied. As seen in Fig. 2C, after the second-order difference was taken, all series became stationary. Augmented Dickey–Fuller (ADF) test was applied to confirm the stationarity of the time series and the results are given in Table 4. ADF test results also show that the time series stabilize after the second difference was taken. This shows us that the parameter d is 2 in the ARIMA model.

Fig. 2.

(A) Original series, (B) first-order difference series, and (C) second-order difference series.

Fig. 3.

Residuals of ARIMA models.

Table 4.

Results of the augmented Dickey–Fuller test of the time series data.

Region	Data	Dickey–Fuller	p-value
Us	Original	−1.048	0.735
	First-ordered	−1.348	0.607
	Second-ordered	−6.249	0.000⁎
Asia	Original	0.132	0.968
	First-ordered	−1.194	0.676
	Second-ordered	−10.130	0.000⁎
Europe	Original	3.790	1.000
	First-ordered	2.169	0.998
	Second-ordered	−5.538	0.000⁎
Africa	Original	0.199	0.972
	First-ordered	−2.786	0.060
	Second-ordered	−9.139	0.000⁎
South America	Original	3.790	1.000
	First-ordered	2.169	0.998
	Second-ordered	−5.537	0.000⁎
World	Original	−1.182	0.681
	First-ordered	−0.655	0.858
	Second-ordered	−7.234	0.000⁎

^*P$<$0.05 and thus stationary at that level.

Candidate ARIMA models’ test results are given in Table 5. ARIMA models with minimum AIC, RMSE and MAPE criteria were chosen as the best models. Accordingly, the ARIMA(5,2,2), ARIMA(1,2,3), ARIMA(5,2,0), ARIMA(2,1,2), ARIMA(2,2,1) and ARIMA(0,2,2) models were selected for the US, Asia, Europe, Africa, South America and the World, respectively. The selected ARIMA models fitted the data reasonably well with a minimum MAPE${}_{\mathrm{US}}$ = 1.27, MAPE${}_{\mathrm{Asia}}$ = 4.80, MAPE${}_{\mathrm{Europe}}$ = 4.24, MAPE${}_{\mathrm{Africa}}$= 11.32, MAPE${}_{\mathrm{SouthAmerica}}$ = 0.90, and MAPE${}_{\mathrm{World}}=1.39$ values.

Table 5.

Performance comparison of candidate ARIMA models for the test dataset.

Region	Candidate models	AIC	RMSE	MAPE	Selected model
US	ARIMA (2,2,2)	3603	3330748	2.38	ARIMA (5,2,2)
	ARIMA (1,2,0)	3626	3151914	2.26
	ARIMA (0,2,1)	3617	3651831	2.62
	ARIMA (1,2,2)	3602	3272585	2.32
	ARIMA (0,2,2)	3603	3349863	2.38
	ARIMA (1,2,1)	3601	3299527	2.35
	ARIMA (2,2,1)	3600	3193971	2.25
	ARIMA (2,2,0)	3628	3060394	2.20
	ARIMA (3,2,1)	3560	2678414	1.83
	ARIMA (3,2,0)	3594	3373309	2.39
	ARIMA (4,2,1)	3558	2536176	1.72
	ARIMA (4,2,0)	3575	3265123	2.28
	ARIMA (5,2,1)	3554	2234625	1.48
	ARIMA (5,2,0)	3559	2398972	1.60
	ARIMA (5,2,2)	3552	1964099	1.27
	ARIMA (4,2,1)	3553	2536176	1.72
	ARIMA (5,2,3)	3554	1983322	1.29
	ARIMA (4,2,3)	3555	1996855	1.30
Asia	ARIMA (2,2,2)	3966	4508909	4.81	ARIMA (1,2,3)
	ARIMA (0,2,0)	4010	13619654	14.08
	ARIMA (1,2,0)	3992	12518718	12.97
	ARIMA (0,2,1)	3964	4480895	4.77
	ARIMA (1,2,1)	3963	4540281	4.84
	ARIMA (2,2,1)	3964	4513366	4.81
	ARIMA (1,2,2)	3964	4475124	4.77
	ARIMA (0,2,2)	3963	4521102	4.82
	ARIMA (0,2,3)	3965	4516004	4.81
	ARIMA (1,2,3)	3966	4503660	4.80
Europe	ARIMA (2,2,2)	4041	6372484	5.78	ARIMA (5,2,0)
	ARIMA (0,2,0)	4087	7442914	6.77
	ARIMA (1,2,0)	4085	8084573	7.37
	ARIMA (0,2,1)	4080	6017086	5.45
	ARIMA (1,2,2)	4062	6364820	5.77
	ARIMA (2,2,1)	4060	6221668	5.64
	ARIMA (3,2,2)	4036	4816791	4.29
	ARIMA (3,2,1)	4052	5759615	5.19
	ARIMA (4,2,1)	4034	5219494	4.66
	ARIMA (4,2,0)	4055	5219494	4.66
	ARIMA (5,2,1)	4030	5075843	4.52
	ARIMA (5,2,0)	3468	4783587	4.24
Africa	ARIMA (2,2,2)	2161	824239	11.33	ARIMA (2,2,1)
	ARIMA (0,2,0)	2188	950504	13.17
	ARIMA (1,2,0)	2170	932713	12.91
	ARIMA (0,2,1)	2155	823725	11.32
	ARIMA (1,2,1)	2157	823566	11.32
	ARIMA (2,2,1)	2159	823488	11.32
	ARIMA (1,2,2)	2159	823568	11.32
	ARIMA (0,2,2)	2457	823448	11.32
South America	ARIMA (2,2,2)	3465	322142	0.91	ARIMA (1,2,1)
	ARIMA (0,2,0)	3529	4085583	11.56
	ARIMA (1,2,0)	3528	3878743	10.97
	ARIMA (0,2,1)	3493	471956	1.22
	ARIMA (1,2,2)	3479	400317	1.07
	ARIMA (2,2,1)	3470	771082	2.06
	ARIMA (2,2,2)	3467	322142	0.91
	ARIMA (1,2,1)	3488	327430	0.90
	ARIMA (1,2,3)	3472	533316	1.51
	ARIMA (3,2,1)	3470	851619	2.36
	ARIMA (3,2,3)	3468	364552	1.02
World	ARIMA (0,2,0)	4352	26246314	6.57	ARIMA (5,2,1)
	ARIMA (1,2,0)	4344	22964805	5.76
	ARIMA (0,2,1)	4332	9017266	2.32
	ARIMA (1,2,1)	4321	9178706	2.37
	ARIMA (2,2,1)	4322	9163123	2.36
	ARIMA (1,2,2)	4323	9172276	2.37
	ARIMA (0,2,2)	4322	8869982	2.29
	ARIMA (2,2,0)	4345	20828062	5.23
	ARIMA (4,2,0)	3070	9321756	2.37
	ARIMA (4,2,1)	3696	5685208	1.46
	ARIMA (5,2,0)	3698	6805696	1.74
	ARIMA (5,2,1)	3693	5412285	1.39
	ARIMA (5,2,2)	3690	5724002	1.46

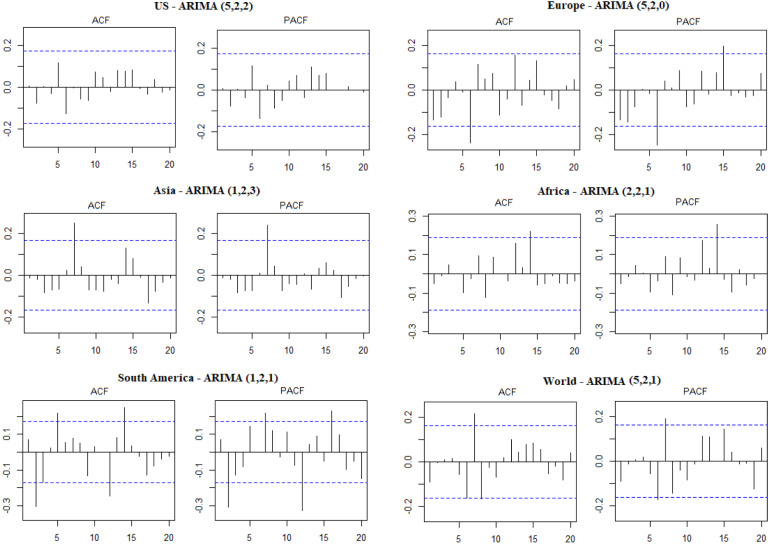
The ACF and PACF graphs of the residuals for the best fitted ARIMA models are presented in Fig. 3. The ACF determine whether the previous value in the series is related to the following value. The PACF shows the amount of correlation between a variable and a lag of itself. When ACF and PACF graphs are examined, it is seen that the residuals generally do not exceed significant boundaries. Box–Ljung test was used to check the residuals are white noise or not. The null hypothesis ($H_0$) for a Box–Ljung test is the residuals are independently distributed. Therefore, it is desirable to reject the null hypothesis. Large $p$-value indicate that the residuals have no remaining autocorrelations, i.e., they resemble white noise. Box–Ljung test results of models are given in Table 6.

Table 6.

Ljung–Box statistic of selected ARIMA models.

	Model	${\chi }^2$	df	p-value
US	ARIMA(5,2,2)	10.55	18	0.91
Asia	ARIMA(1,2,3)	24.15	18	0.15
Europe	ARIMA(5,2,0)	22.26	18	0.22
Africa	ARIMA(2,2,1)	21.09	18	0.27
South America	ARIMA(1,2,1)	27.54	18	0.07
World	ARIMA(5,2,1)	24.64	19	0.17

Fig. 3 shows that the residuals are white noise since all the autocorrelation and partial autocorrelation coefficients are small and within two standard deviations at a 5% level of significance. Also, by Ljung–Box statistic results correlations are not significant and hence the residuals are white noise.

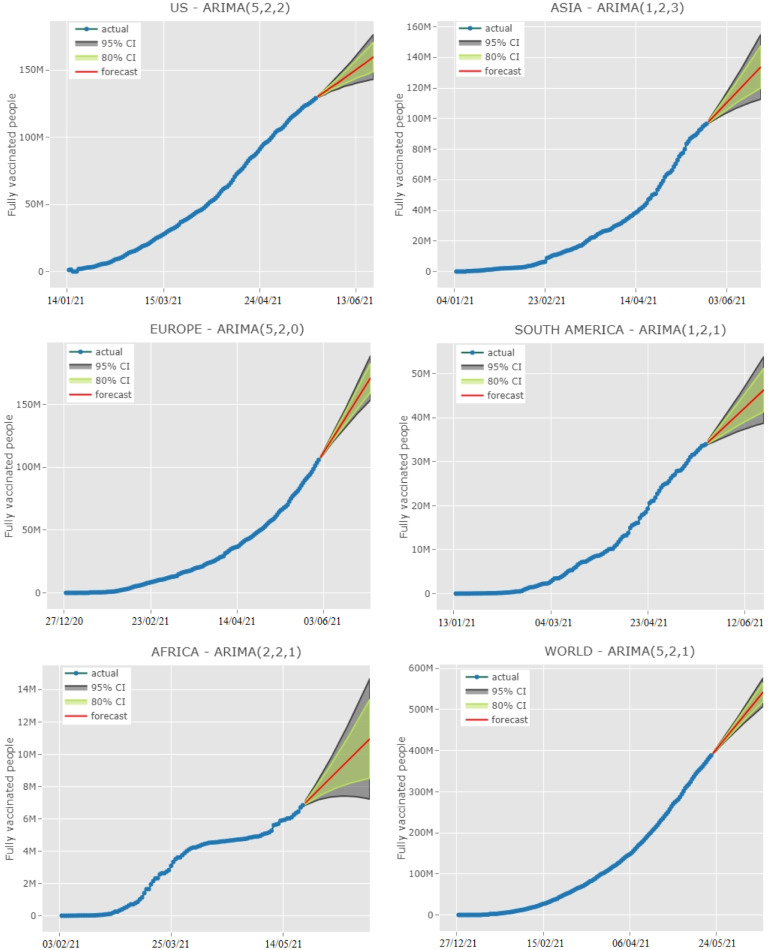
With these best models determined, the number of people fully vaccinated against COVID-19 was forecasted with 80%–95% confidence intervals (CI) (Fig. 4). Forecasting of the number of people fully vaccinated against COVID-19 for the next ten days according to ARIMA models is given in Table 7.

Fig. 4.

Time series plots for the next 30 days according to best ARIMA models with 80%–95% CI.

Table 7.

Forecasting of the number of people fully vaccinated against COVID-19 according to ARIMA models.

Date	US	Asia	Europe	Africa	South America	World
	Forecast	Forecast	Forecast	Forecast	Forecast	Forecast
23.05.2021	130.033 M	97.761 M	107.840 M	6.953 M	34.325 M	393.781 M
24.05.2021	130.923 M	99.004 M	109.760 M	7.081 M	34.729 M	399.043 M
25.05.2021	131.749 M	100.246 M	111.856 M	7.193 M	35.140 M	404.305 M
26.05.2021	132.680 M	101.488 M	114.175 M	7.313 M	35.553 M	409.568 M
27.05.2021	133.755 M	102.730 M	116.558 M	7.423 M	35.967 M	414.830 M
28.05.2021	134.941 M	103.973 M	118.901 M	7.537 M	36.381 M	420.093 M
29.05.2021	136.099 M	105.215 M	121.062 M	7.644 M	36.794 M	425.355 M
30.05.2021	137.144 M	106.457 M	123.110 M	7.753 M	37.208 M	430.617 M
31.05.2021	138.059 M	107.700 M	125.167 M	7.856 M	37.622 M	435.880 M
1.06.2021	138.939 M	108.942 M	127.323 M	7.961 M	38.036 M	441.142 M

4. Discussions

The main purpose of this study is to determine the full vaccination rate in the US, Asia, Europe, Africa, South America, and the World on June 1, 2021. For this purpose, the number of fully vaccinated people in these regions was forecasted using the ARIMA time series model. Thus, they will be able to observe how far countries are from the threshold level required to achieve herd immunity.

With the determined ARIMA models, the number of people fully vaccinated against COVID-19 was estimated on June 1, 2021.

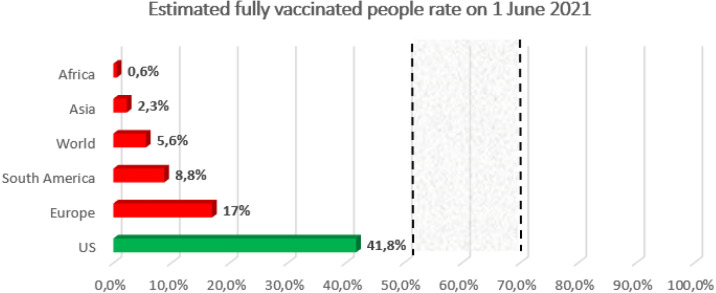
The populations, vaccination information, and the forecasted number of full vaccination people of the regions examined in this study are given in Table 8. Almost all countries desire to administer vaccines to at least 50% of their population until the beginning of the summer. This seems unlikely based on the total number of full vaccinated people estimated by ARIMA models. The ratio of the number of people fully vaccinated against COVID-19 to the population of the examined regions on June 1, 2021 is shown in Fig. 5.

Table 8.

Populations and COVID-19 information of regions.

Region	2021 population	People fully vaccinated (22.05.2021)	People fully vaccinated % (22.05.2021)	Forecasted people fully vaccinated (01.06.2021)
US	332.77 M	129.01 M	38.76	138.94 M
Asia	4.68 B	96.56 M	2.06	108.94 M
Europe	748.05 M	105.92 M	14.16	127.32 M
Africa	1.37 B	6.84 M	0.50	7.96 M
South America	433.99 M	33.95 M	7.82	38.04 M
World	7.87 B	388.60 M	4.93	441.14 M

Fig. 5.

The ratio of the estimated number of fully vaccinated people in examined regions.

According to the estimation results of ARIMA models, about 139 million, 109 million, 127 million, 8 million, 38 million, and 441 million people will be fully vaccinated in the US, Asia, Europe, Africa, South America, and the World, respectively (on June 1, 2021). The 2021 population of these regions are 333 million, 4.68 billion, 748 million, 1.37 billion, 434 million, and 7.87 billion, respectively. On June 1, 2021, it is predicted that fully vaccinated to 41.8% of the people in the US, 2.3% in Asia, 17% in Europe, 0.6% in Africa, 8.8% in South America, and 5.6% in the World. According to the findings obtained as a result of the study, the US reaches the highest level in the fully vaccinated rate on June 1, 2021. Nevertheless, none of the examined regions will reach the herd immunity threshold until June 1, 2021.

These days when the numbers of COVID-19 cases and deaths are at their peak again, the health systems of many countries have collapsed and they have started to impose curfews again. In addition to the tragic deaths, prohibitions affect the country’s economies negatively. To prevent all these negativities, it is thought that vaccination rates should reach quickly the threshold level required to provide herd immunity. Vaccination rates in Fig. 5 show that high-income countries should provide vaccines and healthcare support to low and middle-income countries. In addition, vaccine companies need to make plans to increase vaccine production rates, and countries to provide more vaccines and to apply vaccines quickly. Nevertheless, it has been reported that some mutant viruses are able to vaccine-escaped and antibody-resistant [42]. The rise of new variants may require the monitoring of immune escape variants, force second-generation production that addresses globally circulating variants, and already vaccinated people may be again vaccinated.

5. Conclusion

SARS-Cov-2 virus, which causes COVID-19 disease, is highly contagious. All countries quickly started vaccination development after the coronavirus was declared a global emergency by WHO. Up to now, more than ten COVID-19 vaccines have been approved for use. Although the efficacy of these vaccines is quite high, herd immunity is required to safely slow or stop the COVID-19 epidemic. The fastest way to achieve herd immunity is vaccination.

In this study, the total number of full vaccination people against COVID-19 in the US, Asia, Europe, Africa, South America, and the World on the next ten days was estimated using the ARIMA time series method. ARIMA models have been formulated with different parameters and the most successful models have been selected. AIC, RMSE, and MAPE criteria were used to compare model success. Models with the lowest values were selected to estimate the number of vaccines to be administered in the future. ARIMA(5,2,2), ARIMA(1,2,3), ARIMA(5,2,0), ARIMA(2,2,1), ARIMA(1,2,1) and ARIMA(5,2,1) models were selected for the US, Asia, Europe, Africa, South America, and the World, respectively. The selected ARIMA models fitted the data reasonably well with a minimum MAPE${}_{\mathrm{US}}$ = 1.27, MAPE${}_{\mathrm{Asia}}$ = 4.80, MAPE${}_{\mathrm{Europe}}$ = 4.24, MAPE${}_{\mathrm{Africa}}$ = 11.32, MAPE${}_{\mathrm{SouthAmerica}}$ = 0.90, and MAPE${}_{\mathrm{World}}=1.39$ values. According to the results of this study, on June 1, 2021, in the US, Asia, Europe, Africa, South America, and, the World of 139 million, 109 million, 127 million, 8 million, 38 million, and 441 million people will be fully vaccinated, respectively. This result shows that beginning of the summer, 41.8%, 2.3%, 17%, 0.6%, 8.8%, and 5.6% of people will be fully vaccinated in the US, Asia, Europe, Africa, South America, and the World, respectively. It has been observed that the other regions except the US are quite far from the herd immunity threshold level. The future goal of our study is to forecast the number of fully vaccinated people in the future with deep learning time series models. Thus, the performances of the ARIMA model can be compared with the deep learning methods.

CRediT authorship contribution statement

Pınar Cihan: Writing – original draft, methodology, software, validation, visualization, Writing – review and editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.