Mitigating COVID-19 infection disease transmission in indoor environment using physical barriers

Abstract

During the normalized phase of COVID-19, droplets or aerosol particles produced by infected personnel are considered as the potential source of infection with uncertain exposure risk. As such, in densely populated open spaces, it is necessary to adopt strategies to mitigate the risk of infection disease transmission while providing sufficient ventilation air. An example of such strategies is use of physical barriers. In this study, the impact of barrier heights on the spread of aerosol particles is investigated in an open office environment with the well-designed ventilation mode and supply air rate. The risk of infection disease transmission is evaluated using simulation of particle concentration in different locations and subject to a number of source scenarios. It was found that a barrier height of at least 60 cm above the desk surface is needed to effectively prevent the transmission of viruses. For workstations within 4 m from the outlet, a 70 cm height is considered, and with a proper ventilation mode, it is shown that the barriers can reduce the risk of infection by 72%. However, for the workstations further away from the outlet (beyond 4 m), the effect of physical barrier cannot be that significant. In summary, this study provides a theoretical analysis for implementing physical barriers, as a low-cost mitigation strategy, subject to various height scenarios and investigation of their effectiveness in reducing the infection transmission probability.

Nomenclature

COVID-2019

Corona Virus Disease 2019

SARS

Severe Acute Respiratory Syndrome

CDC

Centers for Disease Control and Prevention

NCCEH

Canadian National Collaborating Center for Environmental Health

HVAC

Heating Ventilation Air Conditioning

S_f

Minimum required fresh air (m³/s)

S_pp

Minimum ventilation requirement per person (m³/s)

O

Number of occupant

S_1L

Multiplication of floor area and S_PA (m³/s)

A

Floor area (m²)

S_PA

Ventilation required per unit floor area in ASHRAE standard 62.1–2016 (m³/s per m²)

S_min

Minimum required supply air rate (m³/s)

OA%

Share of outdoor air (in percentage) in total room loads

CFD

Computational Fluid Dynamics

RANS

Reynolds-averaged Navier-Stokes

RNG

Re-Normalization Group

φ

Solving variables (i.e., velocity, temperature and concentration)

ρ

Density (kg/m³)

$\overline{\mathrm{u}}$

Average velocity (m/s)

Γ_φ

Diffusion coefficient

S_φ

Source term

WHO

World Health Organization

UDS

User-Defined Scalar

D

Brownian diffusion coefficient of particles

ν_p

Turbulent diffusion coefficient of particles

C_ref

Reference value for pollutant concentration

C/C_ref

Relative concentration value

R_inf

Likelihood of infection (%)

IR

Inhalation rate of the exposed subject (m³/h)

t

Exposure time (h)

T

Total exposure time (h)

C (t)

Pollutant concentration (quantum/m³)

ACH

Air change rate per hour

ADPI

Air Diffusion Performance Index

P_i

Measuring points in the target area

N

Total number of P_i

P_EDT

Measuring point meeting the temperature and velocity requirements

M

Number of P_EDT

EDT

Effective draft temperature (°C)

t_x

Air temperature of the measuring points ((°C))

t_m

Indoor mean temperature (°C)

v_x

Velocity of the measuring points (m/s)

LVM

Linear ventilation model

1. Introduction

The outbreak of COVID-19 (Corona Virus Disease 2019) has had unprecedented impacts on the society and governments globally (Feng et al. 2021, Hale et al. 2021, Munzert et al. 2021,Wang 2021). As of March 11, 2021, more than 200 countries, regions or territories around the world have recorded COVID-19 cases, with more than 100 million confirmed cases along with more than 2 million deaths worldwide (https://covid19.who.int/). Transmission of Novel Coronavirus can be divided into direct contact transmission and airborne transmission. The direct contact refers to contact with infected patients, which results in extremely high risk of infection, and airborne transmission through dispersed droplets and aerosol, which presents an uncertain infection risk (Chia et al. 2020, Sakharov and Zhukov 2020). Infected people spread virus particles when talking, coughing or sneezing, which further adhere to the droplets of mucus and saliva (Raj, Velraj and Haghighat 2020). The aerosol propagation is achieved by smaller droplets that could spread to far distances (Jayaweera et al. 2020). In the past, there were studies on other cases of diseases transmission by aerosol, such as influenza (Malik Peiris, Poon and Guan 2009), SARS (Ignatius et al. 2004) and smallpox (Kiang and Krathwohl 2003), which will be revisited in this study.

Earlier studies have shown the influence of air distribution on spread of pollutants in a room. (Liao et al. 2021) reported that airflow pattern could have an important role in the Guangzhou restaurant outbreak. (Choi and Shim 2021, GB50736. 2012) claimed that the infection via aerosol can be airborne beyond the immediate vicinity of infected person. (Anand, Cheong and Sekhar 2020) reported on the role of room air purifiers in the spread of COVID. In this sense, Centers for Disease Control and Prevention (CDC) has recommended the use of physical barriers between the workers to reduce exposure (https://www.cdc.gov/coronavirus/2019-ncov/community/ventilation.html). This approach has been widely applied to separate office workers, manufacturing workers, meat and poultry processing workers, retail food service workers, etc. (Laue 2018, Shirzadi, Tominaga and Mirzaei 2020). The Canadian National Collaborating Center for Environmental Health (NCCEH) published a guideline for use of such partitions (van Hooff and Blocken 2020).

With the prospects of return to public places and workplaces in gradual transition to normal circumstances, implementation of low-cost disease transmission strategies, in particular for open spaces, is rather imperative. Even though physical isolation measures such as wearing masks (Liao et al. 2021) and keeping social distance (Choi and Shim 2021) are reducing the transmission of aerosol particles, there is still a risk of virus infection within indoor environments. In this sense, proper distribution of airflow and use of physical barriers can decrease the spreading of aerosol particles, thus further reducing the risk of human infection (Xu et al. 2020). The critical factors impacting indoor airflow distribution include ventilation mode (location and design of air diffusers) as well as supply airflow rate (Bjorn and Nielsen 2002, Ding et al. 2020, Chen, Feng and Cao 2021, Lv et al. 2019). In case of physical barrier and air deflectors, the focus will be on large and open space (Espinosa and Glicksman 2017, Lv et al. 2019). The goal is to effectively adopt forced interference strategies (e.g., physical barrier) in the premise of appropriate and sufficient airflow. So far, no systematic study has been done to investigate the effectiveness of such physical barriers on preventing the disease transmission and to analyze its interference with HVAC systems under varied operational and air diffuser location scenarios.

This study considers a typical open space office, needing reasonable airflow design with the presence of physical barriers, as low-cost prevention measures, in order to effectively mitigate pollutant spreading from coughing and sneezing of infected occupants. In particular, the aim is to study the effect of physical barrier heights as well as ventilation modes (varied supply air rates) on dispersion and transmission of contaminants generated from infected source. This will be followed by an analysis of the consequent infection risks as a measure of showing the effectiveness of these strategies.

2. Materials and methods

This study investigates the impacts of physical barrier height on mitigating the spread of pollutants and reducing the infection rate considering a well-designed ventilated open office. The ventilation mode and supply air rate is adjusted based on occupancy and load information to ensure sufficient ventilation air. The results of numerical simulation and grid independence are validated with experimental test results. Considering various pollutant source/location scenarios, pollutant dispersion and concentrations are simulated. On that basis, the infection probability (risk) in an open office is analyzed (subject to scenarios of pollution location/source and barrier heights).

2.1. Study design

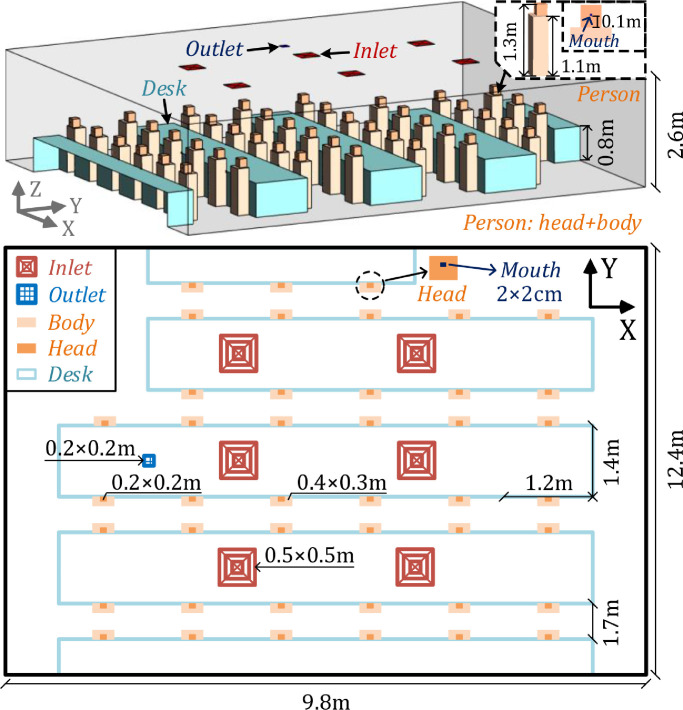
This study was carried out in an open space office located in Sipailou Campus of Southeast University in Nanjing, China, as shown in Fig. 1 . The office dimensions are 9.8 m (length) × 12.4 m (width) × 2.6 m (height) with a volume of about 316 m³. The office is equipped with 43 workstations; each includes a staff member and a desk. The staff member is seated assuming a body size of 0.4 m (length) × 0.3 m (width) × 1.1 m (height), and a head (including neck) size of 0.2 m (length) × 0.2 m (width) × 0.2 m (height) and the mouth size of 2 cm × 2 cm. The dimension of desk is assumed as 1.2 m (length) × 0.7 m (width) × 0.8 m (height) with 5 rows of desks in total.

Fig. 1.

Layout of open office with 43 occupants (including body, head and mouth) and 5 rows of desks under the current ventilation mode with ceiling mounted supply inlets and outlet.

The office is equipped with an HVAC system of 6 ceiling-mounted air supply inlets and 1 ceiling-mounted return outlet (hereinafter referred to as current ventilation mode), as shown in Fig. 1. In current ventilation mode, the inlet size is 0.5 m × 0.5 m, with a square diffuser set up, and the outlet size is 0.2 m × 0.2 m. To reduce energy waste, the minimum supply airflow rate of HVAC unit is designed as 0.45 m³/s according to GB50736-2012 (GB50736. 2012), supplying a minimum fresh air of 30 m³/h per person. Additionally, supply air temperature is set to be a constant value of 25 °C in winter.

The proper design of minimum airflow rate ensures that sufficient ventilation air is delivered to personnel and their activity region to prevent poor air quality while maintaining acceptable energy consumption. Such a design also depends on type and location of air diffusers. To avoid oversupplying or undersupplying the conditioned air, Anand et al's method was adopted to identify a minimum required supply airflow rate based on occupancy and load information (Anand et al. 2020). The fresh airflow rates for targeted zones are calculated as:

$${\left(S_f\right)}_{min}=S_{pp}\times O+S_{1L}$$ (1)

where, (S_f)_min is the minimum required fresh air (m³/s); S_pp is the minimum ventilation requirement (0.0025 m³/s) per person; O is the number of occupants; and S_1L is calculated by the multiplication of floor area A (m²) and S_PA (ventilation required per unit floor area in ASHRAE standard 62.1–2016, i.e., 2 × 10⁻³ m³/s per m²) (Laue 2018). Then, the minimum required supply air rate S_min is calculated as:

$$S_{min}={\left(S_f\right)}_{min}/OA\%$$ (2)

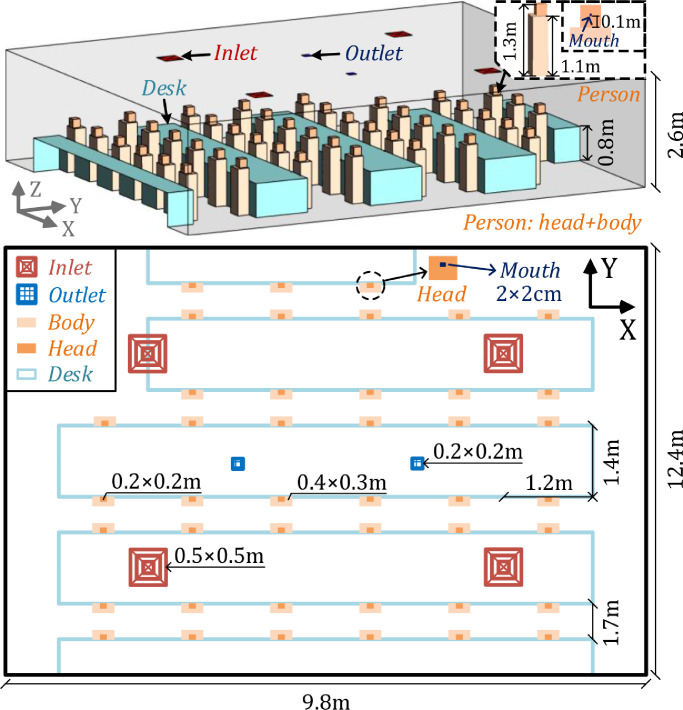
where, OA% is the share of outdoor air (in percentage) in total room loads (including also loads from human body, computers, lighting heat and walls), which are identified as thermal load of 8.1 kW for the current office room. As per Anand's work, S_min is calculated as 1.73 m³/s (considering OA% of 0.31 and a minimum fresh air requirement of 0.35 m³/s). This is rather greater than the minimum requirement set by the current air-conditioning system (0.45 m³/s). In order to achieve a well-mixed airflow distribution and provide sufficient ventilation air for each staff, the current ventilation mode is adjusted with S_min calculated for a uniform distribution of inlets and outlets locations. Fig. 2 displays the adjusted ventilation mode. A total of 4 inlets (square type air diffuser) and 2 outlets were placed, with sizes of 0.5 m × .5 m and 0.2 m × 0.2 m, respectively. The airflow distribution performance of such ventilation modes is further analyzed (see section 3).

Fig. 2.

Layout of open office under the modified ventilation mode with ceiling mounted supply inlets and outlets.

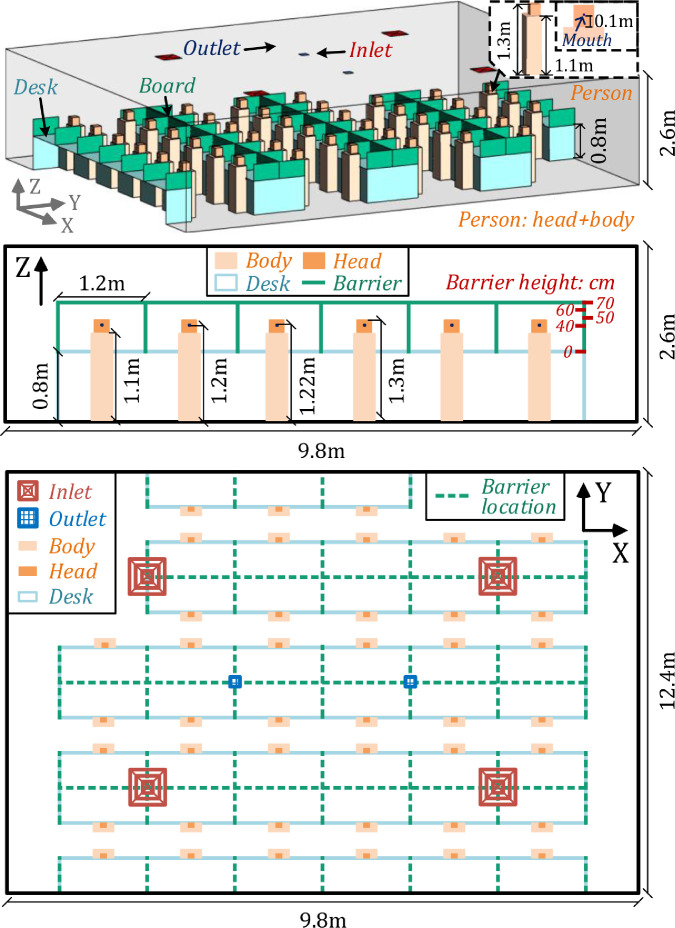
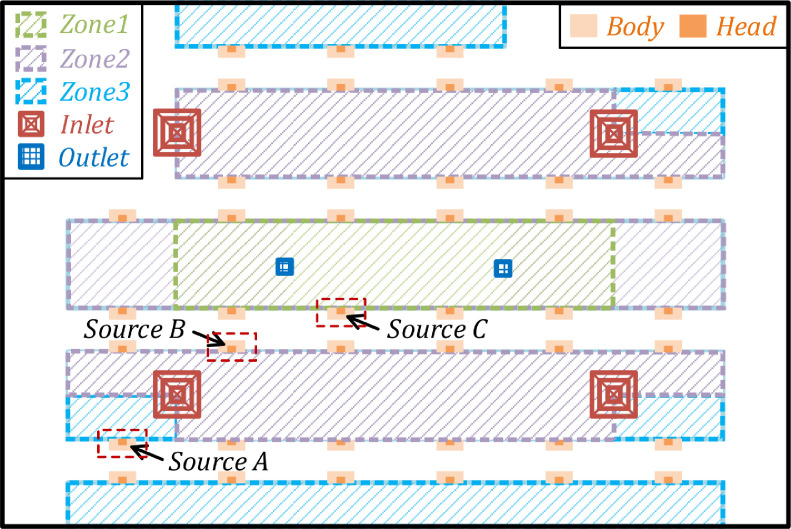
In this study, the physical barriers were located on the desk with heights of 0, 40, 50, 60 and 70 cm (regardless of barrier thickness). Fig. 3 shows the specific setup of barrier heights and locations. In addition, an infected person is considered as the source of COVID-19, who produces droplets or aerosols containing viruses by means of coughing with a coughing speed of 13 m/s downwards at 27.5° (Ai et al. 2020, Kwon et al. 2012). Three typical positions for pollution source (infected person) of A, B and C are selected representing alternative horizontal distances between personnel and air diffusers, as demonstrated in Fig. 4 . By symmetrically dividing the office area into three annular zones, the infected persons are located in zone 1, 2 and 3.

Fig. 3.

Setup of barrier height and location in the office.

Fig. 4.

Arrangement of three annular zones 1, 2 and 3 along with the location of pollutant sources (infected person) A, B and C.

2.2. Experimental study

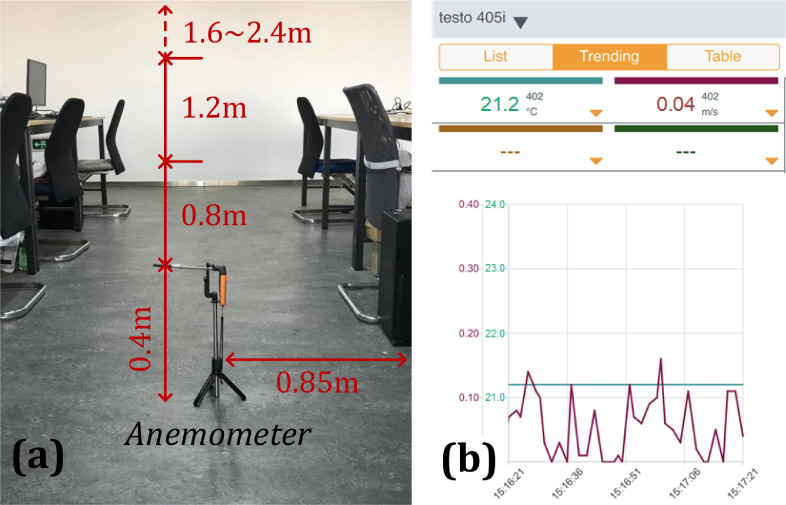
Testo-405i wireless thermal anemometer is used for field measurement of air distribution and temperature parameters, converting flow rate and temperature data into electrical signals via a hot wire. The device can be operated and monitored using smart phones making it suitable for remote measurement of airflow rate, temperature, duct airflow rate, etc. Each measurement sample can last for 2 s. The anemometer measurement range for temperature is from -20°C to + 60°C, and for air speed is from 0 to 30 m/s. The measurement accuracy is estimated at ±0.5°C and ±0.1 m/s with the resolution of 0.1°C and 0.01 m/s, for temperature and airflow rate, respectively. Fig. 5 presents a schematic diagram of the on-site monitoring setup.

Fig. 5.

Schematic diagram of on-site monitoring setup in the office (a): layout of thermal anemometer; (b): monitoring interface for smartphone with green color for temperature (°C) and red color for velocity (m/s).

Table 1 provides information about the experimental measurement conditions. The supply air temperature is assumed to be constant at 25 °C. The supply air velocity is adjusted to 0.3 m/s (corresponding to a minimum supply airflow rate of 0.45 m³/s). The number of seated staff in this experiment is assumed 8, of which five are male and three are female. The coordinate points for test are defined as (x, y) = (4.5 m, 1.55 m), at the alternative heights of 0.4, 0.8, 1.2, 1.6, 2.0 and 2.4 m. For each measurement point, one set of data for velocity and temperature are obtained with 1 min interval. The measurement period is 1 h and 60 groups of measurement samples were acquired.

Table 1.

Outline of field test conditions.

Experimental setup	Personnel location (number = 8)	Location of measuring points
Current ventilation mode Supply air temperature: 25 °C Supply air velocity: 0.3 m/s Outdoor temperature: 15 oC

2.3. CFD simulation

Computational Fluid Dynamics (CFD) has been used to simulate and analyze airflow, temperature and pollutant concentration (Lawrence and Schone 2020). The commercial software of ANSYS Fluent 16.0 was used to conduct numerical simulation, which is widely employed in the built environment (Chen et al. 2021). The simulation cases are configured considering incompressible and steady-state conditions. In order to reduce the computational intensity of CFD simulations, Reynolds-averaged Navier-Stokes (RANS) method is used (Shirzadi et al. 2020). Of RANS models, Re-Normalization Group (RNG) k-ε model shows better performance for simulation of indoor environment (van Hooff and Blocken 2020). The standard form of governing equations is shown as:

$$\nabla ·\left(\rho \overline{u}\phi \right)=\nabla ·\left({\Gamma }_{\phi }\nabla \phi \right)+S_{\phi }$$ (3)

where, $\phi$ is the solving variables (i.e., velocity, temperature and concentration); $\nabla ·\left(\rho \overline{u}\phi \right)$is the convection term; $\rho$ is the density; $\overline{u}$ is the average velocity; $\nabla ·\left({\Gamma }_{\phi }\nabla \phi \right)$ is the diffusion term; ${\Gamma }_{\phi }$ is the diffusion coefficient and $S_{\phi }$ is the source term.

The species-transport equation is solved leading to simulation of pollutant concentration and distribution. We adopt a hypothesis that droplets or aerosols produced by an infected staff are the main cause of airborne viruses and diseases, as small-sized particles can follow the airflow while large-sized coarse particles deviate from the air streamline and deposit on the surfaces (Leng, Wang and Liu 2020). According to the WHO (World Health Organization) (Lawrence and Schone 2020), viruses (e.g., COVID-19) spread primarily through droplets of saliva or discharge when an infected person coughs or sneezes. Droplets generally fall to the ground or other surfaces within 1m, while particles (called aerosols) behave more like a gas compound traveling through the air to longer distances with the risk of airborne transmission to people before settling on surfaces. Furthermore, previous researches have indicated that the transient process from a droplet to a droplet nucleus due to evaporation is also negligible for particles with a diameter less than 1 μm (Chen and Zhao 2010). In this study, a social distance of more than 1 m is maintained between the personnel, and it is thus reasonable to simulate exhaled droplets as gaseous pollutants (Chen et al. 2014). In doing so, a User-Defined Scalar (UDS) is used to simulate pollutant fields, assuming the influence of pollutants on airflow fields is negligible. In this sense, the flow field along with turbulence characteristic determines the distribution of pollutants. Thus, the diffusion coefficient for pollutant is defined as:

$${\Gamma }_p=\rho \left(D+{\nu }_p\right)$$ (4)

where, D is the Brownian diffusion coefficient of particles; ${\nu }_p$ is the turbulent diffusion coefficient of particles. In UDS equations, the coefficient D is calculated with respect to particle diameter. Considering previous studies on identification of droplet nuclei diameter (Ai et al. 2020), the size of human respiratory droplet nuclei is assumed as 1 μm, with a constant source intensity (i.e., releasing concentration) of 1E-04 (quantum/m³), as reference pollutant concentration$C_{ref}$ (Leng et al. 2020).

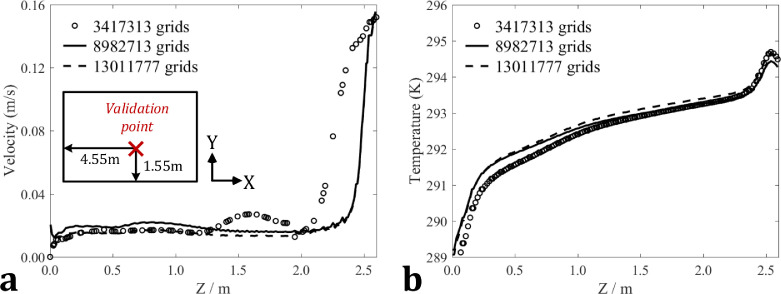
For a simulation case, the solutions might be considered to be converged when the sum of the normalized residuals for all the cells is below 10⁻³for variables of velocity and temperature and less than 10⁻¹²for UDS. Before carrying out the numerical simulations of pollutant, three groups of cases were set up for the grid independence analysis. The corresponding case information is given in Table 2 . The number of mesh grids for three simulation cases is respectively 3417313, 8982713 and 13011777. By using a 64-core supercomputer, the computation time for above three cases is about 1.5 h, 2 h and 2.5 h. The settings related to human personnel (ignoring breathing rate), supply air parameters and ventilation mode are consistent with the experimental conditions given in Table 1. The boundary condition for the diffuser opening is adopted from previous studies (Huo et al. 2000). Moreover, we adopt FLUKE mini IR (Infrared Radiation) thermometer (with laser output of less than 1mW and wavelength range of 630–670 nm) to obtain the temperature parameters of wall, human body, head and mouth in the office. The external wall temperature is set to 15 °C. The temperatures of human body, head and mouth are set as 24 °C, 34 °C and 34 °C respectively. Fig. 6 shows the grid independence analysis for the grid numbers of 3,417,313, 8,982,713 and 13,011,777. According to the analysis results, the simulation results using 8,982,713 and 13,011,777 mesh grids can show good agreement, with a deviation of less than 5%. Therefore, we employ the global setting with the mesh grid number of 8,982,713 to further carry out the simulation of airflow, temperature and pollutant distributions in this work.

Table 2.

Case information for grid independence analysis.

Case No.	Grid number	Person location (red dotted line)	Boundary conditions
Case 1 Case 2 Case 3	3417313 8982713 13011777		Current ventilation mode with airflow velocity of 0.3 m/s and inlet temperature of 25 ℃ external wall temperature: 15 ℃ body temperature: 24 ℃ head (mouth) temperature: 34 ℃ *ignoring personnel breathing rate

Fig. 6.

Grid independence analysis for the grid numbers of 3417313, 8982713 and 13011777 (a): airflow velocity; (b): indoor temperature.

Following the validation of grid independence, a total of 16 simulation cases are set up to calculate the pollution concentration fields based on the velocity-temperature coupling fields considering various combinations of ventilation modes (current and modified ventilation modes), source locations (A, B and C) and barrier heights (0, 40, 50, 60 and 70 cm). Table 3 provides an overview of simulation cases. The current and modified ventilation modes are firstly compared with respect to the airflow characteristics using cases 2 and 4. The parameters of pollutant source location and barrier height are further explored in simulation cases 5–19 under modified ventilation mode. A single pollutant source is considered, assuming an infected personnel with continuous coughing that produces viruses (with an airflow velocity of 13 m/s at the mouth downwards at 27.5°) (Kwon et al. 2012, Li et al. 2021) considering an airflow temperature of mouth as 36 °C (breathing rate for remaining personnel is assumed negligible). In each simulation case, the single pollutant source is placed in positions A, B or C, and the source releasing intensity (i.e., user-defined scalar boundary value at the mouth) is set as 1E-04 (quantum/m³). Additionally, the boundary conditions, including supply air velocity (by adopting diffuser opening) and temperatures of external wall, human body and head are all consistent with the settings in Table 2.

Table 3.

Overview of simulation cases in this work.

Case No.	Mode	Boundary conditions	Pollutant source	Barrier
Case 4	Modified ventilation mode (ref., Fig. 2)	Supply air velocity: 0.3 m/s Supply air temperature: 25 ℃ External wall temperature: 15 ℃ Body temperature: 24 ℃ Head (mouth) temperature: 34 ℃ *ignoring non-source breathing	No source	No barrier
Cases 5-19			Location: A, B and C *coughing rate of 13 m/s downwards at 27.5° with air temperature of 36 ℃	Barrier height of 0, 40, 50, 60 and 70 cm

2.4. Infection risk evaluation model

To analyze the infection risk levels of virus-associated pollutant, the Wells-Riley equation (Riley, Murphy and Riley 1978), an infection risk assessment model is adopted to evaluate the infection risk for personnel in the office. This analysis aims at investigating the potentials of physical barriers in mitigating the transmission of virus in open space offices during the epidemic period. The infection risk assessment model for individual personnel is expressed as follows (Buonanno, Stabile and Morawska 2020):

$$R_{inf}=\left(1-exp\left(-IR*\underset{0}{\overset{T}{\int }}C\left(t\right)dt\right)\right)*100$$ (5)

where, $R_{inf}$ is the likelihood of infection, $IR$ is the inhalation rate of the exposed subject (m³/h), t represents the time (h), T is the total exposure time (h), and $C\left(t\right)$ is the pollutant concentration (quantum/m³). Assuming that the exposed subject is active, the IR value is set as 0.96 (m³/h) (Buonanno et al. 2020). The exposure time is assumed as 1 hour, which is enough to allow an evaluation of human infection possibility in different staff positions. By multiplying the above likelihood with the number of exposed individuals, the number of susceptible people (called risk) can be easily calculated during the exposure time.

3. Results

This section mainly presents the results of the numerical simulations as relate for evaluating the impact of various barrier heights (0, 40, 50, 60 and 70 cm) on air distribution, pollutant dispersion and infection risk. First, the simulation results are validated by the experiment method. The airflow distribution performance of existing and modified ventilation modes is compared without physical barrier and pollutant source. Then, with reference to modified ventilation mode, pollutant dispersion and infection probability of personnel in the open office are calculated and discussed in line with infection risk assessment indicator, aiming to provide guidance on design and implementation of physical barriers as a disease transmission mitigation strategy.

3.1. Validation of numerical simulation and experiment

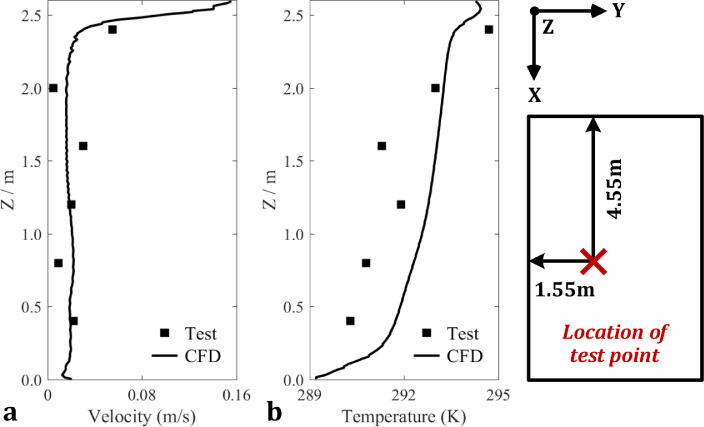
In order to validate the results of numerical simulation, experimental measurements are conducted in the case study office according to Fig. 5. Also, Fig. 7 compares the experimental tests and the results of airflow and temperature provided by the numerical simulation at the location of (x, y) = (4.55, 1.55) m. It can be found that the average deviation between the results of CFD simulation and field test is 18.5% for air velocity and 6.1% for indoor temperature. The distributions for velocity and temperature across the vertical height are acceptable from an engineering perspective. A possible reason for the fluctuation in experimental data is that the targeted office is not air tight, causing air infiltration from outside. However, as the deviation between the experimental and simulation results is at an acceprable level, the validity of numerical simulation results is verified, for the purpose of analyzing the impact of barrier heights on air distribution, pollutant dispersion and infection risk.

Fig. 7.

Validations of experimental tests and numerical simulations (a): airflow velocity; (b): indoor temperature.

3.2. Analysis of airflow distributions of existing and modified ventilation modes

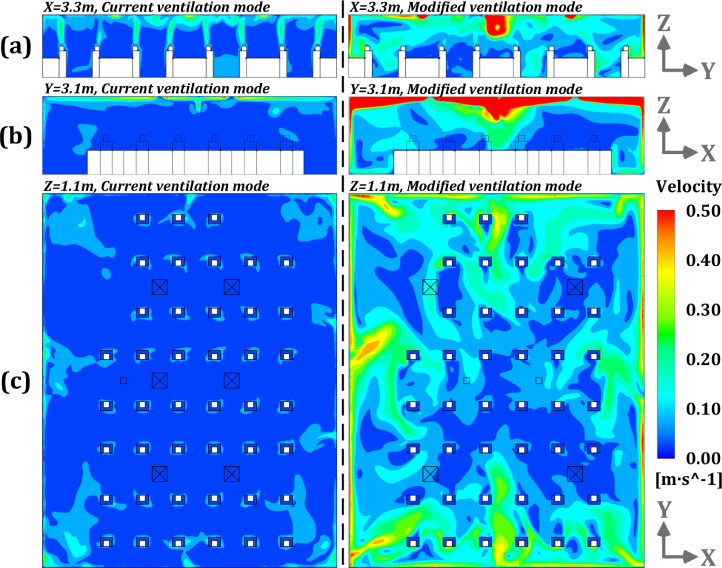
With reference to the existing ventilation system with a supply air volume of 0.45 m³/s (ref., Fig. 1), this study proposes a modified ventilation mode (ref., Fig. 2) with a larger supply air rate (1.73 m³/s), aiming to deliver sufficient ventilation air into the target activity areas. Fig. 8 displays distribution of airflow field under current and modified ventilation modes at planes of x = 3.3 m, y = 3.1 m and z = 1.1 m. The results points to an average velocity magnitude for modified ventilation mode that is about 3.5 times higher than that of current ventilation system. According to Fig. 8 (b–c), the ventilation air supplied to the occupied area is significantly increased in modified ventilation mode due to a larger jet airflow that can be created by diffuser in order to reach the occupied areas along the walls. In addition, it can be observed that the modified airflow pattern has a greater impact on airflow uniformity compared to the current ventilation system, which is one of the disadvantages of increasing the air change rate per hour (ACH).

Fig. 8.

Airflow distributions under current and modified ventilation modes at the planes of x = 3.3 m, y = 3.1 m and z = 1.1 m (without setting physical barrier and pollutant source) [(a): current ventilation mode; (b): modified ventilation mode].

The Air Diffusion Performance Index (ADPI) is used to comprehensively compare the airflow distribution performance of the two ventilation systems. ADPI is defined as the percentage of measurement points that meet the effective blowing temperature and airflow velocity requirements over the total number of measurement points in target areas (e.g., personnel activity areas), as shown in equation (6) (ASHRAE 2009).

$$ADPI=\frac{{\sum }_{j=1}^M{\left(P_{EDT}\right)}_j}{{\sum }_{i=1}^N{P}_i}\times 100\%$$ (6)

where, P_i represents the measurement points in the target area (i = 1, 2, …N, where N is the total number of P_i); P_EDT represents the measurement points that meet the temperature and velocity requirements (j = 1, 2, …M, where M is the number of P_EDT); and EDT is the effective draft temperature (°C) employed to evaluate the degree of blowing sensation in work area, as follows:

$$EDT=\left(t_x-t_m\right)-9.1\left(v_x-0.15\right)$$ (7)

where, t_x represents the air temperature of the measurement points (°C); t_m represents the indoor mean temperature (°C); and v_x represents the air velocity of the measuring points (m/s). When EDT value is varying between -2.2 °C and 2 °C and air speed is greater than 0.2 m/s, most people can feel comfortable (in warm circumstances) (Liu and Novoselac 2015). Table 4 lists ADPI values for the current and modified ventilation modes. The airflow distribution performance is normally accepted when ADPI value is greater than 70% (Ridouane 2011). As shown, airflow distribution of the modified ventilation mode is more comfortable than the current one, with the improvement of three times (63.2%) for air distribution performance. Hence, modified ventilation mode is preferred to ensure sufficient supply air rate and personnel thermal comfort. Thus, in the remaining part of this paper the modified ventilation mode (supply air rate of 1.73 m³/s) is used to investigate the impact of physical barriers height and the infected person location on the infection dispersion.

Table 4.

ADPI for current and modified ventilation systems.

Ventilation mode	Supply air rate (m3/s)	ADPI
Current ventilation mode	0.45	21.0%
Modified ventilation mode	1.73	84.2%

3.3. Influence of barrier height and pollutant source location on the airflow distribution

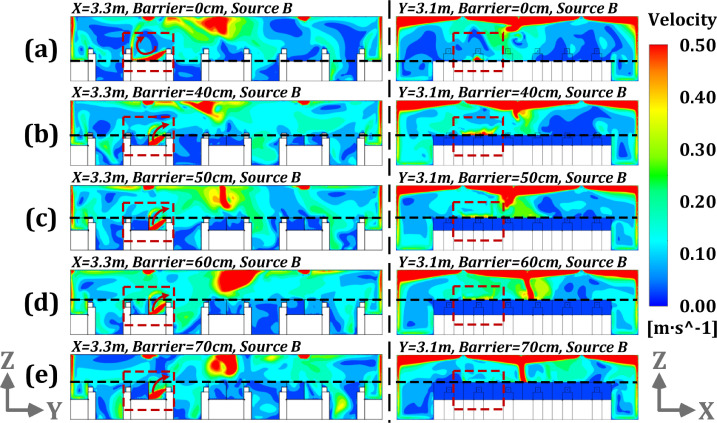
Under modified ventilation mode, the influence of barrier heights (i.e., 0, 40, 50, 60 and 70 cm) on airflow distributions is analyzed for three pollutant source locations (A, B and C). Fig. 9 shows the velocity distribution field at the planes of x = 3.3 m and y = 3.1 m for different physical barrier heights for pollution source at location B. Fig. 10 illustrates the airflow distributions at the plane of z = 1.1 m with the same conditions as Fig. 9. In case of physical barrier absence, the airflow generated by the coughing at location B can directly follow to the breathing area of the opposite staff and spread to the further area, as presented in Fig. 9 (a) and Fig. 10 (a). As the barrier height grows to above 40 cm, the airflow from the pollution source located at B can hit the physical barrier directly to form an upward flow and exit through the outlet, as shown in Fig. 9 (b-e). If the height further increases, the coughing flow from personnel is well blocked by the barrier. According to Fig. 10 (b-d), as the height of barrier gradually increases, less diffusion airflow spreads to the side regions close to source B. With higher barrier heights, collision jet may be introduced into the working area to further increase airflow volatility. In general, barrier height of at least 40 cm has a sufficient effect on airflow obstruction when the pollutant source is located at position B. The corresponding non-uniformity effect can be more obvious for office areas where the height is 60 cm or higher.

Fig. 9.

Airflow distributions at the planes of x = 3.3 m and y = 3.1 m with the barrier heights of 0, 40, 50, 60 and 70 cm under modified ventilation mode and pollution source of B [(a): height of 0 cm; (b): height of 40 cm; (c): height of 50 cm; (d): height of 60 cm; (e): height of 70 cm].

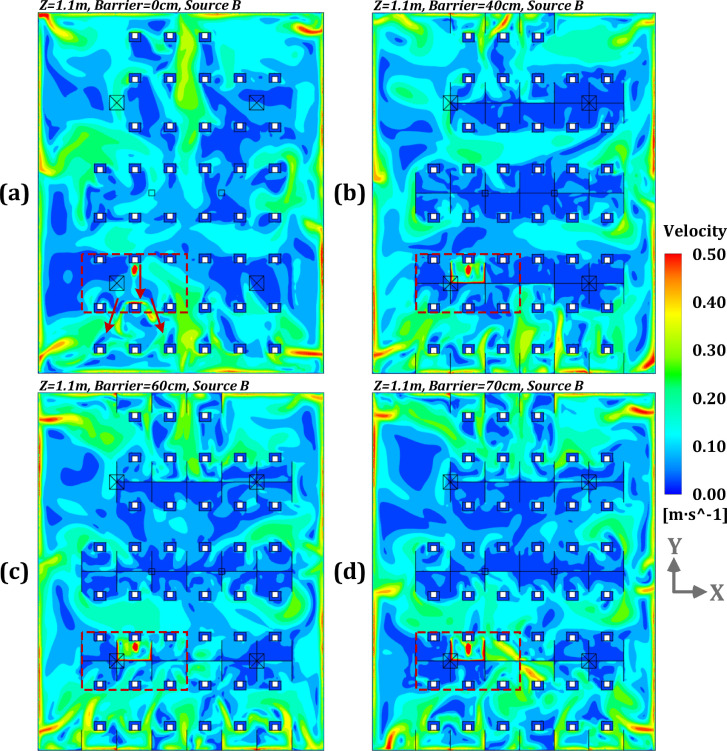
Fig. 10.

Airflow distributions at the plane of z = 1.1 m with the barrier heights of 0, 40, 60 and 70 cm under modified ventilation system and pollution source B [(a): height of 0 cm; (b): height of 40 cm; (c): height of 60 cm; (d): height of 70 cm].

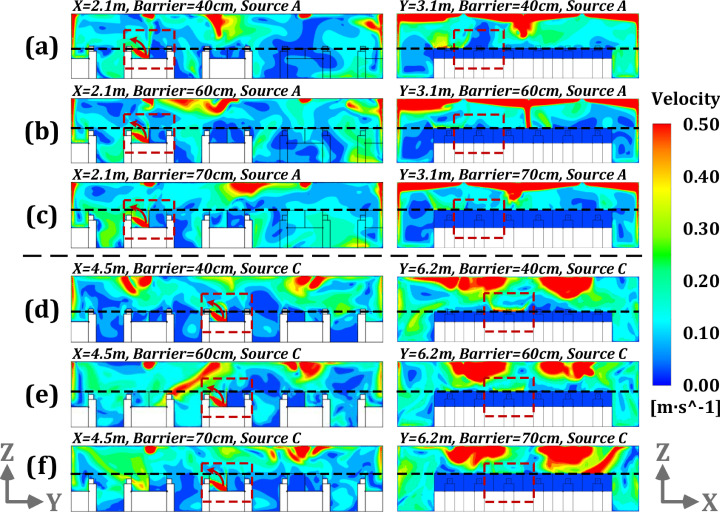
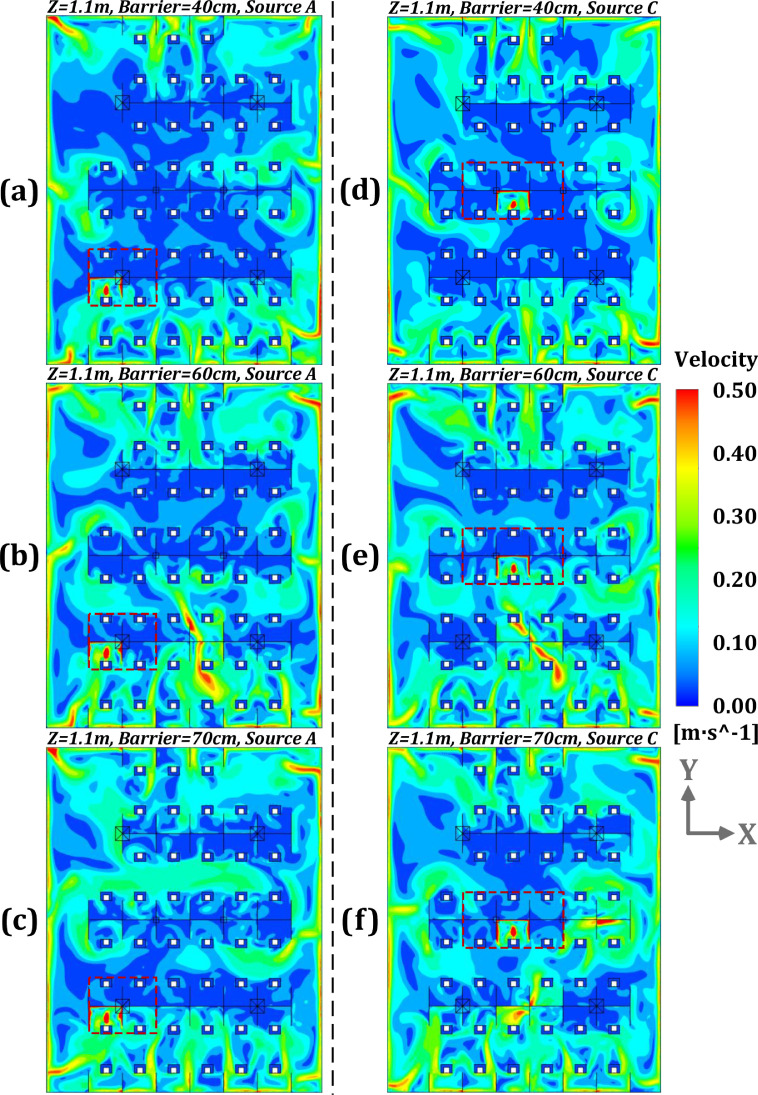
Further simulations were carried out to verify the impact of physical barrier height on the velocity fields through analyzing the cases with pollutant source locations at A and C, as shown in Fig. 11, Fig. 12 . For pollutant source at location A (which is about 4 m away from the outlet), the barrier height of equal or above 40 cm presents effective performance in blocking the airflow generated by human coughing from entering into the adjacent working region. For pollutant source in position C (close to the outlet), the barrier height of at least 40 cm shows sufficient performance for airflow hindering, similar to conditions of pollutant sources A and B. Fig. 12 (b-c) and Fig. 12 (e-f) show the inhomogeneity of indoor airflow is also dramatically increased with the barrier height set to 60 cm or greater values. In summary, a barrier height of at least 40 cm is recommended to prevent the dispersion of virus from an infected occupant with unknown location in an open office.

Fig. 11.

Airflow distributions for different profiles with the barrier heights of 40, 60 and 70 cm and pollution source located A and C [(a): planes of x = 2.1 m and y = 3.1 m with barrier height of 40 cm and source at point A; (b): planes of x = 2.1 m and y = 3.1 m with barrier height of 60 cm and source at point A; (c): planes of x = 2.1 m and y = 3.1 m with barrier height of 70 cm and source at point A; (d): planes of x = 4.5 m and y = 6.2 m with barrier height of 40 cm and source at point C; (e): planes of x = 4.5 m and y = 6.2 m with barrier height of 60 cm and source at point C; (f): planes of x = 4.5 m and y = 6.2 m with barrier height of 70 cm and source at point C].

Fig. 12.

Airflow distributions at the plane of z = 1.1 m with the barrier heights of 40, 60 and 70 cm under modified ventilation mode and pollution sources of A and C [(a): height of 40 cm and source of A; (b): height of 60 cm and source of A; (c): height of 70 cm and source of A; (d): height of 40 cm and source of C; (e): height of 60 cm and source of C; (f): height of 70 cm and source of C].

3.4. Influence of barrier height and pollutant source location on the pollutant dispersion

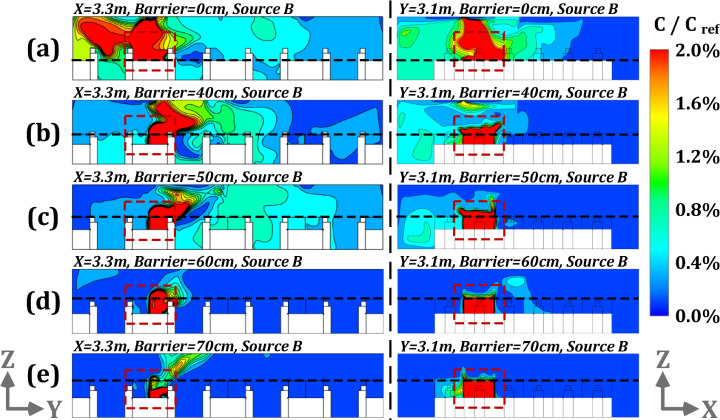
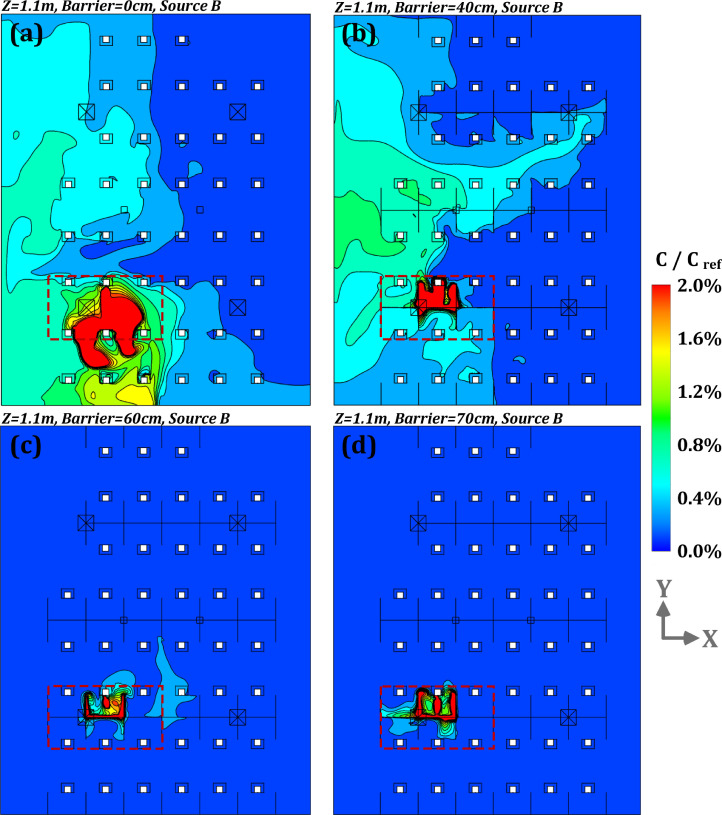
It is necessary to further investigate the performance of barrier height in combination with the influence of airflow on pollutant dispersion. Fig. 13 presents the relative pollutant concentrations (C/C_ref) for the planes of x = 3.3 m and y = 3.1 m for the barrier heights of 0, 40, 50, 60 and 70 = cm and pollutant source located at B. Fig 14 also shows the pollutant distributions at the plane of z = 1.1 m with the same conditions as above. The results of concentration analysis point to the fact that with no barrier, pollutant can disperse to distant regions up to 9 m according to the law of airflow motion, as shown in Fig. 13 (a) and Fig. 14 (a). Roughly 16 occupants have relative concentration values of above 0.6% in their working area. As the height of physical barrier increase to 40 cm, it starts to show a blocking effect on pollutant dispersion as displayed in Fig. 13 (b), corresponding to the work zone of about 11 occupants, as shown in Fig. 14 (b). With the barrier height increases above 50 cm (i.e., 60 cm and 70 cm), the obstructive effect towards pollutant is more obvious, as shown in Fig. 13 (d–e) and Fig. 14 (c–d).

Fig. 13.

Pollutant concentrations (C/C_ref) for the planes of x = 3.3 m and y = 3.1 m under modified ventilation mode with the barrier heights of 0, 40, 50, 60 and 70 cm and pollutant source at point B [(a): height of 0 cm; (b): height of 40 cm; (c): height of 50 cm; (d): height of 60 cm; (d): height of 70 cm].

Fig. 14.

Pollutant concentrations (C/C_ref) for the plane of z = 1.1 m under modified ventilation mode with the barrier heights of 0, 40, 60 and 70 cm and pollutant source at point B [(a): height of 0 cm; (b): height of 40 cm; (c): height of 60 cm; (d): height of 70 cm].

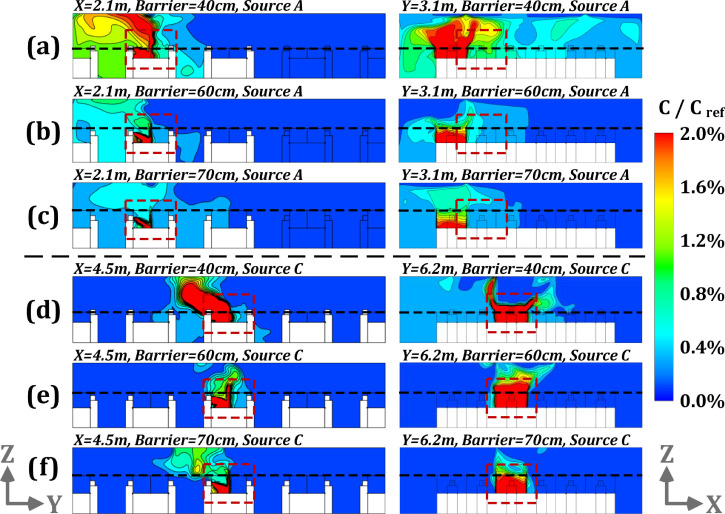
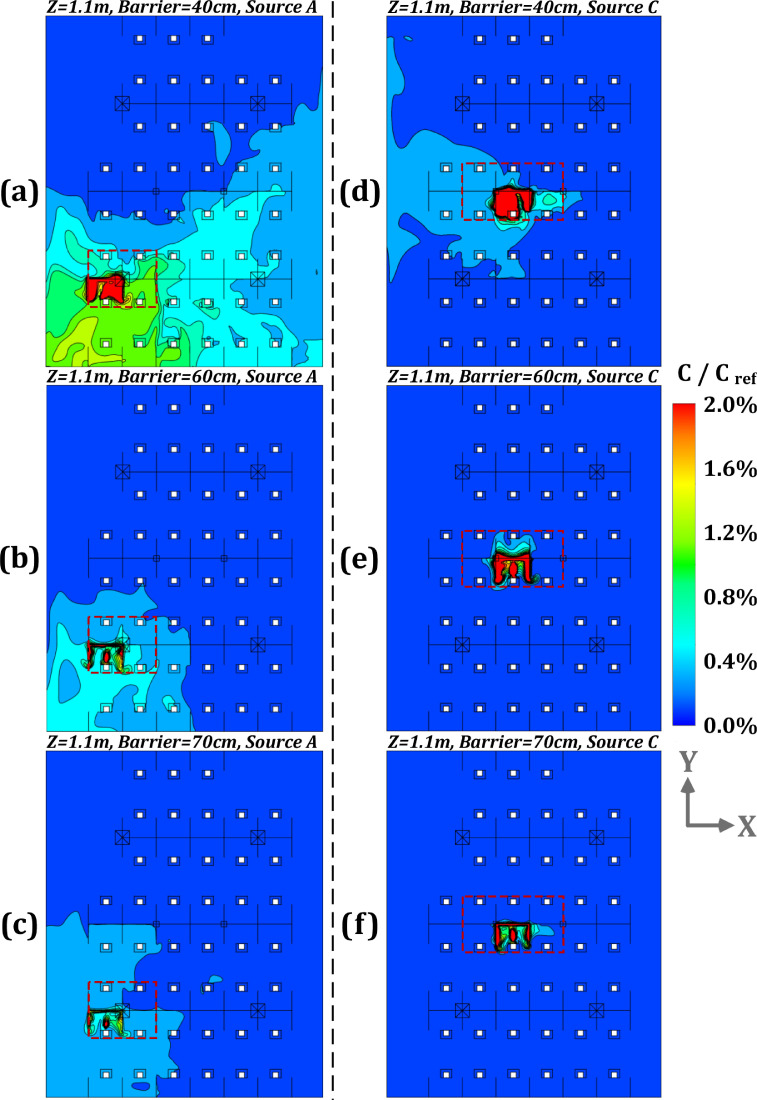
Further analyze was carried out to study the influence of different barrier heights on pollutant dispersion by comparing the simulation results for pollutant source located at point A and C along with barrier heights of 40, 60 and 70 cm, as displayed in Fig. 15, Fig. 16 . For pollutant source at A, the hindering effect of physical barrier on the pollution dispersion is not as obvious as that of source of B, as shown in Fig. 13 and Fig. 15 (a-c). The ranges of relative concentration above 0.6% correspond to the working areas for 18, 3 and 0 occupants with barrier heights of 40, 60 and 70 cm, respectively, according to Fig. 16 (a–c). It is observed that the airflow propagation is affected by the barrier height. However, as pollutant source A is far away from the air outlet, there will be a slow diffusion state for pollutants. For pollution source located at position C, the average relative concentration values are decreased by 23% and 15% in comparison with pollution sources at point A and B, respectively (with a barrier height of 40 cm). As per Fig. 15 (d–f) and Fig. 16 (d–f), most of pollutants produced by a infected person can be directly discharged from indoor space since the location of source C is rather close to the outlet, as shown in Fig. 4. Appendix A shows an unsteady dispersion process of pollutant lasting up to 100s following a cough at position C. In case of pollution source at point C, the number of occupied areas with a relative concentration value (C/C_ref) above 0.6%, will be 1 if the barrier height is 40 cm, as shown in Fig. 16 (d). It is observed that if the height is further increased, the performance of physical barrier will improve with dispersion of pollution becoming negligible such that no relative pollutant concentration of above 0.6% could be observed in occupied areas. In summary, under modified ventilation mode, for a pollution source close to outlet (i.e., pollutant source at B and C), the barrier height of at least 60 cm can show a favorable effect on the pollutant hindering. While for a source position far from the outlet (i.e., pollutant of A), blocking effect of increasing the barrier height is no longer obvious and only reaches an acceptable level with a height of 70 cm or more. Thus, in terms of pollutant dispersion with unclear location of infected person, the barrier height of 60 cm can provide good blocking effect against pollution dispersion. For regions far from the outlet (with a radius distance of larger than 4 m) or those located at zone 3 (shown in Fig. 4), a 70 cm height (or more) may not be effective in obstructing the spread of contaminant. In these circumstances, locations in distant areas of zone 3 and faraway from the air outlet may not be recommended for workstations.

Fig. 15.

Pollutant concentrations (C/C_ref) for different profiles under modified ventilation mode with the barrier heights of 40, 60 and 70 cm and pollutant sources located at A and C [(a): planes of x = 2.1 m and y = 3.1 m with barrier height of 40 cm and source at point A; (b): planes of x = 2.1 m and y = 3.1 m with barrier height of 60 cm and source at point A; (c): planes of x = 2.1 m and y = 3.1 m with barrier height of 70 cm and source at point A; (d): planes of x = 4.5 m and y = 6.2 m with barrier height of 40 cm and source at point C; (e): planes of x = 4.5 m and y = 6.2 m with barrier height of 60 cm and source at point C; (f): planes of x = 4.5 m and y = 6.2 m with barrier height of 70 cm and source at point C].

Fig. 16.

Pollutant concentrations (C/C_ref) at the plane of z = 1.1 m under modified ventilation mode with the barrier heights of 40, 60 and 70 cm and pollutant sources at point A and C [(a): height of 40 cm and source at A; (b): height of 60 cm and source at A; (c): height of 70 cm and source at A; (d): height of 40 cm and source at C; (e): height of 60 cm and source at C; (f): height of 70 cm and source at C].

3.5. Infection risk assessment for different barrier heights and pollution source locations

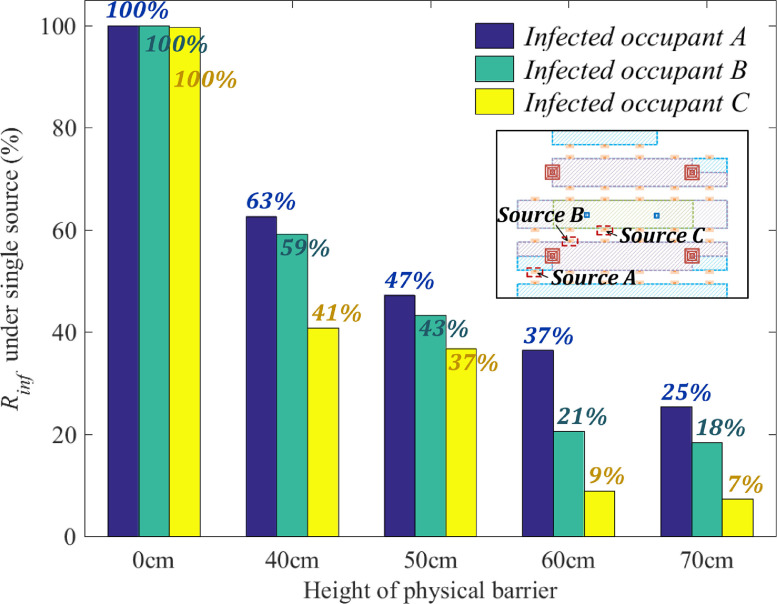
In this section, in line with the infection risk assessment model presented in equation (5), the influence of barrier heights (0, 40, 50, 60 and 70 cm) on occupant infection possibility (likelihood) is analyzed for pollutant source located at A, B and C. With a single source of pollution (one occupant infected out of 43), the maximum infection risk for other 42 occupants is estimated. In case of numerous pollution sources, one could adopt a Linear Ventilation Model (LVM) to rapidly obtain the corresponding concentration fields (Ren and Cao 2020), i.e., utilizing the principle of linear superposition to calculate the infection risk for multiple pollutant sources. Fig. 17 depicts occupant infection risk corresponding to various barrier heights and pollution source locations. Without a physical barrier, the infection risk for a single source of pollution located at point A, B or C positions could be up to 100%. With implementation of barriers of 40 cm and 50 cm, the infection risk can be reduced to 59% and 63%, respectively, for source C. If physical barrier height is above 50 cm, infection probability, with a pollutant source at A, can be decreased to 37% and 25%, corresponding to the barrier heights of 60 cm and 70 cm, respectively. In case of a pollution source at B, a barrier height of 60 cm can reduce the infection risk to about 20%, but infection probability does not significantly decrease with further increase of height. In case of a pollution source at C, infection risk can remain steadily below 10% if barrier height is increased to 60–70 cm. In sense, due to the unknown location of infected personnel in an open office, a barrier height of at least 60 cm would be appropriate for the workstations close to the outlet (with a maximum distance less than 4 m) or located in zones 1 and 2 (as shown in Fig. 4). In case of zone 3 (which is away from the air outlet), a 70 cm physical barrier height shows only a limited effect in reducing infection risk. As such, it may be preferable to recommend occupant to stay away from the certain areas located at zone 3 as shown in Fig. 4.

Fig. 17.

Infection risk (exposure time is 1 h) for single pollutant source at location A, B or C, and barrier heights of 0, 40, 50, 60 and 70 cm.

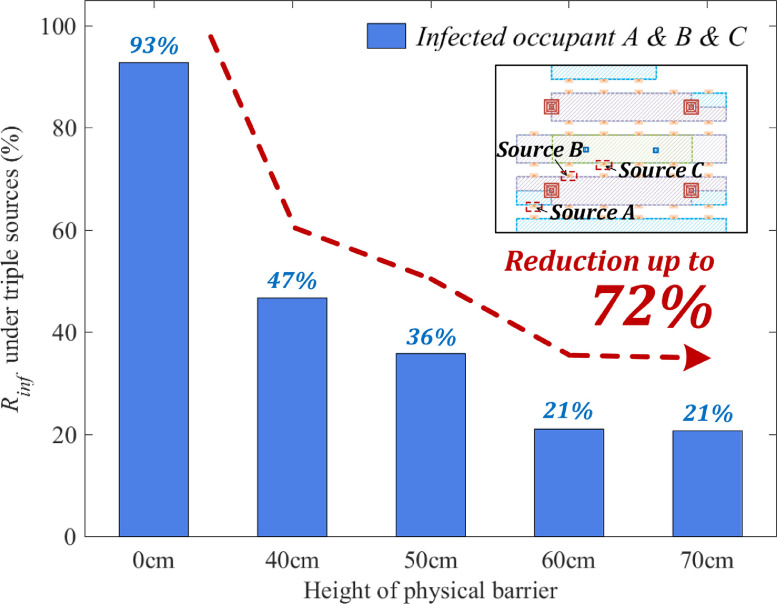
Fig. 18 shows a comparison of infection risks for personnel considering three alternative pollutant source locations of A, B and C, and barrier heights of 0, 40, 50, 60 and 70 cm. As the barrier height increases, the blocking performance is further improved compared to the situation with no physical barrier. The barrier heights of 60–70 cm can prevent the infection risk to 21%. With a physical barrier height of 60 cm, the infection risk has largely decreased to its minimum value, followed by almost no further improvement. In general, if the number of pollutant sources increases to 3, the mitigation of infection risk with barrier heights of above 60 cm is no longer significantly different from that of a single source at either location of A, B and C. In case of an unidentified number of pollution sources, a barrier height of at least 60 cm can be effective for mitigation of infection with sufficient supply air rate (modified ventilation mode).

Fig. 18.

Infection risk (exposure time is 1 h) for multiple pollutant sources (A, B and C) with modified ventilation mode and barrier heights of 0, 40, 50, 60 and 70 cm.

4. Discussion

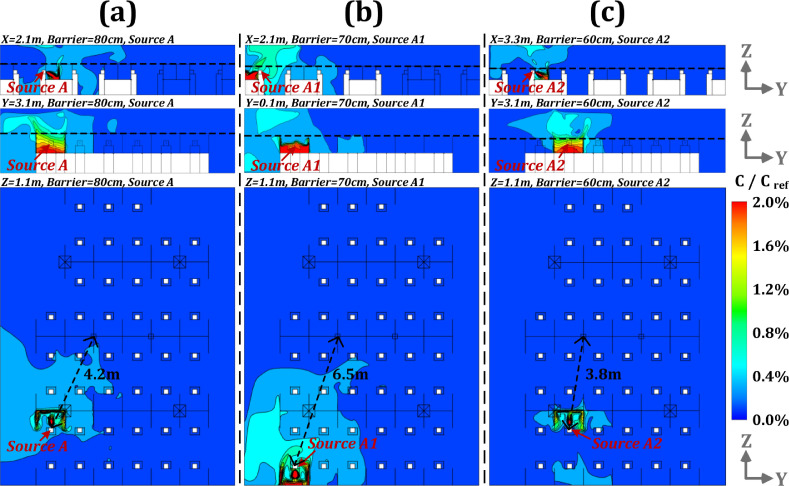
With COVID-19 pandemic, it is critical for open offices to adopt infection mitigation strategies such as use of low-cost physical barriers and/or personnel protection devices. Using CFD simulation, this study analyzed the effectiveness of various heights for physical barriers in hindering pollutant dispersion and reducing infection risk assuming 1 to 3 pollutant sources (infected occupants). It is observed that a barrier height of at least 60 cm can be more suitable for workstations at a distance of less than 4 m from the outlet (i.e., zones 1 and 2 as shown in Fig. 4). The effectiveness of barriers with a height of 70 cm is limited in reducing infection risk for zone 3, which is further away from the air outlet. It may be advisable for occupants to stay away from certain areas such as zone 3, as shown in Fig. 4. Three additional cases are supplemented as shown in Table 5 . Fig. 19 shows the simulation results for distribution of pollutant concentration field (C/C_ref) at different planes in case of pollutant source at location A with a barrier height of 80 cm, and in case of pollutant sources at location A1 and A2 with a barrier height of 70 cm. According to Fig. 19 (a), it could be observed that a barrier height below 80 cm and pollutant source located at A (around 4.2 m away from the outlet), the obstruction effect was not varying from the case with a barrier height of 70 cm (as shown in Fig. 15 and Fig. 16), in which the maximum infection rate was calculated as 24.3% (ref., Table 5). According to the simulation results presented in Fig. 19 (b), for a barrier height of 70 cm and pollutant source location at A1 (6.5 m away from the outlet), dispersion of pollutants cannot be effectively suppressed below an infection risk of 27.3%, as shown in Table 5. If the location of pollutant source is in zone 2, 3.8 m from the air outlet, the pollutant dispersion could be restricted with a barrier height of at least 60 cm, such that the personnel infection rate could be reduced to 23%, as shown in Fig. 19 (c) and Table 5. Hence, it is not suggested for personnel to stay at zone 3 as the mitigation effect of physical barriers cannot be significantly exploited.

Table 5.

Overview of additional cases for validation in this work.

Case No.	Mode	Boundary	Pollutant source	Barrier	Infection risk
Case 20	Modified ventilation mode	As same as Table 3, Supply air velocity: 0.3 m/s Supply air temperature: 25 oC External wall temperature: 15 oC Body temperature: 24 oC Head temperature: 34 oC Mouth temperature: 34 oC *coughing rate of 13 m/s downwards at 27.5° with air temperature of 36 oC *ignoring non-source breathing rate		80 cm	24.3%
Case 21				70 cm	27.3%
Case 22		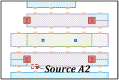		60 cm	23.0%

Fig. 19.

Pollutant concentrations (C/C_ref) at different planes under pollutant source of A with barrier height of 80 cm and under pollutant sources of A1 and A2 with barrier height of 70 cm [(a): planes of x = 2.1 m, y = 3.1 m and z = 1.1 m with barrier height of 80 cm and source of A; (b): planes of x = 2.1 m, y = 0.1 m and z = 1.1 m with barrier height of 70 cm and source of A1; (c): planes of x = 3.3 m, y = 3.1 m and z = 1.1 m with barrier height of 70 cm and source of A2].

In order to further improve the applicability of physical barrier, some limitations of this study need to be focused on. In simulation, it was assumed that pollution (in form of aerosols) behaves like a gas (as shown in Appendix A), while the droplets (large-sized coarse particles) from human coughing are assumed to fall to the ground or other surfaces in about 1m from the source. In a real-life situation, the evaporation of liquid droplets to liquid core (changing from large particles to small ones) is also critical in simulation of pollutant dispersion produced by coughing or sneezing. A detailed source setting (e.g., using tracer mass and particle) needs to be further taken into account to improve the accuracy of pollutant concentration simulations.

To ensure sufficient delivery of ventilation air to workstations, evaluating the influence of different ventilation modes and diffuser types on airflow distribution and pollutant dispersion could be a future avenue of research. It is observed in simulation results, that the infection risk in areas less that 4 m from the outlet is well mitigated. The implementation of physical barriers can further reduce the possibility of infection risk (e.g., at least 60 cm height of physical barrier above the desk surface of 80 cm for region within 4 m away from the outlet) subject to a better understanding of the effect of ventilation system on airflow and pollutant concentration. However, for a poorly-designed air conditioning system without sufficient ventilation air and uniform air diffuser locations, the effect of barrier height in reducing the infection rate remains unverified. In cases with room heights, spaces and ventilation modes different from the targeted office, the performance of physical barrier and effective coverage distance of the outlet could also be the focus of attention. Moreover, it is essential to integrate the prevention strategies (e.g., physical barrier) with appropriate control techniques, such as multi-mode ventilation system (Shao et al. 2017), intelligent and online monitoring of air condition systems (Cao and Ren 2018, Cao and Ding 2020), demand-controlled supply air devices (Wang et al. 2021). Lastly, the design of physical barriers or air conditioning systems (including supply air openings and pipelines) has to be in line with functional and aesthetic requirements. The optimization of design and costing can further help meet the needs of different groups of people and achieve broader application prospects.

5. Conclusions

This study analyzed the influence of barrier heights (0, 40, 50, 60 and 70 cm) on reducing pollutant dispersion and infection risk in an open office with a well-designed ventilation mode and subject to alternative pollutant source locations. This work provides a basis for analysis of the performance of physical protection measures in open spaces through simulating the gaseous pollutant dispersion and calculating an infection possibility. The main conclusions could be listed as follows:

• (1)In terms of airflow blocking, a barrier height of at least 40 cm above the desk level (at 80 cm) is recommended to prevent the coughing flow of an infected person, considering an unknown location in the open office and subject to a modified ventilation mode.
• (2)A barrier height of 60 cm can show a considerable performance in case of pollution sources closer to outlet. In case of source positions more than 4 m from the outlet (at zone 3), a barrier height 70 cm or more is not further effective in obstructing pollutant dispersion, and thus, this area is not recommended for placement of workstations.
• (3)In case location and number of infection personnel is unknown, a barrier height of at least 60 cm above the desk level is recommended provided a sufficient ventilation rate. This could decrease the infection risk by 72%. It is recommended to advise the personnel to work in zones 1 and 2 (within 4 m of the outlet) to enhance the effectiveness of the physical barriers.

Declaration of Competing Interest

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.