Measuring the Kinetics of Molecular Association by Isothermal Titration Calorimetry

Abstract

The real-time power response inherent in an isothermal titration calorimetry (ITC) experiment provides an opportunity to directly analyze association kinetics, which, together with the conventional measurement of thermodynamic quantities, can provide an incredibly rich description of molecular binding in a single experiment. Here we detail our application of this method, in which interactions occurring with relaxation times ranging from slightly below the instrument response time constant (12.5 seconds in this case) to as large as 600 seconds, can be fully detailed in terms of both the thermodynamics and kinetics. In a binding titration scenario, in the most general case an injection can reveal an association rate constant (k_on). Under more restrictive conditions, the instrument time constant-corrected power decay following each injection is simply an exponential decay described by a composite rate constant (k_obs), from which both k_on and the dissociation rate constant (k_off) can be extracted. The data also support the viability of this exponential approach, for k_on only, for a slightly larger set of conditions. Using a bimolecular RNA folding model and a protein-ligand interaction, we demonstrate and have internally validated this approach to experiment design, data processing, and error analysis. An updated guide to thermodynamic and kinetic regimes accessible by ITC is provided.

1. Introduction

In addition to its more traditional application in studying binding thermodynamics, the modern generation power-compensated titration microcalorimeter (Freire, Mayorga, & Straume, 1990; Wiseman, Williston, Brandts, & Lin, 1989) has been applied to the study of enzyme kinetics. The ability to measure the intrinsic heat effect for an enzyme process allows direct real-time monitoring of reaction progress in an unmodified system, circumventing the potential time, cost, or experimental difficulties associated with fluorophore attachment or other chemical modifications. Many of these studies have examined enzyme systems using Michaelis-Menten steady-state kinetics (see for example (Bianconi, 2003; Todd & Gomez, 2001); reviewed in (Bianconi, 2007; Lonhienne & Winzor, 2004; Transtrum, Hansen, & Quinn, 2015)), where the substrate is injected at a sufficiently high concentration so that the initial reaction velocity (V_init) is relatively constant.

Here we examine the alternative approach in which the reaction rate is determined directly from the rate of compensatory power decay following ligand injection, an approach which naturally extends to ligand binding scenarios. Freire and co-workers previously demonstrated the validity of this approach, directly monitoring the decay following substrate injection in enzyme kinetics applications (Mayorga & Freire, 1987; Morin & Freire, 1991). This method was applied sparingly and only to enzymatic systems (Franghanel, Wawra, Luke, Wildemann, & Fischer, 2006; Morin & Freire, 1991; Williams & Toone, 1993), but more recently we adopted it to characterize reversible processes involving RNA-RNA interactions (Vander Meulen & Butcher, 2012). This approach has also been applied to protein-ligand (Burnouf et al., 2012; Egawa, Tsuneshige, Suematsu, & Yonetani, 2007) and RNA-ligand (Burnouf et al., 2012) association. Burnouf et al. performed significant theoretical method development and were able to validate their findings using SPR (Burnouf et al., 2012).

This work provides a practical guide to the rate constant regimes under which time-resolved ITC can be adopted and what information can be obtained, demonstrating these approaches with experimental data and highlighting the numerous processing steps we have developed along the way. We first examine the steps required to obtain kinetic information from the power decay following ligand injection. We then focus on the application of this methodology within a binding titration scenario, for which analysis of each injection yields a series of kinetics experiments. Minimally this reveals a robust association rate constant (k_on); additionally, if the dissociation constant (K_d) can be measured, the dissociation rate constant (k_off) can be subsequently calculated using k_off = k_on·K_d. When the rate constants fall within a subset of values defined by reversibility throughout the full titration, both k_on and k_off can be determined simply and directly. We conclude by demonstrating the seconds-timescale association kinetics profiles accessible to titration calorimetry, which can nicely augment thermodynamics data gathered in the same experiment.

2. Background

2.1. Extraction of Electrical Power due to Molecular Processes

As highlighted previously by Freire (Freire, Vanosdol, Mayorga, & Sanchezruiz, 1990; Mayorga & Freire, 1987), the output from a power-compensation microcalorimeter can be viewed as a convolution of the reaction “impulse” heat evolution function with the calorimeter “response” function, the latter being effectively modeled as first-order with rate constant k_ITC. The “impulse” power function of the process of interest (E*) can be extracted from the raw sample cell excess energy output trace (E_XS), perhaps most simply by way of Laplace Transform:

$$E^{\ast }=\frac{1}{k_{\text{ITC}}}\raisebox{1ex}{$\partial E_{\text{XS}}$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.+E_{\text{XS}}$$ Equation 1

The value of k_ITC depends on instrument design and feedback settings, among other factors (see (Transtrum et al., 2015)). Using a MicroCal VP-ITC in the default ‘high’ (i.e., fast) feedback mode, we found k_ITC = 0.08 (±0.02) s⁻¹, corresponding to a time constant of 12.5 seconds. While the listed specification for the VP-ITC is 20 seconds, it is noteworthy that Burnouf et al. identified a time constant of 3.5 seconds for the MicroCal iTC200, also significantly shorter than the corresponding specification of 10 seconds (Burnouf et al., 2012). With the caveats addressed by Transtrum et al. as backdrop (Transtrum et al., 2015), we simply note that the 12.5 second time constant is within range of two other experimental examinations (Demarse, Killian, Hansen, & Quinn, 2013; Garcia-Fuentes, Baron, & Mayorga, 1998); however, we are not aware of another experimental determination using a VP-ITC, which would be the appropriate comparison.

2.2. ITC Association Kinetics Analysis

E* is approximately equal to the time-dependent rate of new complex formation, ∂[C]/∂t, scaled by the product of the binding enthalpy (ΔH) and the sample cell volume (V₀; for the calorimeter in our RNA experiments, V₀ =1.42 mL).

$$E^{\ast }\approx \Delta H{V}_0\raisebox{1ex}{$\partial \left[C\right]$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.$$ Equation 2

Equation 2 is approximate because the usually minor heat contributions to the cell from the mechanics of injection and ligand dilution are ignored. If the injection period is excluded, kinetics analysis only requires knowledge of the relationship between the rate of complex formation and the underlying kinetic parameters. The remainder of this section derives that relationship.

2.2.1. General Approach

Below we use a general nomenclature in which the calorimeter contains a macromolecule, M, at total concentration, [M]_tot. At the start of the titration, M is at an initial total concentration, [M]_init. Ligand, L, is injected from the syringe and binding generates complex, C. The overall binding process is simply described by a forward rate constant, k_on, and reverse rate constant, k_off

$$\text{M}+\text{L}\underset{koff}{\overset{kon}{\rightleftarrows }}\text{C}$$ Equation 3

The equilibrium involves three species, so knowledge of [M]_tot and [L]_tot for a given injection, as dictated by the experimental setup, reduces the description of all solution concentrations to a single degree of freedom. Here we incorporate that knowledge by using a single displacement from equilibrium variable, λ, which we define as the amount by which the equilibrium concentration of complex, [C]_eq, exceeds the current concentration, [C]. The reaction rate can then be written

$$\raisebox{1ex}{$\partial \left[C\right]$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.=-\raisebox{1ex}{$\partial \lambda $}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.=k_{\text{on}}\left({\left[\text{M}\right]}_{\text{eq}}+\lambda \right)\left({\left[\text{L}\right]}_{\text{eq}}+\lambda \right)-k_{\text{off}}\left({\left[\text{C}\right]}_{\text{eq}}-\lambda \right)$$ Equation 4

Here it is more convenient to reformulate the expression in terms of k_on and the dissociation constant, K_d. Assuming only that K_d = _koff/k_on, Equation 4 can be rearranged to Equation 5.

$$\raisebox{1ex}{$-\partial \lambda $}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.=k_{\text{on}}\left(\lambda \left({\left[\text{M}\right]}_{\text{eq}}+{\left[\text{L}\right]}_{\text{eq}}+{\text{K}}_{\text{d}}+\lambda \right)\right)$$ Equation 5

Integration results in the most general expression for λ.

$$\ln \left(\frac{{\lambda }_{\text{t}=0}}{\lambda }•\frac{{\left[\text{M}\right]}_{\text{eq}}+{\left[\text{L}\right]}_{\text{eq}}+{\text{K}}_{\text{d}}+\lambda }{{\left[\text{M}\right]}_{\text{eq}}+{\left[\text{L}\right]}_{\text{eq}}+{\text{K}}_{\text{d}}+{\lambda }_{\text{t}=0}}\right)=-\left({\left[\text{M}\right]}_{\text{eq}}+{\left[\text{L}\right]}_{\text{eq}}+{\text{K}}_{\text{d}}\right)k_{\text{on}}t$$ Equation 6

In Equation 6, λ_t=0 is the displacement from equilibrium following addition of ligand. More precisely in the case of an ITC experiment, it is the displacement at a hypothetical time point after ligand injection and mixing but preceding formation of any new complexes. λ_t=0 reflects concentration changes caused by the addition of L and the resulting displaced volume (Ltd, 2015). Equation 6 shows that in this most general case, determination of λ requires knowledge of k_on, in addition to K_d and the equilibrium concentrations. In an ITC application, the latter two term categories are known throughout a titration according to analysis of the binding curve and the experimental setup, respectively. Given these quantities and a predicted k_on, λ can then be determined using a root finding routine on Equation 6. Thus the predicted cumulative heat evolution function is given by Equation 2, where λ and subsequently ∂λ/∂t are calculated from Equations 6 and 5, respectively.

2.2.2. Approximation Regime I: The Near-Equilibrium Approximation

The general, non-analytical expression for λ in Equation 6 can be simplified in two limiting cases. First, if the difference between the current and equilibrium concentration (the displacement from equilibrium) is small relative to the sum of the equilibrium concentrations of M, L and the K_d (λ << [M]_eq + [L]_eq + K_d), then the left-hand side of Equation 6 is simplified and the equation can be rearranged into a first-order format. Below we refer to this scenario as “near-equilibrium” (Bernasconi, 1976; Egawa et al., 2007)

$$\lambda ={\lambda }_{t=0}\cdot e^{-k_{obs}\times t}$$ Equation 7 (near-equilibrium)

where

$$k_{\text{obs}}=k_{\text{on}}\cdot \left({\left[\text{M}\right]}_{\text{eq}}+{\left[\text{L}\right]}_{\text{eq}}+k_{\text{off}}\right)$$ Equation 8 (near-equilibrium)

The time derivative of Equation 7 is required for direct analysis of E* and can be simply calculated (see Section 3.3).

The near-equilibrium approximation holds in the following titration scenarios: (1) typically, in the first few injections, when the combined free concentration ([M]_eq + [L]_eq) exceeds λ largely due to the excess of M (i.e., [M]_tot > [L]_tot); (2) throughout a titration for sufficiently weak binding scenarios, so that the K_d is appreciable and the combined free reactant concentration is always in excess of λ. In Section 3.3, we show that this latter scenario holds robustly for titrations designed with a ‘Wiseman’ c parameter (c = [M]_init/K_d (Wiseman et al., 1989)) ≤ 40.

2.2.3. Approximation Regime II: The Tight Binding Approximation

When binding is too strong to measure accurately (c > 200; see 3.5), Equation 6 can instead be simplified using a tight binding approximation. K_d in this case is negligible; removing it from Equation 6 then reformulating reaction progress as the amount of unbound ligand remaining (x) results in the following kinetic equation for a forward titration:

$$\ln \left(\frac{{\left[\text{RR}\right]}_{\text{t}=0}}{{\left[\text{TT}\right]}_{\text{t}=0}}•\frac{{\left[\text{TT}\right]}_{\text{t}=0}-x}{{\left[\text{RR}\right]}_{\text{t}=0}-x}\right)=-\left({\left[\text{RR}\right]}_{\text{t}=0}-{\left[\text{TT}\right]}_{\text{t}=0}\right)k_{\text{on}}t$$ Equation 9 (tight binding)

Though we do not examine this scenario explicitly, it does appear to be highly robust for all injections in an experiment where c > 200, and it is also valid for the initial injections of weaker-binding titrations (pictorially, the ‘plateau region’ of a titration). For example, we found that error due to this approximation is less than 10% for experiments with c ≥ 60 if only injections are analyzed where [L]_tot/[M]_tot < 0.5 (unpublished results).

3. Procedure and Results

Previously we used time-resolved ITC to characterize the thermodynamics of a model RNA system along the folding reaction coordinate (Vander Meulen & Butcher, 2012). This system utilizes a ubiquitous tetraloop – receptor tertiary motif (Cate et al., 1996; Costa & Michel, 1995; Toor, Keating, Taylor, & Pyle, 2008) to drive association of two RNA helices, one containing two receptor motifs (RR), the other containing two cognate GAAA tetraloop sequences (TT) (Figure 1). Because RNA folding kinetics are highly dependent on both salt and temperature, the TT – RR data from our previous study provide a view of kinetics analysis across the range of accessible rate constant regimes.

Figure 1.

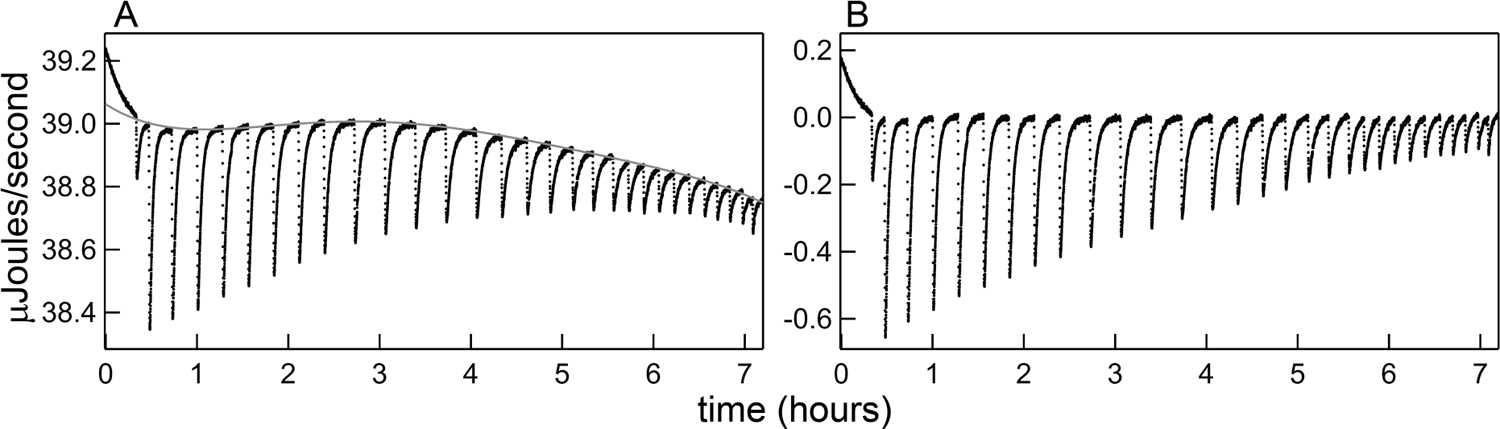
Demonstration of thermogram baseline subtraction (ITC power trace obtained in 0.3 mM MgCl₂ at 30 °C, using starting cell [RR] = 10 µM, syringe [TT] = 171 µM, and 6.5 µL injections.) A) Raw Thermogram (black dots) and fitted baseline (gray curve). B) Following baseline subtraction, the plotted data express only the additional power input in response to ligand injection and binding (referred to here as E_XS).

3.1. Raw thermogram preparation

In principle, one injection of ligand into a solution containing its binding partner is sufficient to measure the forward rate constant, k_on. In our work, as well as that of Burnouf et al (Burnouf et al., 2012), kinetic data was obtained in a full binding titration as a ‘bonus’, and we target that scenario in this guide. We also show in Sections 3.3, 3.4, and 4.3 that there is utility in analyzing multiple injections in a titration, because it reduces uncertainty and additionally yields a concentration-dependent kinetics dataset. However, it is our intention that a practitioner working with even a single injection could easily adapt the appropriate sections.

Thus we begin here from a titration thermogram, as in Figure 1. A representative raw titration power trace for the exothermic TT – RR interaction is plotted in Figure 1A. Because the raw data can exhibit appreciable drift in the baseline power, we first perform a polynomial baseline regression and subsequent subtraction to objectively account for most of the curvature in the instrument baseline, the result of which is shown in Figure 1B. In the regression procedure, we generally mask all data points except those ≤ 10 seconds prior to the next injection.

3.2: Analysis of Individual Injections

Each sharp negative deflection in the thermogram in Figure 1 reflects the real-time compensatory reduction in electrical power following injection of an exothermic binding partner (see Background). Using the Laplace Transform methodology with an instrumental time constant of 12.5 seconds (k_ITC = 0.08 s⁻¹), the instantaneous rate of excess heat input following an injection can be easily recovered by using Equation 1 (Mayorga & Freire, 1987; Morin & Freire, 1991).

Figure 2 plots the 7^th peak from the dataset in Figure 1 as an example with which to highlight the preparation and analysis of an individual injection using a completely general methodology. The first step illustrated is transformation to the real-time power signal; Figure 2A shows the injection signal before and after deconvolution. This example illustrates a relatively slow association process with a half-time of approximately 105 seconds. Here analysis of the raw signal results in only a slight (approximately 3%) underestimate of the rate constant. The effect of the deconvolution and thus the uncertainty related to the instrument time constant increases significantly for faster events (see Sections 3.4 and 4.2.3).

Figure 2.

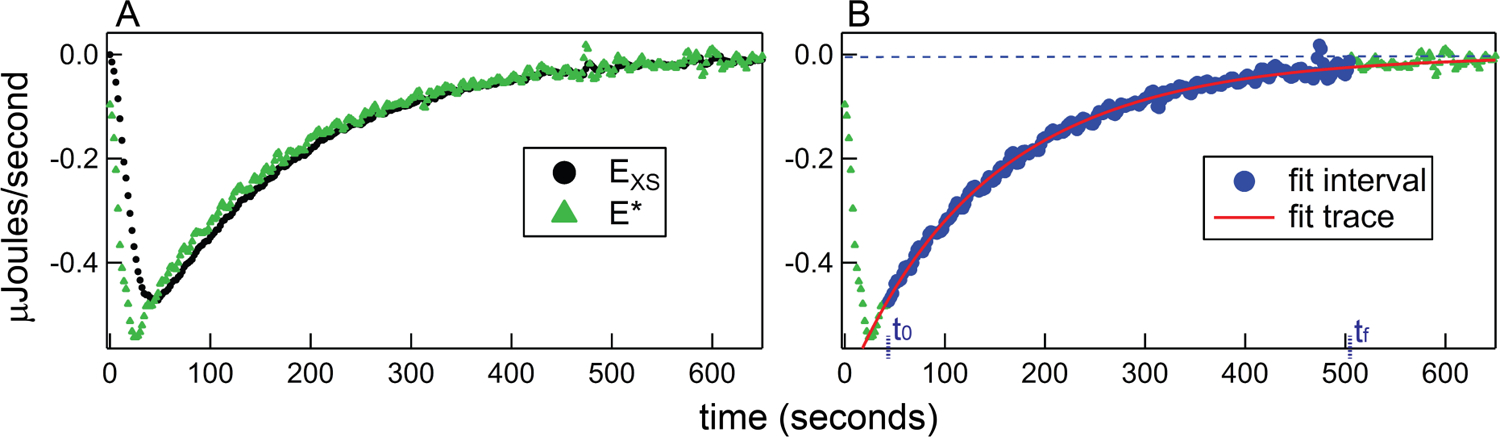
Demonstration of injection peak fit preparation procedure, using the 7^th injection from the titration in Figure 2. A) Deconvolution to recover the instantaneous power signal. The black (raw) data points are referred to as E_XS (the instrument power response) and the green triangles (post-deconvolution) are equivalent to E* (the instantaneous rate of heat evolution due to injection and macromolecular association). B) Baseline, fitting regime, and curve fitting. A final baseline was not fully established in this injection, so the blue dotted line represents the linear and constant terms determined from a preliminary regression procedure. Data within the fitting region are highlighted by large blue circles. The starting point for fitting, t₀, corresponds to the minimum in the pre-deconvolution data (44 seconds) and, in this case, the final point, tf, is determined from the decay in the power signal (504 seconds). The red curve represents the results of regression using the general set of kinetics equations (2, 5 and 6).

Robust kinetics analysis of each injection also requires careful consideration of both the baseline power and the fit region. The first step in baseline treatment is actually handled in the thermogram baseline subtraction (Section 3.1), which largely corrects for sloping and curvature in the baseline power signal and resets the offset to approximately 0 µJ·s⁻¹. However, this procedure cannot be viewed, in general, as having completely removed baseline power from the analysis, since raw thermogram baseline drift is idiosyncratic and miscalculations due to slight imperfections in the subtraction procedure can be acute for fast association processes (see Section 4.3). Thus we use both a linear (slope) and constant (intercept) term in the fitting procedure. Where possible, the baseline terms are determined separately and fixed during regression. Baseline selection and associated error analysis is an important but detail-heavy topic, and is covered in 4.2.2.

The next consideration is fitting interval [t₀, t_f] selection. The first time point, t₀, is the point immediately succeeding the time corresponding to the raw power trace minimum (or maximum for an endothermic process). In our implementation, this effectively excludes the injection and mixing period and the associated heat of dilution. Selection of a final time point, t_f, is also required to prevent baseline overfitting (overrepresentation of a final baseline region) in some cases. t_f is set to the minimum among the following three values: (1), the last point before the next injection; (2), a time-decay boundary point equal to ten times the approximate half-time; (3), a power-decay boundary point corresponding to the time at which the magnitude of the power value offset from the baseline first decreases below a threshold value, which we set to 0.001 µJ·s⁻¹. Figure 2B shows the baseline and fitting range selected for the example injection peak.

The deconvolved real-time excess power input (E*) is defined in Equation 2. The fitting procedure includes ΔH as an unconstrained amplitude parameter (in principle, this could be related to the ΔH for the association process, but the amplitude is complicated by the time offset due to the injection/mixing period). Any obtainable kinetics quantities are buried in the decay term, which is simply the rate of complex formation, ∂[C]/∂t. For a straightforward association process, this can be described in terms of the rate of change in the displacement from equilibrium, ∂λ/∂t, as laid out in Equation 5. The only unknown parameter in Equation 5 is k_on, the rate of complex association. The concentration parameters, [M]_eq and [L]_eq, are obtained from the titration setup and the (potentially ITC titration-derived) equilibrium dissociation constant, K_d. Table 1 displays the underlying set of concentrations ([RR]_eq and [TT]_eq for this specific case, along with λ_t=0) required for analysis of the example data in Figure 2. The fitted curve that follows from the above-described data preparation and general fitting routine is shown in Figure 2B.

Table 1.

Concentrations Relevant to Figure 2

Time Period	Actual Concentrations (µM)			Equilibrium Concentrations (µM)			λ
	[TT]	[RR]	[Complex]	[TT]eq	[RR]eq	[Complex]eq
Pre-Injectiona	0.37	6.90	2.80	0.37	6.90	2.80	0.00
Post-injectiona,b (t=0)	0.95	6.87	2.78	0.46	6.39	3.27	0.49

^aConcentrations include adjustments for activities as included in our previous work (Vander Meulen & Butcher, 2012; Vander Meulen et al., 2008). The K_d was determined separately from the binding titration to be 907 nM.

^bTheoretical state including displaced volume effect, but prior to any changes in binding in response to altered concentration

In a titration scenario, we analyze all of the injection peaks before the stoichiometric equivalence point, where [L]_tot < [M]_tot, as signal-to-noise decreases, sometimes dramatically, beyond this point. The resulting array of k_on data can be averaged to increase the confidence level, although some sources of potential error are correlated and thus cannot be mitigated through averaging (see Sections 3.4 and 4.2.3).

3.3. Near-Equilibrium Approximation

While general, the approach outlined above has drawbacks in implementation (λ cannot be expressed in closed form) and in its ability to only directly calculate k_on. Subsequent determination of the dissociation rate constant (k_off) requires a single step kinetic mechanism assumption, or at least the assumption that there is not a stable intermediate, such that k_off = K_d/k_on.

Where a near-equilibrium approximation can be applied to an entire titration, the kinetics analysis is both simplified and more powerful (Egawa et al., 2007). This approximation holds for titrations in which λ is always small relative to the unbound reactant concentrations (c ≤ 40; see 2.1.2 and below). The near-equilibrium approximation reduces λ(t) to the expression in Equation 7, and subsequent substitution for ∂[C]/∂t in Equation 2 according to Equations 5 and 7 (and the definition ∂λ/∂t = −∂[C]/∂t) results in a description of the rate of reaction heat evolution as pseudo first-order with composite rate constant, k_obs.

$$E^{\ast }\approx \Delta H{V}_0{\lambda }_{t=0}{k}_{\text{obs}}{e}^{-k_{\text{obs}}t}$$ Equation 10 (near-equilibrium)

In Equation 10, k_obs is a composite term that is linear in the sum of the unbound substituent concentrations, with slope k_on and intercept k_off (see Equation 8).

Figure 3 compares rate constant determinations using both the general and near-equilibrium approach for the example titration and injection used in Figures 2 and 3. Fits using these approaches are equally satisfying (Figure 3A); neither residuals (Figure 3A, top) nor χ² are useful in validating or invalidating the near-equilibrium approach. Figure 3B plots the collection of rate constant outputs from the two approaches. The microscopic rate constant k_on, determined using the general equation, is constant over the course of the titration, though the uncertainty increases significantly in later injections where signal-to-noise is reduced (Figure 3B, top). Contrastingly, the composite rate constant k_obs is a strong function of the injection number (Figure 3B, bottom). It decreases to a minimum then increases, mirroring the unbound macromolecular concentration, which decreases as bound complex increases, then subsequently increases for injections in which ligand is in excess. Figure 3C plots this linear relationship between k_obs and unbound reactant concentration.

Figure 3.

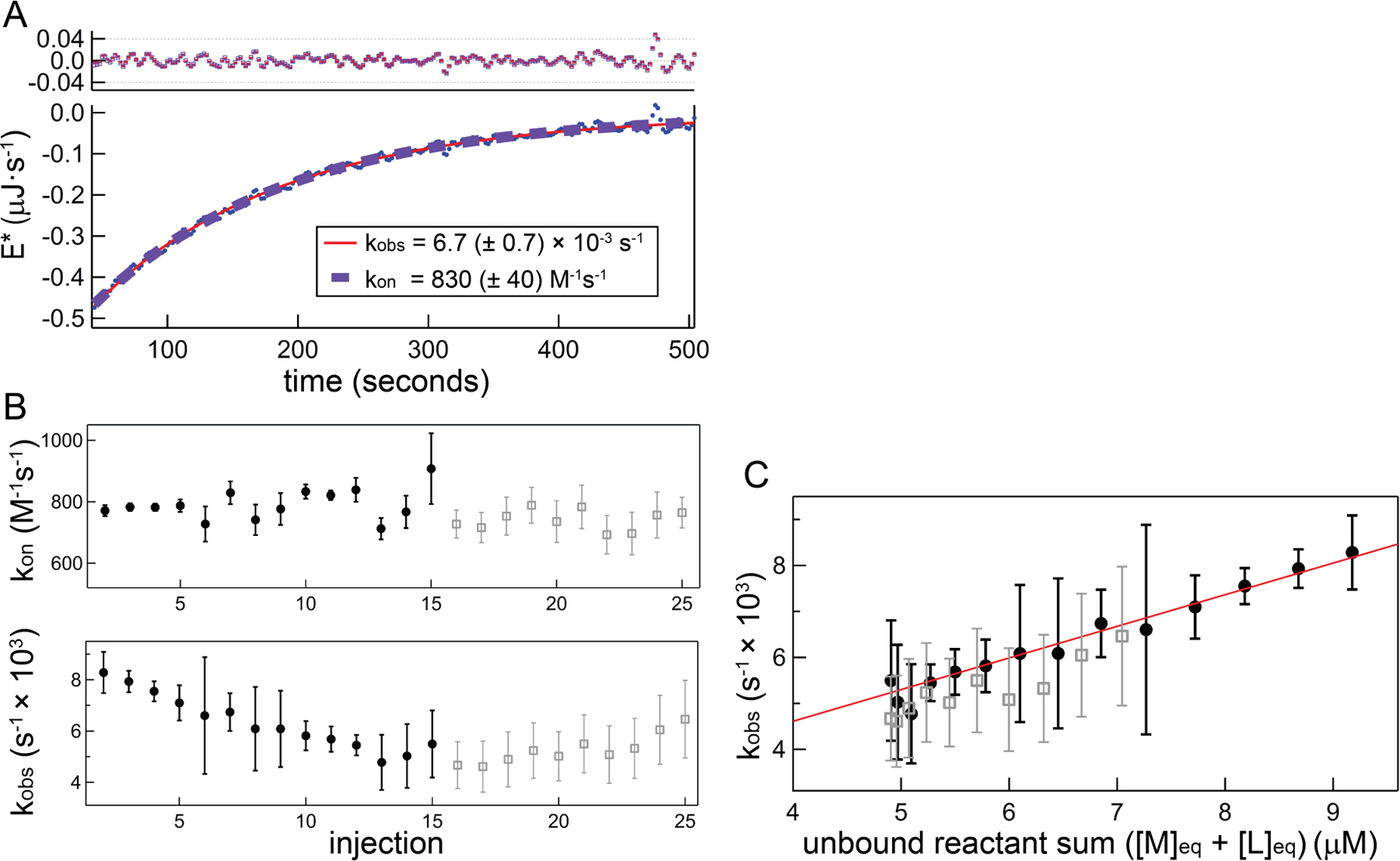
Demonstration and comparison of kinetics analysis using a general equation and the near-equilibrium approximation approach using the same data in Figure 2. A) Main plot: deconvolved data within fitting region (blue circles) and fits using the general equation set (red solid curve) and near-equilibrium approach exponential target function (purple dashed curve). Top plot: corresponding fit residuals. B) Top panel: k_on determinations for each injection using the general approach; bottom panel: composite rate constant (k_obs) determinations using the near-equilibrium approach. In both panels closed black circles show data from the first half of the titration ([L]_tot < [M]_tot), which correspond to the analyzed dataset. For illustration purposes only, open gray squares show the remaining data up to injection 25 ([L]_tot/[M]_tot ~ 2). Error bars represent only the uncertainty that is uncorrelated with other injections (fit parameter variance and baseline uncertainty; termed ‘injection-level uncertainty’ in Section 4.2.3) C) k_obs from near-equilibrium analysis plotted against the free RNA concentration. A linear fit (closed circle data only) yields k_on = 730 (± 110) M⁻¹s⁻¹ from the slope, and from the intercept k_off = 1.6 ± 0.8 × 10⁻³s⁻¹

Demonstration of linearity in k_obs versus ([M]_eq + [L]_eq), as seen in Figure 3C, is necessary for validation of the near-equilibrium approach. To confirm this linearity we examined a more extended range of k_obs by performing a suite of titrations using both higher and lower RNA concentrations (Figure 4). Figure 4A displays k_obs data obtained as described in Figure 3, using the same experimental preparation with [M]_init equal to 5 or 20 µM, in addition to the 10 µM dataset. Plots of k_obs are parallel within error and are nearly completely collinear with the exception being the offset in the 20 µM dataset; a 10% increase in the K_d employed in the 20 µM dataset largely alleviates this discrepancy (Figure 4 inset). Uncertainty in the K_d should be included in a complete error analysis and our implementation of this factor is discussed more fully in Section 4.2.3. Table 2 lists the linear regression parameters (k_on and k_off) obtained from each experiment, along with the dissociation constant and kinetic data determined using the general method.

Figure 4.

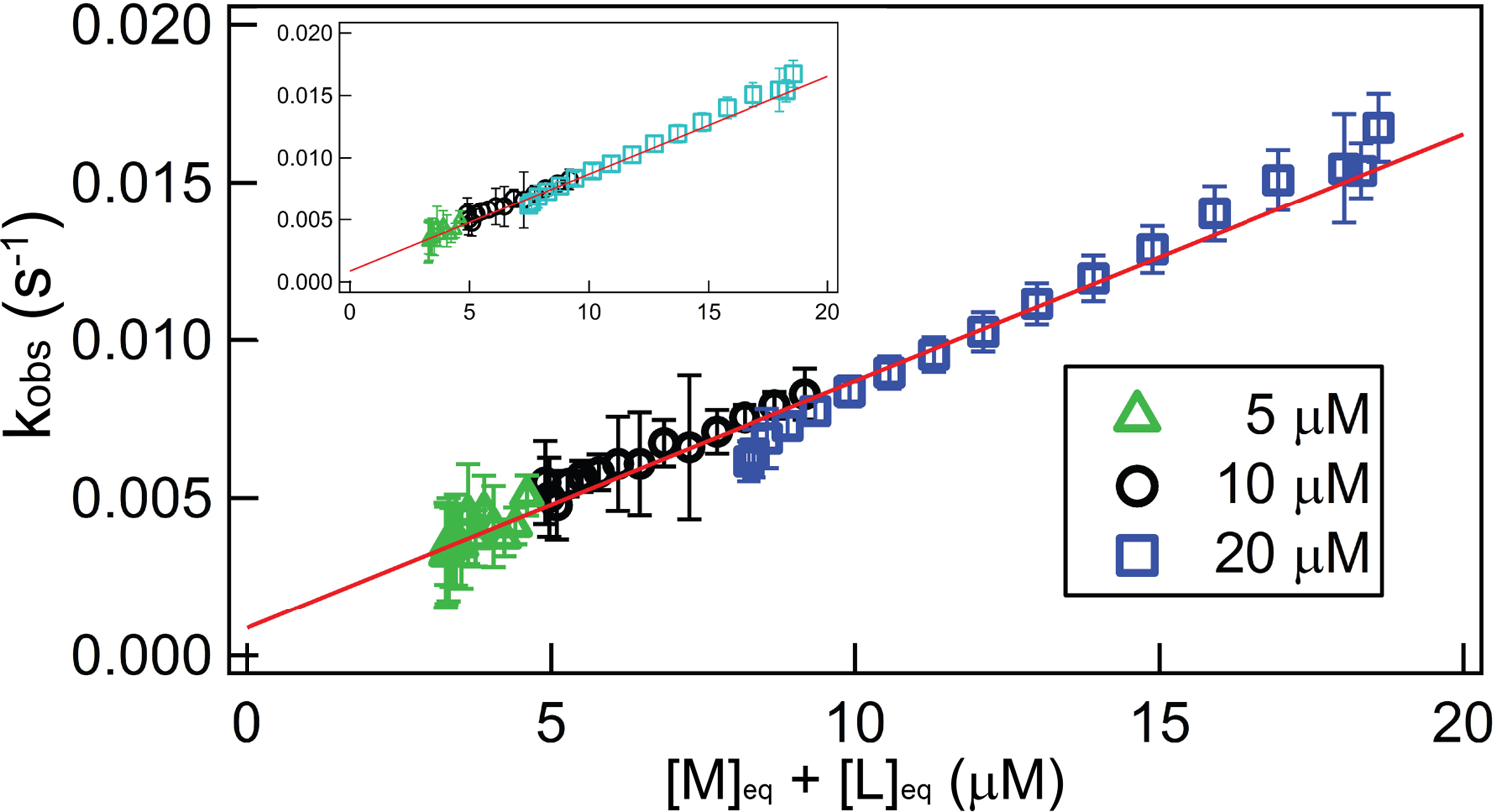
Demonstration of consistency in the near-equilibrium approximation, using TT – RR experiments across a range of [M]_init at the experimental condition 0.3 mM MgCl₂, 30 °C. Main figure: plot of best-fit k_obs against the total unbound RNA concentration ([M]_eq + [L]_eq) for a set of titrations in which the starting cell concentration of a macromolecule, M (RR in this case), was varied and titrated with its ligand, L (TT). For all experiments, the syringe [TT] is 171 µM; green triangles, black circles, and blue squares reflect separate experiments in which [M]_init is 5 µM, 10 µM, or 20 µM, respectively. The red trendline is the result of a global, linear fit; results from the individual datasets are provided in Table 2. The inset figure plots the same data except that the plot for the 20 µM dataset (cyan) employed a K_d that is decreased by 10% over its best-fit value.

Table 2.

Concentration-Dependent Near-Equilibrium Test for TT – RR experiments in 0.3 mM MgCl₂, 30 °C

Dataset(s)	Kd (nM)	Near-Equilibrium Approximation				General Method
		kon (M−1s−1)		koff (s−1) × 10−5		kon (M−1s−1)		kon·Kd (s−1) × 10−5
[M]init = 5 µM RR	900 (± 400)	930	{± 580} [± 630] (± 640)	30	{± 220} [± 240] (± 250)	790	{± 40} [± 190] (± 190)	71	{± 32} [± 36] (± 36)
[M]init = 10 µM RR	910 (± 80)	730	{± 110} [± 180] (± 180)	160	{± 80} [± 110] (± 110)	790	{± 10} [± 150] (± 150)	72	{± 6} [± 15] (± 15)
[M]init = 20 µM RR	1300 (± 200)	940	{± 50} [± 170] (± 170)	−110	{± 60} [± 160] (± 160)	750	{± 10} [± 120] (± 120)	99	{± 10} [± 19] (± 19)
avg (plotted)	1000 (± 200)	840	(± 140)	68	(± 89)	770	(± 80)	84	(± 52)
avg (all)	2000 (± 100)	710	(± 90)	15	(± 65)	470	(± 30)	96	(± 7)

{} includes all injection-level uncertainty terms

[] includes all injection-level and experiment-level uncertainty

() includes all uncertainty contributions

To further test methodology, we also performed a similar set of experiments in a solution containing 200 mM KCl at 25 °C (Figure 5), where K_d is 360 nM. Relatively fast association in this condition means accuracy in the deconvolution procedure is critical, because its effect ranges from relatively minor at the lowest end of the RNA concentration ([M]_init = 4 µM), to much more significant at the upper end ([M]_init = 16 µM). Figure 5 provides representative injections corresponding to these two conditions, for which the deconvolution affects a 20% (Figure 5B) or up to a 70% (Figure 5C) increase in the measured rate constant relative to the raw power trace. The relative collinearity in Figure 5A demonstrates a viable deconvolution procedure.

Figure 5.

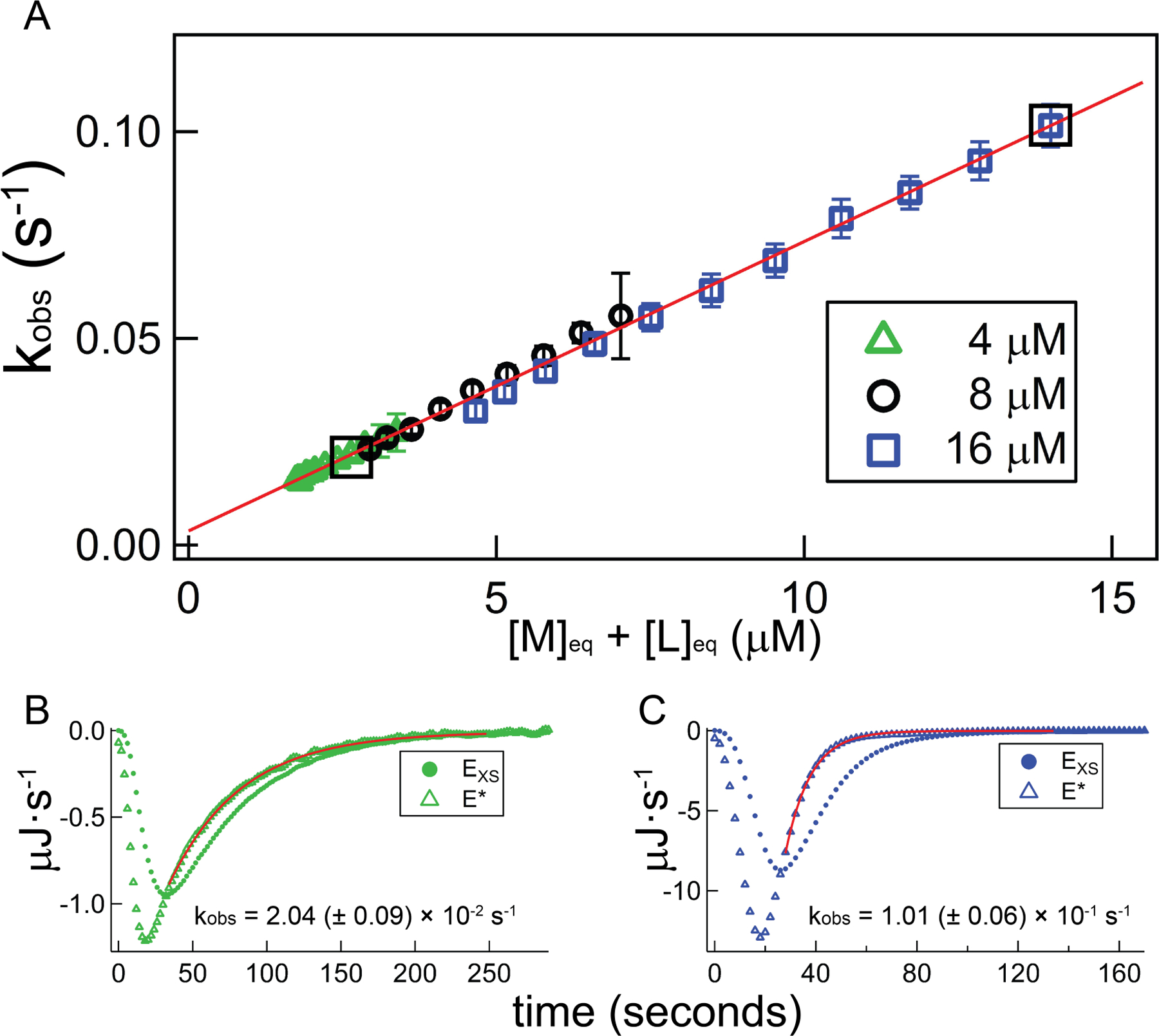
Demonstration of consistency in the near-equilibrium approximation at the upper end of the calorimetry-accessible kinetics window, using TT – RR experiments across a range of [M]_init at the experimental condition 200 mM KCl, 25 °C. A) Plot of best-fit k_obs against unbound RNA for a set of TT – RR titrations in which [M]_init was varied. For all experiments, the syringe ligand (TT) concentration is 240 µM; green triangles, black circles, and blue squares reflect separate experiments in which the starting cell concentration of RR ([M]_init.) is 4 µM, 8 µM, or 16 µM, respectively. The red trendline is the result of a global, linear fit; results from the individual datasets are provided in Table 2. Bottom panels: demonstration of increasing importance of deconvolution for fast association kinetics. Plots depict power traces before (E_XS; closed circles) and after (E*; open triangles) deconvolution using the 6^th injection from the 4 µM dataset (Panel B) and the 2^nd injection from the 16 µM dataset (Panel C) as examples. Red curves plot best-fit exponential functions and fit intervals, and associated composite rate constants (k_obs) are listed. The listed uncertainties reflect only injection-level sources (see 4.2.3). Boxed data points in Panel A correspond to the injections displayed in Panels B and C.

Table 3 lists linear regression parameters corresponding to the k_obs vs free reactants plots in Figure 5. The extracted slopes are similar and in agreement with the k_on values obtained using the general approach, while the intercepts reflecting k_off are inconsistent and exhibit large uncertainties. Encouragingly however, the lowest concentration dataset, which requires the shortest extrapolation and therefore exhibits the smallest confidence interval, is within the injection-level uncertainty band (see Section 4.2.3) of the determinations using the general approach.

Table 3.

Concentration-Dependent Near-Equilibrium Test for TT-RR experiments in 200 mM KCl, 25 °C

Dataset(s)	Kd (nM)	Near-Equilibrium Approximation				General Method
		kon (M−1s−1)		koff (s−1) × 10−5		kon (M−1s−1)		kon·Kd (s−1) × 10−5
[M]init = 4 µM RR	250 (± 60)	7300	{± 700} [± 1700] (± 1800)	280	{± 140} [± 360] (± 360)	7300	{± 100} [± 1200] (± 1200)	180	{± 50} [± 60] (± 60)
[M]init = 8 µM RR	300 (± 20)	8100	{± 500} [± 1400] (± 1900)	–10	{± 210} [± 460] (± 560)	7000	{± 100} [± 1000] (± 1100)	210	{± 10} [± 30] (± 40)
[M]init = 16 µM RR	400 (± 20)	7400	{± 300} [± 1100] (± 2300)	–110	{± 260} [± 580] (± 960)	6800	{± 100} [± 700] (± 1500)	270	{± 10} [± 30] (± 60)
avg (plotted)	360 (± 10)	7600	(± 1500)	100	(± 450)	6900	(± 900)	250	(± 30)

{} includes all injection-level uncertainty terms

[] includes all injection-level and experiment-level uncertainty

() includes all uncertainty contributions

We compared average kinetic parameters determined via the general and near-equilibrium approaches in conditions where both kinetics and affinity measurements are robust (most experiments with c < 200; Table 4). Examining the data according to the average titration c parameter value at that condition is instructive; for c < 43, k_on and k_off measurements generally overlap each other within their confidence intervals (although the uncertainty levels are much higher using the near-equilibrium approach, particularly for k_off). This internal consistency corroborates the viability of either approach.

Table 4.

Comparison of kinetic parameters for all TT-RR datasets with c < 200 and k_on·[M]_init < 0.14

ca	kon[M]init (s−1)b	Kd (nM)	Near-Equilibrium Approximation		General Method		Conditions (No. Replicates)
			kon (M−1s−1)	koff (s−1) × 10−5	kon (M−1s−1)	koff = kon·Kd (s−1) × 10−5
3	0.011	2000 (± 100)	1500 (± 2200)	190 (± 740)	1400 (± 100)	280 (± 30)	0.3 mM MgCl2, 50 mM KCl, 30 °C (4)
4	0.055	1700 (± 100)	6700 (± 2200)	1400 (± 900)	7100 (± 1300)	1200 (± 200)	200 mM NaCl, 30 °C (4)
4	0.019	2100 (± 100)	2400 (± 600)	390 (± 410)	2200 (± 200)	480 (± 40)	150 mM KCl, 25 °C (4)
5	0.007	2100 (± 100)	820 (± 210)	230 (± 130)	690 (± 50)	140 (± 10)	0.3 mM MgCl2, 20 mM KCl, 30 °C (7)
6	0.006	1800 (± 100)	440 (± 120)	83 (± 56)	560 (± 40)	100 (± 10)	100 mM KCl, 15 °C (6)
7	0.050	1100 (± 100)	6900 (± 1400)	620 (± 420)	6500 (± 800)	720 (± 90)	200 mM KCl, 30 °C (11)
8	0.022	1300 (± 100)	3300 (± 600)	−260 (± 340)	1800 (± 200)	230 (± 20)	0.3 mM MgCl2, 80 mM KCl, 30 °C (3)
9	0.008	2000 (± 100)	710 (± 90)	15 (± 65)	470 (± 30)	100 (± 10)	0.3 mM MgCl2, 30 °C (8)
11	0.011	1000 (± 100)	860 (± 210)	340 (± 110)	1100 (± 200)	110 (± 20)	0.3 mM MnCl2, 30 °C (2)
16	0.020	550 (± 20)	2300 (± 300)	250 (± 110)	2400 (± 200)	130 (± 10)	150 mM KCl, 20 °C (3)
17	0.119	440 (± 10)	16,000 (± 5000)	790 (± 980)	16,000 (± 4000)	710 (± 180)	250 mM NaCl, 30 °C (4)
21	0.092	350 (± 10)	13,000 (± 4000)	310 (± 720)	12,000 (± 3000)	440 (± 90)	250 mM KCl, 30 °C (6)
22	0074	490 (± 10)	9100 (± 2300)	340 (± 530)	8600 (± 1600)	420 (± 80)	1.0 mM MgCl2, 40 °C (5)
23	0.015	420 (± 20)	1800 (± 100)	85 (± 51)	1700 (± 100)	69 (± 6)	0.5 mM MgCl2, 30 °C (6)
23	0.005	630 (± 70)	490 (± 60)	61 (± 26)	500 (± 70)	32 (± 6)	0.3 mM MgCl2, 20 mM KCl, 20 °C (2)
27	0.064	360 (± 10)	7600 (± 1500)	100 (± 500)	6900 (± 900)	260 (± 30)	200 mM KCl, 25 °C (3)
29	0.015	360 (± 20)	1500 (± 200)	100 (± 80)	1500 (± 200)	52 (± 8)	0.2 mM MgCl2, 80 mM KCl, 20 °C (2)
36	0.005	560 (± 30)	340 (± 40)	22 (± 32)	240 (± 30)	13 (± 2)	0.3 mM MgCl2, 20 °C (3)
43	0.027	180 (± 50)	3400 (± 400)	170 (± 80)	3500 (± 300)	60 (± 5)	0.7 mM MgCl2, 30 °C (8)
45	0.056	200 (± 10)	7000 (± 1100)	300 (± 210)	7100 (± 800)	140 (± 20)	1mm MgCl2, 35 °C (7)
51	0.022	180 (± 10)	2300 (± 200)	230 (± 60)	2500 (± 200)	45 (± 4)	150 mM KCl, 15 °C (4)
51	0.038	190 (± 10)	4000 (± 500)	190 (± 120)	4000 (± 400)	70 (± 8)	0.7 mM MgCl2, 20 mM KCl, 30 °C (4)
55	0.009	170 (± 10)	850 (± 100)	180 (± 40)	1000 (± 100)	17 (± 2)	0.5 mM MgCl2, 20 °C (6)
60	0.006	190 (± 10)	540 (± 60)	94 (± 29)	600 (± 70)	12 (± 1)	100 mM KCl, 5 °C (5)
62	0.008	110 (± 10)	1100 (± 100)	89 (± 32)	1100 (± 200)	12 (± 3)	0.5 mM MgCl2, 20 mM KCl, 20 °C (2)
62	0.021	160 (± 10)	2000 (± 200)	160 (± 60)	2100 (± 300)	33 (± 4)	0.3 mM MgCl2, 80 mM KCl, 20 °C (2)
76	0.067	130 (± 10)	6400 (± 1100)	290 (± 230)	6600 (± 800)	87 (± 11)	200 mM KCl, 20 °C (3)
83	0.039	120 (± 10)	3800 (± 500)	210 (± 150)	3900 (± 500)	48 (± 6)	0.3 mM MgCl2, 12 0mM KCl, 20 °C (2)
97	0.062	87 (± 2)	7100 (± 1100)	240 (± 200)	7200 (± 700)	63 (± 7)	1.0 mM MgCl2, 20 mM KCl, 30 °C (4)
130	0.013	78 (± 4)	1200 (± 100)	130 (± 30)	1300 (± 200)	10 (± 2)	0.2 mM MgCl2, 80 mM KCl, 10 °C (2)
160	0.025	62 (± 4)	2400 (± 300)	160 (± 60)	2500 (± 300)	16 (± 2)	0.7 mM MgCl2, 20 °C (2)
210	0.048	44 (± 2)	5600 (± 700)	250 (± 100)	6000 (± 700)	26 (± 3)	200 mM NaCl, 10 °C (2)

^ac: average value of [M]_init/K_d for experiments conducted at this condition

^baverage ‘k-parameter’ value for experiments at this condition

For c > 40, the agreement between approaches is maintained for k_on, but not for k_off. Thus, apparently in practice, determination of k_on (but not k_off) may still be conducted according to the near-equilibrium approximation for at least some experiments where 40 < c ≤ 200. This may simply relate to heavier weighting of the initial injections in our implementation, such that case (1), as referred to in Section 2.2.2, is effectively observed. Thus, while this finding is interesting, it may not hold for processes with rates closer to the upper limit of accessibility (see Sections 3.5 and 4.3), and it potentially might not apply at all in another adaptation. More work is required to determine, for each thermodynamic window, the molar ratio at which the near-equilibrium approximation is no longer valid, as well as the amount of data required to accurately determine k_on and k_off.

We add two additional comments on Tables 2 – 4. First, in assembling this method summary, we identified a coding error (the calculation of λ_t=0 prior to kinetics analysis was off by a factor of 2) that affected a uniform 10% underestimate of k_on in our previous work. Fortunately, this in no way affects any conclusions from that work, since the temperature-dependence of k_on and k_off are completely unaffected. Second, the uncertainties reported for K_d simply reflect weighted averaging of the fitting uncertainty. Here we are more interested in rigorous error analysis for the kinetic quantities, so we have not utilized our typical bootstrap approach, in part to simplify the presentation of non-kinetic quantities.

3.4. Maximum accessible rate constant

Kinetic analyses for processes with association rates at the upper limit of the detectable range (composite rate constant → k_ITC) are characterized by significantly increased uncertainty levels. This increased uncertainty is primarily due largely to the increased sensitivity of the measured rate constant to both the Laplace Transform procedure (Equation 1), as well as the baseline parameters employed during fitting.

Figure 6 illustrates the importance of an accurate Laplace Transform, this time using as an example the binding between the catalytic domain of the human SET domain lysine methyltransferase SET7/9 (residues 110–366) and its substrate S-adenosylmethionine (AdoMet) (Horowitz, Yesselman, Al-Hashimi, & Trievel, 2011). A representative titration is shown in Figure 6A. The rate of complex formation is close to the upper limit of the technique (see below), as shown by the fact that only near the middle of the titration do injections evidence a slightly slowed equilibration process. The combination of slightly reduced reactant concentration ([M]_init = 6.0 µM in the example), high data quality, and extended baseline collected following each injection and decay as in these examples, is crucial in examining these upper-limit scenarios.

Figure 6.

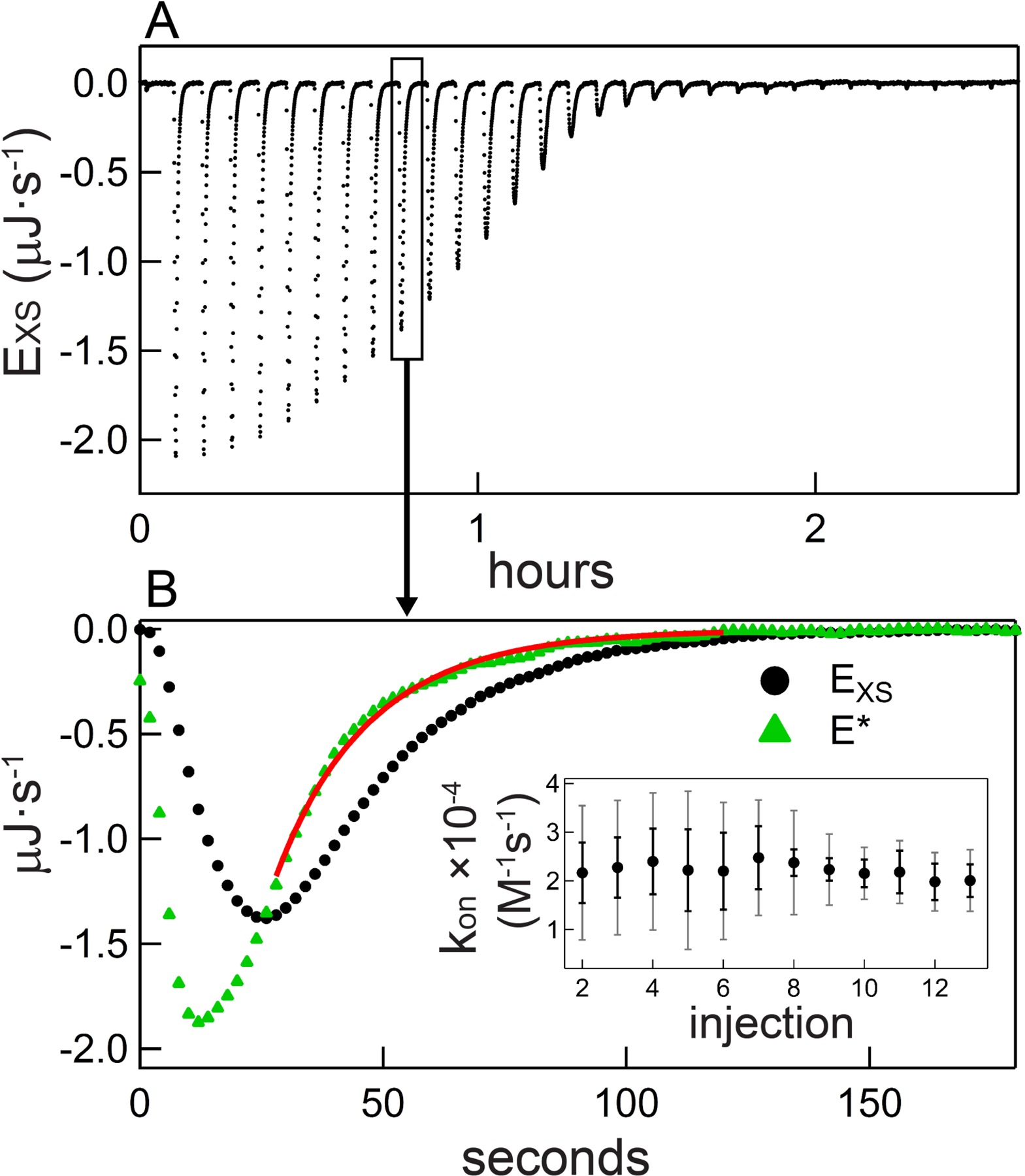
Characterization of the kinetics of SET7/9 – AdoMet binding. A) Thermogram following baseline subtraction for an experiment in which 6.0 µM SET7/9 (residues 110–366) was titrated with 70 µM AdoMet. B) Main figure: injection 10 raw (black circles) and deconvolved (green triangles) power trace. The red curve denotes the graphical result of the general equation set regression procedure as well as the fitting interval. Inset: summary of all k_on values obtained from this titration, with error bars representing uncertainty from injection-level sources (black error bars) or from all sources (gray error bars).

To demonstrate the effect of the deconvolution procedure, Figure 6B displays power signals pre- and post-deconvolution for the representative example 10^th injection. Clearly in this fast-associating condition, with a half-time of ~13 seconds, an accurate deconvolution procedure is essential to robust rate constant measurement. Using the transformed signal, a value k_on = 22,000 M⁻¹s⁻¹ is obtained. Accurate transformation is even more crucial for injections earlier in the titration; for example, the decay following injection 2 exhibits a half-time of approximately 6 seconds (shorter than the example in 6C). In our error analysis, we utilize an empirically-calculated 20% uncertainty in k_ITC (0.067 s⁻¹ < kITC < 0.1 s⁻¹; error analysis is covered in Section 4.2.3).

There is some systematic error in the fit describing the transformed data (Figure 6B), indicating the kinetics are approaching or slightly exceeding applicability. On the other hand, the overall picture of the dataset is mildly encouraging: over the course of the AdoMet-SET7/9 titration, the measured k_on values are consistent (Figure 6B inset). A grossly-incorrect deconvolution procedure might over- or under-correct the early, faster-relaxing injection data, thus manifesting in an injection-dependent k_on (not shown). For comparison, the displayed error bars reflect either the per-injection uncertainty or the total uncertainty for a single measurement, which includes uncertainty propagated through the deconvolution (see Section 4.2.3.3). These large, injection-dependent error bars underscore the massive impact of the deconvolution procedure as well as the importance of the quantity [L]_tot/[M]_tot on the tractability of kinetics analysis for fast processes.

To estimate the accuracy of our measurements at the upper limit of kinetics accessibility, we utilized the generally-observed logarithmic relationship between thermodynamic/kinetic quantities and salt concentration for nucleic acid processes (Record, Zhang, & Anderson, 1998). We predicted k_on for some of the experimental scenarios that lie on the fringe of accessibility; the results are plotted in Figure 7 along with the actual values calculated using our general method. The dotted lines reflect extrapolations from the slower, high-confidence measurements to the conditions exhibiting fast association. Every calculation underestimates the predicted value to a remarkably similar extent, with the average underestimate being 25%. In all cases the error is just outside of that estimated assuming a 20% uncertainty in k_ITC. Curvature in such plots, especially in the mixed salt experiment, is not unprecedented but the consistency of the underestimate is rather convincing. Later, based on our previous observation that processes exhibiting k_on ≤ 8000 M⁻¹s⁻¹ (in more general framing, k_on·[M]_init ≤ 0.08 s⁻¹, comparable to k_ITC) showed no such underestimate for the fastest k_on in a trend (Vander Meulen & Butcher, 2012), we infer a logarithmic systematic uncertainty inherent in our kinetics application throughout the maximal rate regime (i.e., k_ITC < k_on·[M]_init < method maximum).

Figure 7.

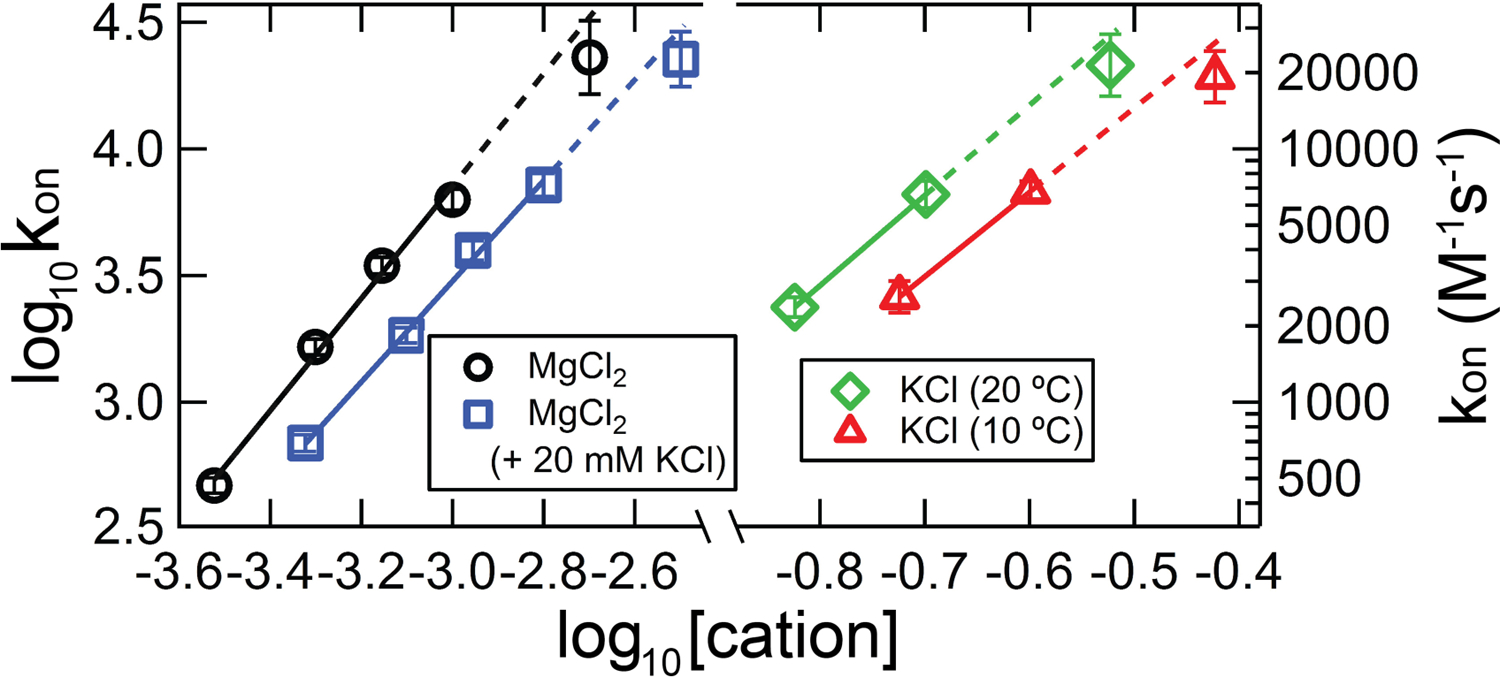
k_on measurements and predictions from extrapolation of the [salt]-dependence, for TT – RR experiments exhibiting kinetics at the upper limit of accessibility by titration calorimetry. Black circles, experiments conducted in solutions containing varying concentrations of MgCl₂ at 30 °C. Blue squares, experiments conducted in varying [MgCl₂] and 20 mM KCl at 30 °C. Green diamonds and red triangles, experiments conducted in 200 mM KCl at 20 °C or 10 °C, respectively. The solid lines represent k_on from titration experiments within the validated region (k_on·[M]_init < k_ITC), and the dotted lines extend those fits to the test data. (For visualization purposes, the blue and red datasets have been shifted to the right by 0.2 and 0.1 log units, respectively, such that they do not overlie the adjacent datasets.)

We examined correcting for this underestimate by simply decreasing k_ITC. A correction would place the k_ITC value would be something between 0.067 s⁻¹ (the minimum value in our error analysis routine) and 0.05 s⁻¹ (which results in a >100% overestimate of k_on in the Figure 7 data). However, it seems at least equally probable that we are approaching a limit where various approximations become invalid, the most important being the first-order approximation of the instrument response. Both factors may be in play, but for the purpose of this work, we use the prior-mentioned k_ITC of 0.08 s⁻¹. This value was determined simply through analysis of an injection under conditions where association is effectively instantaneous, so it and the associated error analysis can be easily transferred to different instrumentation.

3.5. Guidelines for kinetic and thermodynamic analysis

For an association process with appropriate kinetics, time-resolved analysis of ITC binding data significantly enrich its biophysical characterization (Burnouf et al., 2012; Egawa et al., 2007; Vander Meulen & Butcher, 2012). Figure 8 provides an example map of ITC-measurable thermodynamic and kinetic parameters as a function of k_on and k_off. Figure 8 was generated according to the instrument specifications (e.g., VP-ITC with time constant 12.5 seconds) and typical experimental conditions (e.g., [M]_init = 10 µM) employed in our TT – RR study (Vander Meulen & Butcher, 2012).

Figure 8.

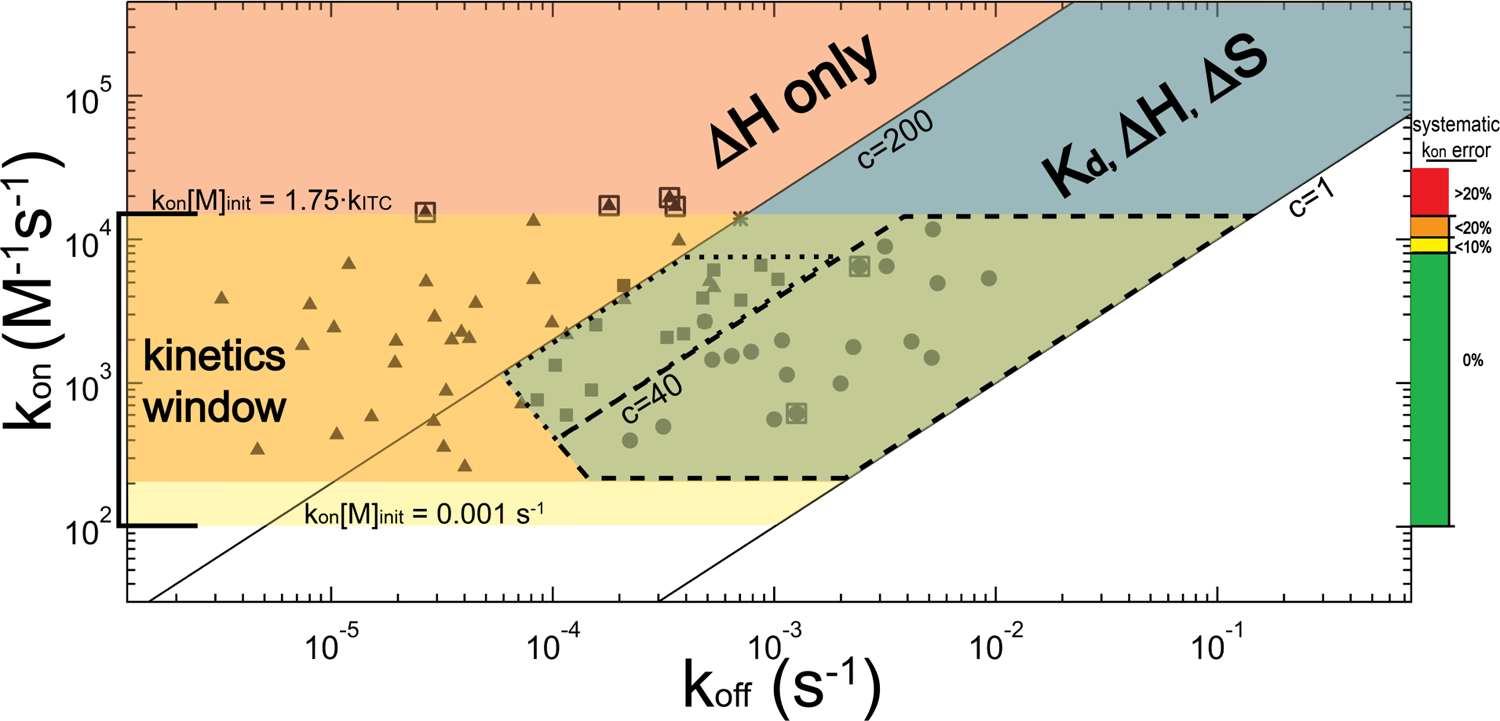
Relationship between the kinetics (k_on and k_off) and the attainable thermodynamic and kinetic parameters by ITC, illustrated for a titration experiment conducted with [M]_init = 10 µM and instrument time constant of 12.5 seconds. The three main regions for consideration are denoted in blue, salmon and yellow; corresponding overlapping regions are colored accordingly. The blue diagonal band represents the optimal thermodynamics regime for ITC in which 1 ≤ c ≤ 200, and for which the full complement of thermodynamic information (K_d, ΔH and subsequently ΔS) can be obtained. The salmon-colored region above the c = 200 line reflects the tight-binding regime for which, thermodynamically, only ΔH can be obtained. The horizontal yellow band represents the kinetics regime (1 × 10² M⁻¹s⁻¹ < k_on ≤ 1.4 × 10⁴ M⁻¹s⁻¹). Within a subrange of the overlap of the kinetic regime with the optimal thermodynamic regime (largely consisting of 1 ≤ c ≤ 40) is the near-equilibrium approximation regime, marked by dashed lines, for which this approximation is valid over the entirety of the titration. A dotted line encloses an adjacent region where, in our experience, the near-equilibrium approximation yields k_on values consistent with the general method. Closed symbols denote the regions within this map that we have examined using TT – RR, and the asterisk reflects the AdoMet-SET7/9 experiment. Symbol positions are “concentration-adjusted” such that they reflect the rate constants that would exhibit the experimentally-observed kinetics if all experiments were conducted at [M]_init = 10 µM. TT – RR closed circles and squares represent average kinetic parameters obtained at an experimental condition where k_on and the full complement of thermodynamic information were obtained (corresponding data are provided in Table 4). For data represented as circles (c < 40) k_off was also obtained independently of the K_d using the near-equilibrium approximation. Triangles represent conditions where we were able to obtain k_on, but only ΔH in terms of thermodynamics. For these experiments, a K_d extrapolated from the [salt]- or temperature-dependence for TT – RR association was employed in the general equation; alternatively, for experiments in which c > 200, the tight-binding approximation could have been used to avoid this extrapolation requirement (additionally ∂k_on/∂K_d is rather negligible if c > 200 so precise knowledge of K_d is not required). The k_off for these datasets (as well as that of AdoMet-SET7/9), however, is known only as accurately as is the K_d and thus the associated uncertainty would be quite high in some cases. Note the truncation at the lower left of the optimal thermodynamics regime: this denotes a region where slow kinetics prevented our accurate measurement of K_d. Boxed triangles represent data used as maximum rate constant test-cases in Figure 7, and boxed circles were used as near-equilibrium test-cases in Figures 4 and 5. The colored scale and labels on the right chart our inferred deconvolution-introduced error: for k_on·[M]_init < 0.14, the error should be less than 20% and we set this as the absolute upper-limit for kinetics analysis.

For a VP-ITC with [M]_init = 10 µM, kinetic analysis using a titration approach requires that 1 × 10² M⁻¹s⁻¹ ≤ k_on ≤ 1.4 × 10⁴ M⁻¹s⁻¹, though in our application exceeding 1.1 × 10⁴ M⁻¹s⁻¹ results in error of at least 10%. Above the upper limit of 1.4 × 10⁴ M⁻¹s⁻¹, we have evidence that the error is even larger than accounted for in our error analysis approach. Systematic deconvolution error inferred from our previous work and the results in Figure 7 are plotted (and color-coded) on the right.

On the low end, if the rate constant is smaller than 1 × 10² M⁻¹s⁻¹, separation of the signal decay from baseline power (i.e., signal-to-noise) becomes problematic. We have not examined data at or below the lower bound, but we suspect a k_on one-half as large as the smallest we have examined is reasonable for a typical scenario with [M]_init = 10µM and |ΔH| ≥ 10 kcal/mol. The figure also highlights the near-equilibrium region (dashed lines) in which, throughout the titration, the decay is exponential with composite rate constant k_obs (Equation 10), allowing direct determination of both k_on and k_off.

Figure 8 overlays the kinetic data obtainable by ITC with an analogous plot illustrating the accessibility to traditional thermodynamic parameters, assuming a single-step reaction mechanism so that K_d = k_off/k_on. The c parameter reveals the thermodynamic parameters that can be measured in an ITC experiment. For measurement of ΔH, c must be minimally equal to one; in Figure 8 this equates to K_d ≤ 10 µM. Measurement of K_d is additionally constrained by a lower limit; in theory this constraint is c ≤ 1000 (Wiseman et al., 1989), though we adhere to an upper limit of c = 200. For c > 200, K_d measurement relies on a small fraction of the titration data, meaning it may similarly rely on a small fraction of the M and/or L population. Thus, the map in Figure 8 reflects a general case where sample homogeneity in all manners cannot be verified to ≥ 99%, so the upper bound of accessibility is set to K_d ≥ 50 nM, reflecting c ≤ 200.

There are two additional regions to note in the figure. Between the green, slightly clipped parallelogram defining the near-equilibrium region and the leftmost band defining the K_d-accessible window (c = 200) is a region where we have demonstrated (Table 4) consistency in applying the near-equilibrium approach to determine k_on (dotted lines; 40 < c ≤ 200). This region is truncated by k_on·[M]_init ≤ 0.07, because we did not collect data above this point and have some reason to doubt its generality outside of it. We also mention here the region defined by extension of the line segment clipping the aforementioned parallelogram to the c = 200 line, below which slow kinetics can sufficiently influence peak integration so that K_d measurements were not possible in our previous work (Vander Meulen & Butcher, 2012).

For an instrument with a similar time constant, Figure 8 can easily be adapted to an experiment using a different [M]_init by noting they are directly related to the actual forward and reverse rates. A change in concentration increases the forward rate while having no effect on the reverse rate. Therefore (at least until signal-to-noise changes significantly), starting concentrations less than 10 µM lead to a simple, corresponding upward shift in all of the windows. For example [M]_init = 5 µM sets the upper limit of kinetics detection at 2.8 × 10⁴ M⁻¹s⁻¹ and the lower limit 2 × 10² M⁻¹s⁻¹. An analog to the c parameter can be conceptualized for kinetics determination. In this respect, using a VP-ITC, kinetics are accessible as long as 0.001 s⁻¹ ≤ k_on·[M]_init ≤ 0.14 s⁻¹. One would expect that the fastest accessible rates will likely depend on instrumentation simply according to the difference in the instrument rate constant, so that the upper limit would be roughly defined according to k_on·[M]_init ≤ 1.75·k_ITC. Similarly, differences in instrument sensitivity will affect the lower end of the kinetics window.

3.6. Summary and Outlook

We have described here our custom-built approach to extracting kinetics from an ITC titration experiment. Our focus has been describing the processing and error analysis details, and in highlighting the regimes in which different types of kinetics analyses may be performed.

Importantly, the approach described here is programmatically successful at both the upper and lower ends of the defined kinetics window. Yet this is still early in method development, and there are several areas where it might be improved to increase the data quality and reduce the final uncertainty. Here we highlight just two possible changes. We think the most crucial improvement would be integrating the kinetics measurements into a global analysis (Zhao, Piszczek, & Schuck, 2015). Our current application requires thermodynamic analysis followed by individual analysis of each injection, first processing then fitting. Direct linking of factors such as the K_d, effective concentrations, and baseline analysis would likely reduce various contributors to what we refer to as injection-level and experiment-level uncertainties. Another area for improvement lies in the analysis of early time points, the accuracy of which may be improved by incorporating mixing lag as put forth by Dumas and co-workers (Burnouf et al., 2012). Along with better modeling of the instrument response time and functional form (Garcia-Fuentes et al., 1998), if possible, this increased level of sophistication might increase the upper limit of the kinetics window.

4. Method Details

4.1. Materials

Preparation and handling of TT and RR RNA was covered in our previous kinetics work (Vander Meulen & Butcher, 2012). SET7/9 expression and enzymatic synthesis of AdoMet were performed using the methods described in (Horowitz et al., 2011). Thermodynamic quantities were determined as described previously (Vander Meulen, Davis, Foster, Record, & Butcher, 2008). All experiments used a MicroCal VP-ITC, with a high feedback setting and a 2 second filtering time. Injections were generally conducted at 0.5 µL/second. All analysis was performed using Igor Pro 6 and its inbuilt programming environment (Wavemetrics, Inc.).

4.2. Methods

4.2.1. Smoothing

We use boxcar-smoothing at various stages in this method. First, we perform the Laplace Transform after minor smoothing of the power derivative term used in Equation 1 (window size 7, 1 pass). This mild procedure is sufficient to minimize significant fluctuations in the raw data without having any measurable impact on the final measured rate constant. A more significant smoothing procedure (window size 7, 3 passes) is used prior to statistical analysis of an injection and decay (Section 3.2) in order to prevent noise-induced settings artifacts, such as an abbreviated fitting regime. Actual fitting utilizes the former, mildly-smoothed data.

4.2.2. Baseline Selection and Associated Uncertainty

All kinetic functions incorporate a linear and constant term representing the underlying power baseline. An optimal approach to baseline selection uses the post-relaxation baseline period whenever possible to eliminate unnecessary fitting parameters, which carry with them inherent uncertainty that must be taken into account in characterizing k_on or k_obs. This ideal situation is most common for injections exhibiting fast kinetics such that a final baseline is quickly established, or similarly for injections that include a long post-injection (equilibration) period. In these cases, which we classify as “constrained”, those pre-determined baseline parameters are set and held during regression; in other cases, they are floated. Baseline classification is discussed next (subsequent propagation of baseline uncertainty is then discussed in Section 4.2.3).

We classify an injection power trace into one of three baseline groups: “constrained”, “moderately constrained”, and “unconstrained”. These groups correspond to how reliably the baseline underlying the entirety of an injection and subsequent decay to a baseline power trace is described by that ending baseline. This procedure is not theoretically-founded but is instead a set of boundary conditions that is based on a combination of observations of ITC power traces and manual tuning from many representative injections across the range of kinetic regimes. The goal of this procedure is to make use of a well-established baseline wherever possible so that uncertainty is not overemphasized, but in all other cases to accurately reflect the sometimes significant impact uncertainty in the baseline can have on analysis of a kinetics measurement.

To classify a baseline, we first select the final baseline region, which we consider to start at the first (boxcar-smoothed) point that is < 0.5% greater in magnitude than a preliminarily-determined baseline, and to conclude at the last point before the next injection. For the baseline to be considered “constrained”, it must meet the following four conditions: first, the reduced χ² (σ_power = 0.02 µJ·s⁻¹ for data collected using our settings, unless a dataset is particularly noisy) must be less than 1.5; second, F-tests for an additional variable with either an exponential or a 2^nd-degree polynomial must be less than 2 and 3, respectively; third, extrapolation of the candidate baseline back to time zero must result in an offset not greater than either 1% of the amplitude of the peak following injection or 0.01 µJ·s⁻¹; fourth, the baseline region must consist of at least 60 seconds. For a baseline to be considered “moderately constrained”, it must meet the first condition above and a second condition that the baseline region time period is at least twice the decay half-time. Thus in our procedure, we first test for the “constrained” category, then for “moderately constrained”. In either case, if the baseline meets the required conditions, it is classified as such and the procedure is concluded. Otherwise, the baseline start time is advanced to the next data point, and the tests are performed again. When the baseline candidate region is too short for the relevant categorization, the process is aborted with the default “unconstrained” baseline status maintained.

4.2.3. Error Analysis

Sources of rate constant uncertainty fall into three groups, according to their level of correlation: injection-level (σ_k,inj), experiment-level (σ_k,exp), and system-level (σ_k,sys). Uncertainty calculations should consider these in turn and incorporate proper nesting to obtain an accurate estimate of the uncertainty in the final measured kinetic parameters, according to the following equations

$${\sigma }_{\text{k},\text{sys},\text{tot}}^2\approx {\sigma }_{\text{k},\text{sys}}^2+{\sigma }_{\text{k},\text{exp},\text{tot}}^2$$ Equation 11

where σ²_k,sys,tot is the final top-level error, which includes unavoidable system-level uncertainty at a given condition, σ²_k,sys (for our purposes, this is simply uncertainty related to k_ITC), as well as the uncertainty resulting from weighted averaging of the results from each experiment (σ²_k,exp,tot) at this condition.

$${\sigma }_{k,\text{exp},tot}^2\approx {\sigma }_{\text{k},\exp }^2+{\sigma }_{\text{k},\text{inj},\text{tot}}^2$$ Equation 12

Similarly to Equation 11, Equation 12 obtains the uncertainty relevant to a particular experiment or titration according to the contribution from uncertainty correlated at the level of that experiment along with the uncertainty resulting from weighted averaging of the results from each injection (σ²_k,inj,tot) in that experiment.

4.2.3.1. Injection-Level Contributions to Uncertainty

Uncorrelated contributions to the uncertainty in kinetics measurements for each injection are related to random and systematic (i.e., drift) noise, and are classified as ‘fitting’ uncertainty and ‘baseline’ uncertainty. Fitting uncertainty (σ_k,fit) comes directly from the variance in the measured k according to nonlinear regression. Baseline uncertainty results from a lack of knowledge of the true baseline underlying the power trace as discussed in Section 4.2.2. For example, the uncertainty in k due to the slope parameter is estimated using Δk/Δslope in place of ∂k/∂slope, with Δslope being set to an estimated σ_slope (determined as discussed below). In this way the combined injection-level uncertainty is calculated as

$${\sigma }_{k,inj}^2\approx {\sigma }_{\text{k},\text{fit}}^2+\Delta k_{\text{slope}}^2+\Delta k_{\text{intercept}}^2$$ Equation 13

where Δk_slope reports the change in k affected by a one-sigma fluctuation in the baseline slope (Δslope). Subsequently, σ_k,inj,tot is calculated through the weighted averaging of injection data.

Determination of Δk_slope and Δk_intercept for a “constrained” baseline (see Section 4.2.2) can be examined as illustrative. For this baseline scenario, Δslope is set to ± 0.25 × 10⁻⁶ µJ·s⁻². Δk_slope is then determined by the maximum change in k affected by either a positive or negative adjustment of this magnitude in the baseline slope. Similarly, the intercept term (Δk_intercept) is determined by a modulation of the intercept (Δintercept) by ±1% of the injection peak’s maximum magnitude. For this baseline uncertainty analysis (Equation 13), and for the experiment-level discussion below, the covariance terms are negligible.

If the baseline is “moderately constrained”, Δintercept is set to the maximum of 1% of the magnitude of the injection peak and the magnitude of the difference between the baseline’s extrapolated time zero intercept and the actual value of the power trace at time zero. Δslope is the value of the slope at that point in the raw thermogram.

For the “unconstrained” case, Δintercept is set similarly to the moderately constrained case, except that the term relative to the peak maximum is 2% instead of 1%. Δslope is the maximum of the fitted slope value and 2.0 × 10⁻⁶ µJ·s⁻².

4.2.3.2. Experiment-Level Contributions to Uncertainty

Experiment-level contributions are those for which error is correlated among the analyses of every injection in a titration. These include uncertainty in the K_d (ΔK_d) and uncertainty in the macromolecular concentrations ([M]_tot, [L]_tot) (Δconc). Calculation of these uncertainties is conducted similarly to the previous section, and incorporates ΔK_d and Δconc values of ±10%. As an example, the uncertainty due to the K_d (Δk_Kd) is determined by calculating the average k for an experiment using the best-fit K_d, then starting the analysis over using a K_d that is increased by 10%, then again for a decrease of 10%. The final experiment-level uncertainty is given by

$${\sigma }_{k,\exp }^2\approx \Delta k_{\text{Kd}}^2+\Delta k_{\text{conc}}^2+\Delta k_{\text{k},\text{inj},\text{tot}}^2$$ Equation 14

Subsequently, σ_k,exp,tot is calculated through the weighted averaging of all experiments at that condition.

4.2.3.3. System-Level Contributions to Uncertainty

Uncertainty in the instrumental rate constant (Δk_ITC) assumes a ± 20% uncertainty (see Section 3.4) and is correlated among all experiments with a given rate constant profile. Most simply, this term is included by propagating the average affected uncertainty (Δk_kITC) with the uncertainty resulting from the weighted average of the final experiment-level uncertainty calculation.

$${\sigma }_{\text{k},\text{sys},\text{tot}}^2\approx \Delta k_{\text{kITC}}^2+{\sigma }_{\text{k},\exp ,\text{tot}}^2$$ Equation 15

For processes with k_on·[M]_init > 0.11, Δk_kITC may be insufficient, and the systematic error plotted alongside Figure 8 could be used instead.

4.3. Example Uncertainties

Figure 9 shows an estimated uncertainty contributed by various error sources throughout titrations we performed at upper and lower limit of accessibility. Each data point in the figure represents the estimated fractional uncertainty in k_on contributed by each potential source of error for a single injection. As discussed above, these error sources contribute at different points in the analysis so that, for example, uncertainty due to noisy data can be minimized by averaging many injections in a titration. Similarly, uncertainty due to potential error in a K_d measurement can be reduced through averaging a number of experiments. However, for experiments with observed rate constants near k_ITC, appreciable uncertainty is unavoidably significant. The data points in the figure are an overlay of data from several experiments at a particular condition as described in the legends.

Figure 9.

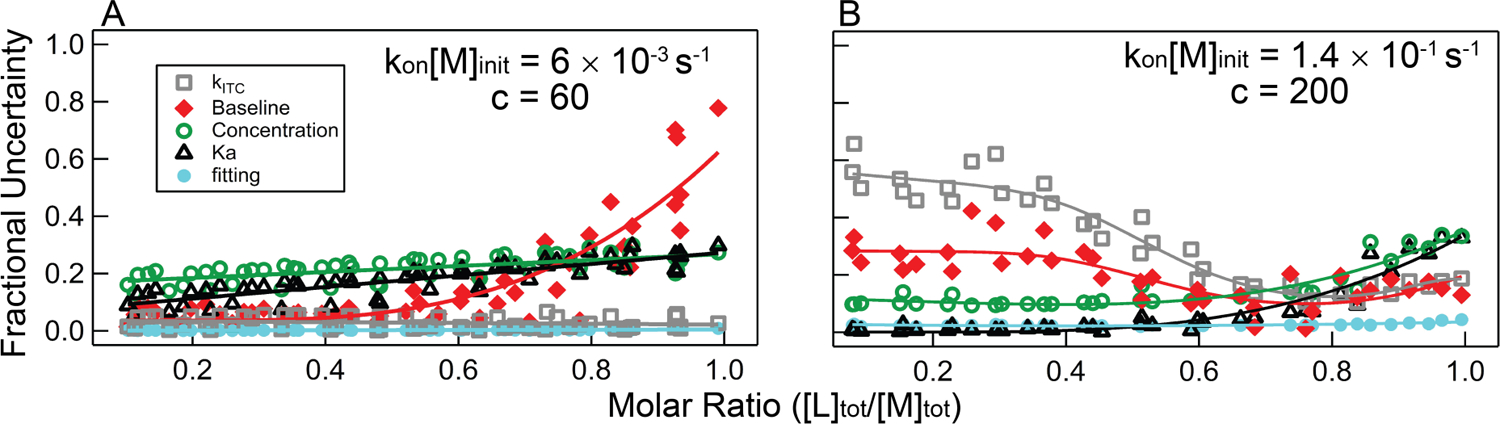
Estimated fractional uncertainty for k_on measurements at the (A) lower and (B) upper end of accessibility. A) Summary data of five experiments collected for TT – RR binding at 5 °C, 100 mM KCl, where the average forward rate constant is 600 M⁻¹s⁻¹. In each experiment the starting cell concentration was 10 µM, so k_on·[M]_init = 0.006 s⁻¹. B) Summary of data collected for the SET7/9 lysine methyltransferase, for which the average forward rate constant is 22,000 M⁻¹s⁻¹, and the average starting cell concentration was 6.4 µM (average k_on·[M]_init = 0.14 s⁻¹). Each symbol reflects the estimated contribution of each source of uncertainty to a single injection at that point in a titration. Averaging of all data points in a titration reduces the uncertainty from uncorrelated sources of error as discussed in Section 4.2.3.

Figure 9A displays the fractional uncertainty in k_on from titrations with a k_on·[M]_init = 0.006 s⁻¹, equivalent to an experiment with k_on = 600 M⁻¹s⁻¹ and [M]_init = 10 µM and significantly below the k_ITC value of 0.08 s⁻¹. In this scenario, all uncertainties are relatively small in the first several injections. At later injections the fitting-related uncertainties (random error fit variance and baseline uncertainty) begin to increase appreciably due to lowered signal-to-noise.

In Figure 9B, the SET7/9-AdoMet experiment at the very upper limit of accessibility is shown, with an average k_on·[M]_init = 0.138 s⁻¹. In this case, the rate of association is largest at the beginning of the titration, so uncertainty related to k_ITC is largest here. Comparison of Figures 7 and 9B suggest the uncertainty may be slightly underestimated in this scenario. The baseline error is also significant early on due to the small fitting range in these scenarios (see, for example Figure 5C and 6B). Both of these major sources of uncertainty decrease as the free macromolecular concentration is reduced and the association relaxation time is correspondingly increased; contrastingly, experiment-level sources of error do increase as the stoichiometric point is approached.

Abbreviations

ITC

isothermal titration calorimetry

µJ

microjoules