Neural coding of cognitive control: The representational similarity analysis approach

Abstract

Cognitive control relies on distributed and potentially high-dimensional frontoparietal task representations. Yet, the classical cognitive neuroscience approach in this domain has focused on aggregating and contrasting neural measures — either via univariate or multivariate methods — along highly abstracted, one-dimensional factors (e.g., Stroop congruency). Here, we present representational similarity analysis (RSA) as a complementary approach that can powerfully inform representational components of cognitive control theories. We review several exemplary uses of RSA in this regard. We further show that most classical paradigms, given their factorial structure, can be optimized for RSA with minimal modification. Our aim is to illustrate how RSA can be incorporated into cognitive control investigations to shed new light on old questions.

Towards modeling cognitive control representations

A healthy human mind can set itself towards achieving a goal. This capacity for cognitive control (see Glossary) seems to be a central part of what it means to be human: it putatively underlies abilities that are most elaborate in our species [1-3], yet which go characteristically awry within prevalent mental health disorders [1,4-6]. Propelled by this notion, cognitive scientists have devoted more than a half-century of collective effort towards understanding how control arises in mind and brain. This understanding has typically been sought through the lens of two complementary cognitive constructs: representations and processes. A “representation” is a description of the information that the activity of a neural unit (e.g., neuron, ensemble, area) encodes [7,8] (Figure 1, Key Figure; Theory, blue components). Conversely, a “process” is a description of the function of a neural unit abstracted over particulars of the information encoded ([9]; Figure 1, Theory, orange components). Analogously, a black-box computing function is not defined by a set of internal state values, but instead by a general input–output mapping. Many fundamental problems in cognitive control reflect our lack of understanding control representations [10]. Studying these representations, however, has been notoriously elusive: classically, their neural markers have only been indirectly observable, through process-level measures.

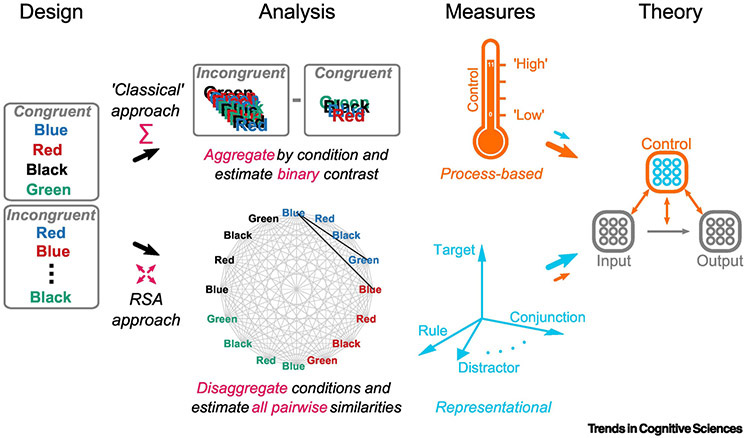
Figure 1, Key Figure.

Schematic of “classical” and RSA-style approaches in cognitive control research. Design, A color-word Stroop task with four colors and four words. The participant is instructed to name the stimulus hue rather than read the written word. Analysis, top, The classical approach begins by defining abstract factor levels (here, congruent and incongruent) to which conditions (e.g., stimuli) are assigned. Within these levels, the outcome variables of interest (e.g., response time) are summed (Σ) then contrasted. Measures, top, These unidimensional measures are typically interpreted in terms of control processes (e.g., slower reaction time on incongruent relative to congruent trials indicates heightened control demands). Analysis, bottom, The RSA approach keeps the task conditions disaggregated (↔↕) in order to examine the set of pairwise similarities among measures (e.g., brain activity patterns) from all conditions — that is, their full similarity structure (grey and black lines). This observed similarity structure is then compared to structures predicted from theory. For example, a model of target representations would predict greater similarity between patterns from trials in which the target response was identical (i.e., between stimuli of same hue: e.g., black line connecting blue-hued “BLUE” and “GREEN” stimuli) versus different (e.g., between stimuli of same word in different hues: black line connecting red-hued and blue-hued “BLUE”s). The RSA approach thus provides indices reflecting the strength which multiple different representational schemes were encoded (e.g., the space defined by the light blue basis vectors, which correspond to potentially encoded variables). Theory, Typically, classical measures support inference (large orange arrow linking Measure to Theory) regarding control processes (entire CONTROL component of model, orange). Conversely, RSA-based measures can map more directly (large blue arrow linking Measures to Theory) onto theorized control representations (blue nodes within CONTROL component).

In this Review, we suggest that progress in understanding the mechanisms of control has arrived in the form of an expansion in experimental approach: from the classical, which focuses on measuring control processes, to the representational, which explicitly models control representations. This expansion was precipitated by the development of neural population-level analytic techniques, including multivariate pattern analysis (MVPA) [11-13] and dimensionality reduction methods [14], which allow neural coding of an unprecedentedly wide range of variables to be measured at the macroscopic scales of functional neuroimaging. But more specifically, we suggest that the MVPA technique of representational similarity analysis (RSA) [15-17] — although it has currently only been sparsely used within cognitive control research — is particularly well-suited for investigation within this domain. This suitability stems from RSA’s flexibility in implementation, and as the name suggests, its explicit focus on modeling representations. First, we discuss how the RSA framework can complement the classical approach. We then illustrate the usefulness of RSA more concretely, by reviewing several recent RSA studies that addressed long-standing issues in cognitive control.

The ‘classical’ approach measures control processes

Classically, cognitive control investigators have designed and analyzed empirical studies using a particular style of experimental psychology. Despite salient differences, most prototypical cognitive control tasks (e.g., [18-28]) share a key design element: an abstract experimental factor that places differential demands on controlled processing. For example, in the color-word Stroop task, the key factor is congruency: whether the task-relevant dimension (hue) is congruent or incongruent with a spatially overlapping, but irrelevant dimension (word; Figure 1, Design). These factors are abstract in the sense that they contain a small number of levels, which collapse across a diverse set of other task-relevant components (e.g., stimuli, rules, response modalities). During analysis, investigators attempt to isolate similarly abstract control processes (e.g., response conflict resolution), by aggregating and contrasting measures along these factors (e.g., Figure 1, Analysis, top).

We refer to this style as the “classical” approach to studying cognitive control: through the scalar lens of process-level contrasts. As a thermometer indicates the temperature, estimates from these one-dimensional contrasts are assumed to indicate the magnitude or efficiency of the control process (i.e., ranging from “high control” to “low control”). Modulations in these indicators — for example, as a function of task parameters or individual difference variables — are then used to shed light on characteristics of the underlying control processes (e.g., boundary conditions [29,30] or relations with other constructs [31,32]; Figure 1, large orange arrow linking Measures to Theory). The classical approach is foundational (e.g., [29,30,33]; see also [34]) and has undoubtedly shaped the kind of information that investigators seek to learn from associated cognitive control paradigms.

With the advent of cognitive neuroscience, control processes have been mapped to the recruitment of particular areas and networks of the brain. To accomplish this, the classical approach was imported into functional neuroimaging studies, under the predominant analytic framework of univariate activation. This framework was used in a manner directly analogous to previous process-based behavioral contrasts — only now these contrasts indicated the amount by which the key control-process manipulation increased aggregate activity within a brain region of interest. Early neuroimaging studies demonstrated that lateral prefrontal cortex (LPFC), dorsomedial frontal cortex (DMFC), and other nodes within frontoparietal and cingulo-opercular networks (FPN, CON), reliably “activate” during situations of controlled processing [35], a result which has been replicated many times over (e.g., [36-39]).

But the classical approach and its focus on measuring control processes — while serving a necessary, anchoring role — is incomplete. Many cognitive control theories are predominantly specified, not in terms of processes, but in terms of representations ([9]; e.g., abstract rules [3,40], high-dimensional [41] task conjunctions [42,43], compositional sub-tasks [44,45], attentional templates [46], hierarchical task schemas [47-49]). In theory, cognitive control representations, encoded and maintained by control networks (FPN, CON), contain the requisite information for performing cognitive control tasks within an appropriately organized form. But investigating the form of these representations, though it is a central goal, is often challenging to pursue with only process-level measures. Possibly, even, the kinds of questions that would be most clarifying for understanding representational format, are those which process-level measures least naturally support. For example, what makes two control-demanding states similar, versus distinct?

Representational approaches explicitly model control representations

Distinguishing among multiple, similarly control-demanding states is exactly the sort of problem that MVPA methods can make more tractable. These methods can be decomposed (non-comprehensively) into two variants: classification-based decoding, which we refer to here as “classification”, and RSA (Box 1; see also encoding methods [50]). There has been a growing body of work using classification within the domain of cognitive control (e.g., for a review [51]), including contributions from our own group ([45,52,53]). But, in contrast to other domains of cognitive neuroscience, (e.g., object recognition or episodic memory; [54-56]), relatively few cognitive control studies have adopted the RSA approach.

Box 1. Strengths of MVPA classification and RSA.

Consider a hypothetical fMRI study of the color-word Stroop task and a researcher interested in the neural coding of congruency information. A one-dimensional research question like this is perhaps most straightforwardly assessed via MVPA classification: can the congruency level of a trial be classified, or “predicted”, by patterns of dACC activation (Figure I, Analysis and Conclusion)? If prediction is successful, dACC would be said to encode congruency information (Figure I, test split; see [117] for an actual example of classification in Stroop; for more general discussion and introductions, see [11,118-120]).

But it is often of interest to compare encoding of multiple task variables — for example, does dACC encode congruency selectively or more strongly than task-relevant target information? Here is where RSA becomes advantageous. A prototypical RSA would frame this as a singular problem of model comparison, in which two models (Figure I, congruency and target model geometries) compete to explain a common outcome: the full condition-by-condition similarity matrix of dACC activity patterns (Figure I, observed geometry, lower). The analysis tests whether the congruency model provides a better fit to the observed dACC geometry than the target model.

This example highlights two key distinctions between MVPA classification and RSA. First, RSA operates at a level once-removed from brain activity patterns, whereas classification operates directly on brain activity patterns (Figure I, Analytic Problem). This “second-order” abstraction (a la [121]) is the key basis for the flexibility of RSA. It allows representations from fundamentally different types of spaces to be easily compared [16].

Second, RSA and classification differ in their direction of inference. In RSA, models are tested in their ability to explain (similarity structure of) brain activity patterns (Analytic Problem, RSA, purple arrow), whereas in classification, activity patterns are tested in their ability to predict (or “recover”) a hypothesized model (Analytic Problem, Classification, orange arrow; [50]). This “forward” direction of inference of RSA — from models, which are (typically) under experimental control, to brain activity measures, which are not — underlies its explicitness for comparing competing coding models. This is a practical consideration that becomes critical with more complex experiments involving balanced factorial designs (e.g., [122]) that include interactions (e.g., [108]), or when there is a need to control for a diversity of confounding similarity structures (e.g., [63]). Further, this strategy enables one to test whether the geometry is completely explained by the models (i.e., with reference to a noise ceiling; [50,59]).

Finally, many strengths of classification are also accessible via RSA. Similarity measures can be chosen that account for certain properties of the data [123] that popular classifiers handle well, such as structured noise (e.g., [96]). Additionally, RSA models can be fit to individual trials, enabling, for example, using RSA model coefficients to predict theoretically-specified single-trial behavioral indices [63].

Box 1 Figure:

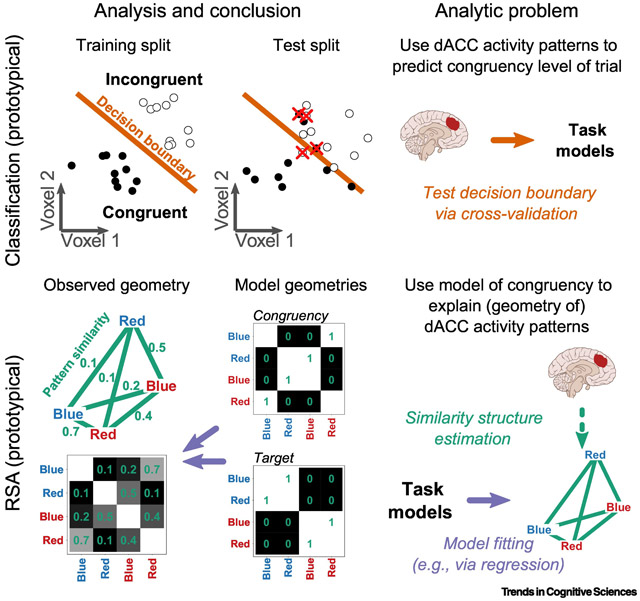
Illustration of prototypical classification and RSA approaches, using a toy example of a four-stimuli color-word Stroop experiment. Classification, Analysis and Conclusion, Trial-level activity patterns from a 2-voxel brain region (dACC) are depicted as points in 2-dimensional space. Classification corresponds to fitting a decision boundary (orange) that separates patterns along a single factor (e.g., congruency; hollow or filled points) and is typically assessed via cross-validation (training and test splits). Classification, Analytic Problem, Classification directly uses brain activity patterns to predict the task model (congruency). RSA, Analysis and Conclusion, Condition-average dACC activity patterns (observed geometry) are depicted as a spatial arrangement (or geometry) of four points (here, the color-word stimuli), with six inter-point distances (green lines). The smaller the distance between patterns, the more similar they are (green numbers). The observed geometry can also be represented as a similarity matrix, as can model geometries. RSA, Analytic Problem, In RSA, brain activity patterns are first transformed into geometries, which are then explained by task models (target, congruency).

We speculate that classification has been used more frequently out of tradition. Classification naturally aligns with the classical approach to cognitive control, as it is well-suited for binary questions — that is, to classify task conditions along a single dimension (e.g., congruency; see Box 1). In contrast, in its original formulation, RSA was developed for the condition-rich naturalistic experimental designs that are common in visual neuroscience [16,57]. Control-oriented researchers may have therefore considered RSA to be more of an exploratory tool for studying sensory and perceptual processes, rather than higher cognitive ones. Yet this would not be accurate. RSA is a general framework in which the central goal is to adjudicate between several competing representational models. Two features of RSA make this a straightforward task: The first is flexibility, due to operating on the similarity structure of activity patterns, or their geometry, rather than on activity patterns per se. The second is explicitness in the goal of modeling representations, due to a “forward” direction of inference, from model to brain (see Box 1).

In fact, the balance of these features makes RSA well-suited for cognitive control research. Seemingly at odds with the original goal of leveraging the continuously varying feature-spaces of naturalistic experiments, RSA can also capitalize on the strengths of factorial designs. These designs are, of course, a bread-and-butter approach used in cognitive control experiments, as they allow confounds to be efficiently orthogonalized and interactions studied. Full factorial RSA provides a simple yet powerful framework for accessing these benefits within analysis of neural representations (Box 2). Indeed, many extant datasets may be amenable to full factorial RSA (e.g., [58]).

Box 2: Full factorial RSA.

Full factorial RSA offers a convenient framework for removing confounds and studying interactions in neural representations. Yet at first, this approach can seem counterintuitive, particularly for those who have primarily employed factorial designs in univariate contexts. Returning to the example of the Stroop task, we illustrate the potential utility of this approach.

In the color-word Stroop task, the target factor (here, four colors) is crossed with the distractor factor (four words; Figure I, A, left). This design permits at least three coding models to be specified: target, distractor, incongruency (Figure I, A, right). Each model describes an “ideal” coding scheme: for example, the target model would be observed in a region that only encoded the hue (or correct response), regardless of the distractor or congruency. Through multiple regression, these model similarity matrices can be jointly fit to the observed similarity matrix. The resulting β weights reflect the strength with which each factor was uniquely encoded within the observed geometry. Indeed, when this approach was recently, retrospectively applied to fMRI activity from sensory, motor, and frontoparietal control regions, predicted dissociations in coding strength were found at the group level (Figure I, B, left) and in relationships with individual differences in behavior (Figure I, B, right; [58]).

But even this example does not reveal the potential precision of full factorial RSA. For example, the target model conflates a variety of coding schemes: sensory coding (of hue), motor coding (of correct response), and more flexible, attentional template coding (Figure I, C, Decomposition). Adding a rule manipulation (Figure I, C, Design, pink) enables these coding schemes to be unconfounded, as regions encoding an attentional template would be expected to reconfigure their coding scheme on the basis of the task rule (Figure I, C, Control-Related Models, target features model; e.g., [108]; see discussion in [58] for additional decomposition). Likewise, a general rule-coding scheme (Figure I, C, rule model) can now be specified to identify task-set representations.

Further, full factorial RSA allows interaction hypotheses to be tested. For example, if increasing the frequency of incongruent trials drives subjects to adopt a mode of proactive control [77], a corresponding increase should be seen the strength of rule coding. This interaction could be tested by comparing the strength of rule coding (Figure I, C, rule model) in blocks with different probability of incongruency. More complex types of interaction hypotheses are testable, too (e.g., [63]; see also [124]).

An important limitation of full factorial designs are constraints on experimental time. Because time is limited, each additional manipulation typically reduces the number of trials per condition. To some extent, though, a larger RSA matrix (due to having more conditions) will counteract instability due to fewer trials. Nevertheless, manipulations should be added judiciously, boosting precision only along specific dimensions. We strongly recommend piloting and simulation to guide concrete design choices.

Box 2 Figure:

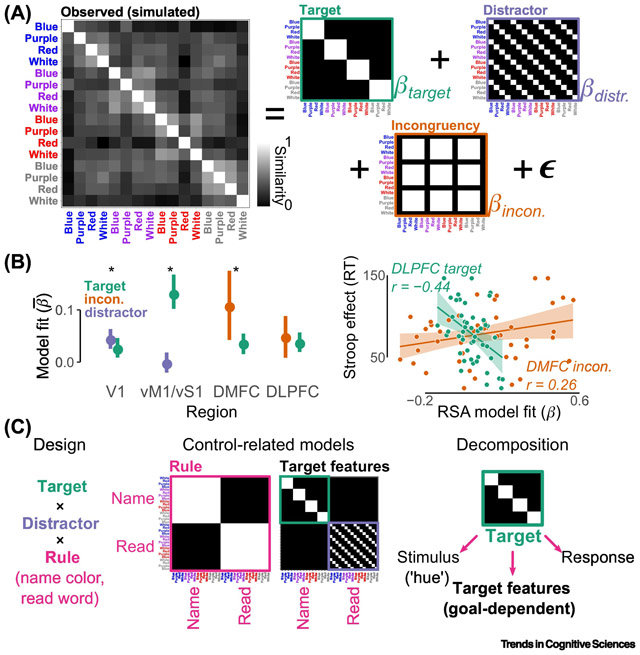
A decomposition of color-word Stroop via full factorial RSA. A, The similarity structure evoked during a Stroop experiment is modeled as a weighted sum of three hypothesized coding schemes (for visibility, white-hued stimuli are displayed in grey). B, Predicted dissociations in coding schemes were found when applying this approach to fMRI data [58]. At the group level (left), target coding predominated in ventral somatomotor cortex (vM1/vS1), whereas distractor coding predominated in V1 (error bars indicate 95% CI of between-subject variance; asterisks indicate significant pairwise model comparison). Relative to DLPFC, coding of incongruency predominated in dorsomedial frontal cortex (DMFC, including dACC and pre-SMA). At the individual level (right), subjects with stronger target coding in DLPFC, but weaker congruency coding in DMFC had smaller Stroop effects. C, In full factorial RSA, the precision of models can be boosted by adding specific manipulations to better isolate representations relevant to cognitive control.

Similarly, cognitive control research can leverage the general inferential strategy of RSA, model comparison, in a more comprehensive manner than perhaps initially anticipated. In the original formulation of RSA, a set of competing models (hypotheses) are fit to an observed geometry (e.g., of a brain region), and evidence for a hypothesis is obtained if its corresponding model clearly provides a better fit. But once fit, the modeled representations (i.e, “coding strengths”) can also be compared in a variety of useful ways: particularly, in their ability to explain behavioral measures (e.g., classical contrasts of control), in their sensitivity to superimposed experimental manipulations [59] (e.g., process-level factors), and in their ability to explain modulations in other modeled representations (e.g., in downstream regions or subsequent timepoints; termed representational connectivity analysis [60], see Table 1). In conjunction, these tools can provide a rigorous means to decompose the black-box of control processes — the gap between process manipulations and controlled behavior — into a more mechanistic path that is mediated by the strength of specific representations.

Table 1.

Summary of various techniques used in RSA.

Technique	Description	Pros (+), Cons (−)	References
ANN-based RSA	Method of specifying RSA models based on artificial neural network representations.	+ more direct link between data and formal models + less computationally intensive than estimating unit-to-unit mappings − cannot predict response to novel conditions	• [82], see also [140] • [13,16]
Full-factorial RSA	Type of experimental approach that uses crossed factors and multiple regression to decompose neural coding.	+ efficiently boost model specificity + test interaction of representations + handles complex designs − number of trials, experimental time	• [63,108]; see also [122], discussion in [58]; see [124] for related technique
Single-trial RSA	Analytic procedure for fitting RSA models at single trial level.	+ test within-subject brain–behavior relationships + supports hierarchical or joint modelling − autocorrelation confounds	• [63,64] • [141-143] • e.g., [144]
Cross-task RSA	Type of analysis that examines similarity structure within battery of tasks.	+ assess “neural construct validity” + use to rigorously assess replication	• [88]; see also [95] • [99]
RSA fingerprinting	Method of assessing presence of stable individual differences in representational structure.	+ mitigates individual differences due to anatomical factors − requires repeated measures	• [114]; see also [54]
Cross-subject RSA	Method of assessing task-dependent similarity in response topographies.	+ useful when individuals can be meaningfully grouped (e.g., by genetic relation) − potential confounds with univariate activity	• [115] see discussion in [92]
Unbiased similarity measures	Type of similarity measure for which the expected value is not impacted by measurement error.	+ useful for unbalanced designs − increased variance − each condition must appear in >1 run	• techniques: [13,96,97,124] • unbalanced design: e.g., [75] • increased variance: [145]
Representational “connectivity” analysis	Type of analysis that examines covariation in coding strength (across region, timepoint). When constrained by RSA models, this covariation is assessed along specific coding variables.	+ test representational interactions (e.g., b/w PFC and downstream coding + constrained or unconstrained by RSA models − third variables, directionality	• PFC–downstream interactions: e.g., [3,146] • unconstrained: [60,147]; constrained: e.g., see interaction analyses in [108]

RSA and cognitive control: a collection of exemplary studies

To demonstrate the advantages of the RSA approach to cognitive control investigation more concretely, we review a number of illustrative studies, focusing on human neuroscience, that touch on long-standing issues within this domain. While the questions differ, many of these studies share a primary goal: to validate a mapping between a theorized control representation and measured neural activity. Results, therefore, primarily provide support for existing theory, rather than advancing or exploring new theoretical ideas. But, with this validating work in place, RSA methodology can now be used to directly refine and challenge existing theoretical models of cognitive control. Relevant techniques are summarized within Table 1.

Task-set representation

A central element of many theoretical models of cognitive control are task set representations (e.g., [2,3]; for a review, see [61]). One expansive cognitive theory proposes that, during goal-driven behavior, perceptual, action, and contextual information are intermediately bound into conjunctive representations, so-called “event files”, that are used to guide action selection [43,62]. Support for this account was recently found using RSA and EEG, in a pair of rule-based action-selection studies [63,64]. The task required a manual response (left, right, up, down button-press) to be determined by applying a spatial translation rule (e.g., horizontal, vertical, diagonal) to a spatial stimulus (a dot in one of the screen’s quadrants). Conjunctive coding was modeled as the components in the EEG geometry that were uniquely but stably evoked by each stimulus, rule, and response combination (i.e., non-linear combinations of these factors). As these constituent factors (i.e., stimulus, rule, response) were orthogonalized in the design, full factorial RSA was used to dissociate conjunctive coding from “pure” coding of each factor, similar to decomposition of main effects from their interaction. Further, in a novel methodological extension, a single-trial RSA method was developed, which enabled within-subject brain–behavior relationships to be tested via hierarchical linear models.

Conjunctive coding emerged relatively early following the stimulus (i.e., prior to response coding), was robustly related to trial-by-trial response time, and — uniquely among the coding schemes — explained a defining behavioral marker of event files (the “partial repetition cost”). A follow-up experiment imposed an additional stop-signal manipulation on the design, to assess which, if any, coding scheme was impacted by inhibitory control processes [64]. Strikingly, only conjunctive coding was suppressed, shortly after the stop signal was presented, selectively on successfully stopped trials, with the degree of suppression uniquely predicting stopping success. Conjunctive coding thus reflects an important locus of action selection, that is both proximal to behavior and a target or intermediary of inhibitory control. A useful direction for future work will be to clarify the neuroanatomical generators of this conjunctive EEG code (e.g., via fMRI, neurophysiology, or perturbative approaches, such as TMS).

Another major focus of control research is to understand how task sets are regulated. Most commonly, this has been studied within multi-tasking and task-switching paradigms, in which competing task sets are activated and frequently switched across trials [65,66]. Foundational to this research has been the behavioral switch cost: across consecutive trials, people typically are slower and more error-prone at switching tasks versus repeating them. In theory, cognitive control processes must overcome this task-set “inertia” [67] and rapidly activate a new task representation when needed (“reconfiguration”) [24]. Task representations within frontoparietal cortices (through interactions with striatum) are thought to mediate these dynamics [2,3,61].

A strong correspondence between this cognitive theory of task-switching and frontoparietal coding dynamics was recently demonstrated via RSA and fMRI [68]. By conducting RSA on consecutive trials within a cued task-switching experiment, this study illustrated that the strength of task representations in these regions closely tracked inertial and reconfiguration phenomena: task representations were stronger (higher trial-to-trial similarity) following repeat versus switch trials (inertia) and were additionally strengthened across the cue-to-target epoch (reconfiguration). Critically, these dynamics were also aligned to behavior, such that stronger reconfiguration of the task representation was associated with reduced switch costs.

Sometimes, though, an irrelevant task set can be a potent competitor, not because of its recent use, but because of stable differences in automaticity. This type of regulation is studied in stimulus–response conflict paradigms such as Stroop. How the brain actually regulates this interference is a matter of ongoing debate. Foundational models of control propose that key mediators of Stroop interference are LPFC rule and attentional template representations (e.g., [3,69]). Recent evidence, however, suggests that cognitive control may play less of a role than originally thought (e.g., [70]; see also [71,72]; but see [73,74]). This debate is undoubtedly complicated by the fact that the classical Stroop interference effect is a highly multi-determined measure. Here, though, the RSA framework can assist, as the Stroop paradigm is amenable to decomposition by full-factorial RSA (Box 2; [58]). Such a decomposition can provide a rich set of coding variables that can be used, in turn, to decompose classical behavioral measures from Stroop (as in [58]), or tracked as a function of interference-modulating manipulations (e.g., proportion congruency; [75]). For example, it is possible that top-down control processes, mediated by LPFC rule coding, are better captured by behavioral measures other than the classical Stroop interference effect (e.g., Stroop-effect variability [76]), or, become crucial only in certain scenarios (e.g., when interference is likely [77] or when task statistics engender habitual responding [78]). Thus, not only can RSA be used to constrain the set of mechanisms that putatively mediate response conflict, but also to clarify how best to measure them within behavior.

Learning latent task structure

Real-world tasks often possess a latent structure that unfolds in time. Learning this structure can facilitate performance and increase the probability of advantageous outcomes by enabling the individual to predict which actions are appropriate in given contexts. Recent accounts have postulated that latent structures are encoded by medial and orbitofrontal cortex, and through interactions with midbrain circuitry, serve to guide the formation of frontoparietal task representations that orchestrate goal-directed behavior (i.e., planning and action preparation) [79,80].

This area, as with many others in cognitive control, is amenable to formal modeling. One useful method of formalizing hypotheses in this domain has been with artificial neural networks (ANNs), which perform tasks via distributed representations [48,81], learned during training. By linking artificial representations to those observed in the brain, neural data can constrain ANN models of cognitive control. Because each of these representations can be high-dimensional, often the simplest way to assess such a link is through their geometry — that is, via RSA ([16]).

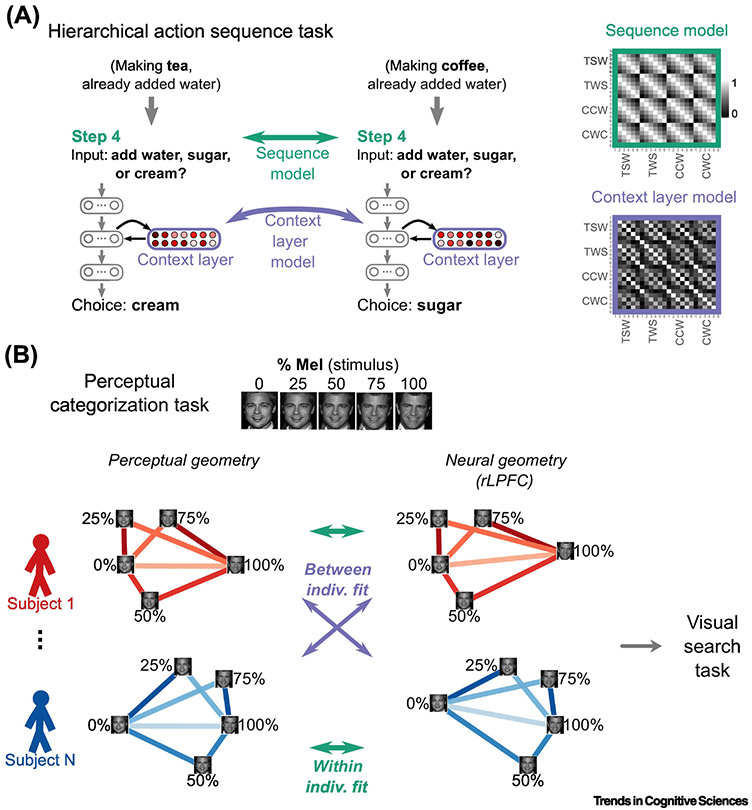
This feature of RSA was effectively used in a recent fMRI study [82], in which both human participants and an ANN learned about the latent sequential structure present in a pair of everyday tasks: making coffee or tea. Although some actions could be freely chosen (e.g., whether to add sugar or water first), others had to be made based on previous choices (e.g., only serve the drink after both ingredients had been added exactly once). Successfully performing such a task requires organizing and maintaining relevant information from preceding timesteps, which the critical “context” layer encoded within the ANN (Figure 2A, left). The similarity structure that emerged within this layer served as the RSA model (Figure 2A, Context Layer Model), and was fit to (the similarity structures of) neural activity patterns recorded from participants during performance of the same task. This model was selectively associated with representations in medial PFC (MPFC; including mid-cingulate cortex) — above and beyond competing models defined from other behaviorally relevant variables (e.g., Figure 2A, Sequence Model). The clear specificity of this result, both to MPFC and to the context model, suggests that MPFC could provide downstream regions with a flexible representation of progress-to-current-goal.

Figure 2.

Diagrams of two reviewed RSA methods. A, Mapping internal representations of an artificial neural network (ANN) to brain activity with RSA [82]. An ANN was trained to perform a hierarchical action sequence task, in which the action at one point in the sequence depended on previously chosen actions (e.g., ingredients could only be added once; cream could only be added to coffee). After training, the ANN simulated each step of each sequence (depicted: the fourth step of two different sequences), and the resulting activation patterns (reddish nodes) within the context layer were extracted; the similarity structure of these patterns served as the Context Layer Model (right). A competing model (Sequence Model), which contained only information regarding position-in-sequence (i.e., not previous choices) was built by taking the distance (absolute difference) between each pair of steps (green arrow). B, RSA “fingerprinting” [114]. Individuals first performed a famous-face classification task, in which an exemplar face, linearly morphed between two famous faces (e.g., Brad Pitt and Mel Gibson), had to be classified (as either Brad or Mel). Each individual's categorizations were expressed in similarity matrix form (here, depicted as 2-dimensional perceptual geometries) then used as models to explain (green and purple arrows) neural similarity matrices (neural geometries) from each and every subject. Idiosyncratic brain–behavior relationships were identified in brain regions (i.e., rLPFC) for which the within-subject models (green arrows) were better fit on average than the between-subject models (purple arrows). Neural geometries were then used to predict the patterns of interference within a separate attentional search task that used the same stimulus set (grey arrow).

Follow-up studies could further strengthen this interpretation by examining how the strength of the MPFC context representation covaries with task representations in other areas and with other manipulations: for example, coordination with LPFC and premotor cortex may be critical during situations of high response conflict, or with hippocampus during learning. Another clarifying direction could be to make the model competition more intense: for example, by testing alternative representations derived from competing network architectures (e.g., [83,84]). Similarly, recent work that could be useful to integrate here, has used classification and RSA methods to identify unique mechanisms for serial-order control, implicating hippocampal and frontoparietal regions in forming hierarchical and “chunked” representations [85-87].

Domain-general cognitive control

A long-standing interest within the field is to refine the constructs of cognitive control (e.g., [1]). Of particular interest is where to draw the boundaries: which functions should be considered general, commonly engaged by different tasks, and which distinct? A construct validation approach is often used to address this issue: measures from a battery of tasks are collected for each individual, and from the covariance structure of individual differences among the tasks, latent factors are estimated that correspond to the hypothesized constructs. Evidence for the construct is provided if factors are interrelated in predicted ways (e.g., [31,32]). Prior studies of the generality of control functions, however, have yielded mixed results (e.g., [71,73]). But, these studies have almost exclusively used behavioral measures to estimate cross-task factors. Brain activity measures may give additional leverage, as they can provide more proximal, higher-dimensional readouts of neural mechanisms.

Through the use of a novel meta-analytic, cross-task RSA, an important first step towards “neural construct validation” of cognitive control was recently reported [88] (see [51] for a complementary voxel-wise meta-analysis). This work included fMRI datasets spanning three domains: cognitive control, negative affect, and pain. The key region of interest was the anterior midcingulate cortex (aMCC), a region that has seemed functionally ubiquitous [89] and challenging to characterize [90]. The researchers found that aMCC representations converged across disparate pain modalities (thermal, mechanical, visceral) and separately, across different sub-domains of negative affect (visual, social, auditory narrative). In contrast, cognitive control representations not only diverged from these two domains, but diverged from each other — regardless of whether they were from common or distinct sub-domains (“working memory”, “response selection”, “response inhibition”). That is, no task-general control representations were detected.

Limitations of this study are important to bear in mind. In particular, site factors (e.g., study location, scanner, research group) confound the manipulations of task domain. Likewise, as their meta-analysis was inherently also a cross-subject RSA (i.e., all pattern similarities were estimated between different subjects), the analysis was not optimized to capture finer-grained representational structure that could be subject-specific (i.e., idiosyncratic [91,92]). Indeed, finer-grained or idiosyncratic response topographies may best define the aMCC signal relevant for cognitive control (as, e.g., suggested by differences in developmental timecourses between domains; c.f., [93,94]). Nevertheless, the potential of cross-task RSA is highly appealing. When tasks form the dimensions of a representational similarity matrix, RSA naturally assesses cross-task convergent and divergent validity at the level of neural (e.g., fMRI BOLD signal) implementation (see also [95]). Indeed, similar to construct validation approaches, several RSA methods have been developed that use unbiased similarity measures in order to explicitly account for measurement error (see Table1; [13,96-98]). More broadly, this cross-task view of representations is also reflected in the recent recommendation to use pattern similarity as a rigorous way to assess replication of task-based fMRI results [99].

Interactions with motivational value

There has been a growing appreciation of the tight relationship between motivation and cognitive control [100,101]. In several recent accounts, deciding whether and how to engage cognitive control is a value-based process, in which the benefits of goal attainment are integrated with the cost of various control strategies [102]. This interaction of motivation and cognitive control is thought to involve dopaminergic signaling and fronto–striatal circuitry [103-107]. One way in which this interaction may manifest is as an increase in the gain (i.e., sharpening) of frontoparietal task rule coding. Indeed, a recent cued task-switching study using MVPA classification, reward incentives (which varied trial-by-trial and were pre-cued) increased the distinctiveness of frontoparietal task-set representations, and these task-set coding changes explained individual differences in performance improvement on incentivized trials [52].

Building on this work, the same question was examined from within the RSA framework, via EEG [108]. Relative to [52], the use of full factorial RSA allowed a richer set of coding variables to be jointly estimated — including task rule (as in [52]), but also two stimulus-feature models (target and distractor) and a response (motor) model. While incentives enhanced target stimulus, response, and rule coding (i.e., all but distractor representations), only rule coding was selectively enhanced during rule updating (i.e., on switch versus repeat trials), and emerged prior to trial onset, consistent with a proactive control mechanism [77]. Completing the link to behavior, individual differences in the strength of this interaction between rule coding and incentive robustly explained the amount by which response latencies decreased as function of incentives, even when controlling for incentive-driven changes in other coding schemes. The results of this elegant study converge with those of [52], but further suggest that this incentive-driven enhancement in rule coding reflects proactive control [77], precedes other incentive-driven representational changes, and may be dependent on updating, as opposed to other types of control processes (e.g., rule maintenance).

From these foundational results, the research paradigm can be expanded to address additional critical questions regarding the motivational properties of incentivized task contexts, such as the effects of motivational valence (i.e., positive/approach, negative/avoidance), incentive categories (i.e., primary, secondary), subjective preferences, and the timing of incentive cues (i.e., preparatory, target-linked) [109,110]. When used with neuroimaging methods of higher spatial resolution (such as fMRI), RSA offers a means of identifying the neural systems underlying these (potentially massively distributed) EEG codes.

Individual differences

Cognitive control is strongly impacted by individual differences [2,77,111]. Some of this variability may be localized to frontoparietal networks, in which functional differences may emerge from, or manifest as variability in task-relevant representations ([2,112]). Studying individual differences in frontoparietal representations can thus be a powerful test-bed for models of control. Likewise, RSA may provide novel ways of approaching such questions, as illustrated by two recent studies.

A long-standing construct in models of control of visual attention is an attentional template representation, encoded by frontoparietal networks, which contains visual information regarding the current target [46] (e.g., an object for which you are searching). At the heart of these models is a computation of similarity, between template features and objects within the visual field: representations of objects are preferentially enhanced, as a function of similarity to template (see [113] for a review). But similarity is, to some degree, subjective [54]. Subjective perceptual differences — idiosyncrasies in perceptual representations — could therefore plausibly drive individual differences in attentional efficiency.

Though this question may seem slippery, it can be naturally addressed with RSA, as demonstrated in a creative fMRI study [114]. Participants first classified identities of faces linearly morphed between two famous individuals (Figure 2B). In an RSA “fingerprinting” procedure adapted from object perception research [54] — which hinges upon on the “second-order” nature of RSA — individuals’ fusiform face area and lateral PFC were found to encode the stimuli in a format that captured their own idiosyncrasies in perceptual categorizations. Critically, an attentional task was performed next, using these same face-morph stimuli as distractors. Only within right lateral PFC did an individual's neural similarity between a given target and distractor — measured during the initial categorization task — predict the degree to which the distractor disrupted (prolonged) their search. This study demonstrates a tight linkage between perceptual categorization, attentional search, and the representational structure in LPFC, while hinting at a privileged role for LPFC in representing categories when relevant for impending decisions. More generally, this study illustrates the utility of the second-order nature of RSA: by abstracting away from brain activity patterns, towards their geometry, investigators can more directly compare individuals on cognitive dimensions of interest. Beyond identifying idiosyncratic representations, such an approach could be an effective medium for comparing subgroups (e.g., older versus younger adults), circumventing issues of gross anatomical change.

But sometimes the functional topographic organization of cortex is of interest. A recent study conducted by our own group [115], used genetic contributions to individual differences in functional organization to explore task coding within the FPN. Cross-subject RSA was applied to fMRI images of the N-back working memory task, in order to examine the similarity structure of activation patterns between paired individuals, contrasting monozygotic (identical) and dizygotic (fraternal) twin pairs, as well as non-twin siblings and unrelated pairs. Two contrasting models were compared: one of working memory load, the other of stimulus category. The coding of these dimensions was anatomically specific, such that frontoparietal regions showed higher pattern similarity in pairs with greater genetic similarity, but critically, only for the load model. Moreover, these patterns exhibited functionally relevant individual differences: in related (but not unrelated) pairs, stronger common coding of working memory load was associated with better N-back performance. These results provide clear support for the idea that genetic factors are entwined with the development of cognitive control functions [116], and suggest that these factors are expressed in the task-dependent functional organization of frontoparietal networks. Here, the use of RSA methods provided an efficient way to both compare different coding models and identify behaviorally relevant individual differences in the strength of a given coding scheme.

Concluding Remarks

RSA provides a convenient yet rich framework for decomposing control-related neural activity into measures that better correspond to representational components of theories. Of course, there are still many unknowns regarding the limitations of these tools (Box 3), as well as important open theoretical questions (Outstanding Questions). But as we have attempted to illustrate, the RSA framework has high potential for constraining mechanistic theories of cognitive control. We hope that this Review inspires other investigators working in this area to consider whether an RSA approach might be usefully applied to their own research questions.

Box 3. Effective fMRI measurement of cognitive control representations.

Cognitive control is complex, and perhaps not coincidentally, the brain regions associated with it, such as DLPFC, are challenging to study. Neurophysiologists have long appreciated the difficulty in characterizing the response profiles of neurons within this region (e.g., [125,126]): neuronal selectivities seem to be dynamic, often changing within single-trials [127], and are highly conjunctive, reflecting a mixture of task attributes [128]. At larger spatial scales, the principles by which lateral PFC is functionally organized have been difficult to establish (e.g., [49]). In fact, a recent, influential model of DLPFC embraces the confounding nature of this region by positing that neural populations are randomly connected to their input layers [42,129]. Random connectivity implies a lack of topographic organization, which would cast doubt on the utility of fMRI pattern analysis methods for identifying localized task representations in DLPFC.

Indeed, recent evidence suggests the signal-to-noise ratio in PFC fMRI activation patterns is relatively low. A meta-analysis of MVPA classification studies concluded that mean classification accuracies were considerably lower in PFC than in posterior sensory cortex [130]. A pair of recent RSA studies also illustrates the potential issue. In the first, macaques were trained on a reward-based decision-making task while single-unit activity was recorded [122]. Full factorial RSA revealed a triple dissociation of coding schemes across PFC regions. Yet this same full factorial RSA design, when adapted for human fMRI, found considerably weaker results in putatively homologous regions [131].

Although the scale of topographic organization (or lack thereof) in PFC is one important open question, there are many other potential limiting factors that also likely impact our ability to measure prefrontal coding effectively. More research on the importance of these factors is needed. For instance, dense sampling approaches (fewer subjects, more data per subject) are critical for maintaining signal in the presence of strong individual variability in functional organization [132]. Yet such an approach is rare in cognitive control research, despite the pronounced sensitivity of the associated frontoparietal brain regions to individual differences [133,134]. Thus, individual-specific areal definitions (e.g., [135,136]) are another important avenue to examine. Conversely, expanding the spatial scale of analysis, from areas to networks, has proven highly effective in other domains [137]. Of course, a loss of anatomical precision necessarily comes with this expansion; but, for many cognitive-level inferences, areal versus network-level specificity may not be critical. Finally, repetition suppression may be an effective means to achieve sub-voxel-level precision in measuring representations [138,139].

Importantly, within each of these alternative approaches, the logic of RSA — explicitly modeling neural similarity structure — is applicable. Thus, for those interested in PFC coding of control, we predict that fluency in RSA will be valuable, regardless of measurement technique.

Outstanding Questions.

• In stimulus–response interference paradigms such as Stroop, how does cognitive control state (e.g., proactive/reactive) or other contextual and state factors (e.g., trial history, proportion congruency, amount of practice) impact target, distractor and task-set (rule) representations?

• Can more detailed representational models of dACC “congruency” coding (based on, e.g., model-derived response conflict, performance-monitoring information, or value computations) be used to shed light on function of this region?

• Can RSA be used to model the trial-by-trial dynamics of task structure learning?

• What is the evidence for domain-generality (i.e., cross-task similarity) of cognitive control representations?

• How do various motivational factors (e.g., valence, incentive type, preferences) modulate cognitive control representations? Is it through a common mechanism of sharpened task-set coding?

• To what degree are cognitive control representations idiosyncratic, that is, serving as a “fingerprint” of the individual?

• What are the psychometric properties of RSA with regard to individual differences analyses (e.g., test–retest reliability)? Can neuroimaging-based RSA be optimized to more powerfully address individual difference questions?

• Within fMRI-based RSA, what methods (e.g., involving amount of data per subject, preprocessing decisions, region definitions, denoising procedures, similarity estimation) are most effective for measuring prefrontal coding?

Highlights.

• Classical measures of cognitive control often only weakly correspond to the theoretical representations they are commonly used to test.

• Representational similarity analysis (RSA) can help better align measures to theory in this domain.

• The power of RSA comes from its flexibility, yet explicitness, in modeling representational structure.

• Full factorial RSA also enhances inferential precision and enables interactions to be tested.

• Useful strategies for applying RSA to inform cognitive control theory are discussed, and recent studies that exemplify these strategies are reviewed.

Glossary

Artificial neural network (ANN):

computing systems, loosely based on biological brains (with units analogous to neurons and weights analogous to synaptic connections) that are trained to perform particular tasks via supervised or reinforcement learning algorithms.

Cognitive control:

the coordination and regulation of thoughts and actions in accordance with internally maintained behavioral goals.

Condition-rich RSA:

an experiment containing diverse and high-dimensional experimental stimuli, such as naturalistic images, that permit description by several different, often continuously varying, feature spaces (e.g., Gabor filters, semantic dimensions). A condition-rich RSA leverages this stimulus diversity to disentangle models built on competing feature spaces.

Full factorial RSA:

an RSA approach that uses a combination of a full factorial design (i.e., with multiple fully crossed factors) and multiple regression to decompose various coding schemes and potentially their interactions.

Multivariate Pattern Analysis (MVPA):

A loose category of data analyses that are sensitive to spatially distributed (e.g., across-voxel, across-electrode, or across-neuron) patterns of brain activity. These include but are not limited to classification-based decoding and RSA.

Process:

an account of the function of a neural or cognitive unit (e.g., neuron, area, model component) in terms of the unit’s outcome or impact on other systems, or more general contexts in which it is engaged. Analogous to a computing function, which is not described by a set of internal state values (representations), but an abstract operation that “acts on” other values.

Representational geometry:

a term equivalent to similarity structure, but that more strongly connotes the geometric or graphical interpretation (of points as activity patterns and similarity as inter-point distances in high-dimensional activity space), and that emphasizes connections with neural population coding frameworks.

Representation:

an account of the function of a neural or cognitive unit (e.g., neuron, area, model component) in terms of the content and format of information that the unit stably encodes. In the black-box computing function analogy, a representation would be the (hidden) internal values (or states) of the function.

Similarity structure:

Given brain activity patterns evoked by a set of task conditions, the set of all pairwise similarities among the conditions. See also representational geometry.

Task set:

The “instructions” for a task — containing information about stimuli, responses, and rules (e.g., stimulus–response mappings) — but represented within a proceduralized, actionable format.

Univariate analysis:

Neuroimaging analysis technique developed to detect spatially uniform (“overall” or mean-level) changes in brain activity resulting from experimental manipulations.