Assessment of Heterogeneous Treatment Effect Estimation Accuracy via Matching

Abstract

We study the assessment of the accuracy of heterogeneous treatment effect (HTE) estimation, where the HTE is not directly observable so standard computation of prediction errors is not applicable. To tackle the difficulty, we propose an assessment approach by constructing pseudo-observations of the HTE based on matching. Our contributions are three-fold: first, we introduce a novel matching distance derived from proximity scores in random forests; second, we formulate the matching problem as an average minimum-cost flow problem and provide an efficient algorithm; third, we propose a match-then-split principle for the assessment with cross-validation. We demonstrate the efficacy of the assessment approach using simulations and a real dataset.

1. Introduction

Nowadays the heterogeneous treatment effect (HTE) estimation under the Neyman-Rubin potential outcome model^1;2 is gaining increasing popularity due to various practical demands, such as personalized medicine^3;4, personalized education⁵, and personalized advertisements⁶. There are a number of works focusing on estimating the HTE using various machine learning tools: LASSO⁷, random forests⁸, boosting⁹, and neural networks¹⁰. Despite the vast literature on HTE estimation, evaluating the accuracy of an HTE estimator is in general open.

An assessment approach measures the performance of estimators on future data and guides estimator comparison. Aware that a large proportion of HTE estimators involve hyper-parameters, such as the amount of penalization in LASSO-based estimators, number of trees in random-forests-based estimators, efficient model selection or tuning methods are ultra-important.

The major difficulty of the HTE assessment is attributed to the “invisibility” of HTE. Standard assessment methods evaluate the performance of a predictor by comparing predictions to observations on a validation dataset. The approach is valid since the observations are unbiased realizations of the values to be predicted. In contrast, in the potential outcome model we observe the response of a unit under treatment or control, whereas the value to be predicted, i.e., HTE, is the difference of the two. Therefore, HTE is not observable, and the standard assessment methods can not be applied.

In this paper, we design a two-step assessment approach. In the first step, we match treated and control units and regard the differences in matched pairs’ responses as the HTE pseudo-observations. In the second step, we compare predictions to the pseudo-observations and compute the prediction error. We propose a distance based on proximity scores in random forests for matching. We also introduce a matching method that minimizes the average pair distance instead of the more commonly used total distance¹¹, and provide an efficient matching algorithm adapted from the average minimum-cost flow problem.

For conducting the assessment approach with cross-validation, we recommend a match-then-split principle. Explicitly, we first perform matching on the complete dataset, then split the matched pairs into different folds for cross-validation. Since the quality of matched pairs deteriorates as the sample size decreases, the pairs constructed by matching first are more similar than those obtained by splitting first. We remark that matching first does not snoop the data since the distance has no access to the HTE.

The organization of the paper is as follows. In Section 2, we introduce the HTE assessment background and discuss related works. In Section 3, we introduce the assessment approach with a hold-out validation dataset. In Section 4, we discuss how to conduct the assessment in the framework of cross-validation. In Section 5, we compare several assessment approaches on synthetic data. In Section 6, we illustrate the assessment approach’s performance on a real data example. In Section 7, we extend the assessment approach to handle various types of responses. In Section 8, we provide discussions on future works.

2. Background

2.1. Potential outcome model

We consider the Neyman-Rubin potential outcome model with two treatment assignments. Each unit is associated with a p dimensional covariate vector X independently sampled from an underlying distribution $\mathbb{P}$. Given covariates X, a binary group assignment W ∈ {0, 1} (1 for the treatment group and 0 for the control group) is generated from the Bernoulli distribution with success probability e(X), i.e., the propensity score^12;13. Each unit is also associated with two potential outcomes Y (0), Y (1). We observe Y (1) if the unit is under treatment and Y (0) if the unit is under control. Let ν(x) and μ(x) be the treatment and control group mean functions respectively. We assume the potential outcomes follow

$$Y(1)\mid X=\nu (X)+\epsilon ,$$

$$Y(0)\mid X=\mu (X)+\epsilon ,$$

where ε is some mean zero noise independent of X, W. We define HTE as the difference of the group mean functions: τ(x) := ν(x) − μ(x). The treatment effect is heterogeneous because it depends on the covariates. We summarize the data generation model as follows,

$$\begin{gathered} X\stackrel{\text{iid}}{~}\mathbb{P}, \\ W\mid X~\mathrm{Ber}(e(X)), \\ Y\mid W,X=\mu (X)+W\cdot \tau (X)+\epsilon . \end{gathered}$$ (1)

Model (1) has implicitly made the following assumptions¹⁴.

Assumption 1

(Stable unit treatment value assumption). The potential outcomes for any unit do not depend on the treatments assigned to other units. There are no different versions of the treatment.

Assumption 2

(Unconfoundedness). The assignment mechanism does not depend on the potential outcomes given confounders:

$$\left(Y^{(1)},Y^{(0)}\right)\text{⫫}W\mid X.$$

2.2. Matching

Matching is commonly used in the estimation of average treatment effect on the treated (ATT) in observational studies^15;16;17. The primary goal of matching is to make the treatment and control groups comparable and reduce the confounding bias. A matching method consists of two parts: matching distance and matching structure¹⁷. Matching distances describe similarities between a pair of units, and matching structures characterize matches’ skeletons.

There are plentiful options for matching distances. Arguably the most popular choice is based on the propensity score^12;13. The propensity score summarizes the information to balance the covariate distribution in a scalar function, and the propensity score matching reduces the confounding bias. Another branch of distances focuses on covariates. To begin with, exact matching pairs a treated unit with a control unit only if they share the same covariates. Though exact matching produces pairs of the best quality, the method is only feasible on the dataset with a limited set of discrete covariates. To enable the matching, metrics like Mahalanobis distance^18;19 reduce the dimension of covariates and encapsulate the similarity regarding covariates in scalars. An alternative distance is based on prognostic scores that summarize the covariates’ dependence on the potential outcomes. The prognostic score matching brings a desirable form of balance to uncontrolled studies²⁰.

In terms of the matching structure, there are also several choices. Pair-matching is the simplest structure, where pairs of one treated unit and one control unit are formed. However, when the group sizes are not balanced¹⁰, pair-matching will discard a considerable number of observations. This gives birth to 1 to k (k to 1) matching²¹, that is each treated (control) unit is matched to k control (treated) units. Nevertheless, 1 to k (k to 1) matching poses a rigid restriction that all treated (control) units should be matched to the same number of control (treated) units. To provide more flexibility, methods allowing treated units matched to a variable number of control units have been discussed²². Nevertheless, those matching methods require each control unit to be used at most once. Full matching^11;23 further relaxes the restriction allowing a set of one-to-multiple and multiple-to-one matches. Furthermore, full matching moves forward from ATT estimation to allow average treatment effect (ATE) estimation.

In the following, we introduce the notations of matching used in the paper. Assume that there are n units in total: n_t treated units ${\left\{t_i\right\}}_{1\le i\le n_t}$ and n_c control units ${\left\{c_j\right\}}_{1\le j\le n_c}$. We define a match π as a function from treated units to the subsets of control units, and let ${\left\{{\pi }_{ij}\right\}}_{1\le i\le n_t,1\le j\le n_c}$ be the indicators whether the treated unit t_i and the control unit c_j are matched. Let Π be the associated set of matched pairs

$$\text{Π}:=\left\{\left(t_i,c_j\right):c_j\in \pi \left(t_i\right)\right\},$$

and denote the number of pairs in set Π as |Π|. There is a bijection between matches and sets of matched pairs, and we use the two notations exchangeably. We define the multiplicity number of the treatment group in match π as

$$M_t^{\pi }:={\max }_{t_i}\sum _{c_j}{\mathbb{1}}_{\left\{c_j\in \pi \left(t_i\right)\right\}},$$

and similarly we define $M_c^{\pi }$. Let $d_{t_i,c_j}$ be a distance defined for each treatment-control pair (t_i, c_j). We denote the total distance and the average distance of a match π under $d_{t_i,c_j}$ by

$$D_{\text{tot}}(\pi ):=\sum _{t_i}\sum _{c_j\in \pi \left(t_i\right)}{d}_{t_i,c_j},D_{\text{ave}}(\pi ):=\frac{D_{\text{tot}}(\pi )}{\left|\text{Π}\right|}.$$

2.3. Related works

In the literature of HTE, a number of works^24;25;26;10 perform accuracy assessment by predicting the response: on the training data, the treatment and control group mean functions are estimated, and the difference of the two is regarded as the HTE estimator; on the validation data, prediction errors of group mean functions are computed and used to assess the HTE estimator’s accuracy. The drawback is that large prediction errors of group mean functions do not ruin out accurate HTE estimation. In other words, the estimators of mean group functions may be of poor quality while the difference is still a reasonably good estimator of the HTE. This may happen when the HTE enjoys better properties than the mean group functions, such as higher sparsity or smoothness²⁷. Moreover, if an HTE estimator comes without estimates of the mean group functions, predicting the response can not be carried out.

Athey and Imbens propose an assessment method based on covariate matching²⁸. Each unit in the validation data is paired with a unit in the opposite treatment status and close concerning the covariates. In this way, a pseudo-observation of HTE is obtained for each pair by taking the difference of the responses, and from here standard prediction error computations can be applied. The method makes considerable progress in avoiding estimating the control group mean function, but is limited to the case where the number of covariates is not too large.

Athey and Imbens also propose the honest validation for causal recursive partitioning²⁹. Honest validation applies some tree structure to the training data and the validation data, and compares the HTE estimates based on the training and validation data. The method relies on the homogeneity of HTE at each terminal node, and it is not obvious how to generalize the method to other HTE estimators.

We finally review two assessment methods for the average treatment effect (ATE) estimation. Synth-validation³⁰ generates synthetic data based on the observed data with a sequence of possible ATEs and evaluates the ATE estimators’ performance by comparing them to the known effects. The approach can not be easily extended to HTE evaluation since the number of possible configurations of HTE increases exponentially with regard to the covariate dimension. Another approach called within-study comparison³¹ contrasts ATE estimators from observational studies with those from randomized experiments. The approach is not effective for assessing HTE estimators due to the small sample size in each heterogeneity subgroup.

3. Assessment with hold-out validation dataset

3.1. General framework

In this section, we consider the HTE assessment with a hold-out validation dataset. We consider the following validation error of an HTE estimator $\widehat{\tau }(x)$

$$\text{error}=\frac{1}{n_t}\sum _{t_i}{\left({\tau }_{t_i}-\widehat{\tau }\left(X_{t_i}\right)\right)}^2.$$ (2)

In the ideal world, for each treated unit, there is an identical copy that goes under control. We can replace ${\tau }_{t_i}$ in (2) by the difference of the two outcomes. In the real world, no identical copy exists. As a surrogate, we construct a match π between treated units and control units, and regard the differences in responses as the HTE pseudo-observations. We then estimate the validation error (2) by

$$\widehat{\mathrm{error}}(\pi )=\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{\left(Y_{t_i}-Y_{c_j}-\widehat{\tau }\left(X_{t_i}\right)\right)}^2.$$ (3)

The proposition below characterizes the bias and variance of the validation error estimator $\widehat{\mathrm{error}}(\pi )$ conditioned on the covariates and the treatment assignments. Define the oracle validation error of a match π as

$$\mathrm{error}(\pi )=\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{\left({\tau }_{t_i}-\widehat{\tau }\left(X_{t_i}\right)\right)}^2.$$ (4)

The validation error estimator equals the oracle validation error if the match π is perfect and the potential outcomes are noiseless. For a treated unit t_i and a control unit c_j, define the difference in the control group mean function values as $b_{t_i,c_j}=\mu \left(X_{t_i}\right)-\mu \left(X_{c_j}\right)$. For a match π, define the mean squared differences in the control group mean function values as $\overline{b_{\pi }^2}=\frac{1}{|\text{Π}|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{b}_{t_i,c_j}^2$.

Proposition 1.

Assuming model (1), Var(ε) = σ², Var(ε²) = κσ⁴, we have

$$\begin{gathered} {\left(1-\sqrt{\frac{\overline{b_{\pi }^2}}{error(\pi )}}\right)}^2\le \frac{\mathbb{E}[\widehat{error}(\pi )]-2{\sigma }^2}{error(\pi )}\le {\left(1+\sqrt{\frac{\overline{b_{\pi }^2}}{error(\pi )}}\right)}^2, \\ \mathrm{Var}(\widehat{error}(\pi ))\le \frac{M_t^{\pi }+M_c^{\pi }-1}{\left|\text{Π}\right|}\left((4\kappa +8){\sigma }^4+32{\sigma }^2\left(\overline{b_{\pi }^2}+error(\pi )\right)\right). \end{gathered}$$

According to Proposition 1, the bias of the validation error is more problematic in match construction. The following example of random matching shows the bias may not vanish even if we have infinite data, while the variance will always go to zero. Assume there is only one binary covariate following the Bernoulli distribution with success probability one half. Let the control group mean function be $\mu (x)={\mathbb{1}}_{\{x=1\}}$, and the propensity score be e(x) = e^2x−1/(1+e^2x−1). On the one hand, the average squared difference $\overline{b_{\pi }^2}$ of random pair-matching is (1 + e²)/(1 + e)² in expectation, and the bias of $\widehat{\mathrm{error}}(\pi )$ is non-zero independent of the sample size. On the other hand, the variance upper bound is inversely proportional to the number of pairs and will vanish as long as the multiplicity numbers $M_t^{\pi }$, $M_c^{\pi }$ go to infinity slower than the number of pairs |Π|, e.g., $M_t^{\pi }$, $M_c^{\pi }$ are fixed at constant level.

Proposition 1 suggests that (1) a smaller average squared difference $\overline{b_{\pi }^2}$ will result in smaller upper bounds for both the bias and the variance; (2) a larger multiplicity numbers $M_t^{\pi }$, $M_c^{\pi }$ will lead to a smaller $\overline{b_{\pi }^2}$ and thus a smaller bias, but possibly a larger variance. Since the bias is the primary concern, we recommend minimizing similar quantities of $\overline{b_{\pi }^2}$ and enforcing constant order multiplicity numbers $M_t^{\pi }$,$M_c^{\pi }$. In the following, we design a matching method following the idea.

3.2. Matching distance

Motivated by Proposition 1, we match treated and control units with similar control group mean function values. On the validation data, we first build a random forest on the control group which learns the control group mean function. Next, we compute each treatment-control pair’s proximity score: the number of trees that the two units end up in the same terminal node. We define the proximity score distance by subtracting the proximity score from the total number of trees. The proximity score distance is a pseudo-metric. A smaller proximity score distance suggests a closer pair in the eye of the random forest.

We compare the proximity score distance with other popular matching distances. Propensity score distances are of little relevance here because two units similar in the control group mean function values are not necessarily close in the propensity scores, and vice versa. Exact covariate matching serves the goal but is usually unrealistic. Besides, distances based solely on covariates often treat covariates equally and are inefficient when only a small proportion of the covariates are informative to the control group mean function.

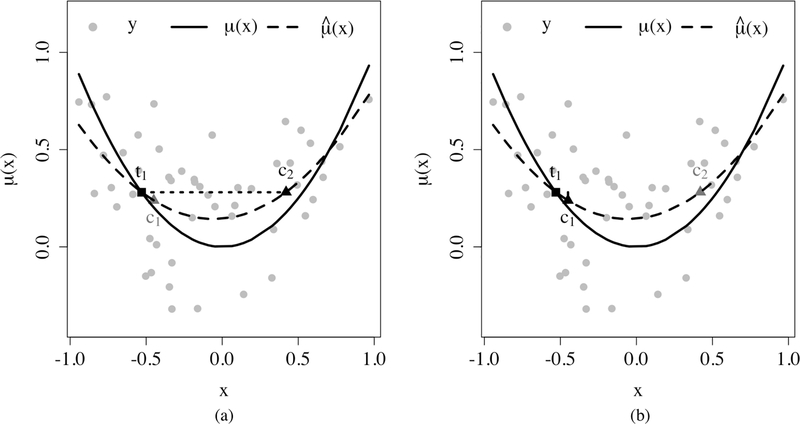
Prognostic score distances²⁰ are the most relevant. Prognostic scores are introduced to provide a form of balance desirable for ATE estimation. Prognostic scores summarize the association between covariates and control group potential outcomes. Mathematically, we call ψ(X) a prognostic score if Y (0) ⫫ X | ψ(X). Prognostic scores are not unique, and the control group mean function is a valid prognostic score. We consider the prognostic score distance: the absolute difference of control group mean function values. In comparison with the prognostic score distance, the proximity score distance admits two advantages. First, the absolute difference of control group mean function values rely more heavily on accurate estimates and are less robust to outliers. The reason is that the proximity scores only depend on the tree structures, while the control group mean function estimates also depend on the responses at each terminal node. Second, as Figure 1 shows, matching on distances based on estimated control group mean functions may pair units close in estimates but far apart in the influential covariates, while matching on the proximity score distance will result in pairs with close estimated control group mean functions as well as similar influential covariates. The latter is less likely to produce spurious treatment-control pairs.

Figure 1.

(a): pair (t₁, c₂) favored by the prognostic score distance

(b): pair (t₁, c₁) favored by the proximity score distance

Comparison of the proximity score distance and the prognostic score distance. The blue curves are the true control group mean function, gray points are observations, and the red curves are the estimated control group mean function via least squares. For the treated unit t₁, there are two candidate control units c₁ and c₂. Candidate c₁ is closer with regard to the true control group mean function, i.e., $\left|\mu \left(x_{t_1}\right)-\mu \left(x_{c_1}\right)\right|<\left|\mu \left(x_{t_1}\right)-\mu \left(x_{c_2}\right)\right|$. Candidate c₂ is closer with regard to the estimated control group mean function, i.e., $\left|\widehat{\mu }\left(x_{t_1}\right)-\widehat{\mu }\left(x_{c_1}\right)\right|>\left|\widehat{\mu }\left(x_{t_1}\right)-\widehat{\mu }\left(x_{c_2}\right)\right|$. In the left panel, the prognostic score distance prefers c₂. In the right panel, the proximity score distance prefers c₁ since there is likely to be a split between $x_{t_1}$ and $x_{c_2}$, and thus t₁ and c₂ will end up in different terminal nodes.

We highlight that to ensure objectivity, only the control group is used for learning the proximity score distance. As discussed by Hansen²⁰, models fitted only to the control units, i.e., the realizations of Y (0), in general do not carry information about the HTE, i.e., the differences Y (1) − Y (0). In other words, the proximity scores based on the control group can be viewed as nuisance to the HTE, and the theoretical foundation of conditioning on such statistics can be traced to the conditionality principles illustrated, for example, by Cox and Hinkley³². In contrast, if both the treatment and the control groups are touched in the proximity score distance construction, the distance is no longer ancillary to the HTE and is prone to data dredging.

3.3. Matching structure

Given a distance, by Proposition 1, we aim to find a match in which (1) paired control units and treated units are close regarding the provided distance; (2) as many units as possible are used; (3) no units are overused.

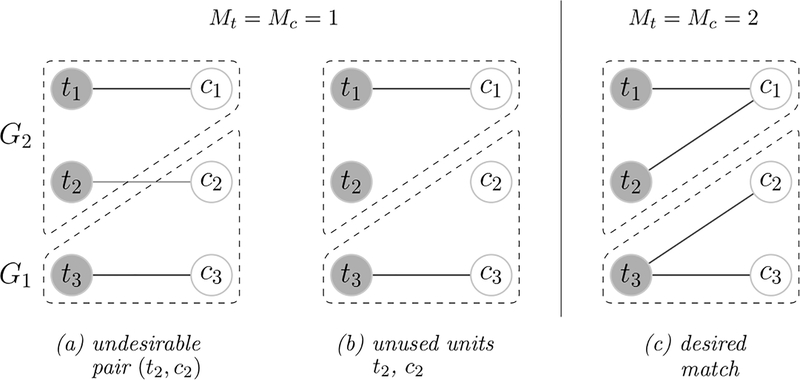
To illustrate the three criteria, we consider the example in Figure 2. There are two clusters G₁, G₂, where units in the same cluster share similar covariates and units in different clusters differ in covariates. As a result, control group mean function values are similar within clusters but different across clusters. We further assume that the units in cluster G₂ are more likely to be treated, and the opposite for cluster G₁. We observe more treated units in cluster G₂ and more control units in cluster G₁. There are three match candidates: in panel (a) each treated unit is matched to exactly one control unit and all the units are used, but there are undesirable matches across clusters; in panel (b) one-to-one matching is conducted and no pairs consist of units from different clusters, but part of the control units and the treated units are not used; in panel (c) there are no across-cluster pairs, every unit is matched, the treated units in cluster G₁ are used twice and similarly for the control units in cluster G₂. Among the three matches, panel (c) satisfies the three properties aforementioned and is the most favorable candidate.

Figure 2.

Example of matching structure. There are two equal-sized clusters G₁, G₂, where units in the same cluster share similar covariates and units not from the same clusters differ in covariates. Control group mean function values are similar within clusters but different across clusters. Cluster G₂ has more treated units, while cluster G₁ has more control units. In (a), (b) $M_t^{\pi }=M_c^{\pi }=1$, and in panel (c) $M_t^{\pi }=M_c^{\pi }=2$.

The example is motivated by the confounding phenomenon in observational studies. Confounders influence both the propensity score and the control group mean function. If we cluster the units according to the confounder values, control group mean function values and proportions of treated units will be different across clusters – the scenario in Figure 2.

To find a match with the desired properties, we propose the following matching structure

$$\underset{\pi }{\min }{D}_{\text{ave}}(\pi )$$ (5)

$$m_c\le \sum _{t_i}{\mathbb{1}}_{\left\{c_j\in \pi \left(t_i\right)\right\}}\le M_c,\forall c_j,$$ (6)

$$m_t\le \sum _{c_j}{\mathbb{1}}_{\left\{c_j\in \pi \left(t_i\right)\right\}}\le M_t,\forall t_i,$$ (7)

with pre-specified m_c, m_t, M_c, M_t ≥ 0. The lower bounds in the multiplicity constraints (6), (7) guarantee that as many units as possible are used. The upper bounds in the multiplicity constraints (6), (7) enforce that no units are matched excessively. The objective function (5), focusing on the average distance, prefers a match with more good quality pairs to fewer poor quality pairs. Particularly for the example in Figure 2, the total distance minimization may rule out panel (c) while the average distance minimization always prefers panel (c). In the following, we discuss the multiplicity constraints (6), (7), and the objective function (5) in detail.

3.3.1. Multiplicity constraints

Arguably the most common multiplicity parameters are M_t = M_c = 1, and m_t = 1, m_c = 0. The constraint requires each treated unit to be matched to one control unit and no control units are used multiple times. The constraint can be stringent if multiple control units are close to one treated unit and vice versa. Consider the example in Figure 2. If M_t = M_c = 1, m_t = 1 are enforced, a proportion of the control units in cluster G₁ will be matched to the treated units in cluster G₂. If we relax m_t = 1 and avoid pairs across clusters, part of the control units in cluster G₁ and part of the treated units in cluster G₂ will not be matched as in panel (b). If we consider M_t = M_c = 2, m_t = m_c = 1, there will be treated units in cluster G₁ matched to multiple control units, and the same for the control units in cluster G₂ as in panel (c). The match contains no pairs of units from different clusters and uses all the data. Therefore, we recommend M_t and M_c to be reasonably large and m_t = 1 if n_t ≤ n_c.

3.3.2. Objective function

The major difference between the aforementioned matching and the full matching¹¹ is the objective function: the former focuses on the average distance, and the latter focuses on the total distance. If the number of matched pairs is fixed, the total distance minimization and the average distance minimization are equivalent. This is the case in pair-matching where the number of matched pairs equals that of the treated units. However, when the number of matched pairs is not fixed, the average distance minimization and the total distance minimization may favor different matches.

The following proposition further illustrates how the average distance minimization and the total distance minimization are different. We call a matching method invariant to the translation of distance if for any distances d₁, d₂ such that d₂(t_i, c_j) = d₁(t_i, c_j) + c for some constant c, the resulted matches are the same. We call a matching method invariant to the scale of distance if for any distances d₁, d₂ such that d₂(t_i, c_j) = c·d₁(t_i, c_j) for some positive constant c, the resulted matches are the same.

Proposition 2.

If the optimization problem (5) is feasible,

1. the average distance minimization is translation and scale-invariant, and the total distance minimization is scale-invariant but not translation-invariant;

2. given multiplicity parameters M_t, M_c, m_t, m_c, let π_ave and π_tot denote an optimal solution of the average distance minimization and the total distance minimization respectively, then

$$D_{ave}\left({\pi }_{ave}\right)\le D_{ave}\left({\pi }_{tot}\right),D_{total}\left({\pi }_{ave}\right)\ge D_{\text{total}}\left({\pi }_{tot}\right),\left|{\text{Π}}_{ave}\right|\ge \left|{\text{Π}}_{tot}\right|\text{.}$$

By Proposition 2, if D_ave(π) is relevant to $\overline{b_{\pi }^2}$, $\widehat{\mathrm{error}}\left({\pi }_{\text{ave}}\right)$ will be less biased and variant compared to $\widehat{\text{error}}\left({\pi }_{\text{tot}}\right)$. In Section 5, we demonstrate that the method minimizes the average proximity score distance is also associated with small $\overline{b_{\pi }^2}$. Besides, the average distance minimization produces a larger number of pairs, which further reduces the variance of $\widehat{\mathrm{error}}\left({\pi }_{\text{ave}}\right)$.

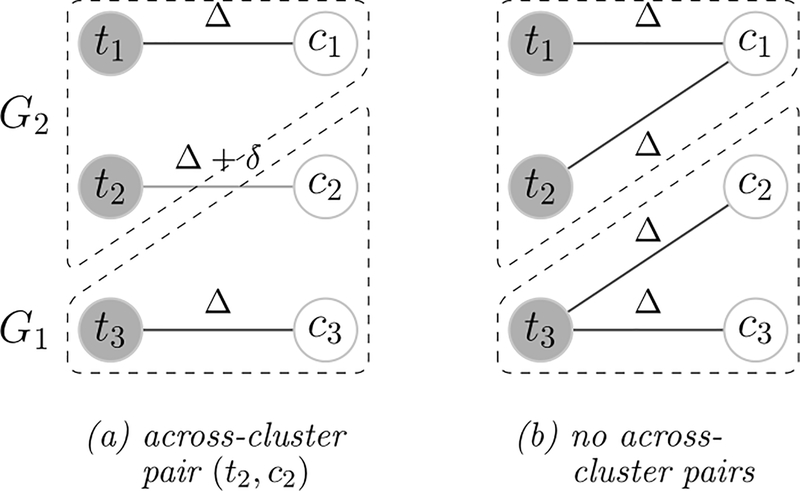
Reconsider the example in Figure 2. We further assume that distances between units in the same cluster are Δ, and those between units across clusters are Δ+δ. As demonstrated in Figure 3, there are two match candidates: in panel (a), there is one across-cluster pair, the total distance is 3Δ+δ and the average distance is Δ+δ/3; in panel (b), there are no across-cluster pairs, the total distance is 4Δ and the average distance is Δ. The average distance minimization always prefers the match with no across-cluster pairs in panel (b). On the contrary, the total distance minimization prefers the match with unfavorable across-cluster pairs in panel (a) if Δ > δ. The translation-invariance makes the average distance minimization robust to distance inflations, i.e., the distance shifts up by a constant.

Figure 3.

Comparison of the average distance minimization and the total distance minimization (continued from the example in Figure 2). Distances between units in the same cluster and across clusters are Δ and Δ + δ respectively. In panel (a), there is one across-cluster pair, the total distance is 3Δ+δ and the average distance is Δ + δ/3; in panel (b), there are no across-cluster pairs, the total distance is 4Δ and the average distance is Δ. The average distance minimization always prefers the match in panel (b), while the total distance minimization prefers the match in panel (a) if Δ > δ.

The example is motivated by multiple popular distances. Consider the semi-oracle distance $d_{t_i,c_j}={\left(Y_{t_i}(0)-Y_{c_j}(0)\right)}^2$. Let μ₁ and μ₂ be the control group mean function values in cluster G₁ and G₂. The expectation of the semi-oracle distance equals 2σ² for within-cluster pairs and 2σ² + (μ₂ − μ₁)² for across-cluster pairs. As the noise magnitude increases, the distance inflates. Another motivating distance is $d_{t_i,c_j}={\Vert X_{t_i}-X_{c_j}\Vert }_2^2$. Suppose that the group mean function only depends on the first covariate and units are clustered according to it, then the distance is ${\sum }_{k=2}^p{\left(X_{k,t_i}-X_{k,c_j}\right)}^2$ for within-cluster pairs and ${\left(X_{1,t_i}-X_{1,c_j}\right)}^2+{\sum }_{k=2}^p{\left(X_{k,t_i}-X_{k,c_j}\right)}^2$ for across-cluster pairs. As the number of nuisance covariates increases, the covariate distance shifts up.

3.3.3. Computation

There are two major approaches to solve the matching problem with total distance minimization. The first approach reformulates the matching problem as a minimum-cost flow problem^22;11. If the distances are positive, there exists a feasible integral flow achieving the minimal cost. The optimal integer flow corresponds to a solution to the aforementioned matching problem. The minimum-cost flow algorithm runs in O(n² log(n)) on sparse graphs (constant order $M_t^{\pi }$, $M_c^{\pi }$ as n → ∞). On dense graphs ($M_t^{\pi }$,$M_c^{\pi }=O(n)$), finding a minimum flow takes O(n³) time.

The second approach casts the matching problem in the language of linear programming. Let π_ij denote whether the treated unit t_i and the control unit c_j are matched. The total distance minimization problem can be rewritten as

$$\begin{gathered} \min \sum _{i=1}^{n_t}\sum _{j=1}^{n_c}{d}_{ij}{\pi }_{ij} \\ {m}_c\le \sum _{i=1}^{n_t}{\pi }_{ij}\le M_c,\forall j, \\ {m}_t\le \sum _{j=1}^{n_c}{\pi }_{ij}\le M_t,\forall i, \\ 0\le {\pi }_{ij}\le 1, \end{gathered}$$

where we relax the integer constraints π_ij ∈ {0, 1} to the linear constraints π_ij ∈ [0, 1]. In fact, as shown in the following, the extremal points defined by the linear constraints are all integer vectors. Thus the simplex method will output an optimal solution of integer values. In this way, we avoid the computationally heavy integer programming.

We show that the extremal points of the feasible regions are integer-valued. We rewrite the linear constraints in the matrix form Aπ ≤ b, where both the coefficient matrix A and the coefficient vector b are integer-valued. The coefficient matrix A defined by the linear constraints is totally unimodular³³, i.e., each subdeterminant of A is 0, 1, or −1. Then for any integer vector b, the polyhedron {π : Aπ ≤ b} is integral³⁴, i.e., a convex polytope whose vertices all have integer coordinates.

Unfortunately, the two major approaches can not be directly applied to the average distance minimization problem. Standard minimum-cost flow problem requires to input the flow value, or equivalently the total number of pairs in the match. However, the flow value is not directly available in the average distance minimization. Linear programming entails a linear objective function, while the average distance is non-linear.

We propose an algorithm for the average distance minimization. The algorithm is derived from the average minimum-cost flow solver designed by Chen³⁵. Explicitly, we search for the optimal flow value via binary search. In each sub-routine, we fix a flow value and solve a minimum-cost flow problem.

Let the time of solving one minimum flow problem on a certain graph be a unit, which ranges from O(n² log(n)) to O(n³) depending on the graph structure. The average distance minimization problem only takes log(n(M_t+M_c)) time units. In other words, the algorithm is of the same time complexity as solving one minimum-cost flow problem up to logarithmic factors of the maximal number of pairs.

Finally, we summarize the assessment approach with a hold-out validation dataset in Algorithm 1.

4. Assessment with cross-validation

In practice, hold-out datasets may be costly. Cross-validation is a popular validation paradigm that uses the whole dataset for training while providing a reasonably good evaluation of the estimation performance. In this section, we discuss how to conduct the assessment approach under the framework of cross-validation.

The standard cross-validation consists of two steps: first, split the data into several folds randomly equally; second, train on all but one fold, conduct validation on the left-out fold, and repeat this for each fold. Naively integrating the assessment approach and the standard cross-validation framework raises the issue: the former splitting hurts the later matching. Consider the most favorable case where the samples are perfectly paired. By splitting first, we may assign two perfectly paired units to different folds, thus missing the ideal match.

To tackle this problem, we propose to do matching before splitting, short as match-then-split. Particularly, on the whole dataset, we obtain proximity score distances and solve the average distance minimization problem to obtain the optimal match. We next split the samples into folds preserving the pair-structures. In this way, we avoid assigning matched units to different folds. Recall the perfectly matched example. If we apply the match-then-split principle, all perfect pairs will be matched and stay in the same fold.

A natural concern of the match-then-split principle is data snooping. Note that the proximity score distance is obtained solely on the control group data, and the treatment group is not touched. The one-sided data provides no information for the differences between the two groups. Therefore, splitting after matching is blind to the validation target and fair.

A new difficulty arises in data splitting to keep matched units together. We represent a match by an undirected graph where each node denotes a unit. There is an edge between two nodes if and only if the two units are matched. The pair-preserving constraint means that connected components should stay together. Since each unit is allowed to be matched multiple times, there may exist large connected components as depicted in Figure 4. The graph may be connected in the extremist scenario, and splitting without breaking pairs is impossible.

Figure 4.

Example of pruning. In panel (a), the graph is a chain of alternate treated units and control units. There are three removable edges (t₂, c₁), (t₂, c₂), (t₃, c₂). We pick the removable edge with the maximal distance, i.e., (t₂, c₂), eliminate the edge and obtain panel (b). After pruning (t₂, c₂), edges (t₂, c₁) and (t₃, c₂) are no longer removable, and the set of removable edges is empty. Therefore, we stop pruning. In the pruned match, units can be split into two connected subgroups: {t₁, t₂, c₁} and {t₃, c₂, c₃}. The connected subgroups either consist of one treated unit and multiple control units or vice versa.

To enable proper splitting, we modify the average distance minimization problem. Beyond the multiplicity constraints (6), (7), we further restrict the maximal path length of the graph to be at most three – a constraint also adopted in full matching¹¹. As proved in Lemma 1, under the maximal depth constraint, only two possible types of connected components are allowed: (1) one treated unit with multiple matched control units; (2) one control unit with multiple matched treated units. The maximal size of the connected components is upper bounded by 1+max{M_t, M_c} – usually small compared to the sample size. In this way, we can assign the connected components randomly into folds without destroying the pair-structures.

In full matching, the constraint is automatically fulfilled. However, this is not true for the average distance minimization. In fact, no known efficient network algorithm works under the path length constraint. As a surrogate, we propose the following heuristic pruning algorithm. Particularly, we start with the solution of the average distance minimization. We call an edge (t_i, c_j) removable if the treated unit t_i is matched to more than one control unit, and the control unit c_j is matched to more than one treated unit. As shown in Lemma 1, the new constraint is equivalent to the condition that there are no removable edges in the graph. We iteratively prune the highest cost removable edge until the set of removable edges is empty. See Figure 4 for an example. The approach is summarized in Algorithm 2. We call the matching with pruning “FACT matching”: “Full matching constraints” and “Average CosT minimization”.

Lemma 1.

In the graph representing a match, the following constraints are equivalent:

1. the maximal path length is at most three;

2. there are only two types of connected components: one treated unit with multiple control units and vice versa;

3. there is no such edge (t_i,c_j) that t_i is connected with multiple control units and c_j is connected with multiple treated units.

The pruned match possesses several appealing properties. First, pairs after pruning are a subset of the matched pairs of the average distance minimization. Thus multiplicity constraints (6) and (7) are satisfied. Second, if the match without the path-length constraint can avoid low-quality pairs, the pruned match will automatically avoid those pairs by choosing from existing pairs. Third, by eliminating the removable pair with the maximal distance each time, we are heading greedily towards the optimal solution with the path-length constraint.

5. Simulation

In this section, we compare various validation methods under the cross-validation framework on the synthetic data generated from model (1).

We consider the following validation methods for comparison.

• Response prediction (prd). On the training data, we estimate the treatment and control group mean functions. On the validation data, we compare the out-of-sample predictions with the observations;

• Covariate distance with FACT matching (cvr). We compute validation errors as described in Section 4 with Mahalanobis distance¹ and FACT matching;

• Proximity score distance with full matching² (full). We compute validation errors as described in Section 4 with the proximity score distance and full matching;

• Proximity score distance with FACT matching and the split-then-match principle (S-M). We first split samples randomly into folds, then match within folds using the proximity score distance and FACT matching. The rest of the steps are the same as described in Section 4;

• Prognostic score distance with FACT matching (prgn)³. We compute estimation errors as described in Section 4 with the prognostic score distance⁴ and FACT matching;

• Proximity score distance with FACT matching (combo). We compute estimation errors as described in Section 4 with the proximity score distance and FACT matching.

Table 1 summarizes the characteristics of the validation methods.

Table 1:

Summary of the validation methods’ characteristics.

method abbreviation	target of comparison13	matching distance	matching structure	split or match first
prd	response	NA	NA	NA
cvr	HTE	covariate dist.	FACT matching	match
full	HTE	proximity score dist.	full matching	match
S-M	HTE	proximity score dist.	FACT matching	split
prgn	HTE	prognostic score dist.	FACT matching	match
combo	HTE	proximity score dist.	FACT matching	match

There are a number of tuning parameters. As for the random forests to compute the proximity score distance and the prognostic score distance, we determine the number of trees and the number of variables randomly sampled as candidates at each splits by the out-of-bag mean-squared errors. In terms of the maximal group sizes in full matching and FACT matching, we experiment with a grid of values. As the group size increases, the distance objectives first decrease then stabilize, and we choose the “elbow point”⁵.

We consider the following four data generation settings.

• Setting I. Setting I serves as the default. There are in total 200 units and each unit is associated with 10 covariates generated i.i.d. uniformly from [−1, 1]. The HTE, treatment and control group mean functions are linear of the first 5 covariates. The treatment assignment is randomized, i.e., the propensity score is always 0.5. We use 10-fold cross-validation;

• Setting II. Compared to setting I, in setting II we only increase the number of covariates from 10 to 100. The HTE, treatment and control group mean functions remain the same, and are independent of the additional covariates. Only 5% of the covariates are meaningful, and the rest are nuisances;

• Setting III. Compared to setting I, in setting III we only increase the number of folds in cross-validation from 10 to 25. After splitting, there are around 8 units in each fold;

• Setting IV. Compared to setting I, setting IV is more realistic with two major changes. First, we let the propensity score depend on the covariates and be correlated with the group mean functions and the HTE. Second, we also change the group mean functions to non-linear functions while keeping the HTE linear. The reason for adding non-linear terms into the control group mean function instead of the HTE is that, according to domain knowledge, the control group mean function, e.g., blood pressure, is usually influenced by more factors than the HTE, e.g., the difference in blood pressure induced by therapy, and in a more complicated way.

The signal-noise-ratios of all settings are below one. Table 2 summarizes the characteristics of the simulation settings.

Table 2:

Summary of the simulation settings’ characteristics.

Simulation setting	group mean functions	number of covariates	propensity score	number of folds
I	linear	10	0.5	10
II	linear	100	0.5	10
III	linear	10	0.5	25
IV	non-linear	10	nonconstant	10

We evaluate the tuning performance of the validation methods applied to the following LASSO-based HTE estimator⁷:

$$(\widehat{\alpha },\widehat{\beta })=\underset{\alpha ,\beta }{\mathrm{argmin}}\frac{1}{2n}\sum _{i=1}^n{\left(Y_i-X_i^{\top }\alpha -W_i\cdot X_i^{\top }\beta \right)}^2+\lambda \left(\Vert \alpha {\Vert }_1+\Vert \beta {\Vert }_1\right).$$ (8)

The approach (8) estimates the control group mean function by $X^{\top }\widehat{\alpha }$ and the HTE by $X^{\top }\widehat{\beta }$. We add ℓ₁ penalties of α and β since the true control group mean function and the true HTE depend on only a few covariates. The approach is not the state-of-art of HTE estimation. However, our emphasis is on the validation step but not the estimation step and the estimator serves our goal well: an HTE estimator making variable selection and involving only one tuning parameter. We expect that a good validation method should be able to select the best tuning parameter for the estimator (8).

To evaluate the tuning performance, for each setting in Table 2, we run the validation methods in Table 1 with a sequence of tuning parameters Λ. We pick the tuning parameters λ_method with the minimal validation errors. We then solve (8) on the whole dataset with the selected hyper-parameters to obtain ${\widehat{\beta }}_{{\lambda }_{\text{method}}}$ and compute the estimation error ${\text{MSE}}_{\text{method}}:={\Vert {\widehat{\beta }}_{{\lambda }_{\text{method}}}-\beta \Vert }_2^2$. Meanwhile, we define the oracle estimation error as ${\text{MSE}}_{\text{oracle}}:={\min }_{\lambda \in \Lambda }{\Vert {\widehat{\beta }}_{\lambda }-\beta \Vert }_2^2$. For comparison, we compute the log ratio of MSE_method over MSE_oracle:

$$\log \left(\frac{{\text{MSE}}_{\text{method}}}{{\text{MSE}}_{\text{oracle}}}\right),$$ (9)

referred to as relative MSE in the following. The smaller the relative MSE is, the better the validation method performs.

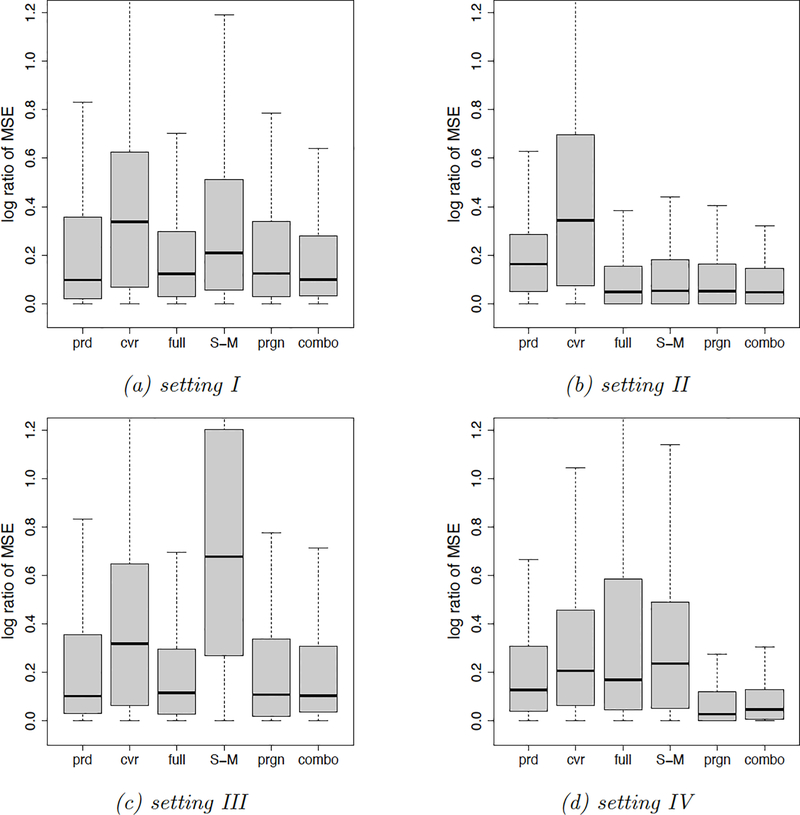
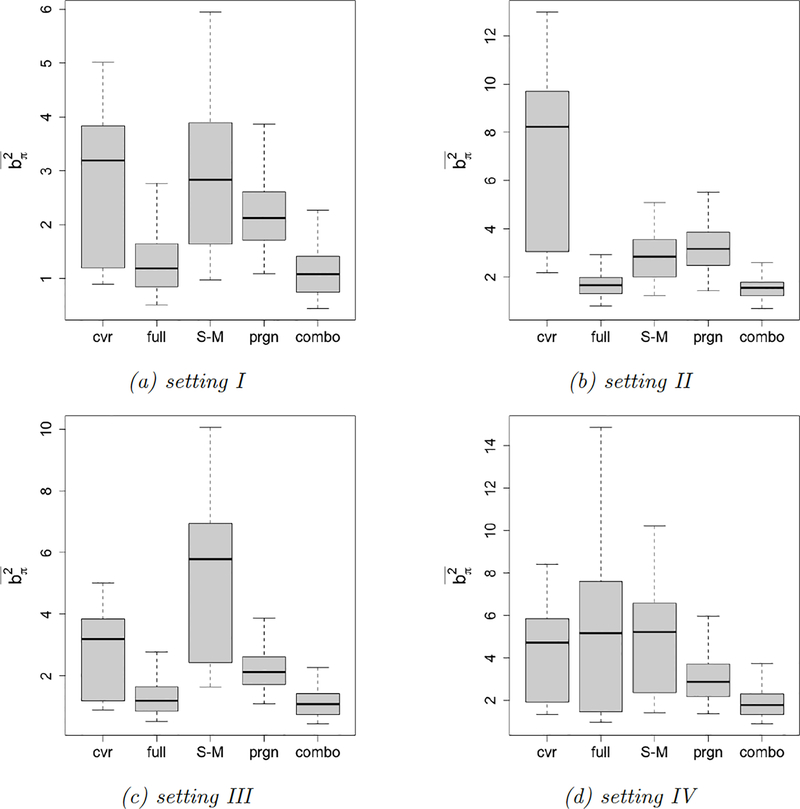
In Figure 5 we present box plots of the relative MSE. Overall, the combo and the prgn methods produce the smallest relative MSEs. The cvr method is problematic in Setting II, since the covariate distance’s quality deteriorates in the presence of many irrelevant covariates. The S-M method produces a large relative MSE in setting III, since there are fewer units in each fold and matched pairs are of lower quality. The full method is less attractive in setting IV – a setting similar to the example in Figure 3 where the average distance minimization (FACT matching) is preferred over the total distance minimization (full matching). The prd method is always dominated by the combo and the prgn methods. We also compare the mean squared differences $\overline{b_{\pi }^2}$ in all simulation settings. The results of $\overline{b_{\pi }^2}$ agree with those of the relative MSE, and the combo method always produces the smallest $\overline{b_{\pi }^2}$. The plots can be found in the appendix.

Figure 5.

Relative MSE box plots. We display the relative MSE of the validation methods in Table 1 under the simulation settings in Table 2. Each setting is repeated 200 times.

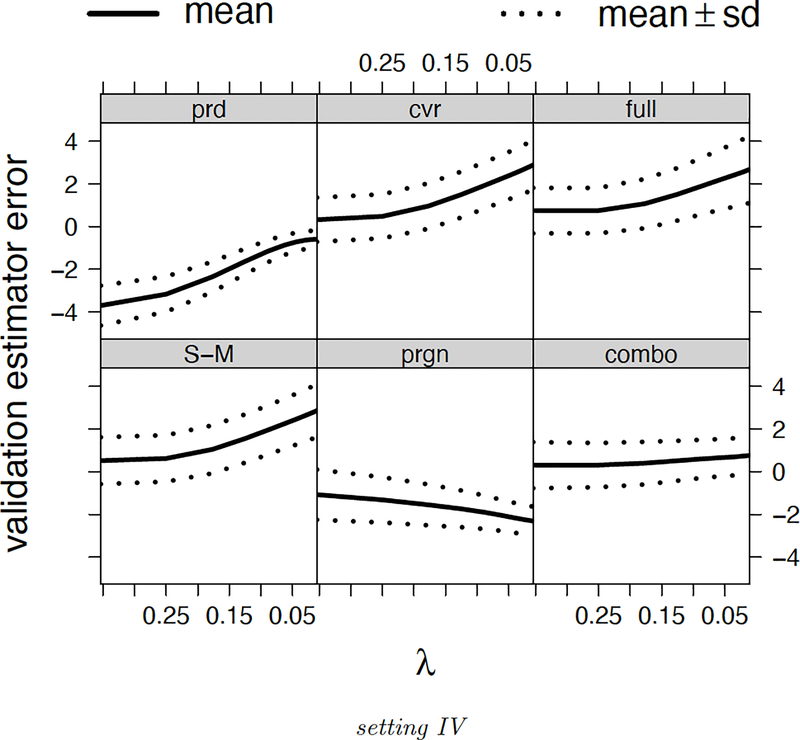
Furthermore, we compare validation error curves. Figure 6 presents the error curves of validation error estimators in the setting IV⁶. The combo method produces the smallest biases across different λ. The validation error estimators’ biases are more problematic than the variances. We also regress average validation error curves over the oracle error curve. In Table 3 we present coefficients and R² of the regressions. Both ideal values are one. The results agree with those of the relative MSE: the combo method leads the performance, and the cvr method, S-M method, full method are not very promising in setting II, III and IV respectively. We also observe that compared to the combo method, the prgn method is performing worse regarding the validation error curve.

Figure 6.

Error curves of validation error estimators (setting IV). The solid curves demonstrate the validation error estimators’ biases. The dotted curves demonstrate the biases plus or minus one standard deviation of $\widehat{\mathrm{error}}(\pi )-\mathrm{error}(\pi )$. Each setting is repeated 200 times.

Table 3:

Comparison of validation error curves. We average the MSEs of the validation methods in Table 1 at each tuning parameter in Λ under the simulation settings in Table 2. We regress validation error curves over the oracle error curve and present the coefficient, R² of each regression.

method	I		II		III		IV
	coef.	R2	coef.	R2	coef.	R2	coef.	R2
prd	2.97	0.99	1.32	0.92	2.95	0.99	4.15	0.95
cvr	1.81	0.88	0.75	0.88	1.78	0.89	2.18	0.81
full	1.05	1.00	1.08	1.00	1.03	1.00	1.76	0.90
S–M	1.56	0.93	0.96	0.99	1.12	0.14	2.02	0.85
prgn	0.68	0.99	1.16	0.98	0.67	0.99	0.78	1.00
combo	0.99	1.00	1.09	1.00	0.98	1.00	1.13	1.00

6. Real data example

We compare the validation methods on the national supported work (NSW) program data^36;37. We use the validation results obtained from a randomized evaluation of the NSW program as the oracle, and compare with the results on an observational dataset combining the treated units from the NSW randomized evaluation and the non-experimental control units from the 1978 panel study of income dynamics (PSID).

The National Supported Work Demonstration is a program aiming to study whether and how employment benefits disadvantaged workers to get and hold unsubsidized jobs. Qualified applicants were randomly assigned to treatment and guaranteed with jobs for 9 to 18 months. We focus on the subset ⁷ with 185 treated units and 260 control units, referred to as the NSW-NSW dataset in the following. Pre-intervention variables include pre-intervention earnings, marital status, race, education and age. The distributions of pre-intervention variables in the treatment and control groups are very similar except hispanic and no-degree ⁸.

We follow Dehejia and Wahba’s analysis and create an observational control group based on the PSID⁹. The control group consists of 128 units with the same set of pre-intervention variables. We then construct an observational study dataset combining the NSW treatment group and the PSID control group, referred to as the NSW-PSID dataset in the following. Unlike the NSW-NSW dataset, the pre-intervention variables in the NSW-PSID dataset are significantly different across the treatment and control groups: the control group are on average 12.4 years older, less likely to be black (45% versus 84%), more likely to be married (70% versus 19%) and earn $1079 more in the year before the program. Table 4 summarizes the pre-intervention variables’ characteristics of the NSW-NSW and the NSW-PSID datasets.

Table 4:

Pre-intervention variables’ characteristics of the NSW-NSW and NSW-PSID datasets. Standard errors are in parentheses. The NSW-NSW dataset contains the NSW treatment group and the NSW control group. The NSW-PSID dataset contains the NSW treatment group and the PSID control group. The pre-intervention variables are: age: age in years; education: number of years of schooling; black : 1 if black and 0 otherwise; hispanic: 1 if hispanic and 0 otherwise; no degree: 1 if no high school degree and 0 otherwise; married: 1 if married and 0 otherwise; pre-intervention income: earnings (in dollars) in the calendar year 1975.

	sample size	Age	education	black	hispanic	married	no-degree	pre-intervention income ($)
NSW treated	185	25.82 (0.34)	10.35 (0.10)	0.84 (0.02)	0.06 (0.01)	0.19 (0.02)	0.71 (0.02)	1532 (153)
NSW control	260	25.05 (0.33)	10.09 (0.08)	0.83 (0.02)	0.11 (0.01)	0.15 (0.02)	0.83 (0.02)	1267 (147)
PSID control	128	38.26 (1.14)	10.30 (0.28)	0.45 (0.04)	0.12 (0.03)	0.70 (0.04)	0.51 (0.04)	2611 (493)

To prepare the data for the LASSO estimator in (8), we log-transform the heavy-tailed pre-intervention income and the post-intervention income¹⁰. We center and normalize the continuous pre-intervention variables education, age and pre-intervention income in both datasets by the means and standard deviations in the NSW-NSW dataset. We add two-way interactions between the 7 pre-intervention variables, which amounts to 28 features in total.

We evaluate the validation methods in Table 1 applied to the LASSO estimator (8). On the NSW-NSW dataset, we compute as described in Section 4 the 20-fold cross-validation errors with a sequence of tuning parameters¹¹. We also obtain the LASSO estimates based on the full NSW-NSW dataset corresponding to the sequence of tuning parameters. On the NSW-PSID dataset, we compute the hold-out validation errors of the LASSO estimates from the full NSW-NSW dataset as described in Section 3. We finally compare the LASSO estimates selected from the two datasets. For each validation method, we regard the selected estimate based on the validation errors of the NSW-NSW dataset as the oracle, and expect it to select the same estimate based on the NSW-PSID dataset. Table 5 demonstrates the results.

Table 5:

Comparison of the LASSO estimates selected from the NSW-NSW dataset and the NSW-PSID dataset by minimizing the validation errors. For each validation method, we compute ${\Vert {\widehat{\tau }}_{NSW}-{\widehat{\tau }}_{PSID}\Vert }_{2,t}:={\left(1/n_t{\sum }_{W_i=1}{\left({\widehat{\tau }}_{NSW}-{\widehat{\tau }}_{PSID}\right)}^2\right)}^{1/2}$ – the treatment group L₂ norm of the difference of the selected LASSO estimates ${\widehat{\tau }}_{NSW}$ from the NSW-NSW dataset and ${\widehat{\tau }}_{PSID}$ from the NSW-PSID dataset. The results regarding the L₂ norm based on the NSW-NSW control group and the NSW-PSID control group are similar and are presented in Table 6 in the appendix.

method	prd	cvr	full	S-M	prgn	combo
${||{\widehat{\tau }}_{\mathrm{NSW}}-{\widehat{\tau }}_{\mathrm{PSID}}||}_{2,\text{t}}$ × 102	0.74	1.36	0.00	1.36	4.36	0.00

According to Table 5, the full method and the combo method select the same LASSO estimates across datasets, while the other validation methods do not pick consistent estimates. In particular, the prgn method selects the most different estimates since the response is rather noisy and the prognostic score distance produces doubtfully close pairs. Often randomized experiment data like the NSW-NSW dataset are rare and expensive to acquire compared to observational study data like the NSW-PSID dataset. With a validation method making consistent selections across datasets, we can assess an HTE estimate using observational study data while arriving at the same result as using randomized experiment data.

The selected LASSO estimates of the combo and the full methods coincide on both datasets. The selected estimate concludes that there is an overall 13.3% improvement in the post-intervention income brought by the NSW program¹². The finding of the overall positive effect agrees with previous works^36;37 though we analyze the log-transformed income while they focus on the original income. The LASSO estimate also suggests that subgroups black and married, young and married, young and high pre-intervention income benefit more from the program.

7. Extension to general exponential family

In the previous sections, we focus on continuous responses. There are other types of outcomes worthwhile to study. For instance, doctors measure whether the patients who underwent the operation or not survive to a certain time spot to study the effectiveness of surgery; agencies compare the times of bicycles used from automated bicycle counters before and after the policy is enforced to investigate the influence of a policy encouraging non-motor vehicles. In this section, we extend the aforementioned assessment approach to address multiple types of responses.

We generalize the model (1) to the general exponential family, which deals with a wide range of responses, including binary data and count data. Mathematically, we assume

$$Y\mid W,X\stackrel{ind}{~}\kappa (Y)\cdot \exp \{\eta (X,W)Y-\psi (\eta (X,W))\},$$ (10)

where η(x, w) represents the natural parameter, ψ(η) is the cumulant generating function, and κ(y) is the carrying density. We write

$$\eta (x,w)=\{\begin{array}{ll}\mu (x),\hfill & w=0,\hfill \\ \nu (x),\hfill & w=1,\hfill \end{array}$$

and focus on the quantity τ(x) := ν(x)−μ(x). The model (10) with Gaussian distribution is a sub-case of the model (1).

Next, we extend the validation criterion, i.e. the mean squared error in (4). We first state the following result regarding conditional likelihoods.

Proposition 3.

Consider n pairs of data {(X_i1,X_i2,W_i1,W_i2, Y_i1, Y_i2)}, where μ(X_i1) = μ(X_i2), W_i1 = 1, W_i2 = 0, and Y_i1, Y_i2 are generated independently from model (10) given X_ij, W_ij. Then the conditional likelihood of {Y_ij} given {Y_i1 + Y_i2} does not depend on μ(x).

Proposition 3 implies that with pairs perfectly matched on control group mean function values, the conditional likelihood, which serves as a valid criterion for the HTE estimation assessment, can be evaluated without μ(x). For example, consider the Gaussian distribution, the log conditional likelihood equals ${\sum }_{i=1}^n{\left(Y_{i2}-Y_{i1}\right)}^2$ up to scale.

If data comes in perfectly matched pairs, the condition μ(X_i1) = μ(X_i2) is automatically satisfied. Examples of Proposition 3 with perfectly matched pairs can be found in the book by Argesti³⁸. When such data are not available, we can apply the matching method based on the proximity score distance to construct pairs such that μ(X_i) ≈ μ(X_j). Based on the matched pairs, we compute the conditional likelihood pretending the pairs are perfectly matched, and use the conditional likelihood as the criterion for assessment.

8. Discussion

The paper discusses an assessment approach of HTE estimators by constructing pseudo-observations based on matching. In terms of the matching, we suggest to use the proximity score distance and minimize the average distance. When conducting the assessment approach under the cross-validation framework, we suggest to match before split.

Our proposed method can be further enhanced by existing matching ideas such as exact and near-exact matching¹⁶. In particular, augmentations motivated by domain knowledge could help HTE assessment when the proximity score learning is onerous, possibly due to limited samples or a large number of covariates. For instance, in the selective serotonin reuptake inhibitors (SSRIs) example discussed by Rosenbaum¹⁷, exact matching on gender is enforced with the belief that the potential outcomes would differ significantly across male and female subjects. To incorporate the gender constraint into our method, we can partition the validation samples according to gender and match within each subgroup. A more flexible alternative is incorporating the restriction into the proximity score distance, e.g., adding a large value to the distance if a treatment-control pair differs in sex.

The pseudo-observations can also be used for data calibration. Given an estimator, the standard calibration tunes the prediction bands’ widths on the hold-out data to achieve the exact coverage. As for the calibration of an HTE estimator, observations’ coverage is not the fundamental goal. We can construct pseudo-observations as discussed and determine the prediction bands’ widths by covering a certain proportion of the pseudo-observations.

A limitation of the assessment approach is the computation of matching. Solving a matching problem exactly is generally computationally heavy. Even if in the simplest case where each treated unit is mapped to exactly one control unit and the distance matrix is not sparse, minimizing the total/average distance takes O(n³) time. Thus, fast approximate matching algorithms are desirable to make the validation method scalable.

12. Appendix

12.1. Proofs

Proof of Proposition 1.

We prove for bias and variance respectively. The expectations are taken with regard to the noise ε.

For bias, under model (1)

$$\begin{gathered} \mathbb{E}[\widehat{\mathrm{error}}(\pi )]=\mathbb{E}\left[\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{\left(Y_{t_i}-Y_{c_j}-\widehat{\tau }\left(X_{t_i}\right)\right)}^2\right] \\ =\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}\mathbb{E}\left[{\left(\mu \left(X_{t_i}\right)-\mu \left(X_{c_j}\right)+\tau \left(X_{t_i}\right)-\widehat{\tau }\left(X_{t_i}\right)+{\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right] \\ =\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{\left(b_{t_i,c_j}+\tau \left(X_{t_i}\right)-\widehat{\tau }\left(X_{t_i}\right)\right)}^2+2{\sigma }^2 \\ =\mathrm{error}(\pi )+\frac{2}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{b}_{t_i,c_j}\cdot \left(\tau \left(X_{t_i}\right)-\widehat{\tau }\left(X_{t_i}\right)\right)+\overline{b_{\pi }^2}+2{\sigma }^2. \end{gathered}$$ (11)

By Cauchy-Schwarz inequality,

$$\begin{gathered} \left|\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{b}_{t_i,c_j}\cdot \left(\widehat{\tau }\left(X_{t_i}\right)-\tau \left(X_{t_i}\right)\right)\right| \\ \le {\left(\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{b}_{t_i,c_j}^2\right)}^{\frac{1}{2}}{\left(\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{\left(\widehat{\tau }\left(X_{t_i}\right)-\tau \left(X_{t_i}\right)\right)}^2\right)}^{\frac{1}{2}} \\ ={\left(\overline{b_{\pi }^2}\right)}^{\frac{1}{2}}\cdot {\left(\text{error}(\pi )\right)}^{\frac{1}{2}}. \end{gathered}$$ (12)

Plug (12) into (11), and divide both sides by error(π),

$$\frac{\mathbb{E}[\widehat{\mathrm{error}}(\pi )]-2{\sigma }^2}{\mathrm{error}(\pi )}\le 1+2\sqrt{\frac{\overline{b_{\pi }^2}}{\mathrm{error}(\pi )}}+\frac{\overline{b_{\pi }^2}}{\mathrm{error}(\pi )}={\left(1+\sqrt{\frac{\overline{b_{\pi }^2}}{\mathrm{error}(\pi )}}\right)}^2.$$

Similarly for the lower bound of the bias.

For variance, let ${\delta }_{t_i,c_j}=\tau \left(X_{t_i}\right)-\widehat{\tau }\left(X_{t_i}\right)$ for simplicity. Define the neighborhood of a matched pair (t_i, c_j) as

$${\mathcal{N}}_{t_i,c_j}^{\pi }=\left\{\left(t_i^{\prime },c_j^{\prime }\right)\in \text{Π}:t_i=t_i^{\prime }\text{or}{c}_j=c_j^{\prime },\left(t_i^{\prime },c_j^{\prime }\right)\ne \left(t_i,c_j\right)\right\}.$$

Since each treated unit falls into at most M_t pairs, and each control unit falls into at most M_c pairs,

$$\left|{\mathcal{N}}_{t_i,c_j}^{\pi }\right|\le M_t+M_c-2.$$ (13)

Under model (1),

$$\begin{gathered} \mathrm{Var}(\widehat{\mathrm{error}}(\pi ))=\mathrm{Var}\left(\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{\left(Y_{t_i}-Y_{c_j}-\widehat{\tau }\left(X_{t_i}\right)\right)}^2\right) \\ =\mathrm{Var}\left(\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j})}^2\right) \\ =\frac{1}{|\text{Π}{|}^2}(\sum _{(t_i,c_j)\in \text{Π}}\mathrm{Var}({(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j})}^2) \\ +\sum _{(t_i,c_j)\in \text{Π}(t_i^{\prime },c_j^{\prime })\in {\mathcal{N}}_{t_i}^{\pi },c_j}\mathrm{Cov}({(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j})}^2,{(b_{t_i^{\prime },c_j^{\prime }}+{\delta }_{t_i^{\prime },c_j^{\prime }}+{\epsilon }_{t_i^{\prime }}-{\epsilon }_{c_j^{\prime }})}^2)). \end{gathered}$$

Since 2 Cov(ξ₁, ξ₂) ≤ Var(ξ₁) + Var(ξ₂) for any random variables ξ₁, ξ₂,

$$\begin{gathered} \mathrm{Var}(\widehat{\mathrm{error}}(\pi ))\le \frac{1}{|\text{Π}{|}^2}(\sum _{\left(t_i,c_j\right)\in \text{Π}}\mathrm{Var}\left({\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right) \\ +\frac{1}{2}\sum _{\left(t_i,c_j\right)\in \text{Π}\left(t_i^{\prime },c_j^{\prime }\right)\in {\mathcal{N}}_{t_i^{\pi },c_j}^{\pi }}\mathrm{Var}\left({\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right)+\mathrm{Var}\left({\left(b_{t_i^{\prime },c_j^{\prime }}+{\delta }_{t_i^{\prime },c_j^{\prime }}+{\epsilon }_{t_i^{\prime }}-{\epsilon }_{c_j^{\prime }}\right)}^2\right)). \end{gathered}$$

By (13),

$$\begin{gathered} \mathrm{Var}(\widehat{\mathrm{error}}(\pi ))\le \frac{1}{|\text{Π}{|}^2}(\sum _{\left(t_i,c_j\right)\in \text{Π}}\mathrm{Var}\left({\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right) \\ +\sum _{\left(t_i,c_j\right)\in \text{Π}}\left|{\mathcal{N}}_{t_i,c_j}^{\pi }\right|\cdot \mathrm{Var}\left({\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right)) \\ \le \frac{M_t+M_c-1}{|\text{Π}{|}^2}\sum _{\left(t_i,c_j\right)\in \text{Π}}\mathrm{Var}\left({\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right). \end{gathered}$$

Recall that Var(ε) = σ², Var(ε²) = κσ⁴,

$$\begin{gathered} \frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}\mathrm{Var}\left({\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}+{\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right) \\ \le \frac{2}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}\mathrm{Var}\left({\left({\epsilon }_{t_i}-{\epsilon }_{c_j}\right)}^2\right)+4{\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}\right)}^2\mathrm{Var}\left({\epsilon }_{t_i}-{\epsilon }_{c_j}\right) \\ =\frac{2}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}(2\kappa +4)\cdot {\sigma }^4+8\cdot {\left(b_{t_i,c_j}+{\delta }_{t_i,c_j}\right)}^2{\sigma }^2 \\ \le (4\kappa +8)\cdot {\sigma }^4+32{\sigma }^2\cdot \left(\overline{b_{\pi }^2}+\mathrm{error}(\pi )\right). \end{gathered}$$

□

Proof of Proposition 2.

For C > 0,

$$\sum _{\left(t_i,c_j\right)\in \text{Π}}C\cdot d_{t_i,c_j}=C\cdot \sum _{\left(t_i,c_j\right)\in \text{Π}}{d}_{t_i,c_j},$$

thus the total distance optimization is invariant to scaling. The example in Figure 3 implies that the total distance minimization is not invariant to translation.

For C₁, C₂ > 0,

$$\frac{1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{C}_1\cdot d_{t_i,c_j}+C_2=C_2+\frac{C_1}{\left|\text{Π}\right|}\sum _{\left(t_i,c_j\right)\in \text{Π}}{d}_{t_i,c_j},$$

thus the average distance minimization is invariant to both scaling and translation.

Let π_ave, π_tot be the optimal solution of average distance minimization. By the optimality condition,

$$\left|{\text{Π}}_{\text{ave}}\right|=\frac{D_{\text{tot}}\left({\text{Π}}_{\text{ave}}\right)}{D_{\text{ave}}\left({\text{Π}}_{\text{ave}}\right)}\ge \frac{D_{\text{tot}}\left({\text{Π}}_{\text{tot}}\right)}{D_{\text{ave}}\left({\text{Π}}_{\text{tot}}\right)}=\left|{\text{Π}}_{\text{tot}}\right|.$$

□

Proof of Lemma 1.

We prove the equivalence by showing (1) ⟹ (2), (2) ⟹ (3), (3) ⟹ (1).

(1) ⟹ (2): we prove by negation. If (2) is not true, then there exists a connected component consisting of at least 2 treated units and 2 control units. Without loss of generality, assume the node with the highest degree in the connected component is treated, and denote the node by t₁. Let t₂ be a treated node other than t₁, by the connectivity, there exists a path connecting t₁ and t₂. Notice that the graph is bipartite, then at least one control unit appears in the path. If there is more than one control unit in the path, the path is of length at least 4. Otherwise, there is only one control unit in the path, denoted by c₁. Then there is another control unit c₂ connected to t₁ since t₁ is connected to at least two control units. The path c₂ −t₁ −c₁ −t₂ is of length 4. Therefore, if the maximal path is of length at most three, then the connected components can consist of either one control or one treated unit.

(2) ⟹ (3): we prove by negation. Assume (3) is not true, i.e. there exists an edge (t₁, c₁) that t₁ is also connected to another control unit c₂, and c₁ is connected to another treated unit t₂. Then the connected component containing c₂ − t₁ − c₁ − t₂ consists of at least two treated and two control units.

(3) ⟹ (1): we prove by negation. Assume (1) is not true, then there exists a path of length 4 of the type c₂ − t₁ − c₁ − t₂. In this way, for edge (t₁, c₁), the treated unit t₁ is connected with two control units and c₁ is connected with two treated units. □

Proof of Proposition 3.

Since Y_i1, Y_i2 are generated independently from model (10), the marginal density of Z_i = Y_i0 + Y_i1 is

$$\begin{gathered} f_{Z_i}(z)=\int f_{Y_{i0}}\left(y_0\right)\cdot f_{Y_{i1}}\left(z-y_0\right)d{y}_0 \\ =\exp \left\{-\psi \left({\eta }_1\right)-\psi \left({\eta }_0\right)\right\}\int \kappa \left(y_0\right)\kappa \left(z-y_0\right)\exp \left\{{\eta }_1{y}_0+{\eta }_0\left(z-y_0\right)\right\}d{y}_0 \\ =\exp \left\{-\psi \left({\eta }_1\right)-\psi \left({\eta }_0\right)\right\}\cdot \exp \left\{{\eta }_{0}z\right\}\int \kappa \left(y_0\right)\kappa \left(z-y_0\right)\exp \left\{\left({\eta }_1-{\eta }_0\right)y_0\right\}d{y}_0. \end{gathered}$$

Then the conditional distribution given Z_i is

$$\begin{gathered} f\left(Y_{i0}=y_0,Y_{i1}=z-y_0\mid Z_i=z\right) \\ =\frac{\kappa \left(z-y_0\right)\exp \left\{{\eta }_1\left(z-y_0\right)-\psi \left({\eta }_1\right)\right\}\cdot \kappa \left(y_0\right)\exp \left\{{\eta }_0{y}_0-\psi \left({\eta }_0\right)\right\}}{\exp \left\{-\psi \left({\eta }_1\right)-\psi \left({\eta }_0\right)\right\}\cdot \exp \left\{{\eta }_{0}z\right\}\int \kappa \left(y_0\right)\kappa \left(z-y_0\right)\exp \left\{\left({\eta }_1-{\eta }_0\right)y_0\right\}d{y}_0} \\ =\frac{\kappa \left(z-y_0\right)\kappa \left(y_0\right)\exp \left\{\left({\eta }_1-{\eta }_0\right)\left(z-y_0\right)\right\}}{\int \kappa \left(y_0\right)\kappa \left(z-y_0\right)\exp \left\{\left({\eta }_1-{\eta }_0\right)y_0\right\}d{y}_0}. \end{gathered}$$ (14)

Since μ(X_i0) = μ(X_i1), then

$${\eta }_1-{\eta }_0=\mu \left(X_{i1}\right)+\tau \left(X_{i1}\right)-\mu \left(X_{i0}\right)=\tau \left(X_{i1}\right).$$

Thus the conditional likelihood does not depend on μ(x). □

12.2. Synthetic data examples

We include the error curves of validation error estimators (Figure 7) in the setting I, II, III. In all settings, the combo method produces the smallest biases across different λ. The validation error estimators’ biases are more problematic than the variances.

Figure 7.

Error curves of validation error estimators (setting I, II, III). The solid curves demonstrate the validation error estimators’ biases. The dotted curves demonstrate the biases plus or minus one standard deviation of $\widehat{\mathrm{error}}(\pi )-\mathrm{error}(\pi )$. Each setting is repeated 200 times.

We compare the mean squared differences $\overline{b_{\pi }^2}$ of five matching-based validation methods in Figure 8. In all simulation settings, the combo method produces the smallest $\overline{b_{\pi }^2}$. The full method comes second except in the setting IV. The cvr method is not very promising in setting I in the presence of many irrelevant covariates. The S-M method is less attractive in setting III with 25-fold cross-validation. According to Proposition 1, a smaller $\overline{b_{\pi }^2}$ implies a less biased and variant validation estimator. As expected, Figure 8 agrees with Figure 5.

Figure 8.

Mean squared differences $\overline{b_{\pi }^2}$ box plots. We display the mean squared differences $\overline{b_{\pi }^2}$ of the five matching-based validation methods in Table 1 under the simulation settings in Table 2. Each setting is repeated 200 times.

12.3. Real data example

We provide more details of the empirical study in Section 6. In complement of Table 5, we demonstrate the differences in selected LASSO estimates under alternative norms in Table 6.

Table 6:

Comparison of selected LASSO estimates from two datasets via different validation methods. For each validation method, we compute the NSW-NSW and NSW-PSID control group L₂ norm of the difference of the selected LASSO estimate ${\widehat{\tau }}_{\mathrm{NSW}}$ from the NSW-NSW dataset and ${\widehat{\tau }}_{\mathrm{PSID}}$ from the NSW-PSID dataset.

method	prd	cvr	full	S-M	prgn	combo
${||{\widehat{\tau }}_{\mathrm{NSW}}-{\widehat{\tau }}_{\mathrm{PSID}}||}_{2,{\text{c}}_{\text{NSW}}}$ × 102	0.60	1.12	0.00	1.49	4.76	0.00
${||{\widehat{\tau }}_{\text{NSW}}-{\widehat{\tau }}_{\text{PSID}}||}_{2,{\text{c}}_{\text{PSID}}}$ × 102	0.60	1.12	0.00	1.53	5.33	0.00

12.4. Maximal group size selection

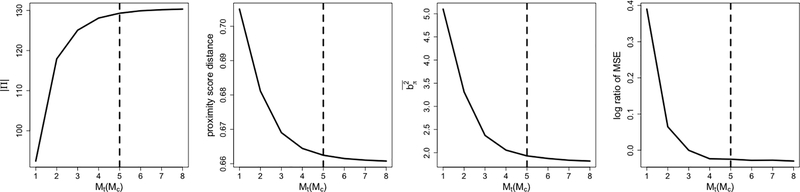
We empirically demonstrate how M_t and M_c affect the assessment of HTE estimators. In particular, we illustrate how the number of matched pairs |Π|, the average proximity score distance of the resulting match D_ave(π) (distance objective), the mean squared difference $\overline{b_{\pi }^2}$, and the relative MSE (9) change as M_t and M_c increase ¹⁴. The former two are available without the underlying truth and can be used for parameter selection. The latter two can not be computed without an oracle and are used as measurements of matching quality and assessment performance. Figure 9 corresponds to setting I in Table 2, where the treatment assignment is randomized. Figure 10 addresses setting IV in Table 2, where the propensity scores vary significantly across subjects¹⁵.

Figure 9.

Selection of multiplicity upper bounds M_t, M_c in setting I. For simplicity, we set M_t = M_c. From the left to the right, we plot in solid curves the number of matched pairs |Π|, the average proximity score distance of the resulting match D_ave(π), the mean squared difference $\overline{b_{\pi }^2}$, and the relative MSE (9) (all aggregated over 200 trials). The dashed lines correspond to the selected multiplicity upper bounds M_t = M_c = 3.

Figure 10.

Selection of multiplicity upper bounds M_t, M_c in setting IV. For simplicity, we set M_t = M_c. From the left to the right, we plot in solid curves the number of matched pairs |Π|, the average proximity score distance of the resulting match D_ave(π), the mean squared difference $\overline{b_{\pi }^2}$, and the relative MSE (9) (all aggregated over 200 trials). The dashed lines correspond to the selected multiplicity upper bounds M_t = M_c = 5.

In both settings, the number of pairs |Π| first increases then stabilizes, and the average proximity score distance D_ave(π) first decreases then stabilizes. As expected in Section 3.3.2, the mean squared difference $\overline{b_{\pi }^2}$ — critical to the validation error estimator’s quality — behaves similarly to the proximity score distance D_ave(π). Finally, the relative MSE first decreases then stabilizes or slightly increases. The relative MSE may rise for M_t, M_c excessively large due to additional variances.

As discussed in Section 5, we choose the “elbow point” of the average proximity score distance D_ave(π) (distance objective) curve. In setting I (Figure 9), we select M_t = M_c = 3 (dashed lines), while in setting IV (Figure 10), we pick M_t = M_c = 5 (dashed lines). Setting IV prefers larger M_t, M_c because the treatment and control groups are imbalanced at subregions with propensity scores far from one half, and the units in the smaller group should be used multiple times. The necessity of larger M_t, M_c in setting IV is also illustrated in the example of Figure 2.

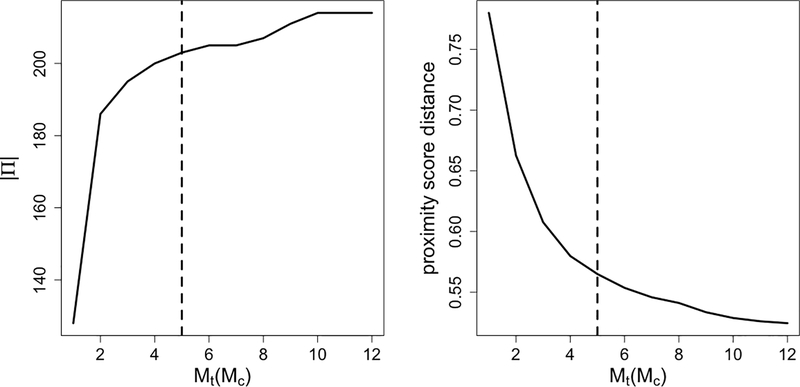
We provide more details of choosing the multiplicity upper bounds M_t, M_c in the real data example (NSW-PSID dataset). In Figure 11, from left to right, we plot the number of matched pairs |Π| and the average proximity score distance D_ave(π) (distance objective) against multiplicity upper bounds M_t, M_c. The number of pairs |Π| first increases then stabilizes, and the average proximity score distance D_ave(π) first decreases then stabilizes. We choose the “elbow point” M_t = M_c = 5 (dashed lines) of the average proximity score distance D_ave(π) (distance objective) curve as discussed in Section 5.

Figure 11.

Selection of multiplicity upper bounds M_t, M_c in the real data example (NSW-PSID dataset). For simplicity, we set M_t = M_c. From the left to the right, we plot in solid curves the number of matched pairs |Π| and the average proximity score distance of the resulting match D_ave(π). The dashed lines correspond to the selected multiplicity upper bounds M_t = M_c = 5.