In situ visualization of long-range defect interactions at the edge of melting

Dark-field X-ray microscopy movies reveal how patterns of microscopic defects in bulk aluminum destabilize from 97-99% of melting.

Abstract

Connecting a bulk material’s microscopic defects to its macroscopic properties is an age-old problem in materials science. Long-range interactions between dislocations (line defects) are known to play a key role in how materials deform or melt, but we lack the tools to connect these dynamics to the macroscopic properties. We introduce time-resolved dark-field x-ray microscopy to directly visualize how dislocations move and interact over hundreds of micrometers deep inside bulk aluminum. With real-time movies, we reveal the thermally activated motion and interactions of dislocations that comprise a boundary and show how weakened binding forces destabilize the structure at 99% of the melting temperature. Connecting dynamics of the microstructure to its stability, we provide important opportunities to guide and validate multiscale models that are yet untested.

INTRODUCTION

Defects underlie many of the mechanical, thermal, and electronic properties of materials. A prominent example is the dislocation, which is an extended linear defect in the atomic lattice that enables crystalline materials to permanently change their shape under mechanical loading. The remarkable range of hardness and workability in ductile materials occurs because of how their dislocations can move and interact. Dislocations have been characterized extensively since the advent of transmission electron microscopy (TEM) (1–6); however, TEM requires submicrometer sample dimensions that introduce size effects and surface stresses that are not representative of bulk materials (7). In situ TEM has thus been limited to resolving the dynamics of dislocation interactions in spatially localized processes (8) including the dynamics of isolated dislocations (9, 10), the operation of dislocation sources (11), and interactions between dislocations and grain boundaries (12).

To understand how defects dictate a material’s macroscopic properties, we must resolve nonlocalized and stochastic processes. Under those conditions, defect motion is governed by unpredictable inhomogeneities and random distributions of defect networks in the sample that span a wide range of length scales in three dimensions (3D). Experiments have explored nonlocalized systems by scaling up the problem: constructing lattices from polymer beads (colloidal crystals); optical microscopy can resolve single-particle motion in such systems with digital image correlation methods (13). This methodology has resolved the motion of dislocations to solve for their mobility and diffusion in equilibrium systems (14) or in the kinetics of phase transitions (15). While colloidal crystals offer deep insight into defects, they do not account for the interaction forces and quantum effects (e.g., tunneling and ballistic motion) that are present in metals or other structural and functional materials. To understand how dislocations pattern into 3D structures, we require the analogous subsurface nanoscale experiments for atomic crystals. Simulations have aided our understanding of such stochastic dislocation dynamics (16–18), but models of realistic patterns that span the necessary nanometer-to-millimeter length scales have proven elusive. At this time, the specific interactions that cause a population of free dislocations to order into a structure (polygonize) are limited to theory and ex situ studies (19), which cannot capture the dynamics. To understand how dislocations in bulk materials pattern into 3D structures and networks, we require new experimental tools.

The limitations of our measurement technology are especially clear at temperatures on the verge of melting. The mechanism by which ordered solids melt into disordered liquids at equilibrium has been actively contested for more than a century (20, 21). The criteria for equilibrium melting were first defined by the Lindemann and Born models, which describe melting as lattice destabilization from high-amplitude vibrational waves (22) or a “rigidity catastrophe” from loss of shear strength (23). Over the years, theory and experiments have studied the validity of these theories and have recently connected them based on contributions from the microstructure (20, 24, 25). Dislocations have been predicted to play a key role in seeding and nucleating melting (26, 27); however, models still lack experimental guidance to determine the relevant physics for the exotic dislocation interactions under conditions at the cusp of melting. The next set of advances in melt theory require experiments to inform the relevant physics over the necessary real-world conditions.

X-ray diffraction–based imaging has become a promising candidate for the necessary multiscale characterization tools, as it can map crystallographic properties in the bulk and in 3D. While several x-ray methods have been able to resolve subsurface dislocations, at this time, they have been unable to measure dynamics with sufficient resolution in space and time over a representative region. Topography (28) and topo-tomography (29) have been used to image dislocations for decades but are limited to spatial resolution in the micrometer range. Recent advancements now enable x-ray nanobeam studies to achieve much higher spatial resolution but they require rastered scans that cannot probe dynamics over the necessary subsecond timescales (30). Dark-field x-ray microscopy (DFXM), analogous to its TEM counterpart, was recently developed to directly map the subtle deformations surrounding defects and boundaries beneath a material’s surface, giving providing views of the microstructure that were previously inaccessible (31). While DFXM has addressed key issues in ferroelectrics (32) and biominerals (33), it has only recently been applied to dislocation studies (34). For materials with sufficiently low dislocation densities, DFXM was demonstrated to resolve single dislocations by mapping the strain fields around dislocation cores (weak-beam contrast) (34, 35).

We present time-resolved DFXM as a new tool to map how dislocations move and interact in delocalized processes deep inside bulk materials. With this approach, we resolve the individual and collective motion of the dislocations that comprise a dislocation boundary (DB) ~200 μm beneath the surface of a single-crystal of aluminum. Our images map how the DB migrates along a very low–angle boundary (LAB) as the crystal is heated from 97 to 99% of the melting temperature, T_m = 660°C. We zoom in on how dislocations enter and leave the boundary, causing two DB segments to coalesce and stabilize into one cohesive structure. As the DB subsequently migrates and increases its spacing between dislocations, we observe how the boundary destabilizes. Connecting this to theory, we reveal the mechanism by which the DB dissolves at the cusp of melting, as thermal forces dominate dislocation interactions. By visualizing and quantifying thermally activated dynamics that were previously limited to theory, we demonstrate a new class of bulk measurements that is now accessible with time-resolved DFXM, offering key opportunities across materials science.

RESULTS AND DISCUSSION

We use in situ DFXM to resolve how an ensemble of dislocations evolves in an aluminum crystal as we slowly heat it, recovering it toward a pristine nondefected form (thermal annealing). As shown in Fig. 1A, the x-rays illuminate a single observation plane in the sample, allowing the microscope to map the local structure over a 200×400×0.6 μm³ internal region with ~300-nm resolution and 250 ms between frames. To minimize effects besides temperature, we apply no external mechanical stress and use a high-purity sample to avoid competing solute-dislocation effects. We present the evolution of structure over 12.5 min, collecting scans of ~120 s at each temperature as we heat the crystal from 0.97 to 0.99 T_m in 2°C increments. Each temperature increase occurs over short 3- to 10-s intervals between movies (see the Supplementary Materials for full thermal history). By slowly heating the crystal in small increments, we allow the internal defect structures and corresponding stresses to recover as it approaches T_m, causing our high-T results to describe the initial conditions for equilibrium melting. These controls ensure that the dislocation motion that we observe arises from the interaction forces between neighboring dislocations, vacancy concentrations, and thermal expansions from local temperature fluctuations.

Fig. 1. Probing dislocations inside a crystal.

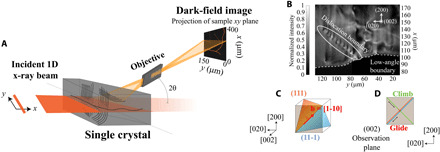
(A) Schematic of the experimental geometry for the dark-field x-ray microscope. We show the single crystal with free dislocations and their arrays inside to demonstrate how the x-rays illuminate a 600-μm-thick observation plane that projects and magnifies the local structure onto the detector. (B) Zoomed-in image of the single domain that we focused on for this study, which includes a collection of dislocations (bright spots) at T = 638°C (0.98 T_m). The white circle outlines an array of dislocations that form a DB, which is pinned to a LAB (dotted white line). We show a schematic (C) of the Burgers vector, b (red), and slip planes (blue and orange) of the edge dislocations in the tilt boundary and (D) how the climb and glide directions for these dislocations trace through the observation plane.

The bulk single crystal in this study forms a large internal pristine domain (Fig. 1B) during the annealing treatment, which is surrounded by LABs. As shown in Fig. 1B, the crystalline domain includes a population of individual free dislocations and collective structures. The dashed white line identifies a LAB that a full scan at lower temperatures confirms is misoriented ~0.01° with respect to the primary domain in the image (see details in the Supplementary Materials). Above the LAB, several alternating bright-dark regions correspond to the long-range deformation fields surrounding individual dislocations. In this case, the dislocation lines slice through the observation plane with a steep incline, as illustrated for an analogous set of dislocation arrays in Fig. 1A. We identify these as edge dislocations on the basis of their directional motion, all of which have identical $[1\overline{1}0]$ Burgers vectors that lie in the observation plane (see details in text S1). Our interpretation is supported by the predicted strain and rotation fields, which are consistent with simulations of the raw images that we collected (35). Circled in white in Fig. 1B, the evenly spaced array of dislocations in the DB packs along the trace of their glide plane in our images (45° from [020]). The geometry agrees with the DB being a tilt boundary that is packed along a plane normal to the Burgers vector. We show the geometry of the Burgers vector and the slip planes for the boundary dislocations in Fig. 1C, projecting the structure onto our (002) observation plane to define the directions that correspond to glide and climb mechanisms of dislocation motion in our images (Fig. 1D). We note that the LAB and the DB are analogous dislocation structures that appear differently in our images due to their orientations. Tilt boundaries of this kind are known to be stabilizing dislocation structures, as their adjacent strain fields counteract each other, reducing the strain energy between neighboring dislocations in a process called stress screening (6).

Snapshots of the progress of DB evolution

We begin this study by showing snapshots that resolve a “static picture” of how the boundary evolves over the temperature range. Even single snapshots from each of the eight movies reveal a previously unseen view of long-range DB motion. Figure 2A includes images of the crystalline domain with one frame for each temperature that shows the position of all DB dislocations at that stage in the recovery. With this view, we see that the dislocations are spaced ~5 to 9 μm apart in this temperature range, which is ~10× larger than previous observations in thin films of deformed metals (3, 5). The wide spacing is not unreasonable for this recovered crystal at near-melt temperatures and demonstrates that stress screening still stabilizes a DB even with weak interaction forces, in the absence of competing interactions.

Fig. 2. Snapshots of the DB.

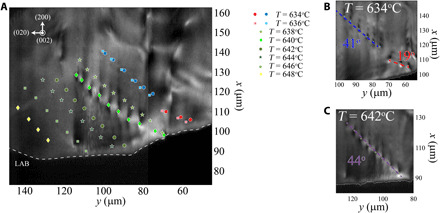
(A) The motion of the DB shown in Fig. 1B with increasing temperature from 634°C (0.97 T_m) to 648°C (0.99 T_m), shown by the positions of all DB dislocation cores, plotted over an image from T = 640°C. We zoom in on the DB at (B) T = 634°C and at (C) T = 642°C to show the joining of the two DB segments. The lines are best fits to straight boundaries. Images and associated linear fits are provided in the Supplementary Materials. The LAB is shown in all frames by a dotted white line.

Figure 2A also reveals that the DB’s trace migrates as the temperature increases, moving a total of ~60 μm until it shifts out of the field of view. The DB shifts along the LAB, suggesting an interaction between the two structures as the number of dislocations in the boundary decreases. Figure 2A also shows that the DB begins as two separate boundary segments (Fig. 2B) that coalesce at 638°C to form a single segment (shown at 642°C in Fig. 2C). A qualitative look at the angle between [020] and the DB trace demonstrates that the lower segment initially has an unfavorable 19° trace that rotates toward the more favorable 45° as it closes the distance between the two DB segments. With only the snapshots in Fig. 2, we cannot resolve how the DB segments join, which dislocations disappear, and how the spacing between dislocations increases as the DB migrates along the LAB.

Coalescence stabilizes the DB structures

To resolve how the two DB segments coalesce, we turn to the real-time movie at 638°C (movie S1). While Fig. 2 (A to C) indicates that the lower segment rotates toward the upper one before they join, the time-resolved view from representative frames and their associated schematics in Fig. 3 (A to E) reveals that a lone dislocation (D3) inserts into the lower boundary to drive the dislocations to ultimately redistribute. Using computer vision tools that we developed with manual corrections to enhance the precision (36), we track the position of each dislocation over the full insertion mechanism, plotting the components along the climb and glide directions that correspond to the different types of dislocation motion (Fig. 3, F and G). The plots and images in Fig. 3 demonstrate that the DB coalescence includes contributions from the four dislocations nearest to the LAB (labeled D2 to D5). In Fig. 3, we plot these with D6 to correlate the insertion mechanism to motion in the remaining DB.

Fig. 3. A direct view of DBs coalescing.

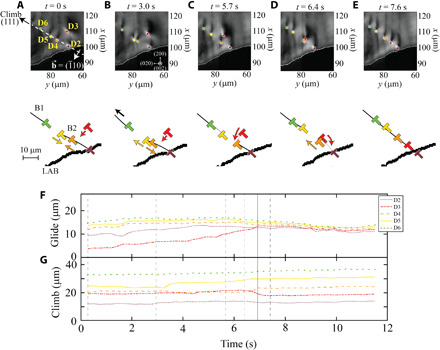
(A to E) Five representative frames with the corresponding schematics to show how dislocation D3 inserts into the lower DB segment at T = 638°C. We label the active dislocations in the first frame and plot their positions in all subsequent frames for clarity. Schematics show the upper (B1) and lower (B2) boundaries with black lines, with a thicker black line showing the LAB. The motion of each dislocation is shown by arrows, with all dislocations and arrows color-coded to the dislocations’ labels in the image frames. We also include plots of the position of each annotated dislocation, projected onto the (F) glide and (G) climb directions [as indicated in (A)]. The time corresponding to each snapshot/schematic pair is shown in the traces in (F) and (G) by vertical dotted lines; the solid vertical line in (F) and (G) marks the time at which D3 enters the DB.

As shown by the frames in Fig. 3 (A and B) and the traces in Fig. 3 (F and G), the free dislocation, D3, initially glides toward the boundary, while D4 and D5 climb gradually toward each other. After ~3 s, D4 and D5 reach a critical distance and repel each other, displacing D4 into a pileup geometry with D3 (Fig. 3C). While the attractive climb between D4 and D5 is slow, their repulsion is faster than our 250-ms time resolution. The newly formed pileup geometry theoretically induces a repulsive force between D4 and D3 along the glide plane, which should require D3 to move via climb to insert into the boundary. We resolve that the deformation fields for D2 and D3 overlap as D3 migrates further toward the boundary, suggesting that D2 and D3 interact to facilitate the climb (Fig. 3D). Passing <300 nm from D4, D3 ultimately climbs into the boundary, changing its apparent shape as it inserts. D3’s shape change indicates that the deformation field changes upon insertion. Following these interactions, all five dislocations slowly migrate along the climb direction until they settle into their most favorable positions, closing the gap between the two segments (Fig. 3E). The insertion mechanism and its associated coalescence of the two DB segments illustrate the stabilizing character of the tilt boundary, demonstrating that this result still occurs in bulk metals.

Dynamics over the full temperature range

Our observations from Fig. 2A of the reduced number of dislocations and increase in spacing between DB dislocations can also be resolved more clearly with time-resolved measurements. We resolve the pathway by which dislocations leave the boundary by tracking the positions of all dislocations in the DB from T = 636° to 646°C. For the full 12.5-min acquisition, we project the components of each position along the glide and climb directions over each temperature, as shown in Fig. 4 (A and B, respectively). The black bars indicate the time over which the temperature increases between each acquisition. Changes to the spacing between neighboring dislocations are clearest along the climb direction, where motion requires vacancy diffusion, while the change of the trace angle and the DB migration is clearest along the glide direction.

Fig. 4. Temporal map of DB evolution.

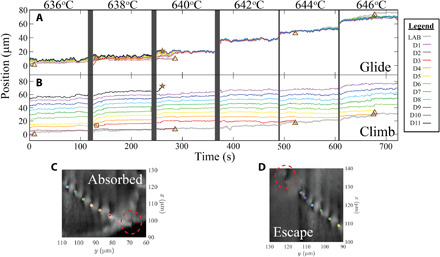
Plots showing the full evolution of the DB over six temperatures, from 0.97 to 0.99 T_m. We show the position of each dislocation in the boundary at each time and resolve the motion along the glide (A) and climb (B) directions. In both plots, 0 corresponds to the position of the first dislocation in the first frame at T = 636°C. The positions where dislocations are absorbed into the LAB are marked by brown triangles, the position where a dislocation escapes into the crystalline domain is marked by a star, and the position at which D3 inserts into the DB is marked by a square. To demonstrate how dislocations exit the boundary, we show representative frames of (C) how D2 is absorbed into the LAB and (D) how D11 escapes into the crystal, both at T = 640°C (exiting dislocations are circled in red).

The full traces in Fig. 4 (A and B) reveal how six dislocations leave the DB. The brown triangles in Fig. 4 (A and B) mark five positions where dislocations exit the boundary via absorption into the LAB, while the brown stars mark the position where one dislocation, D11, escapes the boundary by slowly migrating via climb into the interior of the crystalline domain, likely due to other dislocations that are nearby (see movie S2). Representative frames from T = 640°C are shown for the absorption and escape in Fig. 4 (C and D, respectively), with the exiting dislocations circled in red for clarity. The relative abundance of dislocations exiting the DB at the LAB reveals the importance of the LAB in increasing the spacing between boundary dislocations. Looking more closely at the LAB highlights this point. Dislocations are absorbed by first climbing toward the LAB until they affix to it; the remainder of the DB then glides past the immobile dislocation as the junction dislocation slowly exits the crystalline domain and moves out of our field of view. This mechanism indicates that the LAB can impose stronger interaction forces than those that stabilize the DB; however, these forces only act over much smaller distances. The abundance of dislocations that absorb into the LAB defines it as a dislocation sink, as seen in TEM (37). The successive absorption events in Fig. 4 demonstrate the first direct view of how individual dislocations absorb into a sink in bulk metals. These dynamics present a previously unseen view of how single dislocations navigate through a network of 3D DBs in bulk crystals, at the single-dislocation level.

A closer look at DB stability as T → T_m

Beyond dislocation interactions, Fig. 4 (A and B) also demonstrates collective dislocation motion in the DB with subtle trends at the highest temperatures that reveal key changes under these near-melt conditions. After the DB orients along its preferred 45° trace (t > 300 s), the dislocations oscillate collectively along both the climb and glide directions via thermally activated motion (movie S2). Specifically, the DB migrates along the LAB more quickly at this point, traveling ~30 μm over the final three temperature steps. As DFXM’s intensity scales with stress/strain, the smooth DFXM intensity (movie S2) over the crystal domain implies that any driving stresses are |ε| < 10⁻⁵. This suggests that thermal effects drive the expedited DB migration instead of conventional stress relaxation.

Thermal motion is a stochastic process that arises from local inhomogeneities in the sample; climb motion is driven by vacancy diffusion, while glide motion is driven by the local stresses imposed by long-range dislocation interactions (38). At the verge of melting, thermal motion of lattice defects differs from predictions in classical dislocation theory. The Lindemann theory describes melting as a vibrational catastrophe that destabilizes lattice bonds when the thermally amplified atomic vibrations reach the critical temperature, T_m (22, 23). Larger length scales resolve the Lindemann criteria as increased dislocation mobility as T → T_m, as the additional disorder adds extra pathways to facilitate their motion (25).

Our experiments resolve the increased dislocation mobility as random variation in the position of each dislocation between frames, which we quantify as the temporal variance in dislocation position. We corroborate that variance relates to mobility, as the variance increases just before each dislocation is expelled from the boundary then reduces after the dislocations leave (fig. S4). In the absence of dislocation expulsions, however, we also see an increase in dislocation mobility at the highest temperatures. Figure 5A plots the average variance in the position of boundary dislocations for each temperature, computed from dislocation motion over the full time scan at each temperature from T = 642° to 646°C. The variance in dislocation position jumps by a factor of (∆T)² with increasing temperature from T = 642° to 646°C, corresponding to mean variances at T = 642°, 644°, and 646°C of 0.5, 2, and 8 μm, respectively. Extrapolating this trend to the lower-temperature range shows a nearly imperceptible variance from thermal motion (≤125 nm) that is obscured by the dislocation interactions (shown in the Supplementary Materials). To compare the collective thermal motion to the local motion, Fig. 5B gives a closer look at the dislocation spacing in the DB, plotting histograms for each temperature with colored bars that show the contributions from each D-D pair. The black lines and text show the normal distribution and mean spacing for each temperature. Contributions from each dislocation pair reveal that the increased variance arises from a widening spread in the spacings between each dislocation pair, showing that the boundary becomes more inhomogeneous with each temperature increase.

Fig. 5. Subtle effects destabilize the DB.

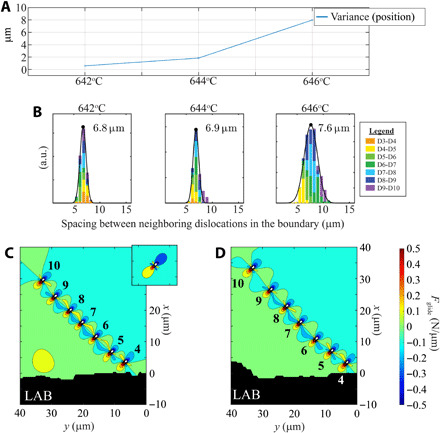
View of the motion of dislocations in the boundary that shows how it destabilizes. (A) Plot showing the variance in the time-averaged position [measured as the distance of each DB dislocation from the (0,0) position], plotted at the highest temperatures. The plot is collected on the basis of the average from all seven dislocations in all 500 frames for each movie (~120-s acquisition). (B) Histograms showing the distribution of the spacing between dislocations in the DB as the boundary destabilizes, with colors in the bars to show contributions from each pair of dislocations (colors are referenced to the higher dislocation of each pair). We plot the normal distribution fitted from all dislocation pairs in black and label the mean spacing for each temperature. a.u., arbitrary units. (C and D) Force field calculations along the glide direction, simulated on the basis of the positions of each boundary dislocation identified in Fig. 4, to show changes to the boundary stability. Traces are computed based on frames (C) shortly after the temperature jump at T = 642°C and (D) at T = 646°C. The inset in (C) shows a lone dislocation. For ease of comparison, all force fields are plotted with the same scaling and contoured to the same thresholds.

The dislocation densities reported here are substantially lower than those of most conventional experiments, allowing us to study dislocation interactions within a DB with minimal competing interaction forces from nearby dislocations. The wide spacing between neighboring dislocations causes their interaction forces to be low (~0.5 N/μm), resulting in minimal stress screening. This indicates that, under these unique conditions, the boundary is likely only stabilized because of the absence of competing interactions due to the very low dislocation density. Figure 5C maps the simulated interaction forces along the glide direction that stabilize the DB for the dislocations that we identify in Fig. 4 at T = 642°C. The primarily isolated boundary allows our simplified model to demonstrate how this wide spacing affects the stress screening. We only predict forces along the glide direction, as the corresponding climb interaction forces are significantly weaker than the ones arising from vacancy diffusion above ~0.9 T_m (see full discussion of force calculations in the Supplementary Materials). At T = 642°C, the variance is quite low, and the spacing between dislocations is relatively uniform; the long-range stress fields for each dislocation are thus screened by their interaction forces along the DB (6). The screening is clearest when comparing the size and magnitude of the stress fields in the DB to those produced by a lone dislocation, as shown in the inset of Fig. 5C.

In contrast, at only 4°C higher temperature, the wider spacing in the DB no longer screens each DB dislocation fully. Figure 5D plots the force fields just after the temperature is increased, at a time where no dislocations interact with the boundary. We note that the enhanced dislocation mobility at this temperature is independent of the two dislocations that are absorbed into the boundary. At this time, we note that another dislocation is pinned to a different structure 15 μm away from the DB, which is stationary for most of the movie. When this dislocation unpins, over the course of 3 s, it approaches the DB-LAB interface and is involved as two dislocations insert into the boundary. The character of this dislocation could not be identified.

The massive increase in the disordered motion and spacing as DB dislocations drift apart at these high temperatures reveals a previously unseen view of how DBs natively destabilize on the verge of melting. The uniform spacing in these types of DBs ultimately gives rise to their inherent stability. Only 8°C earlier, this DB stability causes two DB segments to coalesce (Fig. 3); however, at 0.99 T_m, the boundary dislocations move far more substantially, shifting their spacings. As dislocation motion increases and the dislocation spacing fluctuates more, the boundary loses much of the stability it gains from the long dislocation chain, reducing the stress screening effect and eventually canceling out the inherent stability of the boundary.

While TEM has resolved DB dissolution driven by migration at higher dislocation densities (39), our conditions and long-range interaction forces demonstrate how a DB can unravel, driven only by its internal forces. This statistical view of the stochastic dislocation motion allows us to now quantify a lower bound for the force necessary to stabilize an isolated tilt boundary before it inhomogeneously breaks apart. Our findings demonstrate just one example of the exotic behavior of dislocation structures under the conditions relevant for melting.

Melting theory has demonstrated that, in the absence of surfaces, the behavior of different types of defects is essential to describe how melting proceeds (40, 41). Studies have also suggested that, as T → T_m, the behavior of classical defects (e.g., dislocations and vacancies) deviates significantly from the dynamics under normal high-T conditions (42). At this time, a lack of experimental data on the dynamics of subsurface dislocations as T → T_m has prevented melting theory from understanding which defects and defect interactions are relevant to the lattice conditions at the cusp of melting, without deleterious surface or size effects. Hence, melt theory has been limited to simplified dislocation systems that undersample and may not be relevant to the unique physics at T_m. Other systems have demonstrated that experiments can determine which key defect assemblies play a dominant role in a phase transition, informing models of the simplified set necessary to describe the relevant physics (43). New computational approaches have demonstrated that just as the symmetry of the lattice is about to transform into a disordered liquid, a plethora of defect interactions create numerous degenerate pathways for melting (44). Our novel approach presents an important step forward by directly resolving the relevant initial defect states and behaviors that are required to build a valid model that describes melting, with a first example of these dynamics.

In this first study with time-resolved DFXM, we demonstrate key insight into collective dislocation interactions at temperatures on the verge of melting, resolving length and time scales not previously accessible in a setting representative of bulk behavior. While a static view of the DB’s evolution demonstrates that dislocations come and go as the dislocations spread apart, a time-resolved view of each component dislocation over the full 12.5-min scan reveals how these phenomena occur. We resolve the mechanism by which two DB segments coalesce to stabilize the full structure then extend this to view how successive dislocation absorption and escape events reduce the number of dislocations in the boundary. At the highest temperatures, we reveal how stochastic thermal motion, as the dislocations migrate apart, destabilizes the boundary at temperatures approaching the melt. With force field simulations, we demonstrate that the weakened interaction forces at the highest spacings begin to compete with thermal motion, mobilizing dislocations exponentially over a small increase in T. Our comparison to elastic theory demonstrates how spacing and inhomogeneity reduce the stabilizing forces, causing the DB to begin to unravel at 0.99 T_m.

Linking our microscopic pathways to the dynamics of the material in this way enables us to resolve key multiscale dislocation interactions that models struggle to predict, in the context of melting, deformation, geophysics, and beyond. While current multiscale experiments typically connect the microstructure to bulk properties with only the dislocation density, our study with time-resolved DFXM reveals how previously unseen details about the dynamics provide important metrics to quantify the evolution of dislocation structures and connect them to the bulk. We include an additional movie at slightly lower temperatures (movie S3) to show the rich information about dislocation dynamics that is contained in these DFXM movies, providing further opportunities for multiscale characterization. Further developments in DFXM are pushing the technique to higher temporal and spatial resolution (45, 46). Those developments will extend these capabilities to study faster defect phenomena, samples with higher dislocation densities, and a wider array of defect topologies, presenting opportunities for an even wider range of fields. Our new approach is an important step forward to connect defects to macroscopic properties.

MATERIALS AND METHODS

This experiment was performed at the dedicated dark-field x-ray microscope instrument at ID-06 at the European Synchrotron Radiation Facility (46), with the instrument placed 57 m from the source. A Si(111) Bragg-Bragg monochromator defined a 17.29-keV x-ray beam. The beam was collimated in the vertical direction by a compound refractive lens (CRLs), comprising eight 2D Be CRLs with a radius of curvature of R = 200 μm. Then, it was focused by a condenser comprising 55 1D Be lenses with R = 100 μm corresponding to an effective aperture of 435 μm, a focal length of 816 mm, a divergence of ζ_v = 0.030° [full width at half maximum (FWHM)], and a nominal focal spot height of 220 nm. After illuminating the sample, the {002} diffracted beam was magnified by an x-ray objective (a CRL with 88 2D Be lenses with R = 50 μm, T = 2 mm) positioned 274 mm behind the sample and a far-field charge-coupled device (CCD) camera placed 5.364 m from the sample. The resulting numerical aperture (NA) was 0.720 mrad (root mean square), with a measured magnification of ×18.5. The 2D far-field detector used a scintillator screen coupled to a FReLoN CCD camera via microscope optics, giving an effective pixel size (in the sample plane) of 75 nm per pixel along the y direction and 204 nm per pixel along the x direction. We used a radiation furnace to evenly heat our sample, as described elsewhere (47).

The sample was a 0.5×0.5×20-mm³ single crystal of aluminum with 6N commercial purity, used as purchased from Surface Preparation Laboratory. The mosaic spread of the single crystal was within ~0.2° across our 400-μm region of interest. This spread reduced significantly as the crystal was incrementally annealed in the experiment, following the temperature path detailed in text S4. The instrument was aligned such that it could image the small variations in reciprocal space around the nominal (002) diffraction vector (48, 49), with the associated scattering angle 2θ = 20.73°. Similar to the approach presented in (34), the sample tilt was slightly offset from the peak of the rocking curve to create conditions that approach weak-beam contrast in dark-field microscopy. The spatial resolution is estimated from the sharpest feature in the image to be ~300 nm in the sample plane. The FWHM of our reciprocal space resolution was defined by the NA of the lens: Δ2θ = 0.134° and Δη = 0.134°, respectively (48). The primary reciprocal space contrast in this experiment arises from the divergence of the incoming beam (in the rocking direction), Δχ = 0.015° (35, 48) (for definition of angles, see fig. S1). A full description of the contrast mechanisms in our experimental geometry for DFXM is described in full elsewhere (35).

We used a radiation furnace to evenly heat our sample, as described in (47). Initially, the sample was heated from room temperature to 633°C over ~10 hours. The experiments presented in this work focused on the end of this heating path, during which the temperature was increased by ~2°C increments (in ~5 s) followed by realignment and subsequent data acquisition for 2 to 5 min. Each image was collected over 100-ms integration times, acquired at the 4-Hz frame rate of the camera, with all elements of the microscope and sample remaining stationary. All images were collected with the motor positions and background subtractions from data collected during the experiment. No subsequent normalization was performed.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/29/eabe8311/DC1