Abstract
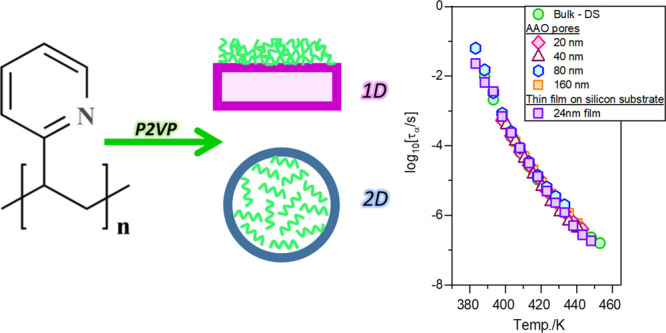
Geometric nanoconfinement, in one and two dimensions, has a fundamental influence on the segmental dynamics of polymer glass-formers and can be markedly different from that observed in the bulk state. In this work, with the use of dielectric spectroscopy, we have investigated the glass transition behavior of poly(2-vinylpyridine) (P2VP) confined within alumina nanopores and prepared as a thin film supported on a silicon substrate. P2VP is known to exhibit strong, attractive interactions with confining surfaces due to the ability to form hydrogen bonds. Obtained results show no changes in the temperature evolution of the α-relaxation time in nanopores down to 20 nm size and 24 nm thin film. There is also no evidence of an out-of-equilibrium behavior observed for other glass-forming systems confined at the nanoscale. Nevertheless, in both cases, the confinement effect is seen as a substantial broadening of the α-relaxation time distribution. We discussed the results in terms of the importance of the interfacial energy between the polymer and various substrates, the sensitivity of the glass-transition temperature to density fluctuations, and the density scaling concept.
Introduction
Over the last few decades, there has been a growing interest in studying the properties of glass-forming materials subjected to geometrical confinement in the nanometer range. These investigations aim to understand better the basic rules governing the glass transition when the system size is comparable to the characteristic length scale associated with such a phenomenon. Recognizing the glass transition dynamics at the nanoscale level also has significant relevance for many technological applications (e.g., photoresistors, smart coatings, adhesives, biosensors, drug delivery systems, flexible organic displays, bendable electronics, and so on).1−4 The key features of novel nanomaterials or functional nanodevices rely on the unique physicochemical properties of the molecular systems confined within such small nanometric size dimensions that, in many cases, are substantially different from the intrinsic bulk behavior.5−8
Among the various available configurations, we can distinguish soft or hard confinement imposed in one (thin films), two (nanopores), or three (nanospheres) dimensions.9−11 Numerous studies have shown that the molecular mobility associated with the glass transition undergoes dramatic changes when reducing the size to the nanometer range.12−14 Changes in the glass transition dynamics include an increase, a decrease, or no effect on the characteristic time scale associated with α-relaxation.10,15−19 The other characteristic feature of geometrically confined glass-forming systems is a large gradient in dynamics.20−22 This includes retarded mobility near the confining surface/substrate and faster dynamics once moving away from the boundary interface. In nanoscale confinement, the surface energy,23 melting/freezing temperature, and overall phase transition behavior might strongly deviate from the bulk.17,24−27 Except for the finite size effect—associated with reducing the space available for the molecular arrangement—interfacial interactions between the confined molecules and the pore walls/solid substrate have a critical influence on the change of the physical properties of spatially constrained materials.5,28−32
Although frequently addressed in the literature, glassy dynamics at the nanometer length scale are far from being completely understood. One of the critical problems is recognizing why some glass-forming systems, including low-molecular-weight liquids and long-chain polymers, are extremely sensitive to confinement effects. In contrast, the others show bulk-like characteristics down to a few nanometers in film thickness or pore size. Can we predict it or rationalize it in some way? Some results indicate that molecular liquids and polymers confined in nanopores vitrify under constant volume conditions instead of constant pressure.33−35 For example, Zhang and co-workers demonstrated that lowering the glass transition temperature of the molecular systems embedded within the nanopores is associated with the buildup of the negative pressure.36 On the other hand, some other reports indicate that the pressure alone has no significant effect on the change of the glass transition temperature in nanoconfinement.37
Various approaches and correlations were investigated to predict or identify some basic parameters controlling changes in soft matter dynamics under nanometer confinement. For example, studying a series of polymers confined within self-ordered alumina nanopores, Alexandris et al. have demonstrated a trend for decreasing the glass transition temperature relative to the bulk with increasing polymer/substrate interactions.38 Talik et al. have found that enhanced dynamics in nanopore confinement correlate with the wettability, surface tension, and interfacial energy induced by increasing the surface curvature in pores of the lowest diameters.39 The surface energy can affect the Tg values in different ways; in case of the materials confined in the nanoporous templates, there is a trend for a decreasing glass temperature relative to the bulk with increasing interfacial energy.38,40 On the other hand, as reported for polymer thin films, the increase of interfacial energy can lead to an increase in Tg values so that they become higher than the bulk values.32
Apart from that, it has been demonstrated that perturbation in the density introduced by geometrical nanoconfinement is responsible for enhanced dynamics in nanopores41,42 or thin polymer films.43 Therefore, one can use information from the high-pressure studies of bulk materials to predict dynamics under confinement.40,44−46
The other problem, related mainly to thin-film dynamics, is that depending on the preparation/processing conditions, even for the same material, opposite effects can be observed in the confined state.15,47−49 This implies that various factors affect out-of-equilibrium glassy dynamics at the nanometer length scale.
As highlighted in a series of recent investigations on confined polymers, there is a decoupling between the calorimetric glass transition temperature Tg and the α-relaxation dynamics. In such cases, when lowering the sample size, a clear reduction of Tg is observed, whereas the molecular mobility still exhibits the bulk-like behavior.50−53 Some of the explanations of this finding consider the presence of interfaces, geometrical factors, and the residual stress present in the confined polymer systems.
In the context of the abovementioned aspects related to the glassy dynamics in the confined space, herein, we have examined the behavior of the polymer system poly(2-vinylpyridine) (P2VP) embedded within cylindrical alumina nanopores and prepared as thin films on silicon wafers. Inorganic nanoporous membranes and flat substrates with nondeformable solid walls as the boundary conditions provide ″hard″ nanoconfinement geometries in two and one dimensions for the polymer systems, respectively. P2VP was chosen for this study because it exhibits very favorable attractive interactions with hydroxyl groups naturally occurring on silica and alumina surfaces. Based on the literature results, the effect of nanoscale confinement on the dynamic glass transition of P2VP remains not very clear. For example, Serghei et al. demonstrated that the thin-film segmental dynamics of P2VP with the free upper interface prepared on ultraflat silicon wafers (rms <0.5 nm) show bulk-like behavior down to a film thickness of ∼10 nm.54 Likewise, no significant changes in the molecular dynamics of P2VP were found upon capillary flow through 18 nm in size cylindrical nanochannels.55 The segmental mobility of (semi-)isolated P2VP chains was also found to be bulk-like. Nevertheless, the broadening of the α-relaxation peak was observed.56 Ultrasensitive differential scanning calorimetry also shows no dependence of the glass transition temperature for P2VP films over the thickness range from hundreds of nanometers down to 3 nm.57 In contrast to that, Madkour et al. demonstrated that while the dynamic glass transition temperature for P2VP remains bulk-like for ∼22 nm films, a more detailed analysis of the calorimetric results gives an argument for a decrease in Tg with decreasing thickness—even by 7 K— as due to the presence of a mobile surface layer.58 Assuming strong interactions of the polymer segments with the substrates’ surface (either silica or aluminum), an increase of Tg for P2VP was also reported.59−62 On the other hand, Glor et al. showed that decoupling between molecular mobility at the free surface and near the substrate produces two distinct Tg’s in ultrathin films of P2VP.63
Since each segment of P2VP carries a dipole moment (effective dipole moment ∼1.2 D),64,65 we have utilized dielectric spectroscopy to probe its relaxation dynamics associated with the glass transition. The dielectric relaxation study in a 2D-confined space was complemented by standard and temperature-modulated differential scanning calorimetry (DSC) measurements, which provide complementary information on the relaxation processes from the analysis of the frequency-dependent heat capacity response. Our results show no evidence of the confinement effect in the temperature evolution of the segmental relaxation times. This feature was observed for P2VP confined in nanoporous alumina templates with the pore size of 20 nm and 24 nm thin films supported on silicon substrates. In contrast to the bulk-like behavior of τα(T), we observed a pronounced broadening of the segmental relaxation peak in confined geometry. We also found no evidence of decoupling between molecular mobility and the glass transition temperature. Interestingly, the broadening of the α-loss peak is not the same for 1D- and 2D-confined P2VP. Namely, the α-relaxation peak at the low-frequency side is slightly broader in the case of the nanopore-confined sample. By characterizing the strength of the interaction between the polymer and the confined surface—alumina or either silicon—we found that they are both favorable. However, P2VP is expected to have more than two times higher interfacial energy with AAO than with silicon oxide surface. To rationalize the bulk-like characteristics of the mean α-relaxation time for P2VP constrained at the nanoscale, we have taken advantage of the information that comes from the high-pressure studies of the bulk material, especially the importance of temperature and density fluctuations on the segmental relaxation of various polymer systems.66 This reasoning also comes from the recent experimental finding demonstrating the connection between 1D and 2D constrained polymer dynamics and bulk behavior via the density scaling approach.44
Experimental Section
Materials
The tested sample is poly(2-vinylpyridine) labeled in the text as P2VP with the averaged molecular weight of Mw ∼54k and PDI 1.43, determined by gel permeation chromatography (GPC). The chemical structure of P2VP is given in Figure 1. The sample was purchased from Polysciences Inc. (US) as a white powder and used without further purification. The glass transition temperature of the bulk polymer determined from the DSC measurements is 375 K (recorded on a second heating run, after cooling from 423 to 293 K with 10 K/min). The literature value for P2VP with Mw of 1020k and PDI 1.33 is 373 K.58 The common convention to determine the glass transition temperature from the dielectric studies is to extrapolate τα(T) to 100 s. By doing so, we get 366 K, which agrees with the value 366.8 K reported by Papadopoulos et al. for P2VP with Mw of 30k and PDI 1.04.65 However, in this study, we use the value of Tg = 372 K (defined as a temperature at which τα = 10 s) to avoid large extrapolation and for consistency with the high-pressure data.
Figure 1.
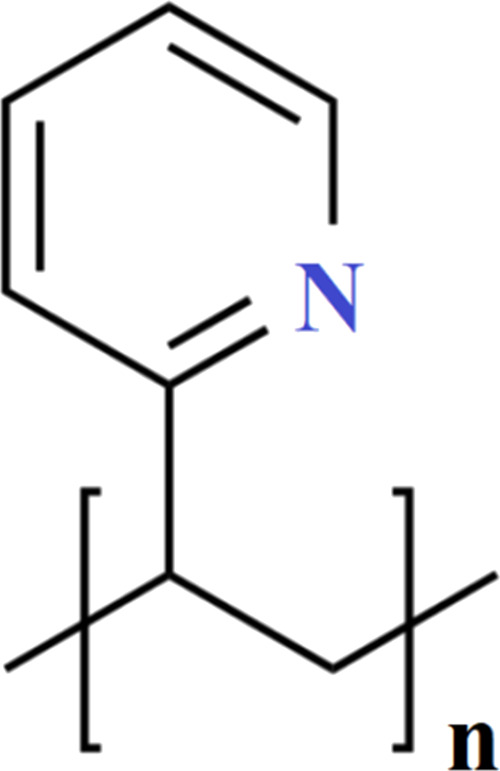
Chemical structure of the poly(2-vinylpyridine) (P2VP).
Preparation of Samples
2D Confinement
Nanoporous Alumina Templates and Infiltration Method
As confining templates, we have used commercially available anodized aluminum oxide (AAO) membranes (Inredox, US) composed of uniform arrays of unidirectional and non-cross-linking nanopores (pore diameter of 20, 40, 80, and 160 nm; pore depth 100 μm). The diameter of the alumina membrane is 13 mm, and its thickness is 100 μm. The porosity of AAO templates used in this study varies from 16% (for 160 nm pores) to 12% (for 20 nm pores). Before filling, AAO membranes were dried at 473 K in a vacuum oven for 24 h to remove any volatile impurities from the nanochannels. Membranes were weighed before and after infiltration. Because of the very high value of the glass transition temperature and chances to decompose the sample upon melting, P2VP was infiltrated into AAO nanopores via the solvent-assisted vapor swelling method, which has been successfully tested for numerous ultraviscous polymeric materials with reduced thermal stability.67,68 For that purpose, a polymer powder was placed on top of the AAO membrane and then moved to a desiccator containing a few milliliters of dichloromethane on the bottom. In the presence of dichloromethane’s vapor, P2VP softens and infiltrates into nanochannels by capillary forces even at room temperature. To achieve high filling rates, the process was carried out for a period of 2 weeks. Every few days, the membranes were taken out of the sealed desiccator and weighed. Each time, their top and bottom surfaces were carefully cleaned from the excess material using delicate wipes soaked in dichloromethane. The infiltration process was repeated until the mass of the AAO membrane with a confined polymer inside did not change with time. Finally, their surfaces were cleaned again. The membranes were put in a vacuum oven overnight (T = 473 K) to remove the residual solvent and weighed thereafter. The estimated degree of filling was calculated by considering the porosity of the membrane, the density of the bulk polymer, and the mass of the template before and after infiltration. The degree of pore filling varies from, in 160 nm pores, ∼60% up to ∼90%, for a pore diameter of 20 nm and 80 nm.
1D Confinement
Thin-Film Preparation
For the supported thin films, a heavily doped 4″ diameter silicon wafer (SIL’TRONIX, France) with a resistivity value in the range within 0.001–0.003 Ω·cm and orientation of (100 ± 0.5°) was used as the substrate. The wafers were diced into pieces of dimension 1 × 1 cm2 and were cleaned using air plasma treatment for 20 min. We used the Henniker Plasma HPT-100 with a power of 98% with 10 sccm ambient airflow for the same. Thin films were then prepared by spin-coating the polymer solution onto the cleaned silicon wafer substrate. The polymer solution, with a mass concentration of 4 g/L, was prepared in anhydrous toluene (99.8%), supplied by Sigma-Aldrich. After, it was filtered, by a 0.2 μm PTFE syringe filter, and used in a film thickness ∼24 nm. For better polymer dissolution in the solvent, we waited for 24 h before the spin coating of the polymer films onto the Si substrate. We used the KLM SCC-200 spin coater with a rotation speed of 2000 rpm, and the time was kept at 60 s. Prepared films were then annealed at 389 K for 24 h under vacuum. This procedure leads to the formation of homogeneous thin films. The film thickness was measured with spectroscopic ellipsometry and confirmed by atomic force microscopy (AFM).
Ellipsometry
The spectroscopic ellipsometer Semilab SE-2000 was used to measure the thin-film thickness. The measurements were done at incident angles of 65, 70, and 75° at ambient conditions. A multilayer model consisting of the Si substrate, SiOx layer, and polymer film was considered. The SiOx layer thickness before the spin coating polymer was measured and is fixed while considering the multilayer model. The thickness was obtained by fitting the ellipsometric angles and bulk material optical constants.
Atomic Force Microscopy
The film thickness measurement was reconciled with JPK’s NanoWizard 3 NanoScience AFM in the air using a tapping mode and a silicon cantilever. The thickness was estimated by making a scratch using a soft pen on the polymer film and measuring the step’s height. The image analysis was done using the WSxM and Gwyddion software.
Methods
Differential Scanning Calorimetry
Calorimetric measurements of nanopore-confined P2VP were carried out using a Mettler-Toledo DSC apparatus equipped with a liquid nitrogen cooling accessory and an HSS8 ceramic sensor (heat flux sensor with 120 thermocouples). Temperature and enthalpy calibrations were performed by using indium and zinc standards. Crucibles with prepared samples (crushed membranes containing confined P2VP) were sealed and cooled down to 293 K at the rate of 10 K/min. DSC thermograms were recorded on heating at the rate 10 K/min over a temperature range from 293 to 473 K. Tg values were determined as the point corresponding to the midpoint inflection of the extrapolated onset and end of the transition curve.
Temperature-Modulated Differential Scanning Calorimetry
For the analysis of the dynamic behavior of the sample in the frequency range from 5 to 25 MHz, we have used temperature-modulated differential scanning calorimetry (TMDSC). Measurements were carried out at a heating rate of 2 K/min and a pulse amplitude of 1.5 K within the temperature range 343–403 K.
Dielectric Spectroscopy
Dielectric relaxation studies for bulk and nanoconfined P2VP were carried out using a Novocontrol Alpha Analyzer. For bulk P2VP, we use standard plate–plate electrodes of 20 mm in diameter separated by a Kapton spacer of 50 μm thickness. Nanoporous AAO templates (of 100 μm thickness and 13 mm diameter) filled with the investigated polymer were placed between two circular electrodes (diameter: 10 mm). Bulk and 2D-confined materials were measured as a function of temperature (on cooling from 443 to 373 K with the rate of ∼0.2 K/min) in the frequency range from 10–1 to 106 Hz. The temperature was controlled with stability better than 0.1 K by the Quatro system.
One should remember that the raw dielectric data collected for the nanopore-confined system represent a combined response of the sample, alumina matrix, and air gaps formed due to incomplete filling of the nanochannels. Therefore, correction of the raw dielectric data is required to access the definite signal of the confined polymer. This can be done according to the procedure described elsewhere.69 In previous works, we have demonstrated that the alumina template oneself and incomplete filling of the nanopores (filling degree ∼90%) do not affect the position of the α-peak and spectral shape for embedded glass-forming liquids and polymers (it only shifts ε″ toward higher values depending on the porosity).70,71 However, in our case, the degree of filling of the nanochannels with the tested polymer was—at least for those AAO membranes with larger pore sizes—much beyond that. Therefore, the dielectric data were corrected accordingly, and it was observed that there are no changes in the position of the α-relaxation peak compared with the bulk. Moreover, Alexandris et al.(38) reported that the air-gap correction is not relevant because it only affects the absolute value of the dielectric permittivity remaining the position of the relaxation peak maximum. Apart from that, such correction is also obligatory when evaluating the dielectric properties of nanopore-confined ionic liquids.72,73
For dielectric studies at elevated pressure, we have utilized a high-pressure setup, which includes the pressure chamber MVX-30 operating in the temperature range from 293 up to 523 K and pressures of 0–200 MPa (Unipress, Institute of High-Pressure Physics, Warsaw, Poland) and a manual pump (Sitec). The pressure was exerted using silicon oil and transmitted to a pressure vessel by a system of flexible capillary tubes (Nova Swiss). The real and imaginary parts of the complex permittivity were measured within the same frequency range as the atmospheric pressure data using an impedance Alpha-A Analyzer (Novocontrol GmbH, Montabaur, Germany). The temperature was controlled by a highly dynamic temperature control system (Huber Tango). The sample was maintained between a 20 mm in diameter plate–plate capacitor with a Kapton spacer and separated from the pressure-transmitting silicon oil by tightly wrapping it with a Teflon tape.
For the dielectric measurements of thin film, the highly conductive silicon substrate on which the polymer film was spin-coated acts as the lower electrode. The 1 × 1 mm counter electrode possesses highly insulating square SiO2 spacers with a side length of 5 μm and height of 60 nm. Such quadratic spacers were supplied by Novocontrol Technologies GmbH (Germany). They are produced by thermal oxidation and optical lithography on the surface of conductive silicon wafers. The two wafer pieces (i.e., the one onto which polymer film was spin-coated and the second one having silica nanospacers) are brought in contact. This gives a capacitor inside which the sample material is with its upper interface free.
Similar, as in the case of nanopore confinement, corrections of the dielectric data measured using a nanostructured electrode arrangement are required to retrieve the pure dielectric response of the thin polymer film. This can be done according to the model introduced by us in a recent paper.74 The model allows to distinguish the confined polymer dynamics from the total dielectric signal that is affected by the contribution coming from the nonzero resistivity of the Si electrodes, the silicon oxide isolating layer, and the spacer posts/air gap between the polymer layer and the upper electrode. The results have led to the conclusion that the most severe change in the loss peak profile in such configuration is due to the air gap that in many cases is much thicker than the polymer film itself. From the analysis of the dielectric response of various polymers within the proposed model, we found that the air-gap effect correlates with the sample polarity. For an ε∞/εs ratio close to 1 (small Δε values), the dielectric response of the sample is not affected significantly by this specific nanostructured-electrode geometry. For the 24 nm P2VP film supported on a silicon substrate (thickness of the oxide layer: 7 nm, air gap: 60 nm, net gap dielectric constant: 1.029, and dielectric constant of the oxide layer: 3.9), the input Havriliak–Negami (HN) fitting parameters describing the shape of the relaxation process recorded at 403 K are ε∞=2.15, Δε = 0.49, τHN = 8.5 × 10–4 s, γ = 0.25, and α = 0.91. These produce a peak shift that amounts only to ∼0.15 decades. Apart from that, they do not affect the breath of the relaxation function. For larger air gaps, the limiting shift in peak position can be estimated using the expression τtot = τsam × ε∞/εs and should not exceed 0.5 decades (assuming that Δε≈2.5 for bulk P2VP). Nevertheless, a more pronounced broadening of the loss profile is expected for the polymer thin film in such a case.
Results and Discussion
Glass Transition Dynamics in Nanopore Confinement
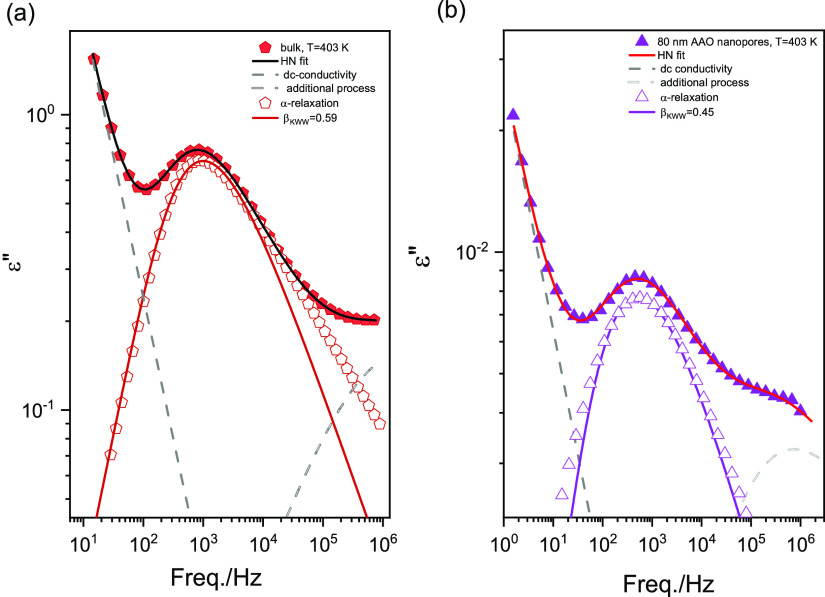
We begin our investigation by demonstrating the effect of nanopore confinement on the glassy dynamics of P2VP. The results of the dielectric relaxation studies are collected together in Figure 2. Representative dielectric loss spectra measured at the indicated range of temperatures for the studied polymer in bulk and confined within 80 nm AAO pores are shown in Figure 2a,b. In both cases, with lowering the temperature, we have observed that the main α-relaxation peak — associated with the dynamics of the polymer’s segments — shifts toward lower frequencies. This effect indicates the slowing down of the molecular movements as the glass-transition temperature Tg is approached.
Figure 2.
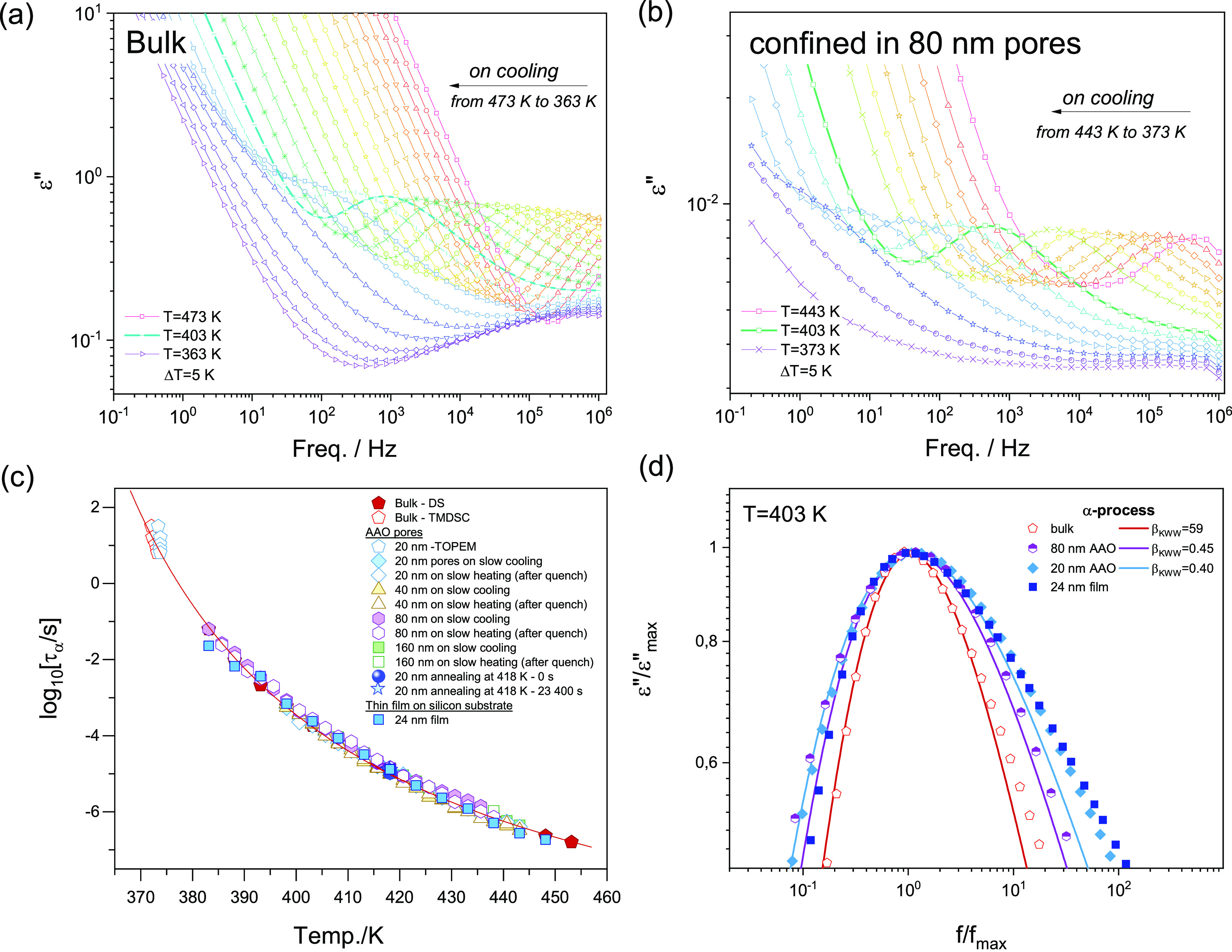
Dielectric loss spectra for P2VP (a) in bulk and (b) confined within 80 nm size alumina nanopores as measured upon cooling with the rate of 0.2 K/min. Dielectric data for nanopore confined polymer were corrected by considering nanoporous matrix permittivity and incomplete filling of the nanochannels with the polymer. (c) Temperature dependence of the segmental relaxation times for P2VP bulk (TMDSC and DS), nanopore-confined, and thin film. The red line represents the VFT fit to the dielectric data. Data in nanopore confinement were measured using two different thermal protocols: (i) on slow cooling from 443 to 383 K with the rate of 0.2 K/min and (ii) on heating with the rate of 0.2 K/min after quenching with 10 K/min from 443 to 383 K. (d) Comparison of the shape of the α-relaxation peak for P2VP confined in alumina nanopores (80 and 20 nm) and 24 nm thin film supported on a silicon substrate as measured at 403 K. Bulk spectra were given as a reference. The dc-conductivity contribution has been subtracted.
The characteristic α-relaxation time is commonly determined as the frequency corresponding to the maximum of the loss peak, 1/(2πfmax). However, when the dc-conductivity contribution shows up as an increase of ε″ at low frequencies, the better description of the relaxation processes is obtained by using the Havriliak–Negami (HN) function with an additional conductivity term given as:75
| 1 |
where Δε is the dielectric strength, ε∞ is the high-frequency limit of the permittivity, τHN denotes the relaxation time, a and b are the shape parameters, and σ0 is the dc-conductivity. The characteristic time constant τHN in the HN function is related to the relaxation time at a maximum of loss peak τmax by the following relation:76
| 2 |
Because of the strong conductivity contribution, not allowing to see clearly the maximum of the loss peak close to the glass-transition temperature, we have also used the derivative method (εder″ = (−π/2)(dε″/dlnf)≈εrel)77 that provides an alternative estimate of the α-relaxation time for bulk and nanopore-confined material. Segmental relaxation times determined for P2VP using both approaches were found to be almost the same (within the error of ±0.2–0.3 decades).
The temperature evolution of the α-relaxation times obtained in this way is shown in Figure 2c. As observed, the τα(T) dependence for P2VP constrained within AAO templates with the pore diameter ranging from 160 to 20 nm follows bulk behavior. This contrasts to most of the glass-forming systems, which show faster dynamics with decreasing pore diameter. The segmental process for P2VP exhibits strong τ(T) dependence that can be described using the Vogel–Fulcher–Tammann (VFT) equation,78,79 as follows:
| 3 |
where log10τ∞ and DT are the fitting parameters, whereas T0 is called ideal glass transition or Vogel temperature. For the investigated compound, we get the following set of parameters: −12.5, 2.4, and 315, respectively. The value of the glass transition temperature for bulk P2VP determined from the dielectric measurements is 372 K, which refers to the temperature at which the segmental relaxation times is equal to 10 s.
Although we cannot actually see the effect of confinement on the temperature evolution of the mean α-relaxation time, a characteristic for nanopore-confined systems broadening of the loss peak is still observed; see the results presented in Figure 2d. This was quantified with the use of the fractional exponent βKWW from the Kohlrausch–Williams–Watts function,80,81 as follows:
| 4 |
where βKWW changes from 0 to 1. The value of βKWW decreases with increasing width of the relaxation spectrum. Values of βKWW that describe the shape of the α-relaxation for P2VP at 403 K in the bulk state and within 20 nm AAO nanopores are 0.59 and 0.4, respectively. The broadening distribution of the relaxation times in nanopores is commonly reported and interpreted in terms of the increasing heterogeneous character of the relaxation dynamics.19,56,82−84 We also note that, in contrast to most glass-forming liquids and polymers confined within AAO nanopores, there is no evidence of an out-of-equilibrium behavior for nanopore-confined P2VP.85−87 Therefore, the shape and the characteristic relaxation time remain constant even upon prolonged annealing (see results presented in Figure 2c). Additionally, in Figure 3a,b, we demonstrate the fitting procedure used to extract the basic features of the α-relaxation for bulk and nanoconfined P2VP. The contribution from the dc-conductivity was subtracted from the total HN fit, same as the additional relaxation process seen at high frequencies (not considered in this work).
Figure 3.
Decomposition of the dielectric loss data into the α-relaxation, conductivity contribution, and additional relaxation seen at high frequencies for bulk and nanopore-confined P2VP at 403 K.
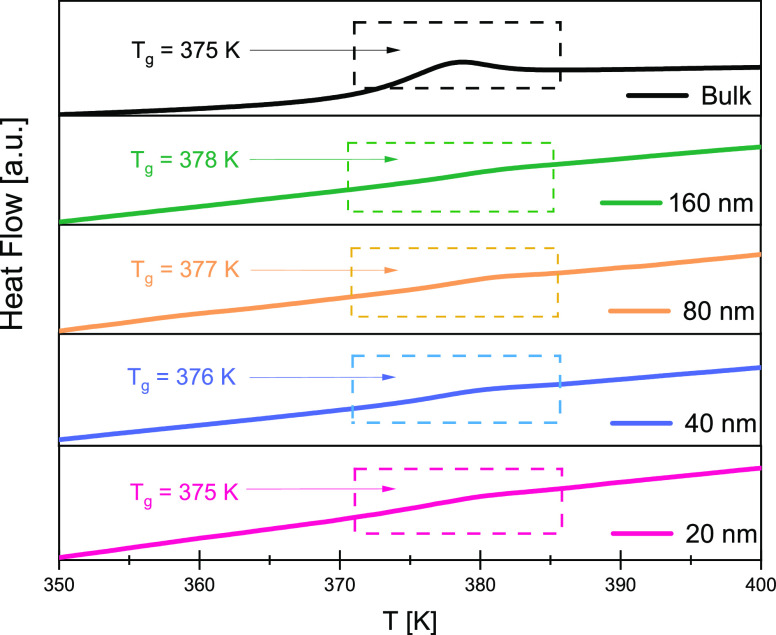
To validate obtained results, we have also performed calorimetric measurements that include stochastic temperature modulation (TOPEM) to determine characteristic relaxation times associated with the glass transition for bulk and P2VP confined within AAO with the pore diameter of 20 nm. The results again show bulk-like behavior, as demonstrated in Figure 2c. In line with this finding, upon standard DSC scans carried out for all P2VP samples constrained within 20–160 nm AAO pores, we detect only one glass transition event located close to that characteristic for the bulk polymer, i.e., at about 375 K; see Figure 4. Therefore, based on calorimetric results, we can conclude that, for P2VP, we have not observed decoupling between molecular mobility and Tg in nanopore confinement. The effect when the dynamic glass transition temperature determined from the τα(T) does not match with calorimetric results is often observed at large confinement length scales, especially for thin polymer films.
Figure 4.
Standard DSC thermograms recorded for P2VP in bulk and confined within AAO templates of pore diameter from 160 to 20 nm. Calorimetric data were measured on heating with the rate of 10 K/min followed by quenching (10 K/min).
Glass Transition Dynamics in Thin Films
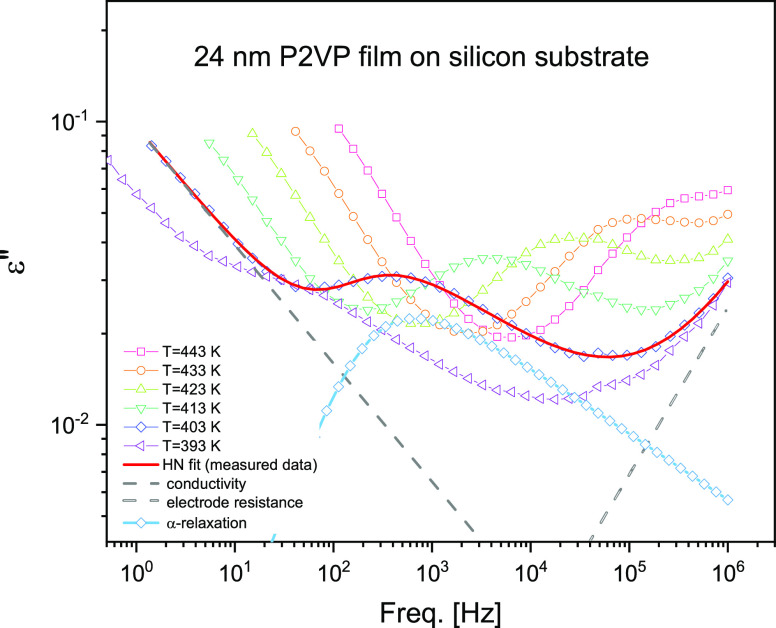
In Figure 5, we show dielectric loss spectra collected at selected temperatures for a 24 nm P2VP film supported on silicon substrate measured using nanostructured electrode configuration. As already noted, to extract the properties of the pure polymer film, correction of the dielectric data is needed according to the model proposed by us recently.74 Therefore, the raw dielectric data as that presented in Figure 5 were fitted accordingly to the proposed model, assuming that the dielectric permittivity of the sample is given by the sum of the Havriliak–Negami (HN) function and a dc-conductivity term. The additional contribution seen on the high-frequency side of the spectrum is due to the nonzero resistivity of the electrodes. As we found, the value of relaxation times determined from the raw dielectric spectrum and that obtained by following the abovementioned correction deviate from each other only very slightly. This relates to the small value of the dielectric strength for the P2VP film. This is consistent with the results by Kremer and co-workers,13,88 who demonstrated that the shape and the mean relaxation rate of the polymer film measured in an air-gap geometry do not change for low values of dielectric strength, as opposed to the case of large strengths. Values of the relaxation times determined in this way were then added to bulk and nanopore data presented in Figure 2c. As observed from the results, the temperature dependence of the α-relaxation times for the 24 nm film follows that of the bulk polymer, whereas the breadth of the relaxation process shows only a difference from that of the 20 nm pore confined sample at the low-frequency side of the loss peak (see Figure 2d). We conclude that stretching of the polymer chains is not sufficient to alter the Tg or the cooperative segmental dynamics of P2VP in confinement. Nevertheless, the width of the α-relaxation process increases under the condition of geometrical confinement. Changes in the distribution of relaxation times reflect the increased heterogeneous character of the environment and a broadening of the glass transition.
Figure 5.
The imaginary component of the total dielectric loss response of the 24 nm P2VP thin film prepared on a silicon substrate as measured at few selected temperatures. The solid line shows the representative fit of the raw data according to the model described in our previous paper.74
Given the results presented above, the question arises why, for P2VP, the segmental dynamics remain bulk when going down with the pore diameter and in thin films. In contrast, for most of the glass-forming systems, we typically observe enhanced dynamics in confined geometry. Can we rationalize it as due to strong interactions (e.g., via hydrogen bonds) with the pore walls, same as expected in thin-film dynamics? On the other hand, strong interfacial interactions should retard the mobility of these polymer segments, which are located close to the pore walls. And this should actually make the gradient in dynamics between core and interfacial layers to be more pronounced. We could use the argumentation of the characteristic length scale on which the glassy dynamics occur. The results suggest that even in 20 nm pores, there are no changes in the cooperativity of the relevant molecular motions. Moreover, it is observed that even with a much higher molecular weight for other polymer systems, these changes are evident. In agreement with recent studies,41,42,89 changes in the molecular packing or frustration in the density are the source of the enhanced mobility of glass-forming systems in nanopores. This immediately leads to a potential role of the pressure effects33,35,44−46 that, together with the temperature variation, are known to be the key factors that control the glass-transition dynamics.90 Therefore, to better understand the bulk-like behavior of P2VP under nanoscale confinement, we have used the information that comes from the high-pressure studies of the bulk material. These results are described in the next part of this paper.
Glass Transition Dynamics for Bulk P2VP on Increased Pressure
Figure 6a illustrates representative dielectric loss spectra measured for P2VP at constant temperature T = 433 K and different pressures. With increasing pressure, the α-relaxation peak moves toward lower frequencies, indicating a systematic slowing down of the segmental dynamics. Due to the high dc-conductivity contribution, the α-relaxation time was extracted using the same procedure as in confinement data. Obtained in this way, pressure dependencies of the α-relaxation times measured along three different isotherms are shown in Figure 6b. The pressure dependencies of the segmental relaxation times have a linear character and therefore were described with the use of the pressure version of the Arrhenius law,91 as follows:
| 5 |
where log10τ0 is a fitting parameter, ΔV* is the activation volume, and R is the gas constant. By extrapolating VFT fits to 10 s, we can determine the corresponding values of the glass-transition pressure, pg (as the equivalent of the glass-transition temperature for isobaric data). The glass transition is usually determined from dielectric relaxation studies as the temperature/pressure at which τα reaches 100 s. Nevertheless, in this work, we have used 10 s to avoid extrapolation of the data.
Figure 6.
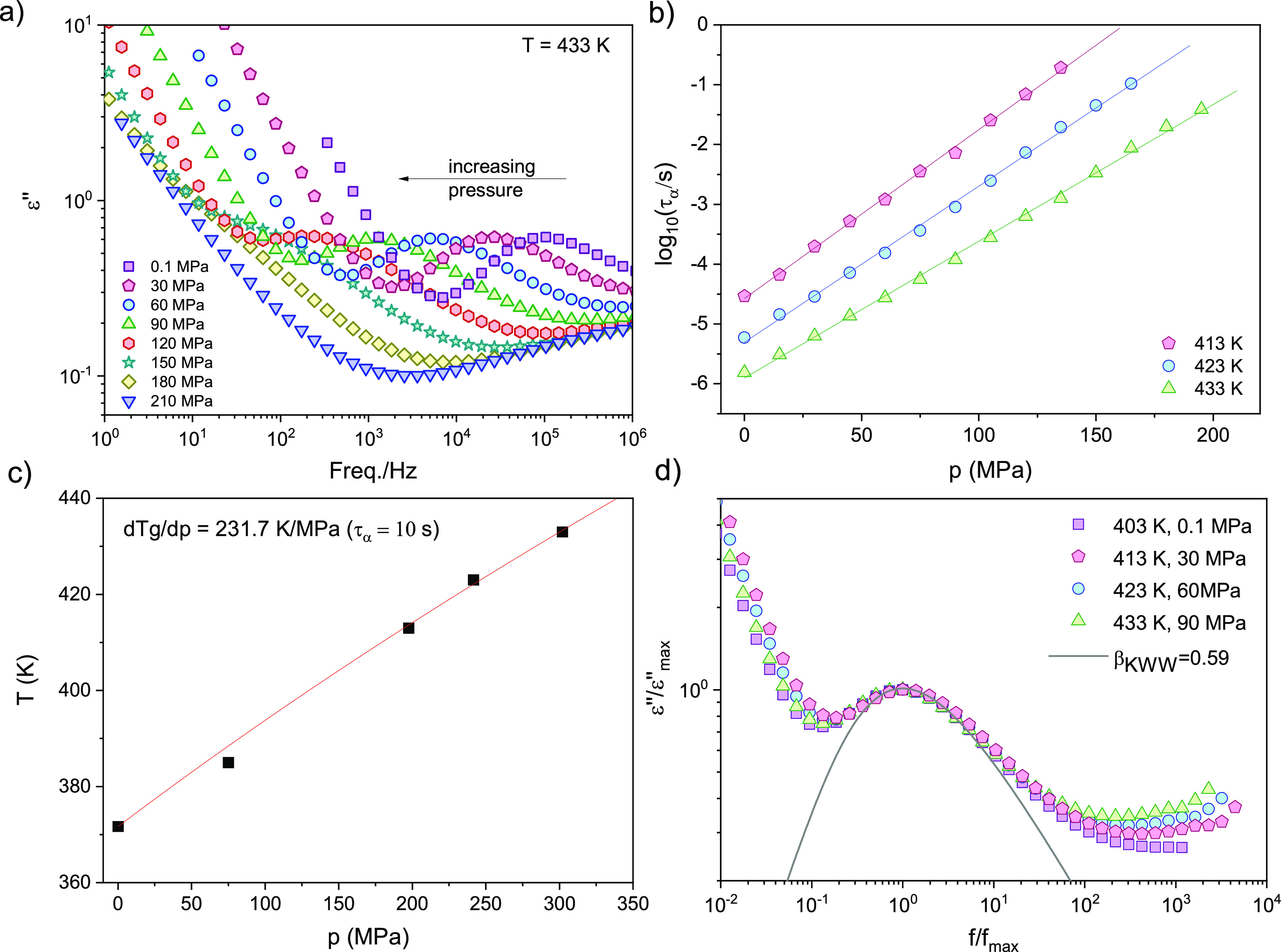
(a). Dielectric loss spectra measured for bulk P2VP along isotherm T = 433 K. (b) α-Relaxation time plotted versus pressure along three different isotherms. Solid lines represent fit to the data with the use of the pressure version of the Arrhenius equation. (c) Variation of the glass transition temperature as a function of pressure. The glass transition was determined from dielectric data as the temperature (pressure) at which τα = 10 s. The red line represents the Andersson–Andersson fit. (d). Comparison of the normalized dielectric loss spectra obtained at different thermodynamic conditions (T, p) for approximately the same α-relaxation time (so-called isochronal superposition plot).
To further quantify the effect of pressure on segmental dynamics of P2VP, we have calculated the pressure coefficient of the glass-transition temperature dTg/dP determined as the first derivative of the experimentally measured Tg(pg) dependence in the limit of ambient pressure. This is presented in Figure 6c. To describe the dependence of the glass transition vs pressure, we have utilized the empirical equation proposed by Andersson and Andersson,92 as follows:
| 6 |
The best fit was obtained with k1 = 371 ± 1, k2 = 2.57 ± 1, and k3 = 1603 ± 173. By dividing k1 by k3, one can estimate the value of the pressure coefficient of the glass-transition temperature dTg/dP, which describes the sensitivity of the glass-transition temperature to pressure changes. For P2VP, we get 232 K/GPa, a relatively low value for a polymeric system and rather more typical for a low-molecular-weight van der Waals liquids. By comparison, the values are 328 K/GPa for polystyrene (PS),66 289 K/GPa for poly(methylphenylsiloxane) (PMPS),93 520 K/GPa for bisphenol-A-polycarbonate,94 and 481 K/GPa for poly-4-chloro-styrene (P4ClS).44 As a matter of fact, the dTg/dP coefficient determined in this study for P2VP is much lower than that reported by Papadopoulos and Peristeraki,65 340 K/GPa, using τα = 100 s and the sample of MW ∼31k. We suppose that the origin of such discrepancy might be the high conductivity contribution, which even made the authors choose dielectric modulus instead of dielectric permittivity representation to analyze the data obtained on increased pressure.
In agreement with recent experimental results, the dTg/dP coefficient’s value might provide a rough estimate on whether the α-relaxation process is sensitive to the density fluctuation in confined geometry. As found by Talik and co-workers,40 the depression of the glass transition in AAO nanopores correlates with the dTg/dP ratio; i.e., the higher the dTg/dP coefficient is, the more deviation from the bulk behavior is observed in confined geometry. Lipson and co-workers also pointed out a similar finding when trying to rationalize the enhanced dynamics of thin films of P4ClS.45 Likewise, the much different behavior of low-molecular-weight liquids glycerol (35 K/GPa) and salol (204 K/GPa) confined in alumina templates was explained in terms of the different contribution of volume and thermal effects in controlling their glassy dynamics.33 In line with this, the relatively weak sensitivity of P2VP to pressure/density effects might be the origin of its bulk-like behavior in AAO nanopores. One can also use the same type of argumentation for 1,4-cis-polyisoprene (dTg/dP = 178 K/GPa),95 in which glass transition temperature was unaffected by 2D confinement, whereas, at the same time, a remarkable broadening of the distribution of relaxation times for both the segmental and chain modes was observed.96
In Figure 6d, we plot the dielectric loss spectra measured at different combinations of (T, p) but with approximately the same α-relaxation time. To have a perfect overlap, their maxima were normalized approximately at frequency f = 103 Hz. The best KWW fit obtained for the relaxation peak of the P2VP is βKWW = 0.59. Although the dc-contribution is relatively high, it is evident that the distribution of the relaxation times for P2VP remains T–p invariant along an isochrone (isochronal superposition). Herein, we wish to note that the isochronal superposition fails for glass-forming systems that reveal strong hydrogen bonding interactions, such as dipropylene glycol.97
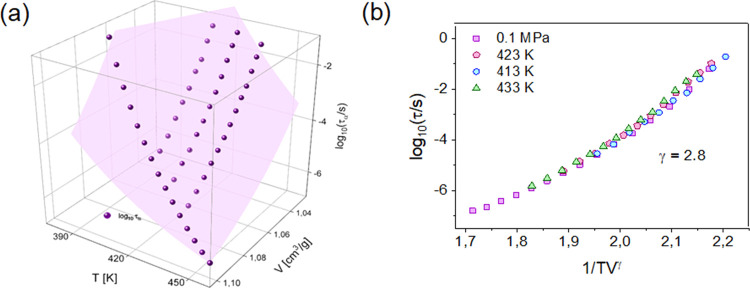
In the next step, with the use of PVT data reported in the literature (for P2VP of similar molecular weight),65 we converted experimentally measured τα (T, p) dependences to τα (T, V) ones. Then, we parameterized them with the use of the modified version of the Avramov model,98 as follows:
| 7 |
where A, B, D, and γ are the fitting parameters. The two-dimensional surface plot described with the set of fitting parameters γ = 2.8, D = 5.5, B = 657, and A = −8.7 is presented for P2VP in Figure 7a. Then, using the value of γ = 2.8 for P2VP, we tested the density scaling, i.e., the ability to describe the relaxation time measured under varying temperature and pressure conditions as a function of the single scaling relation ργ/T.99,100 The gamma exponent found by describing high-pressure data with the use of eq 7 is a material constant, often related to many dynamic and thermodynamic properties of the system.101−103 Therefore, it provides key information about the intermolecular forces or dynamic behavior of the substance. For P2VP, using the scaling exponent value =2.8, we were able to superimpose the α-relaxation times measured under different isobaric and isothermal conditions presented in Figure 7b. The validity of the density scaling for P2VP indicates that its hydrogen bonding tendency is not enough to affect the glass-transition dynamics at varying thermodynamic conditions. In addition to that, the gamma exponent’s value for P2VP is typical for other polymer glass-formers (P4ClS: 3.1, PS: 2.5, and 1,4PI: 3), indicating that we cannot use it to predict any relevant information on confinement effects.
Figure 7.
(a). α-Relaxation times plotted versus temperature (T) and volume (V) for P2VP. The violet area represents the surface fit to the modified Avramov equation. (b) Density scaling dependence of the segmental relaxation times obtained for P2VP using ambient and high-pressure dielectric data.
Surface Free Energy Comparison
The presence of a hard interface is known to cause changes in the local density and affects the dynamics of the confined polymer chains. For example, Fryer et al. showed that the deviation in Tg from the bulk value strongly depends on the interfacial energy.32 The results of the molecular dynamics simulations also show that the Tg of the ultrathin polymer can be tuned by changing the intermolecular potential between the polymer chains and the substrate.104 Recently, Zuo et al. demonstrated that the polymer thin film dynamics can be tuned by the interfacial effects introduced by changing both the strength and degree of chain adsorption via surface modification of the substrates.105 Specifically, the polymer–substrate interfacial effects were affected by attaching silane reagents with phenyl and amino groups onto the surface. As reported, with decreasing surface free energy, Tg of the PMMA films also decreases and deviates more from the bulk polymer.
To understand the type of interaction between P2VP with Al/alumina and SiO2, we calculated the surface free energy between the polymer and the substrates. The total surface free energy of a material, γTotal, can be expressed as follows:
| 8 |
where γLW is the dispersive and γPis the polar component of the surface energy, respectively.106Table 1 shows the γTotal, γLW, and γPvalues for P2VP, Al, alumina, and SiO2 calculated from the contact angle values available in the literature.58,107,108 One can estimate the interfacial energy between two materials, in our case, the polymer ″P″ and the substrate ″S″, as follows:109
| 9 |
Table 1. The Interfacial Energy between P2VP and Various Substrates Calculated from the Total Surface Energy of Material (γTotal) along with Its Dispersive (γLW) and Polar (γP) Components.
| γTotal (mJ m–2) | γLW (mJ m–2) | γP (mJ m–2) | γPS (mJ m–2) | |
|---|---|---|---|---|
| P2VP | 39.5 | 29.8 | 9.7 | |
| Al | 28.32 | 26.5 | 1.82 | 3.21 |
| SiO2 | 47 | 44.6 | 2.3 | 4.14 |
| alumina | 36.3 | 36.3 | 0 | 10 |
The calculated values of γPS are also collected in Table 1. The values of γPS show that the interaction between P2VP and solid substrates increases in the order Al, SiO2, and alumina. In all cases, P2VP possesses strong interaction toward the surface of the substrate. In agreement with the literature, for γSL lower than approximately 2 mJ/m2, the measured Tg should be lower from that of the bulk sample, while for γSL > 2 mJ/m2, an increase in Tg should be observed.32,105 This interfacial energy can possibly affect the broadening of the relaxation in a way that the more the interaction energy is, the more the number density of slowed down segments is at a given temperature. A keen look at Figure 2d reveals that the broadening on the low-frequency side of the α-relaxation is correlated with the interfacial energy values. This broadening (and for some polymers or geometries, a completely new separate mode) is understood to be due to an interphase formed by slowed down segments.110−113 Although we actually have not seen an increase of Tg for confined P2VP, the results of the above calculation, together with the high-pressure data, indicate the pronounced importance of the polymer–substrate interactions and sensitivity of the polymer dynamics on density frustrations as the potential source responsible for changes in the glass transition dynamics in nanoconfinement.
As the last point, it should be noted that free surfaces, substrate interfaces, and confinement can all together significantly perturb the glass transition dynamics of polymers confined at the nanoscale. This can lead to deviations from bulk Tg that can be either barely noticeable (as individual components will counteract each other) or difference of many degrees kelvins (when they reinforce).20,32,114 It is typically believed that the presence of a free surface results in the enhanced mobility of the polymer segments adjacent to the free surface. Simultaneously, attractive substrate interactions reduce the mobility of chain segments anchored to the substrate, which increases Tg. Overall, this might suggest that the absence of change in Tg of P2VP in confinement comes from the conflicting effect of the attractive substrate (increase Tg) and free surface (decrease Tg). However, a significant problem with estimating the impact of free surface on thin-film polymer dynamics is that practically changes in Tg probed as a function of distance from the free surface or supporting substrate can be studied using fluorescent dyes or via computer simulations.20 As showed by Torkelson and co-workers in the case of P2VP, the free-surface effect can be negligible in dictating the Tg behavior of supported ultrathin polymer films. More specifically, it is overdominated by strong attractive interactions of the polymer hydroxyl groups with the silica substrate.62
Conclusions
In this work, we have studied the segmental dynamics of P2VP in one- and two-dimension nanoconfined geometry provided by silicon substrates and porous alumina membranes. The dielectric relaxation studies, together with calorimetric results, show that nanoconfinement does not induce slowing down of the molecular motion of P2VP in AAO nanopores. The α-relaxation time displays bulk-like T-dependence in pores with sizes down to 20 nm. Moreover, we have also not seen deviations in τα(T) for the 24 nm thin film supported on a silicon substrate. On the other hand, the confinement of P2VP in AAO nanopores and thin films results in a substantial broadening of the distribution of relaxation times. Interestingly, we found that the breadth of the α-relaxation time for P2VP in 20 nm size pores and 24 nm thin film does not show a substantial difference, although there is a slight broadening seen on the low-frequency side in the case of the 2D-confined sample.
To understand why the behavior of segment relaxation time for nanoconfined P2VP remains bulk-like, we have made use of the information that comes from the high-pressure studies of the bulk material. The dTg/dP coefficient for P2VP is 232 K/GPa, meaning that its glass-transition dynamics are rather weakly sensitive to pressure/density effects. This most probably explains why the segmental relaxation time is not affected by changes in the density induced by geometrical constraints. Not all polymers are sensitive to confinement effects, same as they are not sensitive to density fluctuations/compression. Hence, by relating these two features, we are able to envisage the potential changes in the dynamics of polymer glass-formers in nanoscale confinement. From the high-pressure studies, we also found that the value of the density scaling exponent, γ = 2.8, for P2VP is quite similar to other polymer systems of much different dTg/dP values. Hence, we cannot use it to explain/predict the effect of geometrical confinement on Tg. The other parameter very useful to understand the properties of P2VP under nanoscale confinement turned out to be the surface free energy between the polymer and the substrates. The estimated γPS values indicate the pronounced importance of the polymer–substrate interactions for all considered cases here. The broadening of the α-relaxation seen at low frequencies seems to correlate with the trend in the calculated surface energies. This broadening is understood to be due to an interphase formed by slowed-down segments. Therefore, by linking the strength of the interaction with the solid substrate and sensitivity of the glass-transition temperature to density variation, we can aim to rationalize the α-relaxation dynamics of the confined polymer system.
Acknowledgments
The authors are grateful for the financial assistance from the National Science Centre (Poland) within the Project OPUS 14 no. UMO-2017/27/B/ST3/00402.
The authors declare no competing financial interest.
References
- Martin C. R. Nanomaterials: A Membrane-Based Synthetic Approach. Science 1994, 266, 1961–1966. 10.1126/science.266.5193.1961. [DOI] [PubMed] [Google Scholar]
- Azzaroni O.; Lau K. H. A. Layer-by-Layer Assemblies in Nanoporous Templates: Nano-Organized Design and Applications of Soft Nanotechnology. Soft Matter 2011, 7, 8709–8724. 10.1039/c1sm05561e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh S.; Kouamé N. A.; Ramos L.; Remita S.; Dazzi A.; Deniset-Besseau A.; Beaunier P.; Goubard F.; Aubert P.-H.; Remita H. Conducting Polymer Nanostructures for Photocatalysis under Visible Light. Nat. Mater. 2015, 14, 505–511. 10.1038/nmat4220. [DOI] [PubMed] [Google Scholar]
- Soppimath K. S.; Aminabhavi T. M.; Kulkarni A. R.; Rudzinski W. E. Biodegradable Polymeric Nanoparticles as Drug Delivery Devices. J. Controlled Release 2001, 70, 1–20. 10.1016/S0168-3659(00)00339-4. [DOI] [PubMed] [Google Scholar]
- Alcoutlabi M.; McKenna G. B. Effects of Confinement on Material Behaviour at the Nanometre Size Scale. J. Phys. Condens. Matter 2005, 17, R461–R524. 10.1088/0953-8984/17/15/R01. [DOI] [Google Scholar]
- Suzuki Y.; Duran H.; Steinhart M.; Kappl M.; Butt H.-J.; Floudas G. Homogeneous Nucleation of Predominantly Cubic Ice Confined in Nanoporous Alumina. Nano Lett. 2015, 15, 1987–1992. 10.1021/nl504855z. [DOI] [PubMed] [Google Scholar]
- Balazs A. C.; Emrick T.; Russell T. P. Nanoparticle Polymer Composites: Where Two Small Worlds Meet. Science 2006, 314, 1107–1110. 10.1126/science.1130557. [DOI] [PubMed] [Google Scholar]
- Napolitano S.; Glynos E.; Tito N. B. Glass Transition of Polymers in Bulk, Confined Geometries, and near Interfaces. Rep. Prog. Phys. 2017, 80, 036602 10.1088/1361-6633/aa5284. [DOI] [PubMed] [Google Scholar]
- Jani A. M. M.; Yazid H.; Habiballah A. S.; Mahmud A. H.; Losic D.. Soft and Hard Surface Manipulation of Nanoporous Anodic Aluminum Oxide (AAO); Springer International Publishing: Switzerland, 2015; Vol. 219. [Google Scholar]
- Richert R. Dynamics of Nanoconfined Supercooled Liquids. Annu. Rev. Phys. Chem. 2011, 62, 65–84. 10.1146/annurev-physchem-032210-103343. [DOI] [PubMed] [Google Scholar]
- Xie S. J.; Qian H. J.; Lu Z. Y. Hard and Soft Confinement Effects on the Glass Transition of Polymers Confined to Nanopores. Polymer 2015, 56, 545–552. 10.1016/j.polymer.2014.11.049. [DOI] [Google Scholar]
- Kremer F.; Huwe A.; Schönhals A.; Różański S. A.. Molecular Dynamics in Confining Space. In Broadband Dielectric Spectroscopy; Springer Berlin Heidelberg: Berlin, Heidelberg, 2003; pp. 171–224. [Google Scholar]
- Kremer F.Dynamics in Geometrical Confinement; Springer: Cham, 2014, 10.1007/978-3-319-06100-9. [DOI] [Google Scholar]
- Napolitano S.Non-Equilibrium Phenomena in Confined Soft Matter: Irreversible Adsorption, Physical Aging and Glass Transition at the Nanoscale; Springer, 2015, 10.1007/978-3-319-21948-6. [DOI] [Google Scholar]
- Ediger M. D.; Forrest J. A. Dynamics near Free Surfaces and the Glass Transition in Thin Polymer Films: A View to the Future. Macromolecules 2014, 47, 471–478. 10.1021/ma4017696. [DOI] [Google Scholar]
- Forrest J. A.; Dalnoki-Veress K. When Does a Glass Transition Temperature Not Signify a Glass Transition?. ACS Macro Lett. 2014, 3, 310–314. 10.1021/mz4006217. [DOI] [PubMed] [Google Scholar]
- Jackson C. L.; McKenna G. B. Vitrification and Crystallization of Organic Liquids Confined to Nanoscale Pores. Chem. Mater. 1996, 8, 2128–2137. 10.1021/cm9601188. [DOI] [Google Scholar]
- Bäumchen O.; McGraw J. D.; Forrest J. A.; Dalnoki-Veress K. Reduced Glass Transition Temperatures in Thin Polymer Films: Surface Effect or Artifact?. Phys. Rev. Lett. 2012, 109, 055701 10.1103/PhysRevLett.109.055701. [DOI] [PubMed] [Google Scholar]
- Arndt M.; Stannarius R.; Gorbatschow W.; Kremer F. Dielectric Investigations of the Dynamic Glass Transition in Nanopores. Phys. Rev. E 1996, 54, 5377–5390. 10.1103/PhysRevE.54.5377. [DOI] [PubMed] [Google Scholar]
- Ellison C. J.; Torkelson J. M. The Distribution of Glass-Transition Temperatures in Nanoscopically Confined Glass Formers. Nat. Mater. 2003, 2, 695–700. 10.1038/nmat980. [DOI] [PubMed] [Google Scholar]
- Hudzinskyy D.; Lyulin A. V.; Baljon A. R.; Balabaev N. K.; Michels M. A. Effects of Strong Confinement on the Glass-Transition Temperature in Simulated Atactic Polystyrene Films. Macromolecules 2011, 44, 2299–2310. 10.1021/ma102567s. [DOI] [Google Scholar]
- Forrest J. A.; Dalnoki-Veress K. The Glass Transition in Thin Polymer Films. Adv. Colloid Interface Sci. 2001, 94, 167–195. 10.1016/S0001-8686(01)00060-4. [DOI] [Google Scholar]
- Ouyang G.; Tan X.; Yang G. Thermodynamic Model of the Surface Energy of Nanocrystals. Phys. Rev. B 2006, 74, 195408. 10.1103/PhysRevB.74.195408. [DOI] [Google Scholar]
- Alba-Simionesco C.; Coasne B.; Dosseh G.; Dudziak G.; Gubbins K. E.; Radhakrishnan R.; Sliwinska-Bartkowiak M. Effects of Confinement on Freezing and Melting. J. Phys. Condens. Matter 2006, 18, R15–R68. 10.1088/0953-8984/18/6/R01. [DOI] [PubMed] [Google Scholar]
- Grigoriadis C.; Duran H.; Steinhart M.; Kappl M.; Butt H.-J.; Floudas G. Suppression of Phase Transitions in a Confined Rodlike Liquid Crystal. ACS Nano 2011, 5, 9208–9215. 10.1021/nn203448c. [DOI] [PubMed] [Google Scholar]
- Duran H.; Steinhart M.; Butt H.-J.; Floudas G. From Heterogeneous to Homogeneous Nucleation of Isotactic Poly(Propylene) Confined to Nanoporous Alumina. Nano Lett. 2011, 11, 1671–1675. 10.1021/nl200153c. [DOI] [PubMed] [Google Scholar]
- Beiner M.; Rengarajan G. T.; Pankaj S.; Enke D.; Steinhart M. Manipulating the Crystalline State of Pharmaceuticals by Nanoconfinement. Nano Lett. 2007, 7, 1381–1385. 10.1021/nl0705081. [DOI] [PubMed] [Google Scholar]
- Park J.-Y. Y.; McKenna G. B. Size and Confinement Effects on the Glass Transition Behavior of Polystyrene/ o -Terphenyl Polymer Solutions. Phys. Rev. B 2000, 61, 6667–6676. 10.1103/PhysRevB.61.6667. [DOI] [Google Scholar]
- Reid D. K.; Alves Freire M.; Yao H.; Sue H.-J.; Lutkenhaus J. L. The Effect of Surface Chemistry on the Glass Transition of Polycarbonate Inside Cylindrical Nanopores. ACS Macro Lett. 2015, 4, 151–154. 10.1021/mz500725s. [DOI] [PubMed] [Google Scholar]
- Li M.; Wu H.; Huang Y.; Su Z. Effects of Temperature and Template Surface on Crystallization of Syndiotactic Polystyrene in Cylindrical Nanopores. Macromolecules 2012, 45, 5196–5200. 10.1021/ma300688h. [DOI] [Google Scholar]
- Keddie J. L.; Jones R. A. L.; Cory R. A. Interface and Surface Effects on the Glass-Transition Temperature in Thin Polymer Films. Faraday Discuss. 1994, 98, 219. 10.1039/fd9949800219. [DOI] [Google Scholar]
- Fryer D. S.; Peters R. D.; Kim E. J.; Tomaszewski J. E.; de Pablo J. J.; Nealey P. F.; White C. C.; Wu W. Dependence of the Glass Transition Temperature of Polymer Films on Interfacial Energy and Thickness. Macromolecules 2001, 34, 5627–5634. 10.1021/ma001932q. [DOI] [Google Scholar]
- Adrjanowicz K.; Kaminski K.; Koperwas K.; Paluch M. Negative Pressure Vitrification of the Isochorically Confined Liquid in Nanopores. Phys. Rev. Lett. 2015, 115, 265702. 10.1103/PhysRevLett.115.265702. [DOI] [PubMed] [Google Scholar]
- Yan X.; Streck C.; Richert R. Structural Relaxation of Glass-Formers Confined to Sol-Gel-Type Porous Glasses. Berichte der Bunsengesellschaft für Phys. Chemie 1996, 100, 1392–1395. 10.1002/bbpc.19961000904. [DOI] [Google Scholar]
- Patkowski A.; Ruths T.; Fischer E. W. Dynamics of Supercooled Liquids Confined to the Pores of Sol-Gel Glass: A Dynamic Light Scattering Study. Phys. Rev. E 2003, 67, 021501 10.1103/PhysRevE.67.021501. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Liu G.; Jonas J. Effects of Confinement on the Glass Transition Temperature of Molecular Liquids. J. Phys. Chem. 1992, 96, 3478–3480. 10.1021/j100187a056. [DOI] [Google Scholar]
- Simon S. L.; Park J. Y.; McKenna G. B. Enthalpy Recovery of a Glass-Forming Liquid Constrained in a Nanoporous Matrix: Negative Pressure Effects. Eur. Phys. J. E: Soft Matter Biol. Phys. 2002, 8, 209–216. 10.1140/epje/i2001-10072-0. [DOI] [PubMed] [Google Scholar]
- Alexandris S.; Papadopoulos P.; Sakellariou G.; Steinhart M.; Butt H. J.; Floudas G. Interfacial Energy and Glass Temperature of Polymers Confined to Nanoporous Alumina. Macromolecules 2016, 49, 7400–7414. 10.1021/acs.macromol.6b01484. [DOI] [Google Scholar]
- Talik A.; Tarnacka M.; Wojtyniak M.; Kaminska E.; Kaminski K.; Paluch M. The Influence of the Nanocurvature on the Surface Interactions Andmolecular Dynamics of Model Liquid Confined in Cylindrical Pores. J. Mol. Liq. 2020, 298, 111973. 10.1016/j.molliq.2019.111973. [DOI] [Google Scholar]
- Talik A.; Tarnacka M.; Geppert-Rybczynska M.; Minecka A.; Kaminska E.; Kaminski K.; Paluch M. Impact of the Interfacial Energy and Density Fluctuations on the Shift of the Glass-Transition Temperature of Liquids Confined in Pores. J. Phys. Chem. C 2019, 123, 5549–5556. 10.1021/acs.jpcc.8b12551. [DOI] [Google Scholar]
- Kipnusu W. K.; Elsayed M.; Kossack W.; Pawlus S.; Adrjanowicz K.; Tress M.; Mapesa E. U.; Krause-Rehberg R.; Kaminski K.; Kremer F. Confinement for More Space: A Larger Free Volume and Enhanced Glassy Dynamics of 2-Ethyl-1-Hexanol in Nanopores. J. Phys. Chem. Lett. 2015, 6, 3708–3712. 10.1021/acs.jpclett.5b01533. [DOI] [PubMed] [Google Scholar]
- Kipnusu W. K.; Elmahdy M. M.; Elsayed M.; Krause-Rehberg R.; Kremer F. Counterbalance between Surface and Confinement Effects As Studied for Amino-Terminated Poly(Propylene Glycol) Constraint in Silica Nanopores. Macromolecules 2019, 52, 1864–1873. 10.1021/acs.macromol.8b02687. [DOI] [Google Scholar]
- Napolitano S.; Capponi S.; Vanroy B. Glassy Dynamics of Soft Matter under 1D Confinement: How Irreversible Adsorption Affects Molecular Packing, Mobility Gradients and Orientational Polarization in Thin Films. Eur. Phys. J. E: Soft Matter Biol. Phys. 2013, 36, 61. 10.1140/epje/i2013-13061-8. [DOI] [PubMed] [Google Scholar]
- Adrjanowicz K.; Winkler R.; Dzienia A.; Paluch M.; Napolitano S. Connecting 1D and 2D Confined Polymer Dynamics to Its Bulk Behavior via Density Scaling. ACS Macro Lett. 2019, 8, 304–309. 10.1021/acsmacrolett.8b01006. [DOI] [PubMed] [Google Scholar]
- White R. P.; Lipson J. E. G. Connecting Pressure-Dependent Dynamics to Dynamics under Confinement: The Cooperative Free Volume Model Applied to Poly(4-Chlorostyrene) Bulk and Thin Films. Macromolecules 2018, 51, 7924–7941. 10.1021/acs.macromol.8b01392. [DOI] [Google Scholar]
- Adrjanowicz K.; Kaminski K.; Tarnacka M.; Szklarz G.; Paluch M. Predicting Nanoscale Dynamics of a Glass-Forming Liquid from Its Macroscopic Bulk Behavior and Vice Versa. J. Phys. Chem. Lett. 2017, 8, 696–702. 10.1021/acs.jpclett.6b02974. [DOI] [PubMed] [Google Scholar]
- Reiter G. G. Dewetting as a Probe of Polymer Mobility in Thin Films. Macromolecules 1994, 27, 3046–3052. 10.1021/ma00089a023. [DOI] [Google Scholar]
- Chandran S.; Baschnagel J.; Cangialosi D.; Fukao K.; Glynos E.; Janssen L. M. C.; Müller M.; Muthukumar M.; Steiner U.; Xu J.; et al. Processing Pathways Decide Polymer Properties at the Molecular Level. Macromolecules 2019, 52, 7146–7156. 10.1021/acs.macromol.9b01195. [DOI] [Google Scholar]
- Grohens Y.; Hamon L.; Reiter G.; Soldera A.; Holl Y. Some Relevant Parameters Affecting the Glass Transition of Supported Ultra-Thin Polymer Films. Eur. Phys. J. E: Soft Matter Biol. Phys. 2002, 8, 217–224. 10.1140/epje/i2001-10088-4. [DOI] [PubMed] [Google Scholar]
- Priestley R. D.; Cangialosi D.; Napolitano S. On the Equivalence between the Thermodynamic and Dynamic Measurements of the Glass Transition in Confined Polymers. J. Non-Cryst. Solids 2015, 407, 288–295. 10.1016/j.jnoncrysol.2014.09.048. [DOI] [Google Scholar]
- Boucher V. M.; Cangialosi D.; Yin H.; Schönhals A.; Alegría A.; Colmenero J. Tg Depression and Invariant Segmental Dynamics in Polystyrene Thin Films. Soft Matter 2012, 8, 5119. 10.1039/c2sm25419k. [DOI] [Google Scholar]
- Zhang C.; Boucher V. M.; Cangialosi D.; Priestley R. D. Mobility and Glass Transition Temperature of Polymer Nanospheres. Polymer 2013, 54, 230–235. 10.1016/j.polymer.2012.11.036. [DOI] [Google Scholar]
- Monnier X.; Cangialosi D. Thermodynamic Ultrastability of a Polymer Glass Confined at the Micrometer Length Scale. Phys. Rev. Lett. 2018, 121, 137801. 10.1103/PhysRevLett.121.137801. [DOI] [PubMed] [Google Scholar]
- Serghei A.; Huth H.; Schick C.; Kremer F. Glassy Dynamics in Thin Polymer Layers Having a Free Upper Interface. Macromolecules 2008, 41, 3636–3639. 10.1021/ma702381t. [DOI] [Google Scholar]
- Serghei A.; Chen D.; Lee D. H.; Russell T. P. Segmental Dynamics of Polymers during Capillary Flow into Nanopores. Soft Matter 2010, 6, 1111–1113. 10.1039/b921757f. [DOI] [Google Scholar]
- Tress M.; Mapesa E. U.; Kossack W.; Kipnusu W. K.; Reiche M.; Kremer F.. Molecular Dynamics of Condensed (Semi-) Isolated Polymer Chains; 2014; pp. 61–93. [DOI] [PubMed]
- Efremov M. Y.; Olson E. A.; Zhang M.; Zhang Z.; Allen L. H. Glass Transition in Ultrathin Polymer Films: Calorimetric Study. Phys. Rev. Lett. 2003, 91, 085703 10.1103/PhysRevLett.91.085703. [DOI] [PubMed] [Google Scholar]
- Madkour S.; Yin H.; Füllbrandt M.; Schönhals A. Calorimetric Evidence for a Mobile Surface Layer in Ultrathin Polymeric Films: Poly(2-Vinyl Pyridine). Soft Matter 2015, 11, 7942–7952. 10.1039/C5SM01558H. [DOI] [PubMed] [Google Scholar]
- Napolitano S.; Lupaşcu V.; Wübbenhorst M. Temperature Dependence of the Deviations from Bulk Behavior in Ultrathin Polymer Films. Macromolecules 2008, 41, 1061–1063. 10.1021/ma702081w. [DOI] [Google Scholar]
- van Zanten J. H.; Wallace W. E.; Wu W. L. Effect of Strongly Favorable Substrate Interactions on the Thermal Properties of Ultrathin Polymer Films. Phys. Rev. E 1996, 53, R2053–R2056. 10.1103/PhysRevE.53.R2053. [DOI] [PubMed] [Google Scholar]
- Park C. H.; Kim J. H.; Ree M.; Sohn B.-H.; Jung J. C.; Zin W. C. Thickness and Composition Dependence of the Glass Transition Temperature in Thin Random Copolymer Films. Polymer 2004, 45, 4507–4513. 10.1016/j.polymer.2004.04.048. [DOI] [Google Scholar]
- Roth C. B.; McNerny K. L.; Jager W. F.; Torkelson J. M. Eliminating the Enhanced Mobility at the Free Surface of Polystyrene: Fluorescence Studies of the Glass Transition Temperature in Thin Bilayer Films of Immiscible Polymers. Macromolecules 2007, 40, 2568–2574. 10.1021/ma062864w. [DOI] [Google Scholar]
- Glor E. C.; Angrand G. V.; Fakhraai Z. Exploring the Broadening and the Existence of Two Glass Transitions Due to Competing Interfacial Effects in Thin, Supported Polymer Films. J. Chem. Phys. 2017, 146, 203330. 10.1063/1.4979944. [DOI] [PubMed] [Google Scholar]
- Uhlmann P.; Tress M.; Reiche M.; Winkler R.; Kipnusu W. K.; Kremer F.; Neubauer N. Glassy Dynamics of Poly(2-Vinyl-Pyridine) Brushes with Varying Grafting Density. Soft Matter 2015, 11, 3062–3066. [DOI] [PubMed] [Google Scholar]
- Papadopoulos P.; Peristeraki D.; Floudas G.; Koutalas G.; Hadjichristidis N. Origin of Glass Transition of Poly(2-Vinylpyridine). A Temperature- and Pressure-Dependent Dielectric Spectroscopy Study. Macromolecules 2004, 37, 8116–8122. 10.1021/ma048555s. [DOI] [Google Scholar]
- Roland C. M.; Hensel-Bielowka S.; Paluch M.; Casalini R. Supercooled Dynamics of Glass-Forming Liquids and Polymers under Hydrostatic Pressure. Rep. Prog. Phys. 2005, 68, 1405–1478. 10.1088/0034-4885/68/6/R03. [DOI] [Google Scholar]
- Mei S.; Feng X.; Jin Z. Polymer Nanofibers by Controllable Infiltration of Vapour Swollen Polymers into Cylindrical Nanopores. Soft Matter 2013, 9, 945–951. 10.1039/C2SM27026A. [DOI] [Google Scholar]
- Kipnusu W. K.; Elmahdy M. M.; Mapesa E. U.; Zhang J.; Böhlmann W.; Smilgies D.-M.; Papadakis C. M.; Kremer F. Structure and Dynamics of Asymmetric Poly(Styrene- b −1,4-Isoprene) Diblock Copolymer under 1D and 2D Nanoconfinement. ACS Appl. Mater. Interfaces 2015, 7, 12328–12338. 10.1021/am506848s. [DOI] [PubMed] [Google Scholar]
- Tu W.; Richert R.; Adrjanowicz K. Dynamics of Pyrrolidinium-Based Ionic Liquids under Confinement. I. Analysis of Dielectric Permittivity. J. Phys. Chem. C 2020, 124, 5389–5394. 10.1021/acs.jpcc.0c00156. [DOI] [Google Scholar]
- Chat K.; Tu W.; Beena Unni A.; Geppert-Rybczyńska M.; Adrjanowicz K. Study on the Glass Transition Dynamics and Crystallization Kinetics of Molecular Liquid, Dimethyl Phthalate, Confined in Anodized Aluminum Oxide (AAO) Nanopores with Atomic Layer Deposition (ALD) Coatings. J. Mol. Liq. 2020, 311, 113296. 10.1016/j.molliq.2020.113296. [DOI] [Google Scholar]
- Winkler R.; Tu W.; Laskowski L.; Adrjanowicz K. Effect of Surface Chemistry on the Glass-Transition Dynamics of Poly(Phenyl Methyl Siloxane) Confined in Alumina Nanopores. Langmuir 2020, 36, 7553–7565. 10.1021/acs.langmuir.0c01194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu W.; Chat K.; Szklarz G.; Laskowski L.; Grzybowska K.; Paluch M.; Richert R.; Adrjanowicz K. Dynamics of Pyrrolidinium-Based Ionic Liquids under Confinement. II. The Effects of Pore Size, Inner Surface, and Cationic Alkyl Chain Length. J. Phys. Chem. C 2020, 124, 5395–5408. 10.1021/acs.jpcc.9b10461. [DOI] [Google Scholar]
- Tu W.; Jurkiewicz K.; Adrjanowicz K. Confinement of Pyrrolidinium-Based Ionic Liquids [CnMPyrr]+[Tf2N]– with Long Cationic Alkyl Side Chains (n = 10 and 16) to Nanoscale Pores: Dielectric and Calorimetric Studies. J. Mol. Liq. 2021, 324, 115115. 10.1016/j.molliq.2020.115115. [DOI] [Google Scholar]
- Beena Unni A.; Chat K.; Duarte D. M.; Wojtyniak M.; Geppert-Rybczyńska M.; Kubacki J.; Wrzalik R.; Richert R.; Adrjanowicz K. Experimental Evidence on the Effect of Substrate Roughness on Segmental Dynamics of Confined Polymer Films. Polymer 2020, 199, 122501. 10.1016/j.polymer.2020.122501. [DOI] [Google Scholar]
- Havriliak S.; Negami S. A Complex Plane Analysis of α-Dispersions in Some Polymer Systems. J. Polym. Sci., Part C: Polym. Symp. 2007, 14, 99–117. 10.1002/polc.5070140111. [DOI] [Google Scholar]
- Kremer F.; Schönhals A.; Volkov A. A.; Prokhorov A. S.; Kremer F.; Schönhals A.. Broadband Dielectric Spectroscopy; Kremer F., Schönhals A. Eds.; Springer Berlin: Berlin, 2003; Vol. 46. [Google Scholar]
- Calderwood J.Dielectric Relaxation in Solids; Chelsea Dielectrics Press, 2003; Vol. 18. [Google Scholar]
- Vogel H. The Law of the Relation between the Viscosity of Liquids and the Temperature. Phys. Z 1921, 22, 645–646. [Google Scholar]
- Fulcher G. S. Analysis of Recent Measurements of the Viscosity of Glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. 10.1111/j.1151-2916.1925.tb16731.x. [DOI] [Google Scholar]
- Williams G.; Watts D. C. Non-Symmetrical Dielectric Relaxation Behaviour Arising from a Simple Empirical Decay Function. Trans. Faraday Soc. 1970, 66, 80–85. 10.1039/tf9706600080. [DOI] [Google Scholar]
- Kohlrausch R. Ueber Das Dellmann’sche Elektrometer. Ann. Phys. 1847, 148, 353–405. 10.1002/andp.18471481102. [DOI] [Google Scholar]
- Yin H.; Napolitano S.; Schönhals A. Molecular Mobility and Glass Transition of Thin Films of Poly(Bisphenol A Carbonate). Macromolecules 2012, 45, 1652–1662. 10.1021/ma202127p. [DOI] [Google Scholar]
- Kremer F.; Huwe A.; Arndt M.; Behrens P.; Schwieger W. How Many Molecules Form a Liquid?. J. Phys. Condens. Matter 1999, 11, A175–A188. 10.1088/0953-8984/11/10A/013. [DOI] [Google Scholar]
- Mel’nichenko Y. B.; Schüller J.; Richert R.; Ewen B.; Loong C.-K. Dynamics of Hydrogen-bonded Liquids Confined to Mesopores: A Dielectric and Neutron Spectroscopy Study. J. Chem. Phys. 1995, 103, 2016–2024. 10.1063/1.469728. [DOI] [Google Scholar]
- Tarnacka M.; Madejczyk O.; Kaminski K.; Paluch M. Time and Temperature as Key Parameters Controlling Dynamics and Properties of Spatially Restricted Polymers. Macromolecules 2017, 50, 5188–5193. 10.1021/acs.macromol.7b00616. [DOI] [Google Scholar]
- Tarnacka M.; Kaminska E.; Kaminski K.; Roland C. M.; Paluch M. Interplay between Core and Interfacial Mobility and Its Impact on the Measured Glass Transition: Dielectric and Calorimetric Studies. J. Phys. Chem. C 2016, 120, 7373–7380. 10.1021/acs.jpcc.5b12745. [DOI] [Google Scholar]
- Adrjanowicz K.; Paluch M. Discharge of the Nanopore Confinement Effect on the Glass Transition Dynamics via Viscous Flow. Phys. Rev. Lett. 2019, 122, 176101. 10.1103/PhysRevLett.122.176101. [DOI] [PubMed] [Google Scholar]
- Serghei A.; Tress M.; Kremer F. The Glass Transition of Thin Polymer Films in Relation to the Interfacial Dynamics. J. Chem. Phys. 2009, 131, 154904. 10.1063/1.3248368. [DOI] [PubMed] [Google Scholar]
- Kipnusu W. K.; Elsayed M.; Krause-Rehberg R.; Kremer F. Glassy Dynamics of Polymethylphenylsiloxane in One- and Two-Dimensional Nanometric Confinement - A Comparison. J. Chem. Phys. 2017, 146, 203302. 10.1063/1.4974767. [DOI] [PubMed] [Google Scholar]
- Floudas G.; Paluch M.; Grzybowski A.; Ngai K.. Molecular Dynamics of Glass-Forming Systems; Advances in Dielectrics; Springer Berlin Heidelberg: Berlin, Heidelberg, 2011; Vol. 1. [Google Scholar]
- Leyser H.; Schulte A.; Doster W.; Petry W. High-Pressure Specific-Heat Spectroscopy at the Glass Transition in o-Terphenyl. Phys. Rev. E 1995, 51, 5899–5904. 10.1103/PhysRevE.51.5899. [DOI] [PubMed] [Google Scholar]
- Andersson S. P.; Andersson O. Relaxation Studies of Poly(Propylene Glycol) under High Pressure. Macromolecules 1998, 31, 2999–3006. 10.1021/ma971282z. [DOI] [Google Scholar]
- Pawlus S.; Rzoska S. J.; Ziolo J.; Paluch M.; Roland C. M. Effect of Temperature and Pressure on Segmental Relaxation in Polymethylphenylsiloxane. Rubber Chem. Technol. 2003, 76, 1106–1115. 10.5254/1.3547790. [DOI] [Google Scholar]
- Mpoukouvalas K.; Gomopoulos N.; Floudas G.; Herrmann C.; Hanewald A.; Best A. Effect of Pressure on the Segmental Dynamics of Bisphenol-A-Polycarbonate. Polymer 2006, 47, 7170–7177. 10.1016/j.polymer.2006.05.068. [DOI] [Google Scholar]
- Dalal E. N.; Phillips P. J. Pressure Dependence of the Glass Transition in Cis-Polyisoprene as Studied by Dielectric Relaxation. Macromolecules 1983, 16, 890–897. 10.1021/ma00240a012. [DOI] [Google Scholar]
- Alexandris S.; Sakellariou G.; Steinhart M.; Floudas G. Dynamics of Unentangled Cis −1,4-Polyisoprene Confined to Nanoporous Alumina. Macromolecules 2014, 47, 3895–3900. 10.1021/ma5006638. [DOI] [Google Scholar]
- Grzybowska K.; Pawlus S.; Mierzwa M.; Paluch M.; Ngai K. L. Changes of Relaxation Dynamics of a Hydrogen-Bonded Glass Former after Removal of the Hydrogen Bonds. J. Chem. Phys. 2006, 125, 144507. 10.1063/1.2354492. [DOI] [PubMed] [Google Scholar]
- Casalini R.; Mohanty U.; Roland C. M. Thermodynamic Interpretation of the Scaling of the Dynamics of Supercooled Liquids. J. Chem. Phys. 2006, 125, 014505 10.1063/1.2206582. [DOI] [PubMed] [Google Scholar]
- Tölle A.; Schober H.; Wuttke J.; Randl O. G.; Fujara F. Fast Relaxation in a Fragile Liquid under Pressure. Phys. Rev. Lett. 1998, 80, 2374–2377. 10.1103/PhysRevLett.80.2374. [DOI] [Google Scholar]
- Dreyfus C.; Aouadi A.; Gapinski J.; Matos-Lopes M.; Steffen W.; Patkowski A.; Pick R. M. Temperature and Pressure Study of Brillouin Transverse Modes in the Organic Glass-Forming Liquid Orthoterphenyl. Phys. Rev. E 2003, 68, 011204 10.1103/PhysRevE.68.011204. [DOI] [PubMed] [Google Scholar]
- Roland C. M.; Casalini R. Density Scaling of the Dynamics of Vitrifying Liquids and Its Relationship to the Dynamic Crossover. J. Non-Cryst. Solids 2005, 351, 2581–2587. 10.1016/j.jnoncrysol.2005.03.056. [DOI] [Google Scholar]
- Casalini R.; Roland C. M. Thermodynamical Scaling of the Glass Transition Dynamics. Phys. Rev. E 2004, 69, 062501 10.1103/PhysRevE.69.062501. [DOI] [PubMed] [Google Scholar]
- Alba-Simionesco C.; Cailliaux A.; Alegría A.; Tarjus G. Scaling out the Density Dependence of the α Relaxation in Glass-Forming Polymers. Europhys. Lett. 2004, 68, 58–64. 10.1209/epl/i2004-10214-6. [DOI] [Google Scholar]
- Torres J. A.; Nealey P. F.; de Pablo J. J. Molecular Simulation of Ultrathin Polymeric Films near the Glass Transition. Phys. Rev. Lett. 2000, 85, 3221–3224. 10.1103/PhysRevLett.85.3221. [DOI] [PubMed] [Google Scholar]
- Xu Q.; Zhu N.; Fang H.; Wang X.; Priestley R. D.; Zuo B. Decoupling Role of Film Thickness and Interfacial Effect on Polymer Thin Film Dynamics. ACS Macro Lett. 2021, 10, 1–8. 10.1021/acsmacrolett.0c00760. [DOI] [PubMed] [Google Scholar]
- Good R. J.; Girifalco L. A. A Theory for Estimation of Surface and Interfacial Energies. III. Estimation of Surface Energies of Solids from Contact Angle Data. J. Phys. Chem. 1960, 64, 561–565. 10.1021/j100834a012. [DOI] [Google Scholar]
- Napolitano S.; Prevosto D.; Lucchesi M.; Pingue P.; D’Acunto M.; Rolla P. Influence of a Reduced Mobility Layer on the Structural Relaxation Dynamics of Aluminum Capped Ultrathin Films of Poly(Ethylene Terephthalate). Langmuir 2007, 23, 2103–2109. 10.1021/la062229j. [DOI] [PubMed] [Google Scholar]
- Tarnacka M.; Talik A.; Kamińska E.; Geppert-Rybczyńska M.; Kaminski K.; Paluch M. The Impact of Molecular Weight on the Behavior of Poly(Propylene Glycol) Derivatives Confined within Alumina Templates. Macromolecules 2019, 52, 3516–3529. 10.1021/acs.macromol.9b00209. [DOI] [Google Scholar]
- Fowkes F. M. Dispersion Force Contributions to Surface and Interfacial Tensions, Contact Angles, and Heats of Immersion. Contact Angle, Wettability, Adhes. 1964, 43, 6–99. [Google Scholar]
- Holt A. P.; Griffin P. J.; Bocharova V.; Agapov A. L.; Imel A. E.; Dadmun M. D.; Sangoro J. R.; Sokolov A. P. Dynamics at the Polymer/Nanoparticle Interface in Poly(2-Vinylpyridine)/ Silica Nanocomposites. Macromolecules 2014, 47, 1837–1843. 10.1021/ma5000317. [DOI] [Google Scholar]
- Mapesa E. U.; Street D. P.; Heres M. F.; Kilbey S. M.; Sangoro J. Wetting and Chain Packing across Interfacial Zones Affect Distribution of Relaxations in Polymer and Polymer-Grafted Nanocomposites. Macromolecules 2020, 53, 5315–5325. 10.1021/acs.macromol.0c00399. [DOI] [Google Scholar]
- Füllbrandt M.; Purohit P. J.; Schönhals A. Combined FTIR and Dielectric Investigation of Poly(Vinyl Acetate) Adsorbed on Silica Particles. Macromolecules 2013, 46, 4626–4632. 10.1021/ma400461p. [DOI] [Google Scholar]
- Mapesa E. U.; Shahidi N.; Kremer F.; Doxastakis M.; Sangoro J. Interfacial Dynamics in Supported Ultrathin Polymer Films—From the Solid to the Free Interface. J. Phys. Chem. Lett. 2021, 12, 117–125. 10.1021/acs.jpclett.0c03211. [DOI] [PubMed] [Google Scholar]
- Keddie J. L.; Jones R. A.; Cory R. A. Size-Dependent Depression of the Glass Transition Temperature in Polymer Films. Europhys. Lett. 1994, 27, 59–64. 10.1209/0295-5075/27/1/011. [DOI] [Google Scholar]