Structural Transitions in Glassy Atactic Polystyrene Using Transition-State Theory

Abstract

Transition pathways on the energy landscape of atactic polystyrene (aPS) glassy specimens are probed below its glass-transition temperature. Each of these transitions is considered an elementary structural relaxation event, whose corresponding rate constant is calculated by applying multidimensional transition-state theory. Initially, a wide spectrum of first-order saddle points surrounding local minima on the energy landscape is discovered by a stabilized hybrid eigenmode-following method. Then, (minimal-energy) “reaction paths” to the adjacent minima are constructed by a quadratic descent method. The heights of the free energy, the potential energy, and the entropy barriers are estimated for every connected triplet of transition state and minima. The resulting distribution of free energy barriers is asymmetric and extremely broad, extending to very high barrier heights (over 50 k_BT); the corresponding distribution of rate constants extends over 30 orders of magnitude, with well-defined peaks at the time scales corresponding to the subglass relaxations of polystyrene. Analysis of the curvature along the reaction paths reveals a multitude of different rearrangement mechanisms; some of them bearing multiple distinct phases. Finally, connections to theoretical models of the glass phenomenology allows for the prediction, based on first-principles, of the “ideal” glass-transition temperature entering the Vogel–Fulcher–Tammann (VFT) equation describing the super-Arrhenius temperature dependence of glassy dynamics. Our predictions of the time scales of the subglass relaxations and the VFT temperature are in favorable agreement with available experimental literature data for systems of similar molecular weight under the same conditions.

1. Introduction

The dynamics of glasses, i.e., amorphous solids formed by quenching a wide class of materials, is of great interest from both a fundamental and industrial point of view. Following Goldstein,¹ theories have been developed that focus on the topography of the potential energy hypersurface and its connection to glassy dynamics and physical aging, which is the relaxation of the glass toward equilibrium. Their main goal is to connect the glass transition and the subglass relaxation with the concept of the “thermodynamic arrest” of the system in the basins surrounding local minima on its energy landscape (also called “inherent structures” following Stillinger and Weber^2,3). Within that framework, the dynamics is governed by the rates associated with the hops from one minimum to another. These infrequent jumps occur through transition states (first-order saddle points) on the potential energy surface. Finally, the physical aging is envisioned as the time-dependent process of vising various minima.

There is a hierarchy of features present in the energy landscape. Neighboring basins (around inherent structures) in configuration space are often separated by an energy barrier that is relatively low. Pairs of fast connected minima communicating mainly via tunneling phenomena, referred to as double-well potentials, give rise to the low-temperature anomalies of the glassy state.⁴ Higher energy barriers between adjacent minima are connected to the faster subglass relaxation processes (β, γ, and δ); i.e., the relaxation of the system occurs as it performs elementary transitions between minima. On the contrary, the slowest α-relaxation has been linked with transitions between nonadjacent minima (or chains of transitions over connected minima), that are distant in configuration space.^5,6

The ability to systematically move on the potential energy hypersurface from one stable geometry (e.g., a local minimum) through a transition state (first-order saddle point) and, subsequently, on to a new stable geometry (another local minimum) is essential for obtaining dynamical trajectories on the energy landscape. A transition state is defined as a structure with a single negative Hessian eigenvalue, following the definition of Murrell and Laidler.⁷ Stationary points (minima, maxima, and saddle points) on energy surfaces bear specific importance because they correspond to equilibrium geometries, where structure or mechanical properties of the system can be studied,^8,9 and the transitions over energy barriers govern the dynamic trajectories; their rate constants can be estimated by means of multidimensional transition state theory (TST).¹⁰

To the best of our knowledge, there is no theoretical framework for discovering the complete set of saddle points around a local minimum. It is typical to study small clusters of atoms for which it has been possible to locate almost all the minima and transition states on the potential energy landscape.^11,12 Doye¹³ has studied the potential energy landscape of a 14-atom Lennard-Jones cluster for which that author found 4196 minima and 87219 transition states. For systems involving more than 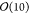atoms, however, knowledge of the complete potential surface as a function of all 3N – 3 atomic coordinates (N being the number of atoms) is out of the question. For many practical applications, generating the full set of saddle points around a minimum (whose count scales exponentially with the number of degrees of freedom^14,15) is of minor importance. One would like to be able to randomly sample saddle points around a minimum, their distribution being representative of the complete set of saddle points surrounding a local minimum.

Even trying to find a finite-sized set of first-order saddle points surrounding a minimum (with the knowledge of only this minimum) is a tough problem. Most methods can be classified into two classes of techniques, the distinguished coordinate^16,17 and the eigenvector-following^18,19 algorithms. Within the second group, a delicate and efficient method for locating stationary points is the eigenmode method with either exact,^12,18−29 or approximate Hessians.²⁷ A review is provided in ref (30). In the eigenmode method, a step toward a stationary point (extremum) of the energy landscape is a combination of orthogonal eigenmodes: the ones corresponding to positive eigenvalues tend to minimize, while those corresponding to negative eigenvalues tend to maximize the potential energy.¹⁸ Unlike the Newton–Raphson method, where the inverse of the Hessian is employed to guide the stepping procedure, a modified Hessian (where eigenvalues along specific modes are shifted) is employed to guide the stepping of the eigenmode method. Several formulations have been suggested for determining the shift parameters. Banerjee et al.²¹ and Baker²² proposed tuning two shift parameters; one for the eigenmodes chosen to be maximized and a different one for those to be minimized. The value of the shift parameters are obtained by either a matrix diagonalization or by employing an iterative procedure (similar to applying Lagrange multipliers to an optimization problem).

Once a first-order saddle point has been found, a minimal-energy path should be unfolded that connects two neighboring minima through this saddle point. In essence, this is done by starting at the saddle point and taking successive small steps in the direction of the negative gradient. If the coordinate system is mass-weighted, the steepest descent path coincides with the intrinsic reaction coordinate (IRC).^31,32 The differential equations for steepest descent paths are stiff; following the reaction path may be challenging even by employing extremely small steps.^33,34 Methods for following the reaction path from the transition state down to connected local minima (reactants and products states) can be classified in three broad categories. Explicit methods comprise the first category; they use information at the current point to move to the next one. One of the first practical techniques was the Ishida–Morokuma–Komornicki method,³⁵ which was based on a suitably stabilized first-order (Euler) method for integrating differential equations. Other numerical methods for integrating ordinary differential equations, like Runge–Kutta, can also be used to follow the path.^34,36−38 The next category consists of the implicit methods that, on top of local information, require derivative information at the end point as well. Müller and Brown developed an implicit Euler procedure.³⁹ The second-order Gonzalez–Schlegel method is similar to an implicit trapezoid method,^40,41 and it has been extended similarly to higher order implicit methods.^42,43 Integrating differential equations by implicit methods allows for larger step sizes along the reaction path but at the cost of solving an optimization problem at every step. Finally, a subcategory of explicit methods, which constitutes a special class on their own, includes the methods based on a local quadratic approximation (LQA) to the potential energy surface. Page and McIver^44,45 developed a series of methods for integrating the IRC equation based on LQA, and corrections based on higher order Taylor expansions. Sun and Rudenberg⁴⁶ extended the LQA method to systems where their Hessian should be approximated,⁴⁷ or it cannot be estimated at all.⁴⁸

Transitions between basins in the configuration space of the system occur when the system goes through first-order saddle points. A simplified one-dimensional potential energy profile is presented in Figure 1. The stationary points are marked by dots (gray for local minima, red for saddle points). In the figure, the corresponding basins of attraction (a steepest descent trajectory initiated anywhere within a basin leads to the local minimum at the bottom of it) and dividing surfaces (points in a single dimension) are also indicated. It has been shown that first-order saddle points correspond to the elementary relaxations of a system.^10,49 Previous works were focused on toy models, like Lennard-Jones glasses,^10,50 or bead–spring polymer systems.⁴⁹ Kopsias and Theodorou¹⁰ studied the elementary structural transitions of an amorphous Lennard-Jones solid by employing the quasi-harmonic approximation for the calculation of the free energies of minima and transition states. Their results indicated an extremely broad and highly asymmetric distribution of free energy and a narrow distribution of entropy barriers. Apart from the energetic characteristics of the barriers encountered by the system on its energy landscape, the underlying mechanisms that allow their crossing are also important. Wales and his collaborators have extensively studied the rearrangements taking place during barrier crossing,⁵¹⁻⁵⁶ and found that they fall into two distinct groups, i.e., “non-diffusive” processes (connected to shallow barriers) and “diffusive” processes; the latter involving changes in the nearest neighbor coordination of at least one atom (“cage-breaking” events).

Figure 1.

Illustration of the terms “convex region” (green), “basin” (blue), and “dividing surface” (red) used in the text. A simple one-dimensional potential energy landscape is employed, where the stationary points are marked with dots (gray for local minima and red for first-order saddle points that are also referred to as transition states).

The purpose of this work is two-fold: first an efficient computational framework is presented for exploring a rugged potential energy landscape; then, the elementary structural transitions of atactic polystyrene are probed, and the corresponding rates are estimated and compared to the experimentally measured time scales of the subglass relaxation processes. The exploration of the energy landscape involves finding as many first-order saddle points around a local minimum as possible. This is accomplished by a hybrid eigenvector-following algorithm. The system is forced to move uphill along randomly chosen eigendirections of the Hessian at the minimum until it exits the convex region of the basin (cf. Figure 1); then, the lowest-curvature path is followed until the discovery of a first-order saddle point. Once a first order saddle point is found, the minimal-energy path to the adjacent minima is followed in both directions by means of a method based on the local quadratic approximation (LQA) to the energy landscape. All steps of the procedure are greatly facilitated by a unified analytical treatment of the local slopes (gradients) and curvatures (Hessians) of the energy landscapes of classical molecular force fields, presented in our earlier work.⁸ For the discovered transition states, the distribution of (free) energy barriers separating the connected minima are studied and the corresponding rate constants are calculated by applying multidimensional transition-state theory (TST). Finally, insightful connections to theoretical models of the glass phenomenology are drawn, allowing us to predict from first-principles important parameters entering macroscopic models.

2. Computational Method

The method for obtaining the elementary structural transitions on the energy landscape consists of five steps, namely the generation of the initial configurations (presented in previous studies), the two parts of the saddle point search (inside and beyond the convex region of the basin), the reaction path following and the calculation of the rate constants by multidimensional TST. The individual steps are followed in a sequential way and are presented in individual enumerated subsections.

2.1. Step 1: Generation of Glassy Configurations

Following our earlier works on glassy atactic PS,^8,57 we employ model systems consisting of monodisperse atactic PS chains of 300 repeat units. Their tacticity obeys Bernoullian statistics with the percentage of meso diads being 50% . They have been generated by employing a hierarchical equilibration strategy.^58,59 First, a coarse-grained representation (every polystyrene repeat unit is mapped onto a single “super-atom”⁶⁰) is used for connectivity-altering Monte Carlo simulations.⁶¹ Then, atomistic configurations are generated by a quasi-Metropolis reverse mapping scheme in the melt state (T = 500 K).^58,62

The protocol of generating the glassy configurations, and the united-atom model governing the atomistic interactions have been described in detail in ref (8). Following the generation of equilibrated reverse-mapped configurations in the melt state, it entails quenching by Molecular Dynamics (MD)⁶³ at a rate of 0.1 K/ns down to 300 K. The applied quenching rates in the simulations are orders of magnitude faster compared to those employed experimentally. This may lead to spurious effects on the properties of the studied systems. However, for the molecular model and preparation methods employed in this work, we operate within the range of quenching rates that were found safe in our previous simulations.^58,64 We consider that well-equilibrated melt configurations are key to obtaining faithful glassy configurations, since the system is trapped close to the melt configuration by quenching. The quality of the melt configurations has been thoroughly tested against nuclear magnetic resonance (NMR) spectra.⁵⁸ We understand that there might be an indirect effect of the cooling rate on the energy landscape (since the volume of the specimens may vary) but we try to alleviate it by a free energy minimization in the glassy state (to be discussed below).

The quenching simulations go through the glass transition, which is considered to occur at 373 K for the system under consideration.⁵⁸ As far as the calculation of the glass-transition temperature is concerned, it is fully elaborated in our previous works on the same model of atactic PS.^58,64 It has been estimated by either the point where the density–temperature relation changes slope or by studying the time decay of the orientational correlation functions of several vectors along the backbone (or between the backbone and the side groups) of the chains. Since fitting long tails of time-correlation functions is inherently inaccurate, we choose to study the system at a considerably lower temperature (300 K) to avoid glass transition related artifacts.

In the glassy state, we tune the dimensions of the specimen in order to ensure that the instantaneous density of the configurations corresponds to the one dictated by its free (Gibbs) energy under given temperature (300 K) and pressure (1 bar).^8,64 The final configurations (after the cooling MD run and the Gibbs energy minimization in the glassy state) are used as the initial configurations for the energy landscape exploration. The results presented in this work are obtained by 40 independent glassy configurations whose neighboring saddle points are discovered, and pathways through them are constructed.

2.2. Quasi-harmonic Approximation

Following our earlier works,⁸ we use the fact that the Helmholtz energy of a basin I, A_I, within the quantum-mechanical quasi-harmonic approximation, can be calculated at the corresponding minimum (IS) at the bottom of the basin and is written as

1

The potential energy at positions r = r_inh, i.e., of the inherent structure, is denoted by 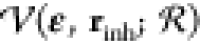, while the Helmholtz energy of the N_DOFs = 3N – 3 vibrational modes^9,65,66 is denoted by A_vib. The quasi-harmonic approximation has limitations, but it has been very successful in describing the free energy of polymer glasses.⁹ As far as glassy polystyrene is concerned, we have shown⁶⁴ that it is a valid approximation, even at elevated temperatures, by comparing our observations against experimental measurements and Molecular Dynamics simulations. The inclusion of higher-order (anharmonic) terms to the free energy is certainly possible; they can be rigorously derived by following our work on obtaining second- and third-order analytical derivatives of the potential energy.⁸

We can now assume that the system is found at a local minimum x_inh of its potential energy 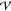, written as a function of all mass-weighted atomic coordinates, x_a = m_a^1/2r_a. Its potential energy, if we consider a slight displacement out of the minimum, can be approximated by a Taylor expansion around x_inh truncated after the second-order term:⁹

2

By definition, H_x is the 3N × 3N Hessian matrix (i.e., second derivatives) of the potential energy with respect to all mass-weighted coordinates

3

which has been evaluated at the minimum. Since a polymer system under periodic boundary conditions is translationally invariant, the Hessian matrix is not positive definite but only positive semidefinite. Excluding the elements of the Hessian matrix corresponding to the first atom, the matrix is left with an effective range of N_DOFs × N_DOFs elements, with N_DOFS = 3N – 3.

The quasi-harmonic approximation to the free energy⁶⁷ assumes that the motion of the microscopic system trapped within its basin can be described by N_DOFs uncoupled, uncorrelated harmonic oscillators, whose vibrational frequencies, ω_j, j = 1, ..., N_DOFs, do not depend on the temperature, T. The normal modes and the corresponding frequencies are determined as eigenvectors, v_j, and eigenvalues, ω_j², of H.⁶⁸ In our case, since the system exhibits translational symmetry, N_DOFs = 3N – 3 with N being the number of atoms present; i.e., three of the eigenvalues of H are zero, and the other ones are equal to the squared angular frequencies of the vibrational modes.

Knowledge of the mode frequencies, ω_j, allows the estimation of the vibrational contribution to the quasi-harmonic Helmholtz energy, A_vib, within a quantum mechanical formulation, as^10,69

4

with k_B the Boltzmann constant and ℏ = h/(2π), h being Planck’s constant. A quantum mechanical treatment of the vibrational partition function is preferred for the hard degrees of freedom.⁶⁴ At temperatures higher than the Debye temperature of glassy atactic polystyrene, θ_D ≃ 100 K,⁷⁰ the classical vibrational partition function is also a reasonable approximation. Furthermore, we can split the Helmholtz energy as A = U – TS, where S is the entropy of the microscopic system,^71,72

5

and U is the internal energy,⁸

6

The latter is independent of temperature and can be calculated from the potential energy of the IS and the vibrational frequencies.

2.3. Step 2: Saddle Point Search—Escaping the Convex Region of a Minimum

A trajectory from a minimum to a saddle point should first exit the convex region around the local minimum. While in convex region, the uphill stepping requires delicate handling. Even if it is relatively straightforward to move along the lowest eigenmode of the Hessian, by means of eigenvalue shifting techniques,^22,23 moving along higher modes becomes prohibitively difficult at rugged landscapes. By construction, the eigenvalue shifting methods will follow the lowest streambed in order to climb out of the convex region; higher modes tend to collapse to the lowest mode, thus reducing the possible ways out of the convex region. When trying to discover as many saddle points as possible around a minimum, the tendency to collapse to the lower mode becomes a weakness. In general, there are less transition structures associated with a system than there are available modes for climbing (degrees of freedom). Even if following every mode were successful, the system would discover the same transition states twice or even more often, i.e., locating states that have already been reached by following a lower mode.

In order to enhance the sampling of exit trajectories from a given minimum, we use a method similar in spirit to the hybrid eigenvector following technique introduced by Munro and Wales²⁹ and the activation–relaxation technique (ART) of Barkema and Mousseau.^73,74 At the minimum, where a diagonalization of the Hessian has been undertaken (essential for the calculation of the quasi-harmonic vibrational contribution to the free energy), all eigenvectors (and the corresponding eigenvalues that are all positive) of the Hessian are obtained and stored. If the goal is to reach a transition state, one should move uphill along one direction that defines a streambed across a valley away from the local minimum. To this end, we randomly choose an eigenvector to follow (direction of the valley floor), and the system is translated in steps from the minimum along the chosen normalized eigenvector ê_m,0,

7

where h_n is the magnitude of the step vector at step n (the choice of h_n is discussed in the following subsection).

At that point, we should note that for every uphill step, the eigenvector calcualated at the minimum, ê_m,0, is used. While it is in principle possible to perform a systematic scan of all eigenvectors, the dimensionality of the problem (thousands of atoms) is prohibiting. Since any systematic scan of a finite subset of eigenvectors may introduce a bias in the method, we prefer to randomly sample the eigenvector space. In that way, lower and higher eigenmodes are equally represented in the final distribution of saddle points. In that respect, a random linear combination of eigenvectors may also be efficient. Following the extended literature on saddle point searching algorithms, we choose to employ Cartesian coordinates for the process of stepping uphill. However, mass-weighted Cartesian coordinates can also be used. Overall, Cartesian coordinates provide several advantages over internal or local coordinates (e.g., bond lengths or bond angles).⁷⁵

At every step, we try to crawl on the canyon floor, which proceeds along the walking direction. This is accomplished by maximizing the potential energy along the walking (parallel to the canyon floor) direction while requiring minimum of the potential energy with respect to all other lateral directions, hence walking along the “stream bed”, which runs in the direction of uphill movement. The minimization in the lateral directions is accomplished by projecting the gradient²⁹

8

and employing it in the framework of a minimization algorithm (either conjugate gradient²⁹ or a limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm as implemented in our previous work⁸).

In most (if not all) circumstances, this algorithm will move toward a first-order saddle point. Since we force the potential energy of the system to be minimal in all but one directions at every step, the uphill trajectory leads to maximization along a single eigendirection; it is expected that the algorithm will not lead to second-order or higher-order saddle points. Cerjan and Miller discussed similar ideas for the location of transition states in low-dimensional energy surfaces,¹⁸ and Wales has later used them for an extensive study of LJ clusters.²⁸ If computational efficiency, rather than uniform sampling of the configuration space, is important, the choice of eigenvectors to be followed can be weighted toward those corresponding to lower eigenvalues. It is expected that moving along an eigenvector corresponding to a lower eigenvalue generally converges to a transition state more rapidly.

The progress of the climbing procedure is monitored by projecting the gradient in directions parallel and perpendicular to the undertaken step. For every step, the norm of the perpendicular component (eq 8), g_⊥ = ∥g_⊥∥, is close to 0, as the lateral minimization dictates. However, the projection of the gradient on the step vector, g_∥ = g·ê_m,0, provides a coarse description of the local topography of the energy landscape. Initially, being close to but stepping away from the minimum, g_∥ increases, since any displacement of the system along the vector h_n tends to increase the gradient along that specific direction. While going uphill, the system goes through a stationary point of g_∥ at step k, where g_∥ stops growing and g_∥,k+1 < g_∥,k. At that point, the system has just left the convex region and the boundaries of the basin are imminent. The process is terminated at step k. The termination point of the method for escaping the convex region will be denoted by r_esc. At the point that the system gets out of the basin, g_∥ changes sign, i.e., g_∥,n–1·g_∥,n < 0; this can also serve as a late termination point for the escape algorithm, if it has overstepped the boundary of the convex region.

2.4. Step 3: Saddle Point Search—Approaching a Transition State

Once the system has escaped the convex region, it can be allowed to continue moving “uphill” along the lowest Hessian eigen-direction while remaining at minima with respect to all other eigen-directions. We can consider a Taylor expansion of the potential energy, 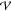, about the point r_esc of configuration r = r_esc + h, then

9

where g is the gradient vector, and H is the second derivative matrix, or Hessian, at r_esc. If we apply the condition 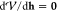to the above equation, this results in the standard Newton–Raphson step

10

Based on a Taylor expansion of the energy landscape around a current position and imposing a constraint on the step length, Cerjan and Miller showed (by introducing a suitable Langrangian multiplier technique¹⁸) that a modified Newton–Raphson process can be converted into an efficient potential energy walker. The step is determined by

11

where 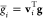is the component of gradient, g, along the local eigenvector v_i of the Hessian. The corresponding eigenvalue, b_i, is shifted by a parameter λ_i. In making a choice for λ_i, some empiricism enters the picture. Cerjan and Miller,¹⁸ Simons et al.,¹⁹ Banerjee et al.,²¹ Baker,²² and Wales²⁸ have proposed algorithms for locating transition states based on the stepping procedure described above; the difference between the several approaches being the recipe for determining the shifting parameters λ_i.

In this work, we adopt the approach of Baker for stepping along the lowest eigenmode of the Hessian.²² The step vector is obtained by introducing two shift parameters, λ₁ = λ_p and λ_n for the lowest and all other eigenvalues, respectively. The step vector can then be formed as²²

12

with

13

14

The shifting parameter for the lowest eigenvalue is obtained analytically as the largest solution to a simple quadratic equation:

15

and λ_n is obtained by solving numerically the optimization problem:

16

The interested reader is referred to the work of Baker²² for the details of the derivation. The optimization problem of eq 16, i.e., obtaining the best possible estimate of the parameter λ_n that balances the two parts of eq 16, is solved by employing a Newton–Raphson method, since the derivative of the above expression with respect to λ_n can be obtained easily.

The algorithm illustrated above for discovering transition states has several beneficial features: it is rigorous, stable and efficient. However, its practical application to realistic systems of interest requires efficient computer codes for the fast analytic evaluation of the Hessian matrix of the potential energy hypersurface. In the case of classical molecular force fields, Vogiatzis et al.⁸ have provided expressions of that kind.

2.5. Step-Length Control by Backtracking

The strength of both algorithms described above lies in the use of the gradient (and the Hessian) to generate a sequence of steps that are followed until the system discovers a neighboring stationary point. The magnitude of the individual steps should be large enough for the system to escape from the local minimum. However, longer steps suffer from “stitching”,²³ i.e., the phenomenon of the system moving back and forth in the traverse, with respect to the streambed of the walk, directions. The essence of our approach to step length control is that any step undergoes step-size reduction, if it is found to be completely inconsistent with its prediction based on a local quadratic approximation of the energy. Our backtracking strategy consists of checking for inconsistencies in energy, the norm and the orientation of the gradient vector. We employ the backtracking process in both parts of the saddle point search, i.e., both for escaping the convex region (Section 2.3) and for approaching the transition state once the system has escaped (Section 2.4).

Since we do not have full knowledge of the whole energy hypersurface except at the point around which a local quadratic approximation is applied (where the potential energy is 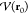), we must restrict the step generated by the algorithms detailed in the previous subsections, h, not to drive the system out of the domain in which the local quadratic approximation holds. The step should be taken (on a trial-and-error basis) if the evaluated (“true”), 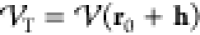, energy at r = r₀ + h can be accurately predicted by the quadratic approximation. If the quadratic prediction

17

accurately reproduces the true energy difference, 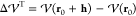, then the step lies within the trusted region for and can be undertaken safely. Otherwise, the step size should be reduced further.²³

As a first criterion for the step-length to be accepted, we demand that the predicted energy difference, , and the true energy difference, , be of the same sign (i.e., exclude moves that seem to walk uphill, while the actual step displaces the system downhill) and be approximately equal, in the sense that

18

with 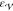being a specified tolerance (in our case, 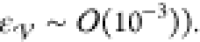If agreement between 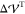and 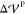is not achieved, the components of h are scaled by the same factor (in our implementation: cut in half). The step to be finally undertaken, which is parallel to the original trial step (because all its elements were scaled by the same factor) is then subjected to the same test, until the condition of eq 18 is satisfied.

Apart from the value of the potential energy, monitoring the gradient vector while moving to the transition state is also important.⁷⁶⁻⁷⁸ We check that the true (if the trial step is undertaken) and the predicted gradient vectors agree to each other, both in magnitude and direction. For the magnitude of the gradient, we apply a criterion similar to eq 18,

19

where the true and predicted differences in gradient are given by

20

21

The tolerance for the norm of the gradient is allowed to be larger than that in energy, i.e., .

As far as the direction of the gradient is concerned, we demand that (Δg)^T and (Δg)^P are parallel to each other. In a high-dimensional space of dimensionality 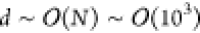, two randomly selected vectors are almost always orthogonal. For the cosine of angles between random vectors in d-dimensional space, the mean is 0 and the standard deviation is 1/√d. Thus, a suitable criterion for the gradient differences to be parallel to each other is

22

considering that for a Gaussian distribution, positive values more than three standard deviations from the mean account for only 0.13% of the distribution.

2.6. Step 4: Reaction Path Following

At the saddle point, all eigenvalues of the Hessian with respect to N_DOFs degrees of freedom (having excluded those affected by the translational invariance of the system; cf. the discussion in Section 2.2) but one are positive. In the neighborhood of the saddle point, the energy landscape bears resemblance to a valley going down along the eigendirection corresponding to the single negative eigenvalue. The reaction path lies along the floor of this valley, being a line in the mass-weighted configuration space, x. According to Fukui,³² the intrinsic reaction coordinate (IRC) is an imaginary trajectory of minimal energy that moves infinitely slowly through the transition state. As that, the trajectory should satisfy the classical equations of motion. Thus, if the coordinate system is chosen such that the kinetic energy can be written as a sum of quadratic terms of the momenta, it can be shown that the steepest descent on the energy landscape coincides with the IRC trajectory. The choice of mass-weighted Cartesian coordinates satisfies this condition.³⁵

The path can be given parametrically in terms of the mass-scaled reaction coordinate, s, which is the actual arc length. This path can be represented by x(s) where x is a column vector whose components are the 3N – 3 mass-weighted Cartesian coordinates of the atoms, i.e., 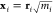. According to Fukui,³²x(s) is the solution to the set of autonomous first order differential equations

23

where v⁽⁰⁾ is a unit vector defined as the negative of the normalized gradient of the potential in mass-weighted coordinates,

24

with and 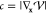. The normalized path tangent with respect to s is denoted by v⁽⁰⁾ with the superscript (0) indicating its zeroth derivative (adopting the notation of Page and McIver⁴⁴). At the saddle point, v⁽⁰⁾ lies along the eigenvector of the mass-weighted Hessian matrix, H_x, corresponding to the single negative eigenvalue. This is not assumed; it is a result of its definition.⁷⁹ In practice, one uses the initial condition that x(s = 0) is the saddle point. Then, eq 23 is integrated from s = 0 to s = s_r where s_r is negative (i.e., on the reactant side in the standard notation), and from s = 0 to s = s_p where s_p is positive (i.e., on the products side). The range (s_r, s_p) should be wide enough for both paths to converge to the neighboring local minima.

In this work, we employ the local quadratic approximation (LQA) method of Page and McIver^44,45 in order to solve eq 23 with eq 24 numerically. The LQA integration of the reaction path is based on a local second-order Taylor expansion of the potential energy with the point around which the potential energy is expanded being shifted stepwise along the reaction path. Derivatives (up to third order) of the potential energy can be efficiently calculated for any classical molecular force field based on tractable analytic expressions.⁸ Truncated at the quadratic term, the Taylor series around a point x₀ in the mass-weighted configuration space is

25

where δx = x – x₀ is the displacement vector from x₀, and g_x|_x0, H_x|_x0 the gradient and the Hessian at x₀, respectively. At an arbitrary point on the path x₀ = x(s₀), we represent the path, x(s), as a Taylor series in s expanded up to second-order terms, about x₀:

26

Here the coefficients v⁽⁰⁾, v⁽¹⁾ depend only on energy derivatives evaluated at x₀:

27

28

Since the path itself is represented as a Taylor series in s, v^(n–1) is the nth derivative of the path, x(s), with respect to s. The notation n – 1 is such that the superscript (0) indicates the zeroth derivative of the normalized path tangent vector, v₀ (eq 24), with respect to s. The first derivative of the path with respect to x, eq 27, stems from the definition of the reaction path as steepest descent trajectory, while the second derivative, eq 28 can be obtained by differentiating eq 27 with respect to s (before setting s = s₀).

Within the LQA, v⁽⁰⁾ and v⁽¹⁾ are computed exactly, since they include up to second-order terms in energy. Stepping along the path, according to eq 26, with consecutive quadratic approximations of the energy offers an improvement over the Euler method (which is based on a local linear expansion of the energy) since a step along the path defined by eq 26 includes the correct path curvature at the point of expansion. That is particularly helpful when stepping away from the saddle point, where simple Euler constructions deviate significantly from the minimum energy paths.

Under the assumptions of the LQA to the energy, eq 23 can be solved analytically.⁴⁴ This is equivalent to summing the aforementioned Taylor series expansion, eq 26, to infinity. Otherwise, a trial and error procedure should be employed for calculating the optimal step size at every point along the path. For the rest of this subsection, we presume that x₀ lies on the reaction path but not at the saddle point. Thus, every term in eq 26 has a nonzero value in the LQA. (Following the reaction path close to the saddle point will be discussed in Section 2.7). The energy gradient within the LQA becomes

29

Substituting eq 29 in eq 23 gives

30

which can be integrated by means of a new independent parameter, t, such that^44,45

31

The steepest descent path is finally obtained by integrating

32

Pechukas⁷⁹ pointed out that eq 32 results in a path identical with that obtained by eq 30 and that it can be solved exactly when the energy is a quadratic function of the coordinates. The integration procedure for eq 32 is briefly described in Appendix A. When approaching the (local) minimum, it may not be possible to take a step along the path with fixed δs because the path may terminate in a shorter arc length. In that case, where during the numerical integration t → ∞, we initiate a Newton minimization. The minimization converges instantly, since the system is already found in the quadratic region around the minimum.

We can now establish the two energy minima connected through the discovered transition state. By following the steepest descent trajectory out of the saddle point twice (one for the positive and one for the negative direction of the eigenvector corresponding to the single negative eigenvalue of the Hessian at the saddle point), we finally arrive at the two neighboring energy minima. After deploying the two paths, we check whether one of the terminal minima of the descent paths coincides with the starting minimum (i.e., where the saddle point search was initiated). The final end product of each such construction is a pair of potential energy minima, A and B, and the transition state in between, denoted by ‡. We have found that step sizes, h_n on the order of 0.1 Å can be safely used.

2.7. Path Initiation at the Saddle Point

At the saddle point, eq 23 is indeterminate and eqs 27 and 28 cannot be used in order to step along the path. Instead, the path tangent v⁽⁰⁾ can be obtained by applying L’Hospital’s rule to the limit v⁽⁰⁾|_s=0 = lim_s→0 (g_x/c), since both numerator, g_x, and denominator, c, approach zero. The result after replacing the gradient and its norm with their derivatives with respect to s is the characteristic polynomial of the Hessian matrix, H_x. Thus, v⁽⁰⁾|_s=0 is proven to coincide with the normalized eigenvector of the Hessian corresponding to the single negative eigenvalue, 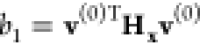, i.e., the lowest solution to

33

The curvature vector at the saddle point can be obtained by differentiating eq 33

34

where H_x⁽¹⁾ is the projection of the third derivatives of the potential energy onto the reaction path. The + symbol indicates the Moore–Penrose inversion,⁸⁰ since the matrix in the first set of brackets is obviously singular (its largest eigenvalue being 0). The above equation parallels the procedure for obtaining derivatives of matrix eigenvalues and eigenvectors proposed by Magnus.⁸¹ It should be noted that the resulting expression for v⁽¹⁾|_s=0, eq 34, is different from the one proposed by Page and McIver.⁴⁴

If third derivatives are not available, it can be easily approximated:

35

By designating a fixed δs and using 34, the first step out of the saddle point is

36

where u₁ denotes to the eigenvector corresponding to the lowest (single negative) eigenvalue of the Hessian at the saddle point. The plus and minus signs in the above equation are used to indicate stepping along both directions of the eigenvector.

The curvature vector, v⁽¹⁾, is a dynamically important property of the reaction path; it is orthogonal to the tangent vector v⁽⁰⁾ but it is not normalized. For quantifying the curvature of the valley around the path, the scalar curvature is defined as

37

2.8. Step 5: Calculation of the Rate Constants

According to the multidimensional transition state theory (TST),¹⁰ a transition from a state A to an adjacent state B occurs every time the system finds itself on the dividing surface between the two states and moves toward the state B. Within this approximation, the fundamental expression of transition rate within the TST framework can be derived,

38

where Q_A is the partition function of the system at the “reactant” state A (s = s_r), and Q^‡ the partition function of the system confined to the dividing surface (passing through the saddle point, s = 0) between states A and B. In the case of the NVT ensemble, A = −k_BT lnQ, and the rate becomes

39

with ΔA being either ΔA = A^‡ – A_A, or ΔA = A^‡ – A_B if the rate k_B→A is to be calculated. In the quasi-harmonic approximation, a way of calculating the Helmholtz energy has been already proposed in Section 2.2. We should note, however, that in the case of the transition state, ‡, the vibrational contribution is calculated by using only the positive eigenvalues of the Hessian.

2.9. Connection to Theoretical Models of the Glass Phenomenology

The calculation of the barrier height, ΔA, directly from atomistic simulations allows connections to theoretical models addressing the phenomenology of the glass transition and the glassy state. A theoretical framework for understanding glassy dynamics is provided by the “trap” models.^82,83 Within the framework of a trap model, the dynamics of the system is represented by the motion of a single phase point traveling in a landscape of “valleys” or “traps”. The valleys are separated by barriers that can be overcome only via activation. A master equation describes the progression of the phase point in the landscape; the corresponding rate constants for hopping over the barriers of the landscape provide the full knowledge of the landscape, i.e., the barrier heights and the geometry of phase space. As a first approximation, the most elementary trap models hypothesize that the top of the landscape is a plateau, and thus the rate of escape from a trap is related only to its depth, E_tr ∈ [0, ∞). Thus, in this class of trap models, the escape rates are dictated by the distribution of trap depths, ρ(E_tr).

The most widely used trap model adopts an exponential distribution of trap energies, i.e.,

40

This exponential form is indicated by phenomenological arguments in the context of glasses,⁸⁴ the random-energy model,⁸⁵ and the mean-field replica theory of spin-glasses.⁸⁶ Another interesting case of a trap model that retains features that are similar to those observed in real glasses is the Gaussian model

41

This also displays glassy phenomenology, such as a stretched exponential decay of time correlations and a super-Arrhenius growth of the relaxation time (aging).^82,83

Trap models were created in order to provide a simplified interpretation for activated aging dynamics.^87,88 Their continuous time dynamics can be extracted by assuming that at each time-step a configuration i is randomly chosen, with a uniform probability 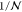among all 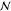configurations at disposal. The system remains trapped in this configuration i for a trapping time τ. By further assuming that escaping a trap of depth E_tr is governed by simple activated dynamics, i.e., the trap lifetime is

42

with τ₀ setting the time unit. Within the TST framework the corresponding time scale is set by τ₀ = ν₀^–1 with ν₀ = (k_BT/h). It has been shown that the exponential model results in a power-law distribution of the mean trapping times^{82−84,89,90}

43

with T₀ being the temperature at which a “strict” glass transition takes place. In contrast, the Gaussian model yields a log-normal distribution of trapping times⁸³

44

The Gaussian trap model results in a dynamics consisting of infinitely many time scales. On every of these scales, the dynamics is in essence identical with that of an exponential trap model with a time scale dependent T₀.⁹¹ An Arrhenius-like probability estimate for the system to escape from its current trapping configuration, i, is provided by the inverse of the average trapping time.

Obtaining the distribution of free energy barrier heights of the energy landscape allows connection to the phenomenological trap models of the glassy state, i.e., predicting the parameters of these models (e.g., T₀) from atomistic simulations. Furthermore, the distribution of rate constants for hopping from one basin to another should share the same characteristics with the distribution of trapping times, e.g., power-law tail at low rates if the exponential model is followed (power-law tail of the distribution of trapping times for long time scales).

3. Results and Discussion

3.1. Sampling of Potential-Energy Minima

We start by examining the distribution of the potential and microscopic Helmholtz energies of the glassy minima visited by the system (Figure 2). The ensemble of minima contains approximately 4000 minima, connected to the 40 independent initial configurations through elementary structural transitions. It can be seen that the sampled minima cover a rather narrow range of Helmholtz energy values; their free energies follow an approximately Gaussian distribution with a mean value of 10.36 (in k_BT per atom) and a variance of 3.44 × 10^–5 (in (Nk_BT)⁻²). While the distribution of free energies is rather symmetric, the distribution of their potential energy contributions is substantially asymmetric with the large majority of the minima explored being located at the lowest part of the energy spectrum (as can be seen in the inset to Figure 2 where the ordinate is logarithmic). This is a remarkable feature: almost all minima lie at the same potential energy level on the energy landscape (85% of the minima have a potential energy between 5.68 and 5.70 Nk_BT); thus, any difference in potential-energy barrier heights (contributing to different transition rates) will be mostly shaped by the position (“altitude”) of the transition states. Moreover, we should note the nontrivial role of the vibrational contribution to the Helmholtz energy which is dictated by the shape (multidimensional curvature) of the energy landscape around every minimum. The incorporation of the vibrational contribution transforms the highly asymmetric distribution of potential energies into a symmetric (albeit narrow) distribution of Helmholtz energies.

Figure 2.

Distribution of Helmholtz energy (per atom) of the sampled potential-energy minima. In the inset to the figure, the distribution of the potential energies is also depicted. Please note the logarithmic ordinate in the inset to the figure.

3.2. Barriers of Elementary Transitions on the Potential-Energy Hypersurface

Having located stable transition states between minima, we can study the distribution of the activation Helmholtz energies of the various elementary structural transitions, ρ(ΔA) with ΔA = A^‡ – A_min, which is depicted in Figure 3. Every triplet of a transitions state with its two adjacent minima contributes with two values of the Helmholtz energy barrier to the figure, corresponding to the two possible directions of crossing the barrier. Even before proceeding to an in-depth analysis of the distribution, it is obvious that the free energy barriers are high compared to the thermal energy scale, k_BT. This observation is in par with the microscopic picture of the system residing in individual basins for long times, before attempting an infrequent jump to a neighboring basin. The distribution exhibits a long tail, up to roughly 70 k_BT, which justifies the use of the transition state theory (TST) for the estimation of the corresponding rate constants. We should also note that slightly negative values of the barrier height, in terms of free energy, are also encountered. Negative barrier heights give rise to transitions faster than the fastest time scale set by the TST rate expression, k_BT/h. Within the quasi-harmonic approximation, the free energy is obtained by a sum of potential energy and vibrational contributions which can make a free energy barrier be slightly negative. The vast majority of the barriers sampled are concentrated around 15 k_BT. Interestingly, the distribution exhibits several pronounced spikes at specific barrier heights, indicating groups of transitions that are characterized by similar energetics. We are going to elaborate on this observation later when discussing the corresponding rate constants.

Figure 3.

Distribution of Helmholtz energy barriers separating the transition states from the minima. For every transition, two values, i.e., the free energy differences between the transition state and the two adjacent minima, are included. In the inset to the figure, the logarithm of the probability distribution of trap energies (E_tr ≡ A^‡ – A_min) is depicted. The solid line corresponds to the fit of a Gaussian trap model, while the dashed line to a fit of an exponential model at large trap depths.

The distribution of the free energy barriers provides fertile ground for connecting the findings of the atomistic calculations to the theoretical “trap” models of the glassy state. The free energy barrier, ΔA, provides an excellent estimate of the trap depth, E_tr ≡ A^‡ – A_min. In the inset to Figure 3, the logarithm of the density of trap depth, ρ(E_tr), is presented as a function of the trap depth, E_tr. A single model cannot fit the entire distribution of barrier heights, since it exhibits a pronounced peak at low E_tr and an extended tail for high E_tr. The distribution can be well fitted by a Gaussian model of trap depths at low values of E_tr < 25 k_BT, eq 41, with E̅_tr ≃ 15.05 k_BT and E₀ ≃ 8.65 k_BT. For higher values of E_tr, the distribution seems to follow an exponential decay according to eq 40. Both models, as discussed in the methodology section, exhibit glassy dynamics. Moreover, the exponential model predicts a finite “ideal” glass-transition temperature T₀ in the interesting case that ρ (E_tr) decays exponentially as exp(−E_tr/(k_BT₀)) for large E_tr. Fitting the tail, E_tr > 25 k_BT, of ρ(E_tr) to an exponential model results in T₀ = 331 K. Interestingly, the glass-transition temperature predicted by the exponential trap model is very close to the temperature corresponding to the point at which the dynamics (viscosity or relaxation times) diverge, i.e., the temperature T_∞ of the Vogel–Fulcher–Tammann (VFT) equation.⁹²⁻⁹⁴ Above the classical glass-transition temperature, T_g, which is arbitrarily defined as the temperature where the relaxation times are longer than 10² s, the viscosity and the relaxation times of the α- process probed by all kinds of spectroscopy, e.g., dielectric, mechanical or Raman, verify the VFT equation, τ = τ₀ exp(B/(T – T_∞)). Dielectric measurements in polystyrene of similar molecular weight as our systems, comply with a VFT equation with T_∞ ≃ 320 K.⁹⁵

The free energy barriers in the glassy state are mainly shaped by the underlying potential energy contribution to the height of the barrier. This is depicted in the inset to Figure 4. The potential energy contribution to the barrier height is always positive; transition states between minima are always higher in terms of potential energy than the minima themselves. In terms of classical thermodynamics, the free energy barrier heights of Figure 3 are split into internal energy, U, and entropy, S according to eqs 6 and 5. The internal energy contribution is presented in the main part of Figure 4. The addition of the vibrational contributions to U causes some of the barriers to exhibit (slightly) negative energy barriers; this is reasonable. Other than that, the internal energy is mainly shaped by the potential energy contribution and exhibits the same shape and breadth.

Figure 4.

Distribution of internal energy barriers separating the transition states from the minima. For every transition, two values, i.e., the internal energy differences between the transition state and the two adjacent minima, are included. In the inset to the figure, the distribution of the potential energy differences is depicted.

The distribution of the entropic contribution to the free energy barrier heights is presented in Figure 5. The distribution is quite symmetric and centered around −5k_B. Mostly negative values of the entropic barriers are expected, since the system should be confined within a narrow (curved) passage in configuration space leading from the one minimum to another. This implies loss of entropy which is clear in Figure 5. However, there are a few cases where the transition state has higher entropy than the minimum. It is generally assumed that entropy differences do not play a major role in transitions in the glassy state.¹⁰ However, it is observed that for a polymer glass, like the aPS studied in this work, elementary transitions through first-order saddle points entail a substantial entropy contribution, lower than, albeit on the same order of magnitude as the internal energy contribution. Despite the fact that entropy is somewhat neglected in the study of organic glasses, it seems to contribute significantly to their properties; the same observation was drawn for the entropic contribution to the elastic constants of aPS.⁸

Figure 5.

Distribution of entropy barriers between the transition states and minima.

The contribution of the vibrational motion to the height of the free energy barriers can be further analyzed by studying the distribution of the vibrational frequencies. The average density of vibrational states, G(ω), is shown in Figure 6, averaged over inherent structures and transition states. The abscissa of the figure, expressed in terms of the phonon energy transfer, allows for connections with experimental studies of the density of vibrational states of polystyrene. In the inset to the figure, the imaginary frequencies of the transition states, related to the negative eigenvalues of the Hessian, are shown along the negative part of the frequency axis. By focusing on the density of states along the positive semiaxis (real frequencies, i.e., the main part of Figure 6) of the two distributions of frequencies, we cannot see any significant difference between minima and transition states over the whole frequency spectrum. The density of vibrational states in the low-energy region below 5 meV, as measured by inelastic and quasi-elastic neutron scattering exhibits several features,^96,97 that are also present in the calculated curves. The position of the peak of G(ω), i.e., around 5 meV, is in good agreement with experimental studies on PS specimens of comparable molecular weight.⁹⁶ As expected, the width of the peak is significantly different from the experimental measurements; this can be mainly attributed to the lack of electronic degrees of freedom in our model. Interestingly, the range of the imaginary frequencies is relatively narrow and dominated by a pronounced peak. The narrowness of the density of the imaginary frequencies at the transition states indicates that most of the barriers the system must overcome have similar curvature in the multidimensional configuration space (detailed analysis of the evolution of the curvature follows).

Figure 6.

Average density of vibrational states, G(ω), of the minima and the transition states versus the phonon energy transfer, ℏω. In the inset to the figure, the imaginary frequencies (of the system found at the saddle points) are plotted along the negative energy semiaxis. The density of vibrational states is normalized so that the area under the curve is unity. Experimental data (neutron scattering) available up to 5 meV are also included (scaled for comparison).⁹⁶

3.3. Structural Transition Pathways

Despite the finite number of atoms employed in our simulations, the elementary structural transitions sampled by our procedure vary from simple to very complicated ones. Figure 7 depicts the reaction profile of three elementary transitions starting from the same minimum. The reaction path has been probed by following the quadratic stepping algorithm presented in the methodology section. The first one (blue line) has a low activation energy; the connected minima are energetically similar and, judging by the length of the path lie close to each other in configuration space. On the contrary, the reaction profile of the third pair (red line Figure 7) links two totally different in energy, but neighboring (connected), minima. Apart from the height of the barrier, the profile includes several “shoulders”, indicating intermediate stages during the rearrangement events.

Figure 7.

Potential energy profile of three elementary transitions, obtained through reaction path following, using the transition state as the starting configuration, as explained in the text. The profile is presented in terms of the configurational distance, i.e., the distance between the current configuration and that of the saddle point, ∥R_cur – R^‡∥, in the multidimensional Cartesian space. Negative values of the abscissa indicate the path leading to the initial minimum (s < 0), where all searches were initiated.

An interesting property of the minimal-energy (reaction) path is its scalar curvature, κ(s), defined by eq 37 in mass-weighted coordinates. In many solid-state problems, transitions between states A and B are made possible only through a narrow passage in the dividing surface between them surrounding the transition state (first-order saddle point). An estimate of the width of a passage of this kind is the scalar curvature, depicted in Figures 8 and 9. The pair of minima considered in Figure 8 are separated by a shallow, relatively symmetric potential energy barrier, whose height is around 3k_BT and the relevant transition rates are on the order of 10¹² s^–1 in both paths. On the contrary, the pair of minima whose reaction path curvature is depicted in Figure 9 are separated by a barrier whose height is slightly more than 40k_BT when approaching from s < 0, and 10k_BT when approaching from s > 0. The transition from the left-hand minimum to the right-hand one is the slowest sampled, with a rate constant of 10^–17 s^–1.

Figure 8.

Scalar curvature as a function of the reaction coordinate (path length) for one of the shallowest barriers encountered in saddle point search (saddle point corresponding to the blue profile of Figure 7) . The numerical integration step is 0.005 u^1/2 nm with u being the atomic mass unit.

Figure 9.

Scalar curvature as a function of the reaction coordinate (path length) for the steepest barrier encountered in saddle point search (saddle point corresponding to the red profile of Figure 7). The numerical integration step is 0.005 u^1/2 nm with u being the atomic mass unit.

The shape of the curvature encountered along the minimal-energy path is important. In the proximity of stationary points on the energy hypersurface, both the tangent and the curvature expressions become ill-defined, since the magnitude of the gradient of the potential energy approaches zero. The curvature of the reaction pathway, κ(s), becomes infinite there. Apart from the neighborhoods around stationary points of the energy landscape, stationary points of the path curvature play an important role. Analysis of the profile of the scalar path curvature along s can help in locating the points along the path where significant changes of the system take place. The profile exhibits both maxima and minima. The former correspond to rearrangement events, while the latter indicate location where the system changes minimally. Therefore, Cremer and Kraka^98,99 introduced the term “reaction phases” in chemical reactions, as the path regions from one curvature minimum to the next, interrupted by a curvature maximum in between. Each reaction (or structural rearrangement in our case) can be composed of different number of reaction phases, each of them with its own characteristic curvature pattern.

Figure 8 presents the curvature and the relative energy (with respect to the saddle point) along the pathway between two fast-communicating minima. It can be seen that the smooth part of the energy profile, connecting the saddle point to the minimum at the reactant side (s < 0), corresponds to an almost featureless evolution of the curvature perpendicular to the path. Apart from a small local maximum at around s ∼ −2, there are no other stationary points. The connection to the right-hand side minimum is also quite smooth. Both directions exhibit mechanisms with at most two or three stages that transform the system from the minimum to the transition state. However, we should note that even a smooth energy profile like that in Figure 8 may be a result of a multistage rearrangement mechanism. On the contrary, the two minima of Figure 9, exhibit a wealth of transformation phases for the system to go from the one to the other minimum and vice versa. There are many local maxima in both directions, of different magnitude and spacing. Thus, even if the connection between these two minima is considered an elementary structural rearrangement, the underlying motion of the system within its phase-space is very complicated.

3.4. Rate Constants

The application of saddle point searching and constructing the minimum-energy paths has resulted in sampling 4346 transitions on the energy landscape of aPS. The combination of methods allowed us to access a wide spectrum of passages between basins, including those going through high-lying terrain (cf. Figure 9) in the rugged energy landscape of the system. The corresponding distribution of transition-rate constants is depicted in Figure 10. The distribution is extremely broad, spanning 31 orders of magnitude (the smallest rate constant being while the largest being 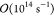). This huge range of values necessitated the use of bins equidistant in a logarithmic scale, with the proper mapping for the density distribution.

Figure 10.

Probability density of the rate constants of the identified distinct transitions between minima on the energy landscape of aPS. In the inset to the figure, a power-law fit (with the exponent a defined in the text) to the lower half (10^–15 ≤ k_A→B ≤ 10⁵) of the distribution is presented in double-log representation. Dashed lines in the main figure correspond to macroscopic relaxation rates of the four relaxation processes, namely α, β*, γ, and δ (from left to right, respectively) obtained by dielectric relaxation experiments.^100,101

The distribution is characterized by a high concentration of rate constants in the range 10⁰ - 10¹² s^–1 and more interestingly, a “wing” extending to very low rate constants, indicating that the system was indeed capable of undergoing elementary transitions through high-energy regions of its energy landscape. The distribution exhibits several local maxima, indicating the existence of several modes of rearrangement. The time scales of those maxima appear close to the dashed lines that mark macroscopic relaxation time scales, probed by Dielectric Spectroscopy (DS). Grigoriadi et al.¹⁰⁰ have succeeded in measuring the dielectric response of freshly quenched aPS. Their experiments identified three distinct relaxation processes, namely the α-relaxation of the glass transition, a β*-relaxation that was present only in the case of freshly quenched glasses and disappeared after aging of the samples, and a γ-relaxation that was always measured irrespectively of the thermal history of the sample. The corresponding inverse time scales of the DS relaxation process, complemented by the inverse time scale of the δ-relaxation obtained by neutron scattering experiments,¹⁰¹ are marked by dashed lines in Figure 10. Their proximity to the maxima of the distribution is remarkable, except for the α-relaxation, which is a cooperative phenomenon consisting of sequences of elementary structural transitions.

The wing of the distribution of rate constants extending to low rate constants is probably too low to be physically relevant at room temperature. However, it bears a wealth of information concerning the topography of the landscape and is presented in the inset to Figure 10, which indicates that a power-law distribution of the rate constants can fit this wing. By transforming the distribution of waiting times of the exponential model, eq 43, to the equivalent distribution of rate constants, a power-law dependence of the rate constants emerges; its form is ρ(k_A→B) ∼ k_A→B^(T/T₀)–1. In a completely equivalent way, the same distribution can be obtained by transforming the density of the trap energies, ρ(E_tr), assuming that they follow an exponential decay (cf. Figure 3 and discussion therein) and by employing the TST expression for the rate constants, eq 39. In the inset to Figure 10, as well as in the main figure, an equally spaced binning on the ln(k)-axis is used for estimating the distribution. By employing equally spaced bins on ln(k), the exponent of a power-law tail of the form k_A→B^(T/T₀)–1 is increased by 1, leading to an exponent a = T/T₀. This is indeed confirmed in the inset to Figure 10; a power-law approximation holds for low rate constants. The actual value of the power-law exponent (a ∼ 0.65) is lower than the one anticipated (T/T₀ = 0.9 based on the fitting of the free energy barrriers, cf. Figure 3). This is due to the sensitivity of ln(k) to poor sampling of slow transitions and the added complexity of getting the exponential of the free energy barrier. At low rate constants, the occupancy of density-calculation bins is binary (0 if no or 1 if a single transition is found), whereby the actual characteristics of the distribution are not represented accordingly. The appearance of a power-law tail resembles the distribution of trapping times at long time scales, eq 43, that was proposed by Bouchard⁸⁷ on the basis of theoretical considerations and the phenomenological models of aging in disordered systems. As discussed above, the existence of the power-law tail indicated a system that exhibits glassy dynamics and has a well-defined finite glass-transition temperature. A similar power-law tail of the distribution of transition rates has been also observed by Tsalikis et al.⁵⁰ in the case of a glass-forming mixture of spherical Lennard-Jones particles.

Finally, we would like to test whether there is any correlation between the transition rate constants and the distance in the multidimensional configuration space between the minimum and the relevant saddle point. These two characteristic quantities are plotted in Figure 11 for each elementary transition. We should note that the distance in configuration space may seem quite large, i.e., 100 nm, but it entails displacements of all atoms on the saddle point with respect to the minimum. By scaling it with the number of atoms 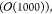we clearly see that the per-atom displacement is minute (on the order of 1 Å). As we can see, there does not seem to be any significant correlation between the transition rate and the distance between the minimum and the saddle point in the configurational space. There is a horizontal bar of fast transitions extending along the full spectrum of distances, indicating that even distant saddle points (with respect to the minimum) can be reached by crossing a shallow free energy barrier. In other words, for a given distance around a minimum, saddle points of different heights can be found and passages with extremely different rate constants can be followed by the system.

Figure 11.

Variation of the distance between a minimum and a saddle point with respect to the transition rate constant.

4. Conclusions

In this paper, we present a set of methods for locating stationary points on the energy landscape of a realistic glassy polymer system described by classical molecular force fields at atomistic resolution. Several aspects of our methods and their application exhibit salient novelties. While most studies of large systems are limited to the energy and gradient calculations for performing saddle point searches and path sampling,^102−104 we have been able to use methods based on the local quadratic approximation that entail analytical calculation of the exact Hessian of multiterm atomistic force fields. These methods were introduced in the framework of ab initio calculations, their use in the community of classical molecular simulations will be beneficial. As far as the saddle point search is concerned, we apply a combination of techniques that allow us to step predictably on a rugged energy landscape. Every step to be undertaken is subjected to a combination of criteria that ensure careful stepping (i.e., reducing the step size to ensure displacement of the system within the region of trust of a local quadratic approximation) and conserve the initial direction of the saddle point search. Next, the minimum energy path is obtained by a quadratic method, which converges faster than brute-force linear Euler methods to the adjacent minima and remains close to the true reaction path by invoking a quadratic (and cubic close to the saddle point) approximation of the true energy landscape. The combination of all methods presented reveals a very broad distribution of elementary transitions sampled on the energy landscape of glassy atactic polystyrene. On top of the energetic characteristics of the barriers, the specific rearrangement mechanisms that allow the system to move in its configuration space are also of major importance. In the case of binary atomic glasses, it has been observed that the main mechanism involves “cage-breaking” events.⁵¹⁻⁵⁶ However, a specific rearrangement mechanism may be difficult to isolate in glassy polystyrene, since the studied system bears bonds between atoms and hard torsional potentials. The connection of transitions to specific changes in structure will be the focus of a future work.

Apart from the several methodological advances presented in this work, there are several salient findings concerning the topography of the potential energy landscape of glassy atactic polystyrene. Differences in barrier heights (and hence rates) are shaped by the height of the transition states on the energy landscape, since all minima visited are characterized by similar potential energy values. Obtaining a rich distribution of barrier heights allows connections to theoretical models of the glass transition and the glassy states, like the “trap” models. The distribution of the free energy barrier heights cannot be fully described by a single trap model; at low values, a Gaussian distribution provides a good representation, while at larger barrier heights the distribution exhibits a clear exponentially decaying tail. The later gives rise to an extended power-law tail of the distribution of rate constants. Connection to theoretical models of the glass phenomenology allows prediction of the “ideal” glass-transition temperature, T₀, entering the VFT equation describing the super-Arrhenius temperature-dependence of dynamics. The free energy barriers include a small but substantial entropic contribution; its distribution being Gaussian and narrow since the barriers are characterized by similar curvatures (also probed by the study of the density of vibrational states). The profile of the curvature along the transition pathway can discern different rearrangement phases in the course of transitions. Even the elementary transitions studied in the present work are characterized by a multitude of rearrangement phases along the minimal-energy path connecting a minimum to the neighboring transition states. Finally, the ultimate goal of this effort was the prediction of the distribution of rate constants. The rate constant distribution in glassy atactic polystyrene is extremely broad with peaks close to the experimentally measured time scales of the subglass relaxation transitions of polystyrene (δ, γ, and β). Those transitions are results of elementary structural transitions of the system, i.e., the system hopping from one basin of the energy landscape to another. As far as the α-relaxation is concerned, despite the fact that traces of its corresponding time scale can be found in single elementary transitions in our simulations, it is a superposition of elementary events. Experimental verification of our predictions is accomplished at three points in the course of the study: (i) the density of vibrational states is in agreement with that obtained by spectroscopic methods, (ii) the estimation of the VFT glass-transition temperature (by the distribution of free energy barriers) is within 3% of the one obtained by fitting macroscopic measurements, and (iii) the peaks of the rate constant distribution correspond to the time scales of the subglass relaxations of polystyrene at the same temperature.

Appendix A. Path Integration within LQA

As discussed in the main text, the steepest descent path can be obtained by integrating eq 32:

32

We can better conceptualize the solution to the above equation by transforming it to generalized normal coordinates.⁴⁴ By considering the eigenvalues, λ_i, and the orthogonal matrix U of column eigenvectors of the Hessian, H_x|_x0, the solution to eq 32 can be obtained as

A1

where

A2

and

A3

where λ_i are the eigenvalues of the Hessian.

In order to integrate eq 30 for a given step in s, δs = (s – s₀), we should determine the corresponding value of t that provides this step. A straightforward Euler integration of eq 31 employing a tiny step size δt suffices. An initial estimate of the Euler step size, δt, is obtained by

A4

where N_Euler is the number of Euler steps to be taken (in our case, N_Euler = 10⁴).

The relationship between the parameter t and the arc length can be obtained from the derivative

A5

By substituting eq A1 into the right-hand side of eq 32 and multiply the result by 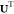,⁴⁴

A6

with g_x′ being the gradient in normal coordinates

A7

By further employing the fact 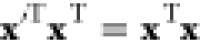, eq A5 becomes upon substitution of eq A6:

A8

which is conveniently rewritten in the Hessian eigenvector space. Given a desired step size in the arc length, eq A8 is readily integrated by employing small steps in t until the predefined arc length, δs is reached.

The authors declare no competing financial interest.