Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 May 25;125(22):5823–5831. doi: 10.1021/acs.jpcb.1c02917

Protein–Ligand Binding Volume Determined from a Single 2D NMR Spectrum with Increasing Pressure

Gediminas Skvarnavičius †, Zigmantas Toleikis †,‡, Vilma Michailovienė †, Christian Roumestand §, Daumantas Matulis †, Vytautas Petrauskas †,*
PMCID: PMC8279561  PMID: 34032445

Abstract

graphic file with name jp1c02917_0012.jpg

Proteins undergo changes in their partial volumes in numerous biological processes such as enzymatic catalysis, unfolding–refolding, and ligand binding. The change in the protein volume upon ligand binding—a parameter termed the protein–ligand binding volume—can be extensively studied by high-pressure NMR spectroscopy. In this study, we developed a method to determine the protein–ligand binding volume from a single two-dimensional (2D) 1H–15N heteronuclear single quantum coherence (HSQC) spectrum at different pressures, if the exchange between ligand-free and ligand-bound states of a protein is slow in the NMR time-scale. This approach required a significantly lower amount of protein and NMR time to determine the protein–ligand binding volume of two carbonic anhydrase isozymes upon binding their ligands. The proposed method can be used in other protein–ligand systems and expand the knowledge about protein volume changes upon small-molecule binding.

Introduction

Most protein–ligand binding studies are performed at ambient pressure and provide the standard Gibbs energy of binding. More in-depth studies often attempt to determine the entropy and enthalpy contributions to the Gibbs energy of ligand binding to a protein. High pressure provides an additional approach to study the protein–ligand binding by revealing the volume changes occurring upon protein interaction with a ligand. This approach provides insight into the changes in the protein partial volume while performing native functions, unfolding, and binding small molecules. These reactions cause the rearrangement of volume-related protein cavities, clefts, and the hydration shell.1−5

High pressure is a key that unlocks various volume-related properties of proteins and reveals their functions. Changes in the protein volume upon unfolding have been extensively investigated.4,6−13 High pressure also allowed one to probe structural properties of protein subdomains,12,14−16 observe folding pathways and switches between protein conformations,17−20 and investigate volume changes that arise upon binding small molecules.21−31 As a quantity of the change in the protein volume upon ligand binding, we use a parameter ΔVb, which is called the protein–ligand binding volume and is defined as the difference between the molar volumes of the bound (hydrated protein–ligand complex plus excess water molecules) and unbound (hydrated protein and hydrated ligand) states. Figure 1 illustrates a simplified definition of the ΔVb. In the literature, this parameter may have alternative names, such as the reaction or interaction volume.

Figure 1.

Figure 1

Open in a new tab

Illustration of the protein–ligand binding volume ΔVb.29,32 W denotes water molecules that the protein (P) and ligand (L) release into bulk water after their partial dehydration upon binding.

Various experimental approaches may be used to measure the protein–ligand binding volume including the density and ultrasound velocity techniques,23,33 small-angle X-ray and elastic incoherent neutron scattering,34 fluorescence spectroscopy at elevated pressures,24,30,31 and high-pressure NMR.16,29,35,36 The NMR spectroscopy is particularly informative in volumetric measurements because it can monitor changes in the local amino acid rearrangement. This allows identification of the binding-affected amino acid residues and analyze changes at the ligand binding site. Such features are unavailable in density- or fluorescence-based techniques, which provide ensemble-averaged properties, and many details remain hidden. Advantages of NMR spectroscopy come at a price: this assay requires relatively high concentrations of 15N-labeled proteins.37 The protein–ligand dissociation constant, Kd, can be accurately determined only if the protein concentration is in the range of Kd, and thus the micromolar concentration of a protein in the NMR experiment limits the range of possible ligand affinities to weak and moderate.38,39 All mentioned techniques reveal different aspects of protein–ligand interactions and have not only advantages but limitations also. We think that the best way to obtain a complementary view of the protein–ligand binding volume is to use several techniques by exploiting their strengths and overcoming possible weaknesses.

In this study, we used recombinant human carbonic anhydrase isozymes I (CA I) and II (CA II) as protein model systems, having a broad spectrum of inhibitors that bear a primary sulfonamide group and exhibit various affinities.40 Carbonic anhydrases are a family of proteins catalyzing the hydration of carbon dioxide to bicarbonate and acid protons and thus performing functions related to the acid–base balance and carbon metabolism in the human body. Several CA isoforms are overexpressed in tumors and thus are investigated as cancer targets.41−44 Despite their vital role in many biological processes, there are very little data in the scientific literature on volume changes that occur when these proteins bind various ligands. The lack of volumetric data limits the application of these methods as standard techniques used in the development of new compounds as drug candidates.

In this manuscript, we exploit high-pressure NMR spectroscopy to determine the changes in the CA I and CA II volumes upon binding two ligands. We present an alternative approach to obtain the volumetric parameters from two-dimensional (2D) 1H–15N heteronuclear single quantum coherence (HSQC) spectra. The proposed analysis can significantly decrease the number of NMR spectra that are required to determine the protein–ligand binding volume.

Materials and Methods

Expression of recombinant human CA I and CA II was performed in Escherichia coli strain BL21(DE). The overnight culture (10 mL) was grown in LB medium with 0.060 mM ZnCl2, then harvested by centrifugation (5 min, 4000g), and resuspended in M9 minimal nutrition medium (containing 42.2 mM (6 g/L) Na2HPO4, 22 mM (3 g/L) KH2PO4, 2 mM MgSO4, 0.10 mM CaCl2, and a mixture of trace metals) with 1 g/L 15N-labeled ammonium chloride, 4 g/L d-glucose, 0.060 mM ZnCl2, and 0.1 g/L ampicillin. The culture was grown at 37 °C, 220 rpm, for approximately 6 h until the optical density at 600 nm reached 0.6–0.8, and the protein expression was induced at this point with 0.20 mM IPTG and 0.4 mM ZnCl2 was added. The culture was harvested by centrifugation after 16 h of protein expression at 20 °C, 220 rpm.

CA I and CA II were purified using nickel-immobilized metal affinity chromatography (chelating Sepharose Fast Flow) and ion-exchange chromatography (SP-Sepharose column for CA I and CM-Sepharose for CA II) as previously described.45,46 The purified proteins were dialyzed against 10 mM Bis-Tris buffer at pH 6.2 (for CA I) and pH 6.4 (for CA II) and freeze-dried.

Protein samples of 0.52 mM or 0.43 mM CA I and 0.34 mM CA II were prepared in buffer (10 mM Bis-Tris, 50 mM NaCl, 10% D2O, 4% dimethyl sulfoxide (DMSO), at pH 6.2 for CA I and pH 6.4 for CA II) with different concentrations of compound 1 or 2, which were prepared in pure DMSO.

High-pressure NMR spectroscopy was used to record 2D 1H–15N HSQC spectra of CA I and CA II at various pressures. The protein solution (0.33 mL) was added into a ceramic tube with an outer diameter of 5 mM and an inner diameter of 3 mM from Daedalus Innovations (Aston, PA). Hydrostatic pressure was applied to the sample directly within the magnet through an inox line filled with low-density paraffin oil (Sigma) using an Xtreme Syringe Pump from Daedalus Innovations. 2D 1H–15N HSQC spectra were recorded at 25 °C and eight different pressures ranging from 5 to 210 MPa on a Bruker AVANCE III 600 MHz equipped with a 5 mM Z-gradient TXI probe head. Water suppression was achieved using the WATERGATE method.471H chemical shifts were directly referenced to the water resonance (4.7 ppm), while 15N chemical shifts were referenced indirectly to the 15N/1H absolute frequency ratios. Water resonance was used as the reference because the most commonly used referencing compound sodium trimethylsilylpropanesulfonate (DSS) might inhibit CA I and CA II. All NMR experiments were processed with TOPSPIN software (Bruker), and the spectra were analyzed with CcpNmr Analysis V2 software.48 A full set of spectra for one sample throughout the pressure range was recorded in approximately 20 h with CA I and 30 h with CA II protein samples.

The resonance assignment of human CA I was determined from previous studies49 and taken from Biological Magnetic Resonance Data Bank (entry number: 4022, doi:10.13018/BMR4022). The assignment of CA II was kindly shared by Ronald A. Venter from Duke University NMR Center.50

Results and Discussion

In this study, we used two compounds that have a primary sulfonamide group in their structures (Figure 2) and exhibit sub-millimolar binding affinities for CA I and CA II.40,51 Two-dimensional 1H–15N HSQC NMR spectra showed that both isoforms of carbonic anhydrase are in the slow exchange (in NMR time-scale) between two protein states—the ligand-bound and ligand-free—for compounds 1 and 2. This exchange rate allowed the monitoring of peaks that correspond to ligand-free and ligand-bound amino acid residues of a protein in the same spectrum. The intensity ratio of ligand-free and ligand-bound peaks is proportional to the fraction of protein molar concentrations in each state.39 In the calculations, we used the volume of amide cross-peaks in 1H–15N HSQC spectra. Many residues showed a second peak corresponding to the ligand-bound state upon addition of either compound 1 or 2. Figure 3 shows the cross-peaks of CA I affected by compound 1 in the overlaid 1H–15N HSQC spectrum at a pressure of 5 MPa.

Figure 2.

Figure 2

Open in a new tab

Compounds that were used to measure the protein–ligand binding volume.

Figure 3.

Figure 3

Open in a new tab

1H–15N HSQC spectrum overlay of CA I (0.52 mM) without a ligand (black) and with 0.70 mM compound 1 (red) at 5 MPa. Magnified peaks of His 107, Gly 111, Gly 145, and Tyr 194 amino acid residues highlight that in the presence of compound 1, both ligand-bound and ligand-free states of the protein were observed in the spectrum of CA I. The resonance assignment was taken from doi:10.13018/BMR4022.

Increasing ligand concentrations enhance the intensity of the peak corresponding to the ligand-bound state of CA I. The left panels in Figure 4A–D show the increase in the intensity of the bound-state Tyr 194 peak of CA I at a fixed pressure. In this case, the positions of both peaks in the spectrum remained steady, and the changes occurred only in their intensities. Pressure can also be used to rearrange the intensity ratio of ligand-bound and ligand-free peaks. The right panels in Figure 4E–H show the behavior of the Tyr 194 peak at different pressures and a fixed concentration of the ligand. As the pressure increases, the intensity of the bound-state peak increases and both peaks propagate along δ(1H) and δ(15N) axes in the 1H–15N HSQC spectra. At elevated pressures, the protein–ligand system tries to occupy a lower volume (Le Chatelier’s principle). Thus, if increasing pressure enhances the peak intensity of the ligand-bound protein state, the partial volume of the protein–ligand complex is lower than that of the sum of individual partial volumes of the protein and the ligand.

Figure 4.

Figure 4

Open in a new tab

Ligand- and pressure-induced shifts of the Tyr 194 residue peak position in the 1H–15N HSQC spectra. The concentrations of Compound 1 ranged from 0 to 2.0 mM (left panels) and pressure values ranged from 5 to 180 MPa (right panels).

The fraction of the bound protein, θi, was calculated from the volumes of amide cross-peaks of the ligand-bound (IPL(i)) and ligand-free (IP(i)) states of the i-th amino acid residue using the following equation

graphic file with name jp1c02917_m001.jpg 1

Fluctuations of the peak intensity in the spectrum can lead to inaccurate values of the protein–ligand binding volume if a single amino acid is analyzed. We used an arbitrary ensemble of amino acid residues, which showed the peaks of ligand-bound and ligand-free protein states upon ligand binding. In further calculations, we used the ensemble-averaged fraction of the ligand-bound protein, θ

graphic file with name jp1c02917_m002.jpg 2

where n is the number of amino acid residues in the ensemble, which was individually arranged for a particular pair of protein and ligand. Many residues in the 1H–15N HSQC spectra showed both ligand-bound and ligand-free forms of the protein, but some of the signals overlapped at high pressures and were hardly distinguishable, and thus, such residues were not used for further analysis. For example, we have chosen an ensemble of nine amino acid residues to monitor the CA I interaction with compound 1: Ile 59, Gly 104, Gly 111, Leu 131, Tyr 194, Gly 196, Thr 208, Ile 211, and His 243. Figure 5 shows the positions of analyzed residues in the crystal structures of CA I (panel A) and CA II (panel B) complexes with compound 1. Most ligand-binding-affected amino acid residues were near the active sites of both enzymes CA I and CA II. However, most probably due to remote rearrangements of the three-dimensional (3D) structure of the protein upon ligand binding, some more distant residues also showed a ligand-bound protein peak in the 1H–15N HSQC spectrum.

Figure 5.

Figure 5

Open in a new tab

Crystal structures of the carbonic anhydrase complex with compound 1: (A) CA I (PDB ID: 1CZM) and (B) CA II (PDB ID: 6RL9). Molecules of compound 1 are shown as blue sticks. Residues that were mostly affected by binding of 1 are colored red and labeled.

The change in volume in textbooks of Thermodynamics is defined as the partial derivative of the Gibbs energy with respect to pressure; thus, the change in volume upon protein–ligand binding at a constant temperature, T, is

graphic file with name jp1c02917_m003.jpg 3

where p denotes the pressure, and ΔGb is the change in the standard Gibbs energy of binding (the standard state is defined as 1 mol/L concentrations of the participating substances at 1 bar pressure and the activity coefficients are equal to 1).32 This equation shows that to obtain ΔVb, we first need to determine ΔGb at various pressures. In experiments, usually the dissociation equilibrium constant, Kd, is determined, while the change in the Gibbs energy is calculated using the equation ΔGb = RT  ln Kd.

In this study, we aimed to show that ΔVb can be obtained from 1H–15N HSQC spectra at various pressures using a single concentration of protein and ligand. To validate this method, we first determined ΔVb values by titrating a protein solution with a ligand at different pressures. The first step of this approach requires to determine Kd from the fraction of ligand-bound protein with the increasing ligand concentration

graphic file with name jp1c02917_m004.jpg 4

where Pt and Lt denote total (initial) concentrations of the added protein and ligand, respectively. We used this equation in nonlinear regression analysis to determine protein–ligand dissociation constants (and subsequently ΔGb) at various pressures. Figure 6A shows experimental data and analyzed results of the CA I interaction with compound 1 at various pressures up to 180 MPa. The resulting ΔGb as a function of pressure (Figure 6B) allows calculating the parameter of interest ΔVb. We assumed that the second pressure derivative of the Gibbs energy at a constant temperature is zero, implying that in the range of investigated pressures, ΔVb is a pressure-independent parameter. This assumption allowed us to calculate ΔVb from the slope of the linear fit to pressure dependence of ΔGb (Figure 6B). The calculated ΔVb of the CA I interaction with compound 1 was (−23 ± 3) mL/mol.

Figure 6.

Figure 6

Open in a new tab

(A) Fractions of the ligand-bound CA I protein determined from 1H–15N HSQC spectra at different pressures. The inset shows a pressure scale with black color corresponding to low pressure and red color corresponding to high pressure. The concentrations of Compound 1 were 0.53, 0.70, 1.3, 1.5, and 2.0 mM. Solid lines show fits to experimental data using eq 4 that yielded Kd values at different pressures. (B) Calculated ΔGb = RT ln(Kd) plotted as a function of pressure. The error bars denote standard errors obtained from the nonlinear fitting of experimental data in panel A.

The described method allows the determination of Kd as a function of pressure, which is necessary to obtain ΔVb. However, this method is time-consuming and requires relatively large amounts of a protein and a ligand. The slow chemical exchange between the ligand-free state of carbonic anhydrases (CA I, CA II) and the ligand-bound state with compounds 1 and 2 allowed an alternative approach to determine Kd using a single concentration of protein and ligand at various pressures. 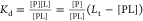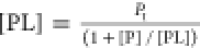In this case, Kd can be determined using the rearranged definition of the dissociation constant Inline graphic, where [L], [P], and [PL] denote the molar concentrations of the free ligand, the unbound protein, and the ligand-bound protein, respectively. We used the mass balance condition Pt = [PL] + [P] = [PL](1 + [P]/[PL]) and expressed as Inline graphic. We obtained the final equation by substituting the [PL] term into the rearranged Kd equation

graphic file with name jp1c02917_m007.jpg 5

The ratio 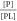Inline graphic is the intensity ratio of the peaks corresponding to the ligand-free and ligand-bound states of a particular amino acid residue in the 1H–15N HSQC spectrum. Equation 5 is used to determine Kds as a function of pressure, using a single concentration of the added protein and ligand. Figure 7 shows the resulting plots of ΔGb versus pressure, which were obtained from several single-concentration experiments. To compare results from different methods, in Figure 7, we also plotted ΔGb dependence on pressure as shown in Figure 6. This comparison shows that different approaches to determine Kd yielded similar ΔGb dependencies on pressure.

Figure 7.

Figure 7

Open in a new tab

Comparison of ΔVb calculations. Colored circles represent ΔGb values calculated from 1H–15N HSQC spectra of CA I that were recorded at 0.70, 1.3, and 2.0 mM concentrations of the added ligand. Data shown as open circles were replotted from Figure 6B to compare different approaches to obtain ΔGbs.

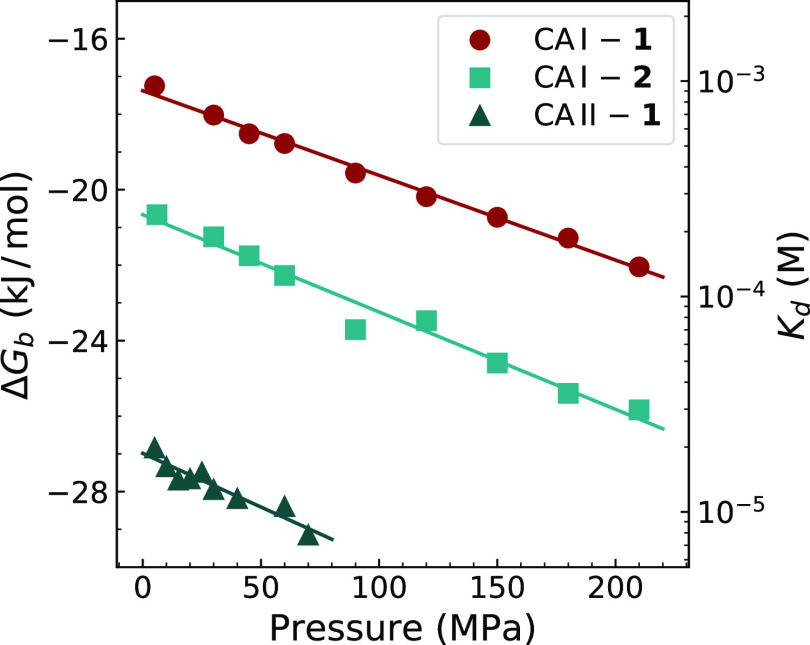
Gibbs energies of CA I and CA II binding to compounds 1 and 2 were calculated for a set of ligand binding-affected protein residues in the 1H–15N HSQC spectra at different pressures. Figure 8 shows averaged ΔGb values as a function of pressure. To determine ΔGb values, we used information from the protein 1H–15N HSQC spectra recorded at 0.7 mM (CA I-1), 0.6 mM (CA I-2), and 0.4 mM (CA II-1) concentrations of the added ligand. A decrease in ΔGb with increasing pressure means negative protein–ligand binding volumes. Linear data fits yielded the ΔVb equal to (−22 ± 4) mL/mol for CA I-1, (−26 ± 4) mL/mol for CA I-2, and (−28 ± 4) mL/mol for CA II-1. The uncertainty given next to the ΔVb values shows the standard deviation, which was evaluated by comparing ΔVb values at different concentrations of the added ligand.

Figure 8.

Figure 8

Open in a new tab

Change in the Gibbs energy of the protein–ligand binding versus applied pressure at a fixed concentration of the added ligand. ΔGb values were obtained from the intensity ratio of peaks in the 1H–15N HSQC spectrum corresponding to ligand-free and ligand-bound states of the protein and averaged over an ensemble of binding-affected residues. The scale on the right shows Kd values that correspond to the ΔGb scale at T = 25 °C.

Discussion

We have described a method to determine the protein–ligand binding volume using a series of 1H–15N HSQC spectra recorded at several different pressures and using a single concentration of the added ligand. Besides the benefits of determining ΔVb with less NMR spectrometry time, this approach could also raise questions about reliability. To examine this, we have determined ΔVb values at several fixed concentrations of the added ligand. The most accurate ΔVb values were obtained when the molar concentration of the added ligand was slightly less than the dissociation constant of the protein–ligand interaction. Such ligand concentrations allow one to expect that both unbound and bound protein populations coexist at a range of pressure values. If the initial ligand concentrations exceed the Kd, the peak intensity of the ligand-bound protein state starts to dominate over the ligand-free state and its peak intensity cannot be determined accurately from the 1H–15N HSQC spectra. Moreover, the intensity of peaks corresponding to the ligand-free protein state decreases further because increasing pressure promotes the protein–ligand binding and diminishes the population of the unbound protein state.

Another potential problem regarding the accuracy of ΔVb is related to the ensemble size and particular selection of amino acid residues for the analysis. Although many peaks in the 1H–15N HSQC spectrum showed both ligand-bound and ligand-free forms of protein, not all of them were suitable for analysis. The doubling of peaks in the 1H–15N HSQC spectrum due to the slow exchange of ligand-free and ligand-bound states complicated the data analysis as some peaks overlapped with each other. This problem forced us to select only clearly visible peaks. We selected groups consisting of 9–13 residues to calculate dissociation constants of the investigated protein–ligand pairs at various pressures. We also questioned, how would ΔVb values change if the number of residues in the ensemble was reduced or selected improperly. To test this, we simulated four case scenarios with reduced ensembles of binding-affected amino acid residues. In CA I-1 analysis, we excluded (1) several more distant residues with respect to the center of the ligand-binding site, (2) all amino acids except nonpolar ones, (3) all Gly residues, and (4) all Gly residues in addition to the second case scenario. Figure 9 shows that these trials resulted in ΔVb values that were similar to those obtained by averaging over the initial ensemble of residues. Case 4 showed the biggest deviation since only three out of nine residues were left after the applied criteria. These tests showed that ΔVb values were less sensitive to the selection of ensemble than to the too high or too low concentration of the added ligand.

Figure 9.

Figure 9

Open in a new tab

Comparison of calculated ΔVb values of the CA I-1 interaction, if analysis was performed on the reduced ensembles of ligand binding-affected residues. Cases 1–4 are described in the text.

A notable advantage of NMR spectroscopy to determine volume-related properties of proteins is its capability to provide simultaneous information about environmental changes of the binding-affected amino acids. This knowledge could reveal the regions of a protein that contribute mostly to the overall change in volume upon binding a ligand. The 1H–15N HSQC spectrum at different pressures also gives insight into compression properties at various sites of the protein and allows one to determine whether the low-lying excited states are populated at high pressures.17 Compressibility is a thermodynamic parameter that reveals the nonlinear response of the Gibbs energy to the applied pressure. It is difficult to obtain this parameter experimentally and very little data are available in the literature about protein compressibility changes upon binding a ligand.33,52−54 It is desirable to determine the change in compressibility by analyzing the corresponding volume changes. In this study, the most ΔGb dependencies on pressure demonstrated a linear decrease in the range of investigated pressures. This could mean that CA I and CA II compressibility changes were very small upon binding compounds 1 and 2. Another possible explanation could be averaging over an ensemble of residues, which might obscure the nonlinear response of a particular residue. Although nonlinear regression analysis could be used to evaluate compressibilities in these protein–ligand systems, we decided not to account for them. Every additional parameter in the nonlinear regression analysis increases the uncertainty and makes fitted parameters less reliable. This problem becomes especially relevant if the parameter of interest describes weakly expressed nonlinear effects, as was the case in our study. Therefore, we assumed that ΔVb was a pressure-independent parameter in our calculations.

Although compressibility was not accounted for in the volume calculation, we analyzed residues showing three different responses to the applied pressure. Ile 59 and Tyr 204 residues of CA I were the most pronounced examples showing distinct linear responses to pressure in ligand-bound and ligand-free protein states. Linear chemical shift variations are due to structural fluctuations within the basic folded state of the protein. In the case of amide chemical shifts, they are essentially related to H-bond compressibility.55 Ligand-free state peaks of both residues experienced relatively high (compared to all residues) chemical shift change, Δδ, in the 15N dimension at 210 MPa. The Δδ(15N) was approximately 10 times lower for the CA I-1-bound state of Ile 59 and up to 3 times lower for the CA I-1-bound state of the Tyr 204 residue compared to that of the ligand-free state of CA I (Figure 10). This result might indicate that compound 1 reduces the volume fluctuations of Ile 59 and Tyr 204 residues in CA I. Similar behavior was observed for CA II amino acid residues Ile 33 and Phe 93. This effect could be either due to the direct ligand interaction with these amino acid residues or the change in protein conformation upon binding compound 1. The reduced volume fluctuations (which are related to protein flexibility) have been reported in several studies of the protein–ligand interaction.35,56−58 As an example, the study of dihydrofolate reductase showed that compressibility is related to enzyme reactivity—the protein–substrate complex was the most compressed (tight structure), but after the product was formed the compression reduced (more flexible or soft state).53

Figure 10.

Figure 10

Open in a new tab

Response of CA I (0.52 mM) residues to the applied pressure in the absence (open circles) and presence (solid circles) of compound 1 (0.70 mM).

The Val 62, Arg 89, and Leu 147 residues in CA I were examples of the second type of response to high pressures. These residues showed the highest linear Δδ, but their responses to pressure were similar for both the ligand-bound and ligand-free CA I states. This suggests high volume fluctuations in these regions that are independent of compound 1 binding to CA I. The chemical shift change of Val 62 is nonlinear up to 210 MPa pressure, suggesting conformational change and possibly populated low-lying excited states of this amino acid residue at a high pressure. Nonlinear chemical shift variations are due to structural fluctuations involving low-lying excited states that differ from the basic folded states.55

His 94 and His 119 showed the third type of response to high pressures. These residues together with His 96 coordinate the Zn ion in the active sites of CA I and CA II. The amide nitrogen chemical shift change of His 94 in CA I-2 was slightly higher at high pressures (not shown in Figure 10) and His 119 in the CA I-1-bound state, compared with that in the ligand-free protein state. This suggests that the change in hydrogen bonds (dependent on the 1H chemical shift change) or dihedral angles of the peptide bond (dependent on 15N chemical shift change) was larger for the ligand-bound state. This was not a clear case for His 94 in the CA I-1 complex state shown in Figure 10. However, the chemical shift changes of these residues were close to the average (Δδ(15N) = 0.4 ppm at 210 MPa) and could not be used to account for CA I and CA II compressibility changes upon binding a ligand. Interestingly, the proton chemical shifts of His 94 and Tyr 204 move to different directions of the ligand-bound and ligand-free states of CA I with increasing pressure. This behavior could indicate that the hydrogen bond changes the length in opposite directions of the ligand-bound and ligand-free states (shorter bond in the case of negative chemical shift change and longer bond in the case of positive chemical shift change) with increasing pressure.59,60

The presented method to determine ΔVb from one concentration pair of protein and ligand at several pressures could not be extended to the fast-exchange regime of the protein interaction with a ligand. In this regime, the ligand-free and ligand-bound states of the protein appear in one averaged peak due to fast-exchange rate compared to the chemical shift difference between these two states. Thus, it is not possible to determine the ratio of ligand-free and ligand-bound states of the protein from a single peak and one has to measure chemical shift changes upon ligand titration to the protein solution. If we could determine the fraction of the ligand-bound protein from one peak, which is a result of the fast-exchange between two states (it is possible if the dissociation constant is known), the peak position with increasing pressure would depend not only on the binding properties but also on the compressibility effect. These two effects would make the analysis difficult to determine ΔVb. The only way to obtain this parameter would be a titration experiment at different pressures, if protein and ligand are in a fast-exchange regime and the compressibility remains unchanged in the ligand-free and ligand-bound protein states.

Despite the discussed limitations, the proposed analysis enables us to determine ΔVb in many protein–ligand systems obeying the described conditions. The obtained ΔVb values of the CA I and CA II interaction with the ligands were within the range of −22 to −28 mL/mol. The binding volume of −32 mL/mol of the CA I interaction with the other compound bearing a primary sulfonamide group in its structure—acetazolamide—was determined previously by a fluorescent pressure shift assay.61 Acetazolamide has a higher affinity toward CA I40 and more negative ΔVb than structurally similar compounds 1 and 2. These results were compatible with previous findings showing correlations between protein–ligand binding volumes and affinities.29 To the best of our knowledge, no other values of ΔVb for the family of carbonic anhydrases were reported in the literature. Other globular protein and ligand systems showed rather similar values of ΔVb.25

Conclusions

The analysis of 2D 1H–15N HSQC spectra of the protein–ligand interaction with increasing pressure enabled us to determine the change in the protein volume upon binding a ligand. If ligand-free and ligand-bound protein states were in a slow-exchange regime in the NMR time-scale, the protein–ligand binding volume could be obtained from a single pair of protein and ligand at several increasing pressures.

Acknowledgments

This work was supported by a grant (No. MIP-004/2014) from the Research Council of Lithuania. HP-NMR work was supported by French Infrastructure for Integrated Structural Biology (FRISBI) grant No. ANR-10-INSB-05. Z.T. acknowledges European Regional Development Fund project No. 1.1.1.2/VIAA/2/18/374 for financial support.

The authors declare no competing financial interest.

References

  1. Chalikian T. V.; Breslauer K. J. On Volume Changes Accompanying Conformational Transitions of Biopolymers. Biopolymers 1996, 39, 619–626. . [DOI] [PubMed] [Google Scholar]
  2. Frye K. J.; Royer C. A. Probing the Contribution of Internal Cavities to the Volume Change of Protein Unfolding Under Pressure. Protein Sci. 1998, 7, 2217–2222. 10.1002/pro.5560071020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chalikian T. V.; Filfil R. How Large Are the Volume Changes Accompanying Protein Transitions and Binding?. Biophys. Chem. 2003, 104, 489–499. 10.1016/S0301-4622(03)00037-1. [DOI] [PubMed] [Google Scholar]
  4. Roche J.; Caro J. A.; Norberto D. R.; Barthe P.; Roumestand C.; Schlessman J. L.; Garcia A. E.; E B. G.-M.; Royer C. A. Cavities Determine the Pressure Unfolding of Proteins. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 6945–6950. 10.1073/pnas.1200915109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Dellarole M.; Kobayashi K.; Rouget J.-B.; Caro J. A.; Roche J.; Islam M. M.; Garcia-Moreno E B.; Kuroda Y.; Royer C. A. Probing the Physical Determinants of Thermal Expansion of Folded Proteins. J. Phys. Chem. B 2013, 117, 12742–12749. 10.1021/jp401113p. [DOI] [PubMed] [Google Scholar]
  6. Brandts J. F.; Oliveira R. J.; Westort C. Thermodynamics of Protein Denaturation. Effect of Pressure on the Denaturation on Ribonuclease A. Biochemistry 1970, 9, 1038–1047. 10.1021/bi00806a045. [DOI] [PubMed] [Google Scholar]
  7. Zipp A.; Kauzmann W. Pressure Denaturation of Metmyoglobin. Biochemistry 1973, 12, 4217–4228. 10.1021/bi00745a028. [DOI] [PubMed] [Google Scholar]
  8. Heremans K.; Smeller L. Protein Structure and Dynamics at High Pressure. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 1998, 1386, 353–370. 10.1016/S0167-4838(98)00102-2. [DOI] [PubMed] [Google Scholar]
  9. Royer C. A. Revisiting Volume Changes in Pressure-Induced Protein Unfolding. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 2002, 1595, 201–209. 10.1016/S0167-4838(01)00344-2. [DOI] [PubMed] [Google Scholar]
  10. Ribó M.; Font J.; Benito A.; Torrent J.; Lange R.; Vilanova M. Pressure as a Tool to Study Protein-Unfolding/Refolding Processes: The Case of Ribonuclease A. Biochim. Biophys. Acta, Proteins Proteomics 2006, 1764, 461–469. 10.1016/j.bbapap.2005.11.011. [DOI] [PubMed] [Google Scholar]
  11. Meersman F.; Smeller L.; Heremans K. Protein Stability and Dynamics in the Pressure–Temperature Plane. Biochim. Biophys. Acta, Proteins Proteomics 2006, 1764, 346–354. 10.1016/j.bbapap.2005.11.019. [DOI] [PubMed] [Google Scholar]
  12. Rouget J.-B.; Schroer M. A.; Jeworrek C.; Pühse M.; Saldana J.-L.; Bessin Y.; Tolan M.; Barrick D.; Winter R.; Royer C. A. Unique Features of the Folding Landscape of a Repeat Protein Revealed by Pressure Perturbation. Biophys. J. 2010, 98, 2712–2721. 10.1016/j.bpj.2010.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Roche J.; Royer C. A.; Roumestand C. Monitoring Protein Folding through High Pressure NMR Spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 102–103, 15–31. 10.1016/j.pnmrs.2017.05.003. [DOI] [PubMed] [Google Scholar]
  14. Paladini A. A.; Weber G. Pressure-Induced Reversible Dissociation of Enolase. Biochemistry 1981, 20, 2587–2593. 10.1021/bi00512a034. [DOI] [PubMed] [Google Scholar]
  15. Royer C. A.; Weber G.; Daly T. J.; Matthews K. S. Dissociation of the Lactose Repressor Protein Tetramer Using High Hydrostatic Pressure. Biochemistry 1986, 25, 8308–8315. 10.1021/bi00373a027. [DOI] [PubMed] [Google Scholar]
  16. Fossat M. J.; Dao T. P.; Jenkins K.; Dellarole M.; Yang Y.; McCallum S. A.; Garcia A. E.; Barrick D.; Roumestand C.; Royer C. A. High-Resolution Mapping of a Repeat Protein Folding Free Energy Landscape. Biophys. J. 2016, 111, 2368–2376. 10.1016/j.bpj.2016.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Akasaka K.; Li H. Low-Lying Excited States of Proteins Revealed from Nonlinear Pressure Shifts in 1 H and 15 N NMR †. Biochemistry 2001, 40, 8665–8671. 10.1021/bi010312u. [DOI] [PubMed] [Google Scholar]
  18. Roche J.; Royer C. A.; Roumestand C. Exploring Protein Conformational Landscapes Using High-Pressure NMR. Methods Enzymol. 2019, 614, 293–320. [DOI] [PubMed] [Google Scholar]
  19. Xu X.; Gagné D.; Aramini J. M.; Gardner K. H. Volume and Compressibility Differences between Protein Conformations Revealed by High-Pressure NMR. Biophys. J. 2021, 120, 924–935. 10.1016/j.bpj.2020.12.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Dubois C.; Herrada I.; Barthe P.; Roumestand C. Combining High-Pressure Perturbation with NMR Spectroscopy for a Structural and Dynamical Characterization of Protein Folding Pathways. Molecules 2020, 25, 5551. 10.3390/molecules25235551. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Li T. M.; Hook J. W.; Drickamer H. G.; Weber G. Effects of Pressure upon the Fluorescence of the Riboflavin Binding Protein and Its Flavin Mononucleotide Complex. Biochemistry 1976, 15, 3205–3211. 10.1021/bi00660a008. [DOI] [PubMed] [Google Scholar]
  22. Torgerson P. M.; Drickame H. G.; Weber G. Inclusion Complexes of Poly-.Beta.-Cyclodextrin: A Model for Pressure Effects upon Ligand-Protein Complexes. Biochemistry 1979, 18, 3079–3083. 10.1021/bi00581a026. [DOI] [PubMed] [Google Scholar]
  23. Filfil R.; Chalikian T. V. Volumetric and Spectroscopic Characterizations of Glucose–Hexokinase Association. FEBS Lett. 2003, 554, 351–356. 10.1016/S0014-5793(03)01187-6. [DOI] [PubMed] [Google Scholar]
  24. Toleikis Z.; Cimmperman P.; Petrauskas V.; Matulis D. Determination of the Volume Changes Induced by Ligand Binding to Heat Shock Protein 90 Using High-Pressure Denaturation. Anal. Biochem. 2011, 413, 171–178. 10.1016/j.ab.2011.02.019. [DOI] [PubMed] [Google Scholar]
  25. Son I.; Shek Y. L.; Dubins D. N.; Chalikian T. V. Volumetric Characterization of Tri- N -Acetylglucosamine Binding to Lysozyme. Biochemistry 2012, 51, 5784–5790. 10.1021/bi3006994. [DOI] [PubMed] [Google Scholar]
  26. Toleikis Z.; Cimmperman P.; Petrauskas V.; Matulis D. Serum Albumin Ligand Binding Volumes Using High Pressure Denaturation. J. Chem. Thermodyn. 2012, 52, 24–29. 10.1016/j.jct.2011.12.026. [DOI] [Google Scholar]
  27. Petrauskas V.; Gylytė J.; Toleikis Z.; Cimmperman P.; Matulis D. Volume of Hsp90 Ligand Binding and the Unfolding Phase Diagram as a Function of Pressure and Temperature. Eur. Biophys. J. 2013, 42, 355–362. 10.1007/s00249-012-0884-7. [DOI] [PubMed] [Google Scholar]
  28. Son I.; Selvaratnam R.; Dubins D. N.; Melacini G.; Chalikian T. V. Ultrasonic and Densimetric Characterization of the Association of Cyclic Amp with the Camp-Binding Domain of the Exchange Protein Epac1. J. Phys. Chem. B 2013, 117, 10779–10784. 10.1021/jp406451p. [DOI] [PubMed] [Google Scholar]
  29. Toleikis Z.; Sirotkin V. A.; Skvarnavičius G.; Smirnovienė J.; Roumestand C.; Matulis D.; Petrauskas V. Volume of Hsp90 Protein–Ligand Binding Determined by Fluorescent Pressure Shift Assay, Densitometry, and NMR. J. Phys. Chem. B 2016, 120, 9903–9912. 10.1021/acs.jpcb.6b06863. [DOI] [PubMed] [Google Scholar]
  30. Oliva R.; Banerjee S.; Cinar H.; Ehrt C.; Winter R. Alteration of Protein Binding Affinities by Aqueous Two-Phase Systems Revealed by Pressure Perturbation. Sci. Rep. 2020, 10, 8074 10.1038/s41598-020-65053-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Oliva R.; Jahmidi-Azizi N.; Mukherjee S.; Winter R. Harnessing Pressure Modulation for Exploring Ligand Binding Reactions in Cosolvent Solutions. J. Phys. Chem. B 2021, 125, 539–546. 10.1021/acs.jpcb.0c10212. [DOI] [PubMed] [Google Scholar]
  32. Skvarnavičius G.; Matulis D.; Petrauskas V.. Carbonic Anhydrase as Drug Target: Thermodynamics and Structure of Inhibitor Binding; Matulis D., Ed.; Springer International Publishing: Cham, 2019; pp 97–106. [Google Scholar]
  33. Barbosa S.; Taboada P.; Mosquera V. Protein-Ligand Interactions: Volumetric and Compressibility Characterization of the Binding of Two Anionic Penicillins to Human Serum Albumin. Langmuir 2003, 19, 1446–1448. 10.1021/la020810j. [DOI] [Google Scholar]
  34. Cinar S.; Al-Ayoubi S.; Sternemann C.; Peters J.; Winter R.; Czeslik C. A High Pressure Study of Calmodulin–Ligand Interactions Using Small-Angle X-Ray and Elastic Incoherent Neutron Scattering. Phys. Chem. Chem. Phys. 2018, 20, 3514–3522. 10.1039/C7CP07399B. [DOI] [PubMed] [Google Scholar]
  35. Wilton D. J.; Kitahara R.; Akasaka K.; Pandya M. J.; Williamson M. P. Pressure-Dependent Structure Changes in Barnase on Ligand Binding Reveal Intermediate Rate Fluctuations. Biophys. J. 2009, 97, 1482–1490. 10.1016/j.bpj.2009.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Dellarole M.; Roumestand C.; Royer C.; Lecomte J. T. J. Volumetric Properties Underlying Ligand Binding in a Monomeric Hemoglobin: A High-Pressure Nmr Study. Biochim. Biophys. Acta, Proteins Proteomics 2013, 1834, 1910–1922. 10.1016/j.bbapap.2013.04.016. [DOI] [PubMed] [Google Scholar]
  37. Gossert A. D.; Jahnke W. NMR in Drug Discovery: A Practical Guide to Identification and Validation of Ligands Interacting with Biological Macromolecules. Prog. Nucl. Magn. Reson. Spectrosc. 2016, 97, 82–125. 10.1016/j.pnmrs.2016.09.001. [DOI] [PubMed] [Google Scholar]
  38. Zhang X.; Sänger A.; Hemmig R.; Jahnke W. Ranking of High-Affinity Ligands by NMR Spectroscopy. Angew. Chem., Int. Ed. 2009, 48, 6691–6694. 10.1002/anie.200902591. [DOI] [PubMed] [Google Scholar]
  39. Kleckner I. R.; Foster M. P. An Introduction to NMR-Based Approaches for Measuring Protein Dynamics. Biochim. Biophys. Acta, Proteins Proteomics 2011, 1814, 942–968. 10.1016/j.bbapap.2010.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Linkuvienė V.; Zubrienė A.; Manakova E.; Petrauskas V.; Baranauskienė L.; Zakšauskas A.; Smirnov A.; Gražulis S.; Ladbury J. E.; Matulis D. Thermodynamic, Kinetic, and Structural Parameterization of Human Carbonic Anhydrase Interactions toward Enhanced Inhibitor Design. Q. Rev. Biophys. 2018, 51, E10 10.1017/S0033583518000082. [DOI] [PubMed] [Google Scholar]
  41. Oosterwijk E.; Ruiter D. J.; Hoedemaeker P. J.; Pauwels E. K.; Jonas U.; Zwartendijk J.; Warnaar S. O. Monoclonal Antibody G 250 Recognizes a Determinant Present in Renal-Cell Carcinoma and Absent from Normal Kidney. Int. J. Cancer 1986, 38, 489–494. 10.1002/ijc.2910380406. [DOI] [PubMed] [Google Scholar]
  42. Pastorek J.; Pastoreková S.; Callebaut I.; Mornon J. P.; Zelník V.; Opavský R.; Zat’ovicová M.; Liao S.; Portetelle D.; Stanbridge E. J. Cloning and Characterization of MN, a Human Tumor-Associated Protein with a Domain Homologous to Carbonic Anhydrase and a Putative Helix-Loop-Helix DNA Binding Segment. Oncogene 1994, 9, 2877–2888. [PubMed] [Google Scholar]
  43. Saarnio J.; Parkkila S.; Parkkila A.-K.; Haukipuro K.; Pastoreková S.; Pastorek J.; Kairaluoma M. I.; Karttunen T. J. Immunohistochemical Study of Colorectal Tumors for Expression of a Novel Transmembrane Carbonic Anhydrase, MN/CA IX, with Potential Value as a Marker of Cell Proliferation. Am. J. Pathol. 1998, 153, 279–285. 10.1016/S0002-9440(10)65569-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Kivelä A. J.; Parkkila S.; Saarnio J.; Karttunen T. J.; Kivelä J.; Parkkila A.-K.; Pastoreková S.; Pastorek J.; Waheed A.; Sly W. S.; et al. Expression of Transmembrane Carbonic Anhydrase Isoenzymes IX and XII in Normal Human Pancreas and Pancreatic Tumours. Histochem. Cell Biol. 2000, 114, 197–204. 10.1007/s004180000181. [DOI] [PubMed] [Google Scholar]
  45. Baranauskienė L.; Hilvo M.; Matulienė J.; Golovenko D.; Manakova E.; Dudutienė V.; Michailovienė V.; Torresan J.; Jachno J.; Parkkila S.; et al. Inhibition and Binding Studies of Carbonic Anhydrase Isozymes I, II and IX with Benzimidazo[1,2-c][1,2,3]Thiadiazole-7-Sulphonamides. J. Enzyme Inhib. Med. Chem. 2010, 25, 863–870. 10.3109/14756360903571685. [DOI] [PubMed] [Google Scholar]
  46. Cimmperman P.; Baranauskienė L.; Jachimovičiu̅tė S.; Jachno J.; Torresan J.; Michailovienė V.; Matulienė J.; Sereikaitė J.; Bumelis V.; Matulis D. A Quantitative Model of Thermal Stabilization and Destabilization of Proteins by Ligands. Biophys. J. 2008, 95, 3222–3231. 10.1529/biophysj.108.134973. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Piotto M.; Saudek V.; Sklenář V. Gradient-Tailored Excitation for Single-Quantum NMR Spectroscopy of Aqueous Solutions. J. Biomol. NMR 1992, 2, 661–665. 10.1007/BF02192855. [DOI] [PubMed] [Google Scholar]
  48. Vranken W. F.; Boucher W.; Stevens T. J.; Fogh R. H.; Pajon A.; Llinas M.; Ulrich E. L.; Markley J. L.; Ionides J.; Laue E. D. The CCPN Data Model for NMR Spectroscopy: Development of a Software Pipeline. Proteins: Struct., Funct., Bioinf. 2005, 59, 687–696. 10.1002/prot.20449. [DOI] [PubMed] [Google Scholar]
  49. Sethson I.; Edlund U.; Holak T. A.; Ross A.; Jonsson B. H. Sequential Assignment of 1H, 13C and 15N Resonances of Human Carbonic Anhydrase I by Triple-Resonance NMR Techniques and Extensive Amino Acid-Specific 15N-Labeling. J. Biomol. NMR 1996, 8, 417–428. 10.1007/BF00228144. [DOI] [PubMed] [Google Scholar]
  50. Venters R. A.; Coggins B. E.; Kojetin D.; Cavanagh J.; Zhou P. (4,2)D Projection-Reconstruction Experiments for Protein Backbone Assignment: Application to Human Carbonic Anhydrase II and Calbindin D 28K. J. Am. Chem. Soc. 2005, 127, 8785–8795. 10.1021/ja0509580. [DOI] [PubMed] [Google Scholar]
  51. Rutkauskas K.; Zubrienė A.; Tumosienė I.; Kantminienė K.; Kažemėkaitė M.; Smirnov A.; Kazokaitė J.; Morku̅naitė V.; Čapkauskaitė E.; Manakova E.; et al. 4-Amino-Substituted Benzenesulfonamides as Inhibitors of Human Carbonic Anhydrases. Molecules 2014, 19, 17356–17380. 10.3390/molecules191117356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Gekko K.; Yamagami K. Compressibility and Volume Changes of Lysozyme Due to Inhibitor Binding. Chem. Lett. 1998, 27, 839–840. 10.1246/cl.1998.839. [DOI] [Google Scholar]
  53. Kamiyama T.; Gekko K. Effect of Ligand Binding on the Flexibility of Dihydrofolate Reductase as Revealed by Compressibility. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 2000, 1478, 257–266. 10.1016/S0167-4838(00)00019-4. [DOI] [PubMed] [Google Scholar]
  54. Chalikian T. V. Volumetric Properties of Proteins. Annu. Rev. Biophys. Biomol. Struct. 2003, 32, 207–235. 10.1146/annurev.biophys.32.110601.141709. [DOI] [PubMed] [Google Scholar]
  55. Kitahara R.; Hata K.; Li H.; Williamson M. P.; Akasaka K. Pressure-Induced Chemical Shifts as Probes for Conformational Fluctuations in Proteins. Prog. Nucl. Magn. Reson. Spectrosc. 2013, 71, 35–58. 10.1016/j.pnmrs.2012.12.001. [DOI] [PubMed] [Google Scholar]
  56. Refaee M.; Tezuka T.; Akasaka K.; Williamson M. P. Pressure-Dependent Changes in the Solution Structure of Hen Egg-White Lysozyme. J. Mol. Biol. 2003, 327, 857–865. 10.1016/S0022-2836(03)00209-2. [DOI] [PubMed] [Google Scholar]
  57. Williamson M. P.; Akasaka K.; Refaee M. The Solution Structure of Bovine Pancreatic Trypsin Inhibitor at High Pressure. Protein Sci. 2003, 12, 1971–1979. 10.1110/ps.0242103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wilton D. J.; Tunnicliffe R. B.; Kamatari Y. O.; Akasaka K.; Williamson M. P. Pressure-Induced Changes in the Solution Structure of the GB1 Domain of Protein G. Proteins: Struct., Funct., Bioinf. 2008, 71, 1432–1440. 10.1002/prot.21832. [DOI] [PubMed] [Google Scholar]
  59. Sitkoff D.; Case D. A. Theories of Chemical Shift Anisotropies in Proteins and Nucleic Acids. Prog. Nucl. Magn. Reson. Spectrosc. 1998, 32, 165–190. 10.1016/S0079-6565(98)00013-2. [DOI] [Google Scholar]
  60. Akasaka K.; Li H.; Yamada H.; Li R.; Thoresen T.; Woodward C. K. Pressure Response of Protein Backbone Structure. Pressure-Induced Amide 15 N Chemical Shifts in BPTI. Protein Sci. 1999, 8, 1946–1953. 10.1110/ps.8.10.1946. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Skvarnavičius G.; Toleikis Z.; Grigaliu̅nas M.; Smirnovienė J.; Norvaišas P.; Cimmperman P.; Matulis D.; V Petrauskas High Pressure Spectrofluorimetry −a Tool to Determine Protein-Ligand Binding Volume. J. Phys.: Conf. Ser. 2017, 950, 042001 10.1088/1742-6596/950/4/042001. [DOI] [Google Scholar]

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES