Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jun 16;125(24):5237–5245. doi: 10.1021/acs.jpca.1c01685

Benzene, Toluene, and Monosubstituted Derivatives: Diabatic Nature of the Oscillator Strengths of S1 ← S0 Transitions

David Robinson †,*, Saleh S Alarfaji ‡, Jonathan D Hirst ‡
PMCID: PMC8279645  PMID: 34132093

Abstract

graphic file with name jp1c01685_0009.jpg

For benzene, toluene, aniline, fluorobenzene, and phenol, even sophisticated treatments of electron correlation, such as MRCI and XMS-CASPT2 calculations, show oscillator strengths typically lower than experiment. Inclusion of a simple pseudo-diabatization approach to perturb the S1 state with approximate vibronic coupling to the S2 state for each molecule results in more accurate oscillator strengths. Their absolute values agree better with experiment for all molecules except aniline. When the coupling between the S1 and S2 states is strong at the S0 geometry, the simple diabatization scheme performs less well with respect to the oscillator strengths relative to the adiabatic values. However, we expect the scheme to be useful in many cases where the coupling is weak to moderate (where the maximum component of the coupling has a magnitude less than 1.5 au). Such calculations give an insight into the effects of vibronic coupling of excited states on UV/vis spectra.

Introduction

Small monosubstituted benzenes serve as model systems for biological chromophores, helping to understand the structure of proteins1 and hydrogels.2 Both their electronically excited states3 and their vibrational spectra have been widely investigated. For example, the aromatic groups of tyrosine and phenylalanine contribute to the electronic circular dichroism of proteins in the near ultraviolet,4 while IR spectroscopy is widely used to probe the conformational landscape of proteins. Toluene plays a role in atmospheric chemistry, oxidizing in the troposphere and playing a role in secondary organic aerosol formation.5−8 Toluene is also important for the synthesis of industrial polymers,9 and excited states have a key role in the radiolysis of aromatic compounds.10 A comprehensive description of the spectroscopy of individual chromophores is a pre-requisite for understanding the often complex spectra of dimers11 and higher aggregates present in many types of macromolecular systems. We have a long-standing interest in the accurate and efficient description of the spectroscopy of toluene as a model of phenylalanine for electronic circular dichroism calculations. Such calculations determine parameters for our DichroCalc software.12,13 In particular, we are interested in a simple, efficient, and quantitative approach to the calculation of vibronic coupling of different electronically excited states in such molecules to improve the fine structure of the electronic transitions and corresponding transition dipole moments.

To glean useful information from calculations of the electronic excited states of benzene and monosubstituted benzene derivatives, one must understand the nature of the transitions being studied: in our case, the S1 ← S0 transition. In benzene, the S1 ← S0 (Ã1B2u ← X̃1A1g) transition is formally forbidden, but it becomes allowed because of vibronic coupling to the optically allowed C̃1E1u state.14,15 Monosubstituted halobenzenes have C2v symmetry, and so the S1 ← S0 transition becomes formally allowed, exhibiting a larger oscillator strength than benzene, although still weak. This is often stated as the electronic structure of monosubstituted benzenes having a “memory” of the D6h symmetry and vibronic nature of the transition. Experimental studies have consistently shown some intensity, with activity in the b2 vibrational modes in the S1 ← S0 spectra.16 The S2 state is known to have a conical intersection, leading to fast internal conversion to the S1 state, with the S2 state having a lifetime of less than 100 fs.17,18 Once on the S1 surface, the excitation wavepacket is able to decay along two channels: the first to the nearby S1/S0 conical intersection and the second to the S1 minimum.19 The S1 state is longer lived, with a lifetime of ∼4 ps.20

There have been several different computational approaches to the accurate description of S1 vibrational frequencies of aromatic molecules and vibronic coupling of S1 states to higher electronic states for benzene, toluene, and other monosubstituted benzene derivatives. The vibronic bands in benzene have been investigated using multireference approaches,21 and coupling between different states22 has been considered in the interpretation of the photochemistry observed experimentally (see also ref (23) for a useful review by Suzuki). Tew et al. investigated the anharmonic nature of the S1 vibrational frequencies of toluene using the CC2/cc-pVTZ approach.24 They found several modes with substantial anharmonicity, and their overall agreement with experiment was within 30 cm–1 for all vibrational modes. Wang et al. studied the quantum dynamics of aniline, discovering vibronic coupling between the S1 state and two Rydberg states.25 Lykhin et al. also showed the importance of triplet states in the photodynamics of aniline, with a competitive photorelaxation route from the 1ππ* state.26 Mondal and Mahapatra determined that the S1 state of fluorobenzene was coupled to a manifold of higher singlet excited states by constructing a vibronic Hamiltonian based on EOM-CCSD calculations.27,28 Phenol exhibits vibronic coupling between the S1 state and the dissociative S2 state of a πσ* character.29 Much theoretical work has been performed, confirming the nature of this conical intersection and tunneling, which is also part of the photodissociation pathway.30−33 While each of these approaches shows good qualitative and quantitative accuracy in the low energy transitions for these molecules, they require specialist work and attention crafted for each individual molecule and are not applicable in an “off-the-shelf” sense, accessible to users from different disciplines.

In the current work, we investigate the S1 ← S0 transition in toluene. We employ a simple diabatization scheme to include vibronic coupling effects approximately. This scheme is applied to benzene and four monosubstituted derivatives to explore oscillator strength enhancement from vibronic coupling for multireference CI (MRCI) and XMS-CASPT2 calculations that is amenable to non-specialist users.

Computational Details

The S0 and S1 equilibrium geometries and S2/S1 minimum energy conical intersection (MECI) geometry for each of the molecules in Figure 1 were calculated at the XMS-CASPT2/cc-pVTZ level of theory (active spaces shown in Figure 1; in each case, the π-electron system plus lone pairs were included).

Figure 1.

Figure 1

Open in a new tab

Benzene and the monosubstituted benzene derivatives investigated in this work. CASSCF active spaces are given in parentheses, where the notation is (number of active electrons, number of active orbitals).

Vibronic coupling is a process where the Born–Oppenheimer approximation breaks down and an adiabatic electronic state, J, mixes with another adiabatic electronic state, I, due to vibrations of the nuclei:

graphic file with name jp1c01685_m001.jpg 1

where fJI are the non-adiabatic coupling matrix elements (NACMEs) and R are the nuclear coordinates. The effects of vibronic coupling were included using the simple diabatization scheme of Simah et al.34 (based on the work by Domcke and Woywod35), in which the overlap of the orbitals from a reference geometry and target geometry is optimized and the resulting pseudo-diabatic orbitals are used to transform the wavefunction at the target geometry. In our case, we chose the reference geometry to be the MECI of the S2/S1 conical intersection seam, as this is the point at which the two states involved in the intensity borrowing process interact most strongly. The target geometry is the S0 optimized geometry as this represents the geometry at which the Franck–Condon (FC) excitation occurs. The diabatic states (denoted by the superscript d) are considered to be a minor perturbation to the adiabatic states and are found by a unitary transformation of the S1 and S2 adiabatic states (denoted by a superscript a)

graphic file with name jp1c01685_m002.jpg 2

The unitary transformation matrix is chosen such that the NACME vector, X2

graphic file with name jp1c01685_m003.jpg 3

is minimized for all of the internal coordinates, q. For a two-state diabatization, the unitary transformation matrix, U, is given as

graphic file with name jp1c01685_m004.jpg 4

where a single non-adiabatic mixing angle, θ, can be used to describe the mixing of the adiabatic states. In the approximate scheme used in this work, the CI coefficients from an MRCI or XMS-CASPT2 calculation were transformed by maximizing the overlap of the CASSCF orbitals at the S0 geometry with those obtained at a reference geometry, generating a pseudo-diabatic set of orbitals:

graphic file with name jp1c01685_m005.jpg 5

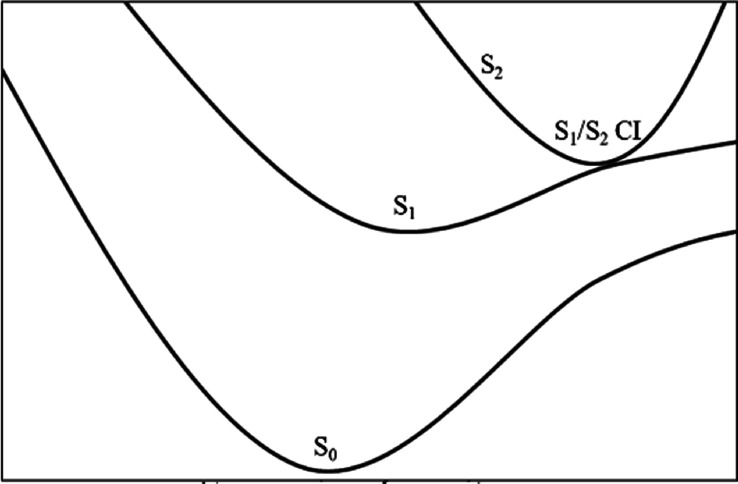
where the overlap is computed over all active orbitals i and j at the current geometry q with those at the reference geometry q′, which in this case was the S2/S1 MECI. In all cases, we assume that this MECI lies close to the S1 minimum and the proximity of the electronic states allows them to interact (see Figure 2 for a qualitative overview). The diabatic wavefunction, Ψmd, is constructed from the pseudo-diabatic orbitals as

graphic file with name jp1c01685_m006.jpg 6

At the target geometry, the matrix d is related to the adiabatic wavefunctions by the transformation d = cU, where c is the coefficient matrix of the adiabatic wavefunctions and U is determined using the condition that d remains as close as possible to the matrix dref at the reference geometry:

graphic file with name jp1c01685_m007.jpg 7

where

graphic file with name jp1c01685_m008.jpg 8

The transition dipole moments can then be calculated for the S1 ← S0 transition, with the approximately diabatic S1 state, as

graphic file with name jp1c01685_m009.jpg 9

and similarly for the Inline graphicy and Inline graphicz components using either the MRCI or XMS-CASPT2 computed densities. Writing the energy expressions explicitly for each of the two states, one obtains

graphic file with name jp1c01685_m012.jpg 10a
graphic file with name jp1c01685_m013.jpg 10b

The oscillator strength can then be calculated:

graphic file with name jp1c01685_m014.jpg 11

While in eq 11, we use an adiabatic description of the S0 state and pseudo-diabatic representation for S1, the pseudo-diabatic representation is essentially only a perturbation to the adiabatic S1 state. As such, where there is very strong coupling between S1 and S2 states, we expect this simple approximation to break down as the pseudo-diabatization scheme is based on the assumption that the orbitals and CI coefficients change very little as a function of geometry; this is not always true in the vicinity of a conical intersection. In the original scheme of Simah et al.,34 the reference geometry is ideally chosen where the adiabatic and diabatic states are identical (e.g., due to symmetry). In the current work, the use of the S2/S1 MECI is a point at which the NACME terms do not vanish completely, but the adiabatic and diabatic states may not be identical. Additionally, the reference orbitals at the MECI geometry may have poor overlap with those at the target geometry (S0). If the MECI is far from the FC region of the S1 state, then the current scheme is likely to show limited vibronic coupling, even if there is true coupling between the two states.

Figure 2.

Figure 2

Open in a new tab

Qualitative schematic of the S0, S1, and S2 potential energy surfaces in the region of the Franck–Condon excitation.

Adiabatic XMS-CASPT236 calculations were performed within the single-state single-reference contraction scheme (SS-SR) and a real shift of 0.2 au, using the cc-pVTZ basis37 and the cc-pVTZ-JKFIT auxiliary basis set,38 using the BAGEL software.39,40 Adiabatic time-dependent density functional theory (TDDFT) calculations within the Tamm–Dancoff approximation41 were performed with the B3LYP,42 CAM-B3LYP,43 M06-2X,44 and ωB97X45 functionals. Single-reference EOM-CCSD,46 ADC(2),47 and ADC(3)48 calculations were also performed. TDDFT and single-reference wavefunction theory calculations were performed using the Q-Chem software.49 The diabatic transformation calculations (using both internally contracted MRCI50−52 and XMS-CASPT2) were performed with the Molpro software suite.53 The S0 and S2/S1 calculated geometries were superposed based on minimizing the RSMD of all atoms. In all cases, the cc-pVTZ basis set37 was employed as it represents a good compromise between accuracy and computational cost.

In addition, for toluene, a vibrationally resolved spectrum was determined by calculating the FC factors between the S0 and S1 harmonic vibrational modes and frequencies. The spectrum was calculated using the ezSpectrum software54,55 at a temperature of 10 K.

Results and Discussion

We first consider the S0 and S1 states of toluene. In Table 1 are the calculated XMS-CASPT2 harmonic vibrational frequencies. The scaled harmonic vibrational frequencies show fair agreement with experiment,16,56−58 with a maximum error of 316 cm–1 for one of the low frequency carbon–carbon bend modes (m18) and average errors of 55 and 29 cm–1 for the S0 and S1 frequencies, respectively, after scaling. The average error for the S0 vibrations is 45 cm–1, neglecting the m18 frequency. Tew et al. employed the CC2/cc-pVTZ approach to calculate anharmonic frequencies of toluene.24 The differences exhibited between the XMS-CASPT2 and experimental S1 frequencies are likely due to a combination of anharmonicity, for which CC2/cc-pVTZ performs well,24 and potential issues in the XMS-CASPT2 accuracy. In particular, the m4, m12, m15, m16, m18, m23, and m25 modes all show larger differences to the CC2 values (and experiment); these were modes identified as genuinely anharmonic.24 Battaglia and Lindh determined XMS-CASPT2 excitations to be poor relative to MS-CASPT2 in regions where potential surfaces are energetically well separated (i.e., at or near minima); they developed an alternative approach to XMS-CASPT2 termed extended dynamically weighted CASPT2 (XDW-CASPT2).59 The results presented here suggest that stationary points and their frequencies may be similarly affected. These frequencies have been used to generate a vibrationally resolved spectrum (Figure 3). The dominant transition is the 0–0 vibrational line, with a handful of other vibrational lines about two orders of magnitude smaller.

Table 1. Calculated Harmonic Frequencies of the S0 and S1 States of Toluene (XMS-CASPT2/cc-pVTZ)c.

  S0
 S1
assignmenta XMS-CASPT2 Expt.b XMS-CASPT2 Expt.b
m1 3072 3087 3086 3097
m2 3052 3063 3076 3077
m3 3038 3055 3066 3063
m4 1560 1605 1411  
m5 1439 1494 1401  
m6 1179 1210 1162 1193
m7 1136 1175 1110 1021
m8 1003 1030 921 935; 934
m9 949 1003 904 966
m10 751 785 719 736; 753
m11 492 521 435 457
m12 798 964 514 687
m13 751 843 511  
m14 379 407 211 228; 226
m15 798 978 583  
m16 751 895 514 697
m17 637 728 511  
m18 379 695 309 423
m19 317 464 287 320; 314
m20 197 216 131 157; 145
m21 3058 3039 3086 3087
m22 3038 3029 3066 3048
m23 1560 1586 1528  
m24 1424 1445 1411  
m25 1340 1312 1331  
m26 1277 1280 1248  
m27 1136 1155 1110  
m28 1049 1080 1000  
m29 587 623 514 532
m30 317 342 309 332; 331
Open in a new tab
a

Assignments taken from ref (14).

b

Experimental data taken from refs (16, 56, 58).

c

Harmonic frequencies are scaled by 0.954. See the Supporting Information for full details of the scaling parameter.

Figure 3.

Figure 3

Open in a new tab

Experimental (line) and computed (stick) spectrum of the S1 ← S0 transition for toluene. The computed spectrum has been shifted by −0.136 eV to match the experimental spectrum.60

We now turn to the calculation of the oscillator strengths for the S1 ← S0 transition for toluene, benzene, and three monosubstituted benzene derivatives. The S2/S1 MECI structures for each of the molecules considered are shown in Figure 4. With the exception of aniline, all exhibit a prefulvene-like structure typical of the MECI geometries of aromatic molecules. Aniline exhibits geometrical distortion of the −NH2 group relative to the ring, with the atoms in the ring remaining planar. This is similar to that seen for the 1ππ*/1πσ* MECI in the recent work of Ray and Ramesh.61 The MECI geometry for toluene has a peaked topology, while the rest have a sloped topology.

Figure 4.

Figure 4

Open in a new tab

XMS-CASPT2/cc-pVTZ structures for the S2/S1 MECI of (a) benzene, (b) toluene, (c) aniline, (d) fluorobenzene, and (e) phenol.

The computed transition energies are given in Table 2 (0–0 transitions) and Table 3 (Franck–Condon transitions), along with the calculated oscillator strengths. The MECIs lie 1.14, 0.89, 0.52, 0.59, and 1.10 eV above the S1 minima and 0.97, 0.73, 0.28, 0.42, and 1.03 eV above the Franck–Condon transition energy (S1 ← S0) for benzene, toluene, aniline, fluorobenzene, and phenol, respectively. The magnitudes of the calculated and experimental oscillator strengths62 are compared in Figure 5. The single-reference methods generally overestimate the oscillator strength, although for benzene (data shown in Table 3) and toluene, they are between 0 and 50% of the experimental value. The multireference methods both underestimate the oscillator strengths in comparison to experiment and the single-reference methods (DFT, EOM-CCSD, and ADC approaches), with the exception of phenol, where the XMS-CASPT2 oscillator strength is the largest of all the methods considered. The pseudo-diabatic oscillator strengths are given in Table 3 and Figure 5 for MRCI and XMS-CASPT2. The calculated oscillator strengths are enhanced relative to the adiabatic values for all molecules except aniline, where the pseudo-diabatic values are ∼50% of the adiabatic values and ∼10% of the experimental value for both MRCI and XMS-CASPT2. In this case, we can see that the S2 state is energetically close to the S1 state across the potential energy surface connecting the S0 minimum and S2/S1 conical intersection (see Figure S1), deviating by no more than ∼1.1 eV. In contrast, the other molecules have energy gaps greater than 1.5 eV at the S0 minima. In Figure 6, we present visual representations of the XMS-CASPT2 calculated non-adiabatic coupling vector between the S2 and S1 states at the S0 geometry. It is clear for aniline that the coupling is much stronger than that seen for the other molecules. This is also reflected in the Franck–Condon excitation energy being less than 0.3 eV lower than the S2/S1 MECI relative to the S0 energy. Interestingly, the coupling is strongest for the atoms in the ring and relatively low for the −NH2 group, in contrast to the 1ππ*/1πσ* conical intersection.61 Worth and co-workers demonstrated two 3p Rydberg states between the S1 and S2 states. These also couple to the S1 state,25 but they are not considered in the current study. We propose that, in this case, the approximate diabatization scheme would need to be replaced with a more robust approach (possibly including Franck–Condon factors and explicit integration of the NACMEs) to give a more accurate oscillator strength as vibronic coupling between the S1 and S2 states is stronger than the other molecules considered. Given in Figure S2 are the maximum and average coupling values compared to the difference in oscillator strength between the calculated and experimental oscillator strengths. For the molecules considered, the accuracy of the current method deteriorates when an individual atom’s NACME vector has a magnitude greater than 1.5 au (or the average magnitude of the NACME vector across all atoms is greater than ∼0.7 au). The coupling between electronically excited states for phenol in this study is between two 1ππ* states, while the true S2 state is of a πσ* character.63 This is a consequence of the approach taken in this study, namely, choosing the simple π-electron active space and not expanding to include σ* orbitals.

Table 2. Calculated Energy Differences (XMS-CASPT2/cc-pVTZ) between the Minima for the S0 and S1 States of Each Molecule and Their S2S1 MECIs.

molecule ΔE (0–0, S1 ← S0) (eV) ΔE (S2/S1 ← S0) (eV)
benzene 4.72 5.86
toluene 4.60 5.49
aniline 4.29 4.81
fluorobenzene 4.69 5.28
phenol 4.53 5.63
Open in a new tab

Table 3. Computed Franck–Condon Excitation Energies (in eV) and Oscillator Strengths in the Adiabatic and Pseudo-diabatic Basisa.

  benzene
 toluene
 aniline
 fluorobenzene
 phenol
method ΔE f ΔE f ΔE f ΔE f ΔE f
Adiabatic
MRCI 5.08 0.0000 4.98 0.0000 4.83 0.0074 5.08 0.0025 4.96 0.0070
XMS-CASPT2 4.89 0.0000 4.76 0.0001 4.53 0.0080 4.86 0.0025 4.59 0.0531
EOM-CCSD 5.18 0.0000 5.12 0.0011 4.78 0.0384 5.24 0.0097 5.07 0.0234
ADC(2) 5.25 0.0000 5.16 0.0013 4.71 0.0464 5.26 0.0152 5.04 0.0323
ADC(3) 4.98 0.0000 4.91 0.0013 4.59 0.0389 5.05 0.0092 4.89 0.0227
B3LYP 5.50 0.0000 5.31 0.0017 4.80 0.0501 5.43 0.0133 5.20 0.0330
CAM-B3LYP 5.66 0.0000 5.43 0.0021 5.04 0.0561 5.60 0.0147 5.39 0.0359
M06-2X 5.71 0.0000 5.51 0.0021 5.10 0.0573 5.67 0.0153 5.47 0.0361
ωB97X 5.69 0.0000 5.49 0.0022 5.12 0.0576 5.63 0.0155 5.44 0.0369
Diabatic
MRCI 5.05 0.0029 5.47 0.0066 4.84 0.0033 5.45 0.0042 5.01 0.0080
XMS-CASPT2 4.91 0.0048 5.21 0.0097 4.80 0.0044 5.38 0.0074 4.99 0.0118
Expt. 4.88 0.0006 4.62 0.0050 3.69 0.0355 4.73 0.0076 4.56 0.0161
Open in a new tab
a

Experimental data taken from ref (62).

Figure 5.

Figure 5

Open in a new tab

Calculated oscillator strengths expressed as a percentage of the experimental value. A value of 100% corresponds to the experimental value. The final two columns of each plot are the pseudo-diabatic MRCI and XMS-CASPT2 oscillator strengths. (a) Toluene; (b) aniline; (c) fluorobenzene; and (d) phenol. Values greater than 200% are depicted with open boxes.

Figure 6.

Figure 6

Open in a new tab

Visual representation of the non-adiabatic coupling vectors between the S2 and S1 states at the S0 optimized geometries for benzene (top left), toluene (bottom left), aniline (center), fluorobenzene (top right), and phenol (bottom right).

For each of the molecules considered, the point-group symmetry of the geometry of the S0 state is D6h (benzene), Cs (toluene), C2v (aniline), C2v (fluorobenzene), and Cs (phenol). Breaking of the planar aromatic ring would therefore be assumed to be responsible for an enhancement in the oscillator strength of the S1 ← S0 transition. The effect of symmetry breaking upon the calculated oscillator strength is given in Figure 7 for toluene. As the torsion angle (between three aromatic carbon atoms and the methyl carbon) is decreased by ∼10°, the energy of the S0 state increases by only 1 kcal mol–1 (Figure 7a). As such, there is effectively little to no barrier to symmetry breaking at finite temperature. While there is a small change in the oscillator strength as the symmetry of the molecule is broken, this is a small effect (Figure 7b).

Figure 7.

Figure 7

Open in a new tab

(a) Two-dimensional potential energy surface scanned along the torsion angle C(aromatic)–C(aromatic)–C(aromatic)–C(methyl) and the bond angle C(aromatic)–C(aromatic)–C(methyl); kcal mol–1, contour value of 0.025 kcal mol–1. (b) Calculated oscillator strength as a function of the bond angle C(aromatic)–C(aromatic)–C(methyl) (see key for details of the methods).

We now consider the extent to which the S1 and S2 states are mixed in the pseudo-diabatization procedure. In Table 4 are the calculated diabatic rotation angles for MRCI and XMS-CASPT2 for each of the molecules considered. While these rotation angles have an effect on the diabatic energies (eq 7), the effect on the oscillator strengths is determined by the mixing of the CI coefficients. As noted above, the coupling between the S2 and S1 states is strong for aniline with analytic NACMEs at the S0 geometry, in contradiction to the rotation angle calculated using the approximate pseudo-diabatization procedure. This provides further evidence that, in the event of strong coupling, the pseudo-diabatization procedure becomes less reliable.

Table 4. Diabatic Rotation Angles Determined Using the Pseudo-diabatization Procedurea.

molecule θ (MRCI) θ (XMS-CASPT2)
benzene 0.02 –0.01
toluene –24.6 –20.6
aniline 0.1 0.1
fluorobenzene –20.8 –21.8
phenol 8.7 11.1
Open in a new tab
a

All angles in °.

Conclusions

We have applied a simple pseudo-diabatization scheme to benzene, toluene, and three other monosubstituted benzenes to account for the vibronic coupling between the S2 and S1 states and the effect this has upon the transition properties of the S1 ← S0 excitation using multireference approaches. In the adiabatic basis, MRCI and XMS-CASPT2 exhibit oscillator strengths lower than the experimental value. Inclusion of approximate vibronic coupling effects through the pseudo-diabatic states results in improved quantitative values of the oscillator strength for all molecules except aniline. In this case, the vibronic coupling was determined to be strong relative to that seen in the other molecules; the success of the simple approach adopted here is predicated on weak coupling of the S2 and S1 states; in the case of aniline, this coupling is strong, leading to a poor description of the oscillator strength.

Acknowledgments

We thank NTU and the University of Nottingham (UoN) for provision of high performance computing facilities used for the present calculations. We thank Zhuo Li (UoN) for useful discussions. S.S.A. thanks the Research Center of Advanced Materials, King Khalid University in Saudi Arabia for a studentship (grant no. RCAMS/KKU/0020/20). J.D.H. is supported by the Royal Academy of Engineering under the Chairs in Emerging Technologies scheme.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.1c01685.

  • Potential energy scans for aniline, NACME magnitudes, and harmonic vibrational frequency scaling data (PDF)

Author Present Address

§ Present address: Research Center for Advanced Materials Science (RCAMS), King Khalid University, P. O. Box 9004, Abha, Saudi Arabia (S.S.A.).

The authors declare no competing financial interest.

Supplementary Material

jp1c01685_si_001.pdf (516.6KB, pdf)

References

  1. Burley S. K.; Petsko G. A. Aromatic-Aromatic Interaction: A Mechanism of Protein Structure Stabilization. Science 1985, 229, 23–28. 10.1126/science.3892686. [DOI] [PubMed] [Google Scholar]
  2. Li J.; Du X.; Hashim S.; Shy A.; Xu B. Aromatic-Aromatic Interactions Enable α-Helix to β-Sheet Transition of Peptides to Form Supramolecular Hydrogels. J. Am. Chem. Soc. 2017, 139, 71–74. 10.1021/jacs.6b11512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Pratt D. W. High Resolution Spectroscopy in the Gas Phase: Even Large Molecules Have Well-Defined Shapes. Annu. Rev. Phys. Chem. 1998, 49, 481–530. 10.1146/annurev.physchem.49.1.481. [DOI] [PubMed] [Google Scholar]
  4. Rogers D. M.; Hirst J. D. First-Principles Calculations of Protein Circular Dichroism in the near Ultraviolet. Biochemistry 2004, 43, 11092–11102. 10.1021/bi049031n. [DOI] [PubMed] [Google Scholar]
  5. Finlayson-Pitts B. J.; Pitts J. N.. Chemistry of the Upper and Lower Atmosphere; Elsevier, 1999. [Google Scholar]
  6. Calvert J. G.; Atkinson R.; Becker K. H.; Kamens R. M.; Seinfeld J. H.; Wallington T. J.; Yarwood G.. The Mechanisms of Atmospheric Oxidation of the Aromatic Hydrocarbons; Oxford University Press, 2002. [Google Scholar]
  7. Steinfeld J. H.; Pandis S. N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. Phys. Today 1998, 51, 88–90. 10.1063/1.882420. [DOI] [Google Scholar]
  8. Ji Y.; Zhao J.; Terazono H.; Misawa K.; Levitt N. P.; Li Y.; Lin Y.; Peng J.; Wang Y.; Duan L.; et al. Reassessing the Atmospheric Oxidation Mechanism of Toluene. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 8169–8174. 10.1073/pnas.1705463114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Schulze M. Industrial Organic Chemicals. Von H. A. Wittcoff, B. G. Reuben, J. S. Plotkin. Chem. Ing. Tech. 2014, 86, 1304–1304. 10.1002/cite.201490073. [DOI] [Google Scholar]
  10. Baidak A.; Badali M.; Laverne J. A. Role of the Low-Energy Excited States in the Radiolysis of Aromatic Liquids. J. Phys. Chem. A 2011, 115, 7418–7427. 10.1021/jp202802a. [DOI] [PubMed] [Google Scholar]
  11. Rogers D. M.; Hirst J. D.; Lee E. P. F.; Wright T. G. Ab Initio Study of the Toluene Dimer. Chem. Phys. Lett. 2006, 427, 410–413. 10.1016/j.cplett.2006.07.022. [DOI] [Google Scholar]
  12. Jasim S. B.; Li Z.; Guest E. E.; Hirst J. D. DichroCalc: Improvements in Computing Protein Circular Dichroism Spectroscopy in the Near-Ultraviolet. J. Mol. Biol. 2018, 430, 2196–2202. 10.1016/j.jmb.2017.12.009. [DOI] [PubMed] [Google Scholar]
  13. Bulheller B. M.; Hirst J. D. DichroCalc—Circular and Linear Dichroism Online. Bioinformatics 2009, 25, 539–540. 10.1093/bioinformatics/btp016. [DOI] [PubMed] [Google Scholar]
  14. Gardner A. M.; Wright T. G. Consistent Assignment of the Vibrations of Monosubstituted Benzenes. J. Chem. Phys. 2011, 135, 114305. 10.1063/1.3638266. [DOI] [PubMed] [Google Scholar]
  15. Douglas I. N.; Grinter R.; Thomson A. J. Vibronic Borrowing of Angular Momentum in The 1B2u State of Benzene. Mol. Phys. 1975, 29, 673–679. 10.1080/00268977500100611. [DOI] [Google Scholar]
  16. Gardner A. M.; Green A. M.; Tamé-Reyes V. M.; Wilton V. H. K.; Wright T. G. Vibrations of the Low Energy States of Toluene (X̃1A1 and Ã1B2) and the Toluene Cation (X̃2B1). J. Chem. Phys. 2013, 138, 134303 10.1063/1.4796204. [DOI] [PubMed] [Google Scholar]
  17. Suzuki Y.-I.; Horio T.; Fuji T.; Suzuki T. Time-Resolved Photoelectron Imaging of S2 → S1 Internal Conversion in Benzene and Toluene. J. Chem. Phys. 2011, 134, 184313 10.1063/1.3586809. [DOI] [PubMed] [Google Scholar]
  18. Radloff W.; Stert V.; Freudenberg T.; Hertel I. V.; Jouvet C.; Dedonder-Lardeux C.; Solgadi D. Internal Conversion in Highly Excited Benzene and Benzene Dimer: Femtosecond Time-Resolved Photoelectron Spectroscopy. Chem. Phys. Lett. 1997, 281, 20–26. 10.1016/S0009-2614(97)01142-1. [DOI] [Google Scholar]
  19. Adachi S.; Suzuki T. Methyl Substitution Effects on the Non-Adiabatic Dynamics of Benzene: Lifting Three-State Quasi-Degeneracy at Conical Intersections. Phys. Chem. Chem. Phys. 2020, 22, 2814–2818. 10.1039/C9CP06164A. [DOI] [PubMed] [Google Scholar]
  20. Farmanara P.; Stert V.; Radloff W.; Hertel I. V. Ultrafast Internal Conversion in Highly Excited Toluene Monomers and Dimers. J. Phys. Chem. A 2001, 105, 5613–5617. 10.1021/jp003818f. [DOI] [Google Scholar]
  21. Bernhardsson A.; Forsberg N.; Malmqvist P. Å.; Roos B. O.; Serrano-Andrés L. A Theoretical Study of the 1B2u and 1B1u Vibronic Bands in Benzene. J. Chem. Phys. 2000, 112, 2798–2809. 10.1063/1.480854. [DOI] [Google Scholar]
  22. Worth G. A. A Model Hamiltonian to Simulate the Complex Photochemistry of Benzene. J. Photochem. Photobiol., A 2007, 190, 190–199. 10.1016/j.jphotochem.2007.01.020. [DOI] [PubMed] [Google Scholar]
  23. Suzuki T. Time-Resolved Photoelectron Spectroscopy of Non-Adiabatic Electronic Dynamics in Gas and Liquid Phases. Int. Rev. Phys. Chem. 2012, 31, 265–318. 10.1080/0144235X.2012.699346. [DOI] [Google Scholar]
  24. Tew D. P.; Hättig C.; Graf N. K. Anharmonic Excited State Frequencies of para-Difluorobenzene, Toluene and Catechol Using Analytic RI-CC2 Second Derivatives. Phys. Chem. Chem. Phys. 2019, 21, 14063–14072. 10.1039/C8CP06952B. [DOI] [PubMed] [Google Scholar]
  25. Wang F.; Neville S. P.; Wang R.; Worth G. A. Quantum Dynamics Study of Photoexcited Aniline. J. Phys. Chem. A 2013, 117, 7298–7307. 10.1021/jp401116c. [DOI] [PubMed] [Google Scholar]
  26. Lykhin A. O.; Truhlar D. G.; Gagliardi L. Role of Triplet States in the Photodynamics of Aniline. J. Am. Chem. Soc. 2021, 143, 5878–5889. 10.1021/jacs.1c00989. [DOI] [PubMed] [Google Scholar]
  27. Mondal T.; Mahapatra S. Photophysics of Fluorinated Benzene. I. Quantum Chemistry. J. Chem. Phys. 2010, 133, 084304 10.1063/1.3465555. [DOI] [PubMed] [Google Scholar]
  28. Mondal T.; Mahapatra S. Photophysics of Fluorinated Benzene. II. Quantum Dynamics. J. Chem. Phys. 2010, 133, 084305 10.1063/1.3465557. [DOI] [PubMed] [Google Scholar]
  29. Lai H. Y.; Jhang W. R.; Tseng C.-M. Communication: Mode-Dependent Excited-State Lifetime of Phenol under the S1/S2 Conical Intersection. J. Chem. Phys. 2018, 149, 031104 10.1063/1.5041992. [DOI] [PubMed] [Google Scholar]
  30. Vieuxmaire O. P. J.; Lan Z.; Sobolewski A. L.; Domcke W. Ab Initio Characterization of the Conical Intersections Involved in the Photochemistry of Phenol. J. Chem. Phys. 2008, 129, 224307 10.1063/1.3028049. [DOI] [PubMed] [Google Scholar]
  31. Xu X.; Zheng J.; Yang K. R.; Truhlar D. G. Photodissociation Dynamics of Phenol: Multistate Trajectory Simulations Including Tunneling. J. Am. Chem. Soc. 2014, 136, 16378–16386. 10.1021/ja509016a. [DOI] [PubMed] [Google Scholar]
  32. Yang K. R.; Xu X.; Zheng J.; Truhlar D. G. Full-Dimensional Potentials and State Couplings and Multidimensional Tunneling Calculations for the Photodissociation of Phenol. Chem. Sci. 2014, 5, 4661–4680. 10.1039/C4SC01967A. [DOI] [Google Scholar]
  33. Xie C.; Ma J.; Zhu X.; Yarkony D. R.; Xie D.; Guo H. Nonadiabatic Tunneling in Photodissociation of Phenol. J. Am. Chem. Soc. 2016, 138, 7828–7831. 10.1021/jacs.6b03288. [DOI] [PubMed] [Google Scholar]
  34. Simah D.; Hartke B.; Werner H.-J. Photodissociation Dynamics of H2S on New Coupled Ab Initio Potential Energy Surfaces. J. Chem. Phys. 1999, 111, 4523–4534. 10.1063/1.479214. [DOI] [Google Scholar]
  35. Domcke W.; Woywod C. Direct Construction of Diabatic States in the CASSCF Approach. Application to the Conical Intersection of the 1A2 and 1B1 Excited States of Ozone. Chem. Phys. Lett. 1993, 216, 362–368. 10.1016/0009-2614(93)90110-M. [DOI] [Google Scholar]
  36. Shiozaki T.; Győrffy W.; Celani P.; Werner H.-J. Communication: Extended Multi-State Complete Active Space Second-Order Perturbation Theory: Energy and Nuclear Gradients. J. Chem. Phys. 2011, 135, 081106 10.1063/1.3633329. [DOI] [PubMed] [Google Scholar]
  37. Dunning T. H. Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  38. Weigend F. A Fully Direct RI-HF Algorithm: Implementation, Optimised Auxiliary Basis Sets, Demonstration of Accuracy and Efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. 10.1039/b204199p. [DOI] [Google Scholar]
  39. Shiozaki T. BAGEL: Brilliantly Advanced General Electronic-Structure Library. WIREs Comput. Mol. Sci. 2018, 8, e1331 10.1002/wcms.1331. [DOI] [Google Scholar]
  40. BAGEL Brilliantly Advanced General Electronic-Structure Library. Http://Www.Nubakery.Org.
  41. Hirata S.; Head-Gordon M. Time-Dependent Density Functional Theory within the Tamm–Dancoff Approximation. Chem. Phys. Lett. 1999, 314, 291–299. 10.1016/S0009-2614(99)01149-5. [DOI] [Google Scholar]
  42. Becke A. D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  43. Yanai T.; Tew D. P.; Handy N. C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  44. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 119, 525–525. 10.1007/s00214-007-0401-8. [DOI] [Google Scholar]
  45. Chai J.-D.; Head-Gordon M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. J. Chem. Phys. 2008, 128, 084106 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
  46. Stanton J. F.; Bartlett R. J. The Equation of Motion Coupled-cluster Method. A Systematic Biorthogonal Approach to Molecular Excitation Energies, Transition Probabilities, and Excited State Properties. J. Chem. Phys. 1993, 98, 7029–7039. 10.1063/1.464746. [DOI] [Google Scholar]
  47. Wormit M.; Rehn D. R.; Harbach P. H. P.; Wenzel J.; Krauter C. M.; Epifanovsky E.; Dreuw A. Investigating Excited Electronic States Using the Algebraic Diagrammatic Construction (ADC) Approach of the Polarisation Propagator. Mol. Phys. 2014, 112, 774–784. 10.1080/00268976.2013.859313. [DOI] [Google Scholar]
  48. Harbach P. H. P.; Wormit M.; Dreuw A. The Third-Order Algebraic Diagrammatic Construction Method (ADC(3)) for the Polarization Propagator for Closed-Shell Molecules: Efficient Implementation and Benchmarking. J. Chem. Phys. 2014, 141, 064113 10.1063/1.4892418. [DOI] [PubMed] [Google Scholar]
  49. Shao Y.; Gan Z.; Epifanovsky E.; Gilbert A. T. B.; Wormit M.; Kussmann J.; Lange A. W.; Behn A.; Deng J.; Feng X.; et al. Advances in Molecular Quantum Chemistry Contained in the Q-Chem 4 Program Package. Mol. Phys. 2015, 113, 184–215. 10.1080/00268976.2014.952696. [DOI] [Google Scholar]
  50. Werner H.-J.; Knowles P. J. An Efficient Internally Contracted Multiconfiguration–Reference Configuration Interaction Method. J. Chem. Phys. 1988, 89, 5803–5814. 10.1063/1.455556. [DOI] [Google Scholar]
  51. Knowles P. J.; Werner H.-J. An Efficient Method for the Evaluation of Coupling Coefficients in Configuration Interaction Calculations. Chem. Phys. Lett. 1988, 145, 514–522. 10.1016/0009-2614(88)87412-8. [DOI] [Google Scholar]
  52. Knowles P. J.; Werner H.-J. Internally Contracted Multiconfiguration-Reference Configuration Interaction Calculations for Excited States. Theor. Chim. Acta 1992, 84, 95–103. 10.1007/BF01117405. [DOI] [Google Scholar]
  53. Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M. Molpro: A General-Purpose Quantum Chemistry Program Package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. 10.1002/wcms.82. [DOI] [Google Scholar]
  54. Mozhayskiy V. A.; Krylov A. I.. EzSpectrum Http://Iopenshell.Usc.Edu/Downloads. [Google Scholar]
  55. This Work Was Conducted Using the Resources from IOpenShell Center for Computational Studies of Electronic Structure and Spectroscopy of Open-Shell and Electronically Excited Species (Http://Iopenshell.Usc.Edu) Supported by the National Science Foundation.
  56. Hickman C. G.; Gascooke J. R.; Lawrance W. D. The S1-S0(1B2-1A1) Transition of Jet-Cooled Toluene: Excitation and Dispersed Fluorescence Spectra, Fluorescence Lifetimes, and Intramolecular Vibrational Energy Redistribution. J. Chem. Phys. 1996, 104, 4887–4901. 10.1063/1.471122. [DOI] [Google Scholar]
  57. Minejima C.; Ebata T.; Mikami N. C-H Stretching Vibrations of Benzene and Toluene in Their S1 States Observed by Double Resonance Vibrational Spectroscopy in Supersonic Jets. Phys. Chem. Chem. Phys. 2002, 4, 1537–1541. 10.1039/b108039c. [DOI] [Google Scholar]
  58. Gardner A. M.; Green A. M.; Tamé-Reyes V. M.; Reid K. L.; Davies J. A.; Parkes V. H. K.; Wright T. G. The 700-1500 cm-1 Region of the S1 (Ã1B2) State of Toluene Studied with Resonance-Enhanced Multiphoton Ionization (REMPI), Zero-Kinetic-Energy (ZEKE) Spectroscopy, and Time-Resolved Slow-Electron Velocity-Map Imaging (Tr-SEVI) Spectroscopy. J. Chem. Phys. 2014, 140, 114308 10.1063/1.4867970. [DOI] [PubMed] [Google Scholar]
  59. Battaglia S.; Lindh R. Extended Dynamically Weighted CASPT2: The Best of Two Worlds. J. Chem. Theory Comput. 2020, 16, 1555–1567. 10.1021/acs.jctc.9b01129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Burton C. S.; Noyes W. A. Jr. Electronic Energy Relaxation in Toluene Vapor. J. Chem. Phys. 1968, 49, 1705–1714. 10.1063/1.1670297. [DOI] [Google Scholar]
  61. Ray J.; Ramesh S. G. Conical Intersections Involving the Lowest 1πσ* State in Aniline: Role of the NH2 Group. Chem. Phys. 2018, 515, 77–87. 10.1016/j.chemphys.2018.03.015. [DOI] [Google Scholar]
  62. Talrose V.; Stern E. B.; Goncharova A. A.; Messineva N. A.; Trusova N. V.; Efimkina M. V.. UV/Visible Spectra. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom P. J.; Mallard W. G. Eds.; National Institute of Standards and Technology: Gaithersburg MD, 2018, 20899. [Google Scholar]
  63. Sobolewski A. L.; Domcke W.; Dedonder-Lardeux C.; Jouvet C. Excited-State Hydrogen Detachment and Hydrogen Transfer Driven by Repulsive 1πσ* States: A New Paradigm for Nonradiative Decay in Aromatic Biomolecules. Phys. Chem. Chem. Phys. 2002, 4, 1093–1100. 10.1039/b110941n. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp1c01685_si_001.pdf (516.6KB, pdf)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES