Hierarchical Study of the Reactions of Hydrogen Atoms with Alkenes: A Theoretical Study of the Reactions of Hydrogen Atoms with C₂–C₄ Alkenes

Abstract

The present study complements our previous studies of the reactions of hydrogen atoms with C₅ alkene species including 1- and 2-pentene and the branched isomers (2-methyl-1-butene, 2-methyl-2-butene, and 3-methyl-1-butene), by studying the reactions of hydrogen atoms with C₂–C₄ alkenes (ethylene, propene, 1- and 2-butene, and isobutene). The aim of the current work is to develop a hierarchical set of rate constants for Ḣ atom addition reactions to C₂–C₅ alkenes, both linear and branched, which can be used in the development of chemical kinetic models. High-pressure limiting and pressure-dependent rate constants are calculated using the Rice–Ramsperger–Kassel–Marcus (RRKM) theory and a one-dimensional master equation (ME). Rate constant recommendations for Ḣ atom addition and abstraction reactions in addition to alkyl radical decomposition reactions are also proposed and provide a useful tool for use in mechanisms of larger alkenes for which calculations do not exist. Additionally, validation of our theoretical results with single-pulse shock-tube pyrolysis experiments is carried out. An improvement in species mole fraction predictions for alkene pyrolysis is observed, showing the relevance of the present study.

1. Introduction

Alkenes are important intermediates formed during the oxidation and pyrolysis of larger alkanes and are key components of hydrocarbon fuels. An understanding of their combustion chemistry is therefore important in our understanding of hydrocarbon fuel combustion. The reactions of Ḣ atom across the C=C double bond play an important role in controlling experimental high-temperature ignition delay times (IDTs), flame speeds, and species profiles measured as a function of temperature and/or time in jet-stirred and flow reactors.¹⁻³

In the current work, the reactions of Ḣ atoms with C₂–C₄ alkenes are studied, while the reactions of Ḣ atom addition to C₅ alkenes were studied previously.^4,5 There have been a number of theoretical and experimental studies of Ḣ atoms with C₂–C₄ alkenes.¹⁷⁻¹⁶ This study aims to complement these by providing a comprehensive hierarchical set of rate constants for Ḣ atom addition and abstraction potential energy surfaces (PESs), including their chemically activated pathways for C₂–C₅ alkenes, determined at the same levels of theory. By having a consistent set of rate constants for C₂–C₅ alkenes + Ḣ atoms calculated at the same level of theory, our results help constrain available models and the development of recommended rate constants, which provide a tool for use in mechanisms of larger alkenes for which calculations do not exist in the literature.

Ethylene is the smallest alkene in our series and has been extensively studied.^17,6−16 Miller and Klippenstein¹⁷ studied the kinetics of Ḣ + C₂H₂ and Ḣ + C₂H₄, including their reverse dissociation reactions using variational transition state theory (VTST) and a two-dimensional (2D) master equation. Matsugi¹⁶ performed direct trajectory calculations on Ċ₂H₅ radical dissociation and discovered a reaction pathway that directly eliminates H₂ from Ċ₂H₅, leading to the formation of vinyl (Ċ₂H₃) radicals. The resulting Ċ₂H₃ radicals can dissociate to C₂H₂ + Ḣ. They suggest that this may be an explanation for the unexpectedly slow Ḣ atom formation previously observed in photodissociation experiments of Ċ₂H₅ radicals.^21,22 Barker et al.⁶ studied the reaction of Ḣ + C₂H₄ as a function of He pressure at room temperature with three experimental techniques: (i) a discharge flow system with Lyman-α photometry, (ii) a time-resolved Lyman-α photometric system, and (iii) a discharge flow system with time-of-flight mass spectrometry. Rate constants were obtained in both excess ethylene and hydrogen environments, and an experimental value for the third-body recombination coefficient for Ḣ + ĊH₃ (+M) was obtained.

Michael et al.¹² used Lyman-α photometry to obtain the pressure dependence of the Ḣ + C₂H₄ reaction at room temperature. Through computer simulation analysis, the rate constants were adjusted for Ḣ atom depletion in reactions subsequent to the initial reaction. Experiments at high pressures of He permitted extrapolation to the high-pressure limiting rate constant. Lee et al.⁹ experimentally measured the rate constant for the Ḣ + C₂H₄ reaction as a function of temperature (198–320 K) at high pressures of Ar bath gas using the flash photolysis-resonance fluorescence technique. Sugawara et al.¹⁴ measured the high-pressure limiting rate constants of Ḣ and Ḋ atom addition to C₂H₄, C₂H₃D, C₂D₄, C₂H₂, and C₂D₂ in the temperature range 206–461 K using pulse radiolysis-resonance absorption.

Pacey et al.¹³ performed pyrolysis experiments on ethane at 902 K and concentrations of 1.8 × 10^–4–4.5 × 10^–3 mol L^–1 in a flow system. Rate constants for the reactions Ċ₂H₅ + Ċ₂H₅ ↔ C₄H₁₀ and Ċ₂H₅ + Ċ₂H₅ ↔ C₂H₆ + C₂H₄ were determined. Moreover, pressure-dependent rate constants for C₂H₆ ↔ ĊH₃ + ĊH₃ and Ċ₂H₅ ↔ C₂H₄ + Ḣ were determined using a unimolecular reaction rate theory. Lightfoot et al.¹⁰ measured the rate constant of the reaction Ḣ + C₂H₄ ↔ Ċ₂H₅ as a function of temperature and pressure, over the temperature and pressure ranges 285–604 K and 50–600 Torr, respectively, using laser flash photolysis/resonance fluorescence, with helium diluent.

Feng et al.⁷ investigated the unimolecular decomposition of Ċ₂H₅ radicals in helium over the temperature and pressure ranges 876–1094 K and 0.8–14.3 Torr, respectively, in time-resolved experiments. The reaction was isolated for a quantitative study in a heated tubular reactor coupled to a photoionization mass spectrometer. Hanning-Lee et al.⁸ studied the reaction Ḣ + C₂H₄ ↔ Ċ₂H₅ at 800 K in He. Exciplex laser flash photolysis at 193.3 nm of ethene–helium mixtures was used to generate Ḣ atoms, which were detected using time-resolved resonance fluorescence. Rate coefficients for the forward and reverse reactions were deduced from measurements of the equilibrium constant and relaxation rate coefficient at nine pressures in the range 97–600 Torr. More recently, Yang et al.¹⁵ investigated the decomposition of ethyl iodide and subsequent dissociation of ethyl radicals behind incident shock waves in a diaphragm-less shock tube using laser schlieren (LS) densitometry (1150 ≤ T ≤ 1870 K, and 55 ≤ p ≤ 123 ± 3 Torr).

Fewer studies exist for the reactions of Ḣ atoms with propene and the butene isomers. Experimental studies of Ḣ atoms with propene include refs (18−19, 23−32), with the most recent one by Chen et al.²⁰ studying the temperature and pressure dependence of the product branching ratio of the Ḣ + propene reaction. This was done behind reflected shock waves in a diaphragm-less shock tube using the Ḣ-ARAS technique in the temperature range 1065–1306 K at 1 and 2 bar. Quantum chemistry calculations were also performed at the CCSD(T)/CBS//CCSD/6-311++G(3df,2p) level of theory. The predicted high-pressure limiting rate constant ratio for terminal versus nonterminal addition agrees well with that reported by Manion et al.¹⁹ for the analogous reaction of Ḣ atoms with butene. Both Chen et al.²⁰ and Manion et al.¹⁹ state that their predicted branching ratio for terminal versus nonterminal addition differ from that calculated by Miller and Klippenstein who studied the dissociation of propyl radicals and other reactions on the Ċ₃H₇ PES.¹⁸ With minor adjustments to several of the barrier heights, Miller and Klippenstein showed excellent agreement between their theoretical values and experimental results available in the literature over a wide range of conditions.

Manion and Awan¹⁹ investigated the kinetics of terminal and internal Ḣ atom addition to 1-alkenes. Single-pulse shock tube methods were employed to thermally generate Ḣ atoms, and their reactions with 1-butene were investigated over the temperature and pressure ranges 880–1120 K and 145–245 kPa, respectively. Relative and absolute rate constants for the displacement of methyl and ethyl radicals by Ḣ atoms were determined and related to the high-pressure limiting rate constant for Ḣ atom addition to the terminal and internal sites of 1-butene. It was found that addition to the terminal site is favored by a factor of 2.6 ± 0.4 at 1000 K. These results were combined with data from lower temperatures and used by Manion and Awan to derive rate constants in the temperature range 220–2000 K. They state that these branching ratio expressions should approximate the behavior of other unbranched 1-olefins and can thus be used as estimates for unstudied 1-olefins in detailed kinetic models describing pyrolysis and combustion conditions. A factor of 3 discrepancy was noted in the branching ratio for terminal to internal Ḣ atom addition by comparing their current experimental results with the theoretical study,¹⁸ and they suggest that the difference observed is well outside the experimental errors of their study and any expected differences for 1-butene.

Wang et al.³³ studied the reaction kinetics of H-atom abstraction from C₄–C₆ alkenes by Ḣ atoms and ĊH₃ radicals using the G4 composite method with CTST and Eckart tunneling corrections. The study provides the first systematic report on the key initiation abstraction reaction classes for alkenes with Ḣ atoms and ĊH₃ radicals. However, large discrepancies are observed between the Wang et al.³³ calculations and those already present in the literature and calculated in this work.

Nagaraja et al.³² performed a single-pulse shock-tube study on the pyrolysis of 2% C₂–C₆ 1-alkenes at 2 bar in the temperature range 900–1800 K, with reactant intermediate and product species obtained and quantified using gas chromatography–mass spectrometry analysis.

One of the aims of the present study is to investigate the ratio of terminal to internal Ḣ atom addition to C₂–C₅ alkenes taking into account our past studies^4,5 of the C₅ alkenes since discrepancies remain in the literature. Rate constant recommendations for Ḣ atom addition, abstraction, and alkyl radical decomposition reactions will also be made and should serve as a useful tool for their use in mechanisms for larger alkenes where calculations do not exist.

Section 2 describes the computational methods employed in the current work, and Section 3 presents the theoretical results including comparisons with literature studies, where available (Table 1). Section 4.0 presents our simulation results compared to the shock tube pyrolysis experiments of Nagaraja et al.^32,35

Table 1. Summary of Experimental and Theoretical Studies Relevant to C₂–C₄ Alkenes + Ḣ.

year	author	reaction(s)	T (K)	p (kPa)	method
2020	Nagaraja et al.32	pyrolysis of C2–C6 1-alkenes	900–1800	200	single-pulse shock tube (SPST)
2020	Chen et al.20	Ḣ + C3H6	1065–1306	100–200	Ḣ-ARAS/shock-tube CCSD(T)/CBS//CCSD/6-311++G(3df,2p)
2018	Wang et al.33	C4–C6 alkenes + Ḣ and ĊH3			G4 composite method
2015	Manion et al.19	Ḣ + C4H8-1	880–1120	145–245	single-pulse shock tube (SPST)
2013	Matsugi et al.16	photodissociation of Ċ2H5			direct trajectory calculations ωB97X-D/6-31+G(d,p)
2013	Miller et al.18	dissociation of propyl radicals and other reactions on Ċ3H7 potential		0–HPL	CCSD(T)/cc-pVTZ MP2/6-311++G(d,p)
2012	Yang et al.15	decomposition of ethyl iodide/dissociation of Ċ2H5 radicals	1150–1870	7.3–16.4	diaphragm-less shock tube/laser schlieren (LS) densitometry
2011	Rosado-Reyes et al.28	Ḣ + C3H6	922–1200	150–340	single-pulse shock tube (SPST)
2004	Miller et al.17	Ḣ + C2H2 and C2H4	300–2000	>0.13/HPL	variational transition state theory (VTST), 2D master equation
1993	Hanning-Lee et al.8	Ḣ + C2H4	800	12.9–80.0	exciplex laser flash photolysis/time-resolved resonance fluorescence
1993	Feng et al.7	unimolecular decomposition of Ċ2H5	876–1094	0.1–1.9	heated tubular reactor/to a photoionization mass spectrometer
1993	Seakins et al.23	iĊ3H7 decomposition	720–910		laser flash photolysis/photoionization mass spectrometry
1992	Tsang36	database for hydrocarbon pyrolysis			estimate
1992	Hidaka et al.29	thermal decomposition of C3H6	1200–1800		laser kinetic absorption spectroscopy/GC
1991	Tsang37	database for hydrocarbon pyrolysis			estimate
1989	Löser et al.30	Ḣ atom abstraction by allyl radicals from hydrocarbons			BSBL
1987	Lightfoot et al.10	Ḣ + C2H4	285–604	6.7–80.0	laser flash photolysis/resonance fluorescence
1986	Munk et al.25	iĊ3H7 and iĊ3H7O2	298	101	UV absorption/pulse photolysis
1984	Pacey et al.13	pyrolysis of C2H6	902	HPL	flow system
1982	Watanabe et al.27	Ḣ + C3H6	200–500		pulse radiolysis-resonance absorption
1982	Harris et al.31	Ḣ + C3H6/C4H8	298–455		flash photolysis-resonance fluorescence
1981	Sugawara et al.14	Ḣ- and D-atom addition to C2H4, C2H3D, C2D4, C2H2, and C2D2	206–461		pulse radiolysis-resonance absorption
1978	Lee et al.9	Ḣ + C2H4	198–320	0.13	flash photolysis-resonance fluorescence (FP-RF) technique
1973	Michael et al.12	Ḣ + C2H4			Lyman α photometry
1972	Kerr et al.24	evaluated kinetic data on gas-phase addition reactions
1971	Kurylo et al.26	Ḣ + C3H6	298		resonance fluorescence of Lyman α radiation
1970	Barker et al.6	Ḣ + C2H4			discharge flow system with Lyman-α photometry, time-resolved Lyman-α photometric system, and discharge flow system with time-of-flight mass spectrometry

2. Computational Details

2.1. Electronic Structure Calculations

As mentioned earlier, we have employed the same methods here as those used in our previous studies^4,5 to carry out all electronic structure calculations; thus, the description here is brief. All calculations carried out using Gaussian 09³⁸ and Gaussian 16³⁹ conformational searches were performed, with the resulting lowest-energy conformer optimized at the ωB97XD⁴⁰/aug-cc-pVTZ⁴¹ level of theory. A harmonic frequency analysis was simultaneously performed at the same level of theory to verify the nature of each stationary point.

Low-frequency torsional modes were treated via relaxed PES scans in 10° increments with the ωB97XD/6-311++G(d,p)⁴⁰ method, with the potential energies as a function of dihedral angle used as input for a one-dimensional (1D) hindered rotor approximation as implemented in the Master Equation System Solver (MESS).⁴²

To compute reaction barrier heights, single point energies for minima and transition states were calculated at the CCSD(T)/cc-pVXZ and MP2/cc-pVXZ (where X = D, T, and Q) levels of theory. The resulting energies were extrapolated to the complete basis set (CBS) limit using the following formula (eq 1):^43,44

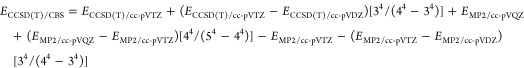1

The T₁ diagnostic for minima and transition state species is ≲ 0.03, indicating that single reference methods to describe the wave function are appropriate.⁴³ However, for the Ċ₂H₃ radical well and the transition states of Ḣ atom addition to and abstraction from C₂H₄, the T₁ diagnostics are 0.04, 0.038, and 0.352, respectively. As a result, for the C₂ and C₃ reaction systems, ROCCSD(T)/aug-cc-pVXZ (where X = T and Q) single point energies were also calculated since they were computationally achievable. The energies were extrapolated to the CBS limit using eq 2:

2

with the resulting T₁ diagnostics falling below 0.03. The largest difference in energy barriers as a result of using the two formulas was for H-atom abstraction from the primary vinylic sites of C₂H₄ and C₃H₆, where differences of 1.57 and 1.39 kJ mol^–1, respectively, were observed. These differences in energy barriers increased the rate constants for these reactions by factors of 1.87 and 1.71 at 298 K.

2.2. Thermochemistry

The methods employed to calculate the thermochemical parameters of species are identical to those used in our previous studies,^4,5 with 0 K formation enthalpies determined via the isodesmic approach using the most recent ATcT values for the molecular and radical chaperones, and uncertainties computed using methods described by Simmie et al.⁴⁵ Temperature-dependent enthalpies, entropies, and heat capacities were calculated using traditional statistical thermodynamic methods as implemented in MESSPF,⁴² with Chemkin format polynomials fitted using PAC99,⁴⁶ and are provided as Supporting Information (SI).

2.3. Transition State Theory (TST), Rice–Ramsperger–Kassel–Marcus (RRKM), and Master Equation (ME) Calculations

High-pressure limiting and pressure-dependent rate constants were calculated for the C₂–C₄ PESs using RRKM/ME as implemented in MESS,⁴² in which tunneling is accounted for via an asymmetric Eckart model.⁴⁷ To model collisional energy transfer, a single exponential down model was used and is estimated to be ⟨ΔE_down(T)⟩ = 75 × (T/300)^1.05 cm^–1 for the Ċ₂H₅ PES¹⁷ and ⟨ΔE_down(T)⟩ = 200 × (T/300)^0.75 cm^–1 for the Ċ₃H₇ and Ċ₄H₉ PESs.⁴⁸⁻⁵¹

3. Theoretical Results

3.1. Thermochemistry

Table 2 presents formation enthalpies, along with their 2σ uncertainties computed via isodesmic and atomization methods. Also presented are ATcT,^52,53 ANL0,⁵⁴ and ANL1⁵⁴ formation enthalpies with 2σ uncertainties. The current study uses the most recent ATcT values for the molecular and radical chaperones.^52,53 Similar to previous work,^4,5 ATcT, ANL0, and ANL1 formation enthalpies do not exist for the species Ċ₄H₇-11, Ċ₄H₇-12, Ċ₄H₇-13, Ċ₄H₇-14, Ċ₄H₇-22, iĊ₄H₇, and iĊ₄H₇-i1. Quantum chemical composite methods (CBS–QB3, CBS–APNO, G3, and G4)⁵⁵⁻⁵⁷ were therefore used to calculate their formation enthalpies at 0 K via isodesmic reactions suitable for each species, using ATcT values as chaperones.

Table 2. Formation Enthalpies and Uncertainties (2σ) Computed via Isodesmic and Atomization Methods, together with ATcT, ANL0, and ANL1 Formation Enthalpies and Uncertainties.

species	isodesmic (0 K, kJ mol–1)	isodesmic (2σ)	atomization (0 K, kJ mol–1)	atomization (2σ)	ATcT52,53 (0 K, kJ mol–1)	ANL054	ANL154	Burcat58 (0 K, kJ mol–1)
C2H4	60.60	0.45	61.36	3.85	60.88	60.20	60.20	61.03
Ċ2H5	131.65	0.74	131.06	6.65	131.06	131.30	131.00	130.77
Ċ2H3	301.49	0.96	301.26	5.41	301.13	300.90	300.50	300.87
C3H6	35.03	0.36	35.85	7.33	34.93	34.50		35.01
nĊ3H7	117.78	0.66	118.15	9.75	118.34	118.20		119.15
iĊ3H7	105.33	0.92	105.71	9.63	105.32	105.10		108.24
Ċ3H5-s	277.86	0.87	278.38	7.53	278.22	278.40		276.29
Ċ3H5-t	262.28	0.95	262.80	6.86	262.98	263.00
Ċ3H5-a	177.44	2.00	179.03	6.69	180.03	179.60		180.40
C4H8-1	21.15	0.20	22.40	10.66	21.00	21.30		20.82
C4H8-2	9.40	0.25	10.63	10.86	9.38	9.60		9.39
Ċ4H9-1	102.20	0.77	102.52	13.08	102.74	103.20		105.91
Ċ4H9-2	90.76	0.74	91.55	12.82	90.84	90.90		94.95
Ċ4H7-11	263.61	0.79	263.97	10.27				262.76
Ċ4H7-12	248.88	0.81	249.16	9.84				248.45
Ċ4H7-13	152.70	0.81	152.04	9.48				153.55
Ċ4H7-14	222.83	0.77	224.34	12.26				220.92
Ċ4H7-22	239.46	1.24	240.21	9.97				239.74
iC4H8	3.61	0.31	5.19	10.72	4.01	4.20		3.46
iĊ4H9	96.14	0.73	96.38	12.91	97.17			97.92
tĊ4H9	73.86	0.73	75.31	13.23	75.60			79.72
iĊ4H7	153.25	0.81	153.73	9.49				155.27
iĊ4H7-i1	250.60	0.70	251.18	10.45

Excellent agreement is observed between this work and the ATcT^52,53 values, with differences, expressed as mean absolute error (MAE ± 2σ), being on average 0.59 ± 1.38 kJ mol^–1. Differences between this work and ANL0⁵⁴ and ANL1⁵⁴ computations are on average 0.57 ± 1.03 and 0.68 ± 0.60 kJ mol^–1, respectively. Differences between this work and Burcat⁵⁸ are slightly higher at 1.58 ± 3.2 kJ mol^–1. Comparisons between isodesmic and atomization values calculated in the current work are in excellent agreement, with an MAE of 0.76 ± 0.93 kJ mol^–1. As discussed in our previous work,^4,5 although the isodesmic and atomization methods give similar nominal 0 K heats of formation, the isodesmic method is often used to achieve “chemical accuracy”. Our computed final heat of formation uncertainties for the isodesmic reactions are between 0.36 and 2.00 kJ mol^–1.

Table 3 presents 298 K formation enthalpies between this work and literature data, with the results generally in good agreement. Differences between this work and Goldsmith⁴³ are on average 1.56 ± 2.61 kJ mol^–1. Excellent agreement is observed between this work and ATcT, with an MAE of 0.76 ± 1.43 kJ mol^–1. The values reported by Burcat⁵⁸ are within 2.01 ± 5.90 kJ mol^–1 of this work.

Table 3. Comparisons of the Formation Enthalpies Computed in This Work with Literature Data.

species	ΔfH298K (this work)	ΔfH298K (Goldsmith)43	ΔfH298K (ATcT)52,53	ΔfH298K (Burcat)58
C2H4	51.99	52.30	52.36	52.50
Ċ2H5	120.61	120.92	119.99	119.70
Ċ2H3	297.29	297.90	296.93	296.58
C3H6	19.88	19.25	19.93	20.00
nĊ3H7	100.23	101.67	100.94	101.32
iĊ3H7	87.92	88.70	88.45	90.19
Ċ3H5-s	267.07	268.19	267.38	265.53
Ċ3H5-t	251.79	253.13	252.58	237.65
Ċ3H5-a	165.55	169.87	168.31	168.60
C4H8-1	–0.21	–0.00	0.05	–0.03
C4H8-2	–11.30	–11.30	–11.18	–11.19
Ċ4H9-1	78.86	80.75	80.23	81.80
Ċ4H9-2	68.02	69.45	66.07	70.22
Ċ4H7-11	246.82	248.11		245.87
Ċ4H7-12	232.66			231.16
Ċ4H7-13	135.21	137.65		136.11
Ċ4H7-14	206.50	208.36		204.60
Ċ4H7-22	223.32	225.10		223.85
iC4H8	–17.60	–17.15	–17.05	–17.57
iĊ4H9	72.29	74.48	73.18	73.79
tĊ4H9	50.77	54.39	50.30	55.04
iĊ4H7	134.68	139.32		137.60
iĊ4H7-i1	233.84

Table 4 presents comparisons of entropies calculated in this work and the literature, with differences being larger than those observed for the enthalpies. Differences between Goldsmith⁴³ and this work are on average 1.13 ± 3.72 J K^–1 mol^–1, while differences between those recommended by Burcat⁵⁸ and calculated here are on average 5.09 ± 11.64 J K^–1 mol^–1. In the case of iĊ₃H₇, the lowest-energy conformer has Cs symmetry, with an assigned symmetry factor of 1. If it is assumed that the symmetry factor of iĊ₃H₇ is 2, the entropy value drops from 295.05 to 289.29 J K^–1 mol^–1, which is now only 1.01 J K^–1 mol^–1 larger than the value computed by Goldsmith and 0.82 J K^–1 mol^–1 lower than that by Burcat.⁵⁸ For the Ċ₄H₇-14 radical, our computed entropy is 5.91 and 4.45 J K^–1 mol^–1 larger than Goldsmith⁴³ and Burcat,⁵⁸ respectively. However, Goldsmith⁴³ reports an uncertainty of 5.86 J K^–1 mol^–1 for their reported entropy for Ċ₄H₇-14, and our value falls within this range.

Table 4. Comparisons of Entropies Computed in This Work with Literature Data.

species	S298K (this work)	S298K (Goldsmith)43	S298K (Burcat)58
C2H4	218.66	218.82	219.32
Ċ2H5	247.38	247.27	242.98
Ċ2H3	233.38	233.47	233.66
C3H6	266.10	266.10	266.66
nĊ3H7	289.91	289.95	290.46
iĊ3H7	295.05	288.28	290.11
Ċ3H5-s	271.27	271.54	271.31
Ċ3H5-t	273.48	273.63	266.06
Ċ3H5-a	257.07	257.32	257.88
C4H8-1	307.77	306.27	305.37
C4H8-2	295.67	295.81	296.33
Ċ4H9-1	331.26	328.44	307.63
Ċ4H9-2	331.85	330.54	327.42
Ċ4H7-11	312.91	311.71	311.28
Ċ4H7-12	315.08		300.37
Ċ4H7-13	300.56	301.25	306.09
Ċ4H7-14	321.80	315.89	317.35
Ċ4H7-22	310.77	311.28	313.26
iC4H8	293.21	293.72	287.45
iĊ4H9	319.07	319.66	304.66
tĊ4H9	318.97	318.82	323.39
iĊ4H7	293.08	293.72	300.80
iĊ4H7-i1	305.54

Table 5 presents heat capacities for the C₂–C₄ species calculated in this work, by Goldsmith⁴³ and present in the Burcat database.⁵⁸ A good agreement is observed, with an MAE of 1.69 ± 1.5 J mol^–1 K^–1 observed between this work and Goldsmith.⁴³ Differences between this work and the Burcat database⁵⁸ are slightly higher, with an MAE of 1.87 ± 3.36 J K^–1 mol^–1.

Table 5. Comparisons of Heat Capacities Computed Here with Literature Data.

	Cp
species	study	300	400	500	600	800	1000	1500
C2H4	this work	42.04	51.22	60.64	69.19	82.07	92.25	108.54
	Goldsmith43	42.68	52.30	61.50	69.87	82.84	92.88	109.20
	Burcat58	43.05	52.64	62.27	70.93	83.89	94.09	109.58
Ċ2H5	this work	50.83	60.85	70.92	80.13	94.66	106.31	125.31
	Goldsmith43	51.46	61.92	71.96	80.75	95.40	107.11	125.94
	Burcat58	50.86	61.26	71.64	81.13	96.05	107.91	126.21
Ċ2H3	this work	43.02	50.42	57.32	63.28	72.12	79.19	90.65
	Goldsmith43	43.51	51.46	58.16	63.60	72.80	79.50	91.21
	Burcat58	42.20	49.42	56.30	62.33	71.37	78.58	89.98
C3H6	this work	62.80	77.74	92.34	105.50	125.94	141.81	166.99
	Goldsmith43	64.43	79.91	94.56	107.11	127.61	143.09	168.20
	Burcat58	64.71	80.19	95.03	108.28	128.79	144.61	168.44
nĊ3H7	this work	71.53	88.04	103.86	117.96	139.72	156.80	184.17
	Goldsmith43	72.38	89.96	105.86	119.24	141.42	158.16	185.35
	Burcat58	71.61	88.44	104.39	118.52	140.27	157.27	183.71
iĊ3H7	this work	67.68	83.16	99.11	113.83	136.88	154.91	183.44
	Goldsmith43	68.62	84.94	100.83	115.06	138.49	156.06	184.51
	Burcat58	65.81	81.67	97.76	112.60	136.04	154.33	182.33
Ċ3H5-s	this work	62.51	75.45	87.65	98.44	115.11	128.06	148.67
	Goldsmith43	64.02	77.40	89.54	99.58	116.32	129.29	149.37
	Burcat58	63.63	76.53	88.46	98.97	115.47	128.30	148.22
Ċ3H5-t	this work	61.98	74.30	86.40	97.33	114.35	127.61	148.57
	Goldsmith43	63.18	76.15	87.86	98.74	115.90	128.87	149.37
	Burcat58	61.94	76.98	90.79	102.80	121.04	134.95	155.57
Ċ3H5-a	this work	61.33	76.91	90.74	102.38	119.28	132.16	152.54
	Goldsmith43	62.34	78.24	92.05	102.93	120.08	133.05	153.13
	Burcat58	62.12	77.74	91.51	103.04	119.77	132.52	152.17
C4H8-1	this work	84.31	105.66	125.90	143.81	171.31	192.50	225.95
	Goldsmith43	87.03	109.20	129.29	146.44	173.64	194.56	227.61
	Burcat58	85.96	106.28	126.08	144.16	173.16	195.04	227.47
C4H8-2	this work	85.63	105.06	124.29	141.89	169.82	191.32	225.43
	Goldsmith43	88.28	108.78	127.61	144.77	172.38	193.30	226.77
	Burcat58	88.03	108.22	127.84	145.62	173.80	195.38	227.77
Ċ4H9-1	this work	93.56	116.39	137.92	156.88	185.81	208.19	243.65
	Goldsmith43	96.23	119.24	140.58	158.57	187.86	210.04	245.18
	Burcat58	94.98	118.67	140.97	160.63	190.76	213.94	249.44
Ċ4H9-2	this work	90.04	111.14	132.42	151.82	181.88	205.36	242.30
	Goldsmith43	91.63	113.80	135.14	153.97	184.10	207.53	243.93
	Burcat58	86.79	109.43	131.47	151.27	181.88	205.47	241.32
Ċ4H7-11	this work	84.17	103.50	121.34	136.89	160.62	178.88	207.72
	Goldsmith43	86.19	106.27	123.85	138.91	162.34	180.33	208.78
	Burcat58	84.05	103.05	120.71	136.20	160.05	178.45	206.63
Ċ4H7-12	this work	83.70	102.27	120.04	135.77	159.75	178.27	207.41
	Goldsmith43
	Burcat58	84.33	103.88	121.97	137.87	162.53	181.46	210.28
Ċ4H7-13	this work	81.56	101.65	120.62	137.24	162.13	181.10	210.74
	Goldsmith43	83.26	103.76	122.59	138.49	163.59	182.42	211.71
	Burcat58	81.15	101.15	120.07	136.69	161.70	180.78	209.69
Ċ4H7-14	this work	83.27	102.21	120.16	135.94	159.76	178.10	207.05
	Goldsmith43	86.61	105.86	123.43	138.49	161.92	179.91	208.36
	Burcat58	85.14	104.57	122.89	138.96	163.17	181.76	210.14
Ċ4H7-22	this work	83.12	99.93	116.93	132.58	157.36	176.52	206.64
	Goldsmith43	84.94	102.81	119.24	134.31	158.41	178.24	207.94
	Burcat58	83.51	99.85	116.58	132.13	157.01	176.30	205.65
iC4H8	this work	86.01	106.46	125.84	143.20	170.72	191.87	225.62
	Goldsmith43	88.28	109.20	128.87	145.60	172.80	193.72	227.19
	Burcat58	86.44	109.53	130.81	149.22	176.71	197.59	228.66
iĊ4H9	this work	95.21	118.37	139.73	158.34	186.70	208.68	243.73
	Goldsmith43	96.65	120.92	142.26	160.25	188.70	210.46	245.18
	Burcat58	98.56	122.36	143.90	162.52	191.01	212.96	246.99
tĊ4H9	this work	88.45	108.45	129.49	149.13	180.04	204.10	241.76
	Goldsmith43	90.79	111.29	132.21	151.04	182.00	205.85	243.09
	Burcat58	82.78	104.42	126.31	146.47	178.31	202.90	240.05
iĊ4H7	this work	80.50	102.35	121.72	138.17	162.72	181.35	210.69
	Goldsmith43	82.01	104.18	123.43	139.33	164.01	182.42	211.71
	Burcat58	82.59	103.51	122.32	138.44	162.74	181.30	209.76
iĊ4H7-i1	this work	85.77	103.91	120.75	135.71	159.46	177.78	207.03
	Goldsmith43
	Burcat58

3.2. Reactions of Ḣ atoms with C₂H₄, C₃H₆, C₄H₈-1, C₄H₈-2, and iC₄H₈

Figure 1 compares the high-pressure limiting rate constants (Table 6) for (a) ethylene + Ḣ, (b) propene + Ḣ, (c) isobutene + Ḣ, and (d) 1- and 2-butene + Ḣ. Hydrogen atom addition to, and abstraction from, ethylene have computed energy barriers of 11.2 and 63.1 kJ mol^–1, respectively. Terminal Ḣ atom addition to propene has a computed energy barrier of 8.4 kJ mol^–1, which is 7.2 kJ mol^–1 lower than that for internal addition. As expected, Ḣ atom abstraction from the primary allylic site of propene is favored, with an energy barrier of 31.1 kJ mol^–1. Abstraction of the two Ḣ atoms on the primary vinylic site have similar barriers of 63.7 and 64.6 kJ mol^–1, leading to cis- and trans-configurations of Ċ₃H₅-s, respectively. Terminal Ḣ atom addition to isobutene forming the tertiary tĊ₄H₉ radical has a computed barrier of 6.1 kJ mol^–1, which is 15.0 kJ mol^–1 lower than internal addition forming the primary iĊ₄H₉ radical. Abstraction from the primary allylic site has a computed barrier of 30.5 kJ mol^–1. Terminal and internal Ḣ atom addition can exist for 1-butene, with respective barriers of 9.3 and 16.0 kJ mol^–1, while abstraction from the primary allylic site has a barrier of 22.85 kJ mol^–1. Internal addition to 2-butene and abstraction from the primary allylic site have respective barriers of 12.5 and 33.5 kJ mol^–1.

Figure 1.

High-pressure limiting rate constants for the reactions of (a) ethylene + Ḣ, (b) propene + Ḣ, (c) isobutene + Ḣ, and (d) 1- and 2-butene + Ḣ.

Table 6. Computed Energy Barriers, Heats of Reaction, and High-Pressure Limiting Rate Constant (298–2000 K) for the Reactions of Ḣ Atoms with C₂–C₄ Alkenes^a.

		reaction	Δ⧧H0K	ΔrH0K	A	n	Ea
C2	R1	C2H4 + Ḣ ↔ Ċ2H5	11.18	–146.48	1.15 × 1015	–0.41	14.73
	R2	C2H4 + Ḣ ↔ Ċ2H3 + H2	63.12	24.09	4.79 × 1005	2.55	51.77
C3	R3	C3H6 + Ḣ ↔ nĊ3H7	15.61	–132.97	6.25 × 1015	–0.73	19.34
	R4	C3H6 + Ḣ ↔ iĊ3H7	8.39	–146.83	1.02 × 1014	–0.03	11.43
	R5	C3H6 + Ḣ ↔ Ċ3H5-s + H2	63.97	27.14	1.21 × 1006	2.43	53.96
	R6	C3H6 + Ḣ ↔ Ċ3H5-t + H2	51.95	12.04	3.11 × 1005	2.51	40.36
	R7	C3H6 + Ḣ ↔ Ċ3H5-a + H2	31.09	–71.88	6.97 × 1002	3.24	13.93
C4	R8	C4H8-1 + Ḣ ↔ Ċ4H9-1	16.04	–136.49	2.23 × 1014	–0.27	18.47
	R9	C4H8-1 + Ḣ ↔ Ċ4H9-2	9.32	–147.65	6.06 × 1015	–0.60	14.59
	R10	C4H8-2 + Ḣ ↔ Ċ4H9-2	12.52	–136.08	1.56 × 1015	–0.42	15.68
	R11	C4H8-1 + Ḣ ↔ Ċ4H7-11 + H2	64.81	27.38	2.01 × 1006	2.44	54.53
	R12	C4H8-1 + Ḣ ↔ Ċ4H7-12 + H2	52.29	13.06	2.11 × 1005	2.54	40.67
	R13	C4H8-1 + Ḣ ↔ Ċ4H7-13 + H2	22.85	–82.85	2.37 × 1005	2.56	12.24
	R14	C4H8-1 + Ḣ ↔ Ċ4H7-14 + H2	42.70	–14.76	1.23 × 1005	2.71	29.03
	R15	C4H8-2 + Ḣ ↔ Ċ4H7-13 + H2	33.51	–69.77	2.60 × 1004	2.95	15.36
	R16	C4H8-2 + Ḣ ↔ Ċ4H7-22 + H2	54.25	15.91	1.21 × 1004	2.41	43.19
	R17	iC4H8 + Ḣ ↔ iĊ4H9	21.15	–124.43	9.67 × 1013	–0.21	22.08
	R18	iC4H8 + Ḣ ↔ tĊ4H9	6.13	–145.60	7.89 × 1015	–0.53	11.98
	R19	iC4H8 + Ḣ ↔ iĊ4H7 + H2	30.50	–63.73	4.45 × 1003	3.08	14.81
	R20	iC4H8 + Ḣ ↔ iĊ4H7-i1 + H2	66.75	32.19	2.60 × 1006	2.34	57.34

^aUnits (ATⁿ = cm³ mol^–1 s^–1, energies kJ mol^–1).

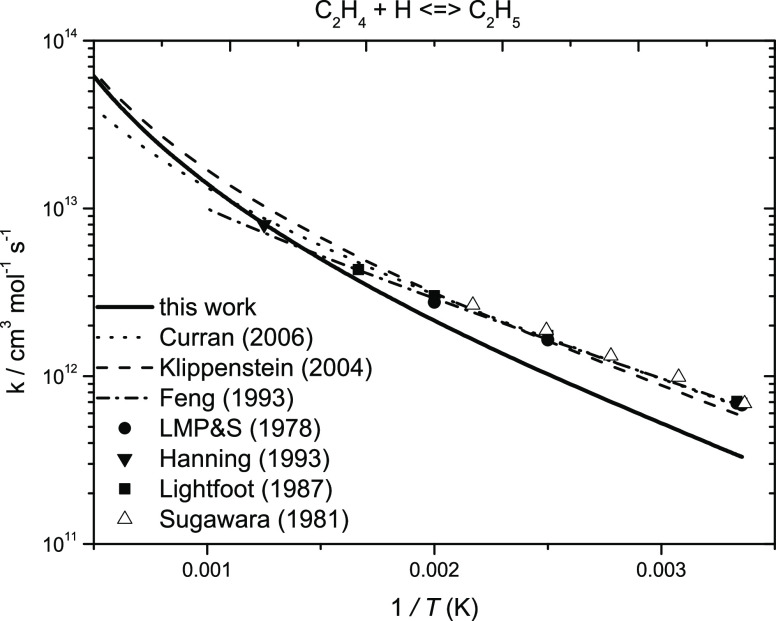
Figure 2 compares theoretical and experimental data^8−10,14 for the reaction C₂H₄ + Ḣ ↔ Ċ₂H₅. Also plotted is the rate constant recommendation from Curran et al.⁵⁹ and the transition state theory fit to the experiments by Feng et al.,⁷ with a good agreement being observed. The largest difference observed between the current work and Miller and Klippenstein¹⁷ is a factor of 1.75 at 300 K. The difference in energy barrier of 0.54 kJ mol^–1 and the quoted uncertainty of their fits to replicate the master equation results of ±20%, which would account for an accumulative difference of ∼1.5.

Figure 2.

High-pressure limiting rate constant comparisons for the reactions of Ḣ atom addition with ethylene. The solid line represents the current work (ROCCSD(T)/aug-cc-pVXZ); dotted line, Curran;⁵⁹ dashed line, Miller and Klippenstein;¹⁷ dashed-dotted line, Feng et al.⁷ and Lee et al.;⁹ ▲, Hanning-Lee et al.;⁸ ■, Lightfoot et al.;¹⁰ and △, Sugawara et al.¹⁴

Figure 3 presents high-pressure limiting rate constant comparisons for the Ḣ atom addition reactions to propene. A relatively good agreement is observed between the current work and theory and experiments from the literature. To improve agreement with experiment, Miller and Klippenstein¹⁸ altered some reaction barriers, including those for terminal and internal H-atom addition and H-atom abstraction from the primary allylic site of propene. The adjusted rate constant for internal addition to propene (red) is in excellent agreement with the one calculated in the current work, and the adjusted energy barrier of 15.5 kJ mol^–1 is almost identical to 15.6 kJ mol^–1 calculated in the current work, as shown in Table 6. The rate constant for terminal addition (black) is approximately a factor of 2 faster than that calculated here. However, as mentioned by Chen et al.,²⁰ the higher values reported by Miller and Klippenstein may be attributed to input data errors. An error in symmetry number affects the energy barriers and pressure-dependent rate constant expressions. If the effect of symmetry reduced the rate constant by a factor of ∼1.5 (dashed blue line, Figure 3), it would be in good agreement with that calculated here.

Figure 3.

High-pressure limiting rate constant comparisons for the reactions of Ḣ atom addition to propene. Solid lines represent the current work (ROCCSD(T)/aug-cc-pVXZ); dotted lines, Curran;⁵⁹ dashed lines, Miller and Klippenstein;¹⁸ dashed-dotted lines, Chen;²⁰ ■, Seakins et al.;²³ △, Watanabe et al.;²⁷ ○, Kurylo et al.;²⁶ ◀, Harris et al.;³¹ and □, Kerr et al.²⁴

The rate constants reported by Chen et al.²⁰ are within a factor of 2 of the current work over the temperature range 298–2000 K. Differences in energy barriers computed in this work and that by Chen are 3.01 and 2.49 kJ mol^–1 for nonterminal addition and terminal addition, respectively. The recommendations by Curran et al.⁵⁹ are in good agreement at T < 800 K, but differences become larger at higher temperatures, with a factor of ∼5 discrepancy observed at 2000 K.

Figure 4 presents the temperature and pressure dependencies of the product branching ratios for Ḣ atom addition to propene in the temperature range 298–2000 K and at pressures of 0.1, 1.0, 10, 100, and 1000 atm. At 0.1 atm, Ḣ atom addition to propene forming iĊ₃H₇ radicals is favored at temperatures up to 800 K, until the formation of C₂H₄ and ĊH₃ dominates. For pressures of 1.0, 10, and 100 atm, the formation of iĊ₃H₇ is favored at temperatures up to ∼1000, 1200, and 1500 K, respectively.

Figure 4.

Temperature- and pressure-dependent branching ratios for propene + Ḣ via hydrogen atom addition reactions at 0.1 (short-dotted lines), 1 (short-dashed lines), 10 (dotted lines), 100 (dashed lines), and 1000 (solid lines) atm.

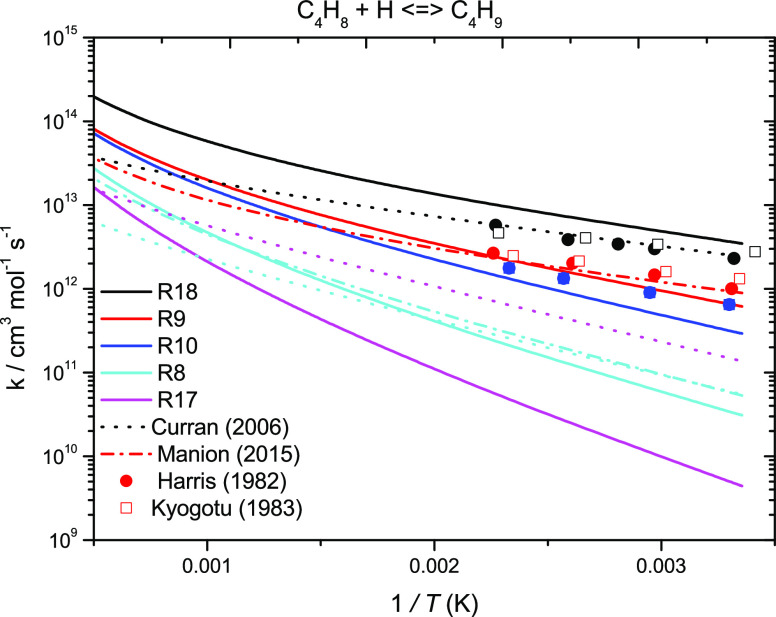
Figure 5 presents high-pressure limiting rate constant comparisons for the reactions of Ḣ atom addition to the butene isomers. Larger differences are observed for the reactions of Ḣ atoms with C₄ alkenes calculated here and in the literature. For terminal addition to 1-butene, the rate constants determined by Manion et al.¹⁹ and in this work are within a factor of ∼2.22 over the temperature range 298–2000 K. The rate constants for internal addition to 1-butene are in excellent agreement and are within a factor of ∼1.3. Additionally, the current calculations are in relatively good agreement with the experimental data by Kyogutu et al.⁶⁰ and Harris et al.³¹ For terminal addition to isobutene, the recommendations by Curran et al.⁵⁹ are again in good agreement at lower temperatures, but there is a larger deviation of a factor of 5 observed at 2000 K. The largest difference is observed for internal addition to isobutene. However, the difference in rate constants calculated in the current work for internal addition to 1-butene and isobutene is consistent with the difference in the computed barrier heights of 5.1 kJ mol^–1, accounting for the factor of 7 discrepancy at low temperatures. Curran’s recommendation is a factor of ∼30 times faster at 298 K. The rate constant recommendation used is 2.5 times the recommendation used for internal addition to propene. However, it was found that our calculation for internal addition to propene is ∼10 times faster than that to isobutene at 298 K, which can be attributed to the energy barrier for internal addition to propene being ∼5.54 kJ mol^–1 lower than that for isobutene.

Figure 5.

High-pressure limiting rate constant comparisons for the reactions of Ḣ atom addition to the butene isomers. Solid lines represent the current work (ROCCSD(T)/aug-cc-pVXZ); dotted lines, Curran;⁵⁹ dash-dotted lines, Manion et al.;¹⁹ red color solid circle, Harris et al.;³¹ and red color square, Kyogotu et al.⁶⁰

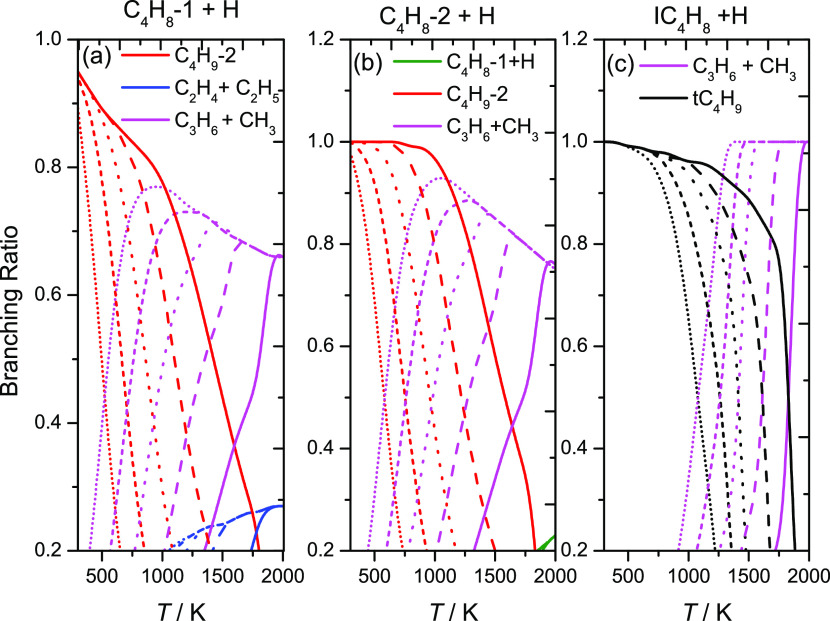
Figure 6 shows the temperature and pressure dependencies of the product branching ratios for Ḣ atom addition to (a) 1-butene, (b) 2-butene, and (c) isobutene in the temperature range 298–2000 K and at pressures of 0.1, 1.0, 10, 100, and 1000 atm. For both 1- and 2-butene, at 0.1 atm, Ḣ atom addition forming the Ċ₄H₉-2 radical is favored at temperatures up to 500 K. The formation of C₃H₆ and ĊH₃ then dominates the reaction flux at higher temperatures. Similar trends are observed in Figure 6a,b at 1.0, 10, and 100 atm. However, the formation of Ċ₄H₉-2 is favored at temperatures up to ∼700, 900, and 1200 K, respectively. In the case of isobutene, Ḣ atom addition forming tĊ₄H₉ radicals is favored at temperatures up to 1000 K at 0.1 atm, whereas at higher temperatures, the formation of C₃H₆ and ĊH₃ dominates. The same trends are observed at 1.0, 10, and 100 atm. However, the formation of tĊ₄H₉ radicals is favored at temperatures up to 1200, 1400, and 1600 K, respectively.

Figure 6.

Temperature- and pressure-dependent branching ratios for (a) 1-butene, (b) 2-butene, and (c) isobutene via hydrogen atom addition reactions at 0.1 (short-dotted lines), 1 (short-dashed lines), 10 (dotted lines), 100 (dashed lines), and 1000 (solid lines) atm.

Figure 7 presents rate constants for Ḣ atom addition reactions, which are reported with no symmetry or optical isomer corrections between the transition state and reactants—i.e., the reaction path degeneracy is set to 1. Table S1 of Supporting Information presents the symmetry factors for the reactants and transition states prior to this change. As expected, external Ḣ atom addition to each of the alkenes (solid lines) dominates over internal addition (dashed lines). For the linear alkenes, both external and internal Ḣ atom additions can lead to the formation of primary (blue) or secondary radicals (red). The rate constants for external addition to propene, 1-butene, and 1-pentene are similar with respective barrier heights of 8.4, 9.3, and 7.8 kJ mol^–1. However, the rate constant for external addition to ethylene is approximately a factor of 2 slower than external addition to propene and 1-butene at 500 K, reducing to a factor of ∼1.4 at 2000 K. This difference can be attributed to the difference in energy barrier of ∼2.8 kJ mol^–1. This can also be correlated with radical stability as a primary radical is formed in the case of ethylene, while secondary radicals are formed for propene, 1-butene, and 1-pentene.

Figure 7.

Rate constants (symmetry-uncorrected) for terminal and internal Ḣ atom addition to (a) linear and (b) branched C₂–C₅ alkenes from previous^4,5 and current works. Solid and dashed lines represent terminal and internal addition, respectively. Different colors represent different radical types formed. Black (tertiary), red (secondary), and blue (primary). Different symbols correspond to the different reactants. Blue box solid (ethylene), blue circle solid (propene), red triangle up solid (1-butene), red triangle down solid (2-butene), black diamond solid (isobutene), red triangle left (1-pentene), red triangle right (2-pentene), hexagon solid (2-methyl-1-butene), black star solid (2-methyl-2-butene), and blue pentagon open solid (3-methyl-1-butene).

Internal Ḣ atom addition to linear alkenes form either primary (C₃H₆ + Ḣ ↔ nĊ₃H₇, C₄H₈-1 + Ḣ ↔ Ċ₄H₉-1, and C₅H₁₀-1 + Ḣ ↔ Ċ₅H₁₁-1) or secondary radicals (C₄H₈-2 + Ḣ ↔ Ċ₄H₉-2, C₅H₁₀-2 + Ḣ ↔ Ċ₅H₁₁-2, and C₅H₁₀-2 + Ḣ ↔ Ċ₅H₁₁-3). Rate constants for internal addition to propene, 1-butene, and 1-pentene are similar. Rate constants for internal addition to 2-pentene are almost identical, with internal addition to 2-butene being slightly slower. However, this can be attributed to an energy barrier difference of ∼1.6 kJ mol^–1. The branched alkenes have been described previously,⁵ so we shall not reiterate here. A trend was observed in that the rate constants for the formation of tertiary radicals are the fastest, followed by secondary and primary radicals, respectively.⁵ In the rate rule determinations, two rules were proposed for internal Ḣ-atom addition to branched alkenes (one for addition to a branched alkene where the branching occurs at the double bond and a second for where the branching does not occur at the double bond). For the cases where branching occurs at the double bond (iC₄H₈ + Ḣ ↔ iĊ₄H₉ and 2M1B + Ḣ ↔ aĊ₅H₁₁), the energy barriers are similar, being 21.15 and 19.9 kJ mol^–1, and are higher than that for 3M1B + Ḣ ↔ dĊ₅H₁₁ (17.15 kJ mol^–1), where the branching does not occur at the double bond (Figure 8).

Figure 8.

Rate constant recommendations (symmetry-uncorrected) for Ḣ atom addition to linear (▲) and branched (■) C₂–C₅ alkenes. Solid, dashed, and dotted lines represent the formation of tertiary, secondary, and primary radicals, respectively. Open symbols are internal C-atom additions; solid symbols are external C-atom additions.

Recommended rate constants were suggested based on (i) whether addition is to a linear or branched alkene, (ii) whether it is terminal or internal addition, and (iii) the type of radical formed. An average of the rate constants within each subclass was taken as the recommended rate constant. If only one rate constant was available, for example, in the case of internal addition to a branched alkene forming a secondary radical (bC₅H₁₀ + Ḣ ↔ cĊ₅H₁₁), the rate constant for the reaction is taken as the recommended rate constant. For the rate constant recommendations presented in Tables 7, 9, and 11, the activation energies are expressed in cal mol^–1 units for ease in implementing into kinetic mechanisms.

Table 7. Rate Constant Recommendations (Symmetry-Uncorrected) for Ḣ Atom Addition to Linear and Branched Alkenes (C₂–C₅).

structure	site	radical formed (deg)	A	n	Ea	uncertainty bounds (upper, lower)
linear	external	1	2.40 × 1008	1.60	1526.
	external	2	4.35 × 1008	1.54	1144.	1.17, 1.23
	internal	1	7.79 × 1007	1.67	2276.	1.32, 1.45
	internal	2	2.74 × 1008	1.52	1621.	1.24, 1.43
branched	external	2	4.21 × 1008	1.54	1292.
	external	3	1.42 × 1009	1.47	836.	1.22,1.29
	Internal_Case1	1	2.27 × 1007	1.78	3326.	1.18, 1.21
	Internal_Case2	1	4.29 × 1007	1.71	2677.
	internal	2	5.09 × 1007	1.65	2401.
	internal	3	5.45 × 1008	1.47	1070.

Table 9. Recommended Rate Constants for H-Atom Abstraction from Alkenes on a Per H-Atom Basis^a,b.

class	A	n	Ea	uncertainty bounds (upper, lower)
primary	4.69 × 1004	2.68	6959	1.42, 1.35
primary allylic: 1-alkenes	9.14 × 1002	3.06	3582	1.10, 1.28
primary allylic: 2-alkenes	1.32 × 1003	3.08	3203	1.19, 1.50
primary vinylic	2.72 × 1005	2.54	12819	2.39, 2.95
secondary	4.08 × 1005	2.44	4734
secondary allylic	1.06 × 1005	2.59	2654	1.67, 2.67
secondary vinylic	2.41 × 1005	2.55	9611	2.09, 2.02
tertiary allylic	2.10 × 1006	2.19	2329

^acm³ mol^–1 s^–1 cal^–1 units.

^b(ATⁿ = cm³ mol^–1 s^–1, energies = cal mol^–1). Fit between 300 and 2000 K.

Table 11. Recommended Rate Constants for Alkyl Radical Decomposition Forming an Olefin + Radical^a.

class	A	n	Ea	uncertainty bounds (upper, lower)
alkyl radical ↔ olefin + ĊH3	2.54 × 1010	1.04	30 573	2.86, 3.71
alkyl radical ↔ olefin + Ċ2H5	5.20 × 1011	0.57	29 308	1.34, 3.11
alkyl radical ↔ olefin + nĊ3H7	9.62 × 1011	0.55	30 678	1.61, 2.60
alkyl radical ↔ olefin + iĊ3H7	6.87 × 1012	0.31	28 225

^a(ATⁿ = s^–1, energies = cal mol^–1). Fit between 300 and 2000 K.

In relation to the uncertainty bounds presented in Tables 7, 9, and 11, upper and lower bounds are given, which are defined as

3

where k_{recommendation} refers to the recommended rate coefficient and k_min and k_max refer to the minimum and maximum rate coefficients used in the determinations of the recommended rate coefficients, respectively. Appropriate symmetry corrections must be applied (Table 8) to these recommendations for use in rate rule determinations (Table 9).

Table 8. Symmetry Corrections to Be Applied to Rate Constant Recommendations for Ḣ Atom Addition to Alkenes.

σ reactant	σ transition state	symmetry-corrected/symmetry-uncorrected
1	0.5	2
2	0.5	4
2	1.0	2
4	2.0	2

Figure 9 illustrates an example of the rules proposed for (a) internal Ḣ addition to a linear alkene forming a secondary radical and (b) external addition to a branched alkene forming a tertiary radical. The rule is represented by a black solid line. Factors of 2 and 4 variations in the rule are represented by dashed and dotted lines, respectively. The colored lines represent the symmetry-corrected rate constants for each respective reaction, with the uncertainty bounds presented in Table 7. Presented in Figure 9a are the recommended rate constants (symmetry-uncorrected), which is multiplied by 4 for C₄H₈-2 + Ḣ ↔ Ċ₄H₉-2 since the reactant has a symmetry factor of 2 and the transition state has a symmetry factor of 0.5. For C₅H₁₀-2 + Ḣ ↔ Ċ₅H₁₁-2 and C₅H₁₀-2 + Ḣ ↔ Ċ₅H₁₁-3, the rule is multiplied by 2, since the reactant has a symmetry factor of 1, and both TSs have a symmetry factor of 0.5. As mentioned earlier, Table S1 of Supporting Information presents the symmetry factors for reactants and transition states prior to changing them to 1. It was found that this change decreased each Ḣ atom addition rate constant for both linear and branched alkenes by a factor of 2, with the exception of C₄H₈-2 + Ḣ ↔ Ċ₄H₉-2, which is explained above.

Figure 9.

Examples of the application of the proposed rules for Ḣ atom addition to alkenes.

3.2.1. Branching Ratios of Terminal/Internal Ḣ Atom Addition to Linear and Branched Alkenes

As discussed earlier, Manion et al.¹⁹ carried out a shock-tube study to investigate the kinetics of terminal and internal Ḣ atom addition to 1-butene. They observed a factor of 3 discrepancy in the branching ratio for terminal/internal Ḣ atom addition compared to that calculated by Miller and Klippenstein¹⁸ for the Ḣ + propene reactions. Manion et al.¹⁹ state that the difference is well outside the experimental error of their experiments or the expected differences for 1-butene. One of the aims of the current work is thus to investigate the branching ratio of terminal to internal Ḣ atom addition in 1-alkenes. Branching ratios for Ḣ atom addition to linear 1-alkenes for C₂–C₅ alkenes are plotted in Figure 10. The branching ratios for propene and 1-butene calculated in the current work are within 5% of each other, while our calculated branching ratio for 1-pentene is approximately 40–48% lower than that for propene. Nonterminal addition to pentene is ca. 1.33–1.92 times faster than that for propene and 1-butene at T < 300 K. However, terminal addition to propene and 1-butene is 1.2–1.38 times faster than for 1-pentene at T > 1000 K. The solid black line represents an average of the calculated rate constants for external addition to a linear 1-alkene forming a secondary radical to internal addition to a linear alkene forming a primary radical and is in excellent agreement with Curran’s recommendation,⁵⁹ with the branching ratios being within 10% of each other. This average branching ratio is also in good agreement with Manion’s branching ratio for 1-butene and is within a factor of 1.57 at 2000 K. The dashed blue line is the branching ratio for terminal/nonterminal addition if the rate constant for terminal addition by Miller and Klippenstein¹⁸ was reduced by a factor of 1.5. This adjusted branching ratio still differs with that of Manion’s by a factor of ∼2.6 and a factor of 1.5–2.0 of the branching ratios calculated in the current work at 2000 K.

Figure 10.

Branching ratio for terminal to internal Ḣ atom addition to (a) linear and (b) branched 1-alkenes.

Figure 11 presents branching ratios for terminal to internal Ḣ atom addition to branched 1-alkenes. 2-Methyl-1-butene (2M1B) and isobutene have branching ratios of 24.2 and 27.2, respectively, at 1000 K. These branching ratios are significantly higher than 3-methyl-1-butene, where the branching ratio of terminal to internal Ḣ atom addition is 6.21 at 1000 K. This is due to branching at the position of the double bond. This results in terminal addition to 2M1B and isobutene forming a tertiary radical, which is more stable than a secondary radical formed through terminal addition to 3M1B, resulting in faster rate constants for terminal addition. Again, the solid black line represents the branching ratio of our recommended rate constants of external addition to branched 1-alkene forming a tertiary radical to internal addition to a branched alkene forming a primary radical. As mentioned earlier, large deviations in rate constants for isobutene are observed between this work and the recommendations by Curran,⁵⁹ particularly for internal Ḣ atom addition. However, Curran does state that no experimental studies for internal Ḣ atom addition existed, so the rate constant recommendation was taken as 2.5 times the rate constant of internal Ḣ atom addition to propene. Manion¹⁹ states in his study that their¹⁹ rates should not be applied to 1-olefins that have branching at the double bond position. We also observe that branching at the double bond significantly influences the branching ratio of 1-olefins and explains the difference as why the branching ratio from Curran is lower than that of the current work. Additionally, Manion¹⁹ states that direct information is lacking on the impact of branching removed from the double bond, but he believes it would have a minimal effect, which is also supported by our calculations here, where our calculated branching ratio for 3M1B is 6.21 at 1000 K. Our calculated branching ratios for propene, 1-butene, and 1-pentene are 4.42, 4.24, and 3.17, respectively, at 1000 K.

Figure 11.

Branching ratio for terminal to internal Ḣ atom addition to branched 1-alkenes.

Rate constant comparisons for the H-atom abstraction reactions from C₂–C₄ alkenes were discussed in our previous studies^4,5 on the reactions of Ḣ atoms with the pentene isomers, so we shall be brief here. As mentioned earlier, excellent agreement is observed for H-atom abstraction from the primary carbon sites (Figure 12). An average of our computed rate constants for abstraction from the primary carbon site as well as the rate calculated by Li et al.² is taken as the recommended rate constant. A good agreement is also observed for the abstraction reactions from the primary allylic and vinylic carbon sites.

Figure 12.

High-pressure limiting rate constants for H-atom abstraction from alkylic (primary) carbon sites on a per Ḣ atom basis.

For H-atom abstraction from the primary allylic carbon sites, a trend was observed in which abstraction from 2-alkenes is faster than that from 1-alkenes (Figure 13a). As a result, two rate constant recommendations were proposed. The average energy barriers for abstraction from the primary allylic site of 1-alkenes and 2-alkenes computed in this work are 31.0 and 28.6 kJ mol^–1, respectively, which accounts for most of the difference observed. The difference observed at higher temperatures can be attributed to the difference in entropy of activation. For the rate constant recommendation for 1-alkenes, an average of the rates calculated in this work and previous studies as well as that by Chen et al.²⁰ is taken.

Figure 13.

High-pressure limiting rate constants for H-atom abstraction from allylic carbon sites on a per Ḣ atom basis.

For 2-alkenes, an average of our computed rate constants and the rate constant by Li et al.² is taken as the recommended value. For comparison purposes, the rate constant calculated by Miller and Klippenstein¹⁸ was decreased by a factor of 2 since this was another reaction for which they altered the energy barrier. The altered rate constant agrees well with the rate constant calculated in the current work and with that from Chen et al.²⁰ Moreover, for abstraction from the secondary allylic and primary vinylic carbon site, an average of our calculated rates and that by Li et al.² is taken as the recommended rate constant. For abstraction from the secondary vinylic site, an average of our computed rate constants, Li et al., Chen et al., and Miller and Klippenstein is taken.^2,18,20 A factor of 2 uncertainty is applied to these recommendations and is represented by dotted purple lines in Figures 12–14. For clarity reasons, the factor of 2 uncertainty is not shown in Figure 13a since there are two recommended rate constants.

Figure 14.

High-pressure limiting rate constants for H-atom abstraction from vinylic carbon sites on a per Ḣ atom basis.

3.3. Reactions of Alkyl Radicals

3.3.1. Ethyl (Ċ₂H₅) Radical

Ethyl radicals are formed via Ḣ atom addition to ethylene (11.2 kJ mol^–1). C–H β-scission of ethyl radicals can also occur with a barrier height of 157.7 kJ mol^–1.

3.3.2. Propyl (nĊ₃H₇ and iĊ₃H₇) Radicals

Once nĊ₃H₇ radicals are formed via internal Ḣ atom addition to propene, they can undergo C–C β-scission to form ethylene and ĊH₃ radicals with an energy barrier of 127.9 kJ mol^–1 (Table 10), which is more favorable (by 30.2 kJ mol^–1) than isomerization to iĊ₃H₇ radicals. They can also undergo C–H β-scission, with an energy barrier of 148.6 kJ mol^–1. The iĊ₃H₇ radicals formed can undergo a Ḣ atom elimination reaction, with an energy barrier of 155.2 kJ mol^–1.

Table 10. Computed Energy Barriers, Heats of Reaction, and High-Pressure Limiting Rate Constant Fits for the Reactions of C₃–C₄ Alkyl Radicals^a,b.

reaction	Δ‡H0K	ΔrH0K	A	n	Ea
nĊ3H7 ⇌ iĊ3H7	158.09	–13.86	2.22 × 1005	2.05	129.83
nĊ3H7 ↔ C2H4 + ĊH3	127.91	91.40	1.10 × 1016	–0.72	135.31
Ċ4H9-1 ⇌ Ċ4H9-2	162.78	–11.15	8.80 × 10–05	4.82	111.84
Ċ4H9-1 ↔ C2H4 + Ċ2H5	124.29	89.93	3.64 × 1015	–0.58	130.33
Ċ4H9-2 ↔ C3H6 + ĊH3	129.45	93.21	1.87 × 1014	–0.20	134.93
iĊ4H9 ⇌ Ċ4H9-t	150.21	–21.17	8.08 × 1001	3.03	116.48
iĊ4H9 ↔ C3H6 + ĊH3	129.86	86.81	1.46 × 1017	–0.91	137.99

^aUnits (ATⁿ = s^–1, energies = kJ mol^–1).

^bFit between 298 and 2000 K.

3.3.3. Butyl (Ċ₄H₉-1 and Ċ₄H₉-2) Radicals

Ċ₄H₉-1 radicals are formed via internal Ḣ atom addition to 1-butene, while terminal addition leads to the formation of Ċ₄H₉-2 radicals. Ċ₄H₉-2 radicals are also formed through internal Ḣ atom addition to 2-butene. C–C β-scission of Ċ₄H₉-1 radicals can occur forming ethylene and Ċ₂H₅ radicals, with a barrier height of 124.3 kJ mol^–1, which is more favorable (by 33.5 kJ mol^–1) than isomerization to Ċ₄H₉-2 radicals. Additionally, C–H β-scission of Ċ₄H₉-1 radicals can occur with a barrier height of 152.5 kJ mol^–1. Two transition states are available for the reaction Ċ₄H₉-1 ⇌ Ċ₄H₉-2, one occurring through a three-membered ring and the second one occurring through a four-membered ring, with barrier heights of 160.6 and 162.8 kJ mol^–1, respectively. C–C β-scission of Ċ₄H₉-2 can also occur, forming propene and a ĊH₃ radical, with an energy barrier of 129.45 kJ mol^–1, while C–H β-scission of Ċ₄H₉-2 has a barrier height of 148.6 kJ mol^–1 (Figure 15).

Figure 15.

Rate constant recommendations for H-atom abstraction from C₂–C₅ alkenes. Solid lines, allylic; dashed lines, alkyl; and dotted lines, vinylic.

3.3.4. Branched Butyl (iĊ₄H₉ and tĊ₄H₉) Radicals

Internal Ḣ atom addition to isobutene forms iĊ₄H₉ radicals, while terminal addition forms tĊ₄H₉ radicals. C–H β-scission of iĊ₄H₉ radicals can occur, with a barrier height of 145.6 kJ mol^–1. However, C–C β-scission of iĊ₄H₉ radicals, forming propene and ĊH₃ radicals is more favored, with a reaction barrier of 129.9 kJ mol^–1. Isomerization of iĊ₄H₉ to tĊ₄H₉ occurs with a higher energy barrier of 150.2 kJ mol^–1. C–H β-scission of tĊ₄H₉ can occur, with a barrier height of 151.7 kJ mol^–1.

Figure 16 presents high-pressure limiting rate constants for alkyl radical decomposition reactions forming an olefin + ĊH₃. For comparison, rate constants for alkyl radical decomposition from our previous work on C₅ alkenes in addition to other literature sources^4,59,61−63 are plotted. The rate constant for the reaction iĊ₄H₉ ↔ C₃H₆ + ĊH₃ recommended by Curran⁵⁹ is a factor of 2.74–1.67 times faster than that calculated in this work in the temperature range 500–2000 K. With the exception of this reaction, all other rate constants calculated in this work for alkyl radicals, leading to the formation of an olefin and a ĊH₃ radical are within a factor of 1.55 of our computed rate constant for nĊ₃H₇ ↔ C₂H₄ + ĊH₃ over the temperature range 298–2000 K. The rate constant calculated in this work for iĊ₄H₉ ↔ C₃H₆ + ĊH₃ is a factor of 2.54–3.08 times faster than nĊ₃H₇ ↔ C₂H₄ + ĊH₃. This may be due to the fact that iĊ₄H₉ radicals have three degenerate sites for C–C β-scission to take place.

Figure 16.

High-pressure limiting rate constants for alkyl radical decomposition, forming an olefin + ĊH₃. Solid line, current work; dashed line, Curran; dotted line, Awan; and short-dotted line, Comandini.

Reasonable agreement is observed for the reactions of alkyl radicals forming an olefin and Ċ₂H₅ radicals calculated previously and in this work. In Figure 17, the rate constant recommendation by Curran⁵⁹ for the reaction Ċ₅H₁₁-2 ↔ C₃H₆ + Ċ₂H₅ is the fastest in comparison to the other analogous reactions. The Curran recommendation⁵⁹ is a factor of ca. 9.5–5.0 times faster than our calculated rate constant for Ċ₅H₁₁-2 ↔ C₃H₆ + Ċ₂H₅ calculated previously over the temperature range 300–2000 K.⁴ The value from Awan and Comandini^61,62 is a factor of ∼3.4 times faster than our previous work⁴ for the same reaction at 500 K, with the rate constants converging at higher temperatures. Jitariu et al.⁶³ are in excellent agreement with our previous work for the reaction Ċ₅H₁₁-2 ↔ C₃H₆ + Ċ₂H₅,⁴ with the rate constants being within a factor of ∼1.3. The rate constant for the reaction aĊ₅H₁₁ ↔ C₃H₆ + Ċ₂H₅ calculated in our most recent study⁵ is a factor of ∼3 times faster at 500 K than our calculated rate constant for Ċ₅H₁₁-2 ↔ C₃H₆ + Ċ₂H₅.⁴ An energy barrier difference of 1.9 kJ mol^–1 accounts for a factor of 1.6 of this difference. For the decomposition of an alkyl radical forming an olefin and an ethyl radical, an average of the rate constants calculated in our current and previous studies^4,5 as well as those by Awan, Comandini, and Jitariu^,61−63 is taken, with a factor of 2 of the recommended represented as orange dotted lines.

Figure 17.

High-pressure limiting rate constants for alkyl radical decomposition, forming an olefin + Ċ₂H₅. Solid line, current work; dashed line, Curran; dotted line, Awan; short-dotted line, Comandini; and dashed-dotted line, Jitariu.

Figure 18 presents rate constant comparisons for alkyl radical decomposition forming olefin and propyl radicals. The reactions Ċ₅H₁₁-1 ↔ C₂H₄ + nĊ₃H₇ and dĊ₅H₁₁ ↔ C₂H₄ + iĊ₃H₇ are plotted for comparison. The rate constants for the reaction Ċ₅H₁₁-1 ↔ C₂H₄ + nĊ₃H₇ by Awan,⁶¹ Comandini,⁶² and Jitariu et al.⁶³ are in good agreement with our previously calculated rate constant.⁴ At 500 K, the values from Awan⁶¹ and Comandini⁶² are a factor of ∼4.5 times faster than our calculated rate constant for this reaction at 500 K, with the rate constants converging at high temperatures. The difference of 7.76 kJ mol^–1 in the energy barrier accounts for the observed difference. Larger differences are observed between the values calculated in this work and by Awan and Comandini at temperatures below 500 K; therefore, the recommended rate constant for Ċ₅H₁₁-1 ↔ C₂H₄ + nĊ₃H₇ is taken as an average of the rate calculated in the current work and by Jitariu et al.⁶³ The rate constant by Jitariu et al. is in excellent agreement with our calculated rate constant for the same reaction.⁴ Our calculated rate constant for dĊ₅H₁₁ ↔ C₂H₄ + iĊ₃H₇ is also plotted in this graph, which is taken as the recommended rate constant for alkyl radical decomposition forming an olefin and an iĊ₃H₇ radical (Table 11).

Figure 18.

High-pressure limiting rate constants for alkyl radical decomposition, forming an olefin + Ċ₃H₇. Solid line, current work; dotted line, Awan; short-dotted line, Comandini; and dashed-dotted line, Jitariu.

4.0. Detailed Kinetic Modeling

All simulations were performed using Chemkin-Pro assuming a constant-volume homogeneous batch reactor. As described in our previous study of the pentene isomers,⁵ test computations implied that the high-pressure limiting rate constant for external Ḣ atom addition to 2M1B was overestimated by a factor of 2–3, which is also in line with the variational effect observed by Jasper and Hansen⁶⁴ for Ḣ atom addition to high-molecular-weight species. To assess the influence of variational effects on predictions of experimental data, indicative simulations are carried out by systematically reducing the rate constants for Ḣ atom addition by a factor of 2 in the RRKM/ME model and recomputing k(T,p). The approximate variational calculation results from the current work for the alkene + Ḣ systems have been included in NUIGMech1.1, which includes our results from our previous studies of the pentene isomers.^4,5 The updated model, NUIGMech1.2, is used to simulate the recent results from a pyrolysis study of 1-alkenes using the NUIG single-pulse shock tube³² and is represented by solid lines. Dashed lines represent model predictions of NUIGMech1.1. The update to the pyrolysis reactions between the two models is solely from the present work. Improvements in species mole fractions are observed, particularly for 2-butene and isobutene pyrolysis.³⁵ The supporting information contains PLOG fits for both the approximate variational results and the original unadjusted results (Figure 19).

Figure 19.

Rate constant recommendations for alkyl radical decomposition to olefin + radical.

4.1. Ethylene Pyrolysis

Figure 20 presents species profiles for ethylene pyrolysis at 2 bar.³² The reaction path analysis was already described by Nagaraja et al.³² so we shall be brief here. H-atom abstraction by Ḣ atoms from ethylene leads to the production of vinyl radicals, with vinyl radicals decomposing to acetylene + Ḣ. Through the incorporation of the rate constants calculated in this work (NUIGMech1.2), there is a slight improvement in the species profiles for both ethylene and acetylene. The rate constant for H-atom abstraction from ethylene is approximately a factor of 2 slower, which reduces the amount of vinyl radical produced, which in turn decreases the production of acetylene and Ḣ atoms.

Figure 20.

Species profiles for ethylene pyrolysis at 2 bar. Dashed lines represent NUIGMech1.1, and solid lines represent NUIGMech1.2.

4.2. Propene Pyrolysis

Figure 21 presents species profiles for propene pyrolysis at 2 bar.³² Both Ḣ atom addition and abstraction reactions are the main consumption pathways for propene. Ḣ atom addition to propene and the subsequent decomposition of propyl radical lead to the formation of ethylene and a methyl radical. The abstraction of an allylic H-atom by Ḣ atoms or ĊH₃ radicals leads to the formation of allyl and H₂ and CH₄. Allyl radicals are converted to allene, which subsequently isomerizes to propyne or undergoes H-atom abstraction to form propargyl radicals, which in turn produces benzene. Acetylene is formed by the decomposition of vinyl radicals, the reaction of Ḣ atoms with allene and propyne, and the β-scission of propen-1-yl radical.

Figure 21.

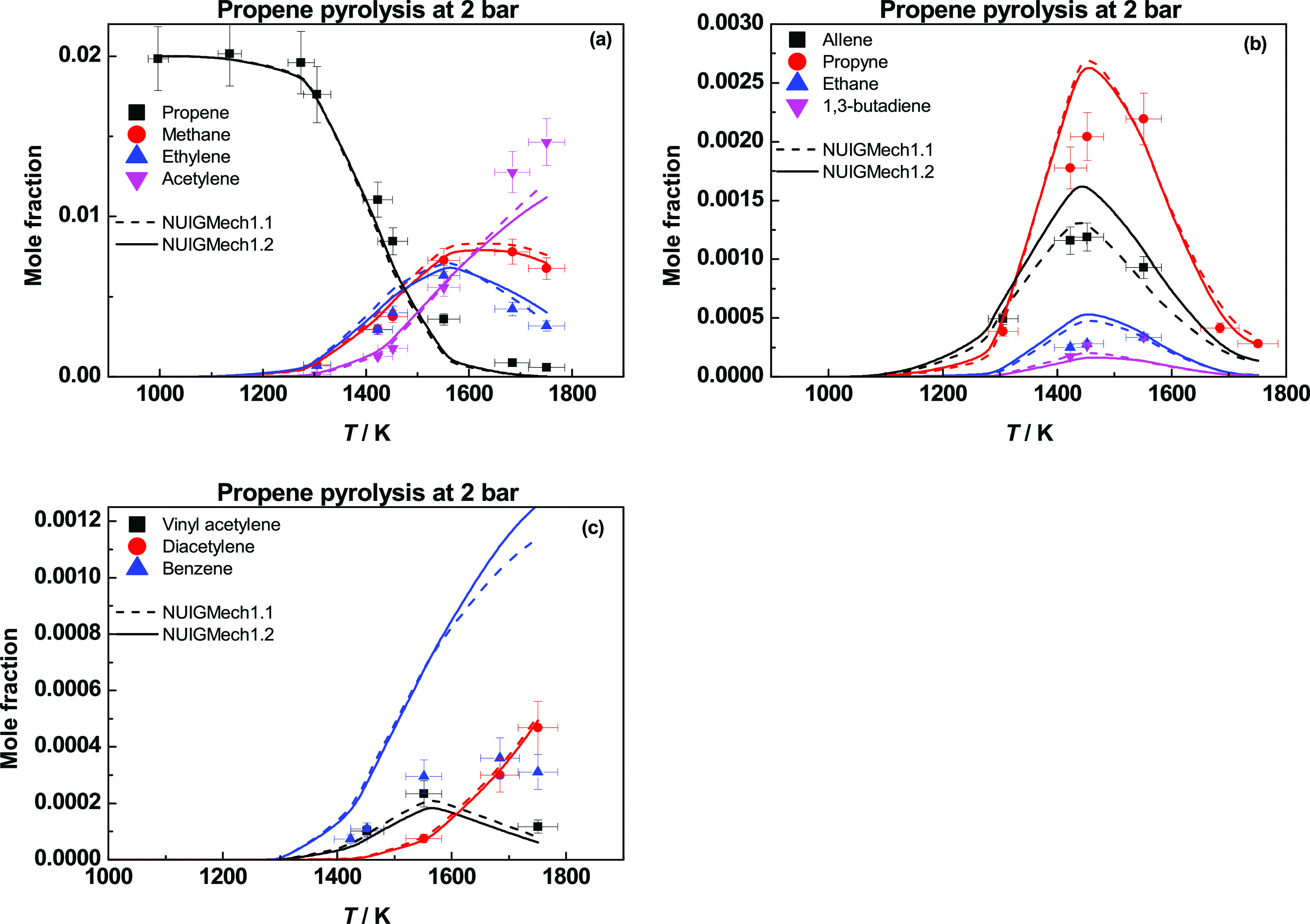
Species profiles for propene pyrolysis at 2 bar. Dashed lines represent NUIGMech1.1, and solid lines represent NUIGMech1.2.

4.3. 1-Butene Pyrolysis

Figure 22 presents species profiles for 1-butene pyrolysis at 2 bar.³² The pyrolysis chemistry is quite similar to that of propene, with both Ḣ atom addition and abstraction reactions being important pathways. H-atom addition to 1-butene produces propene and a ĊH₃ radical and ethylene and a Ċ₂H₅ radical via two chemically activated pathways. Ethyl radicals decompose to ethylene + Ḣ. Hydrogen atom abstraction by Ḣ or ĊH₃ leads to the formation of Ċ₄H₇1–3, which in turn forms 1,3-butadiene. Methane is formed primarily by H-atom abstraction by ĊH₃ radicals from the fuel and other stable species. Acetylene is mainly produced by the decomposition of vinyl radicals and the reactions of Ḣ atoms with allene and propyne.

Figure 22.

Species profiles for 1-butene pyrolysis at 2 bar. Dashed lines represent NUIGMech1.1, and solid lines represent NUIGMech1.2

4.4. Trans 2-Butene Pyrolysis

Figure 23 presents species profiles for 2-butene pyrolysis at 2 bar.³⁵ Again, the pyrolysis chemistry is quite similar to that of propene and 1-butene. Ḣ atom addition to 2-butene forms propene and ĊH₃ radicals through a chemically activated pathway. H-atom abstraction by Ḣ or ĊH₃ leads to the formation of Ċ₄H₇1-3, which in turn forms 1,3-butadiene. The rate constant for H-atom abstraction from 2-butene forming Ċ₄H₇1-3 calculated in this work is a factor of 2.5 times slower than that used in NUIGMech1.1, which in turn reduces the species mole fraction of 1,3-butadiene. For the propene species profiles, there is an improvement in the predictions through the incorporation of the calculations computed in the current work. The production of propene, as previously stated, comes from the chemically activated pathway of Ḣ atom addition to 2-butene. The rate constants in NUIGMech1.1 are based on QRRK/MSC estimates and are approximately a factor of ∼7 times faster than those in NUIGMech1.2 at 1400 K. Again, methane is mainly produced by H-atom abstraction by ĊH₃ from the fuel and other stable species. Acetylene is mainly produced by the decomposition of vinyl radicals and the reactions of Ḣ atoms with allene and propyne.

Figure 23.

Species profiles for 2-butene pyrolysis at 2 bar. Dashed lines represent NUIGMech1.1, and solid lines represent NUIGMech1.2.

4.5. Isobutene Pyrolysis

Figure 24 presents species profiles for isobutene pyrolysis at 2 bar.³⁵ Ḣ atom abstraction from isobutene leads to the formation of iĊ₄H₇ radicals, which decompose to produce allene and ĊH₃ radicals. The resulting allene then isomerizes to propyne. Propene is primarily formed through the chemically activated pathway of Ḣ atom reaction to isobutene. There is an improvement in the propene predictions with the current model, due to the rate constant for the chemically activated pathway of Ḣ atom addition to isobutene being approximately a factor of 7 times slower at 1400 K.

Figure 24.

Species profiles for isobutene pyrolysis at 2 bar. Dashed lines represent NUIGMech1.1, and solid lines represent NUIGMech1.2.

5.0. Chemically Activated Pathways

5.1. Effect of Pressure

From the simulations, it is observed that the chemically activated pathways for the reaction of Ḣ atoms with alkenes are important in capturing the species profiles of the products during pyrolysis and oxidation (Figure 25). Taking propene as an example, which is described in Figure 4, the formation of stabilized iĊ₃H₇ radicals through the reaction of Ḣ atoms with propene dominates at temperatures up to 800, 1000, 1200, and 1500 and pressures of 0.1, 1, 10, and 100 atm, respectively. The chemically activated pathway C₃H₆ + Ḣ ↔ [nĊ₃H₇]* ↔ C₂H₄ + ĊH₃ then dominates the reaction flux at higher temperatures. At 1000 atm, the formation of stabilized iĊ₃H₇ radicals dominates over the entire temperature range.

Figure 25.

Potential energy surface for Ḣ-atom addition reactions of propene. Energies in kJ mol^–1.

At 1000 K and 0.1 atm, 70% of the reaction flux goes through this chemically activated pathway for C₃H₆ + Ḣ. However, as the pressure increases, this percentage reduces, and the stabilization reaction channel becomes more favorable. The percentages of reaction flux going through this chemically activated pathway are 41, 20, 7, and 2% for pressures of 1, 10, 100, and 1000 atm, respectively. It is therefore important to have accurate rate constants for the chemically activated pathways on these potential energy surfaces to predict the species mole fractions across a wide range of temperatures and pressures. Below are a list of some of the chemically activated pathways forming some of the major products of pyrolysis calculated in the current study and in previous ones.^4,5

• C₃H₆ + Ḣ ↔ [nĊ₃H₇]* ↔ C₂H₄ + ĊH₃

• C₄H₈-1 + Ḣ ↔ [Ċ₄H₉-1]* ↔ C₂H₄ + Ċ₂H₅

• C₄H₈-1 + Ḣ ↔ [Ċ₄H₉-2]* ↔ C₃H₆ + ĊH₃

• C₄H₈-2 + Ḣ ↔ [Ċ₄H₉-2]* ↔ C₃H₆ + ĊH₃

• iC₄H₈ + Ḣ ↔ [iĊ₄H₉]*↔ C₃H₆ + ĊH₃

  Moreover, chemically activated pathways were also found to be important for the reactions of Ḣ with the pentene isomers in our previous studies.^4,5

• C₅H₁₀-1 + Ḣ ↔ [Ċ₅H₁₁-1]* ↔ C₂H₄ + n-Ċ₃H₇

• C₅H₁₀-1 + Ḣ ↔ [Ċ₅H₁₁-2]* ↔ C₃H₆ + Ċ₂H₅

• C₅H₁₀-2 + Ḣ ↔ [Ċ₅H₁₁-2]* ↔ C₃H₆ + Ċ₂H₅

• C₅H₁₀-2 + Ḣ ↔ [Ċ₅H₁₁-3]* ↔ C₄H₈-1 + ĊH₃

• aC₅H₁₀ + Ḣ ↔ [aĊ₅H₁₁]* ↔ C₃H₆ + Ċ₂H₅

• aC₅H₁₀ + Ḣ ↔ [aĊ₅H₁₁]* ↔ C₄H₈-1 + ĊH₃

• aC₅H₁₀ + Ḣ ↔ [bĊ₅H₁₁]* ↔ iC₄H₈ + ĊH₃

• bC₅H₁₀ + Ḣ ↔ [bĊ₅H₁₁]* ↔ iC₄H₈ + ĊH₃

• bC₅H₁₀ + Ḣ ↔ [cĊ₅H₁₁]* ↔ C₄H₈-2 + ĊH₃

• cC₅H₁₀ + Ḣ ↔ [cĊ₅H₁₁]* ↔ C₄H₈-2 + ĊH₃

• cC₅H₁₀ + Ḣ ↔ [dĊ₅H₁₁]* ↔ C₂H₄ + iĊ₃H₇

5.2. Effect of Molecular Size

As the size of the molecule increases from propene to 1-butene, the effect of chemical activation becomes greater, especially at lower pressures. At 1000 K and 0.1 atm, for 1-butene, 99% of the reaction flux proceeds through the chemically activated pathways compared to 70% for propene (Figure 26).

Figure 26.

Potential energy surface for Ḣ-atom addition reactions of 1- and 2-butene. Energies in kJ mol^–1.

For the pentene isomers, it was shown that >95% of the reaction flux proceeds through the chemically activated pathways at 1000 K and 0.1 atm,^4,5 which is similar to butene. As the pressure increases, this percentage reduces to 93, 65, 25, and 4% at pressures of 1, 10, 100, and 1000 atm, respectively, for 1-butene, compared to 41, 20, 7, and 2% for propene. The formation of stabilized Ċ₄H₉-2 radicals through the reaction of Ḣ atoms with 1-butene then dominates, which can be seen in Figure 6a. A similar situation prevails for 2-butene (Figure 6b), where 98, 87, 57, 20, and 3% proceed through chemical activation at 0.1, 1, 10, 100, and 1000 atm, respectively. In the case of isobutene, 33% of the reaction flux goes through the chemically activated pathways at 1000 K and 0.1 atm, with the formation of stabilized tĊ₄H₉ radicals then dominating the reaction flux. It is not until a temperature of 1200 K is reached that chemical activation is considerable, accounting for 74% at 0.1 atm (Figure 6c). It is observed that the effect of chemical activation becomes greater as the molecular size increases from propene to butene. However, as the molecular size increases from butene to pentene, the effect of chemical activation is similar (Figure 27).

Figure 27.

Potential energy surface for Ḣ-atom addition reactions of isobutene. Energies in kJ mol^–1.

6. Conclusions

To contribute to the development of combustion models, a hierarchical set of rate constants for the reactions of Ḣ atom with C₂–C₅ alkenes, and the subsequent C–C and C–H β-scission and Ḣ atom transfer reactions using the same level of theory now exist. The reactions for the linear and branched C₅ alkenes were performed in our previous studies, while calculations for C₂–C₄ species are performed in the current work. Thermochemical data are calculated as a function of temperature, with enthalpies of formation determined from an isodesmic network, which is built upon benchmark literature data and electronic structure calculations. High-pressure limiting and temperature- and pressure-dependent rate constants are calculated using RRKM theory with a 1D master equation (ME) analysis. Rate constant recommendations for Ḣ atom addition/abstraction and alkyl radical decomposition are proposed and serve as a useful tool in mechanisms for larger alkenes for which calculations do not exist.

As mentioned in our earlier work,⁵ test computations implied that the high-pressure limiting rate constant for Ḣ atom addition were overestimated by a factor of 2–3, which is also in line with the variational effect observed by others for Ḣ atom addition reactions to high-molecular-weight species.⁶⁴ To determine the influence of variational effects on model predictions, indicative simulations are carried out by systematically reducing the rate constants for Ḣ atom addition by a factor of 2 in the RRKM/ME model and recomputing k(T,p). Similarly to our earlier work,⁵ it is found that the chemically activated pathways for Ḣ atom addition to alkenes, as well as their abstraction reactions, are found to be important in capturing the species profiles of the products from pyrolysis. Although a good agreement is observed between our model predictions and experiment, future work should consider to address VTST, the treatment of multidimensional torsions, and anharmonic effects with the aim of developing a more comprehensive RRKM/ME model for combustion modeling.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.1c03168.

• MESS input and output files and thermochemical values in NASA polynomial format and Chemkin format PLOG rate constant fits (ZIP)

• Symmetry factors for reactants and transition states prior to symmetry-uncorrected rate constants (Table S1) (PDF)

Author Contributions

J.P. performed electronic structure calculations, modeling work, and wrote the manuscript. K.P.S. performed electronic structure calculations and provided input for theoretical and modeling work. S.S.N. performed pyrolysis experiments. H.J.C. managed the project throughout and reviewed the manuscript before and after review process.

The authors declare no competing financial interest.