Cylindrical Similarity Measurement for Helices in Medium-Resolution Cryo-Electron Microscopy Density Maps

Abstract

Cryo-electron microscopy (cryo-EM) density maps at medium resolution (5–10 Å) reveal secondary structural features such as α-helices and β-sheets, but they lack the side chain details that would enable a direct structure determination. Among the more than 800 entries in the Electron Microscopy Data Bank (EMDB) of medium-resolution density maps that are associated with atomic models, a wide variety of similarities can be observed between maps and models. To validate such atomic models and to classify structural features, a local similarity criterion, the F₁ score, is proposed and evaluated in this study. The F₁ score is theoretically normalized to a range from zero to one, providing a local measure of cylindrical agreement between the density and atomic model of a helix. A systematic scan of 30,994 helices (among 3,247 protein chains modeled into medium-resolution density maps) reveals an actual range of observed F₁ scores from 0.171 to 0.848, suggesting that the cylindrical fit of the current data is well stratified by the proposed measure. The best (highest) F₁ scores tend to be associated with regions that exhibit high and spatially homogeneous local resolution (between 5 Å and 7.5 Å) in the helical density. The proposed F₁ scores can be used as a discriminative classifier for validation studies and as a ranking criterion for cryo-EM density features in databases.

Graphical Abstract

INTRODUCTION

The number of atomic structures that are derived from cryo-electron microscopy (cryo-EM) density maps has increased rapidly over the last five years. As of December 1, 2019, there were 824 structures modeled from cryo-EM density maps at reported resolution values in the medium- resolution range (5–10 Å) compared to 3,144 structures derived from resolutions better than 5 Å.^1,2 It is, of course, desirable to obtain high-resolution maps (better than 3.4 Å resolution is typically required to directly solve atomic structures). The quality of a map produced by an experimental cryo-EM laboratory improves over time as more data is collected. Consequently, medium-resolution maps are routinely created in the initial stages of a cryo-EM imaging project, before the specimen preparation protocols are tuned to perfection. Lower-resolution regions can also be present in overall high-resolution maps due to conformational flexibility or libration of the specimen. For these reasons, medium-resolution maps are often the first and only observations available of a new system. Such early glimpses of an unknown system can be of significant biological importance, and there is pressure to interpret them at atomic detail. Understandably, investigators will attempt to build models despite the risks and inaccuracies. Our present work is concerned with assessing the accuracy of the model fit given the increasing number of deposited map/model pairs in the challenging medium-resolution range.

Various structural modeling methods have been developed to utilize known atomic structures as initial templates. Some structures were derived from medium-resolution density maps through rigid-body fitting^3,4 and real space refinement.^5–8 Other structures were derived using comparative modeling methods^9–13 and flexible fitting.^14–18 It remains quite difficult and risky to model atomic structures de novo for most proteins, owing to the resolution limitations. However, in many cases, secondary structure elements, such as α-helices and β-sheets, can be assigned with confidence into medium-resolution maps.^19–26 Our understanding of the quality of density patterns and corresponding atomic models in medium-resolution maps is limited. Without knowledge of reliable density patterns, it is risky to overfit atomic models on erroneous density or to underutilize reliable density patterns in model building.

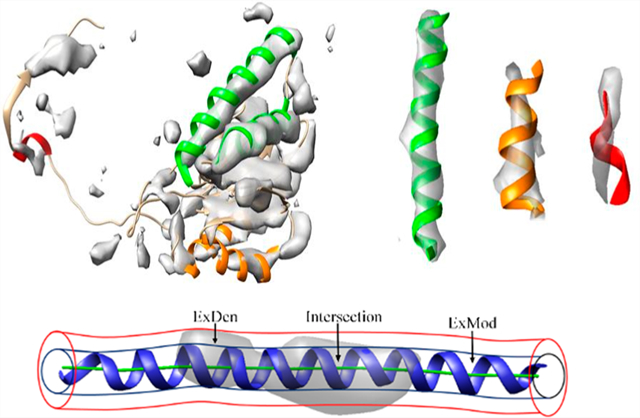
Among secondary structural features, α-helices often appear as cylindrically shaped density regions, and β-sheets appear as thin layers of density in medium-resolution cryo-EM maps. Although the location of α-helices is commonly detectable,^21,22,24,25 density strength varies considerably at helix regions.²⁷ The density of some helices appears to fill almost all of the helix backbone region expected of the atomic structure (green helices in Figure 1) when visualized at a threshold tuned to the surface of secondary structural features. Other helix backbone regions appear to be partially filled (orange helices in Figure 1); but for some outliers, the orientation of the helix appears to be different from the direction of the corresponding density region (red helix in Figure 1). Variations in density strength can be explained by the limitations of systematic image processing, such as image alignment and 3D reconstruction artifacts, or structural flexibility of molecules. To represent a spatially heterogeneous level of detail^28,29 that is often observed in cryo-EM maps, the concept of local resolution has recently been introduced. While local resolution provides important information about the quality of specific regions of a map, it is not clear how the concept can be best utilized in model building. Due to the effects of noise, density sharpening, correction of microscope parameters, and 3D reconstruction, individual voxels may not be reliable; moreover, the voxel spacing is typically much finer than indicated by the medium-spatial resolution.

Figure 1.

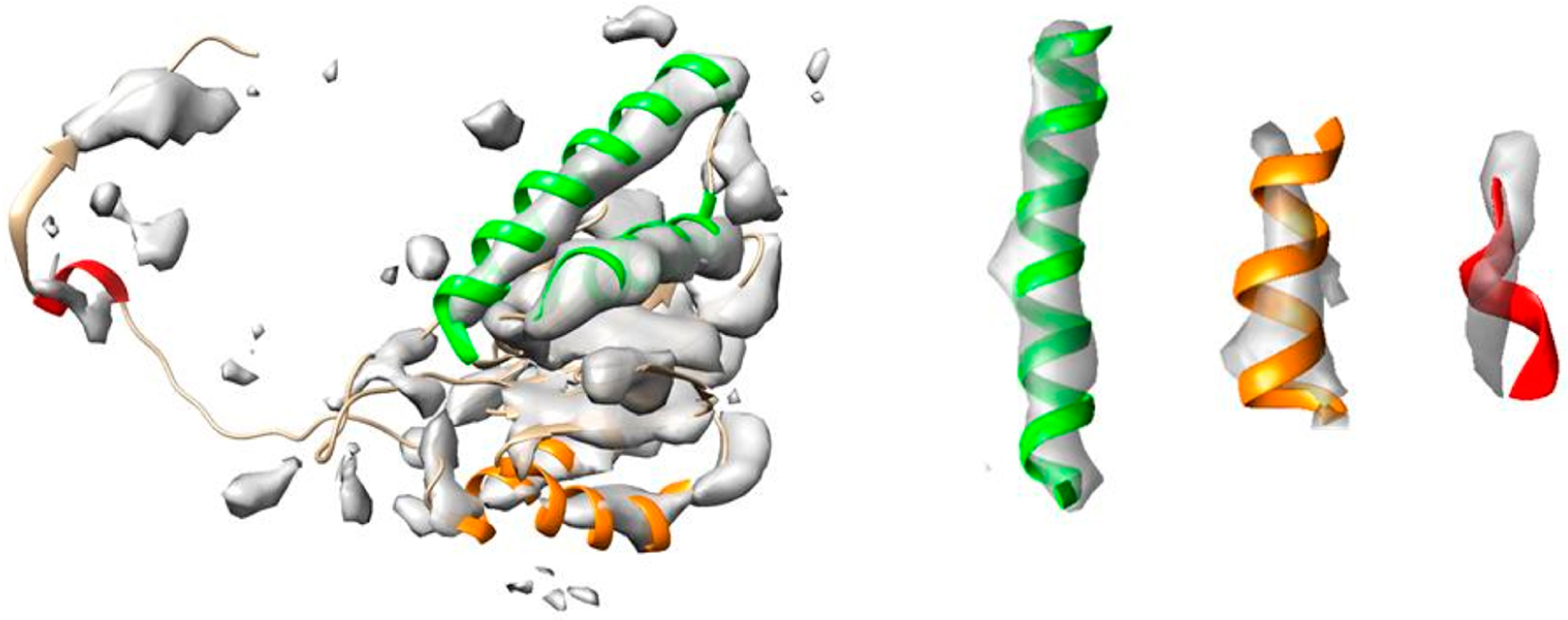
Illustration of different levels of map/model similarity exhibited by helices in the same map. The surface representation of the density map (EMDB ID 4089, gray, corresponding to Chain 2) is superimposed on Protein Data Bank (PDB) ID 5ln3 Chain 2 (ribbon). Helices with different levels of similarity are indicated by green, orange, and red, respectively, from strong similarity to poor similarity (with separate views, on the right, for three examples). For detailed F₁ similarity scores, see the Results section.

In this work, we therefore propose to assess the local quality of a map at the level of secondary structure elements. The level of detail of a similarity measure based on secondary structure elements, such as helices, is, by design, intermediate between individual voxels and the global map. The features are large enough to be robust, but the similarity measure is still a local one, compared to the global cross-correlation coefficient.³⁰

The reproducibility and discriminative ability of a local similarity score is important during the model-building process, because a global score, such as the cross-correlation (CC), varies with the size of the map volume under consideration. Consequently, an earlier application of CC scores in the PHENIX program required a local region mask³¹ to evaluate individual residues. An alternative tool, EM-Ringer, evaluated side chains only and produced a single score to represent the quality of the fit, but the approach did not generalize to the secondary structure level.³² The closest related approach, in terms of applicability to a secondary structure, was the Z-score.³³ A Z-score was calculated from 27 CC scores using ± zero or one voxel shifts in the x, y, and z directions, respectively.³³ The approach did not take specific shape information into account, and by design it depended on the granularity of the map. In contrast, the new F₁ score proposed below uses a simple geometric metric and is invariant when zooming in to the level of residues.

Despite the challenges associated with interpreting medium-resolution density maps, over 800 atomic models have already been derived from such data, mostly through fitting an existing X-ray structure followed by refinement. Since each atomic model often involves multiple chains, and each chain, in turn, often has multiple helices and β-sheets, the large number of map/model pairs provides a solid data set for a quantitative analysis. Since helices are the more distinctive secondary structural feature and visible across the entire medium-resolution range, this study proposes a quantitative score to evaluate cylindrical similarity for helix regions in a medium-resolution density map. Owing to the diverse 3D reconstruction and modeling approaches used in cryo-EM and a resulting multitude of potential algorithmic and experimental limitations, the similarity score was designed to be agnostic of the origin of a specific mismatch (the unaccounted for regions ExMod or ExDen in Figure 2C).

Figure 2.

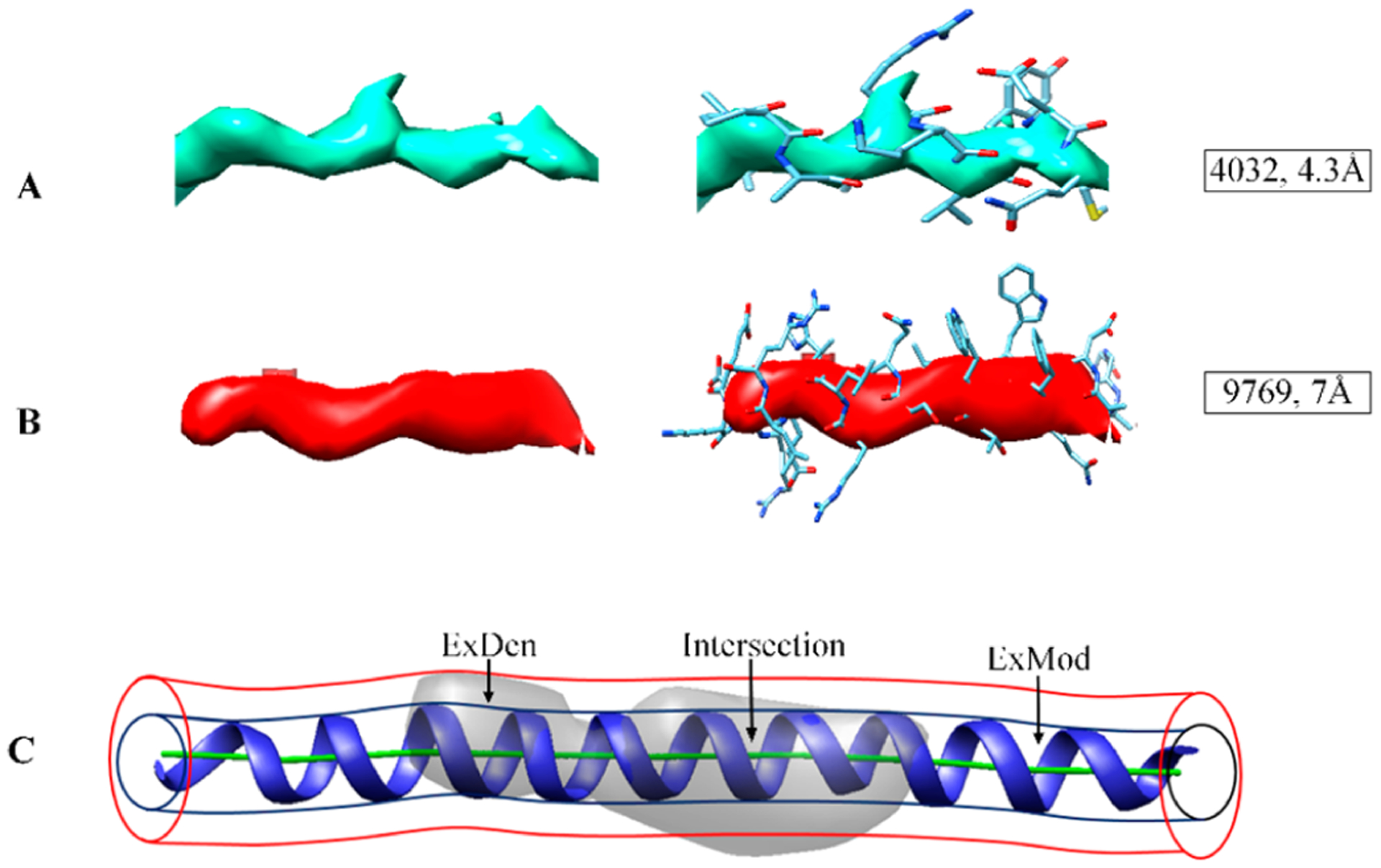
Examples of helix densities at different resolutions and their cylindrical similarity: (A) density for a helix in EMDB ID 4032 with 4.3 Å resolution superimposed on the atomic model; (B) density for a helix in EMDB ID 9769 with 7 Å resolution superimposed on the atomic model; (C) two template cylinders of 2.5 and 4 Å radii, respectively, were used to measure the cylindrical similarity (see section “Cylindrical Similarity Score”). Part (C) shows the intersection of map and model and two mismatched regions, ExDen and ExMod (where density is not accounted for by the model or vice versa).

METHODOLOGY

Data.

On September 9, 2018, we downloaded 654 medium-resolution cryo-EM density maps with corresponding atomic models from the EMDB and PDB, respectively. For a protein with multiple copies of the same chain sequence, only one was included to eliminate redundancies. The final data set consisted of 3,247 protein chains. The cryo-EM density region corresponding to each chain was extracted from the entire density map using UCSF Chimera with a radius of 5 Å around each atom.³ Because the method was designed to measure helices, chains without helices were excluded. Chains that lay completely outside any molecular density were also excluded.

Cylindrical Similarity Score.

The density distribution of a helix closely resembles a cylinder at medium resolution, with highest densities found near the central axis of the helix. The similarity of an atomic model was quantified using two suitably chosen template cylinders, derived from the central line of a helix using Cα atoms (Figure 2C). The central line was produced using the AxisComparison tool from an atomic model in PDB format.^34,35 In the AxisComparison method, every four consecutive Cα atoms of a helix are averaged to generate initial central points, which are interpolated to produce a smooth line (Figure 2C). The radius was selected as 2.5 and 4 Å for the inner and outer cylinders, respectively, to approximate the radius of the helix backbone and a typical radial size of an α-helix. We also explored 3 and 5 Å for inner and outer cylinder radii, respectively, but we found that the use of 4 Å radius for the outer cylinder reduced the density overlap from surrounding nonhelix density. At each density threshold, the number of helix density voxels within the inner cylinder, VxInner, measured the (ideally large) volume of the intersection between the helix density and the model (Figure 2C). The number of helix density voxels between the inner and outer cylinder, VxOut, measured the (ideally small) volume of identifiable helix voxels outside of the helix backbone model (denoted ExDen in Figure 2C). The number of inner cylinder voxels that have lower densities than the threshold, $\overline{\mathit{\text{VxInner}}}$, measured the (ideally small) volume where the atomic helix backbone model was not supported by sufficient map density (denoted ExMod in Figure 2C). Both VxOut and $\overline{\mathit{\text{VxInner}}}$ lowered the F₁ score via eqs 1–3.

$$F_1=\frac{2^{*}Pde{n}^{*}\mathit{\text{Rmod}}}{\mathit{\text{Pden}}+\mathit{\text{Rmod}}}$$ (1)

$$\mathit{\text{Pden}}=\frac{\mathit{\text{Intersection}}}{\mathit{\text{Intersection}}+\mathit{\text{ExDen}}}=\frac{\mathit{\text{VxInner}}}{\mathit{\text{VxInner}}+\mathit{\text{VxOut}}}$$ (2)

$$\mathit{\text{Rmod}}=\frac{\mathit{\text{Intersection}}}{\mathit{\text{Intersection}}+\mathit{\text{Exmod}}}=\frac{\mathit{\text{VxInner}}}{\mathit{\text{VxInner}}+\overline{\mathit{\text{VxInner}}}}$$ (3)

Density thresholds were sampled between the mean and the maximum of the density map, and the threshold that maximized the F₁ score (eq 1) was selected automatically.

The F₁ score is a metric commonly used in machine learning. Our adaptation of the F₁ score (eq 1) was adapted from the standard interpretation in statistics where the F₁ score is the harmonic mean of precision and recall.³⁶ Although it is typically used to compare ground truth and prediction, the F₁ score in our implementation measured similarity between two sets: the density region (above a threshold) in the vicinity of a helix and the region of a helix backbone model. Pden (eq 2) represents the accuracy of the helix density, i.e., the percentage of agreed map/model volume among the total volume of map relevant to the helix. Rmod (eq 3) represents the accuracy of the model, i.e., the percentage of agreed map/model volume among the total volume relevant to the helix backbone model. F₁ scores lie between zero and one, where one indicates perfect similarity between the two sets.

RESULTS

When the resolution is high, such as at about 4 Å, the coil of the helix backbone starts to become visible in cryo-EM density maps (Figure 2A): the helix backbone exhibits a higher density than the side chains. The higher density of the helix backbone thus requires a density threshold for visualization that obscures the expected side chain regions (Figure 2A). At medium resolution, however, instead of the coil of the backbone, only a cylindrically shaped density is observed (Figure 2B): the highest density voxels are often located near the central axis of the cylinder. We used two cylinders to measure the cylindrical character of the density along a helix that is represented by the central axis of a helix atomic model. The inner radius of 2.5 Å was designed to capture the backbone density of a helix: a helix with good map/model similarity is expected to have a density threshold at which the density is primarily located within the inner cylinder of 2.5 Å radius.

The cylindrical similarity of helices was evaluated for 30,994 helices from 3,247 protein chains corresponding to maps with resolutions between 5 Å and 10 Å. Each helix region in Figure 3 was shown using the automatically selected density threshold that maximizes the F₁ score. The observed F₁ scores varied considerably, and those helices with higher F₁ scores appear more cylindrical through the entire length of the model. The F₁ score also appears to stratify the data as intended. As an example, the helix located on chain D of PDB ID 5j4z between amino acid segment 131 to 161 appeared to have a good cylindrical shape (top left in Figure 3). The maximum F₁ score of the helix was 0.863 when the density threshold was at 0.159, at which the inner cylinder was maximally filled, while the density volume between inner and outer cylinder was minimized.

Figure 3.

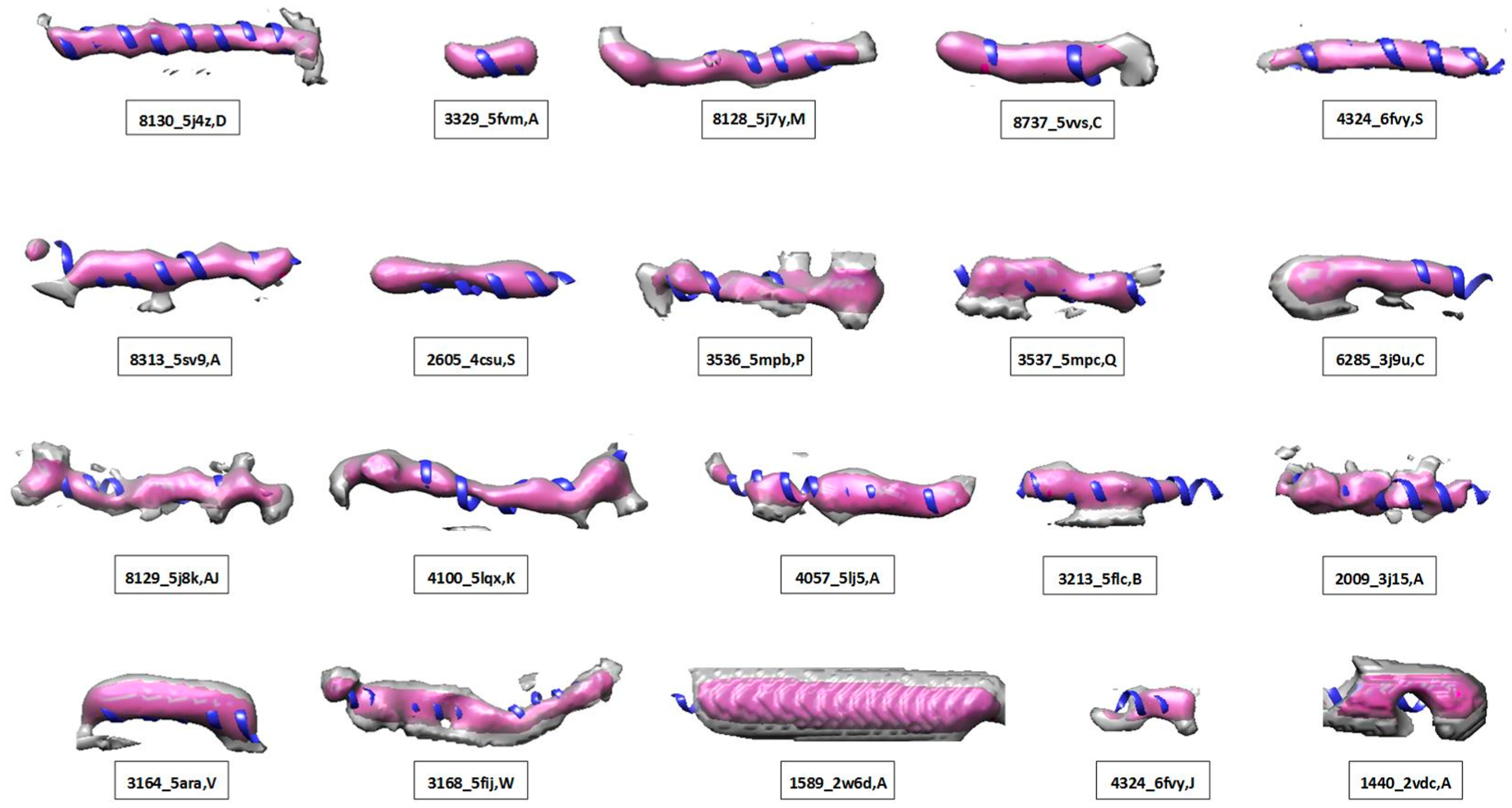
Twenty examples of helical map/model pairs with F₁ similarity scores (see Table 1). The atomic structure of a helix (ribbon) is superimposed on the density extracted using 4 Å radius (pink) and 7 Å radius (gray, to visualize the immediate neighborhood), respectively, around the central axis of the helix. Each helix density is displayed using the threshold that optimizes the F₁ score. Panels are sorted by the F₁ score from top left to lower right (see details in Table 1).

When a helix was not clearly distinguishable from the surrounding density in some spots, such as in EMDB ID 3536 chain P segment 334–356 (middle of the second row in Figure 3), Pden was lower since the indistinguishable density was reflected in VxOut. In this case, the accuracy of the helix density was 0.613, and the F₁ score was 0.698 (Table 1). When a misalignment occurred between helix density and its atomic model, such as in the helix in EMDB ID 3164 chain V from amino acid 29 to 47 (first example in the bottom row in Figure 3), the shifted density contributed to reduced VxInner and increased VxOut. The resulting F₁ score was 0.618 in this case (Table 1).

Table 1.

Various Levels of Cylindrical Similarity Evaluated by Their F₁ Scores for 20 Helices^a

IDA	ChB	segment	F1	PC	RD	TE	resF
8130_5j4z	D	131–161	0.863	0.863	0.863	0.159	5.8
3329_5fvm	A	884–891	0.833	0.851	0.817	0.129	6.7
8128_5j7y	M	63–85	0.794	0.75	0.845	0.137	6.7
8737_5vvs	C	26–39	0.751	0.741	0.76	0.039	6.4
4324_6fvy	S	306–325	0.741	0.817	0.678	0.03	6.1
8313_5sv9	A	161–188	0.738	0.769	0.709	165.048	5.9
2605_4csu	S	43–60	0.717	0.696	0.739	0.105	5.5
3536_5mpb	P	334–356	0.698	0.613	0.809	0.039	7.8
3537_5mpc	Q	253–273	0.688	0.681	0.695	0.046	7.7
6285_3j9u	C	597–616	0.675	0.625	0.734	0.036	7.6
8129_5j8k	AJ	16–47	0.668	0.574	0.797	0.096	7.8
4100_5lqx	K	46–75	0.662	0.592	0.75	0.147	7.9
4057_5lj5	A	841–870	0.646	0.591	0.712	0.035	10
3213_5flc	B	1736–1762	0.632	0.658	0.608	0.085	5.9
2009_3j15	A	176–198	0.621	0.604	0.64	0.132	6.6
3164_5ara	V	29–47	0.618	0.515	0.774	0.192	7.4
3168_5fij	W	138–182	0.597	0.465	0.831	0.159	7.4
1589_2w6d	A	5–44	0.537	0.392	0.854	0.243	9
4324_6fvy	J	131–141	0.452	0.365	0.592	0	6.1
1440_2vdc	A	619–633	0.41	0.326	0.553	35.314	9.5

^aSee Figure 3. Columns from left to right are (A) EMDB ID, PDB ID; (B) chain ID, amino acid segment of the helix, the best F₁ score; (C) Pden, the accuracy of helix density; (D) Rmod, the accuracy of helix backbone model; (E) the density threshold that maximizes the F₁ score; and (F) resolution of the density map.

The histogram of helix F₁ scores shows that the most frequent F₁ scores were at about 0.55 with about 1,600 helices (Figure 4A). Populations with F₁ scores less than 0.55 sharply reduced as the score decreased. Three examples with F₁ scores lower than 0.55 show a poor match with 0.452, 0.537, and 0.410 F₁ scores (Table 1), respectively (right three examples in the last row in Figure 3). The histogram of helix F₁ scores suggests that below an F₁ score of 0.55, there is a poor map/model similarity of helices.

Figure 4.

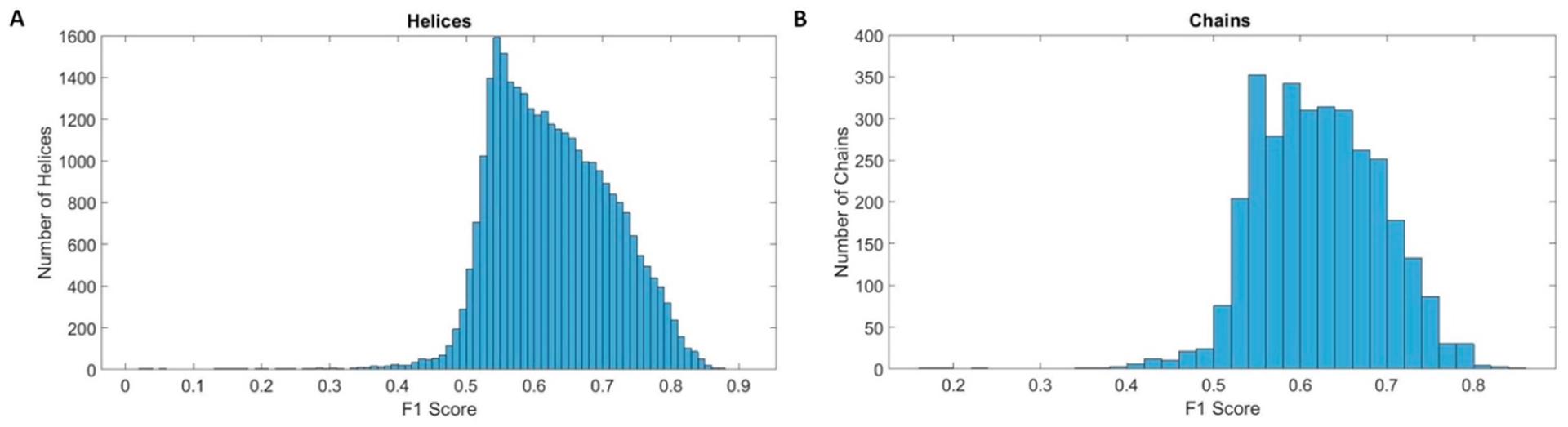
Histograms of F₁ scores in medium-resolution maps: (A) the histograms of F₁ scores for 30,994 helices and (B) the histograms of F₁ scores for 3,247 protein chains.

An averaged F₁ score was calculated at a chain level to represent the overall density fitting at multiple helices in a chain. In some chains, it is possible to have helices with different levels of cylindrical similarity. As an example, in Chain 2 of PDB ID 5ln3, the density regions at five helices have F₁ scores of 0.761, 0.769 (green in Figure 1), 0.631, 0.700 (orange in Figure 1), and 0.567 (red in Figure 1), respectively. The F₁ score of a chain was calculated as a weighted average of F₁ scores of all helices, in which the weights were derived by the lengths of helices. Similar asymmetric distribution of F₁ scores between the left and the right side of the most popular F₁ scores was also observed at the chain level. The most popular score for a chain was between 0.54 and 0.56 (Figure 3B). The results suggest that chains with F₁ scores lower than 0.54 exhibited poor similarity. The scores at the helix level varied greatly, with minimum and maximum F₁ scores of 0.171 and 0.848, respectively.

The F₁ scores are agnostic of the origin of dissimilarities; both errors in maps and in models can lower the score. To compare with another established local measure, we created local resolution maps using the MonoRes tool³⁷ for the 20 helices that were analyzed using cylindrical similarity (shown in Figure 3). MonoRes focuses exclusively on the map quality, and not on the atomic model, so we did not necessarily expect similar results.

To visualize local resolutions in the vicinity of a helix, density regions were extracted using 7 Å radial distance from the central axis determined by AxisComparison. MonoRes produced local resolutions for 18 of the 20 EMDB map entries. All 18 cases were displayed at the density thresholds that maximize the F₁ score in each case. Although local resolution and cylindrical similarity measure different properties at different levels of detail, the two scores share certain similarities. We observed that the best F₁ scores were often associated with more uniform local resolutions at the helix region. The five highest F₁ scores of the 18 cases (top row in Figure 5) had F₁ scores between 0.741 and 0.863. The density at the five helix regions had similar local resolutions of about 5 Å to 7.5 Å (darker blue to light blue in Figure 5). This suggests that helices with the best F₁ scores tended to have similar local resolutions near the high end of the medium-resolution range. We also observed that high F₁ scores were not always associated with high local resolutions. For example, EMDB ID 2605 chain S (second example of the second row in Figure 5) had a good cylindrically shaped density, with an F₁ score of 0.717, whereas voxels on the surface showed about 9 Å resolution (Figure 5). This suggests that cylindrical helix density can be detected accurately in good quality cryo-EM maps, even near the low end of the medium-resolution range. The two cases with the lowest F₁ scores (right two on the bottom row of Figure 5) had missing density regions and hence were weak in cylindrical character. For the helix in EMDB ID 1440, which had an F₁ score of 0.410, many voxels on the surface exhibited low-resolution values of about 10 Å (Figure 5). In the case of the helix in EMDB ID 4324, the F₁ score was 0.452, and voxels with resolutions of about 6 and 10 Å were observed.

Figure 5.

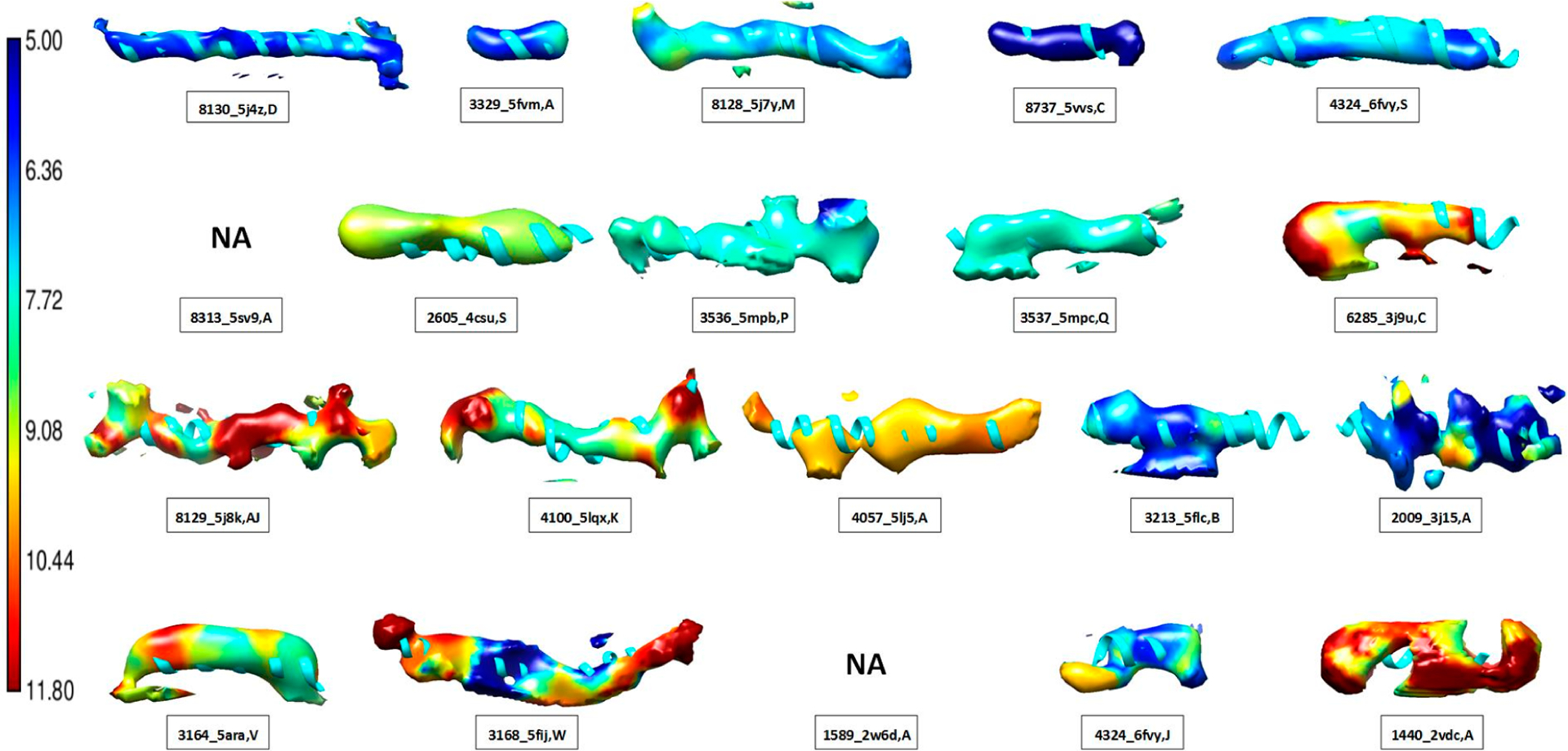
Local resolution of 18 helix regions. Density regions near helices were extracted using a cylinder of 7 Å in radius from the central axis of the corresponding helix model (ribbon). Local resolutions produced using MonoRes²⁹ were used to color the density according to the resolution bar (left). The EMDB ID, PDB ID, and chain ID are provided for each helix. Refer to Table 1 for their amino acid segment and the F₁ score in each case. The threshold that maximizes the F₁ score was used in displaying density. Panels are sorted by the F₁ score such that the upper-left helix has the highest F₁ score and the lower-right has the lowest.

The F₁ score measures the cylindrical similarity between the density and the model at a helix region. This is reflected in the results, showing that the highest scoring densities, such as the top 5 (row 1 in Figure 5), were cylindrical in shape and associated with higher local resolution that is also spatially homogeneous. Those with lower F₁ scores deviated from a cylinder shape and were mostly associated with lower or spatially fluctuating local resolution. F₁ scores collectively compare the density with the model of a helix. Local resolution varies from voxel to voxel, and for poor similarity map/model pairs, we observed that there could be as much as a 5 Å difference in local resolution within the same helix region.

DISCUSSION AND CONCLUSIONS

Quantifying the local fit at the secondary structure level is important for validating medium- (5–10 Å) resolution density maps and their associated atomic models. Earlier local measures focused mainly on the amino acid residue level, which is applicable to higher resolutions at which side chain densities are distinguishable.^31,32 The CC score between the experimental map and a simulated map (based on the model) or the map value at specific side chain atoms was used in earlier work.^31–33 It is more challenging to measure the local fit in medium-resolution maps, since density features at the secondary structure level are less reliable than individual atoms. The proposed F₁ score method is a shape-based geometric measure that does not use CC, and hence it avoids the challenge of producing a realistic expected density map for secondary structures. It also ignores minor differences in side chain appearance and focuses on the shape of a helix backbone that resembles a cylinder. This idea is based on our experience that side chain features are not distinguishable at medium resolution.

Cryo-EM density maps at medium resolution provide significant challenges for interpretation. With a growing number of atomic models derived from such density maps, using both template structures and fitting, it is important to understand how well models fit in reliable density regions of such maps. Since helices often show as cylindrical density in medium resolutions, we proposed a measure of cylindrical similarity for each helix using the natural shape of a helix backbone. The proposed method was applied to 30,994 helices in medium-resolution density maps and shown to be effective in distinguishing different levels of cylindrical similarity. The best F₁ scores tended to be associated with spatially uniform local resolution of about 5 Å to 7.5 Å. Due to its discriminating power, the F₁ score is a potential optimization criterion for the local fitting and refinement of an atomic model at a helix for medium-resolution maps.

In this paper, the F₁ similarity score was designed to be agnostic of the origin of a specific structural mismatch (regions ExMod or ExDen in Figure 2C). This simple design of our score is both an advantage and a limitation. It is an advantage because the measure can be used to quickly extract good matching map/model pairs from the EMDB database without being concerned about lower scoring cases. It is a limitation because, at present, we do not distinguish between regions ExMod or ExDen in Figure 2C for lower levels of similarity (although our Pden and Rmod accuracies in eqs 2 and 3 could provide such a differentiation in future work).

Without knowing the ground truth, it is often difficult to speculate whether density or model is more correct in the lower-scoring cases. For example, algorithmic or conceptual limitations, such as imprecise local refinement or flexible fitting and the use of a global fitting criterion, can place helix fragments into densities that do not support the placement (ExMod). However, heterogeneity of the biomolecular structure, flexibility, or libration of the specimen could conspire to reduce alignment of corresponding image intensities such that an aggressively modeled helix might be more accurate than the weak cryo-EM density in that region. Since models are created with very diverse algorithmic approaches, it is unlikely that a single criterion will do justice to all lower-scoring map/model pairs. However, a low F₁ score could be a starting point for further study of pathological cases detected by it.