Economic Policy Uncertainty Index Meets Ensemble Learning

Abstract

We utilize a battery of ensemble learning techniques [ensemble linear regression (LM), random forest], as well as two gradient boosting techniques [Gradient Boosting Decision Tree and Extreme Gradient Boosting (XGBoost)] to scrutinize the possibilities of enhancing the predictive accuracy of Economic Policy Uncertainty (EPU) index. Applied to a data-rich environment of the Newsbank media database, our LM and XGBoost assessments mostly outperform the other two ensemble learning procedures, as well as the original EPU index. Our LM and XGBoost estimates bring EPU closer to the stylized facts of uncertainty than other uncertainty estimates. LM and XGBoost indicators are more countercyclical and have more pronounced leading properties. We find that EPU is more strongly correlated to financial volatility measures than to consumers’ assessments of uncertainty. This corroborates that the media place a much higher weight on the financial sector than on the economic issues of consumers. Further on, we considerably widen the scope of search terms included in the calculation of EPU index. Using ensemble learning techniques on such a rich set of keywords, we mostly manage to outperform the standard EPU in terms of correlation with standard uncertainty proxies. We also find that the predictive accuracy of EPU index can be considerably increased using a more diversified set of uncertainty-related terms than the original EPU framework. Our estimates perform much better in a monthly setting (targeting the industrial production growth) than targeting quarterly GDP growth. This speaks in favor of uncertainty as a purely short-term phenomenon.

Introduction

After the occurrence of global financial crisis in 2008, the macroeconomic outlook has changed immensely throughout the world. Rising uncertainty has dampened investments, caused considerable disruptions in the financial markets and discouraged entrepreneurs from undertaking any business activity with irreversible costs. In the academic sphere, these circumstances have conditioned the proliferation of research focusing on economic uncertainty, primarily on the methods of quantifying uncertainty and modelling the way it affects various sorts of economic activity. Starting from the position of classical Knightian uncertainty1 (Knight, 1921), the first class of uncertainty indicators uses macroeconomic volatility as a proxy for macro uncertainty (e.g. Asgharian et al., 2015; Cronin et al., 2011). Other authors quantify uncertainty using forecasting disagreement among economic agents (e.g. Bachmann et al., 2013). Finally, there is a vast literature aimed at quantifying uncertainty from media reports. The Economic Policy Uncertainty (EPU) index of Baker et al. (2016) provides possibly the most influential contribution in that respect, and this study aims precisely at assessing the potential methodological improvements of EPU index.

The seminal paper of Baker et al. (2016) utilizes sentiment analysis of articles published in 10 leading US newspapers. They extract articles containing at least one term from each of the following three categories: economic (“economic” or “economy”), policy (“Congress”, “deficit”, “Federal Reserve”, “legislation”, “regulation”, or “White House”) and uncertainty (“uncertain” or “uncertainty”). Scaling and normalizing the monthly count of media articles matching these criteria enables the authors to quantify the EPU index. Baker et al. (2016) investigate the relationship between the EPU index and both firm-level and aggregate level of investments and employment for the US economy. Their results confirm the negative impact of uncertainty shocks on economic activity.

The methodological foundations of Baker et al. (2016) are easily replicable, the search terms can be augmented or altered to match the idiosyncrasies of individual economic sectors or countries, and the quantification procedure can be applied to produce data in basically any preferred frequency from yearly to daily. These useful features have enabled a very wide application scope of EPU index in many economies, rather long time periods and specific economic sectors. Namely, the EPU index is now calculated and regularly published for more than 20 world countries (even its global version is quantified), an extensive range of categorical uncertainty indices is available for a number of countries, and some of them even went a step further to construct the daily version of EPU index.

Such a tremendous applicative scope of the EPU index has also prompted several criticisms, mostly those of methodological nature. Konczal (2012) was one of the first ones to critically assess the index on the account of the chosen set of search terms and the fact that the quantification procedure is automatized (without human reading), making the index upward biased. Krugman (2012, 2013) even amplified this harsh criticism by calling the EPU index a “scam” and a “phony fear factor”. More recent analyses again criticize the lack of human textual analysis in the process of article count (Kaya, 2018).

Such reactions have prompted Baker et al. (2016) to perform a large-scale human audit study of the articles entering the EPU coding, showing that the computer-based EPU is highly correlated to the human-audited one. Moreover, a separate branch of literature has emerged, focusing on the potentials of utilizing machine learning techniques to enhance the accuracy of the EPU index (Azqueta-Gavaldon, 2017; Tobback et al., 2016; Xie, 2020). And this is precisely the niche that we want to tackle with this study.

Our contribution to the literature is manifold. We considerably enrich the set of search terms originally used by Baker et al. (2016) to inspect whether a wider search scope would enhance EPU’s predictive accuracy. Further on, we utilize four separate ensemble learning methods (linear regression model, random forest model, gradient boosting decision tree and extreme gradient boosting) to counteract one of EPU’s nominally most restrictive assumptions: arbitrary set of keywords, chosen with no reference to the theoretical properties of uncertainty. Since economic uncertainty is a latent variable, we rely on the well-established stylized facts of uncertainty as criteria for model fit. Namely, a high-quality uncertainty indicator would have to be highly correlated to other standard uncertainty proxies, it would have to be countercyclical, and have pronounced leading indicator characteristics with regard to economic activity. Therefore, we compare the model fit of the four assessed ensemble learning methods with the original EPU index in terms of the stated criteria. Our analysis reveals that the ensemble linear regression method and the gradient boosting method mostly outperform the original EPU index in that sense, as well as they considerably enhance EPU’s countercyclicality vis-à-vis the industrial production growth rate and its short-term forecasting accuracy with respect to the same target variable. On the other hand, our specifications targeting quarterly GDP growth rate do not bring added value in comparison to the original EPU index. This result speaks in favor of uncertainty as a purely short-term phenomenon, because higher frequency models generate a much better model fit. Finally, we find that uncertainty quantified via ensemble linear regression is highly sensitive to the choice of analyzed keywords. Examining the combinations of keywords that provide the best model fit, we find that EPU might considerably benefit from expanding the uncertainty-related set of search terms.

Literature Review

The technical flexibility of the EPU index has made it tremendously versatile and useful for a wide variety of macroeconometric applications. For example, Nilavongse et al. (2020) utilized a structural vector autoregression (VAR) to find a negative relationship between an EPU shock and industrial production in the USA.

Many authors inspected various types of Granger causality between EPU and economic activity. Just to mention a few, Čižmešija et al. (2017), as well as Škrabić Perić and Sorić (2018) found that the results are rather heterogeneous across countries.

Another strand of literature focuses on uncertainty spillover effects. To that end, Colombo (2013) showed that a one standard deviation shock to US EPU induces a fall in the European industrial production and prices of − 0.12% and − 0.06%, respectively. Lee (2018) revealed that EPU in Korea is significantly affected by US uncertainty. On the other hand, Goodell et al. (2020) analyzed different types of uncertainty, establishing that election uncertainty drives both EPU and financial uncertainty.

Finally, EPU is even found to be a significant driver of house price volatility (Wang et al., 2020) and Bitcoin returns (Demir et al., 2018).

Parallel to these macroeconomic utilizations of EPU index, a separate literature strand has emerged, making an effort to enhance its leading indicator qualities. One of the pioneer attempts in that sense was provided by Baker et al. (2016) themselves. Namely, the authors provided a human reading of more than 12,000 articles that were automatically coded to enter the EPU count because they contain at least one of the pre-defined keywords from the economic, policy, and uncertainty domain. That audit study had revealed negligible false positive and false positive rates since the correlation between computer and human EPU indices is found to be between 0.86 and 0.93, depending on data frequency.

Other similar studies have focused on optimizing the EPU index via advanced machine learning techniques, without the need of human assistance or extensive, costly and time-consuming audit studies. Tobback et al. (2016) construct the Belgian EPU index from six local newspapers in the period from 2000 to 2013, by counteracting two possibly over-restrictive assumptions of Baker et al. (2016). First, the original EPU index assumes that each keyword entering the index quantification has the same weight. Implementing the support vector machine (SVM) model, Tobback et al. (2016) determine specific weights for each considered keyword. Further on, Tobback et al. (2016) construct their uncertainty index by examining all variations of economic uncertainty, i.e. not specifically related to economic policy uncertainty. The modality annotation algorithm is used for word count of uncertainty-related terms. The authors conclude that the SVM method improves the EPU index in comparison to the original index constructed by Baker et al. (2016). Also, they find that the Belgian EPU index has considerable short-term forecasting power with regard to several Belgian macroeconomic and financial variables. Building upon these promising results, more research has followed.

Azqueta-Gavaldon (2017) proposed an unsupervised machine learning algorithm for constructing the EPU index. The Latent Dirichlet Allocation (LDA) model is used to search for topics of unlabeled articles, while the number of topics is chosen with a Bayesian approach. The analysis is conducted on newspaper articles containing all variations of the terms “economy” and “uncertainty” from The Washington Post, The New York Times, and USA Today from January 1989 to August 2016. The author finds a total of 30 topics explaining EPU, and makes a comparison to eight categorical EPU indices established by Baker et al. (2016). Finally, Azqueta-Gavaldon (2017) finds his index to be highly correlated to the original categorical EPU indices of Baker et al. (2016).

Xie (2020) proposed a novel method to construct sentiment indices with Wasserstein Index Generation model (WIG). WIG is an unsupervised machine learning method, so there is no need for human classifying of newspaper articles from The New York Times, as in Baker et al. (2016). Xie (2020) shows that the EPU index constructed with WIG is significantly correlated with the Baker et al. (2016) EPU index, and it also outperforms the LDA approach.

In contrast to the previous literature, Saltzman and Yung (2018) enriched the input data by gathering information from the Federal Reserve Beige Books to improve the construction of the uncertainty index. They applied a natural language processing model, accounting for positive and negative connotations of uncertainty. Applying principal component analysis on a set of 13 uncertainty fields, Saltzman and Yung (2018) quantified two specific types of uncertainty: Politics and Government Uncertainty, and Business and Economics Uncertainty. Within a vector auto-regressive (VAR) framework, the authors established a significant relationship between uncertainty and several US macroeconomic variables. Moreover, the uncertainty measure by Saltzman and Yung (2018) and the original EPU index were found to be moderately correlated.

Uncertainty can also be measured through online searches by Internet users. Castelnuovo and Tran (2016) proposed a new viewpoint for measuring uncertainty with Google Trends through keywords chosen according to the most used uncertainty words from Federal Reserve’s Beige Book for the US and the Reserve Bank’s Monetary Policy Statement for Australia. The authors found that the Google Trends uncertainty index is moderately correlated with the original EPU index for the US and Australia.

Synthetizing the above literature, it seems that several machine learning techniques offer valuable opportunities for constructing the EPU index without any need for human assistance. Here, we add ensemble learning to the set of previously applied machine learning methods. Relying on the mentioned literature (Azqueta-Gavaldon, 2017; Saltzman & Yung, 2018; Tobback et al., 2016), we postulate that enriching the examined set of keywords should provide a more detailed insight into the true dynamics of economic uncertainty, and highlight EPU’s leading properties vis-à-vis economic activity. As opposed to previous studies, we examine a battery of ensemble learning techniques and inspect which of these approaches brings EPU closer to the stylized facts of uncertainty, i.e. countercyclicality, correlation to standard uncertainty proxies from the literature, and leading indicator properties. The proposed methodological framework is thoroughly explained in the following section.

The Apparatus

The following section provides a detailed explanation of the examined dataset and the utilized methodological framework.

Data

The methodological foundation of the original EPU index is a counter that traces the frequency of articles containing a predefined set of keywords organized into three groups: economic, policy, and uncertainty. Most criticisms of EPU (e.g. Konczal, 2012; Krugman, 2012) focus on the choice of these keywords, demanding robustness testing or human-reading to confirm that EPU indeed measures economic policy uncertainty. Here we bring forward a much wider set of search terms, organized into 11 alternatives search categories within the policy group and 28 specifications within the uncertainty group. The set of keywords for each of the three EPU pillars (economy, policy, and uncertainty) is fundamentally chosen on the basis of Baker et al. (2016) original specification, and additionally expanded considering the contributions of other similar papers such as Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016). Regarding the uncertainty-related terms, we expand the assessed set of terms using synonyms for 'uncertainty' taken from https://www.thesaurus.com/. The utilized keywords are listed in the “Description” column of Table 11 in the “Appendix”, while the “Source” column highlights the papers and Internet sources we build upon. To be specific, elements of the policy group are collected and organized by categories: Financial Regulation, Entitlement Programs, Monetary Policy, Government Spending and Other, Healthcare, Trade policy, National security, Sovereign Debt and Currency Crises, Equity Market, Taxes, and Regulation. The keywords are chosen from multiple papers and coherently presented in Table 11 (“Appendix”). We expand the uncertainty category by experimenting with 28 synonyms for words “uncertain” and “uncertainty”. Their full list is given in Table 11 (“Appendix”). These 28 uncertainty combinations and 11 policy combinations provide a total of 28 × 11 = 308 news-based count indicators, obtained as monthly/quarterly proportions of articles that contain a specific combination of keywords published in US newspapers in English language. An article is included in the frequency count if it contains at least one word from all three categories. For example, in Table 11 (“Appendix”), the first assessed policy group of keywords is Financial Regulation, and the first examined uncertainty synonym is the term “ambigu” with arbitrary word ending (e.g. “ambiguous” or “ambiguity”). We would therefore define the first count indicator ($X_1$) as a proportion of articles containing at least one term from the group economic (“business”, “industry”, “industrial”, “commerce”, “commercial”, “economic”, “economy”), at least one word from the Financial Regulation group of keywords, and an ambiguity-related term.

Table 11.

Data description

Variable	Category	Description	Source	Frequency
EPU components
	Economy	Selected keywords: business, industry, industrial, commerce, commercial, economic, economy	Newsbank database, keywords defined in accordance with Baker et al. (2016)	Monthly
	Financial regulation	Selected keywords: banking supervision, bank supervision, Glass-Steagall, tarp, thrift supervision, Dodd-Frank, financial reform, commodity futures trading commission, cftc, house financial services committee, Basel, capital requirement, Volcker rule, bank stress test, securities and exchange commission, sec, deposit insurance, fdic, fslic, ots, occ, firrea, plant, water, energi*, electr*, coal, environment, farm, 1, percent, 2, 3, fell, 4, rose, stock, market, investor, invest, fund, Yellen, wall, federal deposit insurance corporation	Newsbank database, keywords defined in accordance with Baker et al. (2016), Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016)	Monthly
	Entitlement programs	Selected keywords: entitlement program, entitlement spending, government entitlements, social security, Medicaid, medicare, government welfare, welfare reform, unemployment insurance, unemployment benefits, food stamps, afdc, tanf, wic program, disability insurance, part d, oasdi, Supplemental Nutrition Assistance Program, Earned Income Tax Credit, EITC, head start program, public assistance, government subsidized housing, school, student, colleg*, univers*, educ, children, health, airlin*, medic, patient, insur*, hospit*, care, doctor, job security, patient protection and affordable care act, unemployment extension	Newsbank database, keywords defined in accordance with Baker et al. (2016), Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016)	Monthly
	Monetary policy	Selected keywords: federal reserve, the fed, money supply, open market operations, quantitative easing, monetary policy, fed funds rate, overnight lending rate, Bernanke, Volker, Greenspan, Yellen, central bank, interest rates, fed chairman, fed chair, lender of last resort, discount window, European Central Bank, ECB, Bank of England, Bank of Japan, BOJ, Bank of China, Bundesbank, Bank of France, Bank of Italy, fed, economi*, rate, growth, economist, inflat*, econom*, American recovery and reinvestment act of 2009, austerity, bank loan, bank rate, bank regulation, bankruptcy, federal funds rate, price level	Newsbank database, keywords defined in accordance with Baker et al. (2016), Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016)	Monthly
	Government spending and other	Selected keywords: government spending, federal budget, budget battle, balanced budget, defense spending, military spending, entitlement spending, fiscal stimulus, budget deficit, federal debt, national debt, Gramm-Rudman, debt ceiling, fiscal footing, government deficits, balance the budget, budget, cut, bill, congress, propos*, would, spend, legisl*, senat, plan, fiscal, budget cut, fiscal cliff, fiscal policy, military budget	Newsbank database, keywords defined in accordance with Baker et al. (2016), Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016)	Monthly
	Healthcare	Selected keywords: health care, Medicaid, Medicare, health insurance, malpractice tort reform, malpractice reform, prescription drugs, drug policy, food and drug administration, FDA, medical malpractice, prescription drug act, medical insurance reform, medical liability, part d, affordable care act, Obamacare, health, airlin*, medic*, patient, insur*, hospit*, care, doctor	Newsbank database, keywords defined in accordance with Baker et al. (2016) and Azqueta-Gavaldon (2017)	Monthly
	Trade policy	Selected keywords: import tariffs, import duty, import barrier, government subsidies, government subsidy, wto, world trade organization, trade treaty, trade agreement, trade policy, trade act, Doha round, Uruguay round, Gatt, dumping, China, Chines, Japan, India, Beij, Japanes*, Asia, Taiwan, Asian, currenc*, trade, foreign	Newsbank database, keywords defined in accordance with Baker et al. (2016) and Azqueta-Gavaldon (2017)	Monthly
	National security	Selected keywords: national security, war, military conflict, terrorism, terror, 9/11, defense spending, military spending, police action, armed forces, base closure, military procurement, saber rattling, naval blockade, military embargo, no-fly zone, military invasion, Iraq, war, militari, Iraqi, Syria, Afghanistan, attack, troop, Russia, Russian, Soviet, Putin, Ukrain, nuclear, Moscow, Iran, refuge, immigr, polici, migrant, Africa, Cuba, Puerto, border	Newsbank database, keywords defined in accordance with Baker et al. (2016) and Azqueta-Gavaldon (2017)	Monthly
	Sovereign debt and currency crises	Selected keywords: sovereign debt, currency crisis, currency crash, currency devaluation, currency revaluation, currency manipulation, euro crisis, Eurozone crisis, European financial crisis, European debt, Asian financial crisis, Asian crisis, Russian financial crisis, Russian crisis, exchange rate, bank, loan, financi*, debt, credit, lender, billion, lend, default, bond, 2008, rate, 2012, 2013, 2011, 2014, 2016, 2009, yield, financial crisis, real estate bubble, recession, slow economic recovery, United States housing bubble	Newsbank database, keywords defined in accordance with Baker et al. (2016), Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016)	Monthly
	Equity market	Selected keywords: stock price, equity price, stock market, 1, percent, 2, 3, fell, 4, rose, stock, market, investor, invest, fund, Yellen, wall, securities and exchange commission, share price, stock exchange	Newsbank database, keywords defined in accordance with Baker et al. (2016); Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016)	Monthly
	Taxes	Selected keywords: taxes, tax, taxation, taxed	Newsbank database, keywords defined in accordance with Baker et al. (2016)	Monthly
	Regulation	Selected keywords: truth in lending, union rights, card check, collective bargaining law, national labor relations board, nlrb, minimum wage, living wage, right to work, closed shop, wages and hours, workers compensation, advance notice requirement, affirmative action, at-will employment, overtime requirements, trade adjustment assistance, Davis-Bacon, equal employment opportunity, eeo, osha, antitrust, competition policy, merger policy, monopoly, patent, copyright, federal trade commission, ftc, unfair business practice, cartel, competition law, price fixing, class action, healthcare lawsuit, tort reform, tort policy, punitive damages, medical malpractice, energy policy, energy tax, carbon tax, cap and trade, cap and tax, drilling restrictions, offshore drilling, pollution controls, environmental restrictions, clean air act, clean water act, environmental protection agency, epa, immigration policy, court, law, legal, case, justic*, rule, investing*, lawyer, judg*, collective agreement, construction permit, emission trading clean air act, environment protection, food price, fuel price, gas price, home price, home sales, national labor relations act, reform, regulation	Newsbank database, keywords defined in accordance with Baker et al. (2016), Azqueta-Gavaldon (2017) and Castelnuovo and Tran (2016)	Monthly
	Uncertainty	Selected keywords: uncertain*	Synonyms for 'uncertainty' taken from: https://www.thesaurus.com/	Monthly
		Synonyms for ‘uncertainty’: ambigu*, ambivalent*, anxiety, concern*, confusi*, distrust*, dubious*, erratic*, hazy, hesitant*, insecur*, mistrust*, precarious*, questionabl*, risk*, skeptic*, suspicio*, trouble*, unclear*, undecide*, undetermine*, unpredictab*, unreliabl*, unresolve*, unsettle*, unsure, vague*
Uncertainty proxies
SPF_GDP		Cross-sectional dispersion (75th percentile minus 25th percentile) of quarterly forecasts of real GDP growth (4 quarter ahead)	Survey of Professional Forecasters, Federal Reserve Bank of Philadelphia	Quarterly
SPF_FED		Cross-sectional dispersion (75th percentile minus 25th percentile) of quarterly forecasts of chain-weighted real federal government consumption and gross investment (4 quarter ahead)	Survey of Professional Forecasters, Federal Reserve Bank of Philadelphia	Quarterly
SPF_CPI		Cross-sectional dispersion (75th percentile minus 25th percentile) of quarterly forecasts of headline CPI inflation (4 quarter ahead)	Survey of Professional Forecasters, Federal Reserve Bank of Philadelphia	Quarterly
VIX		The Chicago Board Options Exchange (CBOE) Volatility Index, measures expected price fluctuations in the S&P 500 Index options over the next 30 days	Yahoo finance	Monthly
sd10		Monthly standard deviation of the US Treasury Bond (10 years maturity) yield	Yahoo finance	Monthly
sd500		Monthly standard deviation of the daily S&P500 market capitalization index	Yahoo finance	Monthly
govt		A disagreement indicator in the vein of Bachmann et al., (2013: 222), based on the responses to the question coded with GOVT in the University of Michigan Surveys of Consumers Time Series Codebook	University of Michigan Surveys of Consumers	Monthly
dis		An "aggregate" disagreement indicator in the vein of Girardi and Reuter (2016: 5) based on the responses to forward-looking questions (coded with PEXP, RINC, BEXP, BUS12, BUS5, UMEX, RATE, and VEH in the University of Michigan Surveys of Consumers Time Series Codebook)	University of Michigan Surveys of Consumers	Monthly
Macroeconomic variables
IND		Year-on-year growth rate of industrial production: manufacturing (NAICS), seasonally adjusted	Federal Reserve Bank of St. Louis	Monthly
GDP		Year-on-year growth rate of real Gross Domestic Product, seasonally adjusted	Federal Reserve Bank of St. Louis	Quarterly

We extract these indicators from Newsbank, the database that collects, organizes, and presents various news stories from US newspapers. Since the same database was also utilized by Baker et al. (2016) for the quantification of several versions of the EPU index, this also enables comparability of results.

In essence, economic uncertainty is a latent variable. It cannot be directly observed, and no one can know with certainty how large it should actually be in a particular phase of the business cycle. What we do know are the theoretically founded stylized facts of uncertainty. First and foremost, uncertainty rises in recessions and recedes in economic expansions. Bloom (2014) finds such countercyclicality of uncertainty in a wide variety of studies dealing with micro (Campbell et al., 2001) and macro uncertainty (Baker et al., 2016; Jurado et al., 2015). To compare the machine learning extensions of the EPU index introduced here and the original EPU index, we will assess correlation coefficients between the observed uncertainty measures and the targeted macro variables, i.e. year-on-year (y-o-y) growth rate of GDP (in the quarterly setting), and the y-o-y growth rate of industrial production (in the monthly setting). An uncertainty indicator with more pronounced countercyclicality (larger negative correlation with economic growth) should theoretically be better than an indicator exhibiting less countercyclicality.

Second, the existing literature offers a plethora of different uncertainty proxies derived from hard or soft (survey) data. To this end, we assess the following uncertainty proxies: VIX volatility (VIX), standard deviation of the S&P500 index (sd500), standard deviation of the 10 years maturity US Treasury Bond yield (sd10), as well as two University of Michigan Consumer Survey disagreement measures: dispersion of consumers’ satisfaction with regard to government’s economic policy (govt) and an aggregate disagreement indicator, measuring the dispersion in consumers’ responses to all forward-looking questions in the Michigan Consumer Survey (dis). The stated variables are in monthly frequencies. The analyzed data span is 1985 January to 2020 March for all variables except VIX, whose data start in 1990 Jan.

We also observe three separate Survey of Professional Forecasters (SPF) disagreement measures in quarterly frequencies: SPF_GDP, SPF_FED, and SPF_CPI. These three variables refer to the dispersion in forecasters’ assessments of future GDP growth, federal government expenditure, and the general price level (respectively). All monthly target variables are also utilized in the quarterly framework (their quarterly estimates are obtained as simple averages for the corresponding months) to question the robustness of the drawn inferences. A detailed description of all considered variables is given in Table 11 (“Appendix”). The main idea in this part of the analysis is to examine whether the hereby proposed uncertainty indicators (obtained via machine learning) are more closely correlated to the above-mentioned uncertainty proxies than the original EPU index itself.

Finally, EPU index is, inter alia, configured as a leading indicator. One of its main ideas is to foreshadow future economic activity (Baker et al., 2016: 1628). In this phase of the analysis, we estimate simple short-run forecasting regressions. The dependent variable in this setting is the growth rate of GDP (in the quarterly setting) or the growth rate of industrial production (in the monthly setting). We assess different forecasting horizons (h = 0,1, 2, …, 12), and for each of these horizons we use the hth lag of the hereby constructed extension of the EPU index as the regressor.

Methodology

We explore ensemble methods based on a linear regression model (LM) as a benchmark, random forest (RF) model as the most famous machine learning approach, and Gradient Boosting Decision Tree (GBDT) with Extreme Gradient Boosting (XGBoost) as one of the most promising competitors. RF already has the status of the “go-to” method in a variety of fields such as computer science (e.g., Joshi et al., 2017) with gaining significance in business and economics (e.g., Ahmad et al., 2020; Montebruno et al., 2020). But, GBDT and XGBoost seem to be taking over the race, bringing more speed and accuracy (e.g., Chen & Guestrin, 2016). Here we explore all four methods to understand which model provides the best estimates for uncertainty.

First, we explore the setup of our research problem. The main goal is to construct an improved uncertainty indicator from 308 possible predictors within ensemble models based on linear regression and decision tree regressions. The sample size is 423 for monthly data and 141 for quarterly data, which raises concerns about having a “big k and small n” problem—in other words, having a large set of predictors (k) compared with sample size (n). The inspected ensemble models can suffer from the overfitting issue, so it is crucial to overcome this problem with a predictors reduction policy.

Linear Regression Approach

For the linear model, we propose that the maximum number of used predictors is approximately four times less than the training set sample size. This way, we have at least four degrees of freedom per predictor [similar rules can be seen in e.g., Green (1991) and Austin and Steyerberg (2015)]. This restriction amounts to 25 predictors for quarterly data, which we also apply for monthly data to ensure comparability of the monthly and quarterly setups. The algorithm for the ensemble based on linear regression has the following steps:

• (i)In each iteration $i=1,2,\dots ,M$, we draw a random sample (without replacement) of 25 predictors ${\mathit{x}}_{{\pi }_i\left(1\right)},{\mathit{x}}_{{\pi }_i\left(2\right)},\dots {\mathit{x}}_{{\pi }_i\left(25\right)}$ from the full set of 308 news-based predictors ${\mathit{z}}_1,{\mathit{z}}_2,\dots {\mathit{z}}_{308}$.
• (ii)
  For every sample, we estimate a linear regression model on the training dataset and predict target variable $\mathit{y}$ with the following formula:

  $${\widehat{\mathit{y}}}_i={\widehat{\beta }}_0+{\widehat{\beta }}_1{\mathit{x}}_{{\pi }_i\left(1\right)}+\cdots +{\widehat{\beta }}_{25}{\mathit{x}}_{{\pi }_i\left(25\right)}$$ 1

  where ${\widehat{\beta }}_0,{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{25}$ are the estimated coefficients.
• (iii)
  Generate final forecast for series $y$ as an equally-weighted average of single model estimates:

  $${\widehat{\mathit{y}}}_{\mathit{LM}}=\frac{1}{M}\sum _{i=1}^M{\widehat{\mathit{y}}}_i$$ 2

Basically, we estimate $M$ regression models with randomly selected 25 predictors and generate the final prediction of an ensemble as an equally-weighted average of single model estimates as in Eq. (2). We propose using $M=1000$ iterations for which the final assessment does not change significantly. Averaging estimates from multiple models is already a well-established approach that produces more accurate estimates than single model estimates (e.g., Claeskens & Hjort, 2008).

Random Forest

The second approach encompasses random forest ensemble modeling. The random forest consists of multiple decision trees where each tree produces a prediction, and the final estimate is the most frequent individual (decision tree’s) forecast or a simple average. In general, it can be used in a classification problem (binary dependent variable) or in a regression analysis problem (numeric dependent variable). This research is a linear regression set up in a random forest environment where we try to find the model with the most important predictors and the best performing model. The algorithm consists of two steps:

• (i)For $i=1,\dots ,M$ we estimate a decision tree on a random sample of 308 news-based indicators and a random subsample of the testing dataset.
• 1.Generate a sample with replacement (or bootstrapped) from the training dataset.
• 2.Grow a decision tree $T_i$ by rerunning the following steps until the stopping criterium is reached (minimum node size). First, draw a random sample of 25 from available 308 predictors, choose the optimal variable, and split point among selected variables. Finally, the node is split into two daughter nodes, so the mean square error is minimized. This way, randomness is introduced into the decision trees via predictors and via sample.
• (ii)
  The ensemble $\left\{T_i,i=1,\dots ,M\right\}$ of $M$ decision trees together make a random forest, and the RF prediction is an equally-weighted average of decision trees’ forecasts:

  $$\widehat{\mathit{T}}=\frac{1}{M}\sum _{i=1}^M{\widehat{\mathit{T}}}_i$$ 3

  where $\widehat{T}$ is a RF estimate of the corresponding $\text{y}$ target series and $\widehat{T_i}$ is an individual decision tree’s estimate. Estimation and comparison are conducted in R software with package randomForest according to the methods reported in Liaw and Wiener (2002). As commented for LM, the RF model can also suffer from the overfitting problem. We circumvent this issue using the backward selection approach. The algorithm is then modified by adding one more step at the end:
• (iii)Calculate the variable importance measure and eliminate the variable with the lowest contribution. Return to the first step.

The basic idea is to start with the full model and exclude one predictor in each iteration until there is only one left. The elimination criterion is one of the importance measures calculated for each predictor in every iteration (available in randomForest R package). We use the total change in node impurities from splitting on the predictor, averaged over all trees. In RF with a continuous target variable this amounts to calculating the sum of squared residuals (detailed explanation in Sandri & Zuccolotto, 2010). In the end, we compare all estimated random forest models on the testing part of the data by calculating the root mean squared error (RMSE) between the forecasted and observed target series. The model that has the smallest RMSE and the number of predictors smaller than 25 is chosen for the final model. Again, we use 25 as the maximum number of predictors to preserve comparability with LM and ensure parsimony. We explore the sensitivity of parameter $M$ (the number of trees) and the number of predictors (instead of 25) with a grid analysis. The results imply that changing the number of predictors doesn’t have a significant impact on RMSE, while setting $M=500$ provides enough trees for an accurate estimate. Additionally, the results in Biau (2012) confirm that the additional variables do not increase RMSE if strong predictors are included.

Gradient Boosting Decision Tree

Gradient boosting, defined in Friedman (2001) and Friedman et al. (2000), is also one of the ensemble methods based on decision trees. At first glance, it looks like a special case of a RF model (consisting of multiple decision trees), but it approaches the data differently. The main innovation is the learning rate, which improves the accuracy and robustness of the model. The model starts with a single leaf and, in every new iteration, recursively builds a regression tree from the previous one by minimizing Friedman’s mean squared error. The final prediction is not the average as in the previous two models, yet the last iteration prediction. The steps of the algorithm are:

• (i)
  Start the iterations with the initialization for the (observed) target variable $\text{y}$

  $$G_0\left(x\right)=arg\underset{\gamma }{min}\sum _{j=1}^{N}L\left(y_j,\gamma \right)$$ 4

  where $\gamma$ is the predicted value and $L\left(y_j,G\left(x\right)\right)$ is equal to the squared residual (in general, a differentiable loss function).
• (ii)For iterations $i=1,\dots ,M$
• 1.
  Calculate for every observation $j=1,\dots ,N$ in iteration $i$

  $${\gamma }_j^{\left(i\right)}=-{\left(\frac{\partial L\left(y_j,G\left(x_j\right)\right)}{\partial G\left(x_j\right)}\right)}_{G\left(x\right)=G_{j-1}\left(x\right)}$$ 5

  and construct a regression tree to the values $\left\{{\gamma }_j^{\left(i\right)},j=1,\dots ,N\right\}$.
• 2.
  Create terminal regions $\left\{R_k^{\left(i\right)},k=1,\dots ,K^{\left(i\right)}\right\}$. For every terminal region $k=1,\dots ,K^{\left(i\right)}$, compute

  $${\gamma }_k^{\left(i\right)}=arg\underset{\gamma }{min}\sum _{x_j\in R_k^{\left(i\right)}}L\left(y_j,G_{i-1}\left(x_j\right)+\gamma \right)$$ 6
• 3.
  Update the prediction formula:

  $$G_i\left(x\right)=G_{i-1}\left(x\right)+\nu \sum _{k=1}^{K^{\left(i\right)}}{\gamma }_k^{\left(i\right)}I\left(x\in R_k^{\left(i\right)}\right)$$ 7

where $\nu$ is the learning rate.

The final estimate is $G_M\left(x\right)$. We have explored different values for $M$ and $\nu$ with a grid approach in R package gbm (details in Ridgeway, 2020) to reach an improved estimate of LM or RF model. The final model is chosen as $M=1000$ and $\nu =0.001$, but our sensitivity analysis has established that altering these parameters does not change the results by much (results available upon request). This approach could also suffer from the overfitting problem (having many predictors and small sample size), so we investigated backward selection as in the RF model. For the elimination criterion, we used the relative influence value as described in Friedman (2001).

XGBoost

XGBoost is one of the gradient boosting systems that leans on the previously explained GBDT. The main difference lies in the implementation of gradient boosting, which makes XGBoost faster and more efficient than GBDT. The algorithm exploits the advantages of parallel and distributed computing applicable to this optimization problem. The main contribution is a more efficient linear model solver (than in GBDT) and weighted quantile sketch for approximate tree learning. According to the performed comparison, XGBoost usually outperforms GBDT (Chen & Guestrin, 2016).

We utilized the R package XGBoost and explored various parameters in XGBoost setup using the grid approach. We set the number of iterations at $M=100$ and step size of each boosting at $\eta =0.1$, but the performed sensitivity analysis has shown that the results do not change much by altering these parameters (results available upon request). This approach could also suffer from the overfitting problem (having many predictors and small sample size), so we investigated backward selection as in the RF and GBDT model. For the elimination criterion, we used the relative influence value as described in Chen and Guestrin (2016).

Empirical Results

The dataset is separated into two segments: the training set and test set. The training set comprises the first 300 data points (1985Jan–2009Dec), accounting for approximately 70% of data, while the remaining part is the test dataset, covering the period from 2010Jan to 2020Mar. The models are built on the training part, and compared on the test part. Also, the analysis is performed on a monthly and quarterly basis to check for robustness of our results and to examine possible differences and similarities between the high- and low-frequency approaches.

The pursuit of finding a “better” EPU index starts with analyzing the 308 assessed news-based indicators (i.e. monthly/quarterly relative frequencies of articles contain a specific set of keywords). But to find an improved uncertainty indicator, we need to propose a target variable or an uncertainty proxy to choose a combination of 308 potential candidates. The monthly target variables are sd10, sd500, dis, govt, and VIX, as well as SPF_GDP, SPF_FED, SPF_CPI, sd10, sd500, dis, govt, and VIX in the quarterly setting. Monthly variables are averaged to get quarterly figures. We explore the RF, XGBoost, GBDT approach, and ensemble LM framework.

First, we assess the accuracy of these two models relative to the standard EPU index. As explained in Sect. 3, there is no way to measure, observe, or extract the true figures for economic policy uncertainty, so we look at indicator’s characteristics or a set of stylized facts. An uncertainty indicator should: (1) adequately react to important economic/political events, (2) have countercyclical properties (negative correlation with industrial production rate or GDP growth rate), (3) be highly correlated with other plausible uncertainty proxies, and (4) have pronounced leading characteristics vis-à-vis economic activity.

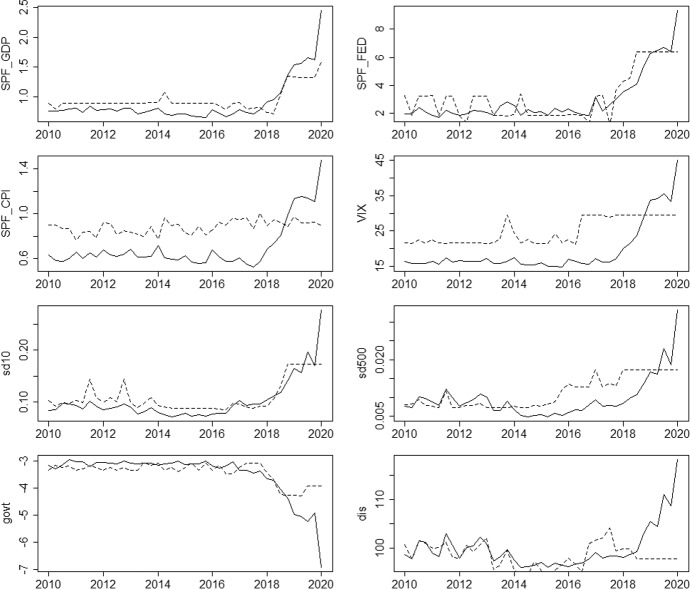
In Figs. 1, 2, 3 and 4 (“Appendix”) we show the estimated uncertainty indicators for the monthly and quarterly setting (respectively). At first glance, it seems that most indicators (excluding SPF_CPI, dis, and govt) strongly spike in the COVID-19 pandemic, giving an initial hint that they might mimic uncertainty well on aggregate.

Fig. 1.

LM and RF estimates for monthly data. Solid and dashed lines represent the LM and RF model, respectively

Fig. 2.

LM and RF estimates for quarterly data. Solid and dashed lines represent the LM and RF model, respectively

Fig. 3.

XGBoost and GBDT estimates for monthly data. Solid and dashed lines represent the XGBoost and GBDT model, respectively

Fig. 4.

XGBoost and GBDT estimates for quarterly data. Solid and dashed lines represent the XGBoost and GBDT model, respectively

Statistically significant and positive correlation coefficients between various assessed indicators should imply that they measure the same phenomenon—uncertainty. Results in Table 1a, b depict how our candidate uncertainty indicators are correlated with other uncertainty proxies that are standard in the literature. For example, the first row of Table 1a implies that the original EPU has a significant correlation coefficient of 0.48 with VIX. Our LM estimates also exhibit significant positive correlation with VIX when the model uses VIX, sd10, and sd500 as target variables (correlation coefficients 0.33, 0.42, and 0.36, respectively), while consumer survey disagreement indicators (dis and govt) do not perform that well. However, overall, our LM-based disagreement indicators (dis and govt, shown in the fourth and fifth row of Table 1a) perform quite better than EPU. It seems safe to say that the obtained correlation coefficients for RF candidates are mostly insignificant or even negatively correlated. Noteworthy exceptions can again be found in the RF-based disagreement indicators (dis and govt), which outperform the standard EPU index.

Table 1.

Correlation coefficients of (a) LM and RF and (b) XGBoost and GBDT uncertainty estimates with standard uncertainty proxies (monthly data)

	LM estimate of					EPU	RF estimate of
	VIX	sd10	sd500	govt	dis		VIX	sd10	sd500	govt	dis
a
VIX	0.33***	0.42***	0.36***	− 0.33***	− 0.11	0.48***	0.11	0.11	0.03	− 0.14	0.01
sd10	0.16*	0.23**	0.18**	− 0.17*	− 0.03	0.35***	0.03	0.1	− 0.01	− 0.12	− 0.02
sd500	0.46***	0.59***	0.51***	− 0.41***	− 0.21**	0.58***	0.19**	0.1	0.13	− 0.1	− 0.03
govt	0.6***	0.41***	0.58***	− 0.63***	− 0.71***	0.18**	0.6***	0.53***	0.68***	− 0.13	0.12
dis	0.41***	0.31***	0.40***	− 0.34***	− 0.47***	0.09	0.39***	0.32***	0.46***	0.05	0.12

	XGBoost estimate of					EPU	GBDT estimate of
	VIX	sd10	sd500	govt	dis		VIX	sd10	sd500	govt	dis
b
VIX	0.39***	0.41***	0.31***	− 0.42***	− 0.28***	0.48***	0.16*	0.04	0.09	− 0.24***	0.09
sd10	0.2**	0.23**	0.16*	− 0.2**	− 0.12	0.35***	0.08	− 0.02	0	− 0.09	0.14
sd500	0.53***	0.57***	0.48***	− 0.26***	− 0.41***	0.58***	0.2**	0.09	0.18**	− 0.22**	− 0.01
govt	0.51***	0.48***	0.65***	0.11	− 0.63***	0.18**	0.5***	0.68***	0.64***	− 0.47***	− 0.42***
dis	0.35***	0.36***	0.43***	0.22**	− 0.42***	0.09	0.25***	0.44***	0.38***	− 0.24***	− 0.19**

Pearson’s correlation coefficient is calculated for the period 2010Jan–2020Mar

*, **, and *** denote 0.1, 0.05, and 0.01 significance (respectively)

The results for XGBoost and GBDT (presented in Table 1b) tell a very similar story. Again, dis and govt (shown in the fourth and fifth row of Table 1b) perform reasonably better than EPU itself. Also, XGBoost estimates seem highly comparable to the LM ones, while GBDT estimates (just as RF indicators from Table 1a) are only sporadically correlated to the main uncertainty proxies.

Uncertainty is a latent variable. No one knows its “true” value and there is no “right” way to quantify it. Furthermore, there is no particular reason why EPU should present the “correct” measure of uncertainty. Even more important, uncertainty is highly multidimensional. Its magnitude in e.g. the financial sector might not at all be related to the magnitude of uncertainty in the consumer sector.

Due to the stated reasons, we opt for a holistic analysis and present the results obtained for a wide variety of uncertainty proxies, ranging from financial volatility indicators, survey disagreement, to the EPU index and our machine learning extensions of EPU.

It is important to realize that news-based uncertainty measures (EPU or its modifications that we propose here) should not necessarily be highly correlated to literally all uncertainty proxies that are usually utilized in the literature. To start with, news media do not reflect all types of uncertainty shocks with the same intensity. This is very important, since the proper choice of an uncertainty indicator highly conditions the empirical results of further macroeconometric analysis (whether uncertainty affects economic activity or not). Researchers should be very meticulous in choosing the proper economic activity indicator as a target variable for a given type of an uncertainty indicator.

In our case, it turned out that EPU is not highly related to consumer disagreement indicators. On the other hand, it is significantly positively correlated to financial volatility indicators. This comes as no surprise since the US economy evolves around the financial market, and the media extensively cover stories related to the financial sector (e.g. Engelberg & Parsons, 2011). Likewise, it seems that the ensemble learning methods utilized on a much wider set of keywords (see Table 11 in the “Appendix”) are able to bring the EPU index much closer to consumers’ assessments of uncertainty (the last two rows of Table 1a, b).

An uncertainty indicator should also be countercyclical, i.e. negatively correlated with economic growth. The results in Table 2 show that the EPU index is not significantly correlated with the industrial production growth rate, while our uncertainty estimates based on sd10, sd500, and VIX are significantly correlated with the industrial production for all four estimation procedures (LM, RF, XGBoost, and GBDT). These results might be interpreted as an initial hint that EPU might benefit from the ensemble learning framework proposed here. Estimates based on average disagreement (dis) and government disagreement (govt) exhibit mixed results (the correlation is sometimes positive or even insignificant).

Table 2.

Correlation coefficient of uncertainty estimates with industrial production y-o-y growth rate

	LM	RF	XGBoost	GBDT
VIX	− 0.33***	− 0.19**	− 0.31***	− 0.21**
sd10	− 0.19**	− 0.12	− 0.26***	− 0.17*
sd500	− 0.32***	− 0.27***	− 0.37***	− 0.36***
govt	0.32***	− 0.21**	− 0.40***	− 0.03
unct_dis	0.41***	0.11	0.41***	0.5***

Pearson’s correlation coefficient is calculated for the period 2010Jan–2020Mar. The correlation of EPU with industrial production is − 0.08

*, **, and *** denote 0.1, 0.05, and 0.01 significance

In the following step, we investigate the predictive accuracy of hereby assessed uncertainty indicators. We explore a simple linear regression model with the industrial production growth rate as the regressand and we use a lagged uncertainty indicator as the regressor. We compare the performance of these indicators by examining the generated Root Mean Squared Errors (RMSEs). If the RMSE is higher than 100, then the indicator in the denominator generates a more accurate prediction. If RMSE is lower than 100 then the indicator in the numerator generates a lower RMSE. Although we consider h = 0,1,2, …, 12 lags of the assessed uncertainty indicators, we summarize the results in Table 3 by presenting only chosen lag lengths (0, 3, 6, and 12). Table 3 suggests that our uncertainty assessments on average exhibit leading characteristics comparable to that of the standard EPU, or even surpass them. A noteworthy example of the latter case is dis-based uncertainty, while the other four sets of indicators (VIX, sd10, sd500, and govt) bring less added value to the examined forecasting accuracy. It is very interesting to notice that the forecasting accuracy of dis considerably rises with the extension of the examined horizon. The other four sets of indicators perform quite similarly in all examined lag lengths. Namely, dis is a “catch-all” survey-based indicator, derived from agents’ expectations about relevant economic variables (predominantly) in the following 12 months. As the forecast horizon approaches that 12 months, the precision of all dis-based indicators rises steadily.

Table 3.

A comparison of predictive accuracy of ensemble learning models with EPU (monthly data)

	VIX	sd10	sd500	govt	dis	Average
RMSE LM (h = 0)	1.65	1.72	1.65	1.63	1.63	–
Ratio EPU to LM	105.8	101.5	105.8	107.6	107.7	105.7
Ratio EPU to RF	99.8	99.7	100.7	104.0	99.6	100.8
Ratio EPU to XGBoost	105.1	103.9	107.7	100.1	110.1	105.4
Ratio EPU to GBDT	99.8	99.5	103.7	99.0	112.3	102.9
Average	102.6	101.2	104.5	102.7	107.4	103.7
RMSE LM (h = 3)	1.69	1.77	1.70	1.66	1.62	–
Ratio EPU to LM	104.8	100.0	103.9	106.4	109.2	104.9
Ratio EPU to RF	101.5	103.6	103.6	102.6	99.9	102.2
Ratio EPU to XGBoost	103.9	101.6	104.8	100.0	109.9	104.0
Ratio EPU to GBDT	101.6	100.9	105.1	100.0	111.2	103.8
Average	103.0	101.5	104.4	102.3	107.6	103.7
RMSE LM (h = 6)	1.68	1.77	1.70	1.68	1.57	–
Ratio EPU to LM	104.5	99.2	103.3	104.7	111.9	104.7
Ratio EPU to RF	100.6	102.4	102.1	99.8	100.6	101.1
Ratio EPU to XGBoost	103.7	100.6	104.9	99.7	112.9	104.4
Ratio EPU to GBDT	99.9	101.1	102.1	99.5	119.5	104.4
Average	102.2	100.8	103.1	100.9	111.2	103.7
RMSE LM (h = 12)	1.68	1.77	1.71	1.73	1.55	–
Ratio EPU to LM	104.8	99.6	103.3	102.0	113.5	104.6
Ratio EPU to RF	102.5	101.5	103.5	99.8	102.6	102.0
Ratio EPU to XGBoost	104.6	100.1	105.2	102.8	114.3	105.4
Ratio EPU to GBDT	101.1	104.7	100.9	101.2	128.3	107.2
Average	103.3	101.5	103.2	101.5	114.7	104.8

RMSEs and corresponding ratios are calculated for the period 2011Jan–2020Mar, after taking the 12th lag of uncertainty indicators into account

Overall, the presented results seem quite promising. Our ensemble learning uncertainty assessments have more pronounced leading characteristics than the original EPU index, LM and XGBoost-based uncertainty generating the most accurate predictions. Almost all of our ensemble learning estimates are more countercyclical than the original EPU, while their correlations with other standard uncertainty proxies reveal somewhat mixed results.

After an in-depth analysis, XGBoost and LM seem to be the best-performing models. There could be several reasons why this happened. XGBoost usually outperforms RF and GBDT on many machine learning competitions, as shown in Nielsen (2016), Chen and Guestrin (2016), or Chen et al. (2015). The main reason is that XGBoost works well for research datasets with a low level of noise. Our research problem consists of 308 news-based indicators covering the same phenomena. In a statistical sense, all variables are proportions, so the noise component is not so pronounced. The LM model mimics the RF model by calculating a final estimate based on regressions instead of decision trees. Again, regression analysis outperforms a decision tree in a setup where there are many predictors and a relatively small noise component, as shown in Rokach and Maimon (2015).

The second part of the analysis concentrates on quarterly data to see if the obtained inferences change when assessing low frequency data. The correlation analysis results in Tables 4 and 5 imply that EPU is more strongly correlated to financial volatility indicators (sd10, sd500, and VIX) than to consumer of professional forecasters’ disagreement. Our LM uncertainty assessments again seem to outperform EPU in the majority of model specifications when it comes to disagreement indicators (SPF_GDP, SPF_FED, SPF_CPI, govt, and dis), although this inference is not that robust across specification. For example, some disagreement estimates even exhibit strong negative correlation with the corresponding disagreement indicators. Again, the results for the LM and XGBoost candidates (Tables 4, 6) show a stronger correlation with other uncertainty proxies than RF and GBDT estimates (Tables 5, 7).

Table 4.

Correlation coefficients of LM estimates and EPU with standard uncertainty proxies (quarterly data)

	LM estimate of								EPU
	SPF_GDP	SPF_FED	SPF_CPI	VIX	sd10	sd500	govt	dis
SPF_GDP	− 0.17	− 0.23	0.47***	− 0.2	− 0.14	− 0.2	0.22	0.3*	0.06
SPF_FED	− 0.3*	− 0.39**	0.43***	− 0.38**	− 0.32**	− 0.38**	0.42***	0.47***	0.05
SPF_CPI	− 0.21	− 0.23	0.26*	− 0.24	− 0.21	− 0.26	0.24	0.35**	0.0
VIX	0.3*	0.2	− 0.22	0.25	0.27*	0.26*	− 0.31**	− 0.15	0.54***
sd10	0.19	0.13	− 0.17	0.15	0.19	0.17	− 0.2	− 0.07	0.43***
sd500	0.42***	0.32**	− 0.35**	0.36**	0.38**	0.38**	− 0.43***	− 0.29*	0.55***
govt	0.62***	0.71***	− 0.36**	0.7***	0.66***	0.7***	− 0.69***	− 0.75***	0.32**
dis	0.43***	0.51***	− 0.31**	0.47***	0.43***	0.48***	− 0.4***	− 0.54***	0.05

Pearson’s correlation coefficient is calculated for the period 2010Q1–2020Q1

*, **, and *** denote 0.1, 0.05, and 0.01 significance

Table 5.

Correlation coefficients of RF estimates and EPU with standard uncertainty proxies (quarterly data)

	RF estimate of								EPU
	SPF_GDP	SPF_FED	SPF_CPI	VIX	sd10	sd500	govt	dis
SPF_GDP	− 0.13	− 0.15	− 0.19	− 0.21	− 0.27*	− 0.04	− 0.04	0.28*	0.06
SPF_FED	− 0.39**	− 0.36**	− 0.2	− 0.37**	− 0.42***	− 0.23	0.15	0.3*	0.05
SPF_CPI	− 0.16	− 0.23	− 0.27*	− 0.16	− 0.24	− 0.15	− 0.15	0.14	0.0
VIX	0.15	0.11	0.04	0.16	0.07	0.18	− 0.19	− 0.01	0.54***
sd10	0.05	0.06	− 0.01	0.01	− 0.02	0.11	− 0.08	0.06	0.43***
sd500	0.24	0.21	0.13	0.26	0.18	0.25	− 0.21	− 0.09	0.55***
govt	0.68***	0.67***	0.55***	0.68***	0.77***	0.61***	− 0.48***	− 0.26*	0.32**
dis	0.41***	0.47***	0.35**	0.47***	0.54***	0.42***	− 0.27*	− 0.14	0.05

Pearson’s correlation coefficient is calculated for the period 2010Q1–2020Q1

*, **, and *** denote 0.1, 0.05, and 0.01 significance

Table 6.

Correlation coefficients of XGBoost estimates and EPU with standard uncertainty proxies (quarterly data)

	XGBoost estimate of								EPU
	SPF_GDP	SPF_FED	SPF_CPI	VIX	sd10	sd500	govt	dis
SPF_GDP	− 0.14	− 0.13	− 0.17	− 0.15	− 0.06	− 0.02	0.2	0.04	0.06
SPF_FED	− 0.31**	− 0.26*	− 0.26*	− 0.26*	− 0.16	− 0.11	0.38**	− 0.03	0.05
SPF_CPI	− 0.15	− 0.16	− 0.14	− 0.14	− 0.06	− 0.05	0.24	0	0.0
VIX	0.28*	0.31**	0.29*	0.3*	0.47***	0.44***	− 0.28*	0.46***	0.54***
sd10	0.17	0.23	0.2	0.21	0.38**	0.34**	− 0.17	0.38**	0.43***
sd500	0.38**	0.4***	0.4**	0.4***	0.55***	0.5***	− 0.41***	0.5***	0.55***
govt	0.66***	0.61***	0.59***	0.61***	0.45***	0.47***	− 0.68***	0.4**	0.32**
dis	0.42***	0.41***	0.38**	0.39**	0.29*	0.28*	− 0.46***	0.21	0.05

Pearson’s correlation coefficient is calculated for the period 2010Q1–2020Q1

*, **, and *** denote 0.1, 0.05, and 0.01 significance

Table 7.

Correlation coefficients of GBDT estimates and EPU with standard uncertainty proxies (quarterly data)

	GBDT estimate of								EPU
	SPF_GDP	SPF_FED	SPF_CPI	VIX	sd10	sd500	govt	dis
SPF_GDP	− 0.08	0.02	− 0.19	− 0.33**	0.05	− 0.33**	0.18	0.32**	0.06
SPF_FED	− 0.22	− 0.24	− 0.44***	− 0.56***	− 0.1	− 0.59***	0.31**	0.28*	0.05
SPF_CPI	− 0.12	− 0.07	− 0.38**	− 0.38**	0	− 0.38**	0.16	0.21	0.0
VIX	0.26	0.14	− 0.26	− 0.26	0.3*	− 0.05	− 0.05	0.04	0.54***
sd10	0.17	− 0.02	− 0.21	− 0.23	0.15	− 0.15	0.01	0.07	0.43***
sd500	0.35**	0.21	− 0.22	− 0.12	0.34**	0.1	− 0.15	− 0.04	0.55***
govt	0.5***	0.62***	0.51***	0.74***	0.47***	0.85***	− 0.7***	− 0.08	0.32**
dis	0.31**	0.42***	0.45***	0.7***	0.23	0.58***	− 0.42***	0.03	0.05

Pearson’s correlation coefficient is calculated for the period 2010Q1–2020Q1

*, **, and *** denote 0.1, 0.05, and 0.01 significance

After inspecting quarterly correlations of observed uncertainty proxies with our candidates for the improved EPU indicator, we conclude that EPU is very robust and it is rather hard to beat its original version. Our uncertainty estimates based on sd10, sd500, and VIX generate very similar results to those of the original EPU index, while our LM estimates based on survey disagreement mostly generate higher positive correlations than EPU, depending on the chosen specification. In line with the inferences obtained from monthly data, our LM and XGBoost predictors seem to outperform the RF and GBDT ones.

The second criterion questions the countercyclical property. The correlation between GDP y-o-y growth rate and EPU is − 0.44 and is statistically significant at 1% level. As shown in Table 8, our machine learning estimates of uncertainty show weak and insignificant correlations with GDP, implying that our quarterly uncertainty estimates are not countercyclical. The only exception is XGBoost, yielding several significant correlations.

Table 8.

Correlation coefficient of uncertainty estimates with GDP y-o-y growth rate

SPF_GDP	SPF_FED	SPF_CPI	VIX	sd10	sd500	govt	dis
Model: LM
− 0.23	− 0.14	0.29*	− 0.19	− 0.22	− 0.21	0.21	0.13
Model: RF
− 0.04	− 0.12	− 0.19	− 0.07	0.09	− 0.15	− 0.09	− 0.02
Model: XGBoost
− 0.21	− 0.17	− 0.23	− 0.19	− 0.37**	− 0.36**	0.2	− 0.35**
Model: GBDT
− 0.2	− 0.01	0.24	0.07	− 0.21	− 0.03	− 0.04	− 0.13

Pearson’s correlation coefficient is calculated for the period 2010Q1–2020Q1

*, **, and *** denote 0.1, 0.05, and 0.01 significance

Further on, we inspect the leading characteristics of ensemble learning uncertainty estimates (Table 9). For shorter prognostic horizons, RMSEs generated by EPU are on average around 10% lower than for the ensemble learning candidates. At longer horizons, the RMSE ratios evolve around 100, implying no particular difference between the RMSEs of EPU and our uncertainty estimates. Overall, it seems very safe to conclude that EPU has far more pronounced leading characteristics in the monthly setting than in the quarterly one.

Table 9.

A comparison of predictive accuracy of ensemble learning models with EPU (quarterly data)

	SPF_GDP	SPF_FED	SPF_CPI	VIX	sd10	sd500	govt	dis	Average
RMSE LM (h = 0)	0.71	0.72	0.71	0.71	0.71	0.73	0.72	0.72	–
Ratio EPU to LM	89.5	88.2	90.0	89.3	89.3	87.9	89.1	88.8	89.0
Ratio EPU to RF	87.5	88.1	87.4	87.8	88.4	89.4	87.7	87.5	88.0
Ratio EPU to XGBoost	88.4	89.8	89.4	94.9	94.3	94.5	88.9	89.6	91.2
Ratio RF to GBDT	89.0	87.4	90.6	89.0	87.4	88.7	87.7	88.0	88.5
	88.6	88.4	89.4	90.3	89.9	90.1	88.4	88.5
RMSE LM (h = 1)	0.72	0.73	0.71	0.72	0.73	0.73	0.73	0.73	–
Ratio EPU to LM	94.0	93.7	95.4	94.1	93.5	93.2	93.4	93.6	93.9
Ratio EPU to RF	93.3	94.9	93.7	93.4	95.6	93.3	93.3	93.3	93.9
Ratio EPU to XGBoost	93.8	94.7	94.3	96.5	97.3	98.7	93.4	94.4	95.4
Ratio RF to GBDT	94.8	93.3	95.0	96.0	93.2	95.2	93.2	93.6	94.3
	94.0	94.2	94.6	95.0	94.9	95.1	93.3	93.7
RMSE LM (h = 2)	0.72	0.72	0.71	0.72	0.72	0.73	0.72	0.72	–
Ratio EPU to LM	92.5	92.4	93.8	93.0	93.1	91.9	93.1	92.9	92.8
Ratio EPU to RF	91.5	93.8	91.6	91.5	94.3	92.0	93.5	91.6	92.5
Ratio EPU to XGBoost	93.0	94.8	93.5	98.0	98.6	101.0	92.1	93.9	95.6
Ratio RF to GBDT	94.1	91.8	95.9	95.0	91.4	92.0	91.8	93.3	93.2
	92.8	93.2	93.7	94.4	94.4	94.2	92.6	92.9
RMSE LM (h = 4)	0.72	0.72	0.71	0.72	0.72	0.72	0.70	0.71	–
Ratio EPU to LM	98.9	99.2	100.2	98.5	99.1	98.3	102.0	99.8	99.5
Ratio EPU to RF	97.9	104.4	97.8	98.7	103.5	97.7	102.0	98.1	100.0
Ratio EPU to XGBoost	103.0	101.5	102.0	100.4	102.3	104.5	100.4	102.2	102.0
Ratio RF to GBDT	101.0	99.6	97.8	100.5	97.7	97.7	102.4	101.5	99.8
	100.2	101.2	99.5	99.5	100.7	99.6	101.7	100.4

RMSEs and corresponding ratios are calculated for the period 2011Q1–2020Q1, after taking the 4th lag of uncertainty indicators into account

After inspecting both monthly and quarterly assessments, we can conclude that there is some room for improvement of EPU’s accuracy via ensemble learning. On the monthly basis, several of our specifications manage to outperform EPU in terms of correlation with standard uncertainty proxies. Our LM estimates based on sd10, sd500, and VIX behave more as an uncertainty indicator than the original EPU does. Our XGBoost estimates provide very similar results, as opposed to standard RF and GBDT. However, looking at quarterly figures, EPU is more strongly correlated to fundamental uncertainty proxies in most specifications. In terms of countercyclicality, our estimates are more closely related to monthly economic activity than the quarterly one, where EPU easily dominates. Although there has been no formal comparison of EPU’s leading properties for different frequencies of economic activity data, Baker et al. (2016) do find that quarterly investments react much more intensely to an EPU shock than monthly industrial production. Contrary to Baker et al. (2016), our estimates suggest that higher frequency data goes hand-in-hand with enhancing EPU’s predictive accuracy. This is also in line with several other researchers who find that various extensions of EPU index can be used for high-frequency daily forecasts of stock market trends (Liu & Zhang, 2015; Yu et al., 2018) or even cryptocurrencies (Demir et al., 2018). Moreover, the found proportional relationship between EPU’s predictive accuracy and data frequency is in line with the concept of disaster myopia, i.e. the notion that short-run uncertainty is not a significant determinant of agents’ long-run economic behavior (Guttentag, 1986). In that context, future research should certainly devote additional attention to the sensitivity of EPU’s leading characteristics on the frequency of target economic variables.

Additionally, one would generally compare the results obtained here with those generated by similar studies. However, although there are papers applying machine learning principles to the construction of EPU index, their ex-post evaluation analysis is mostly based on examining the correlation between the original and machine learning-based EPU index (Azqueta-Gavaldon, 2017; Saltzman & Yung, 2018; Xie, 2020). We take the analysis a step further by providing a formal comparison between the original EPU index and our ensemble learning estimates of uncertainty through the lens of uncertainty-related stylized facts. Our results are in that sense the most comparable to those of Tobback et al. (2016), who find that their SVM strategy considerably improves the forecasting accuracy of EPU index. Again, it should also be noted that Tobback et al. (2016) perform a forecasting exercise of several macroeconomic indicators in a monthly setting. This once again coincides with our conclusion that ensemble learning functions better in the monthly than in the quarterly setting.

This result could have multiple beneficial effects for policy makers on the one hand, and business decision makers on the other. First, policy makers are able to adapt to the recorded changes in EPU to prevent large deviations from the long-run growth path, i.e. to act countercyclically. Also, they have the power of public communication, meaning that they have a direct impact on EPU’s level. Business decision makers can also adapt to rising uncertainty in a timely fashion by developing business plans resistant to possible economic downturns. It is important to mention that such a transmission mechanism is possible only if economic agents trust the public institutions. In that sense, one potentially interesting direction for further research is to include institutional trust while comparing economic cycles with EPU.

The performed textual analysis of Newsbank media articles and the consequent predictive accuracy of the assessed uncertainty indicators might be rather sensitive to the chosen set of keywords. We explore which keywords and combinations are the most important for every uncertainty proxy and propose the following ranking. Since LM and XGBoost estimates clearly outperform RF and GBDT results in all considered models, we only rank the combinations of keywords for these two methods. Table 10 synthetizes the rankings for LM specifications. For every target variable, we estimate 1000 linear regression models and every model is built with 25 randomly selected news-based predictors. We monitor which predictors are statistically significant (p-value in the t test is lower than 0.05) among estimated models. This enables us to rank variables which are statistically significant the most often.

Table 10.

Top ranked combinations of keywords in LM uncertainty estimates

Variable	Rank	Quarterly data		Monthly data
		Policy category	Uncertainty	Policy category	Uncertainty
SPF_GDP	1	Regulation	Uncertaina
SPF_GDP	2	Monetary policy	Unreliablea
SPF_GDP	3	Sovereign debt and currency crises	Concerna
SPF_FED	1	Monetary policy	Ambivalenta
SPF_FED	2	Sovereign debt and currency crises	Unreliablea
SPF_FED	3	Trade policy	Skeptica
SPF_CPI	1	Sovereign debt and currency crises	Concerna
SPF_CPI	2	Trade policy	Unsettlea
SPF_CPI	3	National security	Hesitanta
VIX	1	Regulation	Erratica	Sovereign debt and currency crises	Uncertaina
VIX	2	Sovereign debt and currency crises	Uncertaina	Sovereign debt and currency crises	Concerna
VIX	3	Government spending and other	Undeterminea	Government spending and other	Undeterminea
sd10	1	Trade policy	Erratica	Trade policy	Erratica
sd10	2	Taxes	Unsettlea	Regulation	Uncertaina
sd10	3	Government spending and other	Erratica	National security	Uncleara
sd500	1	Sovereign debt and currency crises	Uncertaina	Sovereign debt and currency crises	Uncertaina
sd500	2	Government spending and other	Erratica	Trade policy	Erratica
sd500	3	Sovereign debt and currency crises	Erratica	Equity market	Riska
govt	1	Equity market	Riska	Monetary policy	Unpredictabea
govt	2	Financial regulation	Riska	Taxes	Ambigua
govt	3	Trade policy	Anxiety	Financial regulation	Riska
dis	1	Healthcare	Undeterminea	Healthcare	Undeterminea
dis	2	Taxes	Undeterminea	Taxes	Anxiety
dis	3	Equity market	Unpredictabea	Entitlement programs	Unpredictabea

^aDenotes a word root

For example, for the target variable sd10 in the monthly setup, the first news-based combination (Trade policy + erratic*) is significant in all specifications, the second combination (regulation + uncertain*) is significant in 92%, and the third (National security + unclear*) in 89% of all specifications.

Several intriguing results emerge from Table 10. First, top-ranked policy keyword combinations seem to be heavily dependent on the underlying uncertainty indicator. Assessments based on professional forecasters’ disagreement are strongly rooted in sovereign debt and currency issues, as well as in trade and monetary policies. This comes as no particular surprise, bearing in mind that our testing dataset (spanning from 2010Jan to 2020Mar) was severely burdened by fiscal, international trade, and monetary uncertainty in the US. Among many relevant sources of uncertainty, it is definitely worth mentioning the fiscal cliff episode (Davig & Foerster, 2019), the US-China trade war (Liu & Woo, 2018), and the monetary uncertainty induced by permanent speculations on federal funds rate increases after the global financial crisis (Kuttner, 2018). The stated episodes did not merely induce an impulse-type transitory growth in uncertainty, but were intensely debated throughout the examined period. In that sense, it is quite expected that professional forecasters heavily react to these specific classes of uncertainty. On the other hand, our uncertainty estimates based on financial volatility indicators are, again as expected, primarily rooted in different kinds of financial variables (government spending, sovereign debt and currency crises, regulation, etc.) The final subgroup of uncertainty indicators (those based on consumer surveys) are rooted in a wide variety of economic subjects. What strikes the most is that our estimates based on the aggregate disagreement indicator (dis) rank healthcare issues first in both monthly and quarterly specifications. It seems that consumers’ aggregate assessment of economic uncertainty is very closely related to the fact that Medicare beneficiaries are extremely vulnerable to high medical costs (Dickman et al., 2017; Narrang & Nicholas, 2017). This tendency was, of course, even more accentuated in the recent COVID-19 pandemic (Ahmed et al., 2020).

Overall, it should be noted that the obtained rankings are extremely robust to the choice of data frequency (monthly vs. quarterly specification).

Our final word of caution refers to the fact that only a few top-ranked combinations of keywords include the “uncertainty” term itself. On the contrary, they include a very diverse set of uncertainty synonyms which are not initially considered in the original Baker et al. (2016) study. This finding should certainly be taken as an impulse for further research. Namely, the combinations of keywords presented in Table 10 (backed up by ensemble learning) mostly outperform the original EPU index in terms of forecasting accuracy and countercyclicality. If nothing else, this should be a stimulus to widen the “uncertainty” category with additional search terms and see whether similar increases in accuracy can be achieved for the original EPU indexed (without the use of machine learning).

An analogous ranking analysis of the examined combinations of keywords is also performed for the XGBoost estimator. The results are not presented here for the sake of brevity, but the main conclusions remain valid. Most importantly, the top ranked combinations of keywords include “uncertainty” very seldomly, indicating that the quantification of EPU index would surely benefit from widening the set of keywords with several uncertainty synonyms. The only notable exception is that, according to XGBoost estimates, health care issues do not rank that high for consumer survey-based uncertainty indicators.

Conclusion

Ever since the global financial crisis, economic uncertainty indicators have been in the spotlight of academics, policymakers and investors. The recent turmoil due to Brexit, US-China trade war, and especially the COVID-19 pandemic has put the focus of researchers back to economic uncertainty. A focal point in that niche of literature is given to the EPU index. We contribute to that specific literature strand by considerably widening the set of keywords utilized for quantifying EPU. Using four ensemble learning methods, we provide several extensions of the EPU index that are more closely correlated to other standard uncertainty proxies than the EPU index itself. Our estimates seem to be particularly countercyclical vis-à-vis the growth rate of industrial production as a monthly indicator of economic activity, while the analysis targeting quarterly GDP data does not bring much added value. EPU seems to heavily dominate over its machine learning extensions in such specifications. Also, our machine learning uncertainty assessments provide more accurate short run predictions of industrial production, considerably above the forecasting accuracy of EPU. This is particularly important since EPU is originally conceptualized (inter alia) to foreshadow economic activity. The analysis presented here validates EPU’s potential to gauge higher-frequency economic uncertainty, yielding motivation for further research on this topic.

Finally, we rank the specific combinations of keywords included in the LM and XGBoost quantification of EPU index according to standard goodness of fit criteria. We show that the top-ranked combinations include a wide scope of uncertainty synonyms, as opposed to the original EPU index, which comprises only the term “uncertain(ty)” in all its variations. Considering that the hereby presented analysis did yield some improvements in EPU’s accuracy, it would be beneficial to scrutinize whether a more diverse set of uncertainty-related terms could lead to further enhancements of EPU’s leading properties, regardless of the underlying statistical framework.

Appendix

See Table 11 and Figs. 1, 2, 3, and 4.

Funding

This work has been fully supported by the Croatian Science Foundation under the project IP-2018-01-4189.

Declarations

Conflict of interest

No conflicts of interest.

Ethical approval

No particular ethical approval was required for this study because it does not entail human participation or personal data.

Informed consent

No consent was required for this study because it does not entail human participation or personal data. The analysis was based on Newsbank data (a commercial database), with all fees being covered by the project IP-2018-01-4189.