Abstract
The interactions between proteins and ligands are involved in various biological functions. While experimental structures provide key static structural information of ligand-unbound and ligand-bound proteins, dynamic information is often insufficient for understanding the detailed mechanism of protein–ligand binding. Here, we studied the conformational changes of the tankyrase 2 binding pocket upon ligand binding using molecular dynamics simulations of the ligand-unbound and ligand-bound proteins. The ligand-binding pocket has two subsites: the nicotinamide and adenosine subsite. Comparative analysis of these molecular dynamics trajectories revealed that the conformational change of the ligand-binding pocket was characterized by four distinct conformations of the ligand-binding pocket. Two of the four conformations were observed only in molecular dynamics simulations. We found that the pocket conformational change on ligand binding was based on the connection between the nicotinamide and adenosine subsites that are located adjacently in the pocket. From the analysis, we proposed the protein–ligand binding mechanism of tankyrase 2. Finally, we discussed the computational prediction of the ligand binding pose using the tankyrase 2 structures obtained from the molecular dynamics simulations.
Introduction
Molecular recognition through protein–ligand binding is at the core of multiple biological functions. During protein–ligand binding, both proteins and ligands are flexible and adjust to complement each other within their environments. It is important to understand the detailed mechanism of protein–ligand binding for drug discovery and to improve understanding of protein function. The experimental structural data (e.g., X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy) provide the key structural information of the ligand-bound (holo) and ligand-unbound (apo) proteins; however, the static information is insufficient for understanding the protein–ligand binding mechanism, especially for a flexible pocket that contains several subsites. Molecular dynamics (MD) simulation is a powerful tool that provides a description of the dynamics and structures of protein–ligand systems with a high spatial and temporal resolution. Thus, in this study, we aimed to investigate the detailed mechanism of the conformational change in the ligand-binding pocket on ligand binding using MD simulations.
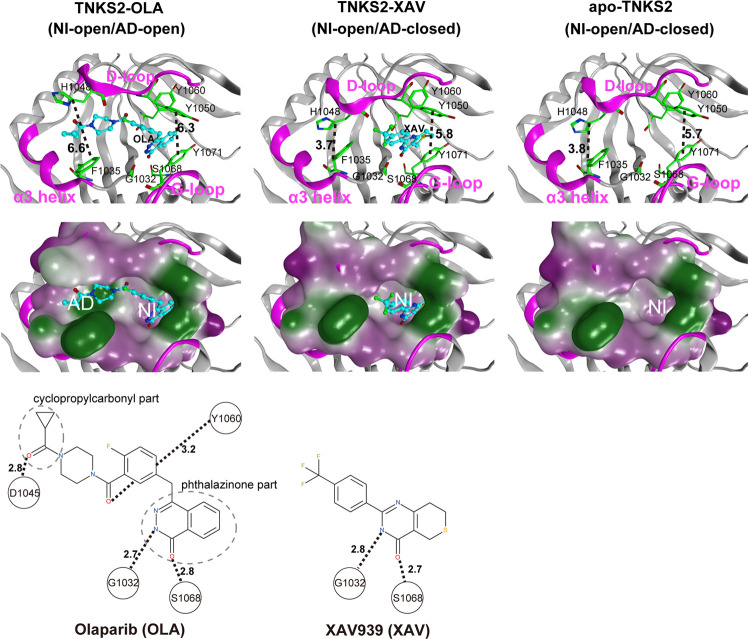
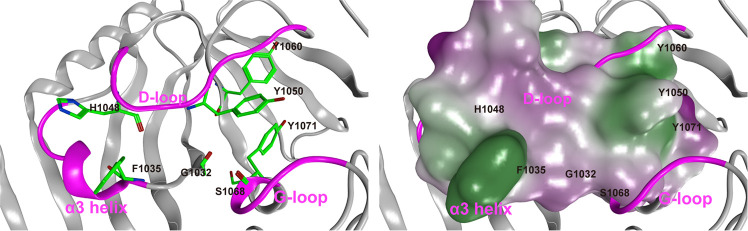
Tankyrase 2 (TNKS2) belongs to the family of poly(ADP-ribose) polymerases (PARPs/EC: 2.4:2.30) that catalyze the transfer of the adenine diphosphate (ADP)-ribose unit from nicotinamide adenine dinucleotide (NAD+) to the substrate protein (PARsylation).1 In this reaction, NAD+ is cleaved into nicotinamide (NI) and an ADP-ribose, while the ADP-ribose covalently binds to the target protein.2 TNKS2 has previously been investigated as a potential drug target because it regulates the activity of the Wnt/β-catenin pathway in colon cancer cells through PARsylation and axin protein destabilization.2−11 Deregulation of the Wnt/β-catenin pathway has been identified in many cancers.3,11,12 Several TNKS2 inhibitors (ligands) have been identified, and the X-ray crystallographic structures of holo- and apo-TNKS2 have been revealed.4,12,13Figure 1 shows the conformations of the ligand-binding pocket of holo- and apo-TNKS2.4,13 The TNKS2 pocket has two subsites: one is the NI subsite and the other is the adenosine (AD) subsite.14,15 The NI and AD subsites are adjacent and share a D-loop. The NI subsite is located between Tyr1050 in the D-loop and Tyr1071 in the G-loop, while the AD subsite is located between His1048 in the D-loop and Phe1035 in the α3 helix. The ligand-binding mode analysis of the X-ray crystallographic structures of TNKS2 complexes revealed that the TNKS2 ligands can be classified into three groups.16−18 The first ligand group contains NI mimetic inhibitors (e.g., XAV939 (XAV)4) that bind only to the NI subsite. A typical ligand from the second group, olaparib (OLA), binds to both NI and AD subsites.13 Finally, the ligands (e.g., IWR-1(IWR1)12) in the third group bind only to the AD subsite. The experimental structure of the TNKS2–XAV complex showed that the XAV molecule from the first ligand group formed hydrogen bonds with Gly1032 and Ser1068 in the NI subsite; however, no hydrogen bond was formed in the AD subsite that was occupied by His1048 and Phe1035 side chains. The experimental structure of the TNKS2–XAV complex assumed the open conformation for the NI subsite and the closed conformation for the AD subsite, which is further described as the NI-open/AD-closed form (Figure 1). Additionally, OLA formed hydrogen bonds with Gly1032 and Ser1068 in the NI subsite and occupied the AD subsite with two hydrogen bonds. Both NI and AD subsites had open conformations, as observed from the structural data of the TNKS2–OLA complex (Figure 1). This type of conformation is henceforth referred to herein as the NI-open/AD-open form. In the experimental structure of the TNKS2–IWR1 complex, IWR1 bound to the AD subsite with two hydrogen bonds; however, no hydrogen bonds with Gly1032 and Ser1068 were formed in the NI subsite, although the IWR1 utilized the entrance of the NI subsite (Figure S1). The ligand-binding pocket took the NI-open/AD-open form. For the structure of apo-TNKS2, the ligand-binding pocket took the NI-open/AD-closed form, which resembles that of the TNKS2–XAV complex despite the absence of a ligand (Figure 1). The comparison of the holo- and apo-TNKS2 structures indicates that although the difference in pocket conformation is explained by the different interactions between the ligand and pocket, the detailed mechanism through which the pocket undergoes conformational changes remains to be elucidated.
Figure 1.
X-ray crystallographic structures of the pocket conformation of tankyrase2-olaparib (TNKS2–OLA) complex, tankyrase2-XAV939 (TNKS2–XAV) complex, and unbound-tankyrase2 (apo-TNKS2). The X-ray crystallographic structures of pocket conformations of the TNKS2–OLA complex, the TNKS2–XAV complex, and apo-TNKS2 are shown in left, center, and right panels, respectively. Top figures show the conformations of the ligand binding pockets. Several key residues (Gly1032, Phe1035, His1048, Tyr1050, Tyr1060, Ser1068, and Tyr1071) are shown using a green stick model. The α3 helix, D-loop, and G-loop regions are shown in magenta. The bound ligands are shown using a ball-and-stick model in cyan. The black dotted lines indicate the distance between the geometric center of the Tyr1050 phenyl ring and that of the Tyr1070 (the ring distance of Tyr1050–Tyr1071) (Å) and the minimum distances between Phe1035 and His1048 (the minimum distance of Phe1035–His1048) (Å). The middle figures show the ligand binding pockets depicted using a molecular surface representation. The hydrophilic and lipophilic regions are drawn in purple and green, respectively. The bottom figures illustrate the structural formula of each ligand. The black dotted lines with numerals represent the distances of hydrogen bonds between the ligand and the amino acids in the binding pocket. AD, adenosine subsite; NI, nicotinamide subsite.
In this study, we investigated the dynamics and conformation of the TNKS2 pocket on ligand binding using MD simulations. By performing four MD simulations of apo- and holo (TNKS2–XAV and TNKS2–OLA)-structures, we identified the four conformations of the TNKS2 pocket: the NI-closed/AD-closed, NI-open/AD-closed, NI-open/AD-semi-open, and NI-open/AD-open forms. The transition between the four conformations was largely influenced by the presence and the structural features of each ligand interacting with the pocket, especially for the NI subsite. In addition, we discussed a computational prediction of the OLA binding pose for the NI-open/AD-open conformation obtained from MD simulations, using molecular docking and molecular mechanics (MM)-based calculations.
Results
Overview of MD Simulations of Apo- and Holo-TNKS2
We investigated the structural behaviors of three MD simulations of apo-TNKS2, the TNKS2–XAV complex, and the TNKS2–OLA complex using the root-mean-square deviation (RMSD) of the Cα atoms of whole proteins and principal component analysis (PCA) of the pocket residues. RMSD analysis showed that the RMSD values of the TNKS2–XAV and TNKS2–OLA complexes were kept at approximately 2.0 Å, while that of apo-TNKS2 increased rapidly from 250 ns to 400 ns and then fluctuated around 2.5 Å (Figure S2). In addition, the projection of the first two principal components clearly indicated that the MD trajectory of apo-TNKS2 during the last 550 ns (250–800 ns) deviated from the other MD trajectories and formed an isolated cluster (Figure S2). Figure 2 illustrates a representative apo-TNKS2 structure during the last 550 ns of MD trajectory simulation. It clearly shows that the NI subsite of apo-TNKS2 became narrow as the Tyr1050 from the D-loop and Tyr1071 from the G-loop approached each other. The distance between the geometric center of the phenyl ring of Tyr1050 and that of Tyr1070 (hereafter referred to as the ring distance of Tyr1050–Ty1071) was 4.5 Å. For all other cases, the ring distances were observed to be >5.0 Å in the experimental and simulation representative structures (Table S1). Conversely, the AD subsite kept a closed conformation resembling that of the experimental structure of apo-TNKS2. The minimum distance between the Phe1035 and His1048 side chains (heavy atoms; hereafter referred to as the minimum distance of Phe1035–His1048) was 4.3 Å. This value was similar to those measured for the experimental structures of apo-TNKS2 and the TNKS2–XAV complex that formed the closed conformation of the AD subsite (Table S1). This structural change in apo-TNKS2 was reproduced by several MD simulations with different initial momenta (data not shown). In the following analysis, we excluded the apo-TNKS2 MD trajectory after 250 ns to focus on identifying the conformational change of TNKS2 upon ligand binding: the observed closing of both the NI and AD subsites was unrelated to the ligand binding structures.
Figure 2.
Representative conformation of apo-TNKS2 during the last 550 ns (250–800 ns) of MD trajectory. (Left) The ligand binding pocket is depicted using a ribbon model. Several key residues (Gly1032, Phe1035, His1048, Tyr1050, Tyr1060, Ser1068, and Tyr1071) are shown using a green stick model. The α3 helix, D-loop, and G-loop regions are shown in magenta. The cyan dotted lines indicate the distance between the geometric center of the Tyr1050 phenyl ring and that of the Tyr1070 (the ring distance of Tyr1050–Tyr1071) (Å) and the minimum distance between the Phe1035 and His1048 side chains (heavy atoms; the minimum distance of Phe1035–His1048) (Å). This conformation shows that the NI-closed/AD-closed formed because the AD subsite remained in the closed conformation and the NI subsites became narrow compared to those observed in the experimental structure of apo-TNKS2 (Figure 1 and Table S1). (Right) The ligand binding pocket is depicted using a molecular surface representation. The hydrophilic and lipophilic regions are drawn in purple and green, respectively. These figures are the same view of the structures depicted in Figure 1.
For a detailed analysis of the change in the pocket conformation on ligand binding, we performed an additional PCA using MD trajectories of apo-TNKS2 (first 250 ns), the TNKS2–XAV complex, and the TNKS2–OLA complex. Figure 3 illustrates the projection of the first and second principal components (PC1 and PC2) and the eigenvectors. The contribution ratios of PC1 and PC2 were 44.4 and 7.8%, respectively. The eigenvector of PC1 corresponds to the open-close motion between the D-loop and the α3 helix, as well as that between the D-loop and G-loop. Alternatively, the eigenvector of PC2 corresponds to the swinging motion of the Phe1035, His1048, Tyr1050, and Tyr1071 side chains in the pocket. The PCA projection shows that the respective MD trajectories of apo-TNKS2 and the TNKS2–OLA complex are classified into nonoverlapping groups; the PC1 distribution of apo-TNKS2 ranged between −25.0 and 5.0, while that of the TNKS2–OLA complex ranged between 5.0 and 25.0. Conversely, PC2 does not largely contribute to the classification of the three MD trajectories. The MD trajectory of the TNKS2–XAV complex has a wide distribution that overlapped with those of apo-TNKS2 and the TNKS2–OLA complex. We noticed that the TNKS2–XAV complex and apo-TNKS2 exhibited similar experimental pocket conformations and showed the NI-open/AD-closed form (Figure 1). The PCA result suggested that the TNKS2–OLA complex and apo-TNKS2 (first 250 ns) pocket maintain conformations similar to their experimental structures (the NI-open/AD-closed form for apo-TNKS2 and NI-open/AD-open form for the TNKS2–OLA complex). Figure 4 shows the time courses of the PC1 values of each MD trajectory. The eigenvector of PC1 corresponding to the open-close motion of the AD subsite shows that the pocket conformation of the TNKS2–XAV complex shuttled between the NI-open/AD-closed and the NI-open/AD-open forms. Figure 5 presents the PC1 values of each MD trajectory in a histogram. The PC1 value distributions are different in each MD trajectory. We selected the representative pocket conformations from the MD trajectories (Figures 3A–F and 6A–F) based on the PC1 value histogram in Figure 5.
Figure 3.
PCA of pocket conformation using MD trajectories of apo-TNKS2, TNKS2–XAV complex, and TNKS2–OLA complex. For the PCA, the first 250 ns of the MD trajectory of apo-TNKS2 and 800 ns trajectories of the TNKS2–XAV complex and the TNKS2–OLA complex were used. The left panel shows the MD trajectories projected onto the plane of the first two components (PC1 and PC2). The contribution ratios of PC1 and PC2 were 44 and 7%, respectively. The black circles represent the projections of the representative conformations of the ligand binding pocket. (A–F) were determined based on the PC1 value histogram shown in Figure 5, and these correspond to conformations of (A–F) of Figure 6. The black circles of 3KR7, 3KR8, and 3U9Y correspond to the ligand-binding pockets of X-ray crystallographic structures of apo-TNKS2, the TNKS2–XAV complex, and the TNKS2–OLA complex. The right panel shows the motions corresponding to the two eigenvectors, respectively. The red regions indicate the position of the 21 amino acid residues used for PCA (see the Methods section). The blue and green arrows represent the motions of PC1 and PC2, respectively.
Figure 4.
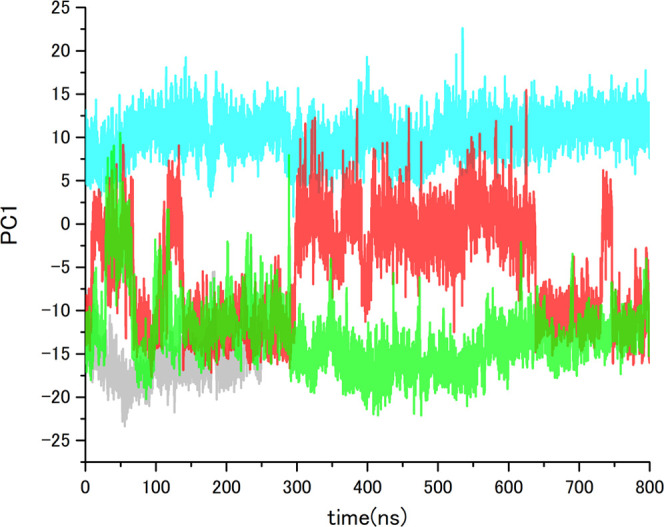
PC1 value time courses of MD trajectories of apo-TNKS2, TNKS2–XAV complex, TNKS2–OLA complex, and apo-TNKS2-CSol. Gray, red, cyan, and green lines indicate the PC1 values of apo-TNKS2, TNKS2–XAV complex, TNKS2–OLA complex, and apo-TNKS2-CSol, respectively. The abscissa is the simulation time (ns), and the ordinate is PC1 value.
Figure 5.
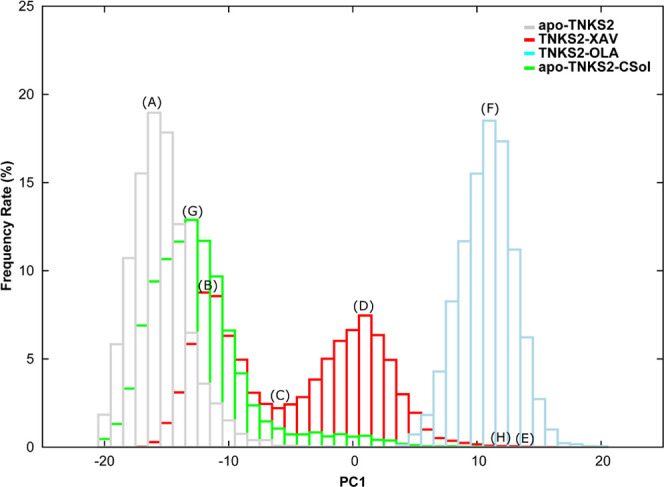
PC1 value histograms of MD simulations of apo-TNKS2, TNKS2–XAV complex, TNKS2–OLA complex, and apo-TNKS2-CSol. Gray, red, cyan, and green boxes indicate the occurrence frequency rate of apo-TNKS2, TNKS2–XAV complex, TNKS2–OLA complex, and apo-TNKS2-CSol, respectively. The abscissa represents the PC1 value, and the ordinate represents the appearance frequency rate (%) of conformations (A–H), thus indicating the representative positions of the respective histograms. (A) The PC1 value peak for apo-TNKS2. (B, D) Two different PC1 value peaks for the TNKS2–XAV complex. (C) The valley between two different PC1 value peaks of the TNKS2–XAV complex. (E) The maximum PC1 value for the TNKS2–XAV complex. (F) The PC1 value peak of the TNKS2–OLA complex. (G, H) The peak and maximum PC1 value of apo-TNKS2-CSol.
Figure 6.
Representative conformations of the ligand binding pocket of MD simulations of apo-TNKS2, TNKS2–XAV complex, TNKS2–OLA complex, and apo-TNKS2-CSol. The conformations (A–H) are labeled with (A–H). The conformations (A–H) in this figure correspond to the positions of (A–H) in Figures 3, 5, and S6. The ligand binding pocket is depicted using molecular surface representations. The hydrophilic and lipophilic regions are drawn in purple and green, respectively. The bound ligands (XAV and OLA) are shown using ball-and-stick models. (A) An apo-TNKS2 conformation (23.3 ns). (B–E) Representative conformations (700.6, 414.5, 580.0, and 549.2 ns, respectively) of the TNKS2–XAV complex. (F) A TNKS2–OLA complex conformation (60.4 ns). Conformations (A–D) exhibit the NI-open/AD-closed form. Conformations (E) and (F) exhibit the NI-open/AD-open form. Conformations (G) and (H) are representative conformations of apo-TNKS2-CSol (616.3 and 49.6 ns), which exhibit the NI-open/AD-closed and NI-open/AD-open forms, respectively.
Pocket Conformation of Apo-TNKS2
Figure 6A shows the representative pocket conformation selected from the first 250 ns of the apo-TNKS2 MD trajectory (conformation A). It can be observed that the NI subsite takes the open conformation, although the ring distance of Tyr1050–Ty1071 (5.0 Å) was shorter than that observed in the experimental structure of apo-TNKS2 (Table S1 and Figure 1). Moreover, the minimum distance of Phe1035–His1048 (4.0 Å) was almost identical to that of the experimental structure of apo-TNKS2. This indicates that the AD subsite remained in the closed conformation (Figure S3) as it did in the experimental structure (Figure 1). In addition, the PCA results suggested (Figure 3) that the MD trajectory of apo-TNKS2 was clustered near the experimental structure and did not overlap with that of the TNKS2–OLA complex. These observations indicate that the opening of the AD subsite did not occur in the MD trajectory of apo-TNKS2 (Figures 3, 6A, and S3). Therefore, the pocket conformation of apo-TNKS2 remained in the NI-open/AD-closed form in the MD simulation.
Pocket Conformation of the TNKS2–OLA Complex
Figure 6F shows the representative pocket conformation of the TNKS2–OLA complex (conformation F). It was observed that the OLA molecule interacted tightly with the pocket; thus, both the NI and AD subsites formed open conformations (Figure S3). Furthermore, the conformation was similar to that observed in the experimental structure of the TNKS2–OLA complex (Table S1 and Figure 1). Moreover, the hydrogen bonds between OLA and the pocket residues (Gly1031, Ser1068, Tyr1060, and Asp1045) were maintained, as in the experimental structure (Figure 1). As discussed in the PCA results mentioned above, the MD trajectory of the TNKS2–OLA complex did not overlap with that of apo-TNKS2. This suggests that the NI and AD subsites maintained the initial conformation in the MD simulation. Conversely, a spread of the trajectory along PC2 indicates that the swinging motion of the Tyr1060, Tyr1071, His1048, and Phe1035 of the NI and AD subsites occurred despite the interaction of OLA and the pocket. These results indicate that the NI-open/AD-open form was maintained in the MD simulation of the TNKS2–OLA complex (Figures 3, 6F, and S3).
Pocket Conformation of the TNKS2–XAV Complex
Further, the PCA projections (Figure 3) showed that the MD trajectory of the TNKS2–XAV complex overlapped with those of apo-TNKS2 and the TNKS2–OLA complex. In addition, the time course of the PC1 values (Figure 4) clearly showed that the PC1 values of the TNKS2–XAV complex repeatedly fluctuated between that of apo-TNKS2 (around −15.0) and the TNKS2–OLA complex (around 10.0) in the MD simulation. The PC1 value histogram of the TNKS2–XAV complex exhibits a bimodal distribution (Figure 5); one peak (approximately −12.0) was located near the apo-TNKS2 peak of distribution, while the other (approximately 1.0) was located near the TNKS2–OLA complex peak of distribution. Based on the PC1 value histogram of the TNKS2–XAV complex shown in Figure 5, the four selected representative conformations (B–E from the MD trajectory) are shown in Figure 6. In the four representative conformations, the XAV molecule tightly interacted with the NI subsite, allowing the NI subsite to form an open conformation. The hydrogen bonds between the XAV molecule and the pocket residues (Gly1031 and Ser1068 in the NI subsite) were maintained as in the experimental structure. In contrast, the AD subsite formed various conformations (Figure 6B–E). As shown in Figure 5, conformation B is observed at one of the two peaks on the bimodal distribution near that of apo-TNKS2 (approximately −12.0). Conformation B took the NI-open/AD-closed form (Figures 6B and S4), as with the experimental structure of the TNKS2–XAV complex (Figure 1 and Table S1). Conformation C (Figure 6C), which was observed at the valley between two different peaks, took the NI-open/AD-closed form. The minimum distance of Phe1035–His1048 was 3.6 Å (Table S1), indicating that the AD subsite was still too narrow to accommodate molecules such as OLA. Conformation D (Figure 6D) was observed at the other peak of the two different peaks on the bimodal distribution (PC1 of around 1.0) (Figure 5). Conformation D indicates a clear difference in the AD subsite from those observed in the experimental conformation of the TNKS2–XAV complex. The minimum distance of Phe1035–His1048 was over 2.0 Å longer than that observed in the experimental conformation of the TNKS2–XAV complex, while it was shorter than that observed in the experimental conformation of the TNKS2–OLA complex (Figures 1 and S4 and Table S1). In comparison to the other conformations with fully opened AD subsites (the experimental conformation and conformation F of the TNKS2–OLA complex), the AD subsite of conformation D did not fully open or exhibit an opening to accommodate the OLA molecule. Hereafter, this conformation was referred to as the “semi-open” conformation. This conformation was specifically observed in the MD trajectory of the TNKS2–XAV complex. Notably, a cavity to accommodate a few water molecules emerged between the D-loop and the XAV molecule. The water molecules occupying the cavity interacted with His1048 and the XAV molecule (Figure S4). Furthermore, the semi-open conformation corresponded to the intermediate state between the closed and open conformations of the AD subsite. The conformation would be further stabilized by the water-mediating interactions. In conformation E (Figure 6E), which was observed at a maximum PC1 value, the AD subsite formed the fully open conformation. Conformation E was similar to the experimental conformation of the TNKS2–OLA complex (Figures 1 and S4 and Table S1). Therefore, conformation E was in the NI-open/AD-open form. Additionally, several water molecules were observed to occupy the fully opened AD subsite and the space between the D-loop and the XAV molecule (Figure S4). The PC1 time course of the TNKS2–XAV complex showed that the fully open conformations emerged transiently (Figure 4). The fully open conformations were stabilized by the binding of OLA to the AD subsite, as observed in the MD simulation of the TNKS2–OLA complex. Alternatively, the ligand interaction with the AD subsite was absent in the TNKS2–XAV complex; thus, we presumed that the fully open conformation transiently appeared in MD simulation of the TNKS2–XAV complex.
Taken together, the PCA results and the structural observations clarified that the pocket conformation of the TNKS2–XAV complex repeatedly changed between the NI-open/AD-closed and the NI-open/AD-open forms in the MD simulation. Furthermore, this conformational change was facilitated by the presence of a stable semi-open conformation, wherein a few water molecules occupied the cavity between the D-loop and the XAV molecule (Figures 6B–E and S4). In contrast, for apo-TNKS2, we observed that the NI subsite became narrower (after 250 ns MD trajectory), while the AD subsite remained in the closed conformation (Figure 2). We also performed additional MD simulations of pseudo-apo-TNKS2 structures derived from the TNKS2–OLA and TNKS2–XAV complex structures to verify the conformational change of the pocket. The results indicated that the AD subsites of both pseudo-apo-TNKS2 structures were limited to the closed conformation after 350 ns, compared with those of the TNKS2–OLA and TNKS2–XAV complexes (Figure S5). Following the comparison of the apo-TNKS2 and TNKS2–XAV complex MD simulations, we hypothesize that a conformational change from an AD-closed conformation to an AD-open conformation can be induced by stabilizing the NI-open conformation in TNKS2. Based on these results, we further hypothesize that the ligand interaction to the NI subsite could affect the overall binding pocket conformation. Therefore, we investigated whether the interactions of the chemical probe molecules with the NI subsite induce the opening of the binding pocket by performing MD simulations of apo-TNKS2 using cosolvent.
Pocket Conformation of Apo-TNKS2 in Cosolvent (Apo-TNKS2-CSol)
We performed an isopropyl alcohol (IPA)–water cosolvent MD simulation of apo-TNKS2 in cosolvent. Apo-TNKS2 in cosolvent was referred to as apo-TNKS2-CSol. The RMSD values of the apo-TNKS2-CSol were maintained stably around 2.0 Å, as observed for the TNKS2–XAV and TNKS2–OLA complexes (Figure S2). The MD trajectory was projected onto the plane defined by the first two PCs shown in Figure 3 (see also Figure S6). The MD trajectory of apo-TNKS2-CSol rarely overlapped with that of the TNKS2–OLA complex. In addition, the PC1 time course showed that the conformation of apo-TNKS2-CSol repeatedly shuttled between the NI-open/AD-closed and the NI-open/AD-open forms in the MD simulation, although the frequency was lower than that of the TNKS2–XAV complex (Figure 4). Furthermore, the PC1 value histogram of apo-TNKS2-CSol showed the difference in distribution compared to those of apo-TNKS2 and the TNKS2–XAV complex. The apo-TNKS2-CSol distribution had a peak (PC1 of approximately −13.0) and the long tail of the right side of the peak overlapped with that of the TNKS2–OLA complex (Figure 5). We selected two representative pocket conformations, G and H, from the MD trajectories based on the PC1 value histogram. These pocket conformations G and H are shown in Figure 6.
Remarkably, for both conformations G and H, the NI subsite maintained an open conformation during apo-TNKS2-CSol MD simulation, despite the absence of a ligand molecule in the NI subsite. In conformation G (Figure 6G), the NI subsite maintained the open conformation and the AD subsite was in the closed conformation. This is supported by the ring distance of Tyr1050–Ty1071 (5.1 Å) and the minimum distance of Phe1035–His1048 in the AD subsite (3.8 Å) (Figure S7), which were almost identical to those of apo-TNKS2 conformation A (Figure S3 and Table S1). Thus, this conformation took the NI-open/AD-closed form. In conformation H (Figure 6H), the NI and AD subsites formed open conformations. The ring distance of Tyr1050–Ty1071 and the minimum distance of Phe1035–His1048 were 7.0 Å and 10.2 Å, respectively. These were longer than those of the experimental conformation of the TNKS2–OLA complex (Figures 1 and S7 and Table S1). Thus, this conformation forms the NI-open/AD-open form.
To investigate the relationship between the behavior of the IPA molecules and the pocket conformation, we counted the IPA molecules in the respective NI and AD subsites (Figure S8). We observed that a few IPA molecules frequently went in and out of the NI subsite. Additionally, it was rare for the IPA molecule to access the AD subsite. The comparison of the apo-TNKS2 MD trajectories with and without IPA molecules suggested that the interactions of IPA molecules with the NI subsite residues prevented the closing of the NI subsite. In addition, the presence of the IPA molecule in the AD subsite was not always identified in the open AD subsite conformation during the MD simulation (Figures 4 and S8). These results suggest that access of the IPA molecule to the AD subsite does not directly contribute to the opening of the subsite, although the interactions between the two might trigger the AD subsite to open.
Interestingly, the semi-open conformation of the AD subsite was not found to be a stable conformation in the histogram of apo-TNKS2-CSol shown in Figure 5. In the TNKS2–XAV complex conformation D (Figures 6D and S4), a cavity between His1048 and the XAV molecule emerged due to the steric hindrance effect between the trifluoromethyl group of the XAV molecule and the D-loop. This cavity was considered to stabilize the semi-open conformation and promote the opening of the AD subsite (Figure S4). Conversely, since the IPA molecule is smaller (only four heavy atoms) than the XAV molecule and diffuses faster on the protein surface, a cavity to accommodate water molecules was hardly formed. Thus, the AD subsite of apo-TNKS2-CSol opened less frequently than that of the TNKS2–XAV complex.
In summary, the apo-TNKS2-CSol MD simulation exhibited repeated conformational changes from the NI-open/AD-closed to the NI-open/AD-open forms, unlike the apo-TNKS2 MD simulations. This reveals that the use of cosolvents prevents the closing of the NI subsite and promotes the opening of the AD subsite. The opening frequency of the AD subsite was lower than that of the TNKS2–XAV complex because the opening mechanism of the AD subsite is a one-step process without a semi-open conformation; meanwhile, the TNKS2–XAV complex has a two-step opening process. The absence of the semi-open conformation would increase the height of the energy barrier to go from a closed to open AD subsite conformation compared to that of the TNKS2–XAV complex.
Discussion
Conformational Change of Ligand-Binding Pocket on OLA Binding
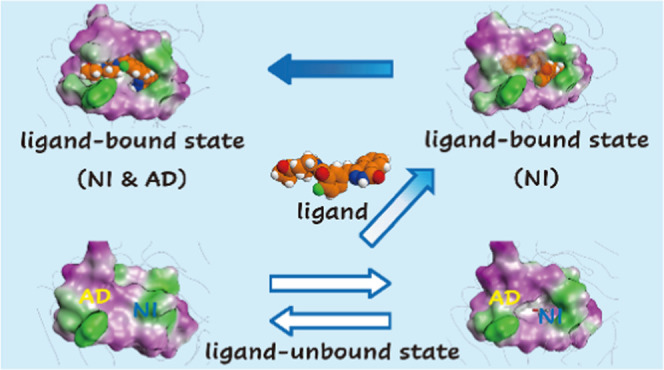
Following analysis of four MD simulations of TNKS2 (apo-TNKS2, TNKS2–XAV complex, TNKS2–OLA complex, and apo-TNKS2-CSol), we identified four representative forms of the ligand-binding pocket: the NI-closed/AD-closed, NI-open/AD-closed, NI-open/AD-semi-open, and NI-open/AD-open forms. The X-ray crystallographic structures of the NI-open/AD-closed and NI-open/AD-open forms have been previously identified, while the NI-closed/AD-closed and NI-open/AD-semi-open forms were detected only in our MD simulations. Furthermore, analysis of the dynamic conformational change of the ligand-binding pocket revealed that the dynamic behavior of the AD subsite was dependent on the conformation of the NI subsite. The conformational transition of the AD subsite occurred when the NI subsite was in the open conformation, while the AD subsite could not open and was limited to the closed conformation when the NI subsite was in the closed conformation. Based on the dynamic information from our MD simulations, we hypothesized that the pocket undergoes conformational changes upon binding the OLA molecule, as shown in Figure 7. We hypothesize that the IWR1 molecule also has a similar binding mechanism to that of the OLA molecule. Further, the different conformations from Figure 7 are referred to as numbers in parentheses.
Figure 7.
Proposed mechanism of conformational changes of ligand-binding pocket on OLA binding. Four conformations (NI-closed/AD-closed (1), NI-open/AD-closed (1′ and 2), NI-open/AD-semi-open (3), and NI-open/AD-open (4) forms) of the ligand binding pocket of TNKS2 are shown. The dotted box indicates the conformational change between the NI-closed/AD-closed (1) and NI-open/AD-closed (1′) forms of apo-TNKS2. The black arrows indicate the main conformational change pathway of TNKS2 upon OLA binding. The ligand binding pocket is depicted using molecular surface representations. IPA molecule shown in the ball-and-stick model is in the NI-open/AD-closed (1′) form. XAV and water molecules shown in ball-and-stick and space-filling models are in the NI-open/AD-closed (2) and NI-open/AD-semi-open (3) forms, respectively. The OLA molecule shown in space-filling model is in the NI-open/AD-open (4) form. The hydrophilic and lipophilic regions are drawn in orange and blue, respectively.
Prior to ligand binding, the NI-closed/AD-closed form (1) and NI-open/AD-closed form (1′) could coexist. The dynamic behavior in the apo state corresponds to those of apo-TNKS2 and apo-TNKS2-CSol. These results suggest that either or both the NI-closed/AD-closed and NI-open/AD-closed conformations emerge as a result of exposure to various experimental solvent conditions. Based on the apo-TNKS2 data, the IPA–water cosolvent revealed that the interactions of IPA molecules with the NI subsite prevented the closing of the NI subsite while inducing the opening of the AD subsite. This suggests that other cosolvents, which correspond to buffer salts and stabilizers existing in the surrounding environment of proteins under physiological conditions, might have a similar effect on the dynamic behavior of the conformation of the ligand-binding pocket.
OLA binding takes place in the two TNKS2 conformations mentioned above. When the OLA molecule binds to the NI-closed/AD-closed form (1), the OLA molecule may access and interact with the NI subsite, inducing a conformational change from the NI-closed/AD-closed form to the NI-open/AD-closed form. Following the conformational change, the phthalazinone part of the OLA molecule would be accommodated in the NI subsite. In the case of the NI-open/AD-closed form (1′) and/or (2), the OLA molecule might bind to the opened NI subsite.
After the formation of hydrogen bonds on the phthalazinone part of the OLA molecule in the NI subsite, the conformational change from the NI-open/AD-closed form (2) to the NI-open/AD-open form (4) occurs through the NI-open/AD-semi-open form (3), as observed in the conformational changes of the TNKS2–XAV complex. The NI-open/AD-semi-open form appeared in the TNKS2–XAV complex and promoted a conformational change from the NI-open/AD-closed form to the NI-open/AD-open form. The frequency with which the NI-open/AD-open form occurred in the TNKS2–XAV complex was approximately 10-fold greater than that in apo-TNKS2-CSol. Finally, the cyclopropylcarbonyl part of the OLA molecule could be accommodated in the AD subsite with the NI-open/AD-open form (4).
Docking Study of the NI-Open/AD-Open Conformations Obtained from MD Simulations
The MD simulations of the TNKS2–OLA complex, TNKS2–XAV complex, and apo-TNKS2–CSol allowed the NI-open/AD-open conformation. Here, we used molecular docking and the single molecular mechanics Poisson–Boltzmann and surface area (MM-PB/SA) method to evaluate the ability to reproduce the experimental binding pose of the OLA molecule (the prediction ability of the OLA binding pose) for a variety of NI-open/AD-open pocket conformations.
Table 1 shows the OLA pose prediction success rates for the sampled conformations. The molecular docking success rates for the TNKS2–OLA complex, TNKS2–XAV complex, and apo-TNKS2-CSol were 88.3, 40.2, and 8.3%, respectively. Interestingly, although the MD trajectory of the TNKS2–OLA complex accommodated the OLA molecule in the binding pocket, approximately 12.0% of the NI-open/AD-open conformations failed to reproduce the experimental pose. In addition, while the molecular docking success rates of both the TNKS2–XAV complex and apo-TNKS2-CSol were low, that of apo-TNKS2-CSol was the lowest. Next, we applied the single MM-PB/SA method to the molecular docking results to take the structural refinement and solvation effect into consideration. The success rates of the single MM-PB/SA method for the TNKS2–OLA complex, TNKS2–XAV complex, and apo-TNKS2-CSol were 98.7, 72.0, and 16.0%, respectively. This result indicates that the single MM-PB/SA method improved the success rates of molecular docking. Thus, while pose prediction based only on molecular docking data is not an effective method to reproduce the experimental binding pose of the OLA molecule, the incorporation of structural refinements and solvation effects can increase the reliability of pose prediction. Remarkably, the success rate of apo-TNKS2-CSol remained low despite using the single MM-PB/SA method. This is mainly due to the conformation differences in the NI subsite of apo-TNKS2-CSol. A comparison between the representative NI-open/AD-open conformations of the TNKS2–OLA and TNKS2–XAV complexes from MD simulations and that of apo-TNKS2-CSol revealed that the shape of the NI subsite in apo-TNKS2-CSol is slightly deformed due to the position of Tyr1050 compared with those in the TNKS2–OLA and TNKS2–XAV complexes (Figure S9). This deformation could prevent binding of the phthalazinone part of the OLA molecule and reduce the molecular docking success rate. Such deformation of the NI subsite is in line with a previous study conducted by Gao et al.19 Their study found that their MD simulations of holo protein lacking ligand, namely, ligand-unbound proteins, did not reproduce holo-like conformations. Therefore, we believe that the protein structures obtained directly from MD simulations of the holo and apo states should be carefully considered before using them for computational drug discovery, including molecular docking and single MM-PB/SA calculations.
Table 1. Success Rate (%) of Olaparib (OLA) Binding Pose Prediction Using MD and X-ray Structures.
| system | number of selected structures | docking | single MM-PB/SA | |
|---|---|---|---|---|
| MD | apo-TNKS2-CSol | 12 | 8.0 (1) | 16.0 (2) |
| TNKS2–XAV | 122 | 40.2 (49) | 72.0 (88) | |
| TNKS2–OLA | 7777 | 88.3 (6871) | 98.7 (7678) | |
| X-ray | TNKS2–XAV | failure | failure | |
| TNKS2–OLA | success | success | ||
Numerals without and with parentheses in the docking and single MM-PB/SA columns indicate the success rate (%) and the number of success poses using docking and the single MM-PB/SA method, respectively.
Conclusions
We performed four conventional MD simulations of apo- and holo-TNKS2 (apo-TNKS2, the TNKS2–XAV complex, the TNKS2–OLA complex, and apo-TNKS2-CSol) conformations and obtained dynamic information regarding the conformation of the ligand-binding pocket. Comparative analysis of the apo- and holo-MD trajectories revealed that the pocket conformation change was characterized by the four representative conformations: the NI-closed/AD-closed, NI-open/AD-closed, NI-open/AD-semi-open, and NI-open/AD-open forms. Furthermore, the NI-closed/AD-closed and NI-open/AD-semi-open conformations were observed only in the MD simulations. The conformational changes in the pocket of TNKS2 were mainly influenced by the presence and structural features of ligands interacting with the NI subsite. Additionally, based on the dynamic behavior of the pocket conformation, we proposed a mechanism through which the pocket conformational changes take place during OLA molecule binding. Furthermore, our results suggested that using cosolvent for MD simulations, which has been used to detect ligand-binding sites, was an effective method to explore the conformational change of a ligand-binding pocket. Moreover, the prediction ability of the OLA molecule binding pose using computational approaches, including molecular docking and MM-based calculations, was not always sufficient, despite the use of the NI-open/AD-open conformation derived from the MD simulations. Our results show the importance of selecting suitable MD simulation structures for computational drug discovery and design.
Methods
Preparation of Initial Systems for MD Simulations
The X-ray crystallographic structures of the TNKS2–OLA complex (PDB ID: 3U9Y),4 TNKS2–XAV complex (PDB ID: 3KR8),13 and apo-TNKS2 (PDB ID: 3KR7)13 were obtained from the Protein Data Bank (PDB).20 Missing atoms from these structures were added using the homology modeling technique with the Molecular Operating Environment software (Chemical Computing Group, Inc.).21 These initially modeled structures were referred to as initial structures, and their pocket conformations were nearly identical to those of the corresponding X-ray crystallographic structures. Next, these initial structures were solvated in a rectangular box containing TIP3P water molecules.22 Each system contained approximately 51 000 atoms. In addition, we prepared a model system of apo-TNKS2-CSol. MD simulations using cosolvents are used in drug discovery to find hidden druggable binding sites, which are named cryptic sites.23−25 For the initial MD simulation system for apo-TNKS2-CSol, the initial TNKS2 structure used in apo-TNKS2 was placed in a rectangular box containing TIP3P water molecules22 and IPA molecules as chemical probes. The IPA molecules were randomly positioned in the box, and the cosolvent contained approximately 2.0 w/w% IPA molecules. The total number of atoms in this system was approximately 54 000.
MD Simulations
MD simulations were performed using the GROMACS version 5.0.6 software.26−30 The AMBER99SB-ildn force field31 was used for proteins and the general amber force field (GAFF)32 was used for OLA, XAV, and IPA (i.e., chemical probe). The partial charges for the ligands were calculated at an RHF/6-31G(d) level using Gaussian 09 software (Gaussian Inc.)33 and the restrained electrostatic potential method. The periodic boundary condition was applied to the initial system, and the temperature and pressure were kept constant using the Nosè–Hoover thermostat34 and Parrinello–Rahman barostat,35 respectively. The linear constraint solver (LINCS) algorithm36 was applied to the covalent bonds, with an integration time step of 2.0 fs taken into consideration. The long-range Coulomb interactions were treated using the particle mesh Ewald method37 and the direct space cutoff distance was set to 10.0 Å. The van der Waals interactions were calculated using a switched cutoff between 8.0 and 10.0 Å. Following solved system energy minimization, the system was gradually heated to 298 K at 100 ps. Next, 800 ns MD simulations under NPT ensemble (P = 1 bar and T = 298 K) were performed. The trajectories of each system were saved every at 100 ps (8000 conformations in each MD trajectory).
RMSD and PCA
To check the conformational change of the entire TNKS2 structure in MD simulations, the RMSD values of Cα atoms from the respective initial structures were calculated. Furthermore, to analyze the dynamical behavior of the ligand-binding pocket in MD simulations, we performed PCA calculations using carefully selected pocket residues. Here, we focused on the 21 amino acid residues (His1031, Gly1032, Ser1033, Phe1035, Ala1038, Ile1039, Gly1043, Phe1044, Asp1045, Glu1046, His1048, Ala1049, Tyr1050, Ile1059, Tyr1060, Phe1061, Ala1062, Lys1067, Ser1068, Tyr1071, and Glu1138) in the pocket. In the experimental structures of the TNKS2–OLA and TNKS2–XAV complexes, these amino acid residues were located near the ligand molecules (OLA and XAV). Heavy atoms of each residue were at a distance shorter than 5.0 Å from any other heavy atom of each ligand. We applied PCA to the Cartesian coordinates of the heavy atoms of the five key residues (Phe1035, His1048, Tyr1050, Tyr1060, and Tyr1071) and the Cα atoms of the other 16 residues to extract the dynamic features of the pocket conformation. RMSD and PCA were performed using the CPPTRAJ module of AmberTools 16.38
Evaluation of Accessibility of IPA Molecules into NI and AD Subsites
To analyze the accessibility of IPA molecules into the NI and AD subsites of the MD simulated apo-TNKS2-CSol, we counted the IPA molecules in the respective subsites and measured the distance to the IPA molecules. To determine accessibility into the NI subsite, we considered that the IPA molecule enters the subsite when both the distances between the IPA C2 atom and the Gly1032 N (main chain nitrogen) atom and between the IPA C2 atom and the Ser1068 OG (hydroxy oxygen) atom were less than 6.0 Å (Figure S10). In addition, to determine accessibility into the AD subsite, we considered that the IPA molecule enters the AD subsite when the distances between the IPA C2 atom and the His1049 Cα atom and between the IPA C2 atom and the Phe1035 Cα atom were less than 6.0 Å. The threshold value of 6.0 Å was determined based on the van der Waals radii information regarding IPA and protein atoms.
Computational Method for Predicting the Binding Pose of the OLA Molecule for TNKS2 Structures Obtained from MD Simulations
We evaluated the ability to reproduce the experimental binding pose of the OLA molecule (i.e., the prediction ability of OLA binding pose) for the TNKS2 structures obtained from MD simulations using molecular docking and MM-based calculations.
Selection of the NI-Open/AD-Open Conformations for Computational Pose Prediction
To evaluate the OLA binding pose prediction, the MD structures with the NI-open/AD-open conformation were used. When selecting these structures, we regarded the TNKS2 structures with PC1 values larger than 5.0 as being in the NI-open/AD-open conformation. These structures were extracted from the MD trajectories of the TNKS2–OLA complex, TNKS2–XAV complex, and apo-TNKS2-CSol. The numbers of the selected conformations of the TNKS2–OLA complex, TNKS2–XAV complex, and apo-TNKS2-CSol were 7777 (of 8000), 122 (of 8000), and 12 (of 8000), respectively.
Molecular Docking
Molecular docking was performed using the Genetic Optimization of Ligand Docking (GOLD) version 5.3.0 (The Cambridge Crystallographic Data Centre) with the GOLD Scoring function.39,40 The standard default settings for the genetic algorithm parameters were used. Before performing molecular docking, the selected protein structures were aligned to the experimental structure of the TNKS2–OLA complex. The center of the binding site for molecular docking was set to the averaged geometrical center of OLA molecule from the MD trajectory of the TNKS2–OLA complex. The binding site radius was set to 10 Å. To rescore and refine the binding poses using the MM-based calculations mentioned below, the 10 highest-scoring docking poses were collected to obtain a variety of binding poses.
Single MM-PB/SA Method
Further, we used the MM-PB/SA method41,42 to incorporate the structural refinement and solvation effect. The MM-PB/SA method was applied to the MM-based energy-minimized structures obtained from molecular docking (hereafter referred to as single MM-PB/SA.43−45) As previously mentioned, the top 10 docking poses of the OLA molecule of each of the selected TNKS2 structures from the MD trajectories were obtained. Each TNKS2–OLA complex was solvated with a rectangular box containing TIP3P water molecules22 and the solvated system was energy-minimized. At this time, OLA molecules, 21 amino acids (His1031, Gly1032, Ser1033, Phe1035, Ala1038, Ile1039, Gly1043, Phe1044, Asp1045, Glu1046, His1048, Ala1049, Tyr1050, Ile1059, Tyr1060, Phe1061, Ala1062, Lys1067, Ser1068, Tyr1071, and Glu1138) of the ligand-binding pocket, and the water molecules were allowed to move for geometry optimization. The single MM-PB/SA binding affinity (ΔGbind) was calculated using the coordinates of the receptor and ligand extracted from an energy-minimized structure of the TNKS2–OLA complex.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
where MM-PB/SA affinity (ΔEbindgas) indicates the binding energy between the receptor and the ligand, which is the difference between the gas-phase potential energy of the complex and the sum of the gas-phase potential energies of the receptor and the ligand, as mentioned in our previous study.44,45 ΔGbind represents the solvation energy difference upon protein–ligand association. The polar solvation term (Gsolv, polar) was estimated using the Poisson–Boltzmann equation and the atomic radii optimized by Tan and Luo, with respect to the reaction field energies computed in the TIP3P explicit solvents and AMBER charges. The grid spacing used was 0.5 A°. The dielectric constants inside and outside the molecule were 1.0 and 80.0, respectively. In the nonpolar solvation term (Gsolv, nonpolar), SASA represents the solvent-accessible surface area that was calculated using Molsurf software, which is based on analytical ideas primarily developed by Connolly.46 Furthermore, SURFTEN and SURFOFF were 0.00542 kcal/(mol Å2) and 0.92 kcal/mol, respectively. The probe radius was 1.4 Å. In this calculation, TΔSbindgas was not taken into consideration.
Success Rate of Ligand Binding Pose Prediction
To evaluate the prediction ability of the OLA binding pose, we calculated the success rate of the OLA binding pose predictions as follows: the RMSD value of the binding pose with the best GOLD score or the highest MM-PB/SA affinity among OLA molecules for each TNKS2 structure was calculated referring to the experimental conformation of the OLA molecule using the SMARTRMS module in GOLD version 5.3.0.39 Pose prediction was considered successful if the RMSD value is ≤2.0 Å. Next, we calculated the success rate for all TNKS2 structures obtained from each MD trajectory using the following equation
where n represents the number of successful poses and N represents the total number of TNKS2 structures selected from each MD trajectory.
Acknowledgments
The authors thank Dr. Takao Otsuka for his valuable comments. The calculations were performed in part using the RIKEN Integrated Cluster of Clusters (RICC) and the HOKUSAI Great Wave and Big Waterfall systems at RIKEN.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c02159.
(Figure S1) The X-ray crystallographic structures of the pocket conformation of TNKS2−IWR1 complex; (Table S1 and Figures S2-S11) Additional data of MD simulations of apo-TNKS2, TNKS2−XAV complex, TNKS2−OLA complex, apo-TNKS2-CSol, and pseudo-apo-TNKS2 structures (PDF)
Author Present Address
§ Faculty of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama, Kanagawa 223-8522, Japan.
Author Contributions
Y.H. and N.O. contributed equally to all calculations and analysis of the results. All authors contributed to the discussion and manuscript presentation.
The authors received no specific funding for this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Hsiao S. J.; Smith S. Tankyrase function at telomeres, spindle poles, and beyond. Biochimie 2008, 90, 83–92. 10.1016/j.biochi.2007.07.012. [DOI] [PubMed] [Google Scholar]
- Narwal M.; Haikarainen T.; Fallarero A.; Vuorela P. M.; Lehtio L. Screening and structural analysis of flavones inhibiting tankyrases. J. Med. Chem. 2013, 56, 3507–3517. 10.1021/jm3018783. [DOI] [PubMed] [Google Scholar]
- Huang S. M. A.; Mishina Y. M.; Liu S.; Cheung A.; Stegmeier F.; Michaud G. A.; Charlat O.; Wiellette E.; Zhang Y.; Wiessner S.; Hild M.; Shi X.; Wilson C. J.; Mickanin C.; Myer V.; Fazal A.; Tomlinson R.; Serluca F.; Shao W.; Cheng H.; Shultz M.; Rau C.; Schirle M.; Schlegl J.; Ghidelli S.; Fawell S.; Lu C.; Curtis D.; Kirschner M. W.; Lengauer C.; Finan P. M.; Tallarico J. A.; Bouwmeester T.; Porter J. A.; Bauer A.; Cong F. Tankyrase inhibition stabilizes axin and antagonizes Wnt signalling. Nature 2009, 461, 614–620. 10.1038/nature08356. [DOI] [PubMed] [Google Scholar]
- Narwal M.; Venkannagari H.; Lehtio L. Structural basis of selective inhibition of human tankyrases. J. Med. Chem. 2012, 55, 1360–1367. 10.1021/jm201510p. [DOI] [PubMed] [Google Scholar]
- Narwal M.; Koivunen J.; Haikarainen T.; Obaji E.; Legala O. E.; Venkannagari H.; Joensuu P.; Pihlajaniemi T.; Lehtio L. Discovery of tankyrase inhibiting flavones with increased potency and isoenzyme selectivity. J. Med. Chem. 2013, 56, 7880–7889. 10.1021/jm401463y. [DOI] [PubMed] [Google Scholar]
- Voronkov A.; Holsworth D. D.; Waaler J.; Wilson S. R.; Ekblad B.; Perdreau-Dahl H.; Dinh H.; Drewes G.; Hopf C.; Morth J. P.; Krauss S. Structural basis and SAR for G007-LK, a lead stage 1,2,4-triazole based specific tankyrase 1/2 inhibitor. J. Med. Chem. 2013, 56, 3012–3023. 10.1021/jm4000566. [DOI] [PubMed] [Google Scholar]
- Huang H.; Guzman-Perez A.; Acquaviva L.; Berry V.; Bregman H.; Dovey J.; Gunaydin H.; Huang X.; Huang L.; Saffran D.; Serafino R.; Schneider S.; Wilson C.; DiMauro E. F. Structure-based design of 2-aminopyridine oxazolidinones as potent and selective tankyrase inhibitors. ACS Med. Chem. Lett. 2013, 4, 1218–1223. 10.1021/ml4003315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bregman H.; Chakka N.; Guzman-Perez A.; Gunaydin H.; Gu Y.; Huang X.; Berry V.; Liu J.; Teffera Y.; Huang L.; Egge B.; Mullady E. L.; Schneider S.; Andrews P. S.; Mishra A.; Newcomb J.; Serafino R.; Strathdee C. A.; Turci S. M.; Wilson C.; DiMauro E. F. Discovery of novel, induced-pocket binding oxazolidinones as potent, selective, and orally bioavailable tankyrase inhibitors. J. Med. Chem. 2013, 56, 4320–4342. 10.1021/jm4000038. [DOI] [PubMed] [Google Scholar]
- Hua Z.; Bregman H.; Buchanan J. L.; Chakka N.; Guzman-Perez A.; Gunaydin H.; Huang X.; Gu Y.; Berry V.; Liu J.; Teffera Y.; Huang L.; Egge B.; Emkey R.; Mullady E. L.; Schneider S.; Andrews P. S.; Acquaviva L.; Dovey J.; Mishra A.; Newcomb J.; Saffran D.; Serafino R.; Strathdee C. A.; Turci S. M.; Stanton M.; Wilson C.; Dimauro E. F. Development of novel dual binders as potent, selective, and orally bioavailable tankyrase inhibitors. J. Med. Chem. 2013, 56, 10003–10015. 10.1021/jm401317z. [DOI] [PubMed] [Google Scholar]
- Anumala U. R.; Waaler J.; Nkizinkiko Y.; Ignatev A.; Lazarow K.; Lindemann P.; Olsen P. A.; Murthy S.; Obaji E.; Majouga A. G.; Leonov S.; von Kries J. P.; Lehtio L.; Krauss S.; Nazare M. Discovery of a Novel Series of Tankyrase Inhibitors by a Hybridization Approach. J. Med. Chem. 2017, 60, 10013–10025. 10.1021/acs.jmedchem.7b00883. [DOI] [PubMed] [Google Scholar]
- Schacke M.; Kumar J.; Colwell N.; Hermanson K.; Folle G. A.; Nechaev S.; Dhasarathy A.; Lafon-Hughes L. PARP-1/2 Inhibitor Olaparib Prevents or Partially Reverts EMT Induced by TGF-beta in NMuMG Cells. Int. J. Mol. Sci. 2019, 20, 518 10.3390/ijms20030518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen B.; Dodge M. E.; Tang W.; Lu J.; Ma Z.; Fan C. W.; Wei S.; Hao W.; Kilgore J.; Williams N. S.; Roth M. G.; Amatruda J. F.; Chen C.; Lum L. Small molecule-mediated disruption of Wnt-dependent signaling in tissue regeneration and cancer. Nat. Chem. Biol. 2009, 5, 100–107. 10.1038/nchembio.137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlberg T.; Markova N.; Johansson I.; Hammarstrom M.; Schutz P.; Weigelt J.; Schuler H. Structural basis for the interaction between tankyrase-2 and a potent Wnt-signaling inhibitor. J. Med. Chem. 2010, 53, 5352–5355. 10.1021/jm100249w. [DOI] [PubMed] [Google Scholar]
- Ruf A.; de Murcia G.; Schulz G. E. Inhibitor and NAD+ binding to poly(ADP-ribose) polymerase as derived from crystal structures and homology modeling. Biochemistry 1998, 37, 3893–3900. 10.1021/bi972383s. [DOI] [PubMed] [Google Scholar]
- Langelier M. F.; Zandarashvili L.; Aguiar P. M.; Black B. E.; Pascal J. M. NAD(+) analog reveals PARP-1 substrate-blocking mechanism and allosteric communication from catalytic center to DNA-binding domains. Nat. Commun. 2018, 9, 844 10.1038/s41467-018-03234-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehtiö L.; Chi N. W.; Krauss S. Tankyrases as drug targets. FEBS J. 2013, 280, 3576–3593. 10.1111/febs.12320. [DOI] [PubMed] [Google Scholar]
- Haikarainen T.; Krauss S.; Lehtio L. Tankyrases: structure, function and therapeutic implications in cancer. Curr. Pharm. Des. 2014, 20, 6472–6488. 10.2174/1381612820666140630101525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferri M.; Liscio P.; Carotti A.; Asciutti S.; Sardella R.; Macchiarulo A.; Camaioni E. Targeting Wnt-driven cancers: Discovery of novel tankyrase inhibitors. Eur. J. Med. Chem. 2017, 142, 506–522. 10.1016/j.ejmech.2017.09.030. [DOI] [PubMed] [Google Scholar]
- Gao C.; Desaphy J.; Vieth M. Are induced fit protein conformational changes caused by ligand-binding predictable? A molecular dynamics investigation. J. Comput. Chem. 2017, 38, 1229–1237. 10.1002/jcc.24714. [DOI] [PubMed] [Google Scholar]
- Berman H. M.; Bhat T. N.; Bourne P. E.; Feng Z.; Gilliland G.; Weissig H.; Westbrook J. The Protein Data Bank and the challenge of structural genomics. Nat. Struct. Biol. 2000, 7, 957–959. 10.1038/80734. [DOI] [PubMed] [Google Scholar]
- MOE, 2016.08; Chemical Computing Group Inc. 1010 Sherbrooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7, 2016.
- Jorgensen W. K.; Rice M. J. Morphology of a very extensible insect muscle. Tissue Cell 1983, 15, 639–644. 10.1016/0040-8166(83)90013-7. [DOI] [PubMed] [Google Scholar]
- Kimura S. R.; Hu H. P.; Ruvinsky A. M.; Sherman W.; Favia A. D. Deciphering Cryptic Binding Sites on Proteins by Mixed-Solvent Molecular Dynamics. J. Chem. Inf. Model. 2017, 57, 1388–1401. 10.1021/acs.jcim.6b00623. [DOI] [PubMed] [Google Scholar]
- Beglov D.; Hall D. R.; Wakefield A. E.; Luo L.; Allen K. N.; Kozakov D.; Whitty A.; Vajda S. Exploring the structural origins of cryptic sites on proteins. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, E3416–E3425. 10.1073/pnas.1711490115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- An X.; Lu S.; Song K.; Shen Q.; Huang M.; Yao X.; Liu H.; Zhang J. Are the Apo Proteins Suitable for the Rational Discovery of Allosteric Drugs?. J. Chem. Inf. Model. 2019, 59, 597–604. 10.1021/acs.jcim.8b00735. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Vanderspoel D.; Vandrunen R. Gromacs - a Message-Passing Parallel Molecular-Dynamics Implementation. Comput. Phys. Commun. 1995, 91, 43–56. 10.1016/0010-4655(95)00042-E. [DOI] [Google Scholar]
- Lindahl E.; Hess B.; van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 2001, 7, 306–317. 10.1007/s008940100045. [DOI] [Google Scholar]
- Van der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- Pronk S.; Pall S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; Hess B.; Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Piana S.; Palmo K.; Maragakis P.; Klepeis J. L.; Dror R. O.; Shaw D. E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; T G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta P. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam N. J.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision A.08; Gaussian, Inc.: Wallingford, CT, 2009.
- Nosé S. A Molecular-Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. 10.1080/00268978400101201. [DOI] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single-Crystals - a New Molecular-Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Case D. A.; B R. M.; Cerutti D. S.; Cheatham T. E. III; Darden T. A.; Duke R. E.; Giese T. J.; Gohlke H.; Goetz A. W.; H N.; Izadi S.; Janowski P.; Kaus J.; Kovalenko A.; Lee T. S.; LeGrand S.; Li P.; Lin C.; L T.; Luo R.; Madej B.; Mermelstein D.; Merz K. M.; Monard G.; Nguyen H.; Nguyen H. T.; Omelyan I.; O A.; Roe D. R.; Roitberg A.; Sagui C.; Simmerling C. L.; Botello-Smith W. M.; Swails J.; Walker R. C.; W J.; Wolf R. M.; Wu X.; Xiao L.; Kollman P. A.. AMBER 2016; University of California: San Francisco, 2016.
- Jones G.; Willett P.; Glen R. C.; Leach A. R.; Taylor R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997, 267, 727–748. 10.1006/jmbi.1996.0897. [DOI] [PubMed] [Google Scholar]
- Verdonk M. L.; Cole J. C.; Hartshorn M. J.; Murray C. W.; Taylor R. D. Improved protein-ligand docking using GOLD. Proteins 2003, 52, 609–623. 10.1002/prot.10465. [DOI] [PubMed] [Google Scholar]
- Srinivasan J.; Cheatham T. E.; Cieplak P.; Kollman P. A.; Case D. A. Continuum Solvent Studies of the Stability of DNA, RNA, and Phosphoramidate–DNA Helices. J. Am. Chem. Soc. 1998, 120, 9401–9409. 10.1021/ja981844+. [DOI] [Google Scholar]
- Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. 3rd Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Kuhn B.; Gerber P.; Schulz-Gasch T.; Stahl M. Validation and use of the MM-PBSA approach for drug discovery. J. Med. Chem. 2005, 48, 4040–4048. 10.1021/jm049081q. [DOI] [PubMed] [Google Scholar]
- Okimoto N.; Futatsugi N.; Fuji H.; Suenaga A.; Morimoto G.; Yanai R.; Ohno Y.; Narumi T.; Taiji M. High-performance drug discovery: computational screening by combining docking and molecular dynamics simulations. PLoS Comput. Biol. 2009, 5, e1000528 10.1371/journal.pcbi.1000528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okimoto N.; Otsuka T.; Hirano Y.; Taiji M. Use of the Multilayer Fragment Molecular Orbital Method to Predict the Rank Order of Protein-Ligand Binding Affinities: A Case Study Using Tankyrase 2 Inhibitors. ACS Omega 2018, 3, 4475–4485. 10.1021/acsomega.8b00175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connolly M. L. Analytical molecular surface calculation. J. Appl. Crystallogr. 1983, 16, 548–558. 10.1107/S0021889883010985. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.