Noncovalent Interactions from Models for the Møller–Plesset Adiabatic Connection

Abstract

Given the omnipresence of noncovalent interactions (NCIs), their accurate simulations are of crucial importance across various scientific disciplines. Here we construct accurate models for the description of NCIs by an interpolation along the Møller–Plesset adiabatic connection (MP AC). Our interpolation approximates the correlation energy, by recovering MP2 at small coupling strengths and the correct large-coupling strength expansion of the MP AC, recently shown to be a functional of the Hartree–Fock density. Our models are size consistent for fragments with nondegenerate ground states, have the same cost as double hybrids, and require no dispersion corrections to capture NCIs accurately. These interpolations greatly reduce large MP2 errors for typical π-stacking complexes (e.g., benzene–pyridine dimers) and for the L7 data set. They are also competitive with state-of-the-art dispersion enhanced functionals and can even significantly outperform them for a variety of data sets, such as CT7 and L7.

An accurate description of noncovalent interactions (NCIs) is crucial for fields ranging from chemistry to biology to materials science, with a plethora of methods being constantly developed, tested, and improved.¹⁻¹⁹ Second-order Møller–Plesset (MP2) perturbation theory has been often considered a relatively safe choice for the treatment of NCIs in chemistry, given its favorable scaling relative to more sophisticated wave function methods and encouraging early successes in capturing NCIs in small systems.^20,21 The described failures of MP2 when applied to NCIs, such as those in stacking complexes, have been often considered accidental. Very recently, Furche and co-workers²² have shown that MP2 relative errors for NCIs can grow systematically with molecular size and that the whole MP series may be even qualitatively unsuitable for the description of large noncovalent complexes. On the other hand, double hybrid (DH) functionals, which mix density-functional theory (DFT) semilocal ingredients with a fraction of Hartree–Fock (HF) exchange and MP2 correlation energy, typically worsen the performance of MP2 for NCIs,²³⁻²⁵ unless dispersion corrections are added on top of them.^12,26,27 A few notable exceptions to this are the XYGn family of functionals^28,29 and recent DHs developed in Martin’s group,³⁰ which give accuracy improvements over MP2 without requiring additional dispersion corrections.

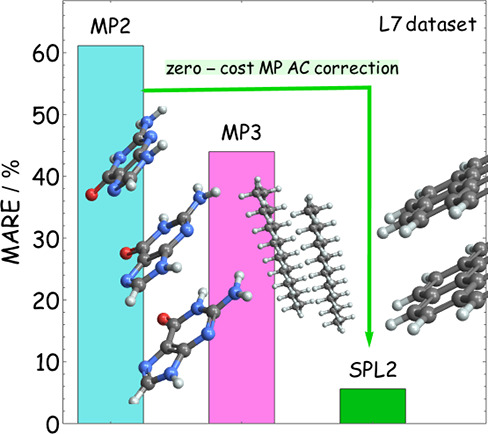
In this work, we use an adiabatic connection (AC) formalism in which the MP series arises in the weak-coupling limit (hereinafter MP AC) to construct a correction to the MP2 interaction energies, which is guaranteed to be size consistent for the case in which the fragments have a nondegenerate ground state. We construct this correction using two different strategies both based on an interpolation between MP2 and the strong-coupling limit of the MP AC, which has been recently studied in detail^31,32 and shown to be given by functionals of the Hartree–Fock (HF) density with a clear physical meaning. The resulting method gives major improvements over MP2, despite coming at a negligible extra computational cost. In Figure 1 we show, in particular, that a specific interpolation form named “SPL2”, an extension of the approach of Seidl, Perdew and Levy³³ (SPL), is competitive with state-of-the art electronic structure methods when applied to the challenging L7 data set.^22,34−36 In what follows, we will describe the theoretical basis for the construction of this new class of functionals based on the MP AC interpolation. We also introduce and analyze the different interpolation schemes within this framework and discuss possible routes to further refinement.

Figure 1.

Mean absolute relative errors (MARE) for selected methods, where TS stands for the Tkatchenko–Shefler method,³⁷ for the L7 data set using the reference data of Grimme and co-workers.³⁶

For the construction of our approximations, we use the Møller–Plesset adiabatic connection (MP AC) framework, whose Hamiltonian reads as

1

with T̂ the kinetic energy and V̂_ee the electron–electron repulsion operators. Here Ĵ = Ĵ[ρ^HF] and K̂ = K̂[{ϕ_i^HF}] are the standard Hartree–Fock (HF) Coulomb and exchange operators in terms of the HF density ρ^HF and the occupied orbitals ϕ_i, respectively. We denote with Ψ_λ the ground state of Ĥ_λ, which at λ = 1 corresponds to the physical system and at λ = 0 to the HF Slater determinant. In terms of these quantities the traditional quantum-chemical definition of the correlation energy is given by

2

with Ĥ = Ĥ_λ=1 and Ψ = Ψ_λ=1. Applying the Hellman–Feynman theorem to eq 1, one obtains the AC expression for the correlation energy, which reads as^{22,31,32,38,39}

3

where W_c,λ is the AC integrand,

4

The small λ expansion of W_c,λ returns the Møller–Plesset (MP) series

5

where E_c^MPn is the nth order correlation energy from the MP perturbation theory.^31,40 Very recently, the large-λ expansion of W_c,λ has been shown to have the following form:³²

6

which is analogous, although with important differences, to the one appearing in the density fixed DFT adiabatic connection (DFT AC).^31,41,42 In the DFT AC the correlation energy is given by^43,44

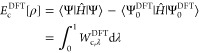7

where Ψ_λ^DFT integrates to the physical density ρ and minimizes the sum of T̂ + λV̂_ee. Defined this way, Ψ_λ is in general equal to Ψ_λ only at λ = 1. Furthermore, the density of Ψ_λ varies with λ, whereas the density of Ψ_λ^DFT is always the same by construction. The DFT AC integrand W_c,λ reads as

8

In the following relations we will also make use of W_λ^DFT, defined to include the exchange energy: W_λ = W_c,λ^DFT + E_x. The functional W_c,λ has large⁴⁵⁻⁴⁷ and small λ^48,49 expansions analogous (but not identical) to those given by eqs 5 and 6. The large-λ limits of the two integrands are related by³¹

9

where dimensionless β[ρ^HF] is system-dependent and known to satisfy³¹ β[ρ^HF] ≥ 1, and for the uniform electron gas (UEG) it is exactly equal to 1.³² By linking W_c,∞ and W_∞^DFT and by knowing some exact features of β[ρ^HF], eq 9 will be used in this work for building approximations to W_c,∞, exploiting the existing approximations for its DFT counterpart.⁵⁰⁻⁵⁴

The AC framework has always played a crucial role in the construction of DFT approximations^28,55−61 and, more recently, also in wave function theories, to approximate missing parts of the correlation energy (see, e.g., the work of Pernal and co-workers^62,63). In the present work, we build upon the interaction strength interpolation (ISI) idea of Seidl and co-workers,^33,64 in which the DFT correlation energy is approximated by interpolating the AC integrand between its weak- and strong-coupling expansions. This construction enables one to include more pieces of information into the approximate correlation energy, avoiding a bias toward the weak correlation regime, present in most of the DFT approximations.^{33,53,61,64,65} The lack of size consistency of the ISI approach had been considered its main drawback, but a recent remarkably simple size-consistency correction (SCC) fixes this problem in an exact way, at least for systems dissociating into fragments with a nondegenerate ground state.^23,66 This SCC has been used for building functionals^23,66,67 in the DFT context and has been already shown to be crucial for the accuracy of model MP AC curves (see Section S3 of ref (66)) that can signal when an MP2 calculation is not reliable.⁶⁶

The idea of this work is to use this approach, originally designed for the DFT AC, in the MP AC context to build accurate approximations to describe NCIs. The mentioned SCC²³ is also used throughout this work to restore size consistency of our MP AC models.

In a previous work on NCI’s,²³ the ISI idea has been applied within the DFT AC framework, by using MP2 as an approximation for the small-λ expansion of the DFT AC. The interpolation function used was the one developed in the DFT AC framework by Seidl, Perdew, and Levy (SPL),³³

10

where b = (4E_c^MP2)/W_c,∞. Such an attempt could be also viewed as an interpolation model for the MP AC in which the large-λ limit was approximated by its DFT counterpart W_c,∞, which is known to be accurately described^41,68 by the point-charge plus continuum (PC) model⁵⁰

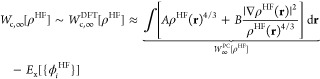11

where A = −1.451 and B = 5.317 × 10^–3. Notice that this approximation is not in line with the exact relation of eq 9, which was not known at the time, but it can still provide reasonable results. By performing a simple MP2 calculation and evaluating W_c,∞ on the HF density, the needed quantities to be fed into eq 10 were easily obtained, yielding^23,66 the SPL approximation to E_c (eq 3). When it comes to NCIs, SPL was found^23,66 to give a major improvement over MP2 (see Figure 2). However, the deficiencies of SPL for NCIs are also already noticeable in Figure 2, where we show results for various NCI’s data sets. On the x-axis, we report the difference between the benchmark CCSD(T) and MP2 correlation energy ΔE_c = E_c – E_c^MP2, and the difference between the benchmark and SPL correlation energies is reported on the y-axis. This way, if SPL had the same level of accuracy as the benchmark, all data points would lie on the y = x line (shown in black). The plotted correlation energies pertain to the interaction energies, i.e., the differences between correlation energies of a complex and its fragments. Since MP2 (with large enough basis set) overbinds most of the complexes,^66,69 ΔE_c is positive for most of the data points. We can see from the same figure that SPL decently corrects MP2 for different ranges of ΔE_c. As ΔE_c becomes large, SPL still substantially reduces the error of MP2. But, the performance of SPL is still not satisfactory as even the reduced errors can easily exceed 5 kcal/mol. Moreover, for few systems where MP2 underbinds, SPL corrects it in the wrong direction (see the inset of Figure 2 that zooms in on the region around ΔE_c = 0). In these cases, a model MP AC integrand should be concave to correct the underbinding of MP2, and the SPL model is not flexible enough to always capture this concavity.⁶⁶

Figure 2.

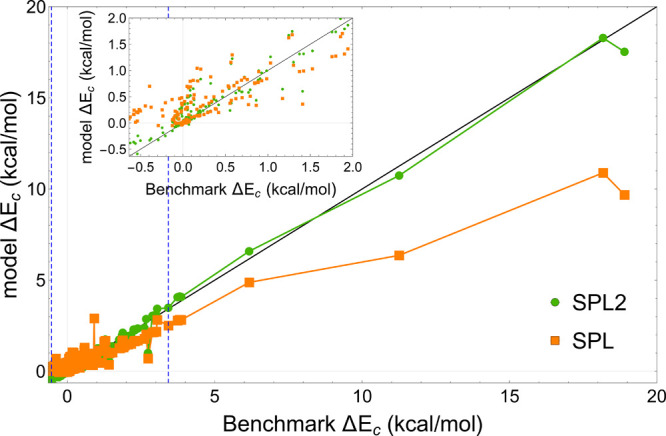
Difference between benchmark CCSD(T) interaction correlation energies and those of MP2 (ΔE_c = E_c – E_c^MP2) vs ΔE_c predicted by our models for a range of interaction energies of the NCI complexes [S22, S66, DI6, CT7, NGD8, and L7 data sets]. The blue vertical dashed lines denote the range in which ΔE_c values of complexes in S22, the data set we used to train empirical parameters in the SPL2 form, lie.

From these examples, it is clear that we need better interpolation forms than SPL to model W_c,λ, and a better description of its λ → ∞ limit, which is known to be different^31,32 from the DFT one used in this SPL construction. To make the interpolation form more flexible in capturing the concavity/convexity correctly when MP2 underbinds/overbinds, respectively, we consider a form containing two SPL terms:

12

We call this form SPL2, with the b₁, m₁, and C₁ parameters fixed by the exact conditions: (i) W_c,λ^SPL2 vanishes at 0, (ii) its initial derivative is equal to 2E_c (eq 5), and (iii) it converges to W_c,∞ in the large λ limit (eq 6),

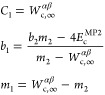where W_c,∞^αβ[ρ^HF] is an approximation to W_c,∞[ρ^HF] inspired by eq 9:

14

In fact, as mentioned, the exact form of W_c,∞ for the MP AC has been recently revealed,^31,32 but it is quite involved, with targeted semilocal approximations still under construction; the use of eq 9 to improve the large-λ description of the MP AC seems a rather effective first step. There are now four parameters left in the SPL2 model for MP AC (b₂, m₂, α, and β that we simplify to be system independent), which we fit in this work to the S22 data set^70,71 by minimizing its mean absolute error (MAE). From Figure 2, we can see that SPL2 fixes the key deficiencies of SPL: it corrects MP2 in the right direction when the latter underbinds and has a better corrective trend than SPL as MP2 errors become large.

In addition to the SPL2 model, we also develop a model for E_c directly. We first generalize E_c as 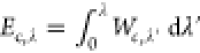, such that E_c = E_c,λ = 1. Then we build the following model for E_c,λ:

with

where W_c,∞^1,1 is W_c,∞ in which α and β are set to 1 by using the UEG argument (see above). This new model is called the Møller–Plesset Adiabatic Connection Functional-1 (MPACF-1) and will be the starting point for a new class of functionals that approximate the MP AC. The underlying MP AC model, W_c,λ^MPACF-1, is simply obtained by taking a derivative of E_c,λ with respect to λ. In contrast to W_c,λ^SPL and W_c,λ, W_c,λ^MPACF-1 contains the 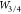term appearing in the large λ limit (eq 6), making this model have a better asymptotic behavior than SPL and SPL2. MPACF-1 is also less empirical than SPL2 since it contains only two parameters (d₁ and d₂), which we again fit to the S22 data sets and report their optimal values in the Computational Details below.

Without the SCC, SPL2 and MPACF-1 have different size-extensivity behaviors. Nevertheless, in this work we always use the SCC ensuring that the interaction energies are correctly computed and vanish in the dissociation limit (see Figure S1 in the Supporting Information for the Kr₂ example and the caption of this figure for a further discussion). From Figure S1, one can also see that the SCC does not affect the shape of the potential energy surfaces (PES), but only shifts a PES by a constant ensuring that binding energies vanish when the fragments are infinitely away from one another. Thus, the SCC would not be required and has no effect for calculating differences in energies at different stationary points of a PES (e.g., reaction energies, barrier heights, isomerization energies, etc.).

In what follows, we compare the performance of SPL2 and MPACF-1 with that of earlier SPL, MP2, and other approximations for NCIs. While our models share some similarities with DHs, there are two key differences. First, our models are based on the full amounts of the exact exchange and MP2 correlation and thus they do not benefit from error cancellations between these quantities and their semilocal counterparts. Furthermore, our models do not require dispersion corrections to be accurate for NCIs.

We start with a light example, showing the Kr₂ binding curve in Figure 3. We can see from the top panel of Figure 3 that SPL significantly improves MP2. At the same time, SPL is significantly improved by MPACF-1 and SPL2, with the latter being slightly more accurate than the former. This happens even though noble gas dimers are beyond our training set (S22). In contrast, the D3 empirical correction can even worsen binding curves of noble gas dimers,⁷³ even though their binding energies have been used in the training of the original D3 parameters.¹² Now we move to the bottom panel of Figure 3, where we look at the accuracy of different AC models for the interaction energies for Kr₂ at equilibrium. To test the accuracy of our AC models, we need a reference W_c,λ for the interaction energies. Ideally, this quantity would be obtained by full-CI or CCSD(T), but we note that the convergence of MPn series for the interaction energy of Kr₂ at equilibrium is fast (see the inset of the lower panel of Figure 3 showing that MP4 gives nearly the same results as CCSD(T)). For this reason, we can safely assume that the right-hand side of eq 5 truncated to fourth order gives us a reliable MP AC reference for the interaction energies of Kr₂. After establishing W_c,λ^MP4 as a reference, we compare the performance of MP3, MP2, SPL, SPL2, and MPACF-1 curves in the lower panel of Figure 3). The error of all MP AC models slowly increases as we move away from λ = 0 since all the curves have the correct initial slope given by 2E_c. On average, SPL2 is the most accurate. MPACF-1 is the most accurate up to λ ∼ 0.7, and then its accuracy deteriorates and at about λ ∼ 0.9 where it is less accurate than even SPL. Overall, all three AC models give significant improvements over MP2 and MP3.

Figure 3.

(a) Interaction energies of MP2, SPL, SPL2, and MPACF-1 as well as reference CCSD(T) curves for Kr₂. (b) Errors of different MP AC models for Kr₂ at equilibrium, ΔW_c,λ = W_c,λ^method – W_c,λ, where the r.h.s. of eq 5 is truncated to fourth order. W_c,λ^MP4 is taken as a reference (the inset justifies this choice given the (fast) convergence of the MPn series).

Now we move to Table 1, where we show the results for several data sets^{34,69,70,74−76} in comparison with the B3LYP hybrid enhanced by D3. Except for noble gas dimers where the differences in MAEs are marginal, SPL improves the performance of MP2 by a factor of 2 on average. SPL2 greatly improves SPL by reducing its errors by the factors ranging from 1.3 (CT7) to more than 4 (L7). MPACF-1 provides still a substantial improvement over SPL, but on average performs worse than SPL2. SPL2 also beats B3LYP-D3 for NGD8, CT7, DI6, and L7, whereas the two approaches display a similar performance for S22 and S66. By looking at MAEs for individual subsets of the S66 data set (see Table S1 in the Supporting Information), we can see that the accuracy of MP2 is high for hydrogen bonded complexes, but it is well-known that it deteriorates for dispersion-bonded and mixed complexes.^66,69 SPL greatly reduces the errors of MP2 for dispersion-bonded and mixed complexes but becomes worse than MP2 for hydrogen bonds. On the other hand, SPL2 greatly improves MP2 for dispersion-bonded and mixed complexes, without deteriorating its accuracy for hydrogen bonds.

Table 1. MAE in kcal/mol of Different Methods for the S22, CT7, DI6, S66, and L7 Data Sets from the Existing Literature^a.

set	MP2	SPL	SPL2	MPACF-1	B3LYP-D3
NGD8	0.04	0.05	0.03	0.03	0.08
CT7	0.92	0.57	0.45	0.60	1.48
DI6	0.48	0.27	0.18	0.20	0.46
S22	0.88	0.38	0.15	0.19	0.15
S66	0.47	0.35	0.21	0.26	0.18
L7	8.74	3.83	0.89	2.32	1.78

^aBest results are highlighted in bold. NGD8 is a set of eight noble gas dimers (Ar₂, He₂, Kr₂, Ne₂, ArKr, C₆H₆–Ne, CH₄Ne, and HeAr) that we construct here.

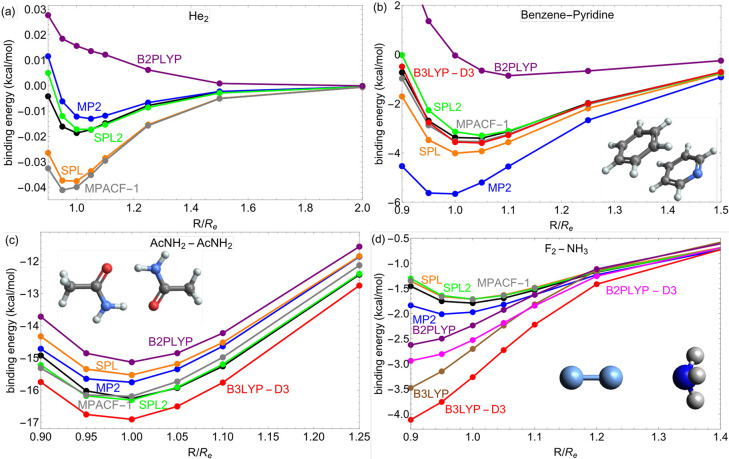
In Figure 4, we show several binding curves representing NCIs of different nature. These includes weakly bonded He₂ [panel a], stacked benzene–pyridine complex [panel b], hydrogen-bonded acetamide dimer [panel c], and the charged-transfer (CT) fluorine–ammonia complex [panel d]. Overall, SPL2 is in the closest agreement with the reference [CCSD(T)] and it corrects MP2 in the right direction in cases when MP2 underbinds (He₂, the acetamide dimer), when it overbinds slightly (the fluorine–ammonia complex), and when it severely overbinds (the benzene–pyridine complex). On the other hand, SPL corrects MP2 in the right direction only in cases when the latter overbinds. MPACF-1 is off for He₂, but in other cases it is on par with SPL2 and even more accurate than SPL2 in the case of the benzene–pyridine dimer. For He₂, SPL is as bad as MPACF-1, whereas empirical SPL2 is very accurate (even though noble gases have not been used in the training of SPL2). Thus, it seems indeed challenging to build a nonempirical MP AC model that will give improvements over MP2 for He₂ but may be achieved in the future by considering approximations to higher-order terms from the large λ limit of the MP AC.³²

Figure 4.

Dissociation curves of He₂ (a), benzene–pyridine (b), acetamide (c), and NH₃–F₂ dimers (d), obtained from various methods. CCSD(T) (black line) has been used as a reference for all complexes. For other binding curves, see Figures S3–S8 in the Supporting Information.

Our models are accurate for NCIs without requiring dispersion corrections (in contrast to, e.g., D3-uncorrected B2PLYP, which is off for all four cases). B3LYP corrected by D3 is completely off for He₂ (see Figure S3 in the Supporting Information). The behavior of B3LYP and B2PLYP is even more interesting in the case of the CT fluorine–ammonia complex where the D3 correction even worsens the original results.⁷⁷ This is not due to the D3 correction itself, but due to the density-driven errors that typically bedevil semilocal DFT calculations of halogen-based CT complexes⁷⁸⁻⁸⁰ (Note also that is not uncommon that the D3 correction worsens the results from semilocal DFT calculations suffering from density-driven errors^78,79). On the contrary, our MP AC models are built only for correlation, and thus the full amount of the exact exchange is used without being mixed with a fraction of its semilocal counterpart. This is probably the reason why all of our MP AC models are very accurate for the studied CT complex (see also Figure S7 in the Supporting Information for another example).

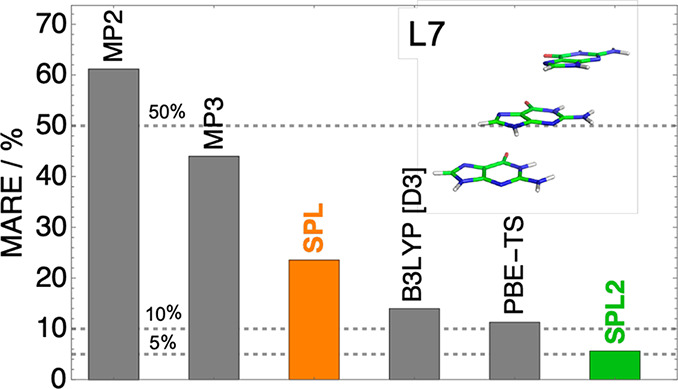
Now we go back to the L7 data set composed by larger complexes for which MP2 displays very large errors.²² Interaction energies for individual L7 complexes are shown in Figure 5, where the reference used is obtained from Grimme et al.³⁶ From Figure 5, we can see that MP2 strongly overbinds most the L7 complexes. SPL corrects it, but not sufficiently, as it is still much less accurate than B3LYP-D3 and B2PLYP-D3. MPACF-1 improves SPL, but a better performance is obtained from our SPL2 model, which very accurately reproduces the reference values. In the SI (Table S2 and Figure S2 in the Supporting Information), we compare the performance of our models against other L7 references from the literature.^34,35 From these results, it can be seen that regardless of what reference is used, SPL greatly reduces the MP2 errors, whereas our new models (SPL2 and MPACF-1) greatly reduce the errors of SPL.

Figure 5.

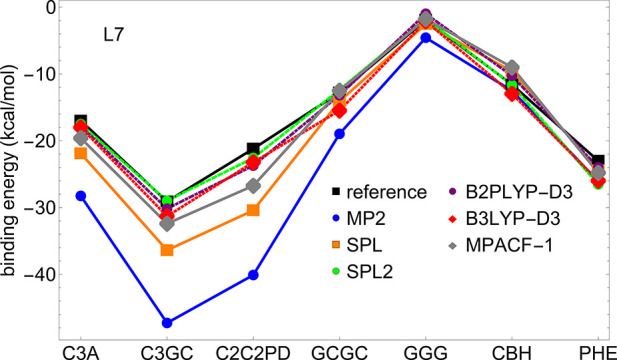
Interaction energies of MP2, SPL, SPL2, B3LYP-D3, and B2PLYP as well as reference data of Grimme and co-workers,³⁶ plotted for individual complexes of the L7 data set. For comparison of the approximations against other reference data, see Figure S2 and Table S2 in the Supporting Information.

In summary, we have introduced a new scheme for the construction of MP AC models providing accurate description of NCIs. Two specific interpolation models, SPL2 and MPACF-1 greatly reduce errors of MP2 and earlier proposed SPL for a variety of NCIs despite coming at a negligible computational cost beyond that of MP2. In comparison with, e.g., modern (double) hybrids,⁸¹⁻⁸³ empirical parameters in our models have been primitively optimized and despite that offer highly competitive accuracy for the description of NCIs. Further improvements can be obtained by better optimization strategies, but also by reducing empiricism using the additional recently revealed exact form of the large λ limit MP AC functionals.³² Furthermore, one can use machine learning to find improved ways for interpolating MP AC (see, e.g., ref (84) for a related work). To lower the cost, in future work we will redesign our models by replacing the exact E_c^MP2 with some of its approximations.⁸⁵⁻⁸⁷ The zero-cost size-consistency correction of ref (23) is an important part of our scheme and for now it can be applied only to systems dissociating into nondegenerate ground states. Generalization of this correction for systems that dissociate into degenerate ground state fragments will be another objective for future works. This and the investigation of the large-coupling limit of the MP AC for open-shell systems should pave the way for the broader applicability of our scheme (i.e., beyond NCIs). The development of analytical gradients enabling further applicability of our method will be then considered following the similar implementation of gradients for standard double hybrids.⁸⁸ Our scheme can also be used to give a formal justification and to improve recently introduced double-hybrid functionals that are applied to Hartree–Fock densities.⁷⁹

Computational Details

All calculations have been performed using a modified version of the TURBOMOLE 7.1 package.^89,90 Computational details are the same as in refs (91) and (92). For all MP2 calculations we have employed aug-cc-pVQZ enhanced with additional basis functions detailed in ref (23). MP2 interaction energies for NCIs within this basis set are close to the MP2/CBS results.⁶⁶ From these MP2 calculations we extract all the quantities needed to construct our MP AC interpolation models (HF densities, E_x[{ϕ_i^HF}], E_c). The B3LYP-D3 results shown in Table 1 for the S22, CT7 DI6, S66, and L7 data sets have been taken from refs (34), (36), (77), (77), and (93), respectively, whereas for NGD8 they were calculated using an aug-cc-pVQZ basis set. The same basis set has been employed to calculate MP3 and MP4 energies for Kr₂. For B2PLYP-D3 the data for L7 was obtained from ref (94). The B2PLYP, B3LYP-D3, and CCSD(T)/CBS data for the S66 dissociation curves were obtained from 69. The B2PLYP(-D3), B3LYP(-D3) and CCSD(T)/CBS data for the CT7 dissociation curves were calculated using an aug-cc-pVQZ basisset. The B3LYP-D3 for the dissociation curves of Ne₂, Kr₂, and Ar₂ were obtained from ref (95), whereas the rest of the B3LYP-D3, B2PLYP, and CCSD(T) data were again calculated with the basis set aug-cc-pVQZ.

For SPL2 the optimal parameters we find are b₂ = 0.117, m₂ = 10.68, α = 1.1472, and β = −0.7397, whereas for MPACF-1 we use the following set of parameters, d₁ = 0.294 and d₂ = 0.934. A few remarks on these parameters are needed. As shown in ref (32), the large-λ limit of the MP AC integrand W_c,λ has a leading term W_c,∞ that is much lower than its DFT counterpart. At the next order, the λ^–1/2 term is, instead, positive and much larger than its DFT counterpart, because the HF exchange operator enhances the zero-point energy, by introducing excited states of the normal modes.³² Finally, the λ^–3/4 term is not present in the DFT AC, and it is a peculiar feature of the MP AC.³² This term is again negative. Overall, these three terms together are needed for an accurate description of W_c,λ, as they balance each other in a delicate way (see Figure 9 of ref (32)). The SPL2 form does not have the λ^–3/4 term. For this reason, its large-λ limit W_c,∞ is an effective description of the three leading terms; this is why in this case β turns out to be negative. In addition, we need to point out that the fitting procedure does not consider the total energies but takes into account only the interaction energies and should only be used within the SCC approach. The new MPACF-1 form, instead, has built in the correct large-λ behavior, including the λ^–3/4 term. This is why in this case the parameters α and β can be set equal to 1. In future work we will build accurate GGA functionals for the first two leading terms of the large-λ MP AC, which are expected to improve our models, when combined with an approximation for the λ^–3/4 term containing the HF density at the nuclei. In Table S3 in the Supporting Information, we give a summary of the three MP AC forms, their parameters, etc., and highlight the differences in models for W_c,∞ that our three forms use.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c01157.

• MAEs for S66 subsets, additional dissociation curves of noncovalent complexes, plots comparing errors for the L7 data set, summary of MP AC forms developed in this work (PDF)

The authors declare no competing financial interest.