Projecting the number of new HIV infections to formulate the “Getting to Zero” strategy in Illinois, USA

Abstract

Objectives:

Getting to Zero (GTZ) initiatives focus on expanding use of antiretroviral treatment (ART) and pre-exposure prophylaxis (PrEP) to eliminate new HIV infections. Computational models help inform policies for implementation of ART and PrEP continuums. Such models, however, vary in their design, and may yield inconsistent predictions. Using multiple approaches can help assess the consistency in results obtained from varied modeling frameworks, and can inform optimal implementation strategies.

Methods:

A study using three different modeling approaches is conducted. Two approaches use statistical time series analysis techniques that incorporate temporal HIV incidence data. A third approach uses stochastic stimulation, conducted using an agent-based network model (ABNM). All three approaches are used to project HIV incidence among a key population, young Black MSM (YBMSM), over the course of the GTZ implementation period (2016–2030).

Results:

All three approaches suggest that simultaneously increasing PrEP and ART uptake is likely to be more effective than increasing only one, but increasing ART and PrEP by 20% points may not eliminate new HIV infections among YBMSM. The results further suggest that a 20% increase in ART is likely to be more effective than a 20% increase in PrEP. All three methods consistently project that increasing ART and PrEP by 30% simultaneously can help reach GTZ goals.

Conclusions:

Increasing PrEP and ART uptake by about 30% might be necessary to accomplish GTZ goals. Such scale-up may require addressing psychosocial and structural barriers to engagement in HIV and PrEP care continuums. ABNMs and other flexible modeling approaches can be extended to examine specific interventions that address these barriers and may provide important data to guide the successful intervention implementation.

1. Introduction

Two seminal HIV prevention policy guidelines were released in 2010: the UNAIDS strategic plan [1] and the United States National HIV/AIDS Strategy (NHAS) [2]. These guidelines precipitated the development of “Getting to Zero” (GTZ) and related HIV elimination initiatives in the United States (US). Following these guidelines, initiatives that focus on HIV elimination within local jurisdictions have been proposed [3]. These plans focus on achieving expanded antiretroviral treatment (ART) and pre-exposure prophylaxis (PrEP) uptake within defined periods. As more ambitious goals are being set to eliminate new HIV infections, the need for improvement at multiple stages of the HIV prevention continuum has been increasingly recognized [4,5]. It is also understood that HIV epidemics in different countries are composed of “microepidemics”, driven by disproportionately large numbers of transmissions occurring within some subpopulations [6]. Indeed, data show lower levels of success in the improvement of the ART and PrEP continuums among younger Black gay, bisexual and other MSM (YBMSM) in the US compared with younger white MSM [7,8]. YBMSM have experienced relatively stable incidence rates, even as overall HIV incidence in the United States has declined [9].

Computational models provide tools to predict the trajectory of localized HIV epidemics, assess the potential effects of interventions, and inform policies for improved implementation of continuums of ART and PrEP care [10,11]. Several computational models demonstrating the potential impact of PrEP, ART and other interventions to promote HIV elimination efforts have been published [12–16]. These models, however, vary in their design, formulation, and input data, and provide predictions that may not always agree [17,18]. Understanding the underlying assumptions of various prediction strategies is important for the interpretation and contextualization of the conflicting findings.

Applying two or more methodological approaches can help compare the impact of model assumptions on model outputs [19–21]. For instance, one can assess the extent to which results from varied approaches are consistent with each other [22] or use data from a variety of sources to examine the range of projected efficacies of prevention mechanisms [23,24]. Studies that compare multiple modeling approaches have been useful in informing HIV prevention policies in Sub Saharan Africa [25,26], but more such studies should be used to guide GTZ planning in the US.

This paper aims to compare predictions from three different modeling approaches that consider ART and PrEP scale-up among YBMSM in Illinois, a population experiencing an ongoing HIV microepidemic. Two of these approaches are derived from statistical time series techniques and project the number of new HIV infections given recent trends in incidence. A third approach uses stochastic simulations generated from an agent-based network model (ABNM), developed previously, that explicitly simulates person-to-person HIV transmission within sexual networks that were parameterized using empirical data [27]. Results from all three approaches are assessed to determine if a “functional zero” HIV incidence is achieved, defined as fewer than 200 new infections annually [28]. Multi-model comparison approaches such as this may offer a powerful tool for implementation scientists interested in rigorously examining the efficacy of interventions before they are implemented.

2. Methods

Three approaches are used to project the number of new infections over the 2016–2030 GTZ implementation period [29]. The two statistical approaches use aggregated incidence data obtained through public health surveillance (further information below). These methods are less computationally intensive compared to most dynamic simulation methods used in HIV intervention planning. The third model type described here is an ABNM, described in detail previously [27], that incorporates more of the real-world complexities affecting HIV transmission rates, particularly parameters that describe behavioral, sexual network, demographic, biological, and treatment-related processes.

All three approaches are used to project HIV incidence among YBMSM over the course of the Illinois GTZ implementation period under the following intervention scenarios: (i) PrEP uptake increased by 20 and 30 percentage points (with no change in ART uptake from the control levels); (ii) ART uptake scaled up by 20 and 30 percentage points (with no change in PrEP uptake from the control levels); (iii) both PrEP and ART scaled up by 20 percentage points each and 30 percentage points each. The increased levels of ART and PrEP use were aligned with the recommended increase in ART and PrEP coverage by the GTZ committee [29]. In addition to the intervention scenarios listed above, a “control” setting assuming baseline uptake levels for PrEP and ART was implemented over the duration of the GTZ implementation. For all interventions, the final outcome was the number of new HIV infections in the last year of GTZ implementation.

2.1. Data sources for model inputs

The two statistical approaches used the annual incidences of HIV diagnoses for YBMSM (18–34 years) obtained from the Enhanced HIV/AIDS Reporting System (eHARS), a database maintained by the Illinois Department of Public Health [30]. Baseline PrEP and ART uptake levels were estimated from a population-based cohort study of YBMSM using data collected between June 2013 and July 2016 [31,32]. Input parameters for the ABNM were selected from several different sources which included systematically sampled data representative of YBMSM. Projected numbers of new infections for each year of the GTZ implementation period as per the three interventions considered here were computed using scaling factors, as described in 2.2.1 below. Derivations for the model equations are detailed in the Appendix.

2.2. Statistical methods

2.2.1. Loess

The Loess technique is a robust local regression technique [33] which optimizes a weighted function that accounts for the closeness of two points in a dataset. The assigned weight is larger if the two points are close to each other and smaller if the points are farther apart. This procedure allows for models to be fit to clusters of data that are close to each other, and specification of a global function that fits all the data is not necessary [33–35]. The flexibility that Loess affords in analyzing trend data has led to its use in a number of public health studies, including the incidence of melanoma [36] and celiac disease [37], as well as in projecting the impact of an HPV vaccination program [38]. Besides its flexibility, Loess is also capable of providing residual standard error, allowing the analyst to quantify the uncertainty of predicted values by using the estimated variance of the prediction at that point.

In the control scenario (where background ART and PrEP does not change), the number of new infections can be projected using the slope parameter which is estimated using existing incidence data. To measure the effect of the various interventions this slope parameter is adjusted by a scaling factor, derived in the Appendix, that accounts for the annual change in ART and PrEP scale-up.

2.2.2. Bonacci-Holtgrave (B&H)

Recent trends in HIV incidence have been used to model whether the goals of the 2010 US National HIV/AIDS Strategy (NHAS) were achieved and to inform future implementation efforts [39]. This analysis projected US HIV incidence from 2013 to 2015, using observed data on HIV incidence from 2010–2012. This approach is implemented by computing the ratios of observed year-to-year change in HIV incidence using the formula, where the annual change is the ratio of the HIV incidence in year t to the HIV incidence in year (t-1), for the three most recent years for which data are available. In the work introducing this method [39], the mean of the observed incidence ratios from 2010 to 2012 was computed and the incidence for 2013–2015 was projected by multiplying this mean by the HIV incidence in the prior year. Studies have used this approach to call for revisions to policies to reduce HIV incidence [40–43].

In the current work, observed HIV incidence ratios for YBMSM in Illinois were computed using data from 2013–2016. HIV incidence for 2017 was computed by multiplying this mean by the observed HIV incidence in 2016. Projected incidences for each of the subsequent years were iteratively computed by considering the mean of the observed incidence ratios for the previous three years.

2.2.3. Agent-based network model

An agent-based network model (ABNM) was used to simulate baseline HIV transmission to capture existing epidemic features among BMSM (age 18 to 34 years). The model was populated with 10,000 individuals at the start of the dynamic simulations. The simulation proceeded in daily time step increments. The substantive model components included arrivals due to agents aging into the model, departures (due to agent mortality or aging out of the model), dynamic sexual network structure, the temporal evolution of CD4 counts and HIV RNA (“viral load”), HIV testing and diagnosis, dynamics of ART and PrEP use, external HIV infections, and HIV transmission dynamics. The ABNM is illustrated in a flow diagram in Figure 1.

Figure 1.

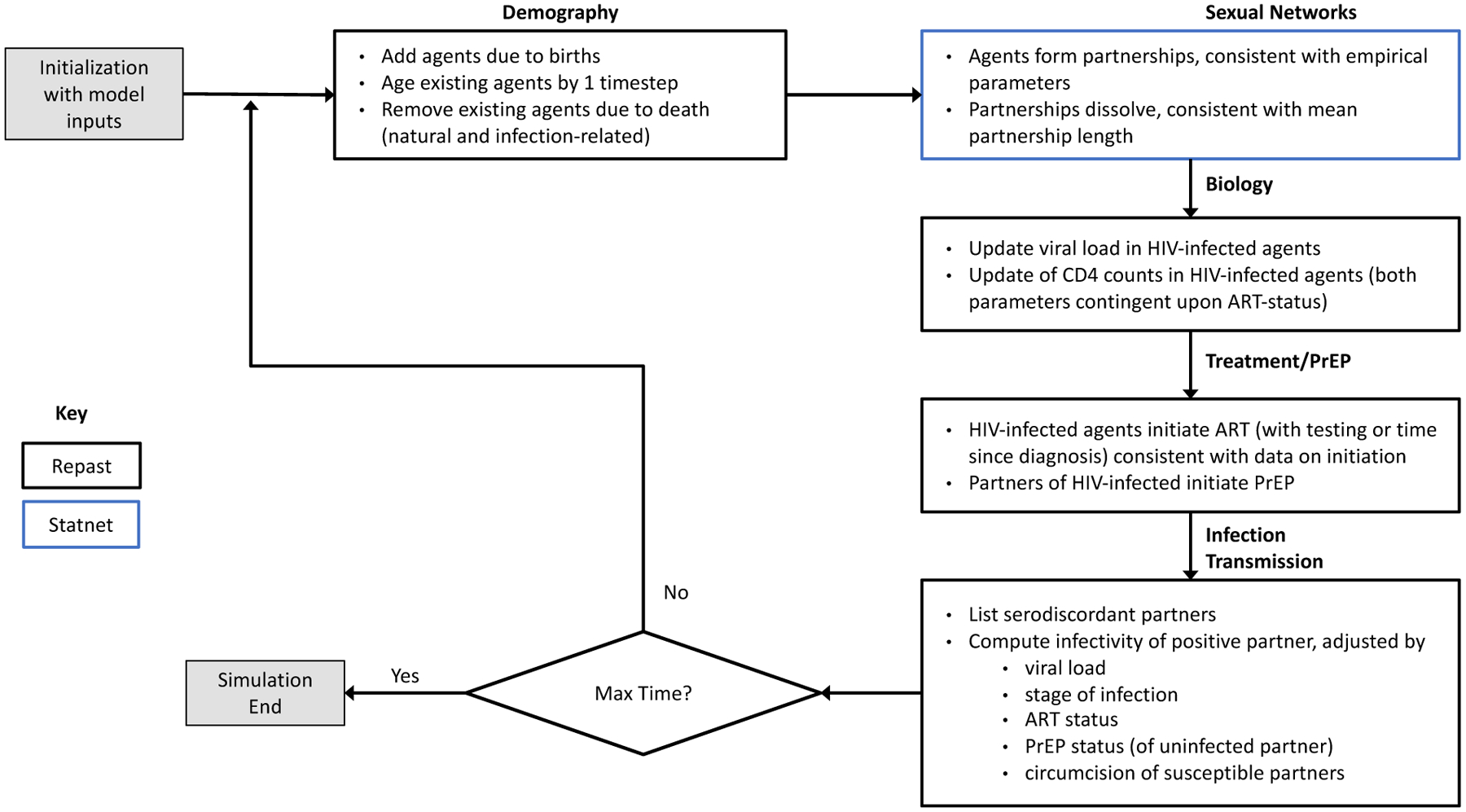
Flowchart illustrating the various components of the agent-based network model (ABNM). Sexual networks are programmed using the statnet [45] package in the R programming language. All other model components are programmed in the C++-based Repast HPC toolkit [46,47].

The sexual network structure was modeled using exponential random graph models (ERGMs) [44], a statistically robust approach to model complex network evolution over time, implemented using the statnet [45] suite of packages in the R programming language. The ABM components were developed with the C++-based Repast HPC ABM toolkit [46,47]. Parameters and computer code to reproduce results are available in a public GitHub repository [48]. A full description of these parameters and the process of model calibration has been published previously [27], and the modeling of engagement in the ART and PrEP continuums, as per the intervention scenarios of interest, is described in the Appendix.

All intervention scenarios and the control were each simulated about 30 times. The primary outcome was the number of new infections per year, averaged across the 30 simulations, along with standard error values calculated over 30 replications at each time point to quantify the uncertainty across the 30 simulations of each scenario (Table 1).

Table 1.

Projected numbers of new infections among younger Black MSM, ages 18–34 years, in the final year (2030) of Getting to Zero implementation in Illinois. Square brackets show the 1-standard error confidence intervals and the round parentheses show the decline in mean number of infections between the control and the intervention scenarios.

	Loess	Bonacci and Holtgravef	Agent-based network model
Control Baseline ART and PrEP coveragea	383 [349, 418]	369	418 [413, 422]
Interventions
ART coverage only increased by 20%b	362 [308, 417] (5%)	181 (51%)	288 [285, 292] (31%)
PrEP coverage only increased by 20%c	367 [317, 417] (4%)	202 (45%)	366 [362, 369] (12%)
ART and PrEP coverage increased by 20%	320 [226, 414] (17%)	99 (73%)	252 [248, 256] (40%)
ART coverage only increased by 30%d	339 [263, 415] (12%)	121 (67%)	246 [242, 251] (41%)
PrEP coverage only increased by 30%e	351 [287, 416] (8%)	145 (61%)	324 [320, 329] (22%)
ART and PrEP coverage increased by 30%	186 [−35, 406] (52%)	48 (87%)	186 [184, 189] (55%)

^aBaseline ART and PrEP coverage are 50% and 10% respectively

^bART coverage only increased from 50% to 70%

^cPrEP coverage only increased from 10% to 30%

^dART coverage only increased from 50% to 80%

^ePrEP coverage only increased from 10% to 40%

^fBonacci and Holtgrave is a deterministic method and no confidence intervals can be computed.

2.2.4. Ethics approval of research

The Institutional Review Board of the Biological Sciences Division at The University of Chicago provided approval for the study and waivers of the consent process, where necessary. Appropriate Data User Agreements with the Chicago and Illinois Departments of Public Health for de-identified eHARS data were established.

3. Results

The numbers of new infections, projected over the 14 years of GTZ implementation in Illinois, are shown in Figure 2 below. The numbers of new infections in 2030 – the last year of GTZ implementation – are given in Table 1. All three models predict somewhat different HIV incidences in the last year of GTZ implementation without any PrEP or ART scale-up. Therefore, the percent decline associated with all three interventions, relative to the infections in the control scenario projected by each approach, is also provided.

Figure 2.

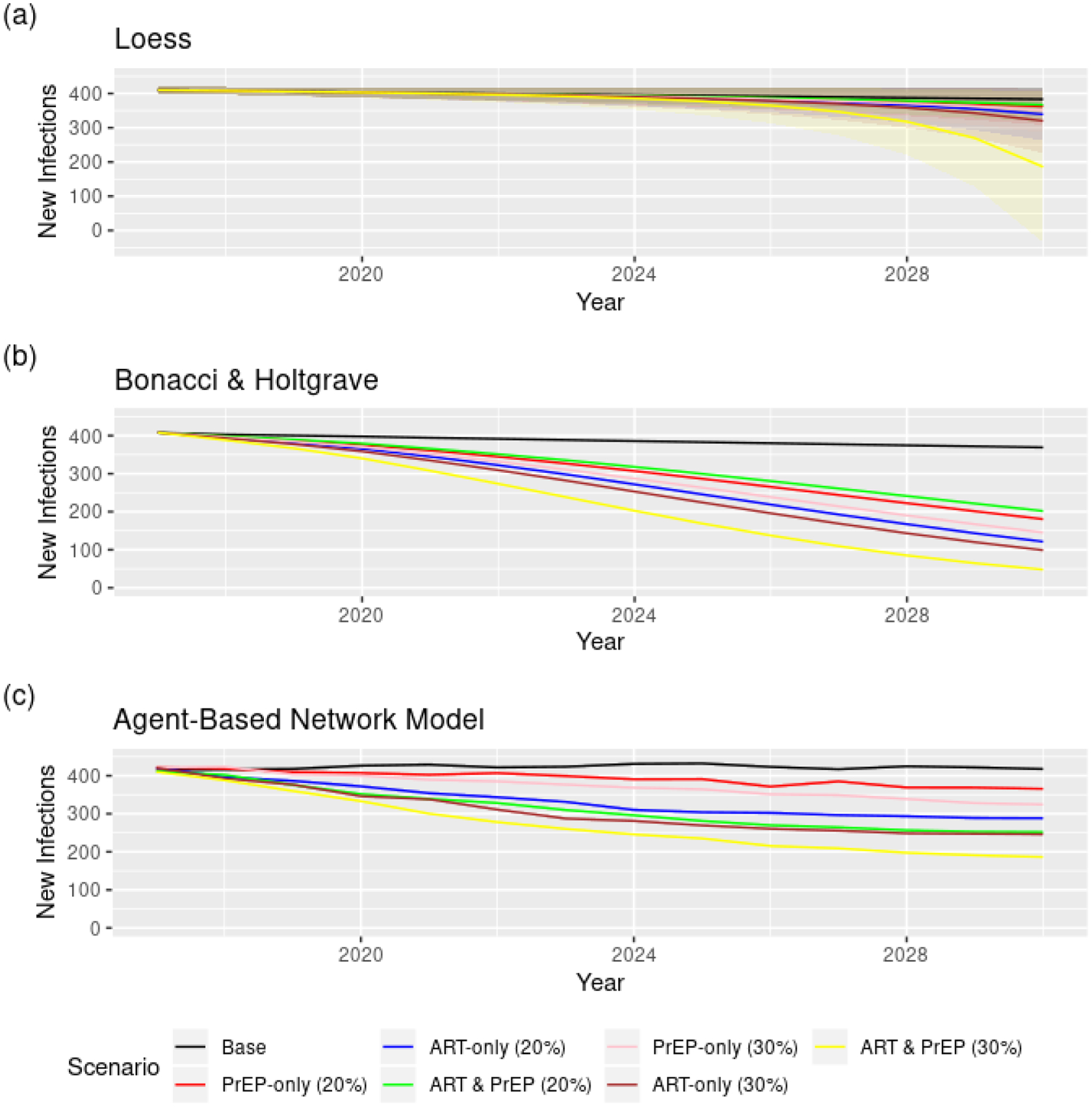
Projected numbers of new infections among younger Black MSM (ages 18–34) in each year of Getting to Zero implementation in Illinois: (a) Loess, (b) Bonacci and Holtgrave, (c) Agent-based network model under baseline and PrEP and ART scale-up interventions.

As expected, all three approaches are consistent in predicting that increasing both ART and PrEP by 20% will be more effective in reducing new HIV infections than increasing only one exclusively. The same pattern was observed for the scenarios where a 30% increase was considered. The approaches, however, differ in their predictions of the effectiveness of each intervention. Except for B&H, the other two approaches suggest that a 20% simultaneous PrEP and ART scale-up among YBMSM may not yield a functional zero HIV incidence. The Loess approach predicted the smallest declines, and the B&H showed the largest declines in the cases when ART was scaled up exclusively and when both ART and PrEP were scaled up simultaneously.

4. Discussion

4.1. Primary findings

We conclude that a 20% increase in current ART and PrEP coverage levels is unlikely to eliminate new HIV infections among YBMSM in Illinois by the end of the GTZ implementation period. However, all three approaches agree that a 30% scale-up in both ART and PrEP uptake levels may help to reach the GTZ targets by 2030. Of the two statistical time series approaches, B&H projected greater efficacy than Loess. The ABNM, which was based on detailed demographic, behavioral, biological and network parameters, projected an intermediate level of efficacy relative to the two time-series approaches. These differences in results are likely driven by the fundamental assumptions behind the approaches: whereas the projections based on the statistical time series methods are highly dependent on trends in recent incidence, the ABNM incorporates a more granular representation of the processes, and the interactions between these processes.

Moreover, of the two time series approaches, the B&H method projected a greater decline than the Loess method. This is because the B&H method projects forward “multiplicatively”, i.e., by computing the mean of the ratios of the HIV incidence for the past three years and multiplying this ratio by a factor that accounts for the increase in ART and PrEP coverage relative to baseline (Equations (4) and (5) in the Appendix). The Loess approach, on the other hand, projects forward “linearly”, i.e., by considering the slope of the line fitted through the last cluster of points, determined by their closeness, and modifying the slope of this straight line by the increase in ART and PrEP scale-up. The Loess method thus projected minimal change in HIV incidence over 14 years, likely driven by the smaller declines in HIV incidence among YBMSM over recent years. In populations with larger recent declines, Loess would predict greater efficacy of proposed interventions, but using the approach as such might mask important considerations that are specific to populations that are experiencing a disproportionate burden of HIV.

The finding that ART and PrEP scale-up by 20% points is unlikely to eliminate new HIV infections among YBMSM is, however, consistent across all three approaches. Indeed, previous research has suggested that exclusively scaling up HIV care and treatment would not accomplish NHAS goals [49] and neither would a 20% scale up in PrEP uptake [27]. This conclusion suggests that scale-up of biomedical prevention interventions will need to be intensified among subpopulations where HIV incidence is highest. Some subpopulations where current ART and PrEP scale-up levels have had substantial impact, for instance, may need lower than 20% scale-up. Other subpopulations experiencing higher incidence may require higher than the 20% scale-up currently planned under the GTZ implementation guidelines.

In scenarios where a 30% scale-up was considered, all three methods show that simultaneous increase in both ART and PrEP uptake levels might help reach GTZ targets, as defined by a functional zero, as described above. Similar to the 20% scale-up level, a 30% increase in ART while keeping PrEP uptake at baseline levels is more effective compared to a 30% increase in PrEP with baseline ART levels.

4.2. Benefits of a comparative modeling approach

Applying multiple methodological approaches allows for an assessment of consistency in the projected findings. The Loess and B&H methods are easier to implement computationally, while the ABNM provides possibilities for a deeper examination of HIV and PrEP continuum variables. Determination of the modeling approach likely depends upon the availability of data and methodological expertise, as well as the projected timelines for modeling findings prior to the implementation of interventions. Our recommended strategy for implementation scientists is to first compute statistical time series type models (for instance, the Loess or B&H, as described in this work), to generate upper and lower bounds of the estimated intervention efficacy. This preliminary work can be followed by longer-term development of more complex ABNM-type models that allow for a more granular examination of specific processes, subpopulations and interventions. The ABNM’s primary advantages are that it provides the capacity to incorporate a wider representation of underlying transmission processes, including network mixing, and to examine specific interventions mechanisms explicitly, and investigate how these interventions might impact different population segments.

Each modeling framework also draws attention to specific contextual considerations. For instance, within Loess and B&H, the uptake of PrEP and ART can be directly controlled, but neither approach has the capacity to model person-to-person transmission explicitly. The impact of ART and PrEP scale-up is realized by considering the multiplicative effects of the number of users at any given time. The ABNM, by contrast, accounted for the HIV care continuum factors that influence ART uptake: testing, linkage, and adherence, but does not provide the flexibility to directly control the number of ART users at any given time. Thus, while the two time-series approaches provided the flexibility of directly controlling an important parameter and were more quickly implemented, the ABNM provided more fine-grained control allowing for explicit examination of key input variables. Identification of a “gold standard” modeling technique is beyond the scope of this study. Rather, this study hopes to compare three modeling frameworks used to project HIV incidence to determine how PrEP and ART scale-up may impact projected HIV incidence. Other modeling approaches, such as deterministic-stochastic modeling choices are available and might be useful in related model comparison studies, depending upon the research questions of interest and the availability of input data [50,51].

4.3. Limitations

All of the modeling approaches described here use recent data to make projections over 14 years of GTZ implementation. Thus, these models assume that other baseline trends will continue to hold, and the changes that occur will be limited to scale-up of ART and PrEP as per the GTZ strategies considered. Therefore, any structural or policy changes that occur over the GTZ implementation period will not be accounted for in the model. Future model iterations must account for such policies, especially if these policy goals are revised. Computation of all models was based upon approximations about how baseline projections might adapt in response to changes in ART and PrEP coverage. Further work in improving these approximations might be necessary, especially if the resources to develop agent-based simulation models are unavailable. A version of the B&H approach that explicitly allows for a consideration of the 90-90-90 goal to improve engagement the ART continuum has been proposed [52]. A similar version for PrEP scale-up, especially to guide GTZ efforts in the U.S., might be helpful in guiding HIV elimination efforts. Finally, the definition of the functional zero might need to be updated as interventions are rolled out in reality and we approach the later stages of the GTZ planning period.

5. Conclusions

Accomplishing GTZ goals will require increased scale-up of ART and PrEP; however, such scale-up may be constrained in part because of the many barriers that prevent effective implementation. Racism, addiction, criminalization, unemployment, lack of access to quality education and health care, and residential segregation are some of the barriers that disproportionately impact young Black men and YBMSM in particular [53,54]. Addressing these barriers is vital to accomplishing HIV elimination goals [55,56]. Indeed, this need to address structural barriers to HIV and PrEP care continuums is recognized in the US [57] and globally [58–61]. The ABNM provides the flexibility to model interventions that are designed to address these barriers and allows for projected effects of interventions before they are implemented. New modeling approaches that can improve our understanding of the underlying mechanisms by which socio-structural and systemic factors impact HIV transmission and that can quantify the effects of interventions to address them can make a critical contribution to the implementation of interventions [62]. The models described here are being expanded to begin the process of incorporating socio-structural and systemic factors. Next-generation modeling tools can help formulate effective strategies that aid in the design of interventions focused on reducing the impact of these barriers. Triangulation studies allow for increasing amounts of complexity to be examined iteratively in order to make the underlying assumptions behind various approaches more explicit and to derive policy prescriptions that utilize the combined strengths of multiple methodological approaches and data sources.

Appendix

A.1. Introduction

This Appendix provides additional methodological details of the models described in the main body of the manuscript. Below, model equations for the Loess and Bonacci and Holtgrave (B&H) methods are derived and the modeling of ART and PrEP continuums in the agent-based network model is described.

A.2. Loess method

The Loess technique is a robust local regression technique [33], which optimizes a weighted function that accounts for the closeness of two points in the dataset. The assigned weight is large if the two points are close to each other and small if the points are farther apart. This procedure allows for models to be fit to clusters of data that are close to each other, and specification of a global function that fits all the data is not necessary [33–35].

A Loess curve was fit to annual incidence data for YBMSM in Illinois, using the loess function in R (version 3.5.3). For any given point, the fitting procedure uses points in the “neighborhood” of that point, defined here as 75% of the points that are closest to it, in accordance with the recommended default value in the R function [63]. These points are weighted by their distance from the point in consideration.

Incidence data were obtained from the Enhanced HIV/AIDS Reporting System (eHARS), a database maintained by the Illinois Department of Public Health [30]. A slope parameter ρ_L,t was computed from the fitted values obtained from the last three years (2013–2016), under the assumption that both PrEP and ART were being used in those years, whereas prior to 2013 PrEP was not being used. The projected number of new infections is iteratively computed as

$$i_{t+1}=i_t+{\rho }_{L,t+1}$$ (1)

where i_t is the HIV incidence in the “current” year t, and i_t+1 is the HIV incidence in the following year, t+1. The slope ρ_L,t+1 is computed as

$${\rho }_{L,t+1}={\rho }_{L,t}{\alpha }_{t+1}$$ (2)

where α is a factor that scales the slope parameter when ART and PrEP are scaled up. The parameter α_t+1 was set to

$$\left(\frac{1-k_A{A}_0}{1-k_A{A}_{t+1}}\right)\left(\frac{1-k_R{R}_0}{1-k_R{R}_{t+1}}\right)$$ (3)

where A_t is the proportion of HIV-positive individuals using ART in year t, R_t is the proportion of HIV-negative individuals using PrEP in year t. Thus, parameters A_t and R_t represent ART and PrEP coverage in year t respectively. The parameters A₀ and R₀ denote ART and PrEP coverage in the first year of the projection, respectively. When ART coverage is scaled up in year t+1, the number of new infections prevented is assumed to be proportional to the relative reduction in the population of the infected individuals, approximated as $\frac{1-A_0}{1-A_{t+1}}$.

Similarly, when PrEP coverage in a given year, R_t, is scaled up, the number of new infections prevented is assumed to be proportional to the population of HIV-negative individuals, approximated as $\frac{1-R_0}{1-R_{t+1}}$. (Note that when ART and PrEP coverage are not scaled up, A₀ = A₁ = … = A_t and R₀ = R₁ = … = R_t , then α_t+1 reduces to 1.)

The factor k_A is a weighted average of the protection conferred on individuals who are always, usually, sometimes, and never adherent to ART. From YBMSM cohort data in Illinois, these proportions were estimated to be 32, 28, 30 and 10% respectively [31,32], and the four respective groups was assumed to receive 100, 67, 33 and 0% protection. The factor k_R indicates PrEP protection, where data from a PrEP demonstration project were used to estimate that 21.1% of men took 0 pills/week (non-adherent), 7.0% took < 2 pills/week (low adherence), 10.0% took 2–3 pills/week (moderate adherence), and 61.9% took 4+ pills/week (high adherence) [64]. PrEP use is assumed to reduce HIV infection probability in these adherence groups by 0, 31, 81, and 95%, for non, low, moderate, and high adherence, respectively, in accordance with previous modeling work [12]. These protection estimates were assumed to be constant across all models.

Equation 2 is iteratively solved over the course of the projection period to yield the number of new HIV infections for each projection time point.

A.3. Bonacci and Holtgrave method

A recent study modeled trends in HIV incidence to assess whether the goals of the 2010 US National HIV/AIDS Strategy (NHAS) were achieved and to inform future implementation efforts [39]. This method is implemented by computing the average of the ratios of observed year-to-year change in HIV incidence using the formula: [annual change = HIV incidence in year t / HIV incidence in year (t-1)] for the three most recent years that data are available for. Thus, the incidence can be iteratively projected as

$$i_{t+1}={\rho }_{BH,t}{i}_t$$ (4)

where ρ_BH,t is the average of the annual change values at the three most recent years as defined above, and i_t is the HIV incidence in the “current” year t. The number of new infections when ART and PrEP are scaled up is given as

$$i_{t+1}={\rho }_{BH,t}{i}_t\left(\frac{1-k_A{A}_{t+1}}{1-k_A{A}_t}\right)\left(\frac{1-k_R{R}_{t+1}}{1-k_R{R}_t}\right)$$ (5)

where parameters are as defined above. Equation 5 is iteratively solved over the course of the projection period to yield the number of new HIV infections for each projection time point.

A.4. Agent-based network model

An agent-based network model (ABNM) was used to simulate baseline HIV transmission to capture existing epidemic features among adolescents and young adults (age 18 to 34 years). The model was populated with 10,000 individuals at the start of the dynamic simulations. The simulation proceeded in daily time step increments. The model was calibrated using published HIV incidence and prevalence estimates. A detailed description of the agent-based network model (ABNM) and its parameterization is available elsewhere [27].

The ABNM is designed to allow for a deeper examination of PrEP and ART care continuums. PrEP uptake was maintained at the base levels by computing a daily initiation probability for HIV-negative individuals not using PrEP. Further, it was assumed that PrEP initiators were retained for an average of one year, consistent with local PrEP continuum data [65]. A dynamic equilibrium was set to balance the PrEP initiation and retention processes to maintain uptake at desired levels. Additionally, PrEP users were divided into four adherence categories, with protection dependent upon adherence. ART uptake, on the other hand, was determined by three care continuum parameters: (a) HIV testing frequency; (b) linkage, defined in the model as distribution of times between HIV diagnosis and ART initiation; (c) ART adherence, modeled by assuming 32, 28, 30, and 10% of ART initiators were always, usually, sometimes, and never adherent, respectively, as estimated from cohort data [31,32].

The PrEP scale-up intervention was implemented by considering a uniform annual increase from base uptake levels to 30 and 40%. Twenty percent ART scale-up level was modeled by assuming an increase in the proportion of individuals who were always adherent to 80% of ART initiators, and a decline in the proportion of individuals who were usually and sometimes adherent to 10% of ART initiators each. (The impact of increased ART adherence on overall ART uptake is further discussed below.) A similar adherence adjustment approach was used to model the 30% ART scale-up. The six interventions and the baseline scenario were simulated 30 times over the course of the GTZ implementation period to account for inherent uncertainty due to the stochastic nature of this model. In addition, standard error values were also calculated over 30 replications at each time point to quantify the uncertainty (Table 1).

Since ART uptake in the ABNM was determined by three care continuum parameters described above, the overall uptake was increased by 20% by assuming an increase in the proportion of individuals who were always adherent to 80% of ART initiators, and a decline in the proportion of individuals who were usually and sometimes adherent to 10% of ART initiators each. In the Loess and B&H methods, on the other hand, ART uptake was controlled by specifying the A_t parameter, as described above. In Figure A1 below, we plot the ART uptake over time in the ABNM, to demonstrate that the increased adherence resulted in a temporal ART scale-up that was comparable to the assumption in the statistical time series methods.

Figure A1.

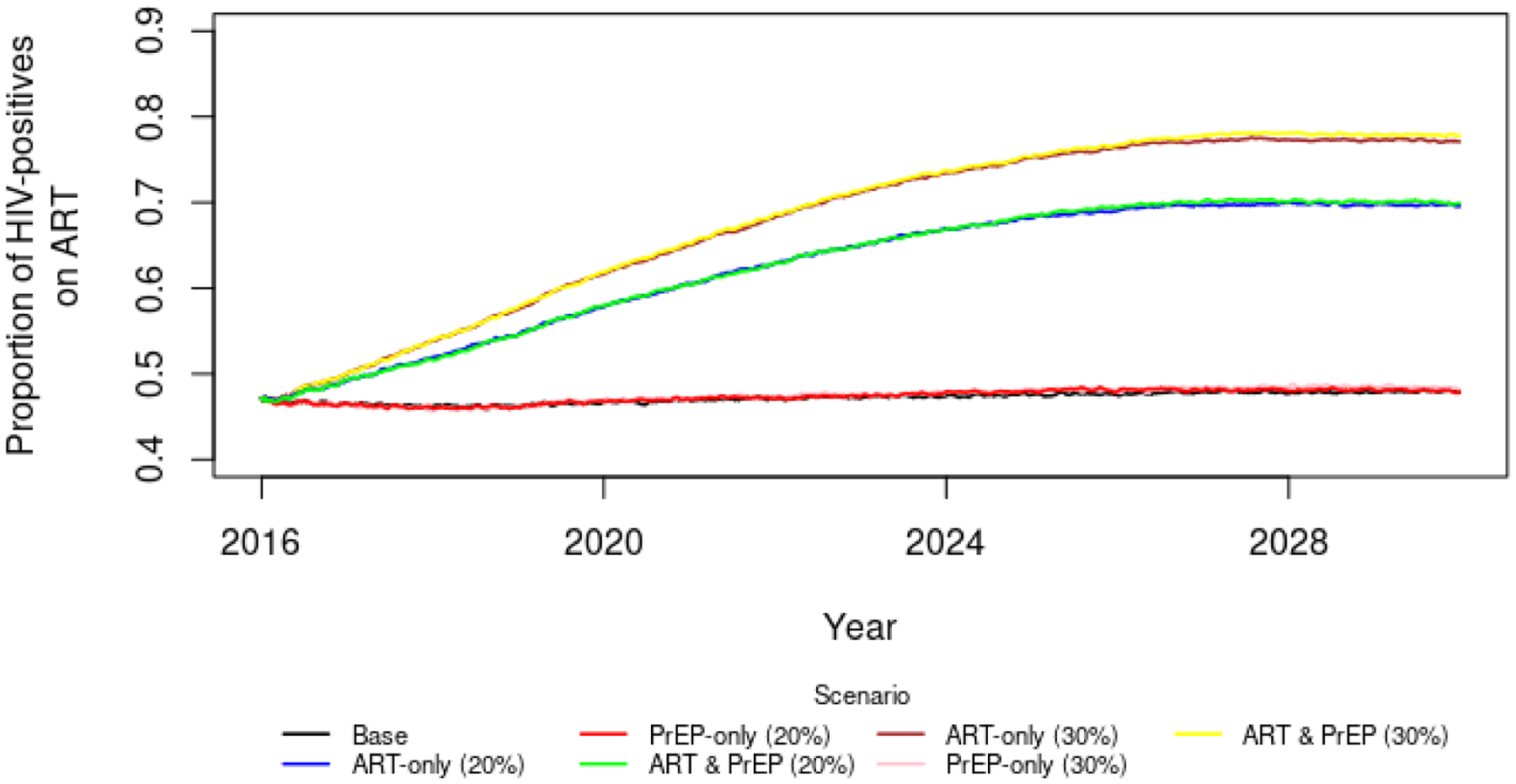
Percentage of HIV-positives using Antiretroviral Treatment under various scenarios of scale-up.