Abstract
We document side-by-side trends in the gender gap of educational achievement and late-life cognition across countries. By and large, we find that, within the cohorts born between 1920 and 1959, women have had significantly lower educational attainment than men, with the gap narrowing over time. Correspondingly, we estimate a pronounced tendency of women’s cognition to improve over time relative to men. We investigate whether these co-movements are likely due to the narrowing gender gap in education inducing a relative improvement in women’s cognition. The data offer little support for such a causal relation. We discuss possible third factors that may underlie the observed parallel trends in education and cognition gender gaps.
Keywords: Cognition, Education, Gender difference, Polygenic risk score, Development
Introduction
With the sharp increase in life expectancy, the number of individuals older than 65 suffering from mild cognitive impairment and dementia is raising rapidly. The trend is striking as dementia cases are projected to reach 140 million worldwide in 2050 from 47 million in 2015 (Livingston et al., 2017). Cognitive impairment, even in the absence of a dementia diagnosis, is often associated with limitations in an individual’s ability to work, to manage finances, and to engage in routine activities, thereby increasing need for care. With the expected rise in the number of cognitively impaired and demented elderly, it is critical to identify opportunities for preventing or delaying cognitive decline.
Education has been recognized as a key contributor to the development of cognitive reserve, which refers to how flexibly and efficiently the brain functions, even in case of or despite Alzheimer’s Disease (AD) pathology. It is also considered a protective factor against cognitive aging (Tucker & Stern, 2011). In fact, there exists empirical evidence that lower educational attainment predicts poorer cognitive performance in late life (Stern, 2002), and having none or only primary school is associated with a 60% higher risk of dementia (Livingston et al., 2017).
The causal effect of early-life education on late-life cognitive ability has been examined by Glymour et al. (2008), Banks & Mazzonna (2012), Crespo et al. (2014), and Schneeweis et al. (2014), among others. All these studies exploit exogenous variation in years of education stemming from differences in compulsory schooling laws across states and/or changes in compulsory schooling laws over time within countries in both the United States and Europe. The estimated relationships between education and late-life cognition provided by these studies are specific to the contexts where particular compulsory schooling laws were in place and reforms were enacted. All such contexts are Western countries, with relatively advanced levels of socioeconomic development. Moreover, the changes in years of education induced by compulsory schooling reforms, which these studies rely upon, are relatively small. In this paper, we examine the extent to which early-life educational achievement has a protective effect on late-life cognition across countries characterized by different levels of economic development, as well as across cohorts exposed to largely different levels of access to education and labor market opportunities. To better account for contextual factors driving both education and cognition within each country, we focus on gender differences in education and late-life cognition across cohorts. This approach nets out the effect of contextual factors, such as level of economic development, that are common to men and women within each country and that are potentially correlated with both educational achievement and cognition. This also allows us to investigate whether heterogeneous effects of education on late-life cognition by gender, which have been documented in the literature, may significantly diverge across places depending on cultural and social norms and their evolution over time.
Recent work suggests that in developed countries older women perform as well as men or better on a wide range of cognitive tests (Langa et al., 2008, 2009). In contrast, older women are at a disadvantage in terms of cognitive functions compared to older men in developing countries, such as India (Lee et al., 2014; Onur and Velamuri, 2016) and China (Zhang, 2006; Lei et al., 2012). The difference in educational attainment between men and women has been proposed as an important contributor to the observed gender gap in late-life cognition in developing countries. It is also a possible explanation for why this gap is reduced in younger cohorts, since women’s access to schooling in developing countries has improved significantly over time. Indeed, several studies, relying on cross-sectional regressions of cognition on gender and education (and other covariates), have documented that education differentials partially account for cognition differences in later life in countries such as China (Zhang, 2006; Weir et al., 2014; Oksuzyan et al., 2018), India (Weir et al., 2014; Onur and Velamuri, 2016; Oksuzyan et al., 2018; Singh et al., 2018), Latin America, and the Caribbean (Maurer, 2011; Díaz-Venegas et al., 2018), and Egypt (Yount, 2008).
Zaninotto et al. (2018) used data from England and estimated a linear growth curve model for cognitive decline over a time span of eight years. They found that women experienced less cognitive decline than men (after controlling for other covariates: age, socioeconomic status and background, health, physical functioning, and health behaviors) and that lower education was associated with steeper cognitive decline. In these data women had more middle-level education than men, who had both more high level and more low level education, which makes interpreting the results less straightforward.
Available causal estimates reveal that the protective effect of education on late-life cognition in the U.S. and Europe is mainly enjoyed by men (and not by women), through better labor market outcomes and, to a lesser extent, through enhanced social participation and quality of life (Banks & Mazzonna, 2012; Schneeweis et al., 2014). Overall, the existing empirical evidence indicates that reducing differences in education between men and women can potentially have very different effects on the gender gap in late-life cognition, depending on contextual circumstances, including the starting level of educational attainment, and on the channels through which the returns to education manifest themselves.
The goal of this paper is to document side-by-side patterns in the gender gap of educational achievement and late-life cognition across countries. Under the premise that education affects late-life cognition (either directly or indirectly), a narrowing gender gap in educational attainment should be reflected into a narrowing gender gap in late-life cognition. However, we expect the magnitude of this relation to depend on the overall level of economic development and educational attainment, as well as on gender differences in access to schooling, labor market, and social opportunities, and, therefore, to exhibit heterogeneity across countries.
An individual’s education level is endogenously determined by one’s characteristics, including innate ability, which, in turn, may affect cognition. Differential trends in access to education by cohort and gender may induce important selection mechanisms that confound the relationship of interest. In other words, observing the parallel narrowing of the gender gap in education and in late-life cognition may not necessarily mean that the latter stems from the former. To address this concern, we evaluate various theoretical scenarios where we vary the strength of the causal links between innate ability on the one hand, and education and cognition on the other hand. We then compare predicted patterns with those observed in the data to assess whether, to what extent, and in what contexts a narrowing gender gap in education might have plausibly contributed to a parallel narrowing gender gap in late-life cognition.
The contribution of this paper is threefold. First, we focus on gender differences in education and late-life cognitive ability, thereby adding an important nuance to the existing debate on how educational achievement affects cognitive health. Compared to existing contributions estimating the relationship between gender differences in education and cognition using cross-sectional regressions, we take advantage of the panel dimension of our data and investigate gender differences in both cognition and education across cohorts while also controlling for age. This approach enables us to examine the differences in cognition across birth cohorts, not confounded with cognitive aging. Second, we analyze this issue from a cross-country perspective. Specifically, we run our analyses for the same cohorts in countries that have experienced different degrees of economic development over time and different evolution of cultural and social norms. This allows us to assess whether and by how much the relationship between education and late-life cognition is shaped by the specific socio-economic circumstances that cohorts have been exposed to. Third, unlike studies that focus only on individuals affected by compulsory education reforms, which exploit relatively small changes in years of schooling induced by such reforms and a narrow range of birth cohorts, we consider all birth cohorts over the period 1920–1959 and the wide range of educational achievement. Our objective is to document the existence (or not) of broad concurrent trends in education and late-life cognition across cohorts and countries and, when they are observed, discuss under what assumptions they can be interpreted as suggestive evidence of a protective effect of education on late-life cognition. While this approach offers an assessment of how education and late-life cognition correlate in general and of context-driven heterogeneity in this relationship, it prevents us from making causal claims. We view the empirical evidence provided by this paper as complementary to the existing causal estimates of the effect of education on late-life cognition.
We use harmonized data, developed by the Gateway to Global Aging Data at the University of Southern California, covering 28 different countries across the world.1 We measure individual cognition in multiple domains, as assessed by comparable cognitive tests in different countries, and rely on a harmonized categorical education variable.
By and large, we observe a tendency towards women’s improvements in educational achievement and cognitive test performance relative to men across cohorts. Yet, we find weak support for the prediction that in countries where the gender gap in education has narrowed, women’s performance in cognitive tests has improved relative to men. We also pool all countries together and relate gender differences in cognitive ability to gender differences in education. In line with country-specific analyses, these aggregate results provide weak evidence for parallel movements of gender differences in education and late-life cognition.
The remainder of the paper proceeds as follows. Section “Data” provides an overview of the data used in the study. Section “Empirical strategy” describes a stylized theoretical setup as well as our empirical specifications. Section “Results” presents the results of the analyses using both country-specific data and aggregated data across countries. Section “Conclusions” concludes with a discussion of our findings.
Data
We use data from the Health and Retirement Study (HRS) in the United States and its sister studies around the world. The HRS is an extraordinarily rich longitudinal study of individuals over the age of 50 in the United States. Since the early 2000 s, an increasing number of studies have been initiated in many countries, purposefully designed to be comparable to the HRS. We use the following surveys alongside the HRS: the English Longitudinal Study of Ageing (ELSA), the Survey of Health, Ageing and Retirement in Europe (SHARE), the Korean Longitudinal Study of Aging (KLoSA), the Chinese Health and Retirement Longitudinal Study (CHARLS), the Mexican Health and Aging Study (MHAS), The Irish Longitudinal Study on Ageing (TILDA), and the Costa Rican Longevity and Healthy Aging Study (CRELES).
The HRS-family surveys are coordinated with the explicit goal of facilitating cross-country comparisons. Characteristics that apply to most or all of these studies are (1) biennial interviews with respondents and their spouses; (2) a multidisciplinary questionnaire design that elicits a wealth of information about health, socioeconomic status, demographics, and other topics; and (3) regular refreshment samples to keep the sample representative of the older population. There are some notable exceptions to the questionnaire frequency, respondent age, and spouse inclusion for these surveys. While the majority of surveys conduct interviews biennially, the MHAS experienced a 9-year interval between the second and third waves. The individual age-eligibility threshold is 51 years in HRS, 50 years in ELSA, SHARE, TILDA, and MHAS, and 45 years in KLoSA and CHARLS. Spouses and partners of age-eligible respondents are interviewed regardless of age by all surveys, except in KLoSA, where they have to be at least 45 years old. The number of countries included in SHARE varies across waves (subject to funding of individual countries). We include all participating SHARE countries with the exception of Ireland for which a larger separate study (TILDA) is available.
Despite the high degree of coordination, there are numerous small differences ranging from different variable names to blocks of questions about country-specific health care systems or pension systems. The Gateway to Global Aging Data at the University of Southern California (g2aging.org) has developed harmonized versions of these surveys. Following the RAND HRS, these consist of user-friendly longitudinal files, where consistent variable names and definitions are adopted. We use the RAND HRS Longitudinal File 2014 (V2) (Bugliari et al., 2018) and the most recent (as of October 2018) Gateway to Global Aging Data harmonized datasets for all other studies (we refer the reader to the supplementary material for details about versions used).
We measure cognition using individual scores on three distinct cognitive tasks, namely total word recall, serial 7 s, and orientation.2 Total word recall, a commonly studied measure of short-term memory that is indicative of everyday cognitive functioning, is available in all the surveys considered in this study. The interviewer reads a list of 10 common words and after that asks the respondent to name as many of these words as possible.3 This gives an immediate word recall score on a scale of 0–10. After a number of intervening questions, the interviewer again asks the respondent to name as many of these words as possible. This gives a delayed word recall score on a scale of 0–10. Total word recall is the sum of these two scores and, thus, is measured on a scale of 0–20. For the serial 7 s test, the interviewer asks the respondent to subtract 7 from 100, and continue subtracting 7 from each subsequent number for a total of five trials. The score is the number of correct subtractions among the five trials (0–5). This test is administered in all surveys except MHAS and CRELES and early waves of SHARE and TILDA. The orientation test, available in all surveys, consists in naming “today’s date” including year, month, day of the month, and day of the week. The score, ranging from 0 to 4, counts how many of these items were correctly named.
Given large differences in education systems across countries, we use a rather coarse measure of educational attainment that ensures reasonable cross-country comparability. In particular, we use a harmonized categorical variable, derived from ISCED-97 codes, which takes the value 1 if the individual has not completed “upper secondary education” (high school or equivalent; ISCED-97 codes 1 and 2), 2 if the individual has completed upper secondary or vocational training (high school graduate or equivalent but below a 4-year college degree; ISCED-97 codes 3 and 4), and 3 if the individual has completed tertiary education (post-secondary education; ISCED-97 codes 5 and 6; for the U.S., this is a 4-year college degree or more). In the regression analyses that follow, we will treat this variable as continuous to ease the presentation and interpretation of our results.
For each country, we examine gender differences in education and cognition across cohorts. These are defined as 10-year birth cohorts, with the oldest born between 1920 and 1929 and the youngest born between 1950 and 1959. This ensures that all cohorts are observed in all countries and, therefore, increases comparability of the results.
More details about how available cross-country measures of cognition and education are used in the empirical strategy are provided in Section “Practicalities” below.
Empirical strategy
Our descriptive analysis consists of comparing average educational achievement and cognition scores by gender and cohort. If education affects cognition positively, higher average education levels should be associated with higher cognition scores. Various confounding factors, exhibiting particular trends over time and correlating with both education and cognition, may lead to spurious correlation between education and cognition. Focusing on gender differences is helpful in this respect: in many countries, women’s education has increased much more than men’s education, whereas many contextual and environmental variables have been equally shared by men and women. Looking at the gender differences allows us to filter out such common confounding factors. The main threat to identifying a relationship between education and cognition through our exercise is the presence of unobserved underlying factors, affecting both outcomes of interest, that vary across birth cohorts and differentially so for men and women. In this section, we first present a fairly stylized setup that will inform us about what patterns we should expect under alternative scenarios characterized by different relationships among education, cognition, cohort, gender, and individuals’ innate (unobserved) ability. We then discuss some practicalities related to the implementation of our empirical strategy.
Stylized setup
Let us consider a simplified setup, in which there are two cohorts (early and late), two levels of education (low and high), two ability levels (low and high), and all individuals’ cognition scores are measured at the same age. The most general model for education is then
| (1) |
where Ei is education of individual i (0 = low, 1 = high), Fi is a dummy indicating whether the individual is female, Bi is a dummy indicating the individual’s birth year (0 = early, 1 = late), and Ai is individual i’s ability (0 = low, 1 = high); vi is the error term that has mean zero conditional on the explanatory variables in the model. In (1), α1–α4 reflect educational attainment for low-ability individuals and α5–α8 reflect the selectivity of education by ability. The coefficients α3 and α7 pertain to trends in educational attainment over time, α2 and α7 to the gender gap in education, and α2 and α6 to changes in this gender gap. We would expect α3 and α3 + α7 to be positive (increasing educational attainment), α2 and α2 + α6 to be negative (women have lower education than men in the earlier cohort), and α4 and α4 + α8 to be positive (narrowing gender gap in education over time).
The most general model for cognition is
| (2) |
where Yi is the cognition score of individual i and εi is an error term, which again has zero conditional mean. Important special cases are the ability-only model
| (3) |
in which education and other environmental factors, as captured by gender and cohort dummies, do not affect cognition, and the education-only model
| (4) |
in which cognition is only determined by educational attainment.
Generally, ability is unobserved, so we will estimate models without it. This leads to a selectivity (or endogeneity) problem if ability affects education and also affects cognition beyond its effect on education. The value of the education-only model is that it is a benchmark model in which there is no selectivity, although we would not expect this to be true.
Empirical specification and theoretical predictions
We estimate models separately by cognition score (word recall, serial 7 s, and orientation) and country. For each of these combinations, we study gender and cohort differences in education and cognition. Specifically, the models we estimate are4
| (5) |
| (6) |
and
| (7) |
Specifications (5) and (6) are simply reduced form specifications that estimate gender and cohort differences in education and cognition. If, as often implied by our narrative, there exist a general increasing trend and a narrowing gender gap in education, then we would expect δ3 to be positive, δ2 to be negative, and δ4 to be positive, with the relative magnitude of δ4 and δ2 differing by country and cohort, depending on whether women still have lower education in the later cohort or have caught up or overtaken men. Eq. (6) is informative of gender- and cohort-specific patterns in cognitive ability. If there are co-movements in education and cognition, we would expect to observe similar trends in the education gender gaps from (5) and the cognition gender gaps from (6). Comparison with (7) helps shed light on the role played by education in shaping late-life cognition.
Suppose that the education-only model (4) is true. Then, the π coefficients in (6) would have the same signs as the δ coefficients in (5). However, when adding education to the model in (7), the coefficients of gender and birth cohort would become zero. So, if the estimated coefficients of gender and birth cohort become noticeably smaller (in absolute value) after including education, this would point toward an important role of education. If, on the other hand, some of the gender and birth cohort coefficients are nonzero in (7), then there exist gender and cohort differences in cognition beyond those explained by education, which in this model (still without ability) would be attributed to other environmental factors. This would raise the question of what other factors affect cognition. Most environmental factors (e.g., air pollution) would likely impact men and women similarly, thereby leading to nonzero coefficients φ3 and φ11. However, we would not expect such common factors to result in nonzero coefficients φ4 and φ12, which measure changes in the gender gap in cognition by educational attainment.
If ability, which is an omitted variable in (7), affects both cognition and education, then φ4 and φ12 may be nonzero and reflect changes in the relative selectivity of education by gender. For example, consider the canonical situation where men have higher education than women in the early cohort and this gender gap narrows (or closes) as education becomes more accessible to women (e.g., for social/cultural reasons). In this scenario, if education and ability are positively correlated and both affect cognition positively, one would expect φ4 and φ12 to be negative. This is because if education is less accessible to women in the early cohort, then one would expect the pool of women with low education in the early cohort to have (on average) higher ability, and therefore higher cognition, than low-educated men. Similarly, women with high education in the early cohort would be positively selected and exhibit higher levels of ability, and in turn of cognition, relative to men. As education becomes more accessible and women start receiving higher education, the average level of ability (and cognition) of both low- and high-educated women in the late cohort decreases relative to the one of men with the same educational attainment, leading to negative φ4 and φ12 coefficients.
Now suppose that education has no causal effect on later-life cognition, and any correlation between the two is a selection effect through ability: the ability-only model (3) is true. Under the plausible assumption that ability does not vary by birth cohort and gender, (6) would have zero coefficients (except for the constant). So, nonzero coefficients in (6) suggest that education matters, especially if the signs of the coefficients in (6), where cognition is the dependent variable, mimic the ones in (5), where education is the dependent variable. Predictions for the parameters in (7) if the ability-only model is true are more complex. Depending on the relation between education and ability, we may see some coefficients (e.g., for the female dummy) positive and others (e.g., female × birth cohort and female × education) negative, although the education coefficient would generally be positive. If we drop the assumption that ability is roughly constant across genders and cohorts, any pattern would be possible. If ability varies by gender but not by birth cohort, our focus on gender gaps and its predictions would be largely unchanged. If ability varies by birth cohort but not by gender, we also would expect our predictions to largely go through. On the other hand, if ability trends are different by gender, a different picture may emerge.
One general prediction is that the implied coefficient of education for each combination of gender and birth cohort should be positive, either because education may have a positive effect on cognition (causal effect), or ability has a positive effect on both cognition and education (selection effect), or both. If we find coefficients of education that are close to zero or negative, this would suggest that ability or education has a negative effect on cognition or ability has a negative effect on education, or neither ability nor education affects cognition appreciably. This would contrast with the theoretical and empirical literature on cognition. The theoretical predictions stemming from our simplified setup are summarized in Table 1.
Table 1.
Theoretical Predictions by Assumption.
| Assumption/true model | Predictions |
|---|---|
| Educationa | |
| Increase in education | δ3 > 0 |
| Initial gender gap | δ2 < 0 |
| Narrowing gender gap | δ4 > 0 |
| Cognition | |
| Education-only | Signs of coefficients in (6) are the same as in (5); φ2 – φ4 are zero |
| Education + environmental factors | φ3and φ11 may be nonzero, but φ4 and φ12 are likely (close to) zero |
| Ability-only (does not vary by gender and cohort) | π2–π4 are zero |
| Ability-only (does not vary by cohort) | π3and π4 are zero |
| Ability-only (does not vary by gender) | π2and π4 are zero |
| Education + ability + narrowing gender gap in education | φ4and φ12 are negative |
| Education + ability | Implied education coefficients are positive and larger than the causal effects of education |
These are not essential for the analysis: predictions for cognition regressions would change accordingly.
Practicalities
The discussion so far in this section has been stylized in several important ways: we have assumed there were only two cohorts and two levels of education, and that we observe every individual at the same age. As mentioned in Section “Data” above, when we take our models to the data we define a birth cohort as the population of individuals born in a decade, 1920–1929, 1930–1939, 1940–1949, or 1950–1959. We use birth cohort as an unordered categorical variable (i.e., a set of dummy variables). This does not restrict the generality of the discussion so far, but it means that there are 4×(4–1)/2 = 6 pairwise combinations of “early” and “late” cohorts. Hence, we will need to condense the results drastically to make them manageable.
For education, we use the harmonized variable derived from ISCED-97 codes. This variable has three ordered categories. Because the effect of education on cognition is expected to be monotonic and education serves as a left-hand side variable in some specifications, we enter this For education, we use the harmonized variable derived from ISCED-variable linearly (after recoding it from 1–3 to 0–2) in the empirical 97 codes. This variable has three ordered categories. Because the effect models.
We observe individuals at a range of ages, and we observe many individuals in more than one wave. Because age is related to cognition in late life, we include a quadratic in age as additional controls in the specification, and to avoid undue influence of outliers at very high ages, we restrict the sample to the 50–89 age range.
Results
Within-country comparisons
We start by documenting trends in the education gender gap across countries. By and large, the estimation results reveal that, for the cohorts surveyed by the HRS-family of studies, education has been increasing over time for men, and women have had significantly lower educational attainment than men, with the gap narrowing over time. With reference to (5), we estimate a positive and significant δ3 coefficient across countries. We find that the δ2 coefficient is negative and statistically significant for 80% of the countries considered in the study, while it is never positive and statistically significant. Most importantly, we observe a robust tendency of the gender gap in education to narrow over time across countries. For each country, we compare the estimated coefficients of the female × cohort interaction (the δ4 coefficient) for two cohorts pairwise across all 6 possible combinations. We then compute the fraction of statistically significant differences where we observe a larger coefficient for the later cohort in a pair. This would indicate a narrowing in the education gender gap over time. Overall, the average fraction of statistically significant differences where the female/cohort interaction coefficient is larger in the later cohort relative the earlier one is 87%. In 19 out of 23 countries, where statistically significant differences across cohorts are observed, this fraction is 1. That is, we estimate that education has systematically increased more for women than for men, leading to a narrowing gender gap.
In Fig. 1, we report trends in the education gender gap in six selected countries, covering three continents and characterized by different levels of economic as well as of social/cultural development over the observation period. These are China, United States, South Korea, Estonia, Germany, and Spain. The coefficient estimates can be found in Table A1 in the appendix.5 As can be seen, in all these selected countries within the 1920–1929 cohort women have less education than men. On a 1–3 point scale, the size of the gap varies from about −0.1 in the U.S. and Spain, to about −0.6 in Germany. The extent to which the gender gap in education narrows over time exhibits substantial heterogeneity across countries as well. The gap is virtually closed in the U.S. and Spain, and is reversed in Estonia. It remains evident in Germany, China, and Korea, with a tendency to narrow down in the former two countries only.
Fig. 1.
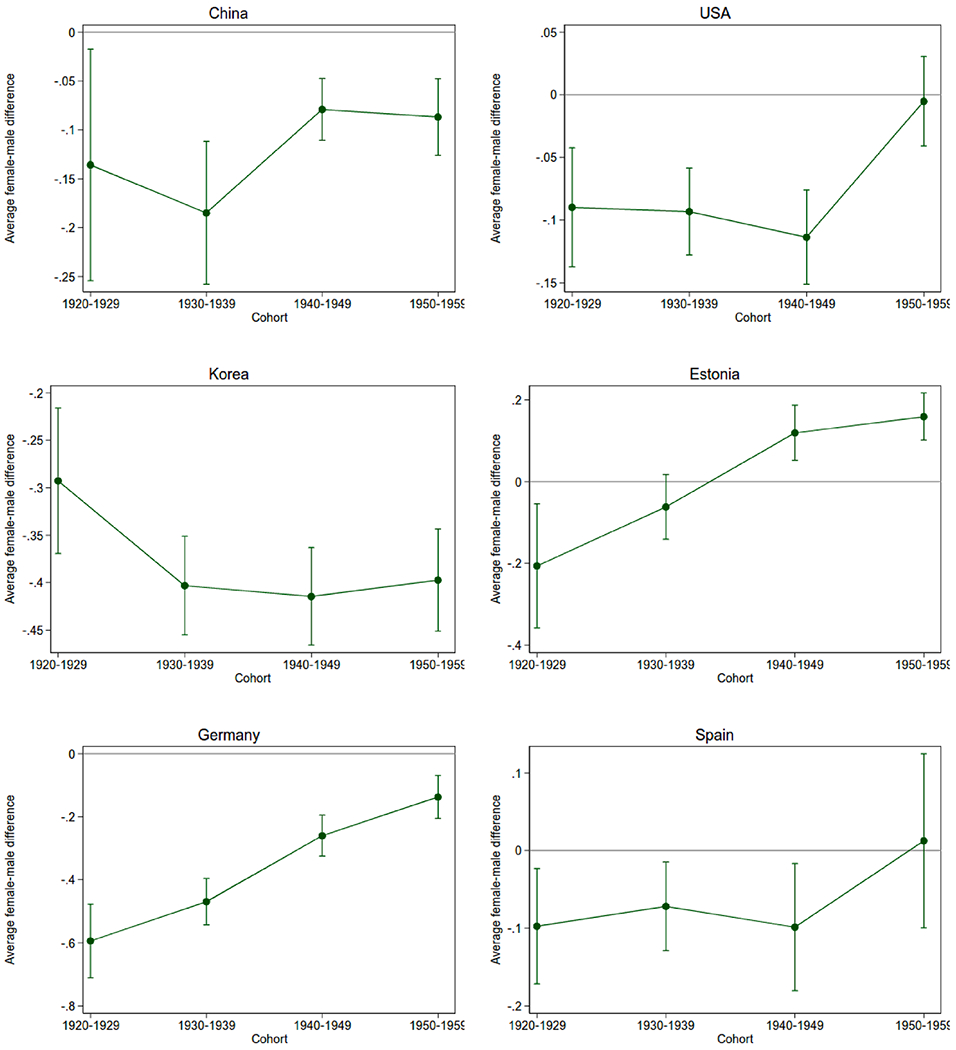
Gender Gap in Education over Time in Selected Countries.
Next, we estimate (6) and study the extent to which the coefficients show similar patterns as the coefficients in (5). In other words, we investigate whether co-movements in education and cognition are observed over time and by gender, in each country. The coefficient estimates for the six selected countries are reported in Tables A2–A4 in the appendix.6
In general, we find that women perform as well as men, if not better, on the word recall test. Specifically, within the 1920–1929 cohort women’s score is statistically indistinguishable from that of men in about two-thirds and higher in about one-quarter of the countries considered in the analysis. However, we observe women performing worse than men in China, South Korea, Greece, and Portugal, which are all nations with relatively lower societal and economic development in the first half of the 20th century. In virtually all countries, we document a positive trend in the word recall score of men over time as well as a substantial improvement in the relative performance of women compared to men. Analogously to the analysis using education as outcome variable, we compare, for each country, the estimated coefficients of the female × cohort interaction for two cohorts pairwise and compute the fraction of statistically significant differences where the later cohort has a larger coefficient. For word recall, this fraction averages 94% and is 100% in 19 out of 21 countries where statistically significant differences across cohorts are estimated. Hence, there is a pronounced tendency of increased women’s performance relative to men, which mimics the narrowing gender gap in education documented above.
In order to gain further insights into these likely co-movements in education and late-life cognition, we compute, for each country, the number of times women’s word recall performance and educational achievement relative to men between two cohorts move in the same direction. With reference to our theoretical setup, this exercise can be thought of as counting the number of times π4 in (6) has the same sign as δ4 in (5), with both being statistically significant at the 5% level. We then compute, for each country, the ratio between this number and the number of times a statistically significant difference in the gender gap in education across cohorts is observed. On average, this fraction is 45%, indicating that in about 1 out of 2 cases where a narrowing gender gap in education is detected, an improvement in women’s word recall performance relative to men is detected too. In only 4% of cases the gaps in education and word recall move in opposite directions, while in 51% of cases we do not find a statistically significant improvement in women’s word recall performance relative to men, even if a significant reduction in the gender gap in education is observed. These figures are suggestive of similar patterns in the trend of education and word recall of women relative to men.
The solid lines in Fig. 2 describe the trend in the word recall performance of women relative to men for the aforementioned six selected countries. As can be seen, women born between 1920 and 1929 appear to perform as well as or better than men in all countries, except for China and Korea, where they exhibit a significant and sizable negative gap. There is a marked improvement in the relative performance of women compared to men over time in 5 out of these 6 countries. In fact, the initial negative gap is substantially reduced and almost closed in China and Korea. In Germany and Spain, a positive gap emerges for later cohorts, while no significant gender difference is observed for the earliest cohort. Finally, a positive gap is either maintained in the U.S. or reinforced in Estonia. Comparing Figs. 1 and 2, it becomes apparent that women’s relative performance in the word recall test and relative educational achievement move in the same direction. This co-movement is especially evident for Germany, Estonia, Spain, and China, but less evident for the U.S. The case of Korea is somewhat atypical since the observed narrowing gender gap in the word recall test score across cohorts is coupled with a broadening gap in education.
Fig. 2.
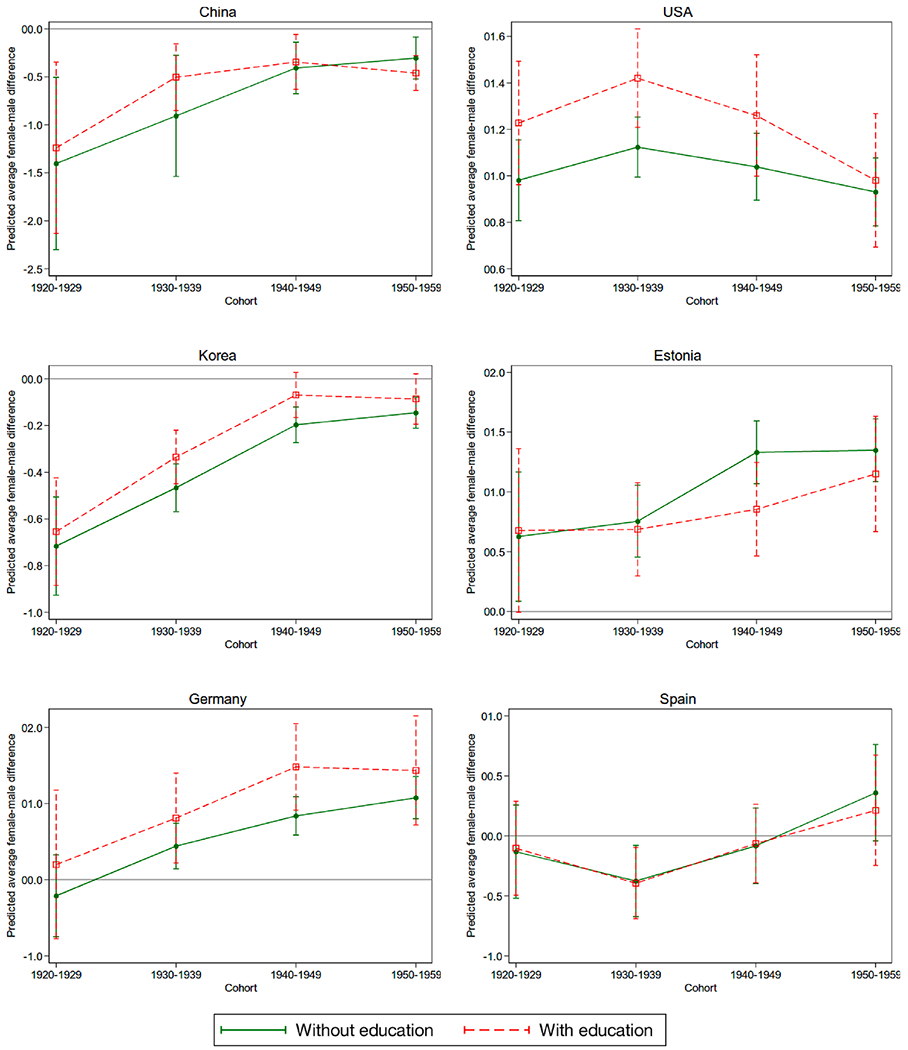
Gender Gap in Word Recall over Time in Selected Countries (with and without education in the model).
Having documented unconditional trends in word recall and co-movements with education trends, we proceed with the estimation of (7), where education is controlled for. Again, the coefficient estimates for the three measures of cognition in the six selected countries are in Tables A2–A4 in the appendix.7 When focusing on word recall, we see mixed evidence of such a role of education.
The number of countries where statistically significant differences across cohorts in the female × cohort interaction coefficient are observed drops from 21, in the model without education, to 15, in the model with education, and the number of countries where all these coefficients are positive correspondingly drops from 19 to 12. This result indicates that the observed improvement in the cognition gender gap over time may be partially accounted for by the narrowing gap in education, but there is a substantial amount that remains unaccounted for. A closer look at the country-specific estimates reveals that in about half of the cases, the magnitudes of the gender and birth cohort coefficients remain unchanged or are even larger when education is added.
The dashed lines in Fig. 2 represent trends in women’s word recall performance relative to men from model (7), net of any education effect. That is, they plot trends implied by coefficients φ1 to φ4 in (7). Since education and late-life cognition are positively correlated and a negative female education gap in the earliest cohort exists in virtually all countries, the theoretical predictions from the previous section imply that we would expect the initial negative female gap in cognition estimated via (6) to be larger than that estimated via (7). That is, we would expect the solid line to start below the dashed line. In countries where a negative female education gap persists over time (e.g., USA, Germany, Korea), the solid line would lie below the dashed line throughout the observation period. However, to the extent that the female education gap narrows over time and education drives the observed gender differences in cognition, the distance between the two lines should decrease over time. In countries where a positive female gap in education emerges (e.g., Estonia), the solid line would lie above the dashed line for the cohorts where women exhibit higher educational achievement compared to men. A growing, positive education gap for women would also imply a diverging trend for the two lines. As can be seen in Fig. 2, there is relatively weak empirical evidence in support of these predictions. In most countries, the solid line starts below the dashed line, but the difference between the two starting points are relatively small. The solid line remains below the dashed line in countries where a negative female education gap persists. However, the two lines do not always become closer to each other as the female education gap narrows (they do in the U.S. and China). The solid and dashed line cross in Estonia, where women move from exhibiting a negative education gap in the earliest cohorts to exhibiting a positive education gap in later cohorts. Nevertheless, they do not indicate diverging paths. In Spain, the two lines virtually overlap throughout the observation period. In general, the estimated gaps in cognition unconditional (solid line) and conditional on education (dashed line) are not particularly different from each other, suggesting only a minor role of education in explaining trends in cognition over time.
With reference to (7), we find that coefficients φ3 and φ11 are nonzero, and in many cases statistically significant. This is consistent with the existence of contextual or environmental factors affecting cognitive performance of men and women in a similar fashion, above and beyond the effect of education. Less than 10% of the φ4 and φ12 coefficients are statistically significant, and of those, only an eighth are negative. This result does not seem to support the argument, made in Section “Empirical specification and theoretical predictions”, according to which φ4 and φ12 would be negative if they were to reflect differential changes by gender in the ability composition of education groups.
We replicate our analyses using the other aforementioned cognitive test scores. With the serial 7 s and orientation scores as dependent variables in (6) and (7), we find that, unlike in the word recall test, women exhibit a clear disadvantage compared to men, especially within the older cohorts. Specifically, within the 1920–1929 cohort, women have a significantly lower serial 7 s test score than men in half of the countries considered in the study. Their performance is statistically indistinguishable from that of men born in the same decade in the other half of the countries, while it is never significantly better. Similarly, within the 1920–1929 cohort, women’s orientation test scores are significantly lower than those of men in one-third of the countries, not statistically different from that of men in 60% of the countries, and significantly higher only in two countries, U.S. and Ireland.
We observe a pronounced tendency of the initial gender gap in serial 7 s and orientation to narrow over time. Again, we compare, for each country, the estimated coefficients of the female × cohort interaction for two cohorts pairwise and compute the fraction of statistically significant differences where the later cohort has a larger coefficient. For serial 7 s, statistically significant differences across cohort pairs are obtained for 15 out of 28 countries. Among those, the fraction where the later cohort has a larger coefficient is 1 in 13 countries and 0 in two countries. For orientation, we see statistically significant differences across cohort pairs for 16 out of 28 countries. Among those, the fraction where the later cohort has a larger coefficient is 1 in 15 countries and 0.5 in one country. Thus, while for serial 7 s and orientation improvements over time in the gender gap are not always precisely estimated, whenever statistically significant differences are observed across cohorts they do point to a narrowing gap.
As far as co-movements with education trends are concerned, the fraction of times when a statistically significant δ4 in (5) is coupled with a statistically significant π4 in (6) with the same sign is 20% for serial 7 s and 16% for orientation; in 3% and 7% of the times, respectively, π4 is statistically significant with the opposite sign. In the remaining 77% and 78% of cases, respectively, where a narrowing education gap is observed, the π coefficients are not statistically significant. Thus, we have rather weak evidence that the gender gaps in education and cognition move in the same direction over time. This pattern is also apparent for the selected countries in Figs. 3 and 4.
Fig. 3.
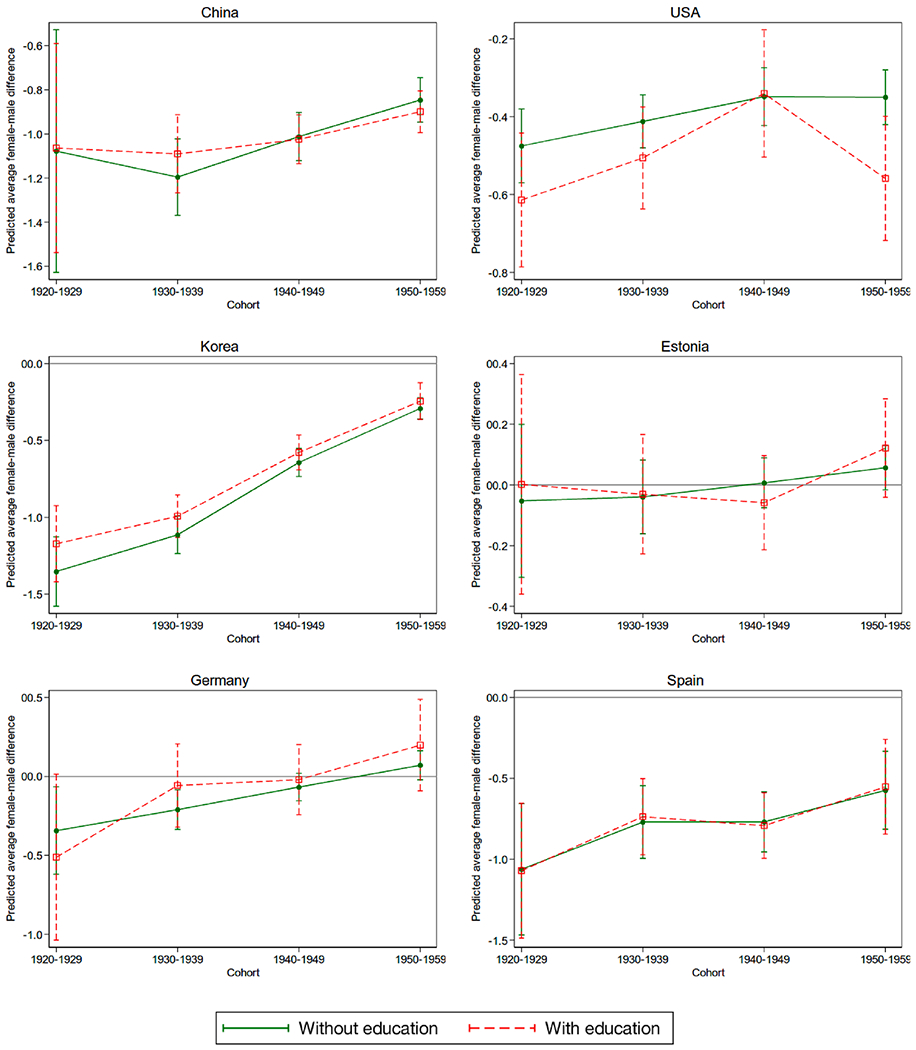
Gender Gap in Serial 7 s over Time in Selected Countries (with and without education in the model).
Fig. 4.
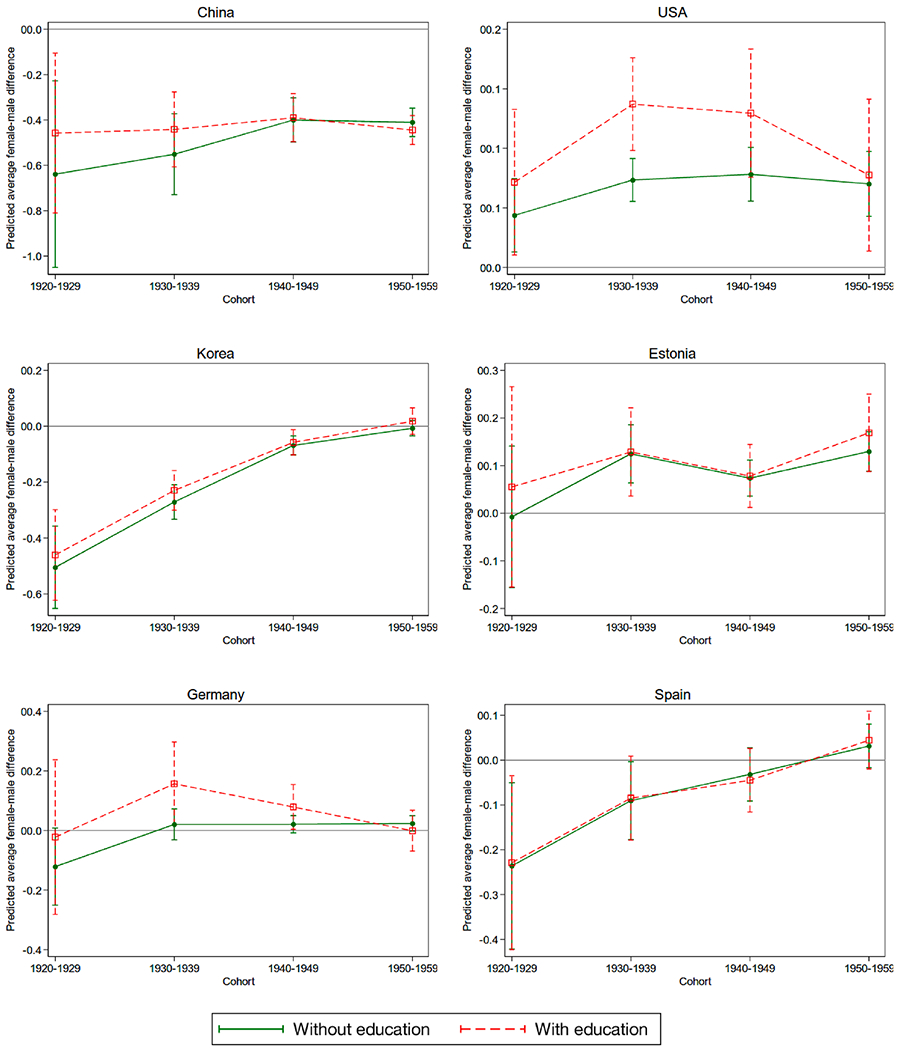
Gender Gap in Orientation over Time in Selected Countries (with and without education in the model).
In the majority of cases, the solid line starts below the dashed line, that is, the negative gender gap in serial 7 s and orientation in the earliest cohort is larger when the observed negative education gender gap in this cohort is not accounted for. However, the difference between the unconditional (solid line) and conditional (dashed line) gaps is relatively modest. The distance between the solid and dashed lines barely changes for the serial 7 s test score. In the case of the orientation score, they do become closer to each other over time in China, the U.S., and Germany, potentially reflecting the narrowing gender gap in education. However, confidence intervals are generally too wide to allow drawing conclusions from these observed patterns.
Gender and birth cohort effects do not change significantly when education is added to the model, for both serial 7 s and orientation. The number of countries where statistically significant differences across cohorts in the female × cohort interaction coefficient are observed drops from 15 to 10 for serial 7 s and from 16 to 15 for orientation. Moreover, for those cases where statistically significant differences across cohorts are observed, the fraction where the later cohort has a larger coefficient is almost always 1. This confirms that the observed unconditional narrowing of the gender gap in serial 7 s and orientation over time is hardly explained by a concurrent narrowing gap in education.
Cross-country analysis
So far, we have estimated separate models for each country. More tentatively, we can also look at differences between countries: If education affects cognition, we expect countries with small gender gaps in education to have small gender gaps in cognition. Thus, we also perform aggregate cross-country regressions, where we estimate the following models:
| (8) |
| (9) |
where represents the average of one of our three cognition measures (word recall, serial 7 s, or orientation), is average education, c and b are subscripts for country and birth cohort, respectively, and F and M are superscripts for females and males, respectively. Hence, in (8) we regress the average cognition gap on the average education gap using a cohort in a particular country as the unit of observation. In (9), we add cohort fixed effects to the specification. If gender differences in education and cognition co-move, we would expect β to be positive in (8). If the observed co-movement is mainly driven by third factors affecting both education and cognition, β should be smaller in (9) than in (8).
The results of this cross-country analysis confirm the conclusions based on the individual-level data: while in general a narrowing gender gap in education is coupled with an improved performance in cognitive tests of women relative to men, there is no evidence that the former is inducing the latter. In Fig. 5, we report the scatter plots and estimated regression lines from the model (8) for the three cognition test scores, with detailed regression results in Table A5 in the appendix. As can be seen, we do estimate a positive and significant relationship between gender differences in education and gender differences in cognition for word recall , but not for serial 7 s and orientation . Most importantly, all these estimated coefficients decrease when estimating (9) and we find no statistical evidence of a positive relationship between gender differences in education and gender differences in cognition when cohort fixed effects are added to the specification.8 This, again, suggests that the observed co-movements in the education and cognition gender gaps are potentially driven by other contextual/environmental variables.
Fig. 5.
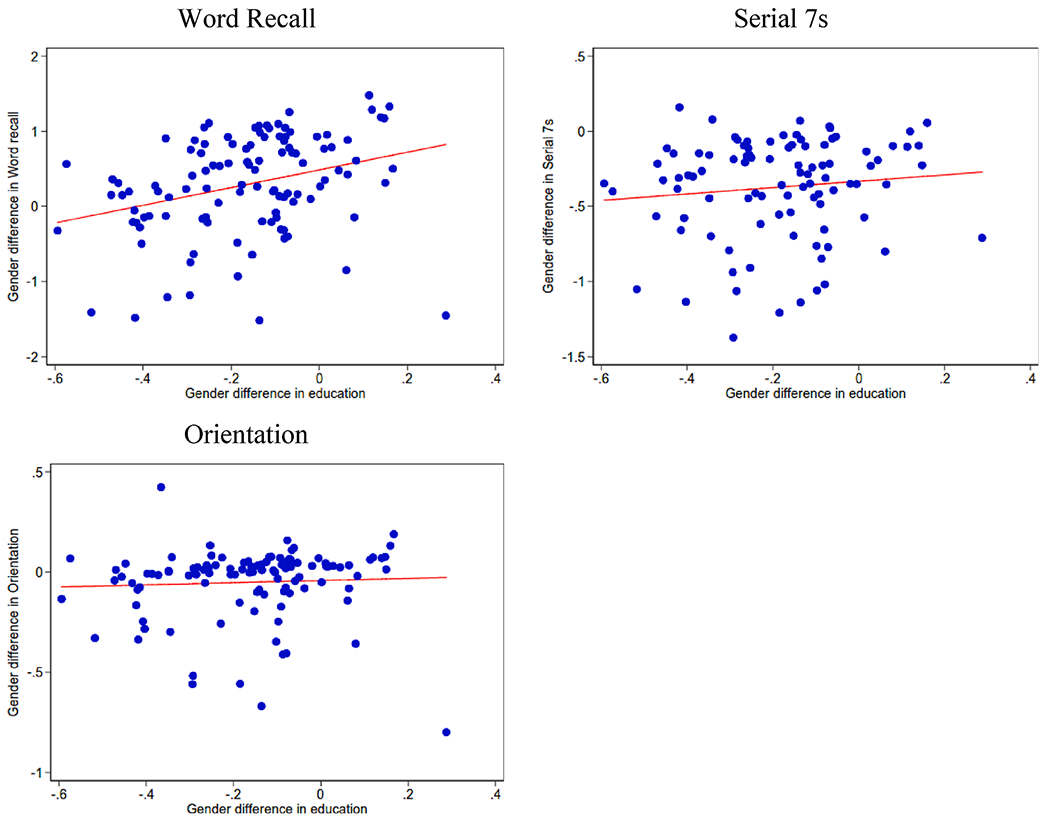
Cross-Country Relationship between Gender Gap in Cognition and Education.
Conclusions
In this paper, we study the relation between educational attainment and late-life cognition, with a focus on differences by gender and cohort. Compared to the literature on the effects of education on cognition, we consider a broader range of cohorts, we look at average effects across the whole educational spectrum, and we study many countries, including middle-income and developing countries, where different circumstances prevail than in the U.S. and Western Europe. An important contribution of our paper is to consider different cognitive domains, as captured by different cognitive test scores, and analyze how the relative performance of women may vary across them.
We document side-by-side trends in the gender gap of educational achievement and late-life cognition across countries. Under the premise that education affects late-life cognition (either directly or indirectly), a narrowing gender gap in educational attainment should be reflected in a narrowing gender gap in late-life cognition. However, the extent to which such a co-movement is observed across countries presumably depends on the degree of economic development as well as on the levels of access to education and labor market opportunities to which different cohorts have been exposed. Also, a parallel narrowing of the gender gap in education and late-life cognition does not necessarily mean that the latter stems from the former, as other context-specific factors may drive women’s improvements in education and cognition relative to men.
By and large, we find that, within the cohorts born between 1920 and 1959, women have had significantly lower educational attainment than men, with the gap narrowing over time. Correspondingly, we estimate a pronounced tendency of women’s cognition to improve over time relative to men. The aforementioned pattern is robust to different test scores concerning different cognitive domains. When focusing on memory status, as assessed by the word recall test score, we see that women have generally performed better than men in earlier cohorts and have either preserved or increased their relative advantage in later cohorts. In countries with relatively lower societal and economic development in the first half of the 20th century, such as China, South Korea, Greece, and Portugal, women start with a substantial negative gap, which is reduced over time. For mental status, as assessed by the serial 7 s and orientation tests, women exhibit a clear disadvantage compared to men throughout the observation period. However, this is more pronounced within older than younger cohorts.
To gain further insights into likely co-movements in education and cognition, we compute the fraction of times a statistically significant narrowing gap in education between a later and an earlier cohort is coupled with a statistically significant improvement in women’s cognitive performance relative to men. This fraction ranges from 45% for word recall to 20% and 16% for serial 7 s and orientation, respectively. Hence, we have from moderate to weak evidence that a narrowing gender gap in education is accompanied by an improvement in women’s cognitive test scores compared to men.
Contrary to the pattern predicted by a model of a causal effect of education on cognition, the trends in the cognition gender gap are virtually the same whether they are computed unconditionally or after including education (and its interactions with gender and cohort). That is, changes in women’s educational achievement relative to men do not appear to be the main driver of the observed improvement in women’s cognitive test performance relative to men.
Thus, the empirical evidence suggests that other factors may underlie the estimated co-movement in the education and cognition gender gaps. One of them could be differential mortality by innate ability and gender. Since men have lower life expectancy than women and higher ability individuals tend to live longer, in older cohorts surviving men would have higher ability than surviving women. As differential mortality by gender and ability is not as prominent in younger cohorts, we may observe a narrowing gender gap in education and a concurrent improved cognitive performance of women relative to men over time. This explanation points at ability and at its differences by gender and cohort as the main drivers of the parallel trends in education and cognition gender gaps. In other words, it presumes that education has little or no causal effect on late-life cognition. Such an assumption is not in contrast with the empirical literature, which has not been able to establish a robust causal link between education and cognition for women.
Other explanations are possible. For instance, improvements in living standards, especially in countries that were less economically and socially developed in the first half of the 20th century, may have enhanced women’s cognitive performance more than men’s. With improved nutrition, health care access, and employment opportunities, women may have experienced a relatively more pronounced improvement in cognition regardless of their relative educational achievement. In this respect, one emblematic case is the one of South Korea, where a significant narrowing gender gap in cognition is coupled with a widening of the gender gap in education. It is possible that the efforts of the Korean government to address gender inequality issues in the late 20th century and improve women’s well-being are reflected in late-life cognition, but not in educational achievement for the cohorts considered in this study. On the other hand, in Northern European countries, where gender bias has been historically less evident (e.g., Denmark and Sweden), we observe a significant narrowing of the gender gap in education, but a virtually constant difference in cognitive test performance between women and men across cohorts (shown in the supplementary material).
In general, increased labor market opportunities, enhanced social participation, and improved quality of life for women, which have been often concurrent to higher educational achievement in most countries, may have contributed to the decreasing female gap in cognition, independently of the narrowing gap in education. We leave the empirical investigation of such potential mechanisms to future research.
In conclusion, we investigate the relationship between early-life educational achievement and late-life cognition through the lenses of trends in education and the cognition gender gap across cohorts and countries. We purposefully focus on gender differences to net out the effect of contextual factors driving both education and cognition that are common to men and women within each country. Yet, our results, which do not support the existence of a causal relationship between education and late-life cognition, seem to indicate that different compositions of cohorts as well as country-specific socio-economic circumstances differentially affecting men and women may underlie the observed parallel narrowing of the gender gaps in education and cognition. These findings are consistent with the fact that a causal link between education and late-life cognition for women has not been established in the literature. They also warn against the broad generalizability of existing causal estimates. First, estimates based on samples where men and women are pooled together may mask heterogeneity by gender. Second, estimates exploiting exogenous variation in years of education induced by changes in compulsory schooling laws may reflect the distinct cultural, economic, and social environments where particular compulsory schooling laws were in place and reforms were enacted. As such, they are not immediately applicable to different cohorts within the same country or to the same cohort across countries, which may have witnessed and operated in very different socio-economic circumstances.
As more detailed and comparable cross-country data become available, future research should help gauge how robust the causal estimates of the effect of education on late-life cognition are to different contexts and point at which factors may drive differences in estimated effects across countries. This would also further our understanding of the specific mechanisms through which the causal effect of education on late-life cognition operates.
Acknowledgments
This research was supported by grant R01 AG030153 from the National Institute on Aging, National Institutes of Health, USA. Zewei Li and Sujeong Park provided excellent research assistance. We thank participants of the Conference on Cross-Country Analysis of Retirement, Health, and Well-Being (October 2018), especially Hidehiko Ichimura (our discussant) and Albert Park, for helpful comments and suggestions. This study uses data from the HRS, ELSA, SHARE, TILDA, MHAS, CRELES, KLoSA, and CHARLS. Detailed acknowledgments for these data are included in the supplementary material.
Appendix. Regression results
Table A1.
Regressions of education on cohort, gender, and their interaction for selected countries.
| Regressor | Country |
|||||
|---|---|---|---|---|---|---|
| China | USA | Korea | Estonia | Germany | Spain | |
| 1930–1939 | 0.0730 | 0.0714*** | 0.164*** | 0.118 | 0.0430 | 0.0190 |
| (0.0695) | (0.0243) | (0.0456) | (0.0749) | (0.0456) | (0.0405) | |
| 1940–1949 | 0.0131 | 0.235*** | 0.304*** | 0.187** | 0.0959** | 0.179*** |
| (0.0610) | (0.0247) | (0.0443) | (0.0729) | (0.0450) | (0.0446) | |
| 1950–1959 | 0.0613 | 0.256*** | 0.603*** | 0.306*** | 0.0696 | 0.349*** |
| (0.0607) | (0.0242) | (0.0440) | (0.0708) | (0.0467) | (0.0528) | |
| Female | −0.136** | −0.0897*** | −0.293*** | −0.206*** | −0.594*** | −0.0973** |
| (0.0605) | (0.0242) | (0.0391) | (0.0774) | (0.0595) | (0.0380) | |
| Female × 1930–1939 | −0.0492 | −0.00342 | −0.111** | 0.144* | 0.124* | 0.0256 |
| (0.0710) | (0.0300) | (0.0473) | (0.0873) | (0.0704) | (0.0479) | |
| Female × 1940–1949 | 0.0567 | −0.0239 | −0.122*** | 0.326*** | 0.334*** | −0.00120 |
| (0.0626) | (0.0309) | (0.0471) | (0.0847) | (0.0682) | (0.0565) | |
| Female × 1950–1959 | 0.0490 | 0.0846*** | −0.105** | 0.366*** | 0.457*** | 0.110 |
| (0.0637) | (0.0303) | (0.0478) | (0.0828) | (0.0689) | (0.0687) | |
| Constant | 0.155*** | 0.962*** | 0.325*** | 0.680*** | 1.229*** | 0.158*** |
| (0.0596) | (0.0200) | (0.0383) | (0.0675) | (0.0392) | (0.0326) | |
| N | 34,561 | 134,399 | 36,553 | 16,659 | 15,389 | 18,918 |
Standard errors in parentheses
p < 0.10,
p < 0.05,
p < 0.01.
Table A2.
Regressions of word recall for selected countries.
| Regressor | Country |
||||||
|---|---|---|---|---|---|---|---|
| China |
USA |
Korea |
|||||
| Without edu | With edu | Without edu | With edu | Without edu | With edu | ||
| 1930–1939 | −0.567 | −1.173*** | 0.233*** | 0.0159 | 0.0655 | −0.00152 | |
| (0.661) | (0.443) | (0.0882) | (0.125) | (0.101) | (0.114) | ||
| 1940–1949 | −0.774 | −1.225** | 0.454*** | −0.226 | 0.0839 | 0.0358 | |
| (0.634) | (0.517) | (0.0989) | (0.141) | (0.117) | (0.129) | ||
| 1950–1959 | −0.964 | −1.196** | 0.231** | −0.248 | 0.0669 | 0.0631 | |
| (0.684) | (0.553) | (0.109) | (0.151) | (0.123) | (0.136) | ||
| Female | −1.403*** | −1.239*** | 0.981*** | 1.228*** | −0.716*** | −0.654*** | |
| (0.458) | (0.456) | (0.0886) | (0.136) | (0.107) | (0.117) | ||
| Female × 1930–1939 | 0.496 | 0.736 | 0.143 | 0.193 | 0.250** | 0.319** | |
| (0.550) | (0.487) | (0.110) | (0.174) | (0.119) | (0.131) | ||
| Female × 1940–1949 | 0.996** | 0.895* | 0.0578 | 0.0319 | 0.519*** | 0.585*** | |
| (0.478) | (0.479) | (0.115) | (0.190) | (0.114) | (0.127) | ||
| Female × 1950–1959 | 1.098** | 0.779* | −0.0505 | −0.247 | 0.57i*** | 0.568*** | |
| (0.472) | (0.465) | (0.116) | (0.200) | (0.112) | (0.130) | ||
| (age-50)/10 | −0.450 | 0.188 | 0.00698 | 0.0626 | −0.247*** | −0.165*** | |
| (0.286) | (0.221) | (0.0695) | (0.0655) | (0.0556) | (0.0552) | ||
| ((age-50)/10)^2 | −0.273** | −0.442*** | −0.320*** | −0.335*** | −0.0910*** | −0.102*** | |
| (0.110) | (0.0810) | (0.0177) | (0.0168) | (0.0183) | (0.0182) | ||
| Education | 1.402*** | 1.529*** | 0.303** | ||||
| (0.343) | (0.0824) | (0.124) | |||||
| Educ × 1930–1939 | 1.007 | 0.0965 | 0.0823 | ||||
| (0.689) | (0.106) | (0.132) | |||||
| Educ × 1940–1949 | 0.374 | 0.270** | 0.0222 | ||||
| (0.377) | (0.112) | (0.128) | |||||
| Educ × 1950–1959 | −0.169 | 0.109 | −0.0701 | ||||
| (0.363) | (0.113) | (0.128) | |||||
| Educ × Female | 2.074 | −0.0913 | 0.801** | ||||
| (1.267) | (0.124) | (0.375) | |||||
| Edu × Fern × 1930 s | −1.660 | −0.0263 | −0.533 | ||||
| (1.408) | (0.155) | (0.389) | |||||
| Edu × Fern × 1940 s | −1.178 | 0.112 | −0.769** | ||||
| (1.297) | (0.161) | (0.379) | |||||
| Edu × Fern × 1950 s | −0.0921 | 0.0668 | −0.734* | ||||
| (1.289) | (0.165) | (0.378) | |||||
| Constant | 8.997*** | 8.570*** | 10.38*** | 8.823*** | 5.311*** | 5.065*** | |
| (0.633) | (0.527) | (0.109) | (0.121) | (0.124) | (0.132) | ||
| N | 29,867 | 29,867 | 126,703 | 126,703 | 28,997 | 28,997 | |
| Regressor | Country |
||||||
| Estonia |
Germany |
Spain |
|||||
| Without edu | With edu | Without edu | With edu | Without edu | With edu | ||
| 1930–1939 | 0.613** | 0.477 | 0.0270 | −0.0546 | 1.115*** | 1.132*** | |
| (0.283) | (0.350) | (0.242) | (0.507) | (0.195) | (0.198) | ||
| 1940–1949 | 0.828** | 0.799** | 0.613** | 0.194 | 2.391*** | 2.246*** | |
| (0.339) | (0.390) | (0.260) | (0.502) | (0.229) | (0.235) | ||
| 1950–1959 | 1.110*** | 0.790* | 1.311*** | 0.930* | 3.557*** | 3.289*** | |
| (0.378) | (0.434) | (0.286) | (0.546) | (0.277) | (0.287) | ||
| Female | 0.627** | 0.677* | −0.211 | 0.200 | −0.131 | −0.102 | |
| (0.276) | (0.349) | (0.274) | (0.498) | (0.198) | (0.200) | ||
| Female × 1930–1939 | 0.128 | 0.00982 | 0.653** | 0.611 | −0.245 | −0.292 | |
| (0.316) | (0.402) | (0.314) | (0.580) | (0.249) | (0.250) | ||
| Female × 1940–1949 | 0.704** | 0.178 | 1.050*** | 1.283** | 0.0486 | 0.0387 | |
| (0.307) | (0.402) | (0.303) | (0.576) | (0.255) | (0.260) | ||
| Female × 1950–1959 | 0.722** | 0.473 | 1.289*** | 1.235** | 0.491* | 0.315 | |
| (0.307) | (0.427) | (0.309) | (0.618) | (0.285) | (0.308) | ||
| (age-50)/10 | −0.617*** | −0.442** | 0.618*** | 0.631*** | 0.547*** | 0.724*** | |
| (0.222) | (0.209) | (0.179) | (0.171) | (0.195) | (0.187) | ||
| ((age-50)/10)”2 | −0.172*** | −0.157*** | −0.354*** | −0.348*** | −0.238*** | −0.260*** | |
| (0.0571) | (0.0536) | (0.0499) | (0.0473) | (0.0482) | (0.0463) | ||
| Education | 1.066*** | 1.169*** | 0.928*** | ||||
| (0.279) | (0.309) | (0.288) | |||||
| Educ × 1930–1939 | 0.266 | 0.0546 | 0.0296 | ||||
| (0.313) | (0.360) | (0.358) | |||||
| Educ × 1940–1949 | 0.311 | 0.286 | 0.317 | ||||
| (0.304) | (0.347) | (0.328) | |||||
| Educ × 1950–1959 | 0.650** | 0.305 | 0.347 | ||||
| (0.316) | (0.368) | (0.335) | |||||
| Educ × Female | 0.299 | 0.406 | 0.849* | ||||
| (0.364) | (0.394) | (0.490) | |||||
| Edu × Fern × 1930s | −0.116 | −0.157 | −0.111 | ||||
| (0.408) | (0.464) | (0.611) | |||||
| Edu × Fern × 1940s | 0.00750 | −0.652 | −0.444 | ||||
| (0.402) | (0.448) | (0.543) | |||||
| Edu × Fern × 1950s | −0.364 | −0.537 | −0.581 | ||||
| (0.413) | (0.472) | (0.542) | |||||
| Constant | 9.215*** | 7.698*** | 8.705*** | 7.154*** | 4.614*** | 4.132*** | |
| (0.409) | (0.433) | (0.301) | (0.484) | (0.294) | (0.287) | ||
| N | 15,681 | 15,681 | 15,102 | 15,102 | 17,834 | 17,834 | |
Standard errors in parentheses
p < 0.10
p < 0.05
p < 0.01.
Table A3.
Regressions of serial 7 s for selected countries.
| Regressor | Country |
|||||
|---|---|---|---|---|---|---|
| China |
USA |
Korea |
||||
| Without edu | With edu | Without edu | With edu | Without edu | with edu | |
| 1930–1939 | −0.0534 | −0.287 | −0.0611 | −0.145* | 0.247** | 0.286** |
| (0.275) | (0.231) | (0.0449) | (0.0816) | (0.117) | (0.132) | |
| 1940–1949 | 0.127 | −0.0585 | −0.0576 | −0.342*** | 0.432*** | 0.539*** |
| (0.304) | (0.260) | (0.0493) | (0.0912) | (0.132) | (0.144) | |
| 1950–1959 | −0.0369 | −0.156 | −0.0195 | 0.516*** | 0.632*** | |
| (0.314) | (0.270) | (0.0531) | (0.0912) | (0.141) | (0.155) | |
| Female | −1.077*** | −1.064*** | −0.475*** | −0.614*** | −1.352*** | −1.172*** |
| (0.281) | (0.242) | (0.0484) | (0.0876) | (0.115) | (0.126) | |
| Female × 1930–1939 | −0.118 | −0.0263 | 0.0629 | 0.108 | 0.239* | 0.179 |
| (0.294) | (0.258) | (0.0595) | (0.110) | (0.131) | (0.145) | |
| Female × 1940–1949 | 0.0656 | 0.0396 | 0.127** | 0.274** | 0.709*** | 0.594*** |
| (0.286) | (0.248) | (0.0614) | (0.121) | (0.124) | (0.139) | |
| Female × 1950–1959 | 0.231 | 0.165 | 0.125** | 0.0553 | 1.060*** | 0.927*** |
| (0.285) | (0.246) | (0.0601) | (0.120) | (0.121) | (0.140) | |
| (age-50)/10 | 0.0351 | 0.276*** | −0.00530 | 0.0280 | −0.134** | −0.0108 |
| (0.107) | (0.101) | (0.0332) | (0.0308) | (0.0595) | (0.0584) | |
| ((age-50)/10)^2 | −0.142*** | −0.202*** | −0.0501*** | −0.0598*** | −0.0766*** | −0.0920*** |
| (0.0329) | (0.0318) | (0.00867) | (0.00800) | (0.0192) | (0.0189) | |
| Education | 0.176 | 0.816*** | 0.691*** | |||
| (0.607) | (0.0438) | (0.129) | ||||
| Educ × 1930–1939 | 0.627 | 0.0177 | −0.234* | |||
| (0.617) | (0.0556) | (0.139) | ||||
| Educ × 1940–1949 | 0.459 | 0.0753 | −0.350*** | |||
| (0.609) | (0.0596) | (0.134) | ||||
| Educ × 1950–1959 | 0.371 | −0.0392 | −0.377*** | |||
| (0.610) | (0.0578) | (0.134) | ||||
| Educ × Female | 1.115 | 0.256*** | 0.585* | |||
| (0.821) | (0.0674) | (0.346) | ||||
| Edu × Fern × 1930 s | −0.399 | −0.0562 | 0.172 | |||
| (0.869) | (0.0835) | (0.362) | ||||
| Edu × Fern × 1940 s | −0.384 | −0.152* | −0.222 | |||
| (0.829) | (0.0877) | (0.352) | ||||
| Edu × Fern × 1950 s | −0.338 | −0.0758 | −0.433 | |||
| (0.826) | (0.0854) | (0.350) | ||||
| Constant | 3.525*** | 3.376*** | 4.102*** | 3.276*** | 4.030*** | 3.571*** |
| (0.313) | (0.269) | (0.0537) | (0.0734) | (0.144) | (0.152) | |
| N | 31,365 | 31,365 | 126,703 | 126,703 | 29,000 | 29,000 |
| Regressor | Country |
|||||
| Estonia |
Germany |
Spain |
||||
| Without edu | With edu | Without edu | With edu | Without edu | With edu | |
| 1930–1939 | −0.109 | −0.154 | −0.0220 | −0.246 | −0.0832 | −0.0415 |
| (0.129) | (0.182) | (0.121) | (0.235) | (0.205) | (0.213) | |
| 1940–1949 | −0.0493 | 0.0625 | −0.0177 | −0.0565 | 0.134 | 0.177 |
| (0.147) | (0.188) | (0.155) | (0.251) | (0.262) | (0.265) | |
| 1950–1959 | −0.0138 | 0.133 | −0.103 | −0.188 | 0.246 | 0.223 |
| (0.157) | (0.197) | (0.170) | (0.282) | (0.290) | (0.299) | |
| Female | −0.0526 | 0.00177 | −0.343** | −0.512* | −1.062*** | −1.070*** |
| (0.129) | (0.185) | (0.141) | (0.268) | (0.207) | (0.213) | |
| Female × 1930–1939 | 0.0131 | −0.0324 | 0.133 | 0.455 | 0.292 | 0.334 |
| (0.143) | (0.210) | (0.156) | (0.301) | (0.237) | (0.244) | |
| Female × 1940–1949 | 0.0594 | −0.0603 | 0.275* | 0.492* | 0.293 | 0.279 |
| (0.135) | (0.201) | (0.148) | (0.291) | (0.228) | (0.236) | |
| Female × 1950–1959 | 0.109 | 0.120 | 0.414*** | 0.710** | 0.488** | 0.518** |
| (0.134) | (0.202) | (0.149) | (0.306) | (0.241) | (0.260) | |
| (age-50)/10 | 0.174** | 0.179** | 0.0523 | 0.0188 | −0.00225 | 0.0358 |
| (0.0733) | (0.0712) | (0.108) | (0.107) | (0.207) | (0.201) | |
| ((age-50)/10)”2 | −0.105*** | −0.0913*** | −0.0308 | −0.0162 | −0.0814 | −0.0838* |
| (0.0216) | (0.0207) | (0.0305) | (0.0297) | (0.0519) | (0.0507) | |
| Education | 0.379*** | 0.112 | 0.645*** | |||
| (0.125) | (0.129) | (0.178) | ||||
| Educ × 1930–1939 | 0.0891 | 0.208 | 0.0228 | |||
| (0.139) | (0.140) | (0.209) | ||||
| Educ × 1940–1949 | −0.0441 | 0.0804 | −0.233 | |||
| (0.132) | (0.137) | (0.196) | ||||
| Educ × 1950–1959 | −0.0753 | 0.125 | −0.190 | |||
| (0.134) | (0.154) | (0.196) | ||||
| Educ × Female | 0.0279 | 0.319 | 0.315 | |||
| (0.155) | (0.212) | (0.275) | ||||
| Edu × Fern × 1930s | −0.00175 | −0.319 | −0.403 | |||
| (0.172) | (0.233) | (0.335) | ||||
| Edu × Fern × 1940s | −0.00130 | −0.313 | −0.0836 | |||
| (0.165) | (0.229) | (0.302) | ||||
| Edu × Fern × 1950s | −0.126 | −0.399* | −0.386 | |||
| (0.166) | (0.232) | (0.302) | ||||
| Constant | 4.430*** | 3.969*** | 4.597*** | 4.389*** | 3.804*** | 3.564*** |
| (0.160) | (0.192) | (0.173) | (0.255) | (0.327) | (0.325) | |
| N | 15,384 | 15,384 | 9,748 | 9,748 | 11,337 | 11,337 |
Standard errors in parentheses
p < 0.10
p < 0.05
p < 0.01.
Table A4.
Regressions of orientation for selected countries.
| Regressor | Country |
|||||
|---|---|---|---|---|---|---|
| China |
USA |
Korea |
||||
| Without edu | With edu | Without edu | With edu | Without edu | With edu | |
| 1930–1939 | −0.0658 | −0.0988 | −0.0536*** | −0.0354 | 0.126* | 0.142* |
| (0.211) | (0.160) | (0.0153) | (0.0299) | (0.0668) | (0.0774) | |
| 1940–1949 | −0.123 | −0.103 | −0.104*** | −0.0744** | 0.126* | 1 |
| (0.231) | (0.185) | (0.0169) | (0.0337) | (0.0759) | (0.0855) | |
| 1950–1959 | −0.235 | −0.157 | −0.0939*** | −0.0416 | 0.104 | 0.161* |
| (0.241) | (0.196) | (0.0250) | (0.0394) | (0.0780) | (0.0882) | |
| Female | −0.638*** | −0.458** | 0.0437*** | 0.0715** | −0.505*** | −0.461*** |
| (0.210) | (0.180) | (0.0157) | (0.0312) | (0.0751) | (0.0828) | |
| Female × 1930–1939 | 0.0877 | 0.0165 | 0.0297 | 0.0656* | 0.234*** | 0.231** |
| (0.229) | (0.199) | (0.0182) | (0.0370) | (0.0815) | (0.0903) | |
| Female × 1940–1949 | 0.238 | 0.0680 | 0.0345* | 0.0581 | 0.436*** | 0.403*** |
| (0.216) | (0.188) | (0.0195) | (0.0416) | (0.0771) | (0.0859) | |
| Female × 1950–1959 | 0.228 | 0.0136 | 0.0264 | 0.00604 | 0.498*** | 0.479*** |
| (0.212) | (0.183) | (0.0210) | (0.0451) | (0.0764) | (0.0862) | |
| (age-50)/10 | −0.105 | 0.0517 | 0.0895*** | 0.105*** | 0.0333 | 0.0421 |
| (0.0787) | (0.0734) | (0.0217) | (0.0216) | (0.0285) | (0.0285) | |
| ((age-50)/10)^2 | −0.0654** | −0.107*** | −0.0570*** | −0.0607*** | −0.0646*** | −0.0640*** |
| (0.0286) | (0.0259) | (0.00514) | (0.00511) | (0.0113) | (0.0113) | |
| Education | 0.875*** | 0.166*** | 0.209** | |||
| (0.258) | (0.0174) | (0.0833) | ||||
| Educ × 1930–1939 | −0.155 | −0.0295 | −0.0782 | |||
| (0.269) | (0.0209) | (0.0866) | ||||
| Educ × 1940–1949 | −0.362 | −0.0536** | −0.160* | |||
| (0.259) | (0.0233) | (0.0846) | ||||
| Educ × 1950–1959 | −0.531** | −0.0632*** | −0.165* | |||
| (0.260) | (0.0239) | (0.0849) | ||||
| Educ × Female | −0.0871 | −0.0109 | 0.500** | |||
| (0.346) | (0.0239) | (0.226) | ||||
| Edu × Fern × 1930 s | 0.443 | −0.0400 | −0.372 | |||
| (0.368) | (0.0281) | (0.233) | ||||
| Edu × Fern × 1940 s | 0.428 | −0.0241 | −0.455** | |||
| (0.352) | (0.0308) | (0.227) | ||||
| Edu × Fern × 1950 s | 0.577 | 0.00480 | −0.514** | |||
| (0.352) | (0.0323) | (0.227) | ||||
| Constant | 3.588*** | 3.339*** | 3.858*** | 3.678*** | 3.767*** | 3.665*** |
| (0.234) | (0.192) | (0.0277) | (0.0352) | (0.0764) | (0.0846) | |
| N | 30,930 | 30,930 | 79,062 | 79,062 | 28,996 | 28,996 |
| Regressor | Country |
|||||
| Estonia |
Germany |
Spain |
||||
| Without edu | With edu | Without edu | With edu | Without edu | With edu | |
| 1930–1939 | −0.0130 | 0.0431 | 0.0372 | 0.0712 | 0.137 | 0.134 |
| (0.0733) | (0.104) | (0.0535) | (0.130) | (0.0861) | (0.0908) | |
| 1940–1949 | 0.0776 | 0.176 | 0.0441 | 0.177 | 0.175* | 0.186* |
| (0.0803) | (0.107) | (0.0556) | (0.119) | (0.0920) | (0.0963) | |
| 1950–1959 | 0.0805 | 0.130 | 0.0531 | 0.274** | 0.214** | 0.212** |
| (0.0842) | (0.111) | (0.0563) | (0.120) | (0.0952) | (0.101) | |
| Female | −0.00754 | 0.0552 | −0.121* | −0.0220 | −0.236** | −0.229** |
| (0.0757) | (0.107) | (0.0660) | (0.132) | (0.0947) | (0.0990) | |
| Female × 1930–1939 | 0.132 | 0.0734 | 0.142** | 0.179 | 0.146 | 0.144 |
| (0.0819) | (0.117) | (0.0711) | (0.151) | (0.105) | (0.110) | |
| Female × 1940–1949 | 0.0813 | 0.0229 | 0.142** | 0.101 | 0.204** | 0.184* |
| (0.0782) | (0.113) | (0.0676) | (0.138) | (0.0995) | (0.105) | |
| Female × 1950–1959 | 0.137* | 0.114 | 1 | 0.0211 | 0.268*** | 0.273*** |
| (0.0786) | (0.115) | (0.0673) | (0.137) | (0.0980) | (0.104) | |
| (age-50)/10 | 0.193*** | 0.197*** | 0.0432 | 0.0461 | 2 | 0.188*** |
| (0.0396) | (0.0396) | (0.0289) | (0.0288) | (0.0461) | (0.0463) | |
| ((age-50)/10)^2 | −0.0565*** | −0.0547*** | −0.0332*** | −0.0338*** | −0.0947*** | −0.0951*** |
| (0.0114) | (0.0113) | (0.0100) | (0.00996) | (0.0149) | (0.0149) | |
| Education | 0.171** | 0.175** | 0.107 | |||
| (0.0735) | (0.0782) | (0.139) | ||||
| Educ × 1930–1939 | −0.0870 | −0.0330 | 0.0169 | |||
| (0.0810) | (0.0891) | (0.144) | ||||
| Educ × 1940–1949 | −0.129* | −0.114 | −0.0608 | |||
| (0.0764) | (0.0800) | (0.142) | ||||
| Educ × 1950–1959 | −0.0789 | −0.179** | −0.0426 | |||
| (0.0778) | (0.0810) | (0.141) | ||||
| Educ × Female | −0.0658 | 0.0132 | 0.0614 | |||
| (0.0954) | (0.0993) | (0.159) | ||||
| Edu × Fern × 1930s | 0.0670 | −0.101 | −0.0288 | |||
| (0.103) | (0.112) | (0.169) | ||||
| Edu × Fern × 1940s | 0.0559 | −0.0523 | 0.00958 | |||
| (0.0988) | (0.103) | (0.163) | ||||
| Edu × Fern × 1950s | 0.0195 | 0.00774 | −0.0850 | |||
| (0.1000) | (0.103) | (0.162) | ||||
| Constant | 3.580*** | 3.434*** | 3.837*** | 3.619*** | 3.563*** | 3.527*** |
| (0.0862) | (0.109) | (0.0557) | (0.117) | (0.0950) | (0.0989) | |
| N | 11,076 | 11,076 | 12,562 | 12,562 | 13,504 | 13,504 |
Standard errors in parentheses
p < 0.10
p < 0.05
p < 0.01.
Table A5.
Regressions of gender difference in cognition on gender difference in education.
| Regressor | Word recall |
Serial 7 s |
Orientation |
|||
|---|---|---|---|---|---|---|
| Controls: None | Cohort | None | Cohort | None | Cohort | |
| Edu gender diff | 1.177** | 0.636 | 0.212 | −0.116 | 0.0540 | −0.0960 |
| (0.502) | (0.542) | (0.243) | (0.288) | (0.128) | (0.152) | |
| 1930–1939 | 0.259*** | 0.0491 | 0.117*** | |||
| (0.0808) | (0.0629) | (0.0338) | ||||
| 1940–1949 | 0.619*** | 0.218*** | 0.181*** | |||
| (0.0902) | (0.0664) | (0.0393) | ||||
| 1950–1959 | 0.659*** | 0.314*** | 0.203*** | |||
| (0.145) | (0.0860) | (0.0547) | ||||
| Constant | 0.487*** | 0.0100 | −0.332*** | −0.538*** | −0.0418 | −0.193** |
| (0.149) | (0.211) | (0.0754) | (0.112) | (0.0403) | (0.0705) | |
| N | 111 | 111 | 96 | 96 | 111 | 111 |
Standard errors in parentheses
p < 0.10
p < 0.05
p < 0.01.
Footnotes
The Gateway to Global Aging Data can be accessed at https://g2aging.org/.
We also examined scores on the verbal fluency test, which asks respondents to name as many animals as possible (the score is simply the number of named animals). The analysis based on the verbal fluency score does not add new insights compared to the analysis based on word recall, serial 7s, and orientation test scores. Hence, we do not report the results of the analysis using this score, which are available upon request.
The list has 4 words in MHAS and 3 in KLoSA and CRELES; the scales are correspondingly different.
For simplicity, we use the same symbols for the error terms as above, but it is understood that they are different error terms.
Coefficient estimates of (5) for all countries are provided in the supplementary material.
Coefficient estimates of (6) for all countries are provided in the supplementary material.
Coefficient estimates of (7) for all countries are provided in the supplementary material.
We also ran cohort-specific regressions where the unit of observation is a country and gender differences in education and cognition pertain to one cohort only. Again, we do not find evidence of a robust positive relationship between education and cognition gender gaps. The interpretation of these results, however, is subject to the caveat that each regression is based on only 25 observations.
References
- Banks J, Mazzonna F, 2012. The effect of education on old age cognitive abilities: evidence from a regression discontinuity design. Econ. J 122, 418–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bugliari D, et al. , 2018. RAND HRS Longitudinal File 2014 (V2) Documentation. RAND Center for the Study of Aging, Santa Monica, CA. [Google Scholar]
- Crespo L, López-Noval B, Mira P, 2014. Compulsory schooling, education, depression and memory: new evidence from SHARELIFE. Econ. Educ. Rev 43, 36–46. [Google Scholar]
- Díaz-Venegas C, Samper-Ternent R, Michaels-Obregón A, Wong R, 2018. The effect of educational attainment on cognition of older adults: results from the Mexican Health and Aging Study 2001 and 2012. Aging Mental Health (Advance online publication). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glymour MM, Kawachi I, Jencks CS, Berkman LF, 2008. Does childhood schooling affect old age memory or mental status? Using state schooling laws as natural experiments. J. Epidemiol. Community Health 62, 532–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langa KM, Larson EB, Karlawish JH, Cutler DM, Kabeto MU, Kim SY, Rosen AB, 2008. Trends in the prevalence and mortality of cognitive impairment in the United States: Is there evidence of a compression of cognitive morbidity? Alzheimer’s Dementia 4, 134–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langa KM, Llewellyn DJ, Lang IA, Weir DR, Wallace RB, Kabeto MU, Huppert FA, 2009. Cognitive health among older adults in the United States and in England. BMC Geriatrics 9, 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Shih R, Feeney K, Langa KM, 2014. Gender disparity in late-life cognitive functioning in India: Findings from the Longitudinal Aging Study in India. J. Gerontol. B Psychol. Sci. Soc. Sci 69, 603–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei X, Hu Y, McArdle JJ, Smith JP, Zhao Y, 2012. Gender differences in cognition among older adults in China. J. Hum. Resources 47, 951–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingston G, et al. , 2017. Dementia prevention, intervention, and care. Lancet 390, 2673–2734. [DOI] [PubMed] [Google Scholar]
- Maurer J, 2011. Education and male-female differences in later-life cognition: International evidence from Latin America and the Caribbean. Demography 48, 915–930. [DOI] [PubMed] [Google Scholar]
- Oksuzyan A, Singh PK, Christensen K, Jasilionis D, 2018. A cross-national study of the gender gap in health among older adults in India and China: Similarities and disparities. Gerontologist 58, 1156–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onur I, Velamuri M, 2016. A life course perspective on gender differences in cognitive functioning in India. J. Hum. Capital 10, 520–563. [Google Scholar]
- Schneeweis N, Skirbekk V, Winter-Ebmer R, 2014. Does education improve cognitive performance four decades after school completion? Demography 51, 619–643. [DOI] [PubMed] [Google Scholar]
- Singh PK, Jasilionis D, Oksuzyan A, 2018. Gender difference in cognitive health among older Indian adults: A cross-sectional multilevel analysis. SSM – Population Health 5, 180–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern Y, 2002. What is cognitive reserve? Theory and research application of the reserve concept. J. Int. Neuropsychol. Soc 8, 448–460. [PubMed] [Google Scholar]
- Tucker AM, Stern Y, 2011. Cognitive reserve in aging. Curr. Alzheimer Res 8, 354–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir D, Lay M, Langa K, 2014. Economic development and gender inequality in cognition: a comparison of China and India, and of SAGE and the HRS sister studies. J. Econ. Ageing 4, 114–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yount KM, 2008. Gender, resources across the life course, and cognitive functioning in Egypt. Demography 45, 907–926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaninotto P, Batty GD, Allerhand M, Deary IJ, 2018. Cognitive function trajectories and their determinants in older people: 8 years of follow-up in the English Longitudinal Study of Ageing. J. Epidemiol. Community Health 72, 685–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, 2006. Gender differentials in cognitive impairment and decline of the oldest old in China. J. Gerontol.: Soc. Sci 61B, S107–S115. [DOI] [PubMed] [Google Scholar]


