Mitigating outbreaks in congregate settings by decreasing the size of the susceptible population

Abstract

While many transmission models have been developed for community spread of respiratory pathogens, less attention has been given to modeling the interdependence of disease introduction and spread seen in congregate settings, such as prisons or nursing homes. As demonstrated by the explosive outbreaks of COVID-19 seen in congregate settings, the need for effective outbreak prevention and mitigation strategies for these settings is critical. Here we consider how interventions that decrease the size of the susceptible populations, such as vaccination or depopulation, impact the expected number of infections due to outbreaks. Introduction of disease into the resident population from the community is modeled as a branching process, while spread between residents is modeled via a compartmental model. Control is modeled as a proportional decrease in both the number of susceptible residents and the reproduction number. We find that vaccination or depopulation can have a greater than linear effect on anticipated infections. For example, assuming a reproduction number of 3.0 for density-dependent COVID-19 transmission, we find that reducing the size of the susceptible population by 20% reduced overall disease burden by 47%. We highlight the California state prison system as an example for how these findings provide a quantitative framework for implementing infection control in congregate settings. Additional applications of our modeling framework include optimizing the distribution of residents into independent residential units, and comparison of preemptive versus reactive vaccination strategies.

1. Introduction

The COVID-19 pandemic has highlighted the need to quickly identify and implement strategies for controlling the spread of a novel respiratory pathogen. A particular challenge in congregate settings such as prisons, nursing homes, and crowded workplaces where transmission is amplified^1–6. The increased risk of transmission in these settings results in a higher potential for an outbreak to cause many infections within a few weeks. In addition, residents of congregate settings often have a higher prevalence of comorbidities that contribute to worse disease outcomes^7,8. The subsequent surge of hospital admissions can strain healthcare capacity and seed increased transmission within the wider community^9,10. Outbreaks in prison settings are further complicated by the additional security, training, and contractual resources needed to hospitalize an incarcerated person. One opportunity to reduce the public health risk associated with congregate settings is simply to decrease the number of susceptible individuals. This might occur via vaccination or depopulation^10,11. Reducing the number of susceptible individuals can both decrease the chance of an outbreak occurring and the size of any outbreaks that occur¹². To provide a quantitative framework to evaluate the impact of reducing the susceptible population, we describe a model for the probability of an outbreak occurring in a congregate setting within a specified time period, as well as the size of an outbreak that may occur. To illustrate the applicability of our model, we utilize publicly available data from the California Department of Corrections and Rehabilitation (CDCR) for the spread of SARS-CoV-2.

2. Methods

2.1. Data

COVID-19 data for all 35 California state prisons operated by the CDCR are reported daily in a public data dashboard. Machine readable time series of these daily reports were acquired from the University of California Los Angeles COVID Behind Bars project which gathers and organizes COVID-19 data from carceral institutions across the United States.¹³ Time series of incident cases were derived by taking the daily difference of reported cumulative cases. Differences in daily cumulative case counts that resulted in negative incidence estimates were ignored and incidence was estimated from the next reported cumulative case count that did not result in a negative incidence estimate.

2.2. Model overview

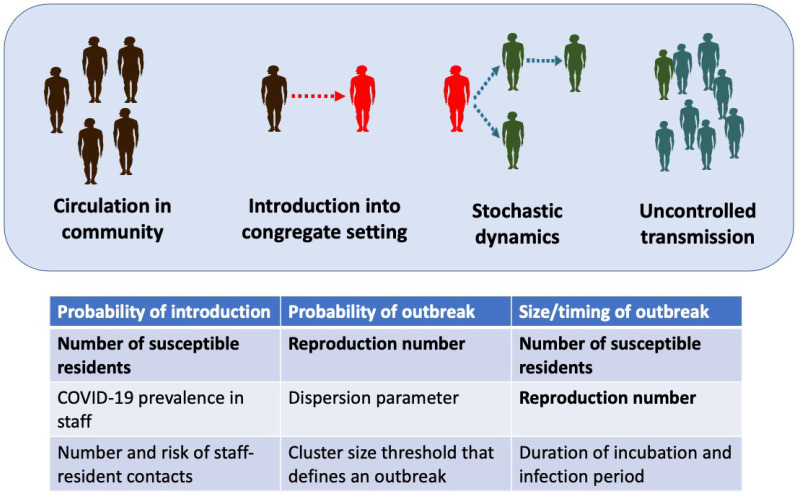
We structure outbreak dynamics in congregate settings into three stages (Figure 1). First, a case has to be introduced into the congregate setting. This may occur due to direct transfer of an infected case into the congregate population, or from transmission from a staff worker or visitor. We model the primary mode of introduction as being from staff introductions, since this is the hardest type of introduction to repress. Second, an introduction of a case (or a few cases) can either be self-limited or progress to a full outbreak. The probability of an outbreak occurring is impacted by the stochastic nature of disease spread, the reproduction number, and the degree of transmission heterogeneity. The reproduction number, R₀, is the average number of cases each new case causes when all of their contacts are susceptible to disease. We use the dispersion parameter, k, to denote the amount of transmission heterogeneity. Third, if an outbreak is established, the overall impact is in proportion to the total number of cases infected. Since the large number of cases overwhelms the stochasticity of transmission, this third stage is deterministic in nature. We employ a deterministic susceptible-exposed-infectious-recovered (SEIR) compartmental model for this stage. Assumptions of the SEIR model include that the duration of natural or acquired immunity is long enough so that re-infections are unlikely within the time frame of a single outbreak.

Figure 1. Stages of an outbreak.

For an outbreak to occur in a congregate setting, an infection that circulates in the community must be introduced into the congregate setting. Then stochastic dynamics determine whether or not an introduction initiates a large outbreak. Once an outbreak occurs, uncontrolled transmission dictates the size and time course of the outbreak. The table lists the variables that are used in each step of the model. The bolded variables are impacted by a reduction in the number of susceptible individuals, as occurs with vaccination or depopulation.

We assume that R₀ > 1, because when R₀ is less than one, transmission is self-limited and outbreaks that involve a large portion of the resident population are not expected. The key outputs for the three stages of the model are the rate of introductions, ϕ, the probability that an introduction results in uncontrolled transmission, P_uc, and the expected size of any outbreaks that occur, I_tot. Our models for each stage of an outbreak are described in the supplementary methods.

2.3. Parameterization

The value of the reproduction number is of particular importance for determining the relative impact of control interventions. For any one disease, there is often great variability of reproduction number estimates. For SARS-CoV-2, there are published estimates of the reproduction number as high as 8.4 in prison settings.¹⁴ Meanwhile less transmissible diseases can also cause outbreaks in congregate settings, such as tuberculosis in prisons or influenza in nursing homes.^15–19 Given the range of estimates for the reproduction number of any single disease, including variants of concern, we explore a range of values for the reproduction number. For the purpose of our analyses, R₀ is defined within the context of system-wide control interventions that are in place before consideration of vaccination or depopulation. That is R₀ may incorporate interventions such as masking, social distancing, ventilation improvements, improved hygiene and other practices that do not specifically reduce the number of susceptible residents. Based on current literature, we assume a latent period of three days (i.e. time between the occurrence of infection and the onset of infectiousness), and an infectious period of seven days.^20–24

Our analyses focus mostly on the relative rather than absolute impact of reducing the size of susceptible populations. As such the specific size of the modeled populations are of secondary importance. However, to provide context for our analyses, we continue to focus on the spread of SARS-CoV-2 within the California prison system for choosing the remaining parameters. The average population size of the 35 CDCR prisons was about 3,300 at the beginning of 2020.²⁵ Meanwhile prisons typically consist of multiple buildings, that have a degree of independence. Thus, to approximate a single congregate population, we choose a population size of 1,000 for our analyses. The prevalence of disease in the staff, the average daily number of staff contacts each resident has, and the probability that an infected staff transmits disease to a resident during a contact were estimated as 0.01%, 10 and 1% respectively based on a combination of community dynamics and the empirical observation of relatively frequent outbreaks occurring in the CDCR institutions¹³.

Numerous studies have shown that infectious diseases tend to exhibit superspreading behavior characterized by a low dispersion parameter²⁶. Recent studies indicate that SARS-CoV-2 follow this pattern and henceforth we assume a value of 0.2 for the dispersion parameter.^27–29.

2.4. Impact of decreasing the susceptible population by vaccination or depopulation

Each of the stages of our model for outbreak dynamics is influenced by either the number of susceptible individuals, R₀, or both. This serves as the basis for assessing how the reduction of the susceptible population by vaccination or depopulation can impact the burden of disease in congregate settings.

We define N₀, and R₀ as the size of the congregate population and the reproduction number prior to any control interventions that decrease the number of susceptibles, and prior to any outbreak occurring. We let γ represent the amount of ‘control’ as determined by the proportional reduction in the size of the susceptible population that occurs with vaccination and/or depopulation,

$$N=(1-\gamma )N_0.$$ (1)

We assume a linear relationship between the effective reproduction number R, and γ,

$$R=(1-\Theta \gamma )R_0.$$ (2)

Here we have defined a susceptibility index, Θ. For Θ = 0, the reproduction number remains constant even when the number of susceptible residents are reduced. This would be equivalent to a vaccine that eliminates disease but has no impact on transmission. In the case of depopulation, Θ = 0 would be consistent with the mean number of contacts per resident remaining constant even when the population size is reduced. In contrast when Θ = 1, the ratio between the size of the susceptible population and the reproduction number remains constant. This corresponds to a vaccine that is equally effective at reducing disease and transmission in a well-mixed population. In the case of depopulation Θ = 1 corresponds to resident contacts being reduced in proportion to the population size. In disease dynamics literature Θ = 0 and Θ = 1 may be referred to as density-independent and density-dependent transmission respectively. We assume that the dispersion parameter is independent of γ. Intermediate values of the susceptibility index (ie. 0 < Θ < 1) may occur in many ways. Examples include vaccines that protect against disease more than against infection, or when poor ventilation implies that halving the number of infected neighbors does not half the risk of acquiring disease.

To model the overall impact of depopulation, we define E to be the average number of cases expected due to outbreaks that are initiated over a defined time interval, T. The expected number of introductions is ϕT. The overall probability, P_ob of an outbreak occurring is one minus the probability that no introductions lead to uncontrolled transmission. The average number of cases expected due to outbreak dynamics is the overall probability that an outbreak occurs times the expected size of an outbreak. That is,

$$P_{ob}=1-{\left(1-p_{uc}\right)}^{\varphi T}$$ (3)

$$E=P_{ob}\cdot I_{tot}$$ (4)

Here we have assumed that only one uncontrolled outbreak can occur in a residential unit because enough individuals would be infected so that there would be subsequent herd immunity. Each of ϕ, P_ob, and I_tot depend on γ. The overall impact of control is probed by evaluating how E depends on γ.

In the supplemental methods, we extend this model to consider two decision-making scenarios. First, we consider how the average number of infections from outbreaks depends on how a fixed number of susceptible residents are distributed into two independent residential units. Second, in contrast to the preemptive strategy of decreasing the susceptible population before an outbreak occurs, we consider how the average number of infection from outbreaks is impacted by a reactive control strategy in which the susceptible population is rapidly reduced once an outbreak is known to occur.

All calculations and simulations are conducted in R, version 4.0.2. Code is available on github (https://github.com/proctor-ucsf/Transmission-in-congregate-settings).

3. Results

3.1. Evaluating model assumptions

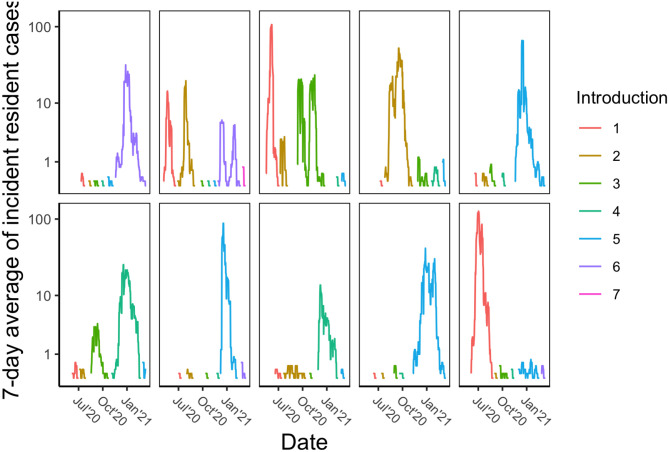
From the beginning of CDCR reporting in April of 2020 through February 2, 2021 there were over 41,000 SARS-CoV2 cases in California State prisons. Within each institution, periods of low disease prevalence were interrupted by focal outbreaks caused by rapid spread (Figure 2). Some institutions have multiple outbreaks, which is consistent with separate residential buildings on a campus having outbreaks at different times. Meanwhile there are many examples of small clusters of cases that do not progress to an outbreak. Upon aggregating case counts by institution and then assigning clusters of infection based on having at least fourteen days of no cases between clusters, we find that 23% of clusters consist of an isolated case and 53% of clusters have greater than ten cases suggestive of a large outbreak. Overall this data supports our key assumptions that outbreak dynamics are supported by sporadic introductions into the residential community and that stochastic dynamics determine the probability that a sporadic introduction progresses into an uncontrolled outbreak.

Figure 2. COVID-19 incidence in California State prisons.

Each panel represents one state institution. For visualization purposes, Y axes are log transformed and 7-day rolling averages of incident counts are displayed. To highlight the stochastic impact of disease introductions, a new color is used for the incidence data whenever there is a period of no cases lasting at least 14 days. Thus the different colors approximate the consequence of individual disease introductions into the residential community. The panels represent all institutions where at least five introductions have occurred. Names of state prisons have been removed, but are available by request.

3.2. Stages of outbreak dynamics

A prerequisite for an outbreak to occur is introduction of disease into the residential community. For our model, the frequency of introductions increases with a larger residential population, increased prevalence of disease in the community, a higher resident-staff contact rate, or higher probability that a resident contact with an infected staff causes disease (Figure S1).

A disease introduction may or may not lead to an outbreak. The probability of an outbreak increases as the number of introductions, or the reproduction number increases (Figure S2). This probability also depends on the dispersion parameter. High values of the dispersion parameter correspond to homogeneous transmission and more predictable dynamics, whereas low values correspond to heterogeneous dynamics that are more likely to produce either explosive outbreaks or dead-ends to transmission. Thus high values of the dispersion parameter lead to a higher outbreak probability (Figure S2).

Once an outbreak occurs, the number of infectious individuals in our model grows exponentially until there is a significant depletion of susceptible individuals (Figure S3). A reproduction number above one is necessary for an outbreak to occur, but even values moderately above one lead to a large attack rate (i.e.proportion of infected residents). A reproduction number as low as 1.5 results in an attack rate of 59%, and a reproduction number of 2.5 leads to an attack rate of 89% (as seen by the asymptotic value for the number of removed individuals in the two panels of Figure S3).

An interactive tool for exploring the relationship between input variables and model outputs for each of the three stages of an outbreak is available at https://phoebelu.shinyapps.io/DepopulationModels/.

3.3. Impact of preemptive control by vaccination or depopulation

When our models of disease introduction, outbreak probability and outbreak size are combined, there is a significant impact of interventions that decrease the size of the susceptible population (Figure 3). Given that there is likely substantial variability in the value of the reproduction number within different congregate settings, it is notable that control interventions have a large impact for a wide array of R₀ values. For example, when the susceptible population is decreased by 20% and transmission decreases linearly with control (i.e. γ = 0.2, and Θ = 1), the expected number of total infections decreases by 73%, 47%, 40%, and 38%, for R₀ of 1.5, 3.0, 5.0, and 8.0 respectively (Bottom panel of Figure 3). These relative proportions hold for a broad range of values for other model parameters (data not shown).

Figure 3. Impact of control measures that decrease the size of the susceptible population.

(Top) The expected number of infections due to outbreaks occurring within 100 days as a function of the level of control. The control value, gamma, shown on the x-axis is the proportion of the number of susceptible individuals that are removed from the resident population via vaccination and/or depopulation. Colors correspond to different values of the baseline reproduction number, R₀, for when no control is implemented. Specific values of the R₀ are specified by the legend. Dashed lines show the result assuming that the control intervention does not change the reproduction number (e.g. Θ = 0 corresponding to a vaccine that immunizes against disease, but not asymptomatic infection). Solid lines show results assuming that the reproduction number changes in proportion to the level of control (e.g. Θ = 1 corresponding to a vaccine that immunizes against disease and asymptomatic infection). (Bottom) Analogous to top panel, except that the rate of infection has been normalized to a rate of one when the level of control is zero. This highlights the relative impact of decreasing the number of susceptible individuals. For both panels superspreading is allowed, which is modeled by a dispersion value of 0.2. We set N_C = 10 and α_ic = 0.01, meaning that residents are assumed to have 10 contacts with staff a day and that contact with an infected staff has a one percent chance of transmitting infection. The other parameters are the same as the defaults for Figures S1 – S3.

Notably, the reduction in the number of cases as a function of control occurs in greater than linear fashion (seen by colored lines falling below the black line in Figure 3). The decrease is even more significant if control impacts both the susceptibility to infection and the transmission potential of individuals, as compared to control affecting susceptibility alone (seen by solid lines falling below the dashed lines in Figure 3). The greater than linear impact of control can be explained by how the expected number of infections is the product of the probability of an introduction, the probability that an introduction leads to an outbreak and the size of an outbreak. All of these factors depends on either the effective reproduction number, the size of the susceptible population, or both. Since control decreases the size of the susceptible population and possibly the effective reproduction number as well, each stage of outbreak dynamics can contribute to the reduction in the number of cases when control is applied (Figures 1 and S4). When the dependency of these individual components of outbreak dynamics are multiplied together, the result is a greater than linear impact of control. The extreme values of the susceptibility index considered here (i.e. Θ = 0 and Θ = 1) provide bounds for the expected dynamics of intermediate values.

If control reduces the reproduction number linearly (i.e. Θ = 1), our model predicts several changes in the dynamics of outbreaks as control is applied (Figure S5). Notably, the attack rate amongst susceptible individuals decreases as the effective reproduction number, R, decreases (Figure S5, upper right panel), particularly as R₀ approaches one. This implies that for relatively small R₀, the decrease in the size of the outbreak seen with control is largely driven by the attack rate rapidly approaching zero, rather than the size of the susceptible population itself. However with higher values of R₀, most of the decrease in the size of the outbreak is driven by a decrease in the number of susceptible residents rather than by a reduction in the attack rate. Reducing the size of the susceptible population also delays the timing of the peak for the number of infectious individuals and reduces the maximum number of individuals infected at once (Figure S5, bottom panels). This can help facilitate roll-out of public health interventions that can further decrease the burden of disease. It also helps to minimize overcrowding of healthcare facilities used to treat severe cases. If control has no impact on the reproduction number (i.e. Θ = 0), our model predicts that the control has no impact on the attack rate or temporal dynamics of uncontrolled outbreaks.

3.4. Adjunctive strategies for disease control

In some circumstances, it may be possible to reduce the risk and burden of disease outbreaks by optimizing the way a group of residents are proportioned into distinct residential units, such as two independent buildings (Supplementary text S7.2.1). For most reasonable parameter values, it appears optimal to distribute residents in a manner that keeps R consistent across the population.

In other circumstances there may be an opportunity to implement reactive disease control measures in which the number of susceptible individuals is rapidly reduced once an outbreak has been detected to occur (Supplementary text S7.2.2). This contrasts with the preemptive approach discussed above of reducing the susceptible population before an outbreak has even occurred. When the efficacy of a reactive control is compared to preemptive control, it appears that reactive control is more likely to be effective when the reproduction number is lower, there is minimal delay in implementing control and the individual-level efficacy of reactive control is high.

4. Discussion

The burden of COVID-19 within prisons, nursing homes and other congregate settings has provided a devastating reminder of the fragility of congregate settings. To reduce unnecessary death, disease, and economic loss, policies are needed to prevent outbreaks from occurring and to mitigate outbreaks that have already started. Besides protecting the residents of congregate settings, interventions that reduce outbreak potential also reduce strain on local health systems and spillover infections in the community. An additional consideration is the strain on staff during outbreaks due to their own health risk, often being overworked, and the emotional burden of taking care of vulnerable populations. Thus the longer term implications of reducing outbreak potential include decreasing the risk of staff burnout, post-traumatic stress disorder, and loss of institutional trust.

Our model for the impact of control on outbreak dynamics can be integrated into a variety of infection control policy decisions. For example, in the context of the COVID-19 pandemic, our study of the impact of decreasing the susceptible population could have provided quantitative context to decisions about how much to prioritize decarceration of prison populations, or whether additional nursing homes for COVID-19 patients are needed to ensure that existing ones are not overburdened with transmission. In particular, we found that relatively small reductions in the susceptible population of congregate settings could have a significant impact on the overall number of cases due to outbreaks. This multiplicative effect occurs due to a combination of decreasing the rate of disease introductions, the probability that an introduction leads to an outbreak and the size of any outbreak that occurs (Figure 1). Consideration of how populations can be divided into distinct residential units as well as the possibility of reactive interventions once an outbreak begins provides further opportunities for disease control.

In order to frame our analysis of control strategies in a manner that was intuitive and transparent, we made many assumptions. Depending on specific circumstances of spread in congregate settings, some assumptions will be more relevant than others. Specifically we ignore the possibility of direct transfer of infected individuals from one building to another as can inadvertently happen for individuals who are transferred during the latent period. We ignore the fluctuation of disease prevalence in the staff, particularly as surges may occur due to staff-staff transmission, resident-to-staff transmission, or increases in community transmission. Similarly we ignore how staff-resident contacts may evolve over the course of a pandemic, particularly as access to personal protective equipment and education about infection control improves over time. Our use of a SEIR transmission model assumes that within a residential unit (e.g. an isolated building) everyone is in equal contact with each other and thus ignores the finer scale structure of population dynamics. Our SEIR model also incorporates the standard assumptions of compartmental models including constant exponential rates of transitions and standard mass-action transmission. These assumptions ignore the possibility of seasonal effects, such as the possibility that transmission is impacted by changes in air circulation when heating or air conditioning is utilized. Except for our modification for reactive vaccination, The SEIR model also ignores how a large outbreak would likely inspire multiple efforts to acutely mitigate disease transmission. Finally, our assumption of a linear, density-dependent relationship between the size of the susceptible population and the reproduction number ignores how factors such as the relationship between duration-of-exposure and infection status may yield a non-linear relationship.

Our model can be adjusted to accommodate more flexible assumptions, but this would come at the cost of adding extra parameters whose values may not be readily identifiable. Importantly, the key finding that decreasing the number of susceptible individuals in congregate settings can have a greater than linear impact on disease burden is expected to be robust to many variants of our model. It is also important to place interventions that reduce the susceptible population into a large context of intervention strategies. Many scenarios may benefit from other control interventions such as improved ventilation, more frequent testing, greater adherence to social distancing, improved utilization of personal protective equipment, or cohorting of staff by residential unit. In addition, besides absolute case counts there are other important considerations for describing the impact of outbreaks on residents of congregate settings including contributions to health inequity, mental health toll, and reduction of ancillary services that are deprioritized during pandemic emergencies. Specific policy-making decisions also need to consider how control strategies will impact the ability of staff to fulfill their normal professional responsibilities, as well as protect their own health.

5. Conclusion

Congregate settings pose a risk of large disease outbreaks. To reduce the burden that outbreaks have on residents, staff and the community at large, it is important to optimize strategies for preventing and mitigating outbreaks. We find that preemptive reduction of the size of the susceptible population via depopulation or vaccination can have a greater than linear affect on outcomes.