A Python Toolbox for Unbiased Statistical Analysis of Fluorescence Intermittency of Multilevel Emitters

Abstract

We report on a Python toolbox for unbiased statistical analysis of fluorescence intermittency properties of single emitters. Intermittency, that is, step-wise temporal variations in the instantaneous emission intensity and fluorescence decay rate properties, is common to organic fluorophores, II–VI quantum dots, and perovskite quantum dots alike. Unbiased statistical analysis of intermittency switching time distributions, involved levels, and lifetimes are important to avoid interpretation artifacts. This work provides an implementation of Bayesian changepoint analysis and level clustering applicable to time-tagged single-photon detection data of single emitters that can be applied to real experimental data and as a tool to verify the ramifications of hypothesized mechanistic intermittency models. We provide a detailed Monte Carlo analysis to illustrate these statistics tools and to benchmark the extent to which conclusions can be drawn on the photophysics of highly complex systems, such as perovskite quantum dots that switch between a plethora of states instead of just two.

Introduction

Since the seminal first observation of single molecule emitters in fluorescence microscopy three decades ago,¹ single quantum emitter photophysics has taken center stage in a large body of research. On the one hand, single quantum emitters as single photon sources² are held to be an essential part of quantum communication networks and are deemed essential for building optically addressed and cavity-quantum electrodynamics-based quantum computing nodes.³ This has particularly spurred research in III–V semiconductor quantum dots,^4,5 color centers in diamond, silicon carbide and 2D materials,⁶⁻⁸ and organic molecules at low temperatures.⁹ On the other hand, classical applications of ensembles of emitters for displays, lighting, lasers, and as microscopy tags drive the continuous development of new types of emitters, such as II–VI self-assembled quantum dots 20 years ago¹⁰⁻¹² and inorganic perovskite quantum dots just recently.¹³⁻²⁰ For all these systems, understanding the photophysics on the single emitter level is instrumental, whether the intended use is at the single or ensemble level. A common challenge for almost all types of emitters is that they exhibit intermittency, also known as blinking.^21,22 Under constant pumping, emitters switch, seemingly at random, between brighter and dimmer states, often corresponding with higher and low quantum yields and different fluorescence decay rates. Frequently, the switching behavior also shows peculiar, power-law distributed, random distributions of durations of events. Determining the mechanisms through which emitters blink, that is, the origin of the involved states, the power-law distribution of residence times, and the cause of switching, have been the topic of a large number of studies particularly for II–VI quantum dots as recently reviewed by Efros and Nesbitt.²³ Recent studies on inorganic perovskite quantum dots uncover intermittency behavior that does not fit common models for intermittency in their II–VI counterparts.¹⁴⁻²⁰

In order to quantify intermittent behavior, the simplest and most commonly employed method is to subdivide a measurement stream of individual photon-arrival times into short bins of a few milliseconds to calculate the intensity (in counts/second) of each bin. Every bin can then be assigned to a state (on, off, or gray) according to its brightness so that on/off times as well as intensity levels can be defined and analyzed.²¹ For pulsed laser excitation, also quasi-instantaneous fluorescence decay rates can be obtained.^24,25 However, it is well known that this method of binning time streams and histogramming binned intensities causes detrimental artifacts.^21,26−32 Retrieved parameters of the quantum dot behavior often exhibit a dependency on the choice of the bin width, which affect estimates of switching time distributions and power laws and also the objective assignment of intensities to intrinsic levels. Narrower bin widths in principle allow better resolution but run into shot noise limits, while conversely choosing larger bins suppresses noise but will render the analysis blind to fast events. To overcome these issues, Watkins and Yang²⁶ proposed changepoint analysis (CPA) as a Bayesian statistics approach for the unbiased determination of switching times that is optimal, that is, gives the best performance given the constraints of shot noise in the data. CPA and clustering are examples of Bayesian inference methods to determine the transitions and underlying levels in single photon trajectories. In the domain of high-throughput single-molecule analysis,³³ many methods to process single photon trajectories have appeared, which one can classify as supervised learning methods with a priori model assumptions on one hand and unsupervised approaches on the other hand. The so-called hidden Markov model (HMM) methods³⁴ that view photon data streams as an experimentally measured output of transitions between hidden transition states are prominent. Bayesian inference can then estimate parameters such as transition probabilities if one a priori postulates the number of levels and the allowed transitions. As this underlying model is a priori often not known, one can apply HMM with different possible models and rank them according to probabilistic criteria, such as the Bayesian information criterion (BIC). Also, the requirement for a priori known models is relaxed in so-called aggregated Markov models³⁵ and non-Markov memory kernel models.³⁶ Juxtaposed to such supervised analysis methods are unsupervised approaches. Such methods apply CPA to partition data into time segments between jumps and subsequent clustering of intensity levels. The CPA method pioneered by Watkins and Yang is essentially such a combination of changepoint detection and hierarchical agglomerative clustering using the BIC to determine the best clustering of measured intensities in distinct levels (states) with as sole assumption that in each segment of time wherein the emitter is in a given level, the counts are Poisson distributed.^26,29 A main drawback is that particularly the clustering is slow. We refer to ref (37) for recent developments in machine learning to mitigate this problem. A main advantage of CPA is that no underlying model is required and that the data are segmented and clustered to the level that the data allow, given that the data is Poisson-distributed in intensity and given a required confidence level stipulated by the user. Variations on CP for other types of noise, such as Gaussian noise, have also appeared.^38,39 Despite the well-documented superior performance over binning of photon counting data, in the domain of single photon counting data from quantum dots, only very few groups have adopted these methods.^{17,26,28,29,32,40,41}

In this paper, we provide, benchmark, and document a Python toolbox for CPA, state clustering, and analysis of fluorescence–intensity–decay rate correlations (Figure 1) that is posted on GitHub.⁴² A main motivation lies in the emergence of new quantum emitter systems with complex photophysics. While II–VI quantum dots for which CPA was originally developed are generally understood to switch between just two or three states, the problem of accurate analysis of intermittency is gaining in prominence with the advent of novel emitters such as perovskite quantum dots, which appear to switch not between just two but instead a multitude of states.¹⁴⁻²⁰ There is hence a large need for a toolbox that provides unbiased, model-free analysis of photon counting data, for which reason we provide a CPA implementation and benchmark it for complex multilevel emitters. Our toolbox is both applicable to real quantum dot data and valuable as a testbed for both testing models and analysis techniques on synthetic, that is, numerically generated, data. Indeed, the code toolbox we supply includes a code to generate numerically random photon time arrival data streams for “synthetic” quantum dots that jump between an arbitrary set of intensity levels and decay rates, with jump time statistics and photon budgets that can be set by the user. As results, we provide benchmarks on the performance of CPA for detecting changepoints in the function of the number of intensity levels and total photon budget, and we explore the limits to the number of distinct states that the clustering analysis can reliably separate. Moreover, the toolbox allows to us test the accuracy of jump time statistic such as power law statistics, for such multilevel dots. Finally, the test suite also allows to benchmark the accuracy of fluorescence decay model fitting with maximum likelihood estimation, and we discuss the construction of fluorescence–intensity–decay rate correlations from CPA-partitioned data. The applicability of the toolbox to experimental data is illustrated by the supplied data sets, which correspond to a related paper in this journal.⁴³ We note that some other approaches such as HMM methods may be more suited for processes where more knowledge on the underlying physical processes is available. In contrast, our toolbox is ideal for cases in which one wants to make no a priori assumption on the physical mechanism behind intermittency. Furthermore, the CPA method in the toolbox operates on the finest level of information available in photon counting, that is, on the distribution of individual photon arrival times, as opposed to methods that are optimized to work on camera frame data.³³ This paper is structured as follows. In the Methods section, we summarize the Bayesian statistics tools we implemented to analyze all aspects of our data. Next, we benchmark the performance of CPA to pinpoint intensity jumps and of level clustering to identify the number of levels between which a dot switches on the basis of Monte Carlo simulations. Next, we present considerations on the dependence of on–off time distributions, decay rate fit, and so-called “fluorescence decay rate intensity diagrams” (FDIDs) on count rates.

Figure 1.

Schematic overview of the working of the toolbox. (A) Illustration of the two methods available to obtain TCSPC data either by photoluminescence TCSPC measurements of a single emitter (top panel) or through simulation of a single emitter (bottom panel). The latter is provided in the toolbox. Both will result in a stream of time stamps that can then be further analyzed by the toolkit. The simulation part of the toolbox simulates dots of m₀ levels, with associated count rates and fluorescence decay rates I_m and γ_m, with the dot visiting levels in random order, and with residence times for each segment chosen drawn according to specified power law exponents α_m. The output simulated data consist of time-stamped photon arrivals over a total time span T, where for each photon k = 1..., a time stamp s_k is recorded. These time stamps are randomly distributed over two detector channels S_A, S_B. The delays of each of the photon time stamps relative to the time stamp in the third channel S_R, representing the periodic pump laser pulse train, is chosen in accordance with the set emitter decay rate. (B) Starting out with this stream of photon events, using CPA (C), the changepoints are found and with these, the instantaneous intensities. (D) Subsequently, these events are grouped in order to find the most likely underlying intensity levels between the behavior. Following this, a number of analyses can be done, such as (E) ascertaining whether the time between switching events is power law-distributed, (F) the visible separation of states in FDIDs/FLIDs, and (G) the presence of memory in the switching behavior. Here, we show an example of a simulated, four-level emitter, with simulation parameters chosen for clarity of illustration.

Methods

In this section, we present all the methods implemented in our Python toolbox as well as the methods for benchmarking them. Benchmark results are presented in the Results section. We refer to the Supporting Information for a manual to the code and the code itself.

Changepoint Analysis

First, we summarize CPA, a Bayesian statistics method for the unbiased determination of jumps or “changepoints” in time traces of discrete events.^{17,26,28,29,32,39,41,44−48} Bayesian statistics is a paradigm that reverses the usual standpoint of probability theory. Usual probability theory views a data set as a random draw from a probability distribution, given a hypothesis on the parameters of the underlying physical process. In this framework, one can calculate the likelihood of drawing the specific measured data set. Bayesian statistics, on the other hand, compares the likelihood of distinct hypotheses, given a measured data set and assumptions on the underlying measurement noise.

We consider time-tagged single photon counting data consisting of an ordered list of measured photon arrival times s_k, collected over a measurement time T. For a single emitter with no memory that emits at a count rate of N photons in a time T, the waiting times—that is, the times between photon arrivals—are exponentially distributed with waiting time τ_w = T/N. In order to determine whether there is a changepoint in some segment q, CPA compares the likelihood of two distinct hypotheses (1) there is a jump in emission intensity (i.e., the average waiting time τ_w jumping from some value to another) against (2) there is the same intensity throughout the measurement interval. When testing for a jump at a photon detection event k at time s_k in this trajectory q with time duration T_q containing N_q photon events, this leads to a log-likelihood ratio, or “Bayes factor””^26,28,29

where V_k = s_k/T_q. Derivation of this log-likelihood ratio involves several steps. First, it incorporates the assumption that in between jumps, the waiting time between photons is exponentially distributed, on the basis of which one can assess the likelihood of measuring the given data set for a given hypothesis on the exponential waiting time τ_w. Second, it uses maximally non-informative priors for 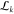to compare the hypothesis of presence versus absence of a changepoint without further restrictive assumptions on the involved intensity levels.

It should be noted that there are other ways to arrive at the same log-likelihood ratio test. One alternative starting point is a binary time series in which there is an underlying uniform and small probability distribution of photon detection per bin [e.g., imagining the time axis binned in by the timing card resolution (of order 0.1 ns for typical hardware)].⁴⁰ Such a uniform distribution would emerge as a direct consequence of exponential waiting time distributions. In this case, one should start from a binomial distribution and ultimately arrive at the same formula after application of Stirling’s formula. Another starting point is CPA applied to binned data with wider bins with multiple counts, that is, to series of Poisson-distributed intensities instead of discrete events.^26,29 However, the binning would introduce an undesirable time scale through the chosen bin width. Of these three methods, working with photon arrival times is the most data-efficient approach and introduces no artificial partitioning whatsoever. We refer to ref (29) for a derivation of the log-likelihood ratio in all these three scenarios, which includes a precise description of the use of maximally non-informative priors.

Following Watkins and Yang²⁶ and Ensign,²⁹ the most likely location of a changepoint, if any, is at the k that maximizes the Bayes factor . The hypothesis that this most likely changepoint is indeed a real event is accepted if 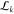exceeds a critical threshold value for or “skepticism”. This value is chosen to balance false positives against missed events. A full data set is partitioned recursively, that is, by recursively checking if data sets between two accepted changepoints themselves contain further changepoints. This results in a division of the data set into segments, each of which starts and ends at an accepted changepoint and with the level of skepticism as the stop criterion for the recursion. The resulting segmentation provides the most likely description of data as consisting of segments within which the intensity is constant, given the value chosen for the degree of “skepticism” and given the amount of data collected. Since the algorithm works with the list of individual photon arrival times, this segmentation entails no arbitrary partitioning. An accepted rule of thumb is that if the Bayes factor exceeds a “skepticism” value of just between 1 and 3, the evidence for a changepoint is highly ambiguous, whereas values in the range 7–10 are deemed strong evidence. The toolbox is supplied with a default value of skepticism of 8, set following the analysis of refs (26) and (29). The reader is warned that for a given photophysics scenario (intensity levels, segment duration statistics), it is advisable to set the level of “skepticism” on the basis of simulations in order to optimize the trade-off between missing changepoints altogether (false negatives) and precision (avoiding false positives). Our Result section provides an example of such an optimization.

Clustering

CPA splits the data in segments separated by jumps (a list of Q jumps delineate Q – 1 segments). One can now ask what the statistical properties are of the segmentation, that is, what the statistics is of the length of segments, the intensity levels most likely corresponding to the segments, and the fluorescence decay times associated with the segments. For instance, it is a nontrivial question how many distinct constant intensity levels or states m_r actually underlie the N – 1 found segments, with intensities I₁...I_Q–1. To answer this question, Watkins and Yang²⁶ proposed a clustering approach. The recent work of Li and Yang³⁹ provides a detailed explanation of the reasoning involved, though quoting results for Gaussian instead of Poissonian distributed data. The idea is that with the Q – 1 found segments, each with their associated recorded intensities I_q, one can use expectation maximization to calculate for a hypothesized and fixed number of levels n_G what the most likely underlying intensity levels are (with m ∈ 1...n_G) and how probable it is that each segment is ascribed to a given level (probability p_mq). Subsequently, Bayesian inference is used to establish the most likely number of levels (i.e., states) m_r and associated intensities 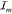, with m ∈ {1...m_r} describing the data.

Following refs (26) and (39), the expectation minimization in our toolbox is implemented as an interactive algorithm started by a first guess of the segmentation. This guess is obtained by a hierarchical clustering of Q – 1 segments in m = 1, 2, ..., Q – 1 levels that proceeds recursively. In each step, it identifies the two segments in the list with the most similar intensity levels as belonging to the same level. This provides an initial clustering of the measured data in any number m = 1, 2, ..., Q – 1 of levels. For the expectation maximization, the idea is to simultaneously and iteratively optimize the probability p_mq for segment q to belong to the mth level as well as an estimate of the intensities of these levels 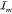. In each iteration, the intensities of all levels are estimated from the level assignment from p_m,q. Following this, the probability distribution p_mq is updated to redistribute the segments over the levels. In this calculation, it is important to understand the type of noise statistics the data obey. In the case of single-photon measurements and for the purpose of this discussion, the intensities are Poisson-distributed. The iteration is repeated until p_mq converges (practically also capped by a maximum number of iterations). The final outcome is a most likely assignment of the measured segments into n_G levels. Next, for each value of n_G one assesses the BIC. This criterion is a measure for how good the description of the segmented intensity trace is with n_G intensity levels, given the assumption of Poisson counting statistics for each fixed intensity level. Beyond a mere “goodness of fit” metric that would simply improve with improved number of parameters available to describe the data, this metric is penalized for the number of parameters to avoid overfitting. For Poisson-distributed data, the criterion is derived in ref (26) as

where Q again is the number of changepoints detected and n_G is the number of available levels. The term 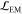is the log-likelihood function optimized in the expectation maximization step, that is, 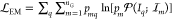with 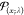the Poisson probability function at mean λ, p_m the probability of drawing level m. The second term in the BIC is the term penalizing the BIC for overfitting. The accepted best description of an emitter in n_G-levels is taken to be the value of n_G where the BIC peaks.

Intensity Cross-/Autocorrelation and Maximum Likelihood Lifetime Fitting

Many single photon counting experiments are set up with pulsed laser excitation for fluorescence decay rate measurements and with multiple detectors to collect intensity autocorrelations (e.g., to verify antibunching in g⁽²⁾(τ) for time intervals τ comparable to the fluorescence decay rate and shorter than the commonly longer detector dead time). In a typical absolute-time tagging setup, this results in multiple data streams S_A, S_B, S_R of time stamps corresponding to the detection events on each detector and the concomitant laser pulses that created them, respectively. Our Python toolbox contains an implementation of the correlation algorithm of Wahl et al.⁴⁹ that operates on time stamp series, and returns, for any combination of channels S₁, S₂ (1, 2 ∈ {A, B, R}), the cross-correlation C(τ)Δτ, that is, the number of events in the time series S₁ and the time series S₂ that coincided when shifted over τ, within a precision Δτ.

Cross-correlating detected photons and laser arrival times, taking Δτ to be the binning precision of the counting electronics and the range of τ equal to the laser pulse repetition rate, returns a histogram of the delay times between photon detection events and laser pulses. To obtain g⁽²⁾(τ) to investigate antibunching, streams of photon events from two detectors in a Hanbury–Brown Twiss setup are cross-correlated. Δτ is taken to be the binning precision of the counting electronics and the sampled range of τ as an interval is taken symmetrically around τ = 0 and several times the laser pulse interval. Finally auto- or cross-correlating detector streams over τ-ranges from nanoseconds to seconds, coarsening both τ and Δτ to obtain equidistant sampling on a logarithmic time axis, results in long-time intensity autocorrelations of use in intermittency analysis.³¹ Our toolbox also provides this logarithmic time-step coarsening version of the correlation algorithm of Wahl et al.⁴⁹

Of particular interest for intermittent single emitters is the analysis of fluorescence decay rates in short segments of data as identified by CPA, which may be so short as to contain only 20 to 1000 photons. For each of the photon detection events in a single CPA segment, cross-correlation with the laser pulse train yields a histogram of the N_q photons in segment q. In each of the bins (with width Δτ), the photon counts are expected to be Poisson-distributed. Therefore, the optimum fit procedure to extract decay rates employs the maximum likelihood estimate procedure for Poisson-distributed data, as described by Bajzer et al.⁵⁰ In brief, for a decay trace sampled at time points τ_i relative to the laser excitation, with counts per bin D(τ_i), the merit function reads

1

Assuming a chosen fit function F_A(t), the parameter set A that minimizes this merit function provides the parameter values that most likely correspond to the data. The estimated errors in these parameters then follow from the diagonal elements of the inverse of the Hessian of M relative to the parameters A. Importantly, the fact that the Poisson distribution is tied to absolute numbers of counts implies that this approach requires that the data are neither scaled nor background-subtracted. Instead, the background should be part of the fit function either as a free parameter or as a known constant. Furthermore, it should be noted that time bins with zero counts are as informative to the fit as non-empty ones and should not be left out.

Generating Synthetic Quantum Dot Data

To benchmark the CPA and clustering method and to test its limits, our toolbox provides an example routine to generate artificial data mimicking quantum dot intermittency. To obtain mimicked quantum dot data, we first choose a number m₀ of intensity level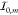s between which we assume the dot to switch. Next, we generate switching times for each of the states. In this work, we choose all switching times from a power law distribution. For benchmark purposes, we will present results with power law exponent α = 1.5, though any exponent can be set in the code. On the assumption that intensity levels appear in a random and uncorrelated order, this segments the time axis in a list of switching events T_0,j, j = 1, 2, ..., m₀, where for each segment, we randomly assign one of the nominal intensities . Next, to mimic a pulsed excitation experiment, we imagine each of these segments to be subdivided in intervals of length τ_L equivalent to a laser repetition rate (τ_L = 100 ns in the examples in this work). We assign each of these intervals to be populated with one photon at probability . This ensures that the number of photons N_q in every segment is drawn from a Poisson distribution at mean 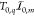. By removal of all empty bins, the binary list is translated into a list S = (t₁, t₂, t₃, ...) of photon arrival time stamps at resolution τ_L to which one can directly apply CPA to attempt a retrieval of switching times and apply clustering to retrieve the number of states.

To also enable fluorescence decay rate analysis, we further refine the photon arrival time list. Recalling that we have generated switching events T_0,q between intensity states , we now also assume fluorescence decay rates γ_0,m. As each segment q was already chosen to correspond to some level m_q, we now impose the decay rate γ_0,mq on the photon arrival times. To do so, for each of the photon events k = 1...N_q already generated at resolution τ_L, we now randomly draw a delay time Δ_k relative to its exciting laser from an exponential distribution characterized by rate γ_0,mq. To mimic the behavior of typical TCSPC counting equipment, the delay time is discretized at a finite time resolution Δτ [in this work, it was chosen as 165 ps to match the hardware in the provided example experimental data measured in our lab (Becker & Hickl DPC-230), though of course in the toolbox, the value can be set to match that of any time-correlated single photon counting (TCSPC) card vendor]. Testing of fluorescence decay trace fitting can operate directly on the generated list of delay times, or alternatively, one can synthesize a TCSPC experiment by re-assigning S to represent laser-pulse arrival times S_R and defining photon arrival times as the events in S_A, SB each shifted by its delay time, that is, S_X = (t₁ + Δ₁, t₁ + Δ₂, ...), with X ∈ A, B. Cross-correlation of S_R and S_X returns the delay time list. We note that although our work does not focus on antibunching, our quantum dot simulation routine provides data distributed over two detector channels, where emission events antibunch, while an uncorrelated background noise level of the detectors can also be set.

Practical Implementation

We have implemented the toolbox ingredients in Python 3.8. As time stamp data can be substantial in size, we use the “parquet” binary format to store time stamps as 64-bit integers. Processing and plotting the data is dependent on Pythons’ standard libraries numpy, matplotlib, while we use Numba, a just-in-time compiler, to accelerate the time stamp correlation algorithms. An example script to generate synthetic data and to run the entire workflow on simulated data is provided. We refer to the Supporting Information for a guide to the practical implementation and use of our toolbox. The toolbox comes also with example experimental data on single CsPbBr₃ quantum dots from a recent experiment.⁴³Table 1 lists scaling and performance metrics for the algorithms contained in the toolbox.

Table 1. Algorithm Scaling and Computation Time as a Function of Number of Photons N and Changepoints Q^a.

algorithm	scaling	timing
CPA		ca. 10 s for N = 106
grouping	initial clustering dominates over iterative algorithm
initializationb		0.5 s for Q = 3 × 102
iterative optimizationc	overhead dominated	0.75 ms per iteration (Q < 500)
g(2)d		8 ms per plot point at N = 106
long-time autocorrelatione		ca. 2 s for full plot

^aTimings were obtained on a standard desktop (Intel I7 4790 at 3.6 GHz, with 16 Gb of DDR3 RAM) and are obtained on the basis of 5 × 100 photon trajectories (100 independent draws for 5 different trajectory record lengths from ca. 10⁴ to 3 × 10⁶ photon events).

^bFor a large Q, this is accelerated by first clustering subsets, merging, and continuing clustering.

^cTypically, 5 to 10 iterations are required when n_G ≈ m.

^dNumba JIT acceleration assuming int64 provides over 2 orders of magnitude acceleration. A typical g⁽²⁾ plot has ca. n_plot points = 2000 and hence requires 10 to 20 s to evaluate.

^eEssentially repeating, g⁽²⁾ and logarithmic coarsening every n_cascade points.

Results

The remainder of this work is devoted to presenting benchmarks of the provided methods. Benchmarks for emitters with “binary”” switching, that is, two well-separated intensity levels as is typical for II–VI quantum dots, have already been presented in literature.^26,32,40 However, emitters under the current study, such as perovskite quantum dots, appear to have a multitude or perhaps even a continuum of intensity levels. Our tests hence focus on determining the performance of CPA and level clustering for many-level single photon emitters.

Precision of Identifying Individual Changepoints

Figure 2A,B shows examples of CPA applied to a simulated quantum dot with a single jump in its behavior, from an intensity level of 10⁴ to 10³ cts/s resp. from 4.5 × 10² to 2.25 × 10², with ∼900 and ∼150 photons left and right of the changepoint, respectively. Purely for visualization purposes, the data are plotted in a binned format as the analysis itself does not make use of any binning. Alongside the binned intensity trace, we also show the log-likelihood ratio 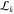. In both cases, the log-likelihood ratio clearly peaks at or close to the point where there is a changepoint in the data. Since the Bayes factor is actually a logarithmic measure for the comparison of hypotheses, the algorithm indeed identifies the changepoint with high probability and to within just a few photon events, even where the jump is far smaller than the shot noise in the binned representation in the plot at a relative intensity contrast of just a factor of 2. Generally, the probability with which the algorithm identifies or misses the changepoint is dependent on the total number of photons recorded both before and after the changepoint and on the contrast in intensities, consistent with the findings of Watkins, and Ensign.²⁶

Figure 2.

Demonstration of changepoint detection applied to a synthesized data set with a single changepoint, with equal photon counts before and after the changepoint. In (A,B) the contrast between intensities is a factor of 10 and 2, respectively, while the total photon budget is approximately 2000 and 300. The bottom panels show the log-likelihood ratio test, which clearly peaks at the changepoint in both cases. The y-axis unit cts/ms stands for counts per millisecond. The robustness of the method is demonstrated in (C,D), where we show the likelihood of detecting a changepoint in such a series for different intensity contrasts, and the variance of the found times, respectively, as a function of the total photon numbers. To gather accurate statistics, 10⁴ photon traces were generated for each data point. The data are plotted in a binned fashion (ms bins) for visualization purposes only.

To identify the limits of CPA,^29,32 we consider the feasibility of identifying changepoints of contrast I₂/I₁ as a function of the total number of photons in the time record. The results are shown in Figure 2C for the likelihood of detecting a changepoint and Figure 2D for the error in identifying the precise event k at which the changepoint that is identified occurred. Here, we only consider the case where there are roughly an equal number of photon events before and after the changepoint. These data are obtained by simulating 10⁴ switching events of the type as shown in Figure 2A,B for each contrast and mean photon count shown. The range of contrasts is chosen commensurate with reported on–off contrasts for typical quantum dots in literature, which generally fall in the 1.5- to 5-fold contrast range. At a high intensity contrast, exceeding a factor 5, a total photon count as low as 300 is enough for near-unity detection. Moreover, for sufficiently high photon count left and right of the changepoint, even very small changes in intensity have a high likelihood of being accurately detected, even if in binned data representations, the jump is not visible within the shot noise. Figure 2D provides a metric for the accuracy within which changepoints are pinpointed. CPA returns the most likely photon event k in which the jump occurred, which in our analysis can be compared to the actual photon event index k₀ at which we programmed the Monte Carlo simulation to show a jump. Figure 2d reports the mean error 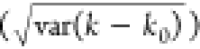as a metric of accuracy. At jump contrasts above a factor 2, changepoints are identified to within an accuracy of almost one photon event even with just 10² photon counts in the total event record. At very small contrasts, the error in determining the location of a changepoint is generally on the level of one or two photon events, only worsening when there are fewer than 200 counts. This observation highlights the fact that if the photon record has just a few counts in total, the error in estimating the count rate before and after the jump becomes comparable to the magnitude of the jump.

Intermittency and On–Off Time Histograms

As the next step in our Monte Carlo benchmarking, we turn to time series with many, instead of a single, jumps. Figure 3A shows a representative example for a simulated intermittent quantum dot with two states, assuming a contrast ratio between states of 2 × 10⁴ and 5 × 10³ s^–1. We generally observe that the recursive CPA algorithm accurately identifies switching events, barring a number of missed events of very short duration. From the CPA, we retrieve the time duration between switching events. Figure 3C shows a histogram of time durations, plotted as a probability density function obtained from a whole series of Monte Carlo simulated time traces of varying contrasts between states (see legend). Notably, if we simulate quantum dots that have switching times that are power-law distributed, the retrieved distribution indeed follows the assumed power-law particularly for long times. At shorter times, the histogram remains significantly below the power law, particularly at low intensity ratios between the two assumed states. This indicates that CPA misses fast switching events and is consistent with the observation from Figure 2C that a minimum photon count is required to observe switching events of a given contrast. As a rule of thumb, usual II–VI colloidal quantum dots have a contrast between dark and bright states of around 5, meaning that of order 200 photons are required to detect a changepoint with near-certainty. At the assumed count rates (2 × 10⁴ s^–1 for the bright state), this means one expects CPA to fail for switching times below 10 ms, where the on–off time histogram indeed shows a distinct roll-off. This result suggests that one should interpret on–off time histograms from changepoint detection with care: one can generally rely on the long-time tail but should determine the shortest time scale below which the histogram is meaningless on basis of the intensity levels present in the data.

Figure 3.

(A) Typical time trace of a simulated quantum dot. The intensity duty cycle switches between 0.5 × 10⁴ and 2 × 10⁴ counts/s. It shows an on/off input duty cycle generated with a power-law distribution (orange), the duty cycle with Poissonian noise (purple), and the retrieved duty cycle (green). Overall, the original intensities and lifetimes (B) are retrieved well. (C) Histogram of the number of switching events as a function of their duration. Each data point represents 10.000, 10 s power-law distributed time traces. The input shows the initial power-law distribution, the lighter colors show the number of retrieved changepoints, after applying Poisson noise and CPA, at different contrasts, with I₁ = 10⁵. counts/s. We can see that even at low contrast, events with long times between switching are retrieved, but each contrast has a characteristic duration below which changepoints cannot be accurately retrieved. This puts a fundamental limit on the information that can be extracted from a given data set. (D) Occupancy diagram illustrating the behavior of the clustering algorithm for a system with m₀ = 4 intensity levels. The color scale indicates the amount of time spent in each state m_i after the assignment of states for a given number of available states n_G. We see that when n_G > m₀, effectively all segments are distributed across only n_G ≤ m₀ intensity levels.

Error Analysis for Trajectories with Multiple Jumps

The CPA results in Figure 2C essentially quantify the algorithm performance in terms of the fraction of correctly identified changepoints (true positives) for traces with a single step in intensity as a function of contrast and photon budget. Actual single emitter photon trajectories have a plethora of steps, where CPA is mainly likely to miss short segments because only those changepoints are accepted for which the evidence in the data is compelling relative to the shot noise in it. Indeed, the short-time roll-off in Figure 3C highlights exactly this tendency of CPA to under-report on closely spaced changepoints (false negative rates high for short segments). The level of skepticism set as a parameter for running CPA sets the overall accuracy of the algorithm, essentially trading off the rates of false positives and false negatives. When using the toolbox for a particular photophysical scenario, the reader is recommended to study the error rates as a function of skepticism. To demonstrate that type of study, here we report on algorithm performance as a function of skepticism using the error metrics accuracy, precision, and recall. To this end, we generate synthetic data and match the list of nominal changepoints and retrieved changepoints to determine the rate TP of true positives, the rate FP (false positives) of detected transitions for which no transition was actually present, and the rate FN of false negatives, in which a true transition is not detected by CPA. The standard definition for the error metrics reads^34,37

2

3

4

The accuracy benchmarks overall performance, whereas precision measures the false positive error rate and recall quantifies the false negative rate. Since, first, changepoint detection is not accurate to the level of a single photon arrival time and, second, the set of stored nominal switching times in our toolbox may fall in between synthesized photon events, such a comparison requires a tolerance range to be meaningful. Figure 4 presents the algorithm performance as a function of the level of skepticism (vertical axis) and as a function of the tolerance range within which changepoints are accepted as true positives, measured in milliseconds. The results are for a more challenging case than a two-level dot, namely, a four-level system with mean count rate 5 × 10⁴ counts per second, four equidistant intensity levels (2, 4, 6, and 8 × 10⁴ counts per second), and power law-distributed segment residence times (exponent 1.5, with shortest residence time of 10 ms in a segment). The presented results are obtained from 200 photon trajectories with on average 5 × 10⁵ photons and 10² changepoints each. If the time axis for the tolerance is chosen as short as the inverse mean count rate, the apparent algorithm precision is low, indicating that changepoints are generally found close to, but not quite at, the moment where the switching event occurs. At tolerances of 2 to 5 ms (containing of order 50–250 photons typically at the given rate and for the various assumed intensity levels), the error rate saturates at above 90%. The accuracy for this example peaks at a skepticism of ca. 7.0 (Figure 4A). At higher levels of skepticism, the precision increases, that is, the number of false positives reduces further (Figure 4B). However, this is at the expense of recall, that is, the number of missed changepoints. The false negatives rate decreases only with skepticism lowered to below 10 (Figure 4C).

Figure 4.

Accuracy (A), precision (B), and recall (C) for CPA as a function of tolerance in milliseconds for which nominal and detected changepoints are matched as equal and as a function of the level of “skepticism” which the Bayes factor needs to exceed for a changepoint to be accepted.

Performance of Level Clustering

Next, we consider the performance of the grouping algorithm applied to the segmentation of simulated time traces. For reference, Figure 5A shows the BIC versus n_G for the example of simulated dots with m₀ = 2, 3, 4 intensity levels. Generally, the BIC rapidly rises as n_G approaches the actual number of levels with which the data were simulated and gently decreases once n_G exceeds the actual number of levels in the data m₀. The fast rise indicates that within the assumption of Poisson-distributed intensities, the data cannot at all be described by fewer than m₀ levels. The slow decrease is due to the penalization of the BIC by the number of fit parameters. Since the BIC criterion actually relates to the logarithm of the probability with which n_G states are the appropriate description of the data, even an apparently gentle maximum in BIC actually coincides with an accurate, unique determination of m₀.

Figure 5.

(A) Examples of the BIC for simulated quantum dots, with m₀ = 2, 3, 4. The most likely number of levels is indicated by a small peak in L_k. In the inset, we show that the distributions indeed peak at their respective m₀. It should be noted that the BIC shows a very sharp rise and then, from m₀ onward appears almost flat. There is in fact a shallow downward slope. Here, one should keep in mind that the BIC is a logarithmic metric. On a linear scale, the maximum is significant. (B–E) Likelihood P of finding m_r levels for a simulated system, given m₀ initial intensity levels and ⟨N⟩ the mean number of photon counts. We see that the photon budget plays a defining role in the total number of states that one can reliably resolve. At low photon budgets, the number of levels is systematically underestimated, whereas at high photon budgets, P(m_i = m₀) remains high even at high m₀. We see that m_r is never overestimated.

To gauge the accuracy of the retrieval of the number of states for multi-state quantum dots, we simulated quantum dot data with power law-distributed (α = 1.5) switching events, assuming switching from m̃₀ = 2 to 10 equally likely levels, where we assumed intensity levels to be assigned to segments randomly and where we assumed levels for simplicity evenly spaced from dark to bright. Lastly, all segments were reassigned an intensity according to Poisson statistics. In other words, we added shot noise.

For many random realizations with different m₀ and ⟨N⟩, we determine the most likely number of states m_r (BIC(m_r) = max(BIC)) according to the clustering algorithm and construct histograms of outcomes. The total photon budget is set by the product of assumed record length and the mean count rates of the different levels. The outcomes of these calculations are shown in Figure 5B–E, where each panel corresponds to a different photon budget. A plot with only diagonal entries signifies that the number of levels retrieved by the clustering algorithm always corresponds to the number of levels assumed, so m_r = m₀. At high photon budgets (Figure 5D,E), the retrieval of the number of states is indeed robust, even for simulated dots that switch between as many as 10 intensity levels. At low total photon budgets (Figure 5B,C), we see that m_r is often underestimated. This signifies that there is high uncertainty due to shot noise in the assigned intensity levels, so that levels cannot be discriminated within the photon budget. It is remarkable that at photon budgets of 10⁶ photons, as many as 10 intensity levels can be robustly discerned even though the smallest contrast between levels is as small as 10% in intensity in view of Figure 2, where it is evident that detecting changepoints for small intensity jumps is difficult. Here, however, one should realize that in contrast to Figure 2C where single small-contrast changepoints are studied, here many levels are visited in a random order. Thus, the correct detection of small level differences is not reliant on the detection of small changepoint contrasts but on having sufficient photon statistics to resolve the segment count rates of already identified segments. A secondary metric, additional to the BIC, is in how the clustering algorithm assigns occupancy to the levels. The clustering algorithm assigns to each data segment the most likely intensity level that it was drawn from. Occupancy is a metric for how often each of the n_G levels available to the algorithm is actually visited by the measured intensity sequence. We find that if one allows the clustering algorithm to use more levels than originally used to synthesize the quantum dot data (n_G > m₀), the additional levels take essentially no occupancy. We show this in Figure 3D for an example of a dot assumed to have four intensity levels with a total photon count of 5 × 10⁵. As soon as additional states (m ≥ 5) are offered to the grouping algorithm, these additional states take no occupancy and do not change the distribution of segments over the states found at the correct m. Thus, we confirm again that the grouping algorithm does not over-estimate the number of states.

Accuracy of Decay Rates versus Photon Budget

Figure 6A shows examples of fitted simulated data for slow and fast decays as examples of the Monte Carlo simulations we have performed to benchmark the accuracy of decay rate fitting in function of photon budget and decay rate (panel (B)). We find that the error in γ very roughly follows roughly a power law with an exponent of 0.9–1.1, with slower decay rates showing higher errors. Consistent with ref (51), we find by Monte Carlo simulation that one requires approx. 200 (50) counts to obtain an error below 10% (20%) in decay rate if one fits mono-exponential decay with free parameters. A problem intrinsic to the use of CPA is that fast switching events may be missed, leading to an averaging of short time intervals with others. This leads to decay traces that are in fact not attributable to a single exponential decay.

Figure 6.

(A) Two examples of decay traces (γ = 0.1, 1 ns^–1) with low photon count (N = 300) fitted to a single-exponential decay. (B) Standard error of the fitted decay rate w.r.t. the input decay rate as a function of the total photon count for different decay rates. Each data point is the average of 10³ simulated decay traces.

FDID Diagrams

Correlative diagrams that plot correlations between intensity levels and fluorescence lifetime^24,25,32 form a powerful visualization of quantum dot photophysics. Our toolbox contains the code to generate both FDIDs and fluorescence lifetime intensity diagrams (FLIDs). The considerations in this section hold equally for FDID and FLID diagrams, although the provided example is for a FDID analysis. Essential to the construction of FDID/FLID diagrams is that for each detected photon also the delay time to the laser pulse that generated it is known so that decay rates can be fitted even to short segments of a time trace segmented by CPA. Here, we discuss the construction of FDID diagrams derived from CPA, again illustrated by examining simulated data for a quantum dot that switches between two states of distinct intensity and lifetime. FDID diagrams are conventionally constructed from time-binned data, where it is interpreted as a simple histogram in which each time-bin contributes a single histogram count to one single intensity-decay rate bin. It is not trivial to extend this notion to CPA-segmented data since CPA segments intrinsically have very different time durations instead of having equal width as in conventional time-binning. We propose two modifications to the construction of a FDID as a histogram. First, instead of representing FDID entries as a single binary entry in just one histogram bin (one time segment contributes one count to a single pixel in an FDID), we propose to incorporate the uncertainty in intensity and decay rate that is associated with each time segment. To this end, each segment contributes to the FDID diagram according to a 2D Gaussian function centered at the CPA-segment decay rate and intensity (total counts C_j in segment j divided by segment duration T_j), where the width is given by the fit error in the decay rate and the shot noise error in the segment 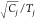. If one would apply this logic to regular time-binned data, giving each Gaussian contributor the same integrated weight, one obtains a diagram similar to a regular FDID histogram except that the results are smooth and with less dependency on a chosen histogram bin width. Instead, the feature size in FDID represents the actual uncertainties in intensity and rate.

As a second modification, we propose to reconsider the weights of the Gaussians—that is, the integrated contribution to each entry in the FDID. For time-binned data, one assigns each segment equal weight so that equal lengths of time contribute to equal weight. Since CPA results in segments of unequal length, several choices for constructing FDID diagrams are possible, which to our knowledge have not been discussed in CPA literature. Giving equal weight to each CPA fragment will lead to FDID diagrams from those obtained from binned data since effectively long time segments are then underrepresented compared to short segments. This leads to under-representation of states with steeper power law distributions in their switching times. The direct equivalent to regular FDID-weighting for CPA-segmented data is that a segment of duration T_i has a weight proportional to T_i (henceforth “duration-weighted FDIDs”). Alternatively one could argue that since time-averaged intensity and fluorescence decay traces are rather set by the contribution in emitted photons, one could instead use the total number of photons C_i in each segment as weight (henceforth “count-weighted FDID”).

It has been established in a multitude of studies of II–VI quantum dots that the distribution of on–off times follows a power law (exponents α_on,off) truncated by an exponential with specific time τ_l, giving the distribution²¹⁻²³t^–α e^–t/τ_l. We analyze Monte Carlo-simulated FDIDs to establish if there are conditions of the truncation time under which a two-state quantum dot would appear not as a bimodal distribution. Figure 7 shows duration-weighted FDIDs for simulated quantum dot data. For (A), we consider a two-state quantum dot with power law-distributed switching times. In (B–D), we show a quantum dot simulated with similar parameters but with the maximum duration of the segments T_c = 10, 1, 0.1 s. Evidently, the bi-modal nature of the quantum dot is faithfully represented by the FDID diagram constructed through CPA. This remains true also for power laws with a long time truncation (t^–α e^–t/τ_l), unless truncation times τ_l are as short as 20 ms, so that there are no segments with over approximately 10² counts. This limit of our benchmarking space zooms in on the regime where CPA intrinsically fails (Figure 2C). In this regime, the originally assumed bimodal quantum dot behavior no longer results in a bi-modal FDID. Instead a significant broadening is evident. We can conclude that for most realistic quantum dot systems, CPA-generated FDIDs will not suffer from this artificial broadening artifact.

Figure 7.

Four FDID diagrams of a simulated bimodal quantum dot with (I, γ) = (2 × 10⁴ s^–1, 0.1 ns^–1) and (0.5 × 10⁴ s^–1, 0.4 ns^–1). In each diagram, we apply a different cutoff time T_c to the simulated power law at ∞, 10, 1, and 0.1 s. We find that a shorter cutoff causes an increasingly strong smearing effect between the two states.

Conclusions

In this work, we have provided a Python toolbox for CPA and for determining the most likely intensity level assignment for intermittent multilevel emitters. We investigated the limits of CPA and clustering as fundamentally set by the photon budget and for the case of many state emitters. We have shown that for long switching times, the typical power law behavior of many quantum emitters can be accurately retrieved. We also show that in the case of many-state emitters, the number of intensity levels can be retrieved with high fidelity, provided the photon count is high enough. At low photon counts, the number of states is systematically underestimated. This shows in which way the photon budget puts a fundamental limit on the amount of information that can be retrieved from a given TCSPC data set. We show that the photon budget also poses a limitation on the accuracy at which the slope of a single-exponential decay can be retrieved. Additionally, we investigate the commonly used intensity-decay time diagrams. We show that with CPA, a two-state simulated quantum dot is well-represented in an FDID, but when a cutoff is introduced to match that commonly found in literature, the states become increasingly poorly defined in an FDID representation. While the Bayesian inference algorithms in this toolbox were reported earlier for application to quantum dots with just two or three intensity states, this toolbox and the provided benchmarks point at the applicability even to emitters that the jump between many closely spaced intensity levels will, in our view, be of large practical use for many workers analyzing the complex photophysics of, for example, perovskite quantum dots. Also, the toolbox can be used for theory development, following a workflow in which hypotheses are cast in synthetic photon counting data, which in turn can be subjected to the CPA suite to assess how hypothesized mechanisms express in observables and how far they are testable. The limit of this testability generally depends on an interplay of total photon budgets, residence time in each level, intensity contrast between levels, and segment durations. For a given photophysics scenario, the user can easily deploy the toolbox to directly assess data segmentation in terms of accuracy, precision, and recall error rates. These rates will depend on the level of skepticism that the user wishes to apply in order to accept assertions regarding the segmentation of data in segments and intensity levels. These error rates, and hence the testability of a hypothesized photophysics scenario, are ultimately limited by the evidence in the counting statistics and not the segmentation algorithm.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.1c01670.

• Detailed manual to the code that is posted on GitHub⁴² and description of the example data set that corresponds to ref (43) (PDF)

The authors declare no competing financial interest.