Effects of I_h and TASK-like shunting current on dendritic impedance in layer 5 pyramidal-tract neurons

Abstract

Pyramidal neurons in neocortex have complex input-output relationships that depend on their morphologies, ion channel distributions, and the nature of their inputs, but which cannot be replicated by simple integrate-and-fire models. The impedance properties of their dendritic arbors, such as resonance and phase shift, shape neuronal responses to synaptic inputs and provide intraneuronal functional maps reflecting their intrinsic dynamics and excitability. Experimental studies of dendritic impedance have shown that neocortical pyramidal tract neurons exhibit distance-dependent changes in resonance and impedance phase with respect to the soma. We, therefore, investigated how well several biophysically detailed multicompartment models of neocortical layer 5 pyramidal tract neurons reproduce the location-dependent impedance profiles observed experimentally. Each model tested here exhibited location-dependent impedance profiles, but most captured either the observed impedance amplitude or phase, not both. The only model that captured features from both incorporates hyperpolarization-activated cyclic nucleotide-gated (HCN) channels and a shunting current, such as that produced by Twik-related acid-sensitive K⁺ (TASK) channels. TASK-like channel density in this model was proportional to local HCN channel density. We found that although this shunting current alone is insufficient to produce resonance or realistic phase response, it modulates all features of dendritic impedance, including resonance frequencies, resonance strength, synchronous frequencies, and total inductive phase. We also explored how the interaction of HCN channel current (I_h) and a TASK-like shunting current shape synaptic potentials and produce degeneracy in dendritic impedance profiles, wherein different combinations of I_h and shunting current can produce the same impedance profile.

NEW & NOTEWORTHY We simulated chirp current stimulation in the apical dendrites of 5 biophysically detailed multicompartment models of neocortical pyramidal tract neurons and found that a combination of HCN channels and TASK-like channels produced the best fit to experimental measurements of dendritic impedance. We then explored how HCN and TASK-like channels can shape the dendritic impedance as well as the voltage response to synaptic currents.

INTRODUCTION

The pyramidal cells (PCs) found in layer 5 (L5) of neocortex generate the main outputs of cortical circuits: spike trains propagating along axons that project to various cortical and subcortical structures, exerting top down control over other brain areas and motor function (1–6). To produce their outputs, L5 PCs integrate inputs from other cortical layers, other cortical areas, and thalamus (7–12). There is great diversity among PCs in L5, not just in their morphologies and projections, but also in their spiking activity, with some PCs having high spontaneous firing rates whereas others’ firing rates are closely correlated with the activity of neurons in the surrounding population (8). The balance of excitatory and inhibitory inputs and the electrotonic structure of PCs are key in understanding how they generate their outputs and exert topdown control over other parts of the nervous system.

In this study, we focused on pyramidal tract neurons (PTs; also called thick-tufted cells), one of the three major classes of cortical PCs. 1) PTs project to subcortical structures and include corticospinal, corticobulbar, and corticopontine cells as well as projections to the medullary pyramids (2, 13). They also send collateral projections to thalamus. 2) Intratelencephalic neurons (ITs), also called thin-tufted or commissural cells, include corticostriatal and corticocortical cells and project to other cortical areas (14). 3) Corticothalamic neurons (CTs) project to ipsilateral thalamus (6). A major physiological factor distinguishing PTs from ITs and CTs is the high expression of the hyperpolarization-activated cyclic nucleotide-gated (HCN) channel, a nonselective voltage-gated cation channel responsible for the h-current (I_h) (13–15). High expression of HCN channels profoundly affects the subthreshold filtering properties of neuronal membranes.

The electrical properties of the passive neuronal membrane are very similar to those of a parallel RC circuit, with the response of membrane potential to currents dropping off at frequencies above the “natural frequency” at 1/2πRC Hz (low-pass filtering). Under the right circumstances, however, voltage-gated ion channels can produce a “phenomenological inductance” (16, 17) that can, like a physical inductor in an RLC circuit, generate resonance: an enhanced voltage response over an intermediate range of frequencies (18, 19). Phenomenological inductance is most likely to be seen when channels with slow gating are present, such as HCN channels and delayed rectifier K channels (20–22). Resonance becomes apparent when currents through these channels are prominent enough and lag sufficiently far behind fluctuations of membrane potential (23).

The filtering properties of the neuronal membrane have been characterized as impedance profiles measured at subthreshold voltages (21, 24–26). A common experimental method for probing neuronal impedance is to stimulate the neuron by injecting a chirp current waveform: a constant-amplitude, sinusoidal waveform whose instantaneous frequency increases from low to high over time (25, 26). In this study, we use a linear chirp stimulus whose instantaneous frequency increases linearly from 0.5 Hz to 20 Hz over 20 s (13, 27) Impedance amplitude (|Z|) characterizes voltage response with respect to stimulus frequency. The resonant peak (resonant frequency, f_res) is found at the frequency where the constant amplitude current stimulus causes the greatest peak-to-peak changes in membrane potential. I_h-mediated resonance has been observed in a wide variety of species and neuronal cell types (23, 27, 28) and is proposed to impart neurons with the ability to discriminate inputs by frequency (20, 25, 29). In addition to responding more strongly at certain frequencies (resonance), I_h also provides another property characteristic of inductive circuits: a shift of response phase (Φ). Given a sinusoidal current stimulus, the peaks of neuronal membrane potential (V_memb) may occur before (lead), after (lag), or synchronous with peaks in the stimulating current (30). The frequency at which peaks in the stimulating current and peaks in V_memb are simultaneous is referred to as the synchronous frequency (13). The phenomenological inductance produced by I_h opposes capacitive delay imparted by the neuronal membrane and produces phase lead at some frequencies. I_h has thus been proposed as a mechanism for compensating location-dependent capacitive delays of dendritic inputs seen at the soma, ensuring that simultaneous synaptic inputs dispersed across the dendritic arbor are coincident in the soma (31).

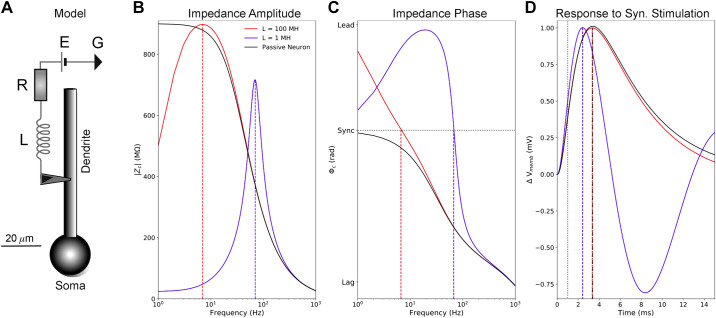
To illustrate these effects, we modified the standard passive neuronal model by adding an inductive circuit which mimics some of the properties of I_h (Fig. 1A). The resistor (R) stands in for the conductance of I_h; the battery (E), its reversal potential; and the inductance (L), the phenomenological inductance it generates. Adding the inductive circuit changed the low-pass filter properties of the passive neuron (Fig. 1B, black lines) to those of a resonator (red and blue lines). Inductance also increased impedance phase, creating phase lead at lower frequencies, where impedance phase is greater than zero (Fig. 1C). The inductance that shapes the impedance amplitude and phase profiles also influences synaptic potentials (Fig. 1D). The effects of the phenomenological inductance imparted by I_h could be recapitulated by our simplified neuronal model with its inductive circuit attached, but no single inductance can capture all the effects of I_h. For instance, when L = 100 MH, resonance frequency (Fig. 1B) and synchronous frequency (Fig. 1C) are both ∼7 Hz, much like what has been seen in real PT dendrites (13, 27). However, there was little effect on excitatory postsynaptic potential (EPSP) timing (Fig. 1D), because impedance phase converges with that of the passive neuron around 50 Hz (Fig. 1C). Conversely, when L = 1 MH, resonance and synchronous frequencies are much higher (∼70 Hz, Fig. 1B), but impedance phase was higher than in the passive neuron over a far larger frequency range (Fig. 1C). The increased impedance phase leads to a shorter lag between peak synaptic current and EPSP peak similar to what we will see in the biophysically detailed PT models (Fig. 1D). The EPSP shape was also narrower, which is consistent with the effects of HCN channels in dendrites, but there was excessive EPSP undershoot, which is not seen experimentally (32, 33). Thus, different inductance values mimicked different aspects of the phenomenological inductance generated by I_h.

Figure 1.

Inductance influences neuronal impedance and the response to synaptic stimulation. A: a simple, passive neuron model (soma and dendrite with membrane capacitance) was connected to a series circuit with an inductor (L = 1 MH or 100 MH), resistor (R = 25 MΩ), and battery (E = −70 mV) to illustrate some of the effects of inductance on impedance and synaptic potentials. We computed impedance between the center of the dendrite and the soma with this circuit attached (blue and red lines) and without it (black lines). B: the inductive circuit combined with membrane capacitance from the neuron produces resonance. When L = 100 MH, resonance frequency (∼7 Hz) is comparable with those seen in PT dendrites (13, 27). They are much higher when L = 1 MH. In the passive neuron alone, impedance amplitude falls off with frequency. Resonance frequencies are indicated with vertical dashed lines. C: the inductive circuit also increases impedance phase, with positive inductive/leading phase (voltage peak precedes current peak for an oscillatory input) seen at low frequencies. The horizontal dotted line indicates 0 radian phase shift between the stimulating current in the dendrite and voltage response at the soma (i.e., synchrony). D: effects of increased inductance on EPSPs measured at the soma: When L = 1 MH, peak EPSP voltage is earlier compared to the passive neuron due to higher impedance phase across the power spectrum of the synaptic current stimulus, but it produces much more undershoot that seen in PTs (32, 33). Conversely, when L = 100 MH, there is little change in peak EPSP time, but EPSP shape is more in line with that observed experimentally (32, 33). Time of peak synaptic conductance is indicated by the vertical dotted line. EPSP, excitatory postsynaptic potential; PT, pyramidal tract neuron; V_memb, neuronal membrane potential; Φ_c, transfer impedance phase.

I_h has other dramatic effects on the intrinsic dynamics and excitability of neurons. It acts as a pacemaker current, supporting regular- and burst-firing modes (34). It mediates the sag potential observed during hyperpolarization and spike-frequency adaptation during suprathreshold depolarization (14, 34). I_h supports coincidence detection, affects temporal summation (35–37), and has been suggested to determine the frequency response of neuronal membrane potential (V_memb) in response to weak alternating electric fields, like that produced by transcranial current stimulation (38). In addition, HCN channels have been shown to have paradoxical effects on excitatory postsynaptic potentials (EPSPs), enhancing spiking in response to EPSPs when the spike threshold is low and inhibiting spiking in response to EPSPs when the spike threshold is high (39). Recent modeling studies have suggested that this dual role could be attributed to interactions between HCN channels and a shunting current, most likely that produced by Twik-related acid-sensitive K⁺(TASK) channels (40, 41).

The relatively high expression of HCN in PTs endows them with resonance, giving the properties of a band-pass filter (13, 23, 27). We here report that five previously developed, biophysically detailed multicompartment models of neocortical PTs exhibit dendrite-location-dependent impedance profiles with resonant frequencies and synchronous frequencies increasing with distance from the soma (40, 42–45). Four of the five models have resonant frequencies in line with experimental findings, ranging from 4 Hz to 9 Hz (13, 27), whereas the fifth produced resonant frequencies above this range. Two of the five models have synchronous frequencies in line with experimental data, ranging from 3.5 Hz to 7 Hz (13), whereas the other three produced synchronous frequencies below this range. Only one PT model, which includes both I_h and a TASK-like shunting current, produced realistic impedance amplitude and phase profiles. We added TASK-like channels to one of the PT models that originally only produced resonant frequencies matching experimental findings. This addition produced realistic impedance amplitude and phase profiles with resonant and synchronous frequencies within the experimental range. We also examined how I_h and the TASK-like shunting current interact to produce and modulate dendritic resonance, inductive phase, and the properties of EPSPs.

METHODS

The biophysically detailed models studied here were developed for and published in previous studies (40, 42–45). All simulations presented here were performed using NEURON v. 7.8.0 (46, 47). The code developed for simulation, data analysis, and visualization was written in Python, and it is available on GitHub and ModelDB (https://github.com/suny-downstate-medical-center/L5PYR_Resonance; https://senselab.med.yale.edu/modeldb/ShowModel?model=266851#tabs-1).

Models

The simplified neuron model presented in Fig. 1 had a single-compartment, spherical soma with radius 5 µm, and a single three-compartment dendrite 75-µm long and 10 µm in diameter. All compartments had a membrane capacitance of 1 µF/cm², passive conductance 0.2 mS/cm², and passive reversal potential of −70 mV. To demonstrate the varied effects of inductance on neuronal impedance and V_memb dynamics, the cell was connected to an inductor (L = 1 MH or 100 MH), resistor (R = 25 MΩ), and a battery (E = −70 mV) placed in series and connected to ground (Fig. 1A).

We focused our study on five biophysically detailed, multi compartment models: three models of rat PTs and two models of mouse PTs (Table 1). Model 1 is based on data from neocortex of Wistar rats, postnatal day (P) 36 (43). The model was fit to perisomatic and backpropagating spiking activity. Dendritic channels were uniformly distributed with the exceptions of HCN channels and high- and low-voltage activated Ca²⁺ channels. I_h was uniform in the basal dendrites, whereas in the apical dendrites I_h channels were distributed using a density function that increased exponentially with distance from the soma (48, 49). The density of Ca²⁺ channels was increased near the nexus of the apical tufts forming a “hot-zone” (43). Model 2 was based on data from frontal cortex of Sprague-Dawley rats, P21–P33, fit using voltage-sensitive dye imaging data with a focus on reproducing dendritic plateau potentials and their propagation toward the soma, dendritic sodium spikelets, and backpropagating action potentials in the basal dendrites (42, 50). The distribution of I_h channels was constant in the basal dendrites and increased exponentially with distance from the soma in the apical dendrites. Model 3 was based on data from somatosensory cortex of Wistar rats (44). Channel densities were adjusted primarily to account for perisomatic spiking activity, particularly fast action potential repolarization, and large amplitude afterhyperpolarization in the axon initial segment. I_h channels were distributed throughout the dendritic arbor with an exponential increase in density with distance from the soma (48). It also had M-type K⁺ channels distributed uniformly throughout the dendritic arbor. Model 4 was based on data from primary motor cortex (M1) of C57Bl/6J mice, P21 (45). The model was fit based on perisomatic spiking activity and validated by simulating subthreshold somatic resonance. I_h conductance was constant in the basal dendrites, increased exponentially with distance from the soma along the apical trunk until the nexus with apical dendrite tufts, beyond which the I_h conductance plateaued at 0.006 S/cm² (51). Model 5 was based on model 4; they had identical morphologies (41). It was modified to include a TASK-like shunting current whose conductivity was coupled to peak I_h conductivity as described by Migliore and Migliore (41), along with small changes to fast sodium channel conductance, membrane capacitance, and passive conductance (40). These changes preserved the perisomatic firing characteristics of the original model and fit experimental data from PT cells in primary motor cortex while also reproducing additional I_h-dependent phenomena observed experimentally (15, 39, 40, 45). TASK-like channels were distributed in proportion to local HCN channel density. In basal dendrites, TASK-like channel density was equivalent to HCN channel density, whereas TASK-like channel density was 20% of HCN channel density in apical dendrites (40). The reversal potential for the TASK-like channels was set to −86 mV. More detailed information regarding the parameters and properties of the models studied here may be found in their original publications (40, 42–45).

Table 1.

Basic model information

Model	Species	Strain	Region	Age	Max gIh in Dendrites, S/cm2	HCN Distribution
1. Hay et al. (43)	Rat	Wistar	Neocortex	P36	0.015	Constant in basal, exponential with distance in apical
2. Gao et al. (42)	Rat	Sprague-Dawley	Frontal cortex	P21–P28	0.0025	Constant in basal, exponential with distance in apical
3. Kole et al. (44)	Rat	Wistar	Somatosensory cortex	P14–P28	0.09	Exponential with distance throughout dendritic arbor
4. Neymotin et al. (45)	Mouse	C57Bl/6	Primary motor cortex	P21	0.006	Constant in basal, exponential with distance in apical below nexus, constant above the nexus
5. Dura-Bernal et al. (40)	Mouse	C57Bl/6	Primary Motor Cortex	P21	0.006	HCN and TASK-like channels both constant in basal, exponential with distance in apical below nexus, constant above the nexus

Models are specified by either the publication in which they first appeared. Ages are specified by postnatal day (P) age. Under the comments on HCN channel distribution, “exponential with distance” is with respect to the soma. HCN, hyperpolarization-activated cyclic nucleotide-gated; I_h, h-current; TASK, Twik-related acid-sensitive K⁺.

We chose these models because they are biophysically and morphologically detailed; many of them were developed with nonlinear, and particularly dendritic, phenomena in mind (40, 42–45). Some of these models are also used in large scale cortical models (40, 43, 45), so their linear transfer functions are of particular importance to the behavior of the network (8, 40). We chose not to include PT models from the Allen Institute’s Cell Types Database (http://celltypes.brain-map.org/). The “all-active biophysical” models, which contain voltage-gated ion channels in the dendrites, have constant channel densities in the dendrites, which is unrealistic: there is strong experimental evidence for location-dependent gradients in I_h distribution and its importance to dendritic impedance properties (25, 31, 51).

Chirp and Impedance

We generated impedance profiles for each of these models by stimulating each compartment along the apical trunk with a chirp current waveform and measuring changes in V_memb at the soma. We used a linear chip stimulus where current (I_in) is defined as:

$$I_{in}(t)=A\sin \hspace{0.17em}[2\pi (\frac{c}{2}{t}^2+f_{0}t)],$$ (1)

where c = (f₁–f₀)/T, f₀ is the initial frequency, f₁ is the final frequency, and T is the duration of the frequency sweep. A, the stimulus amplitude, was chosen such that excursions in V_memb about V_rest were symmetrical to within 0.01 mV. The instantaneous frequency of I_in(t) increases linearly with time. When computing impedance in the biophysically detailed PT models, we used f₀ = 0.5 Hz, f₁ = 20 Hz, and T = 20 s. It should be noted that commonly used scientific computing software packages like SciPy and MATLAB’s Signal Processing Toolbox include chirp functions that use cosine rather than sine, and a phase shift of −90° must be used to ensure smooth transitions in V_memb when using these functions to generate stimuli appropriate for impedance analysis (52, 53).

Linear chirp stimulation has been as used to compute impedance along the apical trunks of PTs in experimental studies (13, 27). We replicated this chirp stimulation in most of our simulations to maintain consistency with experiments. Impedance may also be estimated using other subthreshold current stimuli, such as nonlinear chirps (quadratic, logarithmic, etc.) and white-noise (54–58). White-noise has the advantages of requiring shorter duration stimulations compute impedance over a larger frequency range (up to the Nyquist rate), but it runs the risk of transient nonlinearities dominating the response, which is not an issue for the chirp stimulus. We use this method for a qualitative comparison of impedance phase across a large frequency range.

We focused specifically on the transfer impedance between the stimulated dendrite and the soma, which was computed as:

$$Z_c=\frac{\mathrm{F}\mathrm{F}\mathrm{T}\left({\mathrm{V}}_{\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{a}}\left(t\right)\right)}{\mathrm{F}\mathrm{F}\mathrm{T}\left(I_{in}\left(t\right)\right)}.$$ (2)

Z_c is a complex valued function, where FFT(I_in) is the Fourier transform of the injected current waveform and FFT(V_m) is the Fourier transform of the change in membrane potential at the soma. From the impedance, we extract the real valued resistance (R) and the imaginary valued reactance (X). From R and X, we compute the transfer impedance amplitude as a function of input frequency:

$$\left|Z_c(f)\right|=\sqrt{R^2+X^2}$$ (3)

Transfer frequency, f_transfer, is defined as the frequency at which |Z_c| between the stimulation site and the soma is maximized (13). In other words, f_transfer is the resonant frequency (f_res) of the transfer impedance. Transfer resonance strength (S_c) is a dimensionless quantity defined as:

$$S_c=\frac{\left|Z_c\left(f_{transfer}\right)\right|}{\left|Z_c(0.5)\right|}.$$ (4)

This quantity has been used in previous publications and referred to as “Q factor” or “Q”, but this measure differs entirely from the generally accepted definition of Q factor used in the context of resonant electrical circuits (59, 60). We therefore simply refer to the quantity in Eq. 4 as resonance strength.

Transfer impedance phase (Φ_c), which quantifies the temporal relationship between I(t) and V_memb at the soma, is defined as:

$${\Phi }_c(f)=arctan\left(\frac{X}{R}\right).$$ (5)

Synchronous frequency between the dendrite and soma is defined as the frequency at which Φ_c = 0 and peaks in I_in(t) and V_soma are synchronized. When Φ_c > 0, the peaks in V_soma precede I(t), which is referred to as leading or inductive phase. Total inductive phase (30) is defined as:

$${\Phi }_L={\displaystyle {\int }_{{\Phi }_c(f)>0}{\Phi }_c}(f)df$$ (6)

—the area of the Φ_c curve above zero. If there is no inductive phase and Φ_c < 0 for all frequencies, we set the synchronous frequency to zero.

Transfer impedance is equivalent to the transfer function used in linear systems theory and assumes the linearity of the system in question. In this case, the system is the neuronal membrane between the stimulation site on the apical trunk and the soma. The biophysically detailed models studied here all produce nonlinearities, such as dendritic spikes, action potentials, and backpropagating action potentials (40, 42–45). At V_rest, however, the neuronal membrane responds as an approximately linear system for small subthreshold depolarizations (under ∼10 mV). Therefore, we have taken care to ensure that measurements used to compute Z_c are within a linear operating regime for the neuronal membrane. This was our motivation for ensuring that excursions in V_memb about V_rest were symmetrical to within 0.01 mV. An asymmetrical voltage response would indicate that the neuron/system was in a nonlinear operating regime. In addition, no dendritic spikes or action potentials were produced during these simulations.

Because the chirp waveform is not stationary (its instantaneous frequency increases over time) and the discrete Fourier transforms used in Eq. 2 to compute impedance assume the signal is stationary, we validated the use of chirp to generate impedance profiles. We compared impedance profiles generated using chirp with impedance profiles generated by stimulating the cell with stationary sinusoidal current waveforms at a single frequency for 5 s, computing the impedance phase and amplitude at that frequency, and repeating for each frequency of interest. We found that impedance amplitudes are nearly identical between the two methods, but there are differences in impedance phase (Supplemental Fig. S1; https://doi.org/10.6084/m9.figshare.14058131). For instance, in one of the biophysically detailed models, impedance phase is practically indistinguishable from 0.5 Hz to 13 Hz using both methods, but phase begins to diverge beyond 13 Hz when using chirp. We also see in the simplified models that the errors in impedance phase increase at higher frequencies. As important impedance phase features such as synchronous frequency and Φ_L occur below 13 Hz in PTs, the chirp waveform is suitable for computing impedance phase. However, we recommend caution if one is using chirp to compute impedance phase at higher frequencies. We also evaluated the use of 20-s long, subthreshold white-noise stimuli, rather than linear chirp, to compute impedance amplitude and phase. We found errors in impedance phase estimation at frequencies greater than 100 Hz, but as we only use this method for a qualitative comparison of impedance phase across a large frequency bandwidth, we consider white-noise acceptable for that purpose. We therefore used a 5-s sinusoid at each frequency (0.5 Hz to 1,000 Hz in 0.5 Hz increments) when computing impedance for the simple models seen in Fig. 1 rather than using chirp or white-noise.

Simulations

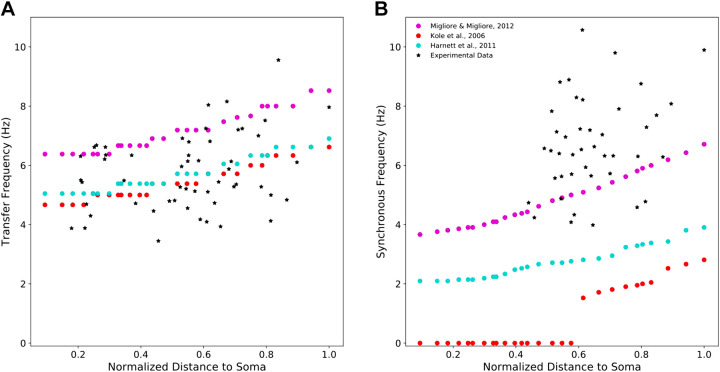
We ran over 4,000 single-cell simulations during the course of this study. For simulating chirp stimulation of the biophysically detailed PT models, 1 s of simulation-time took roughly 40 s of clock-time in NEURON on a Linux system using 2.40 GHz quad-core Intel Xeon CPUs. All simulations used a fixed time step of 0.025 ms. We simulated chirp current stimulation of each compartment along the apical trunks of each PT model and computed the transfer impedance between the stimulated compartment and the soma. By determining the transfer resonance frequencies and synchronous frequencies along the apical trunk, we observed the location dependence of the impedance profiles in these PT cell models. For comparisons between the models and experimental data, transfer frequency and synchronous frequency observations were extracted from published data (13, 27) using WebPlotDigitizer (61) and pooled together. Since each observation was made from a different neuron, and it is not indicated how far each measurement is relative to the apical trunk length, we normalized all position data to the farthest observation from the soma.

All synaptic stimulation simulations were performed using NEURON’s AlphaSynapse with a time constant of 1 ms to mimic a unitary, excitatory α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) synapse (46). Maximal synaptic conductance was chosen to produce an ∼1 mV depolarization in somatic V_memb in each model or condition for all synaptic stimulation simulations.

RESULTS

Impedance Profiles of Model PT Neurons

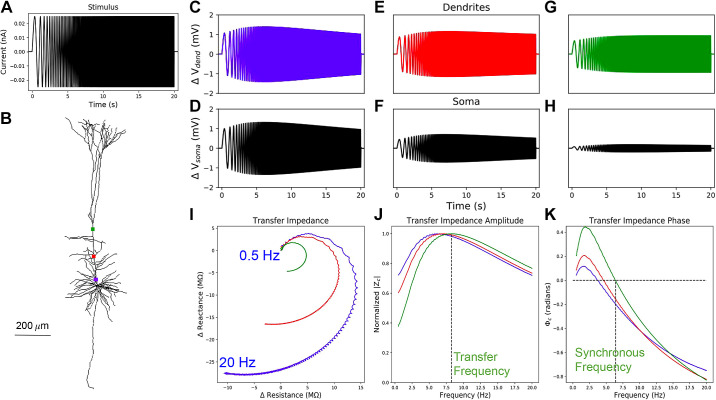
Since location-dependent gradients in resonance and impedance phase were not investigated previously in PT models (57, 62), we explore how both impedance amplitude and phase change with distance from the soma in morphologically and biophysically detailed PT models. We measured the impedance profiles of five biophysically detailed multicompartment models of L5 PTs using a set of simulated 20-s subthreshold chirp-waveform current injections with instantaneous frequency of 0.5–20 Hz (Fig. 2A). We simulated stimulation with a subthreshold chirp-waveform at various locations along the apical trunk (Fig. 2B). Changes in membrane potential in response to chirp stimuli were recorded from the stimulated compartments (Fig. 2, C, E, and G) and at the soma (Fig. 2, D, F, and G). We computed the linear transfer function, or transfer impedance (Z_c), between the dendrite and the soma. Z_c has a real valued component, resistance, and an imaginary valued component, reactance (Fig. 2I). From the resistance and reactance, we computed transfer impedance amplitude and phase profiles via Eqs. 3 and 5, respectively (Fig. 2, J and K). In an example PT model, we see location-dependent changes in the impedance profiles with transfer frequencies, resonance strength, total inductive phase, and synchronous frequencies all increasing along the apical trunk with distance from the soma (Fig. 2, J and K). The peaks and contours of the transfer impedance amplitude and phase profiles shift to the right in frequency with distance from the soma (Fig. 2, J and K).

Figure 2.

Impedance responses in dendrites of model 5. A: constant amplitude, linear chirp, current waveform which is applied to different points along the apical dendrite. B: stimulated locations along the apical trunk: proximal (blue), central (red), and distal (green). We recorded membrane potentials at the stimulated compartments (C, E, and G) and at the soma (D, F, and H). I: Z_c was computed from the changes in the membrane potential at the soma and the current stimulus applied to the dendrites. J: from the transfer impedance amplitude, |Z_c|, we compute the transfer resonance frequency, which is indicated by the vertical dashed line for the most distal recording site. K: from the transfer impedance phase Φ_c, we compute the synchronous frequency, again indicated by a vertical dashed line for the most distal site.

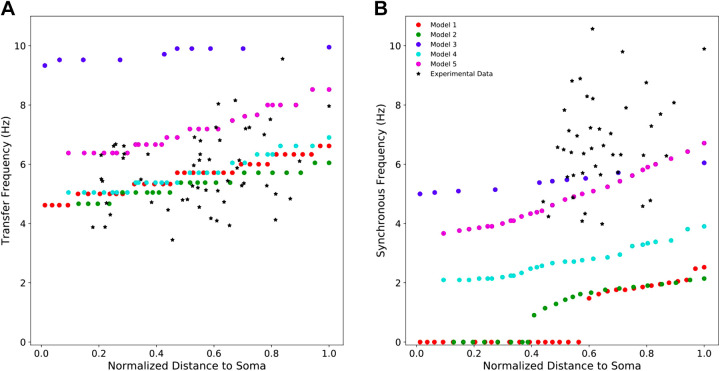
All of the PT cell models exhibit location-dependent impedance profiles with transfer frequencies and synchronous frequencies increasing with distance from the soma (Fig. 3) (13, 27). They varied, however, in how well they replicated the full range of experimental data. Model 3 overestimated the transfer frequency along the apical trunk but exhibited synchronous frequencies within the experimental range. Models 1, 2, and 4 exhibited realistic transfer frequencies along the apical trunk but underestimated the synchronous frequencies. Models 1 and 2 even showed no inductive phase, with Φ_c < 0 at all frequencies (Eq. 5), for large proximal portions of their apical trunks (Fig. 3B). Only model 5 captured both the transfer and synchronous frequencies observed in experiments.

Figure 3.

Resonant frequencies and synchronous frequencies of five PT models compared with experimental data. A: four of the five models show transfer frequencies along the apical trunk within the experimentally observed range. The fifth produced transfer frequencies above this range. Experimental values of transfer frequencies were extracted from Ulrich (27) and Dembrow et al. (13). B: only two models exhibit synchronous frequencies along the apical trunk which are within the experimental range. The other three models produce synchronous frequencies below this range. Experimental values of synchronous frequencies were extracted from Dembrow et al. (13). PT, pyramidal tract neuron.

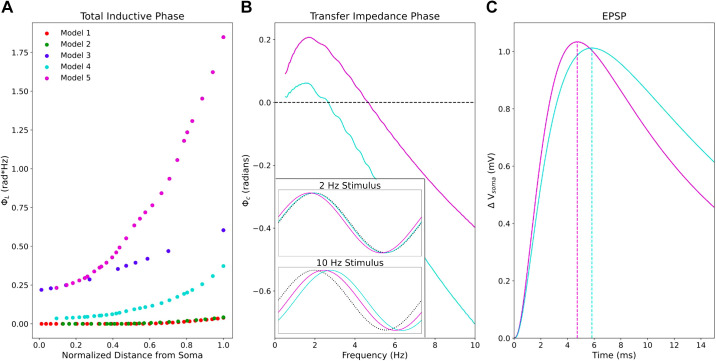
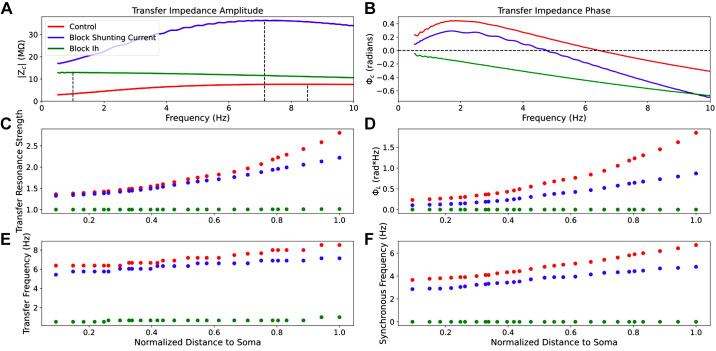
Model 5 produced greater total inductive phase along its apical trunk than any of the other models (Fig. 4). Φ_L (Eq. 6) between the distal end of the apical trunk and the soma was roughly 7 times higher in model 5 with the both HCN and TASK-like channels compared with its earlier incarnation (see methods, Table 1) model 4 (Fig. 4A). As an example, we present transfer impedance phase profiles from the same segment in models 4 and 5, roughly half the length of the apical trunk (136.4 µm) from the soma (Fig. 4B). Peak Φ_c in model 5 is more than double that in model 4, and Φ_c remains higher in model 5 than in model 4 for all frequencies probed. The optimal frequency for leading phase remained around 2 Hz in both models however. In the time domain, this means that V_memb at the soma leads a 2-Hz sinusoidal stimulating current halfway along the apical trunk by roughly 17 ms in model 5, whereas they are practically synchronous in model 4 (Fig. 4B, inset). Although the increased Φ_L is not sufficient to produce phase lead in the EPSP, increased Φ_c partially compensates for the capacitive delay in EPSP arrival time at the soma (Fig. 4C). When synaptic stimulation halfway along the apical trunk produces a 1-mV amplitude EPSP in the soma, peak V_memb occurs roughly 1 ms sooner in model 5 than in model 4. This difference is consistent across a range of EPSP amplitudes (0.5–2 mV, data not shown), and we expect it to remain consistent within the subthreshold range.

Figure 4.

The impedance phase in PT models and its implications for synaptic potentials. A: model 5 exhibits much greater total inductive phase along the apical trunk compared with the other models. B: comparison of two models’ transfer impedance phase profiles from halfway along the apical trunk (136.4 μm from the soma) showing Φ_cis greater in model 5 than in model 4 for all frequencies probed. Inset shows somatic V_memb response to 2 Hz and 10 Hz sinusoidal stimuli in the time domain from both models. At 2 Hz, V_memb leads the stimulating current by roughly 17 ms in model 5, whereas they are nearly synchronous in model 4. At 10 Hz, lag in V_memb is reduced in model 5 compared with model 4. Dotted black lines indicate the stimulating current waveform. C: somatic EPSP in response to synaptic stimulation in both models at the same point along the apical trunk. Peak V_memb occurs more than 1 ms earlier in model 5 than in model 4. EPSP, excitatory post-synaptic potential; PT, pyramidal tract neuron.

I_h, TASK-like Shunting Current, and Dendritic Impedance

A combination of I_h and TASK-like shunting current produced the best approximation of experimentally observed dendritic impedance profiles in PTs (Fig. 5). Model 5 was the only PT model which included a TASK-like shunting current that was coupled to peak I_h conductivity (41). We repeated our simulations on model 5 with different models of the HCN channel that do not include an additional shunting current to determine what produced its biologically realistic impedance profiles. We computed transfer and synchronous frequencies along the apical trunk using models of HCN from Kole et al. (48) and Harnett et al. (51). Although using the other two HCN models reduced the transfer frequencies along the apical trunk, these remained well within the observed range (Fig. 5A). The different models of HCN had dramatic effects on the phase response however. The Harnett et al. (51) model reduced synchronous frequency by roughly one half across the apical trunk. The Kole et al. (48) model produced zero inductive phase along more than half the length of the apical trunk (Fig. 5B).

Figure 5.

A model of HCN including a TASK-like shunting current best approximates experimentally observed impedance profiles. Resulting impedance features when using three different models of HCN channels in the same model neuron. A: compared with the original PT model which uses the HCN and TASK-like channel models from Migliore and Migliore (41), the mechanisms developed by Kole et al. (48) and Harnett et al. (51) reduced transfer frequency along the apical trunk, but the values remain well within the experimental range. B: they led to dramatic reductions in synchronous frequency, however. HCN, hyperpolarization-activated cyclic nucleotide-gated; PT, pyramidal tract neuron; TASK, Twik-related acid-sensitive K⁺.

HCN mediates dendritic resonance and leading-phase response in PTs, but TASK-like shunting current can modulate them (Fig. 6). By simulating the chirp stimulation along the apical trunk of model 5 while blocking either I_h or the TASK-like shunting current across the entire neuron, we observed the independent effects of HCN and TASK-like channels on the impedance profile. Blocking I_h while leaving the shunting current intact increased impedance amplitude across frequencies but eliminated resonance and inductive phase, as expected from experiments (13, 23, 27). Instead, both impedance amplitude and phase fell off with frequency as in a simple, passive parallel RC circuit model. Blocking the shunting current dramatically increased impedance amplitude, more so than blocking I_h, but reduced transfer frequency, resonance strength, synchronous frequency, and impedance phase across frequencies (Fig. 6, A and B). It is noteworthy that blocking the shunting current did not reduce synchronous frequencies along the apical trunk to the level of the other two HCN models from Harnett et al. (51) and Kole et al. (48), but it did reduce them to the low end of the experimental range (Fig. 5). Therefore, the TASK-like shunting current alone does not endow a realistic phase response; the Migliore and Migliore’s model of I_h alone was sufficient for realistic synchronous frequencies. The changes to dendritic impedance caused by blocking I_h and shunting current were consistent along the apical trunk, becoming more pronounced at the distal end of the trunk where HCN and shunting current density were highest (Fig. 6, C–F).

Figure 6.

Selective blockade of I_h and shunting current differentially modulates dendritic impedance. A and B: example transfer impedance amplitude and phase profiles between the distal end of the apical trunk and the soma 288.9 μm away, respectively, under baseline conditions (red) and when either I_h (green) or the shunting current (red) have been blocked. We also observe how resonance strength (C), total inductive phase (D), transfer frequency (E), and synchronous frequency (F) are attenuated along the apical trunk under those same conditions.

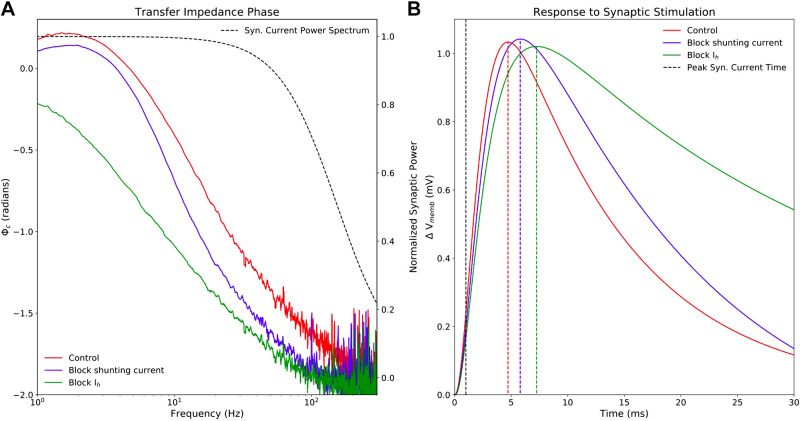
Although the impact of dendritic impedance on neuronal physiology is often linked to oscillatory activity and input-frequency discrimination (20, 25, 29, 31), it is important to emphasize that dendritic impedance, or the linear transfer function between the apical dendrite and the soma, shapes the V_memb response at the soma to a single synaptic stimulation along the apical dendrite. The majority of the power in a single excitatory synaptic current stimulus resides between 0.5 Hz and 100 Hz (Fig. 7A, black dashed lines, right, y-axis), so the transfer impedance amplitude and phase in this frequency range determines the somatic response to synaptic stimulation in the dendrite. Blocking TASK-like channels shifts the transfer impedance phase down across this frequency range, and blocking HCN channels shifts it down further still (Fig. 7A, colored lines, left, y-axis). The downward shifts in transfer impedance phase caused by blocking HCN and TASK-like channels correspond to reductions in the compensation for membrane capacitance, increasing the delay in EPSP peak at the soma. Blocking TASK-like shunting current increases the lag between peak synaptic current halfway along the apical trunk and peak V_memb at the soma by 1 ms. Blocking I_h increases the lag by 2.6 ms. Similarly, blocking these currents reduced resonance strength (Fig. 6C) and the width of the EPSPs were narrowed accordingly. Although the changes to EPSP shape and peak timing were fairly small, they can have a large impact on coincidence detection of synaptic potentials in the soma.

Figure 7.

Selective blockade of I_h and shunting current reduces transfer impedance phase and effects timing and shape of EPSPs. A: model 5 was stimulated with a 20-s long, subthreshold white-noise stimulus roughly halfway along the apical trunk (136.4 μm from the soma), and V_memb was measured at the soma following blockade of HCN (green) and TASK-like channels (blue), as well as under control conditions (red). Transfer impedance phase was reduced by blockade of the shunting current and further reduced by blockade of I_h. The y-axis on the left shows transfer impedance phase. Since the reduction of transfer impedance phase influences the timing of somatic response to synaptic stimulation in the dendrite, the normalized power spectrum of a single AMPA-like excitatory synapse is superimposed (black dashed line), with the y-axis on the right showing normalized synaptic power. The frequencies with the highest synaptic power overlap with the frequency ranges in which the downward transfer impedance phase shifts cause by I_h and shunting current blockade are most prominent. B: model 5 was stimulated with a single excitatory AMPA-like synaptic stimulus at the same location. Maximal synaptic conductance was tuned to produce a ∼1 mV EPSP at the soma, and peak synaptic current occurred at 1 ms (black, vertical dashed line). Maximal EPSP V_memb lagged 3.7 ms behind peak synaptic under control conditions, 4.8 ms after blocking TASK-like shunting current, and 6.3 ms after blocking I_h. EPSPs narrow in accordance with decreasing resonance strength seen in Fig. 6. AMPA, α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid; EPSP, excitatory post-synaptic potential; HCN, hyperpolarization-activated cyclic nucleotide-gated; I_h, h-current; TASK, Twik-related acid-sensitive K⁺.

Degeneracy and the Interplay of I_h and Shunting Current

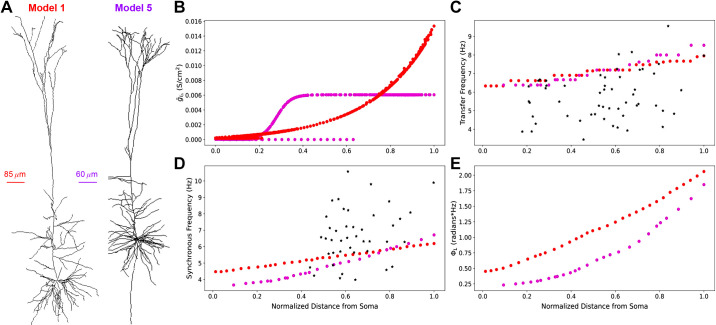
We demonstrated how different distributions of HCN and TASK-like channels can produce realistic impedance profiles (Fig. 8). This is an example of degeneracy, wherein different combinations of elements, parameters, or in this case ion channels can produce the same behavior. We replaced the HCN channel model used in model 1 with the combined HCN and TASK-like channel models described by Migliore and Migliore (41) and used in model 5. Although we preserved the original HCN channel distribution from model 1, this replacement maintained realistic transfer frequencies (Fig. 8C) and produced synchronous frequencies which are in line with experimental observations (Fig. 8D). The location-dependent impedance response in the adjusted model 1 was similar to that of model 5, even though the HCN and TASK-like channel distributions in model 1 was exponentially increasing with distance from the soma across the full length of the apical dendrites, whereas in model 5 their densities were constant in the apical tufts (Fig. 8B). This shows degeneracy of the impedance profile and is consistent with the variability of PTs seen in vivo (13, 27). It also further demonstrates that the Migliore and Migliore (41) implementation of I_h and TASK-like shunting current provides the most biologically plausible sources of inductive phase in neocortical PTs.

Figure 8.

Using a model of HCN channels including a shunting current in model 1 produces realistic impedance amplitude and phase response, comparable with model 5. A: morphologies of model 1 and model 5. B: distribution of g_Ih, which affects both I_h and TASK-like shunting current, in the two models. Distances are normalized to the farthest compartment from the soma in each cell. C: transfer frequencies increase but remain within experimental range as originally. D: synchronous frequencies along the apical trunk are greatly improved compared to the experimental data (red). *Experimental values for transfer and synchronous frequencies. E: total inductive phase between model 5 and the adjusted model 1 are similar. Note that distances in C–E are normalized to the length of each model’s apical trunk. HCN, hyperpolarization-activated cyclic nucleotide-gated; I_h, h-current; TASK, Twik-related acid-sensitive K⁺.

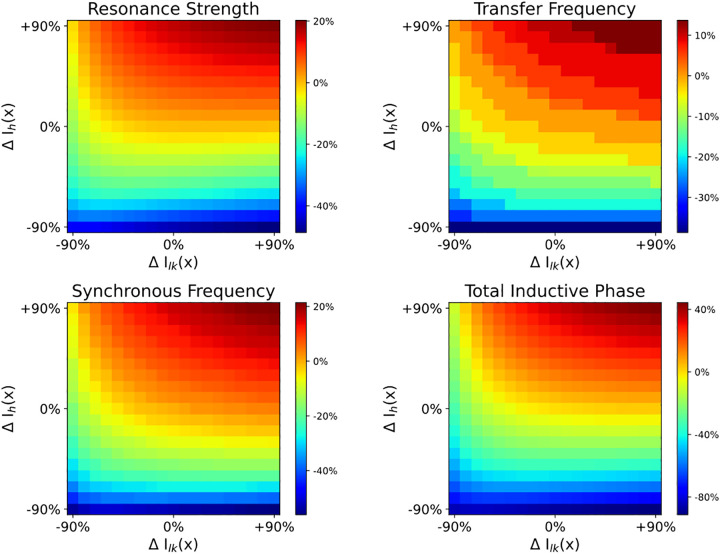
Both I_h and TASK-like shunting current modulated all features of the impedance profile, but they did not contribute to the impedance profile equally (Fig. 9). By varying HCN and/or TASK-like channel density (ΔI_h and ΔI_lk, respectively) by ±90% in increments of 10% uniformly across the dendritic arbor, we explored how different distributions of these channels in model 5 modulated the dendritic impedance profiles. We measured how transfer impedance between the distal end of the apical trunk and the soma was affected by these changes to HCN and TASK-like channel densities (Fig. 9). Changes to HCN channel density had a greater impact on the impedance profile than equivalent changes to TASK-like channel density, but one can compensate for the other. For example, at baseline (ΔI_h = 0%; ΔI_lk = 0%), transfer frequency between the distal dendrite and the soma was 8.26 Hz; transfer resonance strength, 2.65; synchronous frequency, 6.32 Hz; and total inductive phase, 1.60 rad*Hz. By increasing HCN density across the neuron by 60%, transfer frequency increased to 8.97 Hz, resonance strength increased to 2.96, synchronous frequency increased to 7.06 Hz, and total inductive phase increased to 2.01 rad*Hz. These changes may be roughly compensated by also decreasing TASK-like channel density across the neuron by 70%, where transfer frequency was 8.26 Hz; resonance strength, 2.52; synchronous frequency, 6.42 Hz; and total inductive phase, 1.67 rad*Hz. Thus, regions of single color intensity in Fig. 9 represent degenerate combinations of HCN and TASK-like channel densities.

Figure 9.

Combined effects of modulating HCN and TASK-like channel density on dendritic impedance. HCN density (ΔI_h) and/or TASK-like channel density (ΔI_lk) were modulated by ±90% in 10% increments across the entire neuron, which altered resonance strength (A), transfer frequency (B), synchronous frequency (C), and total inductive phase (D). Parameters are presented in percent change from baseline. HCN, hyperpolarization-activated cyclic nucleotide-gated; I_h, h-current; TASK, Twik-related acid-sensitive K⁺.

DISCUSSION

Dendritic Conductances and Impedance Profiles

While none of the models studied were explicitly designed to exhibit realistic dendritic impedance, only model 5 accurately captured features from both impedance amplitude and phase profiles. The combination of I_h with a TASK-like shunting current, which mediated the realistic dendritic impedance we have seen, was intended to account for the paradoxical change from the excitatory to inhibitory effect of I_h in response to increasingly strong synaptic inputs (39–41). The parameters of the shunting current were tuned to reproduce this result while maintaining an F-I curve consistent with experimental observations (40, 45). Importantly, model 5 did not reproduce biologically realistic phase response after eliminating the TASK-like channels and replacing the HCN model with those developed by Kole et al. (48) and Harnett et al. (51) (Fig. 5). With the other HCN channel models, model 5 still maintained the experimentally observed F-I curve, but did not reproduce the paradoxical change from the excitatory to inhibitory effect of I_h in response to increasingly strong synaptic inputs (45, 48, 51). This suggests the model combining I_h and the TASK-like shunting current developed by Migliore and Migliore (41) provides the best approximation of the currents mediating the location-dependent impedance profiles of PT cells.

It is also noteworthy that a combination of dendritic I_h and TASK-like shunting current undermined the hypothesis that the aforementioned paradoxical effect of I_h is mediated by M-type K⁺ channel currents (39). Recent work has demonstrated the effects of M-type K⁺ channels on dendritic impedance in the lobula giant movement detector neurons in grasshoppers (36). We do not, however, expect M-type K⁺ channels to have a significant impact on dendritic impedance in neocortical PTs. Although the distribution of M-type K⁺ channels in neocortical PTs is poorly understood, they are rare in the dendrites of CA1 PCs (63). The only model studied here that included M-type K⁺ channels throughout the dendrites was model 3, which produced reasonable synchronous frequencies but overestimated dendritic transfer frequencies. This can be attributed to model 3’s high HCN channel density, by far the highest of the five studied here (Table 1).

Model 5 provides some insights into the dendritic impedance phase profile of PTs, with total inductive phase increasing by more than 150% along the length of its apical trunk, a far greater increase than seen in the other models (Fig. 4). Similar results were obtained in model 1 after it was adjusted to include TASK-like channels. Though previous experimental studies have not described increases in total inductive phase with distance along the apical trunk in PTs, the relationships seen in models 1 and 5 were comparable with those seen in CA1 PCs (30). Leading or inductive phase is driven by the balance of membrane capacitance and phenomenological inductance and is therefore sensitive to the distribution of dendritic conductances (18, 19, 25, 27, 30, 31, 54, 64–66). Our results support the notion that inductive phase, mediated by I_h and modulated by a TASK-like shunting current, provides a mechanism for compensating the location-dependent capacitive delay of dendritic inputs. This has been hypothesized as ensuring that simultaneous synaptic inputs distributed across the dendritic arbor are coincident at the soma (31). Here we see that HCN channels and TASK-like shunting current, by contributing to inductive phase, both help to reduce the capacitive delay in the arrival of synaptic inputs to the soma (Fig. 7). Some have also suggested that inductive phase provides a mechanism by which subthreshold neuronal membrane oscillations might maintain phase relationships with ongoing local field potentials (25, 30, 31). Although the precise physiological role of inductive phase remains an open question, we believe a model with realistic dendritic phase response is more likely to have realistic distributions of dendritic ion-channels.

The resonance mediated by I_h in PTs qualitatively differs from resonance mediated by K⁺ currents seen in trigeminal root ganglion neurons from guinea pigs or photoreceptors in blowflies (26, 67). Resonant frequencies of the input impedance amplitude profile at the soma in those cells range from 10 Hz to 200 Hz, whereas resonant frequencies in PTs are in the range of 3–10 Hz (13, 20, 27). Furthermore, both location-dependence and impedance phase remain largely unexplored in neurons with K⁺-mediated resonance.

Dendritic impedance profiles are not static. Previous work has demonstrated that subthreshold resonance can be dynamically tuned by ongoing activity (25, 30, 64, 68–72). For instance, long-term potentiation induces changes in the impedance profile of hippocampal PCs (69). Dynamic changes to impedance profiles may have a role in pathophysiology. For example, there is evidence for upregulation of HCN channel expression following epileptic seizure (73–75). And although HCN channels are necessary for resonance in PTs, the dendritic impedance profile can be significantly altered upon modulation of other local conductances or morphological changes to the dendritic tree (23, 62, 65, 70, 76–79). A number of studies have explored the possibility of modulating the dendritic impedance profile by manipulating other channels such as A- and M-type K⁺ channels or Ca²⁺ channel “hot-zones” (36, 62, 78); however, the possibility of modulating dendritic impedance via TASK-like shunting current has not previously been investigated. Our observations of changes to the impedance features through changes to HCN and TASK-like channel density suggest a paradigm by which degeneracy and tunability of the impedance profile may arise (Fig. 9). For instance, changes to the impedance profile caused by changes in I_h, either through changes in HCN channel expression or noradrenergic modulation (37), may be compensated for by appropriate adjustments to the TASK-like channel density, and vice versa . It is important to note, though, that changes to TASK-like shunting current cannot compensate for the complete absence of HCN channels in PTs, but can only modulate the impedance profile in its presence.

Experimentally Verifiable Predictions

1. Model 5 was the only unaltered model to reproduce experimentally observed transfer frequencies and synchronous frequencies, and it also exhibited much larger total inductive phase (Fig. 4A). Therefore, we expect this to be the case in real PTs as well. For instance, 2 Hz was the optimal leading phase between the soma and the center of the apical trunk 136.4-µm away (Fig. 4B). That 0.2 radian lead translates to a roughly 17 ms lead in peaks in somatic V_memb response compared with peaks in the current stimulus. Although there is no doubt variability in PT dendritic impedance profiles, we expect a-17 ms lead is reasonable and probably at the lower end of the possible range.

2. If the shunting current is indeed produced by TASK channels, dendritic impedance should be reversibly alterable by changes to extracellular acidity, as TASK channels are pH sensitive (80).

3. The paradoxical effects of I_h observed by George et al. (39) were abolished with application of the drug XE991. These effects are best accounted for by interaction between I_h and a TASK-like shunting current, and simulation results have suggested that XE991 may block TASK channels (40, 41), though XE991 modulation of TASK channels has not been tested experimentally. XE991 is commonly used as an M-current blocker, and it has been shown to alter the input impedance amplitude profile in the soma of hippocampal PCs at depolarized, but not resting, potentials (81). It may be that XE991 blocks M-current in the soma and blocks the shunting current in the apical dendrites. Similarly, muscarine has been shown to alter K⁺-current in the soma but not in the apical dendrites of PTs (82). Therefore, based on our simulations, we predict that bath application of XE991 to PT cells will produce comparable changes to the dendritic impedance profile as those observed when blocking the shunting current in Fig. 6.

4. We also expect blocking the shunting current to produce an increased lag between peak synaptic current in the apical dendrites and peak somatic V_memb, and blocking I_h should produce an even greater lag (Fig. 7).

Limitations and Future Directions

A major limitation of this study is a limitation of most biophysically detailed models of neurons: the distribution of conductances and passive properties are assumed to be either constant or vary smoothly along the neuronal topography, and this is often not the case (50, 83, 84). Each of these properties can influence the dendritic impedance profile. For instance, hot zones of Ca²⁺ channels have been shown to have an impact on dendritic impedance, but the precise parameters defining these hot-zones differed among the models presented here (40, 43, 45, 62). Differences in the distribution of parameters illustrate the degeneracy of dendritic impedance, however. Both model 5 and the adjusted version of model 1, which includes the TASK-like shunting current, similarly captured the features of the impedance profile observed along the apical trunk (Fig. 8). Vaidya and Johnston (31) demonstrated that realistic transfer resonance frequencies and synchronous frequencies in hippocampal PCs were best achieved with HCN channel density increasing linearly with distance from the soma or distributed following a sigmoid function. Similarly, we found realistic transfer and synchronous frequencies when HCN and TASK-like channel distributions were sigmoidal, as in model 5, but also when the distributions were exponentially increasing with distance from the soma, as in model 1 (Fig. 8). The shape of the sigmoidal distribution can also be varied. Since we chose a sigmoid distribution with a maximal spatial derivative at the midpoint from soma to the nexus of the apical tuft, the shape was dependent on apical trunk length (40, 45, 51). In addition, experimental evidence has shown that dendritic arborization, apical trunk length, and electrophysiological properties of PTs are closely correlated with neocortical thickness and anatomical location, forming rostral-caudal gradients (85). Factors such as dendritic arborization and intracellular resistivity will influence the properties of dendritic impedance, such as resonance, synchrony, and location dependence. It is possible these impedance properties also fall along the same gradients, but we mainly limited ourselves to studying changes related to I_h and TASK-like shunting current.

Two PT models, with different morphologies, apical trunk lengths, passive properties, intracellular resistivities, and voltage-gated ion channel distributions, produced similar dendritic location-dependent impedance properties, and example of parameter degeneracy (86–88). Impedance analysis of the apical trunk could not, however, provide any indication as to whether either exponential or sigmoidal channel distribution scheme is more likely to predominate in PT neurons. Another possibility, not looked at here, is punctate hot spots (89). In fact, differences in channel distribution, dendritic arborization, and intracellular resistivity may be strong contributors to the experimentally observed variance among PTs in impedance properties (13, 27). Systematic investigation of how these parameters contribute to dendritic impedance in PTs is an avenue for future work.

Our explorations modulating dendritic impedance profiles through I_h and TASK-like shunting current was also limited. We observed how uniform changes to HCN and TASK-like channel densities across the entire dendritic arbor produce different impedance profiles (Figs. 6 and 9). This would be analogous to cell-wide changes in channel expression, bath application of agonists or antagonists, or possibly changes to extracellular pH. We did not explore how localized changes to HCN and TASK-like channel activity may affect the impedance profile. For instance, stimulation of postsynaptic alpha2A adrenoceptors has been shown to inhibit HCN channel activity (90). This is not to mention the influences of passive membrane properties, other active channels, or morphology on dendritic impedance (25, 77, 91). Although we showed how HCN channels and TASK-like channels may affect the impedance profile, determining how they interact with these other cell properties to modulate dendritic impedance profiles is a goal for future studies.

Although we have focused on dendritic impedance in neocortical PTs from rodents, how these results relate to PTs in humans remains unclear. Recent studies have shown interesting differences between PTs in humans and rodents regarding I_h-mediated phenomena such as subthreshold resonance and sag potentials in the soma (92, 93). Some of these results may be attributed to differing expression of HCN subtypes between species (93). The I_h-dependent physiological differences between rodents and humans are based on measurements from the soma, so how these results may extend to the dendrites is still an open question (92, 93). Furthermore, the majority of data on resonance from human PTs come from patients with epilepsy, which is associated with pathological effects on HCN channels (73–75). To better understand the relationship between the results presented here and dendritic impedance in human PTs, we need a better picture of the distribution of HCN and TASK-like channels in their dendrites and how they are affected in epilepsy. Considering the relative scarcity of human data compared with rodent data, and the difficulty of performing the experiments necessary for obtaining this information, computational modeling will be indispensable in bridging the gap between species.

GRANTS

This work was supported by National Institutes of Health (NIH) Grants R01EB022903, U01EB017695, and R01MH086638; National Science Foundation (NSF) Grant Internet2 E-CAS 1904444; NYS DOH01-C32250GG-3450000; National Institute on Deafness and Other Communication Disorders (NIDCD) Grant R01DC012947-06A1; and Army Research Office Grant W911NF-19-1-0402.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

C.K., S.D.-B., S.A.N., S.D.A., N.T.C., M.M., and W.W.L. conceived and designed research; C.K. performed experiments; C.K. analyzed data; C.K., S.D.-B., S.A.N., S.D.A., N.T.C., M.M., and W.W.L. interpreted results of experiments; C.K. and S.D.A. prepared figures; C.K. drafted manuscript; C.K., S.D.-B., S.A.N., S.D.A., N.T.C., M.M., and W.W.L. edited and revised manuscript; C.K., S.D.-B., S.A.N., S.D.A., N.C., M.M., and W.W.L. approved final version of manuscript.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at https://github.com/suny-downstate-medical-center/L5PYR_Resonance or https://senselab.med.yale.edu/modeldb/ShowModel?model=266851#tabs-1. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.