Efference copy in kinesthetic perception: a copy of what is it?

Abstract

A number of notions in the fields of motor control and kinesthetic perception have been used without clear definitions. In this review, we consider definitions for efference copy, percept, and sense of effort based on recent studies within the physical approach, which assumes that the neural control of movement is based on principles of parametric control and involves defining time-varying profiles of spatial referent coordinates for the effectors. The apparent redundancy in both motor and perceptual processes is reconsidered based on the principle of abundance. Abundance of efferent and afferent signals is viewed as the means of stabilizing both salient action characteristics and salient percepts formalized as stable manifolds in high-dimensional spaces of relevant elemental variables. This theoretical scheme has led recently to a number of novel predictions and findings. These include, in particular, lower accuracy in perception of variables produced by elements involved in a multielement task compared with the same elements in single-element tasks, dissociation between motor and perceptual effects of muscle coactivation, force illusions induced by muscle vibration, and errors in perception of unintentional drifts in performance. Taken together, these results suggest that participation of efferent signals in perception frequently involves distorted copies of actual neural commands, particularly those to antagonist muscles. Sense of effort is associated with such distorted efferent signals. Distortions in efference copy happen spontaneously and can also be caused by changes in sensory signals, e.g., those produced by muscle vibration.

INTRODUCTION: THE CLASSICAL NOTION OF “EFFERENCE COPY”

It has been well established that perception of various modalities depends on the ongoing action-related, efferent process (reviewed in 1–3). Arguably, the first scientist who paid attention to effects of action on perception was von Helmholtz. He noticed that natural motion of an eye (assume that the other eye is closed) leads to veridical perception of eye motion in the motionless environment. In contrast, if eye position is displaced in an unusual way, e.g., by pressing on the eyeball with a finger, one has an illusory percept that the environment moves. An important step was made in the middle of the XX-th century by von Holst and Mittelstaedt (4) and by Sperry (5) who introduced the notion of a copy of the ongoing efferent process used for perception: efference copy (EC), or efferent copy, or corollary discharge. Despite literally hundreds of papers addressing and exploring these notions, the question posed in the title of this review remains without a clear answer. To search for an answer to this question, “efferent process” and “perception” have to be defined explicitly.

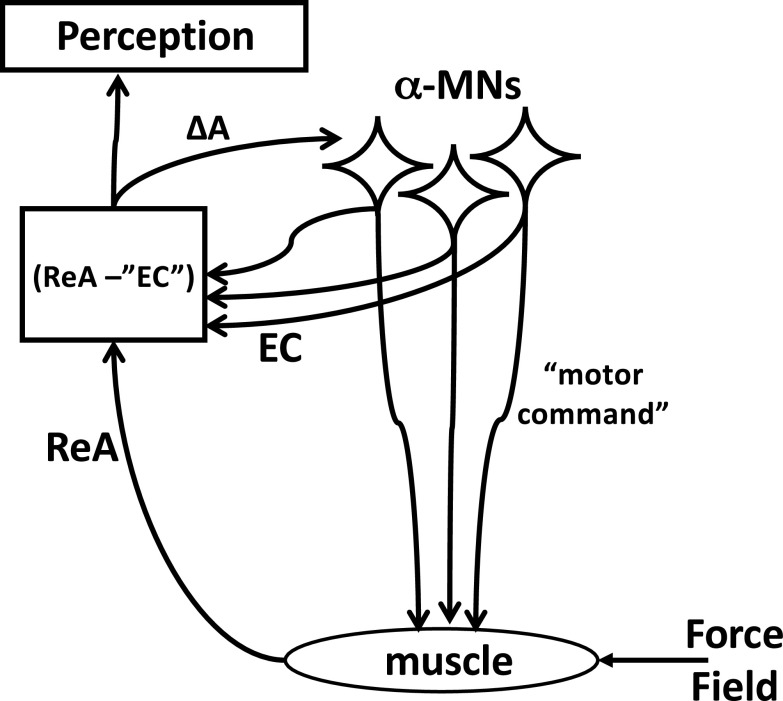
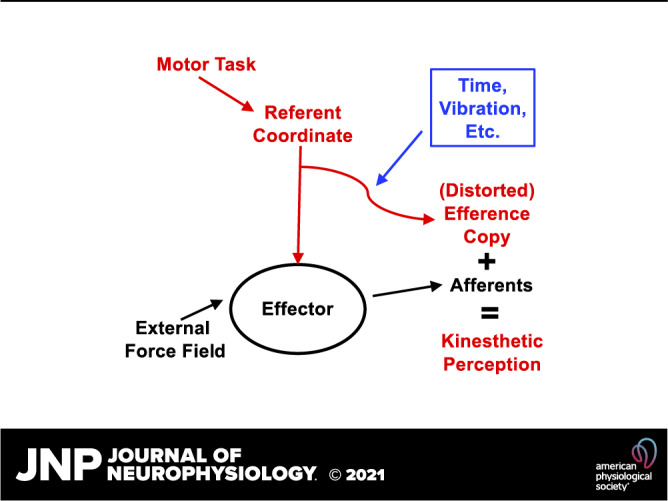
In their original paper, von Holst and Mittelstaedt associated EC with a copy of the signals from alpha-motoneuronal pools (Fig. 1), which were assumed to participate in both perception and correction of the ongoing action in cases of movement errors. In their scheme, a copy of the signals from alpha-motoneurons was used to predict changes in sensory signals from proprioceptors expected from the planned action (so-called, reafference). The quotation marks in “EC” in Fig. 1 emphasize that these signals are somehow transformed into units that make them comparable with signals from proprioceptors. If the prediction was accurate, no correction was issued. If, however, the prediction happened to be wrong, an error signal was sent to the alpha-motoneurons leading to correction of the action. If movement was produced by an external force acting on the effector, changes in proprioceptors were addressed as exafference. They always led to reflex-based corrections. Exafference always affected perception of relevant variables, whereas reafference affected perception only if it differed from the prediction based on EC.

Figure 1.

The classical scheme of the efference copy (EC) as a copy of the output of the alpha-motoneuronal pool. EC is used to predict changes in sensory signals from proprioceptors expected from the planned action (ReA, reafference); this process involves conversion of EC into “EC” expressed in units commensurate with those encoded by afferent signals. If the prediction is wrong, an error signal (ΔA) is sent to the alpha-motoneurons leading to correction of the action. Reafference affects perception only if it differs from the prediction based on EC. MNs, motoneurons.

The scheme in Fig. 1 has been criticized recently by Feldman (6, 7) because of its inability to explain how animals can relax after moving an effector to a different position. Indeed, if the muscles in both positions are relaxed, the output of all alpha-motoneurons is zero, and EC is also zero. Position-sensitive sensory endings, including those in muscle spindles, are expected to show a change in their firing frequency, which cannot be predicted based on the unchanged EC. Hence, this change in afferent signals has to lead to reflex-mediated changes in muscle activation and produce motion of the effector in clear contradiction to the everyday experience that humans can relax muscles at various positions. So, we can conclude that EC is not a copy of the output of alpha-motoneuronal pools.

More recent studies have associated EC with signals in a variety of pathways and structures within the central nervous system associated with movement production. Most commonly the invoked structures have included the cortex of the large hemispheres (8, 9) including the system of mirror neurons (10), the cerebellum (9, 11, 12), the basal ganglia (13, 14), and associated subcortical loops (15). EC has been discussed in relation to motor imagery (16) and to unusual motor and perceptual phenomena, such as the Kohnstamm phenomenon interpreted as motion without EC (17). A number of studies have suggested that EC dysfunctions are responsible for motor, perceptual, and cognitive disorders in a variety of patients including those with schizophrenia (18–20), hallucinations and delusions (21), and vestibular disorders (22).

The notion of EC has been applied to analysis of movements and perceptual processes across species, from insects (23, 24) to Xenopus laevis tadpoles (25), fish (26), horses (27), rodents (28), and monkeys (29). Given the broad spectrum of the mentioned species, EC is likely to be a widespread phenomenon, not tied to any specific anatomic structure or neural loop. The spectrum of explored behaviors and perceptual modalities has also been very broad and included, in particular, whisking in rodents (28), visual perception (1, 29), effects of reaching/grasping (30) and of locomotion (27) on visual perception, sense of direction (31), etc.

Nearly all the mentioned studies have assumed that neural structures within the animal’s body perform computational operations with neural signals, including EC (also see 32), predicting both action mechanics and its sensory consequences. This assumption is far from being trivial, in particular, because it is not based on any known laws of nature. This seems to be proper time to quote a sarcastic statement by Erwin Schrödinger (33): “If you suspend laws of nature in the human body, you can explain anything.” Nikolai Bernstein (34, 35) emphasized that the brain could not in principle predict mechanical consequences of neural efferent signals it generated because of the unpredictable external forces and mechanical coupling among body segments leading to propagation of deviations in mechanical variables. This statement also means that the brain cannot predict sensory consequences of efferent signals, in particular signals from proprioceptors sensitive to mechanical variables such as forces and displacements. This conclusion is not shared by many researchers in our days, in particular those who use models of control and perception based on the concept of internal model. In the next section, we describe briefly this approach and the role of EC in the corresponding schemes.

INTERNAL MODELS AND EFFERENCE COPY

The concept of internal model has been developed over the past years with respect to various biological problems based on the impressive progress in control theory and engineering (reviewed in 36, 37). Its introduction in the fields of motor control and kinesthetic perception was motivated, in particular, by the numerous problems of motor redundancy, complex interactions of the moving body with the external force field, and unavoidable conduction time delays. Internal models are hypothetical neural structures performing computations, which emulate interactions among body parts [including the central nervous system (CNS)] and between the body and the environment. The purpose of these hypothetical neural mechanisms is to produce behavior consistent with model-based control. Direct internal models are sometimes addressed as predictors. They attempt to predict future states of the body based on the available sensory information and ongoing efferent processes. Inverse internal models precompute neural signals required to produce desired motor effects. These concepts have been used broadly, in particular, in discussions of effects of motor learning and adaptation to various changes in the external force field and sensory signals (38, 39, 40, reviewed in 41, 42).

EC has been viewed as an important contributor to direct internal models, which allows them to predict future body states taking into account the recent and current efferent signals, which are expected to contribute to changes in the state of the target effectors (reviewed in 11, 12, 43). A number of brain circuits associated with the efferent process have been implicated as possible contributors to neural predictors. In particular, cortical structures have been discussed as likely predictors, including the supplementary motor area (44), posterior parietal cortex (45, 46), and areas involved in the generation of speech (47, 48).

A large number of studies invoked the cerebellum as one of the likely sites where internal models are formed and predictions are made (reviewed in 42, 49–51). Some of those studies consider circuits limited to the cerebellum and its nuclei (13, 52, 53). Other circuits discussed as contributors to cerebellar internal models have included the cortico-cerebellar loop (9, 54) via the basilar pontine nuclei (55), brainstem structures such as the lateral reticular nucleus involved in the efferent process (56, 57) targeting cervical and limb musculature, nuclei involved in oculomotor control (58, 59), the magnocellular red nucleus (60) involved in the control of limb and facial muscles, afferents from otoliths and semicircular canals (61), and the spinocerebellar tracts reporting activity of spinal motoneurons (62, 63). It is possible that a number of such circuits act in parallel (15, 43).

Internal models have also been invoked in analysis of reflex-like reactions to mechanical perturbations applied to effectors (64, 65). A perturbation to an effector produces a sequence of responses at different delays, from short-latency responses (emerging in different muscles at the latency of 20–35 ms, M1) with likely contributions of monosynaptic Ia projections on alpha-motoneurons, to medium-latency (∼40–50 ms, M2) and long-latency (∼60–90 ms, M3) responses likely mediated by various brain structures including the cortex (66–68). Longer-latency reactions show instruction-specific patterns (69–72), suggesting that the involved circuitry, possibly involving propriospinal connections (56), may also be assigned properties of internal models. Moreover, internal models have been invoked in studies of behavior of a variety of animals, including insects (reviewed in 24), suggesting that qualitatively different neural circuits can form the basis of internal models.

PHYSICAL APPROACH TO BIOLOGICAL MOVEMENT: CONTROL WITH REFERENT COORDINATES

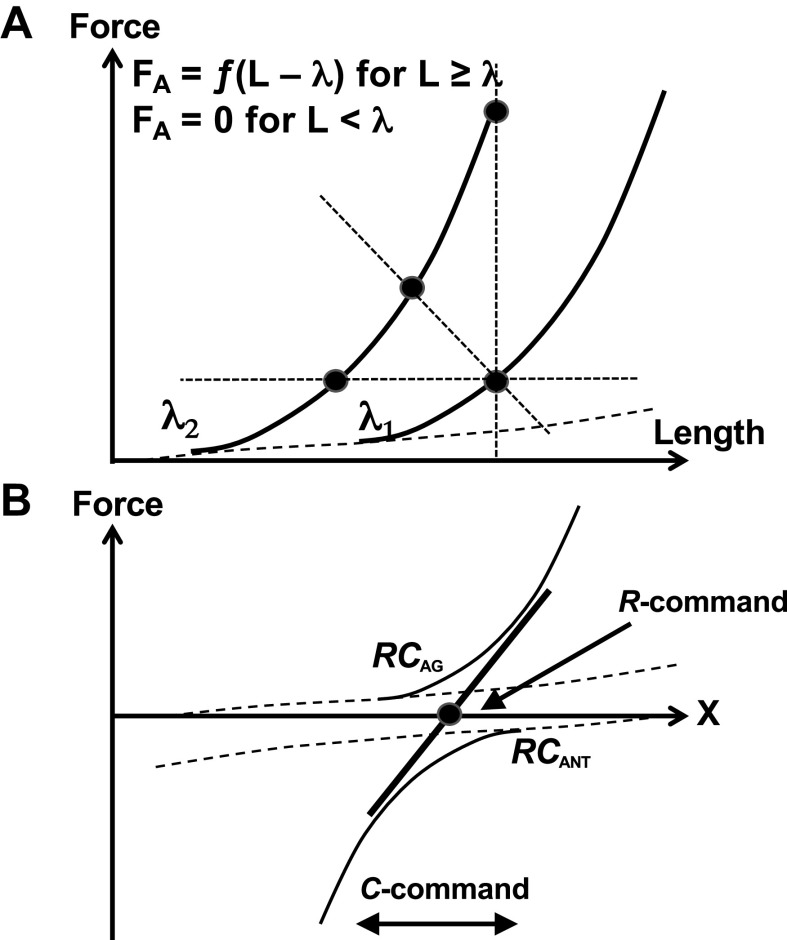
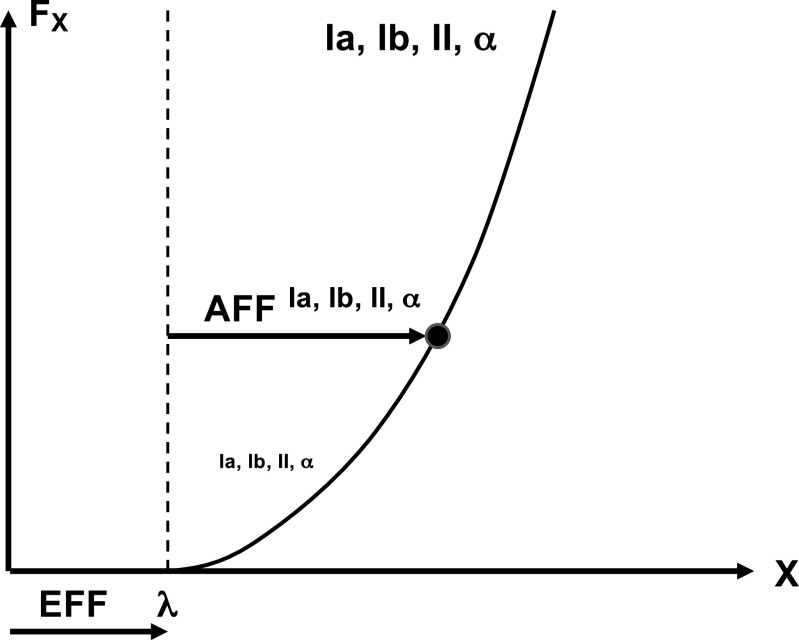
In the subjective opinion of the author, to bring the notion of EC into the field of natural science, it has to be defined exactly within a theory on the neural control of movement that spells out the physical meaning of efferent processes, not only the involved neural circuitry. This approach is based on the assumption that studies in the fields of the neural control of movement and perception have, as their main goal, discovery of relevant laws of nature and specific ways these laws are implemented in biological systems. We are going to address this approach as the physical approach to neural processes (reviewed in 73–75). A major theory within this approach has developed, based on the equilibrium-point hypothesis (76, 77), into a theory of control with parameters representing spatial referent coordinates, RC, for moving effectors (reviewed in 75, 78, 79). According to this approach, the neural control of a single muscle can be adequately described as setting a time course of the threshold of its stretch reflex, λ (RC for the muscle). Using the physical language, λ is a parameter within a law of nature common for all skeletal muscles, which defines the dependence of active muscle force on muscle length (see the equation in Fig. 2A; the functional form of the function ƒ does not matter). A value of λ defines the spatial range where the muscle is active and produces length-dependent active force (Fig. 2A); λ has been associated with a specific physiological variable, namely, subthreshold depolarization of the membranes of alpha-motoneurons within the corresponding pool (reviewed in 78).

Figure 2.

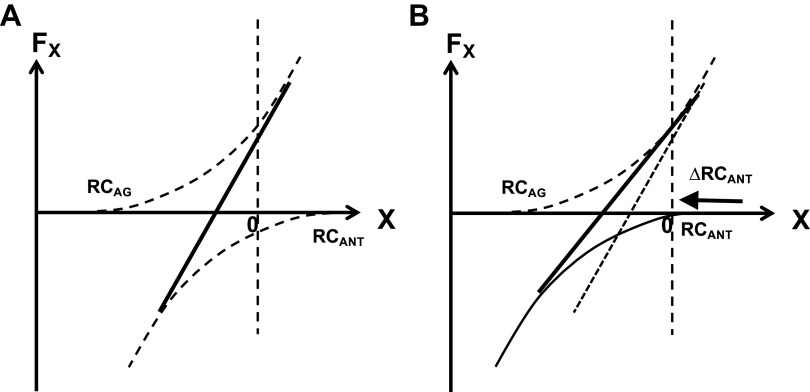
A: the force-length characteristics for a relaxed muscle (dashed curve) and activated muscle (thick, solid curves). Active muscle force (F_A) can be expressed as a function ƒ of the difference between L and λ. A value of λ defines the spatial range where the muscle is active and produces length-dependent active force. A shift of λ (from λ₁ to λ₂) can produce movement, muscle force change, or both depending on the external load (shown with dotted, thin lines). B: the force-coordinate, F(X) characteristics for the agonist muscles (positive force magnitudes) and antagonist muscles (negative force magnitudes). Effector behavior is defined by the algebraic sum of the two muscle characteristics (the thick, slanted line). Its control can be described with referent coordinates to the opposing muscle groups, RC_AG and RC_ANT or, equivalently, by the reciprocal command (R-command, filled circle) and the coactivation command (C-command). The R-command leads to parallel changes in RC_AG and RC_ANT leading to translation of the effector characteristic and in its intercept. The C-command (the distance between RC_AG and RC_ANT) leads to counter-directional changes in RC_AG and RC_ANT leading to rotation of the effector characteristic and in its slope. RC, referent coordinates.

In this review, we do not consider the alpha-model introduced on the basis of experiments on deafferented monkeys (80, 81). The central idea of the alpha-model is to convert the seemingly intractable movement control problem, based on inverse dynamics, into a more tractable problem of posture control using, as control variables, levels of activation of alpha-motoneuronal pools controlling the involved muscles.

Note that shifting λ does not prescribe changes in any of the performance variables produced by the muscle: Muscle length, force, and level of activation change differently depending on the external load characteristic. As illustrated in Fig. 2A, the same shift of λ can produce movement, muscle force change, or both depending on the external load. Muscle activation level increases with deviation from λ along the force-length curve and is different for the three loads illustrated in Fig. 2A.

For an arbitrary effector—from a joint to a digit, to a limb, and to the whole body—moving along a spatial coordinate X, all relevant muscles can be classified into agonists—those that contribute to motion along X in the desired direction, and antagonists—those that oppose this motion. To simplify the analysis, assume that the neural control of this one-dimensional movement can be described with two variables, referent coordinates for these two muscle groups, RC_AG and RC_ANT. Figure 2B illustrates the force-coordinate, F(X) characteristics for the agonist muscles (they produce positive force magnitudes) and antagonist muscles (they produce negative force magnitudes). Effector behavior is defined by the algebraic sum of the two muscle characteristics (the solid, slanted line in Fig. 2B), and its control can be described with two variables, the reciprocal command (R-command), which defines the coordinate where the resultant force of all the muscles is zero (RC for the effector, filled circle in Fig. 2B), and the coactivation command (C-command) reflecting the spatial range where both agonist and antagonist muscles are active (82). For a system controlled by two symmetrical muscle groups, RC of the effector corresponds to the midpoint between RC_AG and RC_ANT, and the range between RC_AG and RC_ANT defines the slope of the effector characteristic, its apparent stiffness, k (cf. 83).

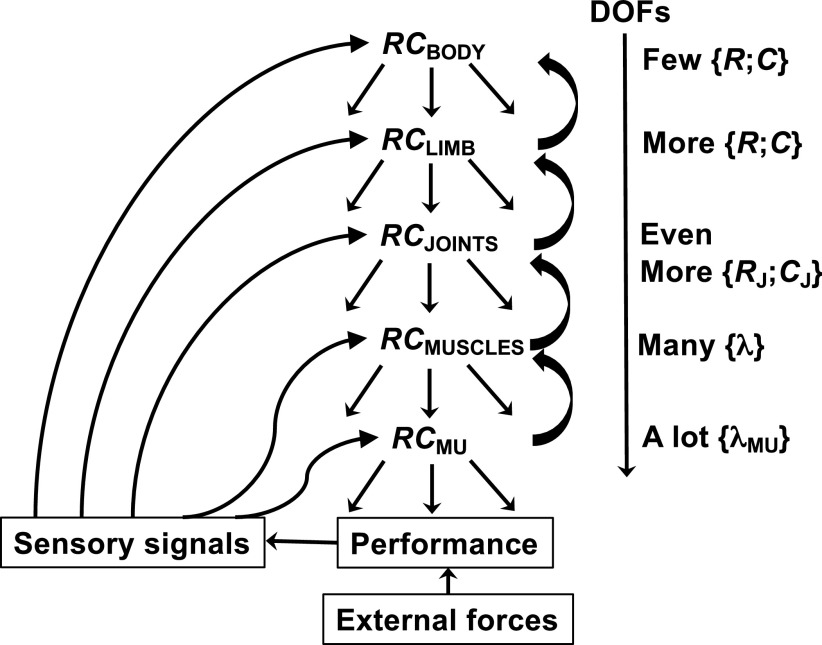
The notions of R- and C-commands can be used for analysis of movements along each coordinate at various levels. For example, the control of fingertip motion during a pointing movement in the three-dimensional space can be described with time functions of three-dimensional vectors R and C. Given the actual body anatomy, these task-level control variables have to be transformed into joint-level variables, R_J and C_J, which in turn have be to transformed into commands to individual muscles, λ(t). A scheme of such hierarchical control is illustrated in Fig. 3. Note that the number of variables manipulated at different levels increases from the relatively low-dimensional task level to the high-dimensional levels of muscle and motor unit involvement. For example, holding an object in the hand with prismatic grasp has been associated with defining referent aperture between the thumb and opposing fingers (84, 85), which is analogous to the one-dimensional R-command at the task level (with a possibility of modifying the C-command). These commands are mapped on the R- and C-commands to the opposing digits, the thumb and “virtual finger” (an imagined digit with the mechanical output equivalent to that of the four actual fingers, 86). Further, the command to the virtual finger is transformed into R- and C-commands to individual fingers (reviewed in 87), and those are mapped on a high-dimensional set of λs to individual muscles. In particular, the well-documented phenomenon of grip force adjustments to self-generated load changes (as during manipulation of the handheld object, 88–91) is interpreted as a change in the referent aperture based on earlier experience with load manipulation (84).

Figure 3.

Body movement in the three-dimensional space can be described by time functions of three-dimensional vectors R and C. Given the actual body anatomy, these task-level control variables have to be transformed into limb-level, joint-level, muscle-level, and motor unit (MU)-level variables. The number of degrees-of-freedom (DOFs) increases as a result of these transformations. Back-coupling loops within the CNS and from peripheral receptors ensure stability of performance. CNS, central nervous system; RC, referent coordinates.

The EP-hypothesis and its recent developments are not accepted by a number of researchers in the field. This hypothesis has been on multiple occasions declared false based on both theoretical considerations and experimental findings (36, 92–95). Although these criticisms have been addressed in many previous publications (75, 78, 96–99), let me discuss them one more time and emphasize a number of crucial points and typical misunderstandings of the EP-hypothesis leading to such claims.

Arguably, the main feature of the EP-hypothesis is that it is based on the idea of parametric control, i.e., on control with specification of time changes of parameters (RC, equivalent to λ for a single muscle) in relevant laws of nature. In the inanimate world, including the world of man-made devices (e.g., robots), movements are produced by specifying time profiles of forces and torques. According to the concept of parametric control, movements are produced by changing salient parameters, and mechanical variables (including forces) change as a consequence of these parameter changes and interaction of the effector with the external force field.

One of the common misinterpretations of the EP-hypothesis is that it represents a mass-spring model with variations in the zero length and stiffness of the “spring.” First, assigning complex systems with feedback loops a single characteristic named “stiffness” is not very much meaningful (reviewed in 83). Attempts to measure the stiffness of such “springs” led even to physically impossible reports of negative stiffness (e.g., 100). Under some conditions, biological effectors (e.g., intact muscles, joints, and limbs) do show spring-like behavior, but these are special cases with numerous exceptions (reviewed in 96).

One of the most commonly cited studies criticizing the EP-hypothesis reported poorly reproducible equilibrium trajectories (time sequences of equilibrium states of the system “effector plus external force field”) with complex shapes, and inadequate stiffness coefficients (92). This study was criticized in detail by Gribble et al. (97) who have shown that these observations were likely consequences of the inadequate model used in the study by Gomi and Kawato. A number of studies showed violations of equifinality during movements under unusual conditions such as being rotated in the centrifuge (101, 102) and moving in an artificial force field with negative damping (94). Assuming the “mass-spring” version of the EP-hypothesis, these results were presented as disproving the hypothesis. In fact, violations of equifinality are common and do not require using complex force fields (e.g., 103–106). They have been naturally incorporated into the framework of the EP-hypothesis.

Although the mechanism of stretch reflex plays a central role in the EP-hypothesis, this does not mean that speed of voluntary movements is limited by the feedback delay in the reflex loop. Specification of control parameters (RC or λ) by the brain can proceed in a feed-forward manner at any speed and produce fast changes in muscle activation and movements given the continuous reflex input into the alpha-motoneuronal pools. So, very fast movement, such as those by great tennis players or during fast speech, are interpreted as defined primarily by the time patterns of descending neural signals, i.e., time profiles RC(t) or λ(t). Movement-related changes in the reflex feedback emerge at appropriate time delays and affect muscle activations later in the movement. This is one of the reasons why models of motor control based on specification of total inputs into alpha-motoneuronal pools (e.g., 107) are relatively successful in describing patterns of muscle activation during the first few tens of milliseconds and are much less impressive in their description of later phenomena affected by the movement-related reflex feedback.

Descending signals are not the only factor that can lead to shifts in the stretch reflex threshold. This was expressed formally as an equation: λ* = λ – µV + ρ + f(t), where λ* is the combined effect on the stretch reflex threshold at the level of alpha-motoneurons, λ is the contribution of descending signals, µ is a coefficient reflecting the effects of velocity (V) sensitivity of the primary spindle endings, ρ reflects effects of other reflex loops, and f(t) reflects history-dependent changes in the stretch reflex threshold (96). In particular, autogenic loops from length-sensitive sensory endings provide for the general form of the dependence of muscle force on length, as shown, in particular, in studies on animal preparations (108, 109). Other reflex loops contribute to shifts of λ* via the ρ term, thus affecting the observed behavior. In this review, we do not distinguish between λ and λ* for brevity.

The issue of neural representation of control variables within the EP-hypothesis remains relatively underexplored. Arguably, one of the most detailed conceptual schemes has been developed by Schöner and colleagues (110, 111). Several studies have suggested that descending signals from different brain structures encode not muscle activation (and not movement mechanics) but changes in λ to target muscles. These involve a study with electrical stimulation of various brain structures in decerebrate cats by Feldman and Orlovsky (108), studies of the effects of transcranial magnetic stimulation to the primary motor cortex in humans (112, 113), and a recent study of the effects of vestibular stimulation also in humans (114). Two recent reviews have offered nontrivial interpretations of the role of agonist-antagonist muscle coactivation (115) and classical results on neuronal population vectors associated with movements (116), both within the framework of the EP-hypothesis.

PHYSICAL APPROACH TO BIOLOGICAL MOVEMENT: REDUNDANCY AND ABUNDANCE

The scheme in Fig. 3 suggests that the efferent process associated with any natural action is always characterized by few-to-many transformations traditionally addressed as redundant leading to the so-called problem of motor redundancy (34, 117). Indeed, how does the CNS select signals at the joint level (R_J and C_J, which are relatively numerous) based on signals from the task level (R and C, which are relatively few)? Typical approaches to this problem have assumed computations within the CNS resulting in selection of optimal with respect to some cost (objective) function solutions (reviewed in 118, 119). Note that all such approaches assume computations of cost functions into future, e.g., over the predicted movement time, before action initiation. There is little argument that movement time is represented in the brain (e.g., 120, 121): Given the importance of proper timing of actions, ignoring time in action generation would have been evolutionary disastrous. Assuming that time integrals of specific variables are computed over future time intervals is a different matter, an assumption that seems to suspend laws of nature in the animal body. It has been suggested that the CNS facilitates actions that are “good enough” according to some criteria (122, 123), which can be done without computing objective functions explicitly.

An alternative approach to few-to-many mappings has been suggested under the name of the principle of abundance (124, 125). According to this principle, no computations are involved in mappings such as those illustrated in Fig. 3. The mappings are allowed to be variable such that no single, optimal or not, solution is selected. The mappings emerge based on the actual state of the system and are shaped by physiological feedback loops. The latter mechanism, addressed as back-coupling, can use feedback loops within the CNS, e.g., similar to those provided by the system of Renshaw cells, as well as signals from peripheral sensory endings (110, 126).

The principle of abundance is readily compatible with the uncontrolled manifold (UCM) hypothesis (127, 128). According to the UCM hypothesis, the CNS can stabilize different salient performance variables by sets of elements contributing to those variables in a task-specific way. In a linear approximation, stabilization of a salient variable leads to a specific signature of intertrial variance in the space of elemental variables. Namely, variance within the subspace where the salient variable does not change (the UCM for that variable) is expected to be larger than variance orthogonal to the UCM, where this variable changes: V_UCM > V_ORT. Recently, the idea of multiple solutions used across trials and preferentially confined to the UCM has been used in analysis of actions at the level of neural control variables such as the R- and C-commands. As mentioned earlier, at the level of effector mechanics, changes in the R-command lead to changes in the intercept of the force-coordinate effector characteristic (RC) and changes in the C-command lead to changes in its apparent stiffness (k). Studies of finger pressing tasks have confirmed that humans use, across trials, broadly varying magnitudes of RC and k, but these magnitudes are mostly confined to the solution space for the desired force magnitude (129).

To summarize, within the scheme in Fig. 3, efferent processes are identified with RCs to the involved muscle groups or, equivalently, with the R and C commands at each of the hierarchical levels. The notion of EC has meaning only after a level of analysis has been defined. For a given level, EC may be defined as a copy of the R- and/or C-commands at the selected level of analysis. Alternatively, EC may be associated with a copy of RC to the agonist and antagonist muscle groups (λs for individual muscles) at the selected level of analysis.

PERCEPTION WITHIN THE PHYSICAL APPROACH

Within the physical approach, perception is the process of measurement with the goal of creating percepts, quantitative or qualitative indices of relevant physical variables. Percepts can be self-reported, reported to others, and used without reporting for a variety of purposes including guiding actions. As mentioned earlier, there is plenty of evidence, from both everyday experiences and laboratory experiments, that both afferent and efferent signals contribute to perception. Note that physiologically the two streams of signals are tightly intertwined, e.g., via the system of gamma-motoneurons that modify sensory signals with action and via reflexes and reflex-like changes in motor output induced by changes in sensory signals. These may be viewed as examples of physiological action-perception coupling. There are numerous examples of more complex action-perception couplings studied, in particular, within the field of ecological psychology (130–132).

One of the striking and poorly understood features of percepts is their stability. There are example of bistable percepts and other cases of compromised stability of perception (133–135) including unstable kinesthetic illusions (136), but they are not typical during behavior in everyday environment. In everyday life, we frequently experience major changes of signals from sensory endings of different modalities and still perceive the environment as stable and our body as preserving anatomical integrity. Indeed, imagine that you press with the palm of a hand on a motionless surface. Signals from all major groups of proprioceptors in the arm would change with activation of both agonist and antagonist muscles, changes in tendon force, joint capsule tension, and activity level of gamma-motoneurons. Nevertheless, the arm configuration is perceived as unchanged. Where does stability of this percept come from?

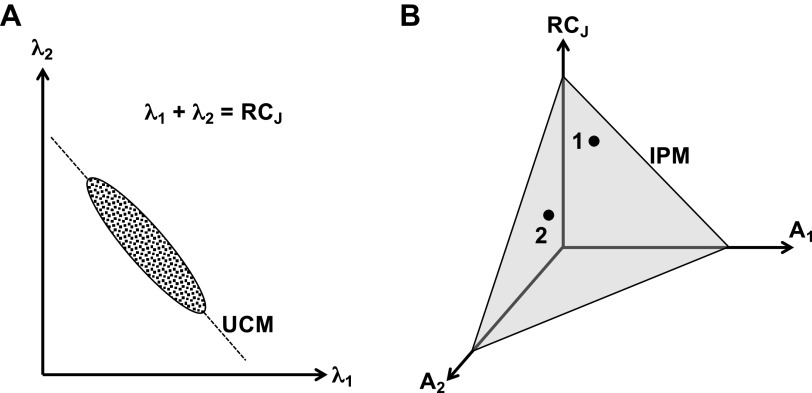
If we assume that percepts come from an unknown interaction of a variety of relevant afferent and efferent signals, stability of percepts under changes in those signals means that these changes are confined to a manifold within the high-dimensional afferent-efferent space, the iso-perceptual manifold (IPM; 137). In other words, a stable percept can be defined as a psychological reflection of an IPM. Covaried changes in afferent and efferent signals correspond to the same percept as long as they do not leave the IPM.

This concept is illustrated in Fig. 4, which uses a cartoon example of two elements, agonist and antagonist muscles acting at a joint, controlled with one neural variable each (λ₁ and λ₂) and equipped with one source of sensory information, e.g., a spindle ending, each (A₁ and A₂). Imagine that the task is to produce and perceive joint angle in isotonic conditions. If we ignore, for the purpose of illustration, the possibility of muscle coactivation, joint control can be reduced to a single variable, RC_J = (λ₁ + λ₂)/2. The left of Fig. 4 shows the solution space for a given magnitude of RC_J—its UCM in the two-dimensional space of commands to muscles. The right shows a linear image of the IPM in the three-dimensional space of RC_J, A₁, and A₂ (the author cannot draw four-dimensional pictures and, hence, the two commands to the muscles are reduced to a single axis; this is also the main reason we do not consider agonist-antagonist coactivation.). Note that covarying changes in commands to the muscles can keep RC_J constant (left), whereas stable perception of a joint angle is compatible with both unchanged RC_J and varying RC_J (right).

Figure 4.

A cartoon example of two elements, agonist and antagonist muscles acting at a joint, controlled with one neural variable each (λ₁ and λ₂) and equipped with one source of sensory information, e.g. a spindle ending, each (A₁ and A₂). Joint control can be reduced to a single variable, RC_J = (λ₁ + λ₂)/2. A: the solution space for a given magnitude of RC_J—its UCM (slanted line) and a theoretical intertrial data distribution (ellipse elongated along the UCM). B: a linear image of the IPM in the three-dimensional space of RC_J, A₁, and A₂. Stable perception of a joint angle is compatible with both unchanged RC_J and varying RC_J (compare points 1 and 2). IPM, iso-perceptual manifold; RC, referent coordinates; UCM, uncontrolled manifold.

The introduced scheme does not have to be limited to kinesthetic perception. In particular, a number of studies emphasized the importance of efferent processes for stability of visual perception (3, 138; see also the earlier Helmholtz example of pressing on one’s eye).

The concept of IPM can be used to offer an interpretation for effects of expectations and preconceptions on perception. For example, a percept of a six-legged cat or dog on the street is likely unstable: The viewer will try to substitute this illegal percept with an alternative one, e.g., a running four-legged animal. In “Star Wars,” however, such a percept may be perfectly legal. During natural movements of a joint, changes in the length of opposing (agonist and antagonist) muscles are matched. High-frequency vibration applied to one of the muscles leads to an increase in the firing rate of primary spindle afferents (139, 140). These changes may be interpreted by the CNS as corresponding to elongation of that muscle, a common interpretation of vibration-induced illusions (141–144). If afferents from the antagonist do not change their firing rate, the overall information stream corresponds to a disallowed percepts of a change in the length of the agonist without a change in the length of the antagonist corresponding to violation of anatomical body integrity. In such cases, actual combinations of afferent and efferent signals correspond to a disallowed IPM. To make the percept allowed, the data are projected on a meaningful (allowed) IPM (illustrated in Fig. 8 in 137). We do not know how such projections are realized. There may be more than one nearby IPM resulting in loss of stability and leading to bistable percepts and reversals of vibration-induced kinesthetic illusions under other sensory modalities, cognitive processes (e.g., counting backwards), and other factors (136).

PREDICTIONS FROM THE SCHEME OF PERCEPTION WITH IPM

The IPM concept generates a number of nontrivial predictions. For example, perception of individual elements participating in a multi-element task of producing a salient performance variable may be expected to be less precise compared with perception of the salient variable. Indeed, motion along the IPM in Fig. 4 can lead to changes in both afferent and efferent signals to each of the elements resulting in changed perception of their outputs compatible with unchanged perception of the salient performance variable. This predictions had been confirmed in recent studies of finger force matching during single- and multi-finger tasks (145, 146). Besides, perception of a functional variable may be based on sensory sources of different modalities as long as they change in a lawful way with that variable. In other words, under specific conditions, spindle endings can contribute to force perception while Golgi tendon organs can contribute to perception of position (cf. 147–149).

Within the IPM concept, efferent and afferent axes are formally equivalent. But this does not have to be the case. According to the generalization of the hypothesis on the neural control with spatial RCs, the efferent process defines a spatial coordinate used as the origin of a referent frame, and afferent signals inform on deviations of the effector from that coordinate (6, 150, 151). Figure 5 illustrates perception of muscle length and force. The efferent process defines a magnitude of λ—threshold of stretch reflex (77). Note that deviations of muscle length from λ are associated with parallel increase in muscle length, force, and activation level. In other words, signals from muscle spindles, Golgi tendon organs, and even from motoneurons can be used to identify a point on the muscle force-length characteristic and contribute to perception of both muscle force and length. This scheme predicts, in particular, that positional illusions may be associated with force illusions—a prediction confirmed in studies of the effects of high-frequency muscle vibration (152, see also 143, 153).

Figure 5.

The efferent process (EFF) defines a magnitude of λ—threshold of stretch reflex. Deviations from λ are associated with an increase in muscle length, force, and activation level. Signals from muscle spindles, Golgi tendon organs, alpha-motoneurons, and even from gamma-motoneurons can be used to identify a point on the muscle force-length characteristic and contribute to perception of both muscle force and length. AFF, afferent contribution; Ia, Ib, and II stand for the corresponding groups of afferent fibers.

Muscle vibration at 50–100 Hz is known as a powerful stimulus for the primary spinal endings (139). The response of the primary spindle afferents is unusually high; they can be driven by vibration, i.e., forced to generate one or more action potentials for each of the vibration cycles (140). The response of muscle spindle endings has been implicated in a variety of motor and perceptual effects caused by muscle vibration including the tonic vibration reflex (154, 155), complex patterns of limb movements resembling those during locomotion (156, 157), and illusions of position and velocity (141–144), which could even lead to perception of anatomically impossible limb configurations (158).

The study by Reschechtko and colleagues (152) has shown consistent effects of vibration applied to finger extensors on force matching. In those experiments, the subjects were asked to match the force produced by one hand (task-hand) at different times after that hand reached a required force level with the other hand (match-hand). No visual feedback was provided for the forces produced by the two hands. During the no-feedback interval, the task-hand force drifted to lower magnitudes (cf. 159, 160), and the match-hand consistently overshot the task-hand force. The amount of the overshoot, however, changed with muscle vibration. The pattern of the effects of vibration has suggested strongly that the vibration affected not only the afferent component of perception but also its efferent component, i.e., RC for the involved muscles. Note that this idea had been suggested earlier (150, 151) to interpret effects of muscle vibration on illusions of position.

The latter group of findings leads us to the following hypothesis: EC is not always a copy of the neural commands to the effector; it may be a distorted copy.

EFFERENCE COPY IS NOT ALWAYS A COPY!

A recent study explored effects of vibration on force production and perception in more detail (161). In that experiment, subjects were required to produce various force levels by pressing on force sensors with fingers of one hand (task-hand) and then, after an interval without visual feedback on the force, to match the perceived force with the other hand (match-hand). Muscle vibration could be applied to either flexor or extensor muscle group of either hand. During the force-matching steady-state episode, the fingers of both hands were smoothly lifted and lower by the “inverse piano” device (162) to estimate referent coordinate and apparent stiffness (RC and k) as mechanical reflections of the R- and C-commands.

Without vibration, the task-hand showed a force drift to lower magnitudes over the time interval without visual feedback (cf. 159, 160), and the match-hand consistently produced higher force as compared with the actual task-hand force (cf. 163). This was associated with significantly lower values of k and significantly higher absolute magnitudes of RC in the match-hand compared with the task-hand (see also 164). Within the idea of control with RC to the agonist and antagonist muscles (RC_AG and RC_ANT in Fig. 6), this combination of findings can only be interpreted as a consequence of RC_ANT in the match-hand being closer to the actual fingertip coordinate compared with the task-hand. This is illustrated in B of Fig. 6.

Figure 6.

A: the task-hand produces a force magnitude in isometric conditions with a combination of RC to the agonist (RC_AG) and antagonist (RC_ANT) muscles. The effector characteristic is shown with the thick, solid line. B: the match-hand shows higher force, smaller apparent stiffness (slope of the effector characteristic), and large absolute magnitude of its RC (n = 11; ANOVA). All three effects can be expected from a shift of RC_ANT toward the actual fingertip coordinate (ΔRC_ANT). Assuming differences in RC_AG between the two hands or between the R- or C-commands is unable to account for the findings (see text). RC, referent coordinates.

Note that assuming differences in RC_AG between the two hands was unable to account for the pattern of differences between the match-hand and task-hand. Indeed, assuming a shift of RC_AG toward the actual effector coordinate would produce a drop in force; assuming RC_AG shift away from the actual effector coordinate would produce an increase in apparent stiffness, i.e., changes in the opposite direction compared with those observed in the experiment. Assuming differences in the R-command or C-command (one at a time!) was also unable to account for the pattern of findings: A difference in the R-command should not lead to different k values and a difference in the C-command should not lead to differences in the RC values between the hands.

Muscle vibration had consistent effects on the main outcome variables (force, RC and k) in the match-hand only. In other words, vibration did not affect force production (no effects in the task-hand!) but did affect force perception (as reflected by the match-hand performance). This was true for any site of vibration. Moreover, effects of vibration of flexors and extensors were qualitatively and statistically the same, but they differed (were in opposite directions compared with the no-vibration conditions) between the conditions with task-hand and match-hand vibration.

The observed pattern of changes in the difference between the two hands in force, RC, and k (ΔF, ΔRC, and Δk) under vibration is illustrated in Fig. 7. It suggests that, during the force matching process, the subjects consistently underestimated the magnitude of RC to the antagonist muscles (extensors). As illustrated in the left of Fig. 7, during vibration of the task-hand, assuming RC_ANT magnitude closer to the actual effector coordinate is able to account for the pattern of findings, which includes an increase in ΔF, an increase in the absolute magnitude of ΔRC, and a drop in Δk. The right of Fig. 7 illustrates opposite effects observed during the vibration of the match-hand: a drop in ΔF, a drop in the absolute magnitude of ΔRC, and an increase in Δk. Within the scheme shown in Fig. 7, vibration applied to the task-hand leads to using a modified copy of RC_ANT in the perceptual process, namely, this copy is shifted toward X = 0 as compared with the current RC_ANT value in the task-hand. When vibration is applied to the match-hand, its RC_ANT is perceived as being closer to X = 0 and, to match the undistorted RC_ANT in the task-hand, the subjects moved actual RC_ANT in the match-hand away from X = 0. This interpretation implies that perceptual effects of RC_ANT (its EC) are unstable and can be distorted by the application of muscle vibration. It is readily compatible with the everyday observation that, during natural actions, antagonist activation is perceived as very weak or not perceived at all (see later).

Figure 7.

Effects of vibration of force matching. Left: during vibration of the task-hand, assuming RC_ANT magnitude closer to the actual effector coordinate accounts for the pattern of findings: an increase in the force difference between the hands ΔF, an increase in the absolute magnitude of ΔRC, and a drop in Δk (n = 11; ANOVA). Right: opposite effects are observed during the vibration of the match-hand: a drop in ΔF, a drop in the absolute magnitude of ΔRC, and an increase in Δk. RC, referent coordinates; RC_AG, RC to the agonist muscles; RC_ANT, RC to the antagonist muscle.

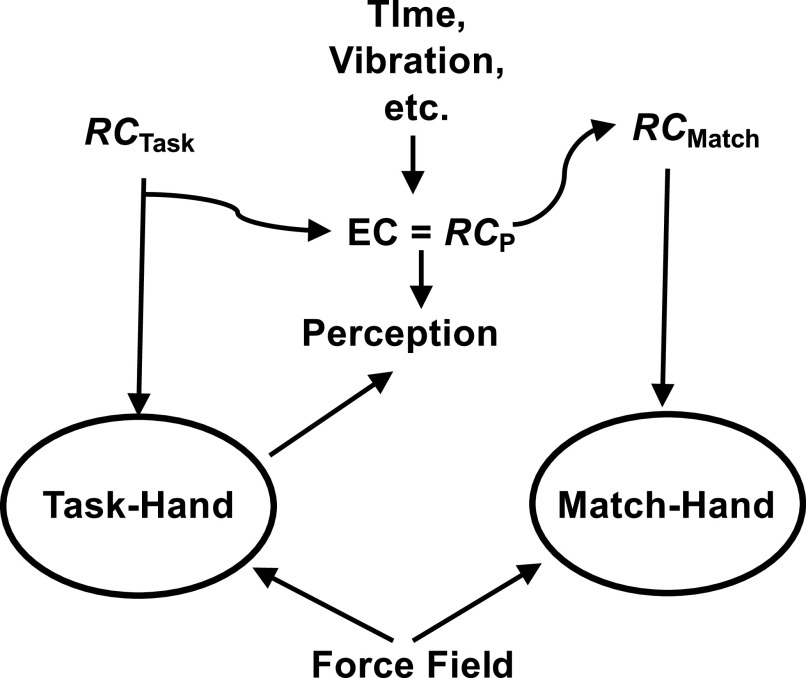
Taken together, these findings support the hypothesis that efferent contributions to perception are not necessarily copies of the current efferent commands. They can differ from the current efferent commands spontaneously, for example, as reflected in force-matching following force drifts in the absence of visual feedback. These differences can be also affected by artificial changes in afferent signals, for example, those produced by high-frequency muscle vibration. This is illustrated schematically in Fig. 8. For simplicity, this figure uses only one variable, RC, directed to the instructed effector (task-hand), which has a corollary stream participating in perception (RC_P). RC_P defines action by the “match-hand.” It can change due to effects from peripheral sensory signals (e.g., caused by vibration) as well as spontaneously.

Figure 8.

For simplicity, this figure uses only one variable, RC, directed to the instructed effector (task-hand), which has a corollary stream participating in perception (RC_P), equivalent to efference copy (EC). RC_P defines action by the match-hand. It can change due to effects from peripheral sensory signals (e.g., caused by vibration) as well as spontaneously. RC, referent coordinates.

There seems to be something special about the role of distorted command to antagonist muscles (RC_ANT, see Figs. 6 and 7) in the overall difference between RC and RC_P in the scheme in Fig. 8. Note that correlations between the antagonist muscle response and kinesthetic illusions produced by vibration have been documented (165) in support of the idea that antagonist muscle reaction to vibration can be associated with perceptual effects. We are going to return to this issue in one of the further sections. As of now, let us make an intuitive observation that, during natural movements (without purposeful agonist-antagonist coactivation), we do not perceive activation of the antagonist muscle, although it can reach substantial magnitudes (e.g., 107, 166). If one asks a subject to match the level of antagonist activation using an action when this muscle is used as an agonist, most naïve subjects are confused by the instruction and report that the level of antagonist activation was zero.

It is possible that the hypothesized underestimation of RC_ANT is related to mechanisms associated with strong persistent inward currents (PIC) generated in dendrites of spinal motoneurons in response to diffuse serotoninergic and noradrenergic descending signals (167, 168). These currents have shown very high sensitivity to reciprocal inhibition between antagonist muscle groups. As a result, local reflex-mediated inputs can have a profound effect on control signals to individual muscles, in particular leading to a drop in RC_ANT. These effects could be amplified under muscle vibration, which leads to higher afferent input from the primary muscle spindles and correspondingly stronger effects of reciprocal inhibition.

EFFERENCE COPY DURING FORCE DRIFTS

Unintentional force drifts in the absence of visual feedback have been a not very well understood group of phenomena. In early studies, such drifts were associated with problems with the working memory (160, 169), and this interpretation has received support from both brain imaging and clinical studies (170, 171, 172). Within the physical approach described in this paper, force drifts are consequences of unintentional drifts in central neural commands, such as RCs to effectors (159, 173).

There have been several puzzling observations in studies of force drifts. First, although the drift magnitude could be relatively large, up to 35%–40% of the initial force level (within the range of forces not leading to fatigue), the drifts did not exceed this magnitude as if limited by an invisible stop. It has not been clear what stopped the force from continuing to drift further down. Second, when the subjects were asked to match the force produced by an effector in the process of force drift with the contralateral homologous effector, the matching effector consistently overshot the actual force. In earlier studies, the matching effector force was reported to be close to the initial force level (152, 163), and these results were interpreted as evidence that the initial force magnitude had not been forgotten. However, the magnitude of the overshoot (∼8% of maximal voluntary contraction force, MVC) does not depend on the initial force magnitude (161): It is about the same for conditions with close to zero drift (when the initial force is ∼10% MVC) and for very large force drifts (when the initial force is ∼25–30% MVC). It seems to be a coincidence that the amount of force drop was nearly perfectly matched by the amount of overshoot in the cited studies that used the initial force levels of ∼25–30% MVC.

Quantitative estimates of the changes in RC and k during the force drift process have suggested that the force drift was primarily caused by a drift of k toward lower magnitudes, while RC drifted less (174, 175). Moreover, drifts in k were also seen during trials of a similar duration when the subject was always presented with visual feedback on the force magnitude. In such conditions, the drifts in k were accompanied by coadjustments of RC that led to no net change in force.

Similar observations were reported in a study of force matching following intentional and unintentional force changes (164). The latter were produced by lifting or lowering fingers using the “inverse piano” (162) under the instruction to the subject not to react to possible force changes produced by these manipulations. Intentional force changes were performed voluntarily, without finger motion, and used visual force targets matched to force magnitudes observed during the finger lifting and lowering. In both conditions, when the contralateral hand was asked to match force, it showed smaller k values and larger absolute magnitudes of RC, which led to underestimation of the force changes in the task-hand: The match-hand showed smaller force magnitudes during force increase by the task-hand and higher force magnitudes during force drop by the task-hand. These observations offer another illustration corroborating the hypothesis that EC used during force perception can be distorted, i.e., it is not a copy of the current efferent command.

WHAT IS “SENSE OF EFFORT”?

The introduced definition of EC allows addressing sense of effort and offering a hypothesis on its origin within the same scheme of control with RC. According to dictionaries, effort is defined as conscious exertion of power, exertion of physical or mental power, physical or mental activity needed to achieve something, and use of physical or mental energy. On the one hand, these definitions link effort to physical variables from mechanics such as power and energy; on the other hand, effort is associated with less precisely defined processes such as mental activity. The vast literature on sense of effort (reviewed in 176, 177) offers a few definitions for this elusive construct including the following: “signals of motor command …, which arise at levels rostral to spinal motoneurons” (178) and “centrally generated sensations arising from the motor command” (179). In more lay terms, effort is an internal measure of how hard one tries to perform the task as reflected in commands to motoneurons, which makes it compatible with the introduced definition of RC and suggests that sense of effort may originate from EC. This definition, as well as a few earlier ones, emphasize central (neural, subjective) origin of this sense in contrast to sense of force, which can be compared with objectively measured forces.

Although sense of effort has been viewed traditionally as being of a primarily central origin, a possibility of modulation from sensory signals has also been emphasized. A number of studies presented examples of dissociation between senses of effort and force, in particular under such manipulations as fatigue, paralysis, or sensory deprivation (176, 178, 179). On the other hand, a few studies have suggested that, when subjects are asked to match forces by two effectors (e.g., the left and right hands), they tend to match efforts, i.e., measures of central neural commands, leading to force mismatch in conditions when the external force fields for the two hands differed (180, 181). This conclusion has been supported recently by a study of force perception, where subjects were required to match force produced by one hand with the other hand and also to report its magnitude verbally using the scale developed during training (145). There were significant differences between the patterns of force-matching and verbal reports, suggesting that the latter represented estimates of central neural commands, i.e., were related to effort. Note that, unlike force, displacement, and related variables, which are produced on the interface with the environment, sense of effort does not need such an interface.

One of the major problems in discussions of the sense of effort is that central neural processes associated with action are typically not being defined. Further, we will try to put this sense within the framework of the neural control of movement with time-varying RC described in earlier sections (see also 6, 7). The purpose of this analysis is not to argue with earlier ideas but to place them into a more concrete, physical framework that appeals to laws of nature.

We start with a hypothesis that effort during an action by an effector equals its RC (i.e., reflects the R-command). In other words, the naturally emerging changes in the C-command have no direct effects on the sense of effort. This hypothesis is readily compatible with Feldman’s idea that the R- and C-commands form a hierarchy: The R-command changes in a task-specific way to produce actions, whereas the C-command may stay unchanged (78). The following section describes recent results corroborating this hypothesis.

MOTOR AND PERCEPTUAL CONSEQUENCES OF COACTIVATION

Unexpected findings, predicted within the introduced framework, have been reported recently in a study of muscle coactivation under the instruction not to change finger pressing force (182). Despite the instruction, the subjects produced a large unintentional increase in the pressing force, on average ∼50% of the original force level. When the subjects were asked to estimate the changed force level verbally, they reported a small drop (!) in force as compared with the level produced before coactivation. To make the situation even more complex, when the subjects were asked to match the force with the contralateral hand, they were relatively accurate and even showed a tendency to overshoot somewhat the actual elevated force level.

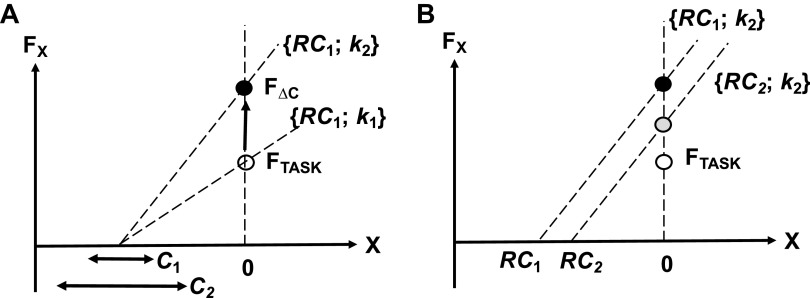
Figure 9 illustrates the interpretation of these findings offered in the original study. Coactivating muscles leads to an increase in the effector’s apparent stiffness, k. This is expected to produce an increase in force unless compensated by an adjustment in RC (Fig. 9A). The observed force increase showed that such adjustments were insufficient. When the subjects were asked to report the force level verbally, they reported sense of effort, i.e., RC magnitude. Note that small, compensatory RC shifts were expected to lead to a drop in the RC absolute magnitude if quantified with respect to the actual hand coordinate (Fig. 9B). During force matching, the subjects could not rely on sense of effort because force magnitude corresponds to a UCM within the {RC; k} space where both RC and k vary (cf. 129, 164). So, they had to attend to all relevant sources of information, which led to relatively accurate results.

Figure 9.

A: coactivating muscles (C₂ > C₁) lead to an increase in the effector’s apparent stiffness, k (k₂ > k₁). This produces an increase in force from the initial level (white circle) to F_ΔC (black circle) (n = 10; ANOVA). B: the force increase can be partly compensated by a shift in RC toward the actual effector coordinate (gray circle, RC₂ < RC₁). Verbal reports reflect sense of effort, i.e., RC magnitude. Modified by permission from Cuadra et al. (182). RC, referent coordinates. F_∆C, force after additional coactivation; F_TASK, force defined by the task; F_X, force along the X coordinate.

This interpretation assumes that sense of effort is dominated by RC magnitude (cf. studies by 180, 181), and natural variations in k have little effect of this sense. Moreover, given the results suggesting gross underestimation of RC_ANT, one may associate sense of effort during force production tasks primarily or even exclusively with the magnitude of RC_AG. RC_ANT seems to represent a poorly perceived or even nonperceived unstable neural variable, which typically does not contribute to sense of effort and leads to distortions of EC.

POSSIBLE NEUROPHYSIOLOGICAL MECHANISMS OF EFFERENCE COPY

Earlier studies associated EC with neurophysiological circuitry in various brain structures including the cerebellum (9, 11, 12), motor cortex (8–10), the basal ganglia (13, 14), and subcortical loops (15). Those studies, however, did not assign physical meaning to the studied neurophysiological signals purported to represent EC.

Within the physical approach accepted in this review, EC is associated with RCs to participating muscle groups. A number of studies in both animal preparations and humans have associated RCs with descending signals along a variety of descending pathways. The classical study by Feldman and Orlovsky (108) on decerebrate cat preparations has shown that electrical stimulation of various supraspinal structures, including the pyramidal tract, mesencephalic reticular formation, and Deiters’ nuclei, leads to nearly parallel displacements of the force-length curves of limb muscles without intersections of those curves. These observations supported the idea that signals from those brain structures encoded only one parameter per muscle, its RC associated with the stretch reflex threshold. More recently, human studies using transcranial magnetic stimulation applied over the primary motor cortex (112, 113) and also studies using galvanic stimulation of the peripheral vestibular organs (114, 183) have confirmed those findings for effector systems ranging from individual joints to the whole body. The idea that multiple systems can contribute to EC is compatible with studies across species with vastly different CNS structures (23–25, 27–29).

A brain-imaging study comparing conditions with muscle vibration associated and not associated with kinesthetic illusions has suggested that perceptual illusions are associated with activation of motor and parietal areas (184). In particular, perception of an illusory movement was specifically related to activation in the left premotor, sensorimotor, and parietal cortices as well as in bilateral supplementary motor and cingulate motor areas. Interactions between vibration-induced illusions and motor imagery have been reported associated with activation of the contralateral cingulate motor areas, supplementary motor area, dorsal premotor cortex, and ipsilateral cerebellum (185, 186). Similar observations have been reported by Casini et al. (187) in a study of vibration-induced illusory movements. The motor network, in particular the primary motor cortex, has been implicated in processing afferent input from skeletal muscles and formation of body representations (188).

EC has been associated with a copy of signals along the corticospinal tract that is fed back to the cerebellum (9, 54), which is part of the cerebellar-thalamo-cortico-cerebellar loop. The question, What is encoded in signals along the corticospinal pathway?, has been discussed at least since the classical studies by Evarts (189) and Asanuma (190). Answers included levels of muscle activation and a variety of kinetic and kinematic variables (forces, coordinates, their derivatives, etc.) at the level of effectors (191–195). Several recent studies have suggested, however, that these signals encode changes in the stretch reflex threshold (λ) for target muscles (112, 113, reviewed in 78, 116). This view, combined with the aforementioned idea that a copy of corticospinal signals sent to the cerebellum plays the role of EC, is readily compatible with the concept advocated in this review that EC represents copies of RC (sometimes distorted) to the involved effectors.

Overall, there seems to be no compelling reason to associate EC with signals within specific brain structures or pathways. On the other hand, the reviewed studies allow formulating a set of specific hypotheses associating EC with a copy, sometimes a distorted copy, of RC to the effector.

CONCLUDING COMMENTS

To summarize, recent studies suggest that efferent contributions to kinesthetic perception involve distorted neural commands, which are associated with spatial referent coordinates for the involved effectors and muscle groups. Such distortions seem to affect primarily neural commands to antagonist muscles, which show spontaneous and vibration-induced drifts. In other words, efference copy is not always a copy of efferent signals. Sense of effort shows distortions compatible with the hypothesis that it is associated with RC to the involved effectors. Neurophysiological mechanisms involved in efferent contributions to sense of force and effort are distributed and involve multiple structures and pathways.

GRANTS

Some of the reviewed studies were in part supported by a grant from the National Institutes of Health (USA) R21 NS095873.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author.

AUTHOR CONTRIBUTIONS

M.L.L. conceived and designed research; M.L.L. analyzed data; M.L.L. interpreted results of experiments; M.L.L. prepared figures; M.L.L. drafted manuscript; M.L.L. edited and revised manuscript; M.L.L. approved final version of manuscript.