Individual differences in proprioception predict the extent of implicit sensorimotor adaptation

Abstract

Recent studies have revealed an upper bound in motor adaptation, beyond which other learning systems may be recruited. The factors determining this upper bound are poorly understood. The multisensory integration hypothesis states that this limit arises from opposing responses to visual and proprioceptive feedback. As individuals adapt to a visual perturbation, they experience an increasing proprioceptive error in the opposite direction, and the upper bound is the point where these two error signals reach an equilibrium. Assuming that visual and proprioceptive feedback are weighted according to their variability, there should be a correlation between proprioceptive variability and the limits of adaptation. Alternatively, the proprioceptive realignment hypothesis states that the upper bound arises when the (visually biased) sensed hand position realigns with the expected sensed position (target). When a visuo-proprioceptive discrepancy is introduced, the sensed hand position is biased toward the visual cursor, and the adaptive system counteracts this discrepancy by driving the hand away from the target. This hypothesis predicts a correlation between the size of the proprioceptive shift and the upper bound of adaptation. We tested these two hypotheses by considering natural variation in proprioception and motor adaptation across individuals. We observed a modest, yet reliable correlation between the upper bound of adaptation with both proprioceptive measures (variability and shift). Although the results do not clearly favor one hypothesis over the other, they underscore the critical role of proprioception in sensorimotor adaptation.

NEW & NOTEWORTHY Although the sensorimotor system uses sensory feedback to remain calibrated, this learning process is constrained, limited by the maximum degree of plasticity. The factors determining this limit remain elusive. Guided by two hypotheses, we show that individual differences in the upper bound of adaptation in response to a visual perturbation can be predicted by the bias and variability in proprioception. These results underscore the critical, but often neglected role of proprioception in human motor learning.

INTRODUCTION

Accurate motor control requires the continuous calibration of the sensorimotor system, a process driven by the sensory feedback experienced over the course of movement. One of the primary learning processes involved in keeping the system calibrated is implicit sensorimotor adaptation (1–3). Here, learning is assumed to be driven by sensory prediction error (SPE), the difference between the predicted feedback from a motor command and the actual sensory feedback.

Recent findings have shown that implicit adaptation in response to a visuomotor rotation (VMR) is remarkably invariant across a large range of error sizes and tasks (4, 5). Even in response to large errors (e.g., 45°), the maximum amount of trial-to-trial change is around 1°–2° (4–9)—not surprising for a system that likely evolved to adjust for subtle changes in the environment and body. More puzzling, the maximum degree of plasticity within this slow learning system is limited, maintaining an asymptotic value of around 15°–25° even after hundreds of trials (4–6, 10–13) or across multiple test sessions (14, 15). As such, learning to compensate for large errors requires the recruitment of other learning processes such as explicit aiming strategies (11, 16–18).

Although the mean upper bound for implicit adaptation to large visuomotor rotations averages around 20°, individual differences can be quite substantial. In standard VMR tasks, these differences are hard to detect during learning since participants eventually exhibit near-perfect performance, independent of the size of the perturbation. With these tasks, the individual differences become evident during the “washout” phase when feedback is eliminated, and participants are instructed to reach directly to the target. An alternative method is to use noncontingent, “clamped” visual feedback in which the angular trajectory of the feedback cursor is invariant, always following a path that is deviated from the target by a fixed angle (e.g., 15°). Despite instructions to ignore this feedback, the participants’ behavior reveals an automatic and implicit adaptation response, deviating across trials in the opposite direction of the clamp (4, 5, 19). With this method, the error remains constant across trials; as such, the asymptote is not tied to changes in task performance (i.e., feedback terminating closer to the target), but rather, the asymptote reflects endogenous constraints. Across both methods (washout performance in tasks using contingent feedback or asymptotic performance in response to noncontingent feedback), the range of values is considerable. For example, in one study (4), the range of asymptotes in response to 15° clamped feedback was between 12° and 43° (mean = 18°, SD = 10°).

The factors that determine the upper bound of implicit adaptation are poorly understood. One hypothesis is that the limit reflects the interaction of visual and proprioceptive feedback. As adaptation progresses, the hand movements are adjusted away from the target, reducing the visual SPE (at least in standard VMR tasks). However, the change in hand direction away from the target results in an increase in a proprioceptive SPE, the difference between the expected and experienced signals of hand position. Importantly, the direction of the proprioceptive SPE is opposite to that of the visual SPE, and thus the response to these two SPEs are in the opposite directions. The asymptotic level of adaptation may thus reflect an equilibrium between learning from visual and proprioceptive error signals.

Studies of multisensory integration have shown that when participants estimate the location of their hand, they use a combination of visual and proprioceptive feedback, weighting each source based on their relative reliability (20–25). Consistent with this hypothesis, in the context of visuomotor adaptation, the response to a visual perturbation is reduced when noise is added to the visual feedback (20, 23, 26–28). The corollary prediction, namely, that the response to a visual perturbation should increase as a function of noise (i.e., variability) within the proprioceptive system, has not been tested.

A second hypothesis relates to another way in which visual and proprioceptive information have been shown to interact during adaptation. The introduction of a visual perturbation creates a discrepancy between the visual and proprioceptive feedback. This discrepancy results in a shift in the perceived location of the hand toward the visual feedback, a phenomenon referred to as a “proprioceptive shift.” The size of the shift tends to range between 5° and 10° and remains relatively stable, evidenced by probing sensed hand position following passive hand displacement at various timepoints in an adaptation study (12, 29–36). Similar to multisensory integration, this shift presumably reflects the operation of a system seeking to establish a unified percept from discrepant sensory signals.

The processes underlying proprioceptive shift may also contribute to the upper bound of implicit adaptation. This shift introduces a different error signal, the discrepancy between the target and the sensed hand position (i.e., the difference between the expected trajectory to the target and the trajectory toward the perceived hand position). A learning process seeking to counteract this error signal would also drive the hand direction away from the perturbation (i.e., the opposite direction of the proprioceptive shift). By this view, implicit adaptation would reach an asymptote when the sensed hand position is “realigned” with the target, and as such, the asymptote would correlate with the size of the proprioceptive shift: A larger deviation in hand angle would be required to counteract a larger proprioceptive shift.

To examine these two hypotheses (Fig. 1) in tandem, we exploit natural variation across individuals, examining the relationship between individual differences in proprioceptive variability and proprioceptive shift with the upper bound of implicit adaptation. To measure proprioception, participants were asked to report the position of their hand after passive displacement. These proprioceptive probes were obtained before, during, and after an extended block of trials in which the visual feedback was perturbed. From these data, we could use standard psychophysical methods to estimate for each participant, the bias and variability in their sense of proprioception, with the bias providing an assay of proprioceptive shift. In experiment 1, the upper bound on implicit adaptation was estimated by measuring the participants’ aftereffect in response to a response-contingent visuomotor rotation. In experiment 2, the upper bound was estimated using the asymptotic response to clamped visual feedback.

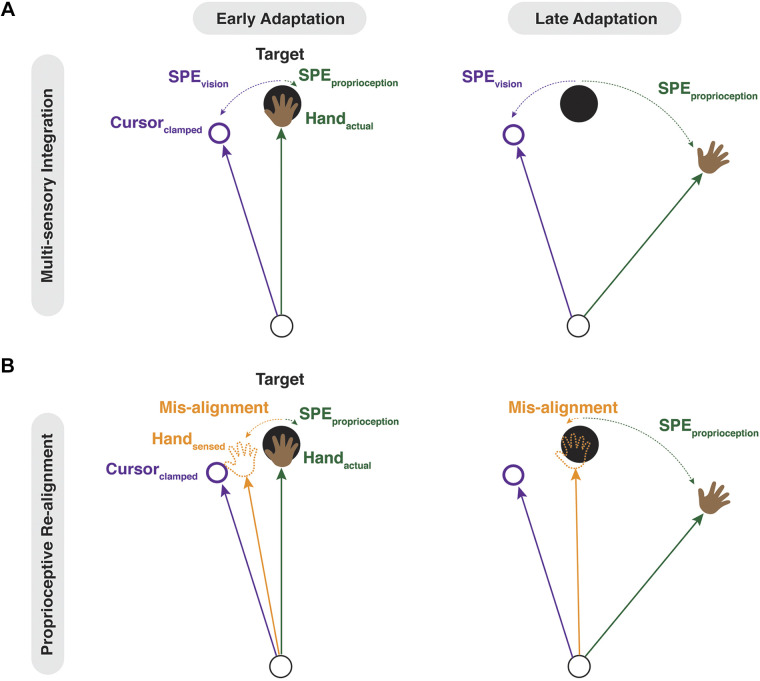
Figure 1.

Two hypotheses concerning constraints on the upper bound of implicit adaptation. A: by the multisensory integration hypothesis, the upper bound of adaptation is the point of equilibrium between the visual SPE and the proprioceptive SPE. Since there is typically more variability in proprioception compared with vision, the proprioceptive SPE may be weighted less, requiring a greater proprioceptive SPE to offset a visual SPE. B: by the proprioceptive realignment hypothesis, the upper bound of adaptation occurs when the participant’s sensed hand position is at the target. Sensed hand position is a composite of visual-based inputs underlying the proprioceptive shift (target and cursor) and proprioception from the actual hand position. SPE, sensory prediction error.

METHODS

Participants

Undergraduate students were recruited from the UC Berkeley community (experiment 1 N = 30; experiment 2 N = 32; age = 18–22; 45 women, 17 men), and either received course credit or financial compensation for their participation. As assessed by the Edinburgh handedness inventory, all of the participants were right handed (37). The protocol was approved by the IRB at UC Berkeley.x Participants provided written informed consent.

Experimental Overview

Each experiment involved a mix of reaching trials and proprioceptive probe trials. For both tasks, the participants were seated in front of a custom tabletop setup and placed their hand on a digitizing graphics tablet (49.3 cm by 32.7 cm, Intuos 4XL; Wacom, Vancouver, WA, sampling rate = 200 Hz) that was horizontally aligned with and positioned below an LCD monitor (53.2 cm by 30 cm, ASUS). The participant’s view of their hand was occluded by the monitor, and the room lights were extinguished to minimize peripheral vision of the arm. On reaching trials, arm movements were made by sliding a digitizing pen, embedded in a custom handle, across the table. On proprioceptive trials, the participant held the digitizing pen, and the experimenter moved the participant’s arm.

Reaching Trials

Reaches were made from a start location to a target, located at various target locations. The start location was indicated by a white ring (6 mm diameter) and the target by a blue circle (6 mm diameter), with the radial distance between the start location and target fixed at 16 cm. To initiate a trial, the participant moved her hand to the start location. Visual feedback of the hand position was given via a cursor (white circle 3.5 mm diameter) only when the hand was within 1 cm of the start position. Once the hand remained within the start location for 500 ms, the target appeared, serving as a cue to indicate the location of the target and an imperative to initiate the reach. To discourage online corrections, participants were instructed to perform “shooting” movements, making a rapid movement that intersected the target.

There were two types of feedback trials: veridical and perturbed. On veridical trials, the cursor corresponded to the position of the hand. On perturbation trials, the cursor was either rotated relative to the hand position (visuomotor rotation, experiment 1) or restricted to an invariant path along a constant angle with respect to the target (visual clamp, experiment 2). On feedback trials, the radial position of the cursor matched the radial position of the hand until the movement amplitude reached 16 cm (the radial distance of the target), at which point the cursor froze. On no-feedback trials, the cursor was blanked when the target appeared, and did not reappear until the participant had completed the reach and returned to the start location for the next trial.

Movement time was defined as the interval between when the hand movement exceeded 1 cm from the start position to when the radial distance of the movement reached 16 cm. To ensure that the movements were made quickly, the computer played a prerecorded message “too slow” if movement time exceeded 300 ms. If the movement time was less than 300 ms, a neutral “knock” sound was generated, informing the participant that the reach speed had fallen in the acceptable window. There were no constraints on reaction time.

Proprioceptive Probe Trials

To probe proprioceptive variability, the experimenter sat at the opposite side of the table, across from the participant. From this position, the experimenter could passively move the participant’s right hand to different probe locations. The participant was instructed to hold the digitizing pen, but to maintain a passive state, one that allowed the experimenter to move the participant’s right hand with minimal resistance. To produce the passive movements, the experimenter used her left hand to move the participant’s right hand, maintaining contact throughout the proprioceptive probe block.

The experimenter initiated each trial by moving the participant’s hand into the start position, at which point the word “Ready” appeared on the screen. The experimenter then hit the space bar with her right hand, at which point the word “Ready” disappeared and a number specifying the desired target location appeared on the corner of the monitor closest to the experimenter (Fig. 2). A small cloth cover was placed at this corner to prevent the participant from seeing the number. The experimenter moved the participant’s hand to the specified target location. Once the participant’s hand was at the target location (2 cm diameter tolerance window), the word “Ready” again appeared and the experimenter hit the space bar to advance the trial. A filled white circle (3.5 mm diameter) then appeared at a random position on the monitor. The participant used her left hand to move a mouse (Logitech Trackman Marble), positioning the cursor above the sensed position of their right hand. When satisfied with the position of the cursor, the participant clicked the mouse button. The participant was allowed to modify their response by repositioning the mouse and clicking again. When the participant confirmed that the trial was complete, the experimenter hit the space bar, at which point the cursor disappeared. The experimenter then moved the participant’s hand back to the start position to initiate the next trial. The start position remained on the screen for the duration of the proprioceptive probe trials.

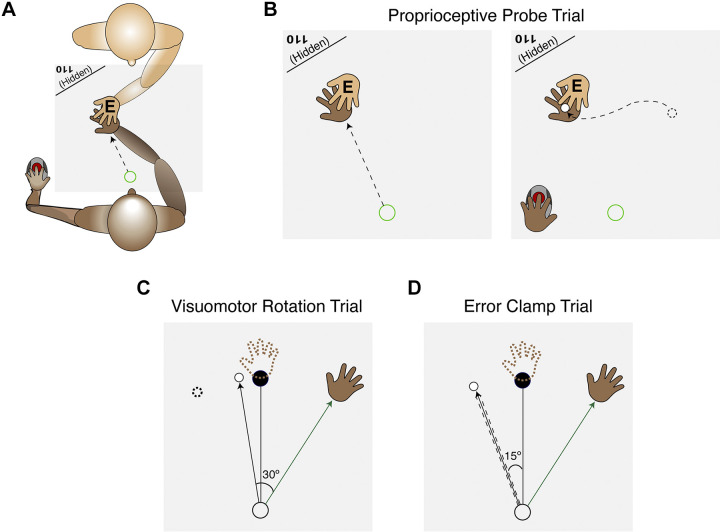
Figure 2.

Experimental overview. A: experimental setup for proprioceptive probe trials. The experimenter (top, with their hand labeled with an “E”) sat opposite the participant (bottom) and moved their hand from the start position to a specified location. The location (e.g. 110°) was signaled to the experimenter via text that appeared on the corner of the horizontal monitor, behind a cloth which prevented the participant from seeing the text. B: after the participant’s hand was passively moved to the probe location, a cursor appeared at a random position on the screen. The participant used their left hand to move the cursor to the sensed hand position. C: in experiment 1, a rotation was applied to the cursor. The task error introduced by the rotation is nullified if the participant moves in the opposite direction of the rotation. D: in experiment 2, the cursor was clamped, independent of hand position. Participants were told to ignore the error clamp and aim straight for the target. The depicted trials in C and D provide examples of performance late in the adaptation block.

We opted to use a tolerance window of 2 cm in positioning the hand, a value that was large enough for the experimenter to guide the participant’s hand to the target location without feedback, but also small enough to ensure minimal variation in target positions across trials. Note that variance in the position of the hand was irrelevant given that the proprioceptive judgments were recorded as the difference from the perceived location of the hand (mouse click) and the actual position of the hand.

Experiment 1, Movement-Contingent, Rotated Feedback

Reaching and proprioceptive trials were performed to five targets located within a wedge (at 70°, 80°, 90°, 100°, 110°, with 90° corresponding to straight ahead). The trials were arranged in cycles of one trial per target, with the order randomized within a cycle.

The experiment began with a brief phase to familiarize the participants with the reaching task. This consisted of 10 baseline reaching trials in which no visual feedback was provided, followed by 10 baseline trials with online, veridical feedback. The latter was used to emphasize that the movement should be produced to shoot through the target and demonstrate that the feedback would disappear once the movement amplitude exceeded the radial distance of the target.

The participant then completed a block of 50 baseline proprioceptive probe trials. Following this, the reaching task resumed but now the feedback perturbed. To minimize awareness of the perturbed feedback, the angular deviation of the cursor was increased in small, incremental steps of 0.33° per trial, reaching a maximum of 30° after 90 trials. Across participants, we counterbalanced the direction of the rotation (clockwise or counterclockwise).

Following the initial 90 perturbation trials, the participant then completed seven more blocks, alternating between proprioceptive probe trials (30 per block) and reaching trials (40 per block, at the full 30° rotation). With this alternating schedule, we sought to obtain stable measures of proprioception following adaptation, while minimizing the effect of temporal decay on adaptation. These blocks were intermixed with four blocks of five no-feedback trials with instructions to reach directly to the target despite the absence of feedback. These no-feedback blocks occurred after the first gradual perturbation block, the second fixed perturbation block, the third perturbation block, and the fourth proprioceptive probe block. These no-feedback trials provided the primary data for our measure of adaptation. By having four of these probes, we were also able to assess the time course of adaptation. To complete the session, the participants completed 50 reaching trials with veridical feedback to ensure that the residual effects of adaptation were removed.

Each participant returned for a second session, 2 to 14 days after the first session. The experimental protocol was identical on day 2, allowing us to assess test-retest reliability of the various measures of adaptation and proprioception.

Experiment 2, Noncontingent, Clamped Feedback

The key change in experiment 2 was the use of the visual clamp method during the perturbation trials. This form of feedback has been shown to produce robust adaptation with minimal awareness (4, 5, 27). Moreover, adaptation with this method will reach an upper bound that is not constrained by performance error (e.g., distance between cursor and target which is reduced over time with contingent feedback as in experiment 1) but presumably reflects factors intrinsic to each participant. Based on previous work, we expected to observe a broad range of upper bounds across our sample, a desirable feature to examine individual differences.

The basic method for the reaching and proprioceptive probe trials was similar to that used in experiment 1 with a few changes. First, we used a finer sampling of the workspace for the proprioception task, with target locations spaced every 5° (70°, 75°, 80°, 85°, 90°, 95°, 100°, 105°, 110°). Although participants were not explicitly queried in experiment 1, we were concerned that some participants may have noticed that there were only five discrete target locations, which could potentially bias their responses; that is, the proprioceptive reports might be based on their memory of a previously reported hand position rather than relying solely on the current proprioceptive signal. The finer sampling should reduce the utility of memory-based reports. Second, for the reaching task, we opted to keep the spacing as in experiment 1 (10° apart) but increased the size of the wedge, with the target locations spanning the range of 50°–130°. This change was motivated by pilot work suggesting that adaptation to a visual clamp is more consistent when the movements are made in a larger workspace. Note that it was necessary to limit reaching in one direction, away from the body, given the workspace limitations imposed by the tablet and our decision to have the movement amplitude be 16 cm.

We also modified the block structure. Experiment 2 began with a proprioception block (one cycle, 1 trial per 9 targets) to familiarize the participant with this task. The participants then completed a block of reaching trials without visual feedback (9 targets, 27 trials total), followed by a block of reaching trials with veridical feedback (72 trials) and another proprioception block (72 trials, with a break after 36 trials).

The participant then completed the perturbation block, composed of 180 trials (break after the first 90). For these trials, the cursor always followed a 16-cm straight trajectory offset by 15° from the target (clockwise or counterclockwise, counterbalanced across participants). The radial distance of the cursor, relative to the start position, was yoked to the participant’s hand. Thus, the motion of the cursor was temporally correlated with the participant’s hand, but its direction was fixed, independent of the angular position of the participant’s hand. Just before the start of this block, the error clamp was described to the participant and she was told to ignore this “feedback” signal, always attempting to reach directly to the target. To help the participant understand the invariant nature of the clamp, three demonstration trials were provided. On all three, the target appeared straight ahead at 90° and the participant was told to reach to the left (demo 1), to the right (demo 2), and backward (demo 3). On all three of these demonstration trials, the cursor moved in a straight line, 15° offset from the target. In this way, the participant could see that the spatial trajectory of the cursor was unrelated to their own reach direction.

Following the initial 90 trials with clamped feedback, the participant completed seven blocks, alternating between the proprioception task (36 trials/block, four blocks) and the reaching task with clamped feedback (90 trials/block, three blocks).

Given the high reliability in our hand angle and proprioceptive measures from experiment 1 (Fig. 4, A–C), we limited testing to a single session.

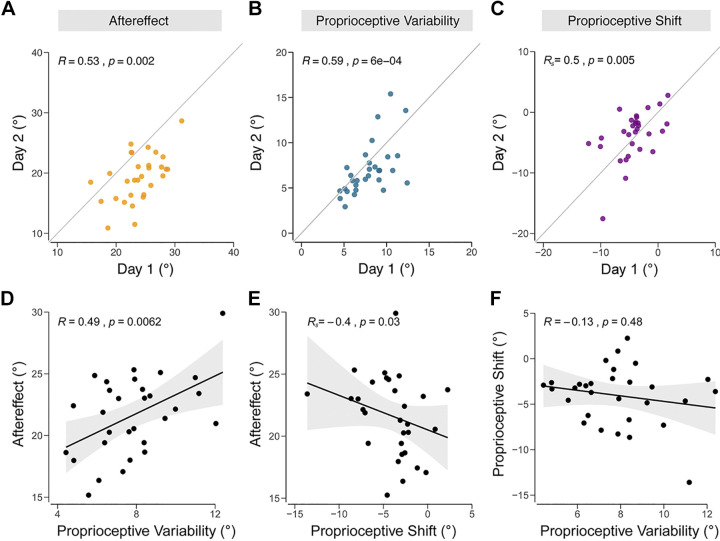
Figure 4.

Interindividual differences analyses in experiment 1. Test–retest reliability, measured across days, for aftereffect from adaptation (yellow; A), proprioceptive variability (blue; B), and proprioceptive shift (purple; C). Correlations between different dependent variables: proprioceptive variability vs. aftereffect (D), proprioceptive shift vs. aftereffect (E), and proprioceptive variability vs. proprioceptive shift (F). Black line denotes the best fit regresion line, and the shaded region indicates the 95% confidence interval.

Data Analysis

The experimental software and analyses were performed using custom scripts in MATLAB and R.

The evaluation of our core hypotheses involves three variables of interest: implicit adaptation, proprioceptive shift, and proprioceptive variability. The dependent variable for implicit adaptation was the change in hand angle from baseline, where hand angle was defined as the signed angular difference between the position of the hand at peak velocity and target, relative to the start location. In experiment 1, the measure of implicit adaptation was the hand angle during the no-feedback aftereffect trials (blocks 2 and 3 averaged across both days since adaptation was at asymptote by block 2). In experiment 2, we used the mean hand angle during the last three blocks (blocks 2–4) of the error clamp trials since adaptation had reached a stable asymptote by block 2. For both experiments, the adaptation analyses were performed after correcting for any bias observed during the last two baseline cycles (experiment 1: 10 trials; experiment 2: 18 trials). Trials in which the hand angle exceeded three standard deviations from a moving five-trial average were excluded from the analyses (experiment 1: 1.2% ± 0.6% per participant; experiment 2: 0.5% ± 0.3% per participant).

For proprioception, we recorded the x and y coordinate of each hand location report and calculated the angular deviation from the target. Proprioceptive shift was operationalized as the angular difference between the mean sensed hand position for each proprioceptive report block and the mean sensed hand position on the baseline block. For each block, we also calculated the standard deviation of the proprioceptive reports for each block, our measure of proprioceptive variability.

Experiment 1 dependent measures were entered into a linear mixed effect model (R function: lmer), with Block and Day as fixed factors, and Participant ID as a random factor. Experiment 2 dependent measures were entered into a linear mixed effect model, with Block as the only fixed factor and Participant ID as the random factor. All post hoc t tests were two-tailed, and Bonferroni corrected for multiple comparisons. Standard effect sizes are reported (η²_p for fixed factors; Cohen’s d_z for within-subjects t tests) (38). When the data met the assumption of normality as assessed with the Shapiro–Wilk test, the parametric Pearson correlation measure was used (R); when normality was violated, we used the nonparametric Spearman correlation (R_s).

We also performed a multiple regression analysis (R function: lm) on the upper bound of adaptation, comparing a model with proprioceptive shift and proprioceptive variability as fixed factors to models in which only one of these was included. Given that the former contains two predictors and the latter two each contain only one predictor, we evaluated these fits with $R_{adj}^2$ (39). $R_{adj}^2$ would only increase if additional parameters improved the model fit more than would be expected by chance.

Formalizing the Relationship between Proprioception and Adaptation

In this section, we outline formalizations of the multisensory integration and proprioceptive realignment hypotheses. In the main body of the paper, these formalizations are provided to make explicit the assumptions underlying each hypothesis and, of primary importance, their respective predictions concerning the relationships between measures of proprioception and the upper bound of implicit adaptation. Model-based analyses are presented in the Supplemental Discussion (see https://doi.org/10.6084/m9.figshare.13585178.v6).

Under the multisensory integration hypothesis, adaptation should reach asymptote when the sensory prediction error created by the discrepancy between the cursor and target (µ_vis) is offset by the sensory prediction error created by the discrepancy between the hand and target (µ_prop). These two error signals are weighted based on uncertainty (${\sigma }_{prop}^2$ for proprioceptive estimate; ${\sigma }_{vis}^2$ for the visual estimate).

$$\frac{{\sigma }_{vis}^2}{{\sigma }_{vis}^2+ {\sigma }_{prop}^2}\times {\mu }_{prop}=\frac{{\sigma }_{prop}^2}{{\sigma }_{vis}^2+ {\sigma }_{prop}^2}\times {\mu }_{vis}$$ (1)

The hand position that corresponds to the upper bound of adaptation (µ_prop,UB) can be calculated based on

$${\mu }_{prop,UB}= \frac{{\sigma }_{prop}^2}{{\sigma }_{vis}^2}\times {\mu }_{vis}$$ (2)

Based on Eq. 2, the upper bound of adaptation (µ_prop,UB) should be positively correlated with proprioceptive variability (${\sigma }_{prop}^2)$.

Under the proprioceptive realignment hypothesis, adaptation will reach asymptote when the sensed hand position is at the target (i.e., 0). The sensed hand position is a combined signal, where actual hand position (µ_prop) (weighted by a prior belief that the hand will be at the target) gets calibrated by (i.e., shifts toward) the visual feedback (proprioceptive shift: PS). This shift is driven by cross-sensory calibration of vision on proprioception.

Although the computational rules governing proprioceptive shifts remain an open question, we assume that the size of this proprioceptive shift is determined solely by the difference between the visual feedback and target position (likely in a nonlinear manner) (40). The literature indicates that this shift occurs quickly (within three trials) (35, 41, 42) and remains relatively invariant. Importantly, for present purposes, the size of the shift should be independent of proprioceptive variability (29, 43) (also see: Figs. 4F and 6C).

$$\frac{{\sigma }_{prior}^2}{{\sigma }_{prior}^2+ {\sigma }_{prop}^2}\times {\mu }_{prop}+ PS=Sensed Hand Position\mathrm{ }$$ (3)

$$\frac{{\sigma }_{prior}^2}{{\sigma }_{prior}^2+ {\sigma }_{prop}^2}\times {\mu }_{prop,UB}+ PS=0$$ (4)

$${\mu }_{prop,UB}= -PS\times \frac{{\sigma }_{prior}^2+ {\sigma }_{prop}^2}{{\sigma }_{prior}^2}$$ (5)

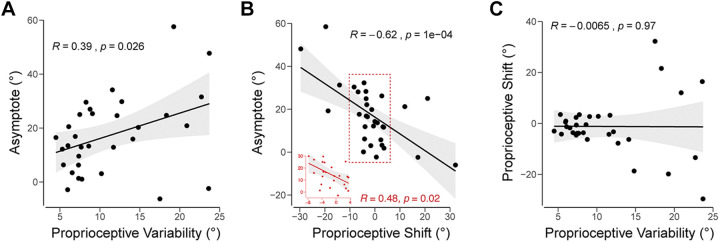
Figure 6.

Interindividual differences analyses in experiment 2. A: proprioceptive variability vs. asymptote in response to the visual clamp. B: proprioceptive shift vs. asymptote. A second correlation was performed on nonoutlier data points contained in the red rectangle, also shown in the inset. C: proprioceptive variability vs. proprioceptive shift. Black line denotes the best fit regresion line, and the shaded region indicates the 95% confidence interval.

Based on Eq. 5, the upper bound of adaptation (µ_prop,UB) should be negatively correlated with proprioceptive shift. In other words, the more proprioception is shifted toward vision, the more adaptation is required to realign sensed hand position with the target. In this model, proprioceptive variability also modulates the upper bound, vis-à-vis its role in determining the optimal hand position in the absence of vision.

RESULTS

Experiment 1

The main goal of experiment 1 was to examine the relationship between individual differences in implicit adaptation and individual differences in proprioception (proprioceptive shift and proprioceptive variability). For implicit adaptation, we focus on the change in heading angle on trials without feedback (aftereffect) following exposure to a 30° rotation of the visual feedback. Since the perturbation was introduced in a gradual manner, we assume the resulting recalibration of the sensorimotor map was implicit.

Implicit adaptation.

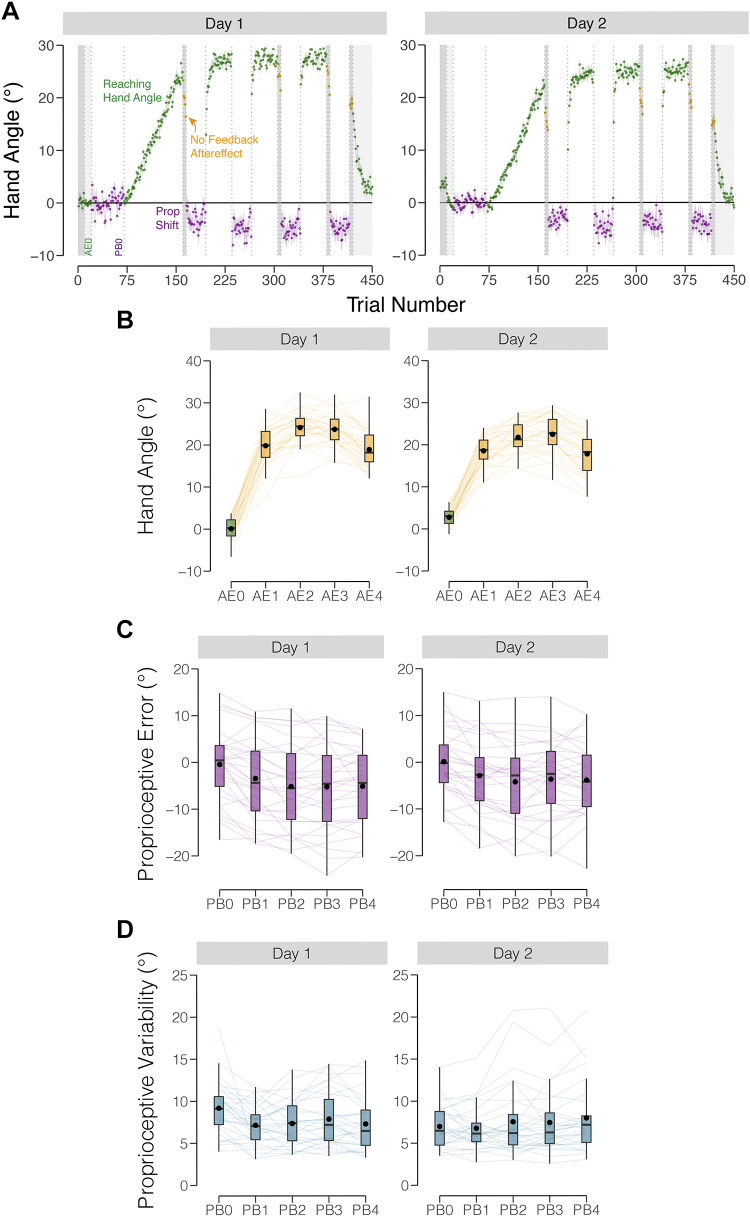
To track the time course of implicit adaptation, we measured mean hand angle during four no-feedback blocks, one at the end of the baseline block and three during the adaptation phase. There was a main effect of block (Fig. 3B; F_4,261 = 93.0, P < 0.001, η² = 0.85), with the mean hand angles in each no-feedback block significantly different from baseline (all t₂₆₁ > 24.1, P_bf < 0.001, d_z > 4.4). The mean hand angle increased from aftereffect block 1 to aftereffect block 2 (Fig. 2A; t₂₆₁ = 5.5, P_bf < 0.001, d_z = 1.0). There was no significant difference between the means in the second and third aftereffect blocks (t₂₆₁ = 0.5, P_bf = 1, d_z = 0.01), suggesting that implicit adaptation in response to a 30° rotation saturated between 22°–26°. The mean hand angle in the fourth aftereffect block was significantly lower than the third aftereffect block (t₂₆₁ = −6.4, P_bf < 0.001, d_z = −1.2). Given that this block occurs after a set of proprioceptive probe trials, the difference here may indicate that proprioceptive trials had an attenuating effect on implicit adaptation (44).

Figure 3.

Performance on adaptation and proprioception probe tasks in experiment 1. A: group means across test session (left—day 1, right—day 2). After a period of baseline trials, participants were exposed to a gradually increasing visuomotor rotation up to 30°, where it was then held constant. Participants performed blocks of visuomotor rotation trials (hand angle shown in green), no feedback aftereffect trials (hand angle shown in yellow), and proprioceptive probe trials (shift in perceived position shown in purple). Vertical dotted lines indicate block breaks. Shaded trials indicate reaching trials either with no feedback (dark gray) or with veridical feedback (light gray). Shaded regions indicate ±SE. Baseline blocks for reaching hand angle (AE0) and proprioceptive probes (PB0) are labeled. B: hand angle during no feedback aftereffect blocks. C: proprioceptive errors for each proprioceptive block. D: variability of proprioceptive judgments for each proprioceptive probe block. Thin lines indicate individual subjects. Box plots indicate min, max, median, and the 1st/3rd interquartile range. Black dots indicate the mean.

We next assessed whether adaptation remained stable across days. Although there was no main effect of Day (F_1,261 = 0, P = 1, η² = 0.04), the Day × Block interaction was significant (F_4,261 = 6.3, P < 0.001, η² = 0.01). Post hoc t tests revealed that the aftereffect was smaller on day 2 compared with day 1 in block 3 (t₂₆₁ = −5.1, P_bf < 0.001, d_z = 0.91). A similar pattern was evident in the other blocks, with the magnitude of the aftereffect lower on day 2 by ∼4°. This attenuation has been observed in previous studies (14, 15, 45, 46).

Proprioceptive shift.

We then assessed whether the exposure to the rotation resulted in a proprioceptive shift, quantified as the angular change, relative to the baseline. The effect of Block was significant (Fig. 3C; F_4,261 = 4, P = 0.003, η² = 0.27), with a ∼4° proprioceptive shift toward the rotated feedback from baseline to PB1 (t₂₆₁ = −3.9, P_bf = 0.005, d_z < −0.7). Consistent with a previous study (41), the shift remained stable across successive blocks (all pairwise comparisons of successive blocks in day 1 were not significant: t₂₆₁ < 0.1, P_bf = 1, d_z < 0.03). In addition, the magnitude of the proprioceptive shift was stable across days, with neither the effect of Day (F_1,261 = 0, P = 1, η² = 0.004), or significant Day × Block interaction (F_{4,261 = 0}.3, p = 0.84, η2 = 0.004), consistent with the findings reported by Liu et al. (47).

Proprioceptive variability.

To operationalize proprioceptive variability, we calculated the standard deviation of the angular hand report data for each block (Fig. 3D). There was no main effect of block (F_4,261 = 0.60, P = 0.66, η² = 0.05). The effect of Day was significant (F_1,261 = 13.0, P < 0.001, η² = 0.08), with proprioceptive variability reduced on day 2 compared with day 1 (t₂₆₁ = −4.9, P_bf < 0.001, d_z < −0.9). This between-day attenuation may be attributed to participants’ increased familiarity with the proprioceptive task on day 2, leading to more consistent proprioceptive judgments (48). Nominally, proprioceptive variability was nonetheless similar across both days (∼7°), with no interaction observed between Block and Day (F_4,261 = 1.0, P = 0.42, η² = 0.01).

Reliability of the dependent variables.

Analyses that involve correlating individual differences across different measures are limited by the reliability of each measure. Thus, before turning to the correlational analyses between the proprioceptive measures and implicit adaptation, we assessed the reliability of our core measures across sessions. For adaptation, we used the mean of the last two aftereffect blocks (AE2–AE3) given that adaptation has reached its limit by these blocks. For proprioceptive shift, we used the mean proprioceptive shift of all blocks (PB1–PB4) after the perturbation was introduced relative to baseline. For proprioceptive reliability, we used the proprioceptive variability from all blocks (PB0–PB4). The between-session correlations were significant for all three dependent variables (Fig. 4, A–C; implicit adaptation: R = 0.53, P = 0.002; proprioceptive variability: R = 0.59, P < 0.001; proprioceptive shift: R_s = 0.5, P = 0.005), indicating that the individual differences were reasonably stable.

Correlating adaptation and proprioception.

Having established that these dependent variables were reliable across days, we next asked whether differences in implicit adaptation could be accounted for by individual differences in proprioception. To obtain more stable measures of proprioception and implicit adaptation, we averaged the mean values for each dependent variable from day 1 and day 2.

According to the multisensory integration hypothesis, we should expect a positive correlation between proprioceptive variability and the extent of adaptation since, all other things being equal, noisier proprioception would diminish the relative weighting given the proprioceptive sensory prediction error. Consistent with this prediction, the two measures were positively correlated (Fig. 4D; R = 0.49, P = 0.006).

According to the proprioceptive realignment hypothesis, we should expect a correlation between the proprioceptive shift and implicit adaptation. Given that these two effects should be in opposite directions, the correlation should be negative: a larger (more negative) proprioceptive shift would require a larger change in hand angle for the hand to be perceived at the target location. Consistent with the proprioceptive realignment hypothesis, there was a significant negative correlation between proprioceptive shift and aftereffect (Fig. 4E; R_s = −0.40, P = 0.03).

We also examined the correlation between proprioceptive shift and proprioceptive variability. Although we had no strong a priori expectations here, a signal-dependent perspective might predict a negative correlation (49) if we assume that variance grows with the magnitude of the shift. Similarly, one might suppose that the perceived location of the hand might be more malleable if the inputs underlying that judgment are more variable. However, proprioceptive variability and proprioceptive shift were not correlated (Fig. 4F; R = −0.13, P = 0.48), an observation in line with previous work reporting the absence of a relationship between the magnitude of cross-sensory calibration and signal reliability (43, 50).

Given that proprioceptive shift and proprioceptive variability were uncorrelated with each other yet both measures correlated with the upper bound of adaptation, we could test a unique prediction of the proprioceptive realignment model: Namely, that the upper bound of adaptation would be better predicted by a model that includes both shift and variability (Eq. 5), compared with models that only include one of these two variables. Our multiple regression analysis was consistent with this prediction: A model that included both shift and variability provided the most parsimonious account of our data ($R_{adj}^2=0.22$) relative to the two single-variable models (proprioceptive shift only: $R_{adj}^2=0.07;$ proprioceptive variability only: $R_{adj}^2=0.21$). This analysis indicates that proprioceptive shift and variability make independent contributions toward predicting the upper bound of adaptation, providing additional support for the proprioceptive realignment account of sensorimotor adaptation.

Experiment 2

Experiment 2 (n = 32 participants) provided a second test of the multisensory integration and proprioceptive realignment hypotheses, using a visual error clamp in which the feedback cursor was always offset from the target by 15°. Compared with experiment 1 where the contingent feedback constrained the degree of adaptation, we expected the clamp to yield a greater range of values for implicit adaptation.

Implicit adaptation.

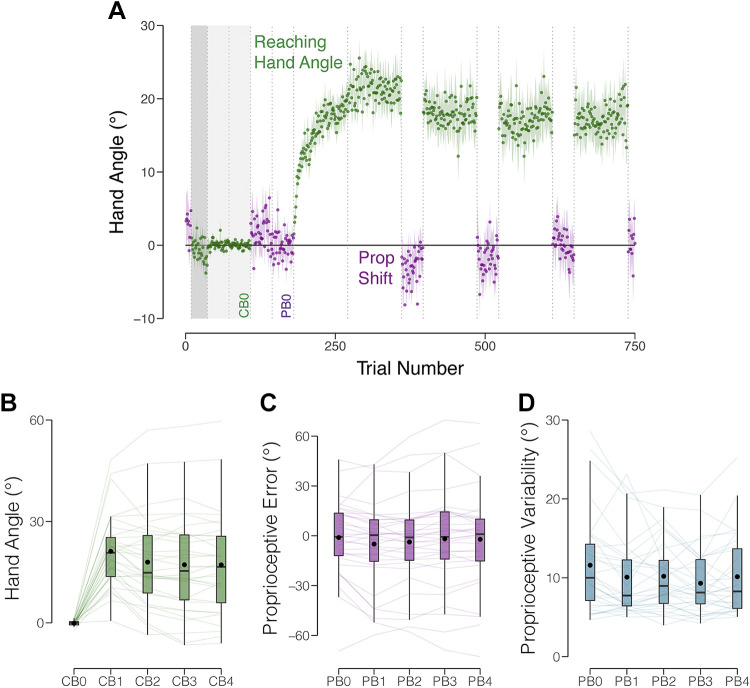
The participants’ reaches shifted in the opposite direction of the error clamp feedback, the signature of implicit adaptation (Fig. 5). The hand angle data (CB0–CB4, using the last 90 trials of CB1, and all 90 trials in CB2–CB4) showed a main effect of Block (F_4,124 = 55.1, P < 0.01, η² = 0.06), with post hoc comparisons indicating that the mean hand angle in each block was significantly greater than baseline (all t₁₂₄ > 10.75, P < 0.001, d_z > 1.9). The mean values were not significantly different from one another for the four clamp blocks (all pairwise t tests: t₁₂₄ < 2.47, P > 0.13, d_z < 0.44), indicating that participants had reached the asymptote of adaptation by the end of the first clamp block. To obtain a single measure of adaptation for each participant, we took the mean hand angle over the last three clamped feedback blocks. The mean change in hand angle was 17.5° ± 13.9°. As expected, the range of asymptotic values was considerably larger in experiment 2 (range = −6.5°–58.5°) compared with experiment 1 (range = 13.5°–33.9°).

Figure 5.

Performance on adaptation and proprioception probe tasks in experiment 2. A: group means across test session. After a period of no feedback (dark gray region) and veridical feedback (light gray region) baseline trials, participants were exposed to a visual clamp in which the feedback was offset by 15° from the target. Participants performed blocks of reaching trials (hand angle shown in green) and proprioceptive probe trials (shift in perceived position shown in purple). Vertical dotted lines indicate block breaks. Shaded regions indicate ±SE. Baseline blocks for reaching hand angle (CB0) and proprioceptive probes (PB0) are labeled. B: mean hand angle averaged over the last three clamped feedback blocks. C: proprioceptive error for each proprioceptive block. D: variability of proprioceptive judgments for each proprioceptive probe block. Thin lines indicate individual subjects. Box plots indicate min, max, median, and the 1st/3rd interquartile range. Black dots indicate the mean.

Proprioceptive measures.

The proprioceptive shift in experiment 2 was modest, and only marginally significant (F_4,124 = 2.17, P = 0.08, η² = 0.06). The mean value was −1.2° (SD = 11.4°), less than 33% of the −4.0° (SD = 3.2°) mean shift observed in experiment 1 (t₅₉ = −4.3, P < 0.001, d = −1.1). In all, 12 of the 32 participants exhibited a shift in the direction opposite to the cursor (compared with 2 out of 30 in experiment 1). Not only was the between-subject variability larger in experiment 2, but we also observed a large increase in within-subject proprioceptive variability (experiment 1, day 1: 7.8 ± 0.4, range = 4.4–12.4, experiment 2: 11.2 ± 1.0, range = 4.5–23.7; t₆₀ = 3.1, P = 0.003, d = 0.8).

Although we will consider these unexpected differences in detail in the Supplemental Discussion section, we note here that the large increase in the variability of the proprioceptive judgments is especially puzzling given that the two experimental protocols are very similar. It is possible that the clamped, noncontingent feedback used in experiment 2 has a different impact on sensed hand position compared with the contingent feedback provided in experiment 1 (see Supplemental Discussion: Between-experiment analysis of the proprioceptive re-alignment integration, https://doi.org/10.6084/m9.figshare.13585178.v6). Alternatively, it may be related to other methodological differences. In particular, the studies were run by different experimenters, and they may have differed in how they passively displaced the participant’s arm, perhaps moving at different speeds.

Nonetheless, the proprioceptive shift and proprioceptive variability scores remained relatively stable across experiment 2. As noted above, in terms of mean values, there was no effect of block for proprioceptive shift. There was also no effect of block on proprioceptive variability (F_4,124 = 1.1, P = 0.34, η² = 0.04). More important in terms of the correlational analyses reported below, individual differences were maintained across the blocks for both proprioceptive shift (all pairwise correlations following the introduction of clamped feedback, from PB1 to PB4: R > 0.87, P < 0.001) and proprioceptive variability (all pairwise correlations between PB0 and PB4: R > 0.76, P < 0.001).

Correlating adaptation and proprioception.

The correlational analysis between the three dependent variables yielded a similar pattern as that observed in experiment 1 (Fig. 6). Consistent with the multisensory integration hypothesis, there was a positive correlation between the asymptote of implicit adaptation and proprioceptive variability (R = 0.39, P = 0.026). Consistent with the proprioceptive realignment hypothesis, there was a negative correlation between the asymptote of adaptation and the magnitude of proprioceptive shift (R = −0.62, P < 0.001). There was no correlation between proprioceptive shift and proprioceptive variability (R = −0.007, P = 0.97).

We note that the correlations with the proprioceptive shift must be qualified. First, the net effect of proprioceptive shift was only marginally significant. Second, there were extreme values in both directions, including participants who showed a large shift in the opposite direction of the expected shift (i.e., away from the clamped feedback). To provide more conservative estimates, we repeated the correlational analyses after applying various inclusion criteria: 1) Limited to participants who showed the expected negative shift (N = 20, R = −0.70, P < 0.001; Fig. 6B inset); 2) Excluding those with a shift >10° in the unexpected direction (N = 28, R = −0.72, P < 0.001); 3) Excluding those showing a shift >10° in either direction (N = 23, R = −0.48, P = 0.02); 4) Only using the proprioceptive shift data from the first block where proprioceptive shifts are most pronounced (R = −0.61, P < 0.001); and 5) using a more conservative, nonparametric Spearman correlation (N = 32, R_s = −0.57, P < 0.001). The correlation, in all cases, remained significant, pointing to a robust relationship between proprioceptive shift (albeit small) and implicit adaptation.

Consistent with experiment 1, the multiple regression analysis also favored the proprioceptive realignment model. The model with both proprioceptive shift and variability ($R_{adj}^2=0.50$) was superior to models that only included one variable (proprioceptive shift only: $R_{adj}^2=0.36$; proprioceptive variability only: $R_{adj}^2=0.12$). This result again points to the relevance of both bias and variability measures of proprioception on sensorimotor adaptation.

DISCUSSION

The sensorimotor system uses visual and proprioceptive feedback to remain properly calibrated. Recent sensorimotor adaptation studies using visual perturbations to induce recalibration have revealed an upper bound on this process, beyond which changes in performance require alternative learning processes. Although the contribution of vision to adaptation has been well characterized (20, 28), the contribution of proprioception to adaptation remains poorly understood. Here, we took an individual differences approach, asking whether the extent of adaptation is correlated with biases and/or variability in the perceived position of the hand during adaptation.

There were two key findings: First, participants with greater proprioceptive variability in both experiments exhibited more implicit adaptation, a finding consistent with the multisensory integration account (20, 21, 23, 28). The asymptotic level of adaptation, in this view, reflects an equilibrium between learning from visual and proprioceptive error signals. This finding is consistent with adaptation being driven by the optimal weighting of proprioception and vision according to their relative variability, whereby greater proprioceptive variability results in greater weighting of visual feedback, and thus greater implicit adaptation. Second, participants with larger proprioceptive shifts toward the visual feedback exhibited larger implicit adaptation, a finding consistent with the proprioceptive realignment hypothesis (30, 31, 34, 42, 51). The multiple regression analysis in each experiment provided further support for the proprioceptive realignment model, highlighting the impact of both the bias and variability in sensed hand position in modulating sensorimotor adaptation (Eq. 5). The asymptotic level of adaptation, in this view, reflects the point of realignment between the sensed hand position and the target.

We note that our focus on how asymptotic performance might arise from the integration of multisensory cues is somewhat orthogonal to the dominant account in the literature. The core idea emphasized in the literature is that the asymptote reflects the point of equilibrium between learning and forgetting processes (52–56), an idea captured in the standard state-space model. This model in its basic form does not specify the sources of information driving learning, although in most applications, the visual (or task) error is treated as the sole contributor to learning. As such, the state-space model does not readily yield predictions concerning the relationship between measures of proprioception and adaptation. The two hypotheses featured here could be taken to extend the conventional notion of learning and forgetting, specifying sensory constraints on both these processes. Rather than assuming that visual errors are the sole contributor of learning, we highlight important proprioceptive constraints on adaptation.

Proprioceptive Variability and Asymptotic Adaptation

Greater proprioceptive variability predicted a greater asymptotic magnitude of implicit adaptation. Although we are unaware of any prior reports of this positive correlation, a recent study asked a related question: Does proprioceptive variability predict the early learning rate in response to the abrupt introduction of a 30° visuomotor rotation (57). This study reported no correlation between proprioceptive variability and early learning in young adults and a negative correlation in older adults. Although these observations may appear inconsistent with the results of our study, their main dependent variable, early learning, likely reflects a strong contribution from explicit processes in response to this large perturbation (6, 11, 13), rather than implicit adaptation. By this view, the null result for the young adults would suggest that proprioceptive variability is not related to explicit learning, whereas the negative correlation observed in older adults may reflect a concurrent age-dependent deterioration of strategy use and proprioceptive acuity (8). Interestingly, older adults have also been shown to exhibit an age-dependent boost in implicit adaptation (8). By the multisensory integration hypothesis, this increase would be expected if a decline in proprioceptive sensitivity is accompanied by an increase in proprioceptive variability, a hypothesis that can be tested using an individual difference approach in an older adult sample.

Previous tests of the multisensory integration account of implicit adaptation have focused exclusively on manipulations of the visual feedback. Increasing visual variability, either by replacing a small cursor with a cloud of dots or a Gaussian blur, has been shown to decrease the rate and extent of implicit adaptation (20, 27, 28). Surprisingly, the sensory integration models put forth to account for these effects have not measured proprioception; rather, this component has either been estimated as a free parameter or ignored entirely. Here we obtained direct measures of proprioceptive variability to test a core prediction of the multisensory integration model. A limitation with our individual difference approach, however, is that the analyses are purely correlational (for further discussion on this point, see the Supplemental Discussion section Addressing concerns with correlational analyses; https://doi.org/10.6084/m9.figshare.13585178.v6). Future studies using experimental methods to perturb proprioception (e.g., tendon vibration) (58–62) could build on our results, asking whether proprioceptive variability has a causal role in modulating the upper bound of adaptation.

One prediction of the multisensory integration hypothesis is that the magnitude of the asymptote will be related to the size of the visual SPE. This holds up to the point where the adaptation response saturates, estimated to be between 6° and 20° (4, 9). Whereas the SPE in experiment 1 is ∼3° (estimated from late adaptation), it is fixed at 15° in experiment 2; as such, the multisensory integration hypothesis would predict a much larger asymptote in experiment 2 to yield the proprioceptive SPE required to produce an equilibrium. At odds with this prediction, the asymptotes were similar (∼20°). From Eq. 2, there are two ways in which a similar asymptote could occur despite a fivefold difference in visual SPE between experiments. First, proprioceptive variability could be smaller in experiment 2 to increase the weight given to proprioception. Our data are inconsistent with this hypothesis, with the trend showing slightly greater proprioceptive variability in experiment 2. Alternatively, an increase in visual variability in experiment 2 would lead to a similar increase in the weight given to proprioception. This seems plausible. More attention is likely directed to the task relevant, contingent cursor in experiment 1 compared with the task irrelevant, noncontingent cursor in experiment 2 (a point emphasized by the instructions). Moreover, the smaller visual SPE in experiment 1 is likely more foveal than the larger visual SPE in experiment 2. Given that visual attention and visual eccentricity modulate visual variability (63–65), it is plausible that visual variability was higher in experiment 2 (see Supplemental Discussion section Between-experiment analysis of the multisensory integration hypothesis, https://doi.org/10.6084/m9.figshare.13585178.v6).

Proprioceptive Shifts and Asymptotic Adaptation

In line with the proprioceptive realignment hypothesis, the upper bound of implicit adaptation was also correlated with the proprioceptive shift induced by the visual perturbation: The proprioception realignment hypothesis offers an alternative multisensory integration perspective on adaptation, albeit one that entails two distinct processes. One process involves the optimal estimate of hand position without the influence of vision, an estimate assumed to be influenced by a prior (i.e., the target location) and the actual hand position. The other process is driven by vision: the biased sense of hand position arises with the introduction of the perturbed visual feedback, the proprioceptive shift. Although the exact computational rules that govern proprioceptive shifts remain an active area of research, the size of the shift presumably depends on the size of the visual feedback (40). The sum of these two signals defines the error signal that drives adaptation. Thus, as the hand adapts in the opposite direction of the target, the signal from the actual hand position can eventually negate the (stable) proprioceptive shift. The current results would suggest that the proprioceptive shift is given much more weight than the actual hand position: In the group means, a proprioceptive shift of ∼3° is only offset when the hand has adapted to around ∼20°.

Verbal reports of sensed hand position obtained in a continuous manner during adaptation provide converging evidence of the dynamics predicted by the proprioceptive realignment hypothesis. The report data followed a striking non-monotonic function, initially biased toward the clamped cursor (away from the target), and then reversing direction (27). However, the asymptotic value of the reports was not at the target. Rather, it was shifted slightly away from the target in the opposite direction of the clamp. This “overshoot” is not predicted by either the multisensory integration or proprioceptive realignment hypotheses, a puzzle that remains to be addressed in future research.

Although proprioceptive shift and implicit adaptation were negatively correlated in both experiments, the net effect of proprioceptive shift was considerably greater in experiment 1 (∼5°) compared with experiment 2 (∼1°). In a post hoc comparison across experiments, we noted a striking difference between subgroups exposed to a clockwise (CW) perturbation compared with those exposed to a counterclockwise (CCW) perturbation. For those exposed to a CW perturbation, the results were quite similar across experiments groups (experiment 1: −5.1 ± 0.6 and experiment 2: −5.4 ± 2.7, both shifted toward the visual cursor). However, for those exposed to a CCW perturbation, the proprioceptive shifts were quite different. In experiment 1, the shift was in the expected direction, toward the visual cursor (3.0 ± 0.9°). In contrast, in experiment 2, the shift was in the opposed direction, away from the visual cursor (−3.0 ± 2.7). The source of this difference and in particular, the highly atypical result for the CCW subgroup in experiment 2 is unclear. It may reflect measurement noise—the proprioceptive data were much nosier in experiment 2. Alternatively, our measure of proprioceptive shift may conflate two types of proprioceptive changes: A change in proprioception due to the visual signal and a change in proprioception within the proprioceptive system itself. A number of studies had described the phenomenon of proprioceptive drift, a shift in perceived hand position with repeated reaches (66, 67). The relative contribution of visually induced proprioceptive shifts and proprioceptive drift may differ across these two experiments, perhaps related to the difference in how the system responds to a contingent and noncontingent feedback signal. (See an extended discussion of this speculative hypothesis in the Supplemental Discussion: Between-experiment analysis of the proprioceptive re-alignment integration, https://doi.org/10.6084/m9.figshare.13585178.v6.)

Reconciling Multisensory and Proprioceptive Realignment Hypotheses

The core predictions for both the multisensory integration and proprioceptive realignment hypotheses were confirmed in the present experiments. The proprioceptive realignment model, in its current form, seems to provide a more parsimonious explanation, as it predicts implicit adaptation to be correlated with both proprioceptive shift and variability. However, our findings do not rule out the possibility that both hypotheses, one based on the variability of proprioception and the other based on the shift in proprioception, operate in parallel manner. The absence of a correlation between the two proprioceptive measures, a finding consistent with several previous reports (29, 30, 50, 68), is consistent with a dual-process model (see also Ref. 29). By this view, the observed asymptote is a composite of these two forms of adaptation. That is, a ∼20° asymptote is actually an equilibrium point between one process that weights the visual and proprioceptive inputs and a second process that seeks to counteract the proprioceptive shift.

Alternatively, there may be a more complex interaction between processes sensitive to proprioceptive variability and bias. We could envision a multistage process in which a reliability weighting rule for each sensory signal operates at an early stage, with the integration of the multiple signals occurring at a later stage (perhaps in a nonweighted manner). Examples of the former are found in the optimal integration literature (9, 69–71). Examples of the latter are also ubiquitous, where proprioception and vision interact in a fixed manner, independent of variability (12, 50, 72, 73). These stages of processing result in a final error signal, one that ultimately drives motor adaptation. Although these ideas remain to be fleshed out in future research, the current results underscore the critical role of proprioception in sensorimotor adaptation.

GRANTS

This work was supported by Grants R35 NS116883, R01 NS105839, and R01 NS1058389 from the National Institutes of Health (NIH). H. E. Kim was funded by Grants K12 HD055931 from the NIH and M3X1934650 from the National Science Foundation.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

H.E.K., D.E.P., A.R.S., and R.B.I. conceived and designed research; D.E.P. and A.R.S. performed experiments; J.S.T., D.E.P., and A.R.S. analyzed data; J.S.T., H.E.K., D.E.P., A.R.S., and R.B.I. interpreted results of experiments; J.S.T. and D.E.P. prepared figures; J.S.T. drafted manuscript; J.S.T., H.E.K., D.E.P., and R.B.I. edited and revised manuscript; J.S.T., H.E.K., D.E.P., A.R.S., and R.B.I. approved final version of manuscript.